空气引射器是利用高压流体引射低压流体后形成具有中间压力的流体的装置,具有结构简单、不易损坏等优点,但其效率偏低,限制了在工业中进一步应用。引射器内部流体流动复杂,不仅存在两股流体混合,还可能产生涡旋、激波等复杂流动现象。为改善内部流场,提高设备引射率,众多研究者从引射器形状、尺寸对引射器性能影响方面开展了大量工作,并取得了系列成果。Kong等[1]对具有锯齿形高压喷嘴的引射器进行了研究分析,证明锯齿形出口结构的高压喷嘴可以优化引射器的性能。Nakagaw等[2]对不同混合室长度两相喷射器进行了实验研究,结果表明,混合室长度不仅影响压力比,还影响喷射制冷系统的引射率。Sicuro等[3]模拟研究了多喷嘴引射器流场,结果显示四喷嘴引射器性能优于其他喷嘴,且在混合室直径与喷嘴出口直径之比在3~9时,引射器性能最佳。史海路等[4]实验研究了喷嘴距对喷射器及双蒸发压缩/喷射制冷系统性能的影响,研究结果表明,喷射器存在最优喷嘴距使喷射以及整个系统性能最好。刘华东等[5]研究发现在最佳结构尺寸和旁路进口压力下,两相旁路喷射器引射系数增大25.7%~56.8%。Banu等[6]、Duan等[7]、姚轶智等[8]发现旋流发生器能够提高喷射器的性能,验证了利用扰流元件诱发驱动流体变化从而提高设备性能的可行性。
分析可知,目前关于引射器的优化研究大多基于单一变量法或正交实验法,优化过程中设置了较多约束条件,限制了引射器优化空间。而拓扑优化技术实现由性能驱动的正向设计,根据目标函数进行优化,避免过多的限制约束[9]。随着近年来拓扑优化技术从固体问题应用到流体问题上,使流体拓扑优化技术得到了快速发展。Kontoleontos等[10]基于Spalart-Allmaras模型对湍流流道进行设计,将拓扑伴随方程应用在不可压缩湍流流动模型中。Dilgen等[11]对二维和三维湍流强制对流换热器进行拓扑优化,实现了湍流模型在拓扑优化中的应用。Yoon等[12]、Zhao等[13]、Cai等[14]提出了基于N-S方程、基于连续表面的惩罚方法以及基于无导数水平集等湍流拓扑优化方法,改善了传统拓扑优化理论在解决湍流模型问题时的弊端。Joo等[15]使用三维拓扑优化方法设计板翅式散热器的最佳通道间距,有效改善了散热性能。Wang等[16]、王定标等[17]、裴元帅等[18]运用变密度拓扑优化方法对设备散热结构进行拓扑优化设计,显示拓扑优化结构在散热方面的优越性。
综上,湍流问题在拓扑优化方法中的验证和发展,极大扩展了拓扑优化技术的应用,并且上述研究也证明了拓扑优化的优势。但少有利用拓扑优化方法进行引射器结构优化方面研究,因此,本文将拓扑优化技术应用到空气引射器结构优化上,并对优化后引射器内部流场进行分析,探究拓扑优化后引射器性能及流场演化规律。
1 拓扑优化数学模型与结果讨论
1.1 设计域
传统空气引射器结构参数[20]见表1,流体介质均设置为空气,图1为传统空气引射器结构图。混合室直径和喷嘴出口位置对引射器性能有显著影响[19],因此本文选取引射器的混合室作为设计域,见图1阴影区域。引射器优化问题描述如下:在既定模型外壁前提下,通过设定目标函数获得自适应引射器最佳流道。
表1 引射器几何尺寸
Table 1 Geometric parameters of the ejector
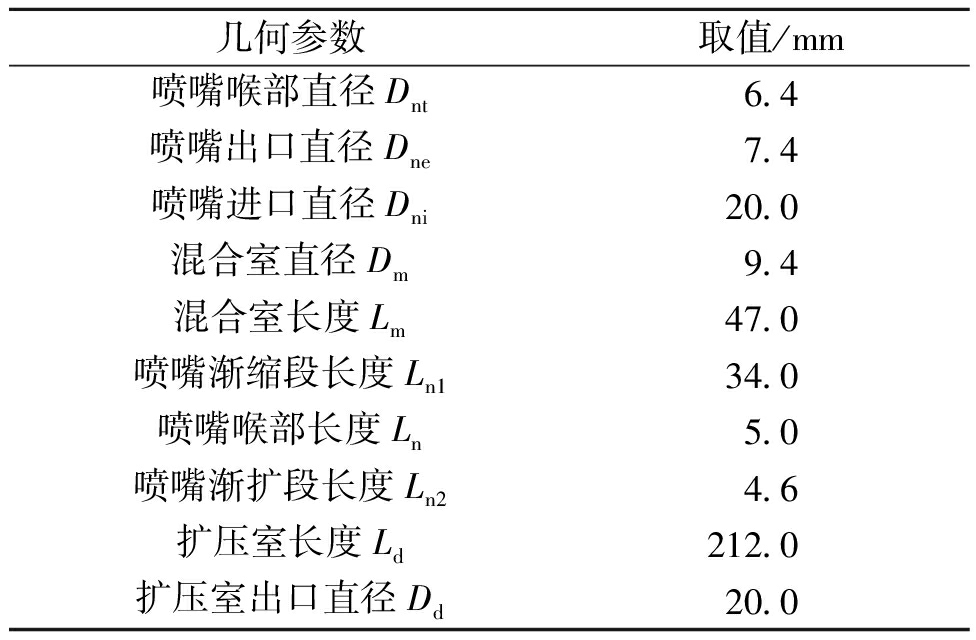
几何参数取值/mm喷嘴喉部直径Dnt6.4喷嘴出口直径Dne7.4喷嘴进口直径Dni20.0混合室直径Dm9.4混合室长度Lm47.0喷嘴渐缩段长度Ln134.0喷嘴喉部长度Ln5.0喷嘴渐扩段长度Ln24.6扩压室长度Ld212.0扩压室出口直径Dd 20.0

图1 引射器几何结构
Figure 1 Geometric structure diagram of the ejector
1.2 拓扑优化设计模型
本文使用变密度法SIMP插值模型进行优化计算。选用布林克曼模型[21]模拟该摩擦阻力,阻尼项为
F=-α*u。
(1)
其中,α*为多孔介质孔隙渗透率,可表示为
(2)
式中:αmax和αmin为多孔介质最大与最小孔隙渗透率,αmax取105 Pa·s/m2;λi取[0,1];q为阻流系数惩罚因子,q取0.001。
为避免出现棋盘格现象,选用亥姆霍兹过滤器[22]对单元敏度值进行正则化,网格过滤半径最小值取0.1 mm。通过对过滤器施加平滑过渡阶梯函数避免结构体灰度较大问题,采用双曲正切函数进行投影:
(3)
式中:θf为该阶梯函数投影前的设计变量;θβ代表投影阈值,取0.5;β取8。
1.3 目标函数及约束条件
以引射器引射率为优化目标函数,引射率ω定义为引射流体与工作流体的质量流量之比:
(4)
式中:me为引射流体质量流量,g/s;mg为工作流体质量流量,g/s。
因引射器需要保证较大流体流通度,控制拓扑生成流道体积与整个模型设计域体积比处于90%~100%内,约束体积表达式为
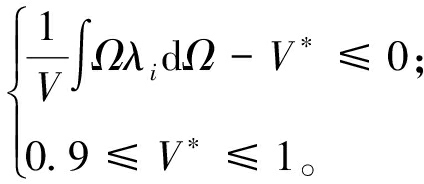
(5)
综上,引射器数学优化模型描述如下:
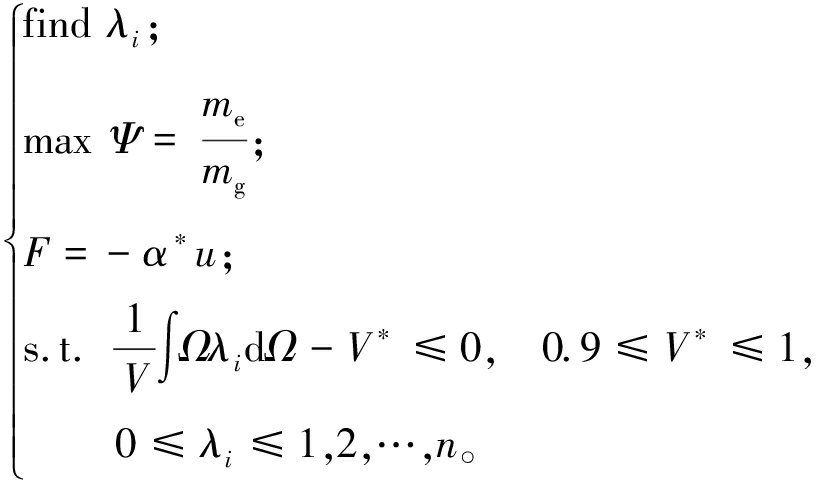
(6)
1.4 拓扑优化结果及流场计算
通过上述优化流程,并对拓扑直接计算结果边界进行规则化设计处理,结果见图2。相比传统引射器,拓扑优化结构在混合室入口处增加一个固体区域,将该固体区域定义为扰流元件。
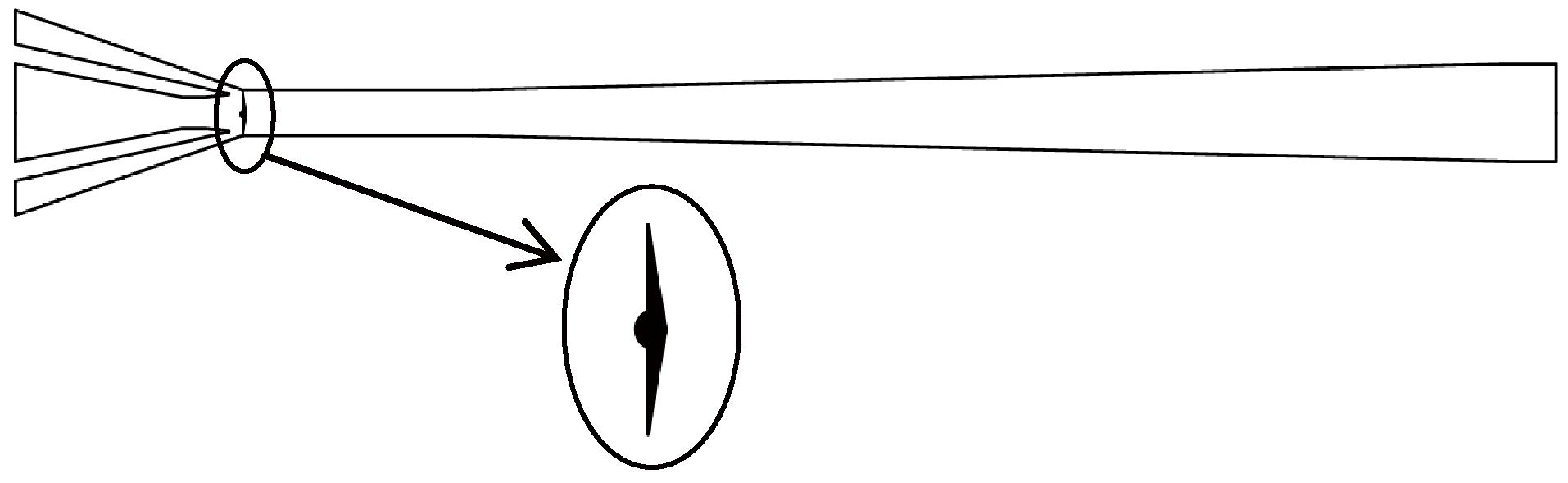
图2 拓扑引射器结构图
Figure 2 Topological ejector structure diagram
1.5 模型设置及验证
采用Ansys Fluent软件对拓扑引射器进行数值模拟。流体介质为可压缩的理想空气,采用RNG k-ε湍流模型,采用SIMPLEC格式的压力-速度耦合项。速度方程、能量方程选用二阶迎风离散格式。体积分数使用QUICK离散格式,空间梯度离散格式为Green-Gauss cell,压力离散格式为PRESTIO。近壁处采用标准壁面函数法。工作喷嘴入口为压力入口,设置为1 MPa;引射室入口为压力入口,设置为0.4 MPa;引射室出口为压力出口,设置为0.5 MPa[20]。
网格划分结果见图3,经网格无关性验证,本文网格数为285 236。将模拟结果与文献[20]实验结果进行对比,引射率结果见表2,相对误差在4.2%~8.6%。
表2 模拟结果与实验结果引射率对比
Table 2 Comparision between numerical simulation results and experimental results of entrainment ratio
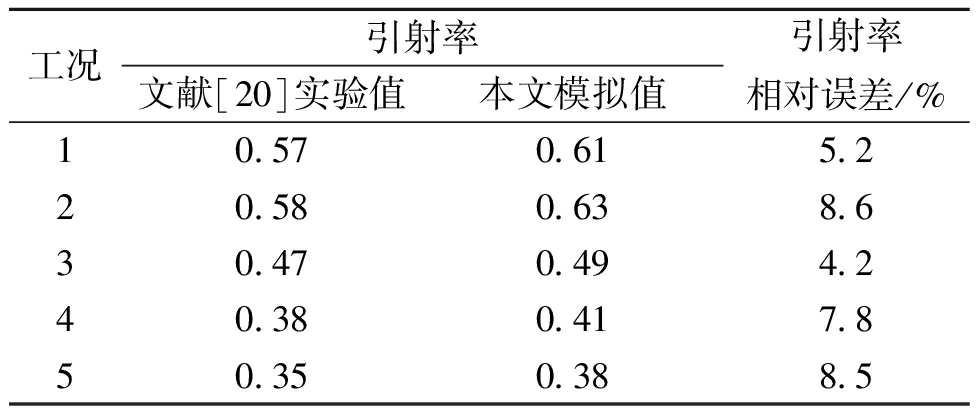
工况引射率文献[20]实验值本文模拟值引射率相对误差/%10.570.615.220.580.638.630.470.494.240.380.417.850.350.388.5
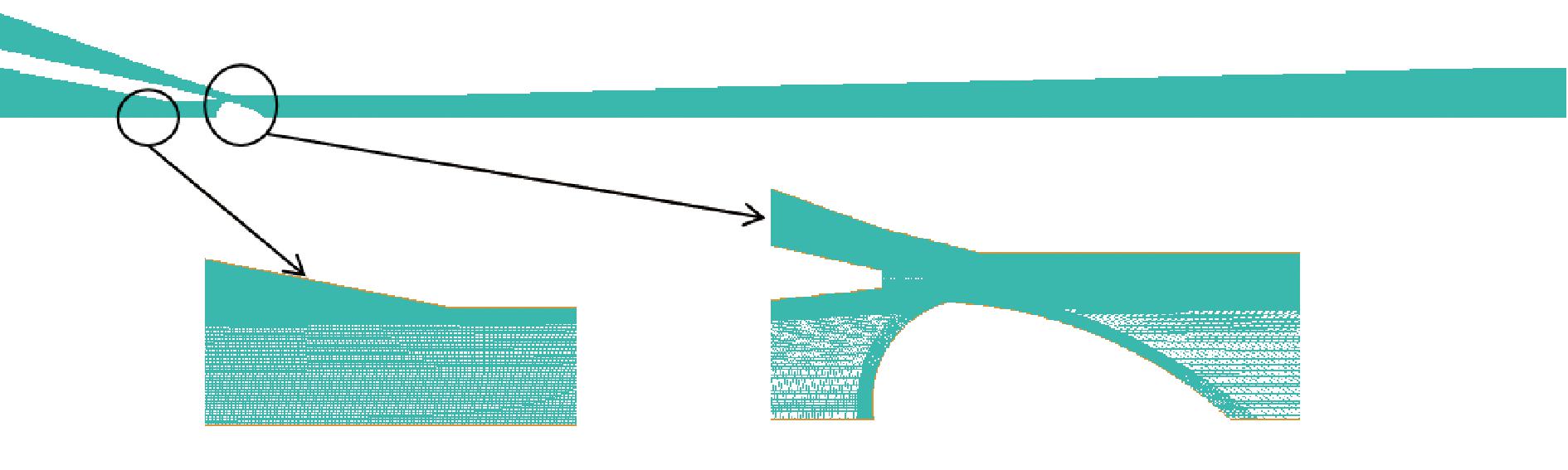
图3 引射器网格划分
Figure 3 Ejector grid division
1.6 结果分析与类翼型扰流元件的提出
图4为引射器结构拓扑优化前后速度云图。从图4拓扑引射器图中可以看出,扰流元件与引射器壁面形成了二次喷嘴,从喷嘴出口流出的工作流体会继续加速,并在流道最窄处达到最大值,且大于传统引射器同位置处工作流体速度。但扰流元件后部出现尾迹涡,形成较大速度亏损区,该区域发生现象及原因与风力机叶片所产生的尾迹类似[23],高马赫数流体的尾迹损失系数较大,会造成较大能量损失。为减小尾迹损失,基于风力机叶片减阻机理[24],将扰流元件调整为类翼型形状[25],图5为调整后扰流元件形状,尺寸见表3。
表3 类翼型扰流元件几何尺寸
Table 3 Geometric parameters of airfoil-like spoiler element

结构参数取值/mm最大高度D3.30前弦长x11.26后弦长x25.04扰流元件与喷嘴喉部距离l5.90
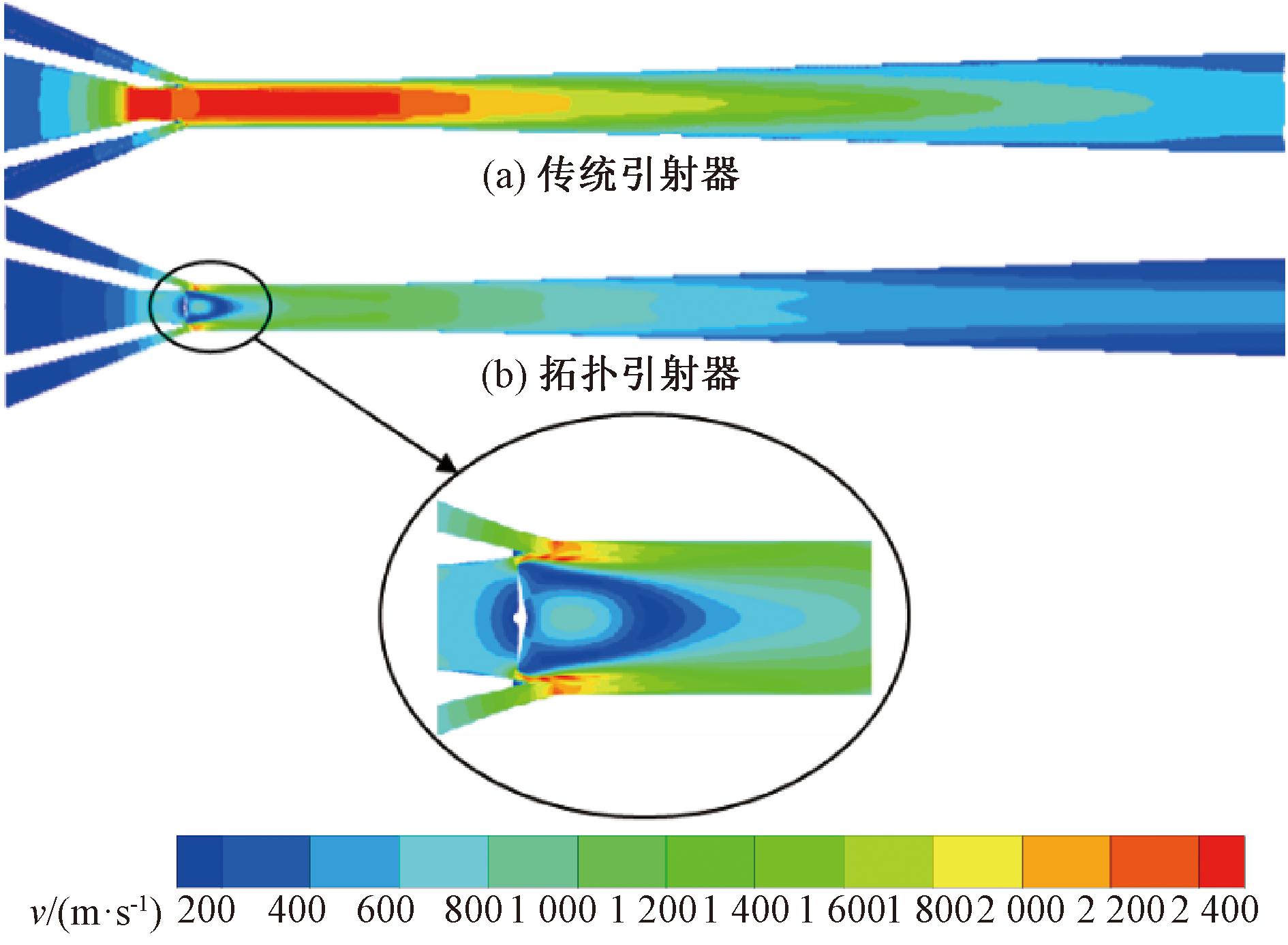
图4 传统引射器与拓扑引射器速度云图
Figure 4 Velocity contours of traditional ejector and topological ejector
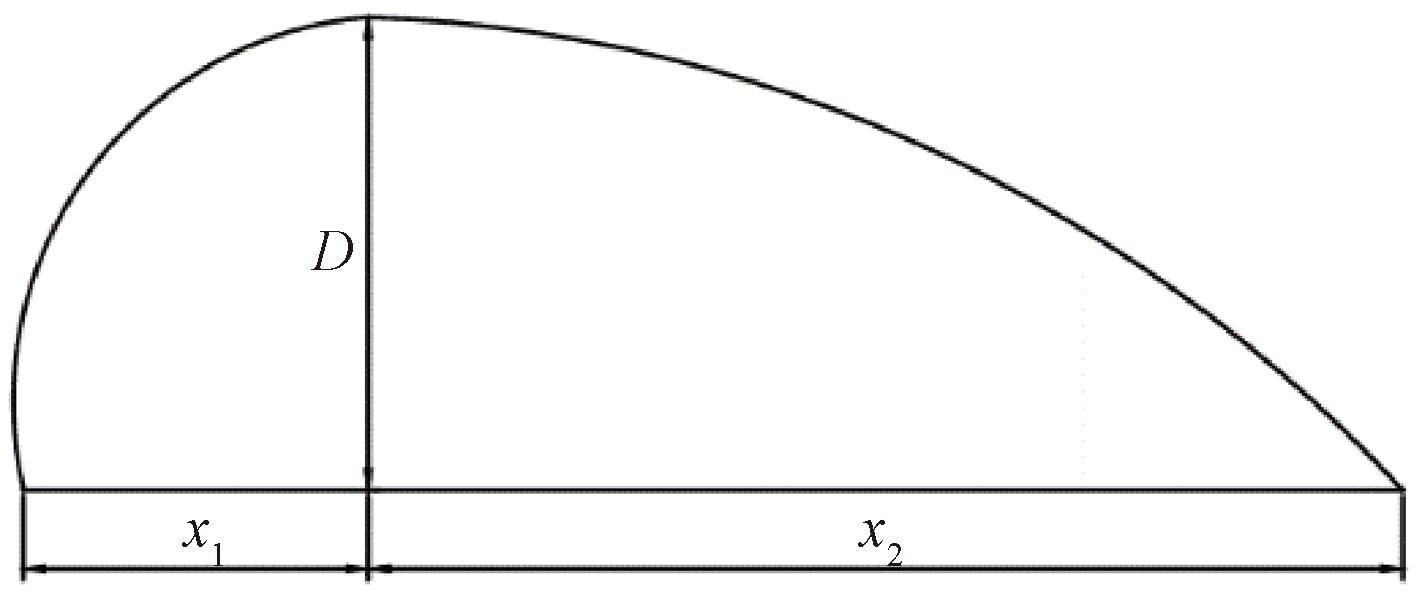
图5 类翼型扰流元件结构
Figure 5 Geometric structure of airfoil-like spoiler element
2 类翼型扰流元件引射器流场与性能分析
2.1 类翼型扰流元件引射器流场分析
图6为类翼型扰流元件引射器与传统引射器速度和压力云图。与拓扑引射器流场类似,类翼型扰流元件与引射器壁面形成的二次喷嘴效应使混合室入口处工作流体速度增加,压力降低。同时,类翼型结构扰流元件尾迹涡旋区显著改善,涡旋能量损失减小。图7为引射器混合室内压力沿扰流元件最大高度轴线分布图。由图7中可见,在混合室入口位置附近压力明显低于传统引射器,而且混合室段压力高于传统引射器,与图6(c)所示压力云图相符。图8为引射器混合室内速度梯度图,在类翼型扰流元件引射器混合室内轴线附近流体速度与靠近壁面流体速度均较低,形成从中心到壁面为低速-中速-低速的速度分布层,该种速度分层能够增大不同速度流体的接触面积,提高流体混合效率。
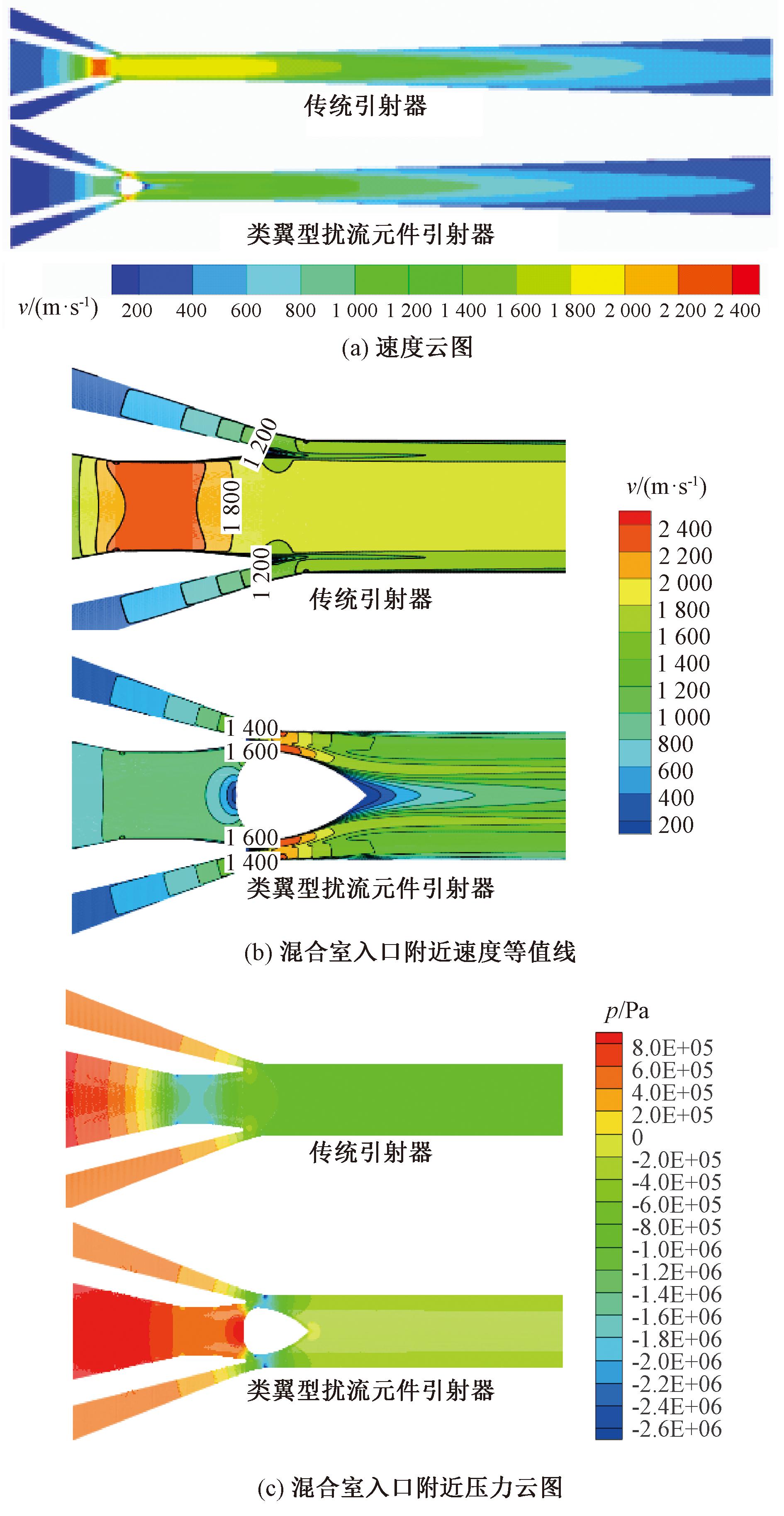
图6 传统引射器与类翼型扰流元件引射器内部流场云图
Figure 6 Internal flow field contours of the traditional ejector and airfoil-like spoiler element ejector
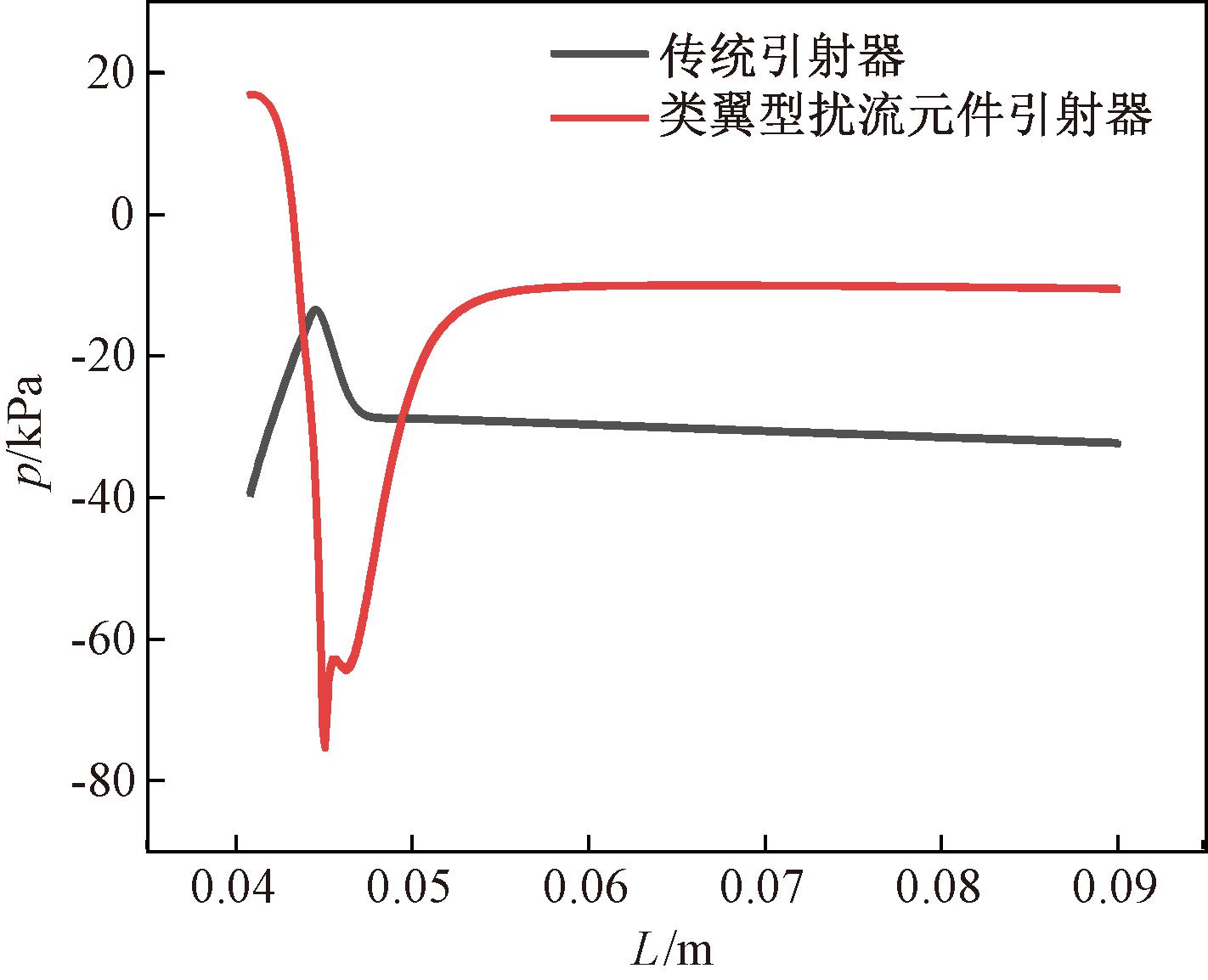
图7 传统引射器与类翼型扰流元件引射器混合室内压力沿扰流元件最大高度轴线方向的变化
Figure 7 Changes of pressure along the axis direction of the maximum height of the spoiler of traditional ejector and airfoil-like spoiler element ejector
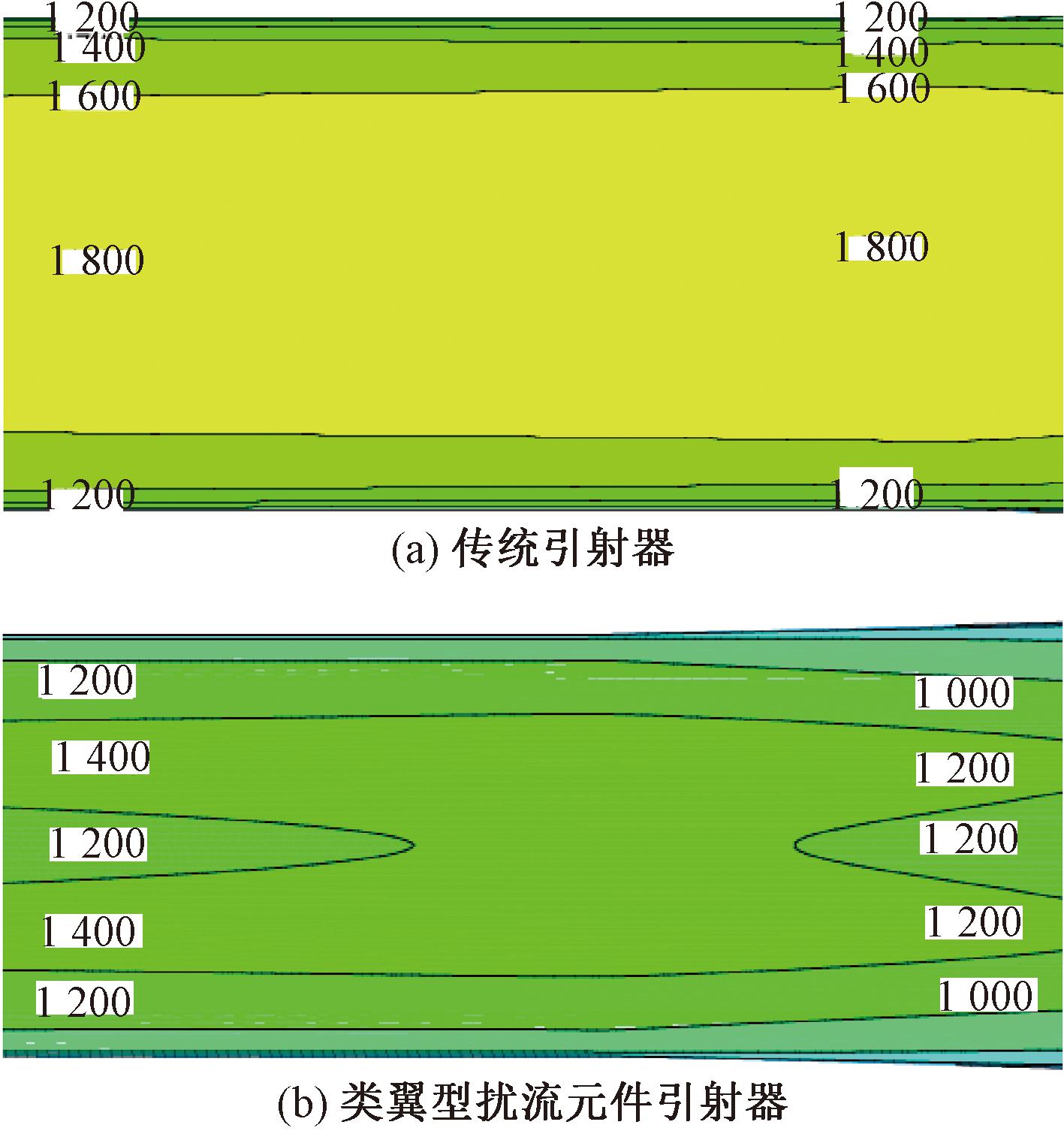
图8 传统引射器与类翼型扰流元件引射器混合室内速度梯度图
Figure 8 Velocity contours of traditional ejector and airfoil-like spoiler element ejector in the mixing chamber
图9所示为引射器内湍动能云图,类翼型扰流元件引射器混合室入口位置附近湍动能显著大于传统引射器,表明在扰流元件作用下,流体之间动量交换剧烈,能量传递效果更好。新型引射器扩压室内湍动能小于传统引射器,表明流体在混合室内混合更充分,扩压室内能量损失较小。

图9 传统引射器与类翼型扰流元件引射器湍动能云图
Figure 9 Turbulent kinetic energy contours of traditional ejector and airfoil-like spoiler element ejector
2.2 扰流元件高度对引射器性能的影响
保持类翼型扰流元件引射器的其他结构尺寸和工况参数不变,改变扰流元件最大高度D从2.8 mm增加到3.9 mm,间隔0.4 mm。图10为工作流体和引射流体流量的变化趋势,随着最大高度值增加,工作流体流量呈下降趋势,引射流体流量先增大后减小,当扰流元件最大高度为3.3 mm时,引射率为1.57,相比于传统引射器增大近146%。
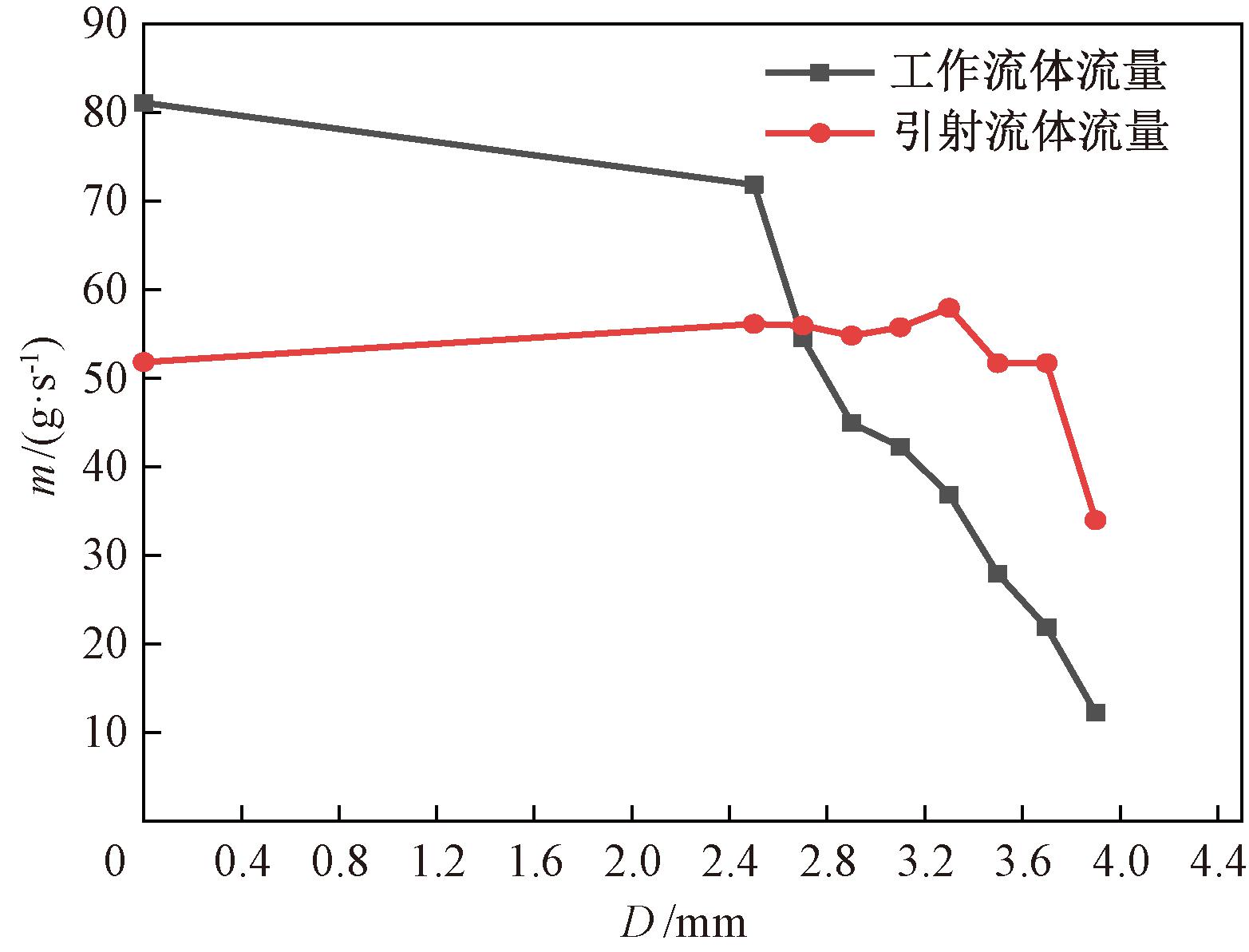
图10 工作流体与引射流体流量随扰流元件高度的变化
Figure 10 Variation of the primary and secondary flow rate with the maximum height of the spoiler element
2.3 扰流元件与喷嘴喉部距离对引射器性能的影响
保持类翼型扰流元件最大高度为3.3 mm、引射器其他结构尺寸参数和工况条件不变,改变扰流元件前端相对于喉部的距离S从0.3 mm增长至2.3 mm,间隔0.5 mm,结果见图11。随S不断增大,工作流体流量呈上升趋势,引射流体流量先增大后减小。当距离为0.8 mm时,引射率达到最大值2.07,相比于传统引射器增大近224%。
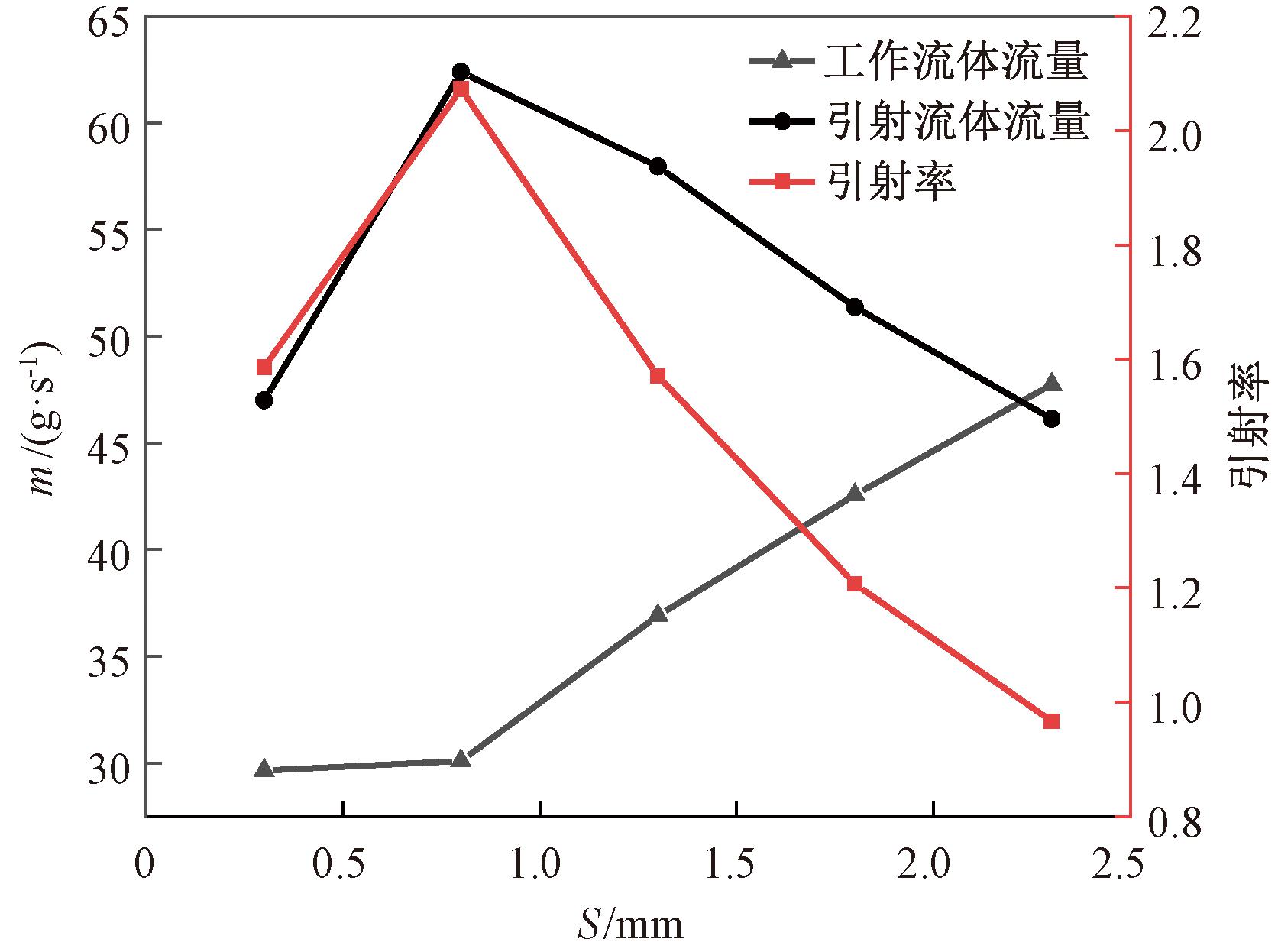
图11 流量与引射率随扰流元件与喷嘴喉部距离的变化
Figure 11 Flow rate and entrainment ratio vary with the distance between the spoiler element and the nozzle throat
3 结论
本文采用拓扑优化方法对空气引射器结构进行了优化,得到了混合室内增加扰流元件拓扑结构引射器,并基于风力机叶片减阻原理分析,提出了类翼型扰流元件引射器。利用数值模拟方法研究了类翼型扰流元件引射器内部流场,分析了类翼型扰流元件高度和扰流元件与距喷嘴喉部距离对引射器性能的影响。主要结论如下。
(1)工况及其他结构参数不变时,增加扰流元件会形成二次喷嘴效应,喷嘴流出的工作流体继续加速,两股流体速度差减小,引射流体驱动压差增大,工作流体引射能力增强,引射率提高。
(2)类翼型扰流元件引射器引射率高于传统引射器。引射率随扰流元件高度增大而增大;随扰流元件与喷嘴喉部距离增加,引射率先增大后减小,引射率较传统引射器可提高146%~224%。当类翼型扰流元件高度为3.3 mm、扰流元件与喷嘴喉部距离为0.8 mm时,引射率达到最大值2.07。
[1] KONG F S, KIM H D, JIN Y Z. Computational study of supersonic chevron ejector flows[J]. Journal of the Korean Society of Propulsion Engineers, 2013, 17(6): 89-96.
[2] NAKAGAWA M, MARASIGAN A R, MATSUKAWA T, et al. Experimental investigation on the effect of mixing length on the performance of two-phase ejector for CO2 refrigeration cycle with and without heat exchanger[J]. International Journal of Refrigeration, 2011, 34(7): 1604-1613.
[3] SICURO B H B, MALATESTA V, PAPA R. Numerical investigation of supersonic air-to-air ejectors including design effects on entrainment efficiency[J]. Journol of Fluids Engineering, 2023, 145(1):011203.
[4] 史海路, 刘华东, 魏新利, 等. 喷嘴距对喷射器及双蒸发压缩/喷射制冷系统性能的影响研究[J]. 高校化学工程学报, 2019, 33(2): 321-328.SHI H L, LIU H D, WEI X L, et al. Effects of nozzle exit position on the performance of ejector and bi-evaporator compression/ejection refrigeration system[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(2): 321-328.
[5] 刘华东, 靳朝阳, 王定标, 等. 旁路结构对亚临界喷射器引射效率的影响[J]. 郑州大学学报(工学版), 2023, 44(6): 48-53.LIU H D, JIN Z Y, WANG D B, et al. Influence analysis of bypass structure on entrainment ratio of subcritical ejector[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(6): 48-53.
[6] BANU J P, MANI A. Numerical studies on ejector with swirl generator[J]. International Journal of Thermal Sciences, 2019, 137: 589-600.
[7] DUAN D L, GE H T, XI X Z, et al. Performance and mixing process investigation of a novel mixing-enhanced ejector [J]. Sustainable Energy Technologies and Assessments, 2023, 58:103322.
[8] 姚轶智, 代玉强, 张博文, 等. 动量增强型喷射器性能实验与分析[J]. 化工进展, 2019, 38(10): 4489-4496.YAO Y Z, DAI Y Q, ZHANG B W, et al. Performance experiment and analysis of momentum-enhanced ejector[J]. Chemical Industry and Engineering Progress, 2019, 38(10): 4489-4496.
[9] 王定标, 王帅, 张浩然, 等. 流体拓扑优化的方法及应用综述[J]. 郑州大学学报(工学版), 2023, 44(2): 1-13.WANG D B, WANG S, ZHANG H R, et al. A review of methods and applications for fluid topology optimization[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(2): 1-13.
[10] KONTOLEONTOS E A, PAPOUTSIS-KIACHAGIAS E M, ZYMARIS A S, et al. Adjoint-based constrained topology optimization for viscous flows, including heat transfer[J]. Engineering Optimization, 2013,45(8): 941-961.
[11] DILGEN C B, DILGEN S B, FUHRMAN D R, et al. Topology optimization of turbulent flows[J]. Mechanics and Engineering, 2018, 331: 363-393.
[12] YOON G H. Topology optimization method with finite elements based on the k-ε turbulence model[J]. 2020, 361:112784.
[13] ZHAO X, ZHOU M D, LIU Y C, et al. Topology optimization of channel cooling structures considering thermomechanical behavior[J]. Structural and Multidisciplinary Optimization, 2019, 59(2): 613-632.
[14] CAI H W, GUO K, LIU H, et al. Derivative-free level-set-based multi-objective topology optimization of flow channel designs using lattice Boltzmann method[J]. Chemical Engineering Science, 2020, 231:116323.
[15] JOO Y, LEE I, KIM S J. Efficient three-dimensional topology optimization of heat sinks in natural convection using the shape-dependent convection model[J]. International Journal of Heat and Mass Transfer, 2018, 127: 32-40.
[16] WANG D B, WU Q T, WANG G H, et al. Experimental and numerical study of plate heat exchanger based on topology optimization[J]. International Journal of Thermal Science, 2024, 195:108659.
[17] 王定标, 李昂, 吴淇涛, 等. 电子元件散热结构的拓扑优化设计[J]. 低温与超导, 2023, 51(5): 37-42.WANG D B, LI H, WU Q T, et al. Topology optimization design of heat dissipation structure of electronic components[J]. Cryogenics/ Refrigeration, 2023, 51(5): 37-42.
[18] 裴元帅, 王定标, 王晓亮, 等. 基于拓扑优化的风冷热沉研究[J]. 机械工程学报, 2020, 56(16): 91-97.PEI Y S, WANG D B, WANG X L, et al. Research on air-cooled heat sink based on topology optimization[J]. Journal of Mechanical Engineering, 2020, 56(16): 91-97.
[19] SALIM I Z, JASSIM N A. Supersonic nozzle location in steam ejector effect on the mass fraction and vacuum of second fluid[J]. International Journal of Heat and Technology, 2023, 41(5): 1121-1128.
[20] CHONG D T, HU M Q, CHEN W X, et al. Experimental and numerical analysis of supersonic air ejector[J]. Applied Energy, 2014, 130: 679-684.
[21] SEOK L J, HA M Y. Study on the aero-thermal topology optimization of single- and multi-fin shapes under two-dimensional external flow conditions[J]. Korean Society of Computational Fluids Engineering, 2018, 4(23): 74-83.
[22] HAJDUK K W, ROBINSOM J C, SADOWSKI W. Robustness of regularity for the 3D convective Brinkman-Forchheimer equations[J]. Journal of Mathematical Analysis and Applications, 2021, 500(1): 125058.
[23] 高伟, 张立茹, 姚慧龙, 等. 基于动网格技术水平轴风力机叶片及尾迹流场旋涡特性[J]. 排灌机械工程学报, 2023, 41(2): 172-178.GAO W, ZHANG L R, YAO H L, et al. Vortex characteristics of horizontal axis wind turbine blade and wake flow field based on dynamic mesh[J]. Journal of Drainage and Irrigation Machinery Engineering, 2023, 41(2): 172-178.
[24] 刘波, 侯为民, 项效镕. 高空低雷诺数二维抗分离叶型研究[J]. 西北工业大学学报, 2008, 26(6): 703-706.LIU B, HOU W M, XIANG X R, et al. Exploring new ideas and new methods in 2D fan/compressor cascade profile optimization design for low Reynolds number and high altitude[J]. Journal of Northwestern Polytechnical University, 2008, 26(6): 703-706.
[25] 孙翀, 田甜, 竺晓程, 等. 风力机翼型非定常流场POD和EPOD分析[J]. 上海交通大学学报, 2022, 56(1): 45-52.SUN C, TIAN T, ZHU X C, et al. Analysis of POD and EPOD for unsteady flow field of wind turbine airfoil[J]. Journal of Shanghai Jiao Tong University, 2022, 56(1): 45-52.