准确的风速预测可以使风电场的管理者及时了解未来的风速变化情况,从而采取相应的调整措施,以确保风力机组的安全可靠运行。当前,风速预测主要有4类,分别为物理模型预测、统计模型预测、机器学习模型预测和混合模型预测[1-3]。相对于其他几类模型,物理模型具有可解释性强的特点。目前,数值天气预报模型(numerical weather prediction, NWP)可用于风速预测[4-6],但NWP建模的过程往往与大气的实际运动规律存在偏差,同时还存在采集相关数据成本偏高的问题。统计模型和机器学习模型都是利用历史风速数据进行预测,以弥补物理模型的一些不足。统计模型中,时间序列模型[7]、自回归滑动平均(ARMA)[8]和差分整合移动平均自回归模型(ARIMA)[9]等通常用于处理线性数据。然而,对于具有较强非线性特征的风速数据等,统计模型的表现相对较差。机器学习模型是目前风速预测的常用方法,主要包括随机森林[10]、梯度提升树[11]、支持向量机[12]等。机器学习方法可以提取到风速序列的非线性特征,对于提升风速预测的精度有较大的帮助。混合模型综合了各个模型的优势,解决了单一模型在预测中表现不佳的问题,通过融合两种及以上预测方法来进行预测,进一步提高预测的精度。
由于风速序列具有较高的随机性和波动性,为提高预测的精度,需采用相关方法分解数据进行预处理。Tian等[13]用经验模态分解(empirical mode decomposition, EMD)完成对风速序列的预处理,但EMD存在模态混叠的局限性。冯义等[14]利用集合经验模态分解(ensemble empirical mode decomposition, EEMD)进行风速数据的预处理,但EEMD的性能易受最终平均问题的影响[15]。对于非线性、非平稳的风速时间序列分解,变分模态分解(variational mode decomposition, VMD)[16]可以在一定程度上抑制模态混叠,且可通过有效确定VMD的相关参数进行预处理以提高最终预测的精确度。
鉴于此,本文采用白鲸优化算法(beluga whale optimization, BWO)[17]对变分模态分解的模态数进行优化,对分解后的风速序列使用鲸鱼优化算法(whale optimization algorithm, WOA)确定长短时记忆神经网络(long short-term memory, LSTM)的隐含层节点数、最大训练次数和初始学习率并完成预测。本文所用预测模型流程如图1所示。
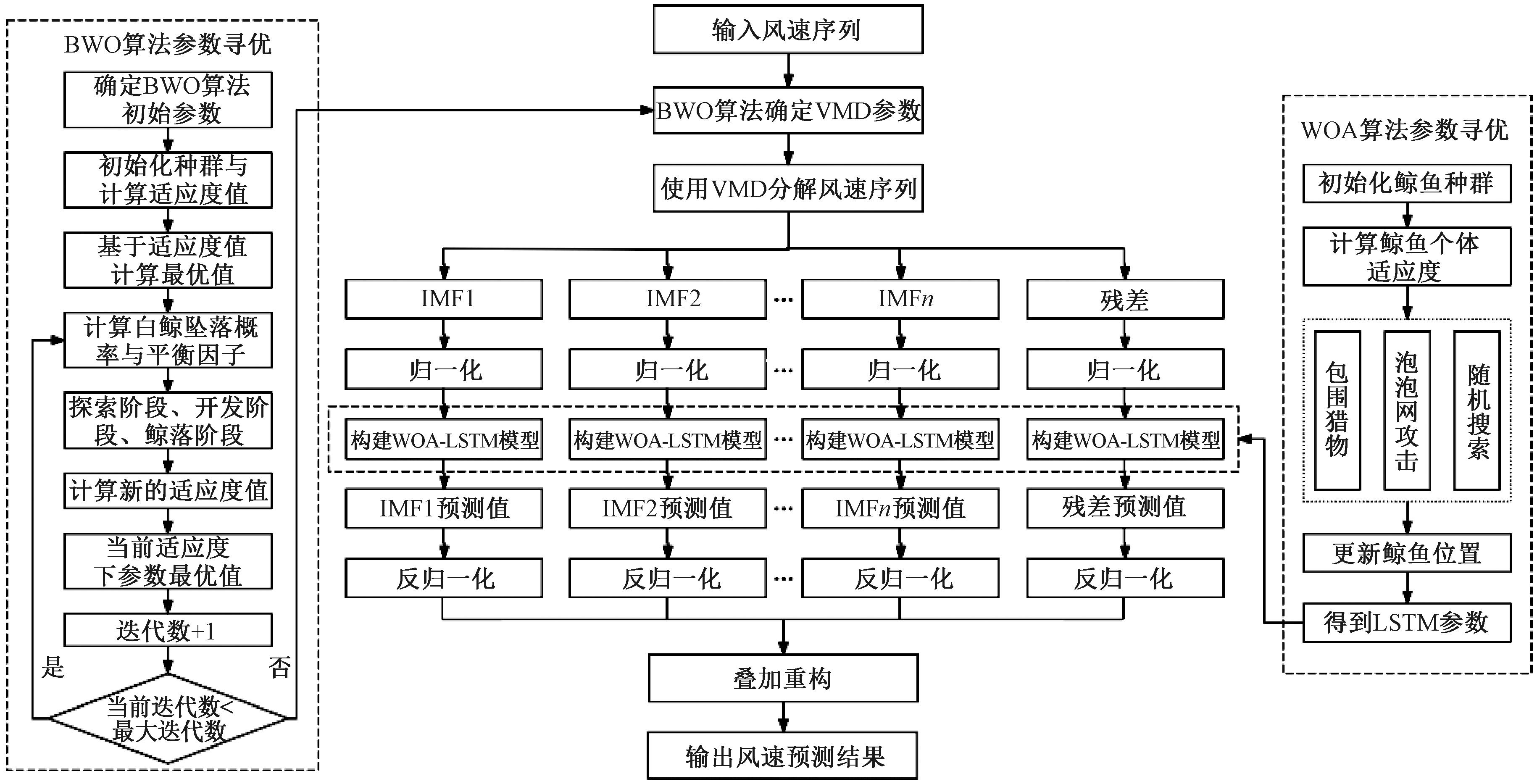
图1 预测模型算法流程图
Figure 1 Prediction model algorithm flow chart
1 基于BWO的变分模态分解
由于VMD算法中相关参数的选择对最终预测结果影响显著,因此,用白鲸优化算法对VMD进行参数优化,确定最佳分解模态数K和惩罚因子α,完成对风速序列的分解。
1.1 白鲸优化算法
白鲸优化算法是Zhong等[17]在2022年提出的一种基于仿生学和自然界中白鲸生态行为的优化算法。BWO模拟了白鲸群体的觅食、社交和生存行为,以帮助解决各种数据优化问题。
白鲸优化算法是一种基于种群的优化算法,将白鲸作为搜索代理,每头白鲸代表了问题的一个候选解。在BWO中,搜索代理的位置通常以矩阵形式来建模,该矩阵包含了每个搜索代理(白鲸)的位置信息。BWO中的搜索代理位置矩阵通常是一个二维矩阵,其中每行代表一个搜索代理(白鲸),而每列代表搜索代理的不同维度或特征。搜索代理的位置矩阵可表示为
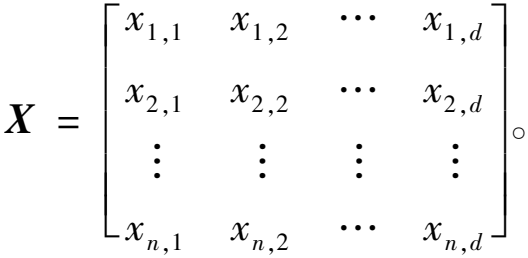
(1)
式中:n为白鲸种群的数量;d为需要优化的变量的维数。
白鲸种群适应度值FX为
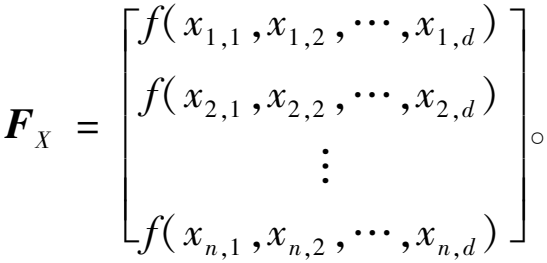
(2)
平衡因子Bf决定探索与开发阶段的转换:
(3)
式中:T表示当前迭代次数;Tmax表示最大迭代次数。Bf在0～1上随机变化,初始阶段时,探索和开发的概率都有可能较高,算法以一种相对平衡的方式进行。随着迭代次数T的增加,Bf逐渐减小至0.5以下。这表示探索阶段的概率逐渐减小,而开发阶段的概率逐渐增加。当Bf<0.5时,说明开发阶段的概率明显增加。
搜索阶段时,搜索代理是以白鲸配对游泳来决定,更新规则为
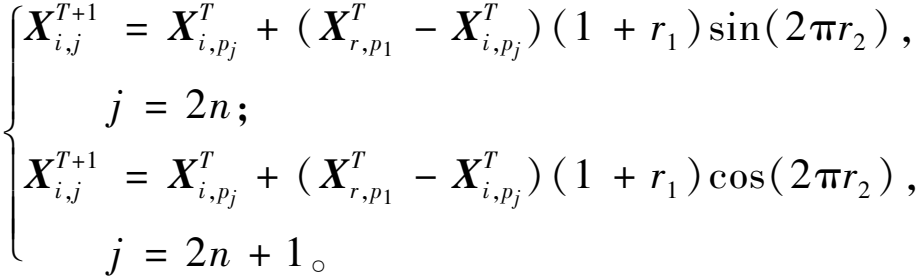
(4)
式中:T为当前迭代次数;
为第i条白鲸在第j维上的新位置;Pj为从d维中选择的随机整数;
为第i条白鲸在第Pj维的位置;
与分别为第r条白鲸和第i条白鲸的当前位置;r1、r2为介于0和1之间的随机数;sin(2πr2)与cos(2πr2)代表镜像白鲸的鳍朝向水面;n为整数。维数通过奇偶数来进行选择。
BWO算法在开发阶段引入了Levy飞行策略,有助于提高白鲸优化算法的搜索效率和全局收敛性。在Levy飞行策略中,白鲸会互相交流各自的位置,以模拟彼此间的猎物捕捉过程,并同时考虑其他白鲸和最佳候选者的位置。开发阶段白鲸的位置更新规则为
(5)
式中:T代表当前的迭代次数;
与
分别代表随机白鲸和第i条白鲸的当前位置;
代表第i条白鲸更新之后的位置;r1、r2为0～1上的随机数;C1代表随机跳跃强度,用来衡量Levy的飞行强度。
C1=2r4(1-r/rmax)。
(6)
LF为Levy飞行函数,其表达式为
(7)
式中:
和ν均为满足正态分布的随机数;β取固定值0.5。
BWO算法中引入了一种模拟鲸鱼坠落的行为来模拟随机性以及白鲸群体中的变化。同时,为了确保种群大小保持不变,BWO算法使用白鲸的位置和鲸鱼落体的步长来建立更新的位置,表达式为
(8)
式中:r5、r6、r7为0～1上的随机数;Xstep为鲸鱼坠落的步长。
(9)
式中:ub与lb分别为变量的上限和下限;C2为种群规模与鲸鱼下降概率相关的阶跃因子。
C2=2Wf×n。
(10)
式中:Wf代表鲸鱼坠落的概率。
(11)
1.2 VMD
VMD[18]是一种用于时间序列分解的替代方法。与EMD不同,VMD使用变分原理来分解时间序列,可以更好地处理一些非平稳和混沌性强的序列,减少模态混叠的问题。
VMD是一种信号处理技术,用于将时间序列分解成一系列模态(或分量),旨在克服传统经验模态分解(EMD)中出现的一些问题,如模态混叠和收敛性不佳。其主要思想是将一个信号分解成多个频率和振幅不同的子模态,子模态间按照它们的频率依次排列。VMD的分解过程是通过优化一个变分问题来实现的,以找到最佳的模态分解,使得分解后的模态尽可能地互相独立。其具体步骤如下。
步骤1 构造变分问题。在各个子模态的和等于原始数据的条件之下表达式为
(12)
式中:{uk}、{ωk}分别为分解的K个模态分量和各个模态分量的频率中心;∂t代表偏导数的计算;δ(t)代表单位脉冲函数;j代表虚数单位;*代表卷积运算。
步骤2 求解变分表达式。在构造变分问题的基础上引入惩罚因子α、Lagrange乘法算子λ,可得增广Lagrange表达式:
(13)
步骤3 求解增广Lagrange表达式的鞍点。首先初始化参数u1、ω1、λ1、n,同时设置n+1循环,uk、ωk、λk根据式(14)～(17)交替更新,当变量满足约束条件时,求解完成。
(14)
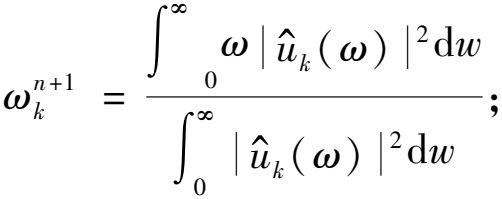
(15)
(16)
(17)
式中:
和
代表傅里叶变换;n代表该算法中的迭代次数;τ代表保真系数。
1.3 白鲸优化算法优化变分模态分解参数
在利用VMD进行信号分解时,需要给定分解模态数K和惩罚因子α,这两个参数的选取将会对分解结果产生重要影响。当设定的分解模态数K较小时,容易造成欠分解,导致重要信息没有被提取;当K较大时,会产生过分解,此时经过分解后的模态分量因中心频率接近形成模态混叠。当设定的惩罚因子α偏大时,分解后得到的模态分量带宽将偏小;若α偏小,则模态分量带宽将偏大,因此,惩罚因子α主要影响模态分量的细节保留度和分解过程的去噪程度。
为提高VMD的分解性能,使用BWO算法对VMD的分解模态数K和惩罚因子α进行寻优。需寻找一个合适的目标函数,使BWO算法可以通过目标函数值的比较来找到VMD的相关最佳参数值。此时将最小包络熵作为BWO的目标函数。
为找出相应的最小包络熵,就需要计算出不同参数组合下的分量的包络熵,然后比较它们的包络熵的大小,即可找出最小包络熵。此时,最小包络熵所对应的参数组合就是VMD算法的最佳参数,具体可以表示为
(18)
式中:
分别表示VMD的惩罚因子和最佳分解模态数的最优参数组;Ep为包络熵。
在利用BWO算法找出VMD最优的分解模态数K和惩罚因子α后,可保证VMD对输入风速序列数据的自适应分解,从而发挥出了VMD的最佳分解性能,避免在分解的过程中出现重要信息的丢失或过分解。
1.4 数值实验
本文选取青海省德令哈市某点位在2022年11月1日0时至2022年12月31日23时的连续风速序列,原始数据采样的时间间隔为1 h,共1 464条数据,如图2所示。根据序列的时间顺序,选择1 464条数据中的前80%即1 171条数据为训练集,后20%为测试集。
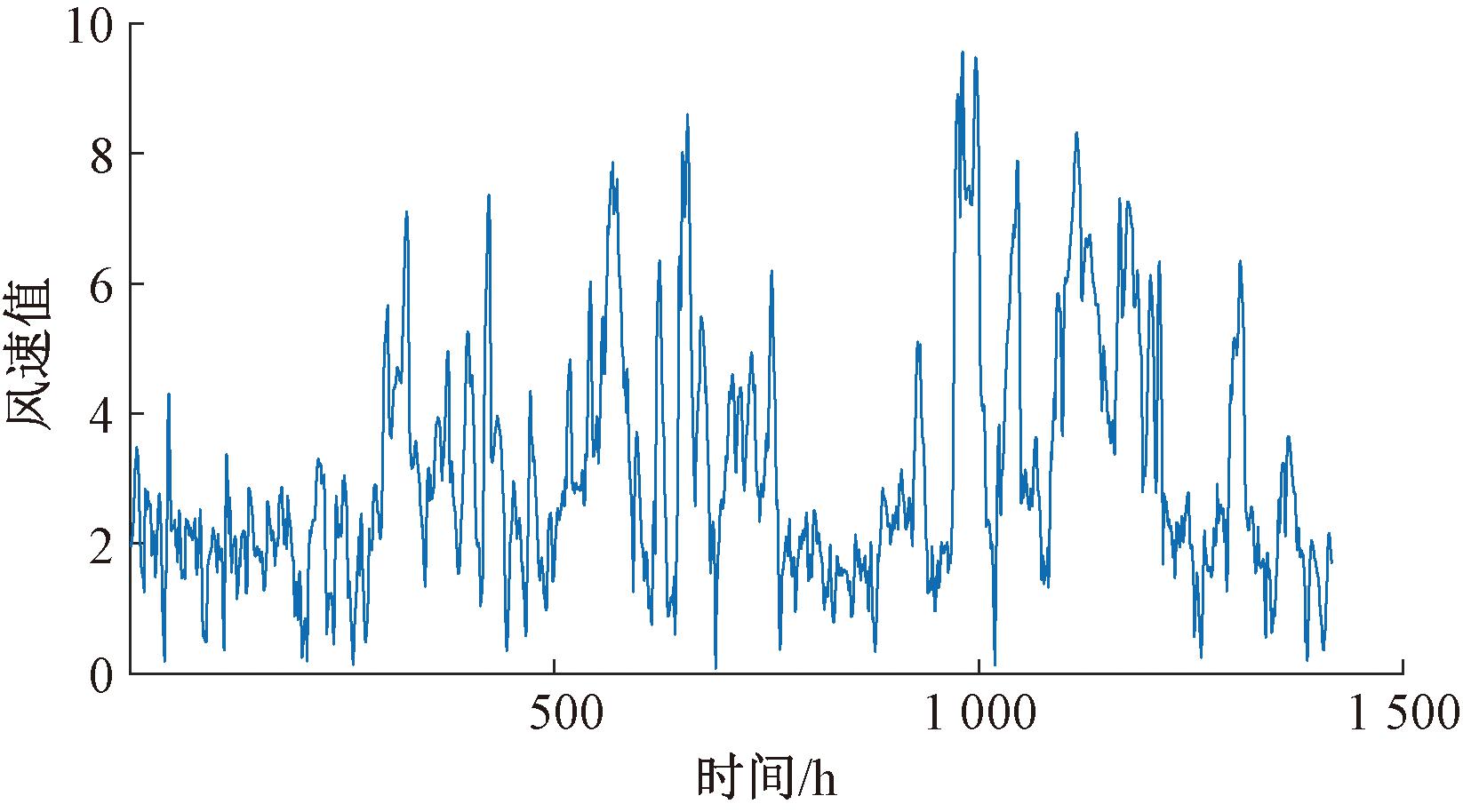
图2 原始风速序列
Figure 2 Original wind speed sequence
设置BWO算法的种群规模为10,最大迭代次数为30,优化变量有2个,分别为分解模态数K和惩罚因子α,并设变量寻优的范围,其中分解模态数K的寻优范围为3～10,惩罚因子α的寻优范围为100～2 500。
经过BWO算法寻优后得到该样本数据的最佳分解模态数K为4,最佳惩罚因子α为1 600。将上述参数数据代入VMD完成风速数据的分解,如图3所示。
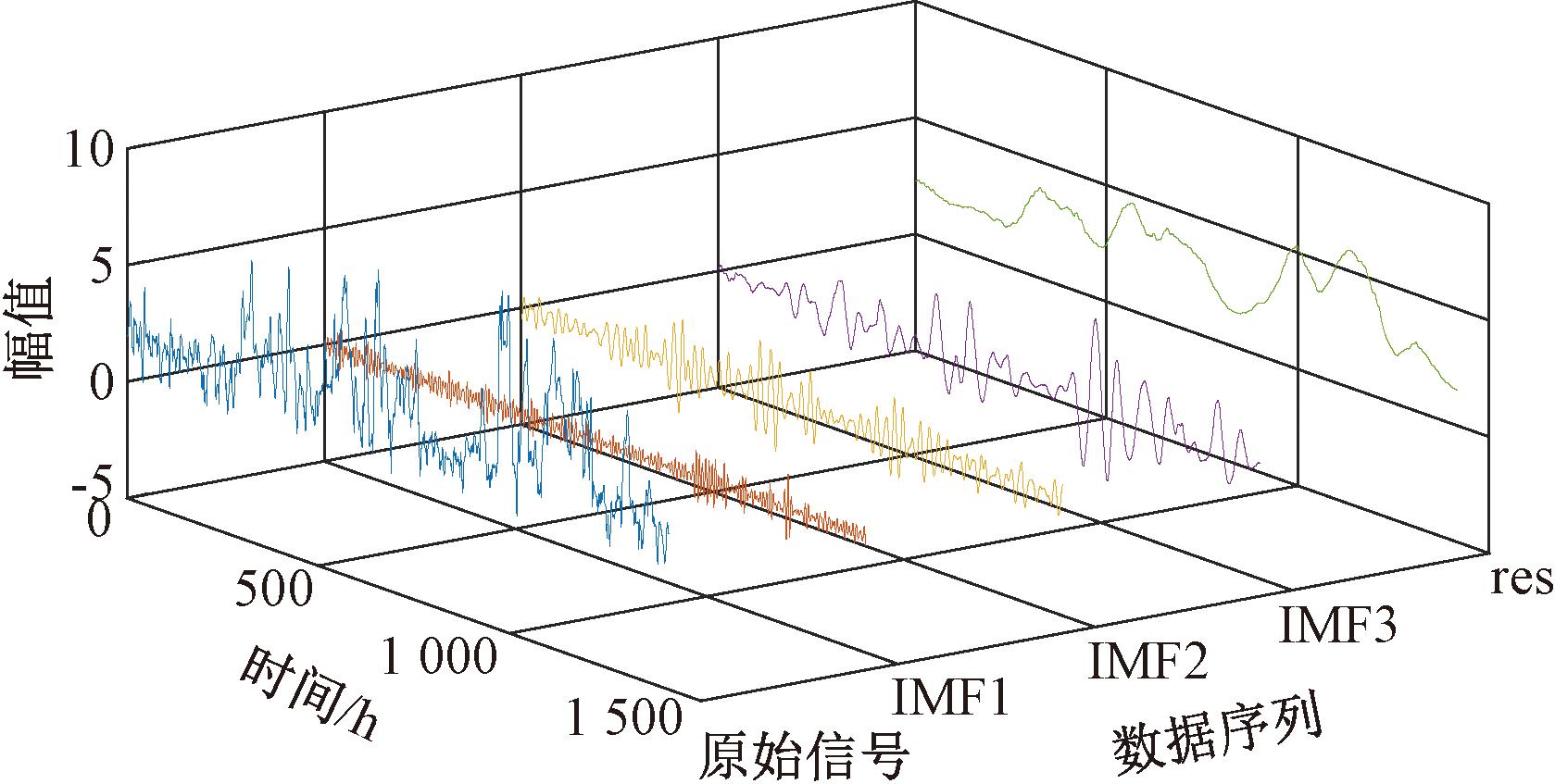
图3 VMD分解序列
Figure 3 VMD decomposition sequence
图3中,蓝色曲线代表的是原始的风速序列,IMF1、IMF2、IMF3和res是VMD分解后的4个子模态,其中IMF1、IMF2和IMF3的频率依次减小,res为VMD分解原始风速序列后形成的残差。
2 基于WOA的LSTM短期风速预测
将训练集的样本输入至长短时记忆神经网络完成预测。为了使LSTM发挥出更好的性能,得到较好预测结果,利用鲸鱼优化算法对LSTM的参数进行优化,完成对测试集样本的预测,并计算预测误差。
2.1 鲸鱼优化算法
鲸鱼优化算法(whale optimization algorithm,WOA)[19]灵感来源于鲸鱼群体的行为。这个算法被设计用来解决优化问题,尤其在连续型优化问题中表现出色。它是一种进化算法,借鉴了鲸鱼群体的社会行为和迁徙模式,由下列三部分组成。
(1)包围猎物。鲸鱼在包围猎物的过程中会自己选择最优路径,具体为
D=|CX*(t)-X(t)|;
(19)
X(t+1)=X*(t)-AD。
(20)
式中:D为猎物与最佳搜索代理间的距离;X*(t)为猎物的位置;X(t)为鲸鱼的位置;t为鲸鱼优化算法的迭代次数;C、A均代表系数向量。
(2)泡泡网攻击。该策略模拟了座头鲸捕猎行为的两种方式,即收缩包围和螺旋更新,这两种方式都允许鲸鱼个体向目标猎物移动,并根据随机生成的概率来决定采用哪种方式进行位置更新。
X(t+1)=D′eblcos(2π)+X*(t);
(21)
D′=|X*(t)-X(t)|。
(22)
式中:b控制着螺旋的形状;l为一个随机数,用于引入随机性,以使鲸鱼个体用不同的方式探索搜索空间。
(3)随机搜索。在搜索阶段,鲸鱼之间采用随机搜索方式,根据最近搜索代理的位置来更新鲸鱼的位置。
D=|CXrand(t)-X(t)|;
(23)
X(t+1)=Xrand(t)-AD。
(24)
式中:Xrand(t)代表猎物的随机位置。
在WOA算法中,还会生成随机数q∈[0,1],用于决定接下来的行为策略:如果生成的随机数q满足q>0.5时,则算法进入泡泡网攻击模式,在这种模式下,鲸鱼个体可能会采取不同的行为策略,以增加搜索的多样性;若q<0.5时,则算法会对系数向量A进行判断,当|A|≥1时,鲸鱼个体选择搜索猎物;当|A|<1时鲸鱼个体选择包围猎物。随着WOA算法的迭代次数增加,算法逐渐从猎物搜索转变为猎物包围状态。
2.2 长短时记忆神经网络LSTM
LSTM[20]是一种特殊的循环神经网络。LSTM在循环神经网络的基础上添加了记忆单元,能够学习到不同长短时间的信息,因而LSTM在处理时间序列问题时的表现更佳。图4为LSTM内部结构。
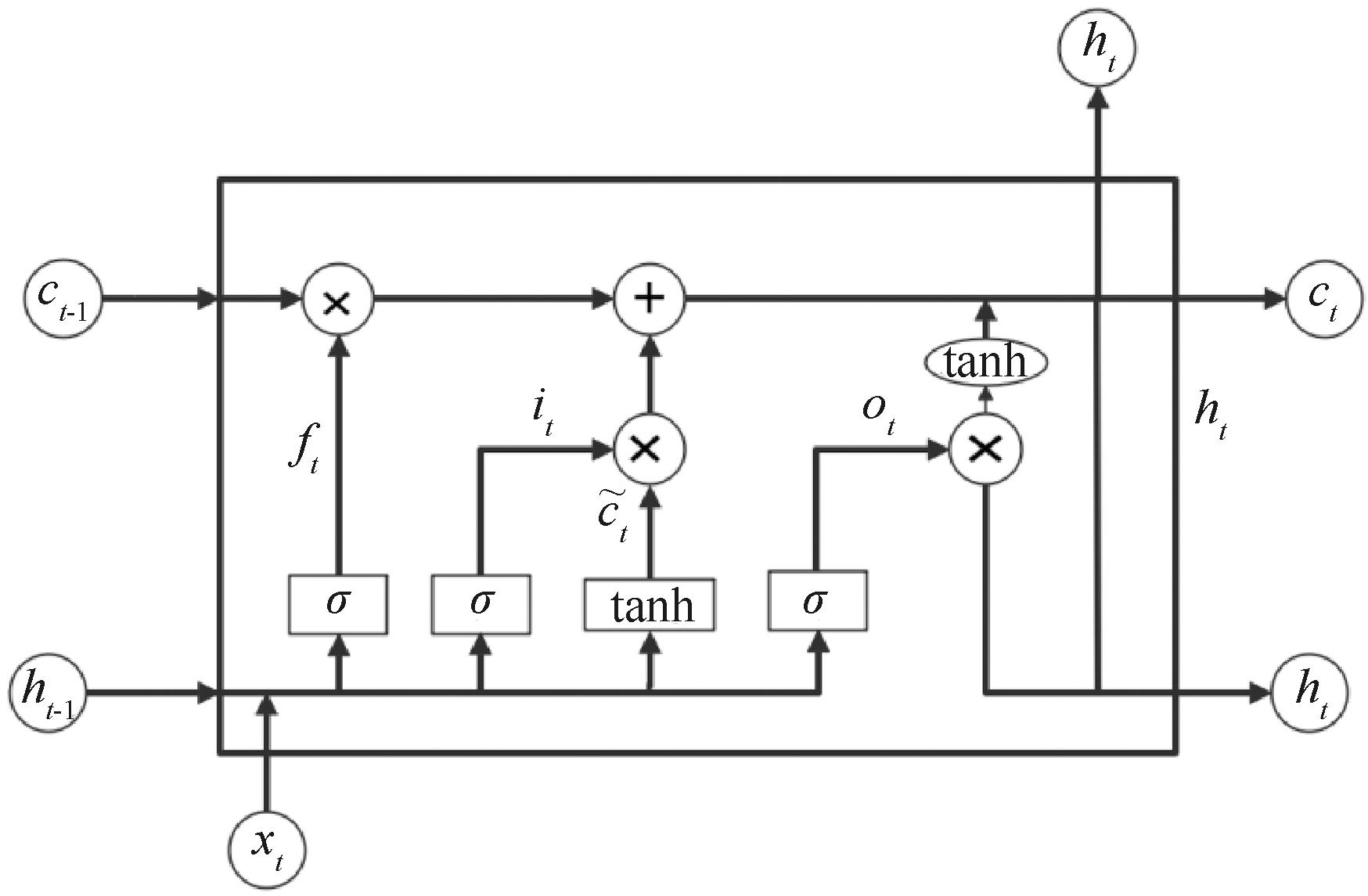
图4 LSTM网络结构
Figure 4 LSTM network structure
LSTM的隐藏层中,单个神经元的计算包括细胞状态的更新和输出值的计算两个重要部分。神经元内部包含3个门函数,分别是遗忘门、输入门和输出门,通过这些门函数可以有效地控制输入值、记忆值和输出值的流动,从而提高网络对长序列信息的处理能力。
假设在t时刻,输入序列为xt、输出序列为yt,则遗忘门ft、输入门it、输出门ot分别为
ft=σ(Wf[ht-1,xt]+bf);
(25)
it=σ(Wi[ht-1,xt]+bi);
(26)
(27)
(28)
ot=σ(Wo[ht-1,xt]+bo);
(29)
ht=ottanh(ct)。
(30)
式中:σ(·)为Sigmoid函数;Wf为遗忘门权重值;ht-1为上一时刻单元的输出;bf为遗忘门偏置项;Wi和Wc分别为输入门和记忆单元c的权重值;bi和bc分别为输入门和记忆单元的偏置项;
为前一时刻记忆单元的状态;ct为当前时刻记忆单元的状态;Wo为输出门的权重值;bo为输出门的偏置项;ht为t时刻单元的输出。
则t时刻输出为
(31)
式中:
为
的权重值;
为的偏置项。
2.3 鲸鱼优化算法优化长短时记忆神经网络参数
LSTM模型具有较强的非线性映射能力和泛化能力,且计算稳定性高,是解决风速预测问题较理想的选择。但LSTM具有依赖性,相关参数的选取没有相对统一的标准,导致目前LSTM的参数大多依靠人为经验设定。这种情况将可能导致LSTM的泛化能力变差,从而导致LSTM模型不能发挥出较好的性能,影响风速预测结果的准确性。因此,针对LSTM模型,恰当选择初始参数同样关键。
为提升LSTM预测的准确性,利用WOA算法对LSTM的最大隐含层节点数、最大迭代次数和初始学习率由全局向局部进行寻优。WOA算法优化LSTM的具体步骤有以下4步。
步骤1 对风速序列数据作零均值和单位方差的标准化处理,确保LSTM网络训练收敛以及得到更好的拟合结果。同时对数据进行划分,以合适的比例确定训练集和测试集。
步骤2 初始化鲸鱼优化算法中的种群和LSTM网络中的相关参数,将需要进行寻优的LSTM参数输入至WOA算法中。
步骤3 在WOA算法寻优的初始阶段,以初始化设定的值作为最佳取值对LSTM网络赋值并进行初步训练。使用均方根误差RMSE作为WOA算法的适应度函数,并计算相应的适应度值。
步骤4 在WOA算法不断迭代的过程中,当适应度值小于终止值时将得到鲸鱼种群和种群中个体的最佳位置,若适应度值大于终止值,则更新鲸鱼搜索代理的位置继续进行寻优,直至满足条件。满足条件后的寻优参数值即为LSTM网络的最佳参数值。
2.4 数值实验
在1.4节的基础上继续完成数值实验。设置WOA算法的种群规模为5,最大迭代次数为20,优化变量的数目为3个,分别为隐含层节点数、最大训练次数、初始学习率,并设变量寻优的范围,其中隐含层节点数的寻优范围为1～100,最大训练次数为1～200,初始学习率为0.001～0.100。
表1为经过WOA算法寻优后得到的子模态的最佳隐含层节点数、最大训练次数和初始学习率。
表1 WOA算法确定的LSTM参数
Table 1 LSTM parameters determined by WOA algorithm
分量 最佳隐含层节点数 最大训练次数 初始学习率 IMF1 53 108 0. 014 IMF2 10 112 0. 024 IMF3 14 105 0. 012 res 99 198 0. 006
本文选用的训练集数据的均值为2.828 3,方差为1.666 0。为了使最终LSTM网络训练收敛以及得到更好的拟合结果,在进行训练之前需将数据转化为零均值和单位方差的标准化数据。
为得到更好的运行结果,可在初始学习率相同的情况下,选择RMSE最小时的最小衰落因子来训练网络。此时学习率衰落因子为0.4,同时使用WOA算法得到的参数数据可使LSTM网络达到较优状态。然后使用训练好的模型对后20%即293条数据进行预测,使用观测值来更新LSTM网络。
图5为本文预测模型与其他模型误差的对比图形,包含仅使用LSTM算法[21]的VMD-LSTM模型预测结果。但仅凭借图形无法直观说明各个模型的预测值与真实值之间的误差。表2为本文模型与其他模型在均方根误差RMSE、平均绝对误差MAE和平均相对误差MAPE的对比。结果表明,相较于VMD-LSTM模型,本文方法可以有效降低风速训练的预测误差,提高预测精度。
表2 消融实验预测值误差
Table 2 Prediction error in ablation experiments
模型 RMSE MAE MAPE LSTM 0. 704 3 0. 513 9 0. 266 9 VMD-LSTM 0. 326 7 0. 257 6 0. 124 6 VMD、WOA-LSTM 0. 282 1 0. 222 0 0. 104 5 BWO-VMD、LSTM 0. 265 5 0. 205 0 0. 093 3 BWO-VMD、WOA-LSTM 0. 223 4 0. 172 7 0. 083 7
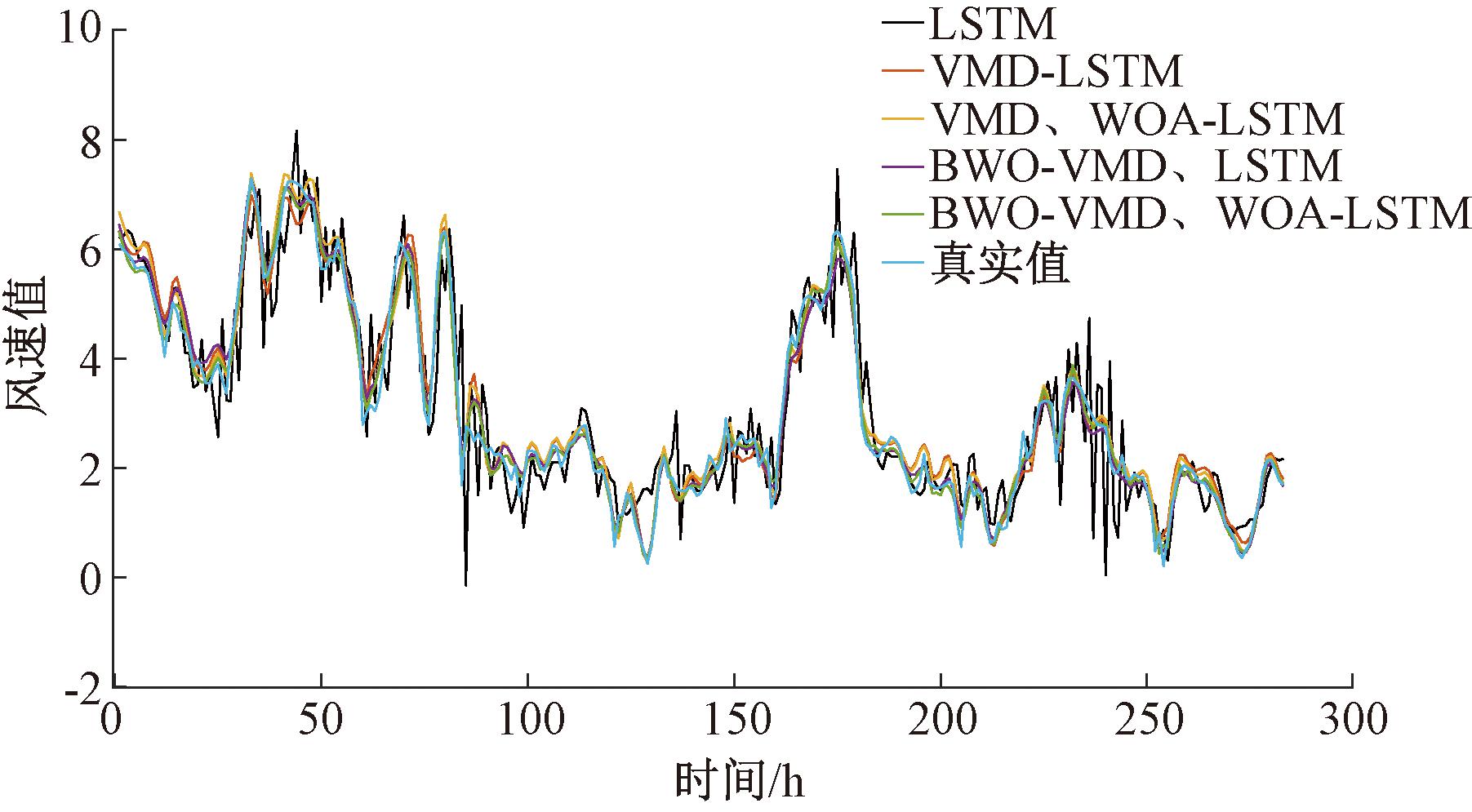
图5 消融实验不同模型预测结果
Figure 5 Prediction results of various models in ablation experiments
为了进一步验证本文模型的优越性,图6和表3为本文与CEEMDAN-GWO-ELM[22]、SSA-BP[23]和CEEMD-SVM[24]模型的对比情况。可以看出,本文模型在RMSE、MAE和MAPE上均优于其他模型,基于BWO和WOA算法的VMD-LSTM模型在短期风速预测上具有更好的精度。
表3 本文模型与其他模型预测值误差
Table 3 The prediction errors of the model in this study compared to those of other models
模型 RMSE MAE MAPE CEEMDAN-GWO-ELM [22] 0. 459 9 0. 358 9 0. 203 1 SSA-BP [23] 0. 394 6 0. 274 0 0. 166 3 CEEMD-SVM [24] 0. 778 6 0. 405 7 0. 265 7 BWO-VMD、WOA-LSTM 0. 223 4 0. 172 7 0. 083 7
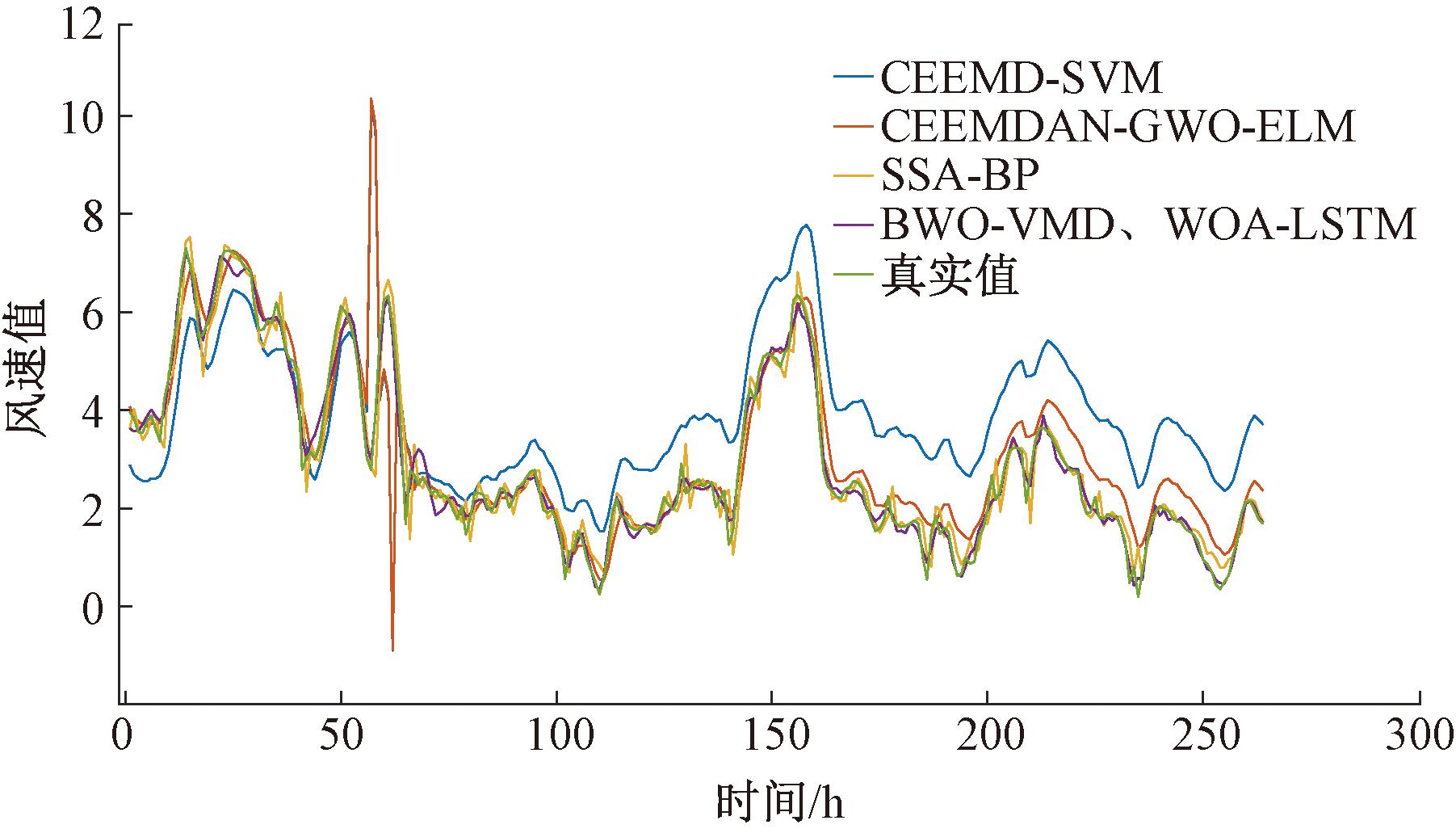
图6 本文模型与其他模型的对比
Figure 6 A comparison of this model with other models
3 结论
(1)利用BWO优化VMD的分解模态数和惩罚因子,可以有效提升VMD分解风速序列后的预测精度。
(2)利用WOA优化LSTM的隐含层节点数、最大训练代数、初始学习率,能够降低LSTM的预测误差。
(3)在对比实验中,本文提出的基于BWO和WOA算法的VMD-LSTM短期风速预测模型都具有较好的预测水平,体现了该模型的优势。
本文采用的寻优算法在运算时间上还有待继续改进,同时还可引入相关影响因素,进一步提高预测结果的准确性。
[1] 张董极, 肖琴. 基于复杂网络的风速预测新方法[J]. 太阳能学报, 2023, 44(3): 90-96.
ZHANG D J, XIAO Q. A new method of wind speed prediction based on complex network[J]. Acta Energiae Solaris Sinica, 2023, 44(3): 90-96.
[2] CHEN G G, TANG B R, ZENG X J, et al. Short-term wind speed forecasting based on long short-term memory and improved BP neural network[J]. International Journal of Electrical Power &Energy Systems, 2022, 134: 107365.
[3] DE MATTOS NETO P S G, DE OLIVEIRA J F L, DE OSANTOS J
NIOR D S, et al. An adaptive hybrid system using deep learning for wind speed forecasting[J]. Information Sciences：an International Journal, 2021, 581(C): 495-514.
[4] DAYAL K K, BELLON G, CATER J E, et al. High-resolution mesoscale wind-resource assessment of Fiji using the weather research and forecasting (WRF) model[J]. Energy, 2021, 232: 121047.
[5] 叶小岭, 顾荣, 邓华, 等. 基于WRF模式和PSO-LSSVM的风电场短期风速订正[J]. 电力系统保护与控制, 2017, 45(22): 48-54.
YE X L, GU R, DENG H, et al. Modification technology research of short-term wind speed in wind farm based on WRF model and PSO-LSSVM method[J]. Power System Protection and Control, 2017, 45(22): 48-54.
[6] YANG D Z, WANG W T, HONG T. A historical weather forecast dataset from the european centre for medium-range weather forecasts (ECMWF) for energy forecasting[J]. Solar Energy, 2022, 232: 263-274.
[7] 姜言, 黄国庆, 彭新艳, 等. 基于GARCH的短时风速预测方法[J]. 西南交通大学学报, 2016, 51(4): 663-669, 742.
JIANG Y, HUANG G Q, PENG X Y, et al. Method of short-term wind speed forecasting based on generalized autoregressive conditional heteroscedasticity model[J]. Journal of Southwest Jiaotong University, 2016, 51(4): 663-669, 742.
[8] WANG Y R, WANG D C, TANG Y. Clustered hybrid wind power prediction model based on ARMA, PSO-SVM, and clustering methods[J]. IEEE Access, 2020, 8: 17071-17079.
[9] 张金良, 刘子毅. 基于混合模型的超短期风速区间预测[J]. 电力系统保护与控制, 2022, 50(22): 49-58.
ZHANG J L, LIU Z Y. Ultra short term wind speed interval prediction based on a hybrid model[J]. Power System Protection and Control, 2022, 50(22): 49-58.
[10] 朱昶胜, 李岁寒. 基于改进果蝇优化算法的随机森林回归模型及其在风速预测中的应用[J]. 兰州理工大学学报, 2021, 47(4): 83-90.
ZHU C S, LI S H. Random forest regression model based on improved fruit fly optimization algorithm and its application in wind speed forecasting[J]. Journal of Lanzhou University of Technology, 2021, 47(4): 83-90.
[11] 孙川永, 彭友兵, 刘志亮, 等. 梯度提升树算法在陕北风电场短期风电功率预测中的应用[J]. 电网与清洁能源, 2022, 38(4): 124-128, 134.
SUN C Y, PENG Y B, LIU Z L, et al. Short-term wind power prediction of the wind farm in northern Shaanxi based on gradient boosting decision tree[J]. Power System and Clean Energy, 2022, 38(4): 124-128, 134.
[12] 柏丹丹, 和敬涵, 王小君, 等. 自适应粒子群支持向量机风速组合预测模型[J]. 太阳能学报, 2015, 36(4): 792-797.
BAI D D, HE J H, WANG X J, et al. Combination model for forecasting wind speed based on adaptive PSO-SVM[J]. Acta Energiae Solaris Sinica, 2015, 36(4): 792-797.
[13] TIAN Z D, CHEN H. A novel decomposition-ensemble prediction model for ultra-short-term wind speed[J]. Energy Conversion and Management, 2021, 248: 114775.
[14] 冯义, 刘慧文, 张宝平, 等. 基于集合经验模态分解和特征选择极端学习机的风速预测[J]. 智慧电力, 2018, 46(12): 30-37.
FENG Y, LIU H W, ZHANG B P, et al. Short-term wind speed forecasting using ensemble empirical mode decomposition and extreme learning machine with feature selection[J]. Smart Power, 2018, 46(12): 30-37.
[15] XIONG D Z, FU W L, WANG K, et al. A blended approach incorporating TVFEMD, PSR, NNCT-based multi-model fusion and hierarchy-based merged optimization algorithm for multi-step wind speed prediction[J]. Energy Conversion and Management, 2021, 230: 113680.
[16] ZHAO Z N, YUN S N, JIA L Y, et al. Hybrid VMD-CNN-GRU-based model for short-term forecasting of wind power considering spatio-temporal features[J]. Engineering Applications of Artificial Intelligence, 2023, 121: 105982.
[17] ZHONG C T, LI G, MENG Z. Beluga whale optimization: a novel nature-inspired metaheuristic algorithm[J]. Knowledge-Based Systems, 2022, 251: 109215.
[18] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[19] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95(C): 51-67.
[20] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780.
[21] 王俊, 李霞, 周昔东, 等. 基于VMD和LSTM的超短期风速预测[J]. 电力系统保护与控制, 2020, 48(11): 45-52.
WANG J, LI X, ZHOU X D, et al. Ultra-short-term wind speed prediction based on VMD-LSTM[J]. Power System Protection and Control, 2020, 48(11): 45-52.
[22] 张文煜, 马可可, 郭振海, 等. 基于灰狼算法和极限学习机的风速多步预测[J]. 郑州大学学报(工学版), 2024, 45(2): 89-96.
ZHANG W Y, MA K K, GUO Z H, et al. Multistep prediction of wind speed based on grey wolf algorithm and extreme learning machine[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(2): 89-96.
[23] 张俱珲, 孟建军, 李德仓, 等. 基于SSA-BP的铁路沿线风速预测方法[J]. 计算机仿真, 2023, 40(12): 209-212, 260.
ZHANG J H, MENG J J, LI D C, et al. A method for predicting wind speed along railway lines based on SSA-BP[J]. Computer Simulation, 2023, 40(12): 209-212, 260.
[24] 田崇翼, 王学睿, 王瑞琪. 基于CEEMD-SVM的风速混合预测模型研究[J]. 计算机时代, 2023(7): 24-28.
TIAN C Y, WANG X R, WANG R Q. Research on hybrid wind speed prediction model based on CEEMD-SVM[J]. Computer Era, 2023(7): 24-28.