社交网络数据是基于节点和边缘的图结构,图神经网络(GNN)可以有效地用于处理图结构数据方面的节点分类任务[1]。在实践中,由于数据采样偏差等原因的影响,节点类在图中可能是不平衡的,即一些类的训练样本比其他类少得多。例如,对于虚假账户检测[2],社交网络平台中的大多数用户都表现良好,但只有小部分是机器人。与多数类节点相比,少数类节点往往包含更有价值的信息[3]。因此,提高GNN的不平衡分类质量,特别是少数类节点的分类精度具有重要意义。
少数类样本表示不足不仅会影响它们的嵌入质量,还会影响相邻节点之间的知识交换过程。因此在生成新节点以形成连通图时,需要获得新节点的边缘信息。然而,现有的过采样方法是基于独立的相同分布假设,认为每个节点都是独立的,不能直接获得两个节点之间的边缘信息。如Park等[4]通过根据2个母节点的ego network为新节点生成邻居,缓解了邻居过拟合问题。Zhao等[5]提出了GraphSMOTE,通过使用边缘预测器为新合成节点生成边缘连通关系,从而在合成节点和现有节点之间生成边缘。但是GraphSMOTE在聚合信息和边缘预测时未能区分多数节点和少数节点的重要性,这使得属于少数类的节点更容易被错误地归类为多数类。Wang等[6]在GraphSMOTE的基础上加入激活函数,并且使用成本敏感学习来改进边缘预测效果。Shi等[7]通过邻域聚合将具有邻域信息的节点特征映射到特征空间,然后通过插值法合成少数节点,省略了边的合成,消除了在边缘构建过程中引入的噪声,但当图中的边不是必需时,就没有充分体现消除边构造的优势。Chen等[8]结合拓扑不平衡与数量不平衡问题,通过计算标记节点到类别边界的距离,提出一个个性化PageRank矩阵以表示标记节点的影响力分布,但是它在标注比例低和图连通性差的场景中效果不明显,并且只在同质连边的图中成立。Song等[9]证明了在与主要节点具有较高链接性的次要节点周围出现了明显的高误报率。通过基于节点拓扑单独调整补偿程度来有效减少过多的误报。
因此针对节点的类别不平衡和图的连通性问题,本文提出一种基于少数类加权聚合(WAMC)和异常连通性裕度(ACM)损失的类不平衡分类算法(WACML-GNN),实验结果表明,该算法增强了聚合过程中少数类节点的特征表示,避免过度平滑现象,并且提高了模型对链接性信息的敏感度。
1 相关工作
1.1 类不平衡
目前关于不平衡数据分类算法的研究主要分为3类:数据级方法、算法级方法以及集成方法。
数据级方法也可称为重采样方法,该类方法关注于通过修改训练数据集以使得标准学习算法也能在其上有效训练。其中最具代表性的是SMOTE过采样方法,其含有许多扩展。Borderline-SMOTE[10]使用边界上的少数类样本来合成新样本;Kernel-SMOTE[11]在邻居密度分布中插值生成新样本。
算法(分类器)级方法专注于利用数据分布不平衡的特点对现有算法进行改进。例如成本敏感学习旨在通过在分类器训练过程中引入惩罚因素,增强少数类的重要性[12]。代价敏感学习给少数类样本分配较高的误分类代价,而给多数类样本分配较小的误分类代价。使用该方法后的算法通常会有更好的表现,并且没有增加训练的计算复杂度,可直接扩展到多分类问题上。
集成学习类方法专注于将一种数据级或算法级方法与集成学习相结合,以获得强大的集成分类器。它们中的大多数基于某种特定的集成学习算法(例如Adaptive Boosting)并在集成的过程中嵌入其他的不平衡学习方法(例如SMOTE)。例如SMOTEBoost方法是boosting和SMOTE过采样的组合[13]。集成学习类方法效果通常较好,可使用迭代过程中的反馈进行动态调整。相比于其他采样方法具有更快的收敛速度和更优的分类性能。
1.2 图神经网络
任何由实体和实体之间的关系组成的系统都可以表示为图,用图结构来表示数据可以从实体以及实体关系表示中提取更有价值的信息。一般来讲,GNN主要分为基于空间和基于频谱两类方法。
基于空间的GNN可以处理大型图,在每个节点执行本地卷积,而不是整个图。并且可以在不同的位置和结构之间共享权重,引入节点采样来提高效率,具有很强的灵活性。NN4G[14]是GNN领域中提出较早的卷积图神经网络模型,其主要通过直接将节点的邻域信息相加来进行图卷积。GraphSage[15]是一种能够利用顶点的属性信息高效产生未知顶点嵌入的一种归纳式学习的框架。
基于频谱的GNN是根据图谱理论和卷积定理,使用特征分解将数据由空域转换到谱域进行处理。ChebNet[16]的出现是为了解决计算复杂度高和无法保证局部链接的问题,其核心在于采用切比雪夫多项式代替谱域的卷积核模型。Kipf等[17]对ChebNet进行一阶近似得到处理结构化数据的新模型GCN,提高了模型学习的泛化能力。基于频谱的GNN只能应用于有向图,并且模型计算成本随着图的大小的增加而急剧增加,难以处理大型图。
2 WACML-GNN模型
本文针对图结构中的类不平衡问题,提出了一种基于少数类加权聚合(WAMC)和异常连通性裕度(ACM)损失的新方法WACML-GNN。该模型由四部分组成,首先输入给定的图结构数据,计算节点的邻接信息后,将其引入第1个GraphSage[18]块进行聚合,之后对节点进行WAMC操作,以增强聚合过程中对少数类节点的特征表示的影响。其次,在生成的嵌入空间中,执行SMOTE过采样操作来生成新的节点。再次,进行边缘预测生成新节点的边,并联合ACML,提高对异常节点的边缘预测能力。最后,将合成节点和现有节点的图结构信息进行组合,并使用第2个GraphSage块对节点进行分类预测。模型的整体框架如图1所示。
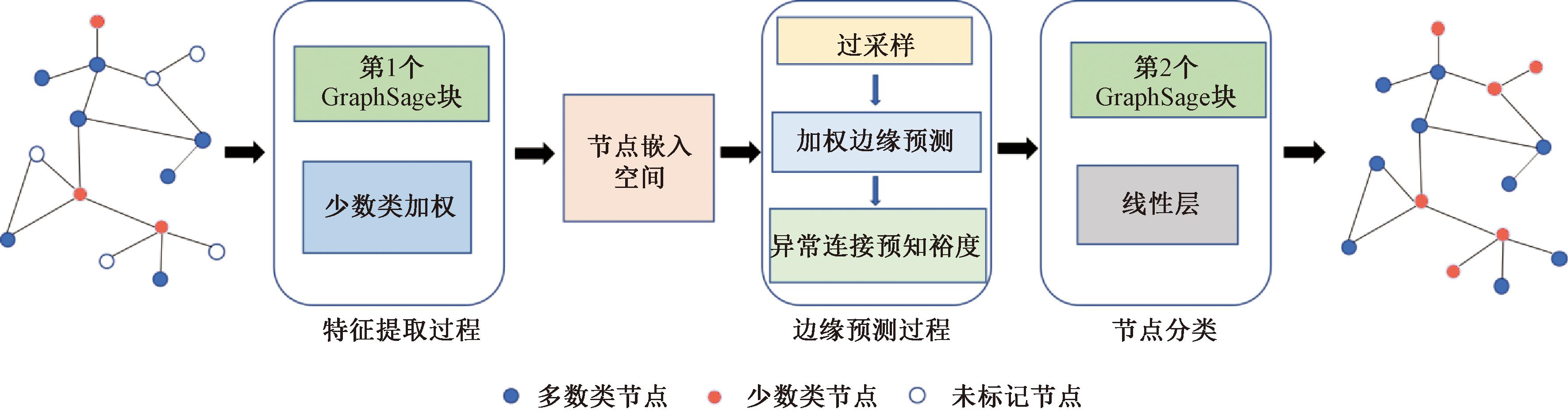
图1 WACML-GNN模型框架
Figure 1 Framework of the WACML-GNN model
2.1 基于WAMC的特征提取器
在处理不平衡数据时忽略了少数节点的重要性,为了提高少数节点对嵌入的影响,采用WAMC操作,增加少数节点对聚合过程的影响,避免过度平滑。使用GraphSage作为主干模型结构来提取特征。在该过程中,节点i的信息传递和融合过程分别为
(1)
(2)
式中:A(·)为聚合函数;C(·)为链接函数;σ(·)为激活函数;N(i)表示链接到节点i的所有节点的集合;
为节点u的输入特征,
为权重参数,
为节点i的嵌入表示。
然而,上述过程在处理不平衡数据时忽略了少数节点的重要性。因此,本文定义并使用WAMC来提高少数节点对嵌入的影响。节点u相对于节点v的WAMC定义为
(3)
式中:μuv为类yu的不平衡比例;I(u)为指示符;ρyu为yu类的不平衡率;yu和yv对应于u和v的标签;p为调整不同类别节点之间聚合过程的比例系数。
如图2所示,节点2和节点3是链接的,并且都属于少数类节点,因此两个节点之间的WAMC是其所属少数类的不平衡比例。如果两个链接的节点都属于多数类,例如节点4和5,则WAMC设置为1,以保持它们之间的邻接关系。当两个节点链接,但它们的类不同时,它们之间的类内相关性会降低。因此,引入比例系数p(0<p<1)来调整不同类别节点对聚合过程的影响。
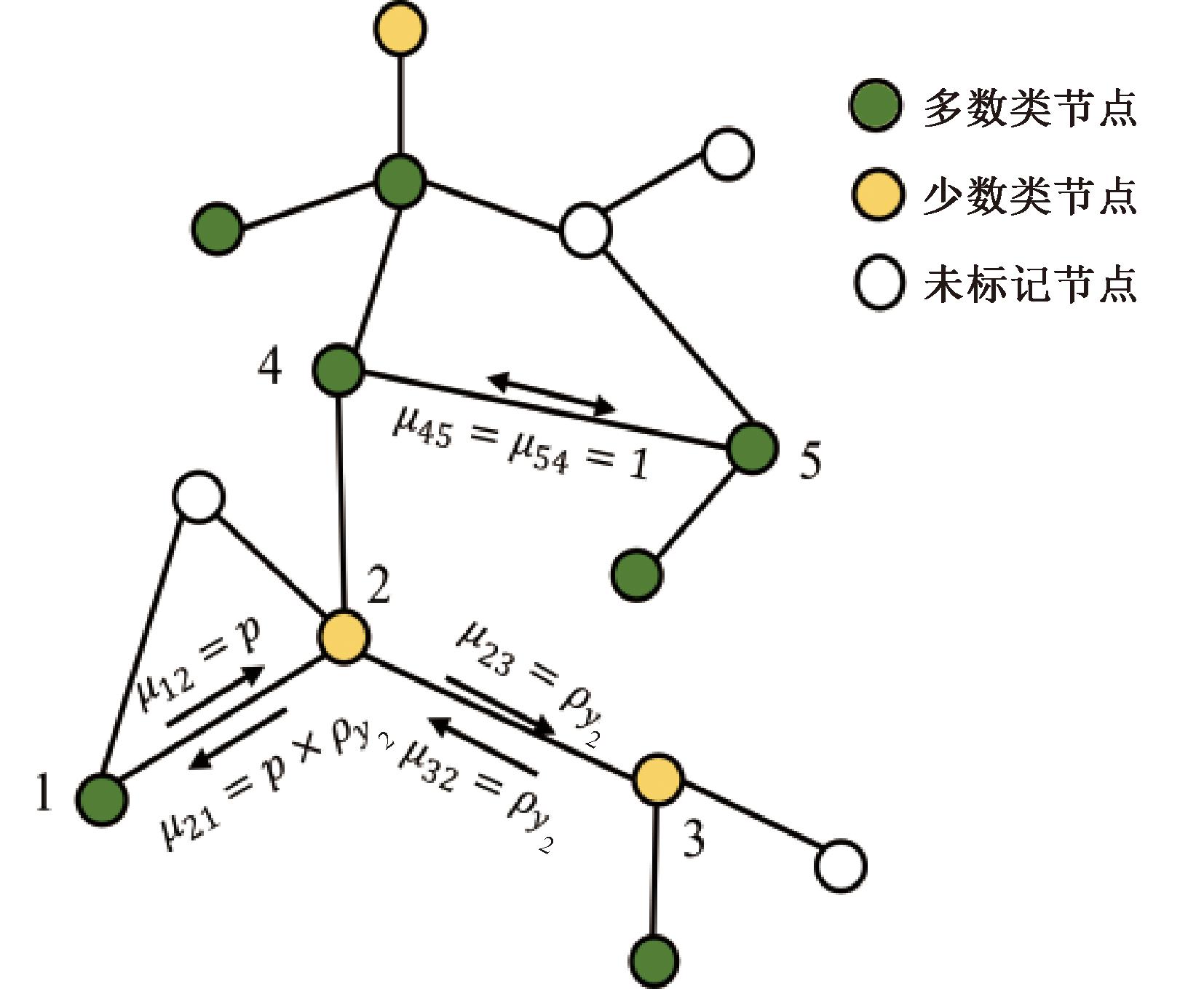
图2 不平衡图结构示例
Figure 2 Example of unbalanced graph structure
基于WAMC,可以将第1个GraphSage块的聚合处理的式(1)更改为式(4)。WAMC的μui由式(3)计算。对于节点i,在获得的聚合特征
之后,获得嵌入空间表示为
(4)
由于原始特征空间十分稀疏,直接在原始特征空间进行插值容易产生域外样本,因此,通过第1个GraphSage块获得嵌入空间中的节点表示,相对于原始的节点特征所获得的节点特征低维且稠密,然后在嵌入空间中进行后续的SMOTE操作以扩展少数类数据。
2.2 基于SMOTE过采样的合成节点生成
在获得由特征提取器构建的嵌入空间中的每个节点的表示之后,本文在此基础上执行过采样。SMOTE[18]算法思想是对目标少数类的样本与嵌入空间中属于同一类的最近邻样本进行插值。设是一个带标记的少数类节点,标记为Yv,第1步是找到与在同一个类中的最近的标记节点,如式(5)所示。
(5)
式中:
为同一类中i的近邻,可以生成节点表示如式(6)所示。
(6)
式中:δ∈[0,1]为随机变量。由于和
属于同一个类,且非常接近,因此生成的合成节点
也与目标节点属于同一类。通过这个生成过程,可以获得标记的合成节点,数据的分布可以变得平衡。
2.3 基于边缘合成预测与ACML
现在已经生成了合成节点来平衡类分布,然而这些节点与原始图G是隔离的,没有链接。因此,本文引入了一个边生成器来对节点之间的边的存在性进行建模。该边缘生成器可以为合成的样本提供关系信息,从而有助于训练基于GNN的分类器。该生成器在真实节点和现有边上进行训练,并用于预测这些合成节点的邻居信息。这些新的节点和边将被添加到初始邻接矩阵A中,并作为基于GNN的分类器的输入。本文采用带权内积解码器(weighted inner product decoder)来计算节点之间的相关性,从而指导边的生成。带权内积解码器本质上是先对Embedding进行一个线性变换,再进行内积解码。利用带权内积解码器计算节点v和节点u的相关性的方式为
(7)
式中:Ev,u为预测的节点之间的关系信息;S为捕捉节点之间的交互的参数矩阵。接下来,用原始图来训练解码器的权重矩阵S,可以计算得到原始图的重构邻接矩阵E,进而计算重构误差,如式(8)所示。
edge=
。
(8)
式中:E为集合V中节点之间的链接预测。在使用edge训练边缘生成器之后,预测合成节点i的邻接性,如式(9)所示。
(9)
式中:Ei′,u表示合成节点i′和节点u之间的邻接关系;
为通过添加合成样本的邻接信息对初始邻接矩阵A的扩展。值得注意的是,此时的S是已经训练的参数矩阵。
为了衡量链接的异常性,本文计算每个链接的异常链接感知裕度(ACM)损失以鼓励模型更好地区分正常链接和异常链接。将ACM损失定义为链接概率的负对数似然是一种常见的方法。ACM损失的具体定义如式(10)所示。
(10)
式中:N为链接的总数(所有i、j组合的数量);Aij为实际链接情况,如果节点i和j之间存在链接,则Aij=1,否则Aij=0;Pij为模型预测的链接概率。
这个损失函数的目标是最小化实际链接情况与模型预测之间的差异,使模型更好地区分正常链接和异常链接。将ACM损失作为额外的损失加入边缘预测任务中,这将鼓励模型在嵌入空间更好地学习链接性信息,以改善边缘预测的性能。
2.4 GNN分类器与目标优化
利用式(7)和式(10)可以获得嵌入空间特征和节点的邻接关系。通过合成节点将现有的图结构G扩展到
含有节点集
邻接矩阵
以及嵌入空间
中的节点的特征矩阵。第2个GraphSage块和一个线性层用于完成最终的分类任务。节点i在两个GraphSage块之后的特征表示如式(11)所示。
(11)
式中:
为节点i在两个GraphSage块之后的特征表示,
为激活函数。H2为第2个GraphSage块中所有节点的特征矩阵。节点分类的损失函数node使用交叉熵损失,并且节点的类别被设置为具有最高概率的类别Yu,具体定义如式(12)所示。
(12)
式中:Pi为节点i的类标签上的概率分布。由于node不是归一化的,因此引入了超参数λ1和λ2来避免node、edge和ACM之间的较大差异。最终的目标函数如式(13)所示。
node+λ1×edge+λ2×ACM。
(13)
2.5 评价指标
本文使用的评价指标具体如下。
准确率(Accuracy)表示在模型预测为正样本的结果中,真正是正样本所占的百分比。
(14)
式中:TP为真阳性,表示正样本正确分类为正类的样本数量;FP为假阳性,表示负样本错分为正类的样本数量。
召回率(Recall)是针对原始样本而言的一个评价指标,表示在实际为正样本中,被预测为正样本所占的百分比。
(15)
式中:FN为假阴性,表示正样本错分为负类的样本数量。
F1Score表示对于Accuracy和Recall的综合考量。F1Score的值越大,表示模型的整体性能越均衡。
(16)
TPR表示预测正确的正类占实际全部正类的比例。FPR表示预测错误的正类占实际全部负类的比例。
(17)
式中:TN为真阴性,表示负样本正确分类为负类的样本数量。
ROC曲线表示不同分类阈值下的真正类率TPR和FPR构成的曲线。AUC表示ROC曲线下的面积。ROC曲线下的面积越大,模型的分类效果越优。
3 实验与结果分析
3.1 数据集和评价指标
本论文采用微博虚假账户公开数据集[19]、Twitter[2]虚假账户数据集以及BlogCatalog[20]数据集进行实验。3个数据集的特性如表1所示。
表1 数据集特性
Table 1 Dataset properties
数据集 真实账户 机器人账户 边 不平衡比例 Kaggle 69 875 2 795 216 799 25∶ 1 Twitter 61 122 2 045 204 547 30∶ 1 BlogCatalog 9 944 368 333 983 28∶ 1
微博虚假账户数据集在Kaggle平台上获取的开源数据集,数据集包含虚假账号和正常账号。数据集中一共包含937 280个正常用户和29 795个虚假用户,不平衡比例大概为31∶1。
Twitter数据集由使用Twitter3中专门的API爬虫对机器人感染问题进行抓取。它总共有5 384 160个用户,其中63 167名用户是机器人,不平衡比例为84∶1。
BlogCatalog数据集是一个从BlogCatalog2抓取的社交网络数据集,有来自38个类的10 312个博主和333 983个友谊边缘。
在不平衡分类下,本文采用了3个标准:分类准确性(ACC)、平均AUC-ROC评分和平均F1Score。ACC是同时对所有测试示例进行计算的,因此可能会低估那些代表性不足的类别。AUC-ROC评分说明了校正类别排名高于其他类别的概率,而F1Score给出了每个类别的精确度和召回率的调和平均值。AUC-ROC评分和F1Score分别为每个类别计算,然后对其进行非加权平均,因此可以更好地反映少数类别的表现。
3.2 结果与分析
将本文方法的分类性能与SMOTE[18]、Re-weight[21]、GraphSMOTE[5]、DR-GCN[22]、mGNN[6]进行比较。SMOTE是一种广泛使用的不平衡学习方法,采用线性插值来合成嵌入空间中新节点的边缘信息。Re-weight是一种经典的成本敏感方法,通过为少数类样本分配更高的损失权重来缓解模型偏向多数类的趋势。GraphSMOTE是在嵌入空间中执行SMOTE,并且没有使用加权边损失来生成新节点的边。DR-GCN提出两种正则化方法来处理多类不平衡图,使用对抗性训练和对齐训练来促进标记节点的分离并保持训练平衡。mGNN是用于社交网络上不平衡节点分类的新方法,应用成本敏感学习来提高现有边缘预测器的性能,并首次使用Gumbel分布作为GNN的激活函数,提高收敛速度与分类性能。
3.2.1 不平衡分类性能
本节将WACML-GNN的不平衡分类性能与上述3个数据集上的方法进行比较。对每个模型进行10次的重复试验,并将每个数据集上不同评估指标的平均数和标准差作为实验结果。实验结果如表2所示。
表2 不同方法下不平衡节点分类效果
Table 2 The classification effect of imbalanced nodes with different methods
方法 Kaggle Twitter BlogCatalog ACC AUC-ROC F1Score ACC AUC-ROC F1Score ACC AUC-ROC F1Score SMOTE 0. 819 4 0. 965 4 0. 799 2 0. 814 4 0. 958 8 0. 797 2 0. 813 0 0. 951 2 0. 795 9 Re-weight 0. 805 6 0. 961 0 0. 795 1 0. 803 3 0. 959 4 0. 788 1 0. 802 1 0. 954 6 0. 781 6 GraphSMOTE 0. 837 7 0. 969 4 0. 823 1 0. 835 5 0. 968 9 0. 822 3 0. 831 2 0. 966 7 0. 821 2 DR-GCN 0. 832 3 0. 961 8 0. 824 9 0. 831 9 0. 961 6 0. 823 1 0. 831 0 0. 961 4 0. 820 5 mGNN 0. 834 1 0. 972 9 0. 823 2 0. 841 8 0. 973 2 0. 822 7 0. 839 5 0. 972 3 0. 821 5 WACML-GNN 0. 845 2 0. 972 3 0. 833 4 0. 843 3 0. 972 3 0. 824 0 0. 840 1 0. 972 8 0. 821 0
与其他5种方法相比,WACML-GNN获得了最好的结果,其平均ACC为84.3%。与GraphSMOTE相比,WACML-GNN在Kaggle数据集上的ACC和F1Score分别提高了0.9%和1.25%,这说明了WACML-GNN在少数类之间加权聚合的有效性,也提高了不平衡分类的准确性。与mGNN相比,WACML-GNN的分类效果也是最优的,表明在类不平衡分类中引入ACM损失能够有效提升分类器的分类效果。
3.2.2 不平衡比例的影响
本小节分析了不同算法在不同的不平衡比例(IR)下的性能,以评估其稳健性。实验在Kaggle数据集上进行,将IR设置为
0.1,0.2,0.4,0.6
,每个实验进行3次,平均结果如表3所示。
表3 在4个不平衡比例下AUC的节点分类性能
Table 3 Classification performance of AUC nodes with four imbalanced ratios
方法 AUC IR = 0. 1 IR = 0. 2 IR = 0. 4 IR = 0. 6 SMOTE 0. 874 2 0. 902 7 0. 916 1 0. 923 7 Re-weight 0. 879 1 0. 888 1 0. 925 7 0. 930 6 GraphSMOTE 0. 911 9 0. 911 1 0. 921 6 0. 932 2 DR-GCN 0. 878 8 0. 891 2 0. 912 0 0. 923 3 mGNN 0. 865 7 0. 896 7 0. 918 8 0. 921 2 WACML-GNN 0. 916 7 0. 913 8 0. 930 3 0. 934 1
从表3中可以看出,所提出的WACML-GNN在4个不同的不平衡比例下实现了最佳性能,这表明了所提出的框架的有效性。当不平衡程度更加极端时,WACML-GNN的改进更为显著。例如,当不平衡比为0.1时,WACML-GNN的AUC比Re-weight算法高0.037 6;当不平衡比为0.6时,AUC减小了0.003 5。这是因为当数据集中的类别相对平衡时,少数过采样就不那么重要了,这使得所提出的算法相对于其他算法的改进没有那么显著。
3.2.3 消融实验
为证明WAMC和ACM损失对不平衡节点分类的有效性,在Kaggle数据集上进行消融实验。将所提的WACML模型去除WAMC后记为M,去除ACM损失后的模型记为A。消融实验结果如图3所示。
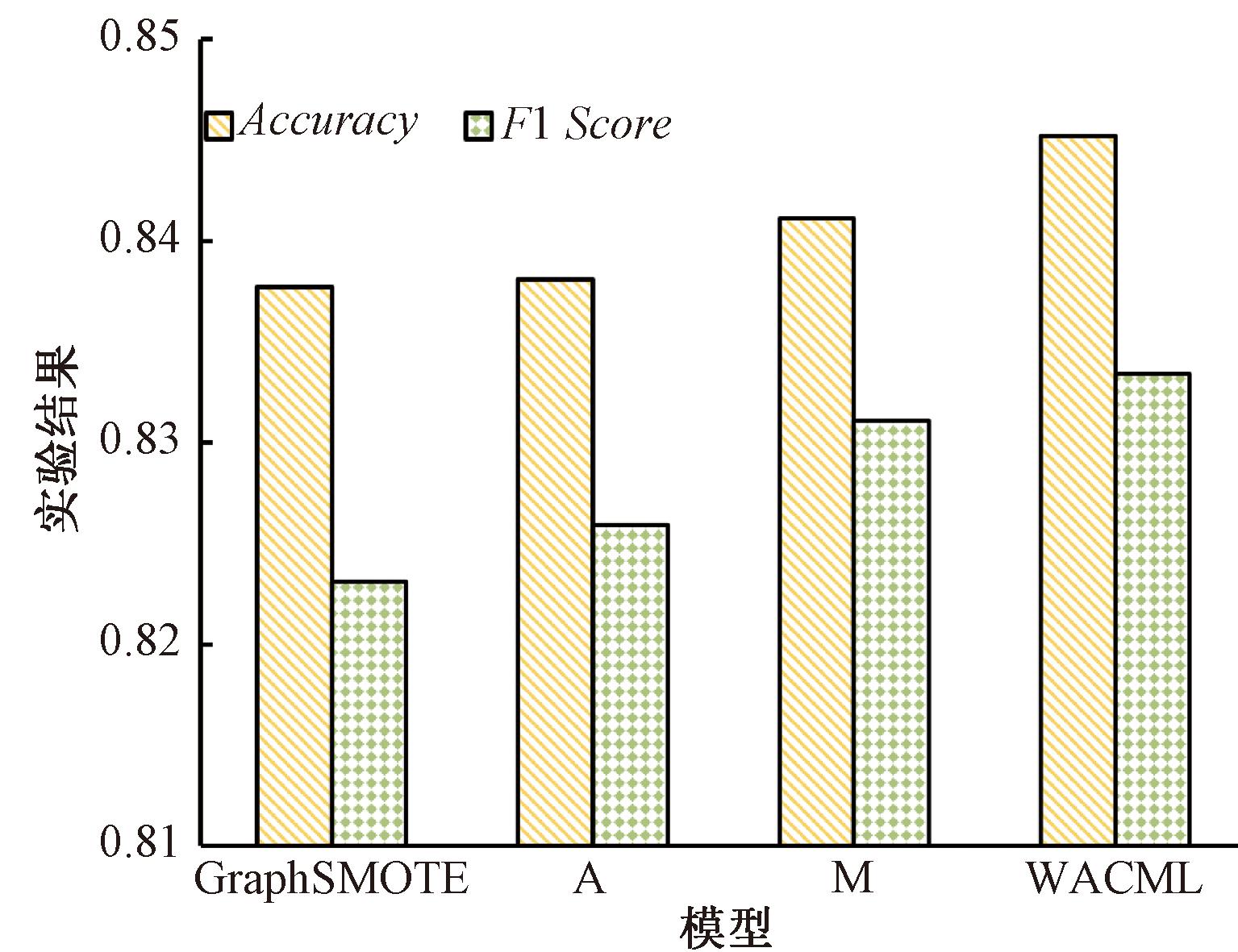
图3 消融实验结果
Figure 3 Results of ablation experiment
实验结果表明,在模型中引入WAMC和ACM损失是有效的,能够提升模型的分类效果。
3.2.4 比例系数p的影响
本节讨论了不同比例系数p对分类结果的影响。比例系数p的值分别取0.2,0.4,0.6,0.8和1.0。使用的数据集是从Kaggle平台获取的微博虚假账户数据集,在5个方法和WACML-GNN方法下进行实验,它们的F1Score和Accuracy结果分别如图4和图5所示。
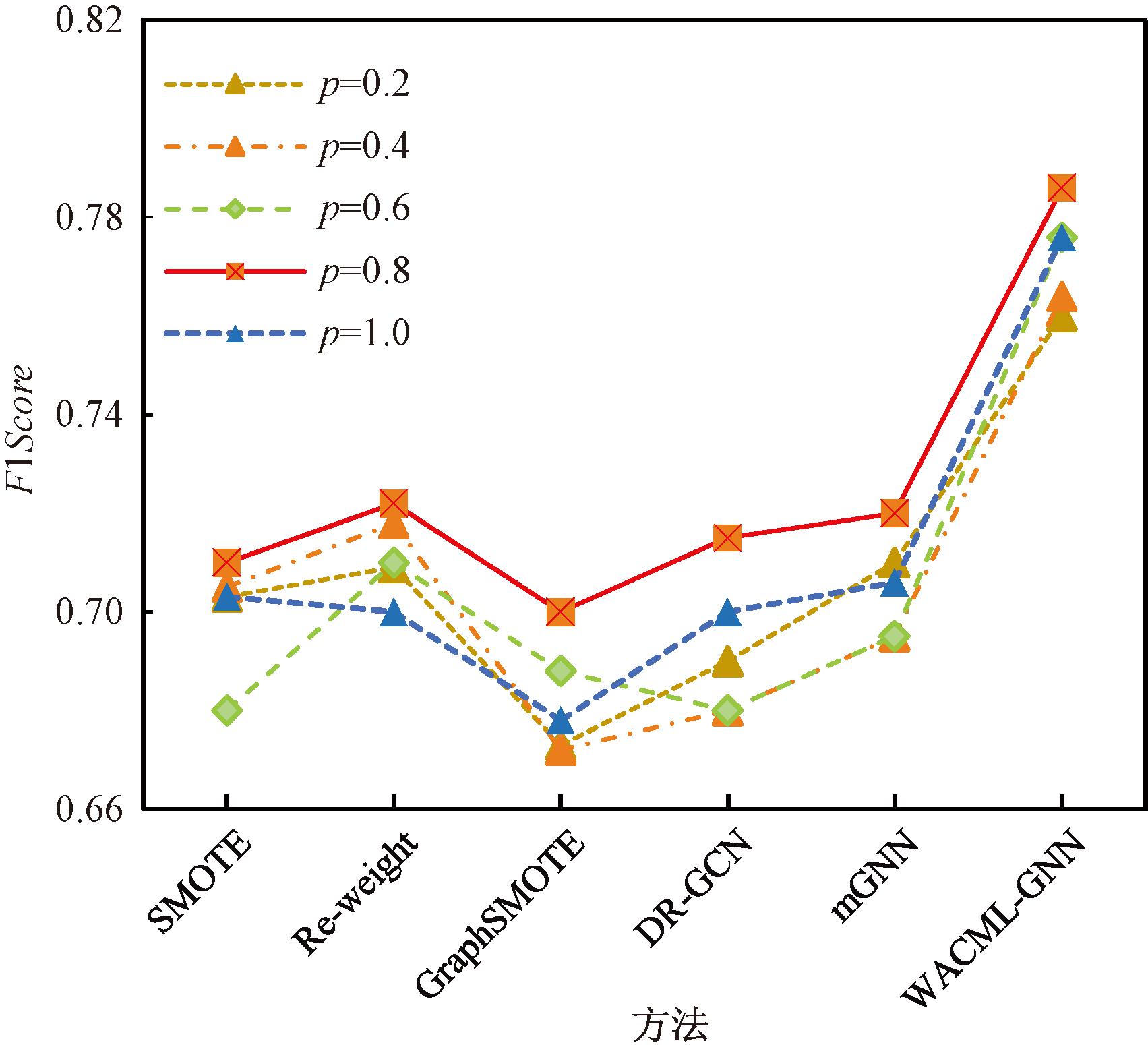
图4 WAMCL-GNN与5种方法下的F1Score折线图
Figure 4 F1Score line chart with WAMCL-GNN and five methods
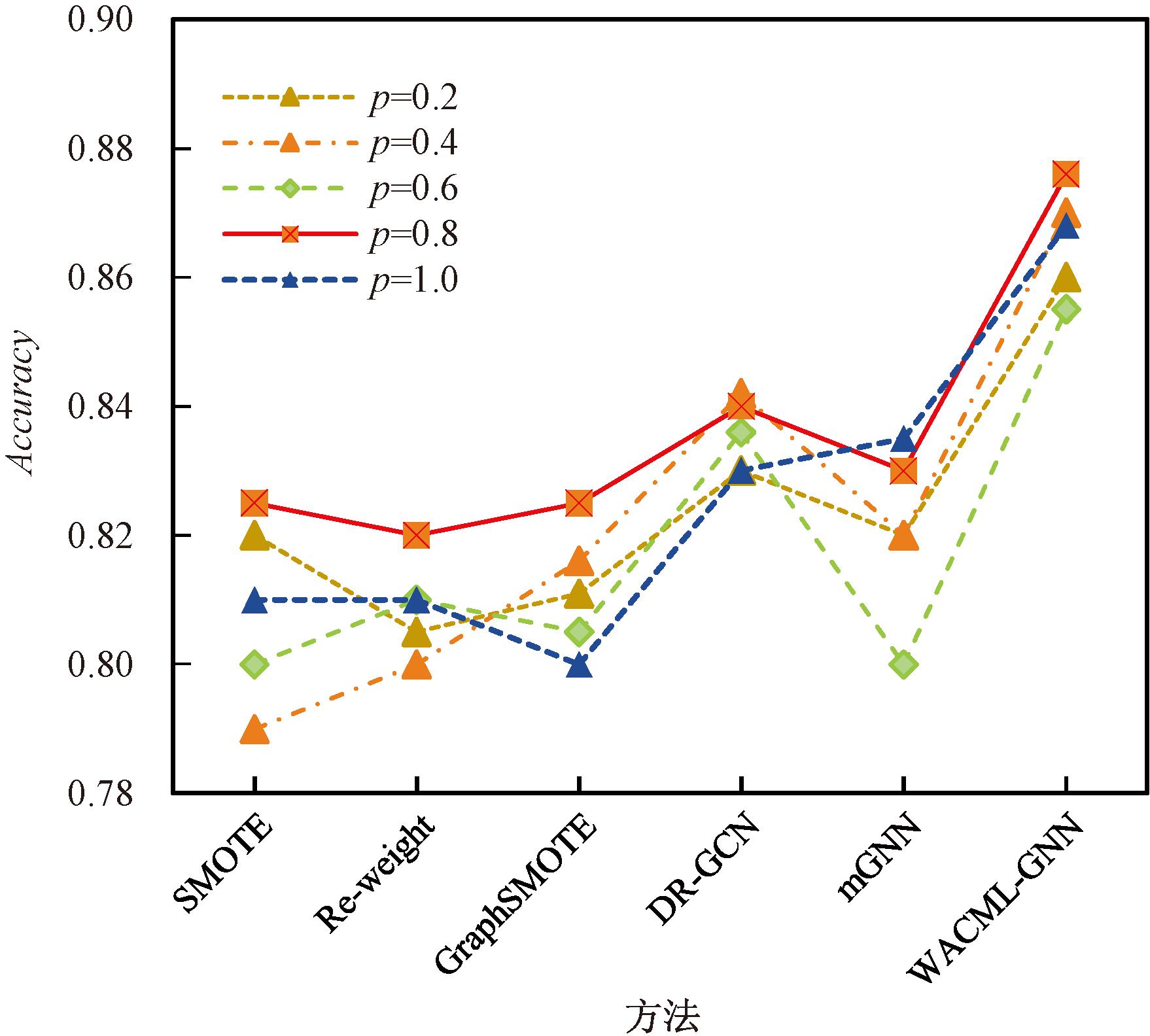
图5 WAMCL-GNN与5种方法的Accuracy折线图
Figure 5 Accuracy line graph with WAMCL-GNN and five methods
从图4和图5可以看出,当p为0.8时,几乎所有模型都实现了最佳的分类性能。通过实验发现,在不同数据集的聚合过程中,链接的大多数节点对节点的特征表示有不同的影响,这就导致p的取值也在影响最终的分类结果。
4 结论
(1)提出了基于少数类加权和异常连通性的不平衡节点分类算法。该方法增强了少数节点的特征表达能力,避免过度平滑现象。同时,引入ACML,提高了模型对链接性信息的敏感度。
(2)实验使用公开的微博、Twitter数据集验证了本文算法的有效性,相比于其他不平衡分类算法,WACML-GNN模型的ACC达到84.3%,相比GraphSMOTE算法的F1Score提升了1.25%。
(3)在下一步研究中,尝试利用边缘类型预测或节点表示学习,来解决少数类中节点表示不足的问题。此外,将不平衡分类与其他优化方法或学习方法相结合也是一种很有前途的研究方法。比如从算法层面进行代价敏感学习。但由于代价敏感学习需要考虑不同类型错误的成本矩阵,如何更加有效地降低学习成本也是未来研究的一个重要方向。
[1] GUO Z W, WANG H. A deep graph neural network-based mechanism for social recommendations[J]. IEEE Transactions on Industrial Informatics, 2021, 17(4): 2776-2783.
[2] MOHAMMADREZAEI M, SHIRI M E, RAHMANI A M. Identifying fake accounts on social networks based on graph analysis and classification algorithms[J]. Security and Communication Networks, 2018, 2018: 5923156.
[3] 田鸿朋, 张震, 张思源, 等. 复合可靠性分析下的不平衡数据证据分类[J]. 郑州大学学报(工学版), 2023, 44(4): 22-28.
TIAN H P, ZHANG Z, ZHANG S Y, et al. Imbalanced data evidential classification with composite reliability[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(4): 22-28.
[4] PARK J, SONG J G, YANG E. GraphENS: neighbor-aware ego network synthesis for class-imbalanced node classification[EB/OL]. (2022-11-09)[2024-01-04].https：∥specialsci.cn/detail/0425c6aa-3711-4e1f-b070-d4e9bea2eb9b?resourceType=0.
[5] ZHAO T X, ZHANG X, WANG S H. GraphSMOTE: imbalanced node classification on graphs with graph neural networks[C]∥Proceedings of the 14th ACM International Conference on Web Search and Data Mining.New York: ACM, 2021: 08826.
[6] WANG K F, AN J, ZHOU M C, et al. Minority-weighted graph neural network for imbalanced node classification in social networks of Internet of people[J]. IEEE Internet of Things Journal, 2023, 10(1): 330-340.
[7] SHI S H, QIAO K, CHEN C, et al. Over-sampling strategy in feature space for graphs based class-imbalanced bot detection[C]∥Companion Proceedings of the ACM on Web Conference 2024. New York: ACM, 2024: 06900.
[8] CHEN D L, LIN Y K, ZHAO G X, et al. Topology-imbalance learning for semi-supervised node classification[EB/OL]. (2021-10-08)[2024-01-04]. http:∥arxiv.org/abs/2110.04099.
[9] SONG J, PARK J, YANG E. TAM: topology-aware margin loss for class-imbalanced node classification[EB/OL]. (2022-06-22)[2024-01-04]. http:∥arxiv.org/abs/2206.12917.
[10] HAN H, WANG W Y, MAO B H. Borderline-SMOTE: a new over-sampling method in imbalanced data sets learning[M]∥Lecture Notes in Computer Science. Heidelberg: Springer Berlin Heidelberg, 2005: 878-887.
[11] MATHEW J, LUO M, PANG C K, et al. Kernel-based SMOTE for SVM classification of imbalanced datasets[C]∥IECON 2015 - 41st Annual Conference of the IEEE Industrial Electronics Society. Piscataway: IEEE, 2015: 1127-1132.
[12] WANG K F, AN J, YU Z B, et al. Kernel local outlier factor-based fuzzy support vector machine for imbalanced classification[J]. Concurrency and Computation: Practice and Experience, 2021, 33(13): 1-10.
[13] CHAWLA N V, LAZAREVIC A, HALL L O, et al. SMOTEBoost：improving prediction of the minority class in boosting[C]∥European Conference on Principles of Data Mining and Knowledge Discovery. Heidelberg: Springer, 2003: 107-119.
[14] BANDINELLI N, BIANCHINI M, SCARSELLI F. Learning long-term dependencies using layered graph neural networks[C]∥The 2010 International Joint Conference on Neural Networks (IJCNN). Piscataway: IEEE, 2010: 1-8.
[15] HAMILTON W L, YING R, LESKOVEC J, et al. Inductive representationlearning on large graphs[C]∥Advances in Neural Information Processing Systems. Lang Beach: NIPS, 2017:1025-1035.
[16] DEFFERRARD M, BRESSON X, VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering[C]∥Proceedings of the 30th International Conference on Neural Information Processing Systems. New York: ACM, 2016: 3844-3852.
[17] KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. (2017-02-22)[2024-01-04]. http:∥arxiv.org/abs/1609.02907.
[18] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16: 321-357.
[19] LIU L Q, LU Y, LUO Y, et al. Detecting "smart" spammers on social network: a topic model approach[EB/OL]. (2016-06-09)[2024-01-04]. http:∥arxiv.org/abs/1604.08504.
[20] TANG L, LIU H. Relational learning via latent social dimensions[C]∥Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2009: 817-826.
[21] BO Y, MA X L. Sampling reweighting: boosting the performance of AdaBoost on imbalanced datasets[C]∥The 2012 International Joint Conference on Neural Networks (IJCNN). Piscataway: IEEE, 2012: 1-6.
[22] SHI M, TANG Y F, ZHU X G, et al. Multi-class imbalancedgraph convolutional network learning[C]∥Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence. Yokohama: IJCAI, 2020: 2879-2885.