现代电力系统的快速发展使得电力系统的实际运行状态充满了不确定性,而这些不确定性也给电力系统的稳定运行带来了巨大挑战[1]。首先,电力系统在实际运行过程中可能会遭受到一些干扰,如故障、发电机投切等。如果这种扰动使电力系统不能过渡到一个新的平稳状态,那么电力系统将持续保持“失稳”状态,最终导致电力系统全面瘫痪。因此,需要在电力系统受到扰动后,及时并准确评估出系统的稳定性,指导工作人员采取相应措施应对系统“失稳”。其次,为了提高电力系统的运行质量和可靠性,避免电力系统因受到突发故障的威胁而导致大面积停电的可能,工作人员必须及时处理相关故障威胁。因此,如何在故障发生后立即准确定位、快速清除故障以达到快速恢复的目的是至关重要的。
传统评估电力系统受扰动之后稳定性的方法主要有2种:时域仿真(time-domain simulation,TDS)法[2]和暂态能量函数(transient energy function,TEF)法[3]。TDS法需要利用系统和扰动的完整信息建立高维非线性微分代数方程,并不适合用来实时地评估扰动后的电力系统稳定性。TEF法则可避免求解描述系统动态特性的微分方程组,但在实际应用过程中该方法存在模型简化、适应性相对较弱等问题[4-5]。
随着人工智能技术的快速发展以及广域测量系统(wide area measurement system,WAMS)的普及,可以通过离线批量训练相量测量单元(phasor measurement unit,PMU)数据建立评估模型,并将模型应用于在线实时稳定性评估中[6-7]。Yu等[8]利用长短期记忆(long short-term memory,LSTM)神经网络挖掘时间数据依赖性,提出了一种时间自适应的电力系统稳定性评估方案。Yan等[9]提出了一种基于卷积神经网络(convolutional neural network,CNN)模型的离线电力系统稳定性评估方案,该方案可以在模拟时间结束前确定稳定性评估结果,但不适用于在线分析场景。
电力系统中故障定位方法主要分为基于阻抗的方法、基于行波的方法和基于机器学习的方法。基于阻抗的故障定位方法使用测量到的电压和电流来估计故障阻抗和故障位置,但该方法的精度会受到故障类型、不平衡负载、架空线路不均匀性、测量误差等因素的影响[10-11]。基于行波的方法借助于由断层产生的原始波和反射波的测量结果来进行故障定位,然而该方法需要较高的采样率和与测量设备进行通信的开销[12]。
随着人工智能技术的发展,多种机器学习模型也被用来实现电力系统中的故障定位[13]。Aslan等[14]提取故障后测量数据的频谱特征,将提取后的特征数据输入人工神经网络进行故障定位。Mora-florez等[15]采用多变量数据分析学习算法进行故障定位,从变电站测量的电压和电流波形中提取描述子,利用描述子对不同类型的故障训练不同的分类器,从而实现故障定位。Thukaram等[16]首先利用支持向量机对故障类型进行分类,然后使用神经网络识别故障位置。然而,随着可测数据数量的增加,传统的故障定位方法无法灵活地结合不同元件的测量数据,特别是在考虑数据丢失的情况下。此外,对于传统的机器学习方法来说,电力系统的拓扑很难建模,更谈不上对拓扑变化建模的可能性。
基于上述问题,本文提出了一种基于图神经网络(graph neural network,GNN)的电力系统运行状态分析与评估模型,首先利用长短时记忆网络对采集的存在不完整的电力系统时序数据进行填补,从而降低数据不完整性对电力系统运行状态的分析与评估造成的影响;其次对填补过后的电力系统量测数据进行图结构表示,准确描述电力系统元件之间的逻辑关系;最后基于图神经网络分别设计了用于故障定位的多分类器和用于稳定性评估的二分类器。
1 智能电网量测数据填补
电力系统的运行数据在传输过程中难免会因为故障等原因而丢失,这会对电力系统运行状态的分析和评估结果产生一定的影响。缺失的某个时刻的量测数据与此前若干时刻的数据具有一定的时序相关性,因此本文采用LSTM对缺失数据进行填补。LSTM作为循环神经网络(RNN)的改进算法,不但继承了RNN针对时序数据的记忆能力,并且解决了RNN无法处理长时序数据依赖的问题。LSTM在RNN的结构上增加了输送带,保存了过去的信息以及增加了3个门控单元,LSTM的每个单元结构如图1所示,式(1)～(6)描述了LSTM单元的工作原理。
i(t)=σ(Wix·x(t)+Wih·h(t-1)+bi);
(1)
f(t)=σ(Wfh·h(t-1)+Wfx·x(t)+bf);
(2)
g(t)=tanh(Wcx·x(t)+Wch·h(t-1)+bg);
(3)
o(t)=σ(Wox·x(t)+Woh·h(t-1)+bo);
(4)
(5)
h(t)=o(t)·tanh C(t)。
(6)
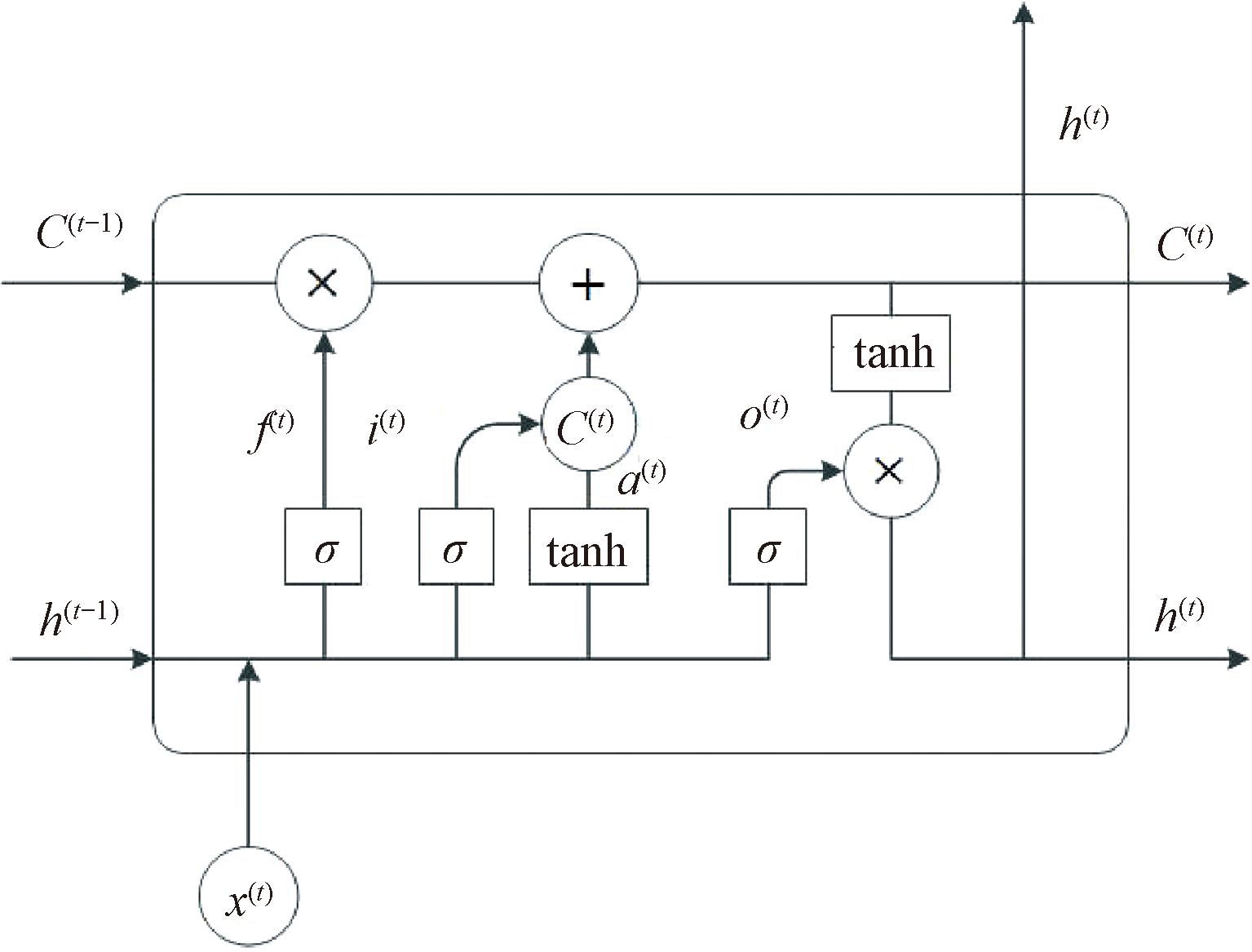
图1 LSTM的内部结构
Figure 1 Internal structure of LSTM
式中:i(t)为输入门,其状态不随时间改变;x(t)为神经网络在t时刻的输入;f(t)为遗忘门;g(t)、h(t)为激活函数;o(t)为输出门;C(t)为细胞状态;σ(·)和tanh(·)分别为Sigmoid函数和双曲正切激活函数。在t时刻,有若干个时序PMU数据按时间顺序输入并分别连接其输入层;再将输入层与LSTM层相连接,通过多个单元学习后连接输出层;最后通过输出层输出预测出的缺失值。可见,最终的输出中包含了前t-1个时刻内的所有隐藏层信息,反映了电力系统量测数据随时间变化的相关性。通过对t-1的选择和划分,可以完成某一时刻或者某一时间尺度内的缺失数据的预测,即完成数据的填补。
2 智能电网运行状态分析与评估模型
实际上,在电力系统受到扰动后元件会产生异常的工作状态,而某个元件的异常也会对其他元件的工作状态产生影响,即元件之间存在着某种逻辑关系。将电力系统的量测数据经过图结构化表示后,就可以利用GNN来对元件节点的特征进行分析,并结合对各个元件节点特征的分析结果来综合分析整个电力系统的运行状态,图2为本文模型的示意图。
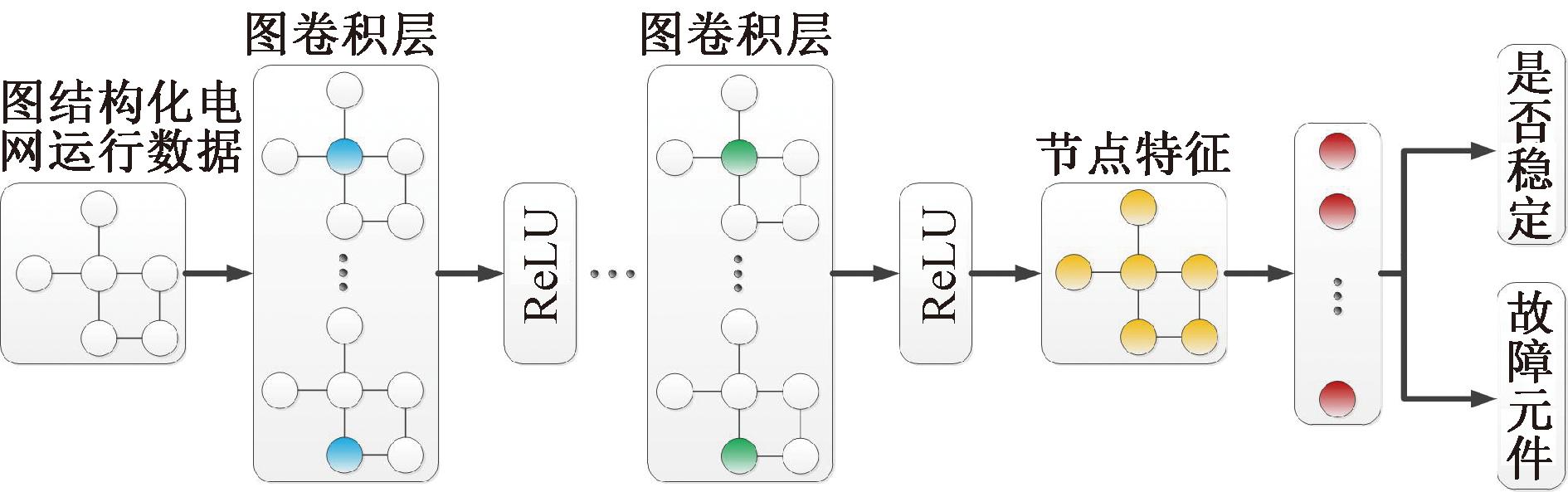
图2 本文模型示意图
Figure 2 The framework of the proposed model
对电力系统量测数据进行图结构化表示后,可以得到元件节点的运行状态信息以及代表节点间关系的邻接矩阵(元件实际的拓扑关系)。因此,可以将电力系统受扰动后的稳定性评估视为一个二分类问题,即通过对元件节点特征进行抽取后形成对于整个电力系统运行状态的全图表示,从而通过对全图表示的分类来实现电力系统受到扰动后的稳定性评估。而对于电力系统受到扰动后的元件节点故障定位,则可以将其视为一个多分类问题。通过将不同元件节点故障后的自身状态信息以及受其影响的其他元件状态信息进行聚合,就可以得到故障节点的特征表示,不同故障元件节点的特征表示将会被划分为不同的类别,只要准确地判断出故障元件节点的类别就能准确地实现元件的故障定位,因此本文采用GNN模型设计2种分类器,分别实现电力系统的稳定性评估和元件故障定位。
GNN的目标是学习节点的隐藏状态hv∈Rs,其中包含了当前节点v和其相邻节点的信息,当前节点v需要不断地从相邻节点收集信息然后用这些信息更新自己的隐藏状态hv,并最终得到适用于相关任务的输出结果ov,如节点标签等。hv和ov分别为
hv=f(xv,xco[v],hne[v],xne[v]);
(7)
ov=g(hv,xv)。
(8)
式中:f(·)为局部转移函数,是一个全局共享函数,根据输入的信息来更新节点状态;g(·)为局部输出函数,描述输出产生的方式;xv、xco[v]、hne[v]和xne[v]分别表示节点v的特征、与v相连的边的特征、与v相邻的节点的隐藏状态以及与v相邻节点的特征。GNN可以使用以下迭代方案计算状态:
Hw+1=F(Hw,X)。
(9)
式中:Hw表示H的第w次迭代的状态;X表示累积所有特征构建的矢量;F(·)表示全局更新函数。由于原始GNN模型对于隐藏状态更新的效率较低,因此本文采用图卷积网络(graph convolutional network,GCN)模型实现系统稳定性评估及故障定位。
传统的GCN模型传播规则可以表示为
H(l+1)=σ(AH(l)W(l))。
(10)
式中:H(0)=X表示第1层的输入,在本文中,X∈RN×C表示电力系统中元件的运行状态;N为元件的个数;C表示元件节点的特征数;A为表示元件间实际拓扑关系的邻接矩阵;W(l)则表示不同层的权重矩阵;σ(·)为激活函数,经过多层处理后就可以得到对于元件节点状态的向量表示。
可以发现元件节点的状态信息在通过每一层操作进行传播时并没有考虑元件节点的自身信息,而是只考虑到了与其相邻元件节点的状态信息,实际上无论实现电力系统的稳定性评估还是故障元件的定位,都需要充分地利用当前故障元件节点,需要在节点状态信息聚合时候增加该节点的状态信息,因此可以将式(10)改写为
(11)
式中:
表示将单位矩阵加到邻接矩阵中;
且
在设计合理的图卷积层数后就可以通过式(11)得到对于每个元件节点的向量表示,由于本文研究的电力系统稳定性评估与故障定位均属于对于整体图结构化的电力系统量测数据的分类问题,因此需要将输出的元件节点状态表示向量进行处理得到对于整图信息的描述才能最终实现整图信息的分类。在本文中,利用两层GCN模型来分别实现电力系统稳定性评估与故障定位,前向传播规则分别为
(12)
(13)
式中:
与
分别表示稳定性评估和故障定位的2个不同层的权重参数;F(·)表示将输出的元件节点状态表示向量进行平均池化操作,从而得到对于整图的特征表示。对于稳定性评估和故障定位,可以分别利用GCN模型实现一个基于整图信息的二分类模型和一个基于整图信息分类的多分类问题,因此2个模型的损失函数可以表示为
(14)
(15)
式中:lossG和lossN分别表示用于电力系统稳定性评估模型和故障定位模型的损失函数;pi表示第i个样本稳定的实际概率;
为第i个样本稳定的可能性;qij表示第i个样本中第j个元件出现故障的实际概率;
表示第i个样本中第j个元件出现故障的可能性。
3 实验结果与分析
针对提出的基于图神经网络的电力系统运行状态分析与评估模型,本文在IEEE39总线电力系统模型中进行仿真验证,该系统包含39总线、10台发电机,并基于此系统模型生成了不同元件发生故障后的5 s内的时序数据。
3.1 模型收敛性验证
如图3所示,当采用的学习率设定为0.000 1时,稳定性评估模型经过5 000次迭代并未完全达到收敛目标。当学习率提升至0.000 5,模型在迭代过程中表现出显著的损失减少趋势,且在经过5 000次迭代后,损失值已有效降低并表现出稳定的态势。针对故障定位模型,当学习率被设定为0.005时,尽管历经5 000次迭代模型趋于稳定,但此时的损失水平依然相对偏高。然而,当学习率进一步调整至0.008或0.010时,模型在经历同样的迭代次数后,不仅损失值急剧下降,而且在5 000次迭代后达到并维持在一个较低且稳定的水平。
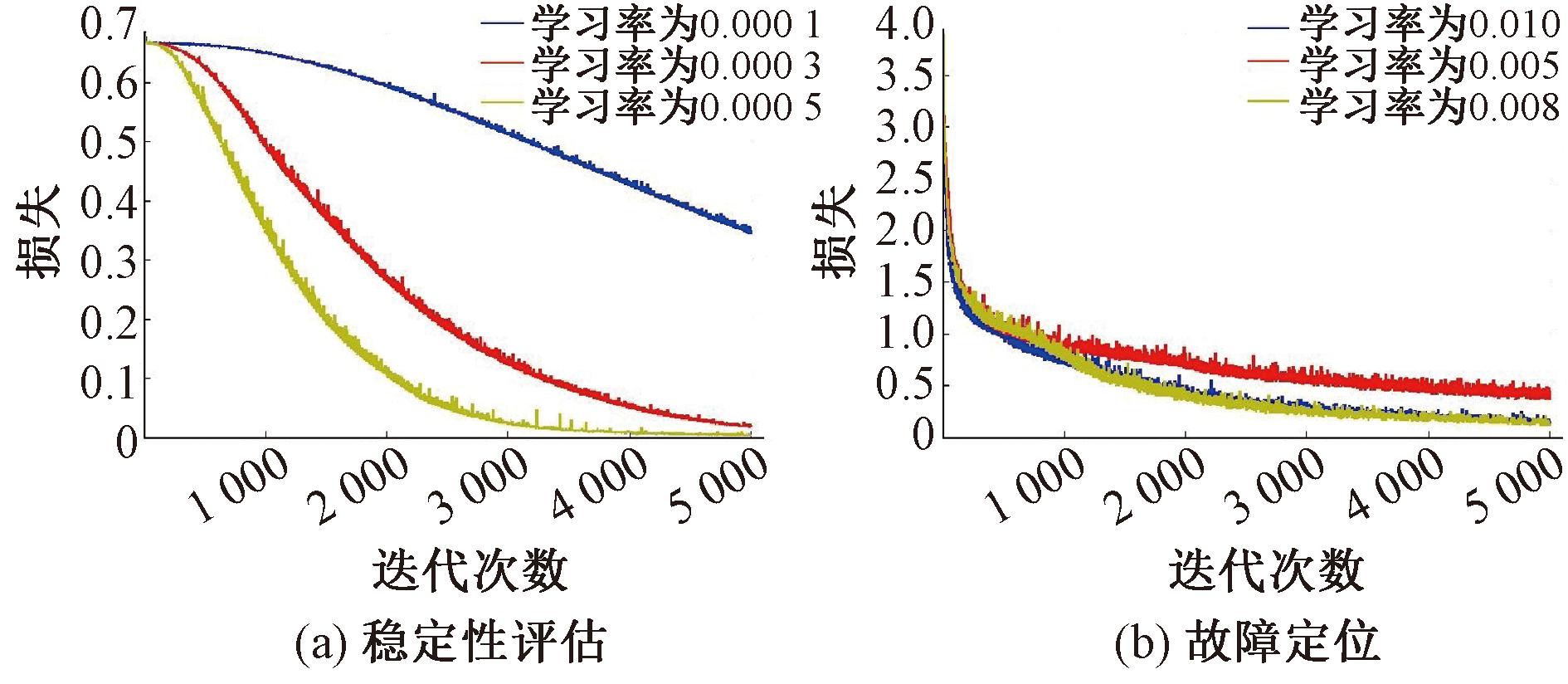
图3 本文模型稳定性评估的训练过程
Figure 3 Training process for stability evaluation
3.2 模型性能评估
为了评估LSTM对缺失数据的填补性能。本文对于元件量测时序数据设置了2种缺失率。本文选取了3种不同指标(MAPE、 MSE和MAE)来评估LSTM对缺失数据的填补性能。3种指标均可以用来评估填补值与真实值之间的偏离程度,值越小则表明模型对缺失数据填补的性能越好。
表1给出了所有元件量测数据填补后的平均MAPE、平均MSE以及平均MAE。由表1可知,LSTM对于PMU的缺失数据的填补值与真实值之间的偏差很小,这表明LSTM模型可以较为准确地填补缺失的PMU量测数据,保证电力系统运行状态分析和评估的准确性。为了进一步验证LSTM对于缺失数据填补的有效性,这里也利用门控神经单元(gated recurrent unit,GRU)网络分别对2种不同缺失率下的数据进行了填补。如表1所示,在缺失率为20%的情况下,LSTM对数据的填补性能要稍微好于GRU,而在缺失率为40%的情况下,GRU的性能则稍微好于LSTM。
表1 所有元件PMU量测数据在不同缺失率下填补的平均结果
Table 1 The average results of data filling with different missing rates
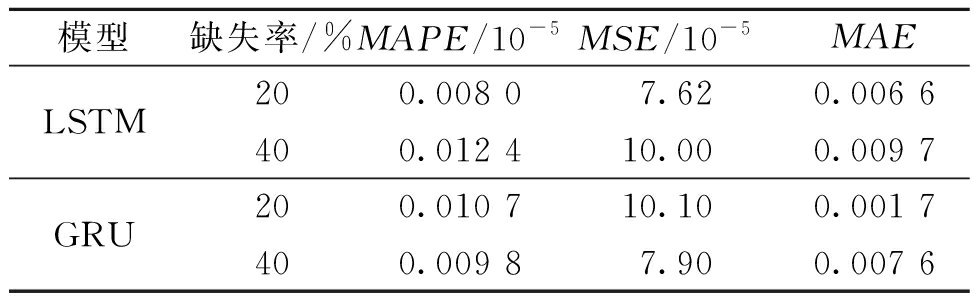
模型缺失率/%MAPE/10-5MSE/10-5MAELSTM200.008 07.620.006 6400.012 410.000.009 7GRU200.010 710.100.001 7400.009 87.900.007 6
为了验证所提出的稳定性评估与故障定位模型的性能,本文选取4种不同的测试集分别对模型性能进行验证,并用准确率来评价稳定性评估的性能[17],对于稳定性评估模型来说,准确率评价了二分类器能够正确识别出系统分别处于稳定或者不稳定状态的能力;而对于故障定位模型来说,准确率衡量了多分类器能够正确识别出哪个元件出现故障的能力。
表2为模型在4种不同测试集上的稳定性评估和故障定位准确率。如表2所示,当进行稳定性评估时,模型在测试集B上的准确率相对较低,但仍在0.98以上。当选取测试集D作为测试集时,准确率可达0.995 3。对于母线的故障定位来说,模型在测试集D上的准确率相对较低,但仍在0.98以上。当选取测试集C作为测试集时,准确率可达0.990 8。对于发电机的故障定位来说,测试集A的准确率相对较低,但也在0.9以上。当选取测试集C作为测试集时,准确率可达0.993 2。
表2 在4种不同测试集上的稳定性评估及故障定位准确率
Table 2 Stability evaluation and fault localization accuracy on four different test sets
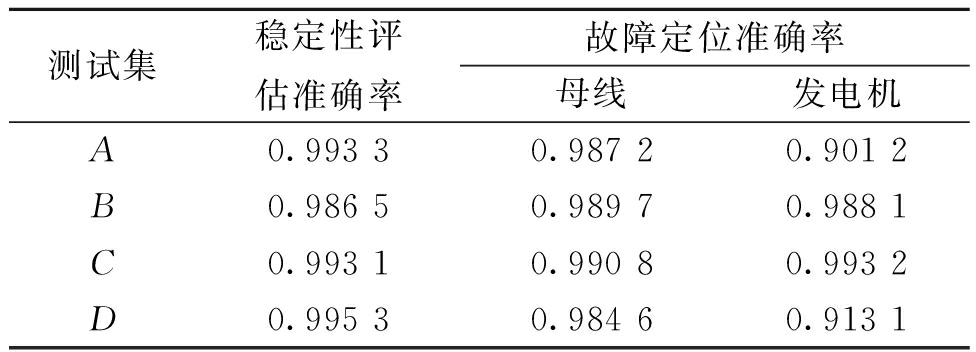
测试集稳定性评估准确率故障定位准确率母线发电机A0.993 30.987 20.901 2B0.986 50.989 70.988 1C0.993 10.990 80.993 2D0.995 30.984 60.913 1
3.3 不同测量条件下的模型性能评估
当模型应用于现实电力系统运行状态的分析和评估时,测量条件并不一定能保证数据的充分性。当电力系统受到扰动之后,往往要求尽可能快地评估出系统的稳定性,这就要求模型输入的时间序列数据尽可能地短(在此小节的实验设置中,即要求输入的数据要小于5 s)。另外,在实际应用过程中PMU的实际部署会受到限制,这就会导致部分元件的数据测量不到。针对这些问题,本文进行了一个扩展验证,以验证所提模型在测量条件受限的情况下的性能表现。
从表3可以看出,尽管随着输入序列的时长逐渐缩短,稳定性评估的准确率呈现出一定的下降趋势,但是当输入序列的时长减少至0.1 s时,稳定性评估的准确率依然保持在0.98以上。同样,尽管随着输入序列的时长逐渐缩短,故障定位的准确率虽然也呈现出一定的下降趋势,但是当输入序列的时长减少至0.1 s时,元件故障定位的准确率依然保持在0.9以上,可见稳定性评估与故障定位模型在输入序列时长较短时依然具有很好的适用性。
表3 不同时长下稳定性评估与故障定位准确率
Table 3 Stability evaluation and fault localization accuracy of time serie with different lengths
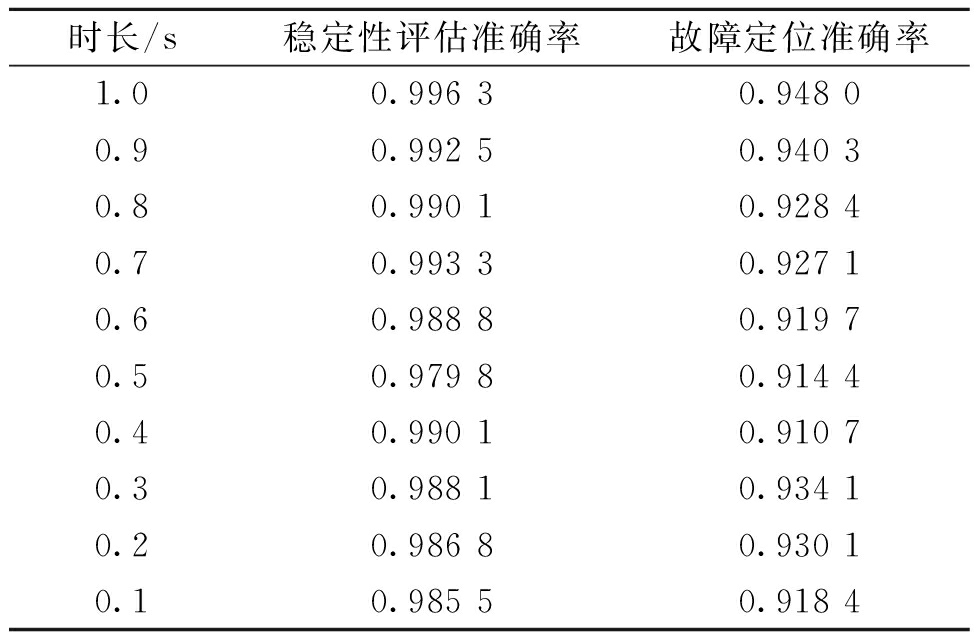
时长/s稳定性评估准确率故障定位准确率1.00.996 30.948 00.90.992 50.940 30.80.990 10.928 40.70.993 30.927 10.60.988 80.919 70.50.979 80.914 40.40.990 10.910 70.30.988 10.934 10.20.986 80.930 10.10.985 50.918 4
为了验证PMU配置受限条件下稳定性评估与故障定位模型的性能,设置了3种实验场景(场景1:仅收集到20条母线的信息或仅收集到5台发电机的信息;场景2:仅收集到1条母线的信息;场景3:仅收集到1台发电机的信息)。表4为不同PMV配置场景下稳定性评估与故障定位准确率。如表4所示,可量测到的元件数量变少,会导致系统稳定性评估的准确率呈现出下降的趋势,但是当仅可量测到一条母线或者一台发电机信息时,稳定性评估的准确率依然保持在0.97以上。PMU配置受限导致部分元件信息不能够收集到,尽管稳定性评估模型会正工作,但是无法判断出是由于哪个故障元件造成系统的不稳定,因此本文只验证模型在只有一半元件状态不可量测情况下的故障定位性能。如表4所示,在只有一半母线信息和一半发电机信息可以量测到的情况下,母线发生故障准确定位的平均准确率为0.960 9,而发电机发生故障准确定位的平均准确率为0.918 2。
表4 不同PMU配置场景下稳定性评估与故障定位准确率
Table 4 Stability evaluation and fault localization accuracy with different PMU configurations
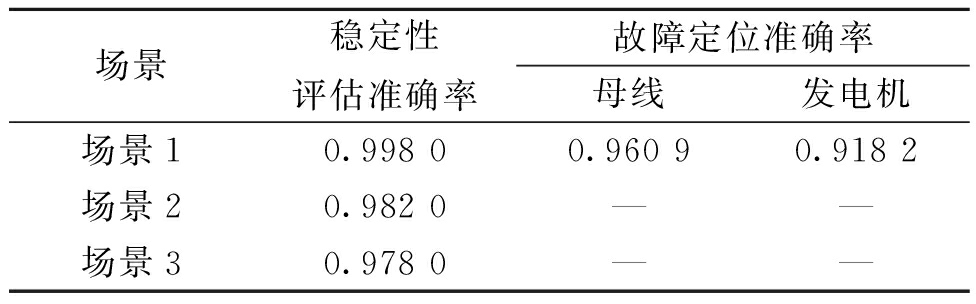
场景稳定性评估准确率故障定位准确率母线发电机场景10.998 00.960 90.918 2场景20.982 0——场景30.978 0——
3.4 消融实验
为了验证数据填补模块对所提模型性能的影响,分别比较了模型在无数据填补、利用LSTM进行数据填补以及利用GRU进行数据填补下的稳定性评估及故障定位的准确率(数据缺失率为20%),如表5所示。在未对缺失数据进行填补时,模型的稳定性评估和故障定位准确率分别为0.931 1和0.909 1。在采用LSTM进行数据填补后,模型的稳定性评估和故障定位准确率则分别提高到0.987 7和0.966 0。而在利用GRU对缺失数据进行填补后,模型的稳定性评估和故障定位准确率分别为0.981 0和0.961 2。可见LSTM与GRU表现出了几乎相同的性能。
表5 不同数据填补情况下稳定性评估与故障定位准确率
Table 5 Stability assessment and fault localization accuracy in different data filling scenarios
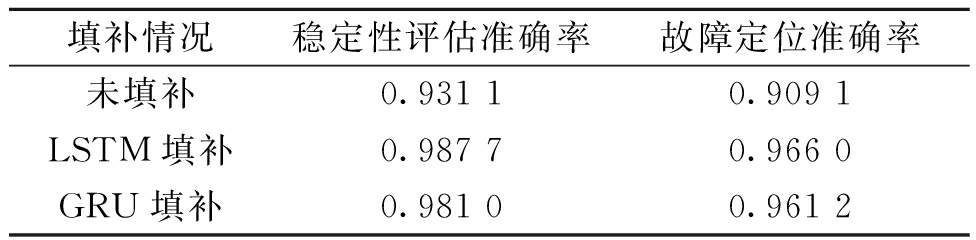
填补情况稳定性评估准确率故障定位准确率未填补0.931 10.909 1LSTM填补0.987 70.966 0GRU填补0.981 00.961 2
3.5 不同模型性能比较
为了进一步验证所提模型对于电网运行状态评估的有效性,选取了LSTM和CNN+LSTM进行稳定性评估和故障定位实验,如表6所示。
表6 不同时长序列下模型性能对比
Table 6 Performance comparison of models with different length time series
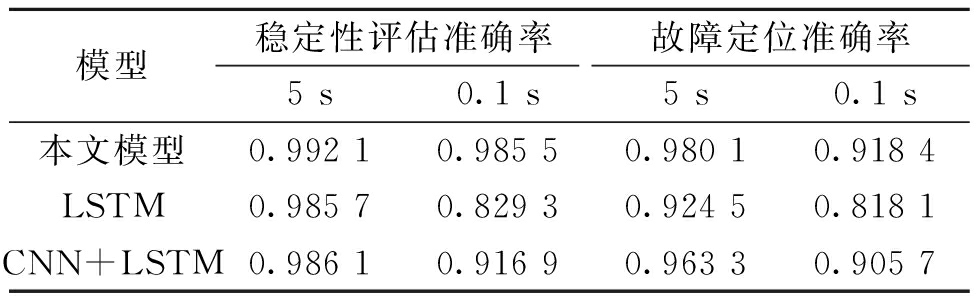
模型稳定性评估准确率故障定位准确率5 s0.1 s5 s0.1 s本文模型0.992 10.985 50.980 10.918 4LSTM0.985 70.829 30.924 50.818 1CNN+LSTM0.986 10.916 90.963 30.905 7
由表6可知,当可量测到5 s内的元件数据时,所提模型、LSTM以及CNN+LSTM均能在对系统进行稳定性评估时表现出良好的性能。量测数据长度的减少会使在时间尺度方向上提取的时序特征受到影响,但是如果能充分发掘元件之间的相互关系则可以保证稳定性评估的准确性。所提模型在仅可量测到0.1 s内的元件数据时,稳定性评估的准确率为0.985 5,依然表现出良好的性能。尽管LSTM此时准确率降低为0.829 3,但当利用CNN在时间、空间尺度进一步提取特征后,CNN+LSTM的准确率虽然有所降低,但依然保持在0.9以上。当仅可量测到0.1 s内的元件数据时,所提模型与CNN+LSTM进行元件故障定位的准确率均下降,但依然保持在0.9以上,而LSTM此时的准确率下降到0.818 1。
表7为一半元件数据可量测情况下模型性能对比。由表7可知,所提模型与CNN+LSTM更好地利用了元件之间的逻辑关系,在PMU配置受限时均能表现出良好的稳定性评估性能。在PMU配置受限时3种模型对母线发生故障准确定位的平均准确率分别为0.960 9,0.929 6和0.953 1,而发电机发生故障准确定位的平均准确率分别为0.918 2,0.893 9以及0.900 0,可见所提模型与CNN+LSTM更适用于此场景下的元件故障定位。
表7 一半元件数据可量测情况下模型性能对比
Table 7 Performance comparison of models with half of the components measured
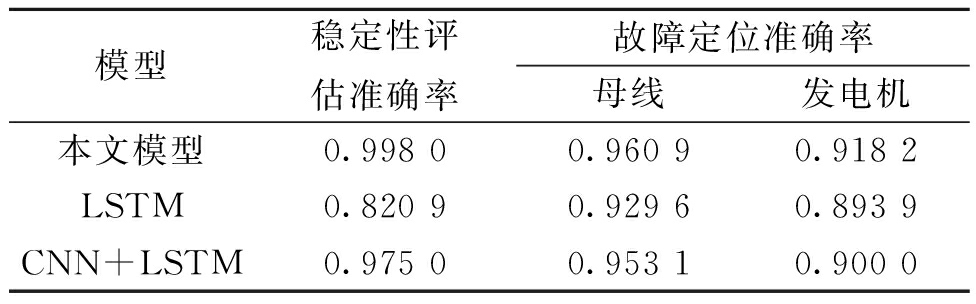
模型稳定性评估准确率故障定位准确率母线发电机本文模型0.998 00.960 90.918 2LSTM0.820 90.929 60.893 9CNN+LSTM0.975 00.953 10.900 0
3.6 实际场景验证
为了进一步验证所提模型对于真实场景的有效性,将模型在冀北电网系统中进行测试,这里主要针对各站点电压等级为220 kV的母线指标进行测试。由于实际电网运行过程中,稳定状态下的运行数据量要远远大于不稳定状态下的数据量,为了降低样本不均衡性对模型带来的影响,这里基于生成对抗网络(generative adversarial network,GAN)在实际不稳定数据的基础上进一步生成该类样本[18-19]。在对实际电网运行状态评估时,利用了系统受扰动(元件故障)后的5 s内的时序数据,由于只利用了部分主要220 kV母线的量测指标,因此评估准确率会比PMU完全配置条件下的结果有所降低。在只有部分220 kV母线指标可以量测到的情况下,系统稳定性评估的平均准确率为0.971 0,而母线发生故障准确定位的平均准确率为0.953 5。
4 结论
本文提出了一种基于图神经网络的智能电网运行状态分析与评估模型。首先利用LSTM对PMU量测的缺失数据进行了填补,进一步保证所提模型具有良好的评估性能。然后基于GNN分别设计了系统稳定评估模型和故障定位模型。实验结果表明,在量测条件受限情况下,所提模型在稳定性评估和故障定位的准确率均好于对比模型。
[1] SHI Z T, YAO W, ZENG L K, et al. Convolutional neural network-based power system transient stability assessment and instability mode prediction[J]. Applied Energy, 2020, 263: 114586.
[2] ZADKHAST P, JATSKEVICH J, VAAHEDI E. A multi-decomposition approach for accelerated time-domain simulation of transient stability problems[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2301-2311.
[3] OUBBATI Y, ARIF S. Securing transient stability assessment using single machine equivalent SIME method[C]∥2015 4th International Conference on Electrical Engineering (ICEE). Piscataway: IEEE, 2015: 1-4.
[4] GUPTA A, GURRALA G, SASTRY P S. An online power system stability monitoring system using convolutional neural networks[J]. IEEE Transactions on Power Systems, 2019, 34(2): 864-872.
[5] CHIANG H D. Foundations of the potential energy boundary surface method[J]. Direct Methods for Stability Analysis of Electric Power Systems: Theoretical Foundation, BCU Methodologies, and Applications, 2011:148-176.
[6] LI S Y, AJJARAPU V, DJUKANOVIC M. Adaptive online monitoring of voltage stability margin via local regression[J]. IEEE Transactions on Power Systems, 2018, 33(1): 701-713.
[7] GUO T Y, 
J V. Online identification of power system dynamic signature using PMU measurements and data mining[J]. IEEE Transactions on Power Systems, 2016, 31(3): 1760-1768.
[8] YU J J Q, HILL D J, LAM A Y S, et al. Intelligent time-adaptive transient stability assessment system[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1049-1058.
[9] YAN R, GENG G C, JIANG Q Y, et al. Fast transient stability batch assessment using cascaded convolutional neural networks[J]. IEEE Transactions on Power Systems, 2019, 34(4): 2802-2813.
[10] KRISHNATHEVAR R, NGU E E. Generalized impedance-based fault location for distribution systems[J]. IEEE Transactions on Power Delivery, 2012, 27(1): 449-451.
[11] MAJIDI M, ETEZADI-AMOLI M. A new fault location technique in smart distribution networks using synchronized/nonsynchronized measurements[J]. IEEE Transactions on Power Delivery, 2018, 33(3): 1358-1368.
[12] LOTFIFARD S, KEZUNOVIC M, MOUSAVI M J. Voltage sag data utilization for distribution fault location[J]. IEEE Transactions on Power Delivery, 2011, 26(2): 1239-1246.
[13] HOSSEINI Z S, MAHOOR M, KHODAEI A. AMI-enabled distribution network line outage identification via multi-label SVM[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5470-5472.
[14] ASLAN Y, 
Y E. Artificial neural-network-based fault location for power distribution lines using the frequency spectra of fault data[J]. Electrical Engineering, 2017, 99(1): 301-311.
[15] MORA-FLOREZ J, BARRERA-NUNEZ V, CARRILLO-CAICEDO G. Fault location in power distribution systems using a learning algorithm for multivariable data analysis[J]. IEEE Transactions on Power Delivery, 2007, 22(3): 1715-1721.
[16] THUKARAM D, KHINCHA H P, VIJAYNARASIMHA H P. Artificial neural network and support vector machine approach for locating faults in radial distribution systems[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 710-721.
[17] WANG Q, BU S Q, HE Z Y, et al. Toward the prediction level of situation awareness for electric power systems using CNN-LSTM network[J]. IEEE Transactions on Industrial Informatics, 2021, 17(10): 6951-6961.
[18] 屈丹, 杨绪魁, 闫红刚, 等. 低资源少样本连续语音识别最新进展[J]. 郑州大学学报(工学版), 2023, 44(4): 1-9.QU D, YANG X K, YAN H G, et al. Overview of recent progress in low-resource few-shot continuous speech recognition[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(4): 1-9.
[19] 成科扬, 荣兰, 蒋森林, 等. 基于深度学习的遥感图像超分辨率重建方法综述[J]. 郑州大学学报(工学版), 2022, 43(5): 8-16.CHENG K Y, RONG L, JIANG S L, et al. Overview of methods for remote sensing image super-resolution reconstruction based on deep learning[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(5): 8-16.