在车辆电动化与智能化进程中,车辆的主动安全控制受到越来越多学者的关注[1]。从车辆横摆稳定性控制的角度分析,如果能提前获取车辆的横摆稳定性信息并加以干预,将有效提升车辆的主动安全性能。因此,如何获取车辆的横摆稳定性信息是一个亟待解决的问题[2]。
准确的横摆稳定性分析是车辆横摆稳定性控制的重要依据。目前常用的横摆稳定性分析方法是相平面法[3],它是在动力学模型的基础上,以车辆状态参数直接构建相平面,采用双线法[4]、菱形法[5]等划分相平面稳定域。周兵等[6]采用前、后轮侧偏角相平面分析车辆横摆稳定性,据此设计主动前轮转向系统和直接横摆力矩控制系统协调控制准则,提高了车辆的行驶稳定性。李子先等[7]针对质心侧偏角-质心侧偏角速度相平面的稳定域划分问题,考虑横摆角速度,提出联合双线法和横摆角速度法的稳定域划分方法。丛森森等[8]基于横向速度-横摆角速度相平面设计基础稳定域偏移的动态稳定域,判断横摆稳定性并控制车辆保持稳定。吴西涛等[9]根据质心侧偏角-横摆角速度相平面设计出基于包络线的横摆稳定性判据,将其添加到路径跟踪控制器的约束条件中,该方法在保证车辆稳定性的前提下,发挥了车辆的动力学极限。以上基于相平面法设计的车辆横摆稳定性分析方法的分析结果单一,只能将车辆划分为稳定或不稳定状态,无法体现车辆横摆稳定性的动态变化。其次,这些横摆稳定性分析方法能否应用于实际车辆,很大程度上依赖于准确的车辆状态信号输入,而这些状态信号大部分无法通过普通传感器测量。
为解决车辆横摆稳定性分析过程中状态参数难以获取、分析结果单一等问题,本文基于相平面法构建车辆横摆稳定性评价指标——横摆稳定度,以描述横摆稳定性的动态变化;提出基于扩展卡尔曼滤波(extended Kalman filter,EKF)状态估计的车辆横摆稳定性分析方法,为横摆稳定性分析过程提供准确的状态参数输入。研究车辆的横摆稳定性分析方法可以为车辆的主动安全控制提供一定的依据。
1 车辆横摆动力学模型
1.1 车辆二自由度模型
车辆的横摆稳定性研究一般需要考虑侧向运动和横摆运动,因此采用二自由度模型描述车辆。如图1所示,o为车辆质心位置,oxy为车辆坐标系。则车辆质心的侧向、横摆运动微分方程为
(1)
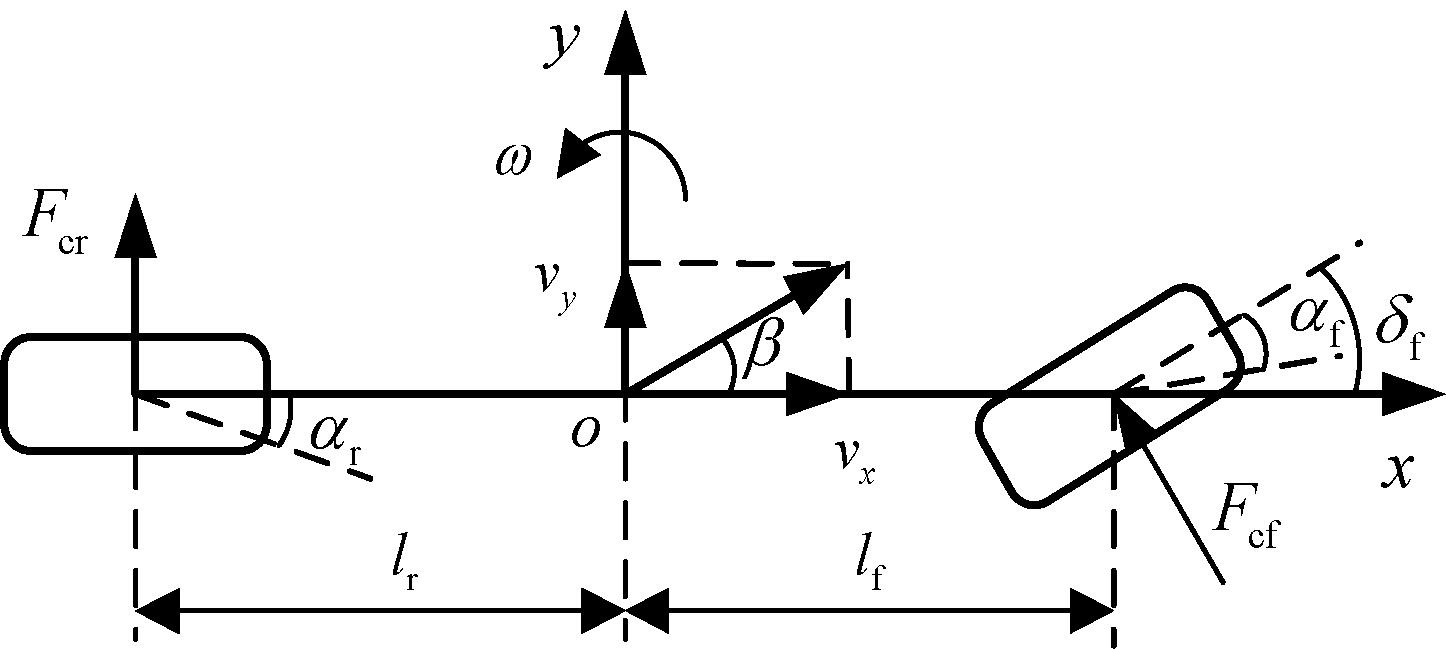
图1 单轨二自由度车辆模型
Figure 1 Monorail two-degree-of-freedom vehicle model
式中:m为车辆的质量,kg;β为车辆的质心侧偏角,rad;vx为车辆的纵向速度,m/s;ω为车辆的横摆角速度,rad/s;Fcf、Fcr分别为前、后轮的轮胎侧向力,N;δf为车辆的前轮转角,rad;Iz为车辆绕z轴的转动惯量,kg·m2;lf、lr分别为车辆质心到前、后轴的距离,m。
1.2 轮胎侧向力模型
采用Pacejka魔术公式轮胎模型[10]计算轮胎侧向力,并引入路面附着系数,当轮胎侧向力作为魔术公式的输出变量时,其表达式为
(2)
式中:μ为路面附着系数;αf、αr分别为前、后轮胎侧偏角,rad;B、C、D、E均为魔术公式轮胎模型参数。
当轮胎侧偏角数值不大(|α|≤5°)时,轮胎侧向力与侧偏角之间近似呈线性相关:
(3)
式中:Ccf、Ccr分别为前、后轮轮胎侧偏刚度,N/rad。
车辆前、后轴侧偏角可表示为
(4)
2 基于相平面法的横摆稳定性指标
2.1 相平面建立
结合式(1)、式(2)得到关于β、ω的二阶自治系统:
(5)
在确定的工况参数vx、μ、δf下,以不同初始条件(β(0),ω(0))绘制车辆系统的相轨迹,即可获得车辆的
相平面,图2为vx=60 km/h,μ=0.8,δf=0°工况下的相平面。
图2 
相平面
Figure 2 
phase plane
2.2 基于MLP的工况自适应稳定域
图2为
相平面。采用双线法[4]划分相平面稳定域,图2中两条虚线之间的区域为双线法确定的稳定域,可表示为
(6)
式中:B0、B1、B2均为稳定域边界系数,采用初始稳定相点法[11]求解。
vx、μ和δf会影响双线法划分的稳定域边界位置,所以不同工况的稳定域边界系数并不相同[12]。为获取不同工况下的稳定域边界系数,首先确定3个工况参数的变化范围和变化步长,得到550个典型工况,如表1所示。分别绘制典型工况的相平面,并求解稳定域边界系数及平衡点坐标
考虑到相平面的平衡点位置基本在
直线上[13],所以只记录平衡点的横坐标βb。记录各个典型工况的稳定域边界系数B0、B1、B2和平衡点横坐标βb,即可得到一个大小为550的相平面稳定域数据集。
表1 参数的变化范围及步长
Table 1 Variation range and step size of parameters
参 数 取 值 步 长 路 面 附 着 系 数 μ 0 . 2 ～ 1 . 0 0 . 2 前 轮 转 角 δ f / ( ° ) - 1 0 ～ 1 0 2 . 0 纵 向 速 度 v x / ( k m · h - 1 ) 3 0 ～ 1 2 0 1 0 . 0
由于工况参数与稳定域系数之间是多输入多输出关系,两者之间的表达式难以求解。为了方便实际使用,采用MLP深度神经网络拟合工况参数与稳定域系数之间的关系。
MLP深度神经网络结构如图3所示,其在单层神经网络的基础上添加若干个隐藏层,使其具备学习和处理非线性函数关系的能力[14]。将550个典型工况对应相平面稳定域数据集用于MLP深度神经网络训练与验证,训练集与验证集数据比例为7∶3。训练完毕后,保存最优权重用于下一步的车辆横摆稳定性分析。
图3 MLP深度神经网络结构
Figure 3 MLP deep neural network structure
2.3 横摆稳定性评价指标
定义横摆稳定度描述车辆横摆稳定性的动态变化,图4为横摆稳定度计算解释图。采用车辆状态点
平衡点B(βb,0)分别与稳定域边界之间距离的比值定义横摆稳定度γ。
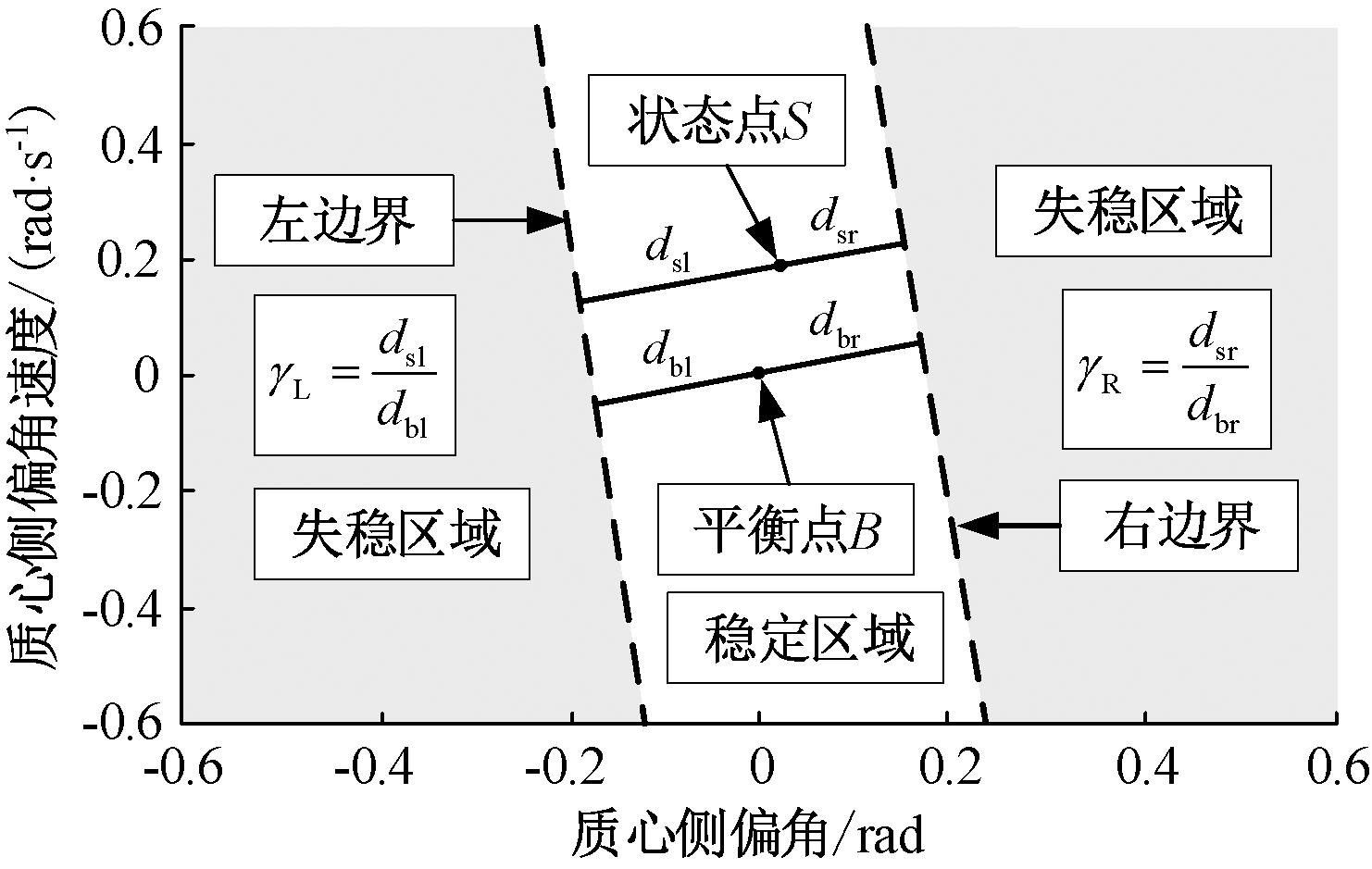
图4 横摆稳定度计算解释图
Figure 4 Explanation diagram of yaw stability calculation
在图4中,横摆稳定度的计算与稳定域边界有关,而稳定域边界包括左、右边界,所以会得到两个横摆稳定度值。为方便后续使用,选择在[0,1]上的横摆稳定度值,即两个值中的较小者作为使用值,其计算表达式为
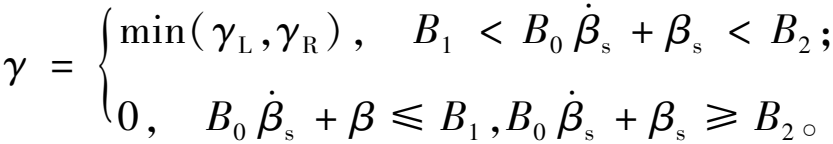
(7)
(8)
式中:γ∈[0,1],γ=1表示状态点与平衡点重合,此时车辆横摆稳定性最佳,γ=0表示状态点处于稳定域边界上或稳定域边界外,车辆已经失稳;γL、γR分别为通过左、右边界计算得到的横摆稳定度值。
3 基于状态估计的横摆稳定性分析
基于相平面法构建的横摆稳定性指标计算需要输入
信号。δf可以通过传感器测量,μ可以通过路面识别获得,而
信号无法通过简单传感器直接测量。为解决此问题,本章节基于EKF设计车辆状态参数估计算法。
3.1 扩展卡尔曼滤波状态估计算法
为保证车辆状态估计的实时性,同时考虑车辆正常行驶时均需符合小角度假设[15],所以将式(1)的非线性二自由度模型进行简化,同时结合式(3)、式(4)得到线性二自由度车辆模型:
(9)
为了估计vx,还需要引入纵向运动学方程:
(10)
式中:ax为纵向加速度,m/s2。
将式(9)与式(10)作为状态估计的状态方程。考虑到实际车辆的加速度信号易于测量,故将观测方程设置为
(11)
式中:ay为侧向加速度,m/s2。
结合式(9)～(11)可得标准化的状态方程和观测方程:
(12)
式中:x(t)为状态变量,
为观测变量,y(t)=ay;u(t)为模型输入,
为过程噪声;v(t)为测量噪声。
采用一阶泰勒展开式[16]对式(12)进行线性化:
(13)
式中:F(t)、H(t)均为非线性函数f(x(t),u(t),w(t))、h(x(t),v(t))对状态变量x(t)求偏导的雅克比矩阵。
EKF算法计算原理如图5所示,其在结构上包括预测模块和校正模块[17],设定初始条件后,EKF在每个采样点迭代估计,实时获取车辆状态参数。
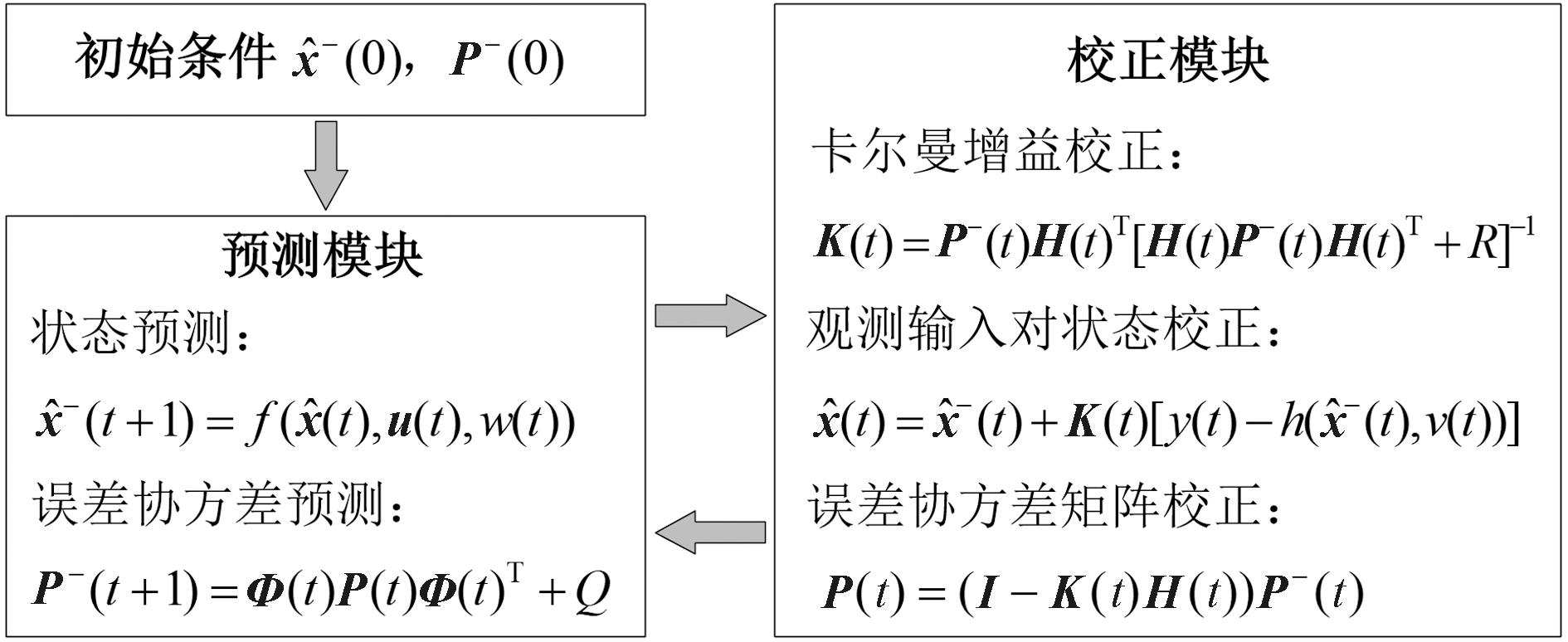
图5 EKF算法原理
Figure 5 Principle of EKF algorithm
3.2 基于状态估计的横摆稳定性分析流程
图6为基于状态估计的横摆稳定性分析方法结构图,该方法主要包括车辆状态估计与基于相平面法的横摆稳定性分析两部分。车辆状态估计模块根据车辆传感系统输入的ax、ay、δf信号,实时估计车辆质心侧偏角、质心侧偏角速度和纵向速度。基于相平面法的横摆稳定性分析模块将估计得到的车辆状态参数作为输入,同时结合μ、δf信号,实时分析车辆横摆稳定性状态,分析结果为车辆的横摆稳定性评价指标——横摆稳定度。
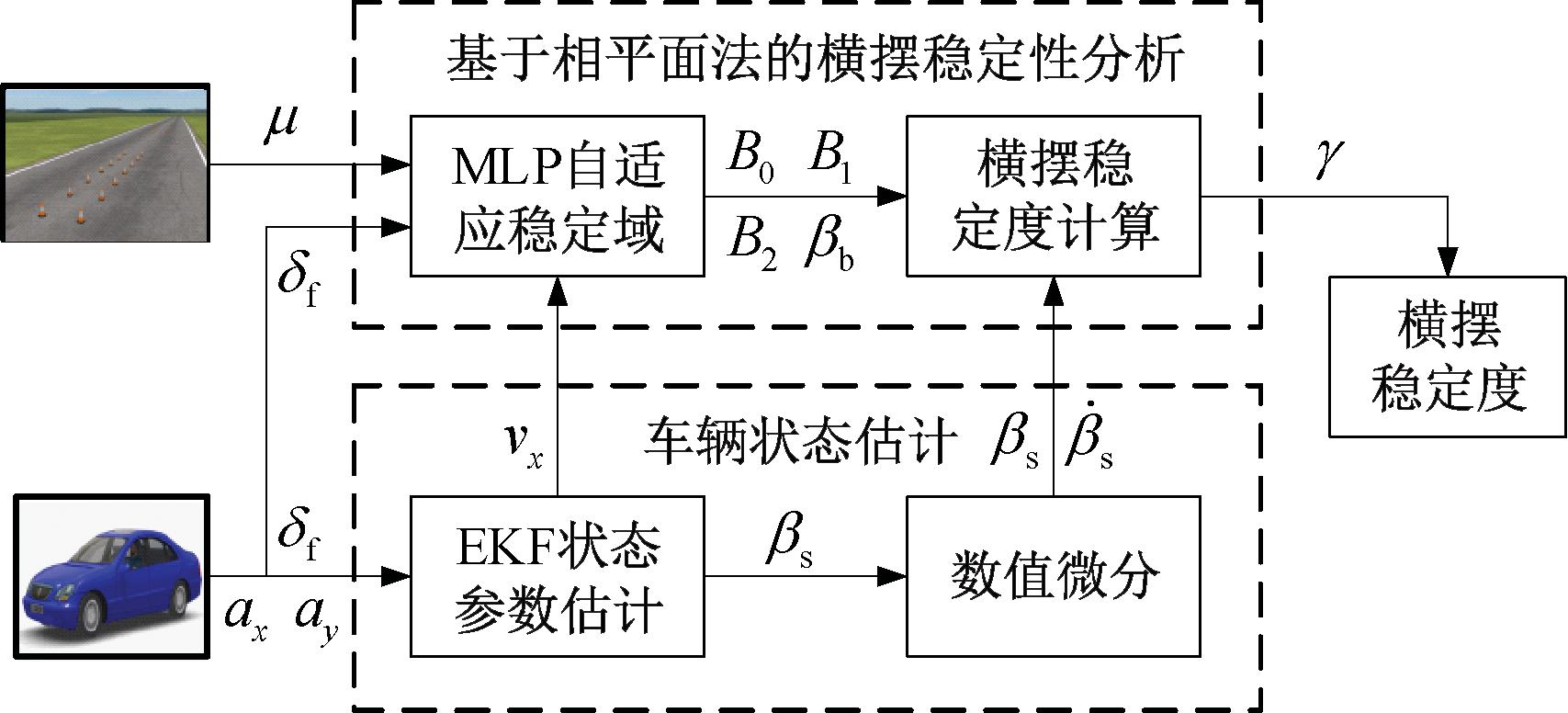
图6 基于状态估计的横摆稳定性分析方法结构图
Figure 6 Structure diagram of yaw stability analysis method based on state estimation
4 试验结果与分析
为验证所提出基于状态估计的横摆稳定性分析方法的有效性与实用性,在双移线工况[18]下分别进行仿真试验与实车试验。
4.1 车辆参数
图7为试验车辆,其配备华测CGI-430组合惯导,博世AP01方向盘转角传感器等,可以测量试验所需的ax、ay、δf、vx、β信号,vx、β可以通过组合惯导的测量输出量进行间接计算[19]：
(14)
图7 试验车辆
Figure 7 Test vehicle
式中:ve、vn分别为车辆的东、北向速度,m/s;φ为车辆横摆角(车辆坐标系),rad;φenu为车辆航向角(东北天坐标系),rad;ve、vn、φ和φenu均为组合惯导的测量输出量。
基于状态估计的横摆稳定性分析方法中使用的部分车辆动力学参数如表2所示。
表2 车辆动力学参数
Table 2 Vehicle dynamics parameters
参数 取值 整车质量 m/ kg 506. 900 转动惯量 Iz / (kg·m 2 ) 220. 057 前轮侧向刚度 Ccf / (N·rad - 1 ) - 16 766. 500 后轮侧向刚度 Ccr / (N·rad - 1 ) - 21 384. 806 质心到前轴距离 l f / m 1. 065 质心到后轴距离 l r / m 0. 835 转向系统传动比 i 21. 667
4.2 仿真试验
依据表2中的车辆参数建立CARSIM/Simulink仿真模型,在双移线工况下进行仿真试验。路面附着系数设置为0.85,车辆速度设置为100 km/h,采样时间为0.001 s。将基于EKF的状态参数估计值与CARSIM中车辆输出的实际值进行对比,并绘制车辆的横摆稳定度曲线,试验结果如表3和图8所示。
表3 100 km/h双移线仿真试验状态估计误差
Table 3 State estimation error of simulation test in 100 km/h double lane change
指 标 质 心 侧 偏 角 / ( ° ) 纵 向 速 度 / ( m · s - 1 ) 最 大 误 差 0 . 3 6 4 0 . 0 4 0 平 均 误 差 0 . 0 9 6 0 . 0 2 9
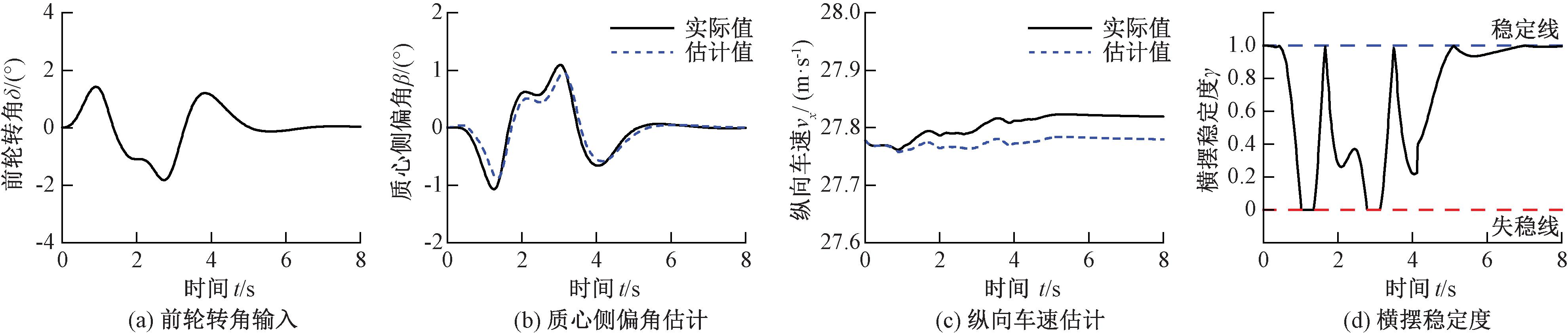
图8 100 km/h双移线仿真试验结果(线性)
Figure 8 Simulation test results of 100 km/h double lane change (umearity)
在100 km/h双移线仿真试验中,由图8(a)可得,试验中车辆前轮转角δf均小于2°,符合小角度假设。结合表3和图8(a)～8(c)可得,质心侧偏角估计的最大误差为0.364°,平均误差为0.096°,纵向速度估计的最大误差为0.040 m/s,平均误差为0.029 m/s,质心侧偏角与纵向速度估计的最大误差均出现前轮转角峰值附近,这是因为在高速转向时,车辆的非线性特性相对较强,导致估计误差有所上升。结合图8(a)和图8(d)可知,在前轮转角0°附近,车辆横摆稳定度值均接近1,此时车辆横摆稳定性最高;而在前轮转角峰值附近,车辆的横摆稳定度值均小于0.3,且分别在1.2,3.0 s附近,车辆的横摆稳定度值等于0,此时车辆已经横摆失稳,需要进行适当的横摆稳定性控制。
4.3 实车试验
控制试验车辆按照双移线轨迹行驶,试验路面为干燥水泥路面,路面附着系数取为0.75,车辆速度控制为30 km/h,采样时间为0.001 s。将基于EKF的状态参数估计值与试验车辆传感系统输出的测量值作对比,并绘制车辆的横摆稳定度曲线,试验结果如表4和图9所示。
表4 30 km/h双移线实车试验状态估计误差
Table 4 State estimation error of real vehicle test in 30 km/h double lane change
指 标 质 心 侧 偏 角 / ( ° ) 纵 向 速 度 / ( m · s - 1 ) 最 大 误 差 0 . 3 6 7 0 . 0 5 4 平 均 误 差 0 . 1 0 0 0 . 0 1 0
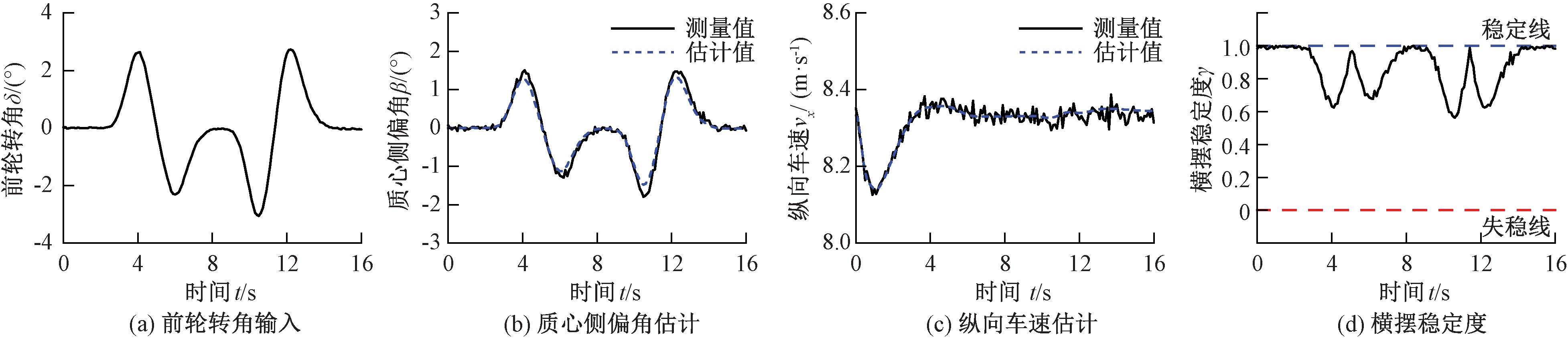
图9 30 km/h双移线实车试验结果
Figure 9 Real vehicle test results of 30 km/h double lane change
在30 km/h双移线实车试验中,结合表4和图9(a)～9(c)可得,质心侧偏角估计的最大误差为0.367°,平均误差为0.100°;纵向速度估计的最大误差为0.054 m/s,平均误差为0.010 m/s,估计值与实际测量值相近。由图9(d)可知,车辆的横摆稳定度值均大于0.5,说明在此工况下,车辆的横摆稳定性较高,不需要稳定性控制系统介入。分析图9(a)和图9(d)可知,车辆横摆稳定度与前轮转角绝对值呈现一定的相关性,说明在低速工况下,前轮转角是影响车辆横摆稳定性的重要因素。
5 结论
(1)基于状态估计的车辆横摆稳定性分析方法,能够依据估计的状态参数对车辆进行横摆稳定性分析,并体现出横摆稳定性的动态变化。
(2)在车速30 km/h双移线实车试验中,车辆的横摆稳定性与前轮转角绝对值呈现一定的相关性,说明低速工况下前轮转角是影响车辆横摆稳定性的重要因素。
[1] 张三川, 马啸. 基于轨迹加权预测的主动避撞安全距离模型及算法[J]. 郑州大学学报(工学版), 2022, 43(3): 104-110.
ZHANG S C, MA X. A safe distance model and algorithm for active collision avoidance based on weighted prediction of trajectory[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(3): 104-110.
[2] 《中国公路学报》编辑部. 中国汽车工程学术研究综述·2023[J]. 中国公路学报, 2023, 36(11): 1-192.
Editorial Department of China Journal of Highways.Review on China′s automotive engineering research progress：2023[J]. China Journal of Highway and Transport, 2023, 36(11): 1-192.
[3] 吴文娟. 基于相平面的车辆稳定性分析与协调控制研究[D]. 重庆: 重庆大学, 2021.
WU W J. Research on vehicle stability analysis and coordinated control based on phase plane[D].Chongqing: Chongqing University, 2021.
[4] 钟龙飞, 彭育辉, 江铭. 基于相平面的分布式驱动电动汽车稳定性控制[J]. 汽车工程, 2021, 43(5): 721-729, 738.
ZHONG L F, PENG Y H, JIANG M. Stability control of distributed driven electric vehicle based on phase plane[J]. Automotive Engineering, 2021, 43(5): 721-729, 738.
[5] 刘飞, 熊璐, 邓律华, 等. 基于相平面法的车辆行驶稳定性判定方法[J]. 华南理工大学学报(自然科学版), 2014, 42(11): 63-70.
LIU F, XIONG L, DENG L, et al. Vehicle stability criterion based on phase plane method[J]. Journal of South China University of Technology (Natural Science Edition), 2014, 42(11): 63-70.
[6] 周兵, 刘阳毅, 吴晓建, 等. 主动前轮转向和直接横摆力矩集成控制[J]. 浙江大学学报(工学版), 2022, 56(12): 2330-2339.
ZHOU B, LIU Y Y, WU X J, et al. Integrated control of active front steering and direct yaw moment[J]. Journal of Zhejiang University (Engineering Science), 2022, 56(12): 2330-2339.
[7] 李子先, 潘世举, 徐友春. 8轮分布式电驱动车辆AFS和DYC协同控制[J]. 汽车工程, 2023, 45(3): 409-420.
LI Z X, PAN S J, XU Y C. Coordinated control of AFS and DYC for 8-wheel distributed electric drive vehicle[J]. Automotive Engineering, 2023, 45(3): 409-420.
[8] 丛森森, 高峰, 许述财. 基于动态稳定域的车辆横纵向稳定性协同控制[J]. 汽车工程, 2022, 44(6): 900-908.
CONG S S, GAO F, XU S C. Cooperative control of vehicle lateral and longitudinal stability based on dynamic stability region[J]. Automotive Engineering, 2022, 44(6): 900-908.
[9] 吴西涛, 魏超, 翟建坤, 等. 考虑横摆稳定性的无人车轨迹跟踪控制优化研究[J]. 机械工程学报, 2022, 58(6): 130-142.
WU X T, WEI C, ZHAI J K, et al. Study on the optimization of autonomous vehicle on path-following considering yaw stability[J]. Journal of Mechanical Engineering, 2022, 58(6): 130-142.
[10] ALAGAPPAN A V, RAO K N, KUMAR R K. A comparison of various algorithms to extract magic formula tyre model coefficients for vehicle dynamics simulations[J]. Vehicle System Dynamics, 2015, 53(2): 154-178.
[11] 罗正. 电动轮驱动汽车差动助力转向与稳定性协调控制[D]. 长春: 吉林大学, 2019.
LUO Z. Coordination control of differential drive assist steering and vehicle stability control for four-wheel-independent-drive EV[D].Changchun: Jilin University, 2019.
[12] 张晨晨, 夏群生, 何乐. 质心侧偏角对车辆稳定性影响的研究[J]. 汽车工程, 2011, 33(4): 277-282.
ZHANG C C, XIA Q S, HE L. A study on the influence of sideslip angle at mass center on vehicle stability[J]. Automotive Engineering, 2011, 33(4): 277-282.
[13] LIANG J H, LU Y B, PI D W, et al. A decentralized cooperative control framework for active steering and active suspension: multi-agent approach[J]. IEEE Transactions on Transportation Electrification, 2022, 8(1): 1414-1429.
[14] 卢佳兴, 刘海鸥, 关海杰, 等. 基于双参数自适应优化的无人履带车辆轨迹跟踪控制[J]. 兵工学报, 2023, 44(4): 960-971.
LU J X, LIU H O, GUAN H J, et al. Trajectory tracking control of unmanned tracked vehicles based on adaptive dual-parameter optimization[J]. Acta Armamentarii, 2023, 44(4): 960-971.
[15] 寇发荣, 郑文博, 张新乾, 等. 采用状态扩展MPC与转角补偿的无人车路径跟踪控制[J]. 机械科学与技术, 2023, 42(9): 1533-1541.
KOU F R, ZHENG W B, ZHANG X Q, et al. Path tracking control of unmanned vehicle using state extended model predictive control and angle compensation[J]. Mechanical Science and Technology for Aerospace Engineering, 2023, 42(9): 1533-1541.
[16] 刘志强, 张晴. 自适应时域参数MPC的智能车辆轨迹跟踪控制[J]. 郑州大学学报(工学版), 2024, 45(1): 47-53.
LIU Z Q, ZHANG Q. Intelligent vehicle trajectory tracking control based on adaptive time domain parameter MPC[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(1): 47-53.
[17] 高自群, 谢桂芝, 周兵, 等. 多方法融合的汽车质心侧偏角估计[J]. 浙江大学学报(工学版), 2023, 57(12): 2391-2400.
GAO Z Q, XIE G Z, ZHOU B, et al. Estimation of vehicle sideslip angle based on multi-method fusion[J]. Journal of Zhejiang University (Engineering Science), 2023, 57(12): 2391-2400.
[18] 寇发荣, 杨慧杰, 张新乾, 等. 采用状态反馈的无人车路径跟踪横向控制[J]. 机械科学与技术, 2022, 41(1): 143-150.
KOU F R, YANG H J, ZHANG X Q, et al. A lateral control strategy for unmanned vehicle path tracking using state feedback[J]. Mechanical Science and Technology for Aerospace Engineering, 2022, 41(1): 143-150.
[19] WU Z W, YAO M L, MA H G, et al. Improving accuracy of the vehicle attitude estimation for low-cost INS/GPS integration aided by the GPS-measured course angle[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 553-564.