近年来,随着气候变化和城市化进程加快,我国城市内涝问题日益严重,严重威胁城市公共安全和可持续发展[1]。为此,构建准确的雨水管网模型以模拟和分析内涝过程变得尤为重要。常用的模型如SWMM(storm water management model)在实际工程中发挥着关键作用[2]。然而,这些模型通常需要大量的模型参数来描述复杂水文水动力过程,使得模型校核变得复杂和具有巨大挑战性[3]。
模型校核是雨水管网模型应用的关键基础[4]。传统的人工经验法在模型校核中存在效率低下和过于依赖个人经验的问题[5]。为提高模型校核效率和准确性,基于智能优化算法的自动校核方法开始被广泛应用,如梯度算法[6]、启发式算法[7]和混合算法[8]。然而,一些研究发现,基于优化的模型校核结果具有高度的案例相关性,受降雨事件[9]、目标函数[10]和校核参数类型[11]的影响显著,导致模型的泛化能力和可靠性不足,难以进行准确可靠的状态预报。
在城市雨水管理中,监测信息的不足是导致模型校核问题的主要原因之一。这主要体现在两个方面:①缺少对雨水管网监测的重视,管网中监测点数量十分有限;②监测点的布置主要依赖工程师的经验,缺乏优化空间布局的研究。由于雨水管网模型涉及的参数众多且具有较大的时空变异性,监测点不足或分布不合理会导致模型校核时出现“异参同效”的问题[12-13],这会严重影响模型对雨水管网状态的预测准确性和模型的泛化能力。因此,为确保雨水管网模型校核的准确性和可靠性,亟须深入分析监测点数量和布局对城市雨水管网模型校核的影响。
本文以丹麦贝灵厄镇的雨水管网模型[14]为例,结合基于模型校核的监测点优化布局方法,系统分析不同监测点数量和空间布局对模型校核特别是对内涝积水点模拟性能的影响,旨在为城市雨水管网监测系统的设计和模型构建提供科学参考。
1 材料与方法
1.1 雨水管网模型
本文的雨水管网模型和数据来自丹麦贝灵厄镇的排水系统数据集[14]。该数据集提供了SWMM模型和多年的降雨观测数据,用于科研目的。研究区域包括38个子汇水区、53根排水管、53个检查井节点和1个排放口,如图1所示。在SWMM模型中,采用Horton法模拟下渗过程,动力波方法计算汇流过程。基于已有的SWMM模型参数校核研究,并参考SWMM手册,选取了8类参数作为模型校核参数[15-17],如表1所示。在实际工程应用中,这些参数往往难以直接测量或无法测量,或具有较大时空变异性,因此需通过模型校核手段进行率定。对于该案例管网,每个子汇水区需校核7个参数,每根管道需校核1个参数,共需校核319个参数。
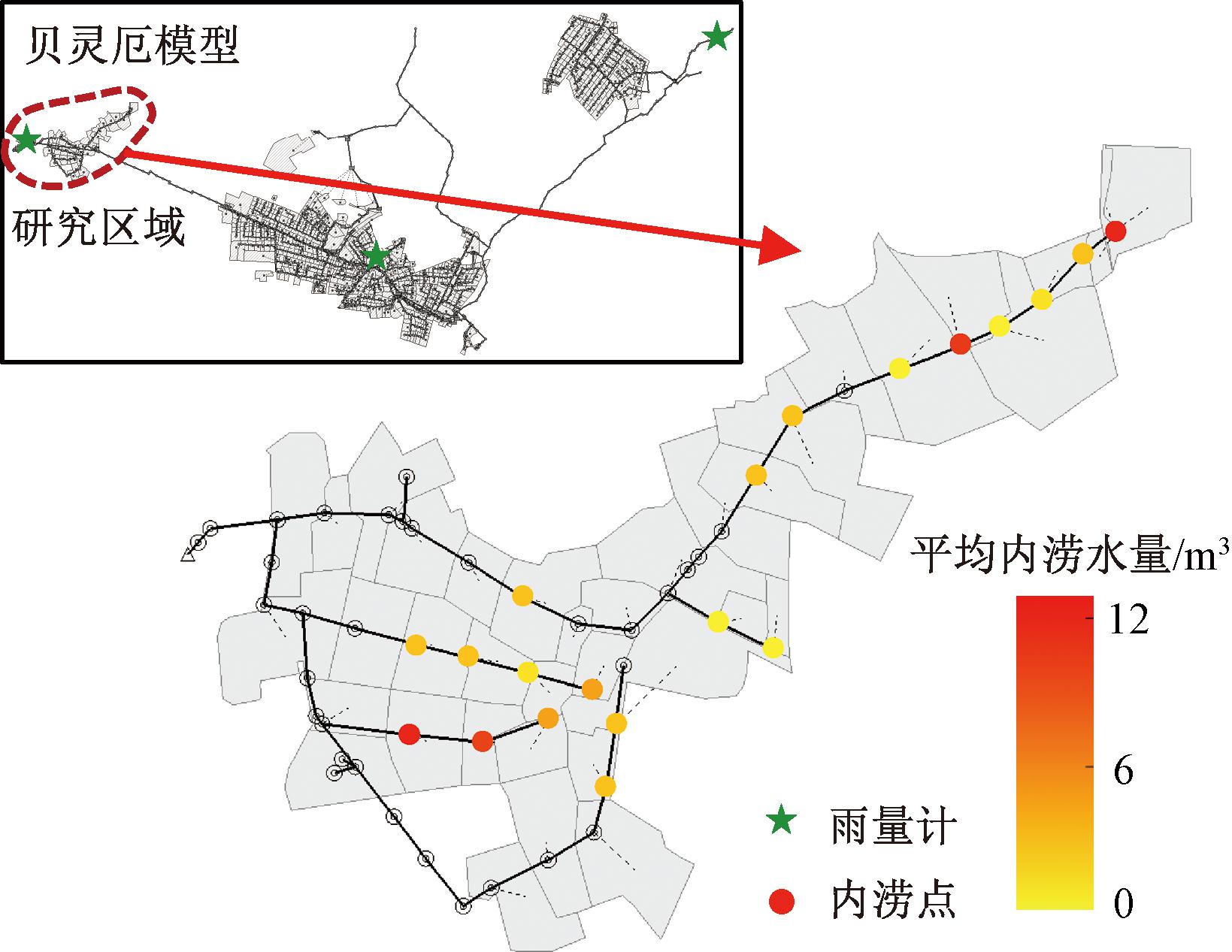
图1 案例雨水管网模型
Figure 1 Layout of urban drainage model
表1 雨水管网模型校核参数
Table 1 Uncertain parameters to be calibrated

校核参数 参数意义 取值 N-Imperv 不透水面曼宁系数 [0. 01,0. 04] N-Perv 透水面曼宁系数 [0. 1,0. 8] Dstore-Imperv/ mm 不透水面洼蓄量 [0. 2,5] Dstore-Perv/ mm 透水面洼蓄量 [2,10] MaxRate/ (mm·h - 1 ) 最大下渗能力 [20,80] MinRate/ (mm·h - 1 ) 最小下渗能力 [0,10] DecayCoeff / h - 1 下渗能力衰减系数 [2,7] Roughness 管道糙率 [0. 01, 0. 03]
需要说明的是,考虑到实际工程中难以准确确定模型参数的真实值,为便于分析监测信息对模型校核效果的影响,本文采用假定的模型参数数值作为真实值,构建基准模型生成“真实”状态数据和监测数据用于研究。
1.2 降雨事件选取
考虑到实际工程中更关注雨水管网模型对内涝积水的模拟情况,在贝灵厄数据集中选取2011 —2012年期间产生显著内涝的9场降雨事件进行研究,见表2(雨量计位置见图1,研究区域降雨数据取自最左侧雨量计)。采用基准模型对这些降雨事件进行模拟分析,所产生的内涝情况(发生内涝的检查井位置和平均内涝水量)如图1所示。考虑到模型校核与降雨事件特征显著相关[18-19],本文同时采用多场历史降雨事件的监测数据进行模型校核,以减少降雨事件差异性对模型校核结果的影响。同时,为充分考察校核模型的准确性和泛化能力,本文采用多场降雨事件进行验证。本文采用2011年的5场降雨事件C1~C5进行模型校核,涵盖的平均降雨强度为1.5~20.8 mm/h,产生内涝量为10~146 m3;采用2012年的4场降雨事件V1~V4进行校核模型验证,涵盖的平均降雨强度为5.5~16.7 mm/h,产生内涝量为19~169 m3,如表2所示。这些降雨事件涵盖了较广的降雨事件特征和内涝响应结果,可基本保证结果的一般性和可靠性。
表2 选取的降雨事件特征汇总
Table 2 Key characteristics of the selected rainfall events

降雨 事件 开始时间 结束时间 持续时长 / min 总降雨量 / mm 降雨强度/ (mm·h - 1 ) 平均值 最大值 内涝量/ m 3 C1 2011 - 06 - 06T05:15 2011 - 06 - 06T09:47 272 7 1. 5 72 17 C2 2011 - 07 - 09T14:13 2011 - 07 - 09T17:56 223 12 3. 1 84 110 C3 2011 - 08 - 06T18:16 2011 - 08 - 06T18:31 15 5 20. 8 60 10 C4 2011 - 08 - 26T21:31 2011 - 08 - 27T01:04 213 13 3. 7 120 146 C5 2011 - 09 - 04T22:11 2011 - 09 - 05T02:11 240 15 3. 7 72 59 V1 2012 - 06 - 29T04:33 2012 - 06 - 29T08:03 210 19 5. 5 108 169 V2 2012 - 07 - 14T16:04 2012 - 07 - 14T18:18 134 9 3. 9 96 53 V3 2012 - 07 - 27T22:37 2012 - 07 - 27T23:18 41 11 16. 7 84 103 V4 2012 - 08 - 22T03:02 2012 - 08 - 22T03:51 49 7 9. 1 96 19
1.3 模型校核方法
考虑到监测的便利性和成本,本文选取检查井内水位(简称水位)作为监测变量。模型校核的目标函数是最小化监测点水位变化的模拟误差。采用监测点处相对标准误差RRMSE (relative root mean square error)来量化监测点处模拟误差:

(1)
式中:![]() 为t时刻的观测水位;
为t时刻的观测水位;![]() 为t时刻的模拟水位;
为t时刻的模拟水位;![]() 为观测水位平均值。
为观测水位平均值。
由此,模型校核的目标函数为
(2)
式中:RRMSEobs为模型校核的目标函数值,即监测点处平均相对标准误差;R为用于校核的降雨事件总数;M为监测点数量;![]() 为第r场降雨事件中第m个监测点处模拟值的标准误差。RRMSE值越接近0表示模拟值和真实值越接近,目标函数值越小。
为第r场降雨事件中第m个监测点处模拟值的标准误差。RRMSE值越接近0表示模拟值和真实值越接近,目标函数值越小。
为最小化目标函数值,本文选取粒子群优化算法(particle swarm optimization,PSO)作为模型校核的求解器。该算法具有全局搜索能力强、收敛速度快、适应性强等特点,已在数值模型领域得到广泛应用[5]。
1.4 监测点优化布局方法
为分析监测信息对模型校核的影响,本文不仅关注于监测点处校核效果,更关注于校核后雨水管网模型的整体性能。因此,提出基于模型校核的监测点优化布局方法,以优化监测点布局,提高校核模型的整体性能。考虑到实际应用中主要关注雨水管网模型对内涝积水的模拟情况,雨水管网模型整体性能采用管网中所有可能发生内涝积水的检查井处水位模拟值与真实值吻合程度的函数来评价,即监测点优化布局的目标函数为最小化所有内涝积水处检查井水位模拟值与真实值的误差,采用相对标准误差RRMSE来量化,即
(3)
式中:RRMSEflood为监测点优化布局的目标函数值,即所有内涝节点处平均相对标准误差;N为所有用于校核的降雨事件中产生内涝的节点总数;![]() 为第r场降雨事件中第n个内涝节点处模拟值的标准误差。本文中,为系统分析监测点优化布局对模型校核的影响,假定所有检查井节点均为可选的监测点位置,即所有检查井内均可安装水位计进行水位全范围监测。
为第r场降雨事件中第n个内涝节点处模拟值的标准误差。本文中,为系统分析监测点优化布局对模型校核的影响,假定所有检查井节点均为可选的监测点位置,即所有检查井内均可安装水位计进行水位全范围监测。
根据上述定义的目标函数,本文所提监测点优化布局方法的基本思路:针对一种监测点布局方案,根据监测数据进行模型校核以确定模型参数数值,由此模拟模型中所有内涝节点处状态变化,与真实值进行对比以评估模型整体性能;进一步采用智能优化算法对不同监测点布局方案进行优化分析,得到模型整体性能最优的监测点布局方案。本文选用遗传算法(genetic algorithm,GA)作为监测点优化布局的求解器。GA算法具有可以在搜索空间中找到全局最优解、适用于非线性问题、可以处理多元化问题等特点,已在监测点优化设计领域得到广泛应用[20]。
本文基于模型校核的监测点优化布局方法的基本流程如图2所示。该方法包括两层优化求解过程,即外层的监测点布局优化(GA求解器)和内层的模型校核优化(PSO求解器)。利用外层GA求解器对设定监测点数量下的监测点布局进行优化,再根据某个个体设定的监测点布局情况利用PSO求解器对模型参数进行校核。由于外层优化的每一代的每一个个体均需进行内层的模型校核优化,导致该优化问题的计算需求急剧增加,计算耗时巨大。为提高该程序计算效率,本文采用蒙特卡洛随机模拟试验:预先计算5×105组不同参数组合下模型模拟值作为模型校核的初始粒子样本库(图2),即在每一次进行内层的模型校核优化时,首先从初始样本库中选择目标函数值较小的样本作为初始粒子,提高初始解质量,以提高模型校核的计算效率。同时,通过多次模型校核试验发现,当模型校核的目标函数值减小至0.25左右时,模拟结果与监测数据之间已拟合良好,由此在内层模型校核优化中设定PSO算法终止条件为目标函数值达到0.25。经对比分析,这两种措施可在保证优化结果相差不大的情况下使程序运算效率提升80%以上。
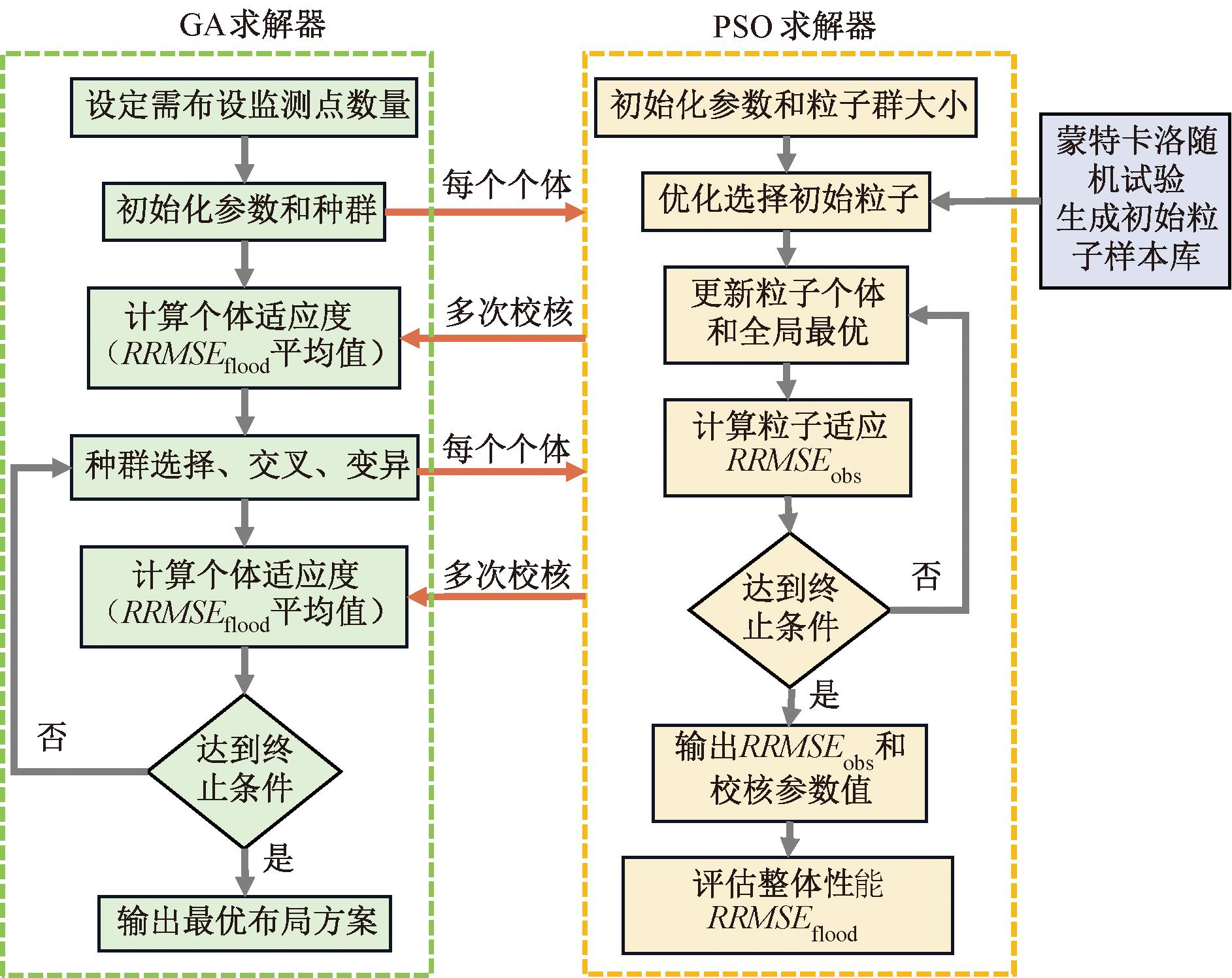
图2 基于模型校核的监测点优化布局方法流程图
Figure 2 Flowchart of the optimization method for sensor placement based on model calibration
此外,为减小优化算法随机性对模型校核结果的影响,每个监测点布设方案的模型校核计算并行进行5次后取平均值作为该方案的目标函数值。同时,为减少优化算法参数设置对优化结果的影响,采用多次数值试验确定了优化算法核心参数的合理取值。具体地,对于GA方法,种群数设为50,采用轮盘选择算子、均匀交叉算子和均匀突变算子,终止条件为20代目标函数不发生明显变化;对于PSO方法,惯性权重为1.1,学习因子为1.49,粒子个数为200,终止条件为RRMSEobs≤0.25。这些参数设置在案例研究中保持不变。
2 结果与分析
2.1 监测点优化布局对模型校核影响分析
首先,以5个水位监测点为例,分析监测点优化布局对模型校核的影响。采用图2所示方法,其基本思路:利用GA方法初始化水位监测点布局方案,其中针对每个布局方案,采用PSO方法进行模型校核(见式(2)),由此评估种群个体的适应度值(见式(3)),通过选择、交叉和变异操作迭代更新种群,最终得到最优的监测点布局方案,如图3所示。
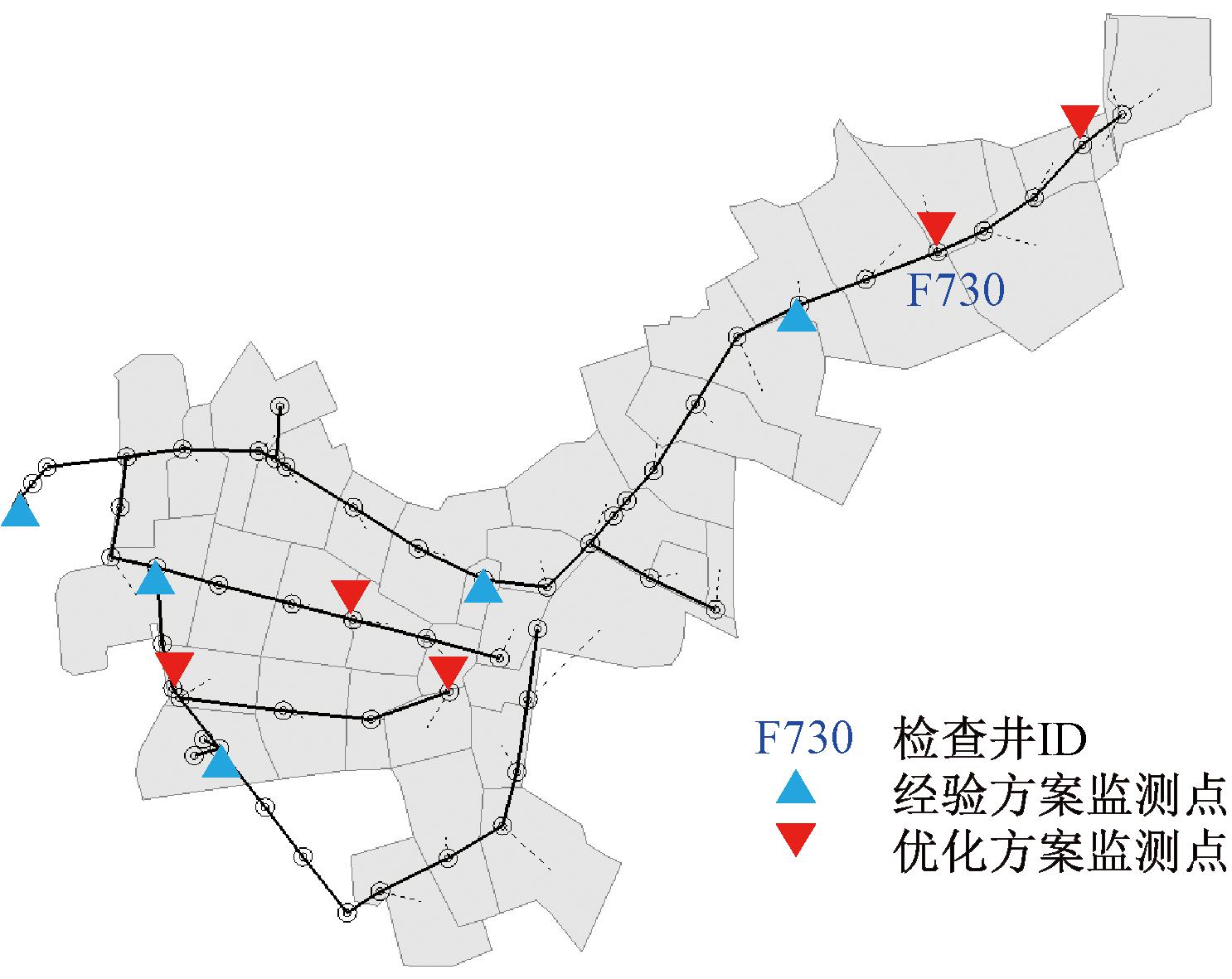
图3 5个监测点的监测点布局
Figure 3 Calibration models at flooding points for 5 sensors
同时,采用空间均匀分布的经验方法布置监测点,用以对比分析。这种经验布局方法的基本原理[21]:监测点处信息是上游水力状态的叠加,在空间上均匀布置监测点,从而使监测信息相对均匀地用于模型参数校核。考虑模型校核优化算法的随机性,同一监测方案下进行5次模型参数校核,并采用4场真实降雨事件进行验证分析。不同降雨事件的模型校核和验证结果对比见表3。
表3 5个监测点的校核模型内涝节点处性能对比
Table 3 Performance comparison of the calibration models at flooding points for 5 sensors

布 局 方 案 校 核 结 果 验 证 结 果 C 1 C 2 C 3 C 4 C 5 平 均 值 V 1 V 2 V 3 V 4 平 均 值 优 化 方 案 0 . 6 4 0 . 6 0 0 . 9 7 0 . 5 8 0 . 7 1 0 . 7 0 1 . 0 3 0 . 8 3 0 . 6 8 1 . 2 3 0 . 9 4 经 验 方 案 3 . 9 3 1 . 4 1 3 . 8 0 1 . 3 7 2 . 2 6 2 . 5 5 1 . 6 8 1 . 3 0 1 . 1 8 3 . 8 7 2 . 0 1
由图3可知,优化方案和经验方案的监测点布局存在显著差异。从表3的对比结果可以看出,对于每一场降雨事件,无论是校核还是验证,优化方案的校核模型对内涝点处的模拟准确性均明显优于经验方案的校核模型(内涝点处的平均模拟准确性分别提升72%和53%)。这说明优化监测点布局可以显著提高校核模型性能。
为进一步展示所提优化布局方法的优越性,选取内涝显著节点F730处的水位变化结果进行对比分析,如图4所示。图4中每根灰实线表示一次模型校核或验证结果,共5次。由图4可知,对于校核事件C1/C2和验证事件V1/V2,优化布局方案下该节点处水位变化曲线与真实值的拟合程度均显著优于经验布局方案。结果表明,通过监测点优化布局可以提供更有效的监测数据,显著提升雨水管网模型校核效果,使校核模型具备更好的模拟预测性能。
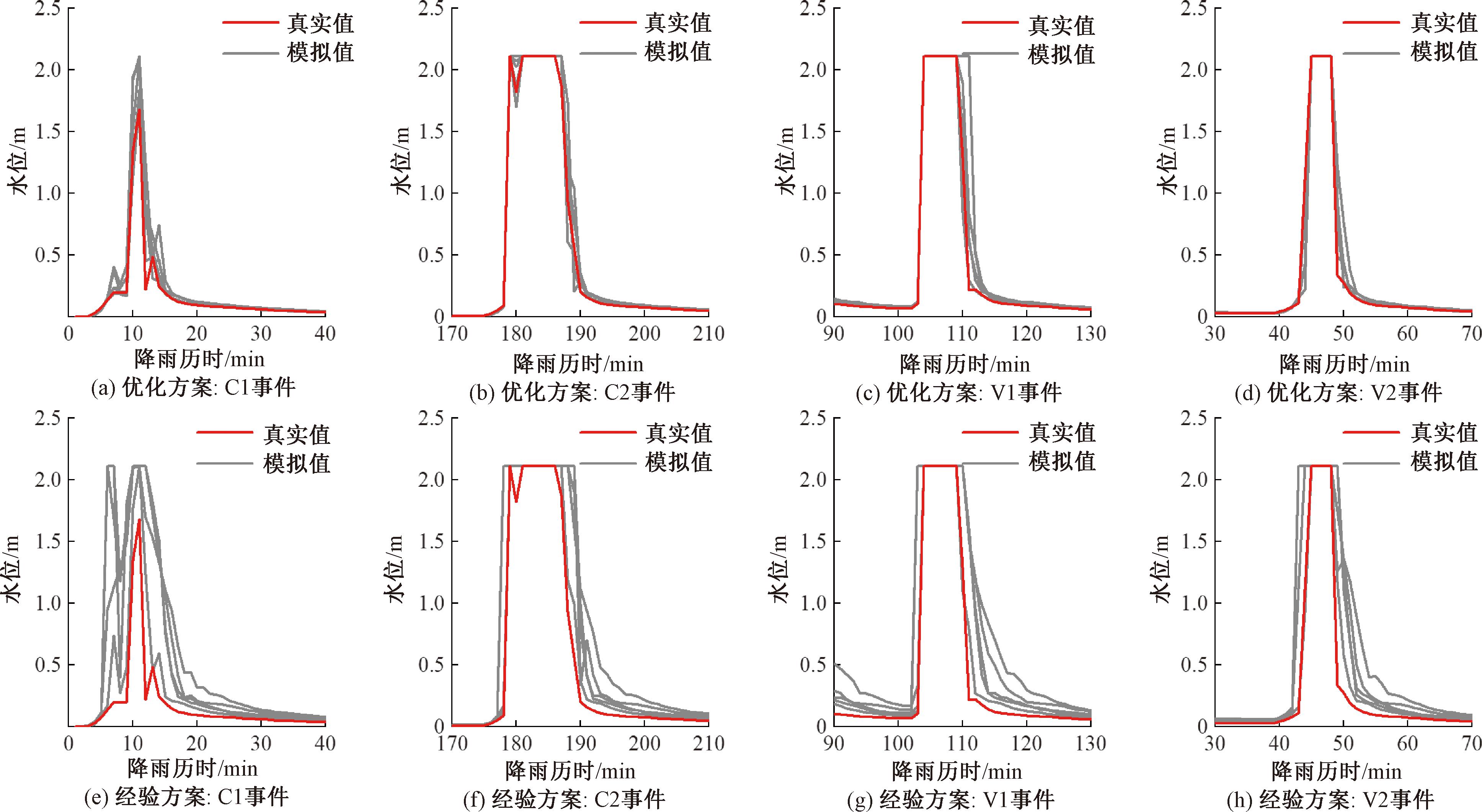
图4 不同校核和验证降雨事件中节点F730处水位变化曲线对比
Figure 4 Comparison of water depth evolution curves at node F730 through different rainfall events for calibration and validation
2.2 监测点数量对模型校核影响分析
采用所提基于模型校核的监测点优化布局方法分别设计监测点数量M为1,3,5,7,10的监测方案,研究监测点数量对模型校核的影响。同时也采用经验方法在管网中均匀布置相应数量的监测点,进一步对比不同监测点数量下两种监测方案对模型校核效果的影响。由此得到的不同数量监测点优化布局和经验布局方案如图5所示。由图5可以看出,不同监测点数量下优化方案的监测点大部分布置于内涝频发区域,少量会布置在非内涝区域的关键节点(见5,7,10个监测点的优化布局方案)。同时,优化布局方案中,监测点并非完全覆盖内涝最严重节点,这说明内涝最严重节点并非一定是模型校核数据最敏感位置,需进行优化分析。相对地,经验布局方案只考虑了监测点在空间分布的均匀性,未能有效体现对内涝积水情况的关注。
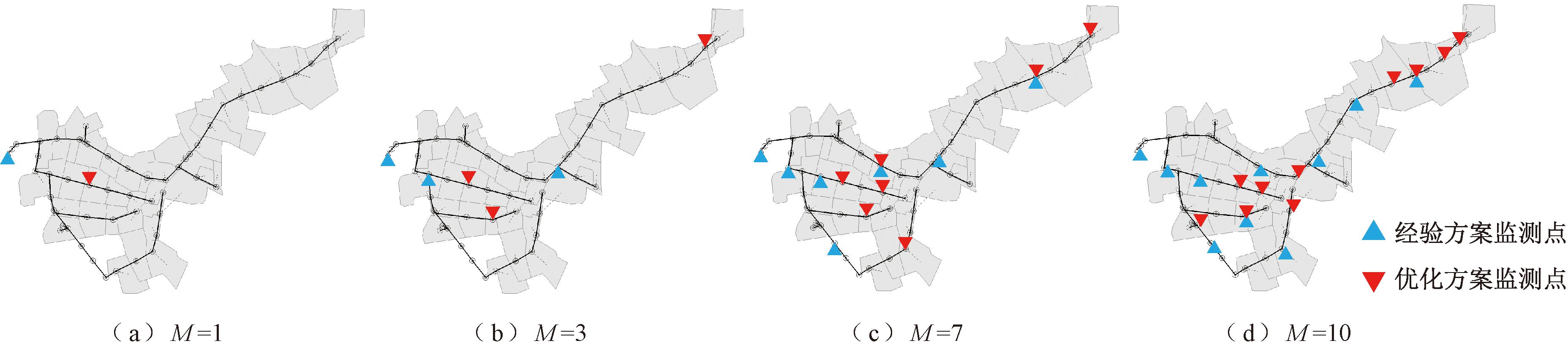
图5 不同监测点数量经验方案和优化方案监测点布局
Figure 5 Layouts of optimal sensor placement for different number of sensors
根据两种监测方案,采用降雨事件C1~C5进行模型参数校核(5次),并采用降雨事件V1~V4进行校核模型验证,分别统计模型校核和验证阶段监测点处模型性能RRMSEobs和内涝点处模型性能RRMSEflood的平均值和标准差,如图6所示。其中,误差条的上下限表示5次模型校核和验证结果的标准差;20个监测点的优化方案表示所有内涝节点处均安装监测点的极端方案,用以展示所有内涝情况均被监测时的模型校核效果。
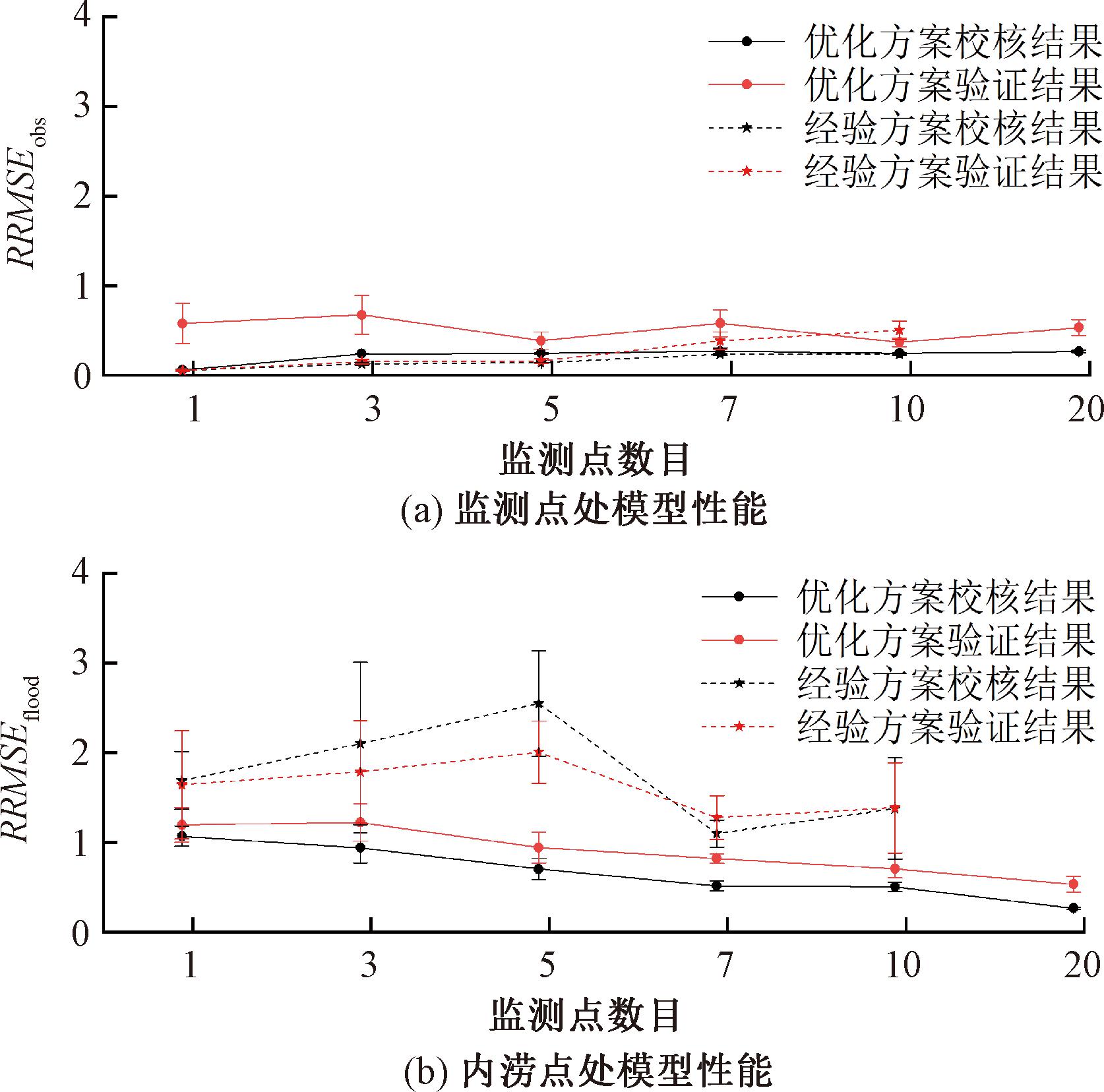
图6 不同监测点数量下监测点处和内涝点处的模型性能
Figure 6 Model performance at sensors and flooding points for different number of sensors
首先对比分析不同监测点数量下基于优化监测方案和经验监测方案的校核模型性能。从图6可以看出,两种监测方案下监测点处的校核和验证结果比较接近,10个监测点以下时经验方案的监测点处验证结果甚至优于优化方案(即RRMSEobs数值更小)。然而,对于内涝点处整体性能,不同监测点数量下优化监测方案的校核和验证结果均显著优于经验监测方案,即优化方案的RRMSEflood数值曲线明显低于经验方案。同时,优化方案的RRMSEflood数值的波动范围(即误差条)也显著小于经验方案,表示优化方案下模型校核结果更加稳定,而经验方案下模型校核结果存在较大的不确定性。上述结果说明,不同监测点数量下优化监测点空间布局均可以显著提升校核模型的准确性和鲁棒性。
进一步,针对优化监测方案下的模型校核和验证结果,深入分析监测点数量对模型校核效果的影响。从图6(a)可以看出,不同监测点数量下,模型校核均使监测点处模拟值与真实值拟合良好(RRMSEobs平均为0.25左右),但验证结果的准确性略有下降(降低至0.50左右)。然而,监测点处校核准确不能确保模型整体性能满足要求,如图6(b)所示。在监测点数量不足时,内涝点处模拟准确性显著低于监测点处。例如,监测点数量为1时,校核和验证阶段的内涝点处RRMSEflood平均值分别为1.07和1.20,显著大于监测点处平均值0.06和0.58。随着监测点数量增多,校核和验证阶段的内涝点处模型性能均逐渐增加(即RRMSEflood逐渐减小),并趋于稳定(标准差减小)。这说明,在雨水管网模型校核时,增加监测点数量可有效提升校核模型的准确性和鲁棒性。经统计分析发现,5个以上的监测点优化布局时,模型预测(即验证阶段)的RRMSEflood值降低至1.0以下(相对于1个监测点的经验布局方案时,模型性能提升38%以上),这说明校核模型具备了较好的整体预测性能。
2.3 模型参数校核结果分析
进一步对不同监测点数量下模型参数校核结果进行分析。为方便对比,采用相对偏差指标RB来量化参数校核的准确性:
(4)
式中:m为参数校核值;m0为参数真实值;m1为参数取值下限;m2为参数取值上限。
图7为不同监测点数量下319个模型参数的5次校核数值的统计结果。
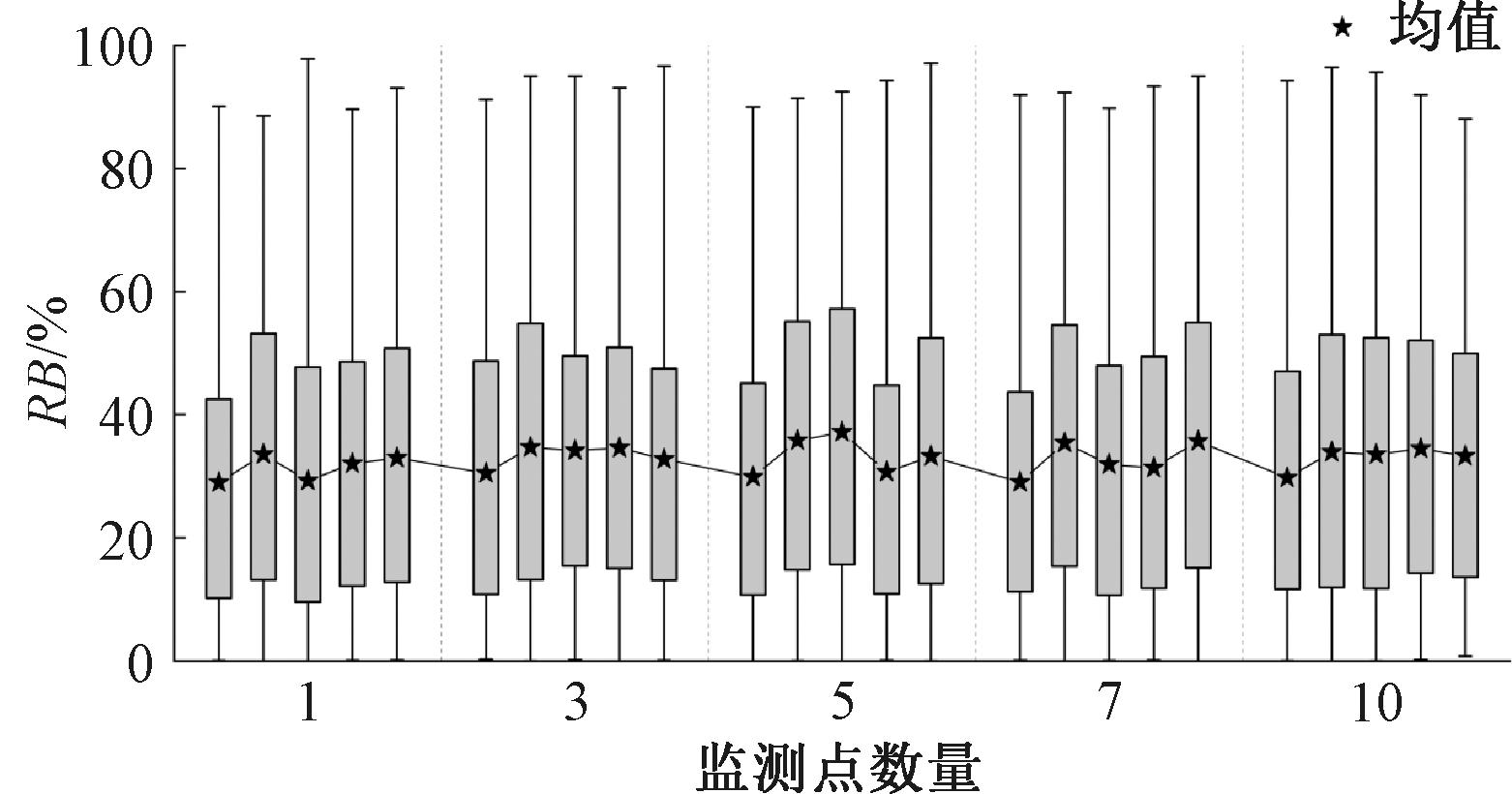
图7 不同监测点数量下模型参数校核结果统计
Figure 7 Model parameter calibration results for different number of sensors
由图7可以看出,随着监测点数量的提升,校核后模型参数的RB值没有发生明显变化,即模型参数校核的准确性并没有显著提高。结合前述发现内涝点处模型性能随监测点数量增多而提升,该现象说明雨水管网模型校核存在显著的“异参同效”问题,即不同的参数组合可以得到监测点处相似的拟合效果。“异参同效”问题使模型校核问题变得复杂,难以通过智能优化算法准确率定模型参数。但是,从上文对图6的分析可知,在监测点数量足够的情况下(如5个监测点以上时),仍然可以得到一个准确性和鲁棒性足够的“等效”模型。这在实际工程应用中往往是可行的。
3 结论
本文利用丹麦贝灵厄雨水管网模型和真实降雨事件,采用基于模型校核的监测点优化布局方法,探讨了监测点数量和布局对城市雨水管网模型校核性能的影响,主要结论如下。
(1)优化监测点空间布局可以显著提升模型校核的准确性和鲁棒性。研究案例中,5个水位监测点的优化布局方案下校核模型相比于空间均匀布局方案对所有内涝点水位的平均预测精度可提升53%。
(2)监测点数量对模型校核效果有显著影响,增加监测点数量可以显著提升校核模型整体的准确性和鲁棒性。研究案例中,监测点数量由1个增加至5个以上时,优化布局监测方案下的校核模型对内涝节点处模拟预测性能可提升38%以上。
(3)雨水管网模型校核存在显著的“异参同效”问题,难以准确率定参数数值。但从实际应用的角度,当监测信息充足时,模型仍能达到满足应用需求的预测性能。
[1] 刘家宏, 裴羽佳, 梅超, 等. 郑州“7·20” 特大暴雨内涝成因及灾害防控[J]. 郑州大学学报(工学版), 2023, 44(2): 38-45.
LIU J H, PEI Y J, MEI C, et al. Waterlogging cause and disaster prevention and control of “7·20” torrential rain in Zhengzhou[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(2): 38-45.
[2] 郑德凤, 高敏, 李钰, 等. 基于GIS的大连市暴雨洪涝灾害综合风险评估[J]. 河海大学学报(自然科学版), 2022, 50(3): 1-8, 22.
ZHENG D F, GAO M, LI Y, et al. Comprehensive risk assessment of rainstorm-flood disaster in Dalian City based on GIS[J]. Journal of Hohai University (Natural Sciences), 2022, 50(3): 1-8, 22.
[3] NIAZI M, NIETCH C, MAGHREBI M, et al. Storm water management model: performance review and gap analysis[J]. Journal of Sustainable Water in the Built Environment, 2017, 3(2): 10.
[4] 宫永伟, 戚海军, 宋瑞宁, 等. 无率定情况下城市雨洪模拟的误差分析[J]. 中国给水排水, 2012, 28(23): 46-50.
GONG Y W, QI H J, SONG R N, et al. Error analysis in simulation of urban stormwater runoff using default parameters[J]. China Water &Wastewater, 2012, 28(23): 46-50.
[5] 郭效琛, 李萌, 赵冬泉, 等. 基于情景模拟的城市排水管网监测点自动识别[J]. 中国给水排水, 2021, 37(9): 130-136.
GUO X C, LI M, ZHAO D Q, et al. Automatic identification of urban drainage pipe monitoring points based on scenario simulation[J]. China Water &Wastewater, 2021, 37(9): 130-136.
[6] 马彦斌, 盛旺, 李江云, 等. 基于遗传算法的SWMM模型参数率定研究[J]. 中国农村水利水电, 2020(7): 46-49, 53.
MA Y B, SHENG W, LI J Y, et al. Parameter calibration of SWMM model based on GA[J]. China Rural Water and Hydropower, 2020(7): 46-49, 53.
[7] 叶陈雷, 徐宗学, 雷晓辉, 等. 基于SWMM和InfoWorks ICM的城市街区洪涝模拟与分析[J]. 水资源保护, 2023, 39(2): 87-94.
YE C L, XU Z X, LEI X H, et al. Flood simulation and risk analysis on urban block scale based on SWMM and InfoWorks ICM[J]. Water Resources Protection, 2023, 39(2): 87-94.
[8] CAI B, YU Y X. Flood forecasting in urban reservoir using hybrid recurrent neural network[J]. Urban Climate, 2022, 42: 101086.
[9] SWATHI V, RAJU K S, VARMA M R R, et al. Automatic calibration of SWMM using NSGA-Ⅲ and the effects of delineation scale on an urban catchment[J]. Journal of Hydroinformatics, 2019, 21(5): 781-797.
[10] REED P M, HADKA D, HERMAN J D, et al. Evolutionary multiobjective optimization in water resources:the past, present, and future[J]. Advances in Water Resources, 2013, 51: 438-456.
[11] KANSO A, GROMAIRE M C, GAUME E, et al. Bayesian approach for the calibration of models:application to an urban stormwater pollution model[J]. Water Science and Technology, 2003, 47(4): 77-84.
[12] HER Y, CHAUBEY I. Impact of the numbers of observations and calibration parameters on equifinality, model performance, and output and parameter uncertainty[J]. Hydrological Processes, 2015, 29(19): 4220-4237.
[13] KELLEHER C, MCGLYNN B, WAGENER T. Characterizing and reducing equifinality by constraining a distributed catchment model with regional signatures, local observations, and process understanding[J]. Hydrology and Earth System Sciences, 2017, 21(7): 3325-3352.
[14] PEDERSEN A N, PEDERSEN J W, VIGUERAS-RODRIGUEZ A, et al. The Bellinge data set:open data and models for community-wide urban drainage systems research[J]. Earth System Science Data, 2021, 13(10): 4779-4798.
[15] 廖如婷, 徐宗学, 叶陈雷, 等. 暴雨洪水管理模型参数敏感性分析[J]. 水力发电学报, 2022, 41(6): 11-21.
LIAO R T, XU Z X, YE C L, et al. Parameter sensitivity analysis methods of Storm Water Management Model[J]. Journal of Hydroelectric Engineering, 2022, 41(6): 11-21.
[16] 赵冬泉, 王浩正, 陈吉宁, 等. 监测技术在排水管网运行管理中的应用及分析[J]. 中国给水排水, 2012, 28(8): 11-14.
ZHAO D Q, WANG H Z, CHEN J N, et al. Application and analysis of monitoring technology in operation and management of urban drainage network[J]. China Water &Wastewater, 2012, 28(8): 11-14.
[17] 陈晓燕, 张娜, 吴芳芳, 等. 雨洪管理模型SWMM的原理、参数和应用[J]. 中国给水排水, 2013, 29(4): 4-7.
CHEN X Y, ZHANG N, WU F F, et al. Stormwater management model(SWMM): principles, parameters and applications[J]. China Water &Wastewater, 2013, 29(4): 4-7.
[18] ZAKIZADEH F, NIA A M, SALAJEGHEH A, et al. Efficient urban runoff quantity and quality modelling using SWMM model and field data in an urban watershed of Tehran metropolis[J]. Sustainability, 2022, 14(3): 1086.
[19] KIM S W, KWON S H, JUNG D. Development of a multiobjective automatic parameter-calibration framework for urban drainage systems[J]. Sustainability, 2022, 14(14): 8350.
[20] WANG K, GONG Y, PENG Y L, et al. An improved fusion crossover genetic algorithm for a time-weighted maximal covering location problem for sensor siting under satellite-borne monitoring[J]. Computers and Geosciences, 2020, 136: 104406.
[21] VONACH T, KLEIDORFER M, RAUCH W, et al. An insight to the cornucopia of possibilities in calibration data collection[J]. Water Resources Management, 2019, 33(5): 1629-1645.