压电换能器因具有能量转换效率高、价格低廉等优势,获得广泛应用[1]。然而,换能器在谐振状态下呈容性,因此需要阻抗匹配以提高换能器的输出功率。阻抗匹配分为静态和动态两种。静态匹配能提升换能器的输出功率,但是换能器的阻抗特性会随着负载、温度等原因发生改变[2-3],造成静态匹配失效,大量无功功率产生。动态阻抗匹配技术能够对换能器阻抗的变化进行实时监测,并且快速地求解出匹配网络中各元件参数[4],使系统时刻处于匹配状态,极大地增强了系统的稳定性。
由于匹配网络复杂度的增加,现有动态阻抗匹配方法研究多集中于智能算法上。何龙富等[5]采用具有并行性与全局搜索性的遗传算法优化得到匹配元件参数值,实验表明匹配后的换能器电抗明显减少;Briones等[6]引入粒子群优化算法来优化匹配参数以获得最佳匹配;Li等[7]采用BP神经网络算法,在算法效率上相较于遗传算法提高了108.5%。这些智能算法在理论上可以获得较好的匹配效果,但是需要复杂的建模和较长的迭代时间。
为了解决当前动态阻抗匹配方法存在的问题。本文提出了一种基于数据拟合的动态阻抗匹配方法用于压电换能器,该方法以换能器两端电阻、电抗分量作为观测值,通过选取合适的模型函数,利用最小二乘方法,得到拟合程度最高的一组换能器等效电路参数,并以此计算出匹配网络元件参数与串联谐振频率,实现换能器的动态阻抗匹配和频率追踪。MATLAB仿真结果表明,本文方法匹配效果良好,并且所需匹配时间较少。
1 基于数据拟合的动态阻抗匹配方法
1.1 压电换能器匹配模型研究
匹配网络的形式多样,其中,T型匹配网络因调节方便而受到重视[8-9]。T型匹配网络与压电换能器等效电路如图1所示,其中Rr为超声波电源内阻。
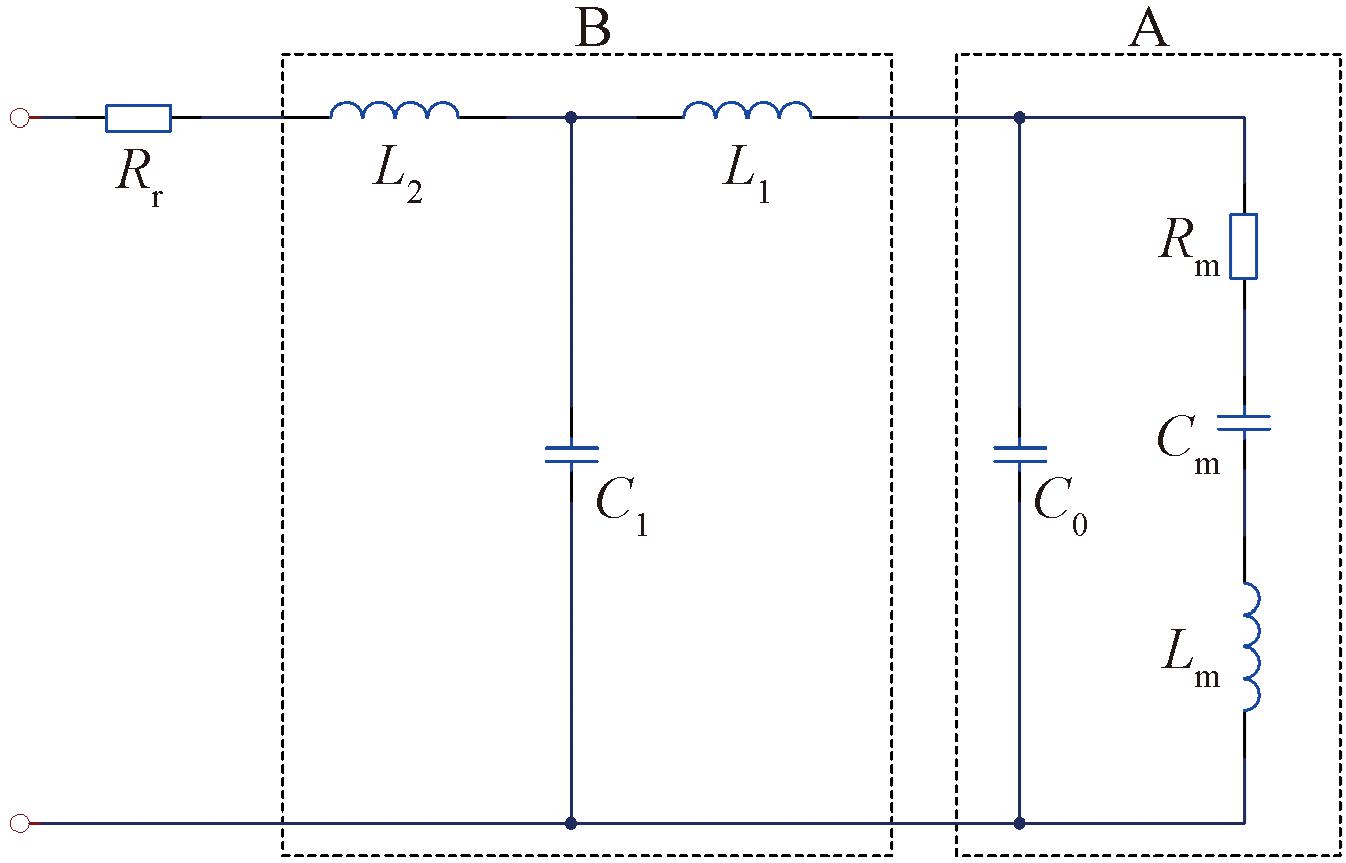
图1 T型匹配网络等效图
Figure 1 Equivalence diagram of T-type matching network
在图1中,A部分为压电换能器在谐振频率的梅森等效电路,其中静态电容C0是压电陶瓷之间的真实电参数,动态电阻Rm、动态电容Cm、动态电感Lm分别代表了压电换能器的机械损耗、弹性刚度和质量[10-11]。
由图1中A部分结合电路理论,可得出压电换能器的阻抗Z=R+jX。其中,电阻分量R和电抗分量X分别为

(1)

(2)
式中:ω为电路信号角频率。
图1中B部分为T型匹配网络,其中L1、L2为匹配电感,C1为匹配电容。当换能器处于串联谐振状态下,匹配网络元件参数分别为式(3)、式(4)和式(5)时,电路可等效为纯电阻。
(3)
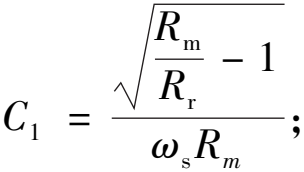
(4)
(5)
式中:ωs为串联谐振角频率。
串联谐振频率Fs为
(6)
1.2 动态阻抗匹配方法的理论分析
由式(3)至式(6)可知,串联谐振频率与T型匹配网络中的元件参数值均可通过压电换能器等效电路参数计算得到。因此,本文提出的动态阻抗匹配方法旨在求出压电换能器在工作中的等效电路参数值,根据上述公式计算出T型匹配网络中的元件参数值与串联谐振频率,实现换能器的动态阻抗匹配与频率追踪。
数据拟合能够确定模型函数中的未知参数,使其能够最好地描述观测值与实验条件的关系[12]。因此,本文使用数据拟合求得换能器在工作中的等效电路参数值。
根据式(1)、式(2),换能器的电阻、电抗分量的表达式可以看作是一个自变量是信号角频率、参数为换能器等效电路参数的函数。并且电阻分量R和电抗分量X的观测值可通过测量换能器阻抗并利用式(7)、式(8)得到,因此本文将式(1)、式(2)用作数据拟合的模型函数。
R=|Z|cos φ;
(7)
X=|Z|sin φ。
(8)
式中:|Z|为阻抗模;φ为阻抗角。
根据最小二乘法原理,若模型函数可表示为y=f(x|a),假设得到一组观测值yi及其相应条件xi,将观测值与基于模型函数计算出的数值之间的残差平方和最小化[12],得到式(9)所示优化模型:
(9)
一般而言,无论选择的模型函数是否正确,由于误差的存在,观测值都不可能精确地匹配函数。因此,本文采用拟合优度作为数据拟合效果的检验,它可以反映出某个统计模型刻画该数据集的准确度[13]。拟合优度R2为
(10)
式中:SSR为回归平方和;SST为总平方和;SSE为残差平方和。
拟合优度R2的值越接近1,回归曲线对观测值的拟合程度越好;反之,R2的值越小,则越差,但是R2不能大于1,大于1说明所选的模型函数不能描述观测值。一般来说,拟合优度到达0.9以上并小于1即可说明拟合效果较好。
2 动态阻抗匹配方案设计
2.1 动态阻抗匹配系统的设计
动态阻抗匹配系统的示意图如图2所示,主要由匹配网络端测量单元、换能器端测量单元、控制单元与动态T型阻抗匹配网络组成。
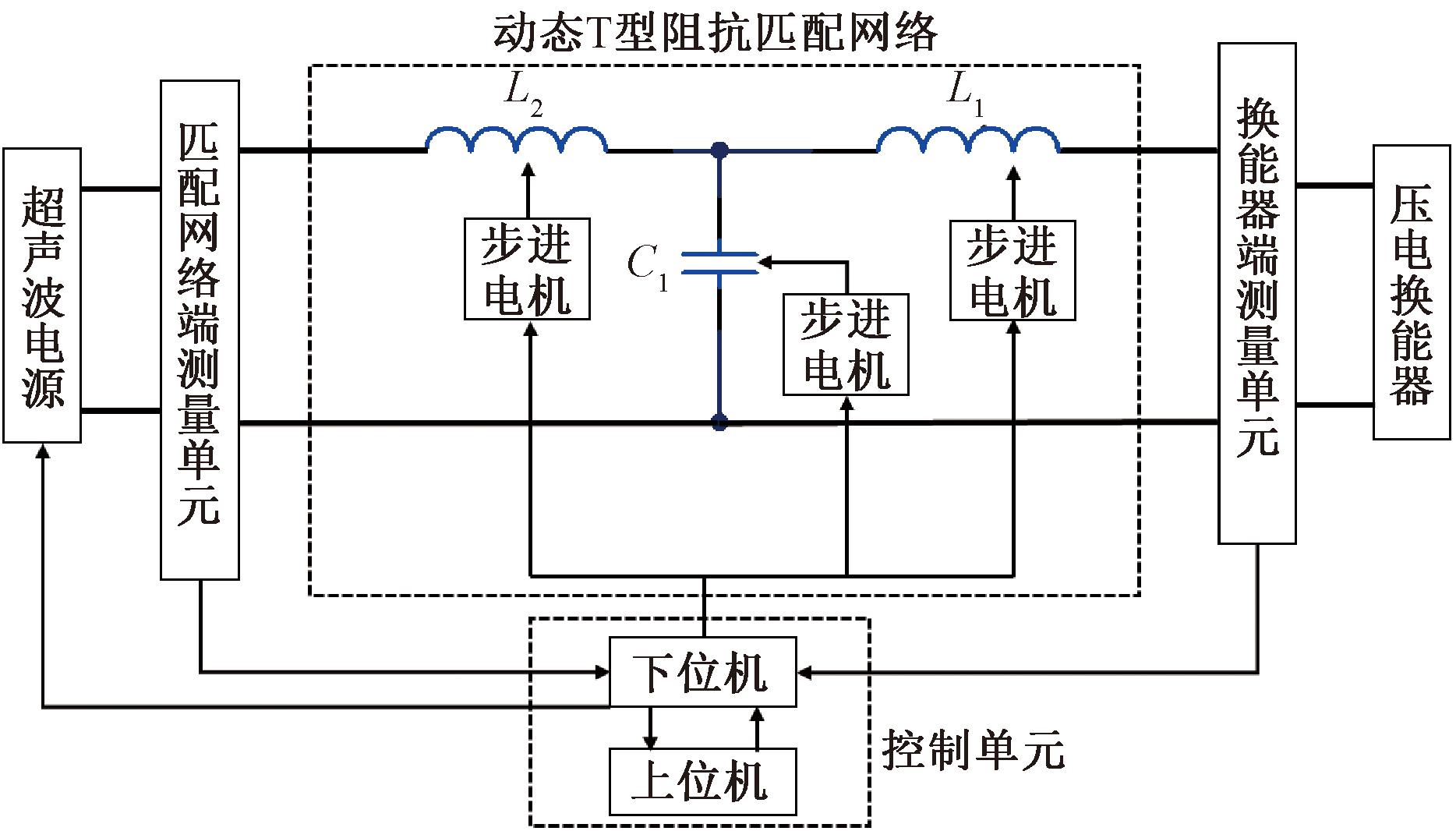
图2 动态阻抗匹配系统示意图
Figure 2 Schematic diagram of dynamic impedance matching system
2.1.1 测量单元
本文中阻抗的测量精度直接影响了动态阻抗匹配方法的准确性。因此,本文选择对阻抗进行在线同步测量。
阻抗测量单元包括两部分,一是对匹配网络端口进行测量,用于评估匹配效果,完成动态阻抗匹配网络的闭环控制;二是对换能器两端进行测量,用于提供数据拟合所需的观测值。图3为阻抗测量流程图。
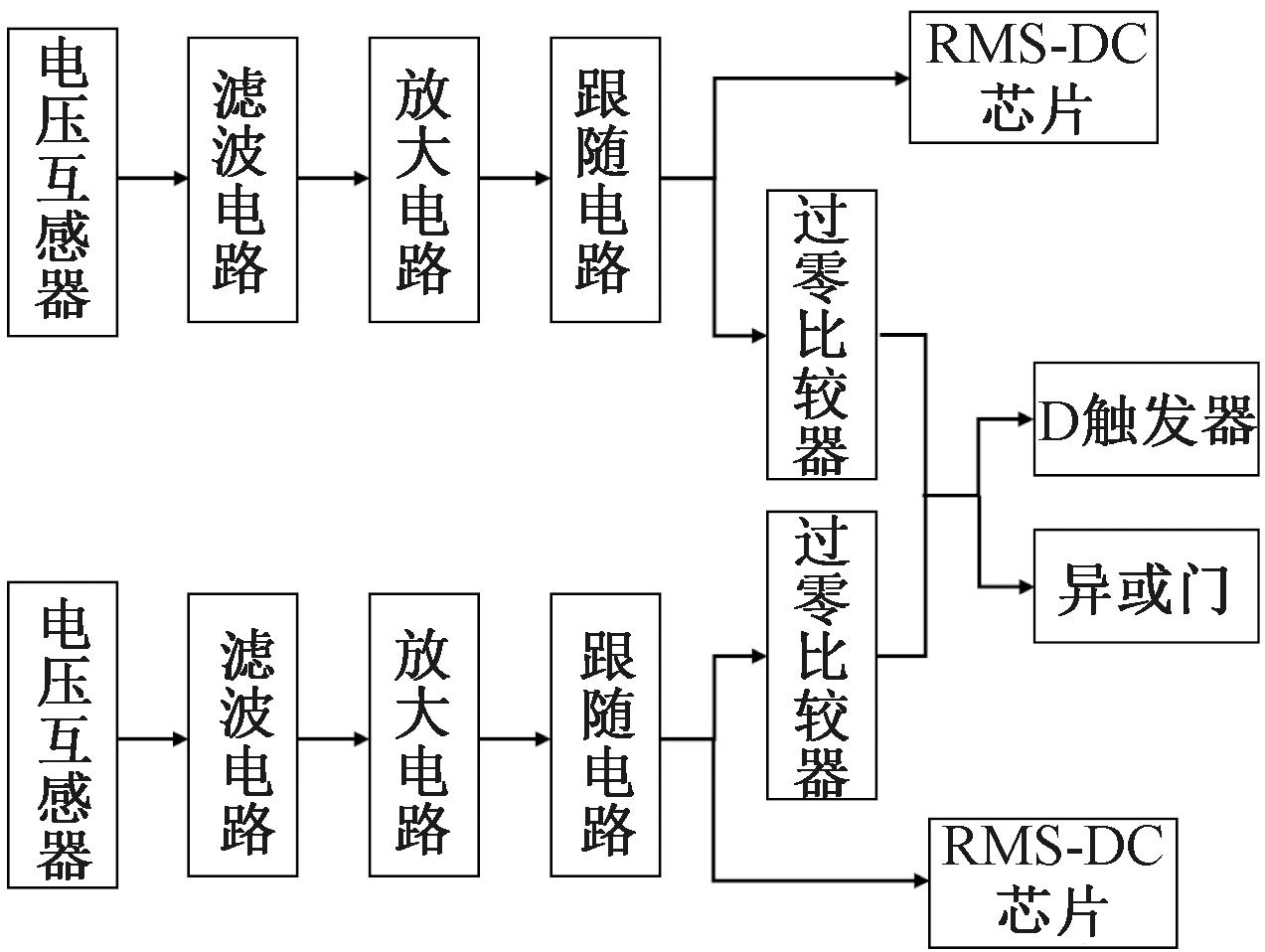
图3 阻抗测量流程图
Figure 3 Impedance measurement flow chart
基于测量实时性、准确性的需要,本文使用电压互感器和电流互感器分别对电压、电流信号进行同步采样。采样得到的电压、电流信号往往含有高次谐波且很微弱,会造成对后续信号的分析处理产生干扰和误差,需要对采样信号进行滤波、放大信号处理[14]。滤波电路选用图4所示的压控电压源二阶带通滤波电路。
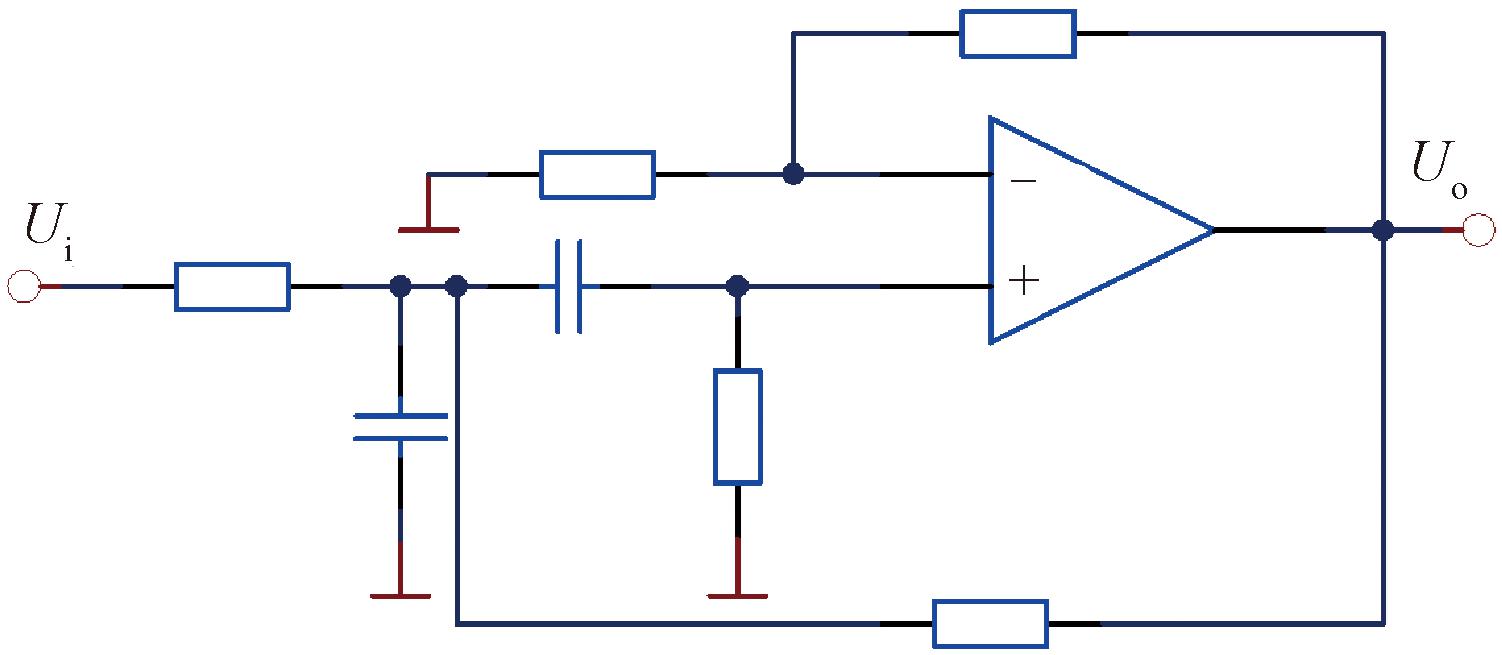
图4 压控电压源二阶带通滤波电路
Figure 4 Voltage-controlled voltage source second-order band-pass filter circuit
经过滤波、放大处理后的电压、电流信号需要经过电压跟随器,以实现信号的隔离和缓冲。随后,信号一方面通过RMS-DC芯片进行电压、电流有效值的计算,另一方面经过零比较电路转变为电压、电流的方波信号,通过异或门和D触发器分别得到代表相位差值的方波和代表相位差方向的电平。这些信号将同时输入到下位机的不同I/O通道中进行处理,实现同步并行测量。
2.1.2 动态T型阻抗匹配网络
可调器件是阻抗匹配网络实现动态调节的基础[15]。为了提高可调元件的调节范围和调节精度,本文使用气隙式可控电感器[16]和空气介质可变电容器作为匹配网络元件,实现T型阻抗匹配网络的无级调节。
气隙式可控电感器如图5(a)所示,步进电机转动丝杆滑块,带动滑块向右移动,通过拉大或减小气隙,实现输出电感量的无级调节;空气介质可变电容器如图5(b)所示,步进电机控制传动轴,通过调节动片与定片之间的相对面积,实现输出电容量的无级调节。
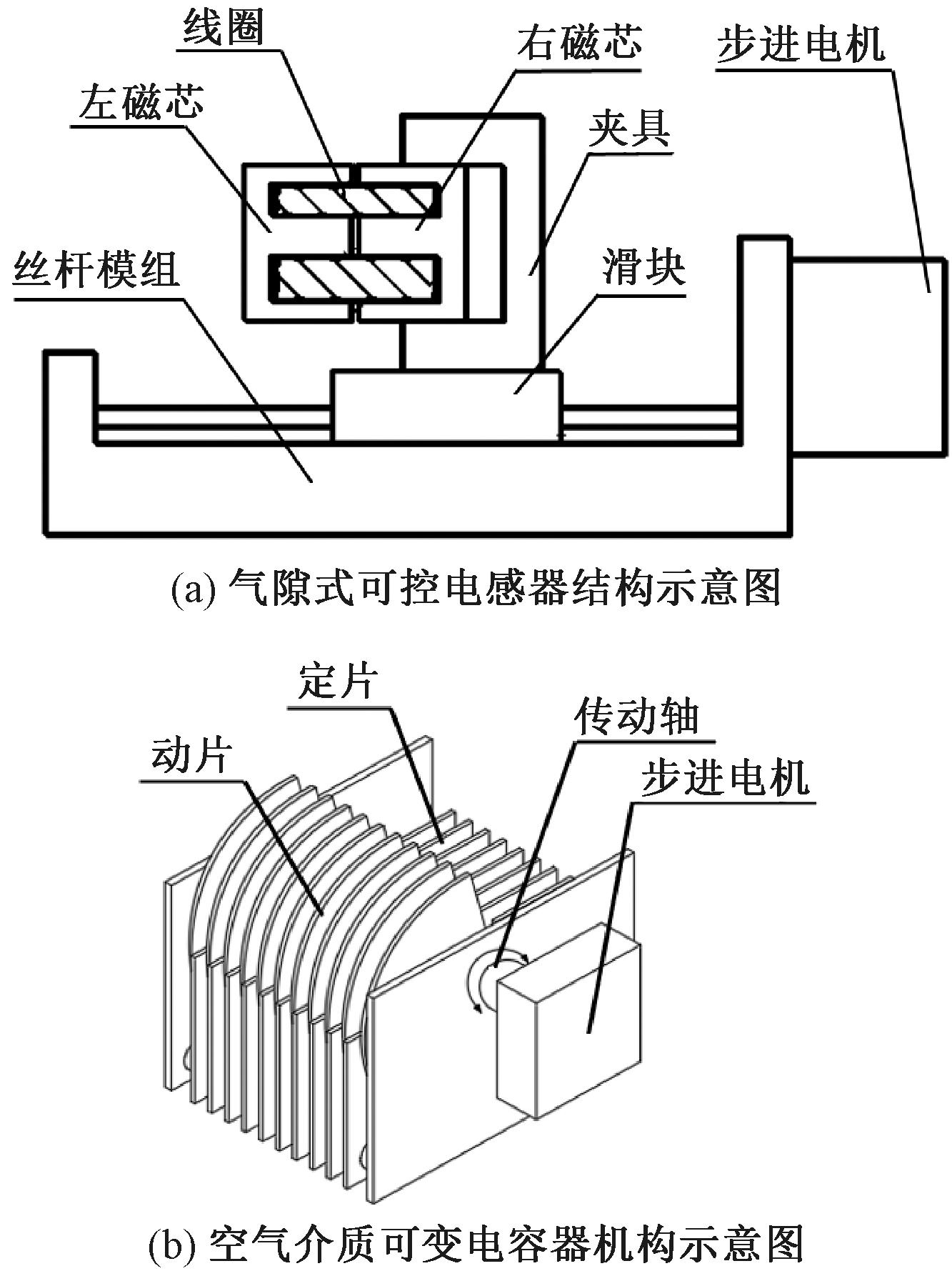
图5 可调器件结构示意图
Figure 5 Structure diagram of adjustable device
为实现气隙式可控电感器输出电感量的精确调节,本文采用数据拟合方法,以可控电感器在不同气隙下的电感值为观测值,以最小残差平方和为判断标准,将拟合程度最高的函数作为气隙式可控电感器的控制算法。将动态阻抗匹配方法得到所需的匹配电感量代入控制算法,求解出所需的气隙大小,控制步进电机进行调节。同理,空气介质可变电容器也可以构造相应的控制模型以实现输出电容量的精确调节。
2.1.3 控制单元
控制单元由上位机和下位机构成,如图6所示。下位机利用ADC转换和输入捕获功能,实现电阻、电抗分量的计算,并将结果发送至上位机。同时,负责对可调器件与超声波电源频率进行控制。
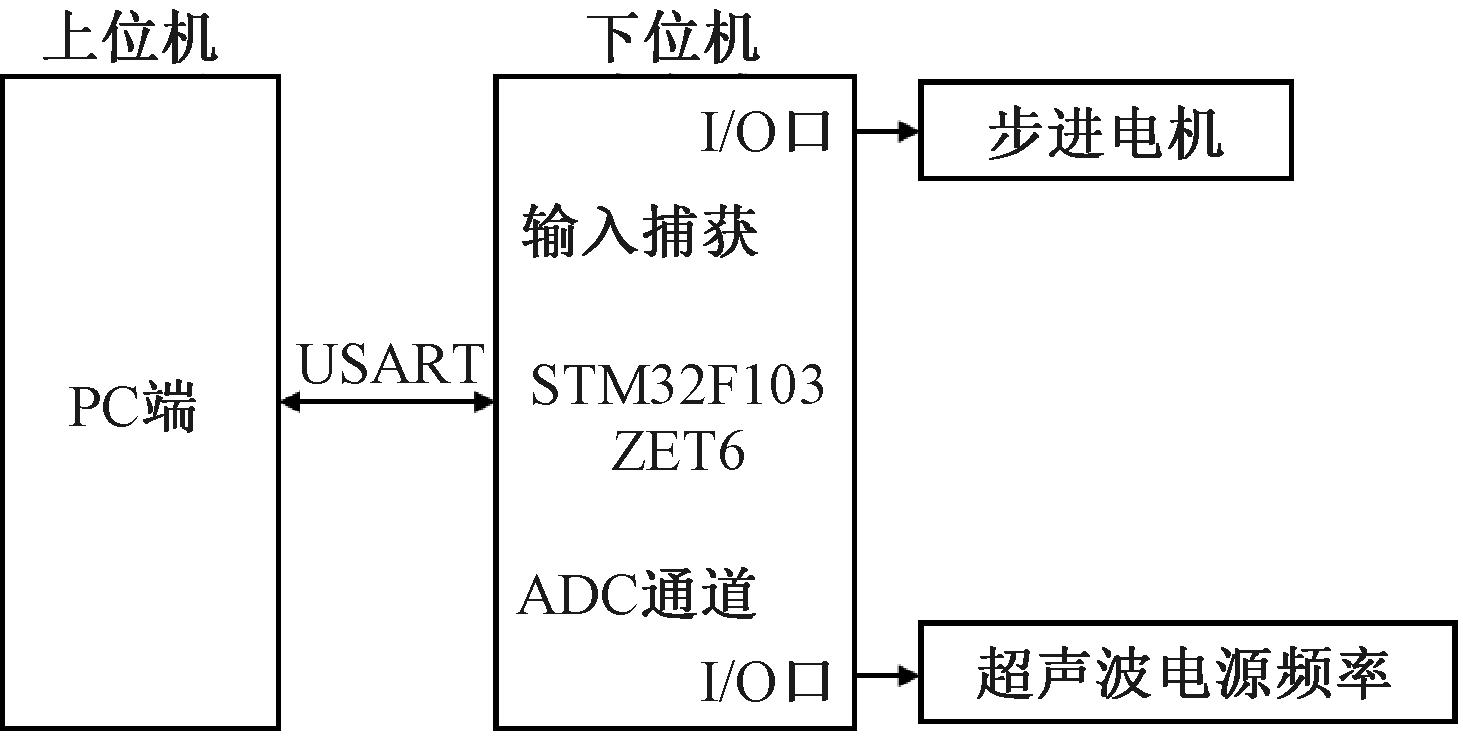
图6 控制单元示意图
Figure 6 Control unit diagram
上位机主要实现动态阻抗匹配方法,得到串联谐振频率和T型匹配网络中的元件参数值,并且根据可调器件的控制模型计算出调节量,并将其传输至下位机。
2.2 动态阻抗匹配的匹配流程
根据匹配原理,本文将T型匹配网络两端的阻抗角φ作为衡量匹配质量的标准。阻抗角φ越小,系统的匹配质量越高。所以让系统不断扫描计算T型匹配网络两端的阻抗角φ,当φ超出允许范围±5°时,判定系统失配并启动匹配测量与控制。鉴于换能器等效电路参数有4个,考虑到拟合准确性和实际应用的需要,本文在当前工作频率周围进行5次频率变化,得到5组电阻、电抗分量的观测值。具体匹配流程如图7所示。
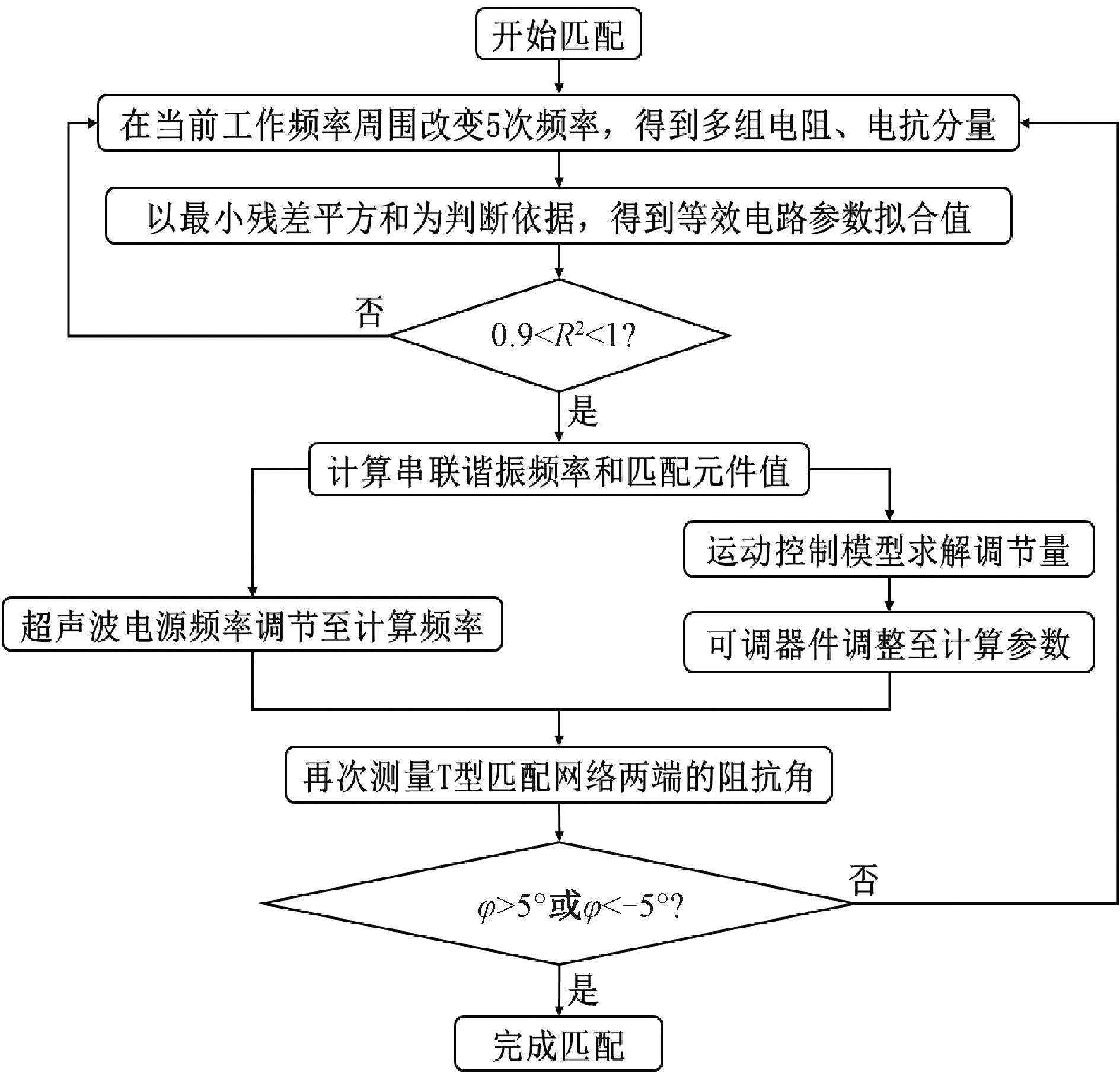
图7 动态阻抗匹配流程图
Figure 7 Dynamic impedance matching flow chart
3 仿真结果及分析
本文选用的压电换能器在空载情况下等效电路参数[17]为C0=17.979 nF;Rm=52.154 5 Ω;Lm=1 965.8 mH;Cm=0.032 1 nF;Fs=20 041 Hz。本文选用串联谐振频率Fs作为工作频率。变负载场景下的换能器等效电路参数变化情况如表1所示。
表1 等效电路参数变化情况
Table 1 Variation of equivalent circuit parameters

Rm / Ω Lm / mH Cm / nF C0 / nF 负载/ N 52. 154 5 1 965. 800 0. 032 1 17. 979 0 0 48. 292 0 1 854. 550 0. 033 9 16. 922 0 10 65. 539 0 2 311. 022 0. 027 2 16. 612 0 20 74. 541 0 1 849. 669 0. 034 0 17. 024 6 30 77. 907 0 1 828. 518 0. 034 4 17. 662 0 40 97. 304 0 2 111. 103 0. 029 7 17. 183 0 50
由式(1)、式(2)可知,电阻、电抗分量的观测值与换能器等效电路参数之间是非线性关系。本文使用Python 3.12版本中的numpy程序库中的concatenate函数将两个模型函数进行拼接,以得到更准确、一致的拟合结果;使用Scipy算法库中的curve_fit函数实现自定义模型函数的非线性最小二乘法拟合,并通过给定初始参数值,设置参数取值范围来减少计算量[18]。
本文使用空载情况下的换能器等效电路参数值作为拟合初始参数值,并将每次拟合得到等效电路参数值作为下一次拟合的初始参数值;对于参数范围,以变工况场景下的换能器等效电路参数变化情况作为参数取值范围的基础。换能器等效电路参数变化情况[17]如表1所示。参数取值如表2所示。
表2 参数取值范围
Table 2 Parameter value domain
R m / Ω L m / m H C m / n F C 0 / n F ( 4 0 , 1 5 0 ) ( 1 7 0 0 , 2 5 0 0 ) ( 0 . 0 2 , 0 . 0 4 ) ( 1 6 , 1 9 )
本文拟合使用的电阻、电抗分量的观测值通过式(1)、式(2)计算得到,并加入高斯噪声模拟测量误差。由于电阻、电抗分量在串联谐振频率周围呈现接近垂直的趋势[19],而最小二乘法在拟合接近垂直数据时拟合效果不佳。因此本文选择串联谐振频率±50 Hz为分界点,设置了两个频率区间,分别为(19 000 Hz,20 000 Hz)和(20 100 Hz,21 000 Hz),每个区间内选取5个观测点,每200 Hz改变一次频率。在(19 000 Hz,20 000 Hz)上参数拟合的结果如图8(a)所示,在(20 100 Hz,21 000 Hz)上的参数拟合结果如图8(b)所示。各区间内拟合得到的换能器等效电路参数与拟合优度R2如表3所示。
表3 数据拟合得到的等效电路参数与拟合优度
Table 3 Equivalent circuit parameters and goodness of fit obtained by data fitting

频率区间/ Hz Rm / Ω Lm / mH Cm / nF C0 / nF 拟合优度 (19 000,20 000) 51. 44 1 972. 64 0. 032 17. 95 0. 998 (20 100,21 000) 55. 46 1 965. 65 0. 032 17. 93 0. 992
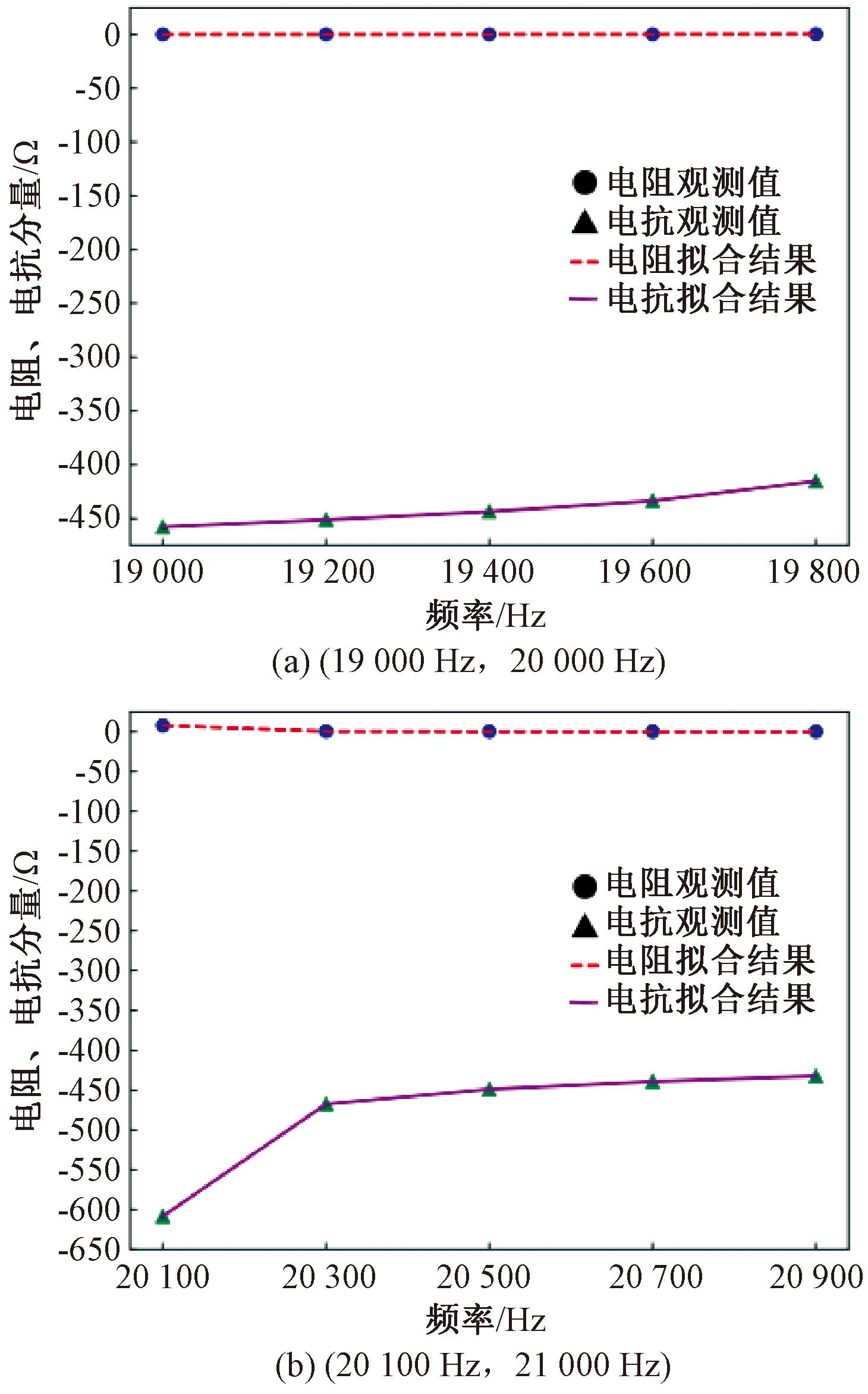
图8 5个观测点的参数拟合效果
Figure 8 Parameter fitting effect of five observation points
由表3可知,频率为(19 000 Hz,20 000 Hz)的拟合优度要略高于(20 100 Hz,21 000 Hz)。因此,本文选择在(19 000 Hz,20 000 Hz)内进行数据拟合。
根据频率(19 000 Hz,20 000 Hz)拟合得到的压电换能器等效电路参数,经过计算得到:Fs=20 032 Hz;L1=46.8 μH;C1=193.6 nF;L2=199.2 μH。
为了验证本文提出的动态阻抗匹配方法和频率追踪的准确性,使用MATLAB R2021版本进行仿真,图9为MATLAB/Simulink中搭建的仿真电路图。图9中,Lm、Rm、Cm和C0构成了压电换能器等效电路;L1、L2、C1组成了T型匹配网络;Rr与交流电压源AC组成了超声波电源;电流测量模块与电压测量模块用来对T型匹配网络两端的电流和电压信号进行测量以评定匹配效果;傅里叶变换模块和加减运算模块用来计算阻抗角;功率计算模块用来检测有功功率和无功功率。超声波电源AC驱动电压峰值为311 V,工作频率为串联谐振频率,内阻Rr取20 Ω。
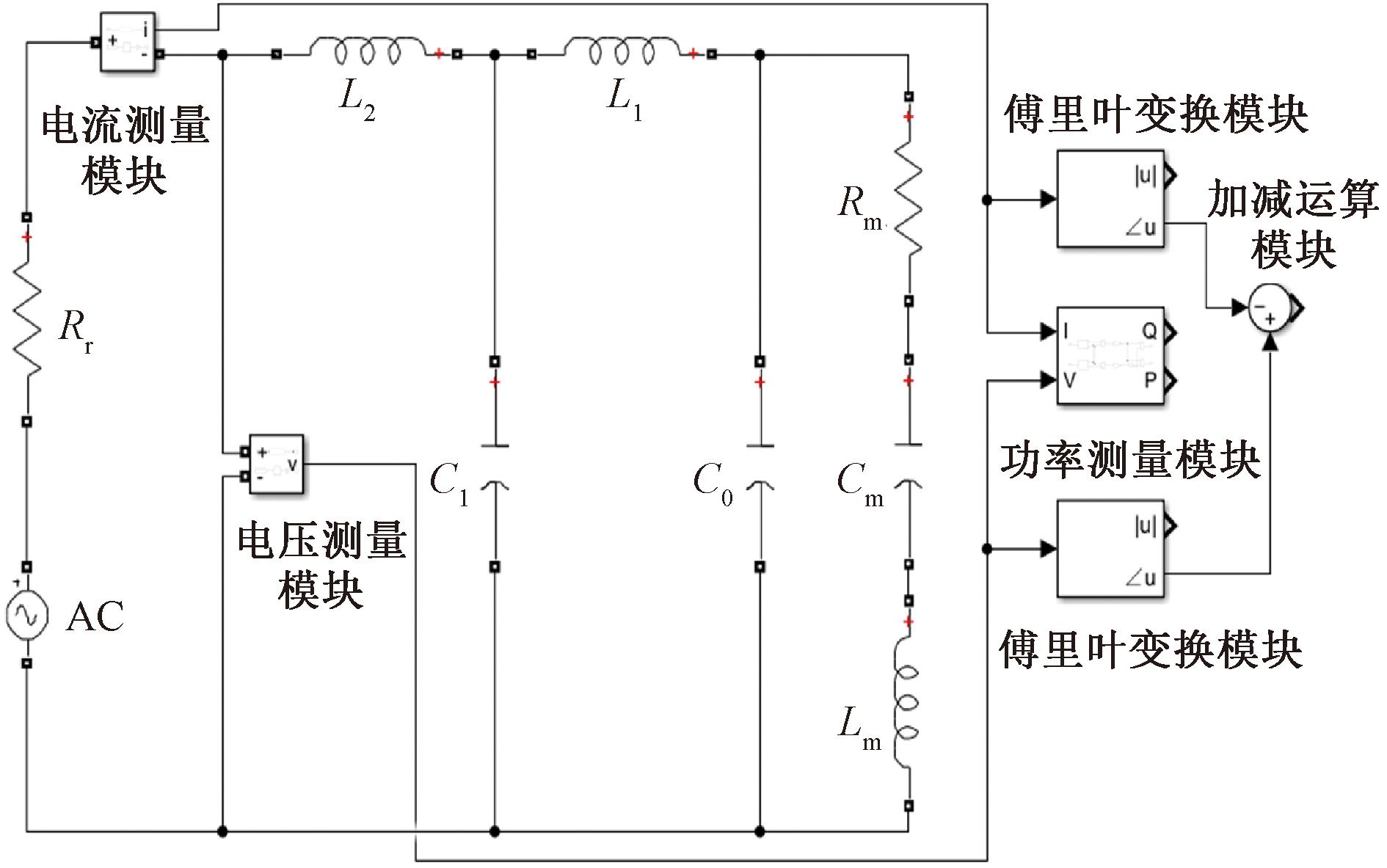
图9 仿真电路图
Figure 9 Simulation circuit diagram
图10(a)为将得到的匹配网络元件参数和串联谐振频率代入仿真电路后,T型匹配网络两端的电压、电流波形。此时,阻抗角为-0.779 1°,电压电流基本同相。有功功率为603.8 W,无功功率仅为-11.72 W。
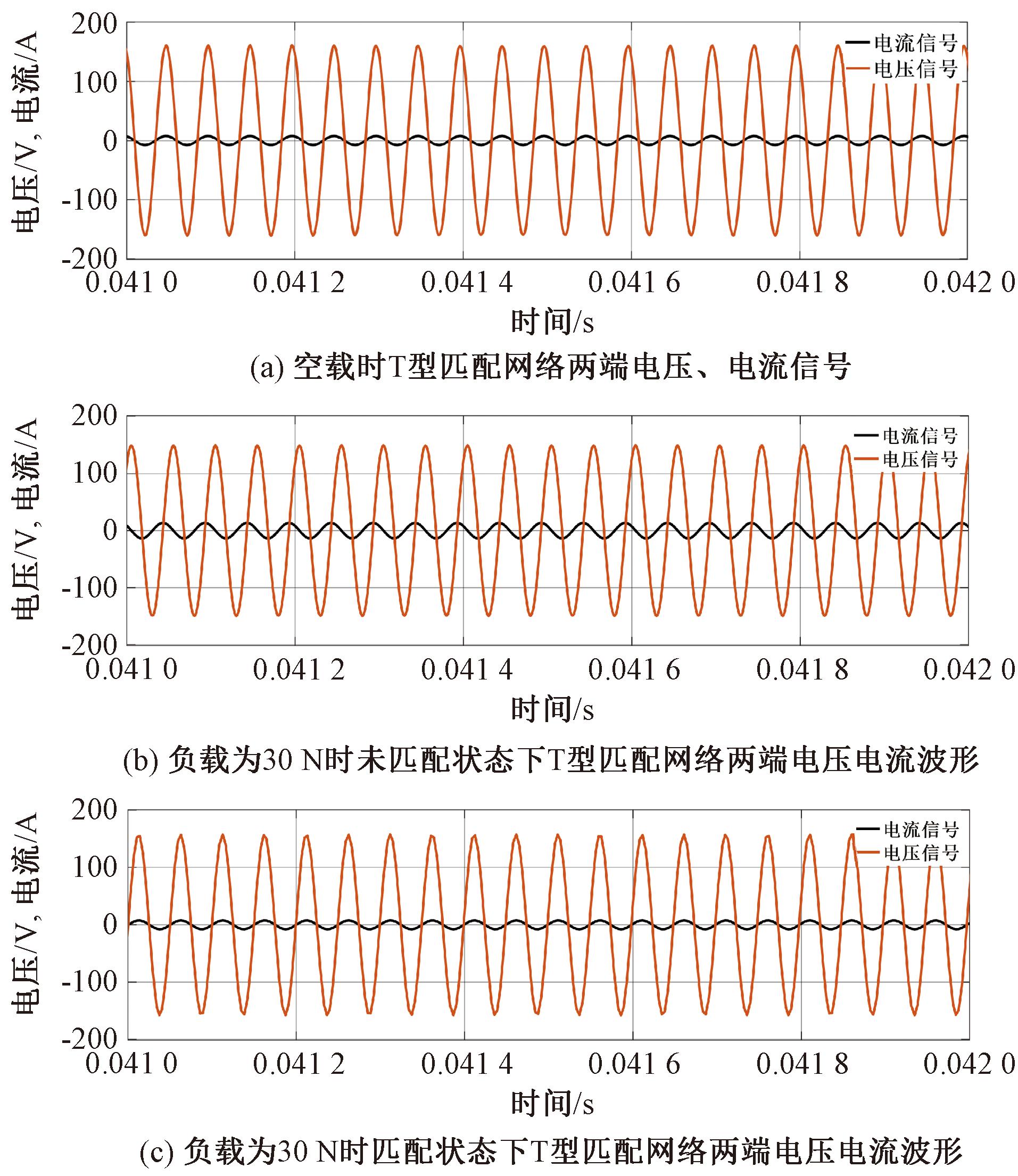
图10 T型匹配网络两端电压、电流波形
Figure 10 Voltage and current waveforms at both ends of T-type matching network
当压电换能器的负载施加在30 N时,在不调整匹配网络元件参数和工作频率的状态下,T型匹配网络两端的电压电流波形如图10(b)所示。
由图10(b)可知,T型匹配网络两端的电压电流信号有较大的相位差,此时的阻抗角为-91.22°,远高于阻抗角允许范围,并且有功功率仅有11.59 W,无功功率则显著提升至-1 011 W,证明阻抗未匹配时会带来大量的无功功率,验证了换能器等效电路参数变化时,如果不调节驱动频率和匹配网络元件参数,会发生匹配失效和频率漂移的现象。
此时,启用动态阻抗匹配方法得到换能器的等效电路参数:C0=17.029 nF;Rm=74.3 Ω;Lm=1 843.2 mH;Cm=0.034 1 nF。根据换能器等效电路参数计算出串联谐振频率和匹配网络元件参数:Fs=20 073 Hz;L1=96.5 μH;C1=174.3 nF;L2=266.06 μH。
将得到的匹配网络元件参数和串联谐振频率代入仿真电路后,得到T型匹配网络两端的电压、电流波形如图10(c)所示。此时电压电流基本同相,阻抗角为1.33°,在允许范围之内,有功功率提升至达到了609.5 W,无功功率则降低至23.59 W。
同时,利用time.perf_counter函数,得到自拟合程序启动至串联谐振频率和T型匹配网络元件参数计算完成的时间通常为10~13 ms,相较于遗传算法[20],匹配时间缩短了约97.5%。
仿真结果表明,本文提出的动态阻抗匹配方法能够较为准确地得到T型阻抗匹配网络中各元件参数和串联谐振频率,从阻抗角、有功功率的提升和无功功率的抑制这3个方面可以看出,匹配和频率追踪的效果良好,并且匹配速度快、计算量少。
4 结论
本文在数据拟合的基础上,针对现有动态阻抗匹配方法匹配速度慢、计算量大等问题,提出一种动态阻抗匹配方法,并以该方法为核心设计了T型动态阻抗匹配网络,通过少量电阻、电抗分量观测值进行拟合分析,即可求解出匹配网络元件参数和串联谐振频率,实现了压电超声换能器的动态阻抗匹配和频率追踪。在Python上进行仿真,结果表明,该方法能够得到较为准确的换能器等效电路参数,这为实现压电换能器动态阻抗匹配奠定关键基础。在MATLAB/Simulink上搭建仿真电路,结果表明,使用所提方法后,T型匹配网络两端电压、电流信号基本同相,有功功率也有明显提升,无功功率受到了抑制,阻抗匹配和频率追踪的效果良好;与使用遗传算法的动态阻抗匹配方法相比,所提方法匹配速度快、计算量较小。
[1] 张云电. 夹心式压电换能器及其应用[M]. 北京: 科学出版社, 2006.
ZHANG Y D. Sandwich piezoelectric transducer and its application[M]. Beijing: Science Press, 2006.
[2] WANG J D, JIANG J J, DUAN F J, et al. A high-tolerance matching method against load fluctuation for ultrasonic transducers[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 1147-1155.
[3] KIJANKA P, PACKO P, ZHU X, et al. Three-dimensional temperature effect modelling of piezoceramic transducers used for Lamb wave based damage detection[J]. Smart Materials and Structures, 2015, 24(6): 065005.
[4] 熊智挺, 谭阳红, 易如方, 等. 射频自动阻抗匹配的分层遗传算法实现[J]. 计算机工程与应用, 2013, 49(23): 261-265.
XIONG Z T, TAN Y H, YI R F, et al. RF impedance automatic-matching with multilevel genetic arithmetic[J]. Computer Engineering and Applications, 2013, 49(23): 261-265.
[5] 何龙富, 陈敏, 李加鑫, 等. 基于遗传算法在水声宽带匹配中的优化[J]. 电子设计工程, 2017, 25(2): 1-4.
HE L F, CHEN M, LI J X, et al. Optimization of underwater acoustic broadband matching based on genetic algorithms[J]. Electronic Design Engineering, 2017, 25(2): 1-4.
[6] BRIONES E, RUIZ-CRUZ R, BRIONES J, et al. Particle swarm optimization of nanoantenna-based infrared detectors[J]. Optics Express, 2018, 26(22): 28484-28496.
[7] LI Y, DONG W H, YANG Q X, et al. An automatic impedance matching method based on the feedforward-backpropagation neural network for a WPT system[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3963-3972.
[8] 王磊, 王时英. 压电换能器T型匹配电路的优化[J]. 压电与声光, 2014, 36(5): 861-864.
WANG L, WANG S Y. Optimization of T-type matching circuits in piezoelectric transducer[J]. Piezoelectrics &Acoustooptics, 2014, 36(5): 861-864.
[9] YANG Y H, WEI X Y, YAO W Q, et al. Broadband electrical impedance matching of sandwiched piezoelectric ultrasonic transducers for structural health monitoring of the rail in-service[J]. Sensors and Actuators A: Physical, 2023, 364: 114819.
[10] 姚震, 莫毅强, 罗子伦, 等. 非线性工作状态压电换能器匹配技术[J]. 应用声学, 2023, 42(2): 379-385.
YAO Z, MO Y Q, LUO Z L, et al. Matching technology of piezoelectric transducer in nonlinear working state[J]. Journal of Applied Acoustics, 2023, 42(2): 379-385.
[11] ZHANG H J, WANG F J, TIAN Y L, et al. Electrical matching of low power piezoelectric ultrasonic transducers for microelectronic bonding[J]. Sensors and Actuators A: Physical, 2013, 199: 241-249.
[12] STRUTZ T. 数据拟合与不确定度: 加权最小二乘拟合及其推广[M]. 北京: 国防工业出版社, 2019.
STRUTZ T. Data fitting and uncertainty[M]. Beijing: National Defense Industry Press, 2019.
[13] XU W, CHEN W, LIANG Y J. Feasibility study on the least square method for fitting non-Gaussian noise data[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 492: 1917-1930.
[14] 王翥, 刘春龙, 罗清华. 超声波传感器特性分析与测试方法的研究[J]. 郑州大学学报(工学版), 2020, 41(2): 13-18.
WANG Z, LIU C L, LUO Q H. Research on ultrasonic sensors characteristics and testing method[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(2): 13-18.
[15] SABERKARI A, ZIABAKHSH S, MARTINEZ H, et al. Active inductor-based tunable impedance matching network for RF power amplifier application[J]. Integration, the VLSI Journal, 2016, 52(C): 301-308.
[16] 东栋. 超声电源换能振动系统的阻抗匹配研究[J]. 电气应用, 2006, 25(9): 125-128.
DONG D. Impedance match of transducer system in ultrasonic frequency power supply[J]. Electrotechnical Application, 2006, 25(9): 125-128.
[17] 吴鹏. 基于气隙式可控电抗器的超声换能器阻抗动态匹配研究[D]. 哈尔滨: 哈尔滨工业大学, 2020.
WU P. Study on dynamic matching of ultrasonic transducer based on air-gap comtrollable reactor[D].Harbin: Harbin Institute of Technology, 2020.
[18] 李辉, 金晓萍, 李丽芬. Python程序设计与数据分析基础[M]. 北京: 清华大学出版社, 2023.
LI H, JIN X P, LI L F. Python programming and data analysis foundation[M]. Beijing: Tsinghua University Press, 2023.
[19] LI J Q, HUANG W C, SHAO W W, et al. An electrical impedance matching method of dual-frequency transducers for ultrasound internal imaging[J]. Measurement, 2023, 221: 113413.
[20] 汪洪波, 黄稳, 陈长琦. 基于遗传算法的真空磁控溅射射频阻抗匹配仿真研究[J]. 真空科学与技术学报, 2011, 31(4): 500-504.
WANG H B, HUANG W, CHEN C Q. Simulation of RF impedance matching of magnetron sputtering based on genetic algorithm[J]. Chinese Journal of Vacuum Science and Technology, 2011, 31(4): 500-504.