近些年,随着城市轨道交通建设加快,我国城市轨道交通里程快速增长。截至2023年11月底,全国已有55个城市开通运营城市轨道交通线路300条,运营里程9 915.6 km,其中地铁占比超过75%。然而,与此同时,突发公共卫生事件、自然灾害、设备故障等各种意外事件的发生频率也在同步增加,严重冲击轨道交通系统的正常运行。据统计,2022年我国共发生5 min及以上延误事件717次,列车退出正线运营故障5 526次[1]。香港地铁每年约有250次中断,外部侵入和设备故障等事件的平均持续时间超过60 min[2]。2018—2019年期间,伦敦城市轨道交通乘客遭受的总延误时长超过3×107 h[3]。这些突发事件导致的不确定性已成为轨道交通面临的新常态。
交通系统的韧性主要包含两个关键部分[4]:一是吸收灾害的能力;二是从灾害中快速恢复的能力[5]。随着交通韧性理论的发展,结合交通系统性能函数与韧性三角形理论所构建的韧性评价体系受到广泛认可。该方法可以很好地评价基础设施网络应对灾害事件的全过程与综合能力[4]。2022年3月,交通运输部发布《交通强国建设评价指标体系》,“交通系统韧性”成为应急保障的重要评价指标[6]。在此背景下,如何提升城市轨道交通韧性、保障其安全平稳运行已成为一个迫在眉睫的新挑战。
目前,地铁网络意外中断后的应急措施有限,多数轨道交通运营公司将公交接驳(安排常规公交在中断站点之间运行以恢复连接)作为首选处置方案[7]。公交接驳具有高度的灵活性和较强的运输能力[7-9],但仍然面临许多现实困难。首先,许多城市的常规公交与轨道交通公司相互独立,导致事故信息无法及时共享,容易出现公交接驳预案启动响应时间过长、组织协调困难等问题。其次,地铁中断持续时间以及客流变化难以预测,导致派出的接驳公交车数量经常难以与真实需求相匹配,容易出现公交车运力不足或运力过剩等问题[10]。最后,常规公交运行容易受到道路、天气等外部因素的影响[11],导致实施效果经常远低于预期。
对于地铁来说,不同方向的轨道线路往往是对外封闭且相互独立的。因此在列车抛锚、屏蔽门故障等突发事件下,地铁线路只在事件发生方向失去运输能力。陈昕[12]对香港地铁2012—2018年的运营事故数据进行分析后发现,其单向运营事故占比高达85.4%。在这种地铁线路局部故障的情况下,部分公司会采取小交路运行以及单轨拉风箱式运行(一辆列车在一条轨道上往返运行)。这类应对措施均利用功能未受影响的轨道进行组织调度以维持整条线路的部分功能。与常规公交接驳相比,这类方法便于组织协调,响应时间快,受外界干扰较小[13],然而在城市早晚高峰,该策略会出现运力严重不足、等待时间过长等问题。
基于此,针对地铁系统韧性,本文首先提出一种以地铁线路性能响应函数为基础的韧性评估模型,包括线路连通率、客流保有率以及出行延误等指标。以地铁线路局部故障为背景,提出一种新的以韧性指标最大化为目标的应急响应策略,并以长沙地铁4号线为研究对象进行实例分析。
1 地铁线路韧性评估模型
1.1 地铁线路韧性
地铁与路面交通在面对突发事件时产生的后果有显著差异。意外事件发生后可能导致一条或若干条车道发生堵塞,从而造成交通拥堵,但车辆仍然可以利用未受影响车道,甚至临时借用对向车道继续通行。相比之下,地铁大部分在封闭空间内运行,当一辆列车甚至一段轨道发生故障后,容易导致更为严重的后果。因此,为了查明事故原因、评估突发事件风险、修复线路故障,全线所有列车就近停靠或暂停运行是各运营公司采取的有效措施。这意味着地铁线路性能将在突发事件发生后短时间内迅速降为0。此外,地铁线路性能无法如道路性能一般渐进式恢复,而是在采取应急运行措施与故障消除的瞬间呈现近似跳跃性的变化。
本文将扰动事件下地铁系统的响应周期划分为 4 个阶段。图1展示了系统性能在受到扰动后随时间的变化情况,横坐标t表示时间,纵坐标Q(t)表示系统性能。系统在te时刻受到扰动,系统性能下降;ta时刻应急方案开始实施;最终系统性能在tr时刻恢复到初始水平。图1中,te~ta为应急策略响应时间,该时间段内地铁运营部门会对突发事件进行评估、制定应急方案并为方案的实施进行列车调度、人员安排与物资准备。
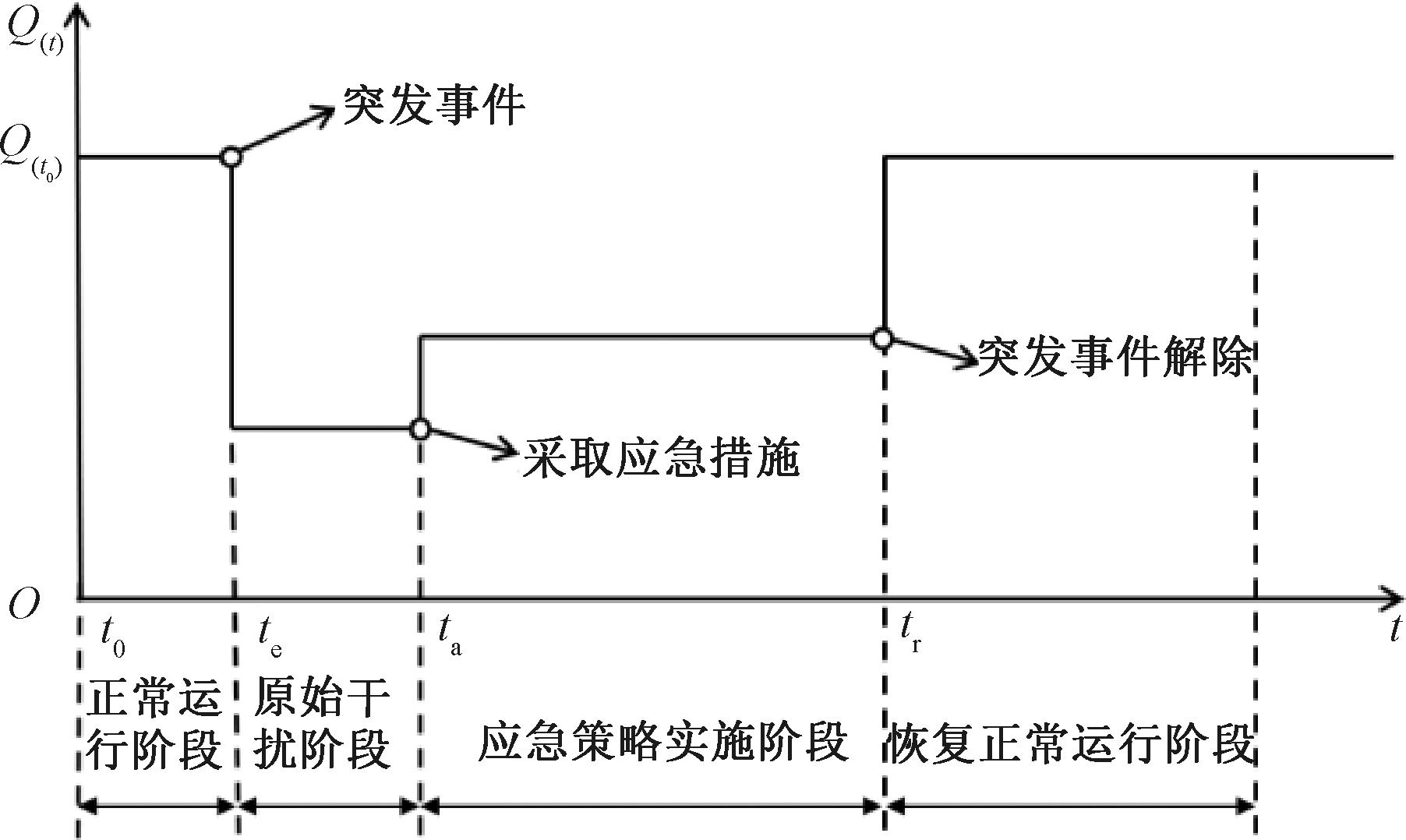
图1 突发事件下地铁性能变化函数
Figure 1 Subway performance change function in emergency
韧性强调系统在一段时间内从损坏到恢复至正常状态的整体性能[14],因此,本文以扰动后系统性能的累积损失程度来度量系统韧性。在扰动事件下,t时刻地铁线路韧性可表示为

(1)
式中:R(t|e)为扰动事件e发生后t时刻的地铁线路韧性,te≤t≤tr;Q(t)为地铁线路在t时刻的性能;Q(t0)为地铁线路正常运行时的性能;te为突发事件发生时刻;tr为突发事件解除时刻。
可见,分子表示从扰动发生时刻te到t时刻地铁线路的累积性能;分母表示从扰动发生时刻te到t时刻地铁线路在正常运行情况下的累积性能。
1.2 性能响应函数
综合考虑地铁线路中断事件对地铁线路结构、服务质量、客流负荷等层面的影响,提出突发事件下地铁线路性能响应函数(式(2)),地铁线路韧性评估框架如图2所示。
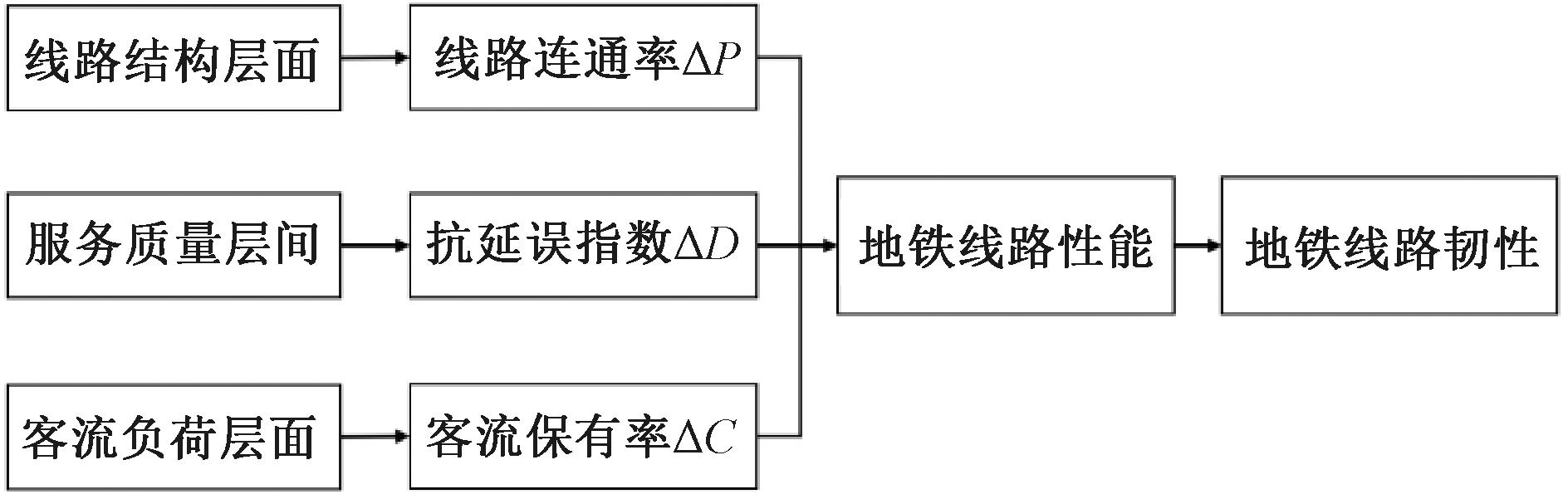
图2 地铁线路韧性评估框架
Figure 2 Framework of evaluating the subway line resilience
线路连通率指采取应急运行策略时,仍有列车途经并停站上下客的站点占全线总站点的比例。应急策略串联起的车站数量越多,其连通率越高。线路连通率计算公式见式(3)。
线路抗延误指数指地铁线路正常运行状态下的加权期望出行时间与突发事件e发生后的加权期望出行时间之比,每一条出行线路的权重由正常运行场景下该线路的客流量决定。线路抗延误指数计算公式见式(4)。
客流保有率指突发事件e发生后的地铁线路客流量与未发生扰动时的地铁线路客流量之比。事件发生后,损失的客流包括无列车停靠的站点损失的客流、出行延误增长损失的客流以及实施应急运行策略前的响应时间内损失的客流三部分。很多学者认为突发事件下,当乘客无法准确预知时间时,轨道交通客流损失率与其等待时间呈显著正相关[15-16],即等待时间越长,客流损失率越大。客流保有率计算公式见式(5)。
(2)
(3)

(4)

(5)
式中:Q(e)为地铁线路遭遇突发事件后,相关部门所采取的最保守策略下的线路性能。运营部门最常见的做法为全线暂停运行,此时的Q(e)等于0;ΔP为线路连通率;ΔD为抗延误指数;ΔC为客流保有率;n代表采取应急运行策略后,仍会有列车途经并停站上下客的站点数;N代表地铁线路正常运营下的站点总数;Vn为应急运行策略下仍会有列车途经并停站上下客的站点集合;i、j分别为站点序号;Tij为正常运行状态下乘客从站点i乘车至站点j的期望出行时间;t′ij为发生突发事件后乘客从站点i乘车至站点j的期望出行时间;Cij为正常运行状态下从站点i乘车至站点j的客流量;CVn表示应急运行策略下仍有列车途经停靠的站点之间的客流总量;CVN表示地铁线路正常运行时的客流总量;F1(t′ij-tij)为期望出行时间增长造成的客流损失率;Tr为从事件发生到采取应急运行措施之间的响应时间长度,Tr=ta-te;F2(Tr)为响应时间内造成的客流损失率。
2 地铁线路突发事件应急运行策略
大部分地铁线路由上下行轨道、地铁列车、地铁站、交叉轨道等要素组成,如图3所示。交叉轨道是除首末站外连接上下行轨道的节点,以交叉轨道为界限把完整的地铁轨道分为A1—A2,A3—A4,A5—A6,A7—A8共4个部分。因此当地铁线路某处发生屏蔽门故障、列车停车故障、人为事故等常见事故时,由于事故仅对单向轨道的部分区域产生实际影响,因此剩下3个部分的轨道仍然具备运输旅客的能力(若A1—A2段发生事故,则A3—A4,A5—A6,A7—A8三段轨道仍具有运输能力)。

图3 地铁线路结构
Figure 3 Subway line structure
小交路运行是一种常见的轨道交通运行模式[17]。在地铁线路局部发生故障时,利用线路中间的交叉轨道实现小交路运行能够保证地铁线路部分路段的运输性能,如图4所示。在这种应急策略下,剩下地铁路段的运输性能完全丧失。为了应对这种情况,Zhang等[13]在无法进行小交路运行的路段上,安排一辆列车进行单轨双向运行。这种小交路与单轨双向运行相结合的应急运行策略在上海等城市已经得到了应用[18]。如图4所示,这种方法虽然使得地铁全线保持了一定的运输能力,但当单轨双向运行区间过长时,一辆列车的运输能力显然远远无法满足乘客需求,并且等待时间急剧增加。
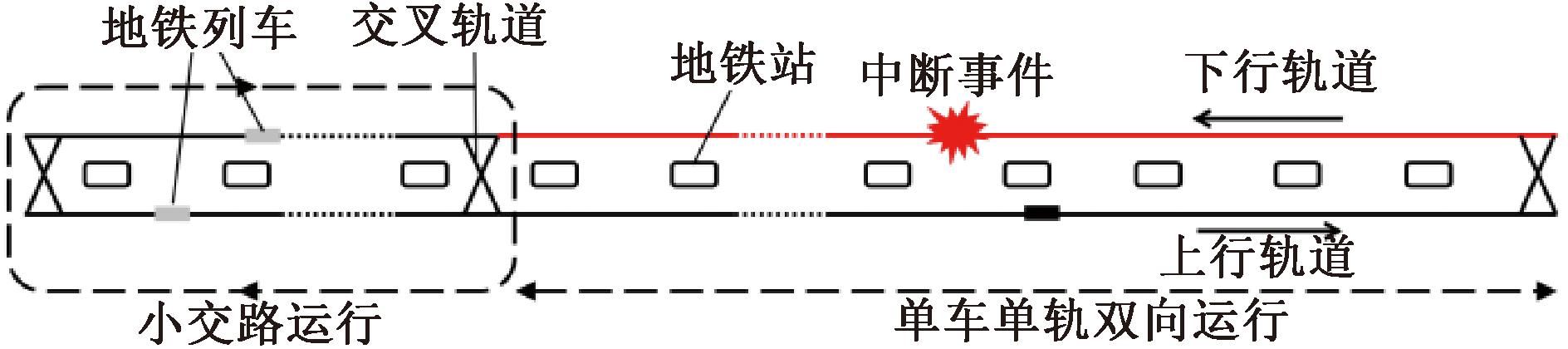
图4 小交路与单车单轨双向运行策略
Figure 4 Small intersection and single-track bidirectional operation strategy
基于以上分析,本文提出一种全新的地铁线路局部中断情况下的应急运行策略。该策略利用交叉轨道实现小交路运行,并将另一侧的可运行单轨道划分为若干个区间,每一个小区间内将安排一辆列车进行单轨双向运行,每一个区间仅首末站与相邻区间重合,为乘客提供不同区间之间的换乘途径,如图5所示。
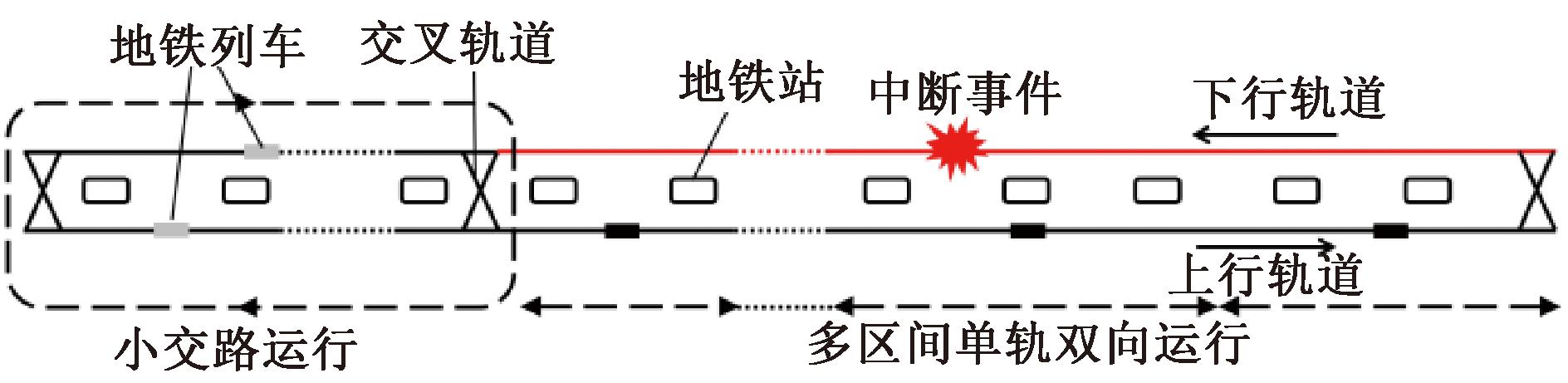
图5 改进的地铁应急运行策略
Figure 5 Improved subway emergency operation strategy
多区间单轨双向运行策略还需满足以下条件:①该策略仅在突发事件导致地铁线路单方向局部失效时可用;②各区间内的列车可根据调度信息避免在交汇站点产生时空冲突,以保证乘客与车辆的安全;③各区间内的列车往返行驶一次的时间应尽量接近,使相同时间内各区间内列车往返次数接近,避免出现各区间因运力不均导致乘客滞留的情况。
与单车单轨双向运行策略相比,本文提出的多区间单轨双向运行策略增加了单轨运行区间上的服务车辆数,将显著提升该区间内的运输容量;此外多个小区间的设置有利于缩短乘客的平均等待时间。
3 案例分析
3.1 线路介绍
长沙地铁4号线全长33.5 km,全部为地下线;共设置车站25座,平均站间距1.44 km,其中换乘站有11站,全为地下站;列车采用6节编组B型列车,最大载客量约为1 950人。目前4号线采用大小交路混合运行模式,大交路为罐子岭站到杜家坪站共25站,小交路为罐子岭站到阜埠河站,共13站,如图6所示。此外,4号线横跨湘江,是连接长沙东西向出行的重要交通工具。
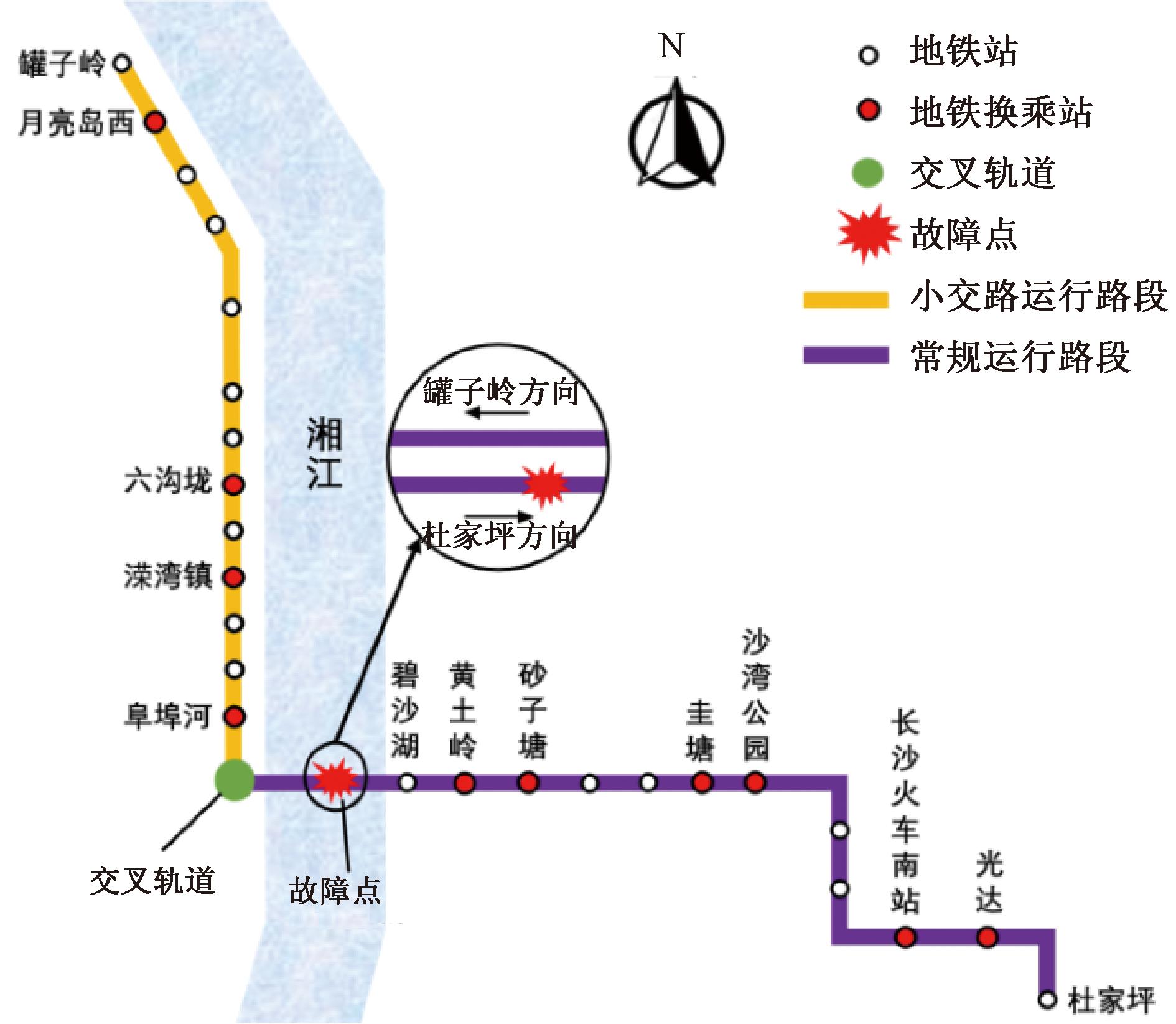
图6 地铁4号线线路示意图
Figure 6 Schematic diagram of Changsha Metro Line 4
3.1.1 突发事件概述
本文假设在某工作日早7点,一列驶向杜家坪方向的列车在阜埠河站与碧沙湖站之间的轨道上因车辆故障抛锚,预计响应时间为15 min,预计事故修复并恢复正常运营的时间为上午9点。由于该地铁为跨江线路,如果选择公交接驳,附近只有一条隧道可以通行,而该隧道及周边路网在早高峰拥堵十分严重,导致公交跨江时间远高于地铁,且可靠性较低。因此,在此假设下,轨道交通公司放弃公交接驳策略,转而考虑以下3种应急运行策略。
方案1:在罐子岭站至阜埠河站启动小交路运行模式(共计13站)。
方案2:在小交路运行的基础上,安排一辆列车在往罐子岭方向的轨道上采取单车单轨双向运行模式(共计12站)。
方案3:在小交路运行的基础上,安排若干辆列车采取多区间单轨双向运行模式(共计12站)。
为了简化计算流程,对以上策略做如下假设:①列车运行速度与早高峰运行速度保持一致,这意味地铁列车通过两站之间的时间与早高峰相同;②为了保障列车安全,多区间单轨双向运行策略下,每个区间不宜过短,至少包含4个站间区间,在不同区间运行的车辆,将在移动闭塞信号系统的保障下避免同时进入换乘站发生碰撞;③由于目前早高峰期间长沙轨道交通4号线运力尚未饱和,没有必要缩短小交路运行区间内列车的到站间隔,而是与早高峰列车到站间隔保持一致,基于前文提出的地铁线路韧性模型对以上3种方案的效果进行评估;④响应时间内,运营公司暂停全线所有车辆的运行以对故障进行检查评估以及制定应急运行策略,此时的地铁线路性能视为0。
3.1.2 地铁4号线早高峰客流
地铁刷卡数据可以反映乘客在地铁网络内的行程轨迹,本文选取了2023年3月20日(周一)到2023年3月24日(周五)5个工作日早高峰的地铁刷卡数据。首先提取07:00—09:00的进站刷卡数据,删除错误值以及在站内逗留超过2 h的数据。接下来根据每条刷卡记录的上车站点与下车站点信息识别得到出行OD。对于进出站分别位于不同线路的数据,将被匹配在连接两站的最短路径上以识别换乘客流。整理后得到正常运行状态下4号线07:00—09:00客流OD矩阵C0。
3.2 相关指标计算
3.2.1 线路连通率
基于不同应急方案下地铁线路的结构完整状况,方案1恢复了13个站点的运行,线路连通率为52%,方案2与方案3的线路连通率均为100%。
3.2.2 线路抗延误指数
乘客的期望出行时间可分为站内候车时间与车上时间,在采取应急运行措施时,乘客可能需要经过1次甚至多次换乘才能到达目的地。根据长沙地铁4号线早高峰运营时刻表,可以得到正常运行状态下的出行时间矩阵T0,从站点i乘车至站点j的期望出行时间为tij。由于各路段列车的运行速度和停靠时间与普通早高峰一致,因此车上时间与普通早高峰相同,故得到突发事件下的出行时间矩阵T′,从站点i乘车至站点j的期望出行时间t′ij为
t′ij=tij-Wi+∑Wk;
(6)
(7)
式中:Wi为正常运营时乘客在i站乘车的期望候车时间;Wk为应急策略下等待k区间列车的期望候车时间;Qk为k区间内的列车往返行驶一次所需时间。
图7展示了计算后得到的不同应急策略下各站点间的期望出行时间矩阵T′1、T′2、T′3。由图7(b)可知,若仅采用小交路运行策略,则小交路范围内的期望出行时间不受影响,而起点或讫点位于小交路外的行程将被完全中断。由图7(c)可知,当对未被破坏的单侧轨道实行单车单轨双向运行策略时,虽然小交路以外的站点都恢复了一部分运输能力,但是所有经过单轨双向运行区间的行程期望出行时间将会显著增长,并且均超过1 h。由图7(d)可知,当对未被破坏的单侧轨道实行3区间单轨双向运行策略时,大部分需要通过单轨双向运行区间的行程期望出行时间明显下降,客流在地铁线路内的转移更为流畅。与正常运行状态相比,延误最大的出行路径期望延误时长约为30 min(1 816 s)。
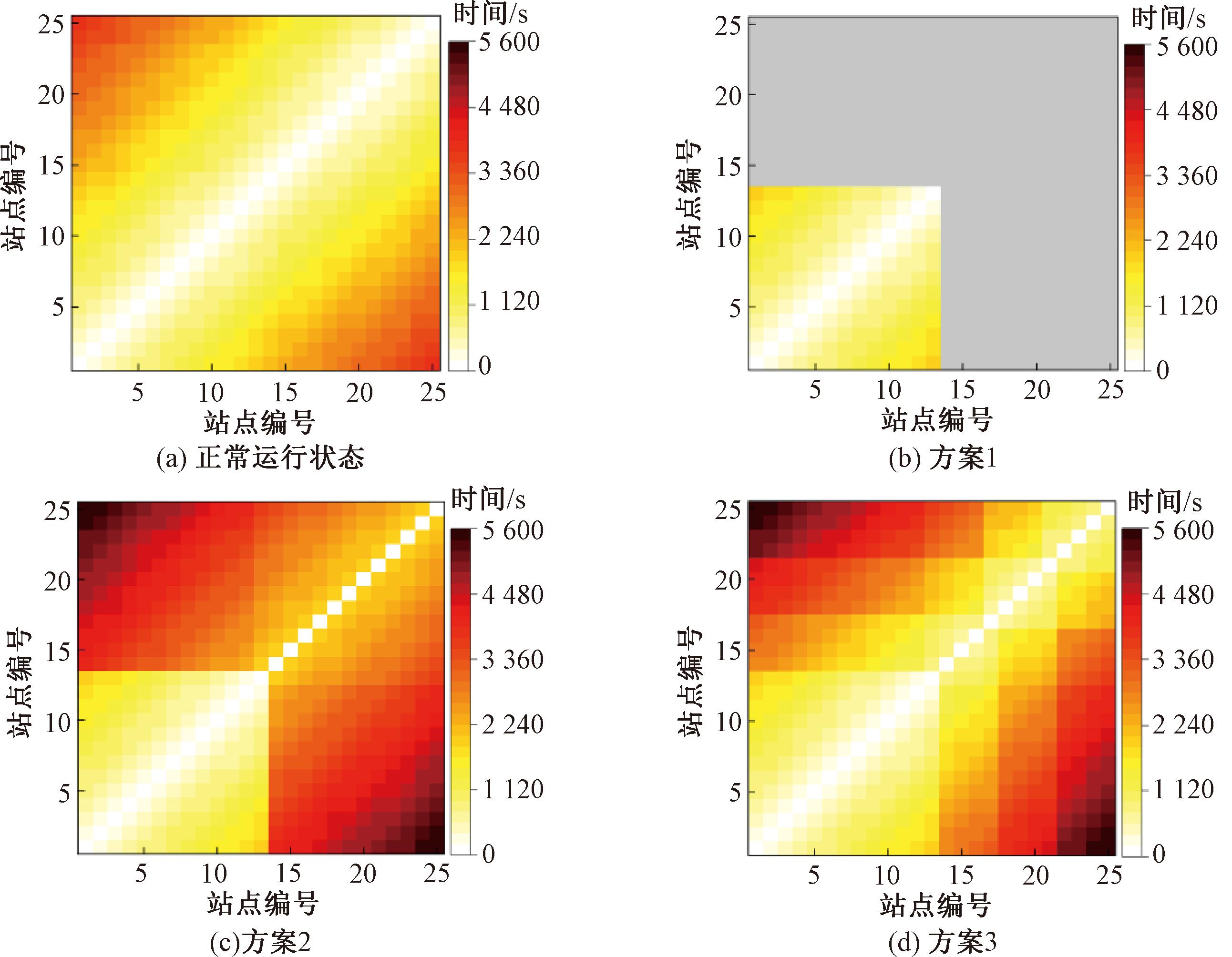
图7 不同响应策略下地铁乘客期望出行时间
Figure 7 Expected travel time of subway passengers with different response strategies
基于前文计算得到的客流OD矩阵C0与突发事件前后的期望出行时间矩阵T0与T′,经式(4)计算可得方案1,2,3的线路抗延误指数ΔD分别等于1.00,0.53,0.69。
3.2.3 线路客流保有率
突发事件下,客流损失主要包含以下3部分。
(1)停运站点客流损失率。方案1中仅维持了罐子岭站到阜埠河站之间的小交路运行。基于3.1.2节中计算得到的客流OD矩阵C0计算得到因线路部分站点停运导致的客流损失率为49.9%。方案2与方案3均维持了4号线全线站点的运行,因此其停运站点客流损失率为0。
(2)响应时间内客流损失率。现有研究大部分通过分析地铁事故期间的客流数据得到地铁突发事件下客流变化特征[19-20]。然而,长沙地铁4号线自开通以来尚未发生造成大面积延误的突发事件,因此本研究利用其他线路的事故案例,探索在突发事件无法准确预估出行时间的背景下客流损失率随时间的变化。
在2019年11月15日07:24,长沙地铁2号线发生设备故障导致全线延误。至09:10,经过地铁专业技术人员的紧急抢修,故障被修复,全线运营恢复正常。本研究对该事故期间的刷卡数据进行分析,筛选出从2号线站点进站后又从同一站点出站的刷卡数据共5 912条,剔除掉等待时间超过1 h的数据后得到乘客等待时间分布,如图8所示。
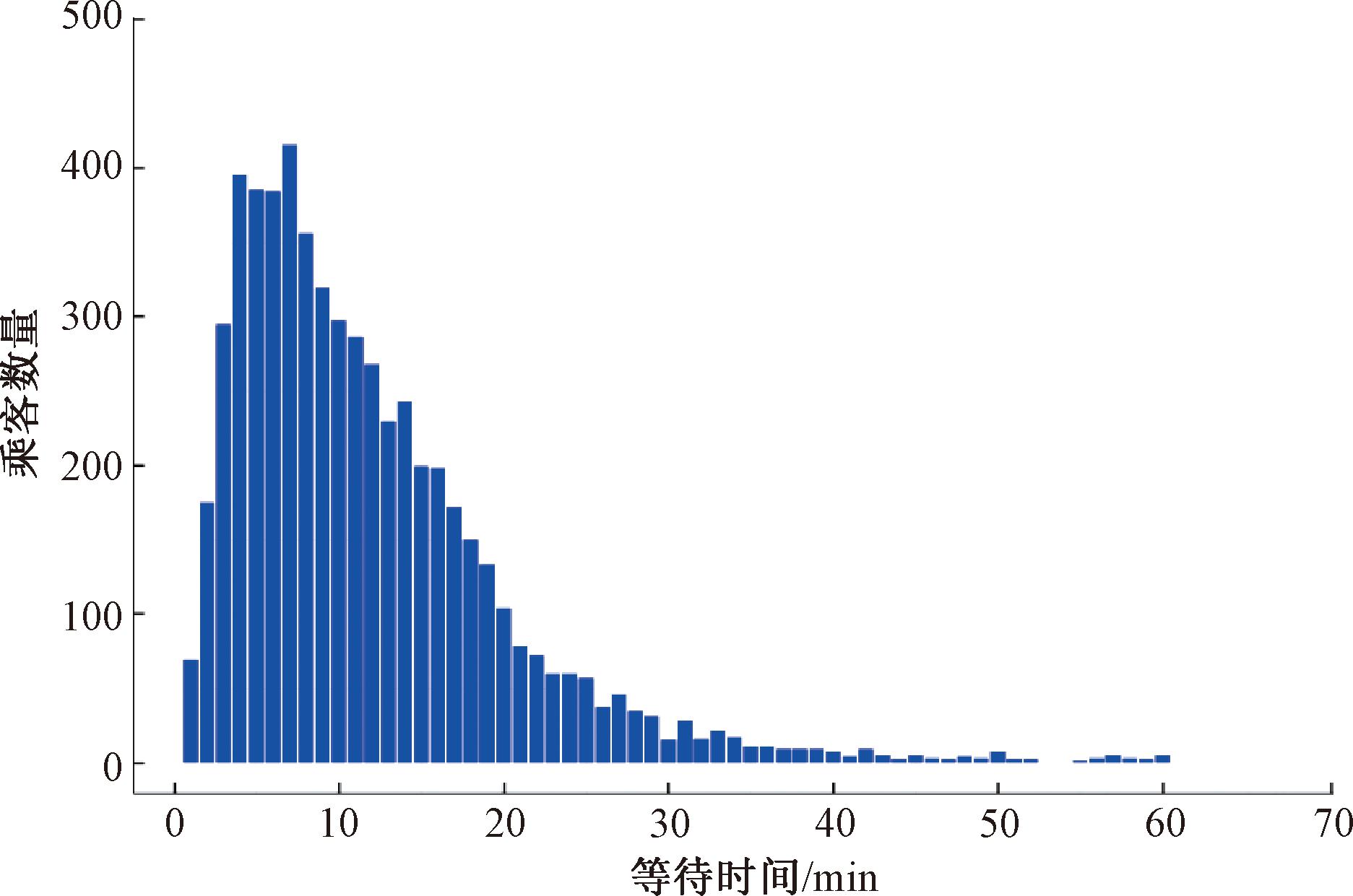
图8 乘客等待时间分布
Figure 8 Passenger waiting time distribution
由图8可知,在面临突发事件时,乘客的平均等待时间为11.8 min。其中,大部分乘客的等待时间集中于5~7 min,等待时间小于10 min的乘客占比53.6%,等待时间超过20 min的乘客所占比例仅为12.1%。图9展示了乘客等待率随等待时间的变化趋势,基于多项式回归模型构建的回归函数f(x)如红线所示。由图9可知,在发生突发事件时,由于无法估计等待时间,乘客对地铁出行的信心显著降低,因此乘客等待率将在10 min内快速下降至50%以下。接下来,下降速度逐渐减慢,并在大约35 min后,乘客等待率趋近于0。因此,提升应急方案实施效率、降低响应时间将有效减少线路客流损失并提升地铁线路韧性。
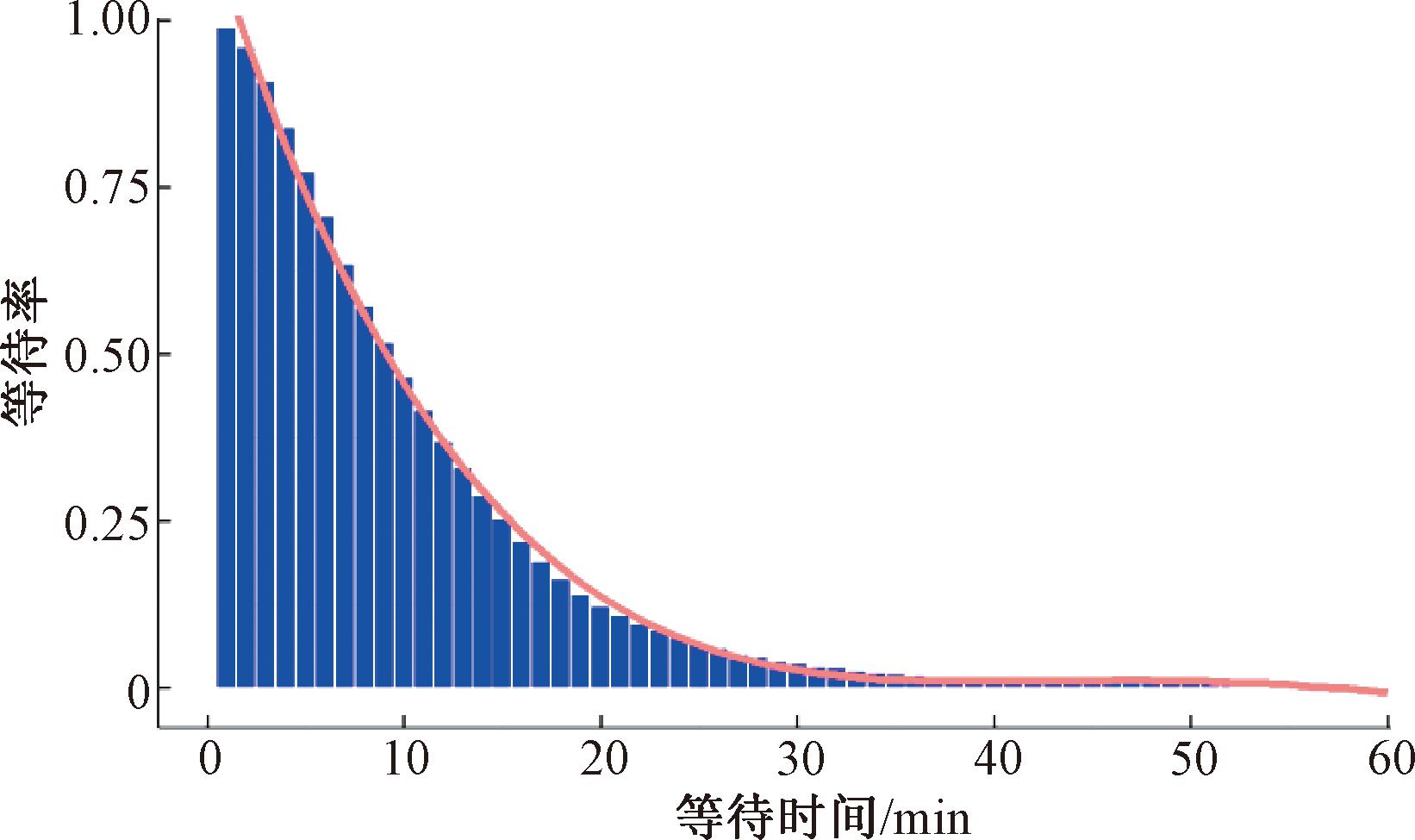
图9 乘客等待率
Figure 9 Passenger waiting rate
响应时间Tr内的客流损失率L为
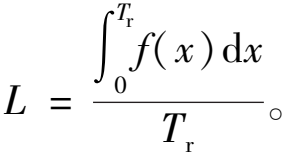
(8)
在地铁线路突发事件下,计算可得15 min应急响应时间内的客流损失率为37.4%,约占总客流的4.7%。
(3)延误客流损失率。当相关部门采取应急响应措施并向乘客提供预估行程时间时,仍会有部分乘客因出行时间的增长而选择换乘别的线路或交通工具(接驳公交、步行、网约车等)。计算得到突发事件下的延误时间矩阵Td=T′-T0;再根据各站点间的客流量估算客流损失率。为了简化计算流程,本文将以表1中的参数近似表述不同延误时间区间内的客流损失率。
表1 客流损失率参数
Table 1 Passenger flow loss rate parameter

延 误 时 间 / m i n 客 流 损 失 率/ % [ 0 , 1 0 ) 5 [ 1 0 , 2 0 ) 1 0 [ 2 0 , 3 0 ) 3 0 [ 3 0 , + ∞ ) 5 0
由于方案1中小交路运行路段的期望出行时间不变,因此其延误客流损失率为0。经计算,方案2与方案3的延误客流损失率分别为18.8%与5.5%。
3.3 方案效果评价
通过以长沙地铁4号线为例的实例分析,首先计算得到本研究提出的新方案(方案3)客流量保有率为90.1%,比方案1高42.4%,比方案2高12.7%。此外,基于本研究提出的地铁线路韧性评价体系,计算得到遇到突发事件时采用方案1的线路韧性为0.22,方案2的线路韧性为0.36,而方案3的线路韧性为0.54,与方案1相比提升了145%,与方案2相比提升了50%。综上所述,可以认为当一条地铁线路发生单侧轨道局部路段中断突发事件的情况下,方案3优于方案2,方案2优于方案1。分析结果体现了新方案的可行性与有效性,计算过程中各参数的计算结果如表2所示。
表2 应急策略下长沙地铁4号线韧性计算结果
Table 2 Calculation result of resilience of Line 4 with emergency strategy

方 案 Tr / m i n Q ( e ) Δ P/ % Δ D 响 应 时 间 内 的 客 流 损 失 率/ % 延 误 客 流 损 失 率/ % 连 通 客 流 损 失 率/ % Δ C/ % Q ( t ) R ( t | e ) 方 案 1 1 5 0 5 2 1 . 0 0 4 . 7 0 4 9 . 9 4 7 . 7 0 . 2 5 0 . 2 2 方 案 2 1 5 0 1 0 0 0 . 5 3 4 . 7 1 8 . 8 0 7 7 . 4 0 . 4 1 0 . 3 6 方 案 3 1 5 0 1 0 0 0 . 6 9 4 . 7 5 . 5 0 9 0 . 1 0 . 6 2 0 . 5 4
4 结论
针对日益频发的城市轨道交通突发事件,本文从提高系统韧性角度研究了应急运行策略,主要成果与结论如下。
(1)针对突发事件下地铁性能的变化过程,综合考虑线路连通度、延误时间与客流损失等指标构建了一套地铁线路韧性评估模型。
(2)针对常见的地铁线路单向轨道局部路段中断事件,以韧性最大化为目标提出了一种利用单侧轨道实行多区间单轨双向运行的应急运行策略。
(3)在面临突发事件时,大部分乘客的等待时间集中于5~7 min。随着等待时间增加,乘客等待率急剧下降,在10 min内快速下降至50%以下。
(4)对长沙地铁4号线进行的实例分析表明,与传统的小交路运行方案和单轨双向运行方案相比,多区间单轨双向运行方案的客流保有率分别提升了44.7%与12.7%,线路韧性分别提升了145%和50%。
与其他研究相比,本文更全面地考虑了导致地铁延误或中断的事件的实际特征,所提出的地铁线路韧性评估模型填补了单地铁线路韧性研究领域的空白。然而本研究仍然存在不足之处,比如客流损失率的计算仅为大概估计,尚未有精准可靠的模型对突发事件发生后的客流变化进行预测;此外,在采取应急响应策略时未考虑到通过提升地铁列车速度等方式进一步提升地铁运行性能。在接下来的研究中将尝试基于新的应急响应策略重新安排列车时刻表,保障列车快速平稳运行,并进一步提升地铁线路韧性。
[1] 中国城市轨道交通协会. 城市轨道交通2022年度统计和分析报告[R/OL].(2023-03-31)[2024-01-05]. https:∥mp.weixin.qq.com/s?__biz=MzI3NzMwODY3OQ==&mid=2247556041&idx=1&sn=599ad2f2a5b5d8692a3ceee2b34a44e1&chksm=a703ff2e681d7e0552c9c9a46e565f64e3d33db91942ba3f2a74b4e74f54cb8b404be87e0e64&scene=27.
China Urban Rail Transit Association. Statistical and analysis report on urban rail transit in 2022 [R/OL]. (2023-03-31) [2024-01-05]. https:∥mp.weixin.qq.com/s?__biz=MzI3NzMwODY3OQ==&mid=2247556041&idx=1&sn=599ad2f2a5b5d8692a3cee e2b34a44e1&chksm=a703ff2e681d7e0552c9c9a46e565f 64e3d33db91942ba3f2a74b4e74f54cb8b404be87e0e64&s cene=27.
[2] ZHANG S Y, LO H K. Metro disruption management:optimal initiation time of substitute bus services under uncertain system recovery time[J]. Transportation Research Part C: Emerging Technologies, 2018, 97: 409-427.
[3] PERELMUTER M. Quantifying passenger impact of disruptions on metro lines[D]. Boston:Massachusetts Institute of Technology, 2020.
[4] 杨琦, 张雅妮, 周雨晴, 等. 复杂网络理论及其在公共交通韧性领域的应用综述[J]. 中国公路学报, 2022, 35(4): 215-229.
YANG Q, ZHANG Y N, ZHOU Y Q, et al. A review of complex network theory and its application in the resilience of public transportation systems[J]. China Journal of Highway and Transport, 2022, 35(4): 215-229.
[5] NAN C, SANSAVINI G. A quantitative method for assessing resilience of interdependent infrastructures[J]. Reliability Engineering &System Safety, 2017, 157: 35-53.
[6] 交通运输部. 交通强国建设评价指标体系[EB/OL].[2024-01-05]. https:∥xueshu.baidu.com/usercenter/paper/show?paperid=1v560tx0aa2m0ef0rn0r0vm0dn325416&site=xueshu_se.
Ministry of Transport. Evaluation index system for the construction of a strong transportation country[EB/OL]. [2024-01-05] https:∥xueshu.baidu.com/usercenter/paper/show?paperid=1v560tx0aa2m0ef0rn0r0vm0dn32 5416&site=xueshu_se.
[7] ADNAN M, PEREIRA F C, AZEVEDO C L, et al. Evaluating disruption management strategies in rail transit using SimMobility mid-term simulator: a study of Singapore MRT North-East line[C]∥ Transportation Research Board 96th Annual Meeting. Washington DC: TRB,2017:1-16.
[8] YANG J F, JIN J G, WU J J, et al. Optimizing passenger flow control and bus-bridging service for commuting metro lines[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(6): 458-473.
[9] WANG Y, ZHOU Y, YANG H, et al. Integrated optimization of bus bridging service design and passenger assignment in response to urban rail transit disruptions[J]. Transportation Research Part C: Emerging Technologies, 2023, 150: 104098.
[10] ITANI A, ABOUDINA A, DIAB E, et al. Managing unplanned rail disruptions:policy implications and guidelines towards an effective bus bridging strategy[J]. Transportation Research Record: Journal of the Transportation Research Board, 2019, 2673(4): 473-489.
[11] NGO N S. Urban bus ridership, income, and extreme weather events[J]. Transportation Research Part D: Transport and Environment, 2019, 77: 464-475.
[12] 陈昕. 基于多源数据的城市地铁系统运营事故特征分析与延误时间预测[D]. 南京: 东南大学, 2022.
CHEN X. Unplanned disruptions characteristics analysis and operational delay prediction in urban railway systems based on multi-source data[D].Nanjing: Southeast University, 2022.
[13] ZHANG S, CHENG Y Q, CHEN K M, et al. A general metro timetable rescheduling approach for the minimisation of the capacity loss after random line disruption[J]. Transportmetrica A: Transport Science, 2024, 20(3): 1-25.
[14] PAN S Z, YAN H, HE J, et al. Vulnerability and resilience of transportation systems:a recent literature review[J]. Physica A: Statistical Mechanics and Its Applications, 2021, 581: 126235.
[15] GUO J W, XIE Z Q, LI Q L, et al. Railway passenger flow recognition algorithm for terminal station based on cost theory and automatic frequency control[J]. IEEE Access, 2020, 8: 26885-26892.
[16] WU J R, LU S G, GE Y E. Identifying factors impacting customers′ perceived waiting time in high density passenger flow waiting areas[J]. Procedia-social and Behavioral Sciences, 2013, 96: 1801-1811.
[17] 戴延泽, 占曙光. 考虑碳排放的城轨开行大小交路方案分析[J]. 铁道科学与工程学报, 2022, 19(12): 3546-3556.
DAI Y Z, ZHAN S G. Analysis of full-length and short-turn routing of urban rail transit considering carbon emission[J]. Journal of Railway Science and Engineering, 2022, 19(12): 3546-3556.
[18] 新民晚报. 上海地铁2号线故障5小时 500多名乘客走出隧道[EB/OL]. [2024-01-05]. https:∥m.haiwainet.cn/middle/456689/2015/0311/content_28510864_1.html.
Xinmin Evening News.More than 500 passengers walked out of the tunnel in 5 hours after the failure of Shanghai Metro Line 2[EB/OL].[2024-01-05]. https:∥m. haiwainet.cn/ middle/ 456689/ 2015/ 0311/ content _28510864_1. html.
[19] CHEN E H, YE Z R, WANG C, et al. Subway passenger flow prediction for special events using smart card data[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(3): 1109-1120.
[20] XING J D, YIN X L, ZHANG J, et al. Resilience modeling and improvement of metro systems considering statistical behaviors of passenger mobility[J]. International Journal of Disaster Risk Reduction, 2023, 96: 103975.