山区公路施工通常具有地质条件复杂、技术难度大的特点。因此,在保证安全的前提下,选出一条经济合理、技术可行的路线尤为重要[1]。路线优选是复杂的多目标决策问题[2],目前的评价方法大多先建立评价体系,然后对各指标进行定性或定量处理,评价结果受各指标的值和权重影响较大[3]。然而,由于路线优选中定性指标具有模糊性、离散性、随机性等不确定性特征,定性指标与定量指标之间无法对比和统一,单一的评价方法难以有效使定性和定量指标相结合。在对定性指标量化时存在个人主观性强的问题[4-5],且较少考虑定性指标不确定性对评价结果的影响[6]。经研究发现,云模型能考虑到定性指标本身所具有的多种不确定性信息[7],对定性评价模糊语言做出具体转换,有效解决了定性指标量化过程中的主观性和不确定性等问题[8]。
在对各指标权重计算及方案评价方面,孙庆珍等[2]建立了山区公路线路评价的指标体系,并求解出了各指标的权重,建立了基于多目标决策的山区公路线路评价模型;邬晓光等[9]指出多属性决策问题各指标间具有优先级的特点,增加专家权向量修正,确定其优先级关系,结合TOPSIS方法对厦蓉高速公路隧道改扩建施工方案进行了评价及优选;鲁海军等[10]针对公路选线方案决策中涉及多维度相互影响数据信息的问题,基于模糊层次分析法对公路路线方案进行评价。然而,现有公路线路方案评价模型中指标权重的确定仅考虑了指标本身的相对重要性,而未考虑不同实际状况中各指标的状态值和各指标组合状态下对权重的影响[11]。现有方案常采用常权权重[12-13],在进行方案评价时容易忽视各指标在极值和突变情况下对评价结果的影响,而变权理论可根据同一指标的实际状态值调整对应权重,其结果相对于常权权重更加合理。
基于上述分析,本文拟建立山区公路线路方案评价指标体系,采用云模型理论量化定性评价指标,基于变权理论[14-15]对常权权重进行修正,最后采用TOPSIS法对山区公路各备选线路方案进行评价,选出最佳线路方案。
1 基于云模型的定性指标量化
1.1 云模型数字特征与基本原理
云模型理论通过3个数值特征P(Ex,En,He)完成定性概念与定量数值之间的转换,首先将一个定性概念用与其对应的某个数值特征P(Ex,En,He)来描述,其中Ex为期望;En为熵,表示指标的模糊程度;超熵He表示指标的离散程度。然后利用云模型的计算机模拟将P(Ex,En,He)进行具体的数字化[16],具体步骤如下。
步骤1 利用正态分布原理,生成模拟数Es=Norm(En,(He)2),其中En和(He)2分别表示期望和方差;
步骤2 以Ex和(Es)2为期望和方差,利用正态分布原理,生成模拟数xi=Norm(Ex,(Es)2);
步骤3 计算隶属度![]() 可得到一个云滴(xi, v(xi));
可得到一个云滴(xi, v(xi));
步骤4 重复上述步骤,即可生成n个云滴,然后取其平均值。
1.2 定性指标量化
针对线路方案中定性指标具有模糊性、不确定性的特点,引入语言类模糊数对定性指标进行评价。将公路线路方案的评价指标分为成本型(属性值越小越优型指标)和效益型(属性值越大越优型指标)。定性指标评价得分范围为0~100分,与之相对应的评语区间见表1[17]。定性概念C(Ex,En,He)对应各评语区间的数值特征由式(1)~(3)计算。根据各定性指标的云模型参数,通过正向云发生器[18]得到的随机云滴即为该指标的量化结果。
Ex=(amax+amin)/2;
(1)
En=(amax-amin)/6;
(2)
He=ρ。
(3)
表1 语言类模糊数和区间数的转换
Table 1 The conversion between linguistic fuzzy numbers and interval numbers

定 性 评 价 成 本 型 效 益 型 评 语 区 间 很 低 很 大 很 差 ( 0 , 2 0 ) 低 大 差 ( 2 0 , 3 0 ) 较 低 较 大 较 差 ( 4 0 , 5 0 ) 一 般 一 般 一 般 ( 5 0 , 6 0 ) 较 高 较 小 较 好 ( 6 0 , 7 0 ) 高 小 好 ( 7 0 , 9 0 ) 很 高 很 小 很 好 ( 9 0 , 1 0 0 )
式中:amax、amin分别为评语区间的最大值和最小值;ρ为标识定性指标模糊程度的常数,根据实际情况取值。
2 基于变权理论的指标权重计算
山区公路线路方案评价中指标权重多是根据各指标本身相对重要性确定的静态常权权重[12-13],但以常权权重应用于不同的实际工程未考虑各指标状态值的变化对评价结果的影响,导致最终评价结果不能准确反映实际情况,存在一定局限性。例如某工程评价方案有3个,分别为Ⅰ、Ⅱ、Ⅲ,评价方案中包含安全性m及经济性n两个指标,其权重都为0.5,则该方案常权权重下评分计算如式(4)所示:
P=0.5m+0.5n。
(4)
式中:P代表方案所得评分。
假设方案Ⅰ、Ⅱ、Ⅲ的安全性与经济性指标分值分别为mⅠ=60,nⅠ=40;mⅡ=90,nⅡ=10;mⅢ=10,nⅢ=90,则方案Ⅰ、Ⅱ、Ⅲ得分都为50。依据最终得分,3个方案都可作为施工方案,从安全性考虑,方案Ⅱ安全性得分最高,但经济性方面得分过低,方案Ⅲ与方案Ⅱ相反。综上分析,虽然3个方案在常权权重下得分相同,但方案Ⅰ最具可行性。
为弥补常权权重的不足,汪培庄[19]率先提出变权思想,Li等[20]在此基础上给出了变权的公理化定义。变权权重通过各因素之间的联系,考虑其本身的相对重要性并根据各指标的实际情况对常权权重进行修正,使指标权重值能随着评价指标状态值的改变而变化。设![]() 为因素常权权重,矩阵Xj=(x1, x2, …, xn)为因素状态变量,Sj(X)=(S1(X), S2(X), …, Sn(X))为状态变权向量,则变权权重Wj(X)=(ω1(X), ω2(X), …, ωn(X))如式(5)所示:
为因素常权权重,矩阵Xj=(x1, x2, …, xn)为因素状态变量,Sj(X)=(S1(X), S2(X), …, Sn(X))为状态变权向量,则变权权重Wj(X)=(ω1(X), ω2(X), …, ωn(X))如式(5)所示:


(5)
式中:w′j为因素常权权重中第j个权重,j∈(1, 2, …, n)。
3 多属性决策模型
TOPSIS法是一种常用的多属性决策方法,通过计算各方案距多属性决策的正、负理想值进行排序并求解[21],其基本步骤如下。
步骤1 假设有m个评价方案,A={A1, A2, …, Am},n个评价指标,C={C1, C2, …, Cn},方案Ai在指标Cj下的取值为xij(i=1, 2, …, m; j=1, 2, …, n),则多属性决策矩阵见式(6):
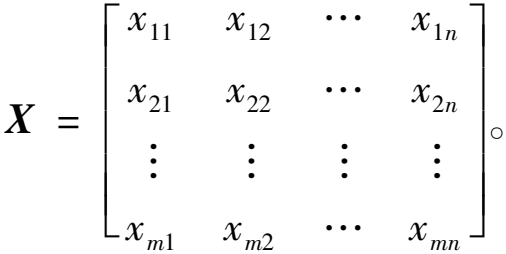
(6)
步骤2 采用式(7)和式(8)对指标进行标准化计算,消除不同量纲的影响,得到矩阵Y1。
效益型指标标准化处理公式:
(7)
成本型指标标准化处理公式:
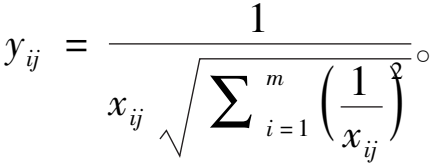
(8)
式中:xij为第i个方案在第j个指标的原始值;yij为数据标准化后第i个方案在第j个指标的值。
步骤3 构建加权规范化决策矩阵:设指标权值为w=[w1, w2, …, wn]T,0<wj<1且![]() 加权规范化矩阵Y2=(uij)m×n,则有uij=wj×yij (i=1, 2, …, m; j=1, 2, …, n)。
加权规范化矩阵Y2=(uij)m×n,则有uij=wj×yij (i=1, 2, …, m; j=1, 2, …, n)。
步骤4 确定正、负理想解![]()
(9)
(10)
式中:uij为数据加权后第i个方案在第j个指标的值;J+代表效益型指标集合;J-为成本型指标集合。
步骤5 计算各方案与正、负理想解的距离![]()
(11)
(12)
步骤6 计算各方案的贴近度:
(13)
式中:Di表示第i方案与最优方案的贴近程度,其值越大,方案越优。
4 线路方案评价计算
4.1 工程概况
艾尔西亚公路是玻利维亚四号公路的关键节点,其中的四号风险点全长5.2 km,是项目施工难度最大的路段。该区域现有公路路况较差,最大纵坡达到10%。该路段要尽量避开黑淤泥体区域,还要满足纵坡不能大于8%的规范要求。根据现场实际地形条件和地质状况,设计方提供了3种路线方案,如图1所示。
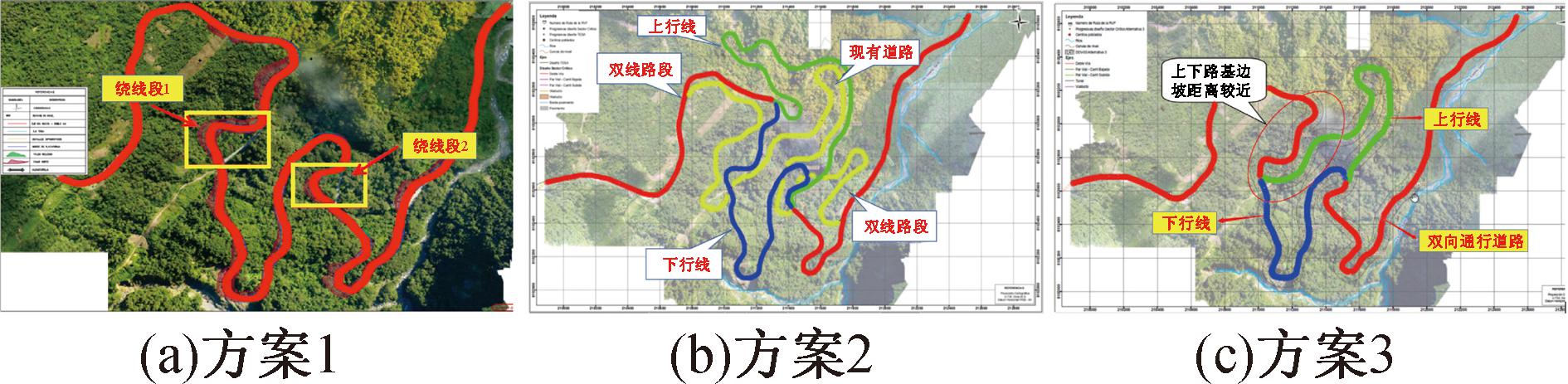
图1 方案1~3设计平面图
Figure 1 Plan view of scheme 1~3
方案1:维持现有道路线形不变,在现有道路的基础上进行拓宽升级改建;对现有道路的平、纵曲线进行优化,在具备条件的地方增加绕线段,改善道路纵坡及行车条件。
方案2:采用分离式路基,在现有道路左侧新修建一条绕山路段作为上行线,使上行线坡度降低,现有道路经过升级改造后作为下行线。
方案3:采用分离式路基,分别修建上行线和下行线,与方案二不同之处在于增加了双线路段的长度,缩短了下行线的长度。
4.2 构建评价指标体系
评价指标体系的构建应遵循科学性、典型性、综合性、系统性和实用性原则[22-24]。本文从技术性、经济性和安全性三方面对线路方案的影响因素进行识别,参考霍尔三维结构,从“时间维、知识维、逻辑维”对线路方案评价影响因素进行分析,如图2所示,初步识别的影响因素如表2所示。对表2中的影响因素进行分析,构建山区公路线路方案评价指标体系如图3所示。
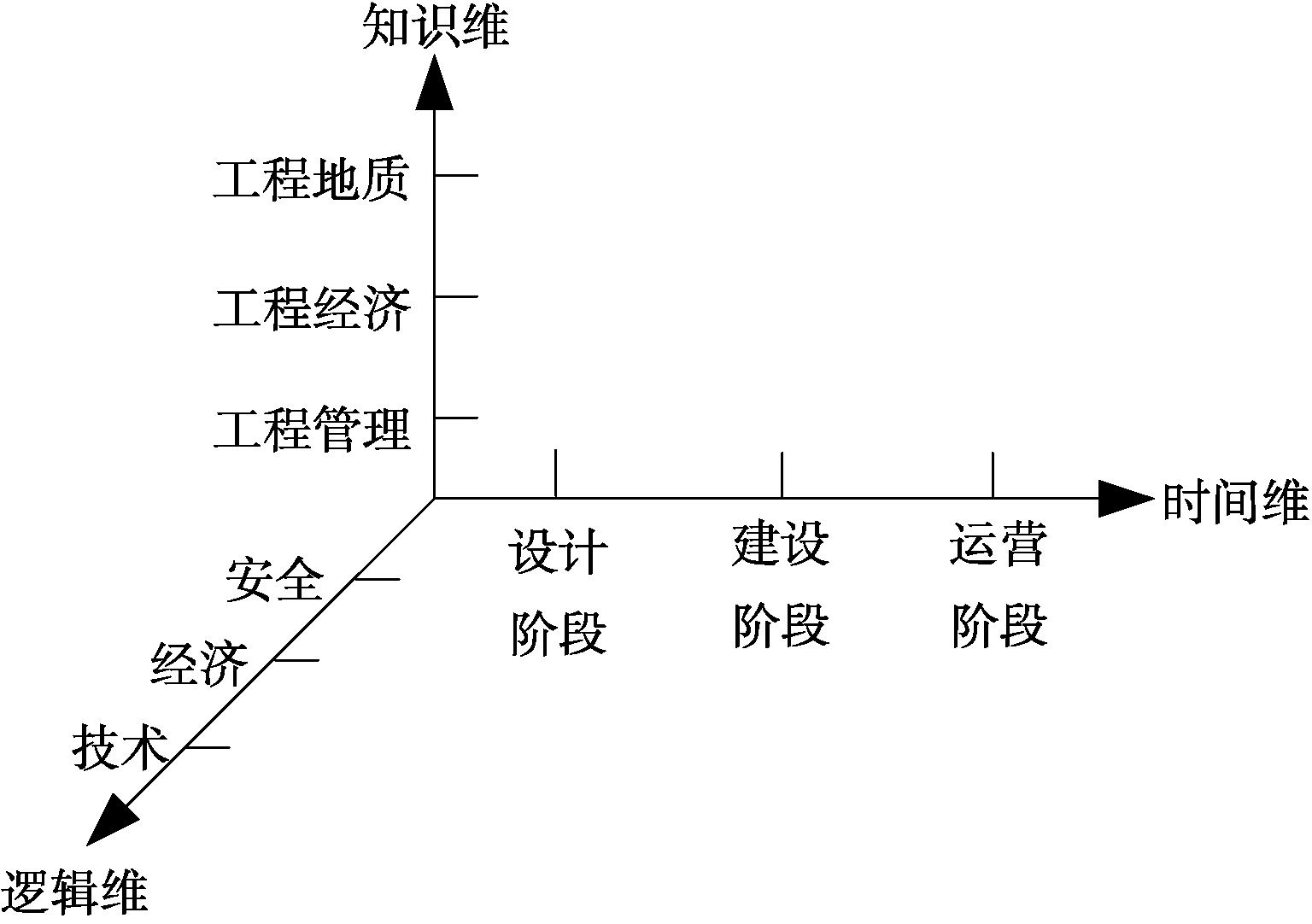
图2 基于霍尔三维结构的线路方案评价影响因素识别
Figure 2 Identification of evaluation factors for route plans based on the Holl three-dimensional structure
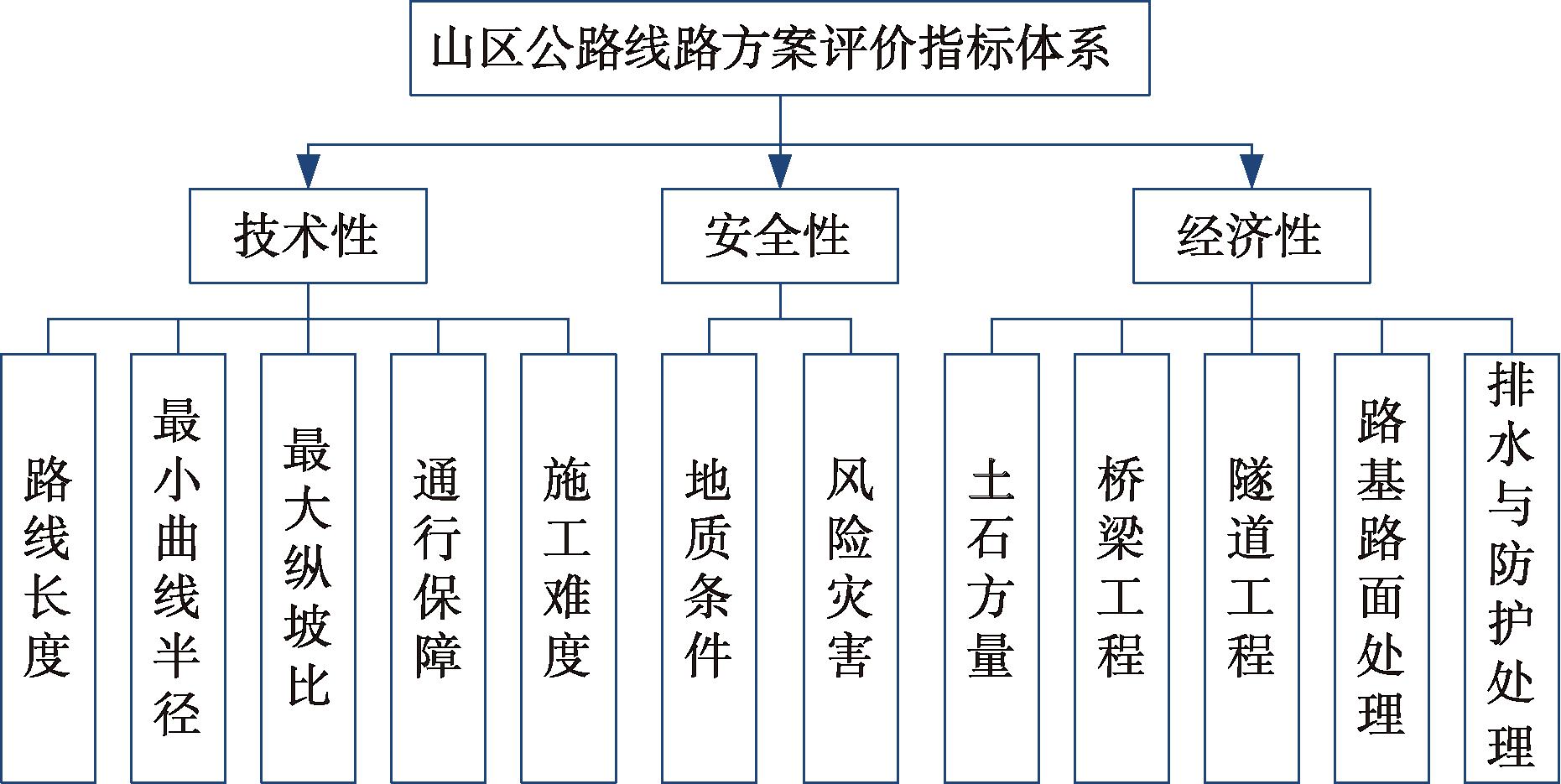
图3 山区公路线路方案评价指标体系
Figure 3 Evaluation index system for highway route evaluation in mountainous areas
表2 线路方案评价影响因素初步识别表
Table 2 Preliminary identification table of influencing factors for route evaluation

影响因素 设计阶段 建设阶段 运营阶段 技 术 经 济 安 全 技 术 经 济 安 全 技 术 经 济 安 全 路线长度 √ √ √ √ √ 最小圆曲线半径 √ √ √ 最大纵坡比 √ √ √ 施工难度 √ √ 交通量 √ √ √ 通行保障 √ √ √ 土石方量 √ √ 隧道工程 √ √ 桥梁工程 √ √ 涵洞工程 √ √ 路基路面处理 √ √ 排水与防护处理 √ √ 地质条件 √ √ √ 滑坡 √ √ √ 塌方 √ √ √ 泥石流 √ √ √ 路基变形沉降 √ √ √
注:√表示考虑了该项因素。
4.3 构建决策矩阵
构建的评价指标体系中既有定量指标又含定性指标,结合艾尔西亚公路工程实际情况确定各评价指标的值如表3所示。根据云模型计算方法和表1的转换规则,结合评语区间的最值和各评价指标的特征,利用式(2)计算其熵值。根据文献[16]中超熵取值,将表2中定性指标转化为定量得分,结果见表4。结合表3和表4得到线路方案的决策矩阵,并根据式(7)~(8)得到规范化决策矩阵Y1:
 。
。
表3 各线路方案评价指标值
Table 3 The values of evaluation indicators for each route plans

指标 指标值 方案 1 方案 2 方案 3 指标 类型 路线长度 C1 / km 3 913 6 644 6 014 定量 最小曲线半径 C2 / m 46 42 42 定量 最大纵坡比 C3 / % 7. 9 5. 4 6. 8 定量 施工难度 C4 小 一般 大 定性 通行保障 C5 较差 较好 较好 定性 土石方量 C6 / m 3 1 221 919 1 279 657 2 910 417 定量 桥梁工程 C7 / m 0 215 260 定量 隧道工程 C8 / m 0 130 130 定量 路基路面处理 C9 / m 3 56 848 58 777 63 550 定量 排水及防护处理 C10 / m 3 10 122 10 634 11 423 定量 地质条件 C11 小 较大 较大 定性 风险灾害 C12 小 一般 很差 定性
表4 定性指标量化结果
Table 4 Quantitative results of qualitative indicators

定 性 指 标 云 模 型 描 述 得 分 方 案 1 方 案 2 方 案 3 方 案 1 方 案 2 方 案 3 C 4 ( 8 0 , 3 . 3 3 3 3 , 0 . 0 2 ) ( 5 5 , 1 . 6 6 6 7 , 0 . 0 2 ) ( 3 0 , 1 . 6 6 6 7 , 0 . 0 2 ) 8 3 . 5 6 6 2 5 5 . 6 5 1 7 3 0 . 6 2 7 1 C 5 ( 4 5 , 1 . 6 6 6 7 , 0 . 0 2 ) ( 6 5 , 1 . 6 6 6 7 , 0 . 0 2 ) ( 6 5 , 1 . 6 6 6 7 , 0 . 0 2 ) 4 4 . 3 6 9 5 6 5 . 8 4 2 8 6 5 . 3 7 1 6 C 1 1 ( 8 0 , 1 . 6 6 6 7 , 0 . 0 2 ) ( 4 5 , 1 . 6 6 6 7 , 0 . 0 2 ) ( 4 5 , 1 . 6 6 6 7 , 0 . 0 2 ) 8 4 . 3 3 7 9 4 4 . 3 9 8 1 4 5 . 1 5 7 1 C 1 2 ( 8 0 , 3 . 3 3 3 3 , 0 . 0 2 ) ( 5 5 , 1 . 6 6 6 7 , 0 . 0 2 ) ( 1 0 , 3 . 3 3 3 3 , 0 . 0 2 ) 8 3 . 9 6 7 7 5 6 . 1 1 2 4 8 . 3 8 2 4
4.4 构建加权决策矩阵
指数型状态变权向量相较于其他状态变权向量具有拟合能力强、决策特点明显等优点[25]。目前指数型状态变权向量已应用于较多领域。公路线路方案评价目标以安全为主,符合指数型状态变权向量决策要求突出的特点,因此本文选择构建指数型状态变权向量如式(14)所示:
Sj(X)=eαxj。
(14)
式中:α为状态变量因子,α>0时Sj(X)为状态变权向量,α<0时Sj(X)为惩罚型变权向量,α=0时,该模型变为了常权模型;xj为因素状态变量中第j个变量。
通过式(7)~(8)对各公路线路方案中的原始评价指标值处理后,各指标值统一为[0,1],此时指标值越小表示指标越差[26],因此Sj(X)为惩罚型状态变权向量,即α<0 [27-28],取α=-1。通过式(5)对熵权法[11]确定的评价指标常权权重进行修正,取得各方案对应的评价指标变权权重,如表5所示。由表5中评价指标变权权重的值和规范化决策矩阵Y1,得到加权规范化决策矩阵Y2:

表5 各指标常权权重与变权权重
Table 5 The constant weight and variable weight of each index

权 重 C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 8 C 9 C 1 0 C 1 1 C 1 2 常 权 权 重 0 . 0 7 3 8 0 . 1 3 1 2 0 . 0 5 7 9 0 . 0 5 5 4 0 . 0 4 8 7 0 . 0 8 1 5 0 . 1 3 1 2 0 . 0 5 0 3 0 . 0 5 2 2 0 . 0 5 5 4 0 . 1 3 1 2 0 . 1 3 1 2 变 权 权 重 一 0 . 0 6 7 0 0 . 1 1 9 2 0 . 1 4 3 0 0 . 0 5 0 6 0 . 0 4 4 4 0 . 0 7 3 9 0 . 1 1 9 1 0 . 0 4 5 5 0 . 0 4 7 5 0 . 0 5 0 4 0 . 1 1 9 7 0 . 1 1 9 7 变 权 权 重 二 0 . 0 8 9 1 0 . 1 5 8 5 0 . 0 2 5 7 0 . 0 4 0 6 0 . 0 2 3 1 0 . 0 8 2 8 0 . 1 5 8 5 0 . 0 2 9 8 0 . 0 3 4 4 0 . 0 4 0 6 0 . 1 5 8 5 0 . 1 5 8 5 变 权 权 重 三 0 . 0 6 0 7 0 . 1 3 6 1 0 . 0 3 8 6 0 . 0 5 7 4 0 . 0 5 0 3 0 . 0 8 4 4 0 . 1 3 6 1 0 . 0 5 2 1 0 . 0 5 4 1 0 . 0 5 7 4 0 . 1 3 6 1 0 . 1 3 6 7
4.5 结果分析
在规范化决策矩阵Y2的基础上,通过式(9)~(14)分别计算各方案采用常权权重和变权权重的贴近度,如表6所示。
表6 各方案的贴近度计算结果
Table 6 The calculation results of closeness degree for each scheme

方 案 所 采 用 权 重 贴 近 度 方 案 1 方 案 2 方 案 3 常 权 权 重 0 . 8 7 2 2 0 . 6 7 1 1 0 . 6 9 1 9 变 权 权 重 0 . 8 3 2 9 0 . 6 0 5 6 0 . 6 8 4 3
表6中引入变权理论前后所得到的最优线路方案结果相同,方案1的贴近度均远超其他方案,说明方案1为最优线路方案,且本模型在线路方案评价中具有可行性和有效性。各方案采用变权理论求得的贴近度均比常权权重求得的结果小,造成此结果的原因是:各方案中均存在较差指标,本模型通过变权理论增大了这些指标的权重值,突出了较差指标对评估结果的影响。
5 结论
(1)从技术性、经济性、安全性三方面考虑,参考霍尔三维结构识别模型,构建了山区公路线路方案评价指标体系。
(2)通过云模型对指标体系中的定性指标进行量化,有效解决了定性指标存在的模糊性问题。
(3)采用变权理论依据各指标值的实际状态对常权权重进行修正,不仅考虑了指标本身的相对重要性,又兼顾了不同实际情况中评价指标值的作用。
(4)基于构建的评价指标体系、定性指标量化结果和指标的变权权重,采用TOPSIS评价模型进行方案的优劣排序,以艾尔西亚公路项目为例验证了理论成果的可行性,使工程项目在技术、经济和安全方面得到有效保障,为工程建设提供了理论和技术支撑。
[1] 王佐, 汪双杰, 屈强. 山区高速公路复杂路段路线方案的比选论证[J]. 公路, 2007, 52(11): 121-125.
WANG Z, WANG S J, QU Q. Comparison and demonstration of route schemes in complex sections of expressway in mountainous areas[J]. Highway, 2007, 52(11): 121-125.
[2] 孙庆珍, 贾燕, 潘春风. 基于多目标决策的山区灾害多发地段公路选线优化[J]. 武汉大学学报(工学版), 2011, 44(5): 633-637.
SUN Q Z, JIA Y, PAN C F. Research on optimization of disaster-prone mountain route selection based on multiobjective decision making method[J]. Engineering Journal of Wuhan University, 2011, 44(5): 633-637.
[3] 葛巍, 焦余铁, 洪辛茜, 等. 基于AHP-BN法的溃坝生命损失风险评价[J]. 郑州大学学报(工学版), 2021, 42(3): 8-12.
GE W, JIAO Y T, HONG X Q, et al. Risk assessment of life loss caused by dam breach based on AHP-BN method[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(3): 8-12.
[4] 陈俊彦. 基于模糊可拓理论的高速公路选线决策研究[J]. 公路, 2021, 66(2): 79-84.
CHEN J Y. Research on expressway route selection decision based on fuzzy extension theory[J]. Highway, 2021, 66(2): 79-84.
[5] 程轩, 关大勇, 夏杰. 基于IAHP-EWM的高速公路路线方案比选研究[J]. 公路, 2021, 66(2): 63-68.
CHENG X, GUAN D Y, XIA J. Research on comparison and selection of route schemes in expressway based on IAHP-EWM[J]. Highway, 2021, 66(2): 63-68.
[6] 高贺, 夏晓英. 基于可拓理论的公路网规划方案评价研究[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(3): 501-505.
GAO H, XIA X Y. Evaluation based on extension theory highway network planning[J]. Journal of Wuhan University of Technology (Transportation Science &Engineering), 2015, 39(3): 501-505.
[7] 杨恒, 刘永强. 基于PP-云模型的河道治理工程效益评价研究[J]. 水利水电技术, 2020, 51(5): 118-125.
YANG H, LIU Y Q. Study on benefit evaluation of river regulation project based on PP-cloud model[J]. Water Resources and Hydropower Engineering, 2020, 51(5): 118-125.
[8] 张鹏, 钟山, 朱锐, 等. 基于熵权法-云模型的石拱桥技术状况评定[J]. 郑州大学学报(工学版), 2022, 43(1): 69-75.
ZHANG P, ZHONG S, ZHU R, et al. Evaluating technical condition of stone arch bridge based on entropy method-cloud model[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(1): 69-75.
[9] 邬晓光, 贺攀, 苏兴矩, 等. 基于海明距离-TOPSIS法的山区公路隧道扩建方案直觉模糊优选[J]. 隧道建设, 2017, 37(8): 926-932.
WU X G, HE P, SU X J, et al. Intuitionistic fuzzy optimization of enlargement scheme of highway tunnel in mountain areas based on hamming distance-TOPSIS method[J]. Tunnel Construction, 2017, 37(8): 926-932.
[10] 鲁海军, 吴卓凡. 基于FAHP评价体系对公路路线方案的优选与应用[J]. 公路工程, 2020, 45(6): 149-154.
LU H J, WU Z F. Optimization and application of highway route scheme based on FAHP evaluation system[J]. Highway Engineering, 2020, 45(6): 149-154.
[11] 李宗坤, 莫向明, 葛巍, 等. 基于变权集对-可拓耦合模型的溃坝后果综合评价[J]. 工程科学与技术, 2022(5): 64-71.
LI Z K, MO X M, GE W, et al. Comprehensive evaluation of dam-break consequences based on variable weight set pair-extenics coupling model[J]. Advanced Engineering Sciences, 2022(5): 64-71.
[12] 曾一凡, 武强, 杜鑫, 等. 再论含水层富水性评价的“富水性指数法”[J]. 煤炭学报, 2020, 45(7): 2423-2431.
ZENG Y F, WU Q, DU X, et al. Further research on “water-richness index method” for evaluation of aquifer water abundance[J]. Journal of China Coal Society, 2020, 45(7): 2423-2431.
[13] 李坦, 陈天宇, 米锋, 等. 基于变权理论和DPSIRM的中国森林生态安全评价[J]. 中国环境科学, 2021, 41(5): 2411-2422.
LI T, CHEN T Y, MI F, et al. Evaluation of China′s forest ecological security based on variable weight theory and DPSIRM[J]. China Environmental Science, 2021, 41(5): 2411-2422.
[14] 刘守强, 武强, 李哲, 等. 多煤层底板单一含水层矿区突水变权脆弱性评价与应用[J]. 中国矿业大学学报, 2021, 50(3): 587-597.
LIU S Q, WU Q, LI Z, et al. Vulnerability evaluation and application of floor water inrush in mining area with multiple coal seams and single aquifer based on variable weight[J]. Journal of China University of Mining &Technology, 2021, 50(3): 587-597.
[15] WANG Y S, JIN Z X, DENG C B, et al. Comprehensive decision making with fuzzy compromised variable weights and its application on maintenance order for entries in underground coal mine[J]. International Journal of Fuzzy Systems, 2019, 21(5): 1379-1388.
[16] 罗圆, 朱颖, 张小强, 等. 基于变权理论的铁路选线方案评价模型[J]. 铁道工程学报, 2018, 35(8): 16-20, 37.
LUO Y, ZHU Y, ZHANG X Q, et al. Scheme evaluation model of railway location designs based on variable weight theory[J]. Journal of Railway Engineering Society, 2018, 35(8): 16-20, 37.
[17] 高玉祥, 董晓峰, 程建军. 基于云模型和改进TOPSIS的风沙地区线路方案优选方法研究[J]. 铁道科学与工程学报, 2023, 20(2): 526-536.
GAO Y X, DONG X F, CHENG J J. Optimization method of railway route scheme in wind-sand areas based on cloud model and improved TOPSIS[J]. Journal of Railway Science and Engineering, 2023, 20(2): 526-536.
[18] 李巍. 基于云模型及改进可变模糊集合的中国溃坝风险后果评价[D]. 郑州: 郑州大学, 2019.
LI W. Risk consequence assessment of dam break in China based on cloud model and improved variable fuzzy set[D].Zhengzhou: Zhengzhou University, 2019.
[19] 汪培庄. 模糊集与随机集落影[M]. 北京: 北京师范大学出版社, 1985.
WANG P Z. Fuzzy set and random set falling shadow[M]. Beijing: Beijing Normal University Press, 1985.
[20] LI H X, LI L X, WANG J Y, et al. Fuzzy decision making based on variable weights[J]. Mathematical and Computer Modelling, 2004, 39(2/3): 163-179.
[21] 杨玉中, 孟祥中, 刘曦, 等. 基于修正熵权的TOPSIS地下水质评价方法[J]. 郑州大学学报(工学版), 2011, 32(2): 121-124.
YANG Y Z, MENG X Z, LIU X, et al. Technique for order preference by similarity to ideal solution(TOPSIS)based on ameliorated entropy weight on the evaluation of groundwater quality[J]. Journal of Zhengzhou University (Engineering Science), 2011, 32(2): 121-124.
[22] 李宗坤, 李巍, 葛巍, 等. 基于集对分析-可变模糊集耦合方法的溃坝环境影响评价[J]. 天津大学学报, 2019, 52(3): 269-276.
LI Z K, LI W, GE W, et al. Dam breach environmental impact evaluation based on set pair analysis-variable fuzzy set coupling model[J]. Journal of Tianjin University (Science and Technology), 2019, 52(3): 269-276.
[23] 李宗坤, 王特, 葛巍, 等. 基于WBS-RBS和AHP的港珠澳大桥人工岛建设风险分析[J]. 郑州大学学报(工学版), 2020, 41(3): 62-66.
LI Z K, WANG T, GE W, et al. Risk analysis of artificial island construction of Hong Kong-Zhuhai-Macao bridge based on WBS-RBS and AHP methods[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(3): 62-66.
[24] 许林新, 郑秉乾, 吴明先, 等. 多目标综合评价方法在山区高速公路选线中的应用[J]. 公路, 2022, 67(5): 15-19.
XU L X, ZHENG B Q, WU M X, et al. Application of multi-objective comprehensive evaluation method in route selection of expressway in mountainous areas[J]. Highway, 2022, 67(5): 15-19.
[25] 张华, 彭朝晖, 张强, 等. 基于DBN的艾尔西亚高等级公路施工进度风险评估[J]. 郑州大学学报(工学版), 2023, 44(5): 108-113.
ZHANG H, PENG Z H, ZHANG Q, et al. Construction progress risk assessment of el sillar highway based on DBN[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(5): 108-113.
[26] LIU S L, LI W P. Indicators sensitivity analysis for environmental engineering geological patterns caused by underground coal mining with integrating variable weight theory and improved matter-element extension model[J]. Science of the Total Environment, 2019, 686: 606-618.
[27] CHEN J H, CHEN Y, YANG S, et al. A prediction model on rockburst intensity grade based on variable weight and matter-element extension[J]. PLoS One, 2019, 14(6): e0218525.
[28] 杜江, 孙铭阳. 基于变权灰云模型的变压器状态层次评估方法[J]. 电工技术学报, 2020, 35(20): 4306-4316.
DU J, SUN M Y. Hierarchical assessment method of transformer condition based on weight-varying grey cloud model[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4306-4316.