谣言通常被理解为对公众感兴趣的未经证实事件的陈述[1]。谣言在社交网络上的传播不仅阻碍了经济的发展,同时也会引起社会恐慌,扰乱社会正常秩序。例如,在日本核泄漏事件中,有人说食用碘盐可以防止核辐射,导致很多人开始疯狂购买碘盐,造成了社会的恐慌。因此,研究网络谣言传播机制和谣言传播动力学性质,对相关职能部门制定谣言控制策略具有重要理论和实践意义。
考虑到谣言传播与传染病传播具有一定的相似性,Daley等[2]提出了DK谣言传播模型。此后,Maki和Thompson对DK模型做了改进并提出了MK谣言传播模型[3]。二者的不同点在于DK模型是假定传播者与传播者接触时均变为免疫者,而MK模型则假定只有初始传播者变为免疫者。为探索网络结构对谣言传播的影响,Zanette等[4]研究了小世界网络上的谣言传播动力学行为并找到了谣言传播临界值。Moreno等[5]研究了无标度网络上的谣言传播动力学行为。复杂网络[6]根据节点度分布特征,可以将其分为均匀网络和非均匀网络,于是,国内外学者围绕均匀网络和非均匀网络结构下的谣言传播动力学进行了研究[7-12]。例如,Guo等[7]考虑媒体对谣言传播产生的影响,提出了均匀网络结构下的SEIMR谣言传播模型。Tong等[8]考虑网络用户的异质性,构造了一个随机IFCD谣言传播模型。以上研究发现网络结构对谣言传播具有重要影响。
当传播者与未知者接触时,传播者需要一定的时间来考虑是否传播谣言,即在谣言传播过程中可能存在一定的时间延迟。基于此,国内外学者开始研究具有时间延迟的谣言传播模型[13-16]。例如,Cheng等[13]建立XY-ISR谣言传播模型,探讨了社交媒体网络与友谊网络之间的谣言传播过程,同时考虑了交互过程中的时间延迟因素。Chang等[14]考虑了非线性关联和传播过程中存在时间延迟,建立了一个ISCR谣言传播模型。考虑到传播者在传播谣言时可能会受到暂时封号等强制措施使传播者无法传播谣言等因素,Zhu等[17]提出了一个在线社交网络中具有强制静默功能的SAIR谣言传播模型,研究了强制静默对传播者的影响。Zhu等[18]考虑到网络监管、时间延迟和网络拓扑结构,建立了一种新的SIR谣言传播模型。此外,学者们通过引入新的种群,建立具有新种群的谣言传播模型。例如,Pan等[19]考虑媒体报道和辟谣群体的影响,提出了SIDRW谣言传播模型。以上研究表明,时间延迟、强制静默和网络监管对谣言传播具有重要影响。
除网络结构、时间延迟和网络监管外,科学进步和社会发展也赋予谣言一些新的传播特性。因此,本文在SIR模型[18]的基础上,结合辟谣机制、时间延迟、强制静默和空格理论,提出了一个新的SICR谣言传播模型,分别围绕该模型的平衡点存在性、基本再生数和模型在平衡点处的稳定性等动力学性质进行分析。
1 SICR谣言传播模型
在线社交网络中,节点表示个体,节点之间的连接边反映个体之间的互动。鉴于个体的迁入和迁出对网络结构的影响,引入空格节点E。当个体迁出时,对应节点变为空格,而新个体只能安置在这些空格节点上。网络中的其余节点根据不同的状态,可分为易感节点S、感染节点I、辟谣节点C和免疫节点R。每个节点最多被一个个体占据。其中,S表示在线社交网络中没有接触过谣言的人;I表示听闻了谣言并积极传播谣言的人;C表示不相信谣言并积极辟谣的人;R表示听到谣言,但不再对谣言进行传播的人。
SICR谣言传播规则如下:①易感节点S有一个恒定的迁入率b,易感节点S、感染节点I、辟谣节点C和免疫节点R可能以ε的概率注销账号;②易感节点S与感染节点I接触时,可能以概率β转变为感染节点I,也可能以概率η转变为辟谣节点C;③辟谣节点C以φ的概率变成免疫节点R,感染节点I因遗忘谣言,以δ的概率变成免疫节点R;④由于网络监管的存在,部分感染节点I被强制屏蔽,结合强制静默函数的定义[18],设强制静默函数T(I)=σI(t)/(1+αI(t)),其中σ表示强制静默率,α≥0描述为因强制静默而延迟感染的影响程度;⑤当易感节点S遇到感染节点I时,感染节点I在传播谣言时存在时间延迟τ。SICR模型的传播示意图如图1所示。
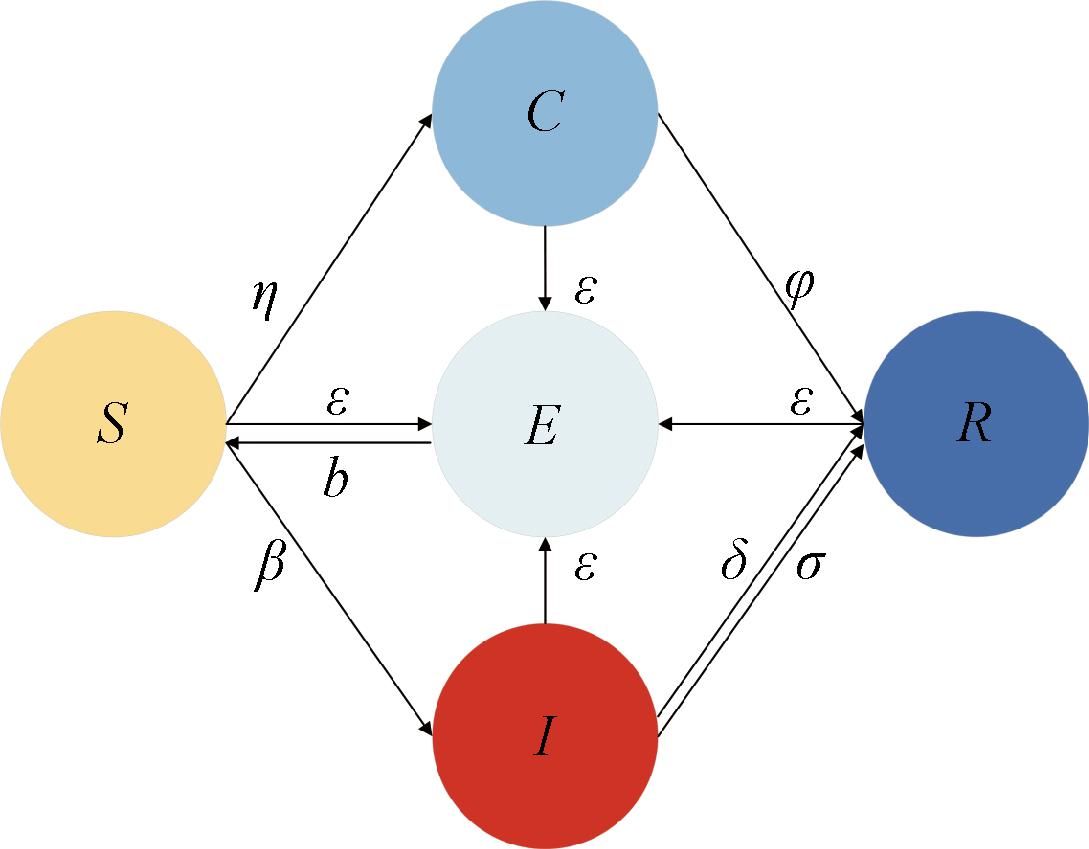
图1 SICR谣言传播模型
Figure 1 SICR rumor propagation model
在t时刻,S(t)、I(t)、C(t)和R(t)分别代表易感节点、感染节点、辟谣节点和免疫节点的密度。其中,E(t)=1-S(t)-I(t)-C(t)-R(t)为空格节点E在t时刻的密度;
表示网络的平均度。根据SICR谣言传播模型的传播机制可以得到该模型在均匀网络上的传播动力学方程:
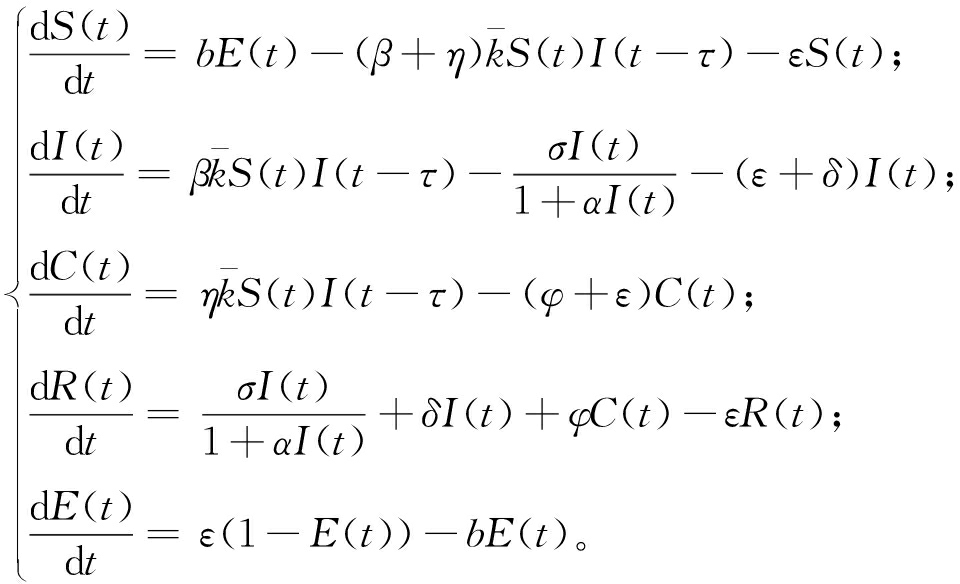
(1)
系统的初始条件为S(θ)=φ1(θ),I(θ)=φ2(θ),C(θ)=φ3(θ),R(θ)=φ4(θ)。其中,θ∈[-τ,0],0≤φi≤1,i=1,2,3,4。
令N(t)=S(t)+I(t)+C(t)+R(t),表示t时刻总种群的密度。由式(1)可得
(2)
由式(2)可得
(3)
结合式(3)和归一化条件有
(4)
将式(4)代入式(1),可以进一步将式(1)化为
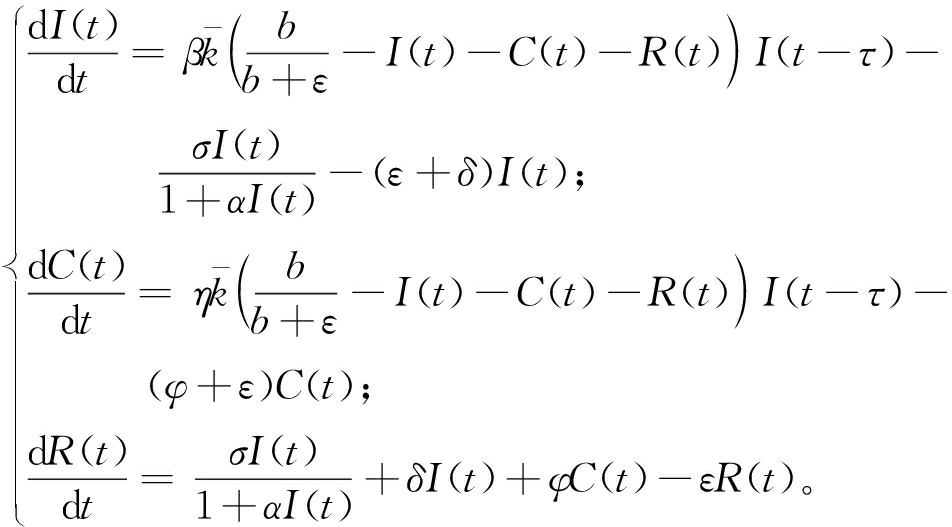
(5)
显然,式(5)的所有可行解均为非负有界,且位于以下正向不变集:
(6)
2 平衡点和基本再生数
基本再生数是评估谣言是否扩散的关键指标,在谣言传播研究中具有重要作用。下面将根据无谣言平衡点E0,利用下一代矩阵法[20]计算模型的基本再生数R0。
无谣言平衡点表示在线社交网络中不存在谣言感染节点,对于式 (5),令所有式子的右端等于0,易知式(5)的无谣言平衡点为E0=(0,0,0)。
令X=[I,C,R]T,可以将系统(5)表示为
(7)
式中:F(X)=
V(X)=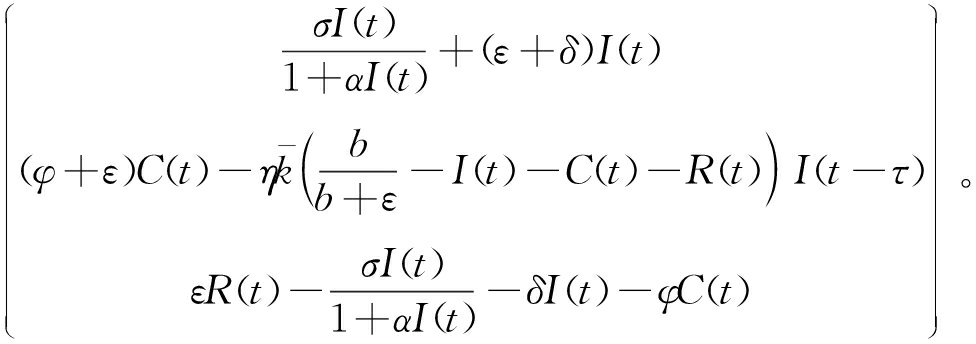
在无谣言平衡点E0处的雅可比矩阵分别为
;
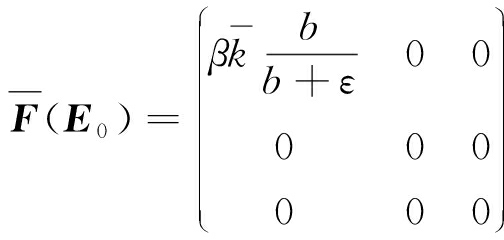(8)
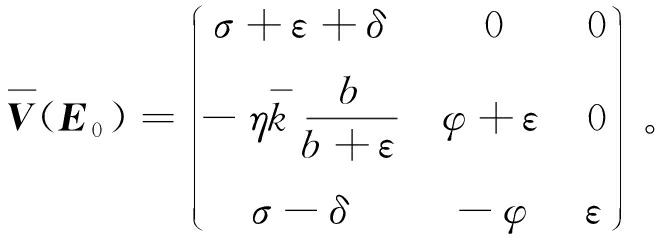
(9)
由下一代矩阵法可得基本再生数R0为
(10)
下面对谣言盛行平衡点的存在性进行分析。假设谣言盛行平衡点E*=(I*,C*,R*),由式(5)可得
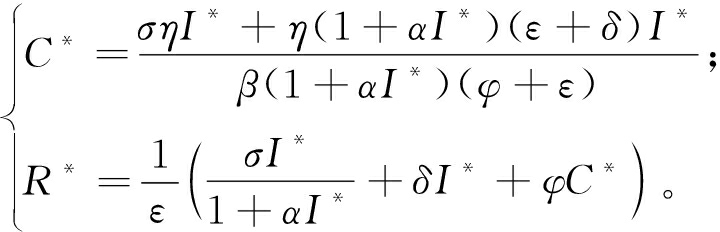
(11)
结合式(5) 和式(11)可得
(12)
根据上述等式,令
M0(I*)2+M1I*+M2=0。
(13)
则有
(ε+δ)(b+ε)εα。
显然M0<0,如果R0>1,那么M2>0,此时方程(13)只有一个正根,意味着式(5)存在唯一的谣言盛行平衡点E*=(I*,C*,R*)。
3 稳定性分析
在控制系统的关键性能指标中,稳定性占据了重要地位,它是确保系统正常运行的前提。下面分别分析系统(式(5))在无谣言平衡点E0=(0,0,0)处的局部渐近稳定性和全局渐近稳定性,以及在谣言盛行平衡点E*=(I*,C*,R*)处的局部渐近稳定性。
3.1 无谣言平衡点E0的稳定性
定理1 如果R0<1,对于∀τ≥0,在无谣言平衡点E0处,系统(式(5))是局部渐近稳定的。
证明 系统(式(5))在E0处的雅可比矩阵为
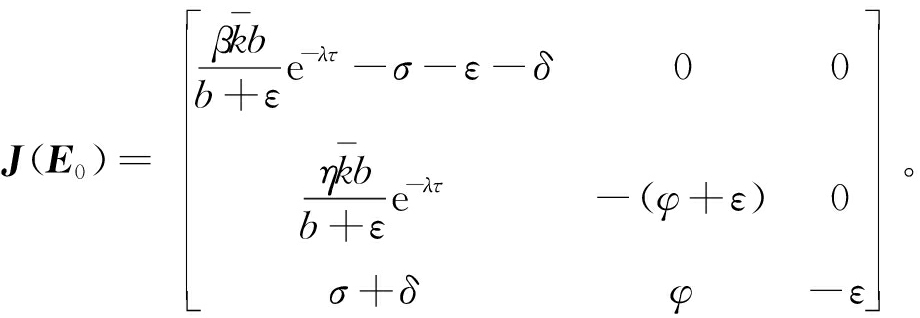
(14)
根据|λE-J(E0)|=0可得特征方程
(15)
(1)当τ=0时,由方程(15)可得
(λ+ε)(λ+φ+ε)[λ-(σ+ε+δ)(R0-1)]=0。
(16)
对应的特征根为λ1=-ε<0,λ2=-(φ+ε)<0,λ3=(σ+ε+δ)(R0-1)。
如果R0<1,那么λ3<0,根据Routh-Hurwitz判据[21-22]可得,在E0处,系统(式(5))是局部渐近稳定的。
(2)当τ>0时,只需考虑:
λ+(σ+ε+δ)(1-R0e-λτ)=0。
(17)
设λ=iω,则有
(18)
将式(18)中的2个等式平方后相加得
ω2=(σ+ε+δ)2(R02-1)。
(19)
如果R0<1,则没有满足式(19)的正实根ω。
综上所述,如果基本再生数R0<1,对于∀τ≥0,在无谣言平衡点E0处,系统(式(5))是局部渐近稳定的。
定理1得证。
定理2 给定
如果Q<1,对于∀τ≥0,在E0处,系统(式(5))是全局渐近稳定的。
证明 构建Lyapunov函数V(t)=V1(t)+V2(t),其中,
V1(t)=I(t)+C(t)+R(t),V2(t)=
I(x)dx。
根据式(5),对V(t)求导可得
令如果Q<1,那么dV(t)/dt≤0。当且仅当I(t)=C(t)=R(t)=0时,有dV(t)/dt=0,式(5)的唯一解是E0=(0,0,0),根据LaSalle不变原理[23],在无谣言平衡点E0处,系统(式(5))是全局渐近稳定的。
定理2得证。
3.2 谣言盛行平衡点E*的稳定性
定理3 对于谣言盛行平衡点E*=(I*,C*,R*),当满足2I*+C*+R*>b/(b+ε)时,如果R0>1,对于∀τ≥0,在谣言盛行平衡点E*处,系统(式(5))是局部渐近稳定的。
证明 式(5)在E*处的雅可比矩阵有以下形式:
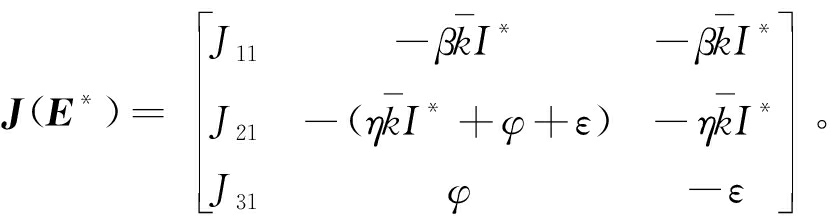
(20)
式中:
根据|λE-J(E*)|=0,可得特征方程
(21)
根据式(21)可得
(22)
式中:
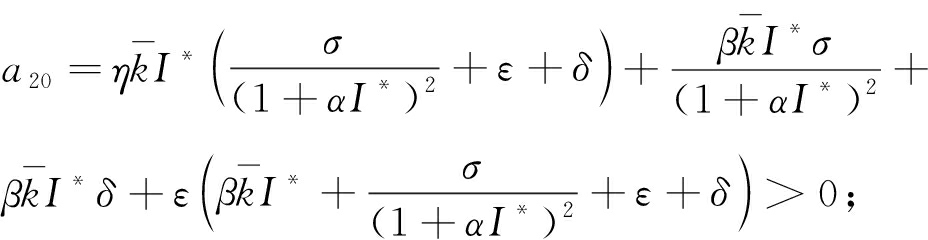
(1)当τ=0时,有
λ2+Aλ+B=0。
(23)
其中,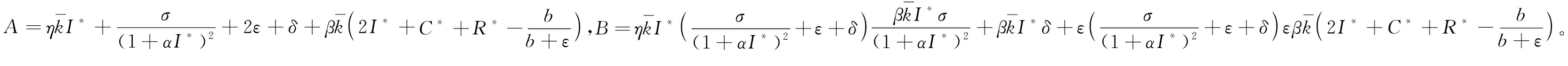
如果2I*+C*+R*>b/(b+ε),那么A>0,B>0,此时方程(23)存在2个负根,根据Routh-Hurwitz判据可知,在E*处,系统(式(5))是局部渐近稳定的。
(2)当τ>0时,令λ=iω为特征方程的根,且满足
λ2+a10λ+a20+(b10λ+b20)e-λτ=0。
(24)
分离实部和虚部得
(25)
将式(25)中的2个等式平方后相加得
ω4+Fω2+G=0。
(26)
式中:
令Z=ω2,方程(26)就等价为
Z2+FZ+G=0。
(27)
其中,如果G>0和F>0可同时满足,那么根据韦达定理可得方程(27)的2个根都为负根,即可证明τ>0情况下,系统(式(5))在E*处的局部渐近稳定性。
由于B=a20+b20,如果A>0,B>0,可得
(28)
其中,
所以有
(29)
如果2I*+C*+R*>b/(b+ε),那么F>0,方程(27)没有正根,此时在E*处,系统(式(5))是局部渐近稳定的。综上所述,当满足2I*+C*+R*>b/(b+ε)时,如果R0>1,对于∀τ≥0,在E*处,系统(式(5))是局部渐近稳定的。
定理3得证。
4 数值仿真
为了验证理论结果的正确性,通过MATLAB进行数值仿真实验。在以下仿真实验中均假设均匀网络的平均度
4.1 基本再生数R0与强制静默率σ、迁入率b和传播率β的关系
在该模型中,强制静默函数为非线性函数,采用强制静默率σ来度量强制静默作用的效果和程度。传播率β反映了谣言的传播能力。因此考虑R0、σ和β三者之间的关系和影响。设参数b=0.4,ε=0.05,δ=0.2,其中σ∈[0,1],β∈[0,1]。由图2(a)可知强制静默率σ越大,R0越小,这说明强制静默措施能够抑制谣言的传播。同理,在图2(b)中考虑R0、b和β三者之间的关系,设参数ε=0.05,δ=0.2,σ=0.3,其中b∈[0,1],β∈[0,1]。通过仿真可知,随着迁入率b和传播率β的增加,基本再生数R0也会随之增加,这导致谣言的传播更加容易。谣言传播有害,控制其传播至关重要。通过等高线图分析相关参数对于R0的影响。由图3可知,将参数分别控制在I～II和I～IV时,有0<R0<1,此时能抑制谣言的传播。
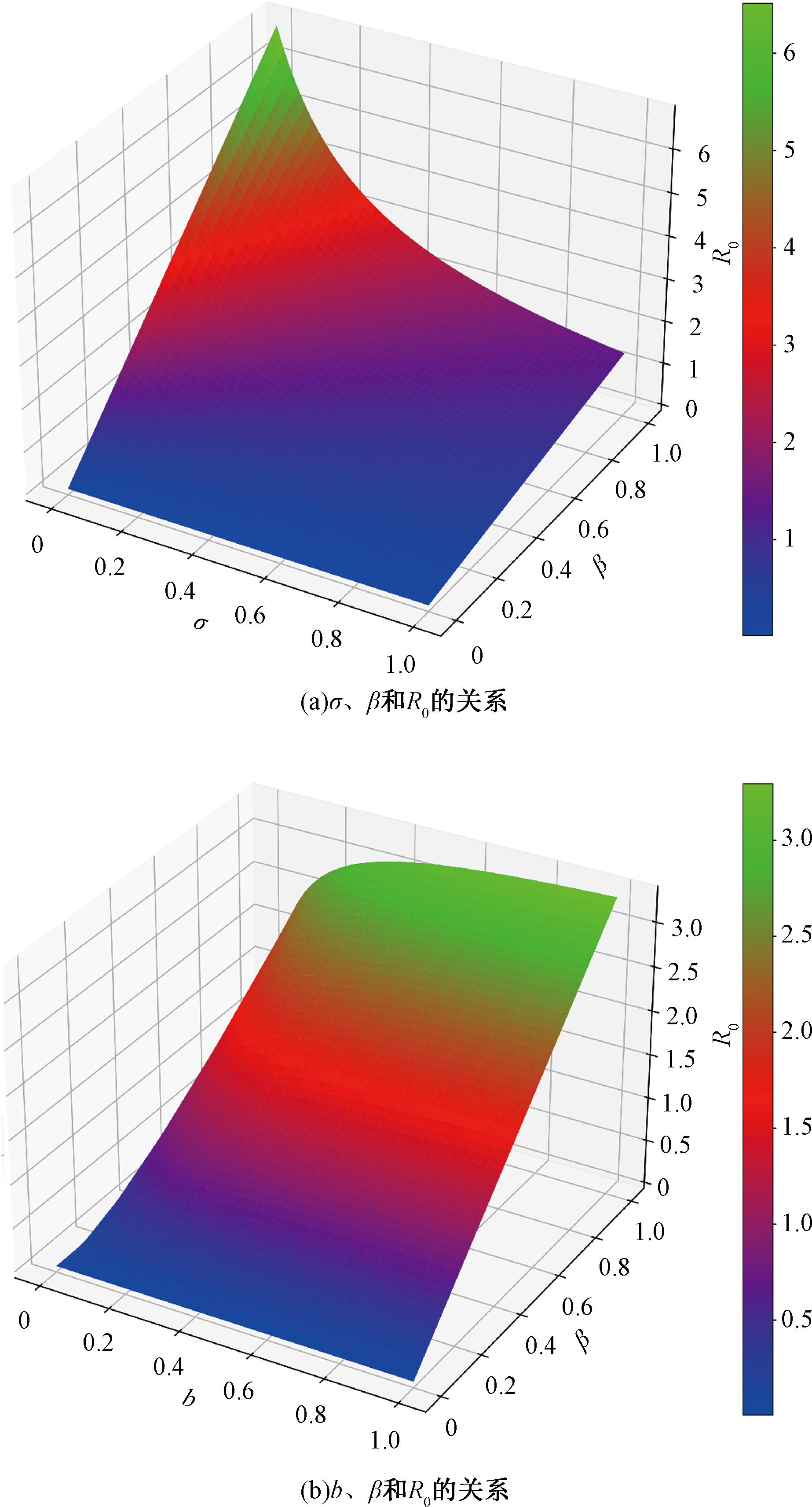
图2 参数与基本再生数R0的关系图
Figure 2 Parameters plotted against the basic reproduction number R0
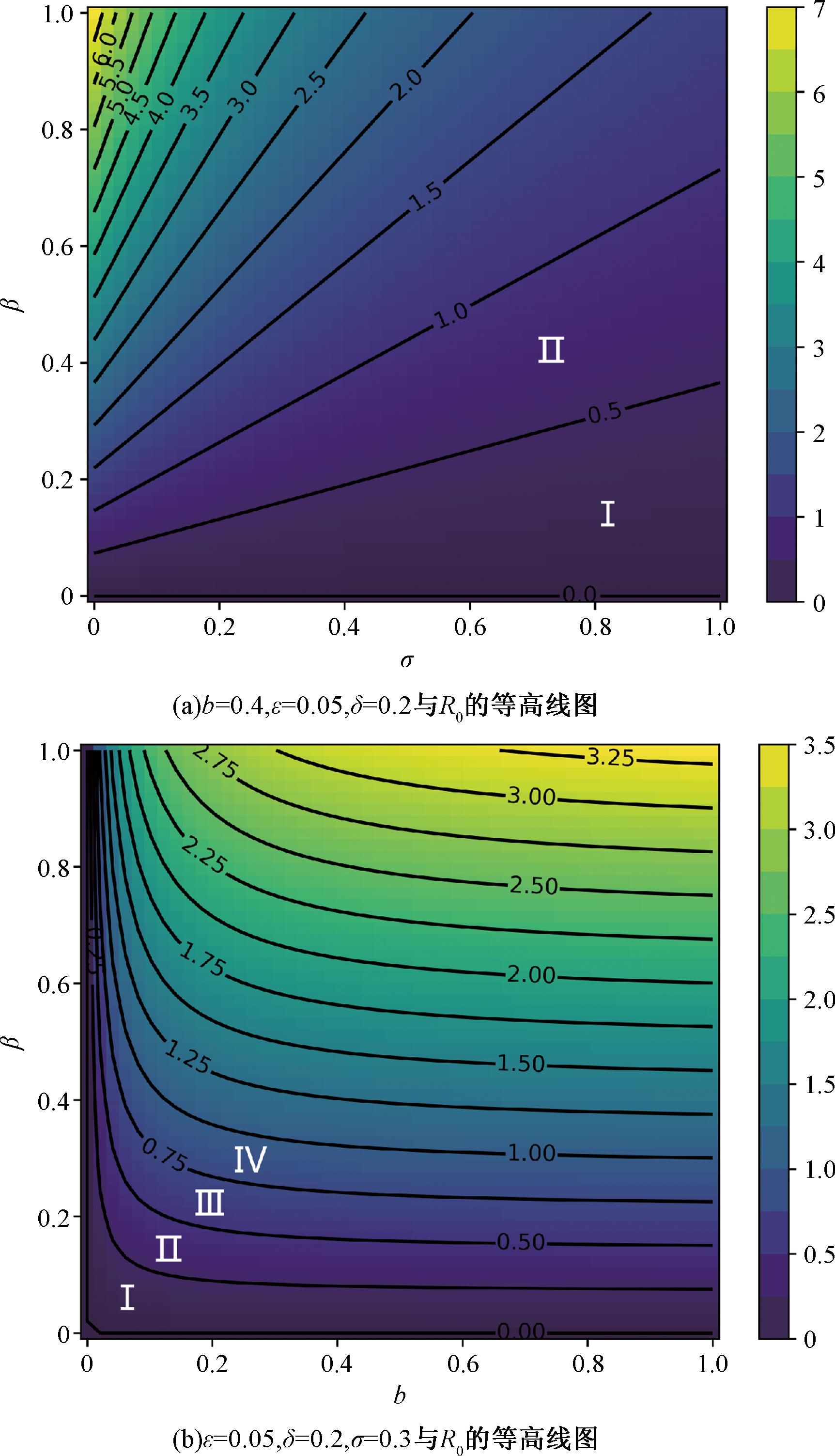
图3 参数与基本再生数R0的等高线图
Figure 3 Contour diagram of parameters and basic reproduction numberR0
4.2 平衡点处的稳定性
设参数b=0.4、ε=0.05、δ=0.2、σ=0.3、β=0.1、η=0.4、α=0.1、φ=0.15,初始条件I(0)=0.1、C(0)=0.1、R(0)=0.01。根据(10)式有R0=0.310 8<1。图4和图5分别为R0<1和R0>1时感染节点、辟谣节点和免疫节点的密度。由图4可知,存在E0=(0,0,0)。根据定理1,如果R0<1,对于∀τ≥0,在E0处,系统(式(5))是局部渐近稳定的。由图4可知,对于任意时间延迟τ=0,2,4,6,感染节点I、辟谣节点C、免疫节点R的密度最终都稳定到0处。由图4和图5可知,时间延迟增大,感染节点密度到达平衡状态的时间随之增加,谣言传播更容易。
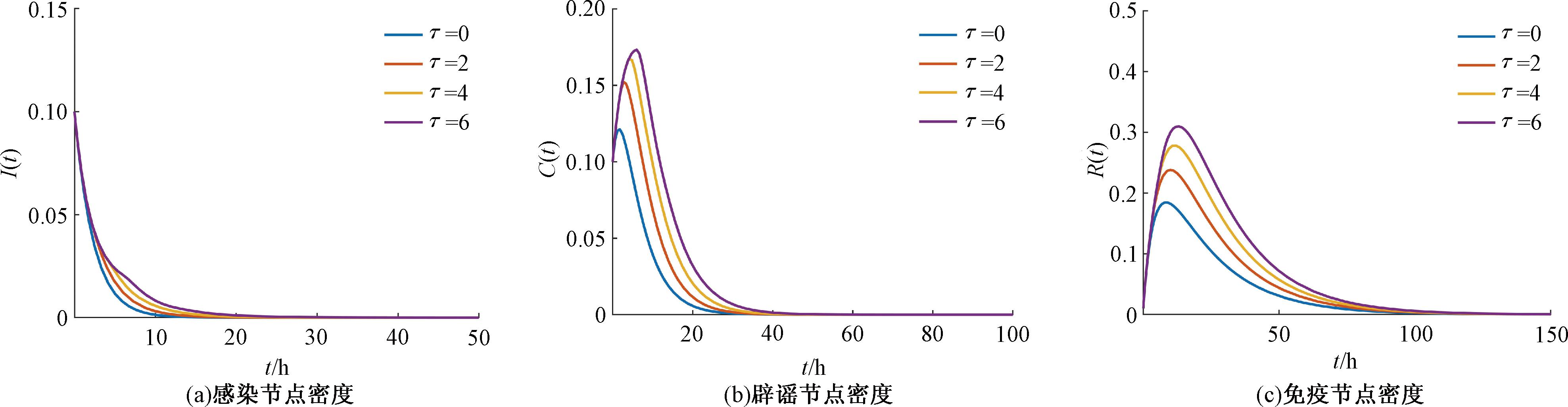
图4 R0<1时,感染节点、辟谣节点和免疫节点密度
Figure 4 When R0<1, the density of infective nodes, rumor refuging and recovered nodes
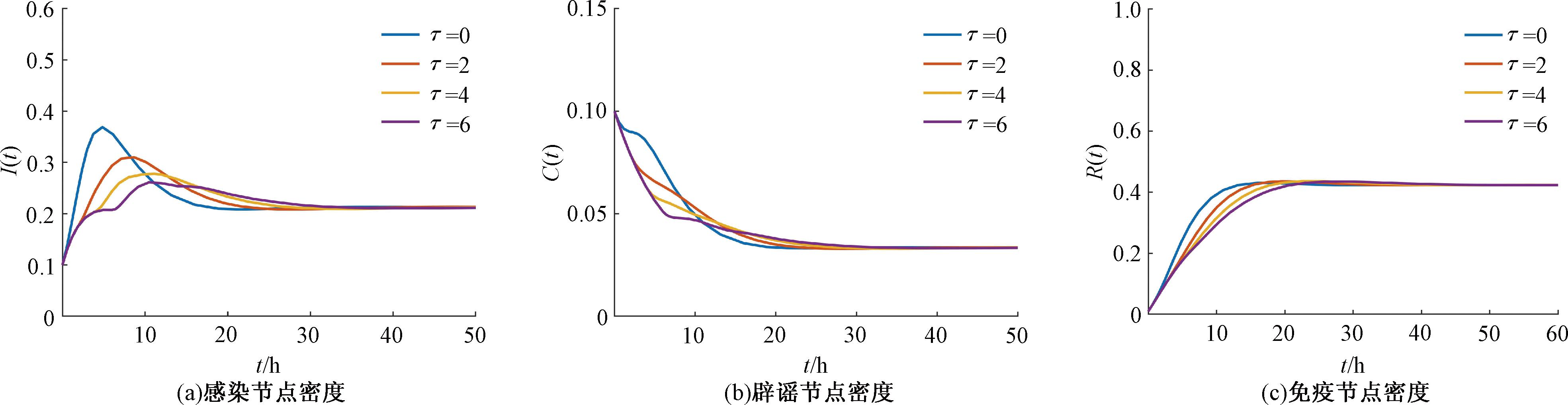
图5 R0>1时,感染节点、辟谣节点和免疫节点密度
Figure 5 When R0>1,the density of infective nodes, rumor-refuging and recovered nodes
设参数b=0.7、ε=0.1、δ=0.05、σ=0.15、β=0.7、η=0.1、α=0.9、φ=0.15,初始条件I(0)=0.1、C(0)=0.1、R(0)=0.01。根据式(10)有R0=3.923 6>1、2I*+C*+R*=0.883 2>b/(b+ε)=0.875,由图5可得,E*=(0.212 7,0.033 5,0.424 3)。根据定理3,当2I*+C*+R*>b/(b+ε),如果R0>1,对于∀τ≥0,在E*处,系统(式(5))是局部渐近稳定的。由图5可知,对于所取的任意时间延迟τ=0,2,4,6,感染节点I、辟谣节点C、免疫节点R的密度最终分别稳定至I*、C*、R*处。
设参数τ=4、b=0.3、ε=0.3、δ=0.2、σ=0.3、β=0.2、η=0.1、α=0.1、φ=0.15,任意取6组初始值(I(t),C(t),R(t))分别为N01=(0.7,0.7,0)、N02=(0.6,0.6,0.1)、N03=(0.5,0.5,0.2)、N04=(0.4,0.4,0.3)、N05=(0.3,0.3,0.4)和N06=(0.2,0.2,0.5)。由式(10)有R0=0.240 4<1,Q=0.961 6<1,对于∀τ≥0,在E0处,系统(式(5))是全局渐近稳定的。图6为系统在无谣言平衡点E0处的全局渐近稳定性。由图6可知,在系统(式(5))中,任意初值最终都收敛至E0处,故系统(式(5))在E0处是全局渐近稳定的。
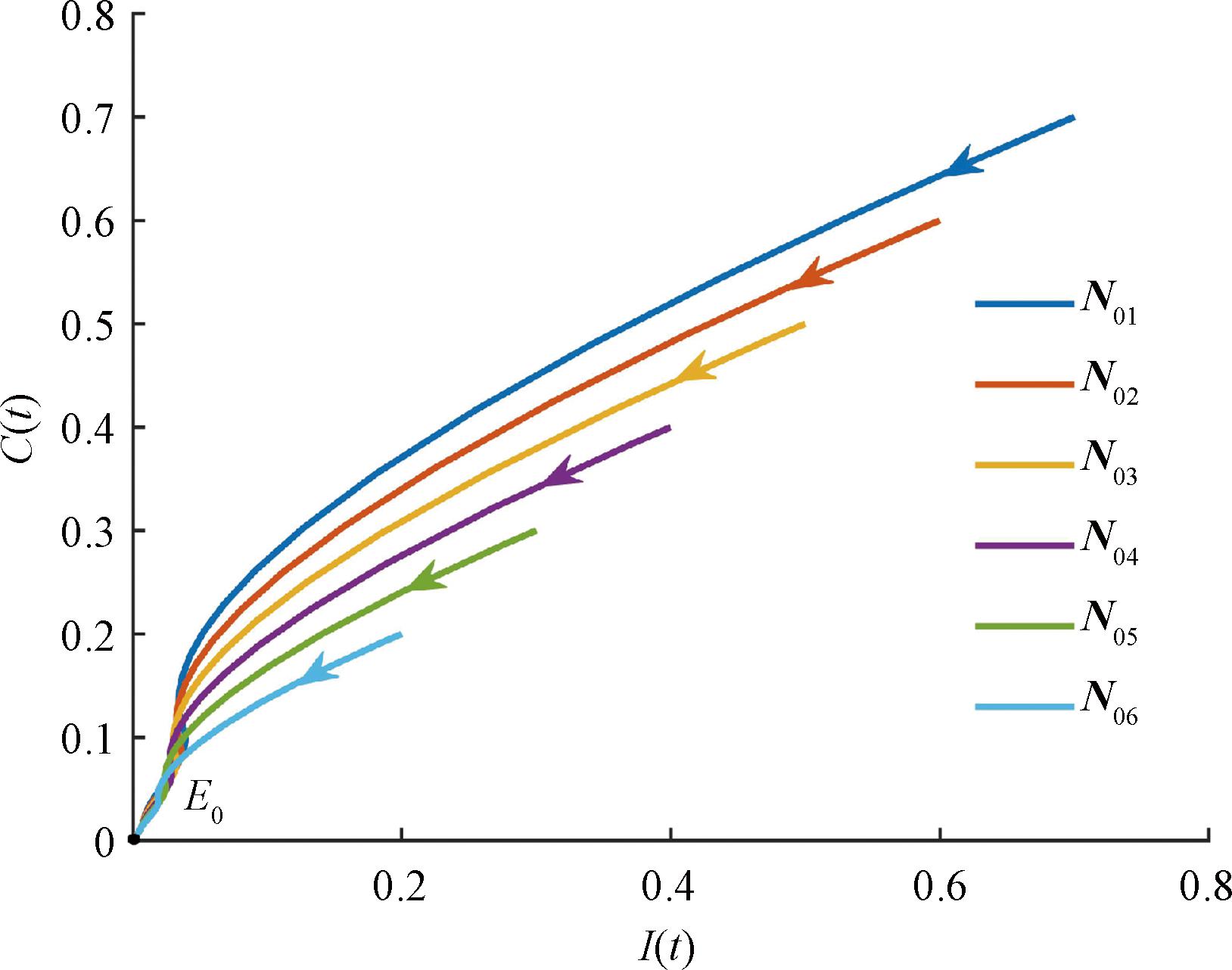
图6 系统在无谣言平衡点E0处的全局渐近稳定性
Figure 6 The global asymptotic stability of system at the rumor-free equilibrium point E0
4.3 模型比较
在本小节中,将SICR谣言传播模型与SIR谣言传播模型[18]进行比较,设参数b=0.7、ε=0.1、δ=0.05、σ=0.15、β=0.7、η=0.2、α=0.9、φ=0.15。图7为SICR模型与SIR模型的比较。由图7可知,SICR模型的感染节点密度峰值比SIR模型小,这意味着考虑辟谣机制能够更好地抑制谣言的传播。因此,当谣言出现时,政府部门可以呼吁广大网友积极辟谣,共同创建绿色网络环境。
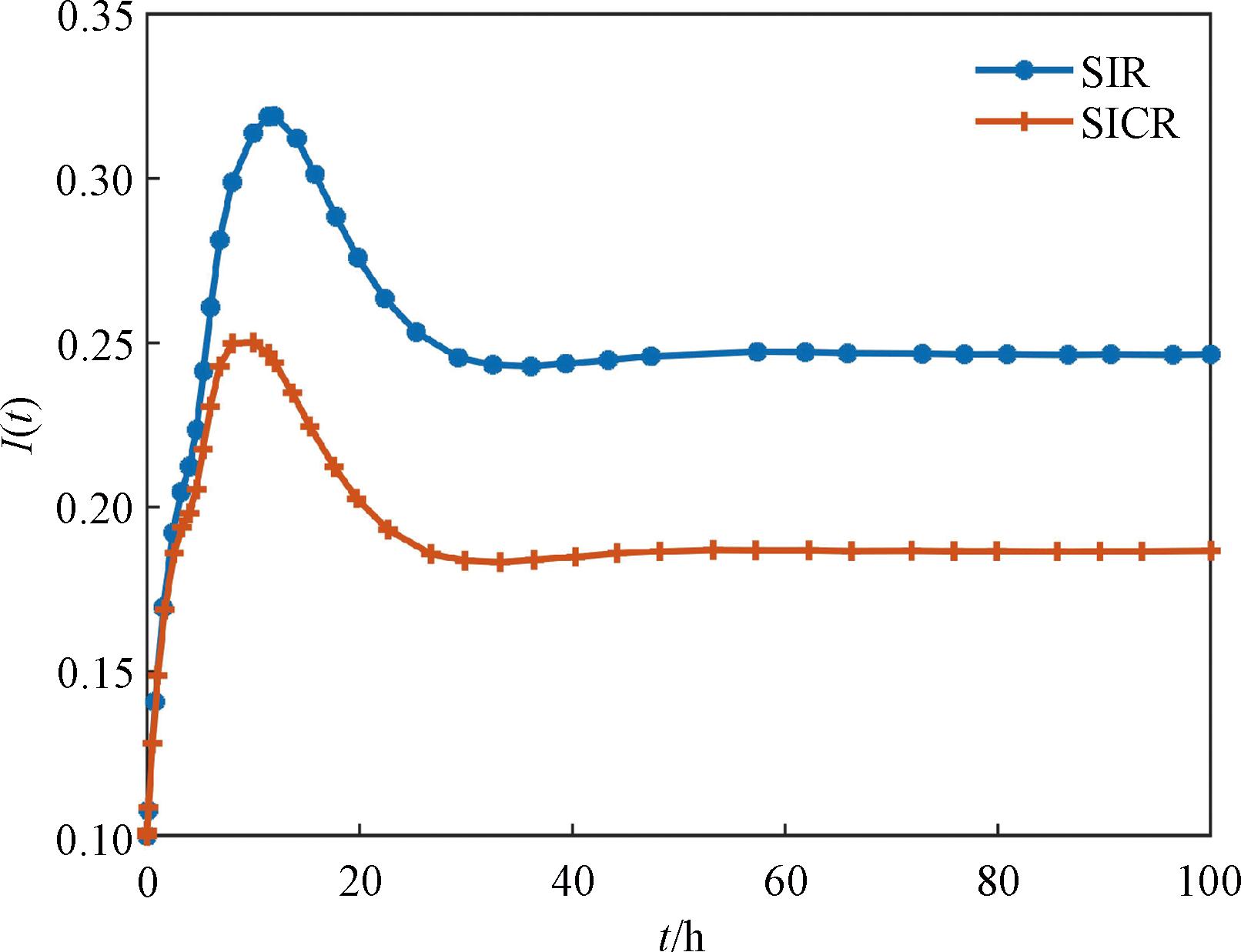
图7 SICR模型与SIR模型的比较
Figure 7 Comparison of the SICR model and the SIR model
5 模型应用
传统的谣言传播模型在随机参数设置方面未充分考虑到实际谣言传播情境。为验证SICR谣言传播模型在实际应用中的有效性,利用推特数据集进行验证。数据集中包含12个关于谣言的统计数据,选择Dataset_R6作为本文的数据集。该数据集收集了从2018年6月28日23时49分04秒至2018年6月30日17时55分51秒,关于“Harley-Davidson′s chief executive officer Matthew Levatich called President Trump ‘a moron’.”的数据。推文总数为754,推文状态为“r”的数量为140。
数据集中状态“r”的推文为谣言推文,与SICR谣言传播模型中感染节点相对应。在数据集中,从起始时间开始每10 min更新并记录一次谣言的数量,并将此数值除以推文总数754,即可得到Rumor-6谣言密度变化数据。图8为模型感染节点密度曲线和真实数据曲线的对比。由图8可知,结合Rumor-6谣言密度数据,使用最小二乘法连续调整模型的参数值,当参数值
b=0.166 6、ε=0.049 1、σ=0.001 0、α=0.487 1、δ=0.001 0、φ=0.436 6、τ=0.500 0时,模型感染节点密度曲线与真实数据的拟合效果最佳。以R2作为评价指标,R2越接近1,模型的拟合度越好。由实验可得R2为0.950 8,说明SICR谣言传播模型具有一定的有效性和适用性。
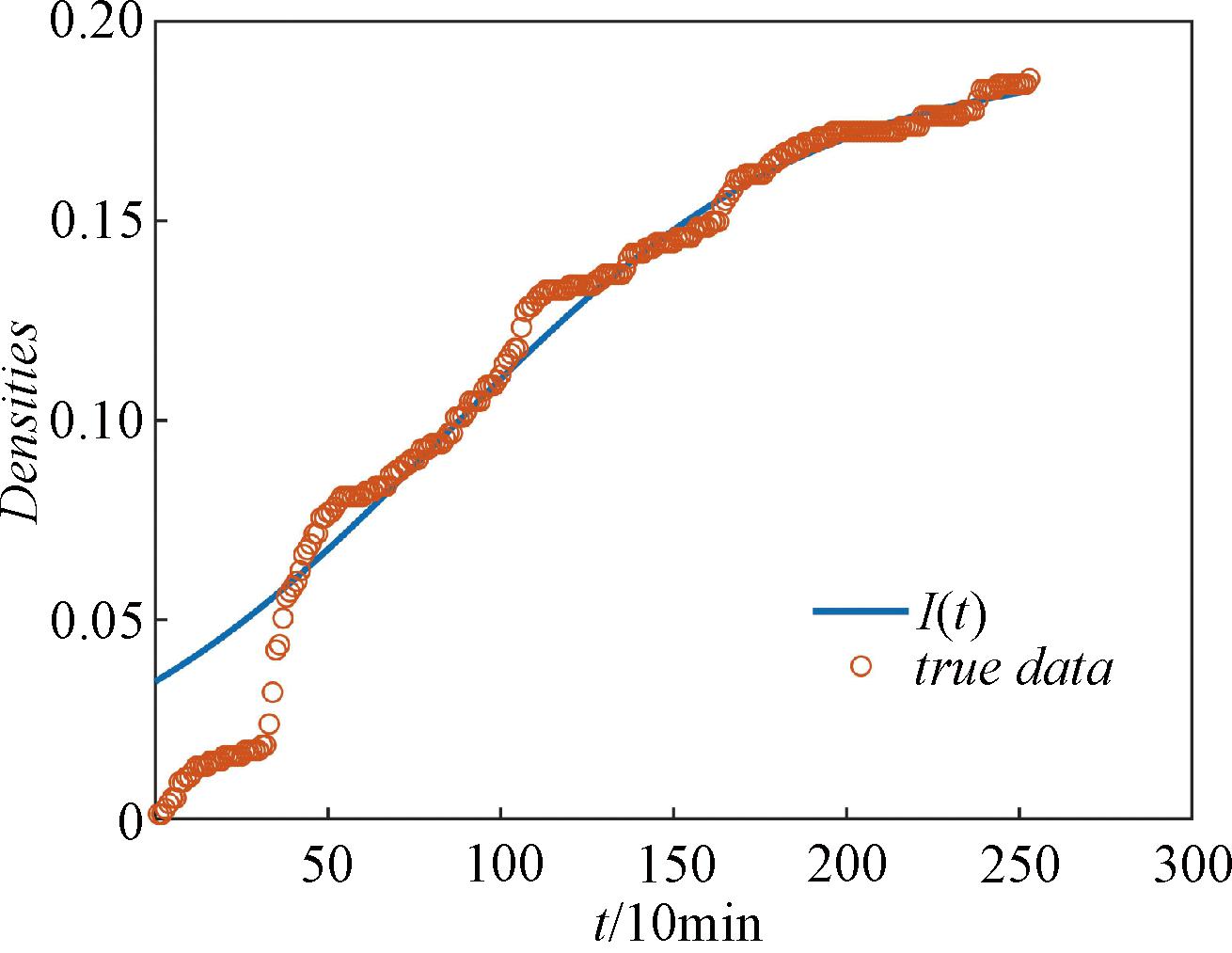
图8 模型感染节点密度曲线和真实数据曲线
Figure 8 Model infective nodes density curve and real data curve
6 结论
考虑时间延迟、强制静默、网络结构和辟谣机制等因素,构造了SICR谣言传播模型。通过下一代矩阵法计算了基本再生数R0,且R0与传播率β、平均度
迁入率b、迁出率ε、强制静默率σ和感染节点恢复率δ有关。在此基础上,当R0<1时,在无谣言平衡点E0处系统是局部渐近稳定的;当R0>1且2I*+C*+R*>b/(b+ε)时,在谣言盛行平衡点E*处系统是局部渐近稳定的;当
时,在E0处系统是全局渐近稳定的。仿真表明,理论与实际相符,且时间延迟、强制静默、网络结构和辟谣机制对谣言传播具有重要影响。最后,通过对推特数据集进行最小二乘拟合,获取了模型的参数数值,R2为0.950 8,表明模型具有一定的有效性和适用性。
[1] CHIERICHETTI F, LATTANZI S, PANCONESI A. Rumor spreading in social networks[J]. Theoretical Computer Science, 2011, 412(24): 2602-2610.
[2] DALEY D J, KENDALL D G. Epidemics and rumours[J]. Nature, 1964, 204: 1118.
[3] MAKI D P, THOMPSON M. Mathematical models and applications: with emphasis on the social life, and management sciences[J]. The Mathematics Teacher, 1974,67(6):541.
[4] ZANETTE D H. Dynamics of rumor propagation on small-world networks[J]. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics, 2002, 65(4): 041908.
[5] MORENO Y, NEKOVEE M, PACHECO A F. Dynamics of rumor spreading in complex networks[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2004, 69(6): 066130.
[6] 方洁, 杜海明, 刘娜. 变时滞耦合不确定复杂网络修正函数投影同步[J]. 郑州大学学报(工学版), 2018, 39(4): 81-85, 91.FANG J, DU H M, LIU N. Modified function projective synchronization of uncertain complex dynamical networks with time-varying coupling delay[J]. Journal of Zhengzhou University (Engineering Science), 2018, 39(4): 81-85, 91.
[7] GUO H M, YAN X F, NIU Y B, et al. Dynamic analysis of rumor propagation model with media report and time delay on social networks[J]. Journal of Applied Mathematics and Computing, 2023, 69(3): 2473-2502.
[8] TONG X R, JIANG H J, QIU J L, et al. Dynamic analysis of the IFCD rumor propagation model under stochastic disturbance on heterogeneous networks[J]. Chaos Solitons and Fractals, 2023, 173: 113637.
[9] LUO X P, JIANG H J, CHEN S S, et al. Stability and optimal control for delayed rumor-spreading model with nonlinear incidence over heterogeneous networks[J]. Chinese Physics B, 2023, 32(5): 058702.
[10] YUAN T Y, GUAN G, SHEN S L, et al. Stability analysis and optimal control of epidemic-like transmission model with nonlinear inhibition mechanism and time delay in both homogeneous and heterogeneous networks[J]. Journal of Mathematical Analysis and Applications, 2023, 526(1): 127273.
[11] JAIN A, DHAR J, GUPTA V K. Optimal control of rumor spreading model on homogeneous social network with consideration of influence delay of thinkers[J]. Differential Equations and Dynamical Systems, 2023, 31(1): 113-134.
[12] CHEN J H, MA H C, YANG S. SEIOR rumor propagation model considering hesitating mechanism and different rumor-refuting ways in complex networks[J]. Mathematics, 2023, 11(2): 283.
[13] CHENG Y Y, HUO L A, ZHAO L J. Dynamical behaviors and control measures of rumor-spreading model in consideration of the infected media and time delay[J]. Information Sciences, 2021, 564: 237-253.
[14] CHANG Z X, JIANG H J, YU S Z, et al. Dynamic analysis and optimal control of ISCR rumor propagation model with nonlinear incidence and time delay on complex networks[J]. Discrete Dynamics in Nature and Society, 2021, 2021: 3935750.
[15] HUO L A, MA C Y. Optimal control of rumor spreading model with consideration of psychological factors and time delay[J]. Discrete Dynamics in Nature and Society, 2018, 2018: 9314907.
[16] ZHU L H, GUAN G. Dynamical analysis of a rumor spreading model with self-discrimination and time delay in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 533: 121953.
[17] ZHU L H, WANG B X. Stability analysis of a SAIR rumor spreading model with control strategies in online social networks[J]. Information Sciences, 2020, 526: 1-19.
[18] ZHU L H, LIU W S, ZHANG Z D. Delay differential equations modeling of rumor propagation in both homogeneous and heterogeneous networks with a forced silence function[J]. Applied Mathematics and Computation, 2020, 370: 124925.
[19] PAN W Q, YAN W J, HU Y H, et al. Dynamic analysis of a SIDRW rumor propagation model considering the effect of media reports and rumor refuters[J]. Nonlinear Dynamics, 2023, 111(4): 3925-3936.
[20] VAN DEN DRIESSCHE P, WATMOUGH J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180: 29-48.
[21] MISRA A K, SHARMA A, SINGH V. Effect of awareness programs in controlling the prevalence of an epidemic with time delay[J]. Journal of Biological Systems, 2011, 19(2): 389-402.
[22] SAHU B K, GUPTA M M, SUBUDHI B. Stability analysis of nonlinear systems using dynamic-Routh′s stability criterion: a new approach[C]∥2013 International Conference on Advances in Computing, Communications and Informatics (ICACCI). Piscataway: IEEE, 2013: 1765-1769.
[23] LA SALLE J P. The stability of dynamical systems[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1976.