水库大坝在给人类带来显著经济和社会效益的同时,对下游人民群众的生命财产安全造成了极大的威胁。2020年5月,由于暴雨等原因,美国Edenville 坝溃决,一万多人紧急疏散。2021年郑州市“7·20”暴雨,造成郭家咀水库、常庄水库以及下游贾鲁河堤岸发生险情,数十万人紧急转移。合理规划和建设避难场所对降低溃坝洪水造成的危害和损失有重要作用。因此,研究潜在溃坝洪灾避难场所选址评价方法至关重要。
现代选址研究起源于20世纪初,Weber等[1]开展了选址研究,提出了单一仓库到各个需求点的距离最小化问题。随着需求的多样化、复杂化,选址研究也更加深入。Dalal等[2]将建设成本作为目标,构建了避难场所选址的单目标模型。单目标模型主要包括p-median方法、p-center方法等,该类模型使用方便,但适用目标较单一[3]。因此,研究人员进一步构建了多目标模型。Zhao等[4]以最小疏散时间和避难场所面积为目标构建了多目标选址模型。Xu等[5]以最小避难场所面积和疏散距离为目标构建了选址模型。张宣峰等[6]以容纳人数最多且避难场所数量最少为目标构建了选址模型。王维莉等[7]以最小避难场所数量和转移距离为目标,建立了优化模型。以上研究通常从建设成本、容纳人数等避难场所自身因素出发来考虑模型的构建,但未充分考虑避难需求地区危险程度的影响,可能会出现规划的避难场所与高危险程度地区的距离相对较远的情况。
因此,Esmaelian等[8]考虑建筑物质量和人口密度构建了避难场所选址模型;Marcelin等[9]考虑年龄分布对飓风救援设施的选址进行了优化分析。以上研究通过考虑避难需求地区特征的影响,使避难场所选址能够重视人口密度大、老龄化严重等因素,但仅考虑了一两个影响因素进行危险程度的识别。然而,避难需求地区的危险程度受多个因素影响,需要对其进行综合评价,以判断出危险程度高的地区,合理选址。
对于溃坝洪灾而言,洪水的潜在淹没区域即为避难需求地区。因此,针对上述问题,在建立潜在淹没区域危险度评价指标体系的基础上,应用改进突变评价法构建了危险度评价模型并制定危险等级划分标准,将避难场所与高级别危险区的距离作为选址评价指标,从而与选址结合构建了潜在溃坝洪灾避难场所选址评价模型。
1 危险度评价及等级划分
危险程度高的潜在淹没区域对避难场所需求更迫切,在规划避难场所时应倾向于该类区域。为识别此类区域,将潜在淹没区域的危险程度定义为危险度并进行评价。根据危险度评价结果将各个潜在淹没区域划分为不同级别的危险区,为避难场所选址评价提供依据。
1.1 危险度评价指标体系
潜在淹没区域危险度与生命损失有一定的契合性,危险程度高的区域生命损失显然更大。参照已有生命损失研究成果[10-14],结合研究目的及实际情况,对相应评价指标进行优选,指标选取的原则如下。
(1)科学性。评价指标体系需要在科学的理论的指导下建立,逻辑必须清晰严谨。
(2)系统性。为便于分析,选取的指标应能形成一个有机的整体,且具有一定的层次性。
(3)指标要符合研究目的及实际情况。要剔除不符合实际情况的评价指标,找出最重要且具有代表性的评价指标。
(4)定性与定量相结合。洪灾认知水平等定性指标难以直接量化,且对危险度也具有重要影响。因此,应坚持定性与定量相结合的原则。
根据以上指标选取原则和灾害理论,从致灾因子、承灾体、孕灾环境3个方面确定危险度的评价指标,选用洪水严重程度、风险人口数量、青壮年比例、洪灾认知水平、与坝址的距离、建筑物质量、具备的救援能力7个评价指标,从而构建危险度评价指标体系,如图1所示。
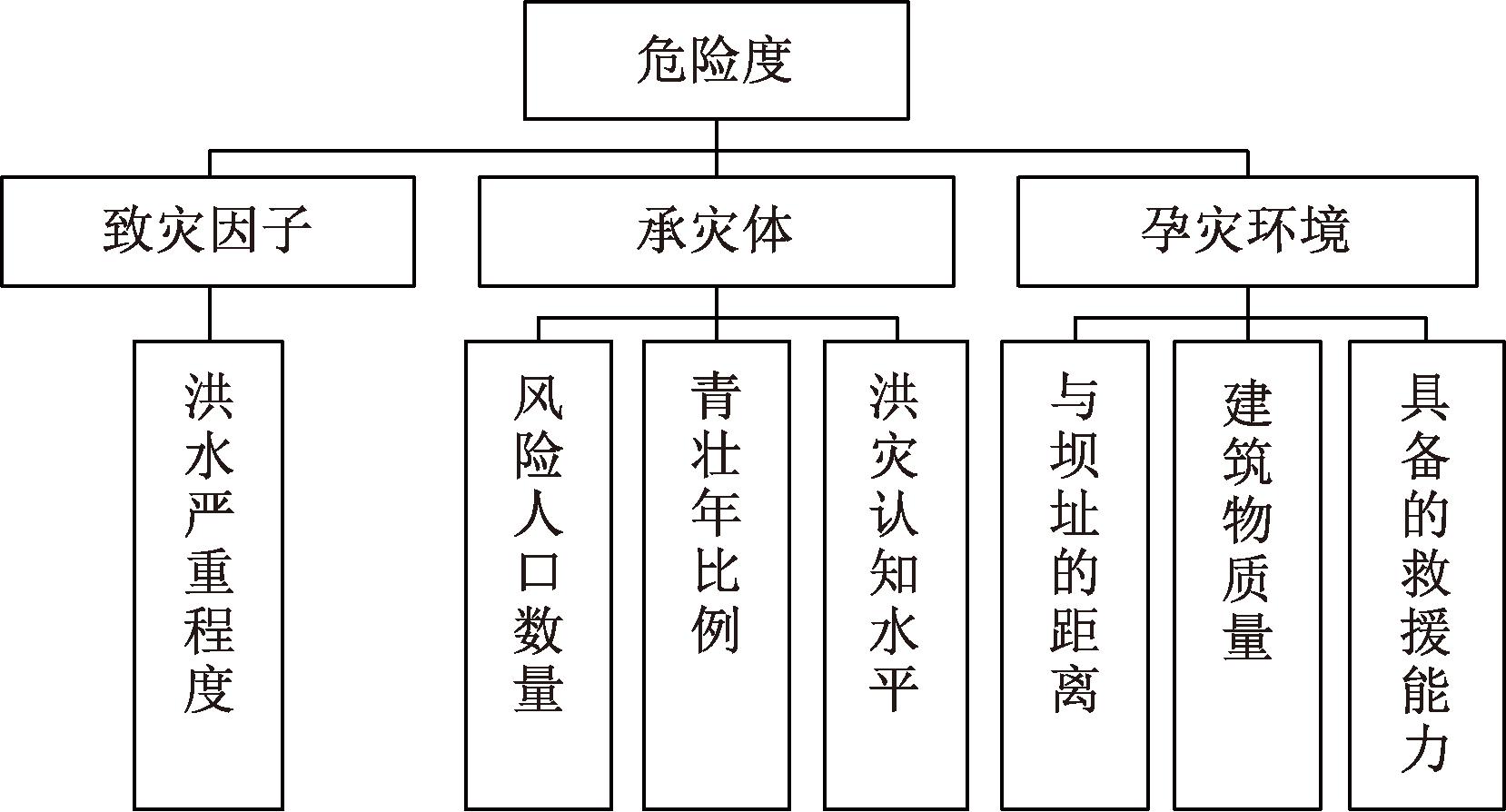
图1 潜在淹没区域危险度评价指标体系
Figure 1 Evaluation index system for risk degree of potential inundation areas
1.2 评价指标标准化及等级划分
结合中国洪涝灾害等级划分标准以及已有溃坝生命损失研究,通常将生命损失及评价指标划分为5个等级。为方便有效地区分不同危险等级的潜在淹没区域,本文将评价指标平均分为D-5级[0,0.2)、D-4级[0.2,0.4)、D-3级[0.4,0.6)、D-2级[0.6,0.8)和D-1级[0.8,1.0]5个等级。
洪水严重程度是危险度的重要影响因素,其取值为洪水深度和流速的乘积。根据已有研究[11],可将洪水严重程度及洪灾认知水平、具备的救援能力2个定性指标划分为5个等级。
危险度评价是受洪水影响区域的内部比较,评价目的是区分不同危险等级的潜在淹没区域。因此对风险人口数量、青壮年比例、与坝址的距离、建筑物质量4个定量指标的初始值进行标准化处理,并平均分为5个等级,以达到区分的目的。其中,风险人口数量按式(1)进行标准化处理,青壮年比例、与坝址的距离、建筑物质量按式(2)进行标准化处理。
(1)
(2)
式中:Ri为指数i标准化处理后的值;ri为指数i的初始值;rmax和rmin分别为所有指标i中的最大值和最小值。
综合以上分析,初步制定各个评价指标的对应等级,如表1所示。
表1 评价指标对应等级
Table 1 Corresponding levels of evaluation index
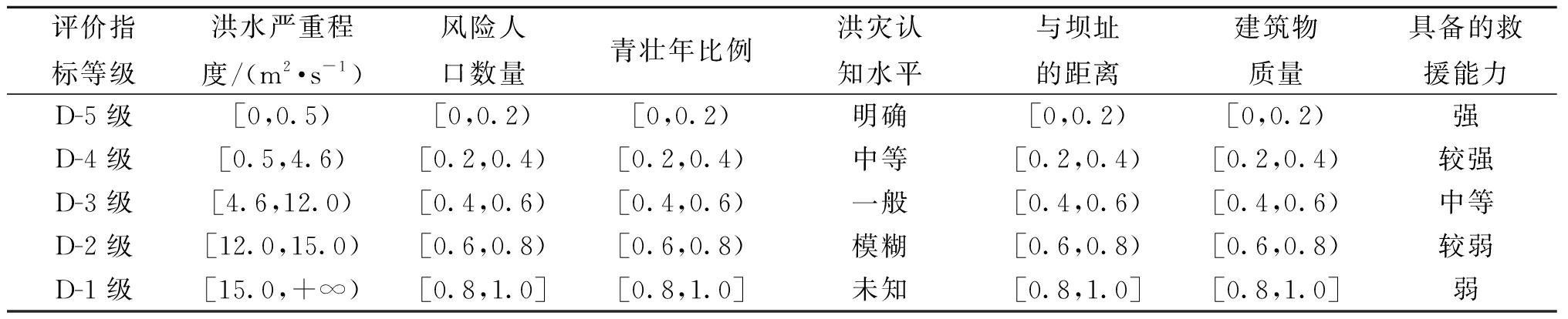
评价指标等级洪水严重程度/(m2·s-1)风险人口数量青壮年比例洪灾认知水平与坝址的距离建筑物质量具备的救援能力D-5级[0,0.5)[0,0.2)[0,0.2)明确[0,0.2)[0,0.2)强D-4级[0.5,4.6)[0.2,0.4)[0.2,0.4)中等[0.2,0.4)[0.2,0.4)较强D-3级[4.6,12.0)[0.4,0.6)[0.4,0.6)一般[0.4,0.6)[0.4,0.6)中等D-2级[12.0,15.0)[0.6,0.8)[0.6,0.8)模糊[0.6,0.8)[0.6,0.8)较弱D-1级[15.0,+∞)[0.8,1.0][0.8,1.0]未知[0.8,1.0][0.8,1.0]弱
对于评价指标初始值的获取,建筑物质量参照Ge等[15]提出的建筑物躲避率计算方法综合分析确定,如式(3)所示:
(3)
式中:R为建筑物躲避率;NUMun-dest为成功抵御洪水冲击的建筑数量;NUMtot为面对洪水冲击的建筑总数。
建筑物对洪水冲击的抵御能力参照王志军等[16]建立的中国房屋破坏参考标准确定,如表2所示。使用水动力模拟软件HEC-RAS进行溃坝洪水模拟,结合ArcGIS软件获取洪水严重程度数据。其余5个评价指标根据已有统计资料确定。
表2 中国房屋破坏参考标准
Table 2 Reference standards for buildings damage in China

房屋类型破坏标准泥土结构平房H≥0.9 m且SF≥2 m2/s砖砌、混凝土结构平房V≥2 m/s且SF≥7 m2/s2层楼房V≥2.4 m/s且SF≥15 m2/s3层楼房V≥2.4 m/s且SF≥22 m2/s4层楼房V≥2.54 m/s且SF≥29 m2/s
注:H为洪水水深;V为洪水流速;SF为洪水严重程度。对于更高的楼房,其抵抗洪水能力很强,可认为不能被破坏。
1.3 基于改进突变评价法的危险度评价步骤
突变理论由法国数学家Rene Thom于1972年提出,用来研究非连续现象。突变评价法是突变理论常见的应用,具有快速准确、有效减少主观因素影响的优点。常用突变模型如表3所示。由于归一公式的聚集性,常规突变评价法所得评价值较为接近,不符合对优劣的直观判断。因此,研究人员提出了改进突变评价法,以提高评价值分辨率水平,便于直观判断评价值的等级[17]。具体评价流程如下。
表3 几种常见的突变模型
Table 3 Several common catastrophe models

类型控制变量势函数归一公式折叠突变1x3/3+axxa=a1/2尖点突变2x4/4+ax2/2+bxxa=a1/2,xb=b1/3燕尾突变3x5/5+ax3/3+bx2/2+cxxa=a1/2,xb=b1/3,xc=c1/4蝴蝶突变4x6/6+ax4/4+bx3/3+cx2/2+dxxa=a1/2,xb=b1/3,xc=c1/4,xd=d1/5
注:在突变评价法的应用中,归一公式的a、b、c、d分别为各评价指标的数据。
步骤1 根据洪水模拟数据和已有统计资料确定所有指标的值。
步骤2 根据指标的特点对指标进行标准化处理。
步骤3 将危险度评价指标根据相对重要性由强到弱依次排列,构建突变模型。采用常规突变评价法计算当所有底层指标的隶属度值均为 xi(i=1,2,…,n,且xi∈[0, 1])时的突变综合评价值 yi(i= 1,2,…,n,且yi∈[0, 1])。
步骤4 通过回归分析拟合 x 与 y 的函数关系。
步骤5 通过常规突变评价法计算各个潜在淹没区域的评价值。
步骤6 根据回归函数将常规突变评价值y转换为隶属度值x,即为危险度。
步骤7 根据得到的危险度x判断潜在淹没区域所属危险等级,如表4所示。
表4 危险度对应危险等级
Table 4 Corresponding levels of risk degree
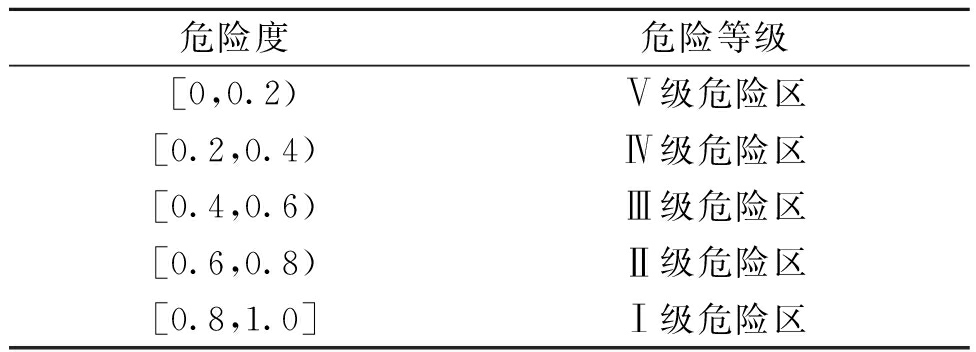
危险度危险等级[0,0.2)Ⅴ级危险区[0.2,0.4)Ⅳ级危险区[0.4,0.6)Ⅲ级危险区[0.6,0.8)Ⅱ级危险区[0.8,1.0]Ⅰ级危险区
2 考虑潜在淹没区域危险度的溃坝洪灾避难场所选址评价
2.1 潜在溃坝洪灾避难场所选址评价指标体系
针对溃坝洪水灾害,结合危险等级划分、已有研究成果以及国家规范[18-19],从灾害风险、位置规模、应急保障、与不同级别危险区的距离4个方面出发,进行潜在溃坝洪灾避难场所选址评价指标体系的构建。
(1)灾害风险。避难场所应选在不易发生地震、滑坡、泥石流等地质灾害的地段。暴雨等极端天气易引起超标准洪水,而超标准洪水是溃坝发生的主要原因之一[20]。极端降雨天气使滑坡、泥石流等地质灾害出现的可能性增加,因此针对潜在溃坝洪灾的避难场所更应避免选址在易出现地质灾害风险的地段。此外,避难场所应远离易燃易爆工厂仓库、储气站等危险源。因此,选取地质灾害、与危险源的距离作为2个评价指标。
(2)位置规模。避难场所是供大量风险人口避难的场所,需考虑可容纳人口的数量。此外,避难场所还应满足不被洪水淹没的要求。因此,可容纳人数、高程是2个重要评价指标。避难场所连通的避难道路、地形情况(如坡度等,高程除外)应满足要求,以便车辆等交通工具能够顺利抵达。
(3)应急保障。灾害发生后,大量避难人口向避难场所转移。为维持秩序和预防紧急情况,避难场所应当靠近当地的医疗机构、公安机关、消防机构,且距离越近越好。
(4)与不同级别危险区的距离。潜在淹没区域与避难场所的距离是风险人口能够顺利进入避难场所的关键影响因素[21]。危险度高的潜在淹没区域对避难场所需求更迫切,避难场所应接近此类区域。因此,根据危险度评价结果,将避难场所与Ⅰ级危险区、Ⅱ级危险区的平均距离以及与危险区的最大距离作为3个评价指标,约束备选避难场所与不同级别危险区的距离,使避难场所选址能够优先考虑高级别危险区的需求。
综上,选取了地质灾害、与危险源的距离等12个评价指标,构建了潜在溃坝洪灾避难场所选址评价指标体系,如图2所示。其中,与医疗机构、公安机关、消防机构的距离3个指标均取最近距离。
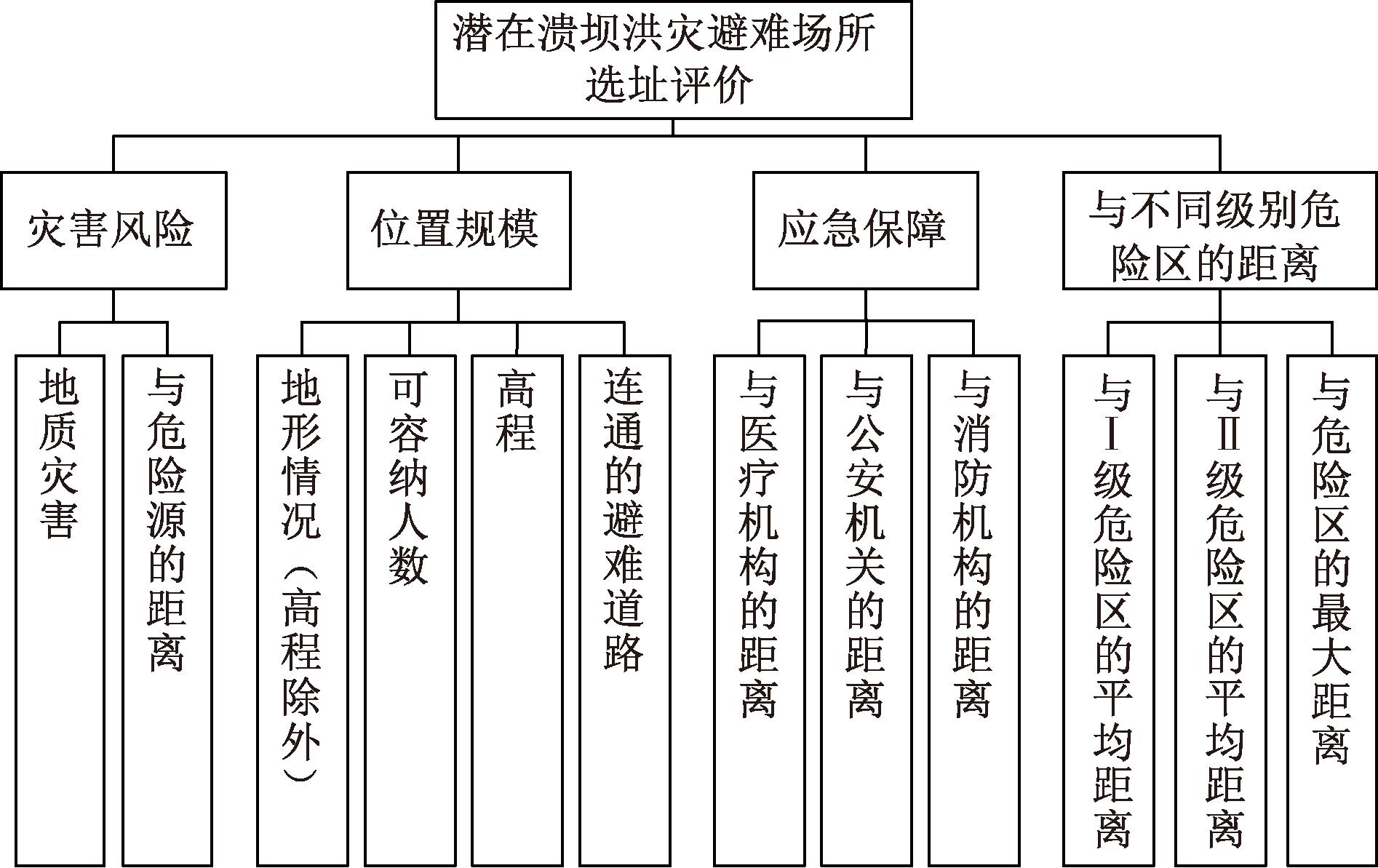
图2 潜在溃坝洪灾避难场所选址评价指标体系
Figure 2 Evaluation index system for site selection of potential dam failure flood shelters
2.2 考虑潜在淹没区域危险度的溃坝洪灾避难场所选址评价模型
(1)备选避难场所初选。在进行备选避难场所的选择时,首先根据地质灾害、与危险源的距离、地形情况(高程除外)3个指标对避难场所进行初选。若3个指标符合条件,则通过初选,对备选避难场所进行评价时不再考虑这3个指标。
(2)层次分析法(AHP)计算权重。层次分析法能够有效处理复杂决策问题,特别是在本研究中,该方法能够反映决策者对不同级别危险区的重视程度。大致计算步骤如下:首先,根据 1~9 标度法则由专家进行打分,并构造判断矩阵;其次,根据判断矩阵的最大特征值求出相应的特征向量,进而得出权重值;最后,进行一致性检验,如式(4)和式(5)所示。若CR<0.10,则通过一致性检验,否则应重新确定判断矩阵。
(4)
(5)
式中:λmax为判断矩阵最大特征值;n为判断矩阵的阶数;RI为随机性指标,可查表取值。
(3)基于AHP-TOPSIS的避难场所选址评价。潜在溃坝洪灾避难场所选址影响因素较多,选用能够有效处理多目标决策问题的TOPSIS综合评价法对备选避难场所进行评价,评价步骤如下。
步骤1 构建决策矩阵并进行标准化处理。
步骤2 将层次分析法计算得到的权重与标准化矩阵相乘得到加权矩阵。
步骤3 确定正期望解和负期望解。
步骤4 计算各个评价对象到正期望解和负期望解的距离,如式(6)所示:
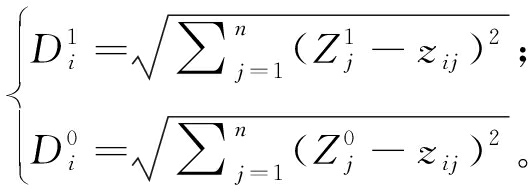
(6)
式中:![]() 和
和![]() 分别为第j个指标的正期望解和负期望解;i=1,2,…,m。
分别为第j个指标的正期望解和负期望解;i=1,2,…,m。
步骤5 计算各个评价对象的相对接近度即综合评价值,如式(7)所示:
(7)
式中:![]() 和
和![]() 分别为第i个评价对象到正期望解和负期望解的距离;i=1,2,…,m。
分别为第i个评价对象到正期望解和负期望解的距离;i=1,2,…,m。
步骤6 将计算得到的综合评价值按由大到小的顺序依次排列,值越大的方案越好,由此得到备选避难场所的优劣次序。
综上,建立了评价潜在淹没区域危险度的模型,并与选址结合构建避难场所选址评价模型,方法流程如图3所示。
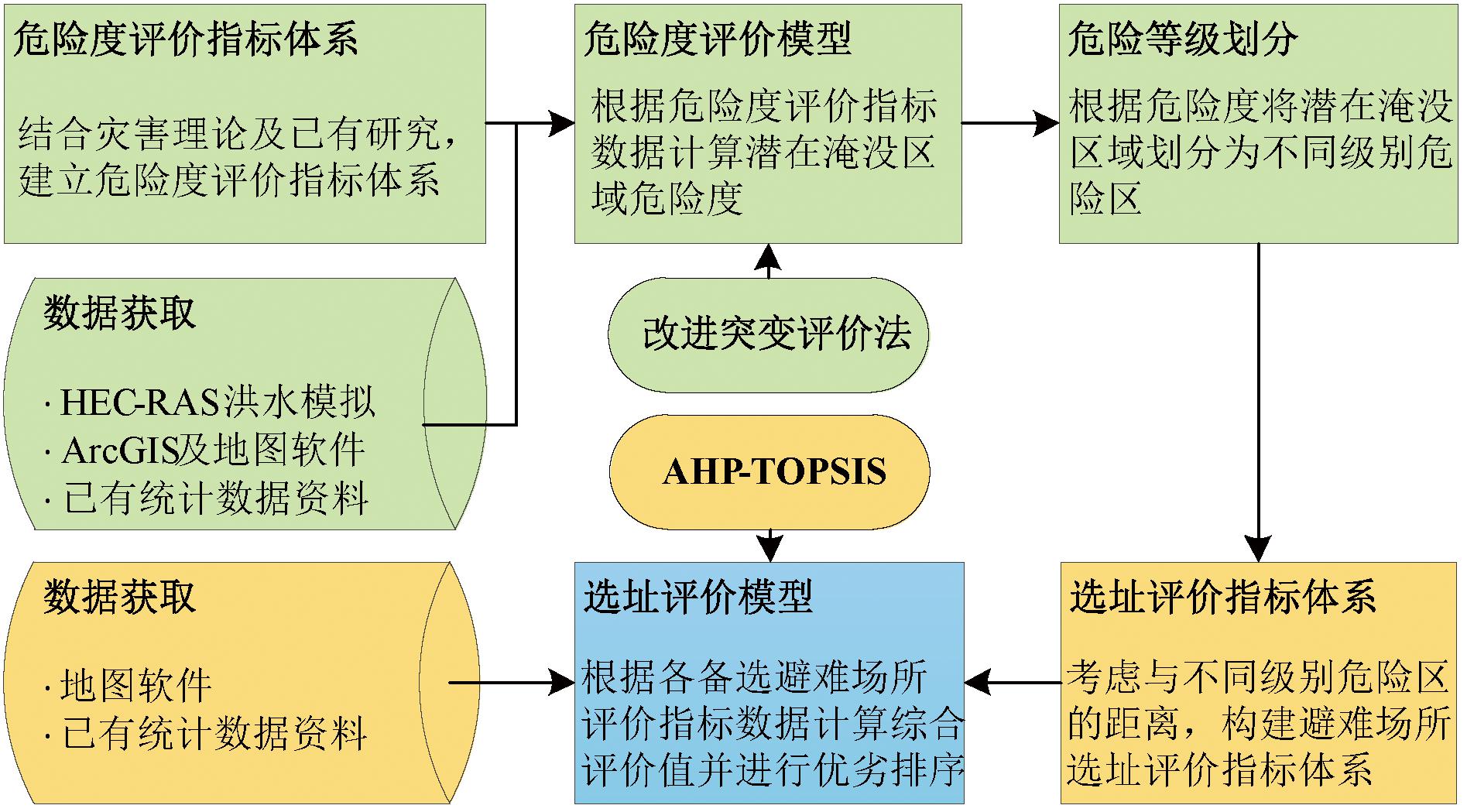
图3 潜在溃坝洪灾避难场所选址评价方法流程图
Figure 3 Flowchart of the methodology for evaluating the site of potential dam failure flood shelters
3 实例分析
3.1 工程概况
陆浑水库位于河南省洛阳市嵩县陆浑峡谷,是一座以防洪为主,兼灌溉、供水、发电等综合利用的大型水库。水库主要建筑物包括大坝、溢洪道、灌溉发电洞等,大坝坝高55 m,为黏土斜墙砂壳坝。水库流域面积3 492 km2,总库容1.32×109 m3。水库距洛阳市67 km,下游地区人口数量众多,发展水平较高,一旦溃坝后果难以接受。因此,研究以陆浑水库下游伊川县、洛龙区等地区为例,进行潜在溃坝洪灾避难场所选址评价。选取水库下游13个潜在淹没区域为研究对象,距离坝址由近到远分别是鸣皋镇(A)、白元镇(B)、城关街道(C)、彭婆镇(D)、龙门石窟街道(E)、龙门镇(F)、诸葛镇(G)、太康东路街道(H)、李楼街道(I)、佃庄镇(J)、庞村镇(K)、翟镇(L)和岳滩镇(M),工程概况如图4所示。
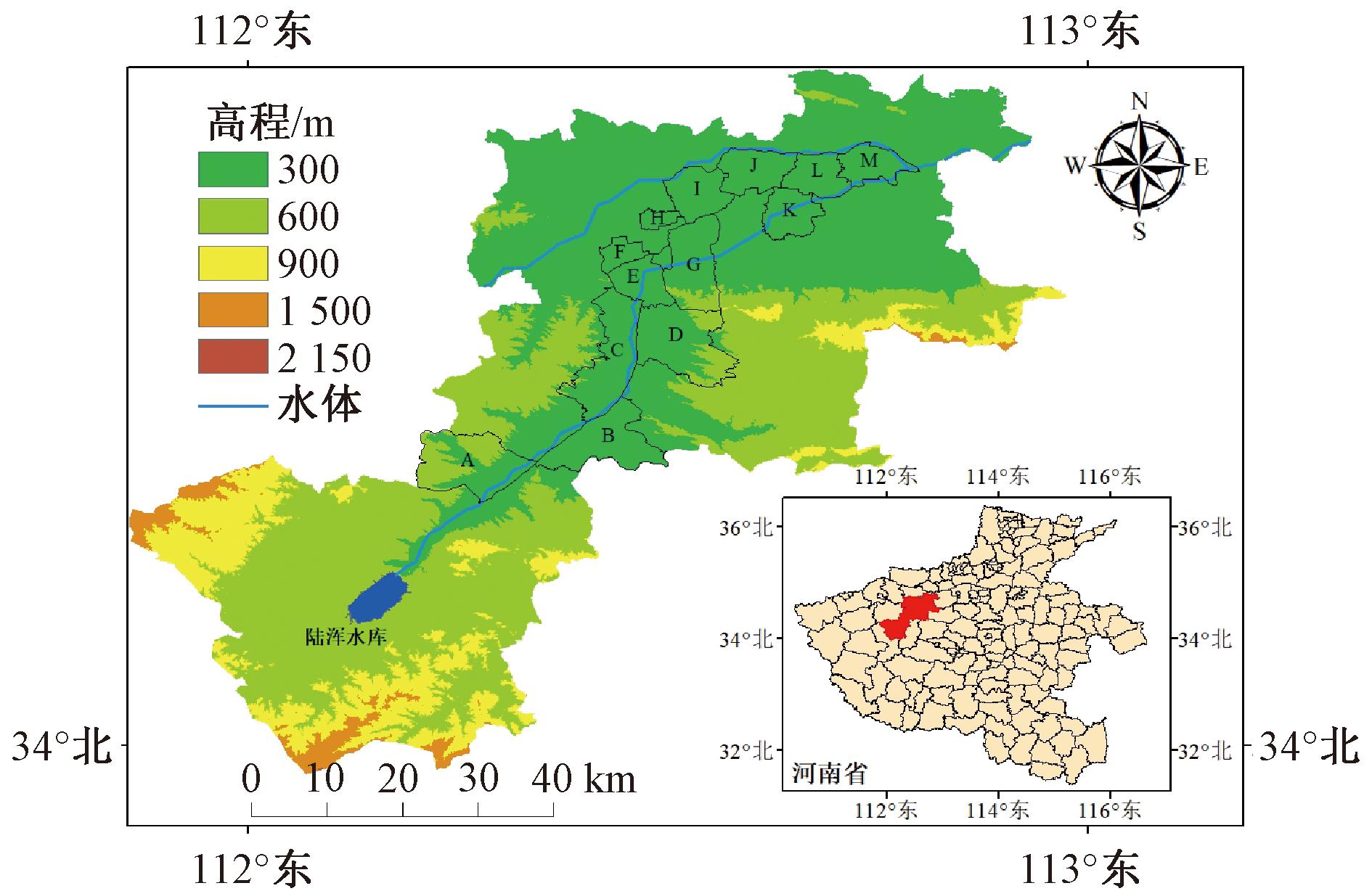
注:该图基于自然资源部标准地图服务网站下载的标准地图(审图号为GS(2020)4619)。
图4 研究区域概况图
Figure 4 Overview of the study area
3.2 危险度评价与危险等级划分
根据统计资料及现有研究[15],得到陆浑水库下游13个潜在淹没区域评价指标的原始数据,如表5所示。其中,青壮年比例由于缺乏具体数据,采用乡镇级别15~59岁年龄分布数据代替;建筑物质量根据式(3)计算得出。在表5中,按照改进突变评价法计算13个潜在淹没区域的危险度,并进行危险等级划分,得到下游13个潜在淹没区域的危险度评价及危险等级划分结果。不同级别危险区的分布如图5所示。
表5 潜在淹没区域危险度评价及危险等级划分结果
Table 5 Risk degree and classification of potential inundation areas
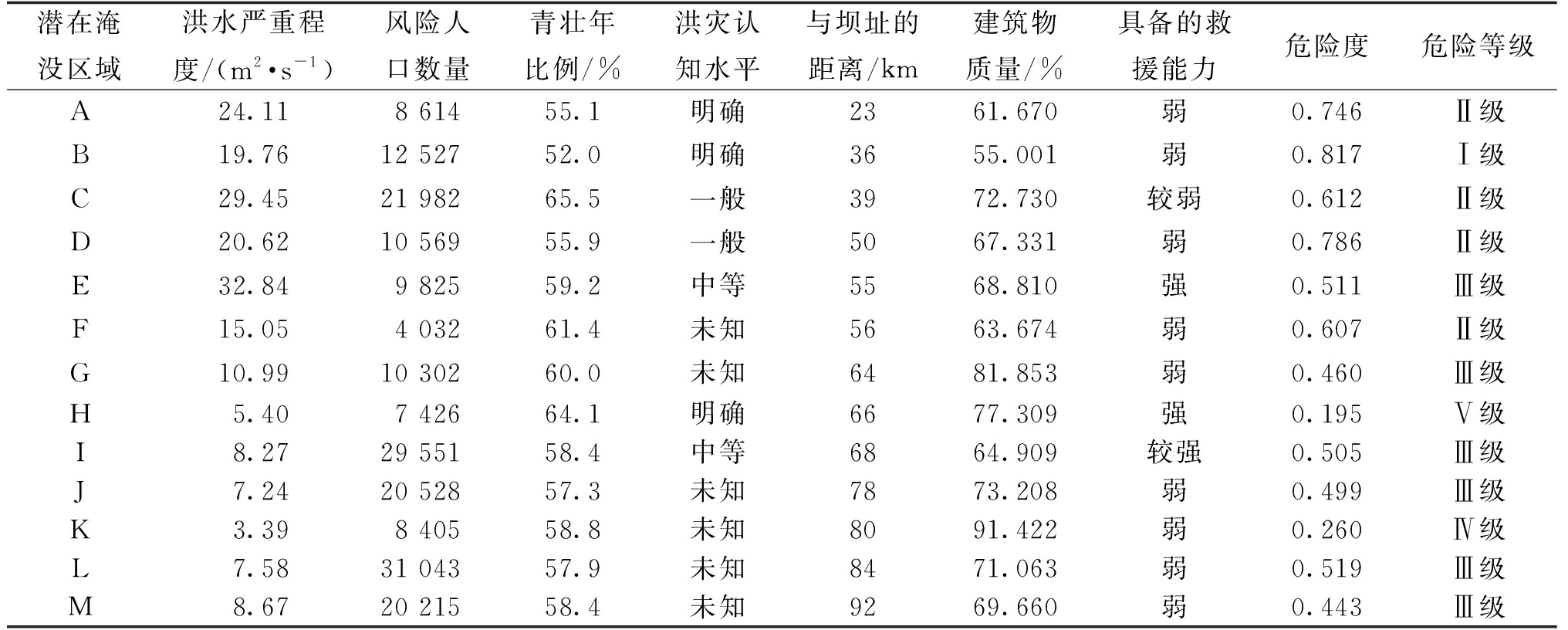
潜在淹没区域洪水严重程度/(m2·s-1)风险人口数量青壮年比例/%洪灾认知水平与坝址的距离/km建筑物质量/%具备的救援能力危险度危险等级A24.118 61455.1明确2361.670弱0.746Ⅱ级B19.7612 52752.0明确3655.001弱0.817Ⅰ级C29.4521 98265.5一般3972.730较弱0.612Ⅱ级D20.6210 56955.9一般5067.331弱0.786Ⅱ级E32.849 82559.2中等5568.810强0.511Ⅲ级F15.054 03261.4未知5663.674弱0.607Ⅱ级G10.9910 30260.0未知6481.853弱0.460Ⅲ级H5.407 42664.1明确6677.309强0.195Ⅴ级I8.2729 55158.4中等6864.909较强0.505Ⅲ级J7.2420 52857.3未知7873.208弱0.499Ⅲ级K3.398 40558.8未知8091.422弱0.260Ⅳ级L7.5831 04357.9未知8471.063弱0.519Ⅲ级M8.6720 21558.4未知9269.660弱0.443Ⅲ级
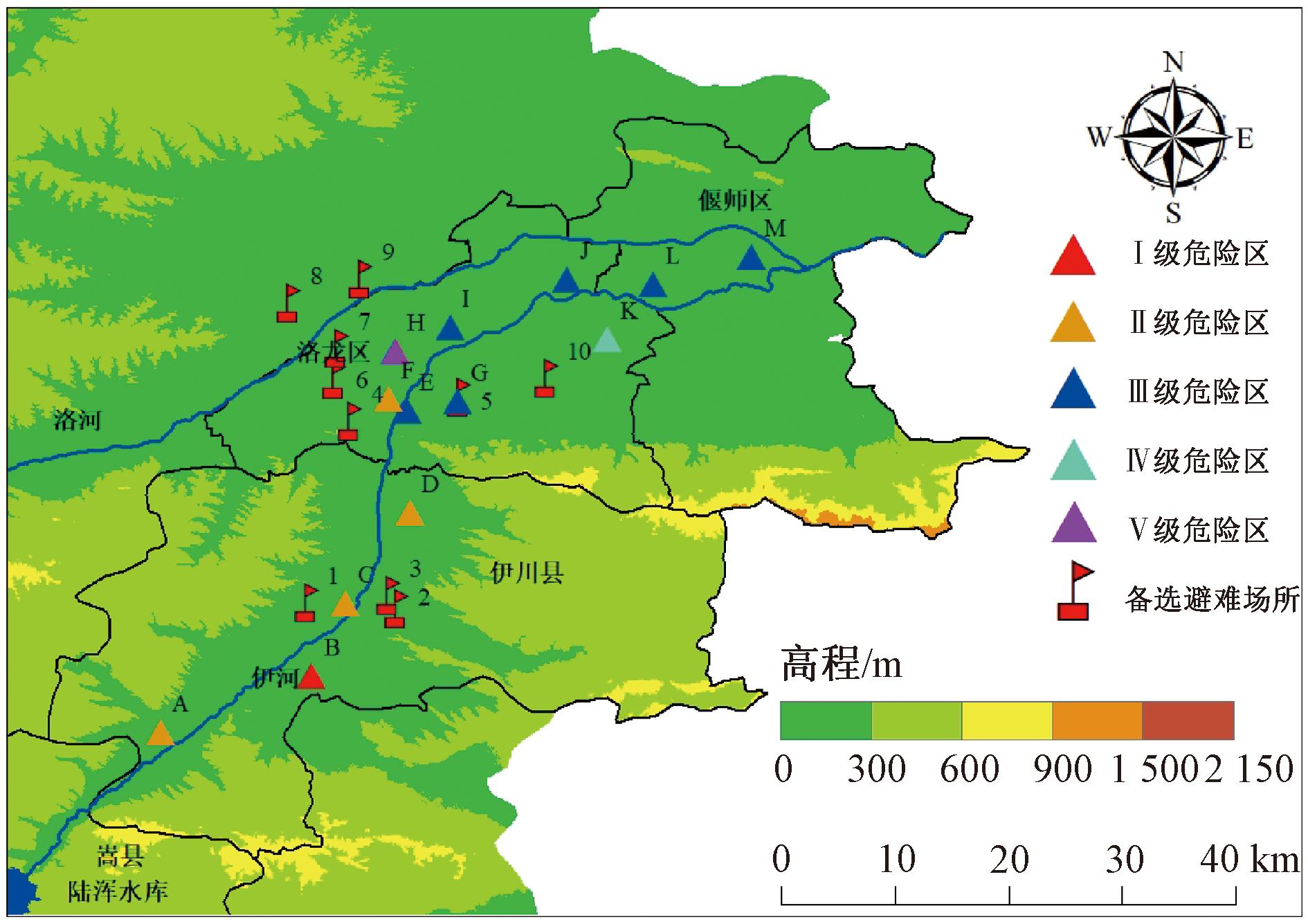
注:该图基于自然资源部标准地图服务网站下载的标准地图(审图号为GS(2020)4619)。
图5 不同级别危险区及备选避难场所分布图
Figure 5 Distribution of areas and alternative shelters
采用葛巍等[10]提出的AHP-BN法进行风险值的计算,将所得结果与危险度评价结果对比,如表6所示。E和G计算得到的风险值较高,原因是2个地区在洪水严重程度方面较危险,而在AHP-BN法中洪水严重程度的权重系数较大。突变评价法无须对评价指标赋权,因此E和G得出的风险值较危险度评价结果高。其余评价结果均一致,验证了危险度评价方法的有效性。
表6 危险度与风险值结果对比
Table 6 Comparison of results

危险度风险值(AHP-BN法)潜在淹没区域排序按危险度按风险值0.8170.861BB0.7860.844DD0.7460.844AA0.6120.841CC0.6070.838FF0.5190.791LE0.5110.601EG0.4950.575IL0.4910.572JI0.4760.563GJ0.4430.561MM0.2550.446KK0.1950.415HH
3.3 潜在溃坝洪灾避难场所选址评价
根据溃坝洪水模拟结果,在潜在淹没范围以外选取出10个备选避难场所。所选取的场所均满足3个初选指标的要求,因此只需考虑容纳人数等9个评价指标。备选避难场所的评价指标数据如表7所示,位置分布如图5所示。
表7 备选避难场所评价指标数据
Table 7 Data of evaluation index for alternative shelters
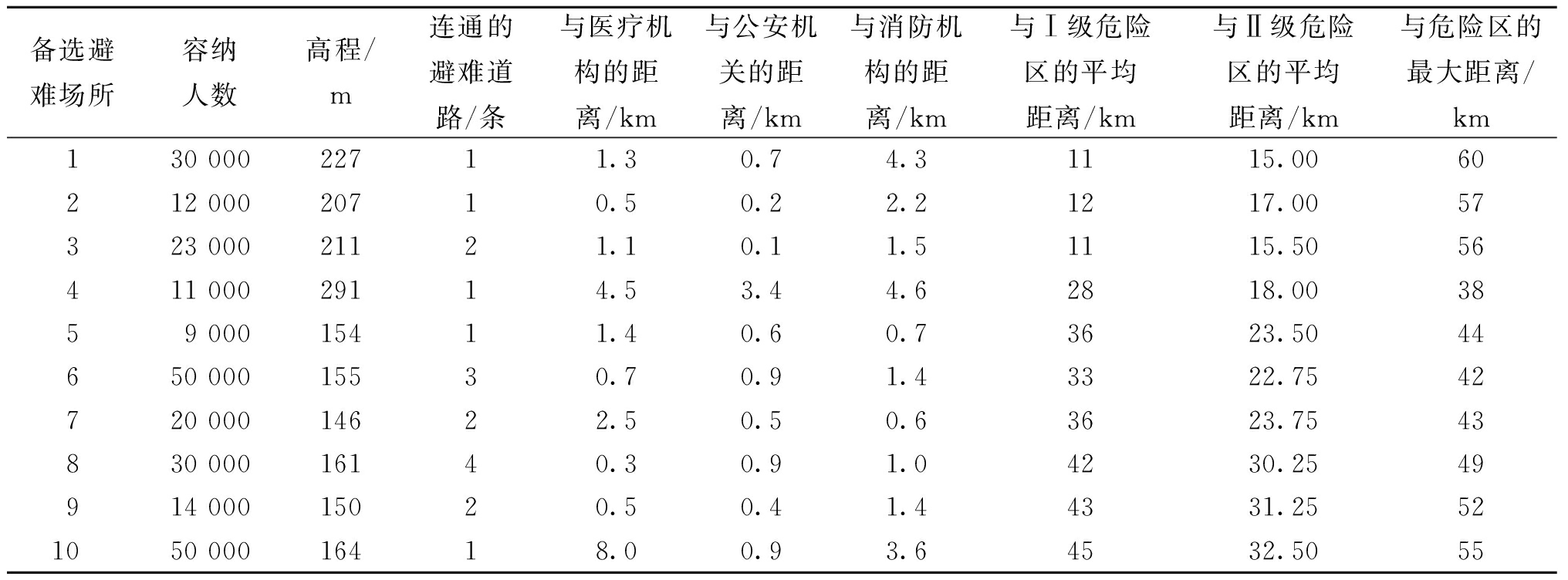
备选避难场所容纳人数高程/m连通的避难道路/条与医疗机构的距离/km与公安机关的距离/km与消防机构的距离/km与Ⅰ级危险区的平均距离/km与Ⅱ级危险区的平均距离/km与危险区的最大距离/km130 00022711.30.74.31115.0060212 00020710.50.22.21217.0057323 00021121.10.11.51115.5056411 00029114.53.44.62818.003859 00015411.40.60.73623.5044650 00015530.70.91.43322.7542720 00014622.50.50.63623.7543830 00016140.30.91.04230.2549914 00015020.50.41.44331.25521050 00016418.00.93.64532.5055
按照层次分析法的步骤计算权重值,并进行一致性检验。将所得权重与决策矩阵相乘从而构造加权矩阵,确定正负期望解,并根据式(6)计算各个评价对象到正期望解和负期望解的距离,通过式(7)计算得到10个评价对象的综合评价值C分别为0.636,0.621,0.675,0.262,0.145,0.350,0.176,0.352,0.212,0.268。将综合评价值从大到小依次排列,可以得出10个备选避难场所的优劣次序为3,1,2,8,6,10,4,9,7,5。
不考虑与高级别危险区的距离,计算备选避难场所的综合评价值,将2种结果进行对比分析,如表8所示。
表8 模型计算结果对比
Table 8 Comparison of calculation results
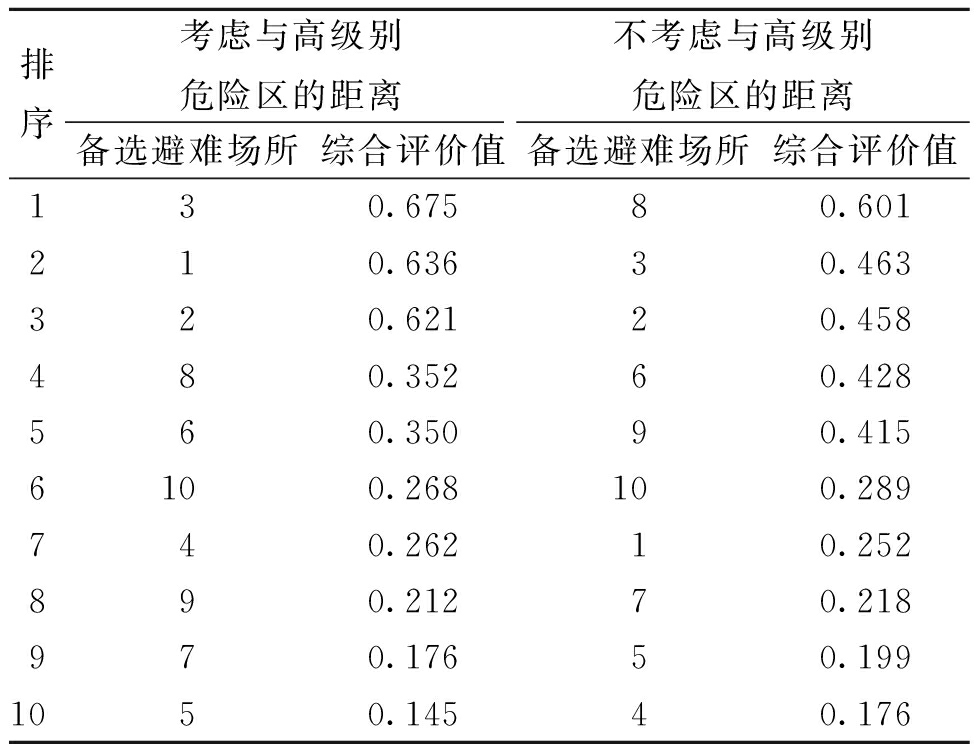
排序考虑与高级别危险区的距离不考虑与高级别危险区的距离备选避难场所综合评价值备选避难场所综合评价值130.67580.601210.63630.463320.62120.458480.35260.428560.35090.4156100.268100.289740.26210.252890.21270.218970.17650.1991050.14540.176
由表8可知,当不考虑与高级别危险区的距离时,备选避难场所8为最优。虽然备选避难场所8的规模、应急保障等条件都较好,但由图5可知,备选避难场所8与Ⅰ级、Ⅱ级危险区的距离较远。而考虑与高级别危险区的距离的模型计算结果中,尽管备选避难场所3,1,2在规模、应急保障方面不是最优的,但综合考虑了与高级别危险区的距离,能够起到重视高危险度潜在淹没区域的效果。可见,所建立的考虑潜在淹没区域危险度的溃坝洪灾避难场所选址评价模型能够充分考虑高级别危险区的需求。因此,可结合实际情况,按照综合评价结果对避难场所进行优选。
该避难场所选址评价方法从灾害风险、位置规模、应急保障、与不同级别危险区的距离4个方面出发确定避难场所的选址评价指标,使用危险度评价结果来反映潜在淹没区域对避难场所的需求程度,运用AHP-TOPSIS评价法对备选避难场所进行优劣排序,能够使选出的避难场所满足远离灾害风险、具备适宜的规模、与应急保障设施距离近、重视高危险度潜在淹没区域等要求。该方法使用方便快捷,能够对大量避难场所进行快速评价、判断相对重要性,可以很好地适用于紧急状态下的避难场所选址、确定避难场所的建设顺序等情况。
4 结论
合理规划和建设避难场所是应对灾害风险的重要措施。避难场所选址应重视高危险程度地区,本文构建了危险度评价模型,并与选址结合建立了潜在溃坝洪灾避难场所选址评价模型。以陆浑水库下游地区为例进行模型的应用,得出5个高级别危险区,危险度由高到低分别为白元镇、彭婆镇、鸣皋镇、城关街道、龙门镇,与层次分析-贝叶斯网络法得出的结果对比,证明了结果的有效性。最后,评价较优的备选避难场所能够在重视高危险度潜在淹没区域的同时满足灾害风险、位置规模、应急保障等要求,验证了方法的可行性。本文方法采用危险度评价结果来判断潜在淹没区域的需求程度,为潜在溃坝洪灾避难场所选址评价提供了新思路。
[1] WEBER E M, SEAMAN V Y, STEWART R N,et al. Census-independent population mapping in northern nigeria[J]. Remote Sensing of Environment, 2018, 204: 786-798.
[2] DALAL J, MOHAPATRA P K J, MITRA G C. Locating cyclone shelters: a case[J]. Disaster Prevention and Management, 2007, 16(2): 235-244.
[3] FADDA E, MANERBA D, CABODI G, et al. Comparative analysis of models and performance indicators for optimal service facility location[J]. Transportation Research Part E: Logistics and Transportation Review, 2021, 145: 102174.
[4] ZHAO X J, XU W, MA Y J, et al. Relationships between evacuation population size, earthquake emergency shelter capacity, and evacuation time[J]. International Journal of Disaster Risk Science, 2017, 8(4): 457-470.
[5] XU W, MA Y J, ZHAO X J, et al. A comparison of scenario-based hybrid bilevel and multi-objective location-allocation models for earthquake emergency shelters: a case study in the central area of Beijing, China[J]. International Journal of Geographical Information Science, 2018, 32(2): 236-256.
[6] 张宣峰, 于善初, 张晓飞. 多目标约束下的固定避难场所选址优化[J]. 城市发展研究, 2020, 27(8): 59-66.ZHANG X F, YU S C, ZHANG X F. Optimized location model of resident emergency congregate shelter based on multi-objective constraints[J]. Urban Development Studies, 2020, 27(8): 59-66.
[7] 王维莉, 王卓. 平灾结合的避难设施选址与灾民安置优化[J]. 安全与环境学报, 2023, 23(10): 3689-3696.WANG W L, WANG Z. Site selection of emergency shelters on the combination of normal times and disaster time and optimization of resettlement scheme for disaster victims[J]. Journal of Safety and Environment, 2023, 23(10): 3689-3696.
[8] ESMAELIAN M, TAVANA M, SANTOS-ARTEAGA F J, et al. A multicriteria spatial decision support system for solving emergency service station location problems[J]. International Journal of Geographical Information Science, 2015, 29(7): 1187-1213.
[9] MARCELIN J M, HORNER M W, OZGUVEN E E, et al. How does accessibility to post-disaster relief compare between the aging and the general population? A spatial network optimization analysis of hurricane relief facility locations[J]. International Journal of Disaster Risk Reduction, 2016, 15: 61-72.
[10] 葛巍, 焦余铁, 洪辛茜, 等. 基于AHP-BN法的溃坝生命损失风险评价[J]. 郑州大学学报(工学版), 2021, 42(3): 8-12.GE W, JIAO Y T, HONG X Q, et al. Risk assessment of life loss caused by dam breach based on AHP-BN method[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(3): 8-12.
[11] 李巍, 李宗坤, 葛巍, 等. 基于改进可变模糊集法的溃坝生命损失评价及其应用[J]. 天津大学学报(自然科学与工程技术版), 2020, 53(4): 419-425.LI W, LI Z K, GE W, et al. Improved variable fuzzy set method and its application in life loss assessment of dam break[J]. Journal of Tianjin University (Science and Technology), 2020, 53(4): 419-425.
[12] PENG M, ZHANG L M. Analysis of human risks due to dam break floods, Part 2, application to Tangjiashan landslide dam failure[J]. Natural Hazards, 2012, 64(2): 1899-1923.
[13] HUANG D J, YU Z B, LI Y P, et al. Calculation method and application of loss of life caused by dam break in China[J]. Natural Hazards, 2017, 85(1): 39-57.
[14] MAHMOUD A A, WANG J T, JIN F. An improved method for estimating life losses from dam failure in China[J]. Stochastic Environmental Research and Risk Assessment, 2020, 34(8): 1263-1279.
[15] GE W, JIAO Y T, WU M M, et al. Estimating loss of life caused by dam breaches based on the simulation of floods routing and evacuation potential of population at risk[J]. Journal of Hydrology, 2022, 612: 128059.
[16] 王志军, 宋文婷. 溃坝生命损失评估模型研究[J]. 河海大学学报(自然科学版), 2014, 42(3): 205-210.WANG Z J, SONG W T. Study of estimation model of loss of life caused by dam break[J]. Journal of Hohai University (Natural Sciences), 2014, 42(3): 205-210.
[17] 李宗坤, 胡义磊, 邓宇, 等. 基于改进突变评价法的黄河凌汛灾害风险评价[J]. 郑州大学学报(工学版), 2023, 44(1): 89-95.LI Z K, HU Y L, DENG Y, et al. The Yellow River ice flood disaster risk assessment based on improved catastrophe theory evaluation method[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(1): 89-95.
[18] 初建宇, 马丹祥, 苏幼坡. 基于组合赋权TOPSIS模型的城镇固定避难场所选址方法研究[J]. 土木工程学报, 2013, 46(增刊2): 307-312.CHU J Y, MA D X, SU Y P. Study on the location method of urban fixed refuge based on TOPSIS model with combined weight[J]. China Civil Engineering Journal, 2013, 46(S2): 307-312.
[19] AMINI H K, ASADZADEH T S, MIRHAKIMI S A. A new index-based model for site selection of emergency shelters after an earthquake for Iran[J]. International Journal of Disaster Risk Reduction, 2022, 77: 103110.
[20] 李宏恩, 马桂珍, 王芳, 等. 2000—2018年中国水库溃坝规律分析与对策[J]. 水利水运工程学报, 2021(5): 101-111.LI H E, MA G Z, WANG F, et al. Analysis of dam failure trend of China from 2000 to 2018 and improvement suggestions[J]. Hydro-Science and Engineering, 2021(5): 101-111.
[21] BERA S, GNYAWALI K, DAHAL K, et al. Assessment of shelter location-allocation for multi-hazard emergency evacuation[J]. International Journal of Disaster Risk Reduction, 2023, 84: 103435.