6G通信融合5G通信与卫星通信,实现万物智联、全球覆盖。调制识别技术能够识别通信信号并分辨干扰,从而保证通信质量,在电子对抗、非协作通信、多元环境通信领域有着重要应用。
6G通信调制体制不断复杂化,通信速率不断提高、容量不断增加,传统单方法识别无法满足实际需求[1-2]。大数据、大容量、高效率的人工智能技术能够有效提升信号调制识别性能。Liu等[3]使用图卷积神经网络进行信号识别,进行多次训练后,能够识别16QAM、32QAM、64QAM、2PSK、4PSK、8PSK等信号调制体制,但信噪比为0 dB时综合识别率仅为70%。Zhang等[4]将深度学习算法用于信号调制识别,能够在同等信噪比状态下将识别率提高至78.3%,并能够保持信号调制识别种类。Zhang等[5]在识别方法中引入深层神经网络与注意力机制,在0 dB情况下调制识别率提高至80%。Deng等[6]基于多模态信息和少镜头学习半监督方法对信号调制种类进行识别,可识别调制体制覆盖FSK、PSK、QAM常用调制阶数,0 dB时调制识别率提高至82%。Wang等[7]融合深度学习算法与多准则决策算法,将IQ两路信号转化的星座图作为视觉线索,利用结构特征对信号调制体制进行识别,0 dB情况下调制识别率可达95%。
信号处理与人工智能技术的融合可提升低信噪比环境下信号调制识别性能。Lin等[8]在研究中引入信号增强的处理方式与多阶注意力机制,信噪比2 dB条件下能够将大部分信号的识别率提高至接近99%,但对高阶QAM调制不具备识别能力。Yang等[9]使用信号高阶累积量,综合卷积神经网络和递归神经网络对信号调制体制进行识别,在信噪比为0 dB的情况下识别率接近100%,但只能区分不同大类的信号调制体制,无法继续识别信号调制阶数。Zhao等[10]融合信号时域与高阶调制域,并使用决策树算法识别信号调制体制,当信噪比达到3 dB时,识别成功率可达到95%以上。Ji等[11]提出时空特征融合的自动调制识别方法,同时在网络中使用记忆网络算法、神经网络算法,经过训练后,0 dB条件下信号调制识别率最高可达到91%。其他研究者对信号的不同特征域,如时频域[12-13]、小波变换域[14]等提取信号特征值以识别其调制体制,但都无法以较高识别率识别6G所需的64QAM、128QAM甚至更高阶数的信号调制体制。
本文针对6G通信信号调制识别阶数要求高、低信噪比环境调制识别难的问题,提出一种基于多准则融合智能决策算法的信号调制识别方法。该方法包含多准则融合网络与智能决策网络。运用信号的高阶累积延伸量,通过遍历局部最优解的方式寻找所有潜在门限值,以基尼系数和确定度增熵确定判决门限;参考多准则决策树中的CART型网络架构,建立初级决策树并迭代剪枝,最终建立最优智能决策树,识别未知信号的调制体制。
1 信号调制识别模型
1.1 信号的高阶累积量及其延伸量
传统的信号调制识别与信号处理方法常对信号的相关函数和功率谱进行分析,由于二阶矩参数具有等价性与多重性,不能辨识非最小相位系统;同时在加性噪声的情况下,二阶统计量抗干扰性弱,无法提供足够精准的调制信息[15]。因此,本文采用信号高阶统计量中的高阶累积量与高阶累积延伸量。高阶量算法复杂度低且具备良好的抗噪声性能,对数字调制信号有着较为突出的识别优势。信号的第二特征函数为随机信号特征函数的自然对数[16-17],按泰勒级数展开为
(1)
式中:Cp为信号的p阶累积量;O(ω)P为ω的高阶无穷小量;P为泰勒级数展开阶数。则信号k阶累积量Ck,l与ψ(ω)的导数之间的关系为
(2)
式中:cum(·)为累积函数;k为累积量且k<K信号序列总数量;l为累积量共轭部分阶数;x1,x2,…,xk为采样信号序列;![]() 为信号xi共轭函数。信号的k阶混合矩Mk,l与ψ(ω)的关系为
为信号xi共轭函数。信号的k阶混合矩Mk,l与ψ(ω)的关系为
(3)
式中:E(·)为均值函数。将式(1)~(3)按照泰勒级数展开并对比(jω)k与(jω)l的同幂项系数,可得信号的高阶累积量Ck,l与高阶混合矩Mk,l的关系如式(4)~(9)所示:
C2,0=cum(X,X)=M2,0;
(4)
C2,1=cum(X,X*)=M2,1;
(5)
(6)
C4,1=cum(X,X,X,X*)=M4,1-3M2,0M2,1;
(7)
(8)
C6,0=cum(X,X,X,X,X,X)=M6,0-
(9)
式中:X为信号采样序列,即x1,x2,…,xk。同种调制类型信号的高阶累积量在比较时具有重复性,导致信号判决门限的确定难度较大。考虑信号偶次矩构成信号功率谱类项,本文对信号二阶、四阶、六阶累积量进行组合筛选,使用高阶累积量组合进行信号调制体制分类,得到信号调制体制的判决门限为
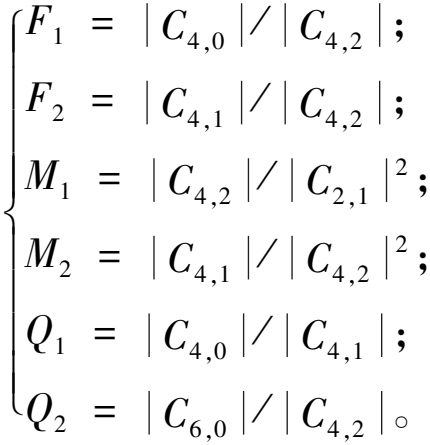
(10)
1.2 基于多准则融合与智能决策的调制识别网络
为提高调制识别的准确度,本文构建基于多准则融合与智能决策的调制识别网络。图1为网络的整体架构,调制识别网络分为多准则融合网络与智能决策网络。在多准则融合网络中,使用局部最优解原则,结合式(10)中高阶累积延伸量筛选出所有潜在判决门限,并基于确定度增熵和基尼系数两种不同的门限确定原则进行比较,得到3层判决门限。将3层判决门限及对应的调制体制输入至智能决策网络,基于CART决策树算法进行网络构建与迭代优化,形成基于多准则融合与智能决策的调制识别网络。
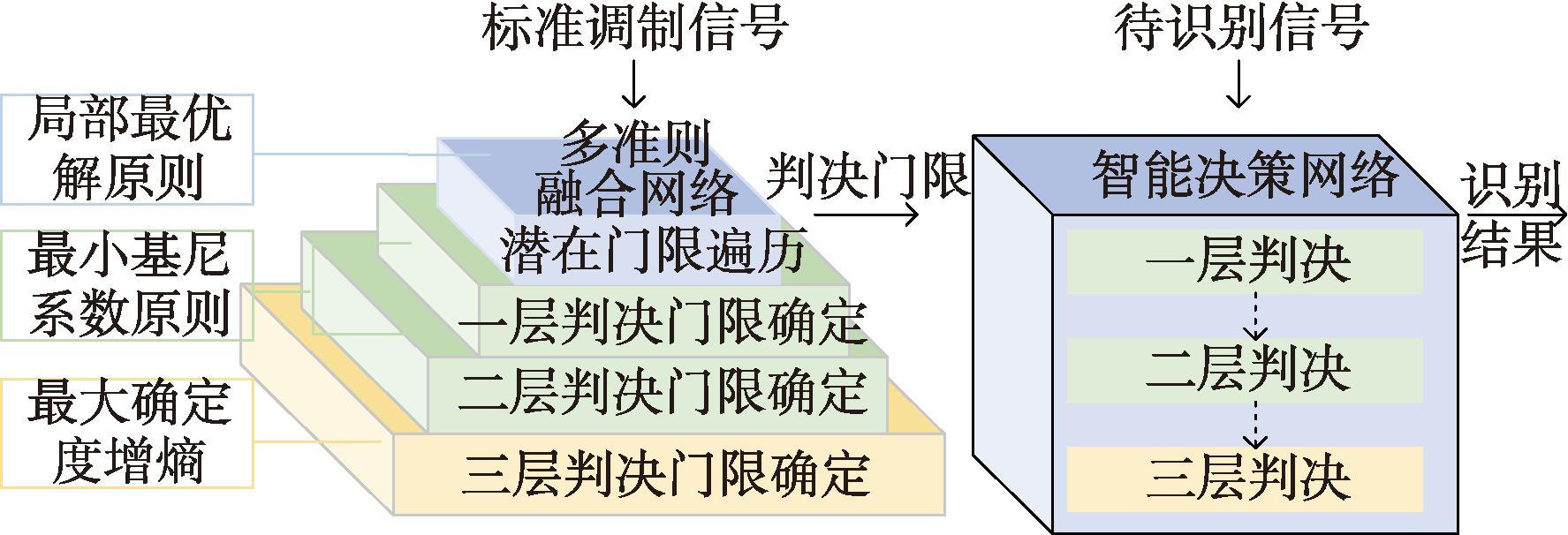
图1 调制识别网络整体架构
Figure 1 Architecture of modulation recognition network
1.2.1 基于基尼系数与确定度增熵的门限融合算法
调制识别的最佳判决门限指能够最大程度减小错误判决概率的门限值,即每个判决门限能够降低的未知信号调制体制不确定度最大。
本文综合考虑判别准则的数量与决策网络的构建,使用遍历局部最优解的方式寻找所有潜在门限,使用确定度增熵和基尼系数两个参考原则寻找并融合最佳的判决门限组合[16-17]。图2为多准则融合网络模型的架构与网络确定调制体制识别时所需门限种类与门限值的具体过程,包含潜在门限遍历、大类门限确定、细分门限确定3个部分。

图2 多准则融合网络架构
Figure 2 Architecture of multi-criteria fusion network
潜在门限值确定过程使用遍历局部最优解的方法,将不同调制体制对应的所有高阶累积量及其延伸量进行对比,计算每种调制体制在不同信噪比下各个量的范围数值。随后遍历数轴上所有的点集并找到没有被调制信号覆盖的区间,以该区间中点为潜在门限,将调制体制分为两个区间,最大程度简化后续算法复杂度。
多准则融合网络遍历所有潜在门限,使用确定度增熵和基尼系数两个参考原则寻找并融合最佳的判决门限组合。门限确定将提高调制体制的确定度,本文采用确定度增熵ΔH(X)表示:
(11)
式中:N为标准调制信号的总采样点数;p(xn)为每种调制体制的概率。ΔH(X)表示调制体制不确定度的变化,确定度增熵越大,判决门限能够提供调制种类的信息量越大,门限有效度越高[18-19]。但面对多个准则融合,且部分准则无法将信号细分为具体的调制体制时,仅以确定度增熵进行判断将严重降低模型效率,增加判决门限选取难度。因此本文引入基尼系数,并按照二分类树模型进行计算和剪枝。标准调制信号集Xst的基尼系数Gini(Xst,T)表示为
(12)
式中:M为标准调制信号的总采样点数;Xm为标准调制信号集Xst的不同分类;T为分类的决策方案,在模型中指信号的判决门限值。在模型中,信号在方案T下的基尼系数Gini(Xst,T)代表该门限进行调制识别时结果的混淆度,基尼系数越小,结果混淆度越低,证明该准则判决能力越好。
模型采用根节点二分方式建立网络子树,在决策门限A的条件下,信号集Xst的基尼系数为
(13)
1.2.2 基于CART决策树的最优智能决策网络
CART决策树是使用基尼系数作为判决标准来进行特征选择并生成二叉树的智能决策算法。本文基于CART模型,通过多准则融合网络计算得到的判决门限与判决分类,构建智能决策网络。智能决策网络将多准则融合网络的3层判决门限作为图3左侧所示的初级决策树判决门限,并通过剪枝算法对决策树进行多次迭代优化,最终得到图3右侧的最优决策树。
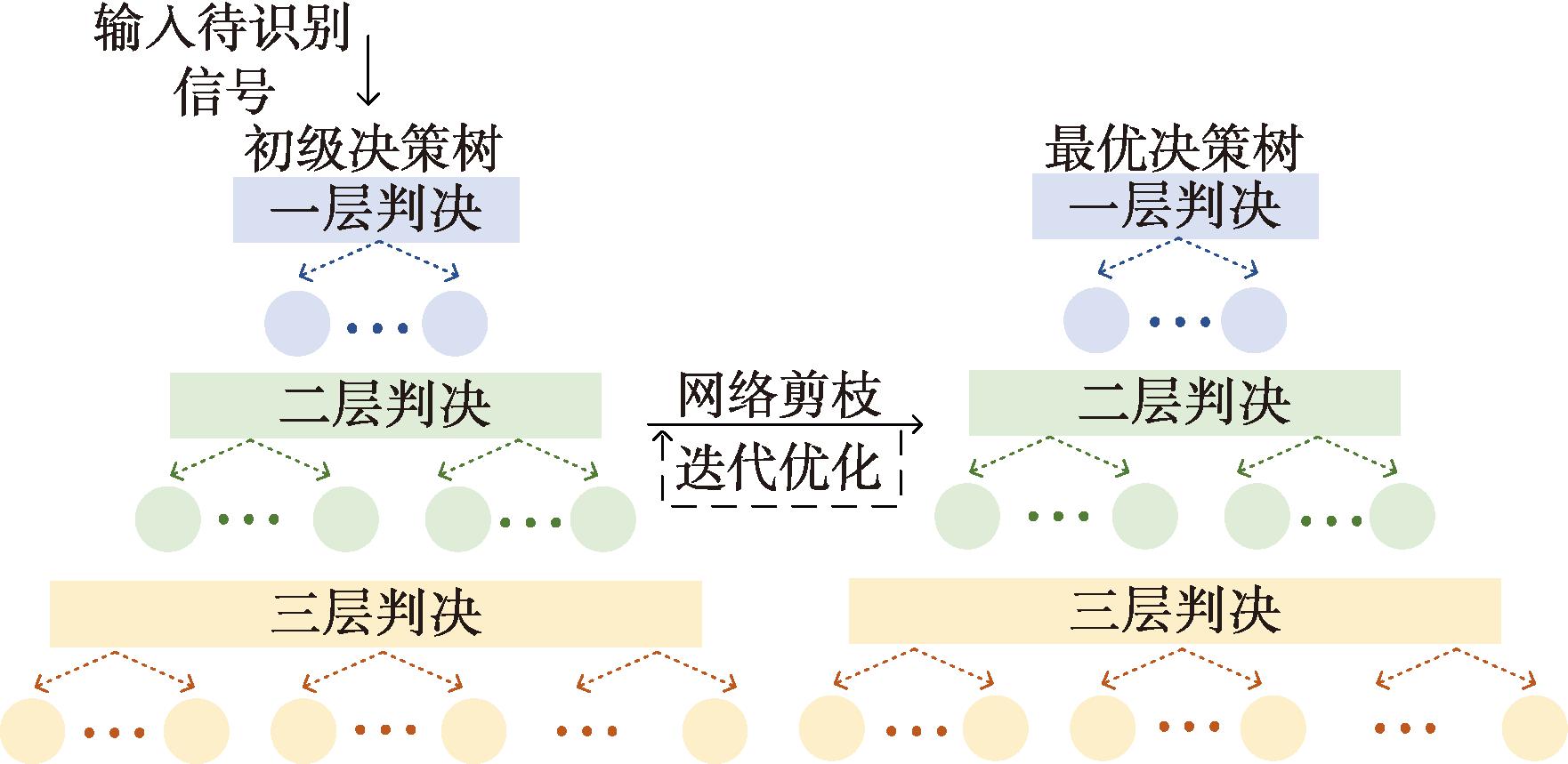
图3 基于CART模型的智能决策网络架构
Figure 3 Intelligent decision network architecture based on CART model
多准则融合网络确定的判决依据与判决门限较多,且不同门限对信号调制体制的分类情况间有重复部分,导致初级决策网络出现较为严重的过拟合情况[20],降低了信号的识别率。因此,本文对初级CART决策树进行剪枝,降低网络过拟合度以提高识别率。CART网络的剪枝算法从初级决策树T0的底端开始不断剪枝,直到T0的根节点,形成一个子树序列T={T0,T1,…,Tn},并通过降低算法的过拟合程度寻找最优决策树。决策树过拟合造成的损失为
Cα(T)=C(T)+α|T|。
(14)
式中:Cα(T)为损失函数;C(T)为过拟合造成的误差;|T|为子树的叶节点数量;α用于权衡过拟合造成的误差与决策树规模的趋势关系。对任意内部节点q,当其作为下一决策子树根节点时,过拟合导致的损失函数为
Cα(Tq+1)=C(Tq+1)+α|Tq+1|。
(15)
对其进行剪枝后,该节点将不再构成决策子树,决策树的损失函数为
Cα(Tq)=C(Tq)+α·1。
(16)
显然此时:
C(Tq+1)>C(Tq)。
(17)
当式(15)与式(16)相等时,剪枝前后达到临界状态,即过拟合造成的损失与决策树规模的损失达到最小值。此时对子树的剪枝不影响决策树整体损失函数。联立式(15)与式(16)可得此时的α为
(18)
具体操作中,第一轮决策从决策树主根节点开始,设α的初值为α0,引入函数g(r)代表任意内部节点r对应的α值,如式(19)、(20)所示:
(19)
α=min(α,g(r))。
(20)
剪枝过程从上至下依次遍历每一内部节点,计算该点的g(r)值并与前一节点的α进行比较。当g(r)=α时,证明该节点的子树损失函数与上一节点一致,在同等损失的情况下剪去以r为根节点的子树,仅将其作为上一级子树的叶节点。如此剪枝下去,直至得到主根节点,从而获得第一轮剪枝的决策树与α。随后算法将依据该轮的α对决策树进行第二轮剪枝,直至最后一轮剪枝得到的α与前一轮相同,证明此时决策树已达最优状态[21]。
多准则融合网络综合局部最优解原则、最小基尼系数原则和最大确定度增熵原则,从不同调制信号的多个高阶累积延伸量中筛选最优判决门限。在该门限的基础上建立基于CART模型的初级决策树,并对决策树进行剪枝,最终得到最优智能决策树,形成智能决策网络,对信号调制体制进行识别。
2 分析与讨论
实验通过MATLAB软件搭建基于基尼系数与确定度增熵的多准则融合网络与基于CART决策树的最优智能决策网络。使用遍历算法与局部最优解算法寻找潜在门限,使用基尼系数与确定度增熵筛选门限,搭建CART决策框架,设计多准则融合智能决策网络模块,在不同信噪比下对未知信号的调制体制进行识别,并与信号实际调制体制对比,得到每种调制的识别率。
2.1 潜在门限寻找与判决门限确定
输入信号进行采样后,依据式(4)~(10)计算信号的高阶累积延伸量。在MATLAB中绘制不同信号高阶量的覆盖区间,遍历所有区间并依据局部最优解原则选出所有的潜在门限。图4中F1、F2、M1、M2、Q1、Q2均为式(10)中定义的高阶累积延伸量。
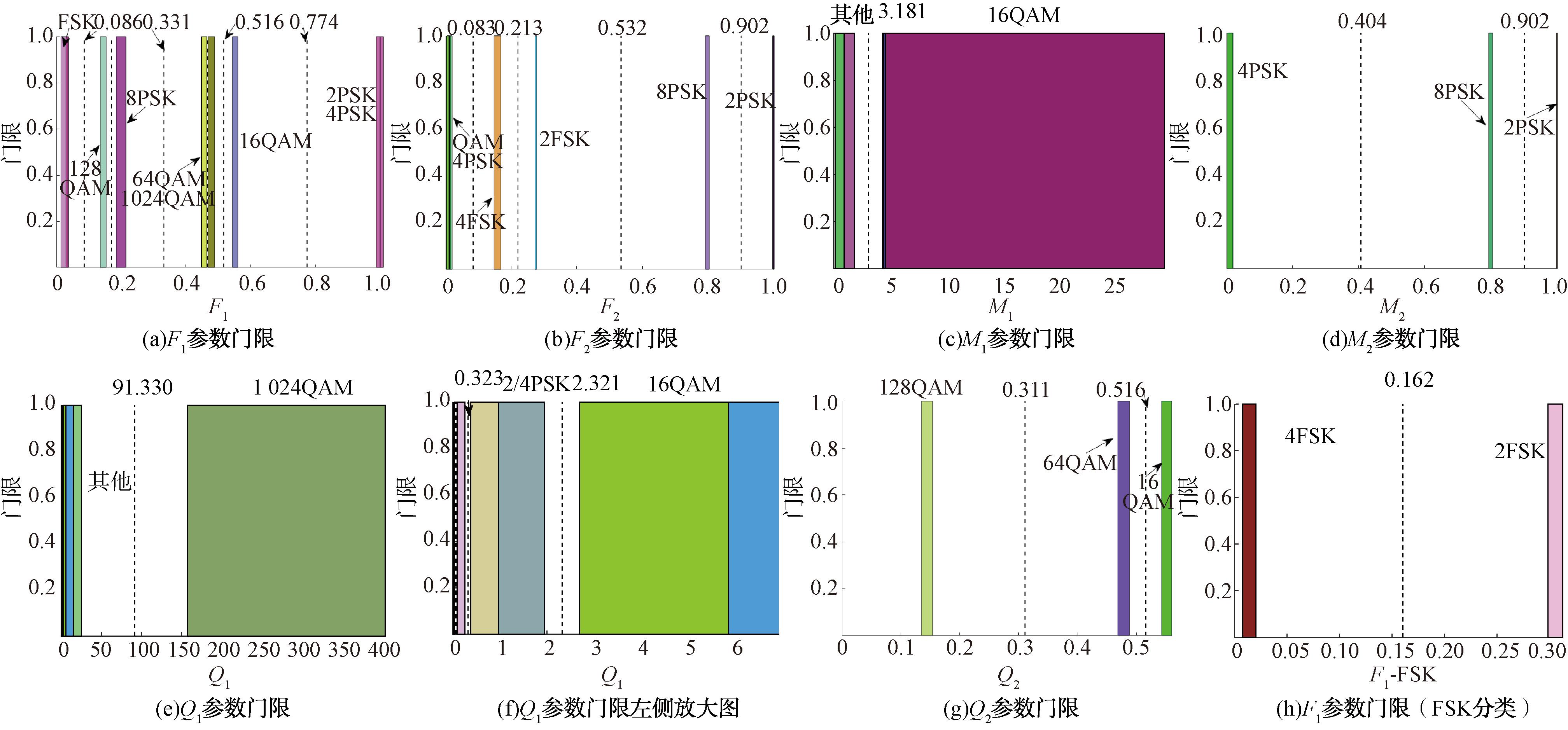
图4 信号潜在判决门限
Figure 4 Signal potential judgment threshold
为提高算法效率,将高阶累积延伸量间区分度较低的值忽略,得到如图4所示的潜在判决门限,并输入至大类门限确定网络。由于FSK信号的特性,在FSK信号大类被筛选出后,需要再次与载波相乘,完成具体的FSK信号调制阶数分类。图4(h)为2FSK、4FSK信号的潜在门限判决结果。基于最小基尼系数原则与最大确定度增熵原则,实验对不同高阶量的门限进行融合判决,并从所有潜在判决门限中,通过基尼系数与确定度增熵因素,最终确定3层判决门限准则,如表1所示。
表1 3层判决准则筛选结果
Table 1 Selection results of three levels judgment criteria

一层判 决准则 F1 > 0. 081 F2≤0. 095 F1≤0. 031 F2≤0. 535 FSK QAM (混杂 PSK) 二层判 决准则 Q1≤2. 3 M1≤3. 175 其余 PSK QAM 三层判 决准则 F3 = 0. 159 Q1 = 89. 965 Q2 M2 0. 311 0. 512 0. 408 0. 902 2 / 4FSK 1024QAM 16 / 64 QAM 64 / 128 QAM 2 / 4 PSK 4 / 8 PSK
2.2 智能决策网络识别结果与剪枝优化
基于多准则融合与智能决策网络得到的3层判决门限,建立初级智能决策树进行未知信号的调制识别,并根据识别结果对决策树剪枝,迭代优化出最优决策树。实验生成16QAM、64QAM、128QAM、1024QAM、2PSK、4PSK、8PSK、2FSK、4FSK共9类信号,设计含有高斯噪声的加性信道,在信号接收端进行采样并按照上述决策门限对信号的调制体制进行识别。实验设置信噪比为-3~10 dB,总采样点数为15 000个点。
实验结果如图5所示。其中,图5(a)为不进行剪枝,使用所有判决门限进行调制识别时的识别率。可以看出,当信号信噪比小于0 dB时,综合识别率低于50%,并且变化较大。造成这种现象的原因是小信噪比情况时门限判决准则过于复杂,且部分门限间距离较小,容易出现误分类情况,降低了算法的识别率。图5(b)、5(c)为经过剪枝后的信号识别结果。图5(b)根据高阶调制体制的子树进行剪枝,在0 dB信噪比情况下,将128QAM识别率从原先稳定在90%左右提高到97.5%以上,将8PSK调制体制的识别率从稳定在85%提高到100%。图5(c)根据低阶调制体制的子树进行剪枝,将64QAM、1024QAM的识别率,尤其是-3 dB信噪比情况下的识别率从60%以下提高到80%以上,在0 dB时达到100%。
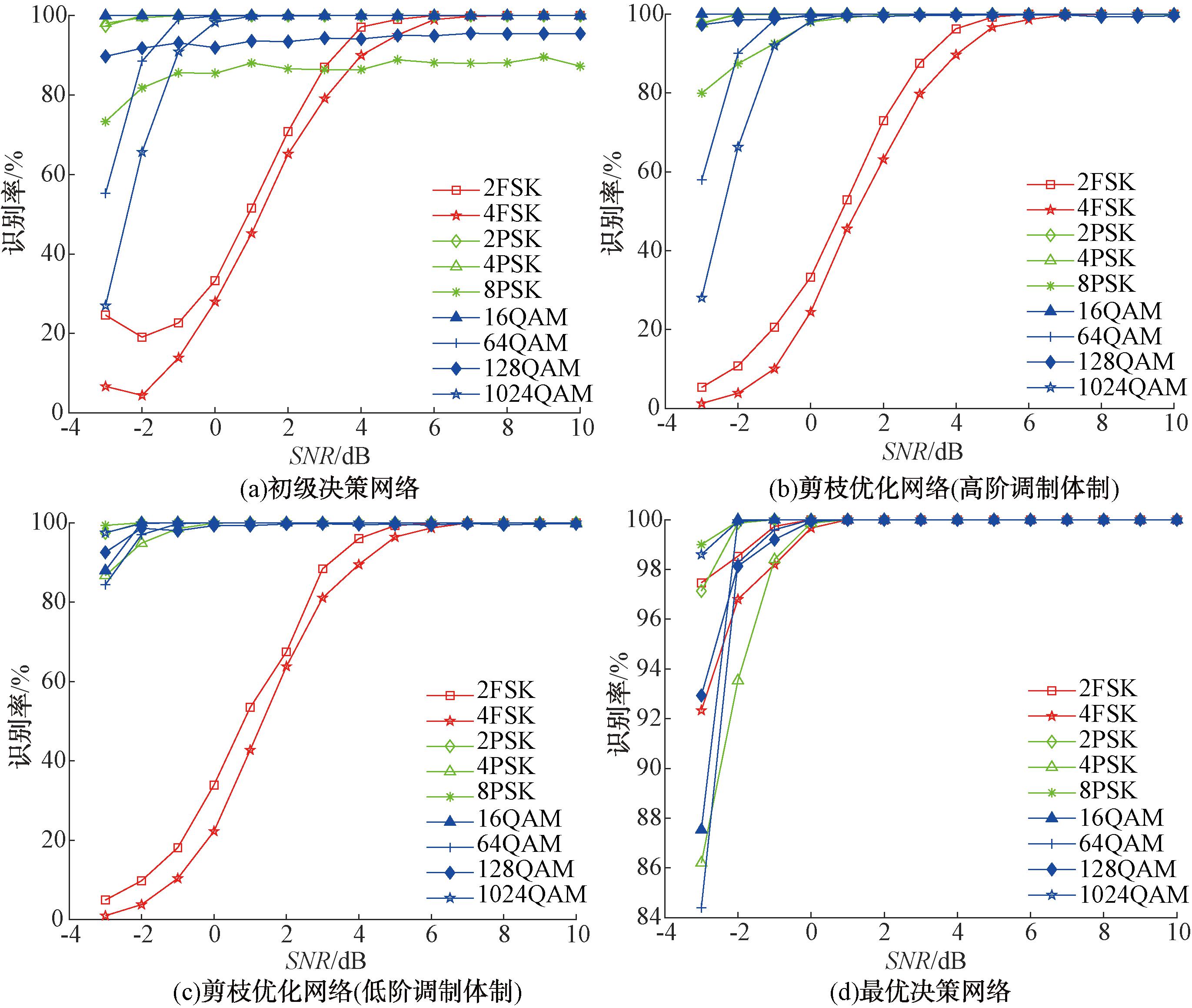
图5 不同剪枝情况下调制识别率
Figure 5 Modulation recognition accuracies with different pruning situations
图5(d)为剪枝至决策树主根节点后得到的最优决策网络,该网络主要对调制识别效果较差的FSK信号为子节点的决策树进行剪枝,能够将2FSK的识别率在0 dB时提高至99.86%,4FSK识别率提高至98.22%,所有调制体制综合识别率达到99.4%。而在-3 dB信噪比的情况下,调制体制的综合识别率也能够达到91.26%以上,识别率最低的64QAM也能超过84%。结果表明,尤其在低信噪比的恶劣情况下,信号的整体识别成功率从71.95%提高至91.26%,同时对于高阶调制体制,剪枝提升效果明显,以0 dB为例,8PSK的识别率从89.67%提升至100%,1024QAM、128QAM均提升至100%。
通过表2的普通信噪比情况下与其他文献的实验结果对比可知,本文实验结果与文献[5,7,11]相比,能够在0 dB处达到99.4%的信号综合识别率,优于典型调制识别率。本文的综合识别率略小于文献[9]的99.8%,但文献[9]只能对信号调制识别的种类进行粗分类,分辨2FSK、4PSK、16QAM这3种信号,而本文能够识别的信号种类共9种,在远多于其识别种类的基础上维持99.4%的信号识别率。
表2 调制综合识别率实验结果与对比
Table 2 Experimental results and comparison of modulation comprehensive recognition accuracy

信噪比 情况 核心算法 可识别调制种类 调制阶数 调制 体制 信噪 比/ dB 综合识 别率/ % 普通信 噪比 多准则融 合与智能 决策网络 信道和空 间自注意 力机制[5] 深度学习 与多准则 融合[7] 深度学习 与神经网 络[9] 多特征值 决策树[11] 2 / 4 FSK 2 / 4 / 8 PSK 16 / 64 / 128 / 1 024 QAM 2 FSK 2 / 4 / 8 PSK 16 / 64 QAM 2 / 4 FSK 2 / 4 / 8 PSK 16 / 64 QAM 2 FSK 4 PSK 16 QAM 2 / 4 FSK 2 / 4 / 8 PSK QAM 0 2 0 0 0 > 99. 40 > 98. 70 > 97. 80 > 99. 80 > 98. 50 低信 噪比 多准则融 合与智能 决策网络 信道和空 间自注意 力机制[5] 多模态智 能决策[6] 2 / 4 FSK 2 / 4 / 8 PSK 16 / 64 / 128 / 1 024 QAM 2 FSK 2 / 4 / 8 PSK 16 / 64 QAM 2 / 4 FSK 2 / 8 PSK 16 / 32 / 64 QAM - 3 - 3 - 3 > 91. 26 > 75. 20 > 72. 00 深度学习 与多准则 融合[7] 多特征值 决策树[11] 2 / 4 FSK 2 / 4 / 8 PSK 16 / 64 QAM 2 / 4 FSK 2 / 4 / 8 PSK QAM - 3 - 3 > 90. 00 > 72. 50
由表2可知,低信噪比条件下本文提出的多准则融合与智能决策网络对信号调制识别具有较优表现。本文多准则融合与智能决策网络能够在-3 dB信噪比情况下,对除64QAM以外的信号达到85%以上的识别率,综合识别率达到91.26%,与文献研究中的调制识别方法相比,均具有更好识别率。
3 结论
本文将人工智能与信号处理技术结合,通过决策网络融合信号高阶量对调制体制进行识别。采用局部最优解方式对不同调制体制的高阶量进行遍历,寻找所有潜在门限,以最小基尼系数和最大确定度增熵为原则,抉择出最优判决门限。基于此建立智能决策网络,并对其进行剪枝,得到最优智能决策树。经实验验证可知,该模型对0 dB信噪比情况下调制体制的综合识别率达到99.4%,在-3 dB下也能达到91.26%的综合识别率,相比其他模型识别率有较大提升,且可识别调制体制在阶数与种类方面更符合6G通信需求。
[1] AN Z L, ZHANG T Q, SHEN M, et al. Series-constellation feature based blind modulation recognition for beyond 5G MIMO-OFDM systems with channel fading[J]. IEEE Transactions on Cognitive Communications and Networking, 2022, 8(2): 793-811.
[2] JANNAH R R, KHAYAM U. Design, implementation, and testing of partial discharge signal pattern recognition and judgment system application using statistical method[C]∥International Conference on Electric Vehicular Technology and Industrial, Mechanical, Electrical and Chemical Engineering (ICEVT &IMECE). Piscataway: IEEE, 2015: 314-318.
[3] LIU Y B, LIU Y, YANG C. Modulation recognition with graph convolutional network[J]. IEEE Wireless Communications Letters, 2020, 9(5): 624-627.
[4] ZHANG X L, LI T Y, GONG P, et al. Open set recognition of communication signal modulation based on deep learning[J]. IEEE Communications Letters, 2022, 26(7): 1588-1592.
[5] ZHANG W N, SUN Y Q, XUE K L, et al. Research on modulation recognition algorithm based on channel and spatial self-attention mechanism[J]. IEEE Access, 2023, 11: 68617-68631.
[6] DENG W, WANG X, HUANG Z T, et al. Modulation classifier: a few-shot learning semi-supervised method based on multimodal information and domain adversarial network[J]. IEEE Communications Letters, 2023, 27(2): 576-580.
[7] WANG T, HOU Y H, ZHANG H Y, et al. Deep learning based modulation recognition with multi-cue fusion[J]. IEEE Wireless Communications Letters, 2021, 10(8): 1757-1760.
[8] LIN S G, ZENG Y, GONG Y. Modulation recognition using signal enhancement and multistage attention mechanism[J]. IEEE Transactions on Wireless Communications, 2022, 21(11): 9921-9935.
[9] YANG C, HE Z M, PENG Y, et al. Deep learning aided method for automatic modulation recognition[J]. IEEE Access, 2019, 7: 109063-109068.
[10] ZHAO X D, ZHOU X H, XIONG J, et al. Automatic modulation recognition based on multi-dimensional feature extraction[C]∥2020 International Conference on Wireless Communications and Signal Processing (WCSP). Piscata-way: IEEE, 2020: 823-828.
[11] JI M R, HUANG C Z, LUO R S. Automatic modulation recognition based on spatio-temporal features fusion[C]∥2022 IEEE 12th International Conference on Electronics Information and Emergency Communication (ICEIEC). Piscataway: IEEE, 2022: 89-93.
[12] XU S, LIU L T, ZHAO Z K. DTFTCNet: radar modulation recognition with deep time-frequency transformation[J]. IEEE Transactions on Cognitive Communications and Networking, 2023, 9(5): 1200-1210.
[13] HOU C B, LIU G W, TIAN Q, et al. Multisignal modulation classification using sliding window detection and complex convolutional network in frequency domain[J]. IEEE Internet of Things Journal, 2022, 9(19): 19438-19449.
[14] YAO R G, WANG P, ZUO X Y, et al. Intelligent modulation pattern recognition based on wavelet approximate coefficient entropy in cognitive radio networks[J]. IEEE Access, 2020, 8: 226176-226187.
[15] ZENG Y, ZHANG M, HAN F, et al. Spectrum analysis and convolutional neural network for automatic modulation recognition[J]. IEEE Wireless Communications Letters, 2019, 8(3): 929-932.
[16] 张贤达. 现代信号处理[M]. 3版. 北京: 清华大学出版社, 2015.
ZHANG X D. Modern signal processing[M]. 3rd ed. Beijing: Tsinghua University Press, 2015.
[17] ZENG L, CHIANG H D, LIANG D, et al. Trust-tech source-point method for systematically computing multiple local optimal solutions: theory and method[J]. IEEE Transactions on Cybernetics, 2022, 52(11): 11686-11697.
[18] ZHAO Z, YANG A Y, GUO P. A modulation format identification method based on information entropy analysis of received optical communication signal[J]. IEEE Access, 2019, 7: 41492-41497.
[19] 韩刚涛, 马瑞鹏, 吴迪. 基于时频图切割的宽带信号智能检测与识别[J]. 郑州大学学报(工学版), 2023, 44(3): 42-49.
HAN G T, MA R P, WU D. Intelligent detection and identification of broadband signals based on time-frequency map cutting[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(3): 42-49.
[20] LAI C M, KUO T J. Available capacity computation model based on long short-term memory recurrent neural network for gelled-electrolyte batteries in golf carts[J]. IEEE Access, 2021, 10: 54433-54444.
[21] 李航. 统计学习方法[M]. 2版. 北京: 清华大学出版社, 2019.
LI H. Statistical learning method[M]. 2nd ed. Beijing: Tsinghua University Press, 2019.