注浆是水利、交通、市政等基础设施修复加固的重要手段,根据注浆方法的特点主要分为压密注浆、劈裂注浆、渗透注浆、裂隙注浆等类型[1]。其中,压密注浆借助浆液对周围土层的挤压效应达到挤密土体、加固地层的目的,在基础设施安全防护领域得到了广泛应用。了解压密注浆机理有利于指导注浆施工。
数值模拟是研究压密注浆机理的重要途径,国内外许多学者在该领域开展了大量研究。李向红[2]采用Mohr-Coulomb准则,用有限元方法对软黏土压密注浆进行了数值模拟,得到了浆柱周围土体位移场与塑性变形范围。巨建勋[3]基于Drucker-Prager准则,利用有限元分析了土体压密注浆过程,确定了注浆加固范围。唐智伟等[4]应用有限差分程序FLAC3D通过在单元上施加各向同性的膨胀压力模拟压密注浆过程,研究了其抬升地层机理。王立中[5]运用二维颗粒流程序PFC2D模拟浆液和土颗粒的运动及其相互作用,研究了围压、注浆压力等对浆液扩散范围的影响。周子龙等[6]运用颗粒流方法分析了影响浆泡半径与注浆效果的因素,结果表明,注浆压力与土体黏聚力对压密注浆效果影响显著,而土体颗粒摩擦因数几乎没有影响。Wang等[7]基于Mohr-Coulomb准则,研究了压密注浆浆体在无黏性土中的径向扩张规律。Shrivastava等[8]基于Mohr-Coulomb准则,将压密注浆模拟为有限介质中圆柱形空腔的膨胀,分析了压密注浆在相对松散、中等和致密3种密实状态土体中的挤密效果。Shrivastava等[9]提出了基于弹塑性理论的压密注浆二维有限元模型,研究了注浆压力、注入点间距、覆土压力和地面初始相对密度等参数对压密注浆效果的影响。
总体来看,目前关于压密注浆仿真方法主要基于弹塑性理论,多采用Mohr-Coulomb、Drucker-Prager等准则模拟土体力学行为,受此类本构模型自身限制,计算结果仅能获得注浆压力作用下浆柱周围土体弹塑性应力分布情况,无法描述土体被挤密后密度、孔隙比、弹性模量等参数变化和分布特征[10],难以全面揭示土体压密注浆机理。
针对这一问题,本文引入修正剑桥模型模拟土体力学行为,基于有限元原理,建立了一种土体压密注浆仿真模型,通过与解析解及现场试验结果的对比检验该模型的适用性,在此基础上分析注浆加固后土体应力、密度、孔隙比、弹性模量分布特征,研究注浆压力、注浆深度等因素对挤密效果的影响,为深入研究压密注浆机理奠定基础。
1 修正剑桥模型
修正剑桥模型具有参数较少且便于获取,能够反映土体压缩回弹过程及破坏前非线性变形等特点[11-12],且考虑了应变硬化特性,屈服面随着应力应变的变化而改变,能够反映土的压密性,能够较好描述压密注浆过程中土体物理和力学特征。
图1为修正剑桥模型屈服面,该模型屈服面和应力应变关系主要涉及3个参数:回弹指数κ、压缩指数λ、临界状态应力比M,其中κ和λ由各向等压试验确定,M由三轴剪切试验确定。
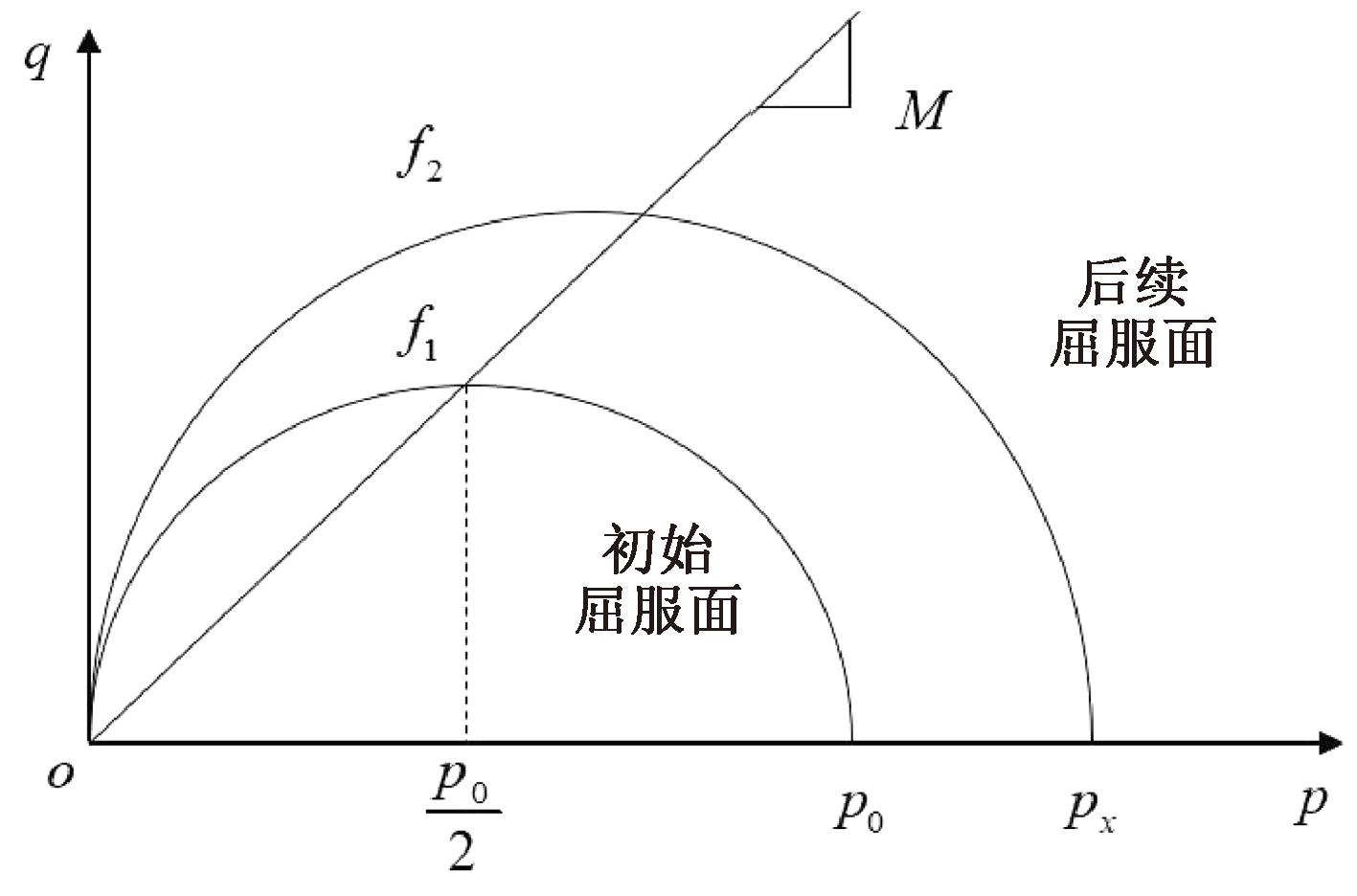
图1 修正剑桥模型屈服面
Figure 1 Modified Cambridge model yield surface
修正剑桥模型屈服函数f为
f=q2+M2p2-M2pxp=0。
(1)
式中:p为平均正应力;q为剪应力;px为屈服面右侧与p轴交点坐标。
修正剑桥模型硬化参量为塑性体积应变,等向固结试验结果如图2所示。
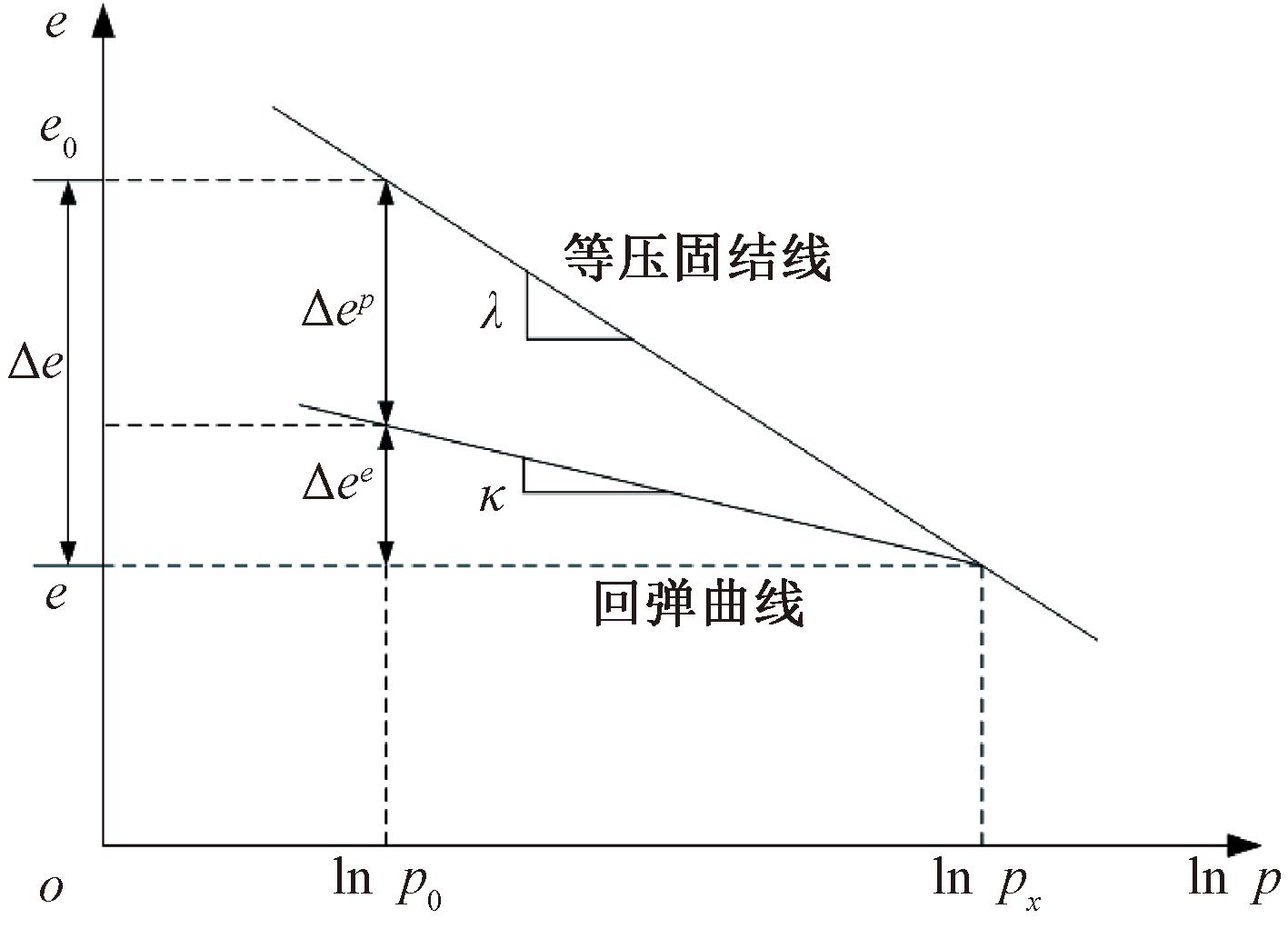
图2 土体等向固结曲线
Figure 2 Isotropic consolidation curve of soil
总体积应变为
(2)
式中:p0为初始状态下平均正应力;e0为初始状态下的孔隙比;Δe为加载过程中孔隙比变化量。
弹性体积应变为
(3)
塑性体积应变为
(4)
联立式(1)与式(4)消去px得到屈服方程为
(5)
结合弹性体积应变增量与式(3),可得弹性模量表达式为
(6)
式中:ν为土体泊松比。
可以看出,随着应力水平的提高,土体孔隙比、弹性模量、密度发生相应改变,能够反映土体受到附加压力作用时产生的挤密效果。
2 算法流程
2.1 基本假定
本文主要研究黏土、粉质黏土等低渗透性土层中的压密注浆机理,借鉴已有成果[13-14],作出如下基本假定:
(1)初始状态下,土体为均质各向同性弹塑性体;
(2)浆液仅对土体产生挤压作用,不向土体内渗透。
2.2 计算流程
本文利用MATLAB开发算法并编写相关程序,首先对计算区域进行剖分,输入注浆压力、注浆深度、土体材料特性等参数,设置边界条件,生成荷载矩阵与刚度矩阵,迭代计算单元初始位移场,达到收敛后更新土体密度、孔隙比和弹性模量,浆液压密过程计算结束后输出应力、密度、孔隙比、弹性模量等计算结果与分布云图,具体步骤如下。
(1)采取有限单元法对计算区域进行离散[15]。
(2)赋予初始土体参数,设置边界条件。
(3)将根据注浆深度得到的地应力作用在模型边界,计算初始时节点位移。
(4)将注浆压力施加于注浆孔周围土体单元。
(5)由土体修正剑桥模型本构关系得到整体刚度矩阵。
(6)集合整体荷载向量,迭代求解位移场。
(7)输出计算结果,程序计算结束。
计算流程图如图3所示。
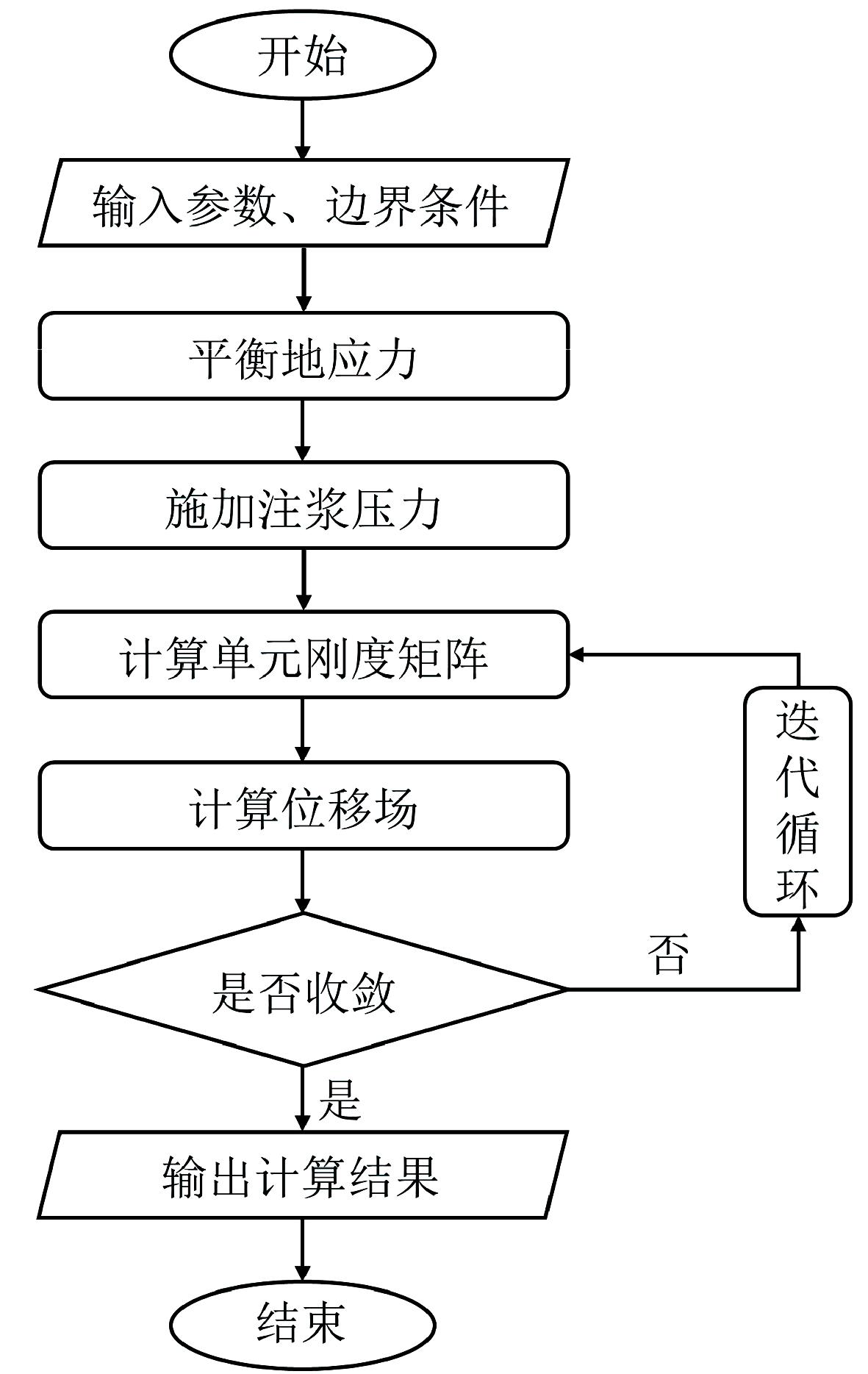
图3 计算流程图
Figure 3 Calculation flowchart
3 算例分析
3.1 计算模型
浆液通过注浆管注入预先钻好的注浆孔中,随后填满注浆孔并对周围孔壁产生压力,如图4所示。本文将垂直钻孔注浆压密土体过程简化为平面应变问题,计算模型所处平面与重力方向垂直,注浆压力作用于孔壁土体单元,计算模型如图5所示。求解区域为5 m×5 m的正方形,采用四节点单元剖分,模型中心设置半径为20 mm的圆形注浆孔,注浆孔附近区域的网格划分如图5(b)所示,四周边界作用相同的均布荷载,用于模拟地层内初始地应力场,土体中任意点的水平应力在各个方向上均相等,为上覆土层重量乘以侧压力系数。
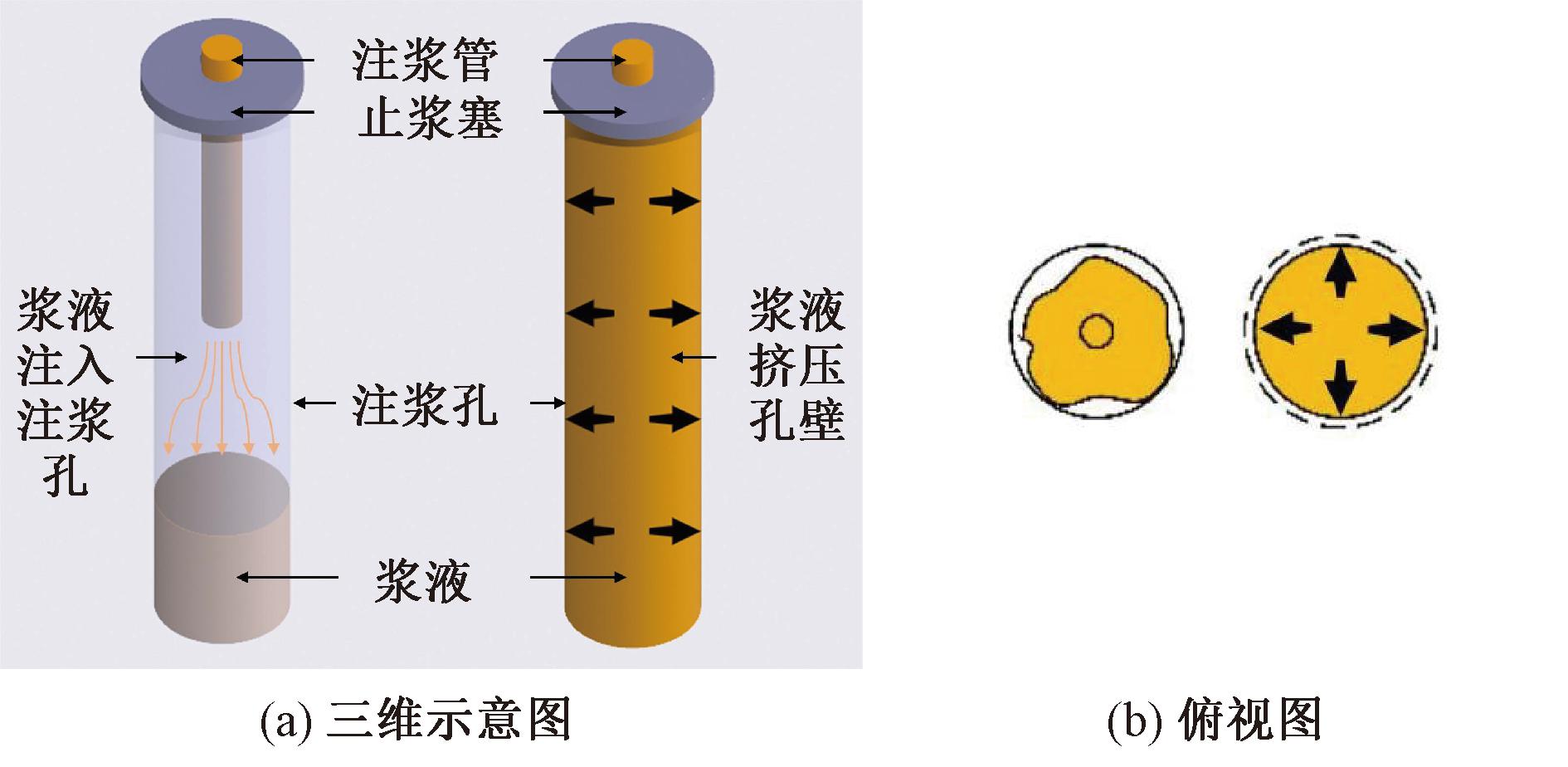
图4 浆液注入注浆孔示意图
Figure 4 Diagram of grout injection into grouting hole
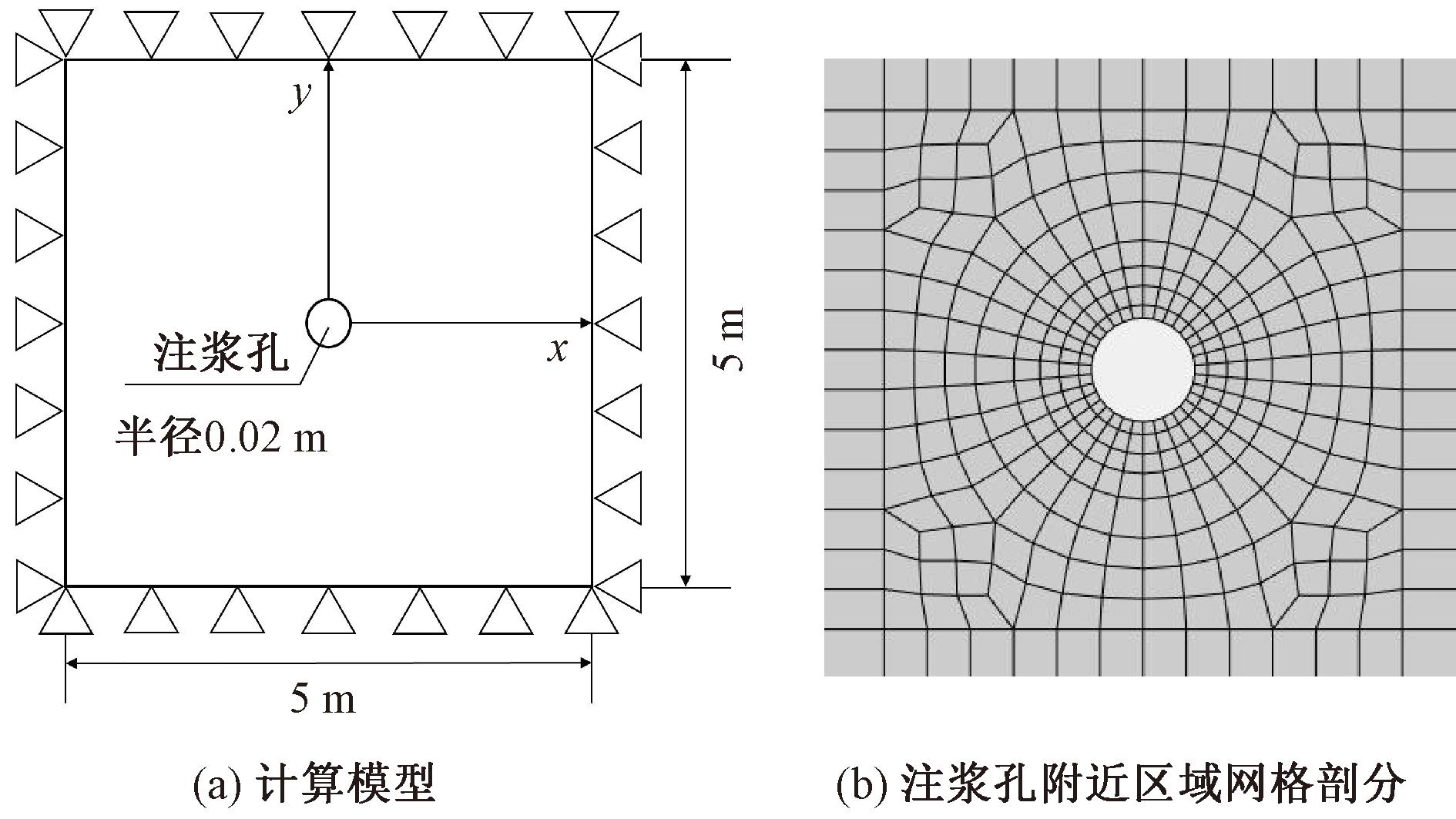
图5 压密注浆计算模型
Figure 5 Compaction grouting calculation model
3.2 模型适用性检验
3.2.1 与解析解对比
柱孔扩张理论结合修正剑桥模型可以得到周边土体响应解析解[16-18]。为检验本文所建仿真模型的适用性,选择文献[19]所提出的基于修正剑桥模型的柱孔扩张问题解析解(式(7)~(9))进行对比分析。图6为柱孔扩张问题示意图,当扩孔压力由σ0增加到σa时,孔径由a0增加到a,半径rp以内为塑性区,以外为弹性区。
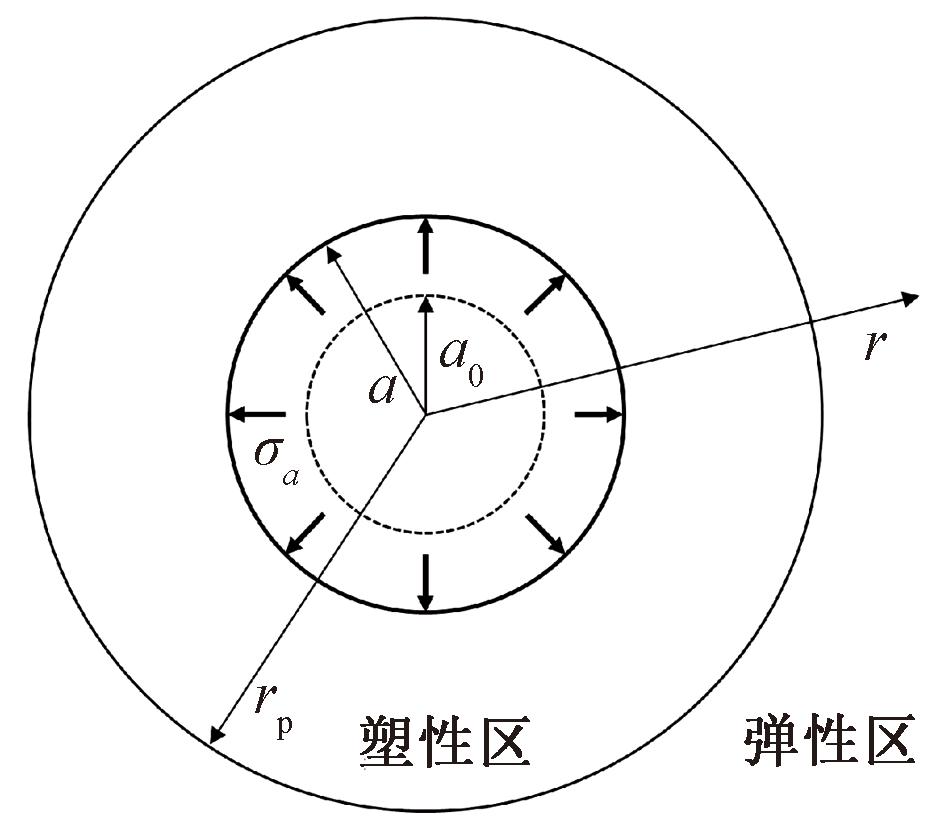
图6 柱孔扩张示意图
Figure 6 Column hole expansion diagram
塑性区径向应力表达式为
(7)
式中:σrp为弹塑性边界径向应力;qu为极限切应力。
弹性区径向应力表达式为
(8)
由图2土体等向固结曲线可得孔隙比与应力关系为
(9)
土层参数取孔隙比为0.79、泊松比ν为0.3、回弹指数κ为0.05、压缩指数λ为0.15、临界状态应力比M为0.983 8。注浆深度1.5 m,注浆压力分别为0.4,0.5,0.6,0.7 MPa时,孔周土体径向应力、孔隙比的解析解与数值模拟结果对比如图7所示,可以看出,4种工况下孔周土体径向应力、孔隙比的数值解与解析解分布规律基本一致,径向应力平均相对误差分别为3.89%,4.61%,3.79%,3.87%;孔隙比平均相对误差分别为0.13%,0.22%,0.31%,0.48%,总体平均相对误差分别为4.04%和0.29%,两种方法所得结果吻合较好。
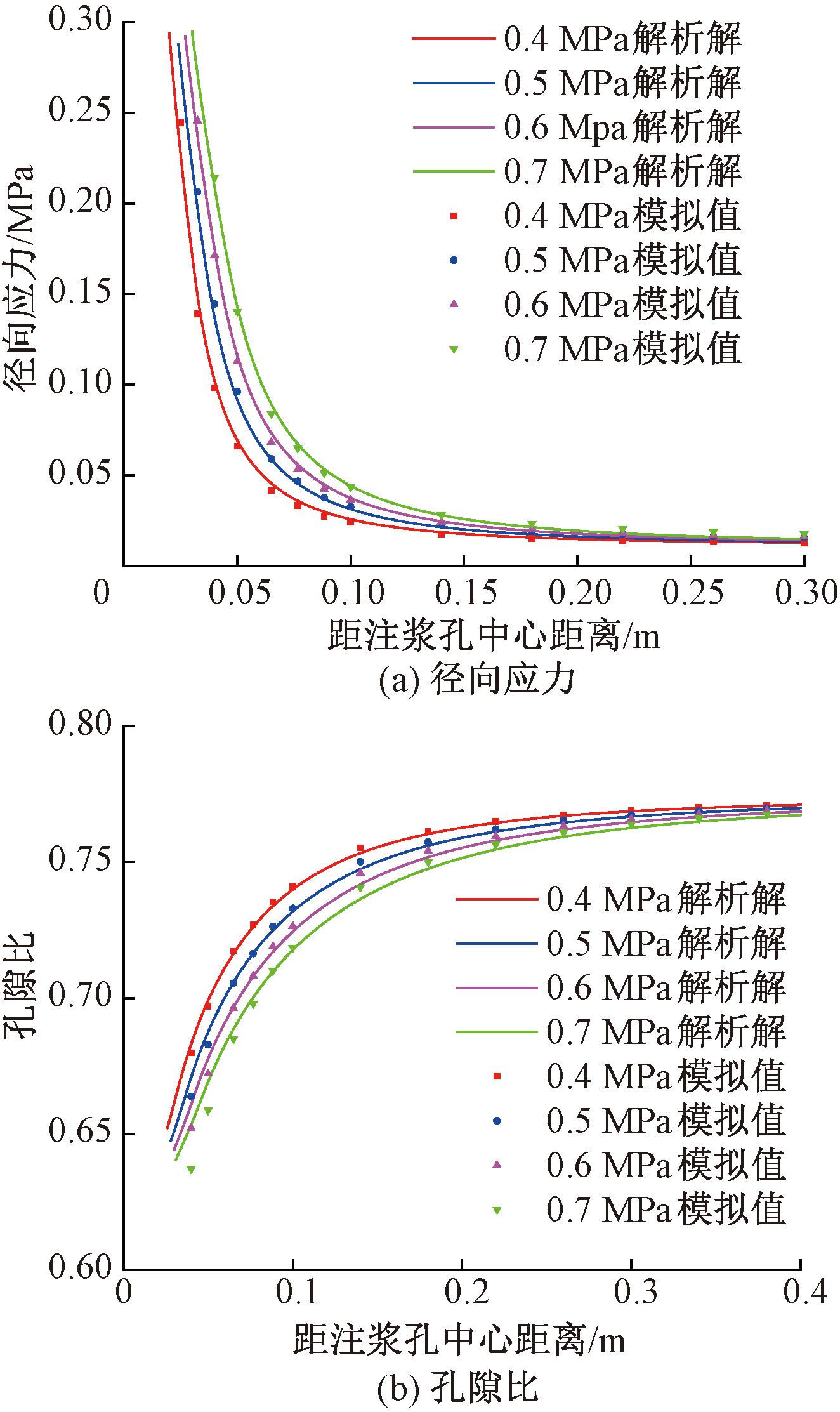
图7 解析解与仿真结果对比
Figure 7 Comparison between the analytical solution and the simulation results
3.2.2 与试验结果对比
参照文献[20]各试验工况,采用本文方法对不同工况下浆液对土体的压密行为进行模拟,注浆压力取1.21 MPa,土体基本参数包括初始孔隙比与弹性模量均按照文献[20]中实测数据进行设置。计算得到的注浆孔附近土体孔隙比、弹性模量值与试验实测值的对比如表1所示。可以看出,不同深度压密注浆后得到的孔隙比试验值、模拟值与初始值相比均明显减小,而弹性模量试验值和模拟值均增大,表明浆液对周围土体产生了显著的挤密作用。总体来看,小深度工况下土体孔隙比、弹性模量变化率要高于大深度工况。与初始值相比,不同工况下孔隙比平均变化率试验值为9.22%,模拟值为8.35%,两者相差0.87%;弹性模量平均变化率试验值为12.84%,模拟值为12.91%,两者相差0.07%。不同工况下孔隙比试验值与模拟结果相对误差平均值为5.70%;弹性模量试验值与模拟结果的相对误差平均值为2.85%。总体来看,模拟结果与试验结果较为吻合。
表1 孔隙比和弹性模量的试验值与模拟结果对比
Table 1 Comparison of void ratio and elastic modulus test values with simulation results

深度/ m 孔隙比 弹性模量 初始值 e0 试验值 et 模拟值 es 相对误差/ % 初始值 E0 / MPa 试验值 Et / MPa 模拟值 Es / MPa 相对误差/ % 1. 2 ~ 1. 5 0. 858 0. 751 0. 750 0. 13 4. 61 5. 31 5. 43 2. 26 2. 2 ~ 2. 5 0. 863 0. 651 0. 758 16. 44 4. 31 5. 37 5. 02 6. 52 3. 6 ~ 3. 9 0. 761 0. 750 0. 712 5. 07 4. 20 4. 67 4. 75 1. 71 4. 2 ~ 4. 5 0. 805 0. 747 0. 762 2. 01 4. 32 4. 69 4. 71 0. 43 4. 6 ~ 4. 9 0. 764 0. 761 0. 724 4. 86 4. 28 4. 48 4. 63 3. 35
3.3 压密注浆机理分析
采用郑州地区的粉质黏土,参数如下所示:孔隙比为0.79、密度为1.78 g/cm3、含水率w为18%、泊松比ν为0.3、黏聚力c为20 kPa、内摩擦角φ为25°、临界状态应力比M为0.983 8、压缩指数λ为0.15、回弹指数κ为0.05。应用本文方法,分析压密注浆后土体应力场、密度、孔隙比、弹性模量分布特征,研究注浆压力、注浆深度对压密注浆效果的影响。
3.3.1 应力场分布特征
图8是注浆压力0.4 MPa、注浆深度1.5 m时浆柱周围土体最大主应力分布云图。
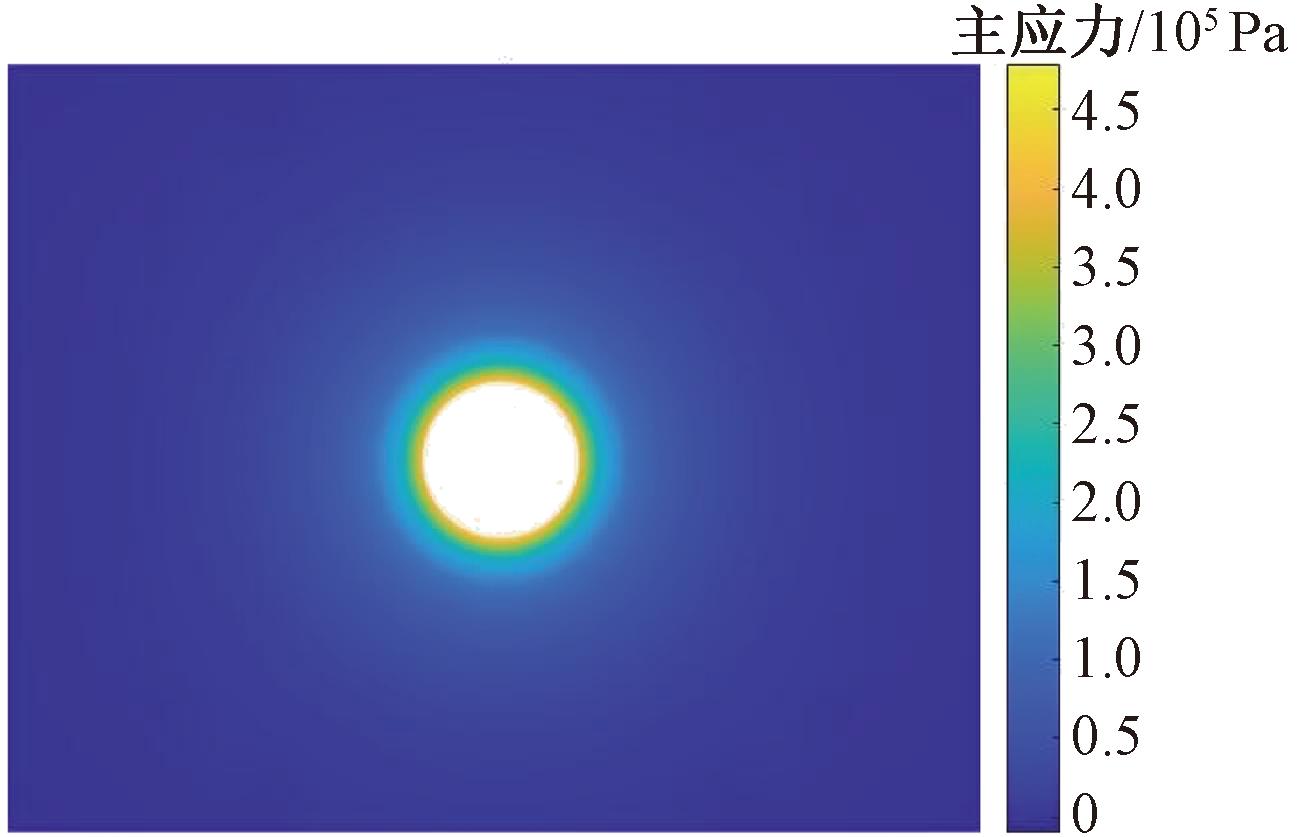
图8 土体最大主应力云图
Figure 8 Soil maximum principal stress cloud diagram
从图8可以看出,注浆加固后,周围土体最大主应力上升,以注浆孔为中心呈中心对称分布,距注浆孔越近,最大主应力越大,随着距离的增大最大主应力逐渐减小,最终趋近于土体初始最大主应力值。
3.3.2 土体密度、孔隙比、弹性模量分布特征
图9为注浆压力0.4 MPa、注浆深度1.5 m时浆柱周围土层密度、孔隙比及弹性模量分布云图,可以看出,3个参数均以注浆孔中心为基点呈圆形对称分布,距注浆孔中心越近,土体参数变化越大;距注浆孔中心越远,土体参数变化越小;当达到一定距离时,土体参数逐渐趋近于注浆前状态。
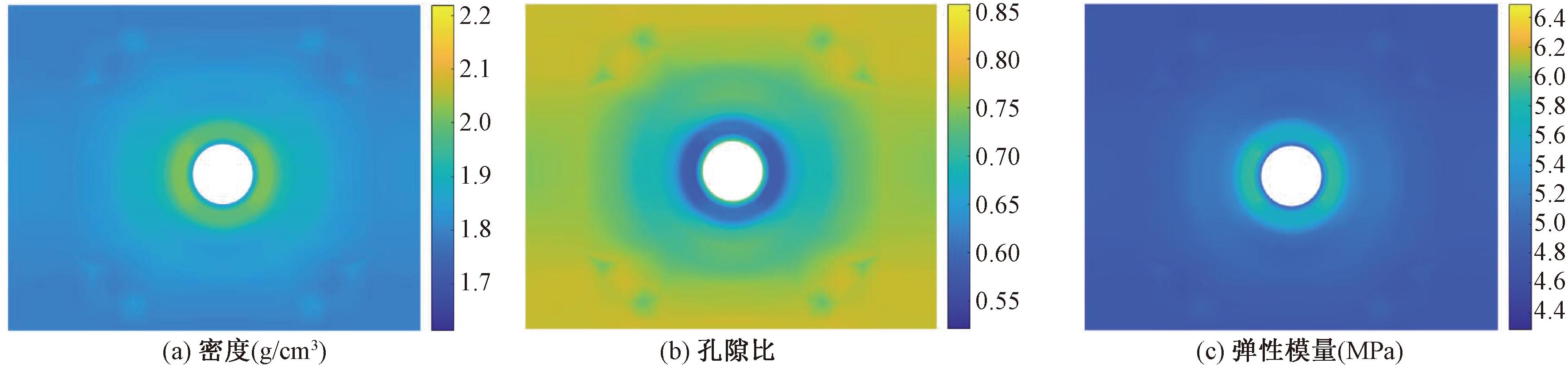
图9 土体参数分布云图
Figure 9 Soil parameters distribution cloud diagram
3.3.3 注浆压力对浆柱半径及土体密度、孔隙比、弹性模量的影响
注浆深度设置为1.5 m,从0.4 MPa到1.0 MPa按0.1 MPa增量设置注浆压力,计算分析不同注浆压力下注浆孔半径及其周围土体的压密情况。
图10为不同注浆压力下浆柱半径变化曲线,可以看出,随着注浆压力的增大,浆柱半径从最初的0.02 m逐渐扩张至1.0 MPa时的0.033 m。图11为不同注浆压力时土体密度、孔隙比及弹性模量沿径向分布曲线,可以看出,注浆挤密后浆柱周围土体孔隙比降低,密度和弹性模量均有较大提升,紧邻注浆孔处密度、孔隙比和弹性模量改变量最大,其变化值随注浆压力的增大而增大。当注浆压力为0.4 MPa时,距注浆孔0.05 m处的土体密度从1.796 g/cm3升高至1.888 g/cm3,提高5.12%,土体孔隙比从0.774降低至0.688,下降11.11%,土体弹性模量从4.792 MPa升高至5.116 MPa,提高6.76%。随着距注浆孔距离的增大,土体参数的改变量逐渐减小,当距注浆孔距离超过0.3 m时,土体密度、孔隙比和弹性模量与注浆前基本相同。
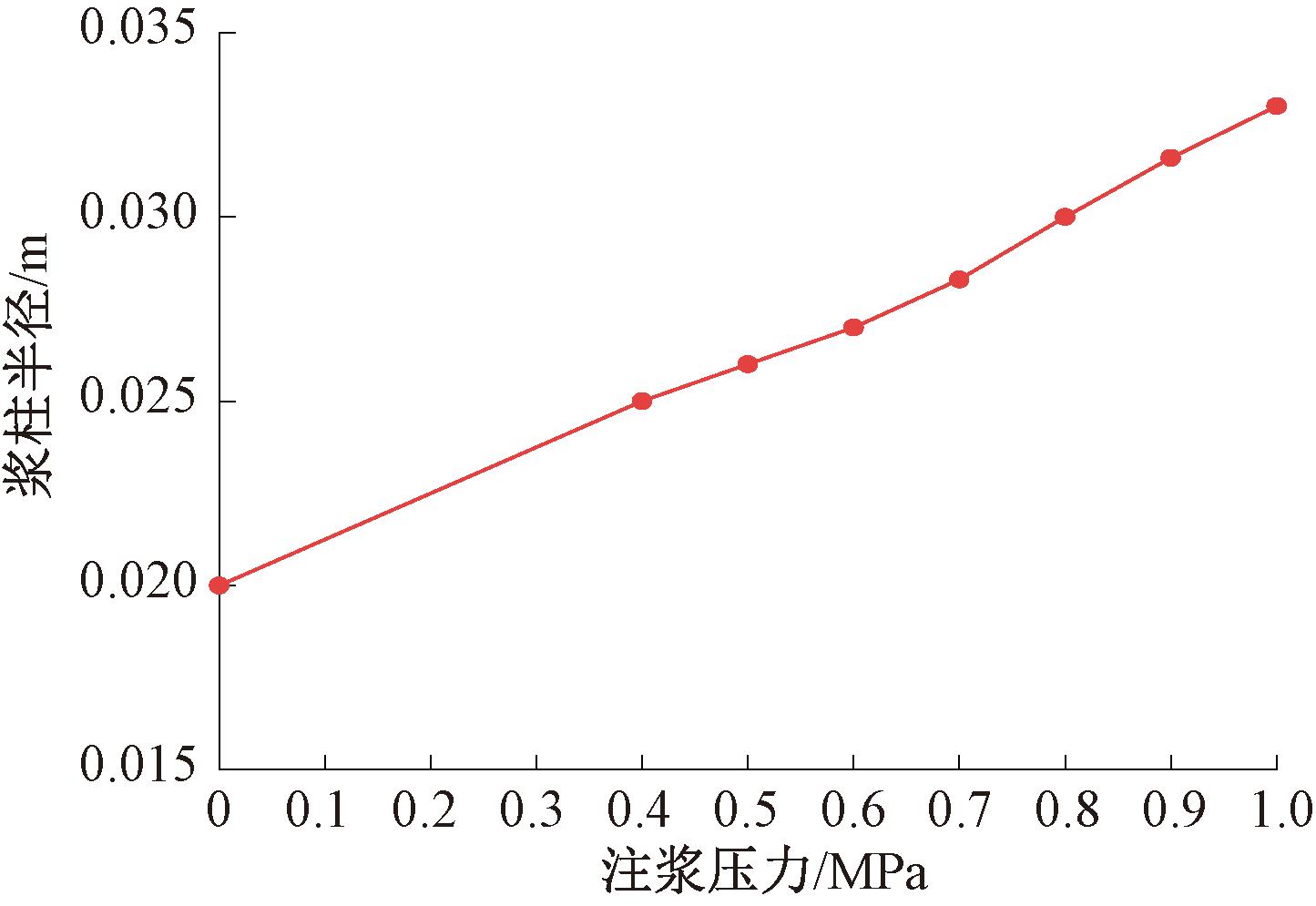
图10 不同注浆压力下浆柱半径变化
Figure 10 Change of grouting column radius with different grouting pressures
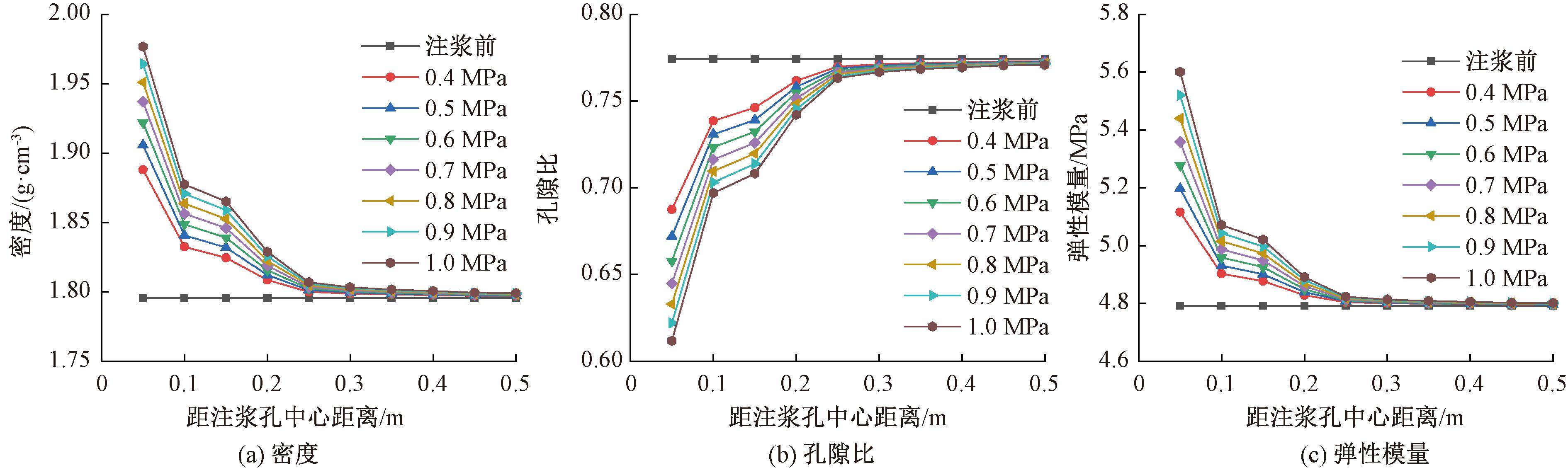
图11 不同注浆压力下土体参数分布曲线
Figure 11 Soil parameters distribution curve with different grouting pressures
不同注浆压力下距注浆孔中心0.05 m处的土体密度、孔隙比和弹性模量变化曲线如图12所示,可以看出,随着注浆压力的增大,监测点处土体密度、弹性模量逐渐增大,孔隙比逐渐减小,在施加的注浆压力范围内,3个参数值随压力近似呈线性变化。当注浆压力从0.4 MPa增加到1.0 MPa时,土体密度由1.888 g/cm3增至1.977 g/cm3,提高率从5.12%升到10.08%,平均变化率为0.148 g/(cm3·MPa);土体弹性模量由5.116 MPa增至5.601 MPa,提高率从6.76%升到16.88%,平均变化率为0.808;孔隙比由0.688减至0.612,降低率从11.11%升至20.93%,平均变化率为-0.127 MPa-1。
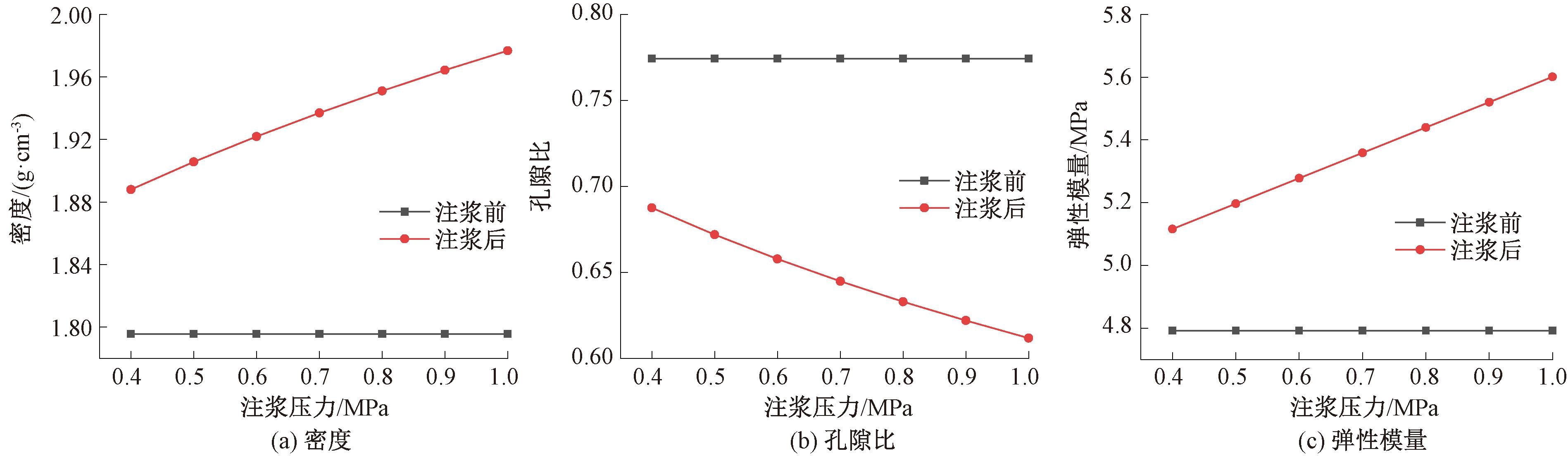
图12 r=0.05 m处土体参数随注浆压力变化曲线
Figure 12 Soil parameters change curve with grouting pressure at r=0.05 m
3.3.4 注浆深度对土体密度、孔隙比、弹性模量的影响
注浆压力0.4 MPa,距注浆孔中心0.05 m处土体密度、孔隙比和弹性模量随注浆深度变化曲线如图13所示,可以看出,在深度1.5 m至5.0 m范围内,随着注浆深度的增大,地层初始应力逐渐增大,注浆前土体密度和弹性模量近似呈线性增长,孔隙比则呈线性下降。注浆后随着注浆深度的增大,土体密度先减小,随后在3.5 m后趋于稳定,与之相对应,孔隙比先增大然后逐渐趋稳,弹性模量则呈线性增加趋势。随着深度的增加,土体密度和孔隙比改变量逐渐减小,弹性模量的增加量基本不变。当注浆深度从1.5 m增加到5.0 m时,测点处土体密度增加量从5.12%降到1.84%,孔隙比降低率从11.11%降到4.24%,弹性模量提高率从6.76%降至5.46%。总体来看,在注浆压力一定的条件下,压密注浆对浅地层的加固效果较为明显,随着注浆深度增加,挤密效果逐渐减弱,原因在于注浆深度越大,地层初始地应力越大,对土体产生了较强的前期挤压作用,注浆压力与初始地应力相比量值较小,难以产生显著的挤密效果。
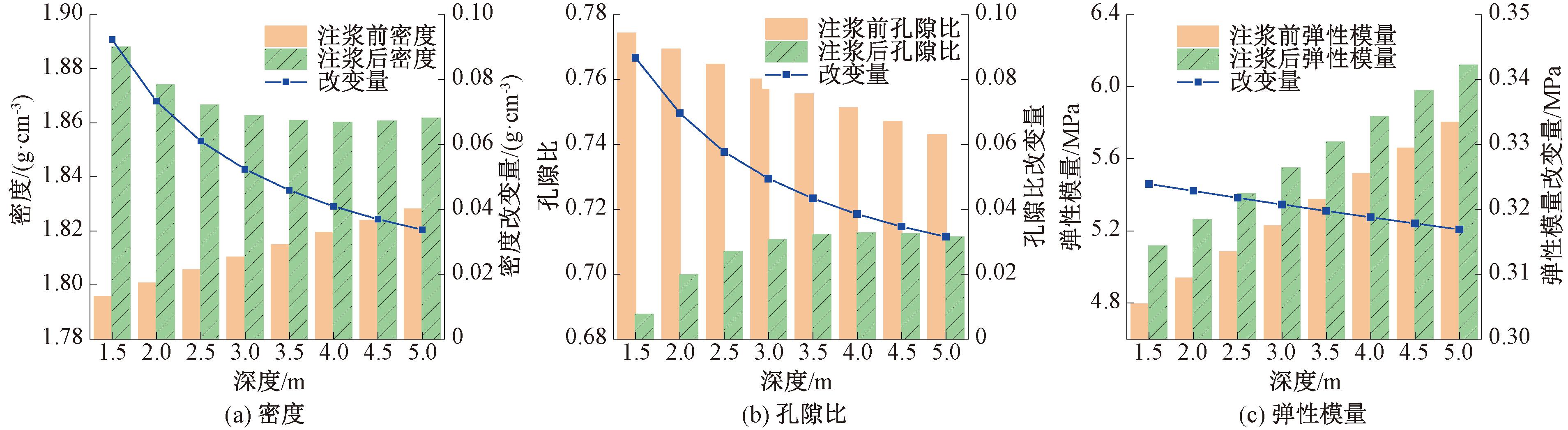
图13 r=0.05 m处土体参数随注浆深度变化曲线
Figure 13 Soil parameters change curve with grouting depth at r=0.05 m
4 结论
(1)针对压密注浆仿真手段尚不完备的现状,引入修正剑桥模型描述土体力学行为,建立了一种模拟常密度浆液在土体中压密注浆过程的仿真模型,利用该模型能够得到压密注浆后浆柱周围土体应力、密度、孔隙比和弹性模量分布特征。与解析解和试验结果的对比表明,不同注浆压力下,不同位置处土体径向应力、孔隙比模拟值与解析解总体平均相对误差分别为4.04%,0.29%;不同深度条件下压密注浆后土体孔隙比、弹性模量模拟值与试验值的平均相对误差分别为5.70%和2.85%,两者吻合较好,验证了本文方法的适用性。
(2)分析了压密注浆加固后浆柱周围土体应力、密度、孔隙比、弹性模量分布特征,并揭示了注浆压力与注浆深度对压密注浆效果的影响。结果表明,均匀的应力条件下,压密注浆后土体应力、孔隙比、密度和弹性模量呈中心对称分布,浆柱周围土体密度及弹性模量有较大提升,孔隙比则明显降低,距注浆孔越远,土体参数较加固前的改变量越小,达到一定距离时逐渐恢复至初始状态。相同深度条件下,注浆压力越大,浆柱半径越大,土体密度、孔隙比和弹性模量等参数较注浆加固前变化值越大,浆液对周围土体挤密作用越显著。相同注浆压力条件下,注浆深度越大,地层初始地应力越大,土体密度和孔隙比改变量逐渐减小,弹性模量的增加量基本不变,对土体的挤密效果逐渐减弱。
[1] 李斌, 方宏远, 王复明. 脱空排水管道高聚物修复前后力学特性分析[J]. 郑州大学学报(工学版), 2019, 40(1): 62-66.
LI B, FANG H Y, WANG F M. Analysis of the mechanical characteristics of disengaging drainage pipe before and after polymer repairing[J]. Journal of Zhengzhou University (Engineering Science), 2019, 40(1): 62-66.
[2] 李向红. CCG注浆技术的理论研究和应用研究[D]. 上海: 同济大学, 2002.
LI X H. Theoretical research and application research of CCG grouting technology[D].Shanghai: Tongji University, 2002.
[3] 巨建勋. 土体压密注浆机理及其抬升作用的研究[D]. 长沙: 中南大学, 2007.
JU J X. Study on the mechanism and the upward-effect of compaction grouting[D].Changsha: Central South University, 2007.
[4] 唐智伟, 赵成刚. 注浆抬升地层的机制、解析解及数值模拟分析[J]. 岩土力学, 2008, 29(6): 1512-1516.
TANG Z W, ZHAO C G. Mechanisms of ground heave by grouting and analytical solutions &numerical modeling[J]. Rock and Soil Mechanics, 2008, 29(6): 1512-1516.
[5] 王立中. 柔性管加筋注浆新技术试验及应用研究[D]. 长沙: 中南大学, 2008.
WANG L Z. Test and application research on new technology of reinforced grouting with flexible pipe[D].Changsha: Central South University, 2008.
[6] 周子龙, 赵云龙, 陈钊, 等. 基于颗粒流方法的土体压密注浆细观机理[J]. 中南大学学报(自然科学版), 2017, 48(2): 465-472.
ZHOU Z L, ZHAO Y L, CHEN Z, et al. Meso-mechanism of compaction grouting in soil based on particle flow method[J]. Journal of Central South University (Science and Technology), 2017, 48(2): 465-472.
[7] WANG D Y, XING X M, QU H H, et al. Simulated radial expansion and heave caused by compaction grouting in noncohesive soils[J]. International Journal of Geomechanics, 2015, 15(4): 1-10.
[8] SHRIVASTAVA N, ZEN K, SHUKLA S K. Modeling of compaction grouting technique with development of cylindrical cavity expansion problem in a finite medium[J]. International Journal of Geosynthetics and Ground Engineering, 2017, 3(4): 1-12.
[9] SHRIVASTAVA N, ZEN K. Finite element modeling of compaction grouting on its densification and confining aspects[J]. Geotechnical and Geological Engineering, 2018, 36(4): 2365-2378.
[10] 周凤玺, 牟占霖, 杨汝贤, 等. 不同排水条件下非饱和土中柱孔扩张问题的解析分析[J]. 力学学报, 2021, 53(5): 1496-1509.
ZHOU F X, MU Z L, YANG R X, et al. Analytical analysis on the expansion of cylindrical cavity in unsaturated soils under different drainage conditions[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(5): 1496-1509.
[11] ROSCOE K H, SCHOFIELD A N, THURAIRAJAH A. Yielding of clays in states wetter than critical[J]. Géotechnique, 1963, 13(3): 211-240.
[12] BURLAND J B. The yielding and dilation of clay[J]. Géotechnique,1965,15(2):211-214.
[13] 叶飞, 陈治, 苟长飞, 等. 基于球孔扩张的盾构隧道壁后注浆压密模型[J]. 交通运输工程学报, 2014, 14(1): 35-42.
YE F, CHEN Z, GOU C F, et al. Back-filled grouting compaction model of shield tunnel based on spherical cavity expansion[J]. Journal of Traffic and Transportation Engineering, 2014, 14(1): 35-42.
[14] 吴悦, 赵春风, 王有宝, 等. 黏土中考虑土体卸荷效应的后注浆压密模型[J]. 哈尔滨工业大学学报, 2020, 52(11): 71-79.
WU Y, ZHAO C F, WANG Y B, et al. Compaction grouting model in clay considering unloading effect[J]. Journal of Harbin Institute of Technology, 2020, 52(11): 71-79.
[15] OWEN D R J, HINTON E. Finite elements in plasticity: theory and practice[M]. Swansea: Pineridge Press, 1980.
[16] 李镜培, 周攀, 李亮, 等. 饱和结构性黄土不排水柱孔扩张问题弹塑性解[J]. 同济大学学报(自然科学版), 2021, 49(2): 163-172.
LI J P, ZHOU P, LI L, et al. Elastic-plastic solution for undrained expansion of cylindrical cavity in saturated structured loess[J]. Journal of Tongji University (Natural Science), 2021, 49(2): 163-172.
[17] 周攀, 李镜培, 李亮, 等. 结构性黄土排水柱孔扩张问题弹塑性解析[J]. 岩石力学与工程学报, 2021, 40(1): 175-186.
ZHOU P, LI J P, LI L, et al. Elastic-plastic solution for drained cylindrical cavity expansion in structured loess[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(1): 175-186.
[18] 周航, 王增亮, 申航, 等. 软黏土中静压桩打桩过程对土体强度和刚度影响的理论分析[J]. 北京工业大学学报, 2021, 47(7): 719-727, 814.
ZHOU H, WANG Z L, SHEN H, et al. Theoretical analysis of the variation of soil strength and rigidity induced by pile penetration in soft clay[J]. Journal of Beijing University of Technology, 2021, 47(7): 719-727, 814.
[19] CAO L F, TEH C I, CHANG M F. Undrained cavity expansion in modified Cam clay I: theoretical analysis[J]. Géotechnique, 2001, 51(4): 323-334.
[20] 徐玉峰. 路基压密注浆加固效果的研究[J]. 公路交通科技(应用技术版), 2012, 8(4): 41-43.
XU Y F. Study on the effect of subgrade compaction grouting reinforcement[J]. Highway Transportation Technology (Applied Technology Edition), 2012, 8(4): 41-43.