近年来,随着经济的快速发展,中国加大了对河道防洪工程的投资建设,截至2022年底,全国已建成5级及以上江河堤防33.2 万公里,已建成流量为5 m3/s及以上的水闸96 348座[1]。这类工程的主要任务是减少洪水灾害、保护国家和人民生命财产安全,其效益并非直接创造社会财富,而是减少洪灾频率和洪灾损失(包括生命损失和经济损失)。在极端降雨事件频发的背景下[2],高标准河道治理可有效减少溃堤频率,从而减少堤防保护区内的人口死亡[3],因此生命效益显著。
近年来,众多学者对防洪工程的防洪效益开展了研究。Hudson等[4]对风险分区措施的成本效益进行了评估;王艳艳等[5]建立了太湖流域防洪效益评估模型,评估了太湖流域遭遇特大洪水时不同防洪措施产生的经济效益;杨丽等[6]采用频率曲线法对北京市中心城防洪排涝系统的经济效益进行了分析;陈卫宾等[7]采用“实际发生年法”对1996—2015年黄河下游防洪保护区的防洪经济效益进行了分析。上述学者在计算防洪效益时,通常只考虑防洪产生的潜在经济效益而忽略了潜在生命效益,导致对工程的防洪效益计算不全面。因此,开展河道治理工程潜在生命效益量化研究是工程防洪效益计算的客观需求,对于根据防洪效益准确开展经济评价,进而决策项目方案意义重大。
河道治理工程潜在生命效益的本质是工程实施前、后洪水造成的生命损失之差,可用减少的死亡人数来衡量。国内外学者在评价生命损失时多以死亡人数为指标。Brown等[8]采用数学统计方法对各国历史溃坝数据进行了回归分析,提出了溃坝生命损失估算方法(B&M法)。Dekay等[9]考虑溃坝洪水严重性的不同,对洪水淹没区域进行分区估算生命损失。Graham[10]以洪水严重性、警报时间及对洪水严重性的理解程度为主要因素,提出了溃坝风险人口死亡率建议表,并建立了相应的经验模型(Graham法)。周克发等[11]基于Graham法对中国8座已溃决大坝资料进行了分析,修正了Graham法,提出了适应中国实际情况的溃坝生命损失评价模型(李-周法)。也有学者以风险等级评价生命损失。Li等[12]基于溃坝洪水风险进行路径分析,采用可变模糊集理论对生命损失进行评价,将生命损失风险划分为轻微、一般、中等、严重和极严重5个等级;葛巍等[13]选取8个影响溃坝生命损失的指标构建指标体系,基于层次分析-贝叶斯网络法,构建溃坝生命损失评价模型。上述生命损失计算方法无论以死亡人数或风险等级为评价指标,均与工程经济投入以货币表达的形式不对等,导致决策者不能准确衡量工程经济投入与效益产出之间的关系。
综上所述,目前在计算河道工程防洪效益时存在未考虑潜在生命效益和生命效益难量化的问题。针对以上问题,本文引入统计生命价值理论,采用收入弹性系数法计算统计生命价值(value of statistical life,VSL),结合李-周法和频率法货币量化河道治理工程防洪效益中潜在生命效益,为计算工程防洪效益和开展国民经济评价提供技术支撑。
1 基于统计生命价值的河道治理工程潜在生命效益量化方法
1.1 洪水生命损失计算方法
根据灾害系统理论,生命损失是由致灾因子、承灾体和孕灾环境共同作用的结果。本文洪水类型为溃堤洪水,根据洪灾作用过程,溃堤洪水与溃坝洪水造成生命损失的致灾因子均以洪水淹没水深和流速为主,它们也是表征洪水严重程度的重要指标[14]。从生命损失影响因素角度分析,溃堤洪水生命损失主要影响因素为洪水淹没水深、流速、警报时间和风险人口对洪水严重性的理解程度,与溃坝洪水生命损失影响因素一致。李-周法的风险人口死亡率主要影响因素洪水严重程度(洪水淹没水深与流速乘积)、警报时间和风险人口对洪水严重性的理解程度均与洪水类型无关,因此认为李-周法同样适用于计算溃堤洪水造成的生命损失。本文采用李-周法计算洪水生命损失,计算公式如下所示:
L=Pf。
(1)
式中:L为洪水造成的风险人口死亡人数;P为处于洪水淹没范围内的风险人口数量;f为风险人口的死亡率,由洪水的严重程度SD、风险人员收到的警报时间WT和对洪水严重性的理解程度UD这3个因素决定,具体取值参考文献[11]。
1.2 统计生命价值计算方法
统计生命价值是人们对死亡风险降低的支付意愿平均值,或者对死亡风险增加接受赔偿意愿的平均值,即统计学意义上的生命价值。统计生命价值的概念广泛应用于生态环境、职业安全、疾病健康、公共安全及交通安全等多个领域[15]。
尽管VSL应用广泛,但许多低收入和中等收入国家仍缺乏对VSL的研究。受地区间收入差异等因素的影响,缺乏VSL研究的国家不能直接使用美国等其他发达国家的VSL值[16-17]。
收入弹性系数法[18]是基于收入差异将VSL从一个研究较为成熟的国家转移至另一个缺乏可靠研究国家的方法,也是世界银行估算中低收入国家VSL值最常用的方法,在国际上应用十分广泛[19-21],其中收入弹性系数是处理收入差异、转移VSL的关键参数。因此,本文采用收入弹性系数法[22]计算中国VSL值,计算公式如下所示:
(2)
式中:VSLA为计算国家的统计生命价值,美元/人;VSLB为被转移国家的统计生命价值,美元/人;YA为计算国家的收入,美元;YB为被转移国家的收入,美元,采用人均国民总收入GNI;η为收入弹性系数。
1.3 河道治理工程潜在生命效益量化方法
河道治理工程多年平均潜在生命效益(简称潜在生命效益)由有、无工程的生命损失货币价值差值以频率为权重计算所得。本文采用生命损失与VSL之积表示生命损失货币价值,构建了生命损失货币价值量化函数,计算公式如下所示:
V=L·VSL。
(3)
式中:V为生命损失的货币价值,元;VSL为研究地区统计生命价值。
由于同时进行河道治理工程实施前、后的数值模拟工作量大,本文将传统频率法进行了简化:根据堤防防洪标准将其分成若干堤防段,当堤防遭遇超本次防洪标准洪水时不发挥作用,遭遇低于原防洪标准洪水时有无工程均不产生生命损失,假设工程面临以上两种情况时不产生生命效益;当堤防遭遇堤防原防洪标准和本次防洪标准之间的洪水时,治理后的堤防因避免治理前洪水造成的生命损失而产生生命效益,因此将工程治理前的生命损失全部视为工程治理后产生的效益,计算河道治理工程潜在生命效益时只需开展工程治理前数值模拟。基于上述分析,本文提出了河道治理工程潜在生命效益量化方法如下所示:
(4)
式中:V0为河道治理工程的多年平均潜在生命效益值,元/a;pi、pi+1为相邻的两次洪水频率,洪水频率上限为堤防本次设计防洪标准,下限为原防洪标准;Vi、Vi+1分别为pi、pi+1频率洪水在工程治理前造成的生命损失货币价值,元。
基于统计生命价值理论的河道治理工程潜在生命效益量化方法主要包括数值模拟、生命损失计算、统计生命价值计算和生命效益量化4个部分,具体流程见图1。
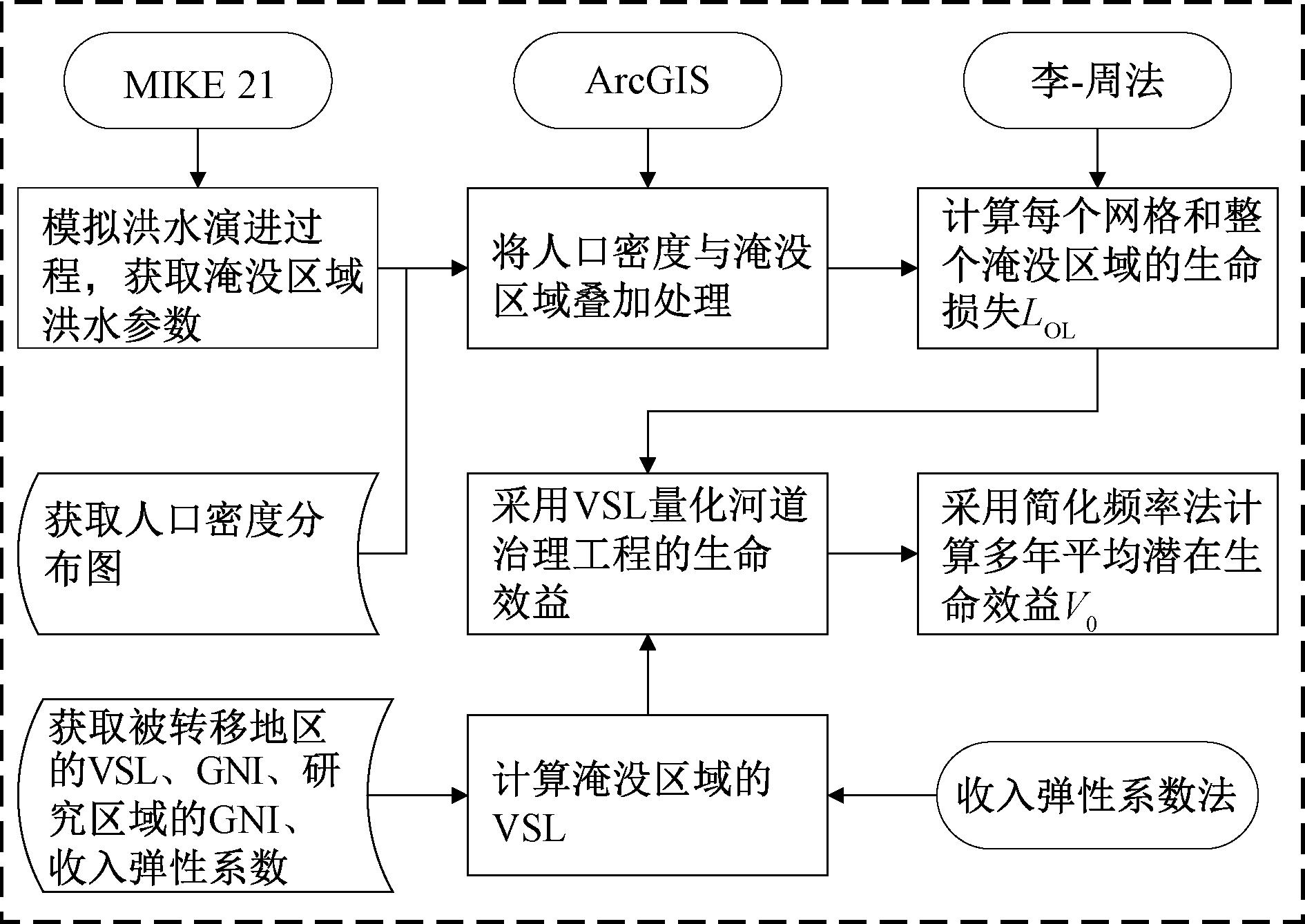
图1 潜在生命效益量化方法流程图
Figure 1 Flow chart of the quantitative method for potential life benefits
2 工程实例
2.1 工程概况
以贾鲁河综合治理工程为研究对象。贾鲁河是淮河支流沙颍河的主要支流,发源于新密、荥阳两市交界处,流经荥阳、郑州、中牟、开封、尉氏、鄢陵、扶沟、西华、周口,在周口市汇入沙颍河,全长共264 km,流域面积共6 137 km2。本次研究贾鲁河治理范围为中牟陇海铁路桥至周口贾鲁河入沙颍河口,治理长度为148.57 km,研究区域概况以及洪水参数示意图如图2所示。
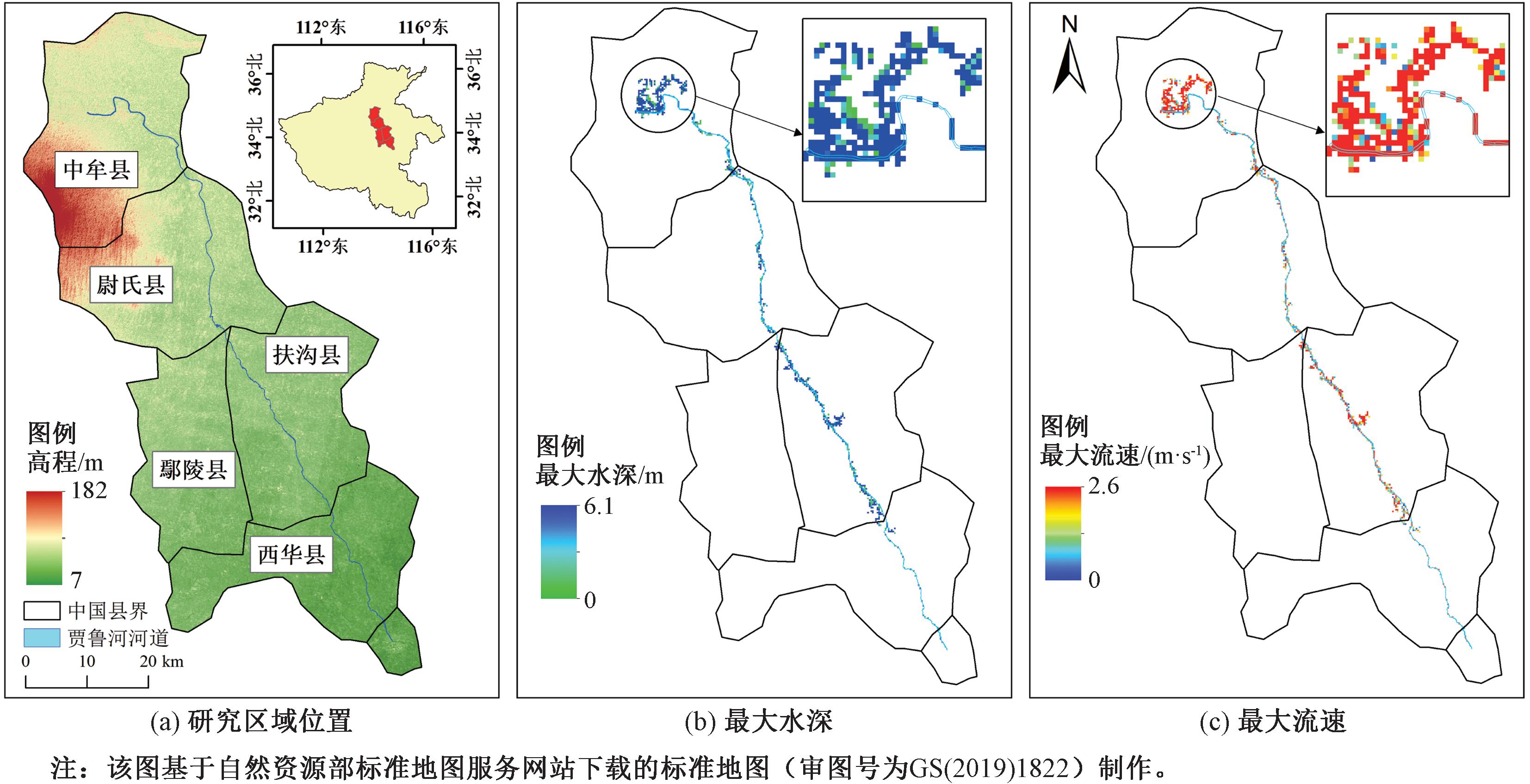
图2 研究区域概况及洪水参数示意图
Figure 2 Study area overview and flood parameter schematic map
贾鲁河综合治理工程是以防洪为主,兼顾水资源利用的大(1)型工程。工程实施前,贾鲁河沿线部分城区段治理标准较低,河槽整治及堤防修筑断断续续,河道整体防洪能力较差。工程治理完成后,防洪标准和建筑物等级全面提高,其中,贾鲁河在中牟县至开封市后曹闸段的防洪标准将达到100 a一遇,尉氏县城区段、扶沟县城区段、西华县城区段和周口市川汇区段的防洪标准达到50 a一遇,其他段的防洪标准达到20 a一遇。
2.2 研究区域水动力模拟
本文采用MIKE 21二维水动力模型对不同频率洪水进行模拟,洪水重现期分别为5 a一遇、10 a一遇、20 a一遇、50 a一遇和100 a一遇。
(1)水动力模型构建。通过MIKE Zero中非结构化网格生成器将研究区域划分为三角形网格,其中河道中网格最大为1 000 m2,河道外最大为30 000 m2,最小角度为30°。根据DEM数字高程数据生成非结构网格,DEM数据采用地理空间数据云的30 m精度数据。洪水演进模拟时在控制断面处添加设计流量,并设置河道主槽及滩地糙率。
(2)水动力模拟结果。以贾鲁河20 a一遇洪水模拟为例,洪水参数如图2所示。由图2可知,大部分淹没区的洪水最大水深为1~3 m、最大流速为0~1.5 m/s,淹没区总面积为94.66 km2。
(3)结果验证。在贾鲁河上中牟水文站选取5组实测流量-水位数据对MIKE水动力模型进行验证,计算两者的相对误差,详见表1。计算得到5组模拟数据和实测数据的平均水深误差为7.74%,说明MIKE水动力模型模拟结果合理,可用于潜在生命效益计算。
表1 中牟水文站误差验证表
Table 1 Error verification table of Zhongmou Hydrological Station

组号 流量/ (m 3·s - 1 ) 实测水位/ m 实测水深/ m 模拟水位/ m 模拟水深/ m 水深相对误差/ % 1 54. 00 74. 58 1. 23 74. 73 1. 38 12. 20 2 80. 20 74. 93 1. 58 75. 09 1. 74 10. 13 3 123. 00 75. 48 2. 13 75. 55 2. 20 3. 29 4 191. 00 76. 25 2. 90 76. 17 2. 82 - 2. 76 5 227. 00 76. 65 3. 30 76. 31 2. 96 - 10. 30
2.3 各重现期洪水生命损失计算结果
采用李-周法计算生命损失,根据式(1),需确定洪水淹没范围内的风险人口数量P和死亡率f。计算得洪水频率在20%,10%,5%,2%和1%时淹没范围内的总风险人口数量分别为30 446,39 597,60 108,75 443和96 501人。f主要由SD、WT和UD这3个因素决定。本文在计算时认为风险人员收到的警报时间WT>1 h,风险人员对洪水严重性的理解程度UD为明确,根据文献[11],f的取值见表2。
表2 风险人口死亡率
Table 2 Mortality rate of population at risk

洪水严重性 SD 水深 × 流速/ (m 2·s - 1 ) 风险人口死亡率 f 高 中 低 > 30 0. 001 0 > 20 ~ 30 0. 000 9 > 12 ~ 20 0. 000 8 > 8 ~ 12 0. 000 7 4. 6 ~ 8 0. 000 6 < 4. 6 0. 000 4
根据每个网格的P和f,结合式(1)计算洪水淹没范围内每个网格的生命损失,汇总可得到各频率洪水的生命损失,并通过式(3)量化生命损失货币价值,结果详见表3,可以看出,贾鲁河综合治理工程面对50 a一遇和100 a一遇洪水减少的生命损失人数少于10 a一遇和20 a一遇洪水,这是因为计算时认为当各堤防段遭遇超标准洪水时不发挥作用,工程遭遇50 a一遇和100 a一遇洪水时20 a一遇防洪标准堤防段不发挥作用,因此计算出工程遭遇高频率洪水减少的生命损失低于部分低频率洪水。
表3 各频率洪水生命损失计算结果
Table 3 Calculation results of loss of life caused by floods of different frequencies

堤防段 生命损失/ 人 生命损失货币价值/ 万元 p = 20% p = 10% p = 5% p = 2% p = 1% p = 20% p = 10% p = 5% p = 2% p = 1% 20 a 一遇防洪标准段 4 5 5 3 824 4 780 4 780 50 a 一遇防洪标准段 5 7 8 10 4 780 6 692 7 648 9 560 100 a 一遇防洪标准段 4 4 11 13 14 3 824 3 824 10 516 12 428 13 384 合计 13 16 24 23 14 12 428 15 296 22 944 21 988 13 384
注:表中的生命损失采用四舍五入的方式取整,部分数据由于差距较小取整后出现生命损失相同的情况。
2.4 研究区域的统计生命价值计算结果
世界银行对不同收入水平的国家设定相应的收入弹性系数,其中高收入国家的弹性系数值为0.8,敏感性分析范围为0.6~1.0;低收入和中等收入国家的弹性系数值为1.2,敏感性分析范围为1.0~1.4,且低收入国家和中等收入国家的收入弹性系数在1.2时,平均传递误差最小。根据世界银行资料[23],2021年中国人均GNI为11 122 美元,处于中高收入国家行列,因此中国的弹性收入系数取1.2。
被转移的VSL采用2015年美国统计生命价值[24],即960 万美元/人,相对应的美国人均GNI为55 980 美元。结合式(2)计算得到中国的VSL值为138 万美元/人,依照当今的汇率计算得出中国的VSL值为956 万元/人。
2.5 工程潜在生命效益计算结果
根据式(4),贾鲁河综合治理工程20 a一遇、50 a一遇、100 a一遇防洪标准堤防段的多年平均潜在生命效益计算结果分别为669.20,1 190.22,1 214.12 万元/a。因此,贾鲁河综合治理工程总的多年平均潜在生命效益为3 073.54 万元/a。根据工程资料,贾鲁河综合治理工程20 a一遇防洪标准堤防段对应位置为沿线非城镇段,50 a一遇防洪标准堤防段对应位置为西华县、扶沟县、尉氏县和周口市川汇区城区段,100 a一遇防洪标准堤防段对应位置为中牟县城区段。根据以上计算结果,贾鲁河综合治理工程在沿线非城镇区域产生的潜在生命效益占工程总潜在生命效益的比例为21.8%,在西华县、扶沟县、尉氏县和周口市川汇区产生的潜在生命效益占工程总潜在生命效益的比例为38.7%,在中牟县产生的潜在生命效益占工程总潜在生命效益的比例为39.5%,在城镇人口密集区域产生的潜在生命效益显著高于非城镇区域。
上述结果中,贾鲁河综合治理工程在100 a一遇防洪标准段产生的潜在生命效益仅比在50 a一遇产生的效益高2.0%。这是因为根据项目设计成果,工程治理完成后,达到100 a一遇防洪标准段的地区为中牟县城区段,其治理长度约为25.7 km,占工程整体治理长度的17.3%;达到50 a一遇防洪标准段的地区包括尉氏县城区段、扶沟县城区段、西华县城区段和周口市川汇区城区段,其治理长度累计达37.7 km,占工程整体治理长度的25.4%。因此,由于治理长度及覆盖区域等因素的差距,使得在分段计算贾鲁河综合治理工程的潜在生命效益时,即便100 a一遇防洪标准安全性更高,其产生的效益也仅略高于50 a一遇防洪标准段。
2.6 结果合理性分析
潜在生命效益计算的关键在于洪水生命损失货币价值量化结果,而后者由生命损失人数和VSL的乘积表示。因此,本文通过分别验证统计生命价值和生命损失计算结果的合理性间接验证贾鲁河综合治理工程潜在生命效益计算结果的合理性。
2.6.1 统计生命价值合理性分析
通过收入弹性系数法将中国学者构建的不同年份不同城市的VSL测算模型转移至2021年,与本文VSL估算结果对比,验证其合理性。本次转移属于相同国家不同年份之间的VSL估算值转移,因此收入弹性系数取1。不同年份VSL转移计算结果见表4。可知,中国2021年VSL估算区间为[614,1 338]。本文VSL的估算值为956 万元/人,处于估算区间内,本文对VSL的估算值合理。
表4 不同年份VSL转移估算表
Table 4 Estimation table for VSL transfer of different years

项目 年份 转移前 2021 年转移后 人均收入/ (元·人-1 ) VSL/ (万元·人-1 ) 人均收入/ (元·人-1 ) VSL/ (万元·人-1 ) 南京[25] 2014 107 545 718 174 520 1 165 长沙[26] 2016 108 652 1 112 130 745 1 338 中国[26] 2016 53 783 408 80 976 614 中国[27] 2005 14 368 181 80 976 1 020
2.6.2 生命损失合理性分析
选用D&M法[9]验证案例中生命损失估算结果的合理性。本文在采用李-周法估算生命损失值时认为WT>1 h,因此,采用D&M法对估算结果进行验证时分别选定WT=1.2 h和WT=1.5 h,验证结果见表5。可以看出,D&M法在WT=1.2 h和1.5 h与李-周法在WT>1 h的估算结果平均相对误差绝对值分别为18.78%和15.97%,即采用D&M法计算的生命损失与李-周法相比误差较小,因此,认定本文计算的洪水淹没区域内的生命损失估算结果合理。
表5 D&M法与李-周法计算结果对比
Table 5 Comparison of calculation results between D&M method and Li-Zhou method

WT / h 洪水频 率/ % 生命损失/ 人 D&M 法 李-周法 相对误 差/ % 平均相对 误差/ % 20 18 13 38. 46 10 21 16 31. 25 1. 2 5 26 24 8. 33 18. 78 2 21 23 - 8. 70 1 13 14 - 7. 14 20 13 13 0 10 16 16 0 1. 5 5 19 24 - 20. 83 15. 97 2 16 23 - 30. 43 1 10 14 - 28. 57
3 结论
本文提出了河道治理工程防洪效益中潜在生命效益货币量化模型,以贾鲁河综合治理工程为例验证了模型的可行性。
(1)贾鲁河综合治理工程多年平均潜在生命效益为3 073.54 万元/a,分别通过验证统计生命价值和生命损失计算结果的合理性,间接证实了贾鲁河综合治理工程潜在生命效益计算结果的合理性。结果表明,河道治理工程的潜在生命效益主要在城区和人口密集区域,因此在工程设计时应重点考虑。
(2)准确的VSL值是货币量化河道治理工程潜在生命效益的关键。本文采用收入弹性系数法转移美国VSL值估算了中国VSL值。但受限于地区财富差异、群众理念差异等因素影响,后续可以开展中国劳动力市场及陈述性偏好等综合分析,能更准确计算中国不同地区的VSL值。
(3)本方法可货币量化水利工程防洪效益中的潜在生命效益,使决策者能更准确地计算工程的防洪效益,为开展国民经济评价和工程建设效果评价提供技术支撑。
[1] 中华人民共和国水利部. 2022年全国水利发展统计公报[M]. 北京: 中国水利水电出版社, 2023.
Ministry of Water Resources of the People′s Republic of China. 2022 statistic bulletin on China water activities[M]. Beijing: China Water &Power Press, 2023.
[2] 李宗坤, 王特, 葛巍, 等. 考虑溃坝后果的水库工程等级划分方法[J]. 水科学进展, 2023, 34(5):753-765.
LI Z K, WANG T, GE W, et al. Research on the rank classification method of reservoir projects considering dam failure consequences[J]. Advances in Water Science,2023, 34(5): 753-765.
[3] BOTZEN W J W, MONTEIRO É, ESTRADA F, et al. Economic assessment of mitigating damage of flood events: cost-benefit analysis of flood-proofing commercial buildings in Umbria, Italy[J]. The Geneva Papers on Risk and Insurance-Issues and Practice, 2017, 42(4):585-608.
[4] HUDSON P, BOTZEN W J W. Cost-benefit analysis of flood-zoning policies: a review of current practice[J]. WIREs Water, 2019, 6(6): e1387.
[5] 王艳艳, 王静, 胡昌伟,等. 太湖流域应对特大洪水防洪工程效益模拟[J]. 水科学进展, 2020, 31(6): 885-896.
WANG Y Y, WANG J, HU C W, et al. Benefit simulation of flood control project in Taihu Lake basin under extreme floods[J]. Advances in Water Science, 2020, 31(6): 885-896.
[6] 杨丽, 申碧峰, 王强. 北京市中心城防洪防涝系统效益分析[J]. 人民长江, 2017, 48(20): 6-9, 34.
YANG L, SHEN B F, WANG Q. Benefit analysis of flood control and waterlogging prevention system for downtown of Beijing[J]. Yangtze River, 2017, 48(20): 6-9, 34.
[7] 陈卫宾, 曹廷立, 李保国, 等. 人民治理黄河70年防洪保护区防洪效益分析[J]. 人民黄河, 2016, 38(12): 11-14.
CHEN W B, CAO T L, LI B G, et al. Benefit of flood protected area in lower Yellow River in recent 70 years[J]. Yellow River, 2016, 38(12): 11-14.
[8] BROWN C A, GRAHAM W J. Assessing the threat to life from dam failure[J]. Journal of the American Water Resources Association, 1988, 24(6): 1303-1309.
[9] DEKAY M L, MCCLELLAND G H. Predicting loss of life in cases of dam failure and flash flood[J]. Risk Analysis, 1993, 13(2): 193-205.
[10] GRAHAM W J. A procedure for estimating loss of life caused by dam failure[J]. Sedimentation &River Hydraulics, 1999, 6(5): 21-43.
[11] 周克发, 李雷, 盛金保. 我国溃坝生命损失评价模型初步研究[J]. 安全与环境学报, 2007, 7(3): 145-149.
ZHOU K F, LI L, SHENG J B. Evaluation model of loss of life due to dam breach in China[J]. Journal of Safety and Environment, 2007, 7(3): 145-149.
[12] LI W, LI Z K, GE W, et al. Risk evaluation model of life loss caused by dam-break flood and its application[J]. Water, 2019, 11(7): 1359.
[13] 葛巍, 焦余铁, 洪辛茜, 等. 基于AHP-BN法的溃坝生命损失风险评价[J]. 郑州大学学报(工学版), 2021, 42(3): 8-12.
GE W, JIAO Y T, HONG X Q, et al. Risk assessment of life loss caused by dam breach based on AHP-BN method[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(3): 8-12.
[14] 尹卫霞, 余瀚, 崔淑娟, 等. 暴雨洪水灾害人口损失评估方法研究进展[J]. 地理科学进展, 2016, 35(2): 148-158.
YIN W X, YU H, CUI S J, et al. Review on methods for estimating the loss of life induced by heavy rain and floods[J]. Progress in Geography, 2016, 35(2): 148-158.
[15] VISCUSI W K. The role of publication selection bias in estimates of the value of a statistical life[J]. American Journal of Health Economics, 2015, 1(1): 27-52.
[16] HAMMITT J K, ZHOU Y. The economic value of air-pollution-related health risks in China: a contingent valuation study[J]. Environmental and Resource Economics, 2006, 33(3): 399-423.
[17] GUO X Q, HAMMITT J K. Compensating wage differentials with unemployment: evidence from China[J]. Environmental and Resource Economics, 2009, 42(2): 187-209.
[18] CAO C J, SONG X K, CAI W J, et al. Estimating the value of a statistical life in China: a contingent valuation study in six representative cities[J]. Chinese Journal of Population, Resources and Environment, 2023, 21(4): 269-278.
[19] HAMMITT J K, HANINGER K. Valuing fatal risks to children and adults: effects of disease, latency, and risk aversion[J]. Journal of Risk and Uncertainty, 2010, 40(1): 57-83.
[20] CARLSSON F, DARUVALA D, JALDELL H. Value of statistical life and cause of accident: a choice experiment[J]. Risk Analysis, 2010, 30(6): 975-986.
[21] VEISTEN K, FLÜGEL S, RIZZI L I, et al. Valuing casualty risk reductions from estimated baseline risk[J]. Research in Transportation Economics, 2013, 43(1): 50-61.
[22] MASTERMAN C J, VISCUSI W K. The income elasticity of global values of a statistical life: stated preference evidence[J]. Journal of Benefit-Cost Analysis, 2018, 9(3): 407-434.
[23] World Bank Group. World bank open data[EB/OL].[2024-10-09]. https://data.worldbank.org.cn/.
[24] VISCUSI W K, MASTERMAN C. Anchoring biases in international estimates of the value of a statistical life[J]. Journal of Risk and Uncertainty, 2017, 54(2): 103-128.
[25] YANG Z, LIU P, XU X. Estimation of social value of statistical life using willingness-to-pay method in Nanjing, China[J]. Accident Analysis and Prevention, 2016, 95: 308-316.
[26] HOFFMANN S, KRUPNICK A, QIN P. Building a set of internationally comparable value of statistical life studies: estimates of Chinese willingness to pay to reduce mortality risk[J]. Journal of Benefit-Cost Analysis, 2017, 8(2): 251-289.
[27] QIN X Z, LI L X, LIU Y Y. The value of life and its regional difference in China[J]. China Agricultural Economic Review, 2013, 5(3): 373-390.