激光超声(LU)检测技术[1]作为一种无损检测新技术涵盖领域广泛。激光超声的原理是利用高能量密度的激光脉冲在材料表面激发超声波,然后用激光干涉仪或探头接收超声波。LU检测技术是非接触式无损检测技术,具有频段宽、空间分辨率高等优点,在缺陷检测方面具有广泛的应用[2]。弓鹏飞等[3]基于LU理论和有限元方法提出了定量表征缺陷的模型,采用时域与飞行散射法的结合来分析缺陷特征信号,发现表面波反射回波信号可以用来确定棒材表面缺陷的深度。杨连杰等[4]利用LU可视化技术生成缺陷处的超声波声场,通过对A扫信号、B扫信号分析发现在一个表面波传播深度内,反射和透射系数与缺陷深度呈近似线性关系,超出其传播深度后,其系数将不再变化。黄燕杰等[5]基于LU理论与有限元方法,成功分辨出横波、纵波和表面波,发现缺陷深度越深,反射表面波的幅值越大,可通过反射表面波的到达时间来计算缺陷的具体位置,而缺陷宽度对于反射波的影响作用有限。Liu等[6]通过分析A扫信号、B扫图像发现,不同直径的缺陷会对纵波的传播造成影响,即通过纵波到达时间可得到内部缺陷大小。Zeng等[7]对脉冲激光激发的超声波传播过程进行可视化,研究了超声波与缺陷相互作用的特性,观察到缺陷会对超声波频率与振幅产生影响。以上的LU检测方法主要是对超声波在缺陷上的反射和透射信号进行特征分析,用信号的振幅、频率和相位等特征值实现缺陷信号的识别与缺陷成像。但这种缺陷检测方法受人为主观因素的影响较大,非常考验分析人员的专业知识水平。
随着计算机技术的发展,机器学习的应用越来越广泛,其强大的数据处理能力、自我学习和适应能力,以及通过数据揭示模式和趋势的能力,比较适合激光超声缺陷检测领域。姜瀚彬等[8]将最大振幅图作为神经网络的输入,利用监督学习训练后的网络对缺陷的识别率可达97.22%。Liu等[9]建立了基于VGG卷积神经网络(CNN)的深度学习缺陷分类模型,发现对于不同类型的亚毫米级尺寸金属表面缺陷、裂纹、气孔和表面划痕的分类精度分别为94.6%、94%、94.6%。Guo等[10]使用小波变换将超声信号转换成尺度图像,这些图像随后作为CNN模型的输入以自动提取缺陷特征,该方法在验证集上的预测准确率达到了98.5%。魏博文等[11]通过激光超声技术获取铸件的最大振幅图像,并将其作为CNN的输入,该CNN架构达到了93.5%的平均识别率,能够有效识别铸件缺陷。可以看出,机器学习在激光超声缺陷检测领域的研究多以监督学习算法为主,但监督学习方法在这一领域的应用存在显著的依赖性,特别是对于大量精确标注数据的需求,这不仅限制了模型训练的可行性和效率,而且可能对模型的泛化能力构成约束。
为了克服监督学习算法在激光超声缺陷检测领域的不足,本文利用LU方法对金属材料缺陷进行检测,并采用机器学习方法实现无监督的缺陷信号分类与识别,进而对缺陷进行可视化成像。首先,利用LU设备采集缺陷试样上的LU信号;其次,利用隔离森林(isolated forest,IF)和局部离群因子(local outlier factor,LOF)两种机器学习方法对异常信号进行识别;最后,将识别到的异常信号进行可视化成像,并与最大振幅图成像进行对比。
1 激光超声实验
1.1 试样
本文采用的试样材料为铝合金,缺陷试样如图1所示,长、宽、厚分别为200、200、3 mm,在试样上预置两个缺陷,缺陷长和宽为10、2 mm,埋藏深度距离表面依次为0.4、0.6 mm。
图1 铝合金试样二维示意图(mm)
Figure 1 Two-dimensional diagram of aluminum alloy sample(mm)
1.2 激光超声检测
激光超声检测系统主要由脉冲激光器、步进位移平台、超声波探头、前置放大器、带通滤波器、A/D采集卡、PC电脑端等设备组成,系统结构示意图如图2所示。
图2 激光超声检测系统
Figure 2 Laser ultrasonic testing system
采用Nd:YAG脉冲激光发射器作为激励源,脉冲激光由聚焦透镜聚焦并经过偏转镜反射后辐照到试样表面。此脉冲激光的特性为峰值能量2 mJ,激光波长1 064 nm,脉冲宽度2 ns,光斑直径200 μm,最大重复频率2 kHz。
试样在脉冲激光辐照下诱发出两种超声波的激发效应:热弹效应和烧蚀效应。热弹效应是由于激光瞬时加热材料表面,诱发瞬态温度场的变化,进而在材料上引起局部的应力,该应力形成的机械波即为超声波[12]。烧蚀效应指激发能量超过材料阈值时,由于辐照区域内的温度过高,材料表面会产生熔融、气化以及形成等离子等现象。在固体表面主要产生垂直于辐照区域的反向力其次产生沿表面的切向应力从而激发出超声波,在材料表面会产生微小的凹坑或刻痕,造成不可逆的损伤。因热弹效应对材料无损的特性,故本文利用热弹效应在试样表面激发超声波。
接收信号部分采用70°超声波斜探头,其中心频率为1 MHz。带通滤波器用来减少杂波干扰。试样和探头放置在步进位移平台上。步进位移平台在x、y方向上的最大移动范围均为400 mm,两个方向上的位移精度均为4 μm。平台控制器负责控制二维步进位移平台的步进电机,使其沿滑轨精确移动。激光超声信号通过A/D采集卡进行记录,采样频率为125 MHz,采样长度为4 000。表1给出了激光超声检测参数。
表1 激光超声检测参数
Table 1 Parameters of laser ultrasonic testing
激光能量/mJ扫描间隔/mm扫描区域/mm采样频率/MHz信号长度1.20.5 20×20 125 4 000
如图3(a)所示,步进位移平台带动试样做S形运动,脉冲激光位置保持不动,探头接收超声波信号。如图3(b)所示,扫描区域内超声波信号保存为一个三维数据矩阵。数据的x坐标和y坐标表示扫描位置,z坐标表示信号时间或采样点数。最终采集到激光超声信号以一个41×41×4 000的三维数据矩阵形式保存,即有1 681个激光超声的时域信号,每个时域信号有4 000个采样点。
图3 激光超声扫描图
Figure 3 Laser ultrasonics scan
图4(a)给出了缺陷深度0.6 mm试样的扫描数据中坐标为(20,20)的时域信号。由于斜探头的入射角为70°,可判定超声波模态为表面波。为了深入分析表面波信号的频域特性,对其进行了快速傅里叶变换(FFT),所得频谱如图4(b)所示,可知其中心频率约为1 MHz。已知表面波在铝合金材料中的传播速度约为2 900 m/s[13],由式(1)可计算出表面波波长约为2.9 mm。
(1)
图4 缺陷深度0.6 mm试样上位置(20,20)的超声信号
Figure 4 Ultrasonic signal at the position (20,20) on the specimen with defect depth 0.6 mm
式中:λ为超声波波长;cp为超声波的相速度;f为表面波中心频率。表面波传播深度约为1个波长,故其传播深度约为2.9 mm,而本实验中缺陷最大埋藏深度为0.6 mm,故表面波与缺陷有相互作用。
为了进行缺陷识别,取每个位置上A扫信号的最大振幅,并绘制出最大振幅图。最大振幅图的成像原理为当结构在受到外部激励时,其振动响应和其内部特性有着密切关系,当结构内存在缺陷或损伤,其在这些缺陷区域的振动响应常与未受损区域存在显著差异。通过对振幅变化的观察,就可以直观地识别并定位异常[14]。如图5所示为缺陷深度0.6 mm对应的最大振幅图,可以看出缺陷处与非缺陷处较为相似,无法直接观测。
图5 缺陷深度0.6 mm的最大振幅图
Figure 5 Maximum amplitude image of defect with depth of 0.6 mm
2 信号处理
机器学习大致可分为3类:监督学习、无监督学习、强化学习。监督学习需要提前给出标记数据,建立输入-输出对的数据集。与监督学习不同,无监督学习不依赖于预先标记的输出,而是依赖数据自身的分布和关系,实现诸如聚类、降维的任务,常见算法有:K-means[15]、主成分分析(PCA)[16]等。强化学习主要通过与环境的互动来学习最佳策略。在激光超声缺陷检测过程中,因缺陷在试样内部,在对缺陷进行激光超声扫查时,并不知道缺陷的位置,且无法对检测信号进行标记,故需要采用无监督算法来对激光超声信号进行分类与识别。
本文技术路线如图6所示,激光超声检测后的测试数据首先经过PCA处理,将复杂高维的数据进行降维处理,方便后面的无监督学习;然后,利用IF和LOF算法处理信号并确定阈值后进行分类;最终,通过信号的各自阈值来判断是否为缺陷信号。
图6 技术路线图
Figure 6 Technology roadmap
2.1 主成分分析
若直接使用原始高维数据进行处理,可能会产生维度灾难、过拟合、冗余信息和计算效率降低等问题,故采用PCA对原始高维数据进行降维处理。PCA通过线性变换将原始特征空间通过投影的方式转换到一个新的特征空间,新空间中的特征就被称为主成分。PCA主要计算数据的协方差矩阵,然后找出此矩阵的特征值和特征向量,第i个主成分可表示为[17]
(2)
式中:ai为协方差矩阵的第i个特征向量;x为中心化后的数据矩阵,是经过中心化处理的数据矩阵。对于原始数据矩阵X的每列(特征),计算其均值uj,然后将每个观测值Xij减去其对应的均值uj来形成中心化后的数据矩阵x。
由图7可知,对于0.4、0.6 mm这两种缺陷深度,分别选取前47个主成分和前40个主成分即可代替原始数据方差的95%,这是因为尽管两次实验参数一致,但受到耦合剂及人为操作的影响,导致采集到的LU信号信噪比并非完全一致。PCA方法在减少数据维度的同时还最大程度地保留了数据的原始信息,减少了过拟合的风险,提高了后续信号异常检测的效率。
图7 A扫数据经PCA处理后的主成分占比图
Figure 7 Principal component ratio of the A scanned data after PCA processing
以图4中的时域信号为例,经过PCA处理后的时域和频域信号如图8所示。从时域信号来看,信号的主要特征成分得以保存,信号信噪比有适当提高;从频域信号来看,PCA算法去除了部分能量占比较低的频率成分。
图8 PCA处理后的结果
Figure 8 Result of PCA processing
2.2 隔离森林法
IF旨在利用其独特的树结构来高效地隔离出异常点[18],即从数据集中随机抽取子样本,然后在所有特征中随机选择一个进行切分,即在树的每个节点上,算法随机选择数据集中的一个特征,并基于该特征的随机阈值将数据分为两部分。这种方法的目的是快速隔离出异常数据点,由于它们在数据集中相对较少且通常在某些特征上与正常数据点明显不同,因此可以在较短的路径内被隔离出来。异常分数计算为[19]
(3)
(4)
(5)
式中:n为训练隔离树的样本数;E(h(x))为所有隔离树的平均路径长度;c(n)为标准化因子,用于比较不同数据集大小构建的隔离树;|leafi(x)|为数据点x落在第i棵树的叶节点中的数据点数量;C(|leafi(x)|)为标准化因子,用于树未完全生长时的调整;H(n-1)=ln(n-1)+0.577 215 664 9,其中常数为欧拉常数。
将IF法应用于经PCA降维后缺陷深度0.4 mm和0.6 mm激光超声检测数据中,结果如图9所示。可以看出数据集异常分数值分布大致呈现正态分布。
图9 IF异常分数直方图
Figure 9 IF anomaly score histogram
尽管IF作为一个无监督学习模型在异常检测中不需要标签即可进行训练,其性能的优劣仍然依赖于适当的阈值设定。这个阈值定义了何种程度的异常分数将被视为异常行为。由于决策函数输出的分数具有统计意义且呈现正态分布的特性,因此阈值的选择不是任意的,而是应该基于数据点的分数分布来决定。
核密度估计(KDE)是一种用于估计随机变量的概率密度函数的非参数方式;累积分布函数(CDF)是一个概率函数,给出了随机变量将处于某一值以下的概率。为了更好地确定阈值,综合考虑不同缺陷深度的核密度估计和累积分布函数,如图10所示。
图10 IF法不同缺陷深度的KDE与CDF图
Figure 10 KDE and CDF images of different defect depths of IF method
以缺陷深度0.6 mm为例,从图10(a)可以看出,IF异常分数出现1个尖峰后迅速下降,在异常分数值约0.1 之后其概率密度较低且下降缓慢;图10(b)表明,概率密度在IF异常分数约为0.1时达到95% 以上。这表明超过95%的数据点拥有低于或等于此阈值的IF异常分数,因其类似正态分布,且分数越高,其异常的可能性越大,故取95%的单边右侧置信区间,其IF异常分数为0.1。因此,可以将IF分数大于0.1的数据点视为异常值。同理,缺陷深度0.4 mm的可取0.1作为确定异常值的阈值。
根据上述阈值判断,将信号异常分数大于阈值的记为缺陷信号标记为黄色,将信号异常分数小于阈值的记为非缺陷信号标记为蓝色,最终成像图如图11所示。超声波探头在扫查区域正上方,故超声波的传播方向自上到下,超声波传播过程中受缺陷影响,一部分超声波被反射,一部分超声波会越过缺陷传播形成透射波;同时,缺陷处的超声波与非缺陷处的反射波在某些特征上会有一定的相似性,因此,当采用IF这种基于全局特征方法进行异常检测时,由于特征的相似性就会产生一定的误判率。
图11 IF成像结果
Figure 11 IF imaging results
2.3 局部离群因子法
与IF不同,LOF并不主要侧重于全局的异常检测策略[20],LOF更强调数据点在其近邻上的相对密度。因此,在处理具有不均匀密度和复杂数据分布结构的数据集时,LOF往往能展现出更优越的性能。
与IF相同,LOF也是基于异常分数来判断数据点是否为异常。可达距离是一种衡量两个数据点之间距离的方法。任意两个数据点p和o间的可达距离为reachability distancek(p,o)=max(distance(p,o), k-distance(o))。局部可达密度[21]为
(6)
式中:Nk(p)为点p的k个最近邻。
数据点p的LOF计算公式为
(7)
当LOFk(p)接近1时,意味着数据点p的密度与其邻居类似,当LOFk(p)大于1时,意味着数据点p的密度比其邻居低,则更可能为一个异常点。将LOF法应用于经PCA降维后缺陷深度0.4 mm和0.6 mm激光超声检测数据中,得到的异常分数如图12所示,可以看出,与IF法相同的是其异常分数分布均大致呈现正态分布形态,不同的在于异常分数评价指标不同,这是因其内部原理所致。
图12 LOF异常分数直方图
Figure 12 LOF anomaly score histogram
绘制缺陷深度0.4、0.6 mm的KDE和CDF图如图13所示。可以看出,在LOF异常分数为1.1附近时,存在着正常和异常值分布的界限,取95%的单边右侧置信区间,其LOF分数为1.2。因此,可以将LOF异常分数大于1.2的数据点视为异常值。
图13 LOF法不同缺陷深度的KDE与CDF图
Figure 13 KDE and CDF images of different defect depths of LOF method
基于上述阈值判断,LOF法最终成像如图14所示。由图14可知,LOF法判断出的异常值更为精确,误判率更低。
图14 LOF成像结果
Figure 14 LOF imaging results
为了验证算法的可靠性,保证实验的严谨性,采集试样无缺陷区域的激光超声实验数据,以LOF算法为例,使用同样的阈值分数,其结果如图15所示。从图15中可看出,绝大多数区域显示为蓝色,表明没有缺陷,而只有极少数的黄色点,表示被误判为有缺陷,这种低误差率是可以接受的。因此,实验结果有效证明了LOF算法能够准确地区分试样中的无缺陷数据和有缺陷数据。
图15 无缺陷数据实验结果
Figure 15 Experiment results of data without defects
3 结果与讨论
最大振幅图如图16所示,颜色变化代表了振幅的变化,深黄色区域表明此处存在显著的物理或结构性缺陷。图16中出现了多处深黄色区域,而实际试样中只存在了一个缺陷,这种不一致性可能与超声波在试样中的反射与透射有关。结合经IF和LOF算法处理后的图11和图14可以看出:LOF可以更清晰地观察到缺陷位置和大小;LOF算法基于局部与全局的密度偏差来识别异常,使其能够有效地处理那些在大体上看似正常,但在某些局部区域存在明显偏差的情况。因此,LOF算法成像不仅展示了缺陷的清晰位置,还较为完整地显示出了缺陷的边界。
图16 最大振幅图
Figure 16 The maximum amplitude images
4 结论
本文首先使用PCA对原始激光超声信号进行降维处理,然后分别采用了IF和LOF算法对降维后的数据执行异常检测,利用KDE和CDF确定阈值0.1和1.2,基于此阈值得到损伤成像图,并与最大振幅图进行了对比。研究表明,LOF算法不仅显示出比IF更佳的识别效果和更低的误判率,而且与最大振幅图相比,其成像效果更为准确和清晰。LOF算法有效规避了传统手工提取特征所带来的误差,为激光超声信号处理开辟了一条新的路径,展示出机器学习方法在激光超声信号后处理方面的优越应用前景。
[1] SEGOVIA RAM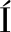
REZ I, GARC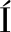A M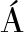
RQUEZ F P, PAPAELIAS M. Review on additive manufacturing and non-destructive testing[J]. Journal of Manufacturing Systems, 2023, 66: 260-286.
[2] 李阳, 彭笑永, 李大磊, 等. 激光超声无损测量40Cr钢渗氮层深度的实验研究[J]. 郑州大学学报(工学版), 2020, 41(6): 7-12.LI Y, PENG X Y, LI D L, et al. Experimental investigation on non-destructive measuring of the nitriding thickness of 40Cr steel by laser ultrasonic[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(6): 7-12.
[3] 弓鹏飞, 张彦杰, 王法雨, 等. 棒材表面缺陷的激光超声无损检测方法研究[J]. 激光杂志, 2022, 43(9): 44-49.GONG P F, ZHANG Y J, WANG F Y, et al. Research on laser ultrasonic nondestructive testing method for surface defects of bar[J]. Laser Journal, 2022, 43(9): 44-49.
[4] 杨连杰, 李阳, 孙俊杰, 等. 激光超声表面波在表面缺陷上的反射与透射[J]. 激光与光电子学进展, 2019, 56(4): 146-151.YANG L J, LI Y, SUN J J, et al. Reflection and transmission of laser ultrasonic waves on surface defects[J]. Laser &Optoelectronics Progress, 2019, 56(4): 146-151.
[5] 黄燕杰, 尚建华, 任立红, 等. 用于铝板缺陷无损检测的激光超声有限元模拟研究[J]. 应用光学, 2019, 40(1): 150-156.HUANG Y J, SHANG J H, REN L H, et al. Finite element simulation in laser ultrasound for non-destructive testing of aluminum defect materials[J]. Journal of Applied Optics, 2019, 40(1): 150-156.
[6] LIU S Y, JIA K N, WAN H P, et al. Inspection of the internal defects with different size in Ni and Ti additive manufactured components using laser ultrasonic technology[J]. Optics &Laser Technology, 2022, 146: 107543.
[7] ZENG W, CAI M M, WANG P, et al. Application of laser ultrasonic technique for detecting weld defect based on FDST method[J]. Optik, 2020, 221: 165366.
[8] 姜瀚彬, 高炜欣, 石萌萌. 基于卷积神经网络的激光超声缺陷检测研究[J]. 激光杂志, 2022, 43(7): 59-64.JIANG H B, GAO W X, SHI M M. Research on laser ultrasonic defect detection based on convolutional neural network[J]. Laser Journal, 2022, 43(7): 59-64.
[9] LIU Z X, HU Z L, WANG L X, et al. Effective detection of metal surface defects based on double-line laser ultrasonic with convolutional neural networks[J]. Modern Physics Letters B, 2021, 35(15): 2150263.
[10] GUO S F, FENG H W, FENG W, et al. Automatic quantification of subsurface defects by analyzing laser ultrasonic signals using convolutional neural networks and wavelet transform[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2021, 68(10): 3216-3225.
[11] 魏博文, 高炜欣, 刘梦溪. 激光超声结合CNN的铸件缺陷检测方法[J]. 激光与红外, 2022, 52(9): 1327-1334.WEI B W, GAO W X, LIU M X. Casting defect detection method combined with laser ultrasound and convolutional neural network[J]. Laser &Infrared, 2022, 52(9): 1327-1334.
[12] ZAREI A, PILLA S. An improved theory of thermoelasticity for ultrafast heating of materials using short and ultrashort laser pulses[J]. International Journal of Heat and Mass Transfer, 2023, 215: 124510.
[13] JAYA RAO V V S, KANNAN E, PRAKASH R V, et al. Fatigue damage characterization using surface acoustic wave nonlinearity in aluminum alloy AA7175-T7351[J]. Journal of Applied Physics, 2008, 104(12):123508.
[14] SOLODOV I, BAI J X, BUSSE G. Resonant ultrasound spectroscopy of defects: case study of flat-bottomed holes[J]. Journal of Applied Physics, 2013, 113(22): 223512.
[15] HU H Z, LIU J X, ZHANG X P, et al. An effective and adaptable K-means algorithm for big data cluster analysis[J]. Pattern Recognition, 2023, 139: 109404.
[16] FAIRLEY N, BARGIELA P, HUANG W M, et al. Principal component analysis (PCA) unravels spectral components present in XPS spectra of complex oxide films on iron foil[J]. Applied Surface Science Advances, 2023, 17: 100447.
[17] MARUKATAT S. Tutorial on PCA and approximate PCA and approximate kernel PCA[J]. Artificial Intelligence Review, 2023, 56(6): 5445-5477.
[18] 吴志强,张胜,包晓玲,等.针对WSN异常数据检测改进的孤立森林方法[J].小型微型计算机系统, 2021, 42(1):127-131.WU Z Q, ZHANG S, BAO X L, et al. Improved isolation forest method for WSN anomaly data detection[J]. Journal of Chinese Computer Systems, 2021, 42(1): 127-131.
[19] WANG H F, JIANG W, DENG X Y, et al. A new method for fault detection of aero-engine based on isolation forest[J]. Measurement, 2021, 185: 110064.
[20] JEONG W, TSINGAS C, ALMUBARAK M S. Local outlier factor as part of a workflow for detecting and attenuating blending noise in simultaneously acquired data[J]. Geophysical Prospecting, 2020, 68(5): 1523-1539.
[21] CHIU A L M, FU A W C. Enhancements on local outlier detection[C]∥The Seventh International Database Engineering and Applications Symposium. Piscataway: IEEE, 2003: 298-307.