大数据时代,电力系统数据呈现出多源异构的特点,电力负荷数据量也在不断增加。然而,由于采集设备故障、极端天气等原因,负荷数据会出现不同程度的缺失,使得可用信息减少,数据结构关联被破坏,给电力负荷特性分析及变化规律研究带来了极大的挑战[1]。对缺失的负荷数据进行较高精度的填充不仅是负荷数据分析与研究的基础,而且对提升负荷预测效果以保障电力系统能够安全稳定地运行具有重要意义。
缺失数据填充是根据观测数据对缺失数据进行估计[2],目前缺失值填充的方法主要分为3类:①基于统计学习的填充方法;②基于传统机器学习的方法;③基于深度学习的方法。
基于统计学习进行填充通常采用均值填充、前值填充、众数填充、热卡填充以及冷卡填充等方法[3],此类方法直接对负荷数据进行拟合,未考虑负荷数据的时序特征以及相关性,使得填充的误差较大。基于传统机器学习的填充方法主要有基于线性回归(linear regression)算法、基于K最近邻KNN(K-nearest neighbors)算法以及支持向量机SVM(support vector machine)等方法。Malarvizhi[4]将KNN用于缺失值填充,其会选择距离缺失数据最近的K个样本来填充,相比K-Means聚类方法,填充精度有所提升,但是该方法每填充一次就需要对所有样本进行一次遍历,十分耗时。Smola等[5]提出了一种基于SVM的缺失值填充方法,其填充缺失数据的过程中采用了时间信息。随着电网环境越来越复杂,负荷变化呈现出较强的随机性、非线性[6]与条件性[7]等特点,传统的机器学习方法难以进行较高精度的缺失值填充。
近年来,基于深度学习的方法被广泛应用于缺失值填充领域。Cao等[8]提出了基于双向循环神经网络的缺失值填充模型,使用估计值作为循环神经网络图的变量,能处理多个相关缺失值,相较于机器学习模型能够提升数据填充精度,但其本质是自回归模型,容易因为误差累积导致填充精度降低。目前基于Transformer[9]的模型多个领域被广泛使用,其核心就是自注意力机制。Du等[10]将自注意力机制应用于时间序列缺失值填充任务,提出了基于自注意力的时间序列填充(self-attention-based imputation for time series,SAITS)模型,其使用两个对角掩码自注意力模块的加权组合进行缺失值填充,相较于其他填充模型提高了数据的填充精度和速度,但是该方法忽略了电力负荷的条件性,对于多维数据间相关性以及时序特征的捕获能力仍有待提升[11]。
针对以上问题,本文提出了一种基于动态融合注意力机制的填充模型(dynamic fusion of attention mechanism imputation model,DFAIM)用于负荷缺失数据填充,相较于其他模型,所提模型填充精度更高。本文贡献如下。
(1)以负荷缺失数据填充为应用背景,构建了动态融合注意机制的填充模型来捕获多维数据间的深层联系,达到更精确的填充效果。
(2)使用了两种不同的缺失值填充实验方法,对两种不同类型的数据集进行实验,更全面地验证了本文模型的效果。
(3)考虑了影响负荷值的主要因素即气象因素,选择了开源的纽约市气象与负荷数据进行处理后作为本文实验数据集之一。
1 方法
1.1 问题定义
电力负荷数据是由多个特征组成的多变量时间序列,本文用矩阵X∈RT×F表示负荷数据,如式(1)所示。
X=[X1,X2,…,XF-1,XF]=
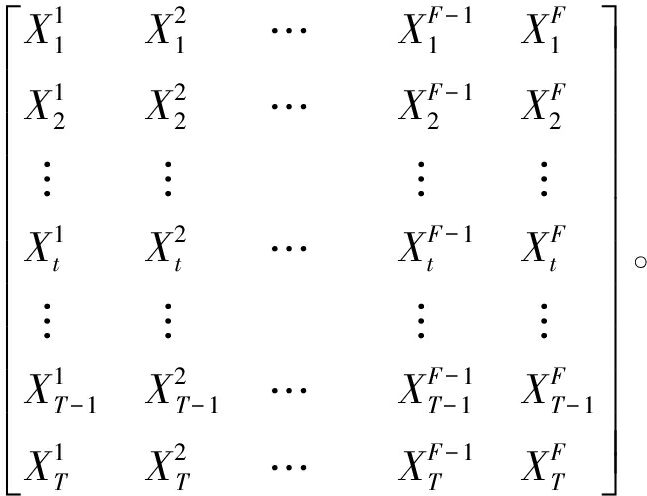
(1)
式中:T为时间戳的数量;F为电力负荷数据特征的维度;X1,X2,…,XF为所有时刻的负荷、温度、降水量等值。
为了更好地标记预处理后的电力负荷数据中缺失值所在位置,本文引入了掩码矩阵M,其中第t个时间戳的第f个特征的掩码值
的计算公式为
(2)
本文目的是通过使用X和M进行训练,得到一个填充模型,从而实现将原始缺失数据X填充为完整数据Ximp,如式(3)所示:
(3)
1.2 两种实验方法
对于不同类型数据集,本文在进行缺失值填充实验时,采用了以下两种方法。
(1)使用完整的数据集进行实验[12]。将数据集以一定比例模拟自然缺失,通过掩码矩阵对模拟缺失的位置进行标记,然后使用填充模型对数据进行填充。由于该方法原始数据集是完整的,因此可以使用真值直接评价模型填充效果。
(2)使用存在缺失数据的数据集进行实验。由于原始数据存在缺失导致无法直接评价模型填充效果,因此需要通过比较人为缺失数据的模型填充精度高低或者比较填充前后的数据对下游预测精度的影响来进行间接评价[13]。缺失值填充实验的两种方法如图1所示。
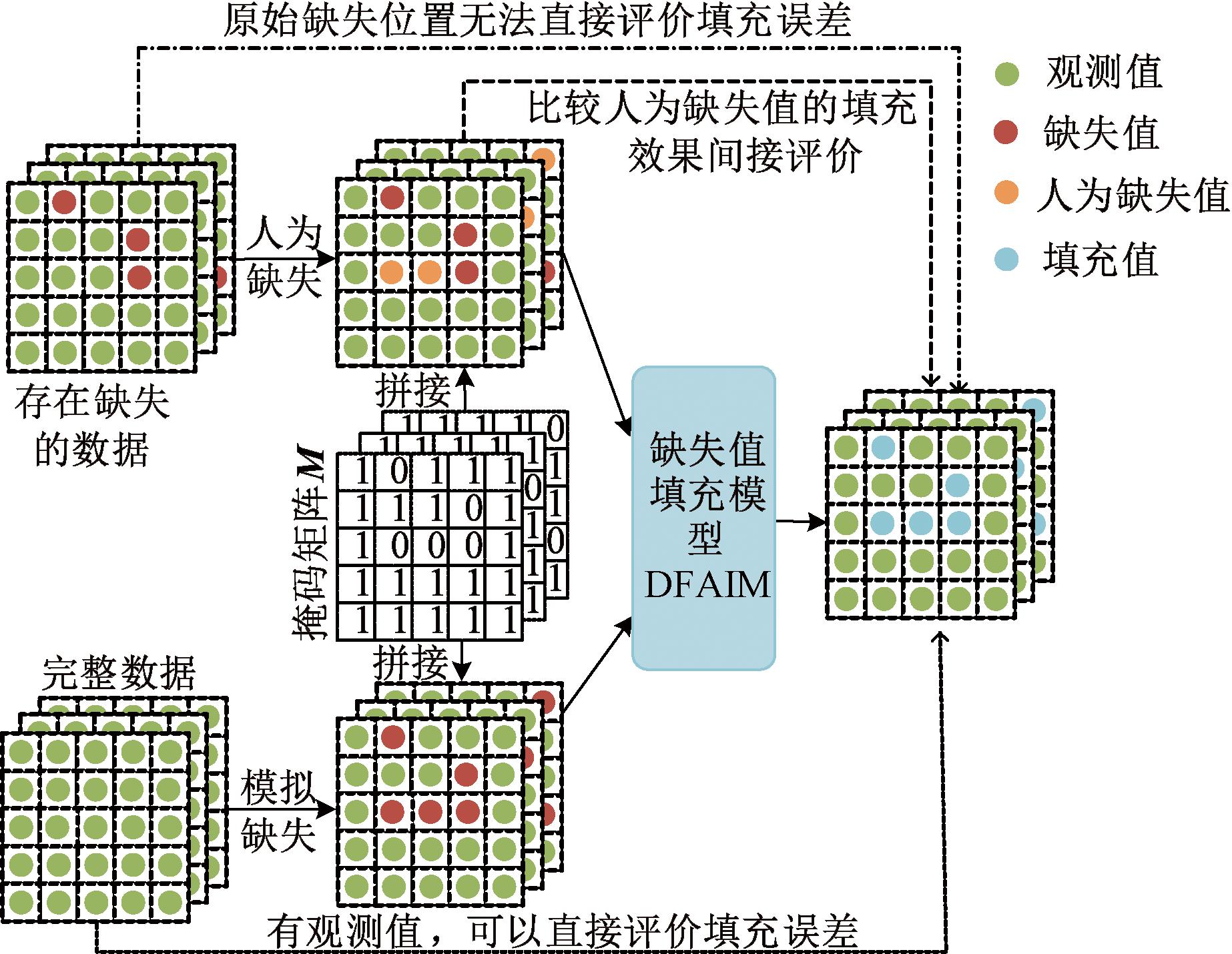
图1 两种缺失值填充实验方法
Figure 1 Two experimental methods for missing values imputation
2 模型设计
本文旨在通过对负荷数据以及相关数据的挖掘,实现缺失数据的准确填充。所提动态融合注意力机制的填充模型DFAIM如图2所示,模型共包括以下两个模块。
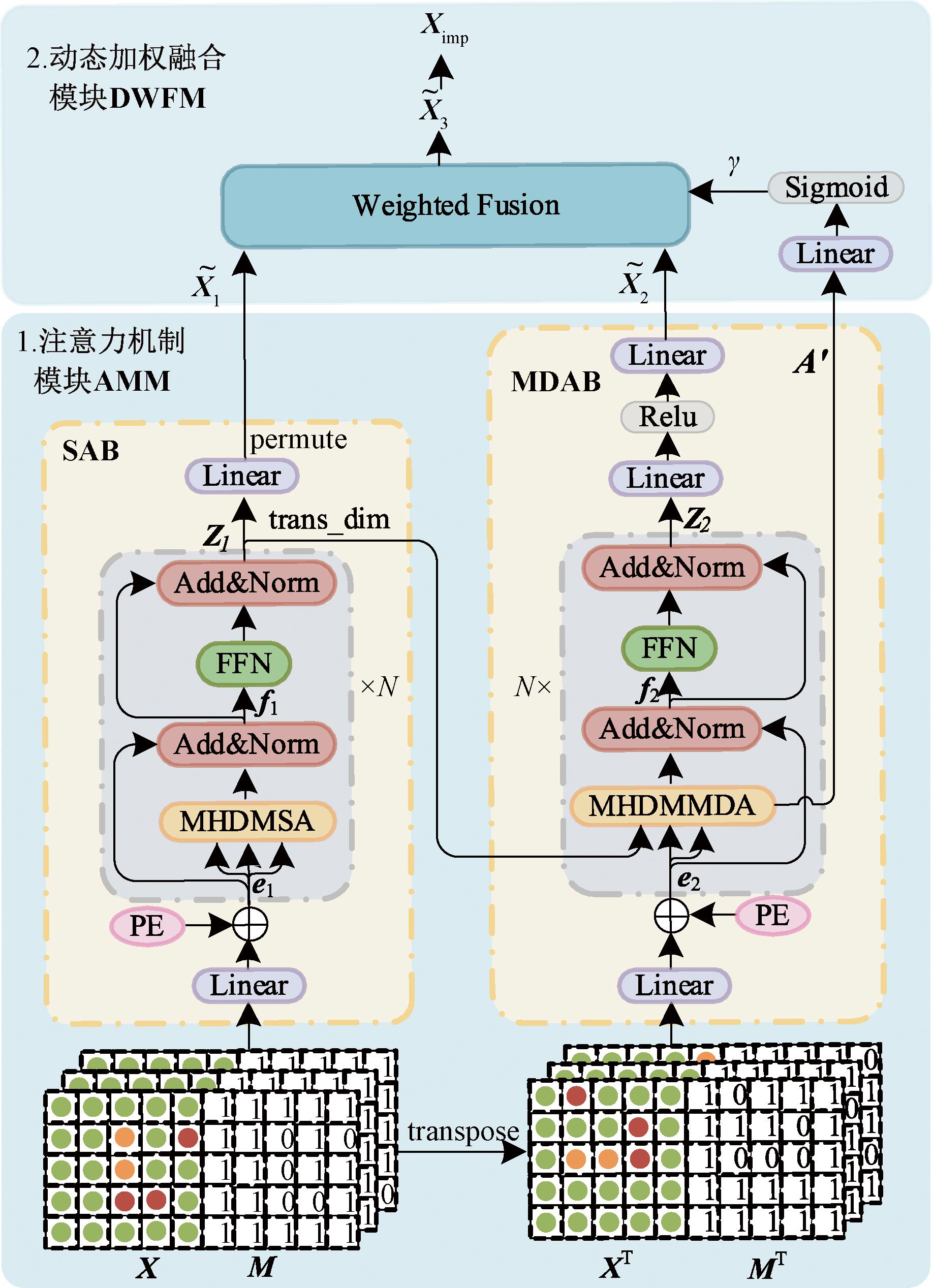
图2 DFAIM结构图
Figure 2 Structure diagram of DFAIM
(1)注意力机制模块(attention mechanism module, AMM)。该模块由自注意力机制块(self-attention mechanism block, SAB)和多维注意力机制块(multi-dim attention mechanism block, MDAB)构成。数据预处理后得到的X和M矩阵通过SAB捕获负荷数据时间步之间的潜在关联,通过MDAB获取到不同时间步与不同特征之间的关联,生成更加准确的特征表示
和
(2)动态加权融合模块(dynamic weighted fusion module, DWFM)。该模块使用可学习的参数γ对AMM的输出
和
赋予不同权重,动态融合得到特征表示
再对
进行非缺失位置值替换得到最终的填充值Ximp。
2.1 注意力机制模块AMM
该模块使用了两种不同注意力机制,分别为自注意力机制和多维注意力机制。
2.1.1 自注意力机制模块SAB
SAB的核心是自注意力机制,将其应用于负荷缺失值填充,可以用来获取不同时间步之间的相关性[14],该模块的具体结构如下。
(1)线性映射与位置编码层。将X和M进行拼接后经过线性层映射到dmodel维度。然后进行位置编码(position embedding, PE)得到特征矩阵e1。PE和e1分别由式(4)、式(5)得到。
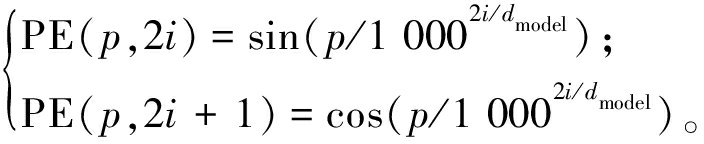
(4)
e1=Linear(Concat(X,M))+PE(p,i)。
(5)
式中:p为元素位置索引;2i为偶数维度;2i+1表示奇数维度;PE(p,2i)为位置编码向量的维度。
(2)多头对角掩码自注意力层。首先,将矩阵e1通过不同的线性变换得到Qt、键矩阵Kt以及值矩阵Vt,如式(6)所示:
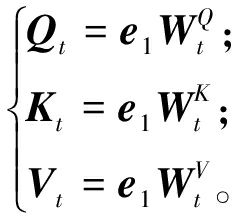
(6)
式中:
为模型需要学习的参数矩阵。
其次,需要在自注意力基础上添加对角掩码,保证填充时估计值只来自其他时刻值或其他特征值,防止数据自身对其估计做出贡献[15]。对角掩码自注意力机制(diagonal masked self-attention mechanism, DMSA)计算公式如式(7)所示:
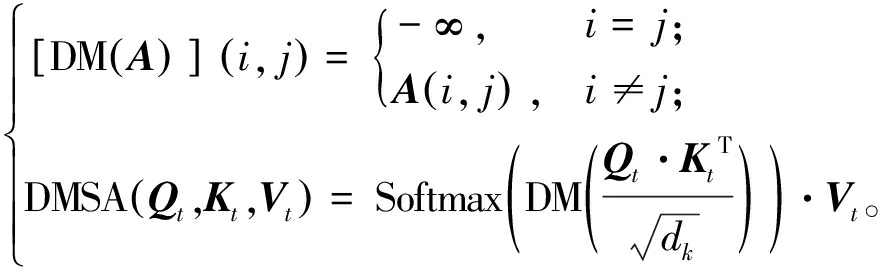
(7)
式中:DM(A)为对角掩码函数;A为Qt与KtT经过点积运算与缩放后得到的矩阵;i和j分别为矩阵A的行索引和列索引;DMSA(Qt,Kt,Vt)为对角掩码自注意力函数。
最后,使用多个注意力头以使模型能获得更为丰富的特征信息,将得到的多个注意力头所有输出进行融合得到f1,计算方法如式(8)所示:
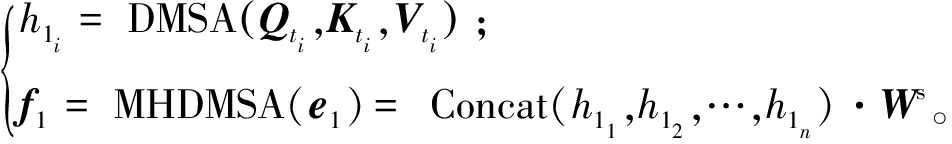
(8)
式中:i⊆(1,n),n为多头机制的头数;Ws为可学习的参数矩阵;MHDMSA(e1)为多头对角掩码自注意力函数。
(3)前馈网络FFN层。该前馈网络由2个线性层和一个Relu激活函数构成。f1通过N次的FFN得到特征表示Z1,如式(9)所示:
Z1=
。
(9)
(4)输出层。对经过线性层的Z1进行第二、三维互换,得到特征表示作为SAB的输出,如式(10)所示:
(10)
2.1.2 多维注意力机制块MDAB
MDAB的核心是多维注意力机制,将其应用于负荷缺失值填充,可以用来获取不同特征与不同时间戳之间的联系,MDAB的具体结构如下。
(1)线性映射与位置编码层。首先,将XT和MT进行拼接,之后通过线性映射并添加位置编码至维度得到特征矩阵e2,如式(11)所示:
e2=Linear(Concat(XT,MT))+PE(p,i)。
(11)
(2)多头对角掩码多维注意力层。不同于自注意力机制的3个矩阵均由一个矩阵变换而来,多维注意力机制的查询矩阵Qf和键矩阵Kf由e2变换得到,值矩阵V′f是由特征表示Z1通过维度变化而来,3个矩阵计算方法如式(12)所示:
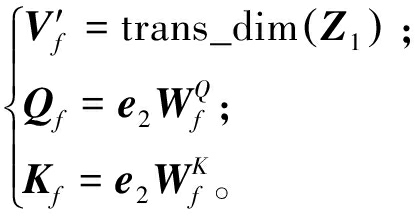
(12)
式中:
和
为模型需要学习的参数矩阵。
矩阵通过对角掩码多维注意力机制(diagonal masked multi-dim attention mechanism, DMMDA) 层以学习特征与时间戳维度深层关联,如式(13)所示:
(13)
Qf和KfT进行了缩放点积运算,可以获取到特征维度的数据相关性,
包含了时间戳维度之间的潜在关联,所以DMMDA能够学习到特征维度与时间戳维度之间的潜在联系。
通过多头机制获取到不同表示空间的多维潜在联系,将多头输出进行融合得到f2,如式(14)所示:
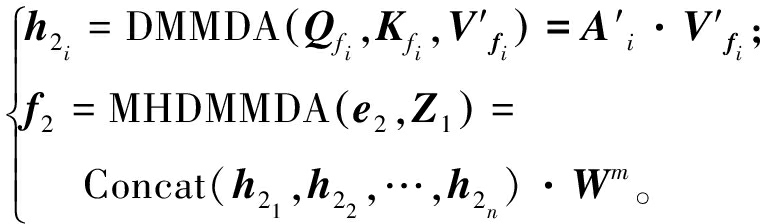
(14)
式中:i⊆(1,n);n为多头机制的头数;A′i为可学习的参数矩阵;MHDMMDA(e2,Z1)为多头对角掩码多维注意力函数。
(3)前馈网络FFN层。将Z2通过N次由2个线性层和1个Sigmoid激活函数构成的FFN层,得到特征表示Z2,计算方式如式(15)所示:
Z2=
。
(15)
(4)输出层。Z2经过线性层、Relu激活函数和线性层得到MDAB的输出
计算方式如式(16)所示:
(16)
2.2 动态加权融合模块DWFM
为提高模型的泛化能力,使模型能够根据负荷数据缺失率的变化动态调整权重,在对注意力机制模块得到的两个特征表示进行融合时,使用动态加权的方式。
首先,将通过MDAB得到的可学习矩阵A′与矩阵MT进行拼接,然后通过线性层进行降维;其次,通过Sigmoid函数得到动态权重γ;最后,将γ作为
的权重,将(1-γ)作为
的权重,加权融合得到
与
计算方式分别如式(17)、式(18)所示:
γ=Sigmoid(Linear(Concat(A′,MT)));
(17)
(18)
最终的填充数据Ximp由提供缺失位置的值,XT提供原本的观测值,如式(19)所示:
(19)
式中:Permute(·)表示第二、三维互换操作,其目的是使Ximp的维度与输入X保持一致;∘表示哈达玛积运算。
3 实验设置及结果分析
3.1 实验环境
本实验采用的编程语言为python,版本为3.8.0,在Windows10操作系统上搭建了基于Pytorch框架的编程环境,框架版本为1.10.0,开发环境为PyCharm11.0.15+10-b2 043.56 amd64,实验所用的处理器为英特尔i5-12400F 2.50 GHz,显卡为英伟达RTX3060,内存为16 GB。
3.2 数据集与预处理
为了验证DFAIM对电力负荷缺失值填充精度的提升效果,本文使用了开源的UCI电力负荷数据集[16],同时考虑到气象因素,构建了纽约气象及负荷数据集作为实验数据集,并对2个数据集进行了预处理操作,具体操作如表1所示,样本构建方法为滑动窗口法。
表1 数据集预处理
Table 1 Datasets preprocessing
数据集是否完整填充实验方法总缺失率/%引入缺失方式特征缩放方式特征维度数据集测试时长/月训练集验证集测试集窗口大小样本总量数据集划分数量训练集验证集测试集UCI电力负荷数据集是方法10 模拟归一化3702810101001 400817292291纽约气象及负荷数据集否方法222.78人为归一化11321110241 602875291235
3.2.1 纽约气象及负荷数据集及预处理
使用开源的纽约市2016年1月1日至2020年5月31日共计53个月的负荷数据和气象数据,通过进行相关性分析以及显著性检验,最终选择了与其关联程度较大的10种气象数据。负荷与气象数据均以1 h为采样间隔,使用外连接的方式进行两种数据拼接,将得到的38 472条数据作为纽约气象负荷数据集。该数据集中含有缺失数据的记录为8 764条,每一属性的数据均存在不同程度缺失,最高缺失达16.27%。为了消除不同量纲之间的影响,先对原数据进行Min-Max归一化处理,将其控制在[0,1]内,归一化公式如式(20)所示:
(20)
式中:t∈(1,T);f∈(1,F);Xfmax和Xfmin分别表示同一特征维度下样本的最大值与最小值。
3.2.2 UCI电力负荷数据集及预处理
该数据集包含从370个客户端收集的2011年1月1日至2014年12月31日共计48个月的负荷数据。采样间隔为15 min,并且没有缺失数据。
3.3 评价指标
本文使用平均绝对误差(MAE)、均方根误差(RMSE)、平均相对误差(MRE)这3个评价指标来评估不同模型对于电力负荷缺失数据的填充效果,计算方法如式(21)～(23)所示:
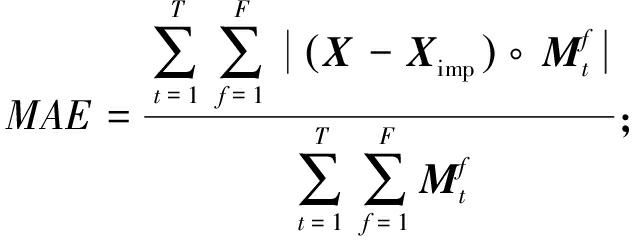
(21)
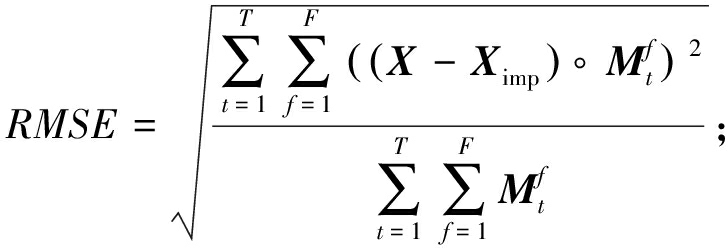
(22)
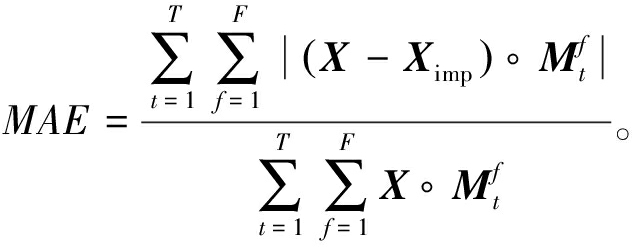
(23)
3.4 参数设置
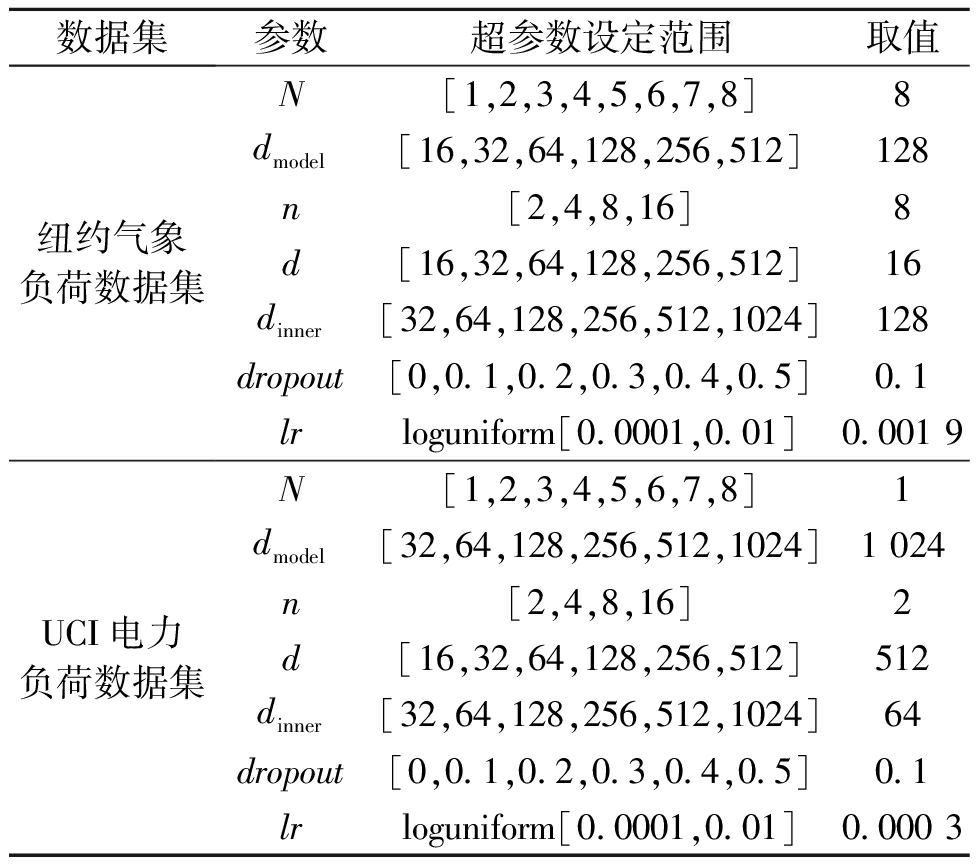
本文在进行超参数的选择时使用了微软自动超参调优工具NNI[17],其可通过定义的超参搜索空间和超参调优算法运行,并报告评价指标,从而更好地选择最佳超参组合。本文对DFAIM模型进行实验时使用随机搜索(random search,RS)作为超参调优算法,该算法相比网格搜索更加高效[18],同时也能够保证模型的准确性。实验设置每个模型的trial为200,即进行200次自动超参搜索,为了兼顾时间效率与模型的可解释性,除学习率lr外超参数范围均设定为离散值。对于纽约气象负荷数据集以及UCI电力负荷数据集,设置的超参搜索范围以及最终确定的模型超参数如表2所示。表2中,N表示2个模块编码器的层数;dmodel表示特征矩阵的e1和e2维度;n表示注意力头数;d表示V的维度;dinner表示中间线性层的维度;dropout表示随机失活率;lr表示模型参数的学习率,采用随机采样的方式进行学习率的选择。
表2 DFAIM在两个数据集上的超参数
Table 2 Hyperparameters of DFAIM for two datasets
数据集参数超参数设定范围取值纽约气象负荷数据集UCI电力负荷数据集N[1,2,3,4,5,6,7,8]8dmodel[16,32,64,128,256,512]128n[2,4,8,16]8d[16,32,64,128,256,512]16dinner[32,64,128,256,512,1024]128dropout[0,0.1,0.2,0.3,0.4,0.5]0.1lrloguniform[0.0001,0.01]0.001 9N[1,2,3,4,5,6,7,8]1dmodel[32,64,128,256,512,1024]1 024n[2,4,8,16]2d[16,32,64,128,256,512]512dinner[32,64,128,256,512,1024]64dropout[0,0.1,0.2,0.3,0.4,0.5]0.1lrloguniform[0.0001,0.01]0.000 3
3.5 对比实验
本文在模型选择上采用了8种基线模型,不仅考虑了传统简单的均值填充法Mean和前值填充法Previous,还考虑了机器学习模型如线性回归模型与多层感知机模型,以及像MRNN、BRITS这样基于双向循环神经网络的深度神经网络,还对比了基于自注意力机制的Transformer模型和SAITS模型。
Mean:均值填充法,使用缺失数据所在属性其余观测数据的平均值进行填充。
Previous:前值填充法,使用缺失数据前一时间戳的值进行填充。
LR:线性回归模型,作为一种基础回归算法,使用线(面)等模型对于现有相对线性的数据进行较小损失的拟合。
MLP:多层感知机,在本实验中隐藏层的维度设置为1 024。
MRNN:基于循环神经网络的填充模型[19],本实验中隐藏层的维度设置为1 024,学习率设置为0.001。
BRITS:基于双向RNN来进行缺失值估算,将缺失值作为双向RNN图的变量参与到反向传播过程中,本实验隐藏层维度设置为1 024,学习率设置为0.001。
Transformer:本文将缺失值填充视为掩码预测任务,因此在实验时只使用了Transformer的编码器部分,未使用解码器部分。
SAITS:基于自注意力机制进行缺失值填充的模型,相比于基于RNN的自回归模型,提高了填充精度,当前在时间序列填充任务上取得SOTA结果。
在10%缺失率的情况下,本文所提DFAIM与其他模型的对比实验结果如表3所示。
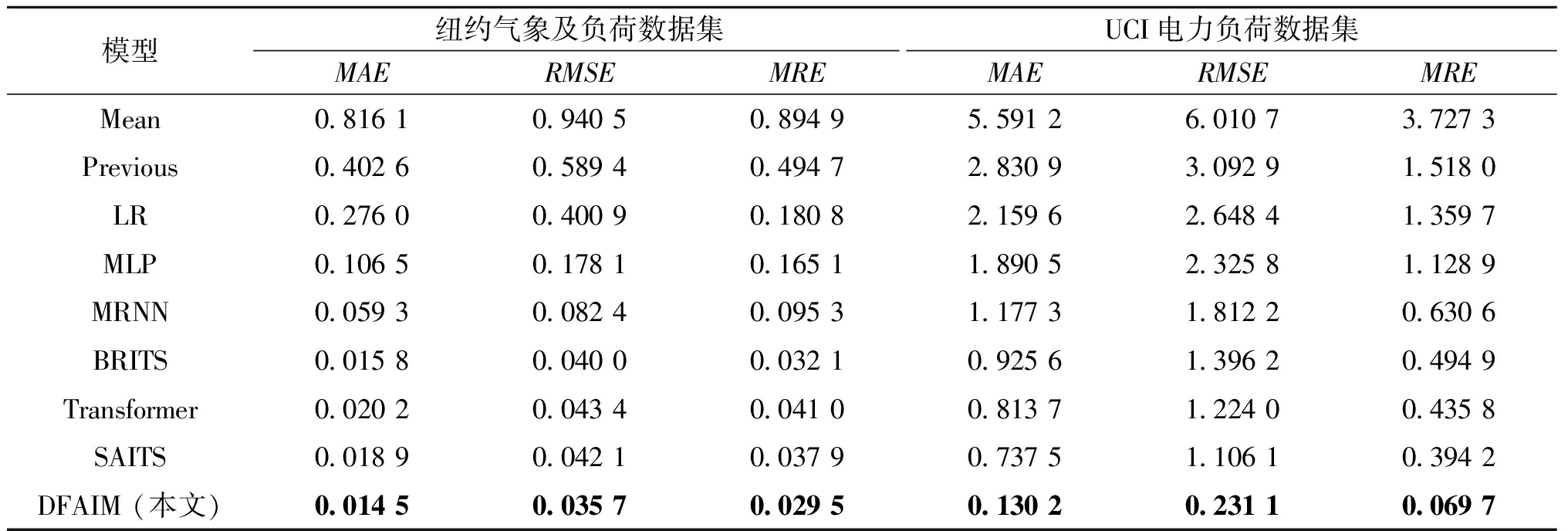
表3 对比实验结果
Table 3 Results of comparative experiments
模型纽约气象及负荷数据集UCI电力负荷数据集MAERMSEMREMAERMSEMREMean0.816 10.940 50.894 95.591 26.010 73.727 3Previous0.402 60.589 40.494 72.830 93.092 91.518 0LR0.276 00.400 90.180 82.159 62.648 41.359 7MLP0.106 50.178 10.165 11.890 52.325 81.128 9MRNN0.059 30.082 40.095 31.177 31.812 20.630 6BRITS0.015 80.040 00.032 10.925 61.396 20.494 9Transformer0.020 20.043 40.041 00.813 71.224 00.435 8SAITS0.018 90.042 10.037 90.737 51.106 10.394 2DFAIM (本文)0.014 50.035 70.029 50.130 20.231 10.069 7
通过对表3数据的对比分析可以看出:
(1)本文所提DFAIM同其他模型相比,MAE、RMSE、MRE值均有降低,取得了最佳填充效果。在其他填充方法中:传统统计方法Mean和Previous的填充效果最差,原因是其仅利用了缺失数据同维度的数据进行填充;简单机器学习模型LR和MLP表现较差,是由于其只能大致拟合数据整体变化;深度学习模型MRNN、BRITS、Transformer和SAITS表现较好,能够较为准确地拟合数据的细节变化,但是捕获数据间深层联系的效果欠佳。
(2)本文所提DFAIM在UCI电力负荷数据集上的填充精度提升十分明显,原因应该在于该数据集特征数量更多,不同维度数据之间的关联性更强,DFAIM模型的多维注意力机制块很好地捕获了多维数据之间的关联性。
3.6 不同缺失率实验
为了进一步验证模型的填充效果,本文还在纽约气象负荷数据集上进行了不同缺失率实验。通过在测试集引入20%～90%缺失比例的自然缺失值,来验证不同缺失率下本模型的有效性,实验结果如图3所示。
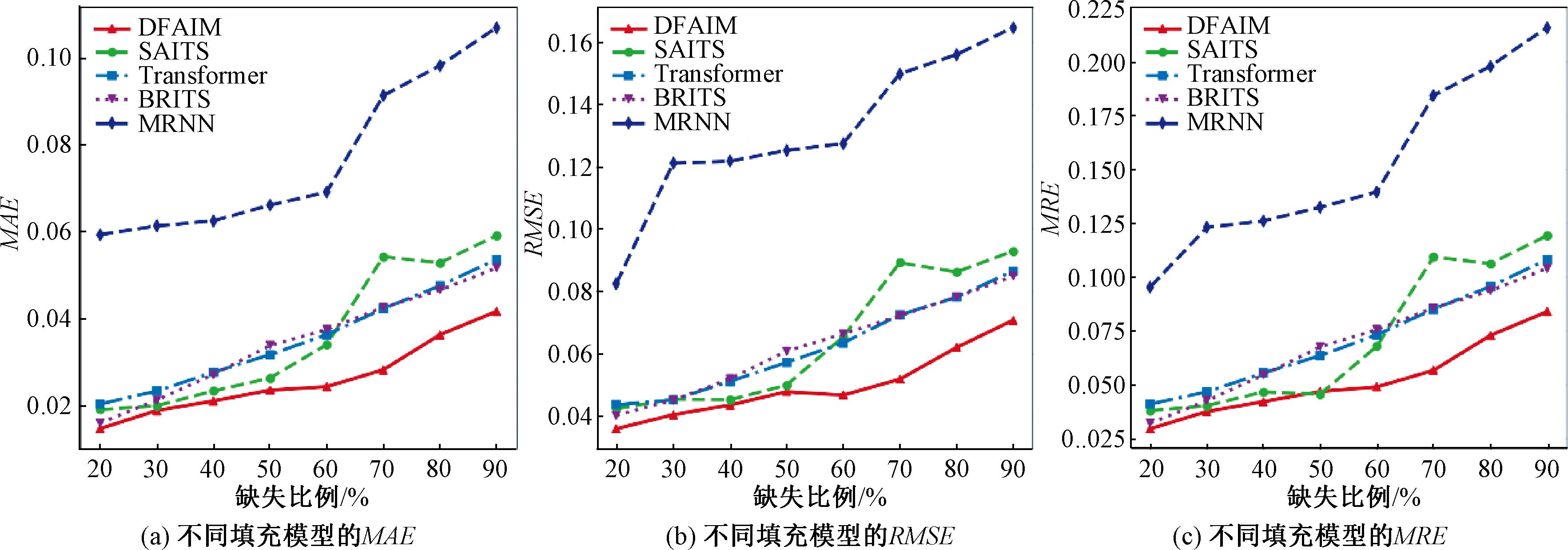
图3 不同缺失率下模型的填充效果
Figure 3 Imputation results of models with different missing rates
从图3可以看出,随着缺失比例的上升,不同模型的MAE、RMSE、MRE值大致呈上升趋势,这表明随着数据缺失比例的上升,填充准确性呈下降趋势,与实际情况一致。DFAIM在不同的缺失率下,都表现出更高的填充精度,实现了最佳效果。
3.7 消融实验
本文使用两个不同的注意力块以深入挖掘数据之间的潜在联系,使用了动态加权融合的方式以根据数据的不同缺失率来自适应地调整权重,因此消融实验重点要探究两个注意力机制块组合的有效性以及动态加权融合方式的有效性。本文在纽约气象及负荷数据集上进行了消融实验,描述如下。
Only SAB:仅使用自注意力机制块的特征表示。
Only MDAB:仅使用多维注意力机制块的特征表示。
AMM+EWFM:使用SAB与MDAB两个模块最终的特征表示,然后使用等权重融合模块(equal weight fusion module, EWFM)。
消融实验结果如表4所示。
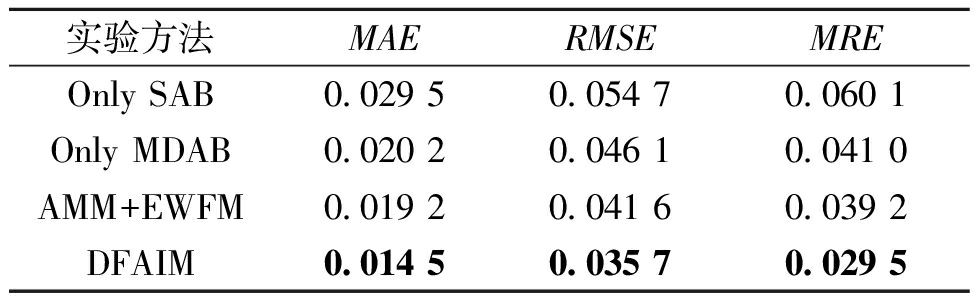
表4 消融实验结果
Table 4 Results of ablation experiment
实验方法MAERMSEMREOnly SAB0.029 50.054 70.060 1Only MDAB0.020 20.046 10.041 0AMM+EWFM0.019 20.041 60.039 2DFAIM0.014 50.035 70.029 5
通过对实验结果的对比分析,可以得出以下结论。
(1)Only SAB的填充误差明显高于其他3个,说明仅使用自注意力机制能捕获浅层的数据关联,但无法捕获更深层的关联。
(2)AMM+EWFM的填充误差低于Only SAB和Only MDAB的结果,说明增加多维注意力机制块能够捕获缺失值与其他时刻值或其他特征值之间更深层的关联,证明了两种注意力机制组合模块AMM挖掘数据潜在联系的能力。
(3)DFAIM的填充误差比AMM+EWFM进一步降低,说明动态加权融合的方式能够根据数据的缺失率学习到更优的权重,证明了动态加权融合模块DWFM对于填充精度提升的有效性。
4 结论
本文设计了动态融合注意力机制的填充模型,通过SAB与MDAB的组合来构建模型,能兼顾时间维度与特征维度之间的关联模式,从而更好地挖掘缺失数据特征间联系。该模型通过动态加权的方式融合两个特征表示,能根据不同的缺失率自适应地调节权重,从而得到更高的填充精度;在两种数据集上与多个填充模型的对比,证明了DFAIM模型能够进一步提升填充精度。另外,消融实验证明了本文所提注意力机制模块及动态加权融合方式的有效性。通过不同缺失比例的实验表明了DFAIM模型能够更好适应现实的不同数据缺失场景。
[1] 朱俊丞, 杨之乐, 郭媛君, 等. 深度学习在电力负荷预测中的应用综述[J]. 郑州大学学报(工学版), 2019, 40(5): 13-22.ZHU J C, YANG Z L, GUO Y J, et al. Deep learning applications in power system load forecasting: a survey[J]. Journal of Zhengzhou University (Engineering Science), 2019, 40(5): 13-22.
[2] SUO Q L, ZHONG W D, XUN G X, et al. GLIMA: global and local time series imputation with multi-directional attention learning[C]∥2020 IEEE International Conference on Big Data (Big Data). Piscataway: IEEE, 2020: 798-807.
[3] LIN W C, TSAI C F. Missing value imputation: a review and analysis of the literature (2006—2017)[J]. Artificial Intelligence Review, 2020, 53(2): 1487-1509.
[4] MALARVIZHI M R. K-NN classifier performs better than K-means clustering in missing value imputation[J]. IOSR Journal of Computer Engineering, 2012, 6(5): 12-15.
[5] SMOLA A J, VISHWANATHAN S V N, HOFMANN T. Kernel methods for missing variables[J]. Society for Artificial Intelligence and Statistics, 2005: 325-332.
[6] 徐岩, 张晓, 周兴华, 等. 基于Prophet-LightGBM的台区短期负荷预测方法[J]. 华北电力大学学报(自然科学版), 2024,51(6):13-19.XU Y, ZHANG X, ZHOU X H, et al. The short-term load forecasting method of transformer based on Prophet-LightGBM[J]. Journal of North China Electric Power University (Natural Science Edition), 2024,51(6):13-19.
[7] 张颖超, 成金杰, 邓华, 等. 基于相似日和特征提取的短期风电功率预测[J]. 郑州大学学报(工学版), 2020, 41(5): 44-49.ZHANG Y C, CHENG J J, DENG H, et al. Short-term wind power prediction based on similar day and feature extraction[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(5): 44-49.
[8] CAO W, WANG D, LI J, et al. BRITS: bidirectional recurrent imputation for time series[C]∥Proceedings of the 32nd International Conference on Neural Information Processing Systems. NewYork: ACM, 2018: 6776-6786.
[9] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]∥Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM, 2017: 6000-6010.
[10] DU W J, C
TÉ D, LIU Y. SAITS: self-attention-based imputation for time series[J]. Expert Systems with Applications, 2023, 219: 119619.
[11] 周远翔, 林孟龙, 陈健宁, 等. 基于自注意力生成对抗网络的电力设备在线监测缺失数据填补[J]. 高电压技术, 2023, 49(5): 1795-1809.ZHOU Y X, LIN M L, CHEN J N, et al. Missing data imputation for online monitoring of power equipment based on self-attention generative adversarial networks[J]. High Voltage Engineering, 2023, 49(5): 1795-1809.
[12] J
GER S, ALLHORN A, BIEßMANN F. A benchmark for data imputation methods[J]. Frontiers in Big Data, 2021, 4: 693674.
[13] AHN H, SUN K, PIO KIM K. Comparison of missing data imputation methods in time series forecasting[J]. Computers, Materials &Continua, 2022, 70(1): 767-779.
[14] 马思远, 焦佳辉, 任晟岐, 等. 基于注意力机制的城市多元空气质量数据缺失值填充[J]. 计算机工程与科学, 2023, 45(8): 1354-1364.MA S Y, JIAO J H, REN S Q, et al. Missing value filling for multi-variable urban air quality data based on attention mechanism[J]. Computer Engineering &Science, 2023, 45(8): 1354-1364.
[15] HAN K, WANG Y H, CHEN H T, et al. A survey on vision transformer[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(1): 87-110.
[16] TRINDADE A. Electricity load diagrams 2011—2014 data set[EB/OL]. (2015-12-03)[2024-08-05]. https:∥archive.ics.uci.edu/ml/datasets/Electricity Load Diagrams20112014.
[17] Microsoft. Neural network intellgence[EB/OL]. (2017-06-01)[2024-08-05]. https:∥github.com/microsoft/nni.
[18] BERGSTRA J, BENGIO Y. Random search for hyper-parameter optimization[J]. Journal of Machine Learning Research, 2012, 13: 281-305.
[19] YOON J, ZAME W R, VAN DER SCHAAR M. Estimating missing data in temporal data streams using multi-directional recurrent neural networks[J]. IEEE Transactions on Biomedical Engineering, 2019, 66(5): 1477-1490.