线控转向(steer-by-wire, SBW)系统作为智能车辆底盘的重要组成部分,因其智能的控制方式及准确的响应特性,使得车辆底盘的灵活性及稳定性都有了进一步提升,因此近年来受到了广泛的研究与关注[1-3]。
变传动比作为SBW系统的关键技术,是影响车辆操纵稳定性及主动安全性的主要因素,国内外学者对此进行了大量研究。目前针对线控转向传动比的设计方法主要可分为两种:第一种方法考虑到线控系统的复杂性和非线性特性,利用神经网络或模糊控制等智能控制算法,将车速和方向盘转角作为输入信号,通过制定特性化的控制策略,得到对应的转向传动比[4-5]。这种方法缺乏准确的设计依据,实用性不强。第二种方法从车辆动力学特性角度出发,将汽车稳态转向的横摆角速度增益作为参考依据,对不同车速下的传动比进行分段研究。赵林峰等[6]以横摆角速度增益不变作为设计依据,分析了汽车理想转向传动比特性,提出了不同车速下的转向传动比设计方案。冯晓志等[7]在稳态横摆角速度增益不变的基础上,引入侧向加速度增益,通过将两者按一定比例综合得到传动比曲线,改善了车辆的转向灵敏度和稳定性。Liu等[8]通过粒子群算法确定稳态横摆角速度增益值,设计可变转向传动比。金智林等[9]将横摆角速度、侧向加速度和侧倾角增益相结合,提出多增益融合变传动比设计方法,并通过遗传算法对增益常量进行优化选取,保障了车辆行驶稳定性的同时,有效提高了汽车的抗侧倾能力。周兵等[10]考虑到传统传动比方案不适用于低附着系数路面,因此基于模糊控制策略,设计了随路面附着系数变化而改变的变角传动比。
上述相关传动比的研究方法中,往往仅考虑将稳态横摆角速度增益设为定值,这样虽保障了汽车在不同车速下转向特性响应一致,但在高速工况下不利于行车安全。此外,虽有研究者在设计传动比时考虑了路面附着系数的影响,在一定程度上改善了汽车在不同附着路面上的行驶稳定性,但基于模糊控制的控制规则制定依据并未明确,路面附着系数与传动比之间的影响关系有待进一步研究。
针对传统定增益传动比设计上的问题,首先,本文对车辆稳态横摆角速度增益特性分析,建立了车速、附着系数与横摆角速度增益之间的数据关系;其次,通过蛇算法优化的BP神经网络(snake optimizer BP, SO-BP)实时地根据附着系数和车速的变化,动态获取对应的横摆角速度增益;最后,基于该增益设计了考虑附着系数和车速因素的线控转向传动比并采用CarSim与Simulink联合仿真平台验证了所设计传动比的有效性。
1 横摆角速度增益特性
横摆角速度增益是评价转向系统好坏的重要指标,常被用来作为稳态变角传动比的设计依据[11],因此对该增益影响因素进行分析。由于本文对变角传动比特性研究是基于车辆稳态响应特性,故后续横摆角速度增益均指其稳态值。
1.1 横摆角速度增益
汽车处于稳态转向时的横摆角速度增益可由二自由度模型计算得到[12],故建立汽车二自由度模型如图1所示。

图1 汽车二自由度模型
Figure 1 Vehicle model with 2-DOF
由图1可得,二自由度汽车受外力沿y轴的合力及绕质心的合力矩为
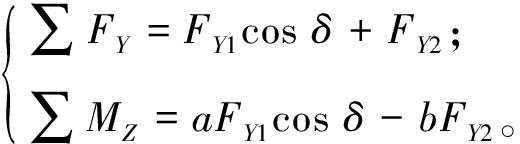
(1)
式中:FY1、FY2为前后轮侧偏力;a、b分别为前后轴到汽车质心的距离;δ为前轮转角。
当汽车前轮δ较小时,式(1)可写为
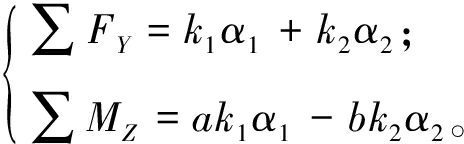
(2)
其中,前后轮侧偏角可表示为
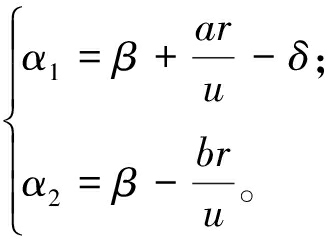
(3)
式中:k1、k2为前后轮轮胎侧偏刚度;r为横摆角速度;β为质心侧偏角;u为汽车沿x轴方向的速度。
因此,二自由度汽车侧向及横摆运动的微分方程表示为
(4)
式中:m为汽车质量;v为汽车侧向速度;IZ为汽车绕z轴的转动惯量。
当汽车稳态转向时,横摆角速度为定值,此时![]() 代入式(4)得
代入式(4)得
(5)
本文将横摆角速度与方向盘转角的比值视为横摆角速度增益,故由式(5)可得横摆角速度增益为

(6)
式中:L为汽车前后轴距离,L=a+b。
1.2 横摆角速度增益影响因素分析
根据1.1节中的式(6),汽车进入稳态行驶时,横摆角速度增益与整车质量、轴距、车速和前轮转角等参数相关。考虑到整车质量和前后轴距离为固有车身参数,在行驶过程中可视为恒定值,故稳态行驶时影响横摆角速度增益的可变因素为车速和前轮转角。
对前轮转角进一步探究,在汽车进入稳态转向的情况下,质心侧偏角β、横摆角速度r和车速u均为常数,根据式(3),此时前轮转角主要受前轮侧偏角α1的制约。结合车辆操纵动力学及轮胎的侧偏力特性曲线(图2)进行分析[13],在轮胎未侧滑之前,为提供稳态转向所需的侧偏力,轮胎在低附着系数路面产生的侧偏角大于高附着系数路面。以附着系数分别为1.0和0.8时为例,轮胎侧偏力为2 900 N对应下的轮胎侧偏角分别为-3.5°和-5.0°。因此,路面附着系数的不同会对轮胎侧偏角产生影响,从而改变前轮转角的取值。
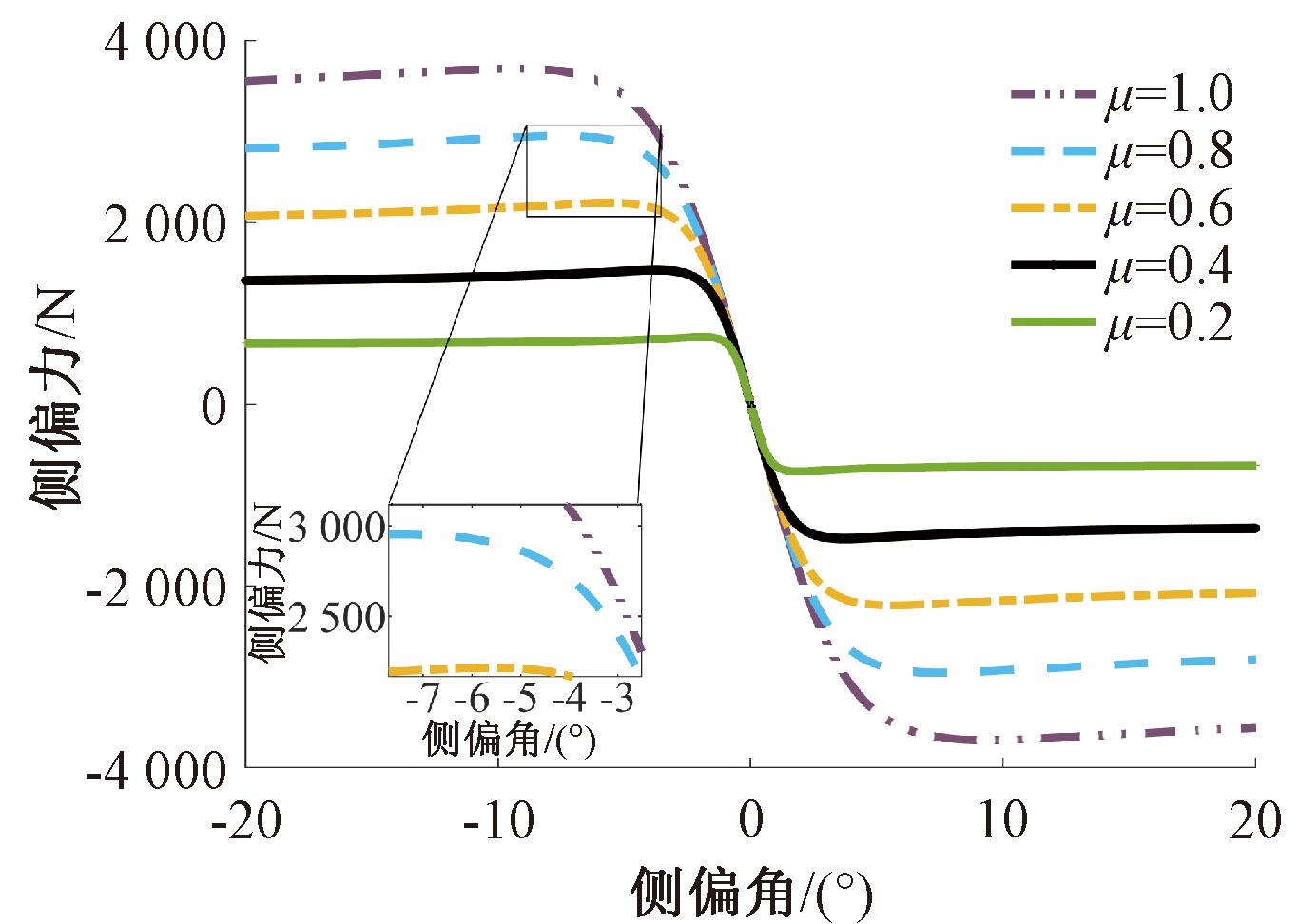
图2 轮胎侧偏力特性曲线
Figure 2 Tire lateral force characteristic curve
通过上述分析,本文选择车速和路面附着系数作为影响横摆角速度增益的因素并进行研究。为得到横摆角速度增益与车速及附着系数之间的关系,基于CarSim实车仿真模块,选取C级轿车,在转向盘转角阶跃工况下进行稳态仿真试验。转向盘转角设为40°,车速区间设为10~150 km/h。附着系数区间设为0.20~0.85,该区间涵盖了从冰雪到干沥青等各种路面类型,仿真结果如图3所示。
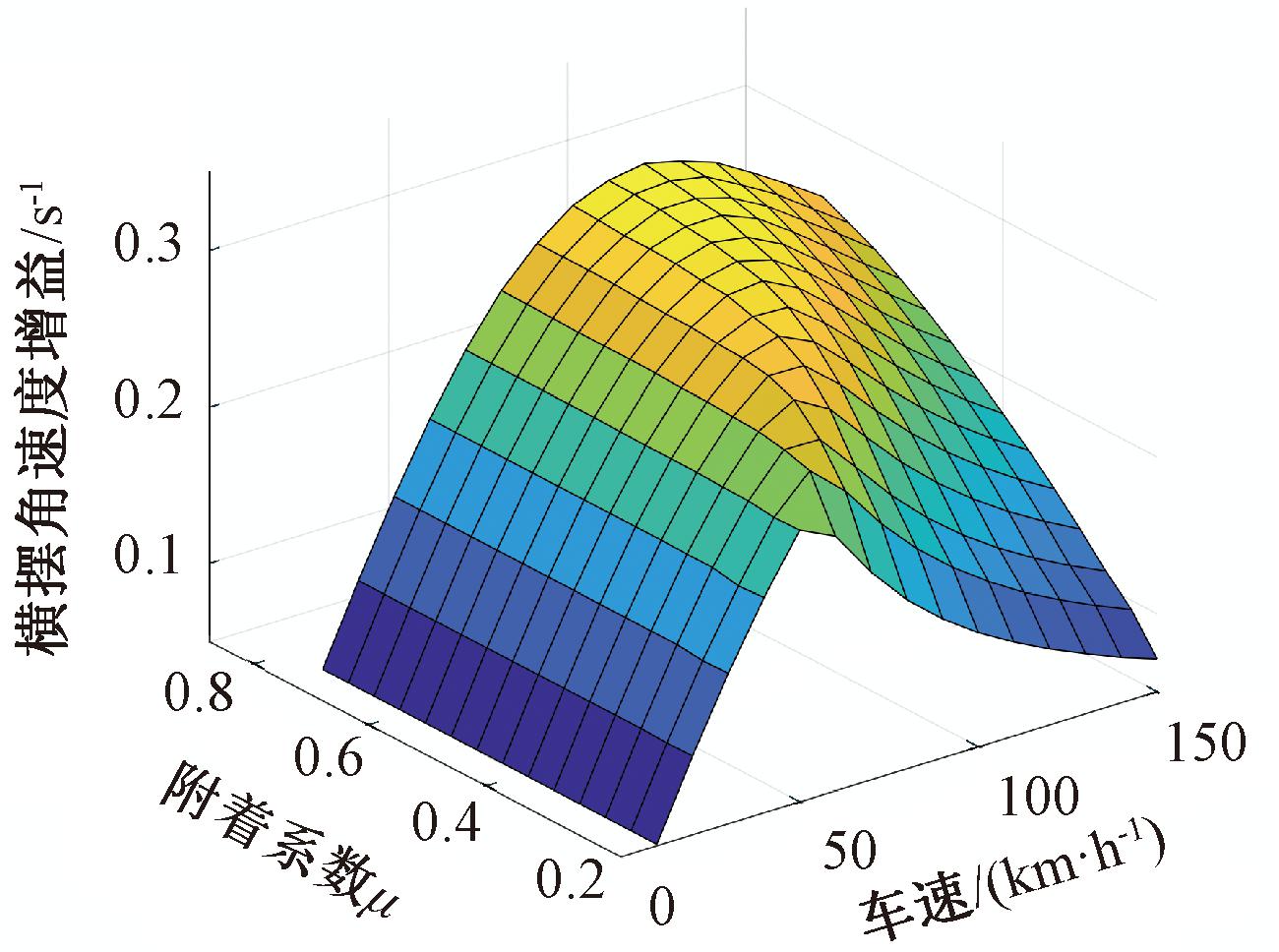
图3 不同工况下横摆角速度增益
Figure 3 Yaw rate gain with different conditions
由图3可知,车速在60 km/h以下时,横摆角速度增益的大小主要与车速有关,路面附着系数对其影响较小,当车速在60 km/h以上时,两者对横摆角速度增益均有影响。在同一附着系数下,随着车速增大,横摆角速度增益出现峰值,随后开始下降,而伴随着附着系数的增大,横摆角速度增益到达峰值所对应的车速也在不断提高,并且后续下降趋势也在逐渐放缓。
2 变横摆角速度增益获取
2.1 数据预处理
1.2节仿真结果表明,横摆角速度增益会随着车速及附着系数变化而改变,但该仿真试验获取的数据并不能直接作为稳态变传动比特性设计依据,根据文献[10]可知,横摆角速度增益的取值范围为0.22~0.38 s-1,本文在该范围内取值,从减轻驾驶员转向操纵负担角度考虑,最终确定横摆角速度增益的取值区间为[0.22,0.32]。
为保留原有横摆角速度增益随车速及路面附着系数变化的趋势,考虑到数据比较集中且均匀分布,能够保障映射之后的数据密度均匀性,因此选择Min-Max归一化方法预处理数据[14]。通过式(7)将1.2节横摆角速度增益数据映射到[0.22,0.32]。经预处理后的横摆角速度增益如图4所示。
(7)
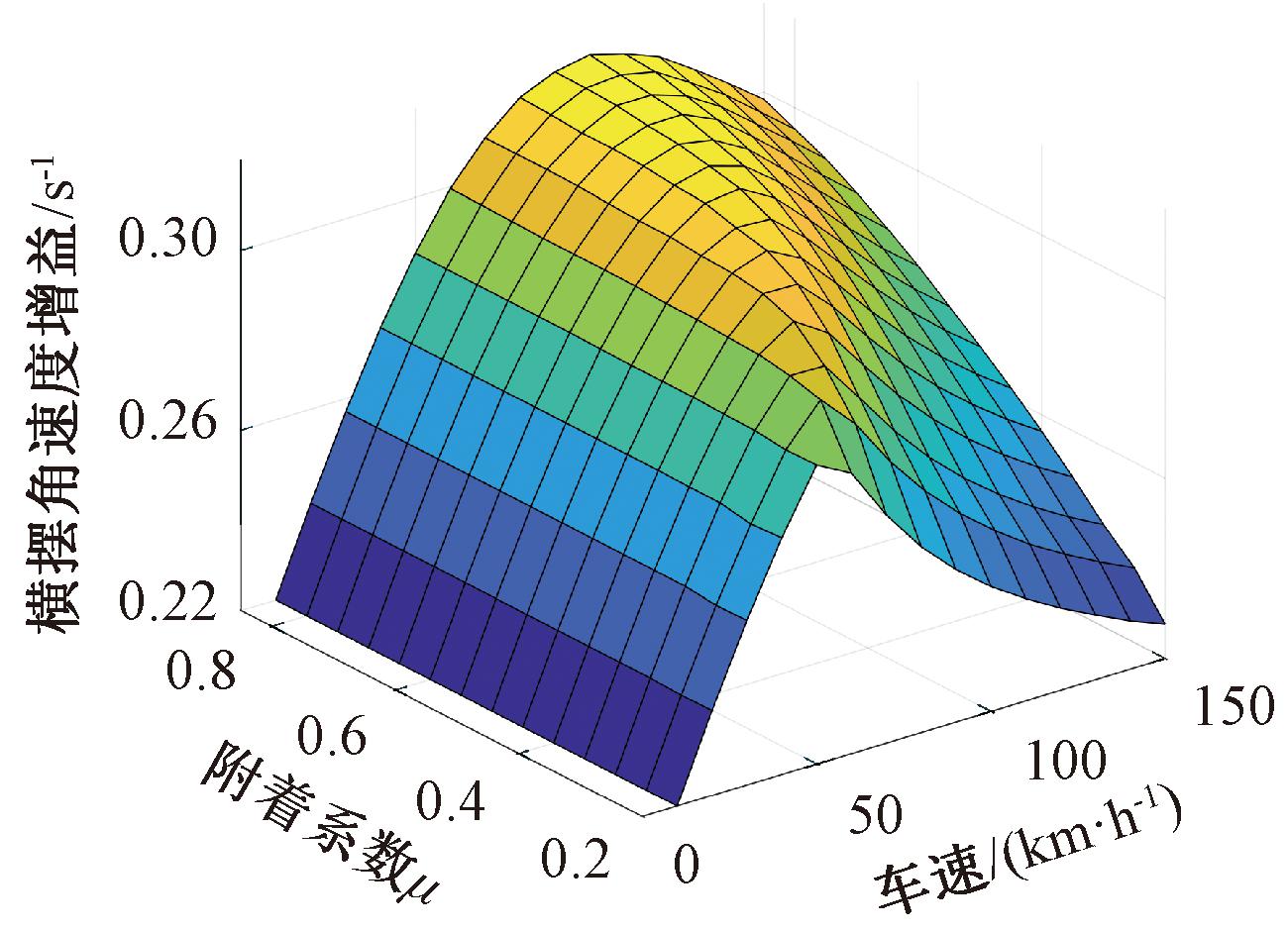
图4 预处理后横摆角速度增益
Figure 4 Yaw rate gain after preprocessing
式中:x表示拟归一化数据;xnew表示x归一化后的数据;xmin和xmax分别为数据中最小值和最大值。
对比图4和图3可知,预处理后的横摆角速度增益变化趋势与原始数据保持一致,取值也保持在选定范围内,为下一步利用神经网络动态获取变横摆角速度增益提供了合理的数据集。
2.2 变横摆角速度增益动态获取
2.1节横摆角速度增益是通过车速和附着系数在仿真时作为离散数据输入得到的,为获得更多可靠的结果,设计了蛇算法优化的BP神经网络(SO-BP),用来动态获取更多附着系数及车速下对应的横摆角速度增益。
传统BP神经网络拟合非线性函数时会产生收敛速度慢、精度低等问题。为解决该问题,引入SO,通过模拟蛇群的觅食及繁殖行为,进而快速高效地得到全局最优解[15]。该算法分为两个阶段,当食物不充分时,蛇群会在任意随机位置探索搜寻食物(全局探索阶段)。当食物充分但温度过高时,蛇群仅会在食物周围探索(局部搜索阶段)。若食物充分且区域寒冷的情况下,蛇群会进入战斗或交配模式。战斗模式下每条蛇都会为获取最好的异性而战斗;交配模式下雌蛇有50%的概率孵化出新的个体,新的个体会与原种群中适应度最差(距离食物位置最远)的个体进行替换。利用SO寻找BP神经网络全局最优的权值及阈值,减少了取值的随机性,避免了传统BP神经网络的缺陷。SO-BP基本流程如图5所示。
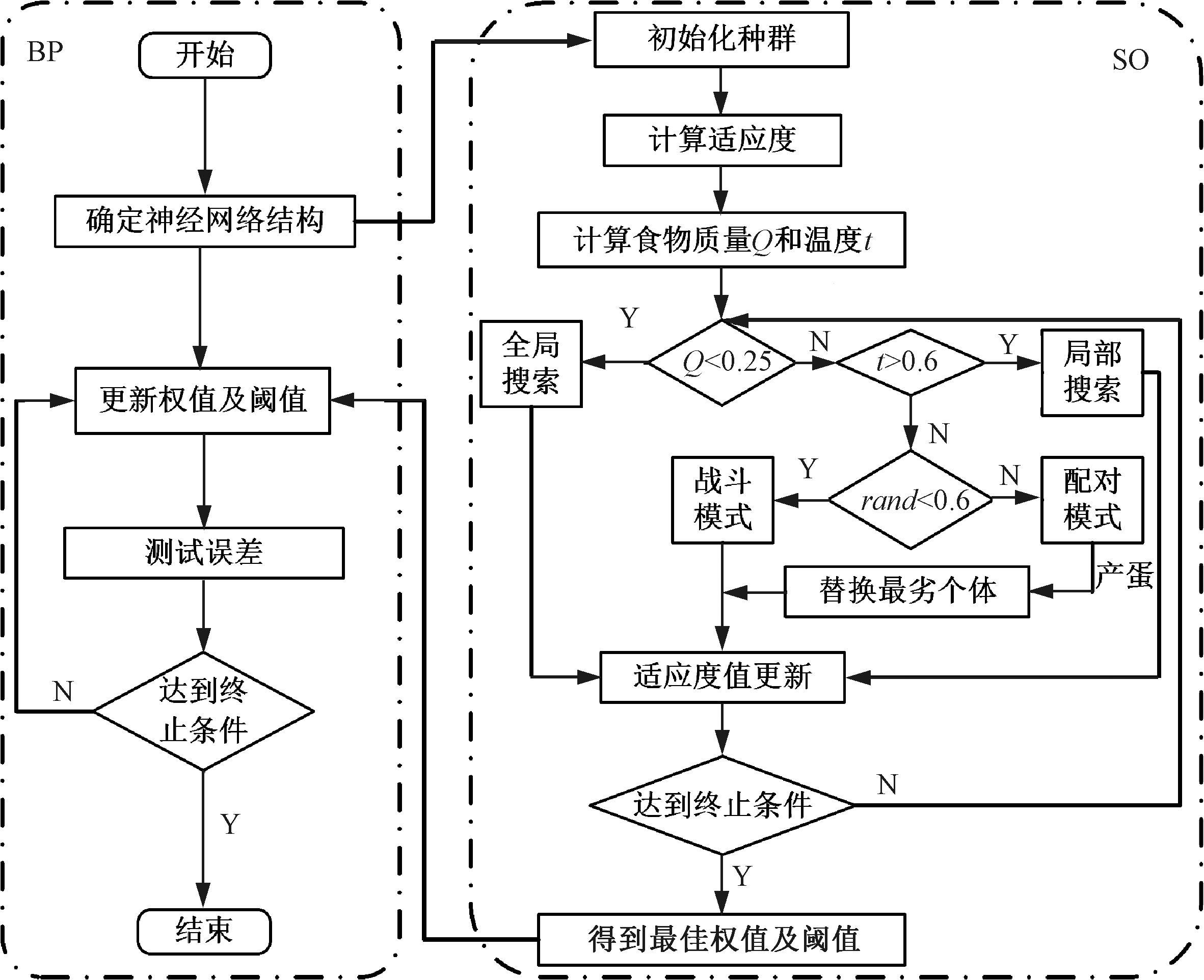
图5 SO-BP神经网络流程
Figure 5 SO-BP neural network process
本文中将SO中种群数目N设为60,最大迭代次数T设为100,当前迭代次数设为i,食物阈值Qm设为0.25,温度阈值tm设为0.6。在神经网络中,将车速及路面附着系数这两个指标作为输入,以2.1节预处理后的同一车型下横摆角速度增益作为输出,构建SO-BP神经网络训练数据集。
SO-BP神经网络数据集包含14种附着系数路面和15种车速工况,同一车型、不同附着系数及不同车速工况下对应的横摆角速度增益共计210种。在210组样本中,将其中90%作为训练样本(共计189组),10%作为测试样本(共计21组),通过训练样本对SO-BP神经网络进行训练,测试样本用来验证SO-BP神经网络的预测效果,神经网络预测值与样本实际值对比如图6所示。
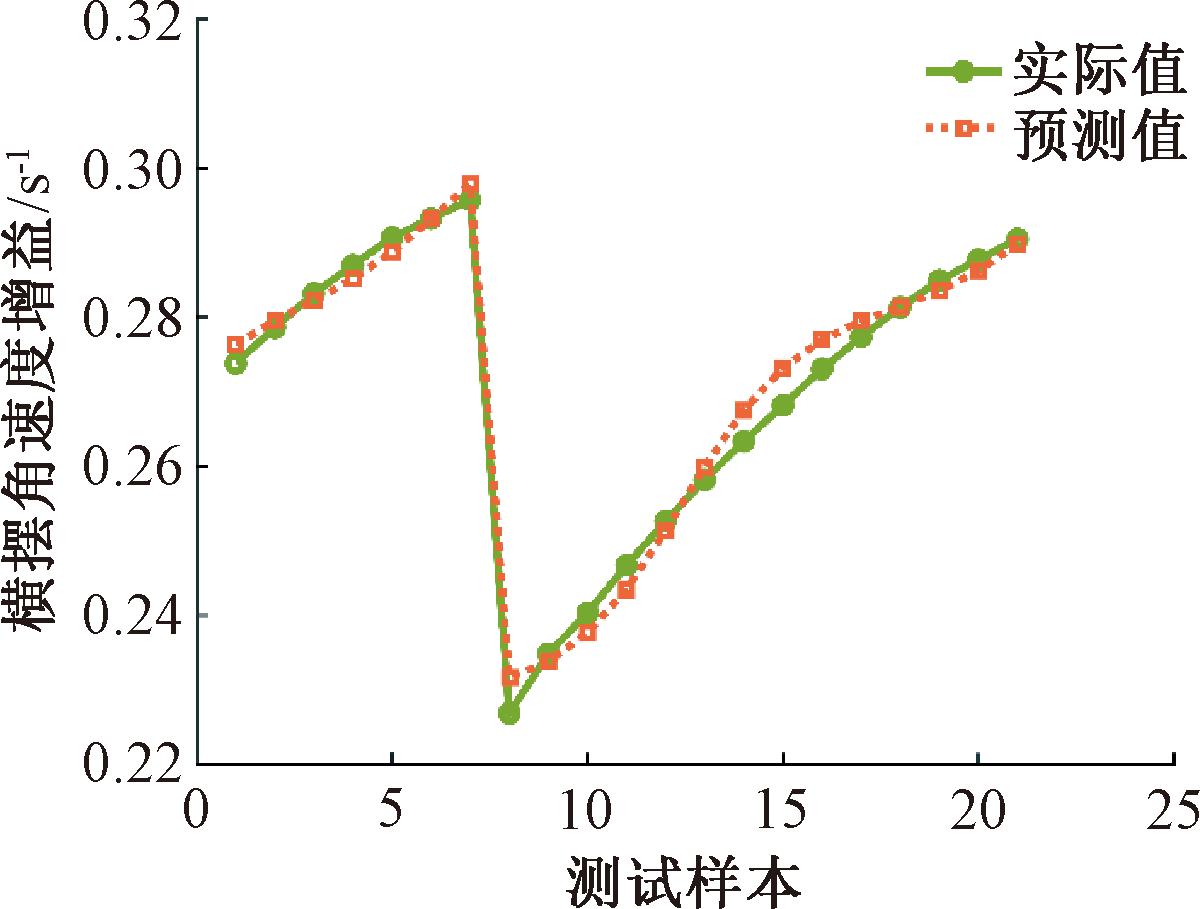
图6 神经网络预测值与样本实际值结果对比
Figure 6 Result comparison between neural network predicted values and actual sample values
从图6中可以看出,SO-BP神经网络的预测结果与实际结果误差极小,经计算最大误差为2.1%、均方误差MSE为0.000 1、平均绝对误差MAE为0.054 1。上述结果表明,SO-BP神经网络预测效果良好,能够动态获取不同车速及不同附着系数下的横摆角速度增益。
3 变增益传动比设计
3.1 变增益传动比设计方法
本文定义汽车转向盘转角δs与前轮转角δ之比为汽车转向传动比[9]:
(8)
横摆角速度增益是评价转向系统好坏的重要指标,侧向加速度增益可以较好地反映转弯时的车辆状态[16]。因此,本文选取这两种增益作为变增益传动比的设计依据。
3.1.1 变横摆角速度增益传动比
为提高汽车在低附着系数路面上的操纵稳定性,应用2.2节经SO-BP动态获取的变横摆角速度增益代替传统固定横摆角速度增益设计传动比,由于
(9)
(10)
结合式(8),则有
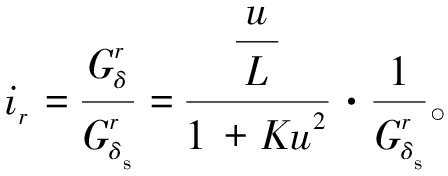
(11)
式中:![]() 为从前轮转角到汽车横摆角的横摆角速度增益。
为从前轮转角到汽车横摆角的横摆角速度增益。
3.1.2 侧向加速度增益传动比
相关研究表明,基于侧向加速度增益不变设计的传动比,在角阶跃工况下到达稳态经历时间最短[17]。本文将从转向盘转角到汽车稳态响应的侧向加速度增益设为定值,则
(12)
式中:ay为汽车侧向加速度。
基于1.1节二自由度模型,从前轮转角到汽车响应的侧向加速度增益为
(13)
结合式(8)、(12)、(13),侧向加速度增益传动比可表示为
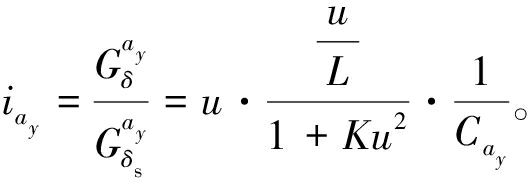
(14)
3.2 变增益传动比确定
在SBW系统中,驾驶员转动转向盘后,控制器会依据所设计的传动比方案来确定对应的目标前轮转角,然后向转向电机发出控制信号,通过转向电机驱动齿轮齿条进行相对运动,进而实现该目标的前轮转角,使车辆沿驾驶员期望轨迹行驶。
简化后的转向盘总成模型为
(15)
式中:Ts为转向盘转矩;Js为转向盘总成等效转动惯量;Bs为转向盘总成等效阻尼系数;km1为转向轴等效扭转刚度;Tf为转向盘总成等效摩擦力矩。
考虑转向电机转动惯量和阻尼,建立转向电机动力学模型为
(16)
式中:Tm为转向电机电磁转矩;Jm为转向电机转动惯量;Bm为转向电机阻尼系数;θm为转向电机转角;km2为转向执行总成等效扭转刚度;gm为转向电机减速器减速比;xr为齿条位移;rp为小齿轮分度圆半径;Tfm为转向电机摩擦力矩。
齿轮齿条转向器动力学模型为
(17)
式中:mr为齿轮齿条质量;Br为齿轮齿条阻尼系数;Tfl、Tfr为左右前轮主销回正力矩;lfl、lfr为左右前轮转向摇臂长。
由3.1节可知,侧向加速度增益传动比需要确定增益常量Cay,在此使用MATLAB遗传算法工具箱,将操纵稳定性综合评价指标作为优化目标函数[18],用来确定增益常量最优值。根据式(15)、(16)和(17),在Simulink中建立SBW系统模型,然后将该转向模型与CarSim中内置的机械转向模块进行替换,搭建SBW整车模型,选定侧向加速度增益传动比方案,在车速为60 km/h的双移线工况下对Cay进行优化选取,迭代结束后Cay取5.25 m/s2,此时操纵稳定性评价指标值最小,故作为最优值代入式(14)确定侧向加速度增益传动比。
为满足汽车“低速轻便”及“高速稳定”的转向需求,定义0~30 km/h为低速段,120 km/h及以上为高速段,将该部分传动比设为定值,具体大小通过式(18)分别在车速为30、120 km/h的计算值来确定。30~120 km/h速度段的传动比曲线应保持较大的变化梯度以保证角位移平滑改变,故将3.1节中设计的两个传动比按一定比例综合获得传动比,即
i=c1ir+c2iay。
(18)
经验证,随着车速提升,3.1节可变横摆角速度增益传动比曲线呈现先增大后减小的趋势,而侧向加速度增益传动比曲线随车速提升则不断变大[19]。根据传动比在30~120 km/h速度段的需求,通过仿真试验优选确定c1、c2的值分别为0.65和0.35。最终得到的变增益传动比为
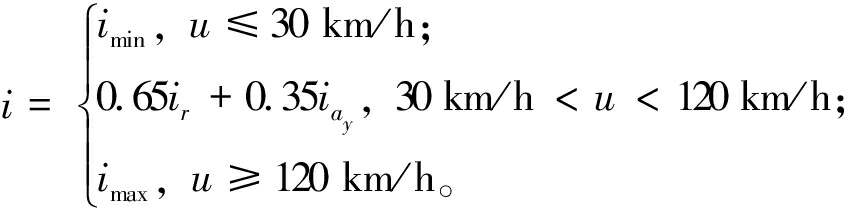
(19)
式中:imin为低速段传动比;imax为高速段传动比。
4 仿真验证
为验证上述工作的合理性及正确性,选择传统定横摆角速度增益传动比(增益值设为0.33 s-1)和本文设计的变增益传动比进行对比,通过CarSim和Simulink联合仿真平台,分别在双移线、角阶跃、稳态回转和转向回正工况下对整车性能进行分析,仿真车辆的部分参数如表1所示,车辆的轮胎型号为215/55 R17。
表1 车辆参数
Table 1 Vehicle parameters

参数取值整车质量m/kg1 341质心高度hg/m0.540质心至前轴距离a/m1.015质心至后轴距离b/m1.895轴距L/m2.910整车绕z轴转动惯量IZ/(kg·m2)1 537前后轮侧偏刚度kf、kr/(N·rad-1)-105 014
4.1 双移线工况
选取CarSim中内置的双移线工况对变增益传动比的合理性进行验证。参考正常行驶路面,将路面附着系数设定为0.8,设定车速为60 km/h,仿真时间为12 s,采样时间为0.01 s,仿真结果如图7和图8所示。
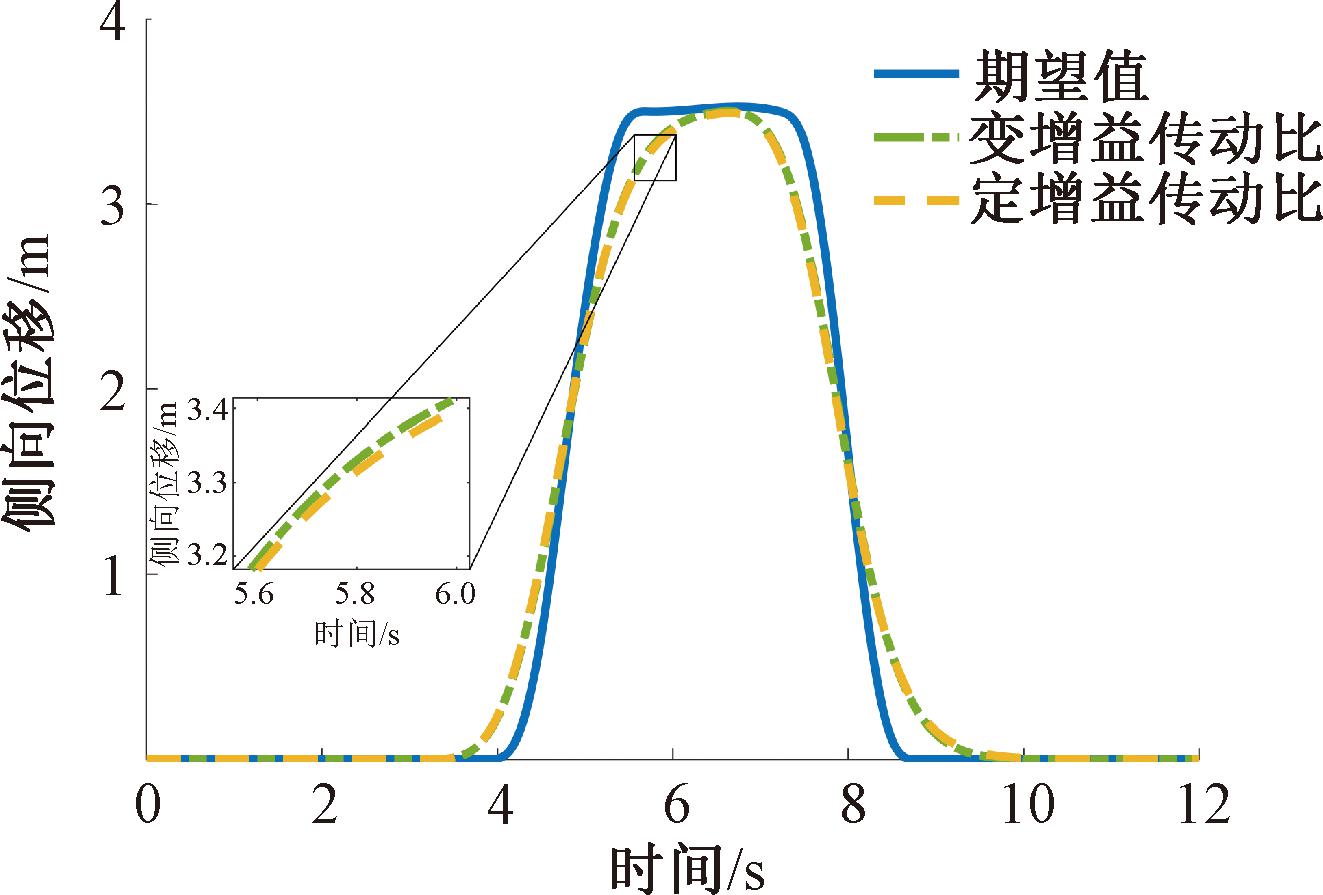
图7 横向位移对比
Figure 7 Comparison of lateral displacement
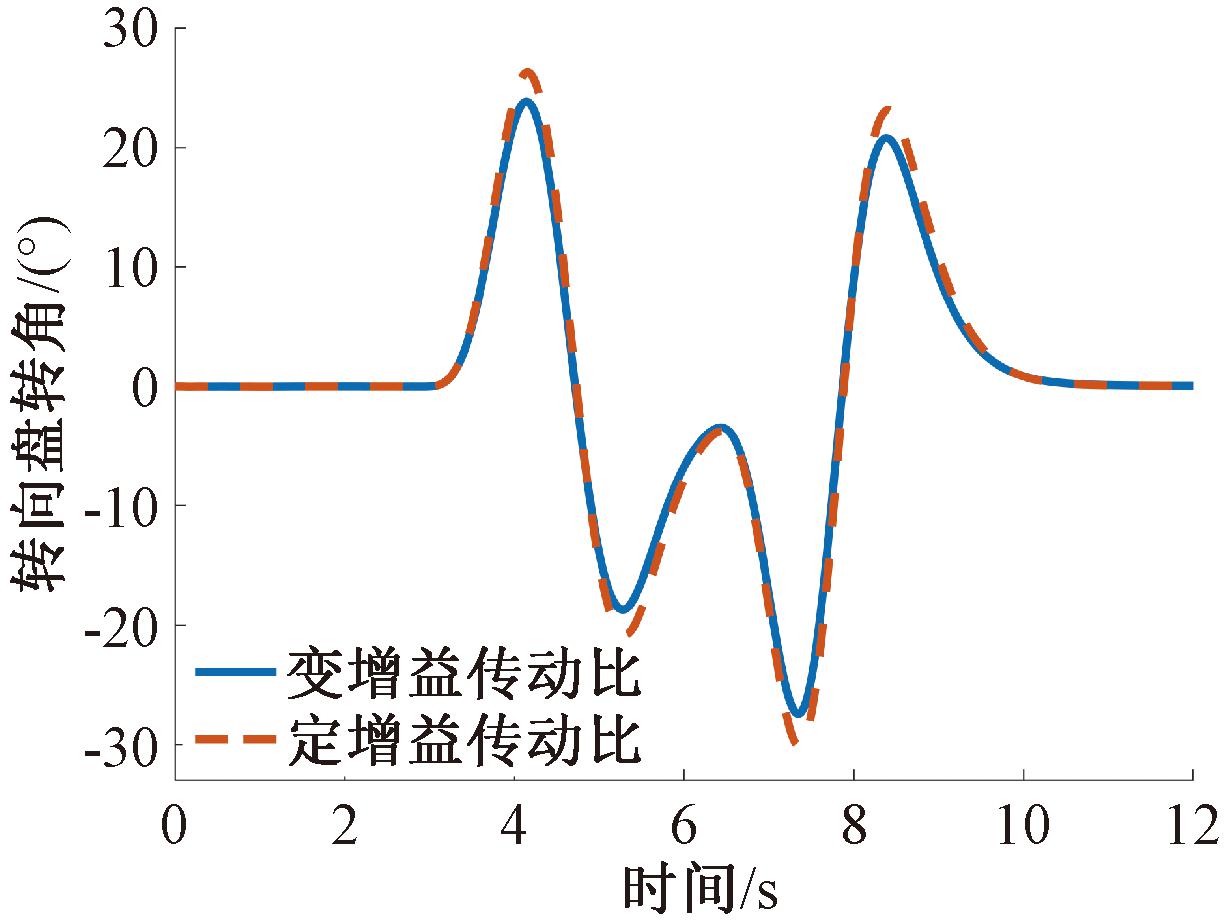
图8 转向盘转角对比
Figure 8 Comparison of steering wheel angle
从图7可以看出,采用变增益传动比车辆能够很好地跟踪期望路径,行驶轨迹与定增益传功比车辆误差保持在3%以内,表明变增益传动比转向特性良好;图8显示,相对定增益传动比,采用变增益传动比车辆转向盘转角有所下降,经计算,转角峰值降低了9.1%,说明变增益传动比在保证路径跟踪精度的同时,也降低了驾驶员的操纵负担。
4.2 角阶跃工况
为验证所设计传动比在低附着系数路面上的表现情况,将路面附着系数设为0.2,在Simulink中设定方向盘转角为30°阶跃输入,车速设定为中低车速(40 km/h)和中高车速(90 km/h)两种情况,仿真时间为10 s,采样时间为0.01 s,仿真结果如图9和图10所示。对比发现,相对于定横摆角速度增益传动比,使用变增益传动比车辆进入稳态响应所需时间降低,并且横摆角速度峰值、稳态值均有所下降。在40 km/h工况下,峰值降低了24.6%,稳态值降低了22.3%;在90 km/h工况下,峰值降低了10.8%,稳态值降低了6.6%。这表明在低附着系数路面下,采用变增益传动比转向系统汽车发生危险的可能性下降,有效提高了汽车在低附着系数路面上的操纵性。
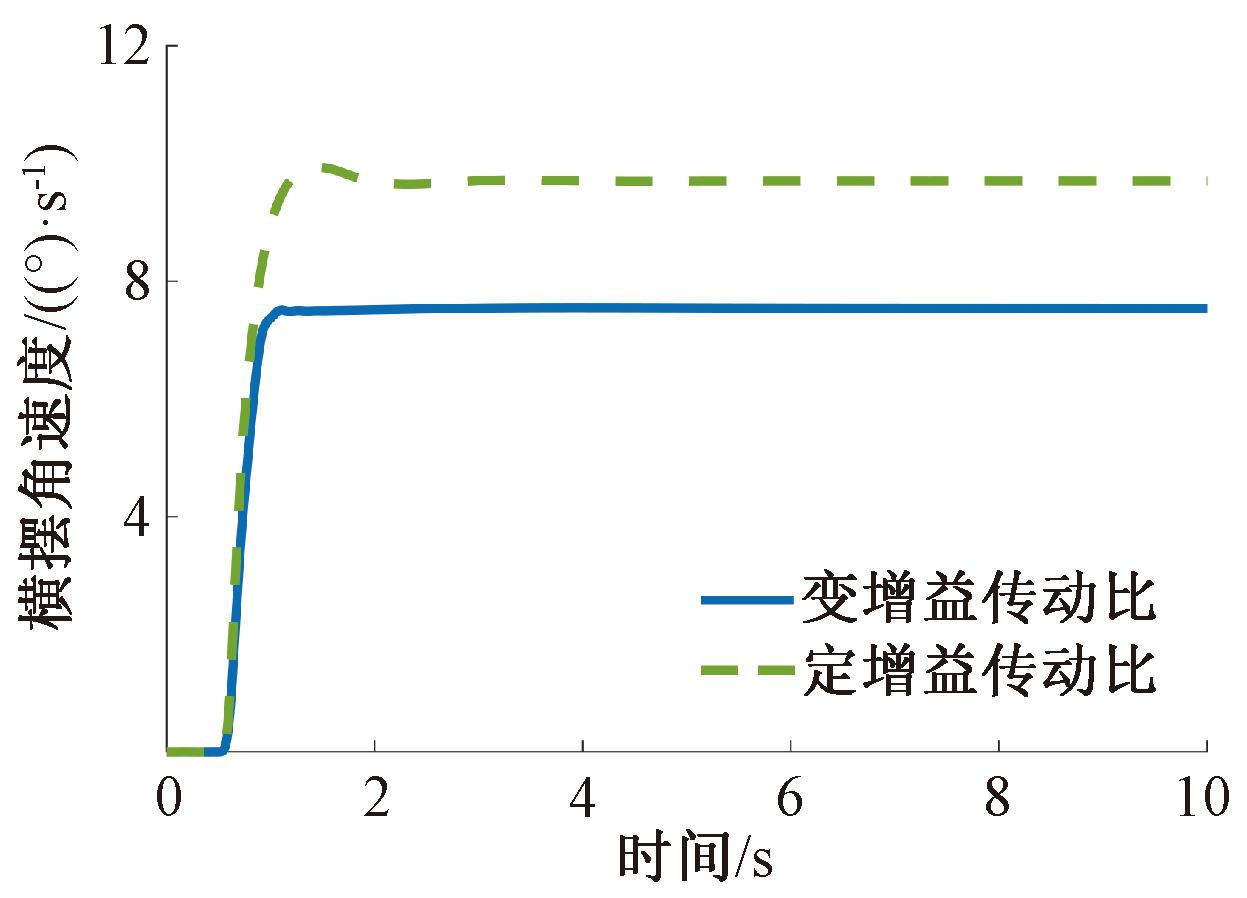
图9 40 km/h工况横摆角速度响应
Figure 9 Yaw rate response for 40 km/h condition
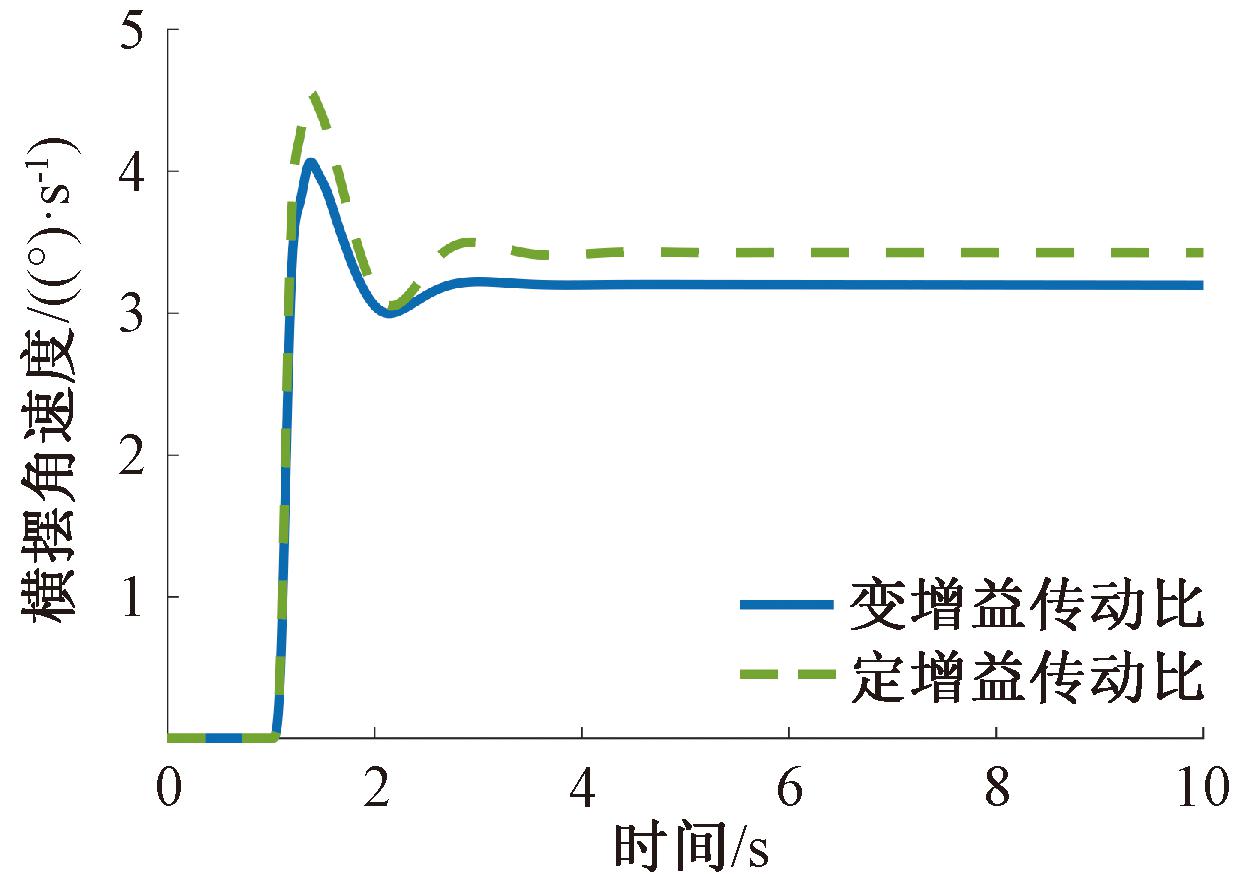
图10 90 km/h工况横摆角速度响应
Figure 10 Yaw rate response for 90 km/h condition
4.3 稳态回转工况
在稳态回转工况下,将采用变增益传动比车辆的车速从40 km/h均匀加速到80 km/h,转向盘转角设为固定值40°,路面附着系数设为0.4,仿真时间为20 s,采样时间为0.01 s,仿真结果如图11所示。由图11可以看出,由于在该速度区间内本文设计传动比是将变横摆角速度增益与侧向加速度增益按比例共同控制,因此在方向盘转角不发生变化时,横摆角速度会随车速增加而适当减小,而且侧向加速度变化趋势变缓,减轻了驾驶员对汽车特性变化的操作补偿,提升了汽车在低附着系数路面上的转向特性,更有利于行车安全。
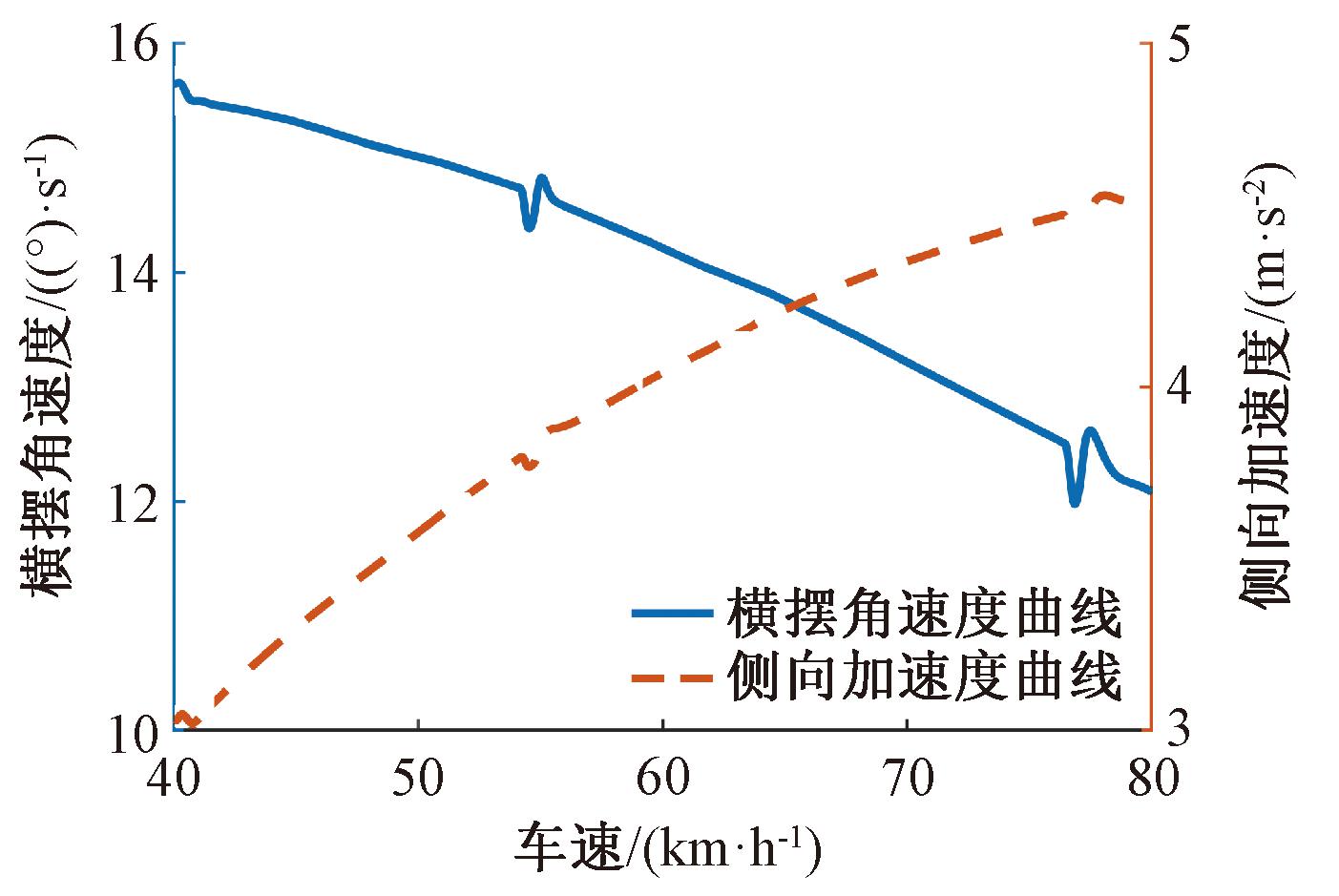
图11 车辆运行参数响应
Figure 11 Vehicle operating parameter response
4.4 转向回正工况
根据GB/T 6323—2014规定,选取低速和高速两种转向回正工况来表征汽车从曲线恢复到直线行驶的过渡过程。在低速回正工况下,车辆沿半径为15 m的圆周进行稳态行驶,调整车速使侧向加速度为(4.0±0.2) m/s2,固定转向盘转角,稳定车速并开始记录,待3 s后快速松开转向盘,记录松手后至少4 s的汽车运动过程,记录时间内加速踏板位置保持不变;在高速工况下,车速设为110 km/h,转动转向盘使侧向加速度达到(2.0±0.2) m/s2,其余设定保持不变。选择稳定时间ts和残留横摆角速度Δr作为转向回正性能评价指标,仿真时间为10 s,采样时间为0.01 s,仿真试验结果如图12、图13、表2所示。
表2 转向回正试验结果
Table 2 Result of steering return

工况时间/s角速度/((°)·s-1)低速工况0.9500.714高速工况1.3300.317
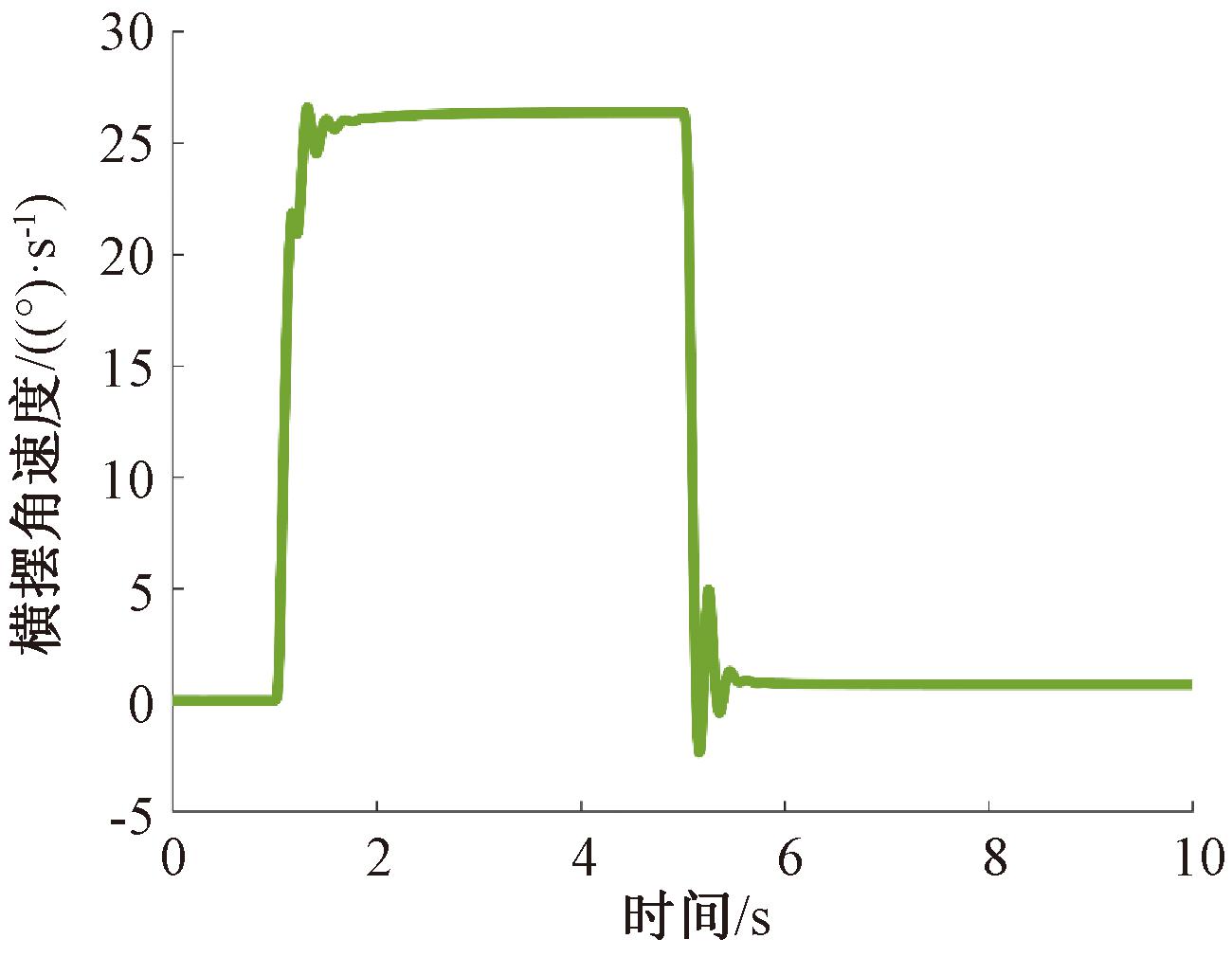
图12 低速工况下横摆角速度响应曲线
Figure 12 Yaw rate response curve under low-speed operating conditions
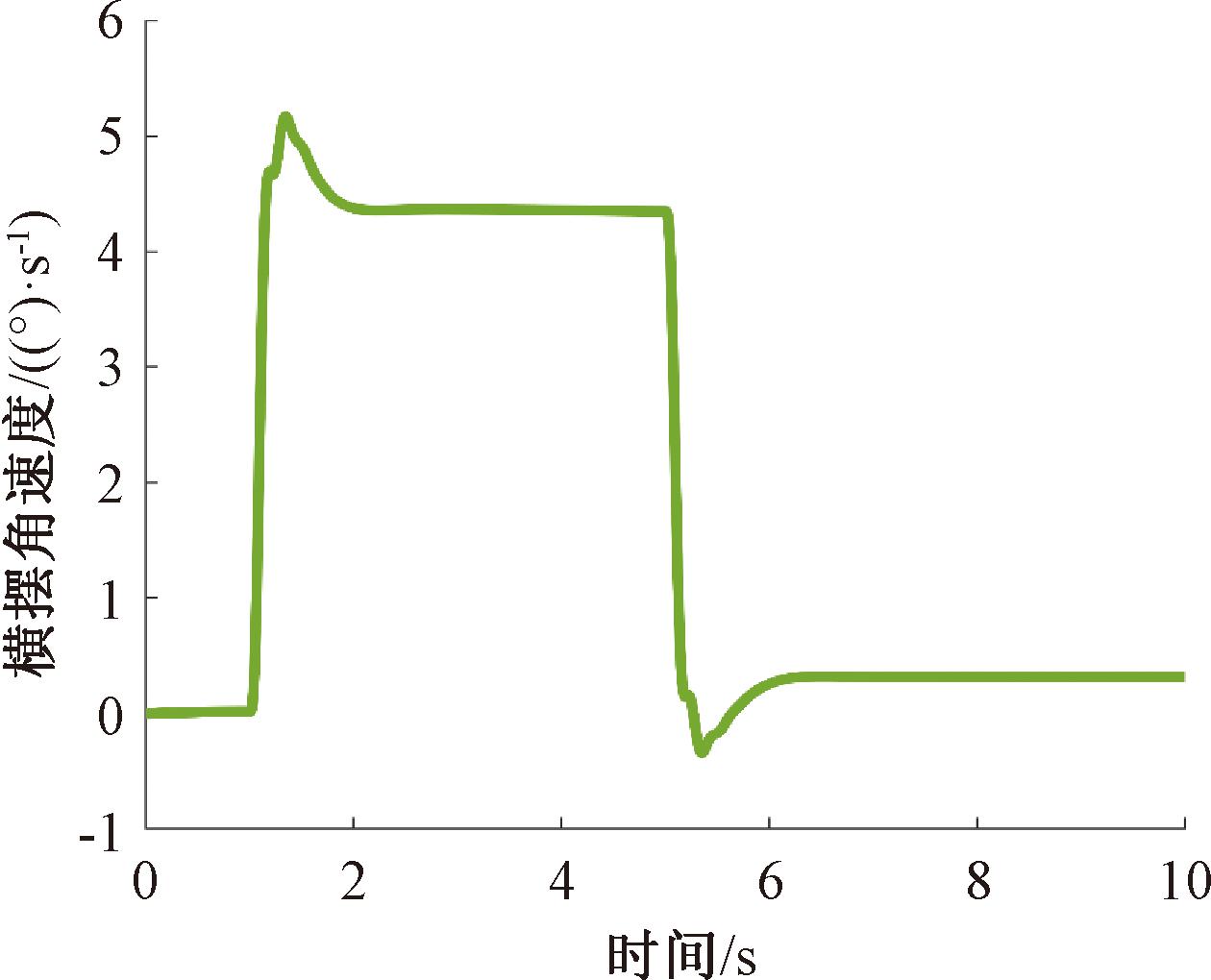
图13 高速工况下横摆角速度响应曲线
Figure 13 Yaw rate response curve under high-speed operating conditions
由试验结果可以看出,变增益传动比车辆在低速转向回正工况下的残留横摆角速度为0.714 (°)/s,横摆角速度到达稳定的时间为0.95 s,高速转向回正工况下的残留横摆角速度为0.317 (°)/s,高速工况稳定时间为1.330 s。两种工况下的残留横摆角速度均小于国标要求的6 (°)/s,到达稳态所需时间较短,表明本文所设计的变增益传动比车辆转向回正性能良好。
5 结论
(1)本文提出一种动态获取横摆角速度增益的方法,由于考虑了路面附着系数及车速因素,通过该方法获取的横摆角速度增益不仅能够随附着系数和车速的改变而自适应调整,而且兼顾了转向特性对驾驶员的影响,保障了取值合理性。
(2)采用可变横摆角速度增益与侧向加速度增益结合的方法设计SBW变增益传动比,搭建了CarSim与Simulink联合仿真平台,在不同工况下对变增益传动比的有效性进行了仿真验证。
(3)仿真试验结果表明:正常附着系数路面,采用变增益传动比的车辆能够保障路径跟踪精度,转向轻便性也得到提高,低附着系数路面,相比传统转向传动比,采用变增益传动比车辆在不同车速下的横摆角速度峰值和稳态值均降低,到达稳态所需的时间下降,提高了车辆在低附着系数路面上的行驶安全性和操纵性,说明本文设计方法有效可行。
[1] MORTAZAVIZADEH S A, GHADERI A, EBRAHIMI M, et al. Recent developments in the vehicle steer-by-wire system[J]. IEEE Transactions on Transportation Electrification, 2020, 6(3): 1226-1235.
[2] 张三川, 叶建明, 师艳娟. 基于毫米波雷达的汽车前防撞预警系统设计[J]. 郑州大学学报(工学版), 2020, 41(6): 13-18.ZHANG S C, YE J M, SHI Y J. Design of vehicle forward collision warning system based on millimeter wave radar[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(6): 13-18.
[3] 陈哲明, 钟诚, 李环宇, 等. 粒子群优化线控转向变角传动比模糊控制器设计[J]. 重庆理工大学学报(自然科学), 2022, 36(12): 41-49.CHEN Z M, ZHONG C, LI H Y, et al. Design of the fuzzy controller for variable angle transmission ratio of steer-by-wire system through particle swarm optimization[J]. Journal of Chongqing University of Technology (Natural Science), 2022, 36(12): 41-49.
[4] 徐飞翔, 周晨, 王军, 等. 基于变传动比的全轮线控转向车辆可拓H∞控制方法研究[J]. 中国公路学报, 2021, 34(9): 133-145.XU F X, ZHOU C, WANG J, et al. Extension H∞ control method for all-wheel steer-by-wire vehicles based on variable transmission ratio[J]. China Journal of Highway and Transport, 2021, 34(9): 133-145.
[5] 程准, 鲁植雄, 龚佳慧, 等. 转向系统传递函数的研究及理想传动比获取[J]. 浙江大学学报(工学版), 2016, 50(7): 1276-1283.CHENG Z, LU Z X, GONG J H, et al. Transfer function of steering system and acquisition method of ideal steering ratio[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(7): 1276-1283.
[6] 赵林峰, 陈无畏, 王俊, 等. 基于可拓滑模线控转向控制策略研究[J]. 机械工程学报, 2019, 55(2): 126-134.ZHAO L F, CHEN W W, WANG J, et al. Research on steering-by-wire control strategy based on Extension sliding mode control[J]. Journal of Mechanical Engineering, 2019, 55(2): 126-134.
[7] 冯晓志, 石沛林, 曹凡, 等. 基于CarSim的线控转向汽车理想传动比的设计研究[J]. 广西大学学报(自然科学版), 2018, 43(6): 2122-2132.FENG X Z, SHI P L, CAO F, et al. Research on ideal transmission ratio design of Steer-By-Wire car based on CarSim[J]. Journal of Guangxi University (Natural Science Edition), 2018, 43(6): 2122-2132.
[8] LIU Z Y, XU X, XIE J, et al. Variable transmission ratio design of a steer-by-wire system for intelligent vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2022, 236(16): 9341-9353.
[9] 金智林, 梁为何, 赵万忠. 汽车多增益融合线控转向传动比及防侧翻控制[J]. 机械工程学报, 2020, 56(10): 172-180.JIN Z L, LIANG W H, ZHAO W Z. Multi-gains ratio of steer-by-wire system and anti-rollover control for vehicle[J]. Journal of Mechanical Engineering, 2020, 56(10): 172-180.
[10] 周兵, 范璐, 吕绪宁. 主动前轮转向系统改进型变传动比曲线设计[J]. 中国机械工程, 2014, 25(20): 2813-2818.ZHOU B, FAN L, LYU X N. Design of modified variable steering ratio curve for active front steering system[J]. China Mechanical Engineering, 2014, 25(20): 2813-2818.
[11] 赵万忠, 张寒, 邹松春, 等. 线控转向系统控制技术综述[J]. 汽车安全与节能学报, 2021, 12(1): 18-34.ZHAO W Z, ZHANG H, ZOU S C, et al. Overview of vehicle steer-by-wire system control technologies[J]. Journal of Automotive Safety and Energy, 2021, 12(1): 18-34.
[12] 李学鋆, 章菊. 考虑路面附着系数和车速的AFS可变传动比设计[J]. 汽车安全与节能学报, 2020, 11(3): 329-336.LI X Y, ZHANG J. Design of AFS variable steering ratio considering road adhesion coefficient and vehicle speed[J]. Journal of Automotive Safety and Energy, 2020, 11(3): 329-336.
[13] 商高高, 张杰. 基于非线性二自由度模型的线控转向系统变角传动比设计[J]. 重庆理工大学学报(自然科学), 2018, 32(9): 6-13.SHANG G G, ZHANG J. Design of variable angle steering ratio for steer by wire system based on nonlinear vehicle model of two degrees of freedom[J]. Journal of Chongqing University of Technology (Natural Science), 2018, 32(9): 6-13.
[14] 杨寒雨, 赵晓永, 王磊. 数据归一化方法综述[J]. 计算机工程与应用, 2023, 59(3): 13-22.YANG H Y, ZHAO X Y, WANG L. Review of data normalization methods[J]. Computer Engineering and Applications, 2023, 59(3): 13-22.
[15] HASHIM F A, HUSSIEN A G. Snake Optimizer: a novel meta-heuristic optimization algorithm[J]. Knowledge-Based Systems, 2022, 242: 108320.
[16] 李文琪, 吴晓东. 线控转向车辆可变角传动比特性的研究[J]. 机电工程, 2019, 36(4): 422-427.LI W Q, WU X D. Variable steering ratio characteristics for steer-by-wire vehicle[J]. Journal of Mechanical &Electrical Engineering, 2019, 36(4): 422-427.
[17] 李亮, 王翔宇, 程硕, 等. 汽车底盘线控与动力学域控制技术[J]. 汽车安全与节能学报, 2020, 11(2): 143-160.LI L, WANG X Y, CHENG S, et al. Technologies of control-by-wire and dynamic domain control for automotive chassis[J]. Journal of Automotive Safety and Energy, 2020, 11(2): 143-160.
[18] TIAN Y T, ZHAO Y B, SHI Y R, et al. The indirect shared steering control under double loop structure of driver and automation[J]. IEEE/CAA Journal of Automatica Sinica, 2020, 7(5): 1403-1416.
[19] ZHAO B, FAN X B, QI G X. Variable transmission ratio and active steering control for steer-by-wire steering[J]. International Journal of Vehicle Systems Modelling and Testing, 2022, 16(4): 290-312.