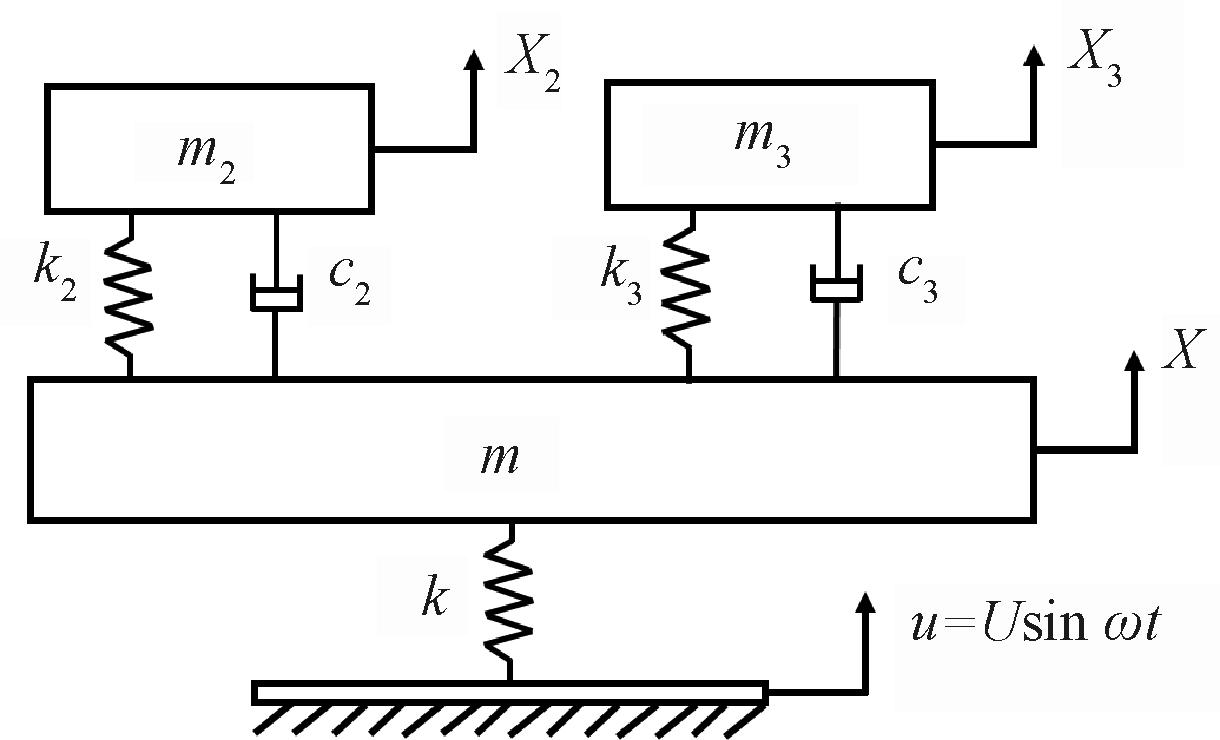
图1 有阻尼二重动力吸振器动力学模型
Figure 1 Dynamic model of double dynamic vibration absorber with damping
管路系统是用来输送液体、气体的系统,广泛应用于核电领域,其首尾部包含压缩机、泵等设备,在运行时会产生循环的吸、排效应,产生的间接性气液流动会导致许多管路振动问题,如结构变化、涡流、湍流情况等。此外,管路系统还会受到不规则外力作用,导致管路产生无规律的振动[1]。频繁的机械振动会对机械加工等生产活动造成严重的影响,引起结构疲劳导致失效,甚至破坏管路,从而影响机械加工的质量和效率,并容易产生生产安全事故[2]。因此,对管路进行振动抑制是至关重要的。
当前,抑制机械振动的方法主要有两种:一是可以进行防振设备的开发;二是使用振动抑制方法最大化地降低振动带来的危害。其中,振动抑制的方法有消除振动、隔离振动、阻尼减振、吸收振动和修改结构[3]。动力吸振器因不需要改变现有结构,是抑制振动的有效方法之一[4]。其工作原理为在主系统上添加子系统,当受到外部激励频率与子系统固有频率一致时,振动能量就会转移到子系统上,并被子系统吸收耗散[5]。也可以理解为在共振系统上添加质量弹簧阻尼结构,这种添加的结构在系统共振时产生一个相反的力,从而减小主系统的振动。由于这种子系统结构简单,且能够抑制小范围频段内的设备振动,在工程实践中应用广泛。
动力吸振器是由质量块、弹簧和阻尼器组成的吸振装置[6-7]。一般情况下,当动力吸振器的吸振频率与振动系统的某一阶固有频率相近时,在这一阶固有频率附近,吸振效果非常明显[8]。许多学者从理论分析和工程应用角度进行了研究,通过改变质量、刚度、阻尼这3个参数,可以吸收不同频段的振动。如何获得最优的动力吸振器参数,是当下比较热门的研究。目前,学者通过改变质量比、刚度、阻尼、使用复合式动力吸振器、采用多重动力吸振器等一系列方法,拓宽动力吸振器抑制共振时的吸振频段[9]。
动力吸振器是一种经济实惠且维护简单的振动抑制装置,可以有效地减少管路在一定频段内的振动[10]。但是传统动力吸振器往往只是针对某一方向上特定频率进行吸振,吸振效率较低,无法满足工程宽频带、多向的吸振需求,且传统阻尼材料在高温下易老化。针对这一问题,本文设计了一种基于金属橡胶材料的二重多向动力吸振器,并采用环形结构,便于安装。通过动力学建模、定点理论以及最优同调,得到动力吸振器的最优设计公式,然后设计动力吸振器的结构,并通过改变动力吸振器的参数获得最优吸振性能,最后通过仿真与试验进行验证。
本文所设计的二重动力吸振器结构和小支管部分可简化为有阻尼三自由度系统,忽略主系统阻尼,构建系统的动力学模型,如图1所示。

图1 有阻尼二重动力吸振器动力学模型
Figure 1 Dynamic model of double dynamic vibration absorber with damping
图1中符号m、k分别表示主系统的质量与刚度,两个动力吸振器的质量、刚度、阻尼分别用m2、m3、k2、k3、c2、c3表示,主系统与两个动力吸振器的位移分别用X、X2、X3表示,主系统受到一个方向竖直向上的基础位移输入u,运动微分方程表示为
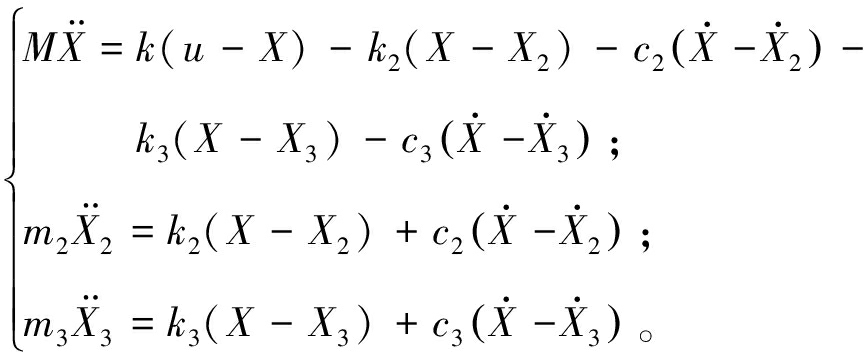
(1)
将与小支管相连设备引起的强制性位移表示为u=Uejωt,将主系统与两个动力吸振器位移变换为![]() 则小支管复数位移振幅大小为
则小支管复数位移振幅大小为![]() 可以由实部RN、RD与虚部IN、ID所构成的表达式表示:
可以由实部RN、RD与虚部IN、ID所构成的表达式表示:
(2)
主系统的位移动力放大系数为
(3)
其中,实部RN、RD与虚部IN、ID表达式分别为
(γ1γ2))·λ2+1;
(4)
IN=-(2/(γ1γ2))(ξ2/γ1+ξ1/γ2)λ3+
2(ξ1/γ1+ξ2/γ2)λ;
(5)
(1+μ2)+4(ξ1ξ2/(γ1γ2))(1+2μ2))·
(6)
ID=(2/(γ1γ2))((ξ2/γ1)(1+μ2)+(ξ1/γ2)·
(1+μ2))λ5-2((ξ2/γ1+ξ1/γ2)/(γ1γ2)+(ξ1/γ1+ξ2/γ2)(1+2μ2))λ3+2(ξ1/γ1+ξ2/γ2)λ。
(7)
式中:吸振器固有频率比![]() 主系统固有频率比
主系统固有频率比![]() 吸振器质量比μ1=m2/m,μ2=m3/m;吸振器阻尼比
吸振器质量比μ1=m2/m,μ2=m3/m;吸振器阻尼比![]()
根据式(3),研究不同阻尼比ξ1、ξ2和主系统的位移动力放大系数。设定动力吸振器固有频率比γ1= 0.98,γ2=1.10,质量比μ1=μ2=0.05,可以绘制出3种不同阻尼比情况下的主系统位移动力放大系数,如图2所示。
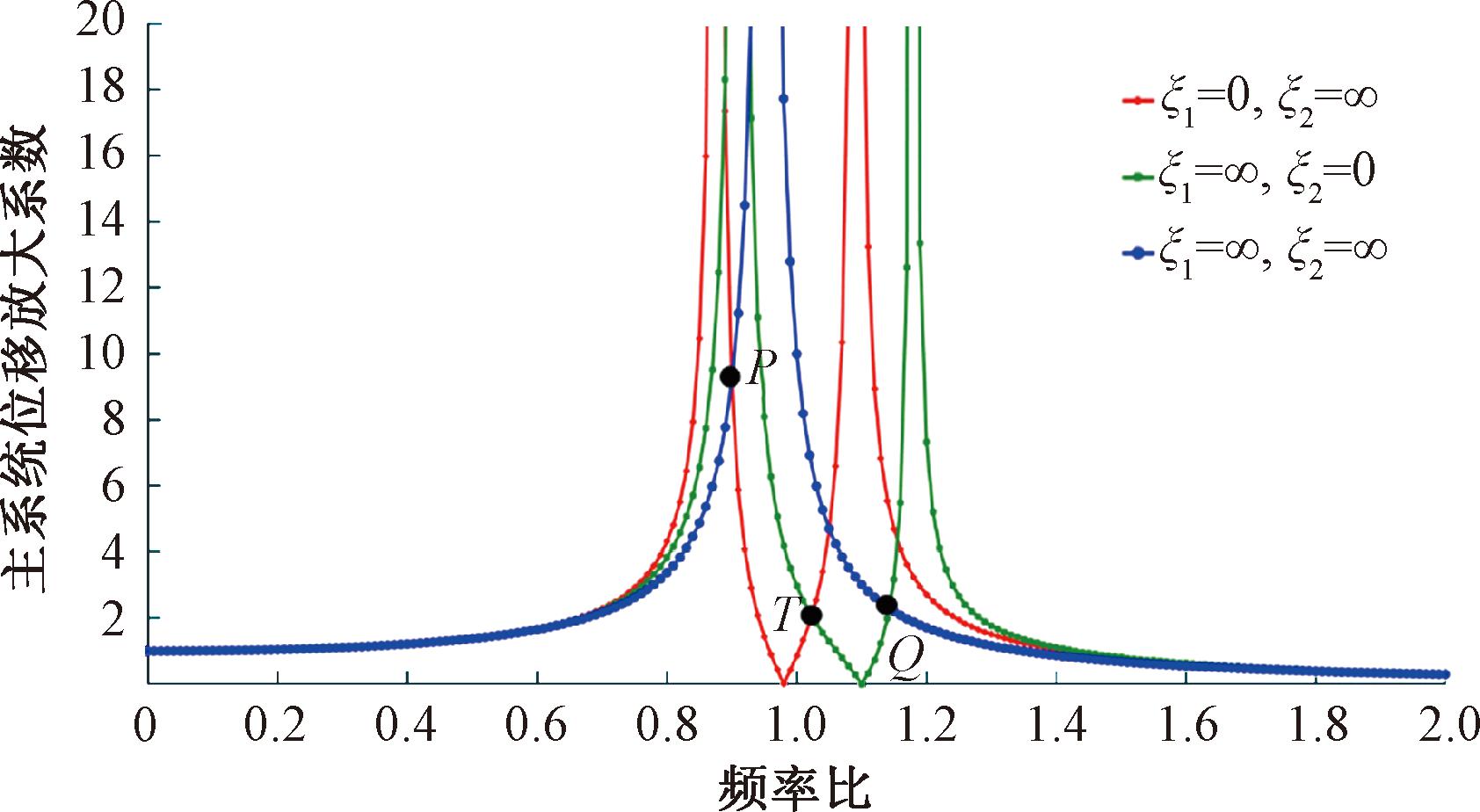
图2 不同阻尼比条件下二重动力吸振器的主系统位移动力放大系数
Figure 2 Displacement dynamic amplification coefficient of the main system of double dynamic vibration absorber with different damping ratios
由图2可知,所有曲线都会穿过P、T、Q 3点,即不动点。优化二重动力吸振器基本参数:将3点设置为相同高度,为最优同调的过程;将3点设置为最大位置所对应的阻尼为最优阻尼。
首先,对P、T、Q 3点进行等高处理,假设3点的频率值分别为λP、λT、λQ。由P、Q点等高条件λP=λQ,可得
(8)
由P、T点等高条件λP=λT,可得
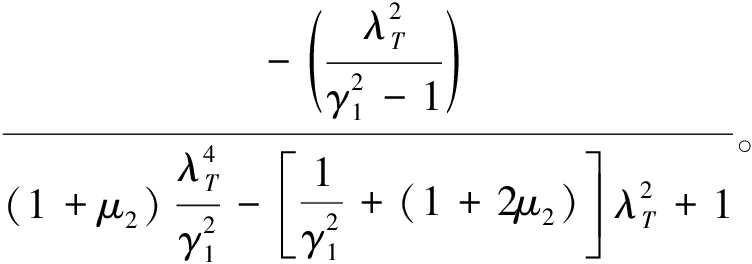
(9)
对P、T、Q 3点进行等高处理,即式(8)与式(9)联立,并在3点附近函数能够取到最大值。根据不同质量比μ2计算出来的结果,绘制成曲线,然后进行曲线拟合,最优频率比为
(10)
从而得到二重动力吸振器刚度为
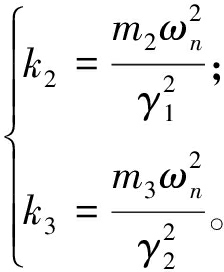
(11)
最优阻尼比为
(12)
根据表1中小支管的相关参数,建立如图3所示的三维模型,整个模型设置为绑定接触,图3中工装位置设置为固定支撑,简谐力方向为沿Z轴方向,并添加如图3所示位置的检测点。
表1 小支管相关参数
Table 1 Minor branch related parameters

材质类型外径/mm壁厚/mm长度/mm质量/kg不锈钢B1421 2200.726
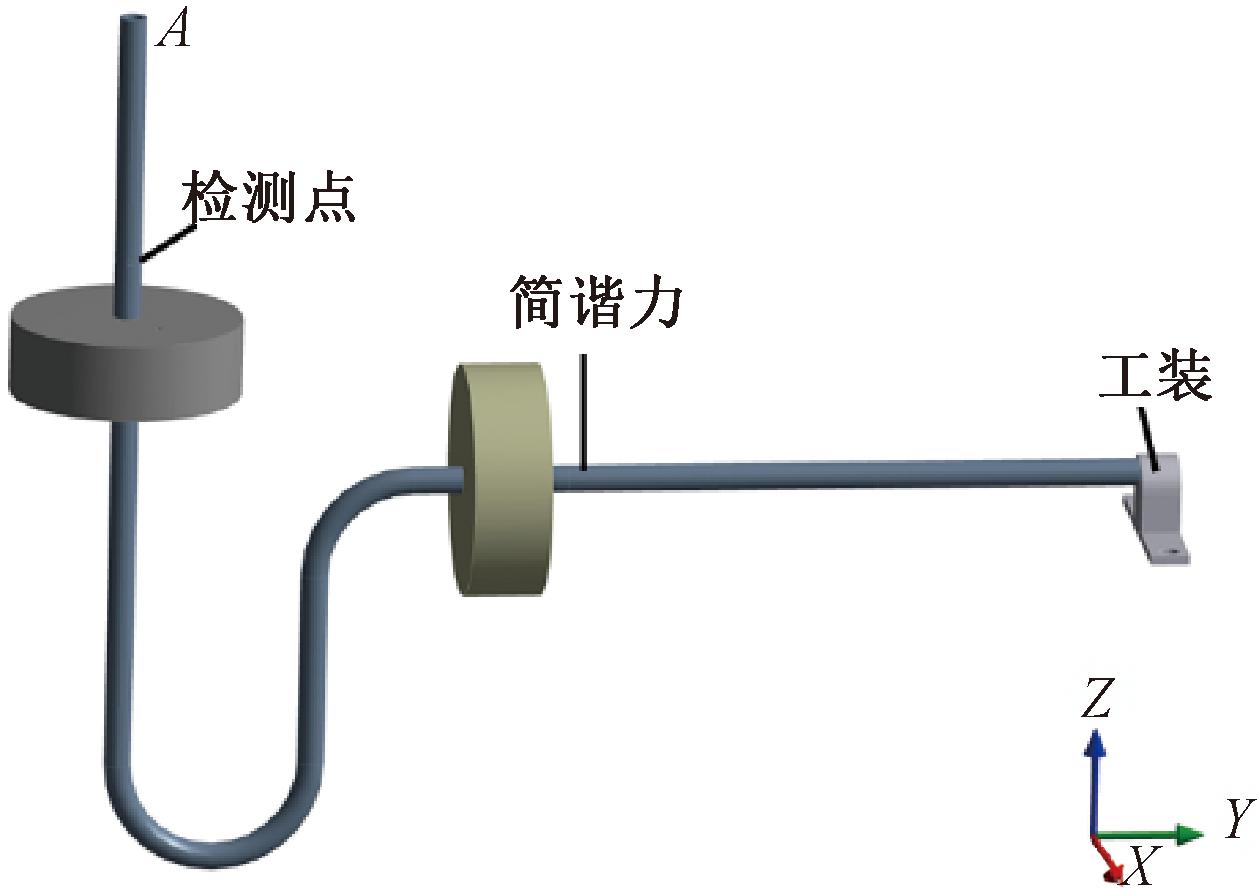
图3 小支管三维结构模型
Figure 3 Small branch three dimensional structure model
根据工程实际得到的小支管吸振频率为117 Hz附近(目标频率),对小支管进行前10阶模态分析,并将分析结果列在表2中。
表2 小支管的模态结果
Table 2 Modal results of small branch tubes Hz
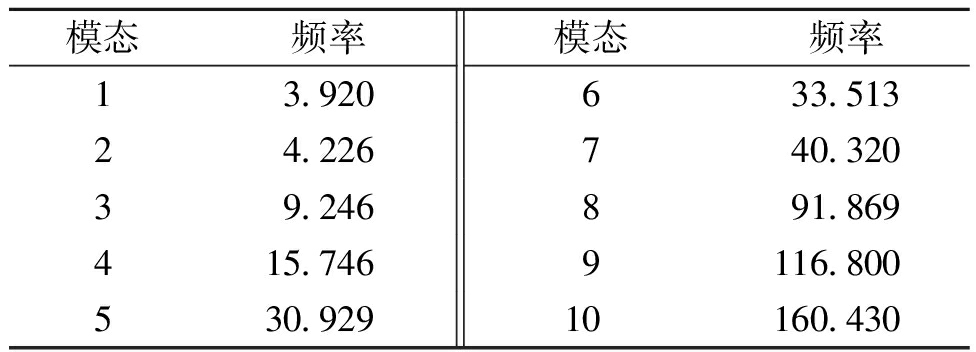
模态频率模态频率13.920633.51324.226740.32039.246891.869415.7469116.800530.92910160.430
由表2可知,当小支管固有频率在第9阶时,与工程实际产生共振峰的频率接近,小支管第8~10阶模态振型如图4所示。根据文献[11]可知,动力吸振器安装的位置一是固有频率的最大位移处,二是主系统最容易安装的地方。图4中红色位置为固有频率位移振型最大处。
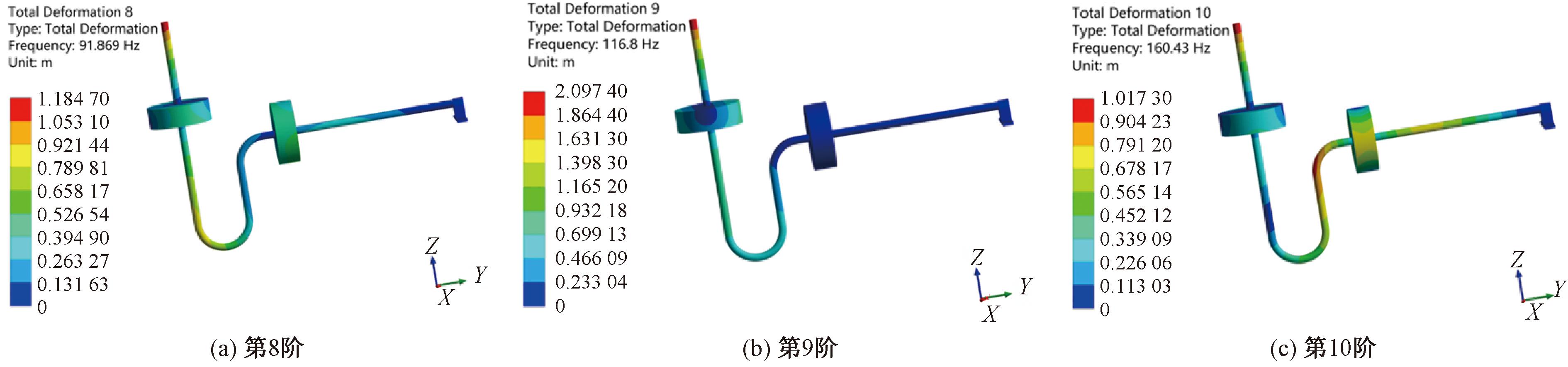
图4 小支管第8~10阶模态振型
Figure 4 Small branch tube mode 8~10
对小支管施加大小为5 N的简谐力,频率为0~150 Hz,记录检测点3个方向加速度输出数据。如表3所示。
表3 检测点X、Y、Z方向最大加速度
Table 3 Maximum acceleration in X, Y and Zdirections at the detection point m/s2
设备名称X向Y向Z向027YP0.02551.44123.930
小支管在该振动条件下的加速度响应如图5所示。由图5可以看出,小支管在Y和Z方向振动比较剧烈,因为激振力作用方向为Z轴方向,而小支管沿YZ平面放置,因此输入能量大部分作用于YZ平面,同时结合小支管模型的模态分析可知,模型的第8、9、10阶模态的振型同样位于YZ平面,因此使得小支管在Y和Z方向振动响应比较剧烈。其中,最大共振峰所对应的频率均为117 Hz附近,从加速度大小上可知,吸振器应主要吸收Y、Z方向上的振动。综上所述,选择目标吸振频率为117 Hz。共振峰所对应固有频率为第9阶。从图4(b)可知,当前模态振型的最大位移处为图3所示A处,且较容易安装,因此选择将动力吸振器安装在A处。
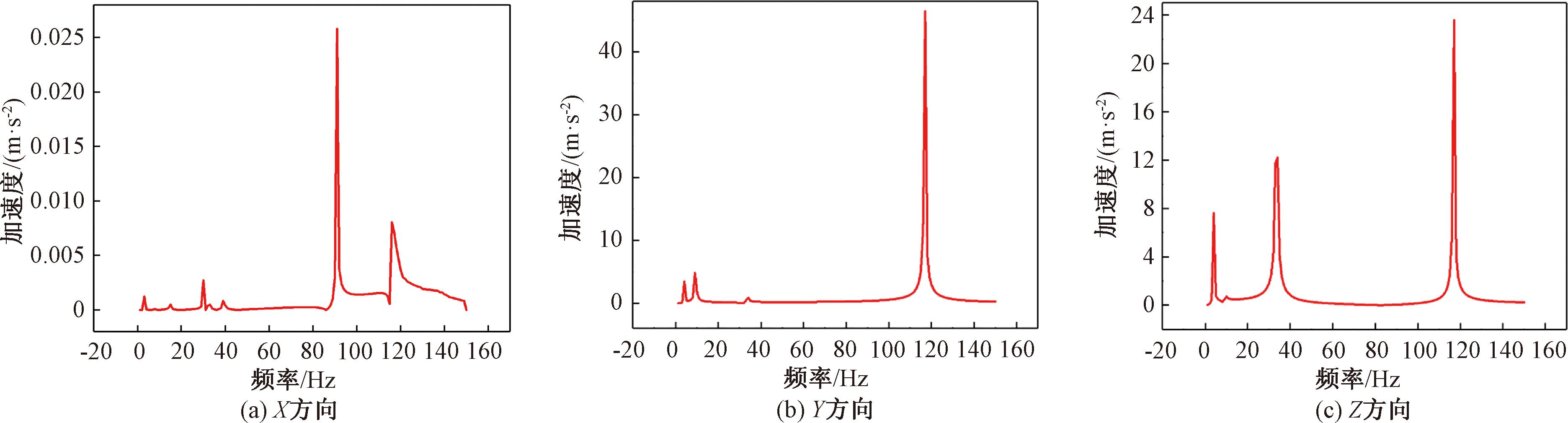
图5 小支管谐响应分析中3个方向加速度频响曲线
Figure 5 Three-way acceleration frequency response curves in small branch tube harmonic response analysis
本文利用质量感应法对小支管的等效质量进行计算,其中,i阶模态在j点的等效质量m4的计算式为
(13)
i阶模态在j点的等效刚度k4的计算式为
(14)
式中:Δmj为在j点添加的质量;Ωji为未在j点添加质量的第i阶模态的固有频率;ωji为在j点添加Δmj后的第i阶模态的固有频率。
由于本节中所涉及小支管由管道以及阀门组成,不是简单的连续体,而式(13)、式(14)适用于纯管道或者没有附加结构的系统。因此,本节将小支管简化为如图6所示的等效弯管。

图6 等效弯管
Figure 6 Equivalent bend
保证等效弯管的质量、固有频率与本节小支管相似,使用单自由度质量感应法求解等效质量,得到的参数结果如表4所示。通过最小二乘法进行曲线拟合[12]得
(15)
表4 等效弯管参数
Table 4 Equivalent bending parameters
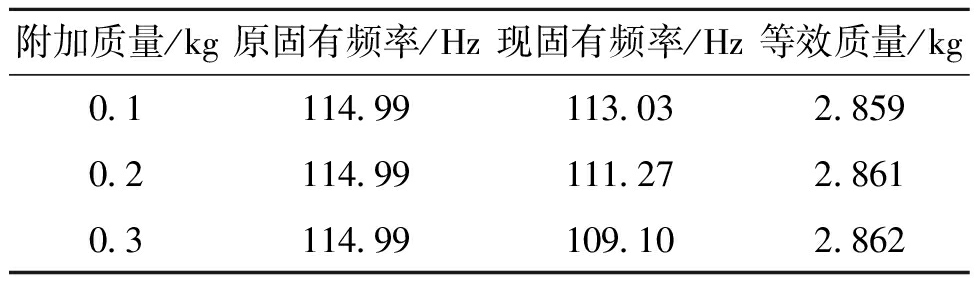
附加质量/kg原固有频率/Hz现固有频率/Hz等效质量/kg0.1114.99113.032.8590.2114.99111.272.8610.3114.99109.102.862
计算附加质量为0时的等效质量,确定本文小支管的等效质量m4约为2.8 kg。从理论上来说,质量比越大,吸振效果越好。一般动力吸振器质量比在0.1及以下,主系统质量越大,质量比应该更小一些,主系统质量越小,质量比应该更大一些[13]。本文通过初步仿真手段,选取吸振器质量比为0.06~0.10,其他参数均为该条件下最优,进行简易的单一动力吸振器谐响应分析,输出检测点3个方向(X、Y、Z)的加速度,加速度响应曲线如图7所示。
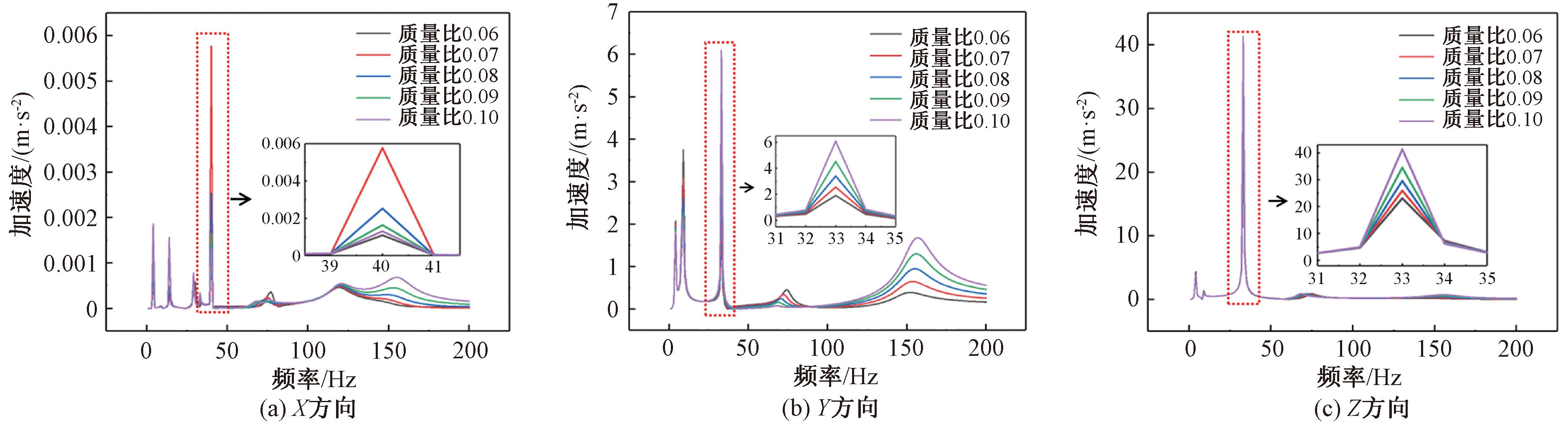
图7 不同质量比单一动力吸振器的小支管3个方向加速度频响曲线 Figure 7 Three-way acceleration frequency response curves of small branch tube of single power absorber with different mass ratio
由图7(a)可知,质量比越大,X方向上的加速度峰值不断减小,应该往大取值。由图7(b)可知,质量比越大,Y方向上的加速度峰值不断增大,应该往小取值。由图7(c)可知,质量比越大,Z方向上的加速度峰值不断增大,应该往小取值。考虑吸振器主要吸收Y、Z方向振动,实际上选取单一动力吸振器质量比为0.06具有最好的吸振效果。同时,二重动力吸振器单个质量为单一动力吸振器质量的一半,等效质量m6=m7=0.084 kg,阻尼比ξ1=0.138,ξ2=0.177,刚度k2=15.67 N/mm,k3=22.15 N/mm。
二重动力吸振器的质量块总质量为0.084 kg,材质为铝合金,密度为2.7 g/cm3,体积为31.11 cm3,使用外径12 mm、高度25 mm的弹簧,预压缩2 mm,使用直径10 mm、高度13 mm的金属橡胶,预压缩1 mm。动力吸振器的外形为环形,如图8所示。图8中工装夹具与小支管固定连接,其质量约为0.05 kg,远远小于小支管质量,因此在计算等效弯管质量中往往将其忽略不计。
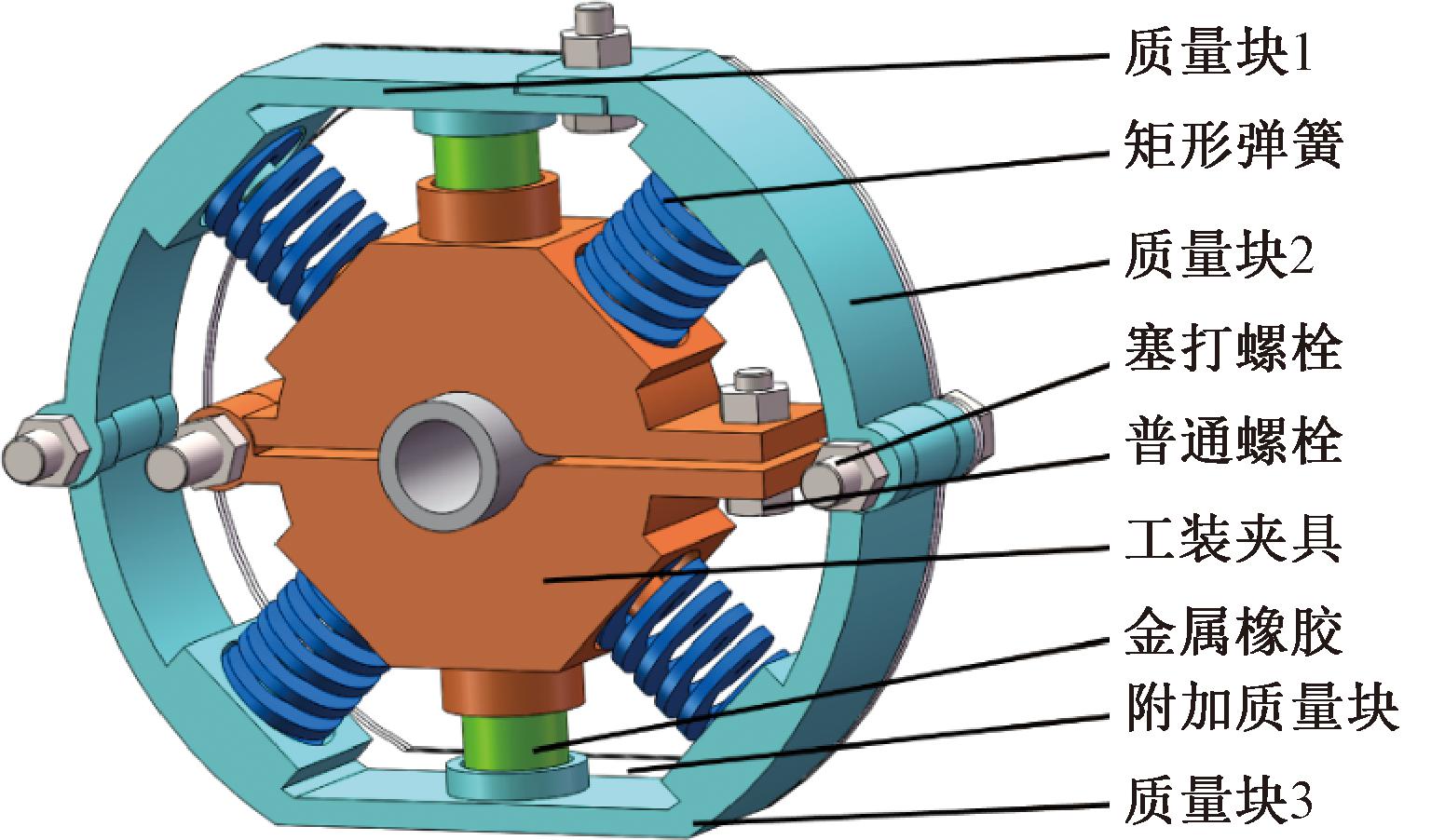
图8 三重动力吸振器结构示意图
Figure 8 Structure diagram of double dynamic vibration absorber
使用塞打螺栓紧固,3块质量块旋转拼接,使得安装便捷,工装夹具也便于安装到小支管上。金属橡胶与弹簧交替安装,避免产生相互作用,也方便安装。附加质量块添加在两侧的塞打螺栓上,同时,质量块以及工装夹具与弹簧及金属橡胶接触的位置均设置一定的凸起,保证弹簧不飞出。
安装二重动力吸振器的小支管有限元模型如图9所示。将小支管、工装夹具以及吸振器工装夹具等连为一体,如灰色部分所示。将质量块,螺栓螺母连为一体,如绿色部分所示,同时在质量块与工装夹具的圆柱面处设置8根弹簧,添加刚度属性,最后,在金属橡胶材料属性中添加阻尼比,如红色部分所示。
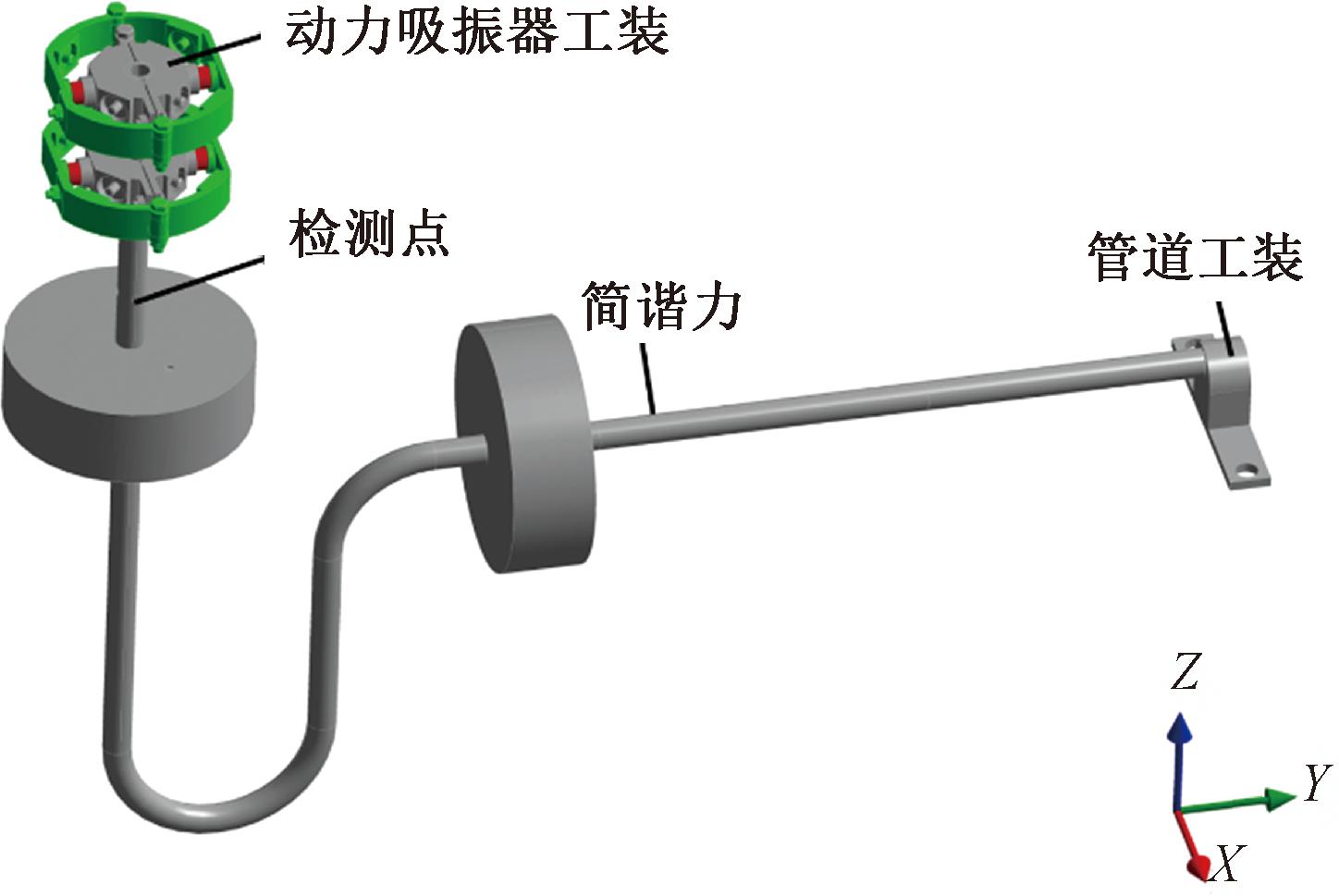
图9 安装二重动力吸振器小支管的有限元模型
Figure 9 Finite element model of the small branch tube installed with double dynamic vibration absorber
对安装最优参数二重动力吸振器的小支管进行谐响应分析,记录检测点3个方向(X、Y、Z)的加速度输出数据,与未安装动力吸振器小支管的加速度频谱图对比结果如图10所示。目标频段与未安装动力吸振器小支管的振动对比,如表5所示。
表5 117 Hz处无动力吸振器与二重动力吸振器吸振效果对比
Table 5 Comparison of vibration absorption effects of unpowered obsorber and double dynamic vibration absorber at 117 Hz
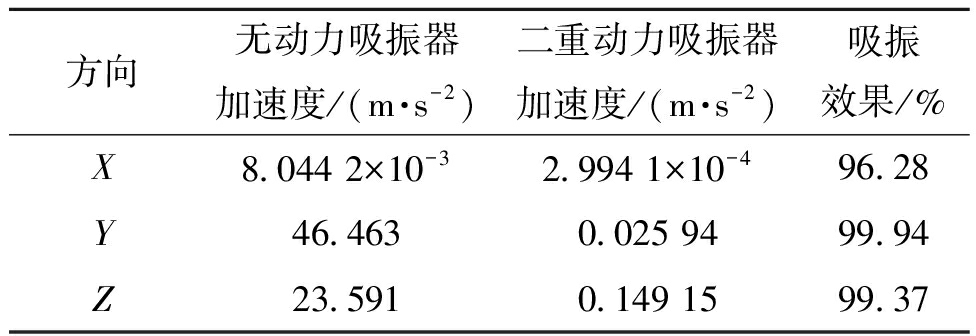
方向无动力吸振器加速度/(m·s-2)二重动力吸振器加速度/(m·s-2)吸振效果/%X8.044 2×10-32.994 1×10-496.28Y46.4630.025 9499.94Z23.5910.149 1599.37
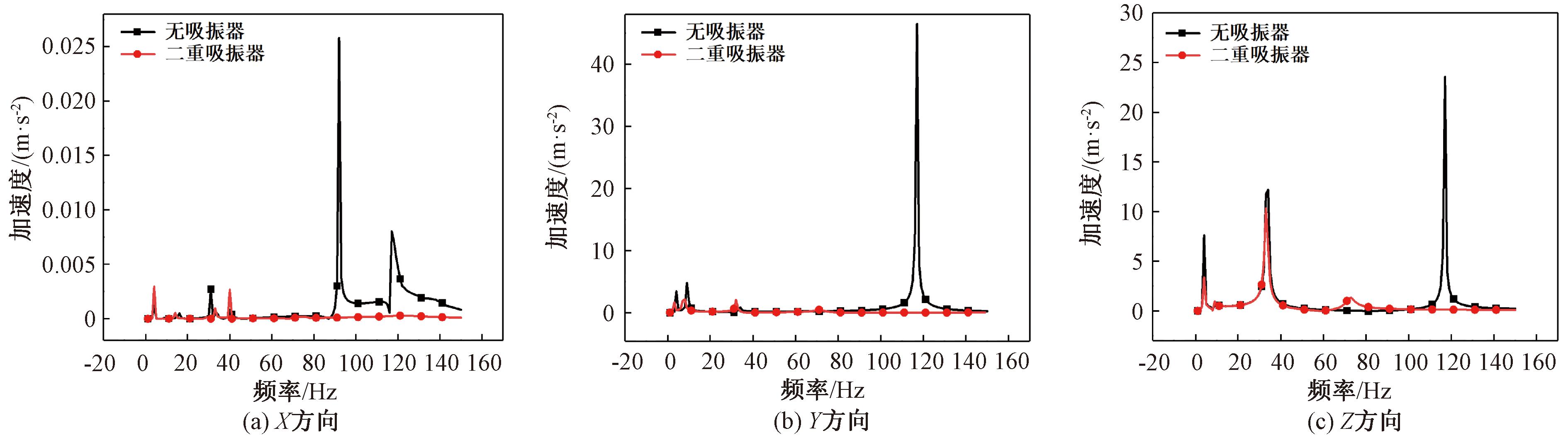
图10 安装二重动力吸振器的小支管3个方向加速度频响曲线
Figure 10 Three-way acceleration frequency response curves of the small branch tube installed with double dynamic vibration absorber
由图10可知,安装质量比为0.06的二重动力吸振器的小支管在3个方向上的共振峰都明显降低,尤其是在目标频段。由表5可知,3个方向上,目标频段的吸振效果达到95%以上(大于25 dB)。
二重动力吸振器强度分析如图11所示。首先,对二重动力吸振器进行静力学分析,选取刚度以及阻尼较大的动力吸振器,只有弹簧作用力。将二重动力吸振器导入静力学分析,弹簧的刚度设置为22.15 N/mm,原长设置为25 mm,压缩2 mm,刚好与工装夹具和质量块接触。对工装夹具与小支管接触面设置固定,应力图如图11(a)所示,应力主要分布在质量块上,且最大应力为4.44 MPa,远低于铝合金的屈服强度108 MPa,静态分析符合强度要求,不会导致永久变形。
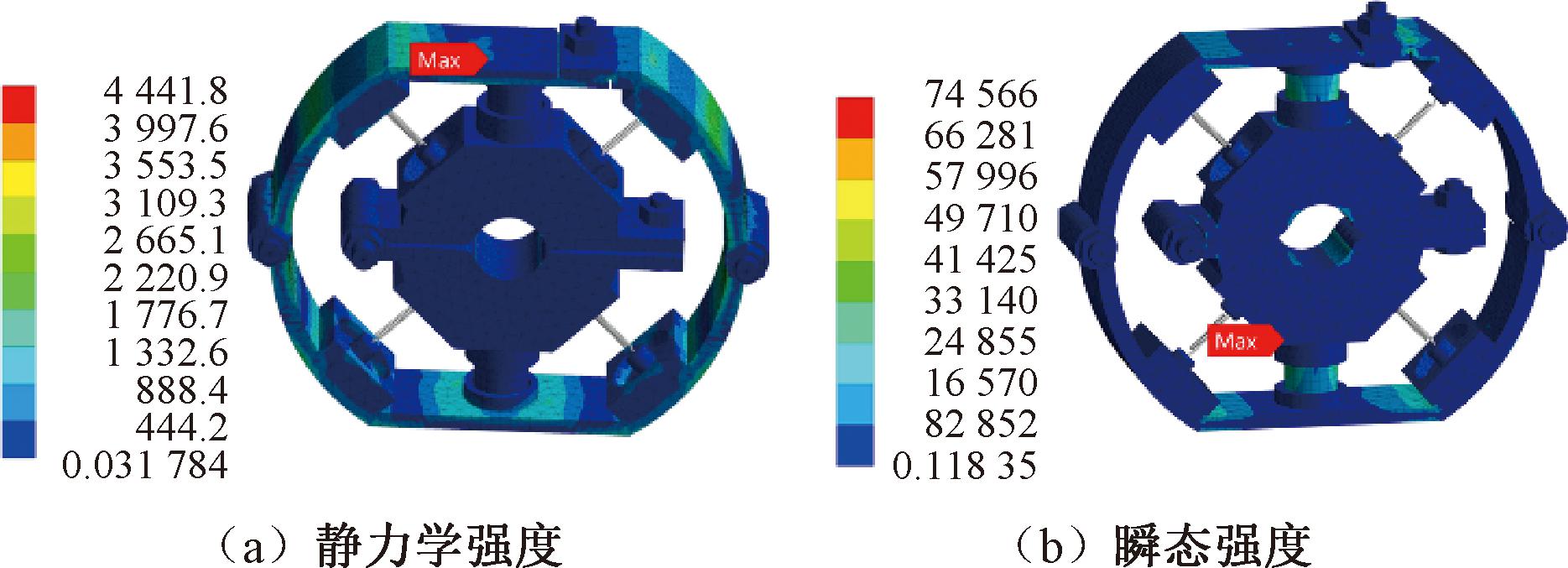
图11 二重动力吸振器强度分析
Figure 11 Strength analysis of double dynamic vibration absorber
在谐响应分析条件下,最大应力:X、Y方向的应力较小,Z方向的应力达到16.75 MPa。对二重动力吸振器进行瞬态分析,弹簧的设置以及固定的部位与静力学分析相同。由于工装夹具通过螺栓,与小支管固定,设置工装夹具的位移限制:3个方向都为12 mm。工装夹具圆柱孔处,设置Z方向应力为16.75 MPa的正弦扫频,频率为117 Hz。输出应力图像,如图11(b)所示,应力主要分布在质量块上,且最大应力为74.566 MPa,远低于铝合金的屈服强度108 MPa,瞬态分析符合强度要求。
按照3.1节中二重动力吸振器的结构设计,加工相关零件如环形质量块、工装夹具、购置螺栓螺母、矩形弹簧。由于矩形弹簧是按照标准表选取,和最优同调得到的刚度略有偏差,本文选取了两种刚度的矩形弹簧,分别为15、20 N/mm。二重动力吸振器实物如图12所示,其中,矩形弹簧①的刚度为15 N/mm,矩形弹簧②的刚度为20 N/mm。

图12 二重动力吸振器实物
Figure 12 Physical double dynamic vibration absorber
本文所采用的动力吸振器阻尼为金属橡胶,不锈钢金属丝丝径为0.1 mm,质量分别为1.6、1.8、2.0 g,密度分别为1.20、1.35、1.50 g/cm3,直径为10 mm、高度为13 mm,不同密度的金属橡胶如图13所示。

图13 不同密度的金属橡胶
Figure 13 Metal rubber with different densities
将二重动力吸振器安装于小支管吸振器安装位置,如图14所示。将小支管一端进行固定,激振器安装位置与仿真简谐力位置一致,幅值为5 N,频率为0~150 Hz,记录检测点3个方向(X、Y、Z)的加速度输出数据,进行3次试验取平均值。

图14 安装二重动力吸振器的小支管
Figure 14 Install the small branch tube of the double dynamic vibration absorber
经过不断调试二重动力吸振器基本参数,最终确定下来二重动力吸振器的最优质量比为0.06,矩形弹簧刚度为上面安装20 N/mm,下面安装15 N/mm,金属橡胶密度上下均为1.50 g/cm3。对安装最优参数二重动力吸振器小支管、未安装二重动力吸振器小支管的振动进行对比,如图15所示,无动力吸振器与二重动力吸振器在目标频率117 Hz处的吸振效果,如表6所示。
表6 试验中117 Hz处无动力吸振器与二重动力吸振器吸振效果对比
Table 6 Comparison of vibration absorption effects of unpowered absorber and double dynamic vibration absorber at 117 Hz in the experiment
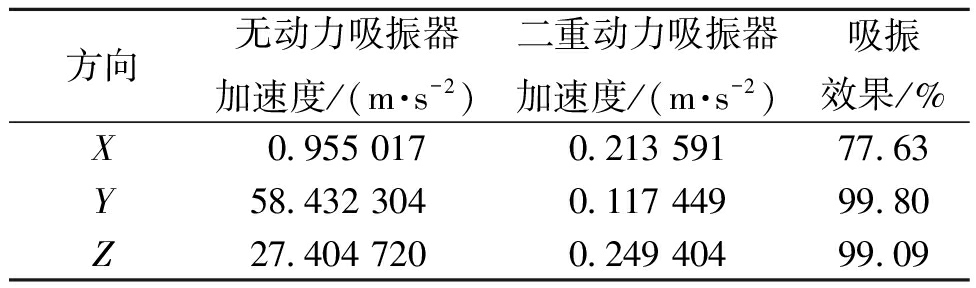
方向无动力吸振器加速度/(m·s-2)二重动力吸振器加速度/(m·s-2)吸振效果/%X0.955 0170.213 59177.63Y58.432 3040.117 44999.80Z27.404 7200.249 40499.09
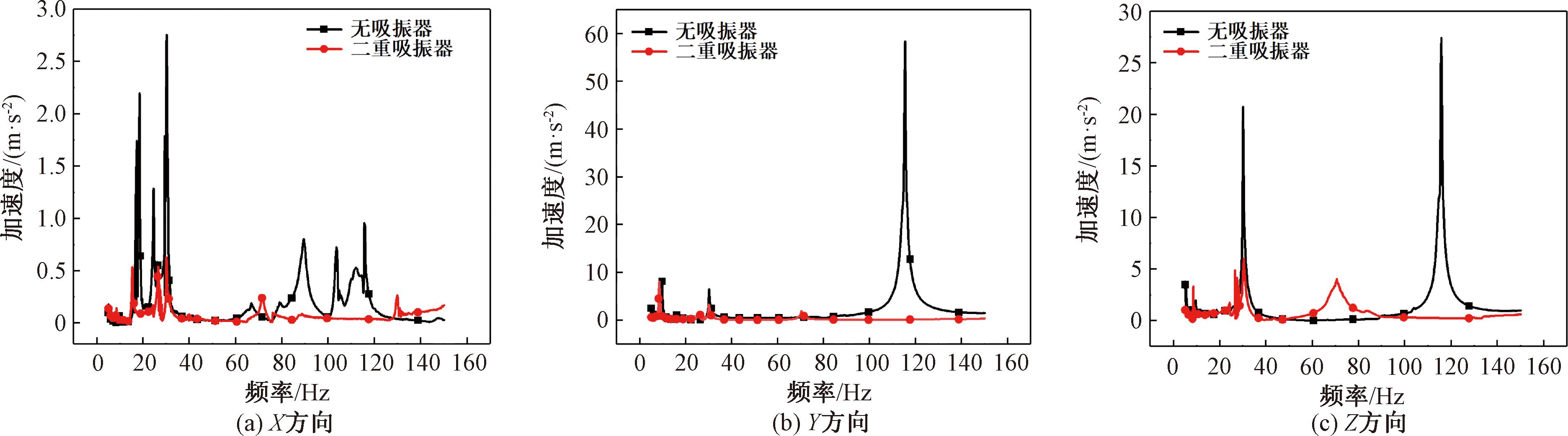
图15 动力吸振器小支管试验的3个方向频响曲线
Figure 15 Three-way frequency response curve of small branch tube test for dynamic vibration absorber
由图15可知,安装最优参数二重动力吸振器的小支管,在3个方向上的共振峰都存在明显降低,尤其是在频率为117 Hz附近的目标频率下。由表6可知,安装最优参数二重动力吸振器的小支管,在Y、Z方向上的吸振效果达到95%以上。同时,X方向上的吸振效果偏低,但是满足工程需求,这是由于小支管在Y和Z方向的振动比较剧烈,在Y和Z方向上的位移程度远大于X方向,因此吸振器的工作行程也远大于X方向,最终导致减振效果也大于X方向。
(1)通过动力学建模、定点理论、最优同调,得到二重动力吸振器的最优频率比、刚度以及最优阻尼比,进一步分析小支管的模态确定目标吸振频率,将固有频率的最大位移处作为吸振器安装位置,并使用质量感应法求解简化小支管的等效质量。
(2)为了实现3个方向的吸振,采用3个质量与金属橡胶弹簧组合的二重吸振器结构,并对该结构进行仿真分析,结果表明:安装二重动力吸振器,3个方向上的吸振效果达到95%以上;动力吸振器满足强度要求。
(3)完成吸振器相关零件的设计并进行小支管激振试验。结果表明,安装最优同调参数下的二重动力吸振器的小支管具有最优的吸振效果:在Y、Z方向上的吸振效果均达到95%以上。小支管在Y和Z方向的振动比较剧烈,在Y和Z方向上的位移程度远大于X方向,因此其吸振器的工作行程也远大于X方向,最终导致减振效果也大于X方向。
[1] 刘昉,张鲁丰,庞博慧,等.基于CEEMDAN和MPE的导墙振动信号降噪方法及应用[J].郑州大学学报(工学版),2022,43(5):91-97.LIU F,ZHANG L F,PANG B H,et al. Denoising method of discharge guide wall vibration signal based on ceemdan and mpe and its application[J]. Journal of Zhengzhou University (Engineering Science),2022,43(5):91-97.
[2] 樊强博, 范信江.试析机械加工中的振动消除与利用[J]. 装备维修技术, 2019(1): 101-103.FAN Q B, FAN X J. Analysis on vibration elimination and utilization in machining[J]. Equipment Technology, 2019(1): 101-103.
[3] 顾仲权.振动主动控制[M]. 北京: 国防工业出版社, 1997.GU Z Q. Active vibration control[M]. Beijing: National Defense Industry Press, 1997.
[4] ASAMI T, YAMADA K, KAWAGUCHI N. A quasi-optimal design formula of a parallel-type double-mass dynamic vibration absorber based on the stability criterion[J]. Mechanical Engineering Journal, 2021, 8(3): 20-00545.
[5] 李晨阳,刘鹏,陈宏,等.基于驾驶室舱内声学特性的动力吸振器设计研究[J].郑州大学学报(工学版),2021,42(4):47-52.LI C Y, LIU P, CHEN H, et al. Design and research of dynamic vibration absorber based on acoustic characteristics of interior sound field in a cab[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(4): 47-52.
[6] ASAMI T, YAMADA K. Numerical solutions for optimal double-mass dynamic vibration absorbers attached to a damped primary system[J]. Mechanical Engineering Journal, 2020, 7(2): 19-00051.
[7] CHEN X Y, LENG Y G, SUN F, et al. A novel triple-magnet magnetic suspension dynamic vibration absorber[J]. Journal of Sound and Vibration, 2023, 546: 117483.
[8] 张成林, 张建润, 孙庆鸿, 等. 两种宽频调谐质量阻尼器仿真及应用[J]. 制造业自动化, 2006, 28(8): 7-9.ZHANG C L, ZHANG J R, SUN Q H, et al. The simulation and application of two kinds of wide frequency rang TMD[J]. Manufacturing Automation, 2006, 28(8): 7-9.
[9] 樊长博, 张来斌, 王朝晖, 等. 往复式压缩机气体管道振动分析及消振方法[J]. 科学技术与工程, 2007, 7(7): 1309-1312.FAN C B, ZHANG L B, WANG Z H, et al. Analysis of reciprocating compressor gas pipeline vibration and control methods[J]. Science Technology and Engineering, 2007, 7(7): 1309-1312.
[10] 杨恺, 张针粒. 基于反共振原理的管路吸振器调谐方法[J]. 噪声与振动控制, 2017, 37(5): 55-60.YANG K, ZHANG Z L. Tuning method for pipeline vibration absorbers based on anti-resonance principle[J]. Noise and Vibration Control, 2017, 37(5): 55-60.
[11] 刘彬彬, 陈果, 赵正大, 等. 一种新型动力吸振器的液压管道减振试验研究[J]. 噪声与振动控制, 2017, 37(1): 152-157, 187.LIU B B, CHEN G, ZHAO Z D, et al. Experimental study on a new dynamic vibration absorber with adjustable frequency for vibration reduction of hydraulic pipelines[J]. Noise and Vibration Control, 2017, 37(1): 152-157, 187.
[12] 申翼. 泻湖潮汐通道地形演变数值模拟研究[D]. 天津: 天津大学, 2016.SHEN Y. Numerical simulation of morphological evolution of lagoon inlets[D].Tianjin: Tianjin University, 2016.
[13] 郭吉祥. 轮毂加工机床主轴动力吸振器设计及实验研究[D]. 杭州: 浙江工业大学, 2020.GUO J X. Design and experiment of dynamic vibration absorber for spindle of wheel hub maching machine[D].Hangzhou: Zhejiang University of Technology, 2020.