近年来,容器技术凭借其灵活性和高效性,被广泛用作虚拟机的替代方案。然而容器在为云原生技术赋能的同时,也带来了诸多安全问题。攻击者通过利用容器弱隔离的特点,在云环境中建立侧信道发起同驻攻击,甚至进一步利用目标容器软硬件层漏洞发起逃逸攻击,严重威胁宿主机和系统安全。Han等[1]提出一种容器镜像访问控制架构,通过阻止对容器映像的非授权直接访问,确保应用运行环境的安全性。Gao等[2]发现了容器内可访问的信息泄漏通道,通过挖掘实际漏洞并抽象攻击范式,对容器脆弱点进行保护。Lim等[3]针对容器系统缺乏捕获高保真容器日志的能力,提出了一种扩展的eBPF框架saBPF,通过检测容器环境下的异常行为进行安全防护。然而,上述被动防御手段面对未知漏洞和后门等问题无法有效解决。
移动目标防御(moving target defense, MTD)技术是国际上比较有代表性的主动防御技术,目前已广泛运用在网络安全领域,成为保护云上安全的重要防御手段。Abed等[4]提出了一种基于云计算容器弹性入侵检测与解决系统,检测恶意行为容器,采用一种容器迁移的MTD方法隔离容器,防止攻击扩散。Hyder等[5]从预防容器环境攻击的角度研究MTD技术,提出了一种基于云中虚拟专用网络的资源变换来欺骗攻击者的方法。但是在容器云环境下盲目地使用MTD技术会给系统带来较大的开销,如何采取有效的方法选取MTD策略保护容器云系统的安全是当前研究的重点。
张帅等[6]建立了微服务攻击模型,归纳了容器动态轮换策略的周期配置问题,并提出了一种基于深度强化学习的SmartSCR算法求解最优轮换周期。但是基于深度强化学习的算法求解容器云安全问题存在局限性,微服务之间复杂的调用关系可能导致状态空间爆炸,容器云环境实时变化导致模型训练有效性降低。在网络安全场景中,博弈论[7]可以指导MTD策略的选取。博弈论可以合理地对防御者和攻击者的决策和行动建模,假设攻防双方在理性的情况下寻求最优策略以最大化双方效用。Wang等[8]针对云的科学工作流环境中多租户共存面临被入侵的风险,提出了一种基于非零和博弈模型的调度算法,求解最优的调度策略。李凌书等[9]针对同驻攻击给容器云环境带来的安全威胁,提出一种基于信号博弈的容器迁移与蜜罐部署策略。曾威等[10]提出了一种基于Stackelberg博弈的动态异构容器调度方法,建立攻防博弈模型,求解各容器动态调度的最优混合概率。综上,采用博弈论的方法解决MTD策略选取问题逐渐成熟,但是当前研究基于博弈论选取异构容器动态调度策略,缺乏针对多阶段、不完全信息的攻防场景构建博弈模型,并进行策略求解。
本文针对当前多阶段、不完全信息的攻防场景提出了一种基于信号博弈的异构容器动态调度策略选取方法。首先,提出了容器云系统动态异构调度模型,使用异构镜像构造异构容器副本,对容器进行动态轮换;其次,构建动态调度信号博弈模型,考虑攻击者对容器信息获取程度的动态变化,设计容器信息获取程度集合;最后,对攻防收益量化,提出了异构容器动态调度策略选取算法。
1 威胁分析
本节对容器云环境中存在的安全威胁进行分析,主要关注虚拟化层引入的安全威胁问题,分析虚拟化环境下常见的安全威胁。如图1所示,虚拟化环境下的安全威胁一般指逃逸攻击和同驻攻击等[11]。
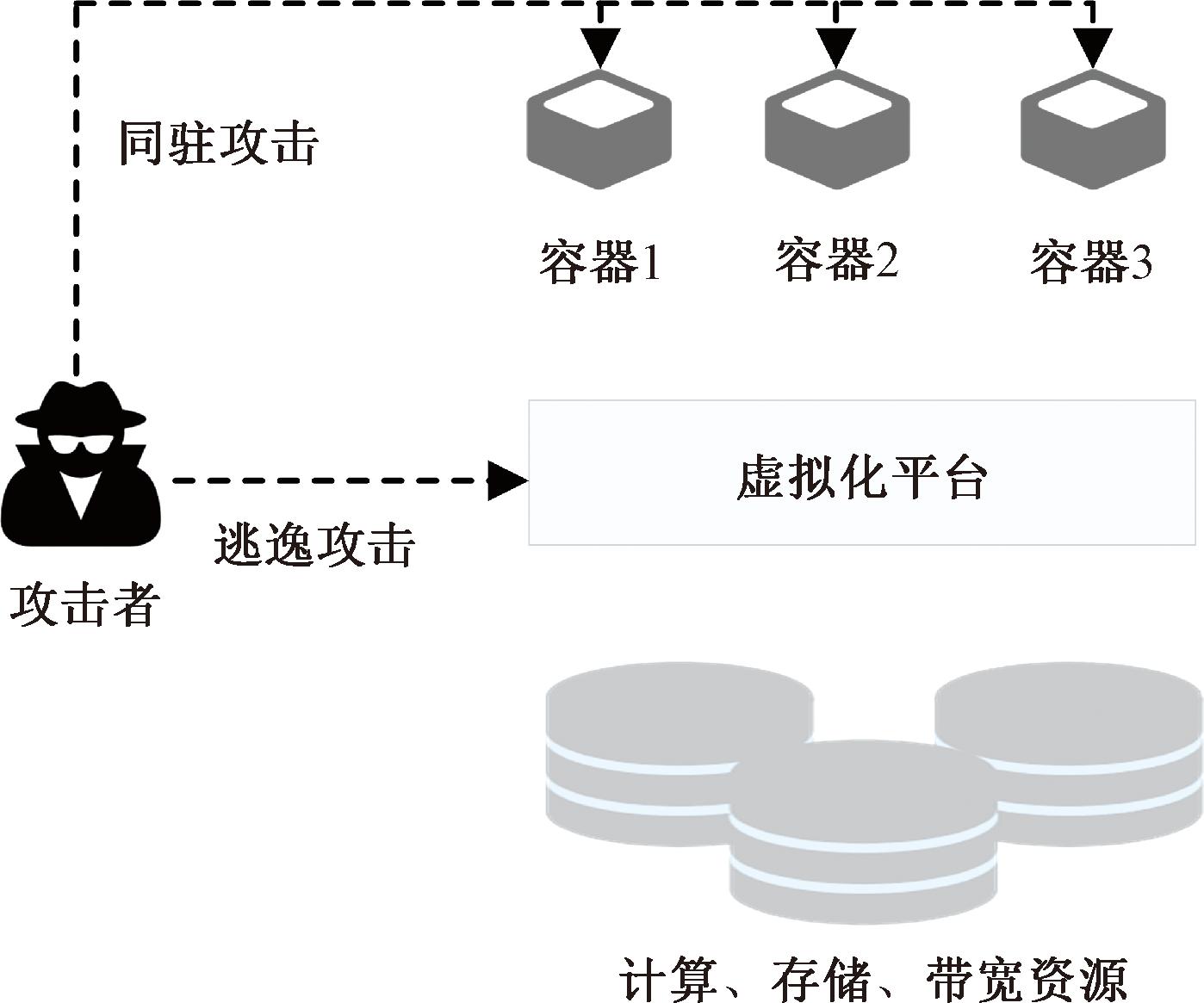
图1 容器云环境攻击威胁图
Figure 1 Attack threat diagram of container cloud environment
逃逸攻击是攻击者通过对探测到的虚拟环境下软硬件漏洞发起攻击,达到扰乱或掌控虚拟化层或宿主机操作系统的目的。首先,容器引擎调用操作系统的隔离机制实现隔离,如果容器引擎存在后门或漏洞,攻击者可以加以利用实现容器逃逸;其次,容器引擎的一些挂载和危险配置易导致容器逃逸;最后,由于同宿主机容器运行在同一操作系统上,如果操作系统的安全机制存在漏洞,攻击者便可以越过容器直接对操作系统进行攻击,实现容器逃逸。同驻攻击是攻击者以建立云环境侧信道的形式,从位于同一节点上的容器中窃取隐私信息。攻击者还可以利用同驻攻击控制多个容器发起DOS攻击消耗系统资源,降低系统服务质量。
2 动态调度模型
在对容器云环境中存在的安全威胁进行分析的基础上,本节提出了容器云系统动态异构调度模型[10]。通过构建容器镜像的异构资源池,增强应用系统容器实例的多样性、动态性和不确定性。不断切换攻击表面,提升攻击者长时间探测和攻击的难度,增强容器云系统的安全性。如图2所示,虚拟化层提供计算、网络带宽、存储等资源为上层提供服务。异构资源池提供功能等价的异构镜像,应用容器实例为系统中实际部署运行的容器副本,各实例在基础架构、容器运行、操作系统等方面实现差异化。将上层服务层应用程序拆分成多个微服务,然后分别进行部署和运行。考虑到同时对所有微服务容器动态轮换开销大,甚至影响用户正常的服务请求,本文采取部分轮换策略。当系统未检测到异常时,云管理调度层对系统资源进行调度管理,以固定时间间隔顺序选取一种微服务的容器进行动态轮换;当系统检测到异常告警时,将攻防双方的策略选取建模成信号博弈的过程,在博弈的每个阶段,云管理调度层采取本文提出的动态调度策略选取算法选择容器的最优调度策略,对可能受到攻击的容器进行动态轮换。
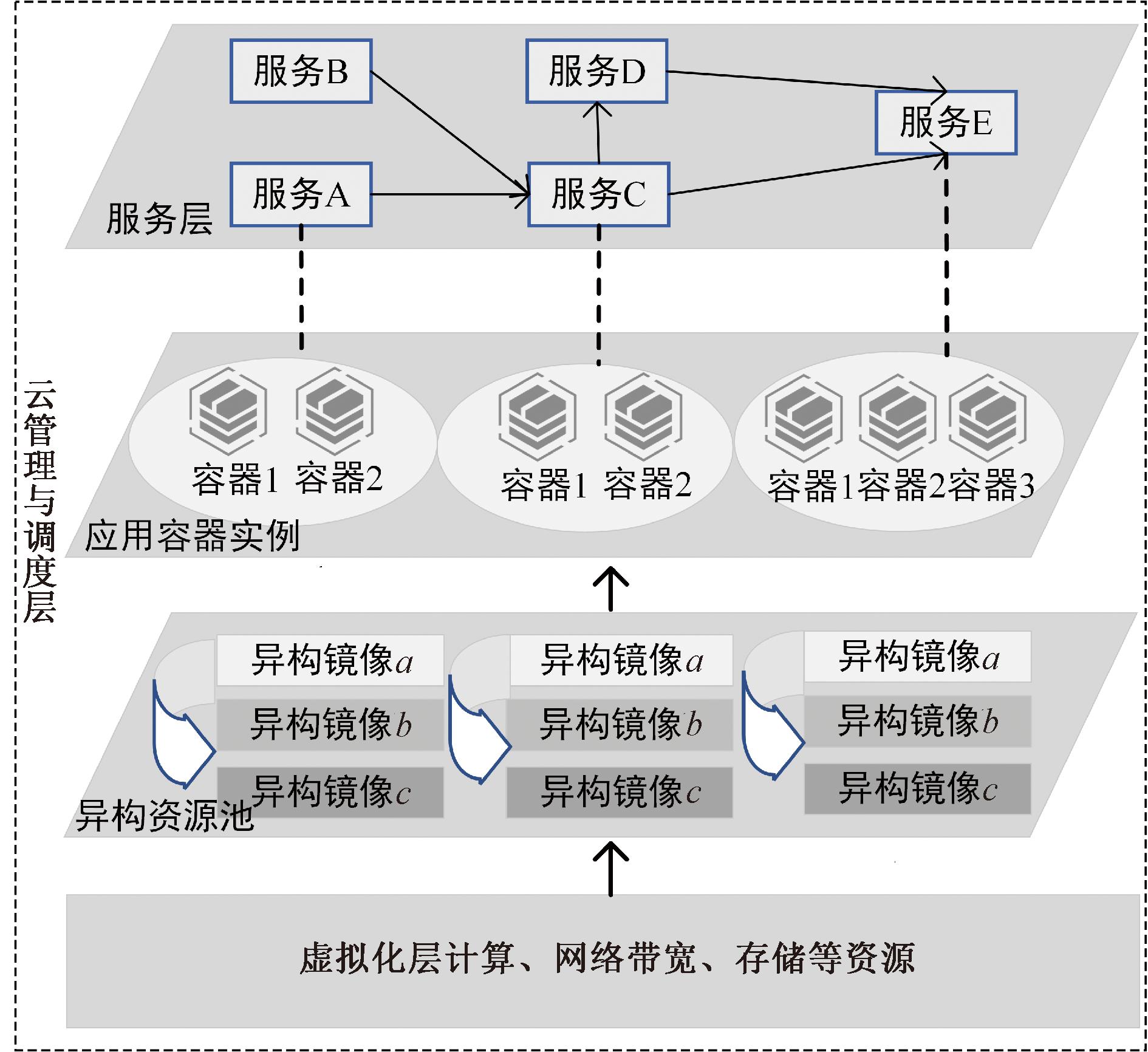
图2 容器云系统动态异构调度模型
Figure 2 Dynamic heterogeneous scheduling model for container cloud system
3 动态调度信号博弈模型
本文提出了一种基于信号博弈的调度策略选取方法,根据实际攻防场景构建信号博弈模型,对攻防收益进行量化分析,所提算法结合精炼贝叶斯均衡求解最优轮换策略。
3.1 防御类型空间确定
信号博弈首先要确定防御类型,本文根据应用程序的功能模块对防御类型进行划分,防御者在采取动态调度策略时首先选择一个应用,然后再对应选择一种微服务的容器进行动态轮换。如图3所示,假设部署在容器云中共有4个应用程序,每个应用对应一种或多种微服务,则容器云环境的防御类型空间表示为{D1,D2,D3,D4},其中D1对应于选择应用1,那么D1防御类型空间对应的防御策略分别为微服务1对应的容器进行动态轮换、微服务2对应的容器进行动态轮换、微服务3对应的容器进行动态轮换,其他对应关系以此类推。
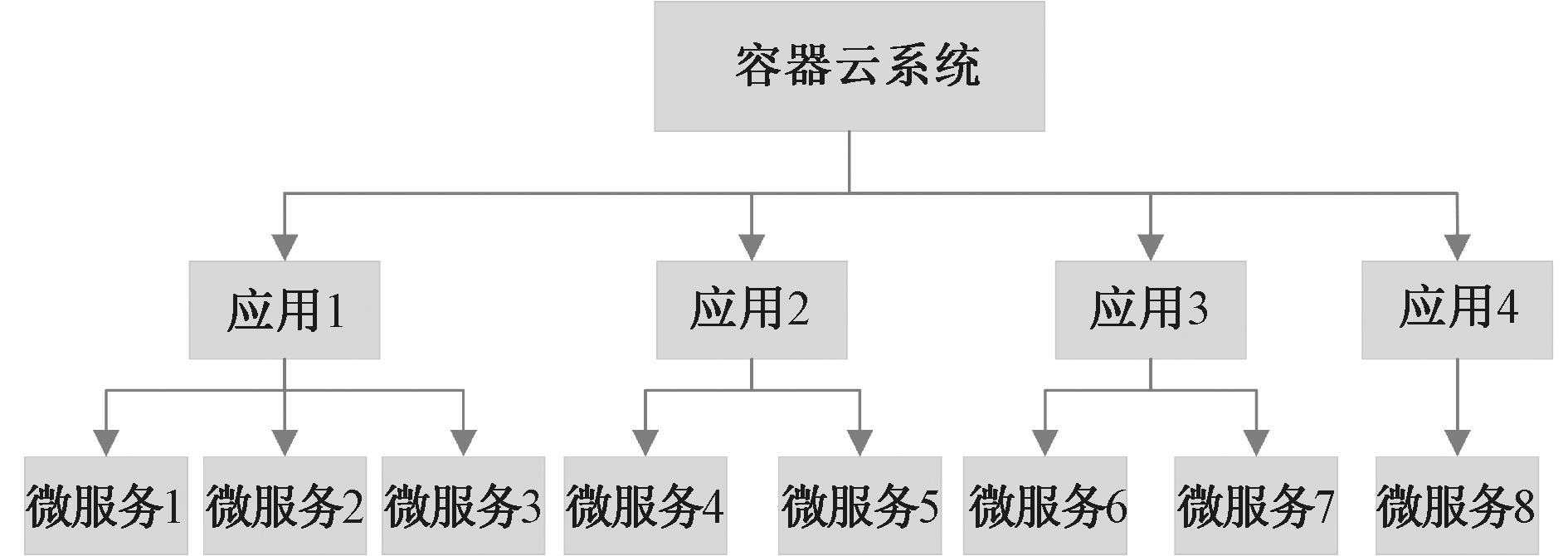
图3 容器云系统层次结构示例图
Figure 3 Example diagram of the container cloud system hierarchy
3.2 异构度量化
本文防御策略采取异构的功能等价的容器进行动态轮换,容器动态轮换的开销以及防御效果都与容器的异构度相关。因此要构建信号博弈模型对攻防收益进行量化,需要对容器的异构度进行量化。容器异构包括应用程序的异构、容器运行时的异构、操作系统的异构等。容器异构度量算法从多个维度量化容器的异构程度,作为攻防收益的重要影响因素。
首先,整个容器云环境如式(1)所示:
C={C1,C2,…,Ci,…,Cn}。
(1)
式中:C表示整个容器云环境;元素Ci表示容器云环境中第i类微服务的集合。
其次,容器云环境中微服务与异构容器的对应关系表示如式(2)所示,异构容器与多层次异构方法之间的关系如式(3)所示:
Ci={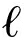 i1,
i1,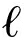 i2,…,
i2,…,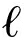 ij,…,
ij,…,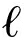 im};
im};
(2)
(3)
式中: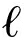 ij表示微服务Ci的一种异构容器,由多个“label-value”描述项组成,每个标签表示一个维度;
ij表示微服务Ci的一种异构容器,由多个“label-value”描述项组成,每个标签表示一个维度;![]() 表示异构容器
表示异构容器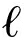 ij在第k个维度分配的标签值;维度d表示对容器进行d种不同层次的异构,例如CPU的异构、容器运行时的异构、容器操作系统的异构等。
ij在第k个维度分配的标签值;维度d表示对容器进行d种不同层次的异构,例如CPU的异构、容器运行时的异构、容器操作系统的异构等。
对微服务的异构度进行量化求解,通过异构容器标签值来计算微服务Ci所有异构容器的平均异构度如式(4)所示,微服务中任意两异构容器间平均距离如式(5)所示:
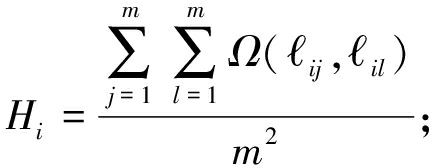
(4)
(5)
设标签值取值为0~1,结合式(4)、(5)和标签值取值范围可知异构度指标值为0≤Hi<1。
3.3 博弈模型定义
动态调度信号博弈模型(dynamic scheduling signal game model, DSSGM)可以表示为十一元组![]() 以下是各参数的详细定义。
以下是各参数的详细定义。
(1)N=(ND,NA)为信号博弈模型中攻防双方的参与者空间,其中,ND作为容器云系统的防御者,向攻击者发送诱导信号;NA代表攻击者。
(2)本文假设容器云系统层次结构如图3所示,则应用程序的集合F={F1,F2,F3,F4},每个应用程序有一个或多个微服务部署在容器中提供服务。
(3)H={H1,H2,H3,H4,H5,H6,H7,H8}为系统中各微服务所有异构容器的平均异构度集合,![]() 与应用一一对应,表示整个应用所有异构容器的平均异构度。
与应用一一对应,表示整个应用所有异构容器的平均异构度。
(4)攻防双方的类型空间T={TD,TA},防御类型空间集合TD={D1,D2,…,Dn}。该模型中TD与F应用集合对应,基于(2)中假设,本文防御类型空间TD={D1,D2,D3,D4},其中D1表示选择应用F1中微服务的容器进行动态轮换,依此类推。TA={A1,A2,A3,A4}表示攻击者的类型集合。
(5)η{D,A}为攻防双方策略空间,防御者策略集合D={d1,d2,…,dg|g∈N+},本文防御策略D={d1,d2,d3,d4,d5,d6,d7,d8},其中di表示选择微服务Ci的容器进行轮换。A={a1,a2,…,ah|h∈N+}表示攻击者策略集合;A={a1,a2,a3,a4}为本文攻击者策略集合;ai表示攻击者对应用Fi的容器发起攻击。
(6)Pk表示攻击者在博弈第k个阶段对防御者类型空间的先验信念集合,其中![]() 本文攻击者先验信念集合Pk={pk(D1),pk(D2),pk(D3),pk(D4)}。
本文攻击者先验信念集合Pk={pk(D1),pk(D2),pk(D3),pk(D4)}。
(7)M={m1,m2,…,mn|n∈N+}为防御者信号空间,M={m1,m2,m3,m4}为本文防御者的信号空间集合,其中mi表示发送对应用Fi的容器进行动态轮换的信号。
![]() 代表攻击者收到防御信号mj后,结合先验信念集合计算得到的后验信念概率推断。
代表攻击者收到防御信号mj后,结合先验信念集合计算得到的后验信念概率推断。
![]() 为收益函数集合,其中
为收益函数集合,其中![]() 代表攻击者在博弈的第k个阶段的收益函数;
代表攻击者在博弈的第k个阶段的收益函数;![]() 表示防御者在博弈第k个阶段的收益函数。
表示防御者在博弈第k个阶段的收益函数。
(10)λ为多阶段信号博弈回合总数,k表示当前博弈阶段,k={1,2,…,λ},其中k∈[1,λ],k∈N+。
![]() 表示攻击者在第k阶段微服务对应容器的信息获取程度的集合。
表示攻击者在第k阶段微服务对应容器的信息获取程度的集合。![]() 与Ci一一对应,其中
与Ci一一对应,其中![]() 值越大表示攻击者对该微服务容器信息获取越多,攻击微服务Ci对应容器的成功率越高。
值越大表示攻击者对该微服务容器信息获取越多,攻击微服务Ci对应容器的成功率越高。
3.4 博弈收益量化
攻击者发起一轮攻击的收益主要由攻击成本(AC)和系统损失(SDC)[12]共同决定。攻击成本指攻击者探测收集系统信息,针对容器发起攻击产生的开销。系统损失主要指攻防双方在对抗过程中导致的系统功能故障或敏感信息丢失带来的损失,结合本文攻防对抗场景,主要由安全属性损失(SAD)、攻击致命度(AL)[13]、资源重要程度(CR)[14]组成。安全属性损失代表当前攻击对系统性能的影响;攻击致命度由攻防两端采取策略决定,本文主要通过攻击成功率体现;资源重要程度文中表示微服务对应容器在系统中的价值。攻击者在第k轮博弈收到诱导信号为ml时,防御者选定防御类型空间Dj时,攻击者采取攻击策略ai时的期望收益如式(6)所示;防御者选择防御类型Dj中的防御策略dp时,攻击者的收益如式(7)所示;系统损失(SDC)如式(8)所示。
(6)
![]() ;
;
(7)
SAD(ai,dp)。
(8)
式中:λp表示防御者在对应防御类型下选择防御策略dp的概率。在系统损失SDC的收益计算中,CR由攻击者采取的攻击策略ai决定;SAD由攻防双方采取的策略决定;AL以攻击成功率的形式呈现,由攻防两端采取的策略、容器异构度以及攻击者对容器信息获取程度共同决定。
防御者收益由防御成本(DC)[12]、系统损失、诱导信号开销(SC)和防御者收益(DE)[13]共同构成。防御成本表示一轮博弈容器动态轮换的开销,每轮博弈选取一种微服务对应的容器进行动态轮换,开销与微服务中异构容器的平均异构度正相关;系统损失同攻击者收益部分的描述;诱导信号开销代表防御者主动发送诱导信号诱骗、引导攻击行为的开销;防御者收益表示防御者保护目标容器正常运行的收益,包括直接收益和间接收益[10]。在第k轮博弈中,攻击者采取攻击策略ai,防御信号为ml时,防御者在防御类型Dj下的期望收益如式(9)所示。在此基础上,防御者选择防御策略dp时,防御者收益如式(10)所示。
(9)
SDC(ai,dp,TRk)-SC(ml)。
(10)
3.5 均衡求解
文中信号博弈模型的精炼贝叶斯均衡求解与攻击者后验概率推断![]() 以及攻防策略组合(m*(D),a*(m))相关。其中,攻击者计算最优攻击策略的过程如式(11)所示;在考虑均衡策略的情况下,防御者获取最优防御信号的过程如式(12)所示;攻击者根据贝叶斯公式计算后验概率过程如式(13)所示。
以及攻防策略组合(m*(D),a*(m))相关。其中,攻击者计算最优攻击策略的过程如式(11)所示;在考虑均衡策略的情况下,防御者获取最优防御信号的过程如式(12)所示;攻击者根据贝叶斯公式计算后验概率过程如式(13)所示。
(11)
(12)
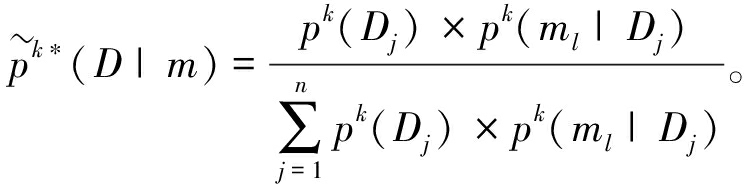
(13)
式中:argmax表示求解自变量最大值。
3.6 博弈均衡分析
本文构建了动态调度信号博弈模型,使用精炼贝叶斯均衡求解攻防最优策略。
纯策略精炼贝叶斯均衡可以表示为![]() 其中m*(Dj)表示防御类型空间为Dj时,防御者对应的信号策略集对应为{m(D1),m(D2),m(D3),m(D4)};a*(m)表示在收到防御者发送的信号ml后,攻击者的最佳攻击策略有序对
其中m*(Dj)表示防御类型空间为Dj时,防御者对应的信号策略集对应为{m(D1),m(D2),m(D3),m(D4)};a*(m)表示在收到防御者发送的信号ml后,攻击者的最佳攻击策略有序对![]() 表示攻击者的后验概率推断。
表示攻击者的后验概率推断。
在求解不完全信息动态博弈均衡过程中,本文考虑采取纯策略的情况下求解均衡,对分离均衡和混同均衡进行分析。
(1)分离均衡。分离均衡指防御者选择在不同防御类型空间下发送不同的信号。若防御者发送的诱导信号对应防御类型空间为(m1,m2,m3,m4),需要确保防御者在防御类型下发送对应的诱导信号可以获得最大收益,并且攻击者在收到诱导信号后,采取的攻击策略与之一一对应,满足以上条件该分离均衡策略存在。
(2)混同均衡。混同均衡指对于不同的防御类型空间发送同一种诱导信号。这里假设防御者的纯策略有序对为(m4,m4,m4,m4),在混同均衡约束下需要保证防御者在各防御类型空间下选择其他诱导信号获取的收益均小于选择上述诱导信号的收益,并且对于攻击者,在收到防御者发来诱导信号为m4的情况下选取攻击策略a4,满足以上条件该混同均衡策略存在。
3.7 算法设计
算法1 异构容器动态调度策略选取算法。
输入:![]()
输出:最优调度策略和最优动态调度策略信号。
① 初始化博弈模型![]()
② 初始化攻防双方类型空间T={TD,TA},防御者类型空间为TD={D1,D2,D3,D4},攻击者类型空间为TA={A1,A2,A3,A4};
③ 初始化攻击者和防御者策略集合,攻击者策略集合为A={a1,a2,a3,a4},防御者策略集合为D={d1,d2,d3,d4,d5,d6,d7,d8};
④ 初始化防御信号空间M={m1,m2,m3,m4};
⑤ 采用容器异构量化算法计算容器异构度,计算得到集合H={H1,H2,H3,H4,H5,H6,H7,H8};
⑥ 初始化![]()
⑦ 自然选择防御类型的概率分布;
⑧ for(k=1;攻击者发起攻击并且系统未被攻破;k++)
⑨ 攻击者通过网络嗅探得到当前阶段先验概率集合为Pk={pk(D1),pk(D2),pk(D3),pk(D4)},收到诱导信号后计算得到后验信念集合为![]() mj)|i,j∈[1,4]};
mj)|i,j∈[1,4]};
⑩ 根据攻防收益函数分别计算攻防两端收益;
 基于式(11)~式(13)求解最优攻防策略a*(m)和m*(D);
基于式(11)~式(13)求解最优攻防策略a*(m)和m*(D);
 计算攻击者的后验概率推断
计算攻击者的后验概率推断![]() 更新信念集合Pk为Pk+1;
更新信念集合Pk为Pk+1;

![]() 误差在一定范围内
误差在一定范围内
 then求解博弈模型下精炼贝叶斯均衡
then求解博弈模型下精炼贝叶斯均衡![]() 该均衡解为分离策略或混同策略均衡;
该均衡解为分离策略或混同策略均衡;
 output k阶段博弈均衡的攻防策略集合;
output k阶段博弈均衡的攻防策略集合;
 else不满足条件,重新计算m*(Dj);
else不满足条件,重新计算m*(Dj);
 end if;
end if;
 根据当前攻击者对容器信息获取程度集合及攻防双方采取的策略更新TRk集合为TRk+1;
根据当前攻击者对容器信息获取程度集合及攻防双方采取的策略更新TRk集合为TRk+1;
 根据k阶段攻防策略更新防御策略概率集合、防御类型空间概率集合以及攻击者先验信念集合;
根据k阶段攻防策略更新防御策略概率集合、防御类型空间概率集合以及攻击者先验信念集合;
 end。
end。
算法首先初始动态调度信号博弈模型十一元组,结合容器异构度量算法计算得到H。然后,攻防双方根据收益函数计算收益,通过均衡策略选择攻防最优策略,并不断更新攻防双方概率集合,防御者在多阶段动态博弈过程中发送诱导信号,选择最佳的防御策略,有效保证了系统的安全性。根据攻防博弈过程,建立了攻防博弈树如图4所示。dk表示在对应防御类型下防御者的防御策略;pi表示自然选择防御类型的概率;pij表示攻击者的后验信念概率。
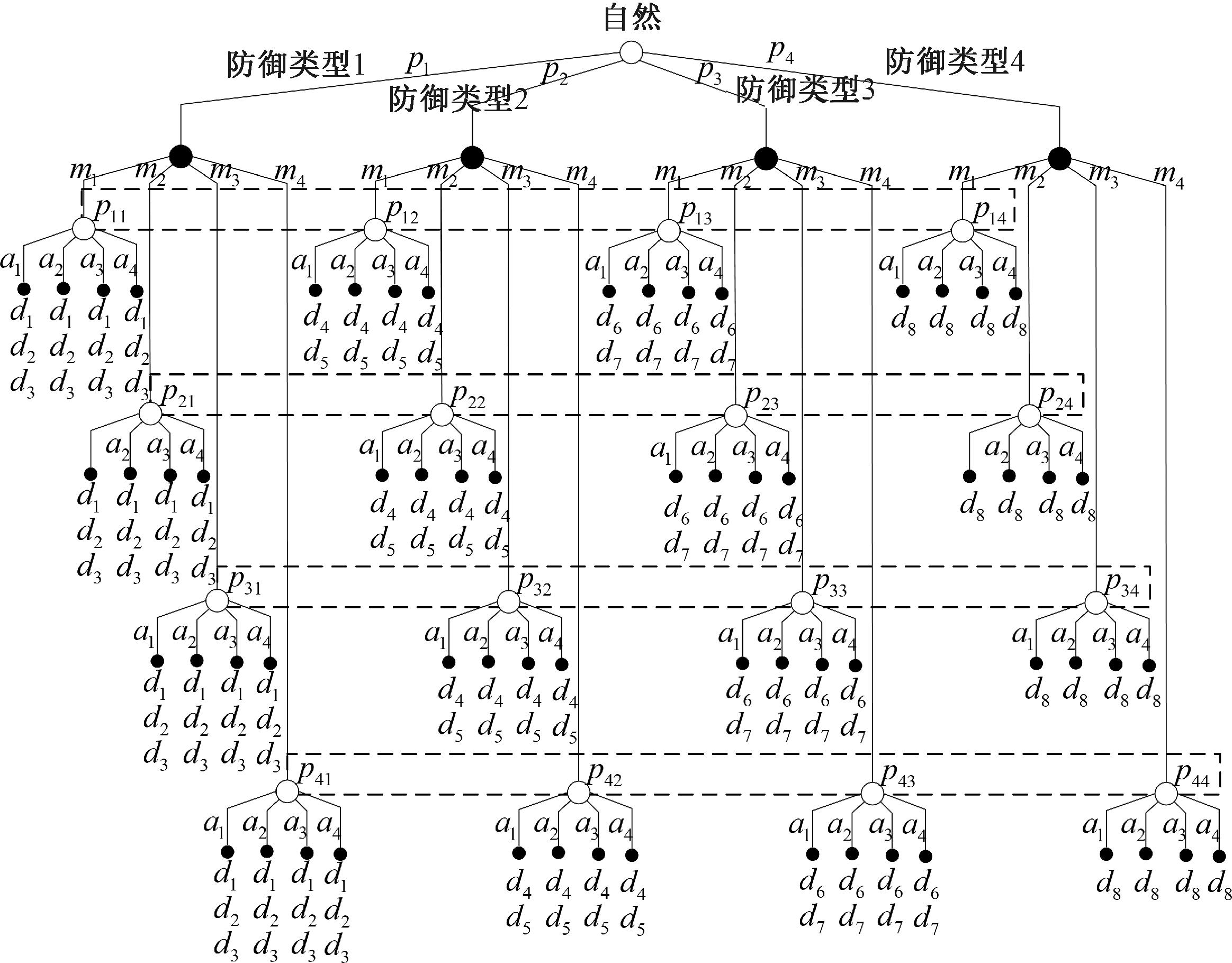
图4 攻防博弈树
Figure 4 Attack defense game tree
4 仿真实验与分析
4.1 实验设置
为了验证本文提出的动态调度信号博弈模型、异构度量化算法以及异构容器动态调度策略选取算法的有效性,本节构建容器云集群环境通过仿真实验对比现有的防御方法进行验证。
仿真实验环境包括1台X86服务器(2.40 GHz,48核,2 TB磁盘)用于集群中控制节点,两台X86服务器(2.40 GHz,64核,1 TB磁盘)用于集群中计算节点以及两台ARM服务器(2.00 GHz,64核,1 TB磁盘)用于集群中计算节点。5台基础设施服务器中,分别使用Ubuntu、RedHat、CentOS 3种不同的操作系统,并采取Kubernetes 对容器化应用和服务进行管理。在容器中部署Kata和Runc 两种容器引擎,使用Harbor作为异构容器镜像仓库,GitLab作为应用的代码仓库,同时将集成异构镜像构建工具和多样化编译构建工具提供容器镜像的异构性。在容器云集群中,部署4个Web应用,共有8个微服务提供服务,当前容器云系统的层次结构如图3所示,仿真工具使用MATLAB R2022a。本实验假设攻击者攻击策略是不断变化的,可以多阶段选取最优的攻击策略,将本文提出的方法分别与SmartSCR[6]和基于Stackelberg博弈的动态异构容器调度方法[10]进行对比。
(1)SmartSCR采用深度强化学习求解最优配置策略,本文设置SmartSCR使用DQN算法动态求解全服务容器动态轮换的周期。
(2)基于Stackelberg博弈的动态异构容器调度算法为部分服务动态轮换策略,算法求解的是各容器进行动态轮换的最优概率。
4.2 实验结果分析
4.2.1 防御策略多阶段效果对比
如图5(a),Stackelberg方法因缺乏动态更新机制,策略设定相对单一,导致防御收益逐渐下降。SmartSCR虽然能随环境动态调整,但全服务轮换开销大,防御者难以取得高收益。本文提出基于信号博弈的多阶段动态防御策略,通过选取部分微服务容器进行轮换,并主动发送诱导信号以引导攻击者的行为。实验数据表明,本文方法下多阶段防御者的平均收益达到最高,相较于SmartSCR提升14.2%,相较于Stackelberg提升65.73%。图5(b)表明,采取Stackelberg方法攻击者收益最高,SmartSCR通过深度强化学习算法计算最优配置,有效降低攻击者的平均收益,而本文策略在信号博弈指导下多阶段诱导攻击者的攻击行为,选取最优轮换策略,对攻击者收益抑制效果与SmartSCR持平。
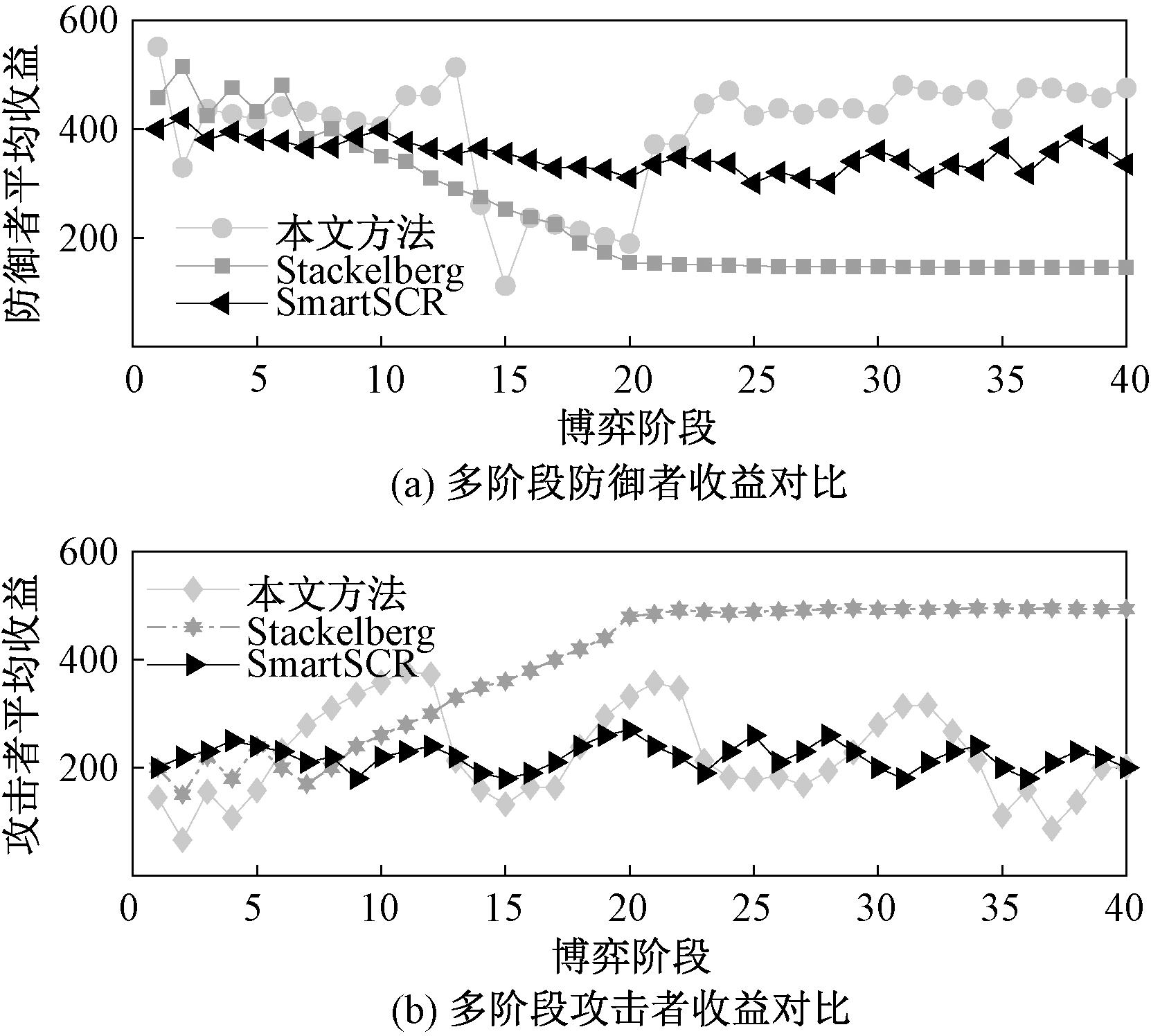
图5 不同方法下攻防两端收益对比
Figure 5 Comparison of attack-defense benefits under different methods
同时,对实验过程中防御者采取防御策略的动态轮换开销DC进行计算分析。SmartSCR采取全服务动态轮换的策略,轮换开销显著高于另外两种方法。本文方法与stackelberg动态轮换开销基本持平,对比SmartSCR开销降低了47.3%。综上所述,本文方法在保持系统轮换低开销的同时,显著提升了防御者的收益,并有效制约了攻击者的攻击行为。
4.2.2 TR值对攻击者的影响
本文提出了TR集合的概念,用来描述攻击者对容器云中各微服务容器的信息获取程度。TR值随着攻击者对容器的探测攻击以及系统防御策略的选取不断变化,TR值在文中设定为2~10。本节对比了40个阶段信号博弈过程中,攻击者收益与TR平均值的变化曲线,如图6所示,两者的曲线走势基本吻合。这表明当TR值越大时,攻击者对容器云系统整体的信息获取程度越高,该阶段采取攻击策略获取收益会越高,反之攻击者获取收益越低。量化攻击者对容器信息获取程度作为收益的影响因素符合动态变化的攻防场景,TR值可以表示防御方法的有效性,TR值整体越低,表示防御者采取的轮换策略选取方法效果越好。
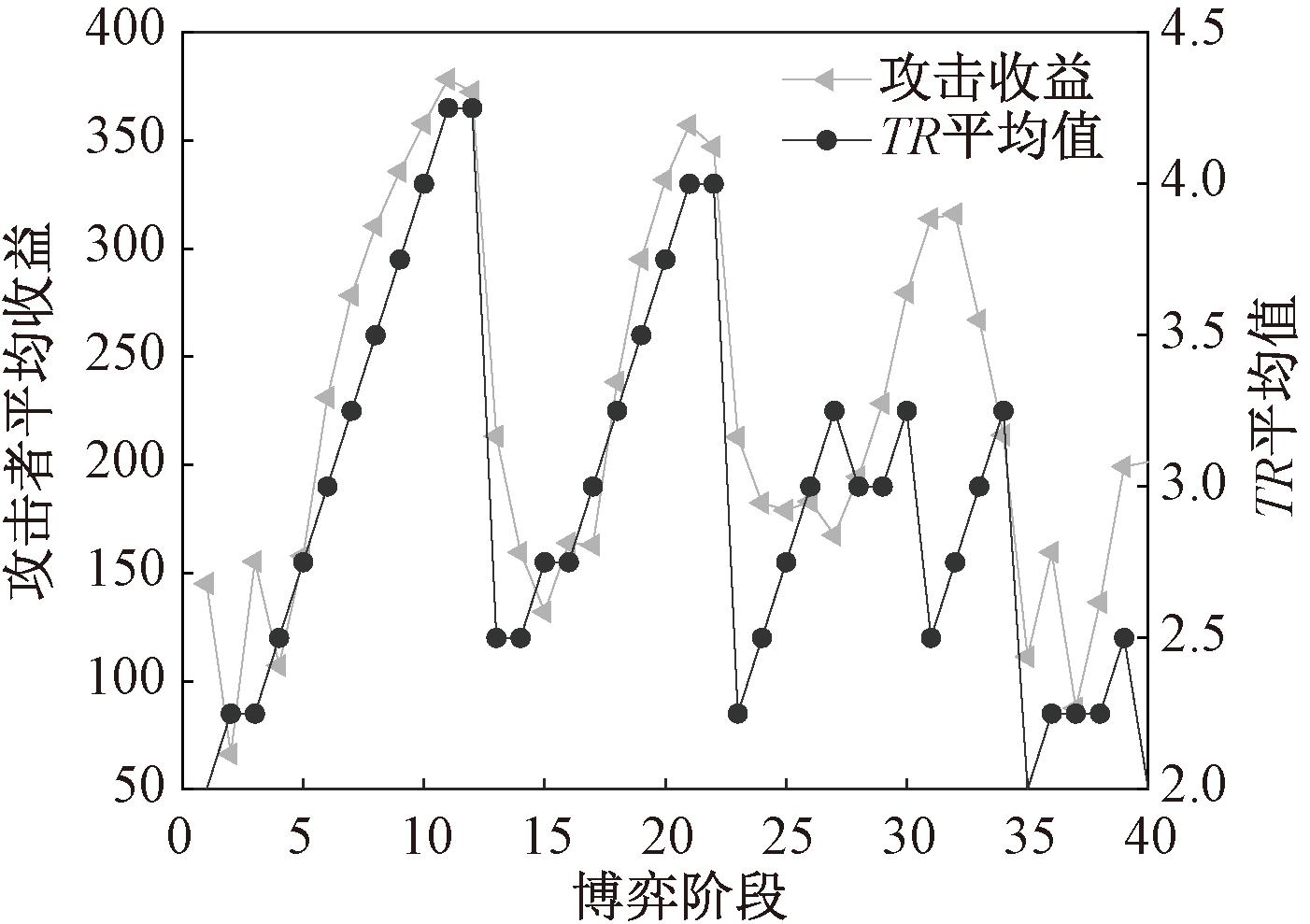
图6 多阶段攻击收益与TR平均值对比
Figure 6 Comparison of multi-stage attack benefits with TR average
4.2.3 异构度值对攻防两端的影响
本文提出了多维度量化容器异构度的算法,容器异构度影响容器云系统动态轮换的防御效果,本节通过实验数据验证提出的容器异构度量算法的有效性。设Hp代表整个容器云系统的容器异构程度,通过集合H计算得到Hp的值。前文实验均建立在Hp为0.435的条件下,本节分别设置Hp值为0.435、0.550、0.200条件下攻防两端进行40阶段信号博弈。图7为不同Hp值下多阶段攻防收益对比。
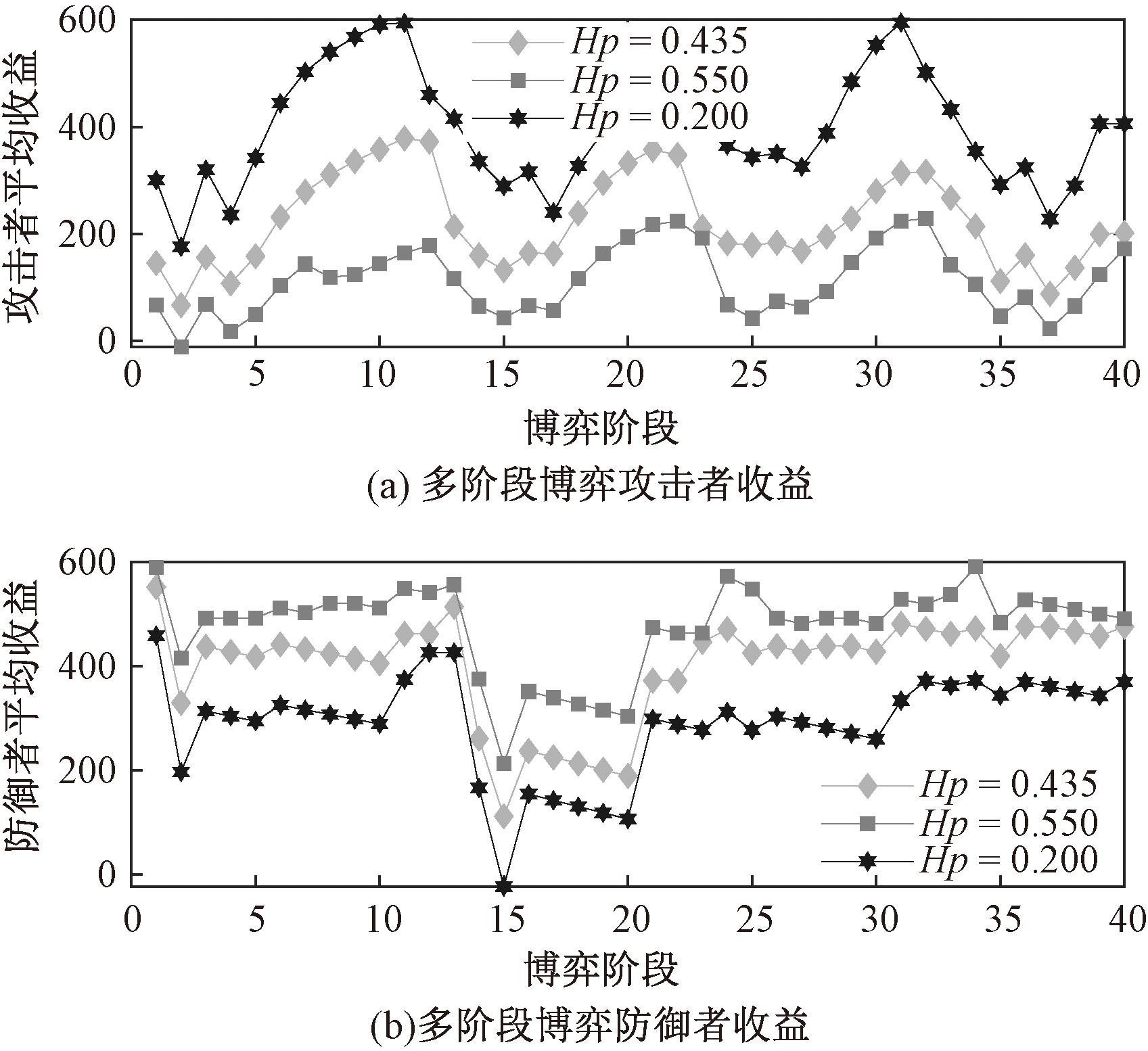
图7 不同Hp值下攻防收益对比
Figure 7 Comparison of attack-defense benefits under different Hp values
图7(a)中3条曲线表示攻击者在不同Hp值条件下40个阶段收益的变化情况,Hp值越大,攻击者越难对系统发起有效攻击,攻击者获取收益越少。图7(b)为防御者在不同Hp值条件下40个阶段收益的变化情况,Hp值越大,容器云系统的防御效果越好,防御者进行动态轮换的整体收益越高。因此,本文提出的多维度量化容器异构度的算法可以有效度量容器异构程度,是收益量化的重要影响因素。
5 结论
本文针对容器云环境存在的安全威胁,首先,提出了容器异构量化算法,从多维度计算容器异构程度;在此基础上,设计了攻击者对容器信息获取程度的动态集合,将攻防交互过程建模成动态调度信号博弈模型;最后,提出了动态调度策略选取算法,通过精炼贝叶斯均衡求解最优的动态防御策略。实验结果证明,本文方法在最大程度降低系统开销的基础上,提升了防御者的主导性,保证了系统的安全性。下一步工作重点是提升收益量化函数的准确性和实时性,在真实容器云攻防场景进行测试,优化调整模型参数,提升容器云系统的安全性。
[1] HAN S H, LEE H K, LEE S T, et al. Container image access control architecture to protect applications[J]. IEEE Access, 2012, 8: 162012-162021.
[2] GAO X, STEENKAMER B, GU Z S, et al. A study on the security implications of information leakages in container clouds[J]. IEEE Transactions on Dependable and Secure Computing, 2021, 18(1): 174-191.
[3] LIM S Y, STELEA B, HAN X Y, et al. Secure namespaced kernel audit for containers[C]∥Proceedings of the ACM Symposium on Cloud Computing. New York: ACM, 2021: 518-532.
[4] ABED A S, AZAB M, CLANCY C, et al. Resilient intrusion detection system for cloud containers[J]. International Journal of Communication Networks and Distributed Systems, 2020, 24(1): 1-22.
[5] HYDER M F, AHMED W, AHMED M. Toward deceiving the intrusion attacks in containerized cloud environment using virtual private cloud-based moving target defense[J]. Concurrency and Computation: Practice and Experience, 2023, 35(5): e7549.
[6] 张帅, 郭云飞, 孙鹏浩, 等. 云原生下基于深度强化学习的移动目标防御策略优化方案[J]. 电子与信息学报, 2023, 45(2): 608-616.ZHANG S, GUO Y F, SUN P H, et al. Moving target defense strategy optimization scheme for cloud native environment based on deep reinforcement learning[J]. Journal of Electronics &Information Technology, 2023, 45(2): 608-616.
[7] 黄万伟, 袁博, 王苏南, 等. 基于非零和信号博弈的主动防御模型[J]. 郑州大学学报(工学版), 2022, 43(1): 90-96.HUANG W W, YUAN B, WANG S N, et al. Proactive defense model based on non-zero-sum signal game[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(1): 90-96.
[8] WANG Y W, GUO Y F, GUO Z H, et al. CLOSURE: a cloud scientific workflow scheduling algorithm based on attack-defense game model[J]. Future Generation Computer Systems, 2020, 111: 460-474.
[9] 李凌书, 邬江兴, 曾威, 等. 容器云中基于信号博弈的容器迁移与蜜罐部署策略[J]. 网络与信息安全学报, 2022, 8(3): 87-96.LI L S, WU J X, ZENG W, et al. Strategy of container migration and honeypot deployment based on signal game in cloud environment[J]. Chinese Journal of Network and Information Security, 2022, 8(3): 87-96.
[10] 曾威, 扈红超, 李凌书, 等. 容器云中基于Stackelberg博弈的动态异构调度方法[J]. 网络与信息安全学报, 2021, 7(3): 95-104.ZENG W, HU H C, LI L S, et al. Dynamic heterogeneous scheduling method based on Stackelberg game model in container cloud[J]. Chinese Journal of Network and Information Security, 2021, 7(3): 95-104.
[11] SULTAN S, AHMAD I, DIMITRIOU T. Container security: issues, challenges, and the road ahead[J]. IEEE Access, 2019, 7: 52976-52996.
[12] 张恒巍, 余定坤, 韩继红, 等. 基于攻防信号博弈模型的防御策略选取方法[J]. 通信学报, 2016, 37(5): 51-61.ZHANG H W, YU D K, HAN J H, et al. Defense policies selection method based on attack-defense signaling game model[J]. Journal on Communications, 2016, 37(5): 51-61.
[13] 刘道清, 扈红超, 霍树民. 基于移动目标防御信号博弈的容器迁移策略[J]. 计算机应用研究, 2023, 40(3): 890-897.LIU D Q, HU H C, HUO S M. Container migration strategy based on moving target defense signaling game[J]. Application Research of Computers, 2023, 40(3): 890-897.
[14] LEI C, ZHANG H Q, WAN L M, et al. Incomplete information Markov game theoretic approach to strategy generation for moving target defense[J]. Computer Communications, 2018, 116: 184-199.