锂离子电池因具有能量密度高、自放电率低、体积小和循环寿命长等优点[1-2],目前被广泛应用于包括电动汽车、储能系统在内的绿色能源行业[3-4]。然而,由于制造技术和生产工艺的复杂性,在成组使用时单体电池间不可避免地会存在不一致性[5-6]。为了确保电动汽车和其他由电池供电设备的运行稳定性,必须消除或降低电池之间的不一致性,以提高电池组的整体可用容量[7]。因此,需要有一种有效的电池均衡系统来实现电池组中不同单体电池电量的快速均衡控制。
被动均衡作为最传统的均衡方式,原理简单、易于实现,但由于其是通过均衡电路中的耗能元件消耗掉高能电池的能量来实现均衡[8],因此,电池产热量增大,可能会加重电池热管理系统的负担。主动均衡是目前研究的主要方向[9],其通过在电路中添加电感、电容类储能元件实现能量从高能电池转移到低能电池,最终实现均衡。但主动均衡电路的结构复杂度一般较高,另外其成本和均衡速度也是其使用场景受限的原因。
Daowd等[10]改进了多电容器均衡电路,并率先提出了单电容均衡结构,实现了任意单体电池之间的能量传输。但在基于电容的均衡拓扑中,电压是唯一的均衡变量,且当电压差较小时均衡效率降低。基于变压器的均衡拓扑解决了电压差较小时均衡效率低下的问题[11],但其体积大、成本高、扩展性差,难以应用到电池数量多的场合。
基于变换器的均衡拓扑结构较为灵活,适用性广。Das等[12]提出的Buck-Boost均衡拓扑实现了相邻电池之间的能量传输,但当需要均衡的电池相距较远时,其效率会大大降低。Wu等[13]提出了一种基于Buck-Boost变换器的分层均衡拓扑,将均衡过程分为多个不同层级同时进行,从而有效地加快了均衡速度。但其控制策略复杂,拓展性差。为了解决这个问题,郭向伟等[14]提出一种基于LC储能的主动均衡电路,该电路使用单个电感电容可以实现任意单体电池间的直接均衡。Chen等[15]也提出一种基于单电感的双向主动均衡方法,同样允许均衡能量直接从任意电池传递到任意电池。
均衡能量转移效率也是评判均衡拓扑优劣的标准之一,为了减少能量损失,Ji等[16]提出了无须DC-DC转换器的可重构均衡拓扑,电池组的容量利用率达到99.8%。针对可重构电路在均衡过程中电压波动的问题,Zhang等[17]提出了一种具有额外电源的可重构电路,以稳定输出电压。但可重构电路只适用于电池充放电状态,不适用于电池的静置状态。
综上所述,目前有关主动均衡方法的研究主要针对的是单体电池对单体电池均衡、电池组与单体电池均衡以及相邻电池成组进行均衡,均衡拓扑存在均衡时间长、均衡路径灵活性差等问题,对不相邻电池成组均衡的研究较少,而实际使用过程中,电池包中电池的电量分布较为复杂,需要更加灵活的均衡路径来缩短均衡时间。因此,本文将Buck-Boost均衡电路与可重构电路相结合提出一种均衡电路,同时提出配套的均衡控制策略,由于增加了均衡路径,均衡时间和能量转移次数都有不同程度的减少。
1 新型拓扑结构及验证
1.1 均衡拓扑结构
本文将可重构电路与Buck-Boost电路相结合,提出了一种新型均衡拓扑结构和相应的控制策略。均衡拓扑如图1所示。均衡电路由电池模块、开关阵列和均衡单元组成。开关阵列包括电池正极开关(S11~Sn1)、电池负极开关(S12~Sn2)和与每个电池配对的一对互斥开关(K11~Kn1、K12~Kn2)。均衡电路采用非隔离的Buck-Boost电路,电路元件包括电感(L)和MOSFET(Q1~Q4)。(在以下描述中,颜色用于表示不同的电池能量水平:红色表示低电量电池,黄色表示高电量电池,绿色表示正常电池。)
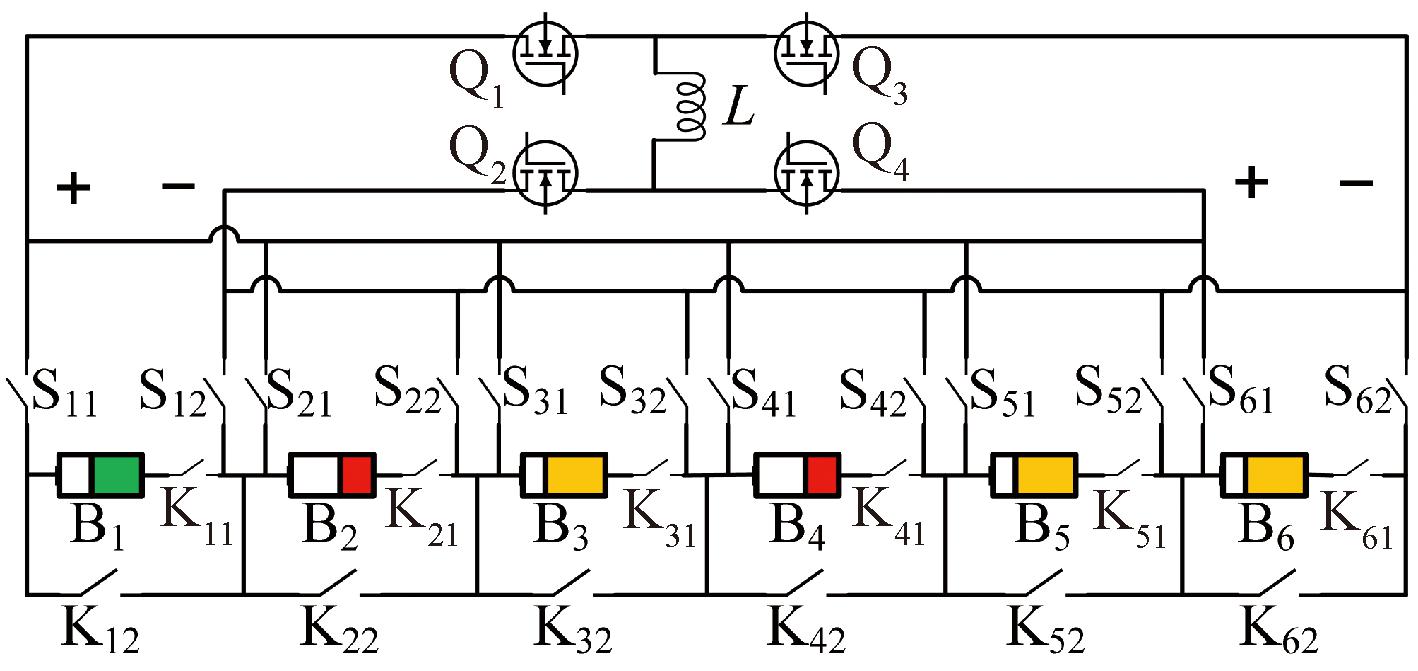
图1 所提均衡拓扑结构
Figure 1 Proposed balanced topology
所提出的拓扑结构有3种工作模式,即任意单元到任意单元的平衡(模式1)、多单元到任意单元的平衡(模式2)和多单元到多单元的平衡(模式3),且在进行多单元均衡时,可以实现不相邻电池成组。
所提均衡拓扑具有以下优点。
(1)可同时对多个电池进行均衡,大大缩短了均衡时间。
(2)可以将问题电池及时隔离出电路,提高电路安全性和均衡性能。
(3)减少了均衡过程中的能量传递次数,有利于提高电池寿命。
1.2 电路模型验证
均衡电路在工作时主要包括两部分,即先由高能电池对电感进行充电,之后再由电感对低能电池进行充电。因此,为了验证均衡电路是否能按照预期进行工作,将均衡电路进行以下等效。高能电池所在的回路为放电回路,等效元件有高能电压源E1、总内阻R1以及开关Q1;低能电池所在的回路为充电回路,等效元件有低能电压源E2、总内阻R2,以及开关Q2。将计算结果与仿真结果进行比较,以验证模型是否正确。均衡拓扑等效电路如图2所示,MOSFET驱动波形如图3所示。
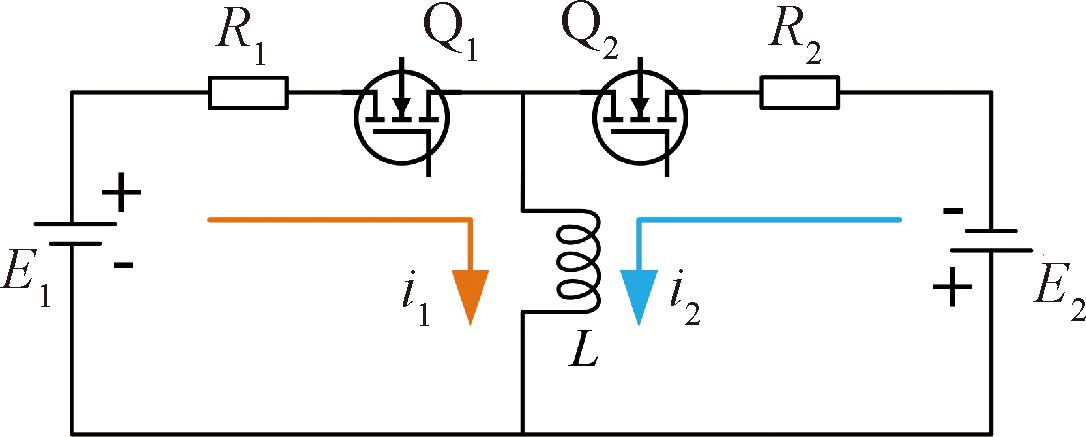
图2 均衡拓扑等效电路模型
Figure 2 Balanced topology equivalent model
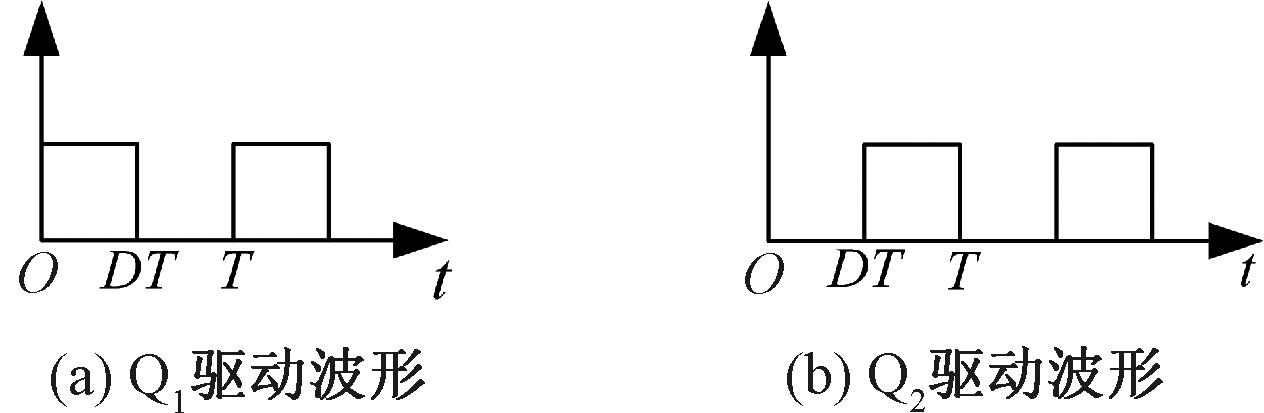
图3 MOSFET驱动波形
Figure 3 MOSFET driving waveform
假设所用开关和MOSFET的响应时间为0,并且它们的内阻计入电路总内阻中。充电电路中的开关和组件的总内阻记为R1,放电电路中的开关和组件的总内阻记为R2。假设B1表示高能电池,B2表示低能电池,则均衡过程可分为以下2个步骤。
步骤1 0≤t≤DT时,Q1导通,Q2断开,形成放电回路。此时,高能电池B1的电能转换为电感L的磁能。放电电流的方向如图2中的黄色箭头所示,放电电流i1(t)表示为[18]
(1)
步骤2 DT<t≤T时,Q1断开,Q2导通,形成充电回路。此时,存储在电感L中的磁能转换为低能电池B2的电能。充电电流的方向如图2中的蓝色箭头所示,充电电流i2(t)表示为
(2)
T=1/f。
(3)
式中:E1为高能电池B1的电压,V;E2为低能电池B2的电压,V;R1为放电回路的总电阻,Ω;R2为充电回路的总电阻,Ω;L为电感值,H;D为PWM信号的占空比;T为开关晶体管的开关周期,s;f为开关频率,Hz。
为了降低电感磁饱和的风险并提高能量传输效率,在每个周期结束时让充电电流为零。将i2(t)=0代入式(2),可以简化得到方程(4)。
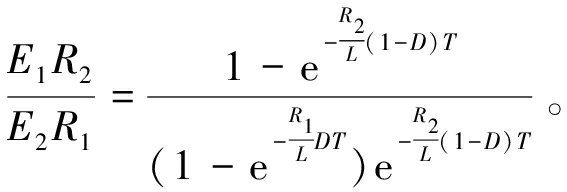
(4)
假设高能电池B1电压E1=3.4 V,低能电池B2电压E2=3.2 V,电感值L=100 μH,开关频率f=10 kHz,充放电回路内阻R1=R2=0.2 Ω。将上述参数代入式(4)中可以得出占空比D=0.51。在进行均衡拓扑和控制策略的联合仿真时,所选用的占空比应小于最大占空比0.51。
电感电流的理论值可以通过将上述参数代入式(1)和式(2)计算得到。同时,将上述参数代入等效电路的Simulink仿真模型中,可以得到电感电流的仿真值。对比结果如图4所示。
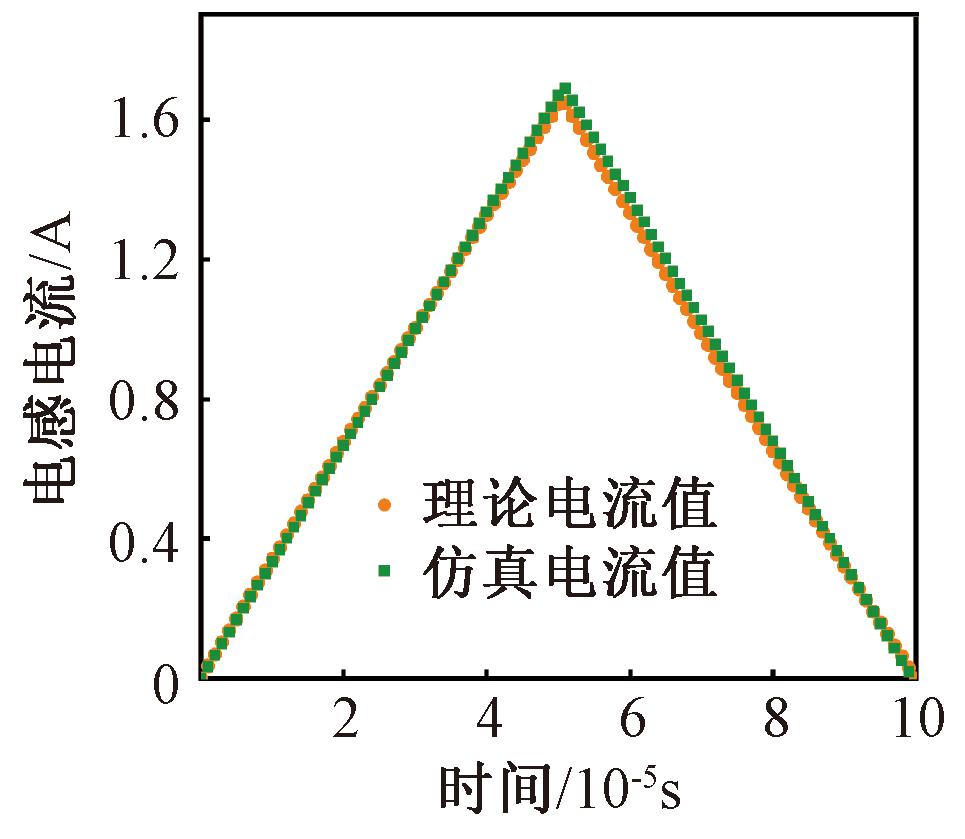
图4 单个周期电感电流理论值与仿真值对比
Figure 4 Calculated and simulated values of inductance current in a single cycle
从图4可以看出,在均衡过程中,电感电流近似线性变化。计算得到的均衡电流理论最大值为1.65 A,出现在t=5.1×10-5 s时。仿真得到的均衡电流的最大值为1.69 A,出现在t=5.1×10-5 s时。它们之间的相对误差为2.4%,但这是由于仿真时间步长设定所导致的,并且误差在可接受范围。因此,从图4可以清楚地看出,仿真模型能够真实地表达均衡过程。
2 影响均衡性能的因素分析
目前用于确定均衡系统有效性的指标主要是均衡时间和均衡损耗。因此,下文对所提拓扑的均衡电流和损耗进行了分析。根据上文推导的电路模型,均衡过程中的平均电流计算如下:
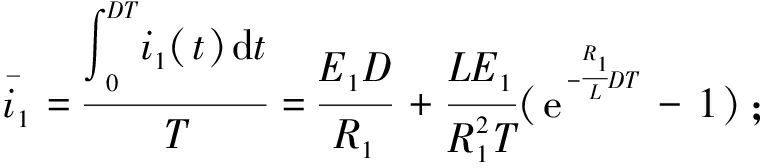
(5)
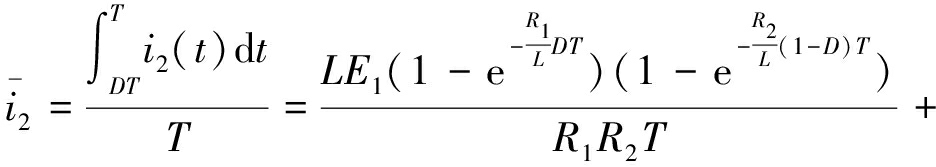
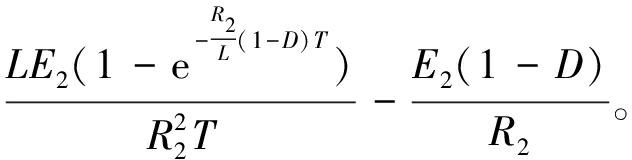
(6)
热损失率可以由以下公式计算得出[19]:
(7)
(8)
(9)
η=(WR1+WR2)/W1。
(10)
单个周期T内转移到低电量电池中的电荷量Q的表达式如下:
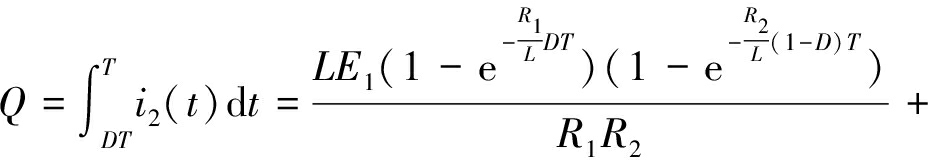
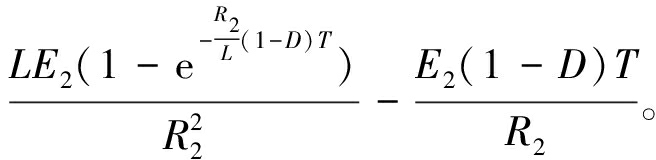
(11)
其中,式(5)和式(6)为整个周期T内放电电流和充电电流的平均值;式(7)为高能电池在一个周期内释放的总能量;式(8)为由于放电回路的总电阻产生热量而损失的总能量;式(9)为由于充电回路的总电阻产生热量而损失的总能量;式(10)表示热损失率。式(5)中包括的参数是电池电压、开关频率和占空比,其中,电池电压、开关频率是自变量,而占空比随这些参数变化而变化,因此,下文分析了电压差和开关频率对均衡性能的影响。
2.1 电池电压对均衡效果的影响
由于本文提出的均衡拓扑主要工作模式是多单元到多单元均衡,因此在均衡过程中,放电电池和充电电池数量会不断变化。E1为高电量电池的电压,E2为低电量电池的电压。为了便于分析,引入了电压差ΔE,如式(12)所示:
ΔE=E1-E2。
(12)
假设E2=3.2 V,电感值L=100 μH,开关频率f=10 kHz,充放电回路总电阻R1=R2=0.2 Ω。首先,根据式(5)来确定不同电压对应的占空比。随后,将D、E1、E2、L、R1、R2、f等参数代入式(5)~(11)中进行计算。
电压差对均衡电流、热损失率和单个周期内转移电荷量的影响如图5所示。从图5可以看出,在均衡过程中,随着电压差的增加,一个周期内的平均电流、热损失率和转移电荷量Q均呈上升趋势。以电压差ΔE=0时的均衡数据为参考,具体数据如表1所示。
表1 电压差对均衡效果的影响
Table 1 influence of battery voltage on the equalization effect
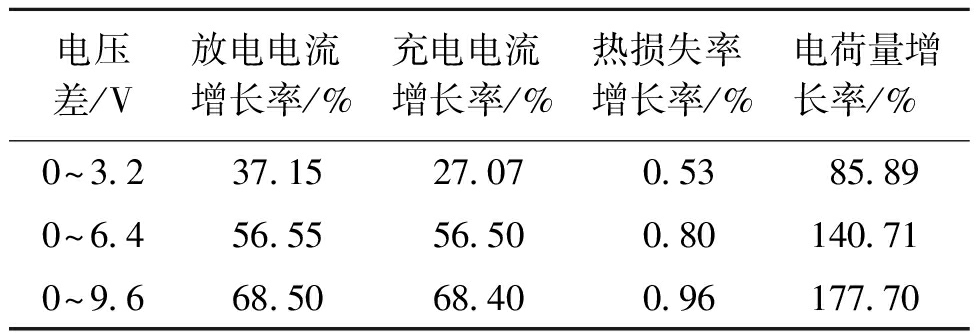
电压差/V放电电流增长率/%充电电流增长率/%热损失率增长率/%电荷量增长率/%0~3.237.1527.070.5385.890~6.456.5556.500.80140.710~9.668.5068.400.96177.70
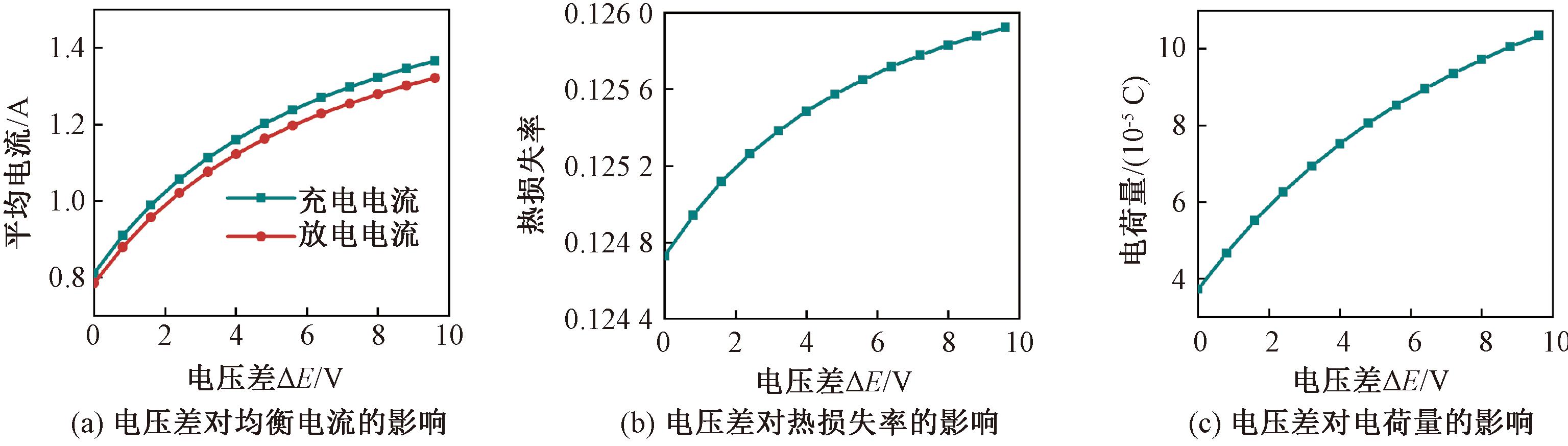
图5 电压差对均衡效果的影响
Figure 5 Influence of battery voltage on the equalization effect
从表1可以看出,平均电流和电荷量Q随着电压差的增加而大幅增加,最小增长率为27.07%。这表明增加电压差可以有效地缩短均衡时间。同时,可以看出,当电压差由0 V变为9.6 V时,热损失率增长率为0.96%。这表明热损失率没有随电压差增加而显著变化。因此,增加电压差可以提高均衡系统性能。
2.2 开关频率对均衡效果的影响
假设E1=3.4 V,E2=3.2 V,电感值L=100 μH,充放电回路的总电阻R1=R2=0.2 Ω,开关频率对均衡电流、热损失率和单个周期内转移电荷量的影响如图6所示。
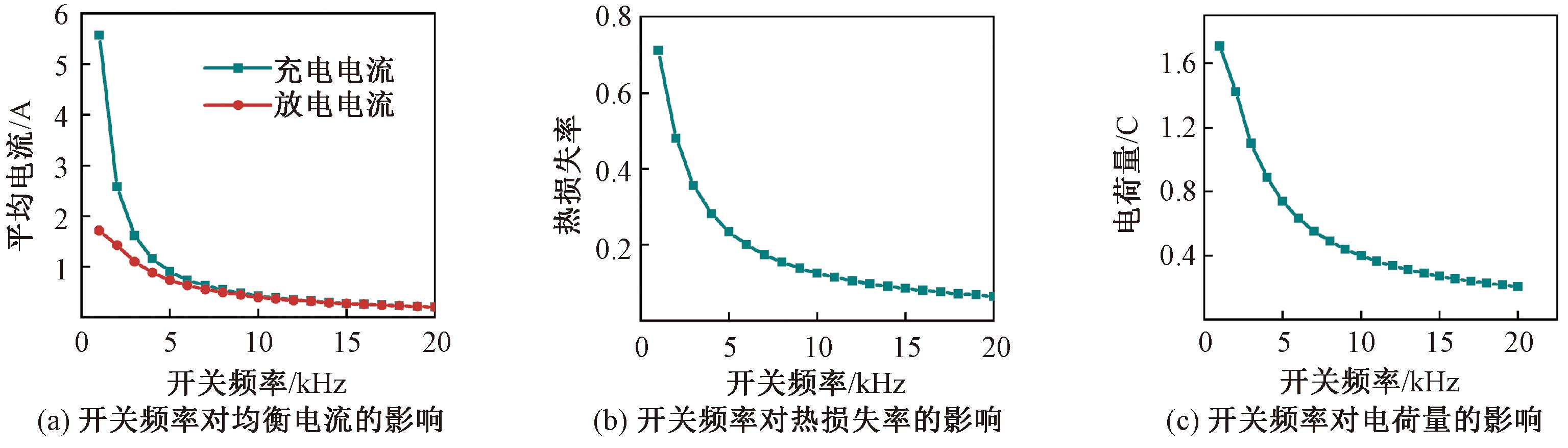
图6 开关频率对均衡效果的影响
Figure 6 Influence of switching frequency on the equalization effect
从图6可以看出,在均衡过程中,随着开关频率的增加,一个周期内的平均电流、热损失率和电荷量Q均呈下降趋势。以开关频率f=1 kHz时的均衡数据为参考,具体数据如表2所示。
表2 开关频率对均衡效果的影响
Table 2 Influence of switching frequency on equalization effect
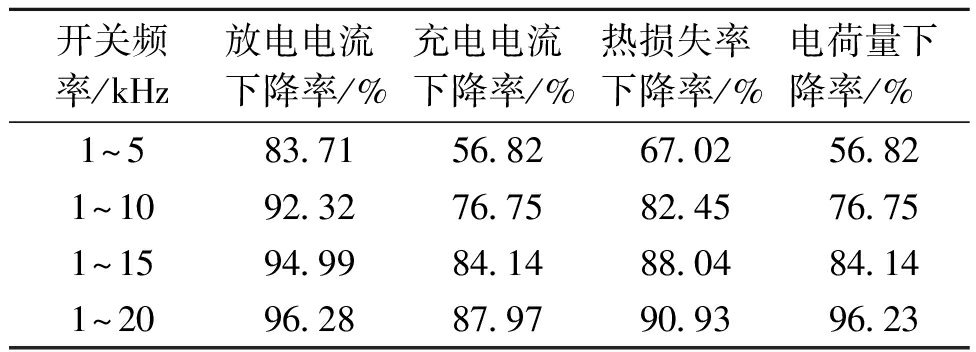
开关频率/kHz放电电流下降率/%充电电流下降率/%热损失率下降率/%电荷量下降率/%1~583.7156.8267.0256.821~1092.3276.7582.4576.751~1594.9984.1488.0484.141~2096.2887.9790.9396.23
从表2可以看出,平均电流和电荷量Q随开关频率的增加而大幅下降,最小下降率为56.82%。这表明,对于本文提出的拓扑结构,增加开关频率会导致均衡时间的增加。同时可以看出,随着开关频率的增加,热损失率有所降低。因此,开关频率不应该太大或太小,应选择中等的开关频率。在本文中,选择开关频率f=10 kHz。
3 仿真结果对比
3.1 均衡控制策略
电池组静置状态的均衡控制策略如图7所示,图7中,SOC1表示电量最高电池的SOC,SOC2表示电量最低电池SOC。对于电池的静置状态,首先根据各电池初始荷电状态SOC计算高能电池和低能电池的个数,工况有以下4种(对应3种工作模式)。
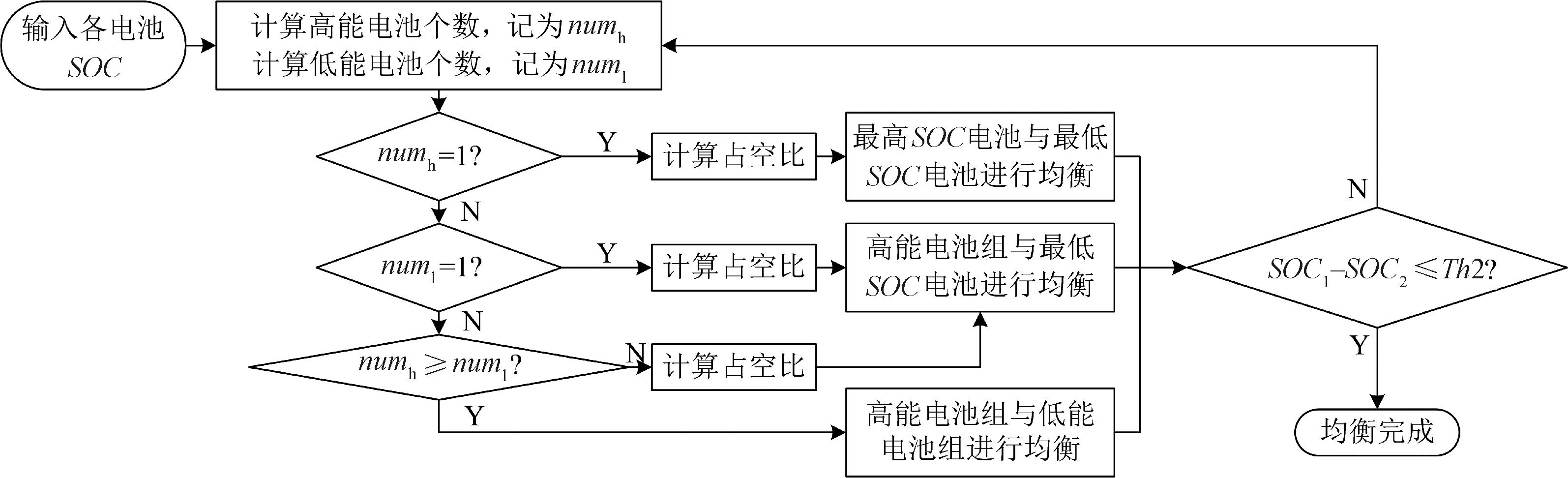
图7 基于可变占空比的均衡控制策略
Figure 7 Balanced control strategy based on variable duty cycle
①如果高能电池个数为1,则进行单对单均衡;②如果高能电池个数大于1,但低能电池个数为1,则进行多对单均衡;③如果高能电池个数和低能电池个数均大于1,但高能电池个数小于低能电池个数,则仍进行多对单均衡;④如果高能电池数和低能电池数均大于1,同时高能电池个数大于等于低能电池个数,此时进行多对多均衡。
文中选用8个串联电池进行模拟验证,但提出的均衡算法可以很方便地应用于更加复杂的电池组。在实际使用过程中,用户可以根据实际需求及成本预算,确定电路中具体元器件的参数,比如需要均衡的电池容量,所选电感可以承受的最大均衡电流。根据这些参数,结合电路的数学模型,即可求得在保证电路元件安全的情况下,均衡系统最多可承受多少电池同时参与均衡。例如:计算出电路元件可承受的最大均衡电流最高可满足n个高能电池对n个低能电池进行均衡,同时假设大规模电池组中的高低能量电池个数均大于n,那么只需在均衡算法中设置最大成组电池数为n即可,由高至低依次选择n个高能电池,由低至高依次选择n个低能电池进行均衡。
仿真采用Simulink的内置电池模型,每个锂离子电池的额定电压为3.2 V,额定容量为2 Ah。在MATLAB R2021b/Simulink中建立拓扑仿真模型,模型包括电池模块、开关阵列、电池分组模块、占空比计算模块、开关控制模块和Buck-Boost均衡单元。选择SOC作为均衡变量。在本文中,均衡开始阈值Th1为3,终止阈值Th2为1。
3.2 电池静息状态仿真结果对比
均衡仿真结果对比如图8所示。SOC为0~100%,假设8节串联电池的SOC值分别为46.5%、4.1%、45.9%、42.8%、45.5%、44.5%、43.1%、45.7%。定义若某电池SOC值满足SOCi≥SOCavg+Th2/2,则该电池为高能电池,用黄色表示;若某电池SOC值满足SOCi≤SOCavg-Th2/2,SOCavg为平均值,则该电池为低能电池,用红色表示;其余电池为正常电池,用绿色表示。绘制电池组初始能量状态分布如图8(a)所示,仿真验证如图8(b)和8(c)所示。Th_high和Th_low为电量正常电池的SOC上、下限。
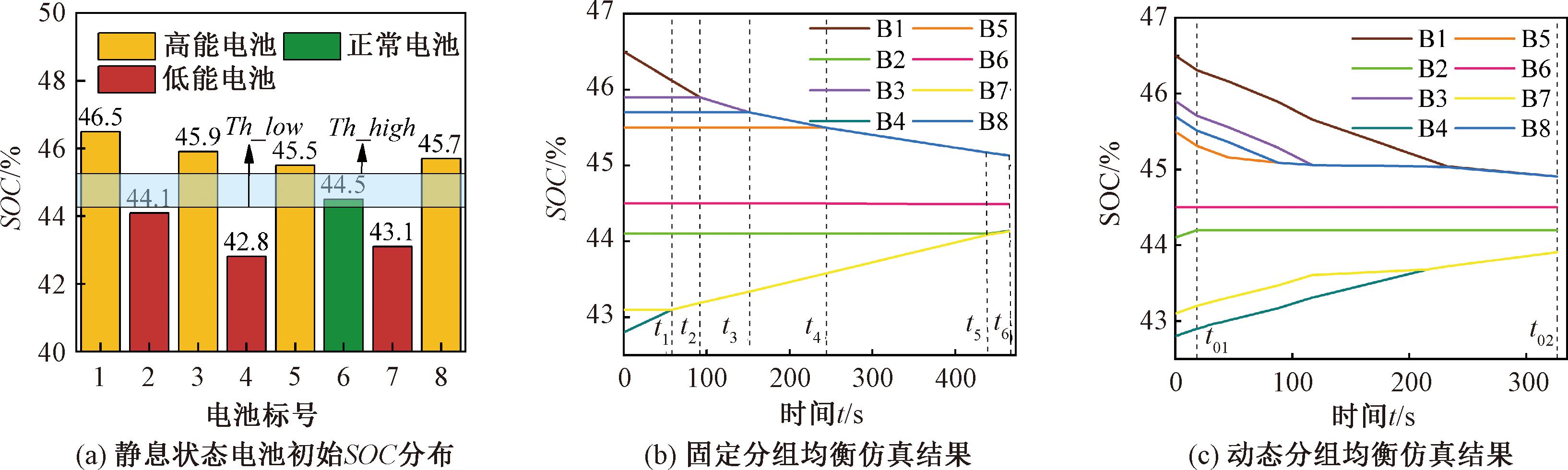
图8 均衡仿真结果对比
Figure 8 Comparison of equalization Simulation Results
固定分组控制策略[20]的仿真结果如图8(b)所示。由于电池的初始SOC分布,相邻的电池无法形成电池组,因此,在均衡开始时,应采用任意单元到任意单元的均衡模式,直到相邻电池可以形成电池组,切换为多单元到多单元均衡模式。达到均衡时间为464.528 s,均衡结束后电池组SOC的方差为0.216 5。
动态分组均衡控制策略的仿真结果如图8(c)所示。由于可重构电路的优点,无论电池SOC初始分布如何,均可实现多单元到多单元的均衡。因此,在均衡开始时,除了具有正常能量的电池B6之外,其余7个电池同时参与均衡。达到均衡时间为326.53 s,均衡结束后电池组SOC的方差为0.182。
两组均衡策略均衡后的具体数据如表3所示。由表3中数据可以得出,与固定分组控制策略相比,动态分组控制策略具有以下优点:可以有效地缩短均衡时间,均衡时间减少29.71%;方差降低16.13%。因此,动态分组控制策略相比固定分组控制策略具有显著的优势。
表3 固定分组和动态分组控制策略的均衡结果
Table 3 Equalization results for fixed and dynamic control strategies
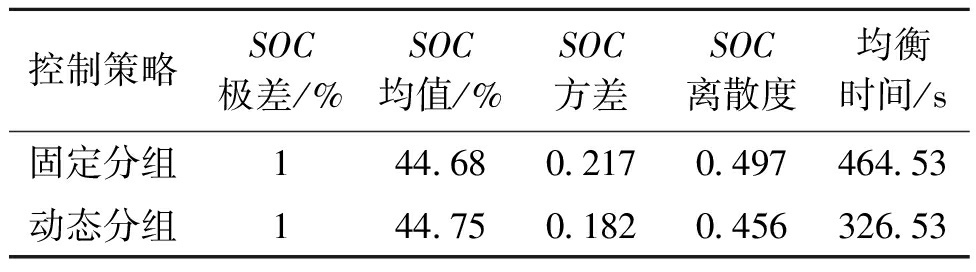
控制策略SOC极差/%SOC均值/%SOC方差SOC离散度均衡时间/s固定分组144.680.2170.497464.53动态分组144.750.1820.456326.53
电池之间的能量转移次数会影响电池的循环寿命,为了从能量转移次数的角度定量分析动态分组的优势,以电池静息状态为例分析能量转移次数的差别。均衡过程可以根据SOC变化曲线分为几个阶段。假设在单个开关周期中,电感对低能量电池的充电被记录为一次均衡。接下来以此为基础分析能量转移次数。固定分组均衡次数如表4所示,动态分组均衡次数如表5所示。
表4 固定分组均衡控制策略能量转移次数
Table 4 Number of energy transfers for fixed grouping control strategy
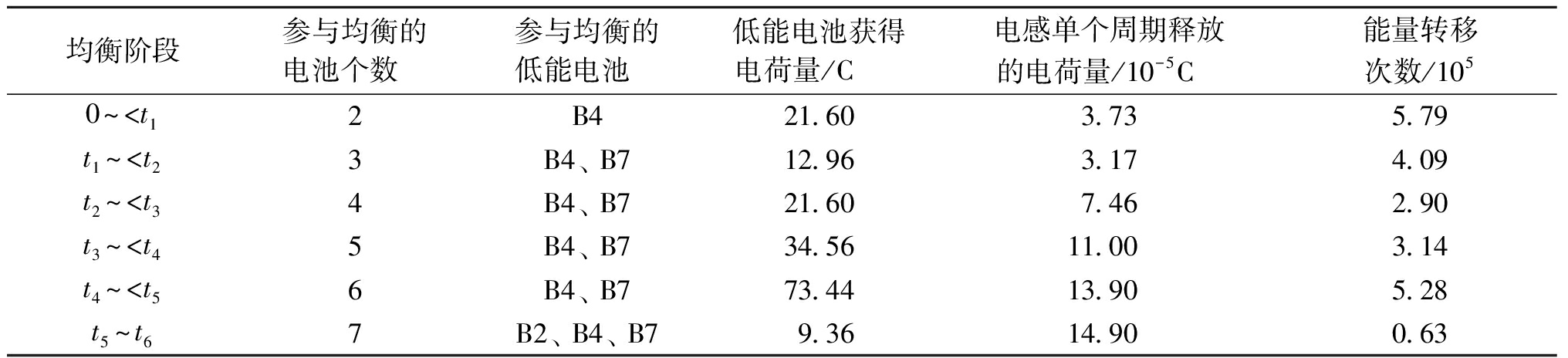
均衡阶段参与均衡的电池个数 参与均衡的低能电池 低能电池获得电荷量/C 电感单个周期释放的电荷量/10-5C 能量转移次数/1050~
表5 动态分组均衡控制策略能量转移次数
Table 5 Number of energy transfers for dynamic grouping control strategy

均衡阶段参与均衡的电池个数 参与均衡的低能电池 低能电池获得电荷量/C 电感单个周期释放的电荷量/10-4C能量转移次数/1050~
根据表4和表5中的数据绘制能量转移次数对比图如图9所示。
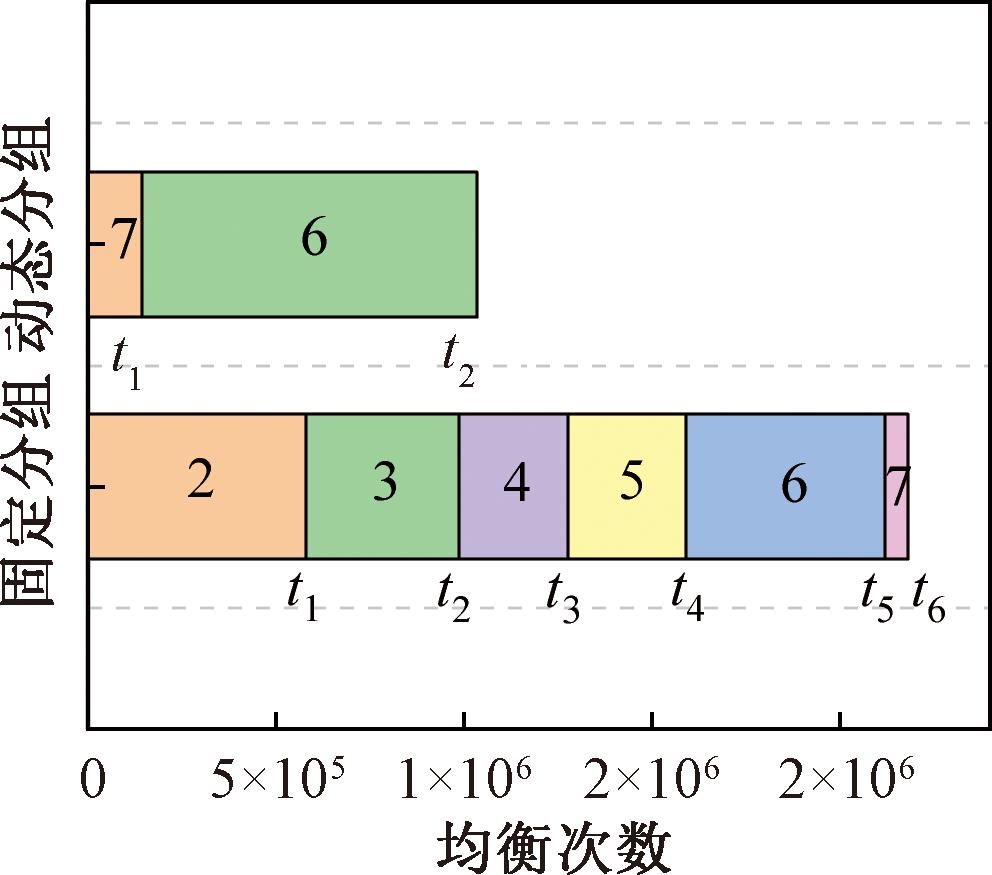
图9 能量转移次数对比
Figure 9 Comparison of the number of balancing energy transfers
结合表4、表5和图9可以看出,动态分组控制策略在减少能量转移次数方面具有显著优势,能量转移次数减少了52.5%,可以达到提高电池寿命的目的。
4 结论
本文提出了一种实现串联电池动态分组的均衡拓扑结构和控制策略。分析了可重构Buck-Boost均衡电路的工作模式和工作原理,并对模型进行了验证。此外,还分析了影响均衡性能的因素。结果表明,开关频率与均衡电流呈正相关,与热损失率呈负相关。因此,综合考虑均衡时间和均衡损耗,选择中等的开关频率来提高均衡系统的性能。电压差对占空比的影响不容忽视,因此在均衡控制策略中增加了可变占空比。最后,选取8个电池建立仿真模型。仿真结果表明,与固定分组控制策略相比,动态分组控制策略具有以下优点:均衡时间减少29.71%;方差降低16.13%;均衡能量转移次数减少52.5%。
[1] 陈港欣, 孙现众, 张熊, 等. 高功率锂离子电池研究进展[J]. 工程科学学报, 2022, 44(4): 612-624.CHEN G X, SUN X Z, ZHANG X, et al. Progress of high-power lithium-ion batteries[J]. Chinese Journal of Engineering, 2022, 44(4): 612-624.
[2] LU L G, HAN X B, LI J Q, et al. A review on the key issues for lithium-ion battery management in electric vehicles[J]. Journal of Power Sources, 2013, 226: 272-288.
[3] 李节宾, 孟海军, 皮正杰, 等. 锂原电池应用现状及发展趋势[J]. 电源技术, 2018, 42(5): 725-727.LI J B, MENG H J, PI Z J, et al. Application status and development trends of the lithium primary batteries[J]. Chinese Journal of Power Sources, 2018, 42(5): 725-727.
[4] ZENG X Q, LI M, ABDEL-HADY D, et al. Commercialization of lithium battery technologies for electric vehicles[J]. Advanced Energy Materials, 2019, 9(27): 1900161.
[5] CUI H Y, WEI Z B, HE H W, et al. Novel reconfigurable topology-enabled hierarchical equalization of lithium-ion battery for maximum capacity utilization[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 396-406.
[6] FAN X Y, ZHANG W G, WANG Z G, et al. Simplified battery pack modeling considering inconsistency and evolution of current distribution[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(1): 630-639.
[7] WU L, PANG K, ZHENG Y, et al. Amulti-module equalization system for lithium-ion battery packs[J]. International Journal of Energy Research, 2022, 46(3): 2771-2782.
[8] 刘嘉林. 电动汽车电池组被动均衡策略与SOC估算研究[D]. 昆明: 昆明理工大学, 2019.LIU J L. Research on passive equalization strategy and SOC estimation of electric vehicle battery pack[D].Kunming: Kunming University of Science and Technology, 2019.
[9] LI Y, XU J, MEI X S, et al. A unitized multiwinding transformer-based equalization method for series-connected battery strings[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11981-11989.
[10] DAOWD M, ANTOINE M, OMAR N, et al. Single switched capacitor battery balancing system enhancements[J]. Energies, 2013, 6(4): 2149-2179.
[11] SHANG Y L, CUI N X, ZHANG C H. An optimized any-cell-to-any-cell equalizer based on coupled half-bridge converters for series-connected battery strings[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 8831-8841.
[12] DAS U K, SHRIVASTAVA P, TEY K S, et al. Advancement of lithium-ion battery cells voltage equalization techniques: a review[J]. Renewable and Sustainable Energy Reviews, 2020,134:110227.
[13] WU X G, CUI Z H, LI X F, et al. Control strategy for active hierarchical equalization circuits of series battery packs[J]. Energies, 2019, 12(11): 2071.
[14] 郭向伟, 刘震, 耿佳豪, 等. 基于LC储能的串联电池组主动均衡方法研究[J]. 仪器仪表学报, 2020, 41(9): 242-251.GUO X W, LIU Z, GENG J H, et al. Research on the active balancing method of series battery pack based on LC energy storage[J]. Chinese Journal of Scientific Instrument, 2020, 41(9): 242-251.
[15] CHEN Y, LIU X, SHEN T, et al. An any-cell(s)-to-cell(s) equalization method with a single magnetic component for lithium-ion battery pack[J]. Journal of Energy Storage, 2020, 33(9): 102071.
[16] JI F, LIAO L, WU T, et al. Self-reconfiguration batteries with stable voltage during the full cycle without the DC-DC converter[J]. Journal of Energy Storage, 2020, 28:101213.
[17] ZHANG Y, HUANG M M, WU T Z, et al. Reconfigurable equilibrium circuit with additional power supply[J]. International Journal of Low-Carbon Technologies, 2020, 15(1): 106-111.
[18] 熊永华, 杨艳, 李浩, 等. 基于SOC的锂动力电池多层双向自均衡方法[J]. 电子学报, 2014, 42(4): 766-773.XIONG Y H, YANG Y, LI H, et al. Multi-level bi-directional active equalization method in lithium-ion power battery based on state-of-charge[J]. Acta Electronica Sinica, 2014, 42(4): 766-773.
[19] FAN T E, LIU S M, YANG H, et al. A fast active balancing strategy based on model predictive control for lithium-ion battery packs[J]. Energy, 2023, 279: 128028.
[20] LUO S Y, QIN D C, WU H X, et al. Multi-cell-to-multi-cell battery equalization in series battery packs based on variable duty cycle[J]. Energies, 2022, 15(9): 3263.