基于硫酸盐环境下混凝土耐久性的大量研究,硫酸盐的侵蚀机理已经有了较为清晰的认知[1]。硫酸盐侵蚀主要发生在混凝土砂浆中,而对其粗骨料的影响较小,硫酸根离子随溶液扩散至混凝土内部后,与水泥砂浆中的水化产物等发生化学反应,生成膨胀性产物石膏和钙矾石[2]。侵蚀产物不断积累造成混凝土内部产生开裂损伤,该现象被认为是受硫酸盐侵蚀后混凝土性能退化的重要原因[3]。
位于沿海、盐渍土及地下水等恶劣环境下的混凝土建筑在承受荷载的同时,受到硫酸盐等外部环境中腐蚀性介质的侵蚀。目前有关承载状态下混凝土结构的抗硫酸盐侵蚀性能的研究表明:压力能够抑制硫酸根离子在混凝土中的扩散,拉力则促进硫酸根离子在混凝土中的扩散[4]。数值模拟能够很大程度上避免试验耗时长、耗力大的缺点[5]。Wang等[6]也利用有限元软件实现了硫酸盐侵蚀混凝土的数值模拟。但有关荷载和硫酸盐侵蚀耦合作用于混凝土的细观数值模拟方法少见报道。有限元软件提供的多物理场耦合能更加真实、稳定地模拟混凝土结构的工作状态,并实现结构长期性能的预测[7]。
针对上述研究中的不足,本研究通过量化应力对混凝土孔隙率的影响,建立了荷载和硫酸盐耦合作用下混凝土中硫酸根离子扩散的细观数值模型。定量分析了不同硫酸盐浓度和水灰比下压应力水平对离子扩散的影响程度,并从细观层面对混凝土的损伤机理进行了分析。研究能够为荷载和硫酸盐侵蚀耦合作用下混凝土结构长期性能的改善提供新的理论借鉴和创新思路。
1 受压状态下的离子扩散方程
1.1 离子扩散方程
硫酸根离子的扩散通常发生在非稳态情况下。在这种情况下,离子浓度梯度变化较大且时间历程较长,而Fick第一定律更适用于浓度随时间变化较小或可忽略不计的情况,因此无法对扩散过程进行准确描述。考虑到硫酸根离子扩散过程中的化学反应消耗,通过Fick第二定律和化学反应动力方程的联立对硫酸根离子在混凝土内的扩散进行描述,如下式[8]:
(1)
式中:Cs为混凝土内硫酸根离子浓度,mol/m3;Cb为化学反应消耗的硫酸根离子浓度,mol/m3;t为侵蚀时间,d;x为侵蚀深度,mm;Deff为混凝土中硫酸根离子扩散系数,m2/s。
考虑到微观结构中孔隙率和曲折度的变化对离子扩散的影响,将硫酸根离子在水泥砂浆中的扩散系数描述为[9-10]
(2)
(3)
式中:φσ为应力作用下混凝土的孔隙率;Ds0为溶液中硫酸根离子扩散系数,取3.5×10-10 m2/s [11];τ为混凝土曲折度,指离子在传输时的实际路径与最短路径长度的比值,由式(3)确定;fs为砂子体积分数;fa为石子体积分数。
1.2 化学反应
研究表明,硫酸根离子扩散至混凝土内部后与水泥水化产物等发生化学反应,生成膨胀性侵蚀产物石膏和钙矾石对混凝土微观结构造成的长期损害,并且这种损伤会随着侵蚀的进行逐渐加重。为方便量化各物质含量的关系,对化学反应方程进行简化[12]:
(4)
(5)
上式表明,硫酸根离子的化学反应消耗发生在式(4),且离子的消耗量与石膏的生成量、钙离子的消耗量相同。化学反应引起的物质浓度变化可以通过建立化学反应动力学方程进行求解,如式(6),式中的负号表示物质的消耗:
(6)
式中:k1为反应速率,取1.22×10-8 s-1[12];CC为孔溶液中钙离子浓度,与温度有关[13]。
1.3 应力作用下混凝土的孔隙率
离子扩散过程中,水化作用、侵蚀造成的损伤和外部应力的作用均会造成混凝土内部孔隙的变化,从而对侵蚀离子的扩散产生影响。研究表明,无应力作用下,混凝土的孔隙率可写为水化程度和损伤演化的函数[14]:
φ(t)=φw+D(t);
(7)
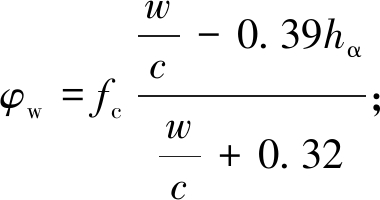
(8)
hα=1-0.5·[(1+1.67ts)-0.6+
(1+0.29ts)-0.48];
(9)
(10)
式中:φ为无应力作用下混凝土的孔隙率;φw为水化引起孔隙率的变化;D(t)为损伤演化函数;fc为水泥体积分数;
为水灰比;hα为水泥水化程度[15];ts为养护龄期与侵蚀时间之和;a、b为试验参数,
时按线性插值法分别取0.475 4和0.889 1;td=730 d [14]。
应力的作用会引起混凝土内部孔隙率发生变化:适当的压应力能够抑制裂缝的形成和开展,使结构变得致密,从而减小孔隙率;拉应力则能够促进裂缝的形成和开展,使结构损伤加快,从而增大孔隙率。
将应力引起的体积应变定义为
(11)
式中:εσ为应力引起的体积应变;ΔVσ为应力引起的混凝土体积变化量;V为混凝土初始体积。
混凝土的孔隙率是指混凝土内的孔隙体积与混凝土总体积V的比值,则无应力作用下孔隙率可表示为
(12)
式中:Vk为无应力作用下混凝土内孔隙体积。
应力作用下,混凝土内的总体积和孔隙体积均会发生变化,并通过下式表示为
Vσ=V+ΔVσ;
(13)
(14)
式中:Vσ和
分别为应力作用下混凝土的总体积和孔隙体积;
为应力引起的混凝土孔隙体积的变化量。
根据质量守恒定律,当混凝土受应力作用时,其总体积的变化量是由于内部孔隙的变化导致,也就是孔隙的变化量等于体积变化量:
(15)
经过上述分析,应力作用下混凝土的孔隙率可以表示为
(16)
将式(16)分子分母同时除以V后,得到应力作用下混凝土孔隙率的表达式为
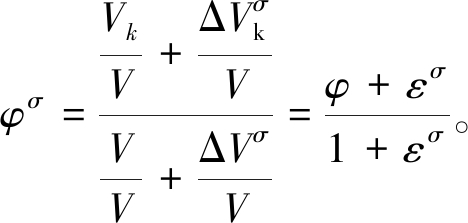
(17)
当施加应力的大小确定时,即可由混凝土的应力-应变关系求解出对应的应变值εσ,从而计算出应力作用下侵蚀时间t时混凝土的孔隙率。
2 细观模型的创建及验证
2.1 混凝土的细观模型
考虑到粗骨料位置和形状的随机性对离子扩散的影响,构建混凝土二维随机凸多边形骨料模型来验证第1节建立的离子扩散方程。该模型基于随机骨料基本原理编程程序建立:
(1)在确定骨料的投放范围和粒径等信息后,在投料范围内随机生成圆。
(2)判断圆投放位置合理后,在圆上随机生成点作为随机凸多边形骨料的顶点。如图1(a)所示,②-1超出边界、②-2与上一骨料重合,所以返回第一步继续生成②-3中的圆。
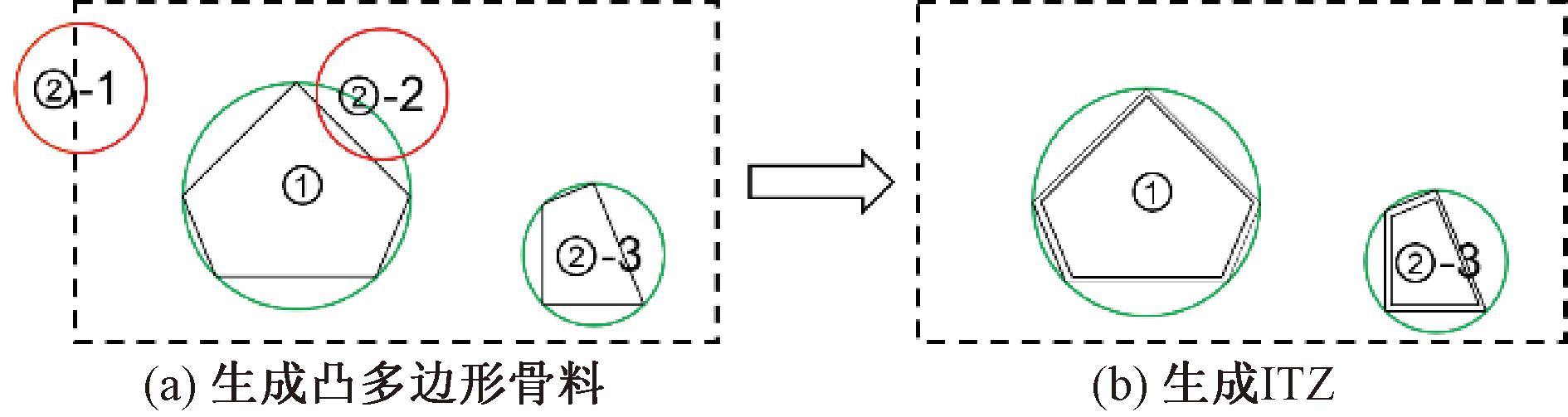
图1 凸多边形骨料投放
Figure 1 Placement of convex polygonal aggregates
(3)确定相邻点与圆心连线形成的夹角角度合理后,连接各点形成凸多边形骨料。当3个步骤持续循环到生成的骨料面积达到预定值时,通过缩进各顶点与圆心的连线方向的长度形成界面过渡区(ITZ),如图1(b)所示。
最后混凝土的细观模型由粗骨料、砂浆和界面过渡区三相构成。其中骨料粒径分为5～10 mm、10～15 mm和15～20 mm 3个级别,分布遵循Fuller级配[16];界面过渡区和砂浆厚度分别为0.1 mm和1 mm[17],界面过渡区的离子扩散系数取5倍的Deff;天然骨料为不可渗透项,离子扩散系数取0[18-19]。模型的计算和网格划分均在COMSOL Multiphysics中完成。处理后的细观模型如图2所示。
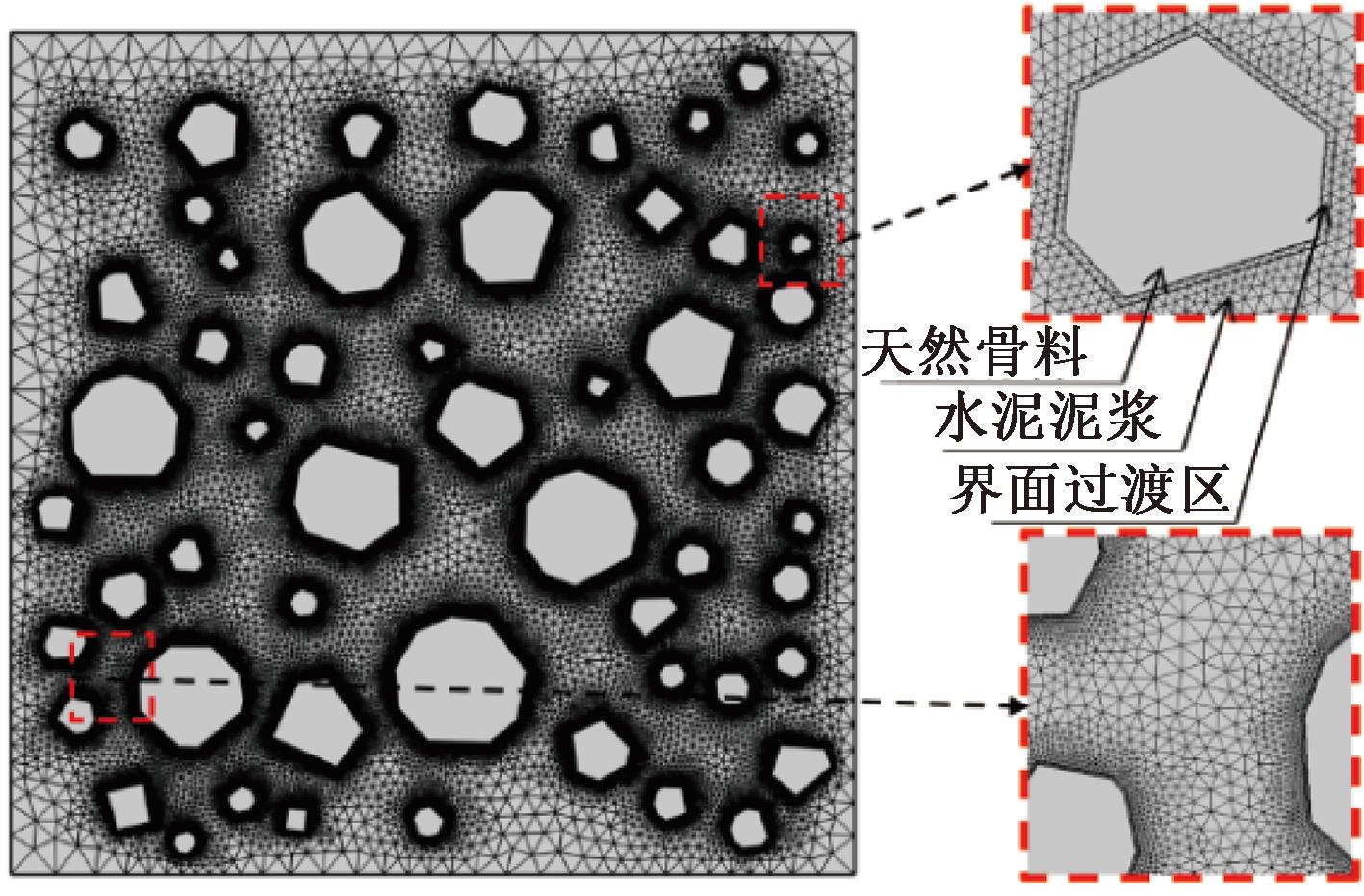
图2 混凝土细观模型
Figure 2 Mesoscopic model of concrete
图3给出了计算简图,模型尺寸100 mm×100 mm。硫酸盐从混凝土一侧侵入,压应力作用在混凝土细观模型的上部和下部,同时该图中的坐标轴为下文特征点的选取提供依据。
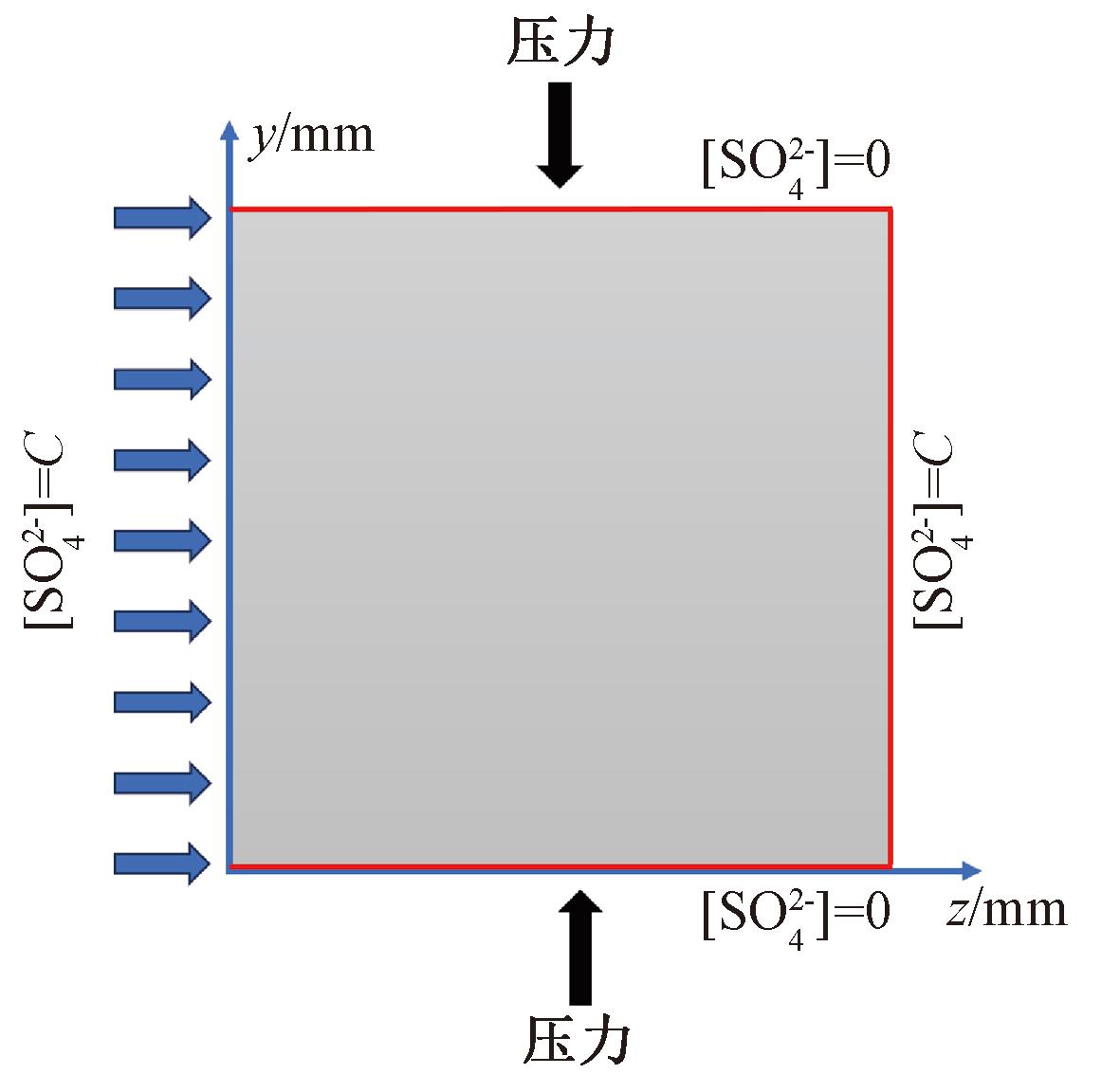
图3 计算模型简图
Figure 3 Sketch of the computational model
2.2 理论及细观模型的验证
引用文献[4]中压力作用下硫酸根离子在混凝土中分布情况的试验数据对本文模型的可行性进行验证,试验设置的压应力水平
为0、0.2、0.3、0.4。初始硫酸根离子C0=44.31 mol/m3;侵蚀溶液C=352 mol/m3;水灰比
环境温度T=298.15 K;fc=0.191、fs=0.31、fa=0.417;混凝土抗压强度fcr=32 MPa;弹性模量Ec=30 GPa,CC=21.25 mol/m3,以上数据取自文献[4],确保模拟参数与试验吻合。根据规范GB 50010—2010《混凝土结构设计规范》,由应力水平等力学参数计算出4个应力水平对应的应变值分别为0、212×10-6、318×10-6、424×10-6。
图4(a)～4(d)分别给出了文献[4]中0、0.2、0.3、0.4应力水平下,距离侵蚀表面6.25 mm处硫酸根离子浓度随侵蚀时间变化的试验与模拟结果。能够看出图4(d)在0.4压应力水平下,侵蚀56 d时的试验数据可能测量误差较大,误差值达18%,小于30%,考虑到人工取粉和后续特征点选取可能出现偏差,该误差在合理范围内[20]。除去该点之外的数值模拟与试验测试结果均随侵蚀时间的延长而逐渐增加,二者吻合度较高。说明本文建立的数值模型能够有效模拟硫酸根离子的扩散行为。其中,取(x, y)坐标为(6.25, 25)、(6.25, 50)、(6.25, 75),3点的平均值作为距离侵蚀表面6.25 mm处硫酸根离子浓度的模拟结果,坐标轴见图3。以同样方式对文献[21]中侵蚀溶液704 mol/m3、水灰比w/c=0.4、压应力水平为0和0.4时的试验数据进行了验证,如图4(e)～4(f)。结果与试验吻合较好,进一步说明了模型的有效性。
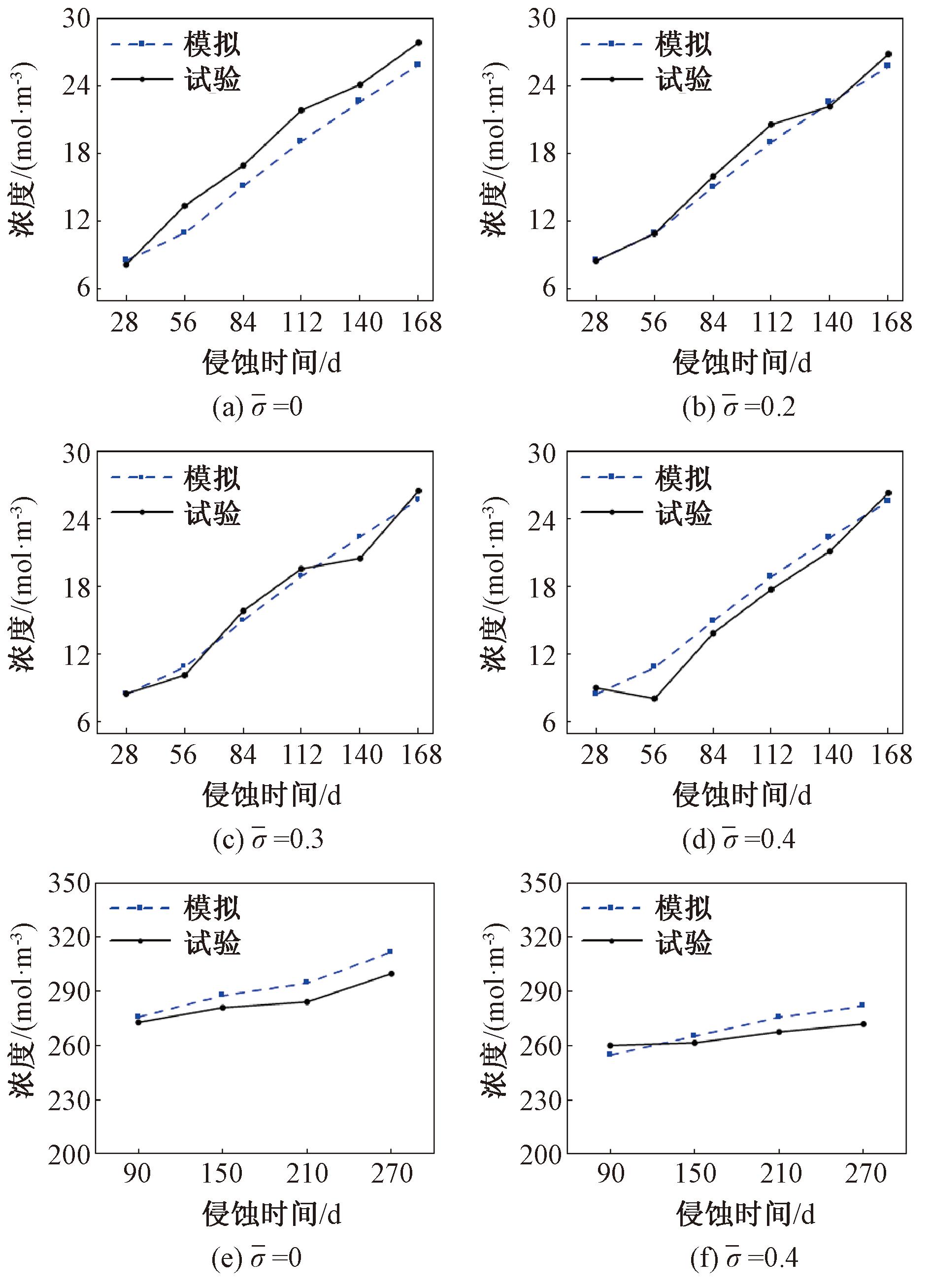
图4 模拟和试验结果对比
Figure 4 Comparison of simulation and experimental results
3 模拟结果及分析
3.1 细观模拟结果
图5给出了2.2节中不同应力水平下硫酸根离子浓度随深度的变化情况。分析可知,随着压应力水平从0增加到0.4,同一深度处的硫酸根离子浓度逐渐减小。
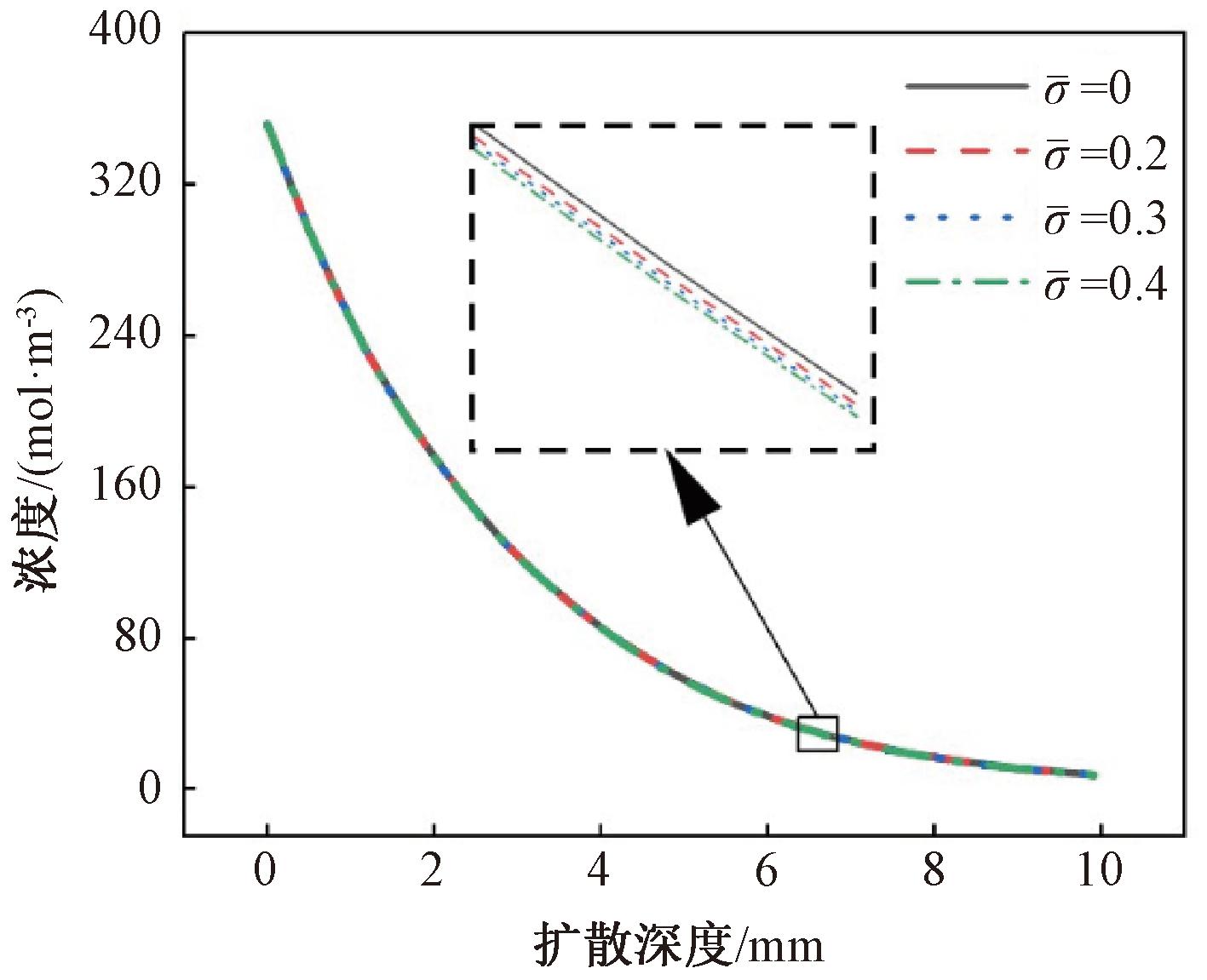
图5 应力水平对硫酸根离子扩散的影响
Figure 5 Effect of stress level on sulfate ion diffusion
图6则给出了不同应力水平下侵蚀时间为336 d时,距侵蚀表面6.25 mm点处的硫酸根离子浓度随侵蚀时间的变化。相较于没有施加压应力的情况,0.2和0.4压应力水平下该点处的硫酸根离子浓度分别降低了0.59%和1.17%。说明当施加的应力水平不大于0.4时,随着应力水平的升高硫酸根离子浓度逐渐降低。
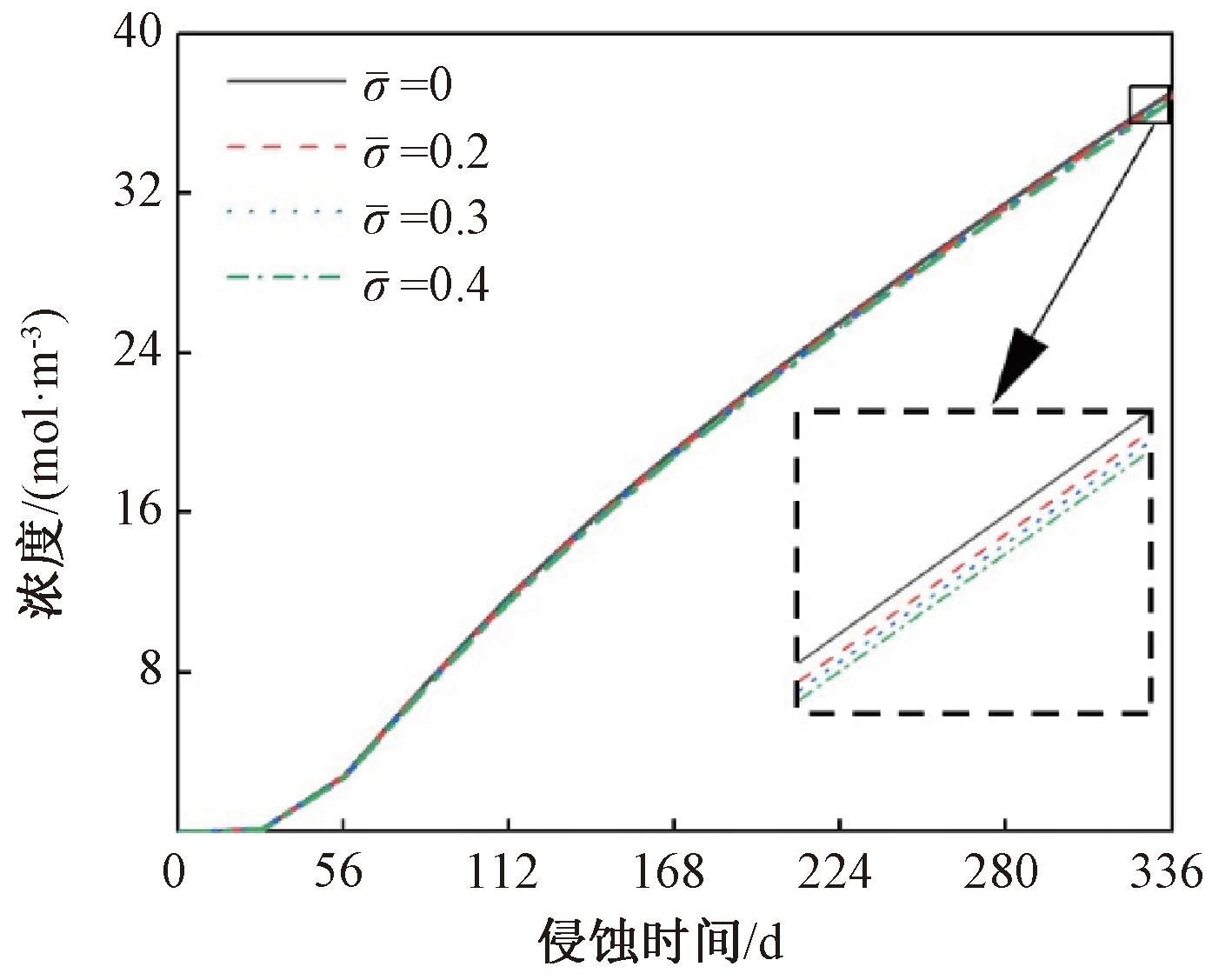
图6 6.25 mm处硫酸根离子浓度随侵蚀时间变化
Figure 6 Variation of sulfate ion concentration at 6.25 mm with erosion time
压应力的作用能够压缩混凝土内部孔隙,使混凝土孔隙率降低,减少硫酸根离子的传输空间;同时压应力能够抑制由侵蚀和收缩引起裂缝的发展,进一步阻碍离子扩散。
3.2 硫酸盐浓度和压应力水平对离子扩散的影响
图7给出了侵蚀336 d时,不同应力水平和硫酸盐溶液浓度下硫酸根离子浓度随扩散深度的变化情况。由图7可知,对于压应力来说,侵蚀溶液浓度对离子扩散的影响更加明显。同时,随着侵蚀溶液浓度从211.2 mol/m3依次增加到352 mol/m3和563.2 mol/m3,6.25 mm处硫酸根离子浓度比无应力作用下依次降低了1.31%、1.15%和1.13%,说明压应力的作用效果变化并不明显。这是由于随着侵蚀溶液浓度的增大,应力阻碍的硫酸根离子增多,但相同位置硫酸根离子的浓度也就越大,使得二者的比值变化不明显。
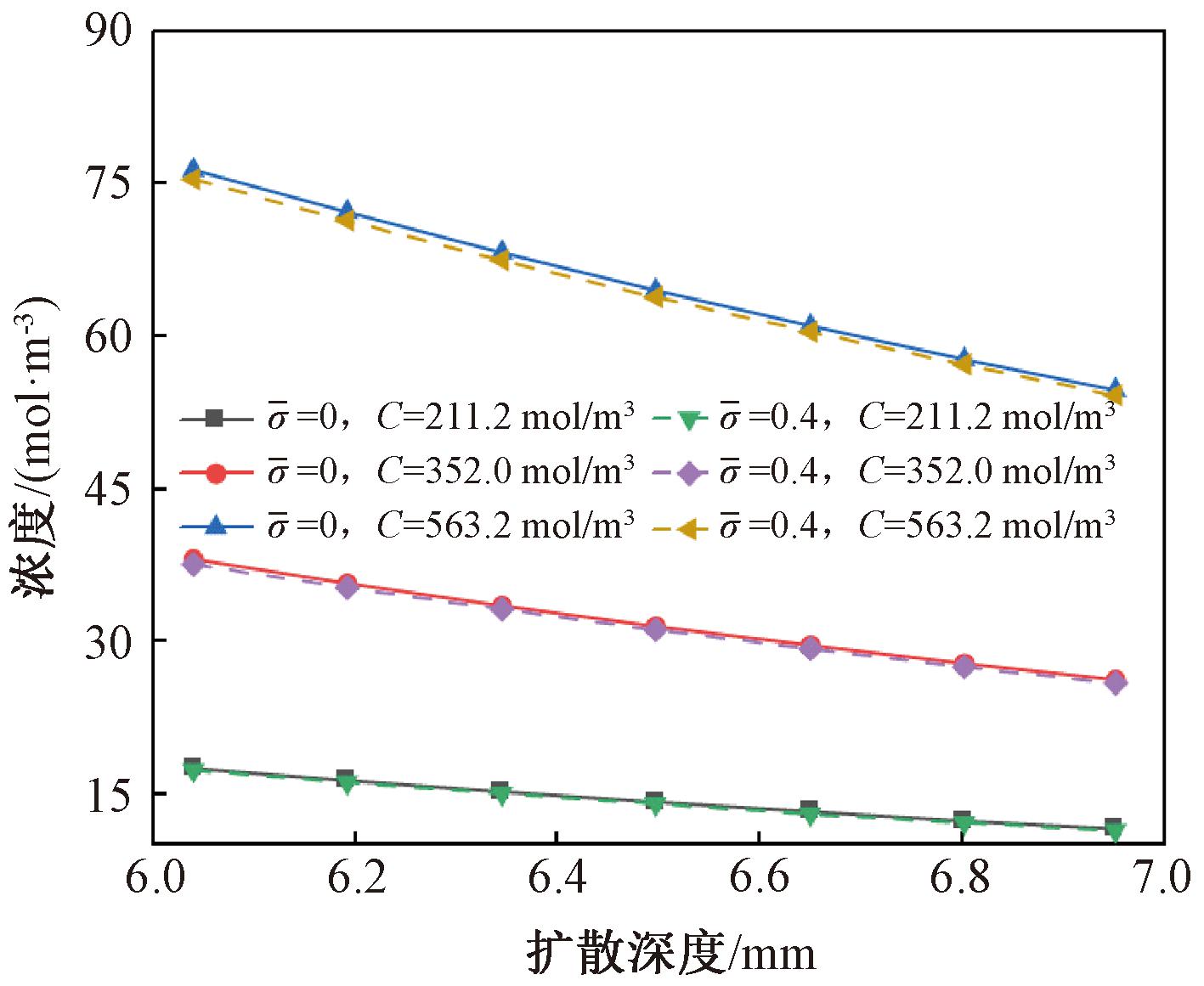
图7 浓度和应力对硫酸根离子扩散的影响
Figure 7 Effect of concentration and stress on the sulfate ion diffusion
图8则给出了C=563.2 mol/m3和应力水平0.4共同作用下 (4.25, 75)、(6.25, 75)、(8.25, 75)3点处硫酸根离子浓度随侵蚀时间的变化情况。能够看出距离侵蚀表面越近的点越早出现硫酸根离子,且离子浓度的增长也越快。基于Fick定律来看:由于某点处离子浓度的变化率与扩散系数及浓度梯度的一阶导数呈正相关,而随着深度的增加,硫酸根离子浓度梯度的逐渐减小,导致其一阶导数随之减小,因此浓度增长也随之减慢[22]。
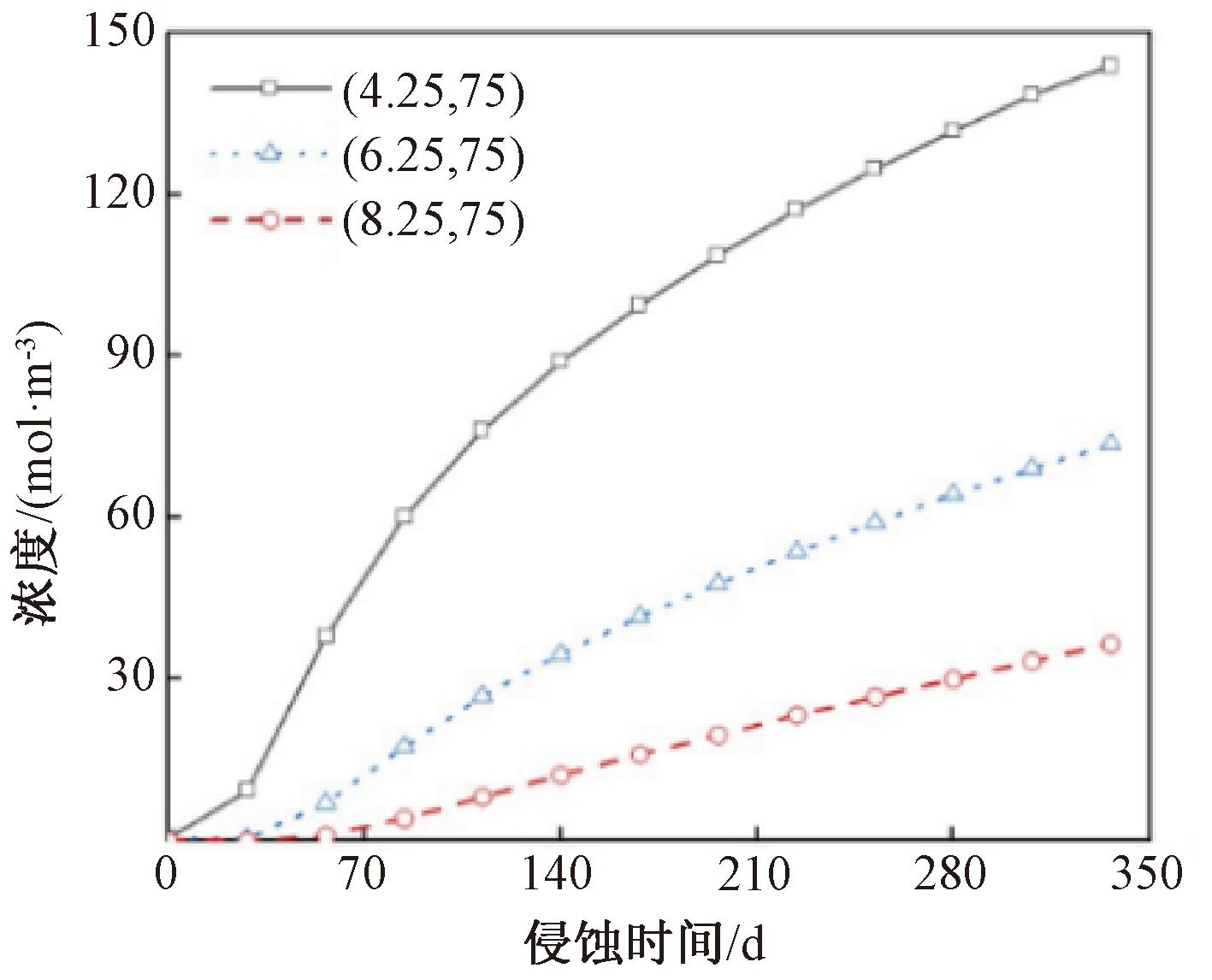
图8 不同点处硫酸根离子浓度随侵蚀时间变化
Figure 8 Variation of sulfate ion concentration at different points with erosion time
细观模拟结果能够直观地给出不同因素、不同侵蚀时间下离子的扩散情况和细观组成对离子扩散的影响。图9给出了侵蚀336 d时,不同应力水平及浓度下硫酸根离子的分布云图。能够看出,由于界面过渡区的硫酸根离子扩散系数大于水泥砂浆区域,因此粗骨料附近区域的离子浓度略大于远离骨料的水泥砂浆区域。
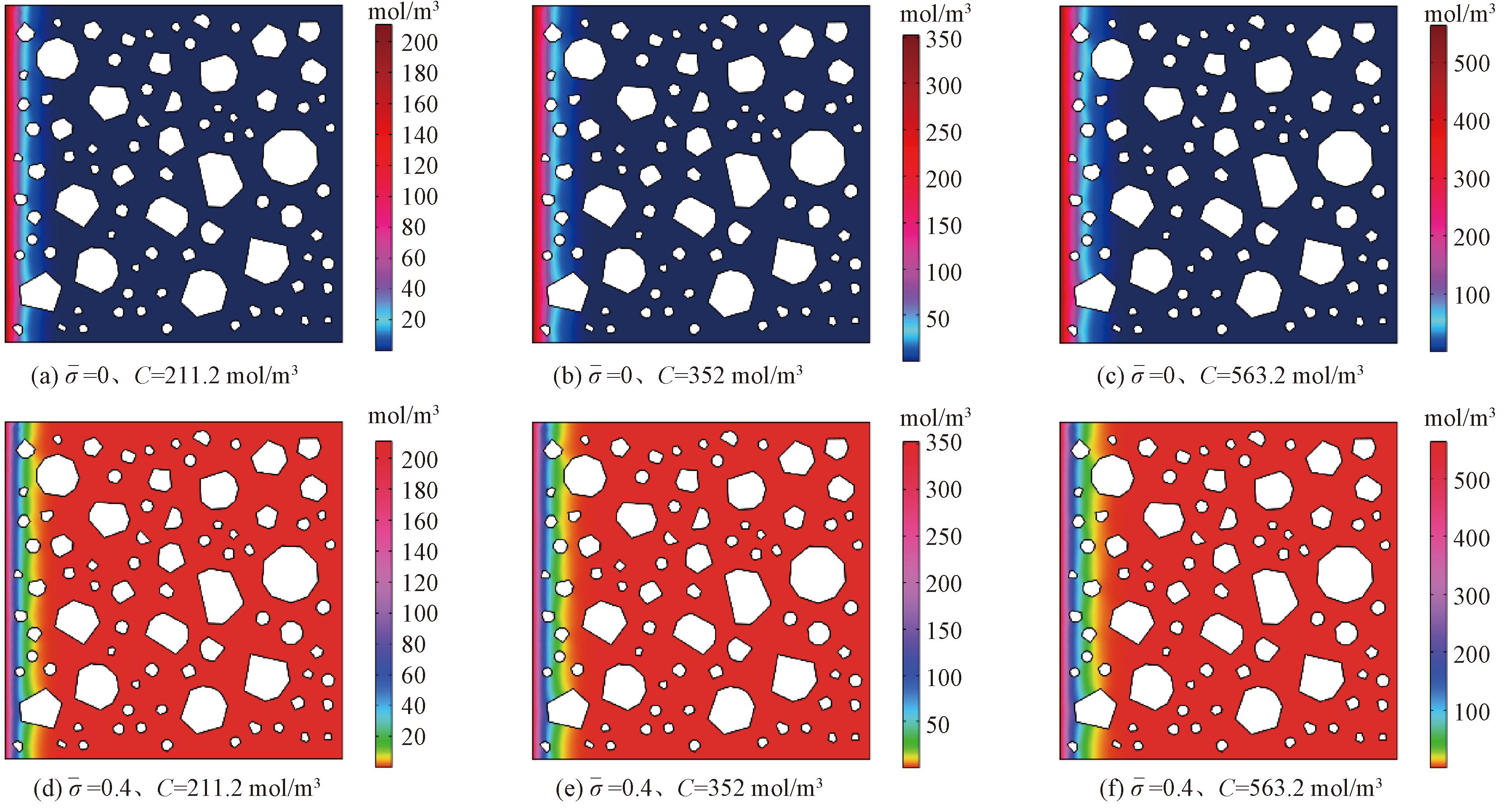
图9 不同应力水平及溶液浓度下硫酸根离子的分布云图
Figure 9 Cloud map of the distribution of sulfate ions at different stress levels and solution concentrations
3.3 水灰比和压应力水平对离子扩散的影响
为分析不同水灰比下压应力对硫酸根离子扩散的影响,增加w/c=0.4、0.7的情况,C=563.2 mol/m3,应力水平为0和0.4。图10给出了侵蚀336 d时,不同应力水平和水灰比下硫酸根离子浓度随扩散深度的变化情况。与3.2节相似,水灰比对硫酸根离子浓度的影响同样明显大于压应力对离子浓度的影响。不同的是,随水灰比从0.4依次增加到0.6和0.7时,0.4应力水平作用下6.25 mm处硫酸根离子浓度比无应力作用时依次降低12.1%、1.12%和0.85%,说明压应力对离子扩散的抑制效果在水灰比较低时更加明显,这可能是由于水灰比引起孔隙率的变化较大所致。
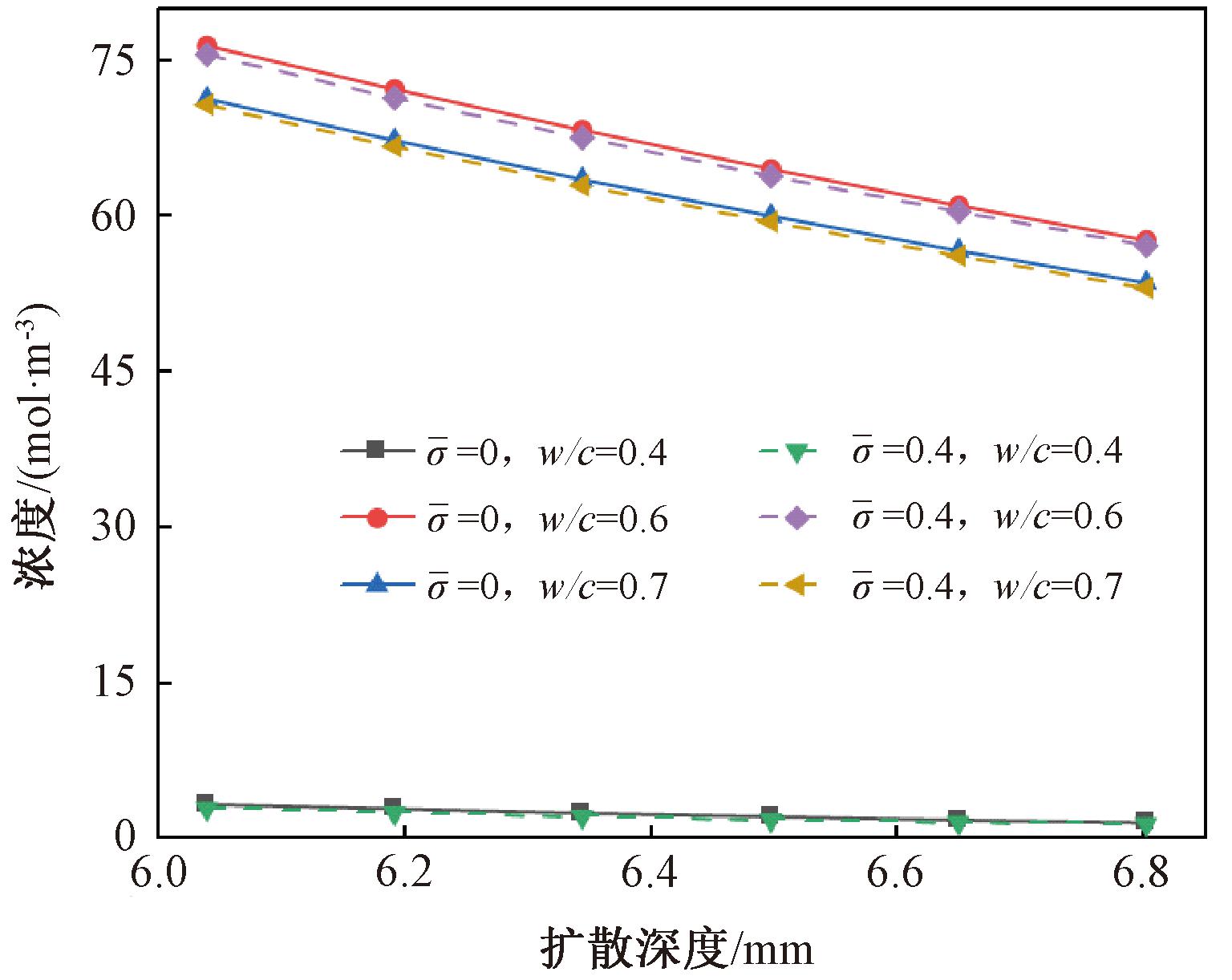
图10 水灰比和应力对硫酸根离子扩散的影响
Figure 10 Effect of water-cement and stress on the sulfate ion diffusion
同时,受压状态下较小的水灰比更有利于混凝土试件抵抗硫酸盐侵蚀。但从图10中了解到,侵蚀336 d时w/c=0.7时硫酸根离子浓度随深度变化的曲线位于w/c=0.6时曲线的下方,下面从无压力作用下孔隙率和扩散系数的变化对该情况进行分析。
从图11(a)中能够看出,w/c=0.6时的孔隙率K要小于w/c=0.7时,孔隙率较大也就会提供更多硫酸根离子扩散的通道,这也就是侵蚀初期w/c=0.7时硫酸根离子扩散系数较大的原因之一。但从公式(2)和(7)中能够看出,硫酸根离子扩散系数由孔隙率、曲折度和损伤函数决定,前两者可归为与侵蚀时间相关的函数,由此扩散系数可由侵蚀时间和损伤函数值确定。因此可以判断某个侵蚀时间下w/c=0.6时的损伤函数值大于w/c=0.7时的情况,这就是后来w/c=0.6时硫酸根离子扩散系数较大而导致硫酸根离子浓度大于w/c=0.6时硫酸根离子浓度的原因。
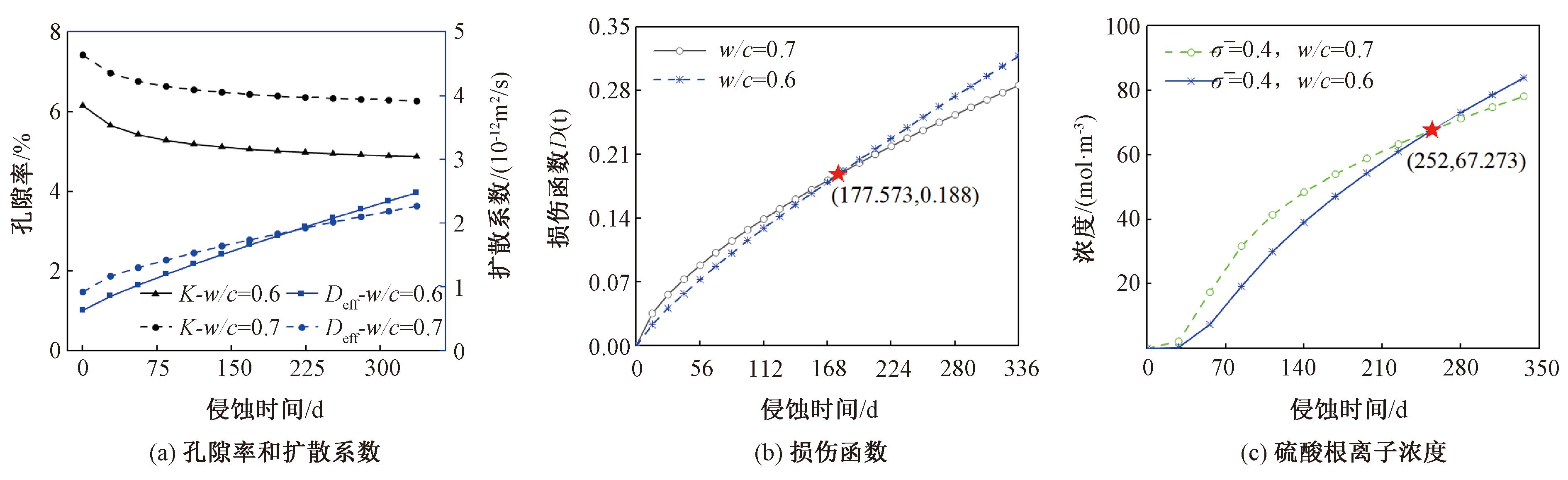
图11 不同变量随侵蚀时间的变化
Figure 11 Variation of different variables with erosion time
图11(b)中给出了w/c=0.6和0.7时的损伤函数变化曲线,二者相交发生在侵蚀时间为177.573 d。之后随着侵蚀的继续,会出现硫酸根离子浓度逐渐增加并大于w/c=0.6的情况。如图11(c)中绘制的2种水灰比下,距离侵蚀表面6.25 mm处硫酸根离子浓度随侵蚀时间的变化,在侵蚀时间达到252 d时,离子浓度的大小顺序发生变化。
图12给出侵蚀336 d时,不同应力水平及硫酸盐浓度下硫酸根离子的分布图。同样可知水灰比对离子分布的影响比较明显,图12(a)、12(d)也表明低水灰比时混凝土具有更好的抗硫酸盐侵蚀性能。
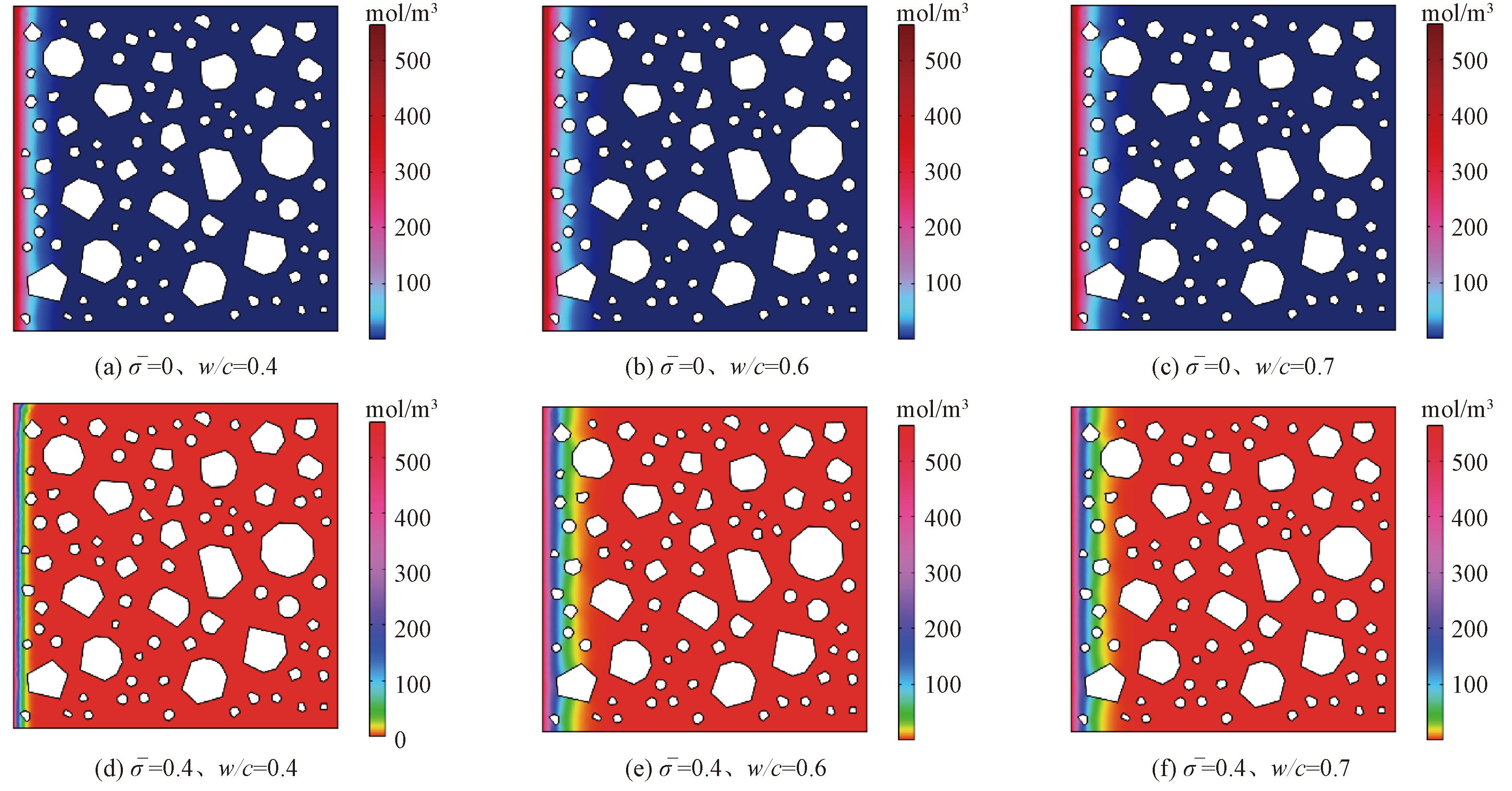
图12 不同应力水平及水灰比下硫酸根离子的分布云图
Figure 12 Cloud map of the distribution of sulfate ions at different stress levels and water-cement ratio
4 结论
(1) 将硫酸根离子扩散模型的数值结果与硫酸盐全浸泡试验结果对比,二者吻合度较高,表明该模型能有效预测受压混凝土中硫酸根离子的扩散行为。
(2) 压应力对离子扩散具有抑制作用,随着应力水平从0增加到0.4,硫酸根离子浓度随深度变化的曲线逐渐降低。侵蚀336 d时,0.2和0.4应力水平下距侵蚀表面6.25 mm点处的硫酸根离子浓度比无应力作用时分别降低了0.59%和1.17%。
(3) 溶液浓度和水灰比对离子扩散的影响程度大于应力水平,同时随着溶液浓度或水灰比的变化,应力水平对离子扩散的影响程度变化不同。0.4压应力水平下侵蚀336 d时:硫酸盐浓度取211.2、563.2 mol/m3,6.25 mm处硫酸根离子浓度比无应力作用下分别降低了1.31%和1.13%;水灰比取0.4和0.6时,离子浓度分别降低了12.1%和1.12%。
(4) 较小的水灰比更有利于受压混凝土抵抗硫酸盐侵蚀。水灰比过大会导致更多的硫酸根离子进入混凝土,但因含有更多容纳侵蚀产物填充的孔隙,会使得混凝土的损伤减慢。
[1] MIN H G, SONG Z G. Investigation on the sulfuric acid corrosion mechanism for concrete in soaking environment[J]. Advances in Materials Science and Engineering, 2018, 2018: 3258123.
[2] BROWN P W, BADGER S. The distributions of bound sulfates and chlorides in concrete subjected to mixed NaCl, MgSO4, Na2SO4 attack[J]. Cement and Concrete Research, 2000, 30(10): 1535-1542.
[3] XIE F, LI J P, ZHAO G W, et al. Experimental investigations on the durability and degradation mechanism of cast-in-situ recycled aggregate concrete under chemical sulfate attack[J]. Construction and Building Materials, 2021, 297: 123771.
[4] 黄冬. 不同机制下混凝土内SO42-传输-劣化机理研究[D]. 徐州: 中国矿业大学, 2019.
HUANG D. Study on the transport-degradation mechanism of SO42- in concrete under different conditions[D]. Xuzhou: China University of Mining and Technology, 2019.
[5] 张浩, 乔文靖, 杨帆, 等. 强腐蚀桥梁钢Q345的J-C本构模型及数值模拟[J]. 郑州大学学报(工学版), 2021, 42(6): 99-104.
ZHANG H, QIAO W J, YANG F, et al. Tensile finite element simulation of Q345 bridge steel with strong corrosion based on J-C model[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(6): 99-104.
[6] WANG H L, CHEN Z W, LI H D, et al. Numerical simulation of external sulphate attack in concrete considering coupled chemo-diffusion-mechanical effect[J]. Construction and Building Materials, 2021, 292: 123325.
[7] IKUMI T, SEGURA I. Numerical assessment of external sulfate attack in concrete structures[J]. Cement and Concrete Research, 2019, 121: 91-105.
[8] WU T, JIN L B, FAN T, et al. A multi-phase numerical simulation method for the changing process of expansion products on concrete under sulfate attack[J]. Case Studies in Construction Materials, 2023, 19: e02458.
[9] YIN G J, ZUO X B, SUN X H, et al. Numerical investigation of the external sulfate attack induced expansion response of cement paste by using crystallization pressure[J]. Modelling and Simulation in Materials Science and Engineering, 2019, 27(2): 025006.
[10] ZUO X B, SUN W, LI H, et al. Geometrical model for tortuosity of transport paths in hardened cement pastes[J]. Advances in Cement Research, 2012, 24(3): 145-154.
[11] 左晓宝, 孙伟. 硫酸盐侵蚀下的混凝土损伤破坏全过程[J]. 硅酸盐学报, 2009, 37(7): 1063-1067.
ZUO X B, SUN W. Full process analysis of damage and failure of concrete subjected to external sulfate attack[J]. Journal of the Chinese Ceramic Society, 2009, 37(7): 1063-1067.
[12] ZUO X B, SUN W, YU C. Numerical investigation on expansive volume strain in concrete subjected to sulfate attack[J]. Construction and Building Materials, 2012, 36: 404-410.
[13] 万旭荣. 硫酸盐侵蚀环境下的混凝土扩散反应规律研究及数值模拟[D]. 南京: 南京理工大学, 2010.
WAN X R. Study and numerical simulation of concrete diffusion reaction law under sulfate attack environment[D].Nanjing: Nanjing University of Science and Technology, 2010.
[14] 关博文, 刘佳楠, 吴佳育, 等. 基于侵蚀损伤的混凝土硫酸根离子传输行为[J]. 硅酸盐通报, 2020, 39(10): 3169-3174, 3183.
GUAN B W, LIU J N, WU J Y, et al. Transport behavior of sulfate ions in concrete with attack damage[J]. Bulletin of the Chinese Ceramic Society, 2020, 39(10): 3169-3174, 3183.
[15] MASI M, COLELLA D, RADAELLI G, et al. Simulation of chloride penetration in cement-based materials[J]. Cement and Concrete Research, 1997, 27(10): 1591-1601.
[16] 苗艳春, 张玉, 雷闯, 等. 热力耦合途径下再生保温混凝土的细观力学性能[J]. 郑州大学学报(工学版), 2021, 42(5): 79-85.
MIAO Y C, ZHANG Y, LEI C, et al. Meso-scale response of recycled aggregate thermal insulation concrete based on coupled thermo-mechanical modeling[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(5): 79-85.
[17] 金立兵, 余化龙, 王振清, 等. 再生混凝土抗氯离子渗透的五相细观数值模拟[J]. 郑州大学学报(工学版), 2022, 43(1): 83-89.
JIN L B, YU H L, WANG Z Q, et al. Five-phase mesoscopic numerical simulation of chloride permeation resistance in recycled aggregate concrete[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(1): 83-89.
[18] JIN L B, YU H L, FAN T, et al. Experimental and computational modeling of chloride transport behavior in fully recycled coarse aggregate concrete[J]. Construction and Building Materials, 2022, 360: 129592.
[19] JIANG Z L, HUANG Q H, XI Y P, et al. Experimental study of diffusivity of the interfacial transition zone between cement paste and aggregate[J]. Journal of Materials in Civil Engineering, 2016, 28(10): 129592.
[20] CHEN J K, JIANG M Q, ZHU J. Damage evolution in cement mortar due to erosion of sulphate[J]. Corrosion Science, 2008, 50(9): 2478-2483.
[21] 徐惠. 硫酸盐腐蚀下混凝土损伤行为研究[D]. 徐州: 中国矿业大学, 2012.
XU H. Research on damage behavior of concrete under sulfate corrosion[D]. Xuzhou: China University of Mining and Technology, 2012.
[22] PAUL A, LAURILA T, VUORINEN V, et al. Fick′s laws of diffusion[M]∥ Thermodynamics, Diffusion and the Kirkendall Effect in Solids. Cham: Springer, 2014: 115-139.