在城市现代化进程迅速推进的今天,综合管廊整合了电力、通信、燃气、供热、给排水等多条管道,并设置了专用的检修口、吊装口和监控系统,实行统一规划、设计、建设、管理,是保证城市正常运转的关键基础和“生命线”。近几年地震频繁发生,其对城市地下综合管廊具有极大的威胁。因此,加强对地下综合管廊抗震能力的研究,对城市的发展和运转具有至关重要的意义。
史晓军等[1]通过管廊振动台试验得出地下综合管廊的地震响应受周围土体影响,内力集中在角部,接触面土压力随地震强度增加而增大,顶底板产生相对位移和刚体转动。阮滨等[2]为解决管廊穿越液化场地的抗震问题,提出了一种改进的广义反应位移法,建立模型,验证了该方法的可行性。王鹏宇等[3]建立数值分析模型,研究了地震和冻土条件下综合管廊的结构性能。魏奇科等[4]以体积配箍率和纵筋锚固长度为参数,进行叠合装配式地下管廊节点试验,研究了其力学特征,给出提高其抗震性能的建议。Shamsabadi等[5]开展了管廊抗震研究,分析了土与结构的作用机理,提出了加固方案,指导了实际工程。
在管廊抗震性能研究中,学者们对影响管廊结构动力响应的因素也进行了分析。施有志等[6]建立非线性有限元三维动力数值模型,研究了Rayleigh波平行入射对综合管廊动力响应的影响,探讨了管廊结构的断面尺寸、覆土厚度、入射角和土体本构模型等因素对其的影响。杨仕升等[7]建立综合管廊的二维模型,对4种不同峰值的地震波进行了数值模拟。Debiasi等[8]数值模拟了影响浅埋地下结构抗震的因素。Gebremedhn等[9]以ABAQUS有限元软件为平台,模拟了两个纵向邻近浅埋预制管廊不同幅值的地震响应。甘梦云等[10]提出预制管廊横向抗震分析的壳-弹簧计算模型,通过ABAQUS有限元软件对天津某在建的地下综合管廊进行数值模拟。
以上研究通过试验和数值模拟的方法分析了矩形和圆形断面的综合管廊受地震作用时的响应以及影响管廊抗震的各种因素,为综合管廊的抗震设计提供了理论和实践指导。但对于三心拱断面形式的管廊未进行分析。由于综合管廊结构的复杂性以及地震的不确定性等因素,对此种新型断面的管廊抗震性能需深入探讨,以提高其在地震灾害中的安全性和可靠性。本文以郑州城区耿河变电站到博文变电站之间的地下管廊为研究对象,利用ANSYS Workbench软件建立三维实体模型,对其进行前6阶的模态分析、横向和竖向地震的地震响应分析,为此种断面的管廊抗震设计提供参考。
1 管廊结构动力响应
郑州城区耿河变电站到博文变电站之间的单仓三心拱形断面管廊结构宽3.1 m,高3.2 m。管廊结构采用C35混凝土,场地类别为Ⅱ类,设计地震分组为第2组,抗震设防烈度为7度,设计基本加速度为0.15g。地震波选用适用于Ⅱ类场地且经调幅后的EL-Centro波,截取前12 s加速度数据作为地震动输入到Transient Structural模块,分600步计算,时间间隔0.02 s,调幅后的地震波见图1。

图1 调幅后的地震波
Figure 1 Seismic wave after amplitude modulation
1.1 有限元计算模型
1.1.1 材料参数
本文以综合管廊结构为研究重点,考虑到地震作用下土-管廊结构之间的非线性关系,简化其周边土的地震响应,同时忽略土的液化效应,所以将土的复杂层状特性简化为单一特性。结合管廊所处位置的地质勘查报告及其埋设深度,确定出土体具体的物理力学参数,见表1。土的本构模型采用ANSYS Workbench中D-P模型。
表1 土体参数
Table 1 Soil parameters

土体名称密度/(kg·m-3)弹性模量/MPa泊松比摩擦角/(°)黏聚力/kPa粉质黏土1 85030.60.32827
管廊结构采用强度为C35的混凝土,由于管廊结构在地震作用的整个过程中均处于弹性阶段,因此采用线弹性本构模型。具体参数见表2。
表2 管廊结构材料参数
Table 2 Material parameters of pipe gallery structure
强度等级密度/(kg·m-3)弹性模量/MPa泊松比C352 30031 5000.18
1.1.2 模型建立
图2为有限元模型图及监测点图。在模型计算区域的选择方面,为减小界面上的地震波反射,应将模拟区域的横向尺寸设置为大于5倍管廊结构的宽度,这样可保证模拟结果的稳定性[11]。在计算土体模型深度的取值方面,通常是土层截断面位置离管廊结构底部的距离大于管廊高度的3倍,且大于结构底部以下10 m。土与管廊均选用实体单元模拟,管廊单元尺寸为200 mm,土体单元尺寸为500 mm。在XZ平面内建立土-管廊结构断面形状,然后沿Y轴方向进行拉伸,获得三维有限元实体模型见图2(a)。模型横向宽度25 m,为管廊结构宽度的8.06倍,竖向高度为18 m(管廊顶面距离地面距离为3 m),纵向长度是10 m。
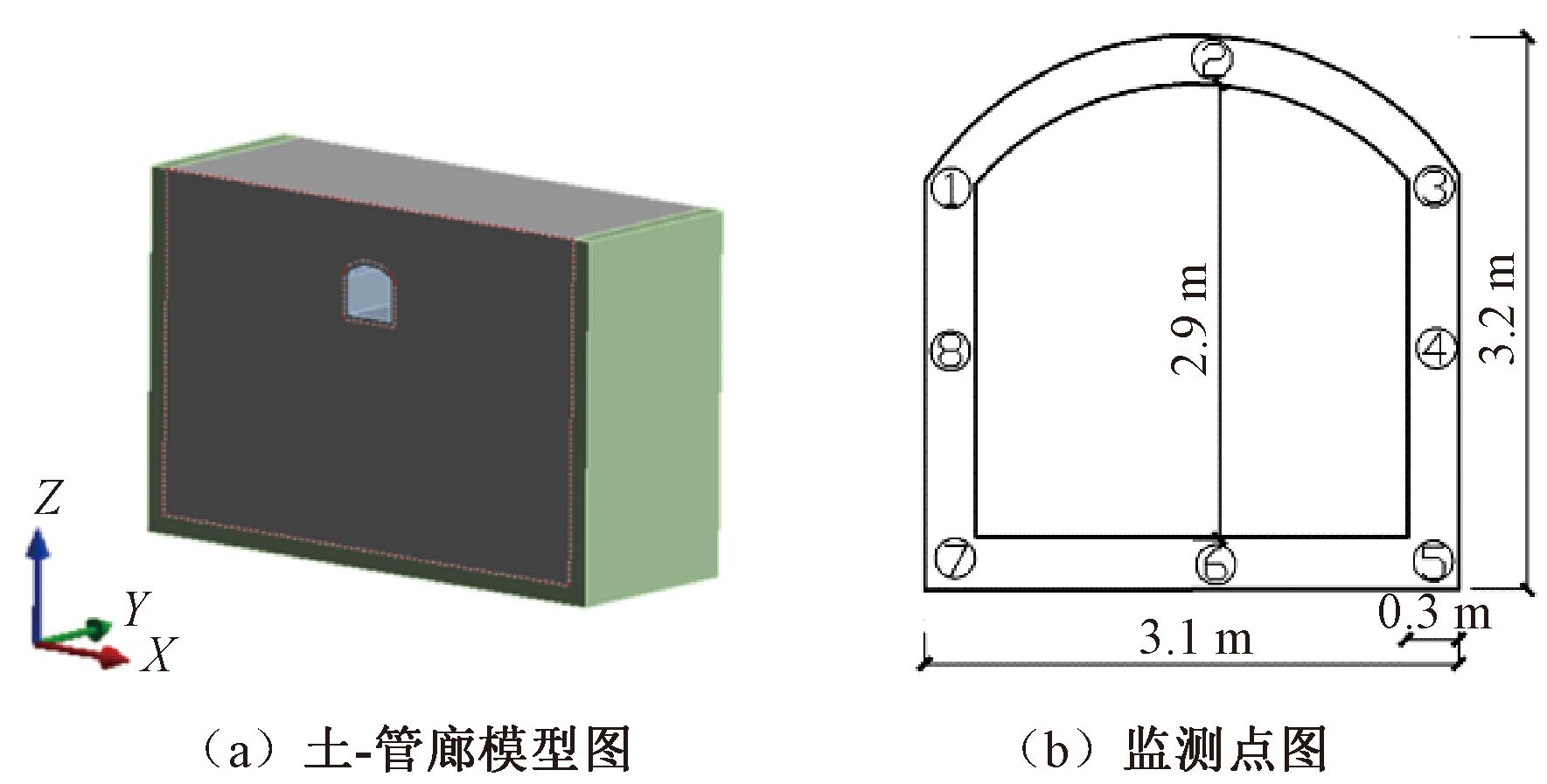
图2 有限元模型图及监测点图
Figure 2 Finite element model diagram and monitoring point diagram
在土体结构模型的外围,设置一层厚度为1 m的黏弹性人工边界单元[12-13]。在数值模拟中,将黏弹性人工边界单元设为固定,且与土体外围边界的接触状态设置为绑定,从而实现黏弹性边界单元对行波更好地吸收[14-16]。针对土体与管廊之间的相互作用,考虑了土与管廊滑移和脱开时,其内力和变形程度要小于不考虑时的内力和变形程度,后者计算的结果有较高的安全储备。所以本文在对土-管廊结构模型进行动力时程分析中,不考虑相互滑动和脱离的情况,土与管廊结构的状态为摩擦接触,摩擦系数设置为0.3。在管廊结构中选取8个监测点,具体点位置见图2(b)。
1.2 模态分析
采用Block Lanczos法进行土与管廊结构的模态分析。因为前几个模态的振型是结构振动中最主要的振型,这些振型对结构的响应和应力贡献最大。因此,提取前几阶模态进行分析。提取土与管廊整体结构前6阶模态,得到管廊结构体系的自振频率与周期见表3。
表3 结构体系自振频率、周期
Table 3 Natural vibration frequency and period of structural system

振型阶次频率/Hz周期/s振型特征10.616 51.621 95纵向振动21.012 60.987 56竖向振动31.081 80.924 39横向振动41.198 40.834 45绕管廊对角线轴旋转51.198 40.834 45绕管廊对角线轴旋转61.405 10.711 69绕Z轴转动
取2、3阶振动频率,依据式(1)与式(2)(土体与管廊结构的阻尼比取ξ=ξi=ξj=0.05),计算得α=0.328 46,β=0.007 60。
(1)
(2)
式中:α为质量阻尼系数;β为刚度阻尼系数;ωi、ωj分别为结构的第i和第j阶固有频率;ξi、ξj为对应的第i和j阶振型阻尼比。
1.3 水平和竖向地震下的动力响应
1.3.1 位移响应分析
管廊结构在水平地震和竖向地震作用下,提取管廊关键部位节点的各自方向的位移时程曲线反映结构的位移时程响应,见图3。
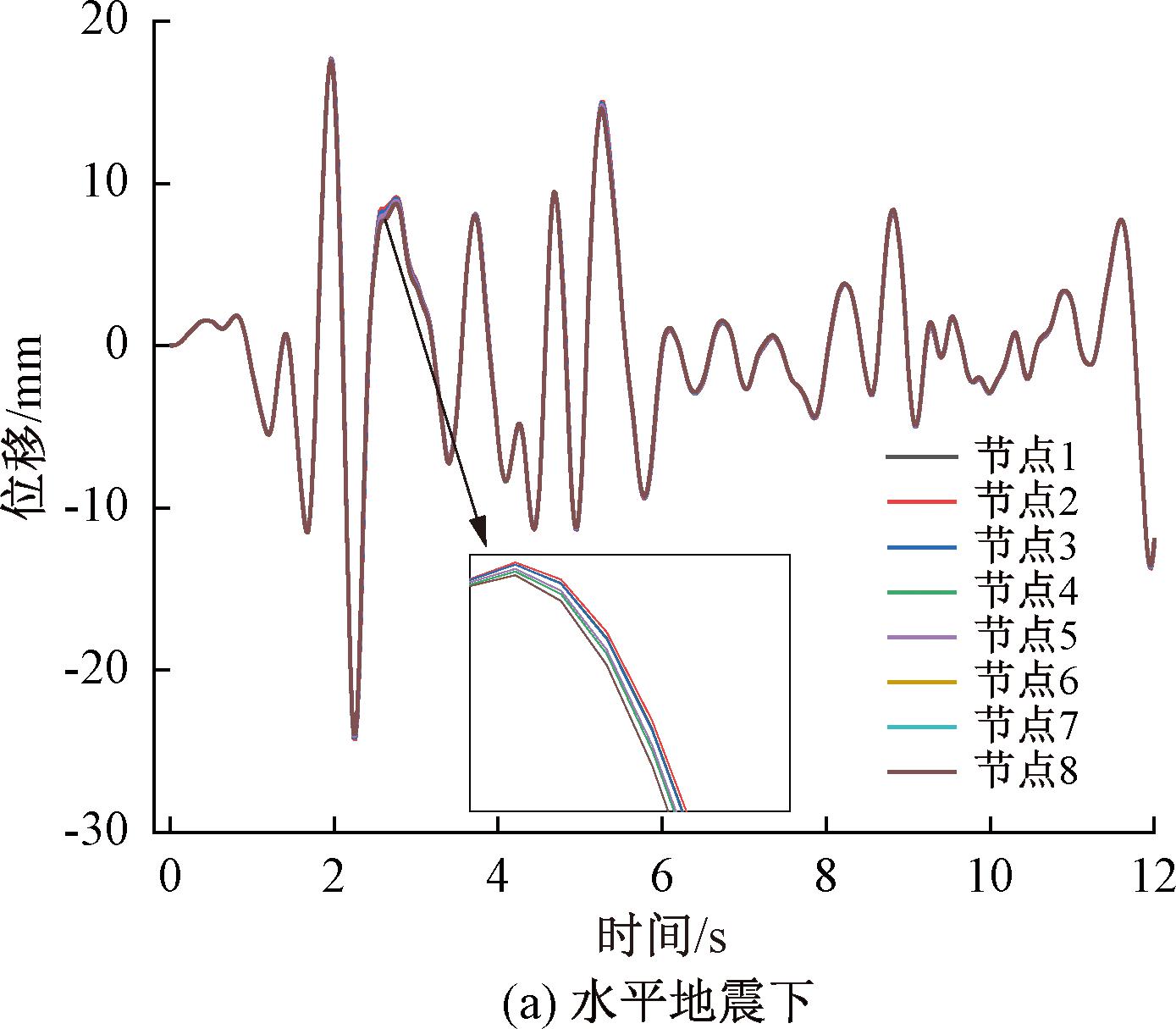
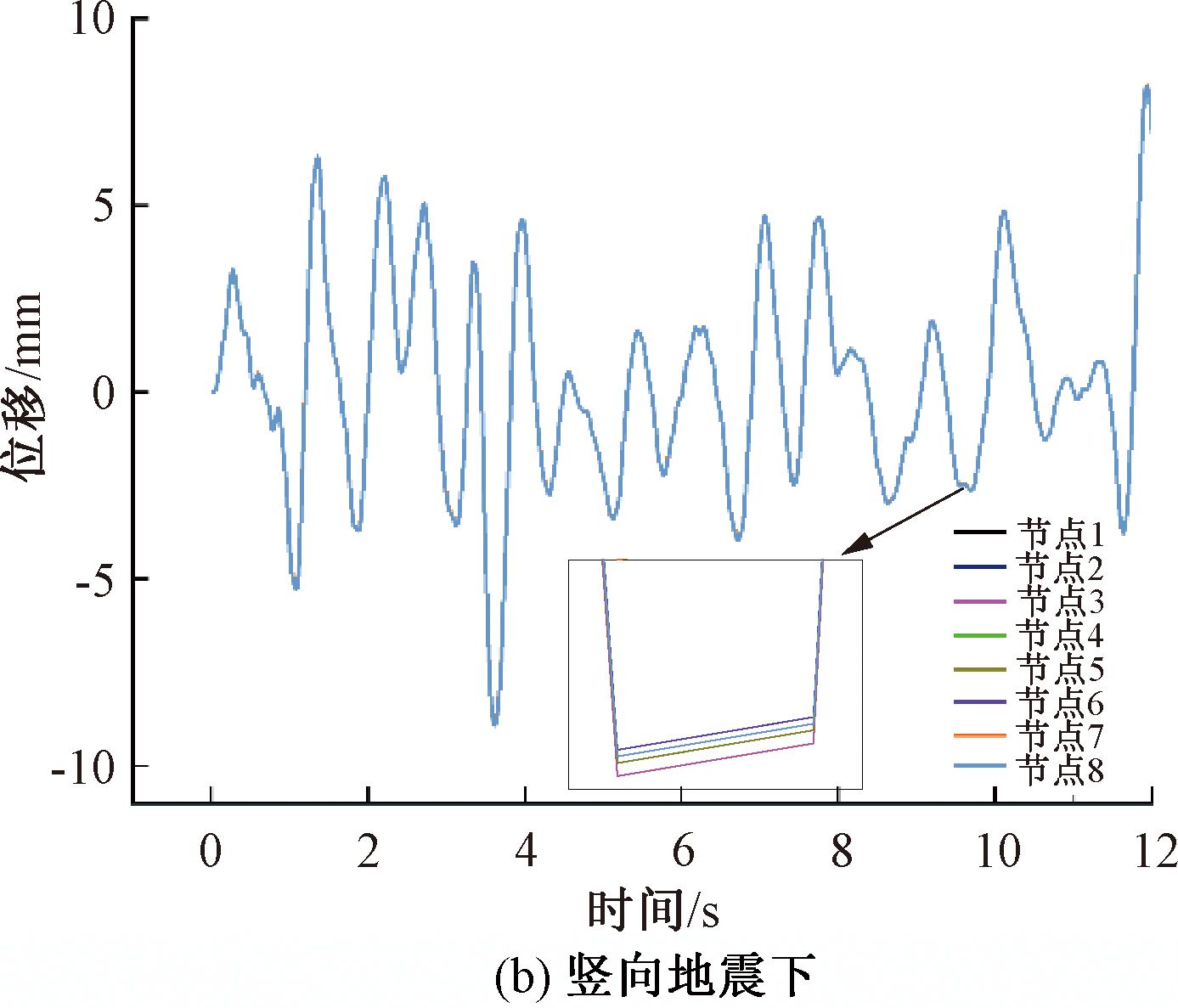
图3 水平和竖向地震下各监测点的位移时程曲线
Figure 3 The displacement time history curve of each monitoring point under horizontal and vertical earthquake
由图3知,各关键节点的时程曲线趋势基本相同,说明管廊结构呈整体运动;水平地震下,最大位移发生在2~3 s;竖向地震下,最大位移发生在3~4 s,说明该时间段管廊结构承受的地震作用较大。根据各监测点的位移时程曲线,列出最大位移峰值,见表4。
表4 监测点出现峰值位移
Table 4 The peak displacement of the monitoring point and the corresponding time mm
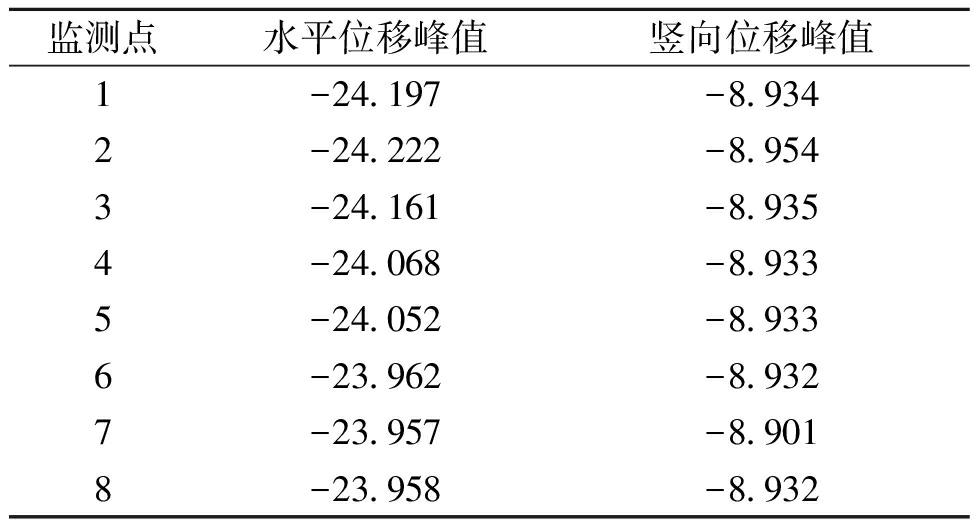
监测点水平位移峰值竖向位移峰值1-24.197-8.9342-24.222-8.9543-24.161-8.9354-24.068-8.9335-24.052-8.9336-23.962-8.9327-23.957-8.9018-23.958-8.932
注:负号“-”表示与正方向相反的方向。
由表4可知,最大水平位移峰值出现在顶部2号节点,峰值为-24.222 mm,最小水平位移峰值出现在底部7号节点,峰值为-23.957 mm。管廊各节点水平位移在2.24 s均达到峰值,且峰值大小分布在-23.957~-24.222 mm的范围内,最大差值绝对值是0.265 mm。表明水平地震下管廊结构水平向移动呈一致性移动,但是仍有部分水平层间位移存在,并且位移由下而上呈缓慢增加趋势。
竖向地震作用下,管廊结构各节点均在3.62 s达到峰值,最小位移峰值出现在管廊底部中间节点,数值为-8.901 mm;最大位移峰值出现在管廊顶部中间节点,数值为-8.954 mm;在竖直方向上,从下往上位移峰值渐渐增大;管廊其余监测节点的位移峰值处于最小值与最大值之间。其原因是管廊结构的中间土体被掏空,上部中间刚度稍微小于下部中间刚度,因此上部分的位移幅值稍大于下部分。
1.3.2 加速度响应分析
在水平和竖向地震作用下,在管廊断面中取监测点2和监测点7的加速度时程曲线,用于分析管廊结构的动力特征。水平和竖向地震下监测点2与监测点7的加速度时程曲线,见图4。

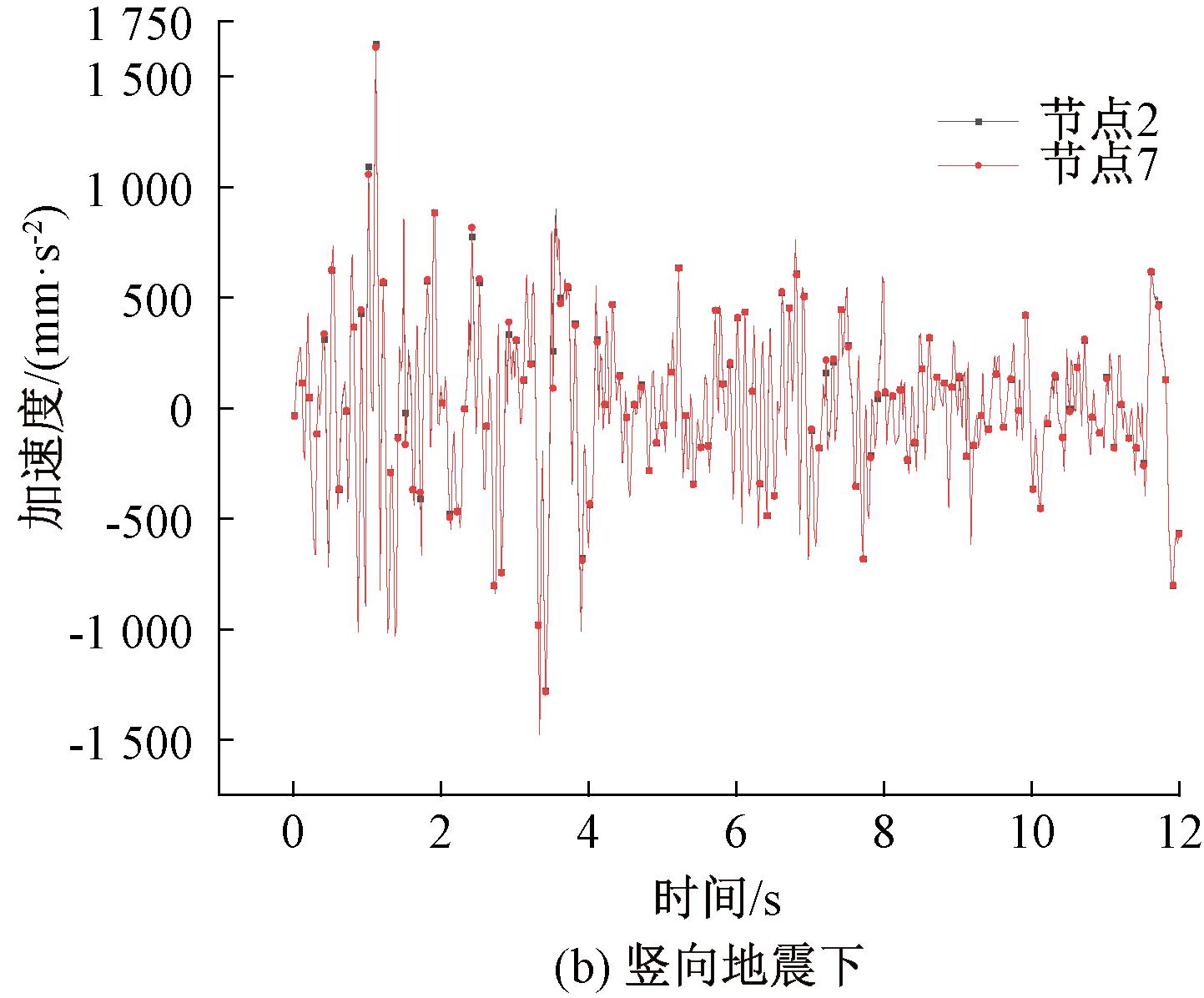
图4 水平和竖向地震下加速度时程曲线图
Figure 4 Acceleration time history curve under horizontal and vertical earthquake
由图4可知,管廊结构关键节点处加速度时程曲线基本类似,不再逐一罗列。仅提取各关键节点峰值加速度,并计算各点的加速度放大倍数,见表5。由表5可知,在水平地震作用下,最小峰值加速度出现在管廊结构的底板中心处(即监测点7),其数值为3 297.9 mm/s2,且放大系数为2.199;最大峰值加速度发生在管廊顶板中心处(即监测点2),其数值是3 354.2 mm/s2,且放大系数为2.236。说明地震波从底层向高层自由表面传播时土体起放大加速度作用;沿高度方向加速度幅值从下到上逐渐增加,且加速度幅值在同一水平线上基本相同。
表5 各节点的峰值加速度
Table 5 The peak acceleration of each node mm/s2

监测点输入峰值加速度水平地震下监测点峰值加速度竖向地震下监测点峰值加速度11 5003 339.21 640.121 5003 354.21 646.031 5003 337.41 640.241 5003 310.31 639.751 5003 311.61 639.861 5003 298.21 639.371 5003 297.91 631.781 5003 297.81 639.4
在竖向地震作用下,管廊顶部中间节点加速度峰值最大,达到1 646.0 mm/s2;底部中间节点幅值最小,达到1 631.7 mm/s2。竖向地震波在向上传递的过程中,沿着传递方向,加速度幅值呈现稍微增大的趋势;同时土层对其起到了放大效应。另外,管廊结构在竖向地震作用下,各节点的加速度峰值相比横向地震时较小,并且加速度放大系数比较稳定,在1.088~1.097,这也说明管廊结构几乎不受竖向EL-Centro波的影响。
1.3.3 主应力响应分析
管廊结构在水平和竖向地震作用下,各自的第一主应力峰值云图和第三主应力云图见图5、图6。
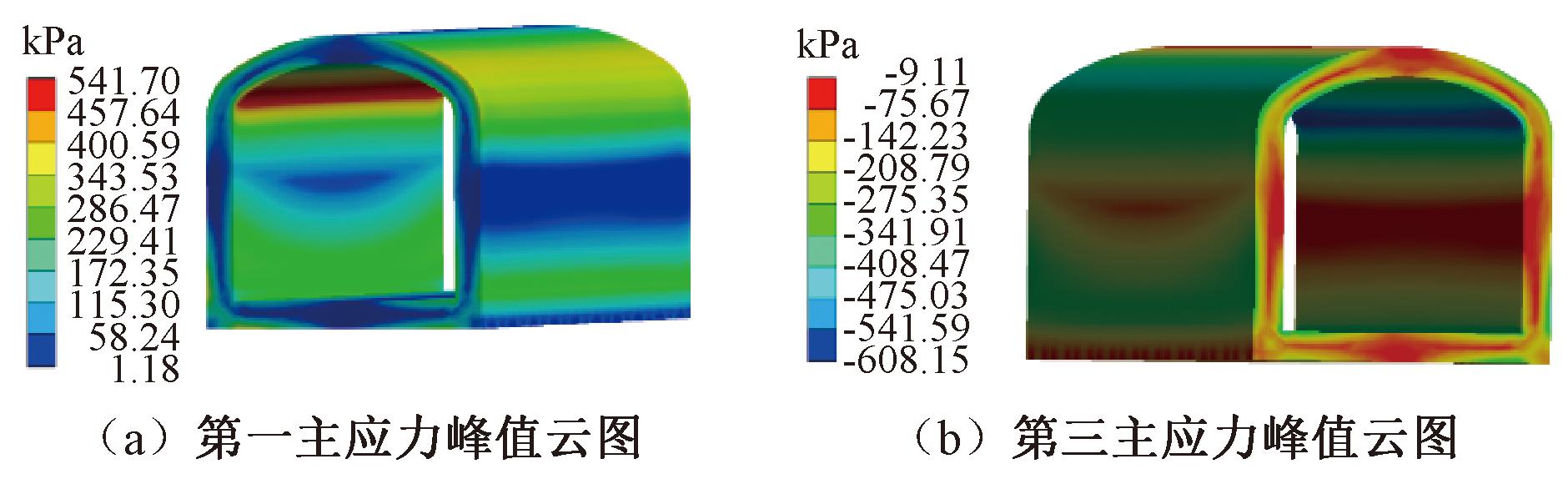
图5 水平地震下应力峰值云图
Figure 5 Peak stress cloud diagram under horizontal earthquake
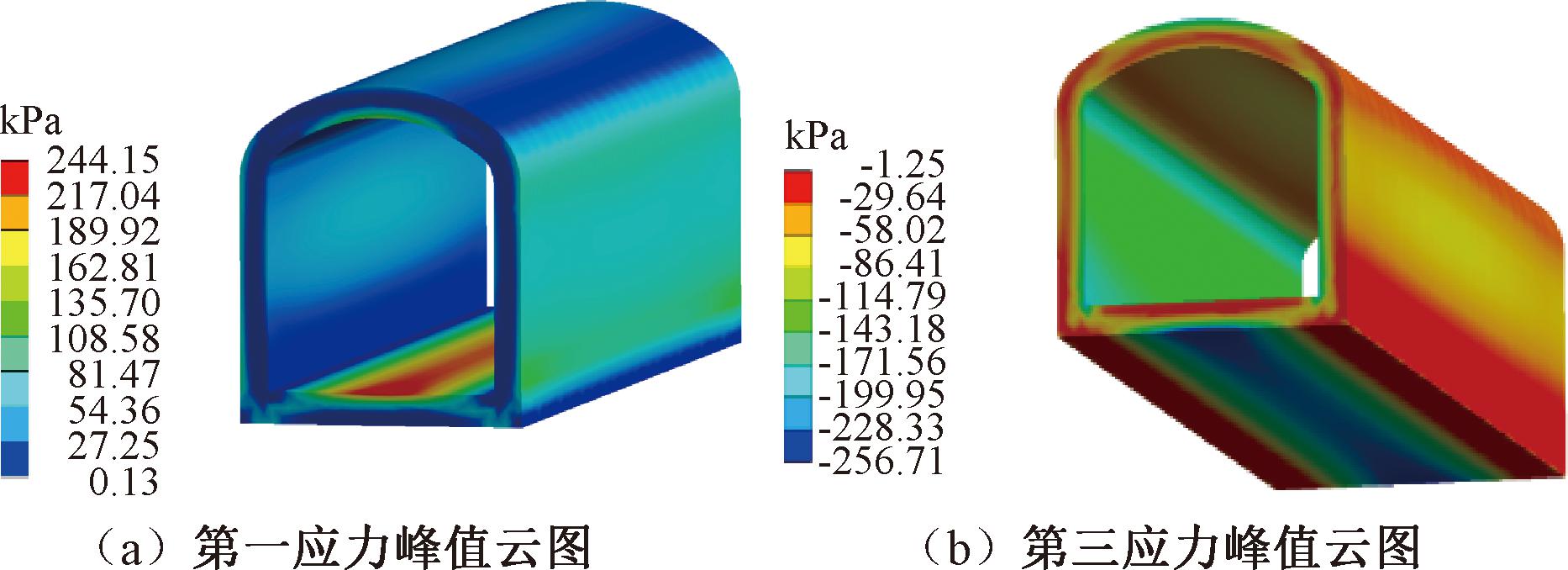
图6 竖向地震下应力峰值云图
Figure 6 Stress peak cloud diagram under vertical earthquake
由图5可知,第一主应力峰值为514.70 kPa,出现在上部弧形与方形的交界处,管廊上部与管廊下部的最大应力值大于管廊中部。第三主应力峰值为-608.15 kPa,同样发生在上部弧形与方形的交界处,为第一主应力发生的对称处。可以得出,管廊结构在水平地震动的作用下,其结构的一个角部的受压应力比较大,另一个角部受拉应力较大,角部更容易破坏。因此,管廊结构在抗震设计时需要对角部采取加强措施。
由图6知,在竖向地震作用下,管廊的第一主应力最大值为244.15 kPa,出现在管廊底板的上部,管廊结构的应力主要分布在外侧面以及内侧面的上部位置。管廊第三主应力最小值为-256.71 kPa,出现在管廊底板的下部,管廊的第三主应力主要分布在管廊的外侧面上部及内侧面。
因此,如果管廊结构考虑到竖向地震作用时,其设计的重点应该加固底板。竖向地震与水平地震第一主应力小270.55 kPa,比第三主应力小351.44 kPa。表明管廊结构受竖向地震影响程度较小,且相比于水平地震的影响较轻。
2 管廊抗震影响因素
管廊抗震设计是一个涉及多个因素的复杂问题。一般来说,管廊抗震设计需要考虑以下几个方面的因素:土质条件、设防烈度、管廊结构形式、埋置深度、地震波类型、管廊材料和连接方式等。本节通过ANSYS Workbench软件从频谱特性、混凝土材料强度以及结构的埋置深度3个方面,用相对位移和主应力响应指标来进行管廊结构的地震响应分析,激励方向均为坐标系中的X方向,与Y轴夹角90°。
2.1 频谱特性的影响
频谱特性是指地震动中构成各种简谐振动的振幅与相位特征,频谱表现出不同频率成分的强度分布情况,体现地震的动力特性。选取4种经调幅后的地震波用于动力时程分析,4种地震波分别为EL-Centro波(简称EL波)、Pasdena波(简称PAS1-4波)、Courthouse波(简称OLY1-4波)以及Oroville Earl Broadbe波(简称EAR-2波)。对应的卓越频率分别为1.17、1.08、1.67、2.67 Hz。
2.1.1 对位移响应的影响
在输入地震波的峰值加速度幅值均为0.15g的情况下,由于地震波频谱特征的不同,导致地下管廊结构顶底间的水平相对位移最大值的不同。在本节所选的4条地震波作用中,EAR-2波作用下,综合管廊顶底部的相对水平位移最小,仅有0.473 mm;PAS1-4波作用下,管廊结构顶底部的相对位移最大,达到1.5 mm。4条地震波按顶底板最大水平相对位移值排序,从小到大是EAR-2波、OLY1-4波、EL波、PAS1-4波。
2.1.2 对主应力的影响
管廊结构的第一主应力最大值(以下简称最大主应力)与第三主应力最小值(以下简称最小主应力)见表6。
表6 不同频谱下最大主应力值
Table 6 The maximum principal stress value under different spectrums kPa

不同频谱特性的波最大主应力最小主应力PAS1-4波517.38-670.04EAR-2波218.80-267.70OLY1-4波476.15-586.33EL波514.70-608.15
由表6可知,管廊结构在不同频谱特性的地震波作用下,其产生的最大、最小主应力均不相同。4条地震波形中,根据结构内部产生的最大主应力值从小到大排列依次是EAR-2 波、OLY1-4波、EL波、PAS1-4 波。由此可见,本文研究的管廊结构对于卓越频率为1.10 Hz左右的地震波较为敏感。
2.2 结构材料的影响
为研究管廊材料强度对其动力响应的影响,依次选取C25、C30、C35及C40共4种强度级别的混凝土。在软件中改变材料的弹性模量,就可以得到不同强度的混凝土,从而实现不同结构材料对管廊结构的抗震分析。
2.2.1 对位移响应的影响
在管廊断面中,监测点2与监测点7的相对水平位移最大值依次为0.897 1 mm、0.895 8 mm、0.895 0 mm、0.894 4 mm。分析可得:随着管廊材料强度的提高,其结构顶底板相对水平位移峰值逐渐减小。但是,混凝土强度由C25提高到C40时,管廊结构相对水平位移只减少了0.002 7 mm,可忽略不计,可认为管廊材料强度的改变不影响结构的相对位移。
2.2.2 对主应力的影响
不同强度混凝土下的管廊结构在水平地震作用下产生的最大主应力和最小主应力见表7。
表7 不同强度混凝土下管廊的主应力峰值
Table 7 The peak principal stress of pipe gallery under different strength concrete kPa
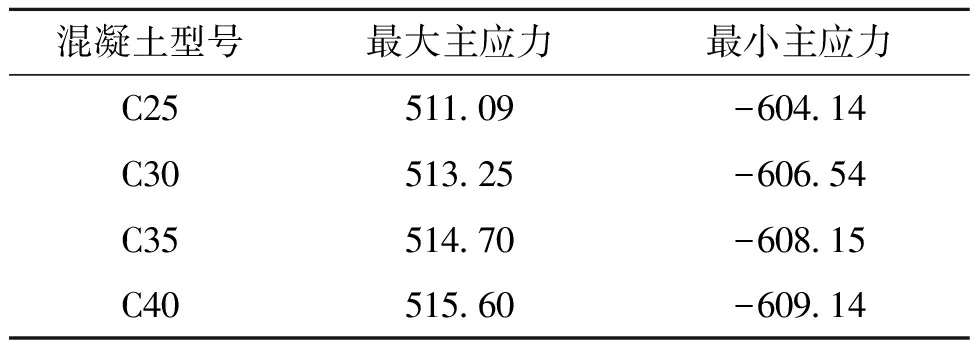
混凝土型号最大主应力最小主应力C25511.09-604.14C30513.25-606.54C35514.70-608.15C40515.60-609.14
由表7可知,随着管廊结构材料强度的增加,其最大主应力峰值与最小主应力峰值都得到了小幅度的提高。当混凝土型号从C25增加到C40时,结构的最大主应力从511.09 kPa增加到515.60 kPa,增幅为0.88%;最小主应力从604.14 kPa增加到609.14 kPa,增幅为0.83%,但两个主应力的增幅程度都较小。可见混凝土强度的提高并不影响管廊结构的主应力响应。另外,因为管廊结构的压应力远远小于相关规范规定的混凝土抗压强度。拉应力是影响管廊整体受力的一个重要因素,且随其强度的提高,其最大主应力也随之增加,这意味着其所受的地震作用也随之增强,这对结构的整体受力是不利的。
2.3 结构埋深的影响
结构埋深也是影响管廊结构抗震性能的因素之一,这里的埋深是指管廊主体结构顶板到地面的垂直距离。本节在前面模型的基础上,依次将管廊埋深设置为1.5、2.0、2.5、3 m,对不同埋深的管廊结构进行地震响应分析。
2.3.1 对位移响应的影响
随着管廊结构埋深的增加,管廊结构的顶、底板最大水平相对位移分别为1.24、1.15、1.12、1.09 mm。表明管廊在埋深1.5~3 m这个区间里,管廊结构顶、底板的相对水平位移逐渐减小。这是由于管廊结构随埋置深度加大而引起所受周边土压力增大,同时对土体的约束能力得到加强。
2.3.2 对主应力的影响
在水平地震作用下,4种工况下的管廊结构的最大主应力值和最小主应力值见表8。
表8 不同埋深下管廊的主应力峰值
Table 8 The peak principal stress of pipe gallery under different buried depths

埋深/m最大主应力/kPa最小主应力/kPa1.5406.64-481.492.0445.11-526.592.5482.11-570.563.0514.70-608.15
由表8可知,随着埋设深度的增加,管廊结构的最大、最小主应力也随之增加。当埋深从1.5 m分别增加到2.0、2.5、3.0 m时,管廊结构的最大主应力峰值从406.64 kPa分别增加到445.11、482.11、514.70 kPa,增幅分别为9.46%、18.56%和26.57%;而最小主应力峰值从481.49 kPa分别增加到526.59、570.56、608.15 kPa,增幅分别为9.35%、18.50%和26.31%,最大、最小主应力随着管廊埋置深度的增加,增幅基本相同。其主要原因是:管廊结构浅埋于地下,受到土体的约束,埋深加深使这一约束作用更强,因此管廊结构应力随埋置深度而增加。
3 结论
(1)土-管廊结构前6阶模态存在纵向振动、竖向振动、横向振动以及转动。
(2)管廊在水平地震作用下,位移由上而下呈缓慢增加趋势;地震波从底层向高层传播时土体放大加速度作用,沿高度方向加速度幅值从下到上逐渐增加;结构角部受力较大,因此管廊结构在抗震设计时需要对角部采取加强措施。
(3)管廊在竖向地震作用下,从下往上位移峰值渐渐增大,加速度幅值呈现稍微增大的趋势。管廊的主应力主要发生在底板和侧面。对比管廊水平和竖向地震作用计算结果,竖向地震作用下的位移、加速度及主应力响应都小于水平地震的工况,水平地震在管廊动力分析中占主导作用。
(4)管廊在不同频谱特性地震波作用下,管廊响应指标有所差异。本文所研究的管廊结构在地震波频谱特性约为1.1 Hz时最为敏感。因此在对管廊抗震设计时,需要找出管廊频率最为敏感范围,以保障管廊安全。
(5)混凝土强度的改变对管廊结构的动力响应影响不大。
(6)随管廊埋设深度的增加,周边土压力加大,使其内力逐步上升。但由于土体的约束作用,使其顶底板相对变形受限,更利于结构抗震。因此在综合管廊的抗震设计中建议考虑埋深的变化对管廊的影响。
[1] 史晓军, 陈隽, 李杰. 地下综合管廊大型振动台模型试验研究[J]. 地震工程与工程振动, 2008, 28(6): 116-123.SHI X J, CHEN J, LI J. Shaking table test on underground utility tunnel[J]. Journal of Earthquake Engineering and Engineering Vibration, 2008, 28(6): 116-123.
[2] 阮滨, 吉瀚文, 刘华北, 等. 大尺度可液化场地综合管廊纵向抗震分析方法[J]. 华中科技大学学报(自然科学版), 2022, 50(8): 99-104.RUAN B, JI H W, LIU H B, et al. Longitudinal seismic analysis method of utility tunnel in large-scale liquefiable site[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2022, 50(8): 99-104.
[3] 王鹏宇, 王述红, 朱承金. 城市地下管廊结构地震动力响应分析[J]. 东北大学学报(自然科学版), 2019, 40(7): 1020-1027.WANG P Y, WANG S H, ZHU C J. Seismic dynamic response analysis of urban underground utility tunnel structure[J]. Journal of Northeastern University (Natural Science), 2019, 40(7): 1020-1027.
[4] 魏奇科, 王宇航, 王永超, 等. 叠合装配式地下综合管廊节点抗震性能试验研究[J]. 建筑结构学报, 2019, 40(2): 246-254.WEI Q K, WANG Y H, WANG Y C, et al. Experiment study on seismic performance of joints in prefabricated sandwich structures of utility tunnels[J]. Journal of Building Structures, 2019, 40(2): 246-254.
[5] SHAMSABADI A, LAW H, AMINI M. Seismic rock-tunnel-structure interaction analysis[C]∥12 th European Conference on Earthquake Engineering. Oxford: Elsevier Science, 2002:91-98.
[6] 施有志, 孙爱琴, 林树枝, 等. Rayleigh波作用下地下综合管廊动力响应三维数值分析[J]. 世界地震工程, 2017, 33(4): 196-210.SHI Y Z, SUN A Q, LIN S Z, et al. Three dimensional(3 D) numerical analysis of dynamic response of underground utility tunnels to Rayleigh wave effects[J]. World Earthquake Engineering, 2017, 33(4): 196-210.
[7] 杨仕升, 姜龙, 谢开仲. 城市地下综合管廊典型节点地震响应分析[J]. 地震工程与工程振动, 2018, 38(5): 103-110.YANG S S, JIANG L, XIE K Z. Seismic response analysis of typical node of urban underground utility tunnel[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(5): 103-110.
[8] DEBIASI E, GAJO A, ZONTA D. On the seismic response of shallow-buried rectangular structures[J]. Tunnelling and Underground Space Technology, 2013, 38: 99-113.
[9] GEBREMEDHN Z, QIAO G F, SUN L. Seismic effect analysis of the adjacent longitudinal box culvert for the utility tunnel[J]. IOP Conference Series: Materials Science and Engineering, 2020, 758(1): 012084.
[10] 甘梦云, 梁建文, 李东桥, 等. 基于壳-弹簧模型的预制地下管廊横向抗震分析[J]. 自然灾害学报, 2022, 31(2): 102-110.GAN M Y, LIANG J W, LI D Q, et al. Lateral seismic analysis of precast utility tunnels using the shell-spring model[J]. Journal of Natural Disasters, 2022, 31(2): 102-110.
[11] 刘述虹. 典型综合管廊体系地震响应分析[D]. 哈尔滨: 中国地震局工程力学研究所, 2016.LIU S H. Seismic response analysis of typical urban utility tunnel system[D].Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2016.
[12] LYSMER J, WAAS G. Shear waves in plane infinite structures[J]. Journal of the Engineering Mechanics Division, 1972, 98(1): 85-105.
[13] DEEKS A J, RANDOLPH M F. Axisymmetric time-domain transmitting boundaries[J]. Journal of Engineering Mechanics, 1994, 120(1): 25-42.
[14] 廖智麒. 综合管廊地震响应分析及影响因素研究[D]. 广州: 华南理工大学, 2019.LIAO Z Q. Study on seismic response analysis and influencing factors of utility tunnel[D].Guangzhou: South China University of Technology, 2019.
[15] 吴晔, 许紫刚, 杜修力. 软弱夹层对地下结构地震响应的影响分析[J]. 郑州大学学报(工学版), 2021, 42(4): 91-97.WU Y, XU Z G, DU X L. Analysis of effects of weak interlayer on seismic responses of underground structures[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(4): 91-97.
[16] 谷音, 刘晶波, 杜义欣. 三维一致粘弹性人工边界及等效粘弹性边界单元[J]. 工程力学, 2007, 24(12): 31-37.GU Y, LIU J B, DU Y X. 3 d consistent viscous-spring artificial boundary and viscous-spring boundary element[J]. Engineering Mechanics, 2007, 24(12): 31-37.