单元的刚度矩阵和质量矩阵(质量矩阵有集中质量矩阵和一致质量矩阵两种形式,下文所指均为一致质量矩阵)是有限元计算的基础,既有文献往往侧重对单元刚度矩阵的分析,对结构动力分析[1-2]中必不可少的质量矩阵,却关注较少[3-4]。相关研究仅给出了不考虑剪切变形的欧拉梁的质量矩阵,且未考虑弯曲受力状态下截面转角引发的轴向变形对质量矩阵的影响[5-8]。基于有限元的思想和形函数及虚功原理,在Archer等[9-10]的基础上,Przemieniecki[11]给出了考虑剪切变形的欧拉梁的单元质量矩阵推导过程,但仅针对等截面单元,这在刘瑞岩[12]的研究中亦有介绍,杜柏松等[13]也给出了相同的推导过程。李明瑞[14]仅给出了分析思路但没有给出具体结果。Yokoyama[15]基于最小势能原理所给出的质量矩阵与Przemieniecki[11]的研究一致,这也是ANSYS中Beam4单元质量矩阵的来源。Clough等[16]详细介绍了质量矩阵概念,即将运动单元的分布质量附以相应的分布惯性力,并基于虚位移原理给出节点等效惯性力。
但是,既有研究对质量矩阵的分析仅针对等截面欧拉梁单元,对工程中常用的变截面梁单元却未见分析。另外,在质量矩阵分析中,如何计入弯曲受力状态下截面转角引发的轴向变形,亦需关注。因此,本文在考虑剪切变形的等/变截面欧拉梁刚度矩阵[17-19]的基础上,根据质量矩阵分析的基本原理[11],分析探究考虑剪切变形的等/变欧拉梁的质量矩阵分析过程,并着重讨论弯曲受力状态下截面转角引发的轴向变形对质量矩阵的影响。为简化分析过程,仅以一个梁单元为例进行分析,且仅考虑其自身分布质量而不考虑其他附加集中质量,同时对受弯仅限于XY平面内进行分析,但包括其轴向伸缩和扭转问题。
1 理论基础
对于具有分布质量的杆件,设其密度为常量ρ,按照达朗贝尔原理,当其处于运动状态时可视为具有惯性力,并且是一种分布的体积力,这就需要明确杆件上各点的位移状态,以表示这种惯性力,然后进一步根据虚功原理,将这种分布的惯性力表示为沿节点自由度方向的集中力[5,16]。
形函数是确定杆件变形状态的基本方法,也是刚度和质量矩阵分析的基础。由于伸缩、扭转和弯曲受力与变形本身是独立的,因此在分析中可对3种变形模式对应的矩阵进行独立分析,这也是下文的分析方式。对于图1所示xy平面内的欧拉梁单元,其刚度矩阵分析中所涉及的位移函数也即杆轴线的变形,包括伸缩、扭转和弯曲3种,并可统一表示为式(1)[3,18]形式,图2为形函数示意图。
(1)
图1 单元坐标系示意图
Figure 1 Element in the uniform coordinate system
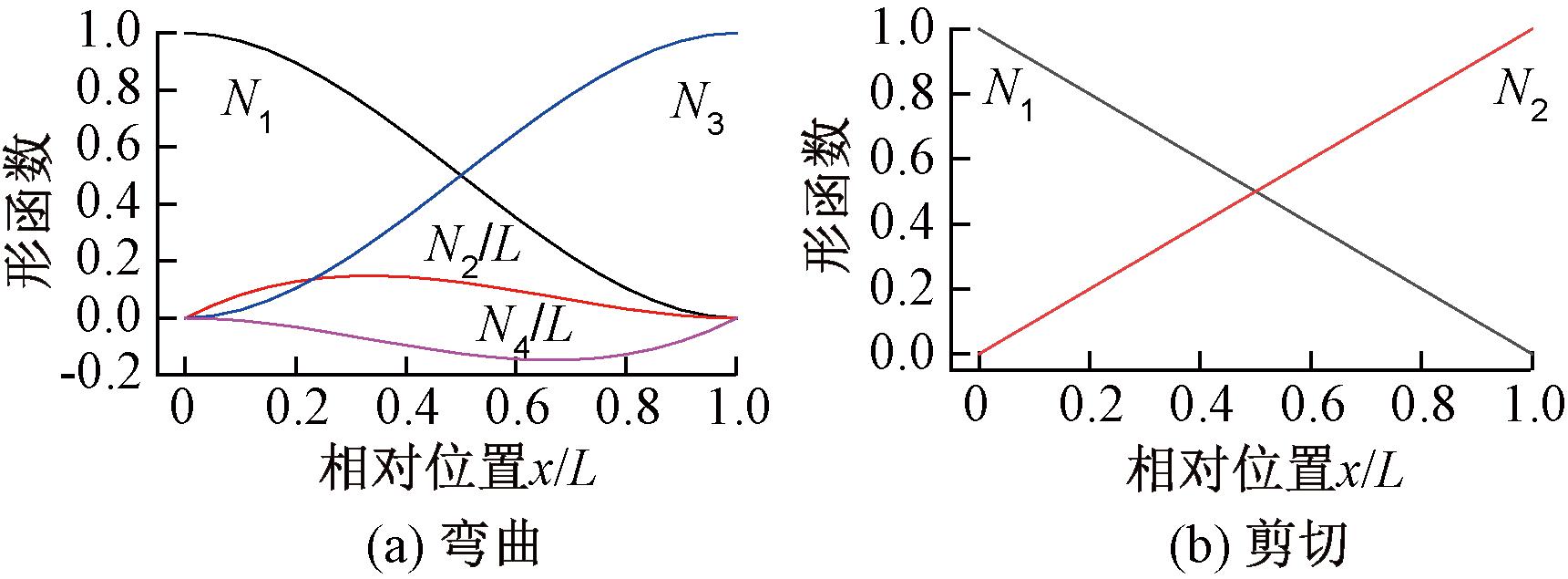
图2 形函数示意图
Figure 2 Drafts of shape functions
式中:N和Φ分别为形函数行向量和节点位移列向量(见表1);ψr表示节点i和j的位移,包括节点的轴向位移u或扭转角θ、竖向位移w和截面转角α;n为独立节点位移数量,除弯曲变形对应的r=4外,其他两种变形均为r=2(见表1);Nr(x)表示形函数,图2和表1给出两种形函数的形式和适用变形[3,18]。如果考虑剪切变形,伸缩和扭转变形不受影响,但弯曲形函数则有所不同(表1),其中参数
和G分别为弹性模量和剪切模量,A和I为截面惯性矩,k为截面剪切系数[18]。
表1 不同变形的形函数
Table 1 Shape functions for different deformations
变形形函数向量节点位移向量伸缩NA=l-xl,xl[]ΦA=[uI,uJ]T扭转NT=l-xl,xl[]ΦT=[θI,θJ]T弯曲(不考虑剪切)NB=2x3-3lx2+l3l3,x3-2lx2+l2xl2,3lx2-2x3l3,x3-lx2l2éëêêùûúúΩB=6(x2-lx)l3,3x2-4lx+l2l2,6(lx-x2)l3,3x2-2lxl2éëêêùûúúΦB=[ωI,αI,ωJ,αJ]T弯曲(考虑剪切)NB=2x3-3lx2+l3+(l3-xl2)ϕl3(1+ϕ),x3-2lx2+l2x+12(xl2-x2l)ϕl2(1+ϕ),éëêêê 3lx2-2x3+xl2ϕl3(1+ϕ),x3-lx2-12(xl2-x2l)ϕl2(1+ϕ)ùûúúúΩB=6(x2-lx)l3(1+ϕ),3x2-4lx+l2+(l2-lx)ϕl2(1+ϕ),6(lx-x2)l3(1+ϕ),3x2-2lx+lxϕl2(1+ϕ)éëêêùûúúΦB=[ωI,αI,ωJ,αJ]T
上述各种变形的形函数,均可借助结构力学的方法对两端固结梁进行位移计算得到,此处以受弯状态的N1(x)和N2(x)为例给出计算方法(图3)。对于N1(x),首先将两端固结梁解除左侧竖向约束并施加单位竖向力,根据力法求解杆件的弯矩和剪力,并进一步计算左侧单位竖向力作用下任意位置x的竖向位移w(x),将此竖向位移w(x)以左端竖向位移归一化,即可得N1(x)。对于N2(x),则解除左侧转动约束并施加单位力矩,同样计算左侧单位力矩作用下任意位置x的竖向位移w(x),将此竖向位移w(x)以左端转角位移归一化即可得N2(x)。N3(x)和N4(x)的计算与此类似。如果在整个计算过程包括求解图3所示杆件内力以及变形w(x)中考虑剪力的贡献,则所得即为考虑剪切变形的形函数。另外,根据结构力学分析可知,变截面梁的形函数更为复杂,故在有限元中对变截面梁依然直接使用等截面梁的形函数以简化分析,这也是后续对变截面梁分析时的基本假定。
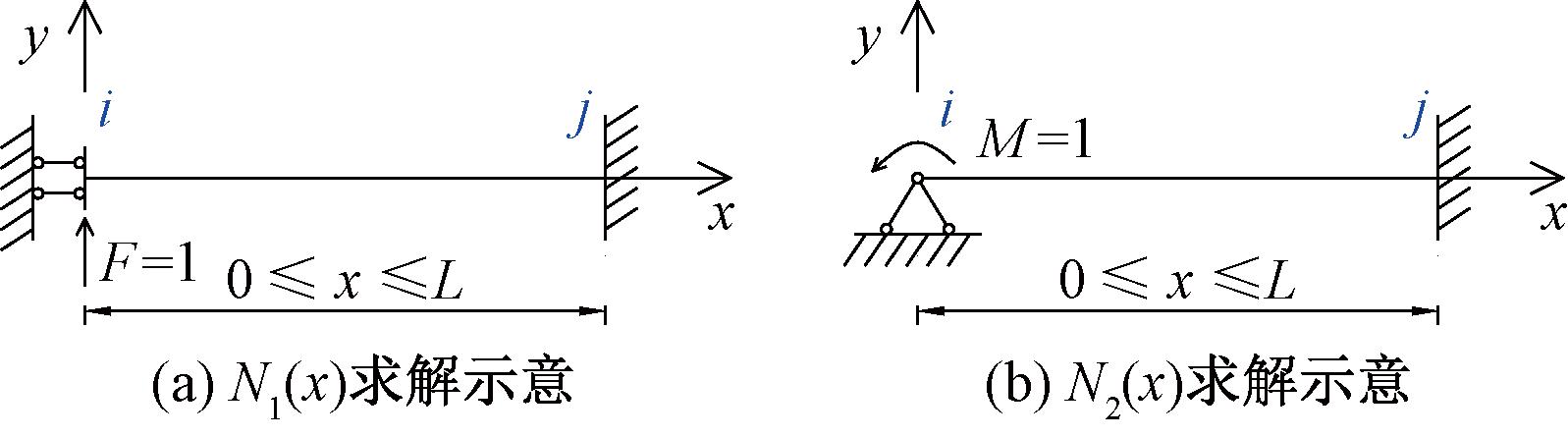
图3 形函数计算示意图
Figure 3 Calculation of shape functions diagram
形函数本质上仅是杆轴线上各点的水平位移、转角位移和竖向位移,利用形函数即可表示杆件的变形能,从而进行刚度矩阵分析。但在质量矩阵分析中,需要明确杆件上各点的变形或位移状态,对于受弯状态,仅有形函数仍不充分,因为此时杆件上各微元体的位移并非都沿y方向,中性轴以外的微元体还会因截面转角产生沿x方向的位移,因此需要定义新的位移关系矩阵H以完整表示杆件上各位置的位移(式(2)):该位移关系矩阵H不仅包括表示y向位移的形函数向量NB,还增加了一行表示任意位置(x, y)微元体x向位移的向量-ΩBy。类似式(1)即可得到在弯曲受力状态下节点位移向量ΦB所引发的杆件任意位置(x, y)微元体在平面x和y方向的位移向量。
(2)
式中:ΩB为截面的转角形函数;y为微元体偏离杆轴线的距离。ΩB的计算与NB类似,只是所求为任意位置x的转角位移α(x)而非竖向位移w(x)。还需要说明,如果不考虑剪切变形,则截面转角位移α(x)始终为竖向位移w(x)的导数,这也是不考虑剪切变形的欧拉梁的基本性质[18]。但在考虑剪切变形时,由于剪应变γ0的参与,截面转角α(x)不再是w(x)的导数,也即
(见图4)。
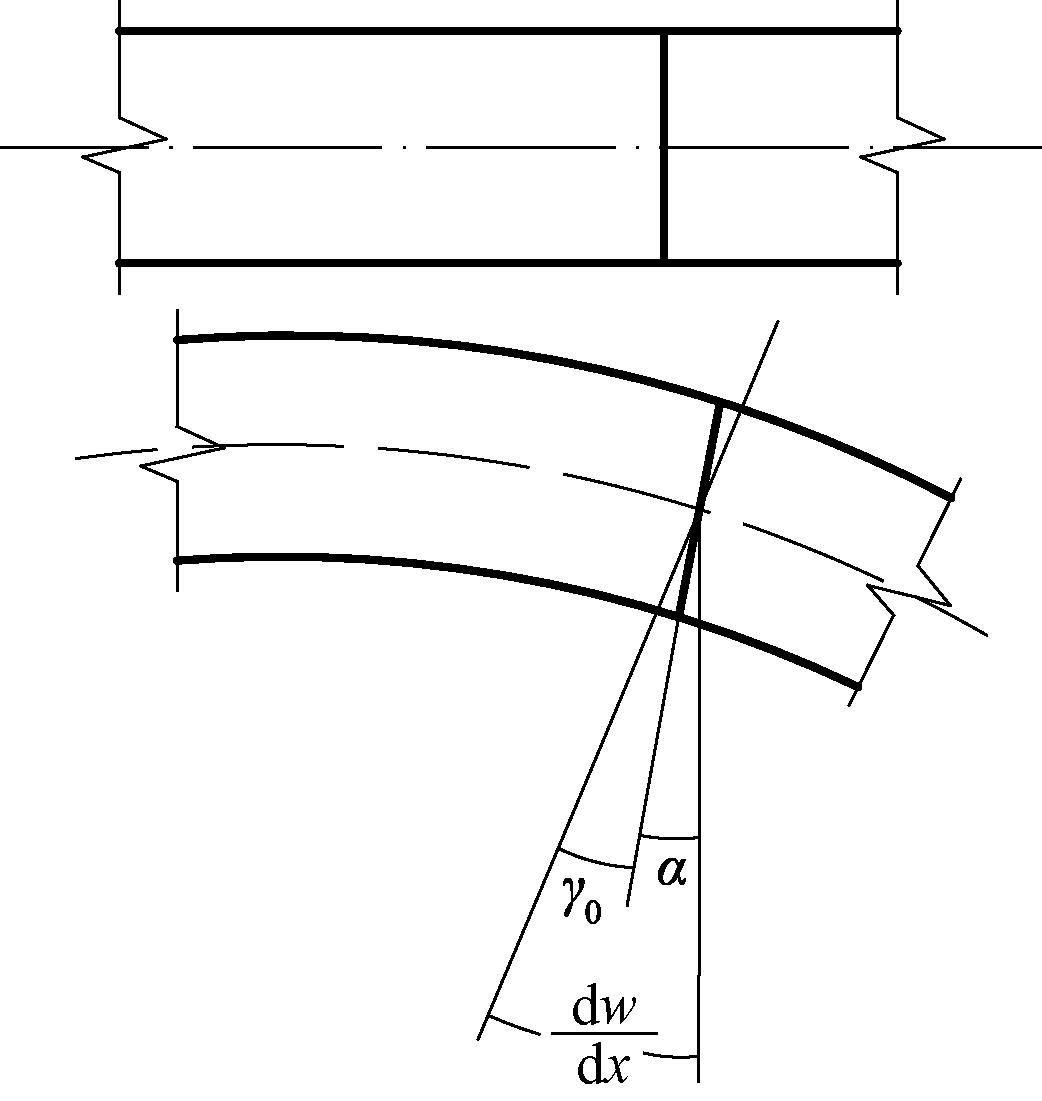
图4 截面转角示意图
Figure 4 Section rotation diagram
2 质量矩阵分析
2.1 伸缩和扭转
单元在伸缩时,整个杆件所有微元体都仅发生沿x轴的位移(在小变形假设下忽略微元体垂直于杆轴线的位移),且整个截面的位移相同,故整个截面的位移可用伸缩状态下的形函数(见表1)表示。类似的,伸缩运动状态下的加速度同样可以用该形函数表示,则在杆端加速度
作用下,杆件上各截面x位置的惯性力为
(3)
根据虚位移原理,虚设节点i、j依次发生单位轴向位移并引发杆件变形,则分布惯性力fA(x)在相应杆件变形上做的虚功即节点等效惯性力Fi,A列向量:
(4)
式中:
即为伸缩运动对应的一致质量矩阵,该式其实也是动力学方程的第1项。对于等截面单元,A(x)为常数A0,代入计算得
(5)
对于变截面单元,即使截面尺寸线性变化,其A(x)也为2次函数,再考虑
之后则为4次函数,积分表达式过于复杂,理论解已无实用价值。在ANSYS中,对于变截面梁单元Beam44的一致质量矩阵,则在式(5)中的主对角元分别使用i、j端的面积Ai和Aj,副对角元则使用两端的平均面积
即
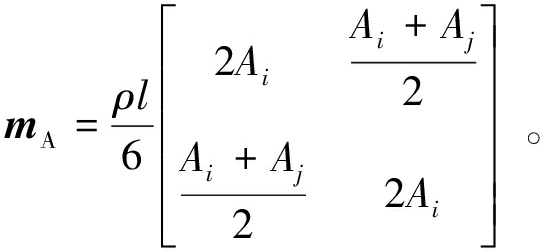
(6)
对于扭转变形对应的质量矩阵,其推导过程与伸缩类似,只是将上述推导过程中的截面面积A(x)替换为截面极惯性矩J(x),所得结果也与式(5)、式(6)类似,不再给出。
2.2 考虑剪切的杆件弯曲变形状态质量矩阵
推导考虑剪切的杆件弯曲变形状态的质量矩阵时,需要同时考虑各微元体在x向和y向的惯性力,在杆端加速度
作用下,杆件上各位置(x, y)处的惯性力分布为
(7)
式中:fB,x和fB,y分别为坐标(x,y)位置微元体在x和y方向的惯性力。显然弯曲状态下的惯性力分布更为复杂,不能类似伸缩或扭转时给出整个截面的惯性力,尤其是对于x方向的惯性力fB,x,因为其来自于截面转角α引发的截面微元体在x方向的位移,其在截面上的分布还与坐标y有关。这种既考虑剪切变形,又考虑x方向惯性力的单元在文献[12]中称为全耦合单元。根据虚位移原理,虚设节点i、j依次发生单位竖向和转角位移并引发杆件变形,则分布惯性力fB在相应杆件变形上做的虚功也即节点等效惯性力FB列向量,即
(8)
式中:
即为弯曲运动对应的一致质量矩阵。对于等截面单元,A(x)=A0,代入得
mB=ρA0l·
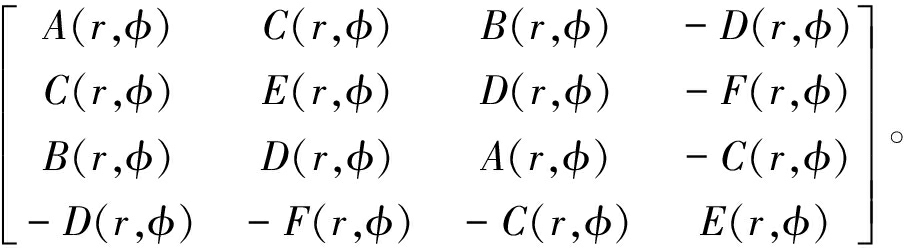
(9)
式(9)中各参数分别为
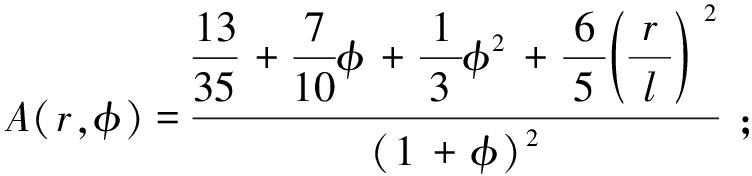
(10)
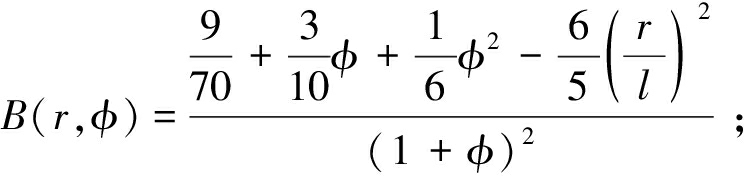
(11)
C(r,φ)=
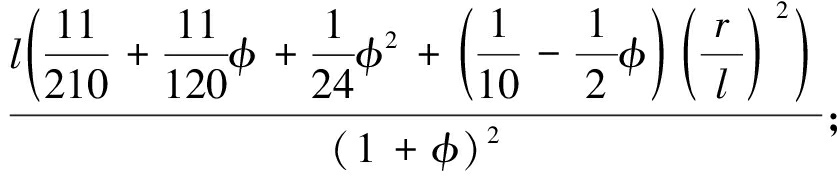
(12)
D(r,φ)=
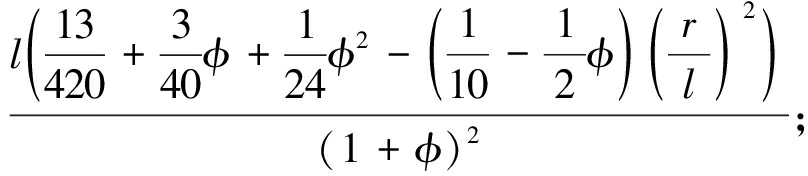
(13)
E(r,φ)=
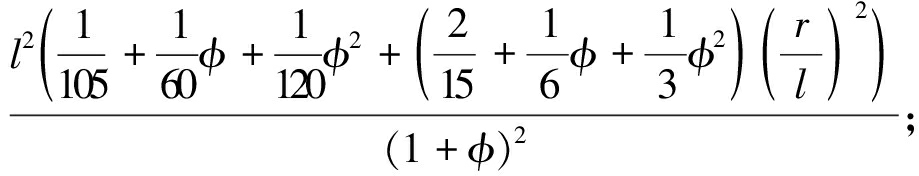
(14)
F(r,φ)=
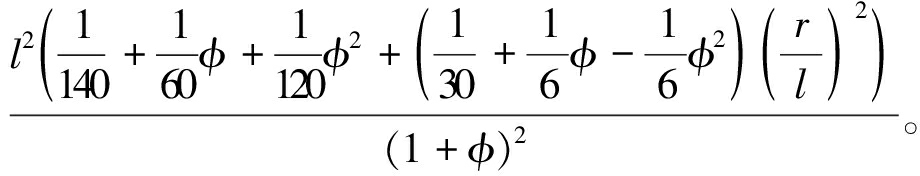
(15)
显然,对于变截面单元,截面面积A(x)作为变量,会使式(8)更为复杂,其理论解亦无实际价值。在ANSYS中,变截面梁单元Beam44的质量矩阵同样通过对式(9)中元素的调整来实现(式(16)),即对式(9)中左上角4个元素,也即仅与i端节点加速度相关的元素匹配i端面积Ai,右下角4个元素,也即仅与j端节点加速度相关的元素匹配j端面积Aj,其他元素则匹配两端面积均值。
2.3 不考虑剪切的杆件弯曲变形状态质量矩阵
不考虑剪切变形时弯曲变形状态的质量矩阵推导过程与前节一致,只是对位移关系矩阵H中的形函数使用不考虑剪切变形式的形函数而已。对于等截面梁单元,所得结果为式(17)。
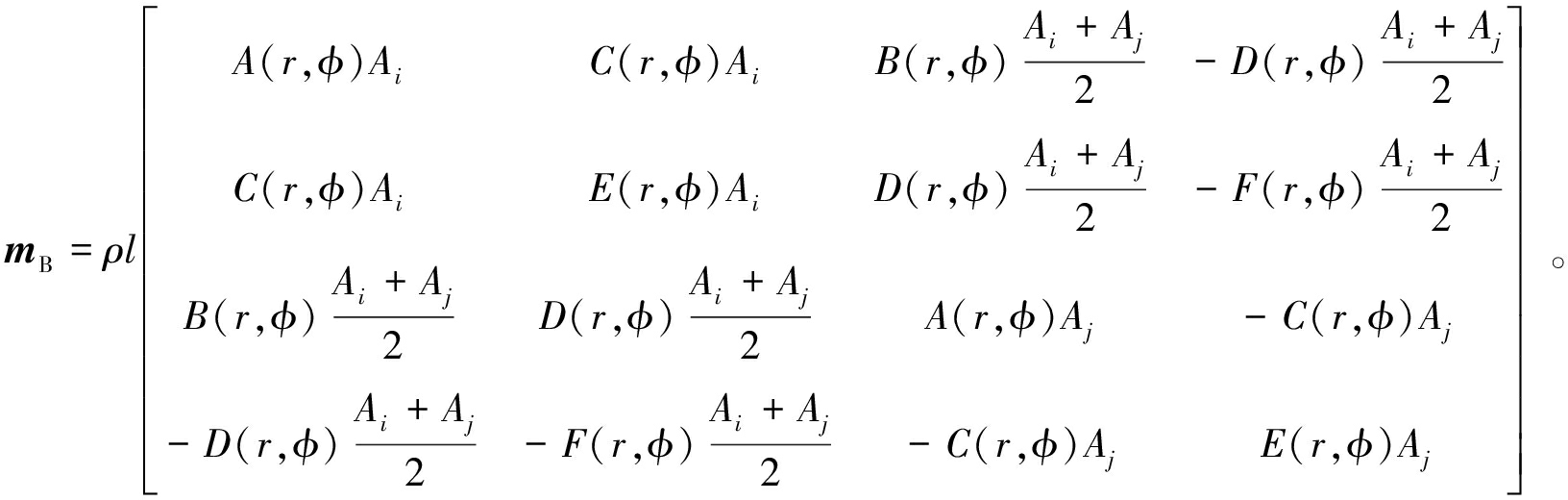
(16)
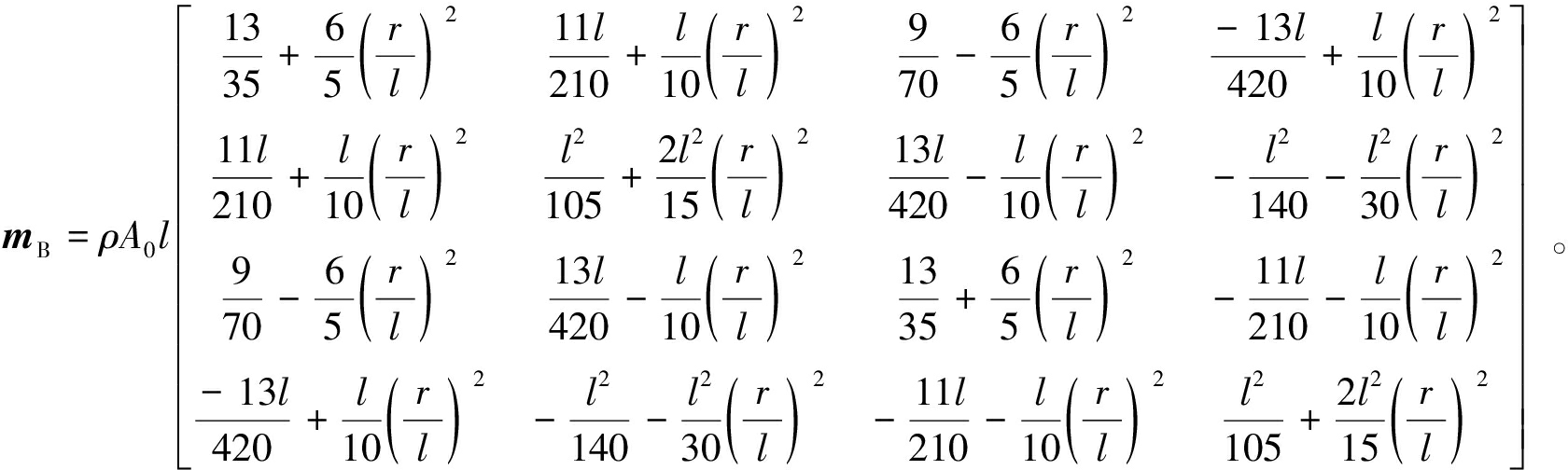
(17)
式中:
为截面的惯性半径,
为截面的惯性矩。显然,这一结果与文献[5-7, 16]所给质量矩阵(式(18))并不一致,矩阵中每一个元素都多了一个与
有关的项,而这一项正是由于在分布惯性力的表达式(式(7))中考虑了杆件截面转角的影响,或者说考虑了杆件微元体沿x方向的惯性力,这本身正是完善的表达式。
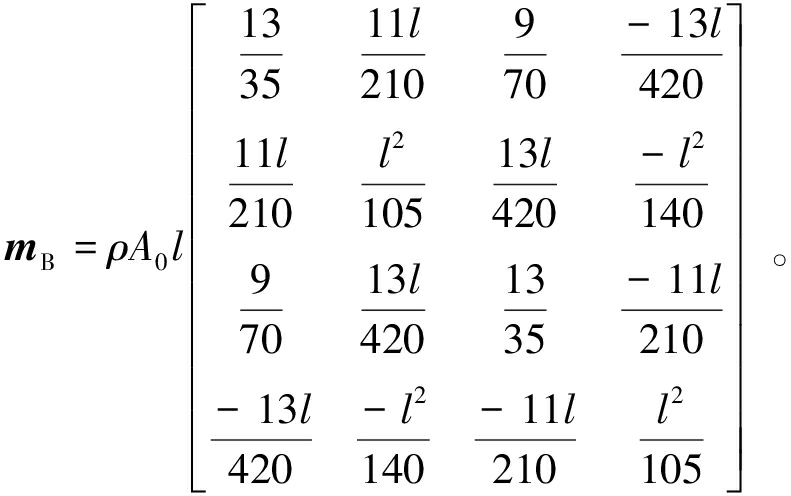
(18)
对比式(18)可知,研究者们在一致质量分析中并未考虑剪切变形的影响,也未考虑弯曲受力状态下截面转角引发的轴向变形对质量矩阵的影响[5-7,16],这显然是一种近似的方法和结果。此时因忽略了x方向的惯性力,而整个截面y向位移相同,故可类似式(3)直接给出杆件上的各截面的惯性力分布为式(19),再类似式(4)即可得式(18)的质量矩阵。
(19)
对于ANSYS的Beam44单元,在不考虑剪切变形时,其所得质量矩阵亦是式(18),说明其亦未考虑截面转角引发的轴向变形对质量矩阵的影响;其变截面梁单元Beam44的质量矩阵依然通过对式(18)中元素的调整来实现,过程类似式(9)和式(16)。综合伸缩和扭转运动状态的质量矩阵分析可知,Beam44单元的一致质量矩阵是对矩阵中仅与i、j端有关的元素分别考虑i、j端的截面面积或截面极惯性矩,与两端都有关的元素则取两端参数的均值。
2.4 受弯状态下质量矩阵和刚度矩阵分析方法的差异和联系
由前文可知,对于等截面欧拉梁的伸缩和扭转,由于受力特征简单,其质量和刚度矩阵的分析也较为简单,均只需要相应单一的形函数即可[17-19]。但对于等截面欧拉梁的弯曲问题,因剪力和弯矩的耦合性,给其刚度矩阵和质量矩阵分析带来一定的困难,因此传统欧拉梁采用忽略杆件剪切变形这一基本特征。此时在其刚度矩阵的分析中,由于忽略剪应变和剪切应变能,仅计入其弯曲应变能,也仅需其竖向位移形函数NB(纯弯曲竖向位移形函数)即可;在质量矩阵分析中,完善的分析应类似式(7)计入各微元体x向的惯性力,这就需要截面转角形函数ΩB,但实际使用中往往均忽略了x向的惯性力,仅采用式(19)和纯弯曲竖向位移形函数保留了y向的惯性力,这也实现了不考虑剪切变形的欧拉梁刚度和质量矩阵分析过程的统一。
为了提高欧拉梁的适用性,仍可计入剪切变形的影响。此时推导刚度矩阵时,为计入剪切应变和剪切应变能,往往再专门指定剪切位移形函数,且此形函数与表1伸缩和扭转形函数一致,通过纯弯曲竖向位移形函数和剪切位移形函数分别得到弯曲应变能和剪切应变能,将两者叠加并考虑弯矩和剪力的微分关系以及剪切竖向位移、纯弯曲竖向位移和总竖向位移之间的叠加关系,最终可得考虑剪切变形的欧拉梁单元刚度矩阵,此过程在文献[18]中有详细介绍,不再赘述。但是,对考虑剪切变形的欧拉梁单元的质量矩阵进行推导时,则要通过式(7)和式(8)直接使用考虑剪切变形的形函数,而非对纯弯曲变形和剪切变形分别考虑各自的惯性效应。这也是因为在刚度矩阵分析中,涉及的弯曲应变能和剪切应变能两者之间是独立的,弯曲正应变和剪切剪应变之间不会相互产生应变能,因此可以独立分析。但在质量矩阵分析中,需要关注分布惯性力在相应节点位移引发的变形上做的功,不管是纯弯曲变形还是剪切变形,都会使微元体产生y向的位移,两者是耦合的,因此必须在形函数中同时考虑纯弯曲变形和剪切变形。
当然,利用考虑剪切变形的形函数亦可进行刚度矩阵分析。对于等截面梁,通过图4可知,需通过截面转角α的一阶导数(而非竖向位移w的二阶导数)得到正应变ε和正应力σ,通过竖向位移w的一阶导数和截面转角α的差得到截面平均剪切应变γ0和平均剪应力
0,从而得到弯曲正应变能UM、剪切应变能UQ和总应变能U,进而根据文献[18]得刚度矩阵表达式如式(21)所示。
U=UM+UQ;
(20)
(21)
式中:
dx;
dx。
对比张军锋等[18]对计入剪切变形的刚度矩阵K推导过程可知,在上述过程中尽管已经在变形中计入了剪切变形的影响,但可以得到独立的正应变ε和平均剪切应变γ0,从而进行刚度矩阵的推导,而无须对剪切变形本身设定形函数。实际上,对比表1所列考虑与不考虑剪切变形的竖向及转角位移形函数可知,考虑剪切变形的形函数,本身就是不考虑剪切的形函数与纯剪切变形形函数的线性叠加,直接采用考虑剪切变形形函数进行刚度矩阵推导在本质上也与张军锋等[18]的推导过程是相通的。
3 结论
(1)不考虑剪切变形时,欧拉梁受弯状态的一致质量分析一般忽略了单元上微元体水平方向的惯性力,此时仅考虑弯曲变形引发的竖向位移形函数而无须转角位移形函数。
(2)考虑剪切变形时,欧拉梁受弯状态的一致质量分析不再忽略单元上微元体水平方向的惯性力,此时同时需要完整的竖向位移形函数和纯弯曲转角位移形函数。
(3)对于变截面欧拉梁单元,即使是截面尺寸线性变化的情况,其一致质量的理论表达式已过于复杂,较为实用的办法是对质量矩阵中仅与i、j端有关的质量元素分别考虑i、j端的截面面积或截面极惯性矩,与两端都有关的质量元素则取两端参数的均值。
(4)考虑剪切变形时,欧拉梁的刚度矩阵亦可经竖向位移和纯弯曲转角位移形函数计算得到,这一过程与使用纯弯曲竖向位移和纯剪切竖向位移形函数的过程在本质上是一致的。
[1] 梁岩, 闫士昌, 赵博洋, 等. 近断层高速铁路刚构桥地震易损性分析[J]. 郑州大学学报(工学版), 2022, 43(4): 80-85, 91.LIANG Y, YAN S C, ZHAO B Y, et al. Seismic fragility analysis of rigid frame bridge near-fault high-speed railway[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(4): 80-85, 91.
[2] 杨雅勋, 王成之, 柴文浩, 等. 断索对曲线斜拉桥力学性能的影响[J]. 郑州大学学报(工学版), 2023, 44(5): 101-107.YANG Y X, WANG C Z, CHAI W H, et al. Effect of broken cable on mechanical properties of curved cable-stayed bridge[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(5): 101-107.
[3] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.WANG X C. Finite element method[M]. Beijing: Tsinghua University Press, 2003.
[4] 王焕定,焦兆平. 有限单元法基础[M]. 北京: 高等教育出版社, 2002.WANG H D, JIAO Z P. Fundament of finite element methods [M]. Beijing: Higher Education Press, 2002.
[5] 朱伯芳. 有限单元法原理与应用[M]. 4版. 北京: 中国水利水电出版社, 2018.ZHU B F. Finite element method theory and applications[M]. 4th ed. Beijing: China Water &Power Press, 2018.
[6] 胡于进, 王璋奇. 有限元分析及应用[M]. 北京: 清华大学出版社, 2009.HU Y J, WANG Z Q. Finite element analysis and applications[M]. Beijing: Tsinghua University Press, 2009.
[7] 杜平安, 甘娥忠, 于亚婷. 有限元法——原理、建模及应用[M]. 北京: 国防工业出版社, 2004.DU P A, GAN E Z, YU Y T. Finite element method——principles, modelling and applications [M]. Beijing: National Defense Industry Press, 2004.
[8] COOK R D, MALKUS, D S, PLESHA M E, et al. Concepts and applications of finite element analysis[M]. New York: John Wily &Sons. Inc., 2002.
[9] ARCHER J S. Consistent mass matrix for distributed mass systems[J]. Journal of the Structural Division, 1963, 89(4): 161-178.
[10] ARCHER J S. Consistent matrix formulations for structural analysis using finite-element techniques[J]. AIAA Journal, 1965, 3(10): 1910-1918.
[11] PRZEMIENIECKI J S. Theory of matrix structural analysis [M]. New York: McGraw-Hill, 1968.
[12] 刘瑞岩. 全耦合梁单元的一致质量矩阵[J]. 国防科技大学学报, 1984, 6(1): 101-108.LIU R Y. Consistent mass matrix for complete coupled beam elements[J]. Journal of National University of Defense Technology, 1984, 6(1): 101-108.
[13] 杜柏松, 项海帆, 葛耀君, 等. 剪切效应梁单元刚度和质量矩阵的推导及应用[J]. 重庆交通大学学报(自然科学版), 2008, 27(4): 502-507.DU B S, XIANG H F, GE Y J, et al. Derivation and application of 3D-beam′s element stiffness and mass matrix with shear effect[J]. Journal of Chongqing Jiaotong University (Natural Science), 2008, 27(4): 502-507.
[14] 李明瑞. 考虑剪切的梁单元的等效节点载荷和质量矩阵[J]. 北京农业工程大学学报, 1990, 10(2): 85-90.LI M R. Equivalent nodal load and consistent mass matrix of beam element considering shearing effect[J]. Journal of Beijing Agricultural Engineering University, 1990, 10(2): 85-90.
[15] YOKOYAMA T. Vibrations of a hanging Timoshenko beam under gravity[J]. Journal of Sound and Vibration, 1990, 141(2): 245-258.
[16] CLOUGH R W, PENZIEN J. Dynamics of structures[M]. New York: McGraw-Hill, 2003.
[17] 张军锋, 尹会娜, 李杰, 等. 欧拉-伯努利梁单元刚度矩阵推导[J]. 水利与建筑工程学报, 2019, 17(3): 89-93, 131.ZHANG J F, YIN H N, LI J, et al. Derivation of element stiffness matrix of Euler-Bernoulli beam element[J]. Journal of Water Resources and Architectural Engineering, 2019, 17(3): 89-93, 131.
[18] 张军锋, 尹会娜, 孙大勇, 等. 基于形函数推导考虑剪切变形的欧拉梁单元刚度矩阵[J]. 重庆交通大学学报(自然科学版), 2020, 39(9): 59-66.ZHANG J F, YIN H N, SUN D Y, et al. Euler beam element stiffness matrix considering shear deformation based on shape function derivation[J]. Journal of Chongqing Jiaotong University (Natural Science), 2020, 39(9): 59-66.
[19] 张军锋, 李杰, 尹会娜, 等. 考虑剪切变形的变截面欧拉梁单元刚度矩阵[J]. 结构工程师, 2020, 36(2): 43-50.ZHANG J F, LI J, YIN H N, et al. Element stiffness matrix of tapered Euler beam element including shear deformation[J]. Structural Engineers, 2020, 36(2): 43-50.