随着经济发展,汽车保有量增加,城市中车位不足、泊车环境复杂等问题愈发突出,研究自动泊车系统对解决停车难的问题有巨大帮助[1]。完整的自动泊车系统可分为环境感知、路径规划、跟踪控制3部分[2]。根据环境信息,快速规划出一条安全无碰撞且易于跟踪控制的路径,是实现自动泊车的关键一环,具有重要研究意义。目前,常用的路径规划方法包括几何曲线法、随机采样法、图搜索法等。
基于几何曲线法,张家旭等[3]采用双圆弧规划泊车路径,并使用回旋曲线进行平滑,其规划方法所得路径需要较大的泊车空间,否则可能规划失败;胡杰等[4]采用5次多项式规划泊车路径,以碰撞和汽车运动学性能为约束,求解最优泊车路径,但该路径只适用于能一次泊入的库位,无法进行库内调整泊车路径;胡杰等[5]将泊车路径分为入库段与库内调整段,通过重复使用“之”字形的库内调整路径,使车辆通过不断前进后退,最终停至目标位置,但调整次数过多,舒适性较差,对跟踪控制的要求较高。几何曲线法的优势在于计算效率高,可快速求得泊车路径。由于使用预设的曲线类型作为泊车路径,然后根据车辆参数与环境信息确定曲线具体参数,当泊车空间较小,车辆无法通过预设曲线泊入车位时,几何曲线法就无法计算出所需路径。
基于随机采样法,Jhang等[6]采用RRT*算法规划泊车路径,通过对状态空间进行采样,使用Reeds-Shepp (R-S)曲线连接一系列采样点,得到泊车路径,但该方法实时性差;王海芳等[7]针对RRT算法搜索效率差的问题,提出了Bi-RRT*算法,其在起点与终点同时开始搜索,最后交汇于一点,但该方法仅适用于移动机器人,不能满足汽车的运动学约束;Tahir等[8]在Bi-RRT*的基础上对采样空间进行限制,减少了采样次数,提高了实时性,但对于狭窄空间下的泊车适应性不佳。随机采样法的优势在于其直接对状态空间进行采样,因此具有完备性,即当采样点足够多时,一定能得到可行解。但由于车辆自身的非完整性约束,车辆具有横纵坐标与航向角3个状态变量,采样维度的上升会导致采样数成指数级增长,同时由于采样的随机性,在自动泊车这个对于规划路径的精度要求较高的场景下,规划所用时间较长,且规划路径一般不是最优的。
基于图搜索的方法,段书用等[9]使用A*算法,并加入安全距离矩阵,保证机器人搜索出路径的安全性,但未考虑运动学约束;曹彦博等[10]对混合A*算法的启发值获取方式进行改进,预先创建离线的代价地图,后续搜索过程中无须逐一计算,提高了算法的实时性,但未解决曲率不连续的问题;Zhang等[11]针对搜索曲线连接点曲率不连续的问题,使用螺旋线代替R-S曲线中的圆弧连接节点,但未能提高搜索效率。图搜索法中的A*算法通过遍历整个状态空间,可搜索出最短路径,但未考虑车辆运动学约束,不能直接用于自动泊车的路径规划。混合A*算法引入了车辆非完整性约束,所得路径可直接跟踪,但由于其通过采样控制变量,经过计算间接获得状态变量,不具有完备性。
针对受限泊车通道下路径规划时间长、路径质量差等问题,本文改进混合A*算法的节点扩展与碰撞检测方式,提高实时性,并通过二次规划对初始路径进行平滑,改善了曲率突变的问题。
1 混合A*算法
混合A*算法是由斯坦福大学Dolgov等[12]提出的一种算法,是一种在离散x-y-θ状态空间使用A*策略并融合R-S曲线机制的路径规划方法,并在DARPA挑战赛中得到了应用。
在A*算法的基础上,混合A*算法考虑到了车辆的运动学约束,引入航向角θ这一状态量,并使用R-S曲线进行节点扩展,如图1所示,同时在扩展一定次数后,尝试使用R-S曲线连接当前节点与终点,以加快搜索速度。
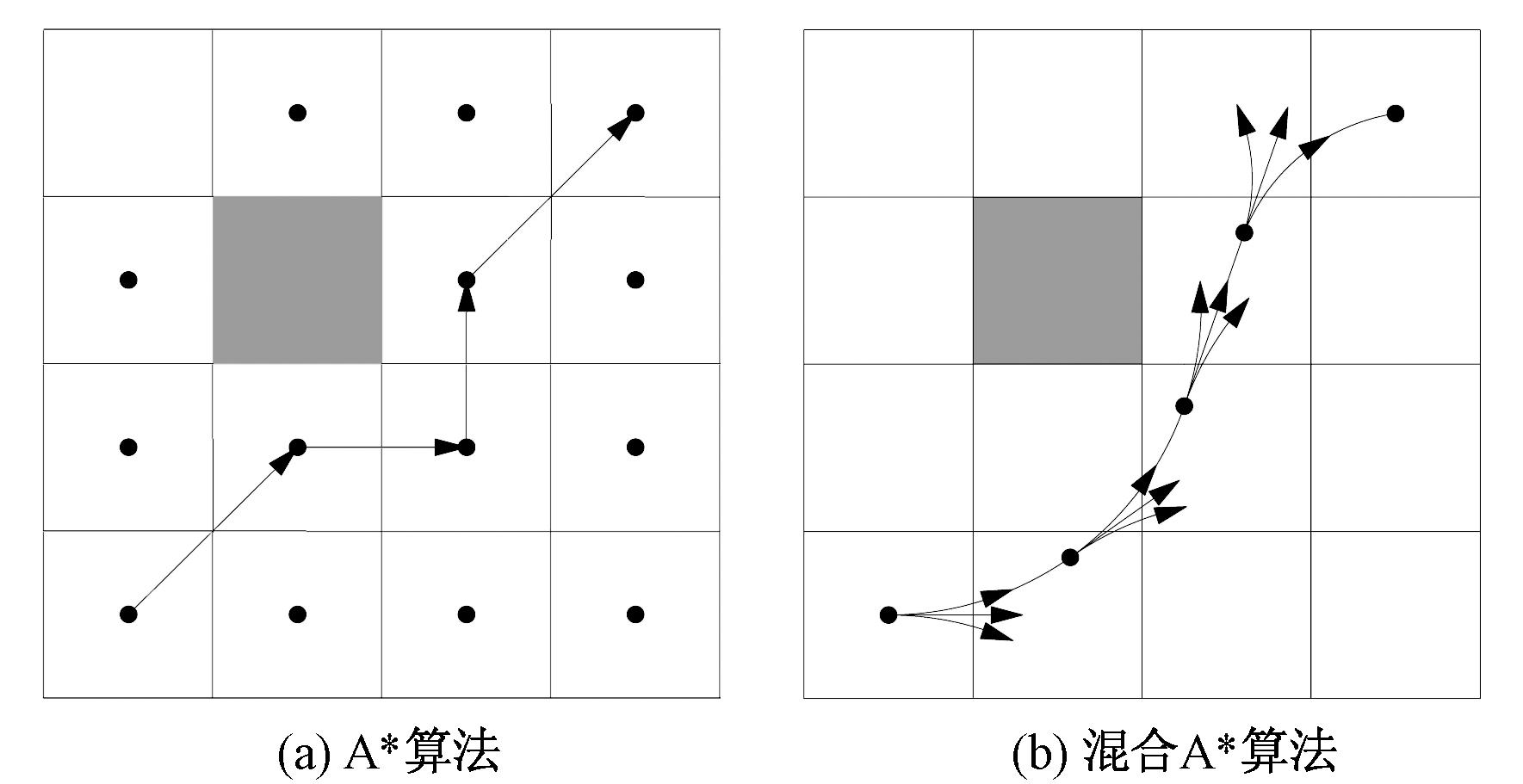
图1 两种算法节点拓展方式对比
Figure 1 Comparison of node expansion methods in two algorithm
同时,混合A*算法更改了启发函数h的定义,将h定义为两个子启发函数h1和h2的较大者,其中h1代表一条符合车辆运动学约束但无视碰撞的路径长度,通常用R-S曲线表征,h2代表一条考虑避障但未必运动学可行的路径长度,通常用A*路径长度和曼哈顿距离的较大值来表征。然而,对于平行泊车工况这一局部路径规划,由于汽车的运动学约束,起始点与目标点的h2距离一般远小于实际距离,h2无法真实反映情况。而R-S曲线由于没有考虑障碍物的影响,同样会远短于实际距离,h1同样无法反映真实情况。这两种子启发函数在算法刚启动开始搜索时误差格外明显,导致搜索了大量的无用节点,延长了搜索时间,且可能导致搜索失败。
因此,将泊车路径分为两段,其中前进段路径由于空间有限,相对简单固定,使用曲线构造,并得到倒车起始点,后退段考虑到目标点周围环境更复杂,不利于混合A*算法的加速搜索机制,因此从目标点到倒车起始点进行反向搜索。
2 平行泊车规划
2.1 前进调整段
当车位旁通道足够宽且足够长时,位姿调整路径可以是一条直线。而在通道长宽受限时,位姿调整段需要借用车位空间,以实现在有限空间内的平行泊车,如图2所示。首先要确定的是车辆借用车位进行位姿调整的路径,确定倒车起始点,然后规划从目标位置到倒车起始点的路径。
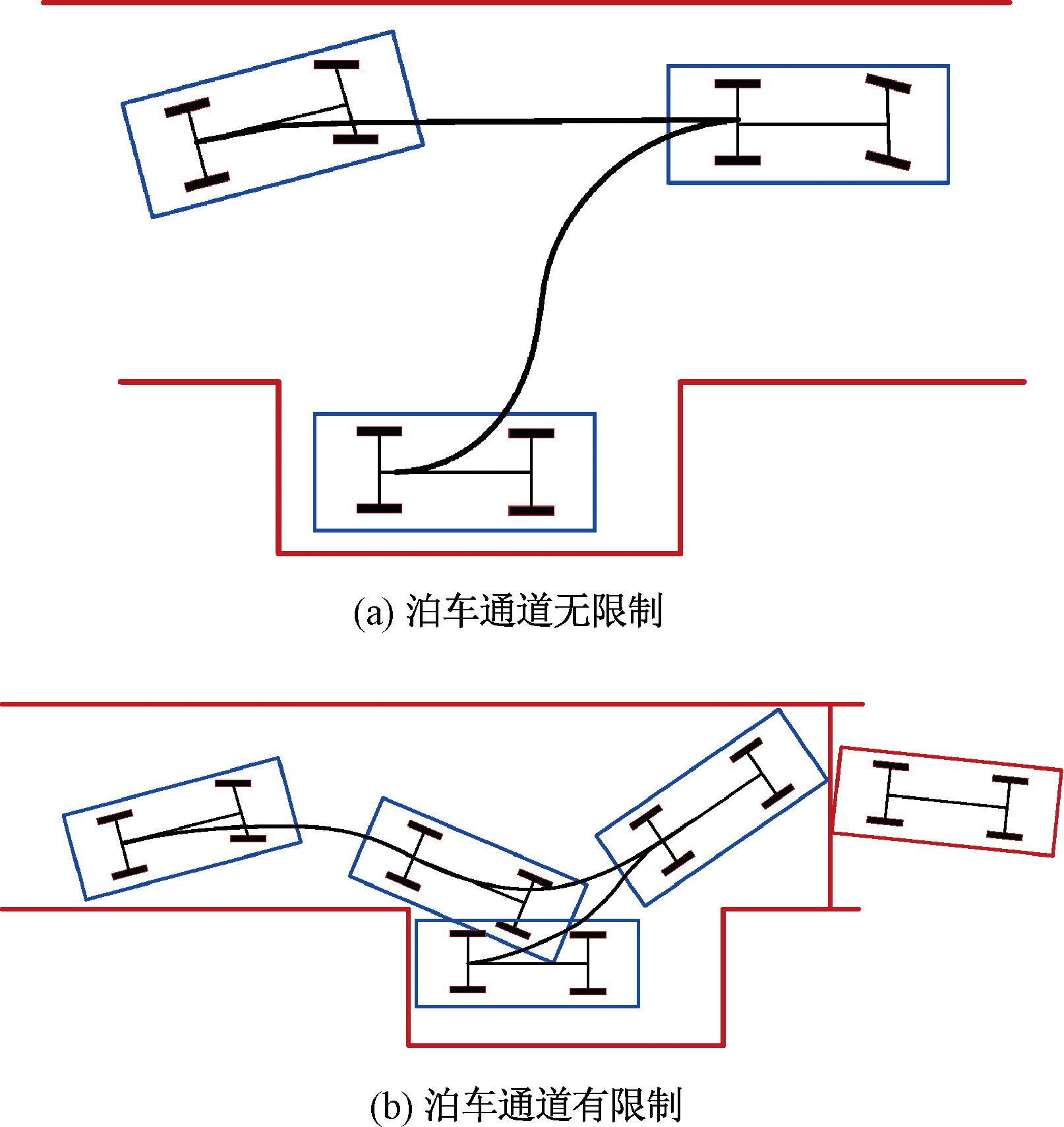
图2 平行泊车路径对比
Figure 2 Comparison of parallel parking paths
首先,要确定从何处开始借用车位空间;其次,确定汽车与过道边界不发生碰撞的极限位置;最后,规划一条从极限位置到泊车位置的无碰撞路径。
如图3所示,当借用车位空间时,车辆侧面不能与障碍物发生碰撞。为尽可能利用车位空间,B点纵坐标应尽可能小,即目标函数和约束为
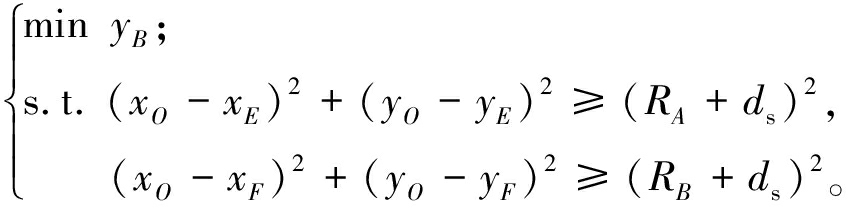
(1)
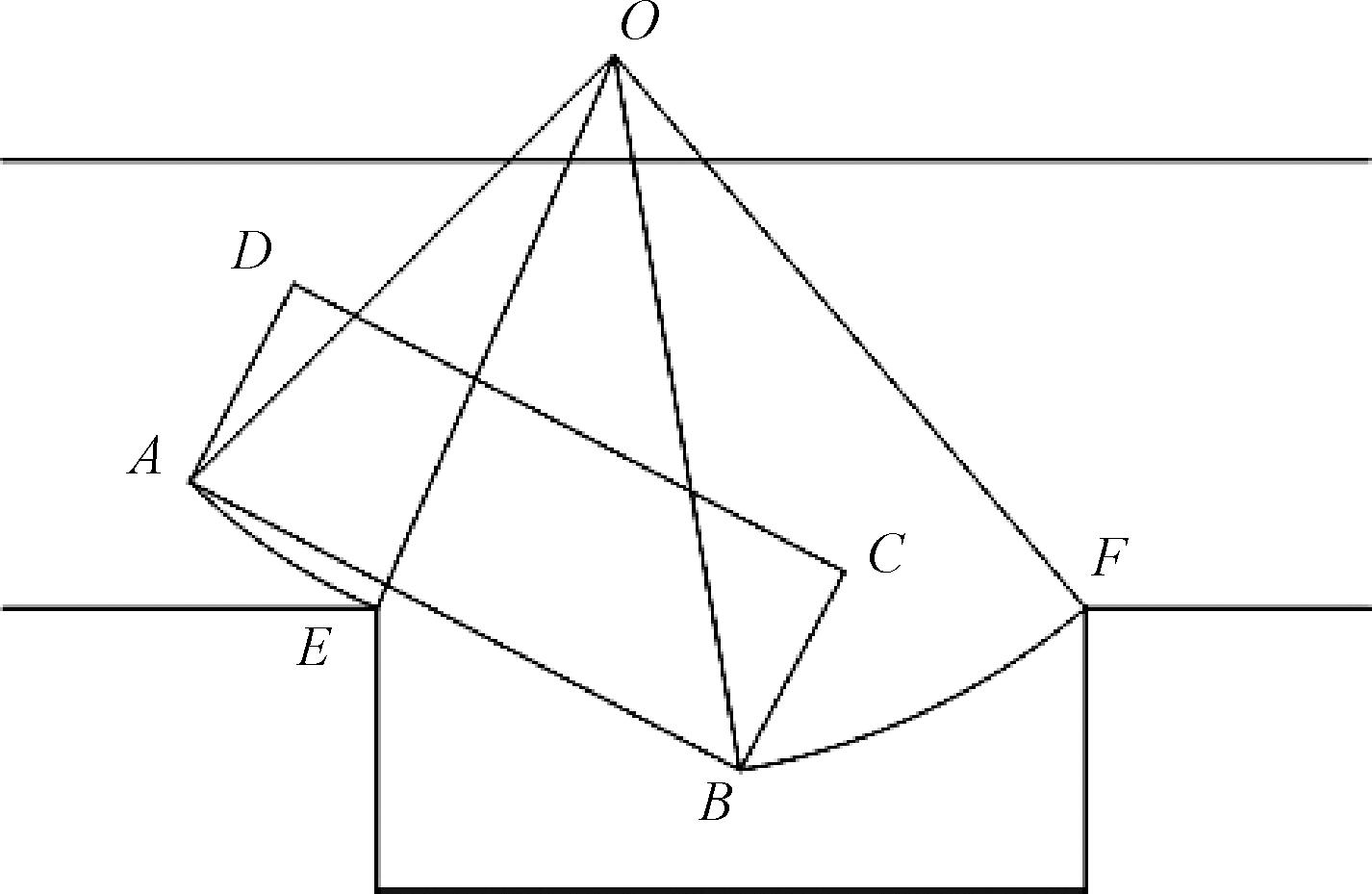
图3 确定借用车位的位置
Figure 3 Determination of the location of the parking space used
式中:xO、yO为汽车转向中心O点的横纵坐标;xE、yE为图3中E点的横纵坐标;xF、yF为图3中F点的横纵坐标;RA、RB为汽车转向中心O点到图3中A点、B点的距离;ds为安全距离。
相关参数均可用汽车后轴中心坐标x1、y1和车辆航向角θ表示:
(2)
(3)
yB=y1+(Lw+Lf)sin θ-0.5Wcos θ;
(4)
xO=x1+Rcos(θ+π/2);
(5)
yO=y1+Rsin(θ+π/2)。
(6)
式中:R为汽车最小转弯半径,m;W为汽车宽度,m;Lf为车辆前悬,m;Lw为车辆轴距,m;Lr为车辆后悬,m;θ为车辆航向角,rad;x1、y1为汽车后轴中心横纵坐标。
得到车辆的转向中心坐标(xO,yO)和位置1的后轴中心坐标(x1,y1)及航向角θ1后,进一步计算后退泊车段的起始点。如图4所示,C点纵坐标应尽可能大,且B点和C点不与障碍物发生碰撞,即目标函数和约束为
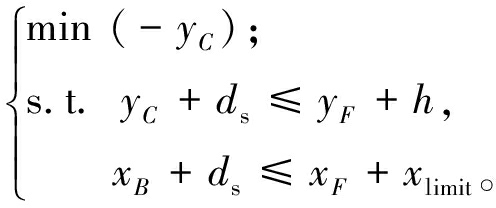
(7)

图4 确定泊车起始点
Figure 4 Determination of the starting point for parking
相关参数均可使用变量α表示,其为车辆从位置1驶至位置2时,后轴中心与转向中心连接所得线段旋转的角度。
(8)
yC=y2+(Lw+Lf)sin θ2+0.5Wcos θ2;
(9)
xB=x2+(Lw+Lf)cos θ2+0.5Wsin θ2。
(10)
2.2 后退泊车段
后退泊车段采用混合A*算法从目标点到泊车起始点反向搜索,针对采用原始混合A*算法碰撞检测精度低、规划路径过于靠近障碍物的问题,改变其碰撞检测方式,并引入新的代价函数。
2.2.1 碰撞检测
混合A*算法使用栅格地图来描绘环境信息,其碰撞检测通过判断障碍物所占据的栅格与车身所占栅格的距离来判断是否发生碰撞。混合A*算法最初是一种用于全局路径规划的算法,这种碰撞检测方法可以较快判断车辆是否与数个复杂障碍物发生碰撞,但其对障碍物与车辆的描述不准确,存在一定的误差,而栅格划分的分辨率越低,这一误差越大[13]。在泊车这一局部路径规划时,栅格划分分辨率过低会导致无法规划出可行路径,而分辨率过高会显著增加规划时间。
由于泊车工况车辆周围环境较为简单,不存在复杂障碍物,因此,只需要考虑车辆停入库位时的碰撞。同时,考虑到泊车时对碰撞检测的精度要求较高,用矩形表示车辆轮廓,用折线段表示车位及障碍物轮廓,通过快速排斥试验与跨立试验判断车辆轮廓线是否与车位及障碍物轮廓线相交来判断是否发生碰撞。这种方法在世界坐标系下进行计算,简单方便,同时精度较高,能准确描述车辆与障碍物的关系。
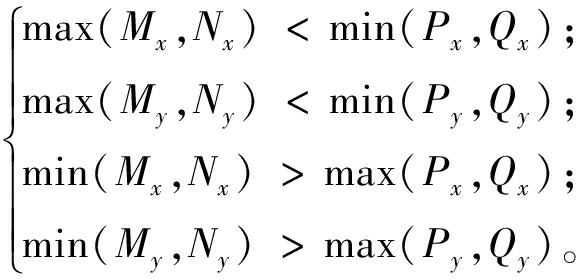
(11)
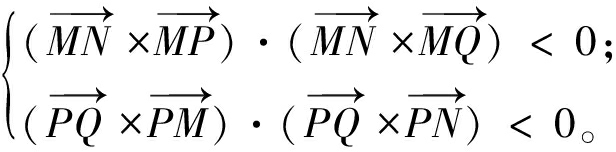
(12)
对于线段MN和线段PQ,首先判断是否满足式(11)中任意一个条件,若满足,两条线段不相交。若都不满足,再判断是否同时满足式(12)中条件,若同时满足,则两条线段相交,否则不相交。
2.2.2 代价函数
混合A*算法搜索出的路径通常较为靠近障碍物,在泊车场景下,这会对跟踪控制提出更高的要求。解决方案通常是对车辆或障碍物进行膨胀处理,而在泊车场景中,空间狭窄,可行驶区域较小,膨胀处理可能导致算法无法搜索到可行解。为解决这一问题,在代价函数中额外引入碰撞风险函数,即代价函数的形式变为
f=g+h+d。
(13)
式中:f为扩展节点的代价函数;g为历史路径长度,表示从起始节点扩展至当前节点的累积代价值;h为启发函数,表示从当前节点扩展至终止节点代价的估计值;d为碰撞风险函数。
碰撞风险函数应能快速且较为准确地反映车辆与障碍物之间的距离。扩展节点包含车辆的位姿信息(x0,y0,θ0),以此构造互相垂直的两条直线:
y-y0=(x-x0)tan θ0;
(14)
(15)
两条直线可与障碍物轮廓线产生4个交点,各交点到车辆后轴中心的距离分别为l1、l2、l3、l4,如图5所示。
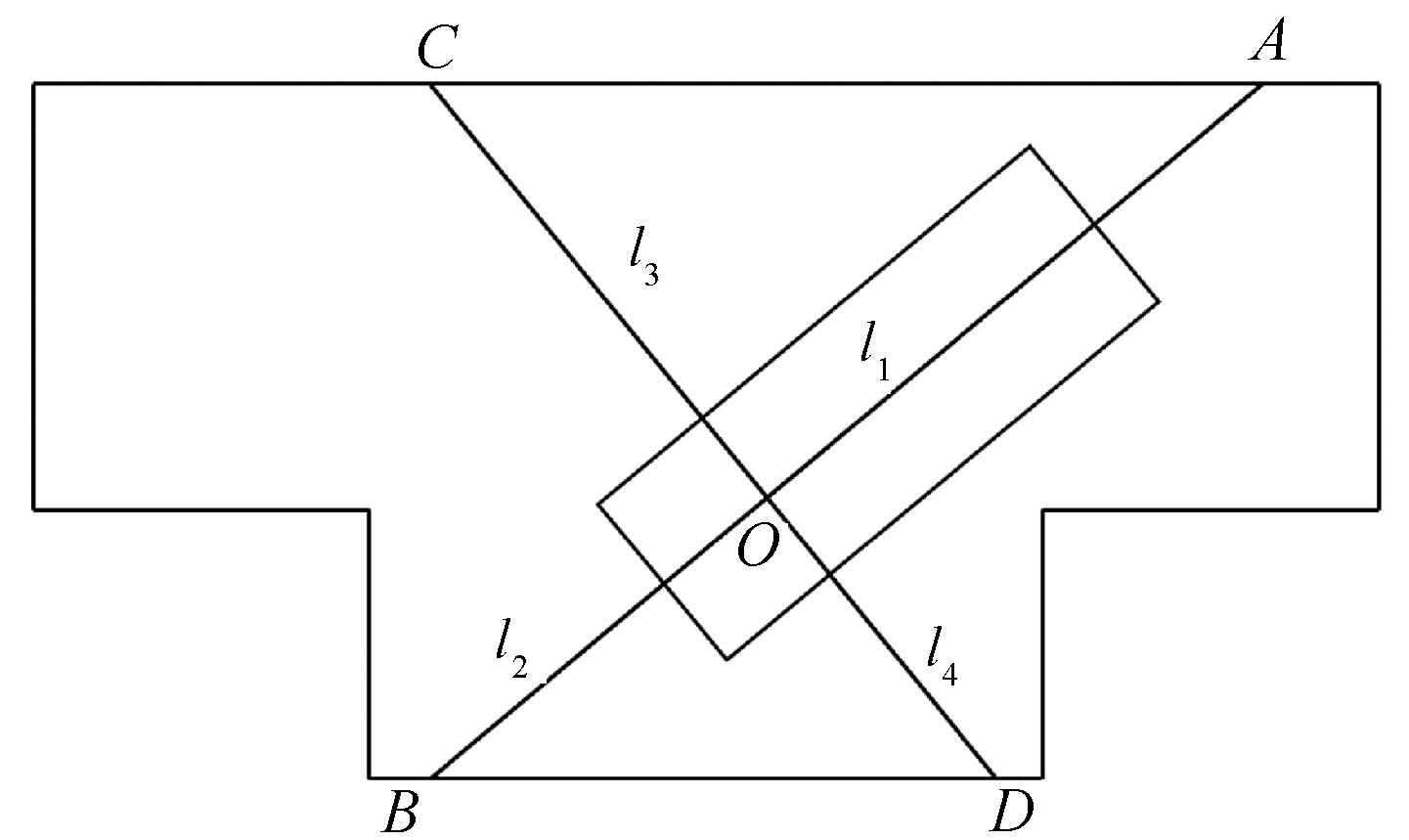
图5 碰撞风险函数示意图
Figure 5 Schematic diagram of collision risk function
考虑到车辆自身轮廓,令:
(16)
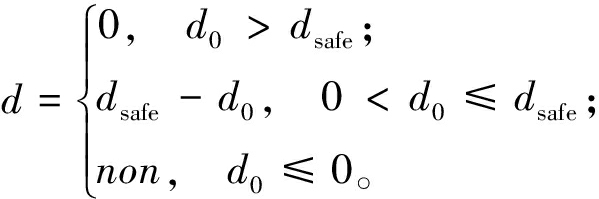
(17)
式中:dsafe表示安全距离;non表示车辆与障碍物发生碰撞,不向该节点进行扩展。
在向节点扩展时,优先考虑碰撞风险函数d更小的子节点。当碰撞风险差距不大时,优先向原代价函数g+h更小的节点扩展。这样,在不影响搜索可行解成功率的情况下,可以使车辆尽可能远离障碍物,减少跟踪难度。
2.3 路径平滑
由于前文所得路径为通过前轮转角进行离散采样获得的,初始路径存在曲率不连续的问题,因此需要对初始路径进行平滑的后处理。在泊车场景中,存在进退挡位切换的情况,因而对初始路径进行分段处理,每段的处理如下。
混合A*算法通过采样可获得m个等距的离散路径点,记为p0(x0,y0),p1(x1,y1),…,pm-1(xm-1,ym-1)。目标函数由3项组成,表示形式如下:
(18)
式中:ω1、ω2、ω3为各项优化目标的权重系数。等式右侧第1项优化目标是使优化路径尽可能平滑,其物理意义为向量![]() 和向量
和向量![]() 相加所得
相加所得![]() 的模的平方,其值越小,代表P0、P1、P2 这3点组成的曲线越趋于平直,因此可反映路径的平滑性;第2项优化目标是使优化路径尽可能短;第3项优化目标是使优化路径尽可能不过于偏离初始路径。
的模的平方,其值越小,代表P0、P1、P2 这3点组成的曲线越趋于平直,因此可反映路径的平滑性;第2项优化目标是使优化路径尽可能短;第3项优化目标是使优化路径尽可能不过于偏离初始路径。
由于本文对泊车路径分段进行优化处理,因此每段的起始点和终点的位置和航向角均保持不变,可得到位置约束:
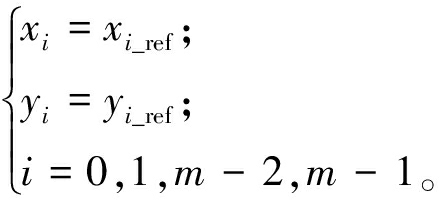
(19)
在优化过程中,需要对坐标(xi,yi)的变化范围进行一定的限制,以防优化后的路径与障碍物发生碰撞,可得碰撞约束:
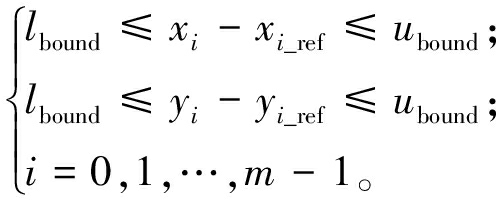
(20)
由于车辆自身的运动学特性,优化路径存在最大曲率的限制,可得曲率约束:
(Δs2cur)2≥(xi+1+xi-1-2xi)2+(yi+1+yi-1-2yi)2,
i=1,2,…,m-1。
(21)
由于曲率约束为非线性约束,可通过线性化方法将其转化为线性约束。令F=(xi+1+xi-1-2xi)2+(yi+1+yi-1-2yi)2,在参考路径处泰勒展开,保留线性项可得
(22)
综上所述,路径平滑可以看作以式(18)为目标函数,以式(19)、(20)、(22)为约束条件的优化问题,使用二次规划的方法求解。
3 仿真分析
3.1 平行泊车路径规划
路径搜索仿真所用车辆长度为4.6 m,宽度为1.8 m,轴距为2.7 m,前悬为0.9 m,后悬为1.0 m,最大前轮转角为34 °。车位长6.0 m,宽2.4 m,泊车通道宽3.8 m,长度方向受限。起点位姿为(1.1,3.9,0),终点位姿为(7.1,1.4,0)。分别使用混合A*算法与本文方法进行泊车路径搜索,路径规划结果如图6所示。
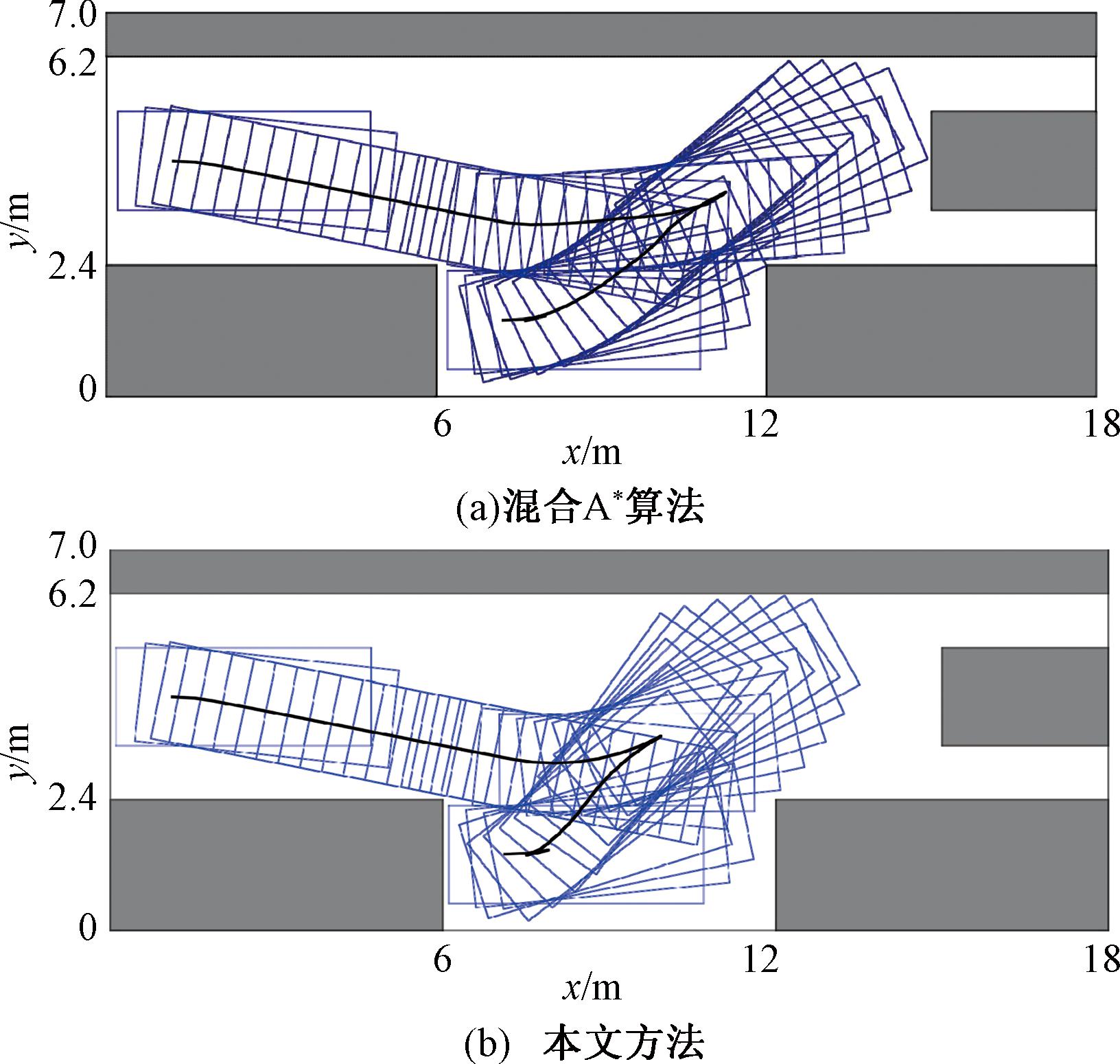
图6 工况1路径规划结果
Figure 6 Path planning results of case one
对比两种方法所得结果可知,两种方法都可以搜索出无碰撞且符合车辆运动学约束的泊车路径,但混合A*算法所得路径在车辆后退驶入库位时,右前方车头过于靠近障碍物,存在碰撞风险,对路径跟踪的精度要求较高。而本文方法由于引入了代表碰撞风险的代价函数,使节点扩展时尽量远离障碍物,因此所得路径与障碍物间保持着较为安全的距离,降低了后续进行跟踪控制的难度。两种方法所得结果的主要参数如表1所示,相较于混合A*算法,本文所提方法搜索节点数减少了19.4%,搜索时间减少了23.8%,提高了路径搜索的实时性。
表1 工况1仿真结果
Table 1 Test results of case one

算法搜索节点数搜索时间/s混合A∗算法2160.863本文方法1740.658
在工况1的基础上,将起点位姿改变为(1.1,3.9,0.2),以进一步验证本文方法在不同起始位姿时的路径规划效果,泊车路径搜索结果如图7和表2所示。
表2 工况2仿真结果
Table 2 Test results of case two
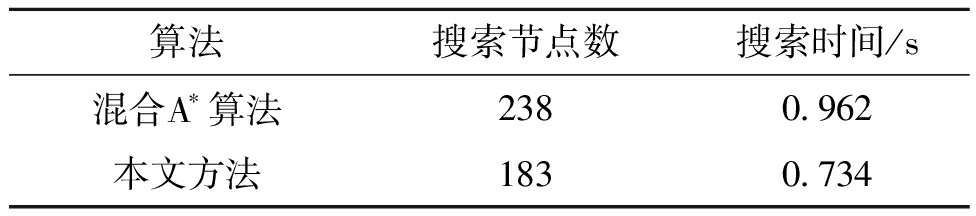
算法搜索节点数搜索时间/s混合A∗算法2380.962本文方法1830.734
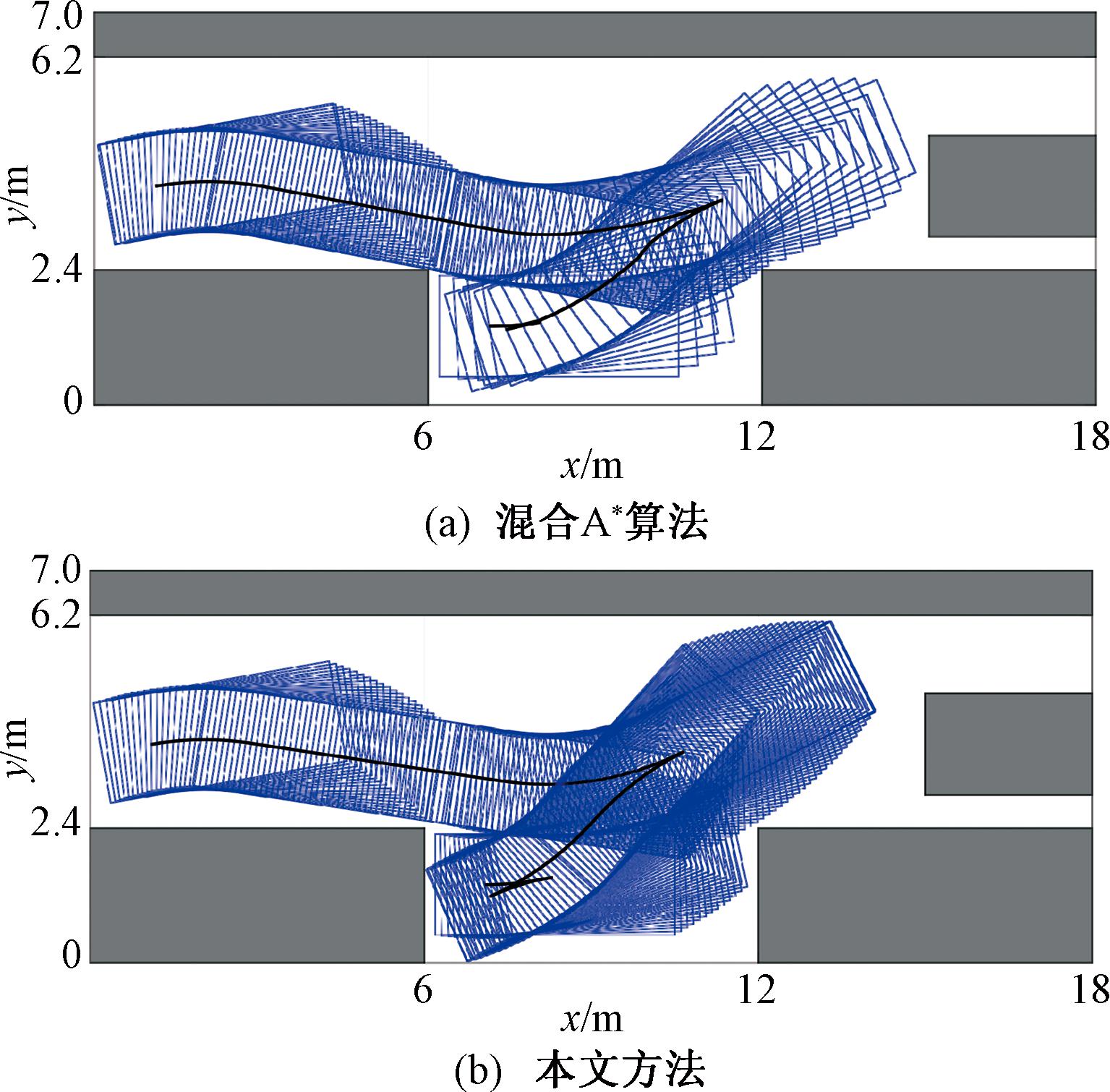
图7 工况2路径规划结果
Figure 7 Path planning results of case two
根据图7和表2可知,在起点位姿的航向角不为零时,本文方法仍能快速地搜索出一条无碰撞泊车路径,相较于混合A*算法,本文方法搜索节点数减少了23.1%,搜索时间减少了23.7%,提升了实时性。
为进一步验证本文方法在泊车通道受限情况下的路径规划能力,在工况1基础上,进一步限制泊车通道的宽度,将其设为3 m,其他设置保持不变。分别使用混合A*算法与本文所提方法进行路径搜索,路径规划结果如表3和图8所示。
表3 工况3仿真结果
Table 3 Test results of case three
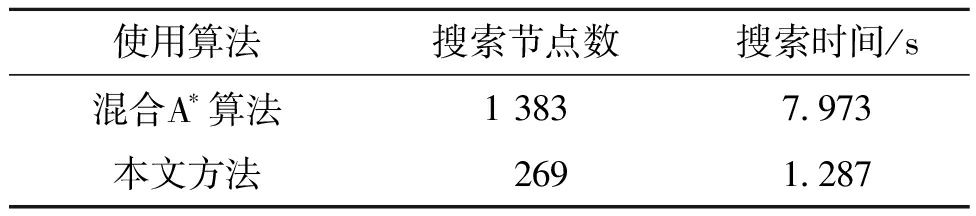
使用算法搜索节点数搜索时间/s混合A∗算法1 3837.973本文方法2691.287

图8 工况3路径规划结果
Figure 8 Path planning results of case three
根据表3及图8可知,两种方法均可得到可行路径。混合A*算法搜索节点个数与耗费时间显著增加,搜索得到的路径在车位中多次改变行车方向,增加了跟踪控制的难度,影响行车的舒适性。观察车位内的路径可得,车辆在调整位姿时过多进行直线行驶,降低了车辆泊入车位的效率。而本文方法所得路径由于碰撞风险函数影响,在位姿调整时更多以最小转向半径前进后退,更符合驾驶员操作习惯,整个泊车流程共切换挡位5次,显著少于混合A*算法的规划结果。
3.2 路径平滑
使用本文路径平滑方法对图6(b)中规划路径进行平滑,耗时约为0.152 s,满足实时性要求,所得结果如图9、图10所示。
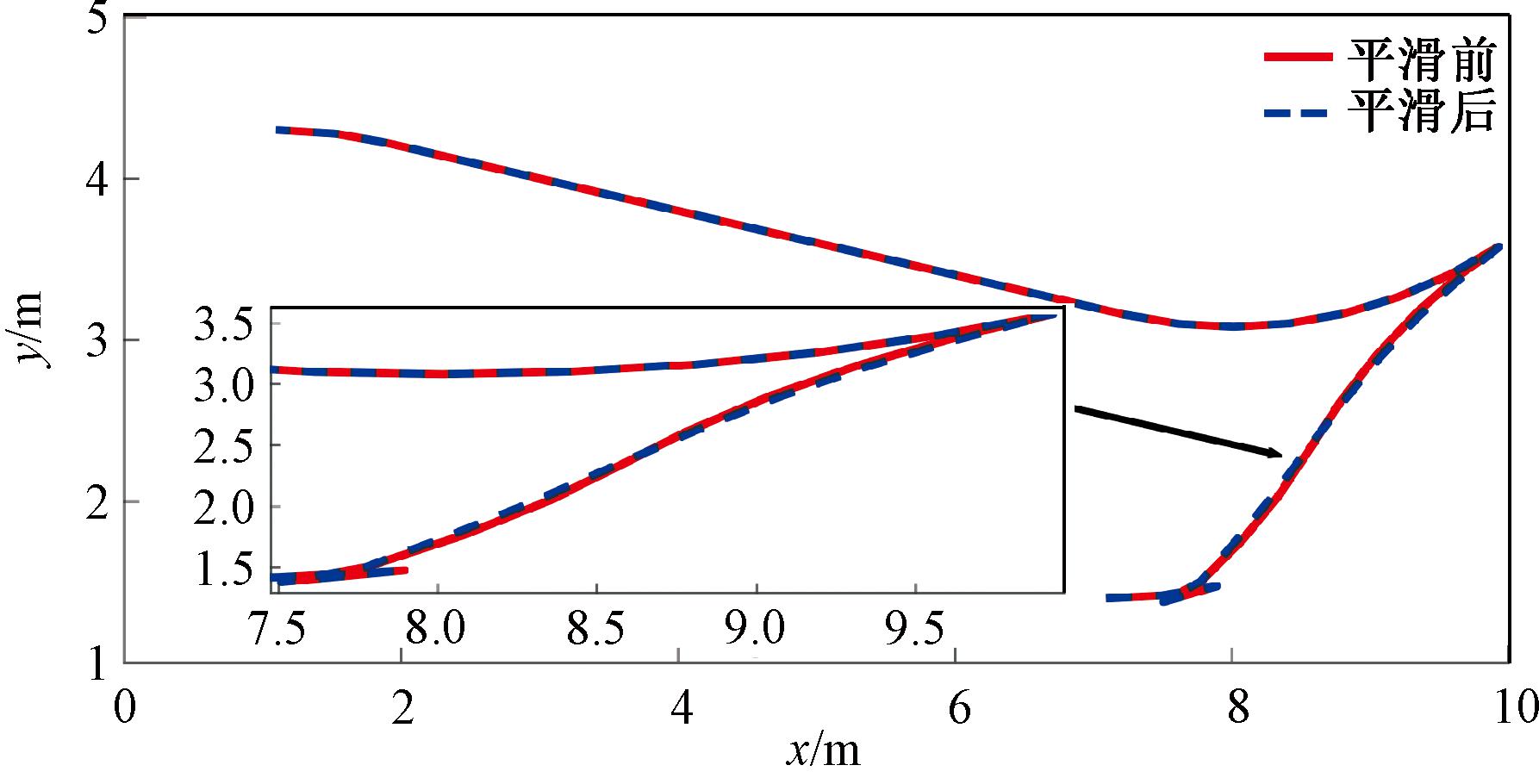
图9 路径平滑结果
Figure 9 Results of path smoothing
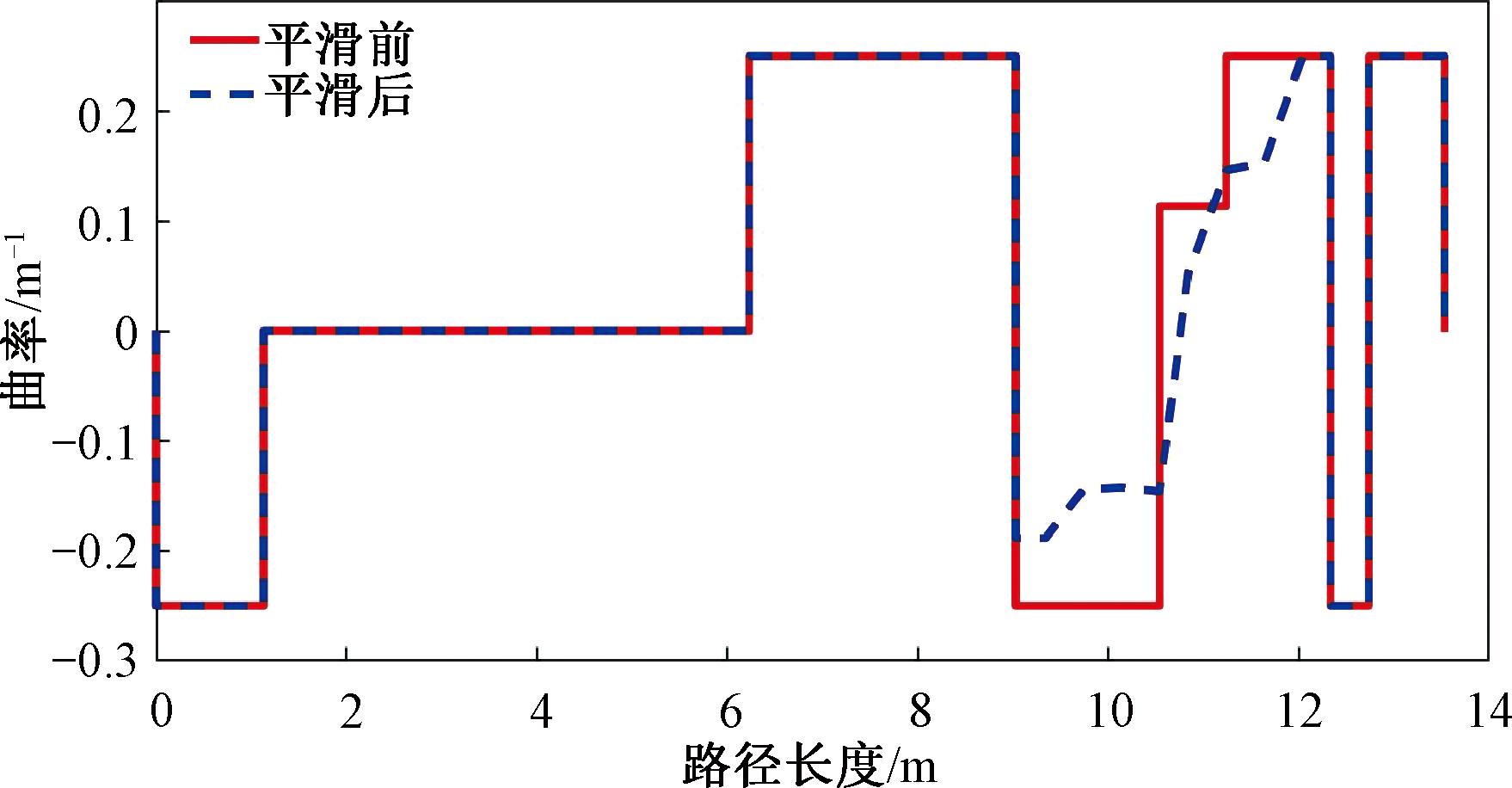
图10 路径平滑后的曲率变化
Figure 10 Curvature change after path smoothing
结合图9和图10可以看出,在开始段与结束段,车辆始终以最小转向半径进行转向,因此平滑后的路径与原始路径相同,保证了进退挡位切换点的车辆位姿保持不变。而在中间段存在曲率变化时,经平滑方法处理后的路径曲率变化更合理,改善了曲率突变的情况。
4 结论
本文提出了一种针对泊车通道受限情况下的平行泊车路径规划方法,该方法首先构造前进的位姿调整段路径,确定合适的泊车起始点;其次,改变混合A*算法的碰撞检测方式并引入代表碰撞风险的代价函数,搜索后退的泊车路径;再次,使用二次规划对所得初始路径进行平滑;最后,设计仿真试验进行验证。结果表明,本文所提方法满足路径搜索的实时性和安全性要求。
[1] 孙超, 李世杰, 张鹏, 等. 出行系统最优配置下共享停车选择及泊位分配[J]. 郑州大学学报(工学版), 2023, 44(1): 38-43.SUN C, LI S J, ZHANG P, et al. Shared parking selection and berth allocation for optimal configuration of travel system[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(1): 38-43.
[2] 黄江, 魏德奎, 秦良艳, 等. 自动泊车系统路径规划与跟踪控制方法研究[J]. 汽车技术, 2019(8): 39-45.HUANG J, WEI D K, QIN L Y, et al. Research on path planning and path tracking control method of automatic parking system[J]. Automobile Technology, 2019(8): 39-45.
[3] 张家旭, 赵健, 施正堂, 等. 基于回旋曲线的平行泊车路径规划和跟踪控制[J]. 吉林大学学报(工学版), 2020, 50(6): 2247-2257.ZHANG J X, ZHAO J, SHI Z T, et al. Path planning and tracking control for parallel parking based on clothoid curve[J]. Journal of Jilin University (Engineering and Technology Edition), 2020, 50(6): 2247-2257.
[4] 胡杰, 张敏超, 徐文才, 等. 自动驾驶车辆的平行泊车轨迹规划[J]. 汽车工程, 2022, 44(3): 330-339.HU J, ZHANG M C, XU W C, et al. Parallel parking trajectory planning for autonomous vehicles[J]. Automotive Engineering, 2022, 44(3): 330-339.
[5] 胡杰, 朱令磊, 陈瑞楠, 等. 狭小车位平行泊车路径规划方法研究[J]. 汽车工程, 2022, 44(7): 1040-1048.HU J, ZHU L L, CHEN R N, et al. Research on parallel parking path planning method for narrow parking space[J]. Automotive Engineering, 2022, 44(7): 1040-1048.
[6] JHANG J, LIAN F L, HAO Y. Human-like motion planning for autonomous parking based on revised bidirectional rapidly-exploring random tree* with Reeds-Shepp curve[J]. Asian Journal of Control, 2021, 23(3): 1146-1160.
[7] 王海芳, 张瑶, 朱亚锟, 等. 基于改进双向RRT*的移动机器人路径规划算法[J]. 东北大学学报(自然科学版), 2021, 42(8): 1065-1070, 1142.WANG H F, ZHANG Y, ZHU Y K, et al. Mobile robot path planning based on improved bidirectional RRT*[J]. Journal of Northeastern University (Natural Science), 2021, 42(8): 1065-1070, 1142.
[8] TAHIR Z, QURESHI A H, AYAZ Y, et al. Potentially guided bidirectionalized RRT* for fast optimal path planning in cluttered environments[J]. Robotics and Autonomous Systems, 2018,108:13-27.
[9] 段书用, 王启帆, 韩旭, 等. 具有确保安全距离的A*路径优化方法[J]. 机械工程学报, 2020, 56(18): 205-215.DUAN S Y, WANG Q F, HAN X, et al. Improved A-star algorithm for safety insured optimal path with smoothed corner turns[J]. Journal of Mechanical Engineering, 2020, 56(18): 205-215.
[10] 曹彦博, 颜京才, 李旭升, 等. 基于改进混合A*算法的自动泊车系统路径搜索方法[J]. 汽车技术, 2023(6): 37-41.CAO Y B, YAN J C, LI X S, et al. A method of path search for automatic parking system based on improved hybrid A* algorithm[J]. Automobile Technology, 2023(6): 37-41.
[11] ZHANG S Y, CHEN Y, CHEN S T, et al. Hybrid A-based curvature continuous path planning in complex dynamic environments[C]∥2019 IEEE Intelligent Transportation Systems Conference (ITSC). Piscataway: IEEE, 2019: 1468-1474.
[12] DOLGOV D, THRUN S, MONTEMERLO M, et al. Path planning for autonomous vehicles in unknown semi-structured environments[J]. International Journal of Robotics Research, 2010, 29(5): 485-501.
[13] 陈翔翔. 基于Hybrid A*算法的自动泊车路径规划与跟踪控制研究[D]. 西安: 长安大学, 2022.CHEN X X. Research on Hybrid A* algorithm path planning and tracking control for automatic parking[D].Xi’an: Chang’an University, 2022.