CT机主轴承主要用于传递和承受X线管、准直仪、探测器、滑环等装置产生的径向载荷和倾覆力矩[1]。由于其运转稳定性直接影响到医学成像的清晰程度,故对于CT机主轴承在运行过程中的振动特性也提出了更高的要求。
轴承产生振动的因素[2]是多方面的,包括制造误差、结构振动、运行工况等。陈月等[3]分析了4点接触球轴承内外圈圆度误差及阶次对轴承旋转精度的影响。余永健等[4]在考虑轴承内外圈滚道形状误差对轴承回转误差的影响时进一步考虑了轴承零件几何误差引起的滚子-滚道接触位置变化,使得分析模型更加准确、精度更高。余光伟等[5]通过建立6201深沟球动力学模型,分析了波纹度波数对轴承振动的影响。吕润楠等[6]在波纹度理论分析的基础上通过Adams建立了更加接近轴承实际运行状态下的双列圆锥滚子波纹度动力学模型,分析了波纹度波数对轴承振动的影响。Zmarzy[7]通过测针轮廓仪对轴承表面进行测量,以实验为基础分析了二维、三维轴承表面形貌对振动的影响。汪凯等[8]以2-DOF滚动轴承为例分析了游隙对轴承振动特性的研究,但模型未考虑保持架的影响。唐志霖等[9]以压缩机用球轴承为例,综合考虑保持架以及流体动压摩擦力的情况,分析了轴承初始游隙对振动特性的影响。邓四二等[10]、田凯文等[11]分别通过对低噪音深沟球轴承、4点接触球轴承建立振动数学模型,进一步分析了轴承自身结构参数对其振动加速度值的影响。Parmar等[12]研究了双列角接触球轴承在承受径向不对中载荷下的振动响应。Gunduz等[13]以车轮所用的双列角接触球轴承为研究对象分析了轴向、径向预紧力对轴承固有频率和谐振幅的影响。欧旭鹏等[14]基于赫兹接触理论、弹性力学、轴承运动学以及几何学建立了4自由度深沟球轴承动力学模型,分析了轴承在受到不平衡扰动力影响下的振动响应机理。Tong等[15]以圆锥滚子轴承为例,在考虑轴承存在滚子直径误差的情况下,建立了5自由度振动数学模型,分析了轴向预紧力以及组合载荷对轴承振动频率的影响。
综上所述,有关轴承振动特性的研究主要针对的是小型轴承,而大型转盘轴承主要应用于风电、盾构等重型设备,其工作环境对于轴承的振动特性要求不高,故有关转盘轴承的振动分析很少见。鉴于此,本文针对洛轴研制的双列角接触CT机主轴承进行建模和振动特性分析,建立3自由度双列角接触球转盘轴承非线性振动模型,采用4阶Runge-Kutta法对振动微分方程组进行简化求解。通过研究轴承结构参数对振动特性的影响,从而确定出满足CT机主轴承低振动下的最优结构参数,为CT机主轴承的设计提供一定的理论依据。
1 CT机主轴承振动数学模型
CT机双列角接触球转盘轴承的结构示意图如图1所示,其中,cj、Kj、φj分别为第j个滚动体处的阻尼、刚度系数和位置角;A为轴承右端面。本文基于Hertz接触理论建立3自由度振动数学模型。为便于研究其结构振动特点,特进行如下假设:轴承零部件表面为理想光滑的几何形状; 滚动体元素间的接触简化为弹簧和阻尼单元。
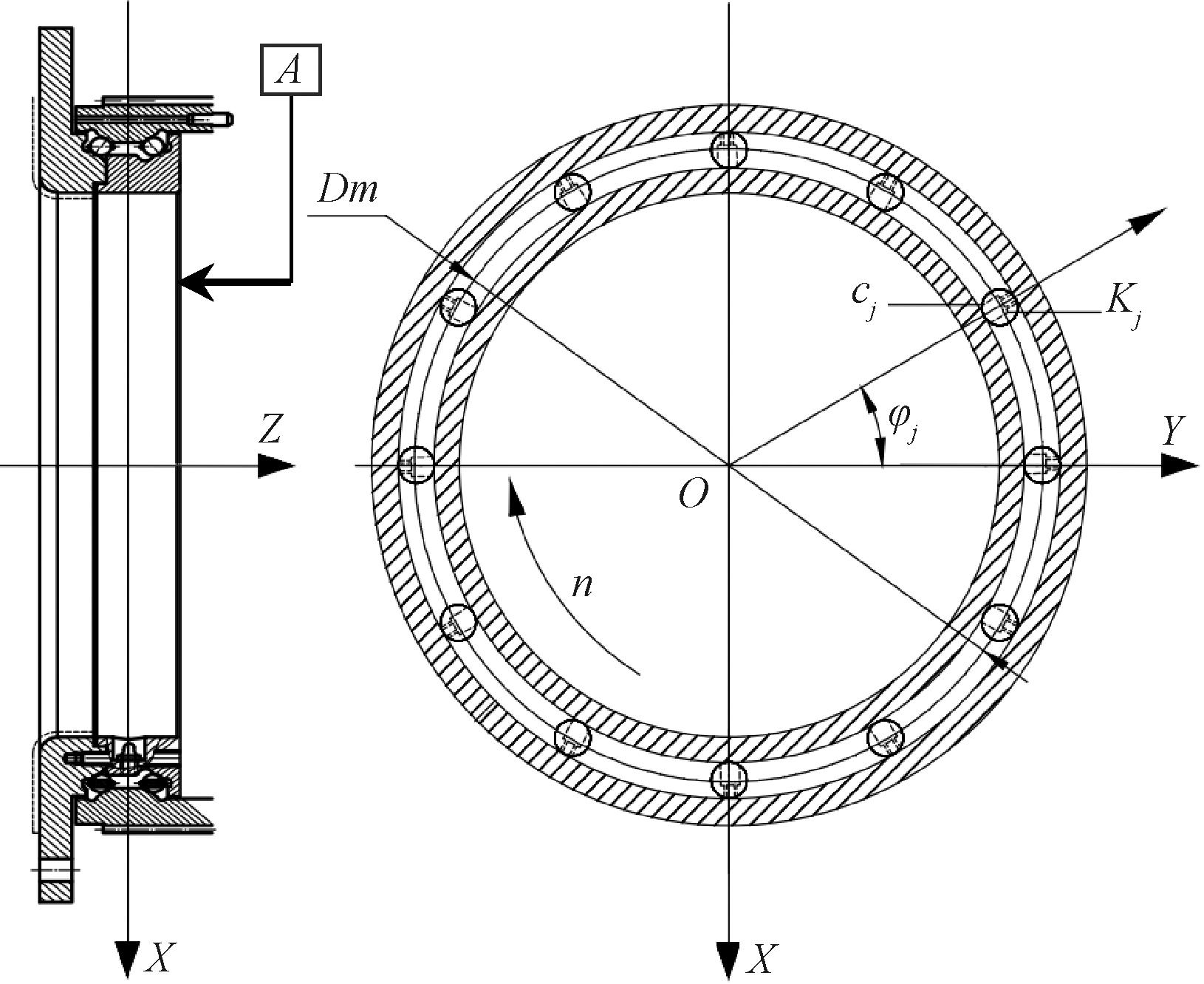
图1 CT机主轴承结构示意图
Figure 1 Schematic diagram of the structure of the main bearing of CT machine
1.1 轴承接触刚度与阻尼
1.1.1 等效刚度计算
由Hertz接触理论可知,球轴承滚动体和内外滚道接触刚度计算式如下:
(1)
(2)
式中:∑ρi、∑ρo分别为滚动体与内外圈滚道曲率中心和;
分别为内外滚道量纲为1的接触位移。
1.1.2 等效阻尼计算
阻尼为振动方程不可或缺的一部分。润滑阻尼可以表示为[16]
(3)
式中:a为钢球与套圈接触区的短半轴长。
由于滚动体在运行过程中与内外圈同时接触,故润滑阻尼为内外圈阻尼复合而成:
(4)
式中:ci表示内圈阻尼;co表示外圈阻尼。
上述阻尼分析为单个滚动体接触时的润滑阻尼,对于整个轴承而言,需要将所有滚动体产生的阻尼进行叠加。方程如下所示:
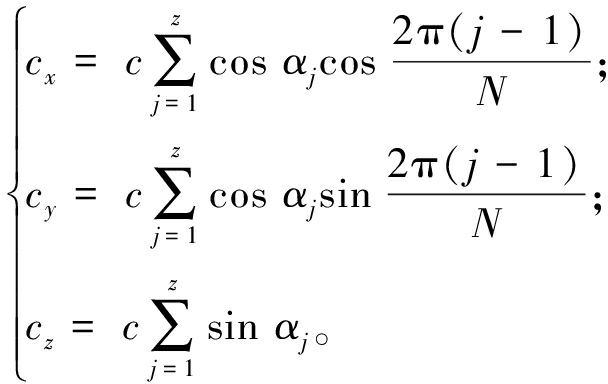
(5)
式中:N为滚动体的数量;αj为接触角。
1.2 CT机双列角接触球转盘轴承力学模型
由于轴承内圈固定于机架,外圈以180 r/min的转速旋转,属于低速运转轴承,因此,力学分析以静力学分析为主。通过上述介绍可知,轴承主要承受X线管、准直仪、探测器、滑环等装置产生的复合载荷,其在载荷作用下轴承内外圈会产生相对形变,这种形变等同相应位置的内外圈沟曲率中心的变形。根据轴承运动特点可用5个自由度对轴承的运动加以描述,即δ=(δx,δy,δz,θx,θy)。
如图2所示,分别以轴承质心以及两列轴承内圈中心建立坐标系。
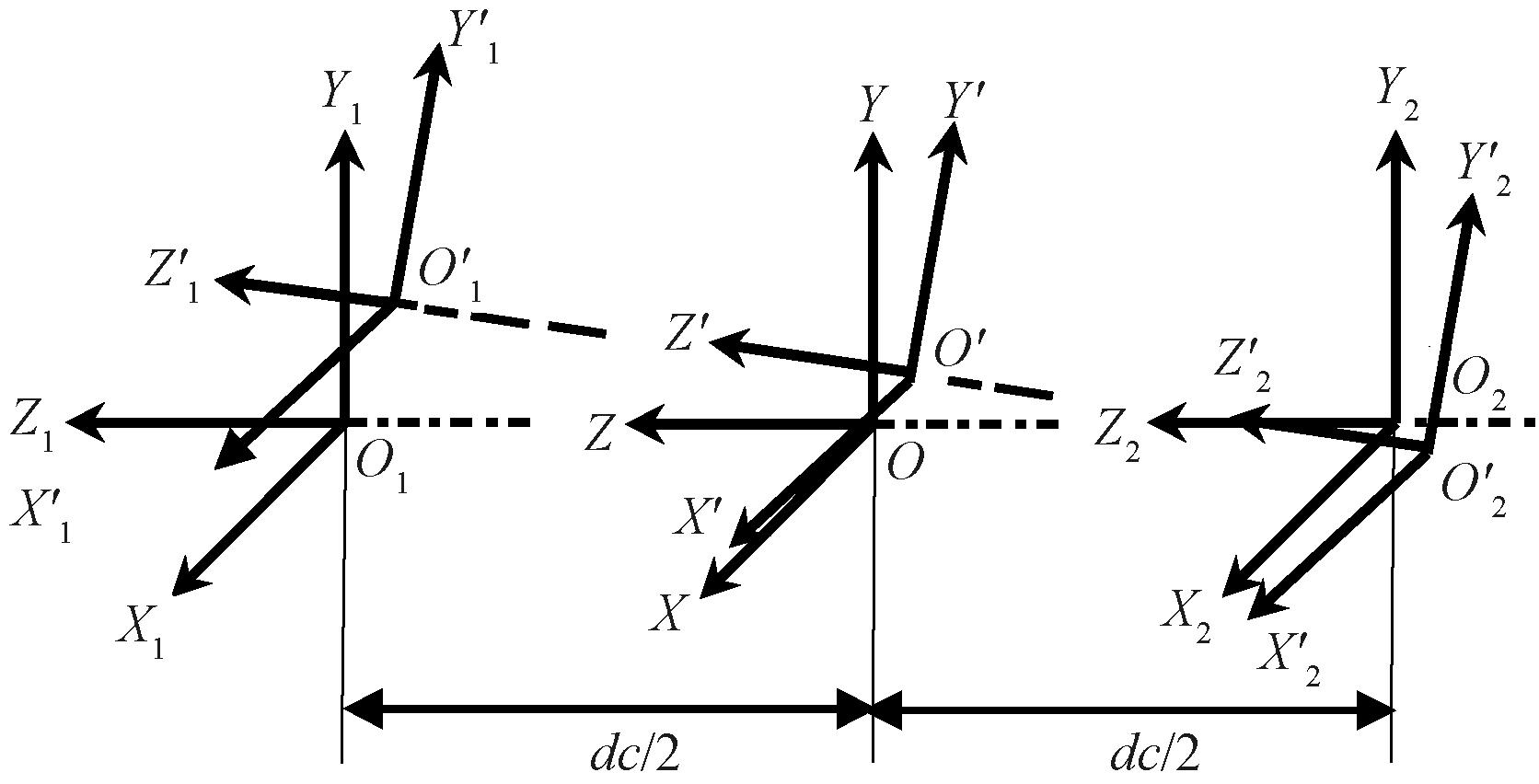
图2 轴承坐标变换示意图
Figure 2 Schematic diagram of bearing coordinate transformation
由坐标转换原理可得转换矩阵T如下所示:
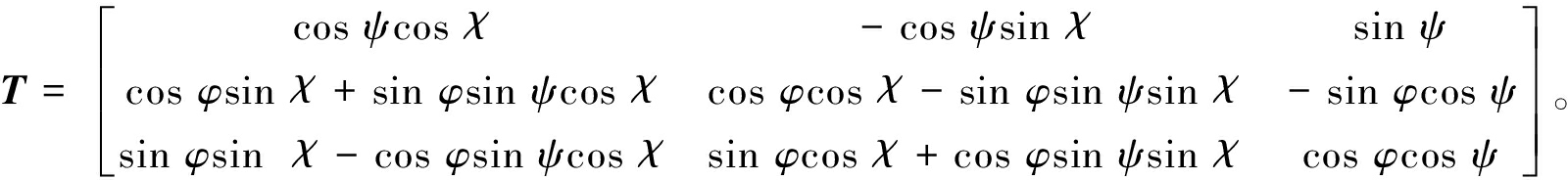
(6)
式中:φ为X轴的旋转角; ψ为Y轴的旋转角; χ为Z轴的旋转角。将φ=θx、ψ=θy、 χ=0代入转换矩阵得
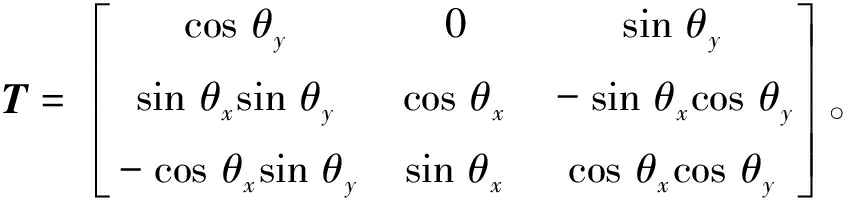
(7)
由坐标变换原理可得轴承受载后坐标系
相对于O1X1Y1Z1的变换矩阵T1,如式(8)所示,同理可得轴承受载后坐标系
相对于O2X2Y2Z2的变换矩阵T2,如式(9)所示,其中,dc为两列滚动体的中心距。
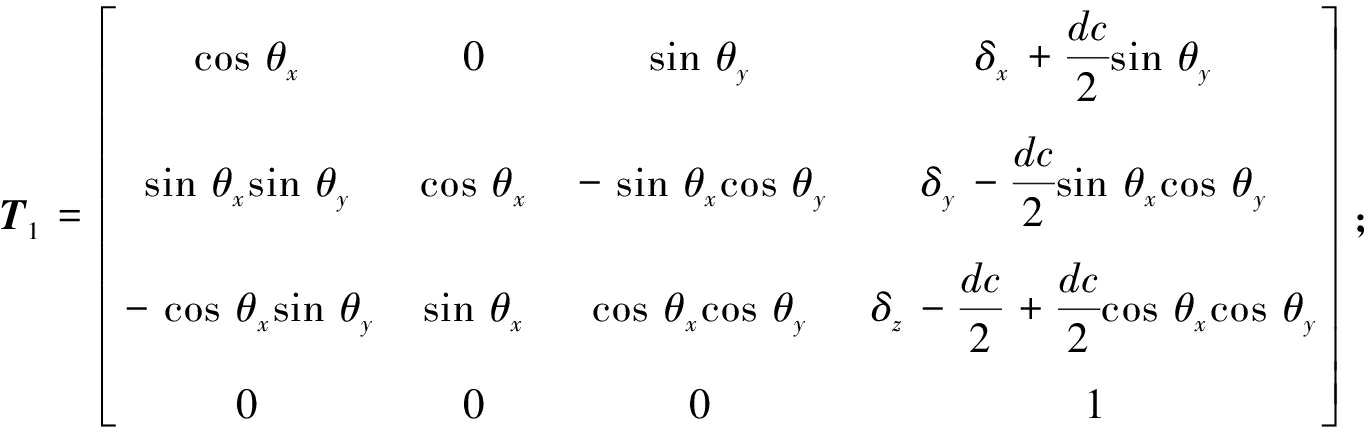
(8)
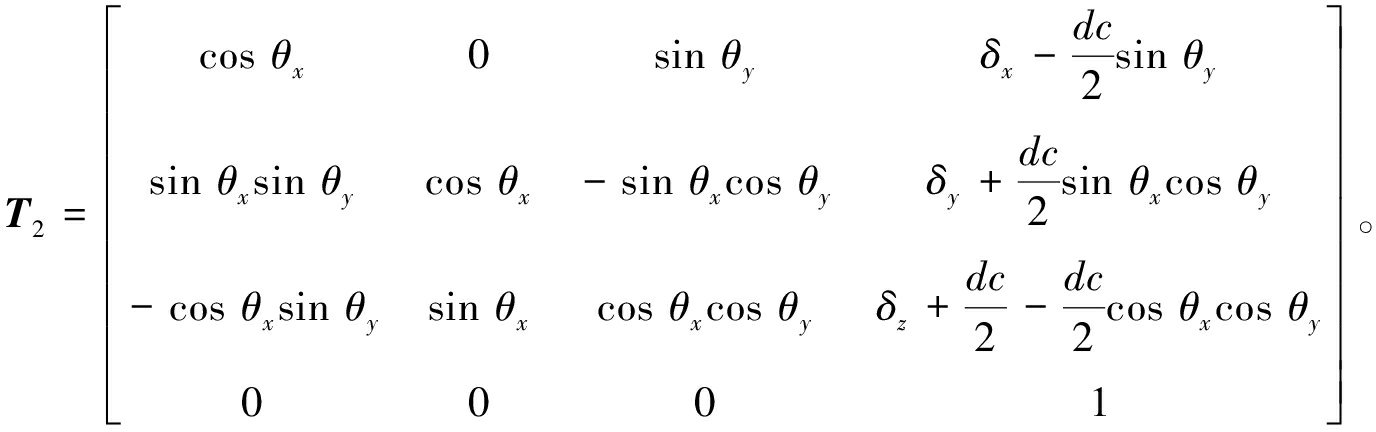
(9)
变形前,第1列轴承外圈滚道曲率中心线上一点Pj1在O1X1Y1Z1坐标系中的坐标为
Pj1=(Rosin φj,Rocos φj,0,1)。
(10)
式中:Ro为轴承外圈沟道曲率中心圆的半径;φj为滚动体所在的位置角。
(11)
式中:ωc为轴承保持架的角速度。
轴承在受载变形后外圈沟曲率一点Pj1坐标变化为
中的
将
坐标转换到O1X1Y1Z1坐标系下:
Rosin φjsin θxsin θy+Rocos φjcos θx+δy-
θxcos θy,-Rosin φjcos θxsin θy+Rocos φj·
(12)
由于接触过程中产生的弹性变形量通常为微小量,因此可取sin θ=θ,cos θ=1,则在第j个滚动体处,滚动体在XYZ方向上的弹性变形量:
(13)
考虑轴承游隙,可得滚动体与内外圈在法向上的接触的总变形量为
δj1=δφa1sin αj1+δφr1cos αj1-C。
(14)
式中:δφa1=Δz1为轴向位移量;δφr1=Δx1sin φj+Δy1cos φj为径向位移量;αj1为轴承接触角;C为轴承初始游隙。由Hertz接触理论可知,双列滚动体第1列中第j个滚动体处的接触载荷为
(15)
同理可得第二列中第j个滚动体处的Hertz接触应力为
(16)
则所有滚动体在各个方向上产生的合力如下。
在X轴方向上(径向):
(17)
在Z轴方向上(轴向):
(18)
绕Y轴产生的倾覆力矩:
(19)
1.3 CT机双列角接触球转盘轴承振动方程确立
由于轴承在设计之初已经经过动平衡,且其挂载的X线管、准直仪、探测器、滑环等装置为圆周分布,故在计算过程中忽略部件自重产生的离心力。如图1所示,部件简化质量ms为距A端面283 mm处施加平行于X轴6 800 N的径向载荷。简化上述方程,建立X轴、Z轴方向的平动以及Y轴方向的转动,则CT机双列角接触球转盘轴承3自由度非线性振动方程如下所示:
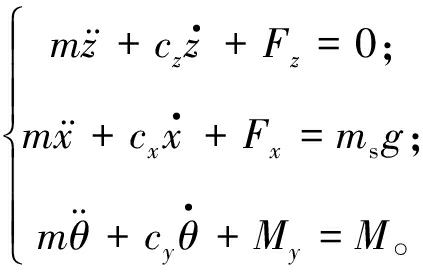
(20)
式中:m为双列角接触球转盘轴承的外圈质量。
2 CT机主轴承振动特性分析
上述振动方程为二阶非线性微分方程组,本文采用4阶Runge-Kutta数值方法对其进行求解,得到轴承外圈在各个方向上的振动加速度信号。假设轴承外圈初始位移x=z=θ=0;初始速度
时间间隔Δt=0.000 1(采样频率为10 000 Hz),起始时间t1=0.01 s,结束时间t2=0.03 s。轴承的结构参数如表1所示,设定轴承外圈转速为180 r/min,轴承外圈质量为46.3 kg,轴承受到的轴向载荷为0,径向载荷为6 800 N,倾覆力矩为2 100 N·m。
表1 CT机主轴承结构参数
Table 1 Structural parameters of main bearings of CT machine
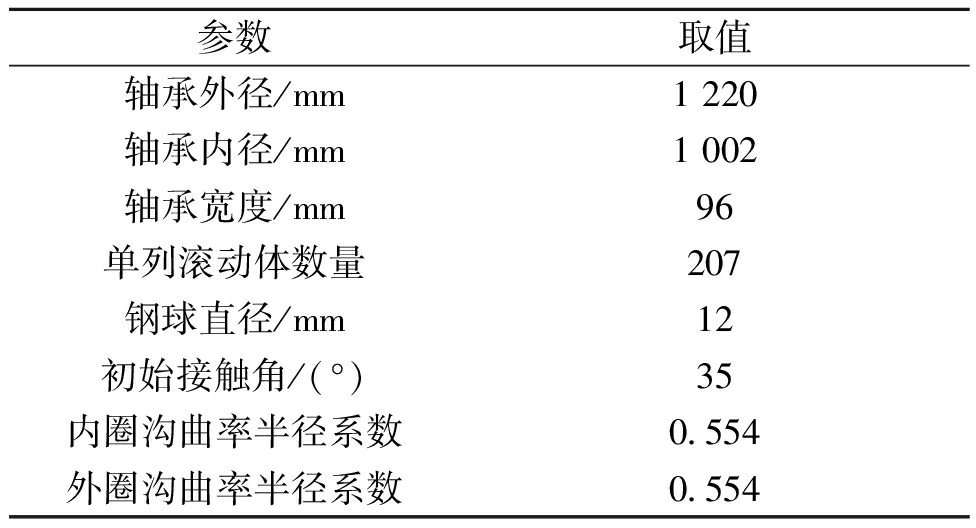
参数取值轴承外径/mm1 220轴承内径/mm1 002轴承宽度/mm96单列滚动体数量207钢球直径/mm12初始接触角/(°)35内圈沟曲率半径系数0.554外圈沟曲率半径系数0.554
为描述轴承的整体振动水平,本文对振动方程求解后的径向振动数据进行分析,采用轴承振动加速度级L对轴承振动水平进行评价[17]:
(21)
式中:ai为振动加速度的均方根值;ao为振动标准参考值,其值为9.81×10-3m/s2。
2.1 结构参数与工况对轴承振动的影响
图3与图4分别为CT机主轴承在径向载荷为6 800 N,倾覆力矩为2 100 N·m时,各参数与工况对轴承振动加速度与振动级的影响。
图3 各参数对轴承振动加速度的影响
Figure 3 Influence of each parameter on the vibration acceleration of the bearing
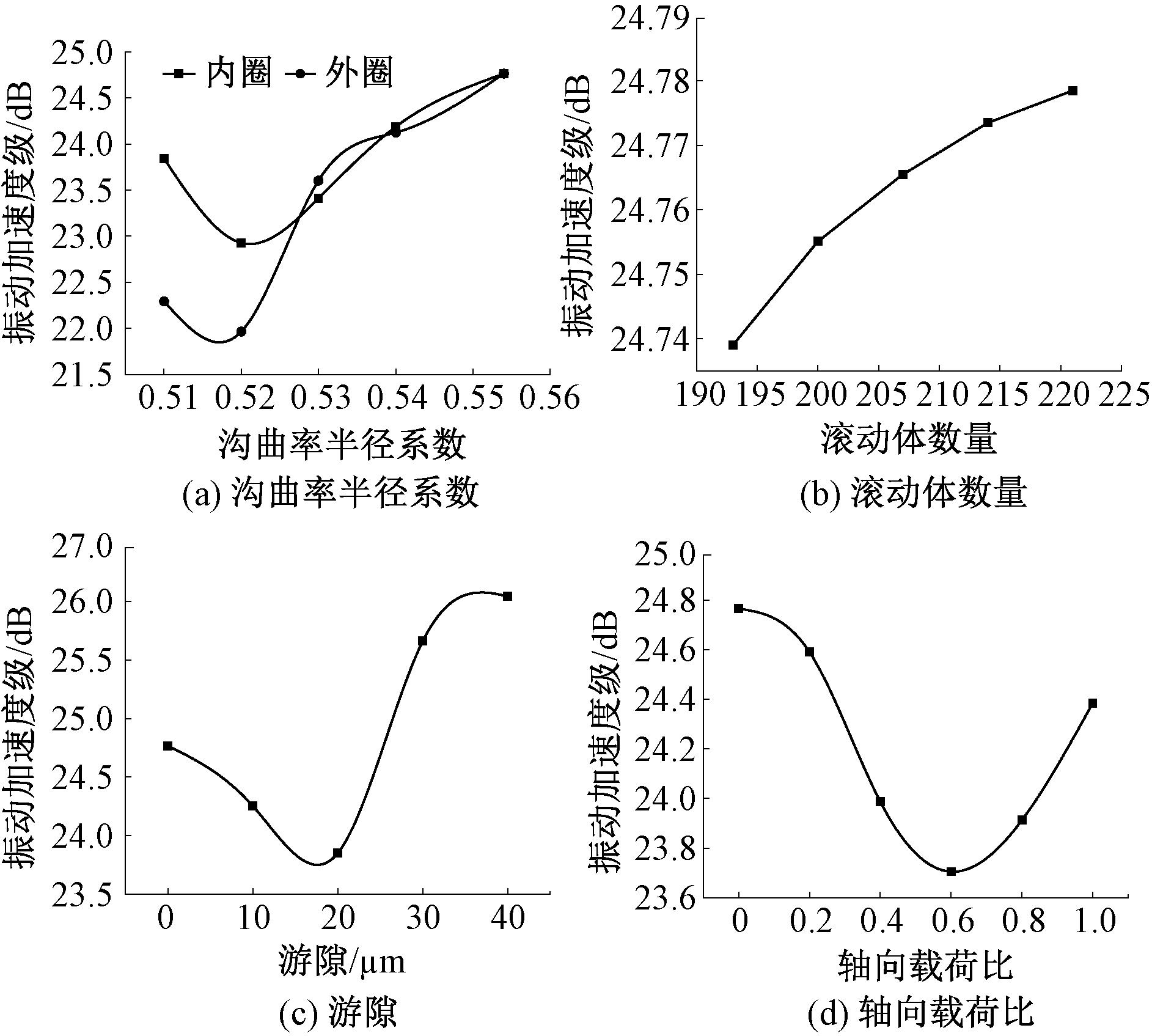
图4 各参数对轴承振动加速度级的影响
Figure 4 Influence of each parameter bearing on the vibration acceleration level of the bearing
2.1.1 内圈沟曲率半径系数对轴承振动的影响
从图4(a)可以看出,随着内圈沟曲率的增加,轴承的振动呈现先减小后增加的趋势,且在沟曲率为0.522附近振动达到最小。故在选取轴承内圈沟曲率半径系数时,将其控制在0.515～0.525更有利于降低轴承的振动。
2.1.2 外圈沟曲率半径系数对轴承振动的影响
从图4(a)可以看出,随着外圈沟曲率的增加,轴承振动趋势和内圈沟曲率变化趋势一致,表现为先减小后增大且在曲率为0.518附近达到最小。故在选取轴承外圈沟曲率半径系数时将其控制在0.510～0.525更有利于降低轴承的振动。
2.1.3 滚动体数量对轴承振动的影响
从图4(b)可知,随着滚动体数量的增加,轴承振动趋势也随之增加,但其总体振动幅值变化平稳,无剧烈变化。滚动体数量增加虽然降低了单个滚动体承载的载荷,但也增加了振动源。从振动角度分析,减小滚动体的数量有利于降低轴承的振动。故在轴承设计之初,在满足轴承的承载能力条件下可以减少滚动体的数量从而降低振动,但降低的幅值有限。
2.1.4 游隙对轴承振动的影响
由图4(c)可知,随着游隙的增加,轴承的振动先减小后急剧增大,在18 μm处达到最小,且当轴承游隙大于20 μm后,轴承振动幅值随着游隙的增加而增加。这主要是由于当轴承游隙过小时,游隙限制了滚动体在交替受载过程中的相对位移能力,导致振动无法得到充分缓解,从而使振动幅值增加,且当游隙过小时无法形成有效润滑从而增加轴承的摩擦与磨损。而当轴承游隙过大时,会引起滚动体与内外圈的剧烈碰撞,造成振动的急剧增加,故轴承游隙应控制在18 μm附近。
2.1.5 轴向载荷对轴承振动的影响
轴向载荷比Ca定义为轴承轴向载荷与径向载荷之比:Ca=Fa/Fr。从图4(d)可以看出,随着轴向力的增加,轴承的振动幅值呈现先减小后增加的趋势,在轴向载荷比0.6附近时,振动幅值达到最小。故对轴承施加合适的轴向载荷可以有效降低轴承的振动幅值。
3 结论
(1)通过Hertz接触理论建立了CT机双列角接触球转盘力学模型,并进一步对其非线性振动模型进行分析。
(2)通过对CT机双列角接触球转盘轴承振动模型分析,发现存在最优的结构参数使得轴承的振动降低。如减少滚动体的数量,将轴承内圈沟曲率控制在0.515～0.525,外圈沟曲率控制在0.510～0.525,游隙控制在18 μm附近。
(3)轴承在运行过程中存在合适的轴向载荷使得轴承振动降低,因此可通过两内圈相连的螺栓对轴承进行一定的预紧从而降低轴承的振动。
[1] 温景波, 周琳, 谢兴会, 等. 高速CT机主轴承[J]. 轴承, 2012(9): 9-10.WEN J B, ZHOU L, XIE X H, et al. Main bearing of high-speed CT[J]. Bearing, 2012(9): 9-10.
[2] 梁杰, 张志强, 高金刚. 40Cr/石墨关节轴承摩擦学性能及磨损机理研究[J]. 郑州大学学报(工学版), 2022, 43(2): 65-70.LIANG J, ZHANG Z Q, GAO J G. Study on tribological properties and wear mechanism of 40Cr/graphite spherical plain bearings[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(2): 65-70.
[3] 陈月, 邱明, 杜辉, 等. 机器人用四点接触球轴承旋转精度影响因素[J]. 中国机械工程, 2020, 31(14): 1678-1685, 1692.CHEN Y, QIU M, DU H, et al. Factors influencing rotation accuracy of four-point contact ball bearings for robots[J]. China Mechanical Engineering, 2020, 31(14): 1678-1685, 1692.
[4] 余永健, 陈国定, 李济顺, 等. 轴承零件几何误差对圆柱滚子轴承回转误差的影响: 第一部分 计算方法[J]. 机械工程学报, 2019, 55(1): 62-71.YU Y J, CHEN G D, LI J S, et al. Effect of geometric errors of bearing components on motion error of cylindrical roller bearings: part Ⅰ calculation method[J]. Journal of Mechanical Engineering, 2019, 55(1): 62-71.
[5] 余光伟, 方党生, 蔡翔宇, 等. 波纹度波数对深沟球轴承振动特性的影响[J]. 轴承, 2021(4): 18-22.YU G W, FANG D S, CAI X Y, et al. Influence of waviness wave number on vibration characteristics of deep groove ball bearing[J]. Bearing, 2021(4): 18-22.
[6] 吕润楠, 郝旭, 于长鑫, 等. 双列圆锥滚子轴承滚道表面波纹度对轴承振动特性的影响研究[J]. 振动与冲击, 2022, 41(20): 126-132.LYU R N, HAO X, YU C X, et al. Effects of vibration characteristics of a double row tapered roller bearing with raceway surface waviness[J]. Journal of Vibration and Shock, 2022, 41(20): 126-132.
[7] ZMARZY P .Influence of bearing raceway surface topography on the level of generated vibration as an example of operational heredity[J].Indian Journal of Engineering and Materials Sciences, 2020, 27(2):356-364.
[8] 汪凯, 江胜飞, 胡波, 等. 轴承间隙对轴承振动影响的理论模型与试验研究[J]. 机械科学与技术, 2023, 42(1): 67-74.WANG K, JIANG S F, HU B, et al. Theoretical model and experimental study on influence of bearing inner clearance on bearing vibration[J]. Mechanical Science and Technology for Aerospace Engineering, 2023, 42(1): 67-74.
[9] 唐志霖, 蒋迪永, 张文虎, 等. 时变载荷激励的空调滑片式压缩机用球轴承振动特性分析[J]. 振动与冲击, 2023, 42(1): 169-180, 223.TANG Z L, JIANG D Y, ZHANG W H, et al. Vibration characteristics of ball bearing for air conditioning sliding vane compressor excited by time-varying load[J]. Journal of Vibration and Shock, 2023, 42(1): 169-180, 223.
[10] 邓四二, 孙朝阳, 顾金芳, 等. 低噪音深沟球轴承振动特性研究[J]. 振动与冲击, 2015, 34(10): 12-19.DENG S E, SUN C Y, GU J F, et al. Vibration characteristics of low-noise deep groove ball bearings[J]. Journal of Vibration and Shock, 2015, 34(10): 12-19.
[11] 田凯文, 邱明, 王东峰. 动力传动机构四点接触球轴承的振动特性分析[J]. 振动与冲击, 2023, 42(4): 39-47.TIAN K W, QIU M, WANG D F. Analysis of vibration characteristics of four-point contact ball bearings for power transmission[J]. Journal of Vibration and Shock, 2023, 42(4): 39-47.
[12] PARMAR V, SARAN V H, HARSHA S P. Effect of dynamic misalignment on the vibration response, trajectory followed and defect-depth achieved by the rolling-elements in a double-row spherical rolling-element bearing[J]. Mechanism and Machine Theory, 2021, 162: 104366.
[13] GUNDUZ A, DREYER J T, SINGH R. Effect of bearing preloads on the modal characteristics of a shaft-bearing assembly: experiments on double row angular contact ball bearings[J]. Mechanical Systems and Signal Processing, 2012, 31: 176-195.
[14] 欧旭鹏, 张义民, 张凯, 等. 考虑不平衡力与扰动力的深沟球轴承动力学模型[J]. 机械设计与制造, 2022(12): 6-10.OU X P, ZHANG Y M, ZHANG K, et al. Dynamic model of deep groove bearing considering unbalanced force and disturbing force[J]. Machinery Design &Manufacture, 2022(12): 6-10.
[15] TONG V C, HONG S W. Vibration characteristics of tapered roller bearings with roller diameter error[J]. MATEC Web of Conferences, 2016, 51: 01004.
[16] 杜秋华. 球轴承振动的非线性模型及信号分析方法研究[D]. 武汉: 华中科技大学, 2007. DU Q H. Research on nonlinear models and signal analysis methods of ball bearing vibrations[D].Wuhan: Huazhong University of Science and Technology, 2007.
[17] 中华人民共和国工业和信息化部.滚动轴承振动(加速度)测量方法:JB/T 5314—2013[S].北京:机械工业出版社,2013.Ministry of Industry and Information Technology of the People′s Republic of China. Rolling bearing vibration (acceleration) measurement method: JB/T 5314—2013[S].Beijing:China Machine Press,2013.