车辆高速行驶产生的噪声以轮胎路面噪声为主,约为90%[1]。降低交通噪声的措施,主要有声屏障、汽车吸震[2]、多孔沥青路面等,其中路面能够就近吸收噪声[3],较为经济实用。
多孔沥青混合料具有的多孔结构,能够使入射的噪声声波在与空隙结构的摩擦和热交换中完成一部分声能的耗散[4],吸收声能与入射声能的比即为吸声系数,是吸声性能的重要表征[5]。目前,针对混合料吸声性能的研究集中在使用驻波管测试吸声系数,分析空隙率、级配、厚度、表面粗糙程度、单双层结构等对吸声性能的影响[6-7],这些特征多为结构特征参数,且多是基于实验测试开展的,尚不能从机理上指导多孔沥青混合料的声学性能设计。
吸声系数的唯象模型在结构特征参数的基础上引入了声学参数,建立空隙结构特征、声学特征与吸声性能的联系[8-9]。基于声学参数建立的声学模型可为吸声性能的预测与优化提供便利。Rochat等[10]实地测量了多种路面的有效流阻率,发现开级配沥青路面具有较小的有效流阻率,较密级配沥青路面更有利于噪声声波的吸收。Sachakamol等[11]通过空隙率、流阻率、曲折因子、厚度等参数,建立了橡胶沥青混合料的吸声系数模型,该模型可在较宽频率范围内对吸声系数提供较为准确的定量预测。Luong等[12]通过超薄多孔沥青路面的空隙率、流阻率和曲折因子来预测吸声系数。
混合料的声学参数中,结构特征参数相对容易获取,而声学特征参数获取困难[13]。本文基于唯象模型,以开级配沥青磨耗层(OGFC)为对象,通过驻波管测试吸声系数,通过实测与算法反演结合的方法获得声学参数并使用声学有限元方法验证,最后从声学参数的角度对吸声性能进行优化。
1 多孔材料声学模型
多孔沥青混合料是一种刚性骨架的多孔材料。刚性骨架的声学模型分为经验模型与唯象模型[14],前者基于大量吸声系数测试建立,预测的准确性和普适性均较差,后者从微观考虑声波在空隙中的传播及损耗,对声波的吸收作用以黏性、热效应表示,预测效果较好。
Johnson-Champoux-Allard(JCA)模型是一种应用广泛的唯象模型[15],黏性、热效应分别使用有效密度与有效体积模量表征,并通过5个声学参数进行描述,分别为空隙率φ(材料空隙内的流体体积)、流阻率σ(材料单位厚度的流阻)、曲折因子α∞(流体通过多孔材料路径的曲折程度,α∞越大路径越曲折)、黏性特征长度Λ(表征流体通过材料时与空隙壁摩擦产生的黏滞作用)和热效特征长度Λ′(表征流体通过材料时与空隙壁发生的热交换作用)。声学参数的准确获取,是JCA模型能够准确预测吸声系数的关键。JCA模型的表达式为
(1)
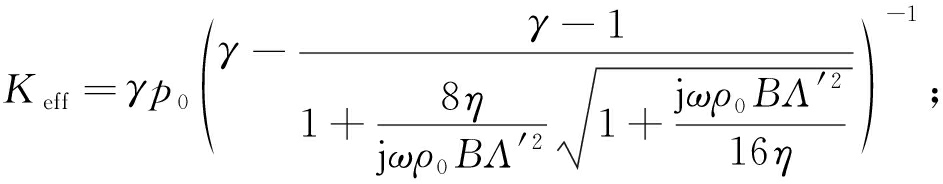
(2)
(3)
(4)
(5)
(6)
(7)
(8)
α=1-![]() 。
。
(9)
式中:d为材料的厚度,m;c为形状因子;c′为尺度因子;Zs为表面阻抗,Ω;Z0为空气的特征阻抗,416.5 Ω;ρ0为空气的密度,1.21 kg/m3;p0为空气的压强,1.01×105 Pa;ω为入射声波的角频率,rad/s;η为空气的动力黏度,1.88×10-5 N·s/m2;γ为空气的比热比,1.4;B为普朗克常数,0.71;R为反射系数;α为吸声系数。
2 多孔沥青混合料的声学参数
2.1 吸声系数测试
OGFC是一种典型的多孔沥青混合料,空隙率为18%~25%。为了分析空隙率、级配对吸声性能的影响,采用的级配如表1所示。制备混合料使用的原材料为辉绿岩集料、高黏改性沥青、木质素纤维、水泥和石灰岩矿粉,技术指标均满足要求。
表1 混合料的级配组成
Table 1 Gradation composition of the mixture %
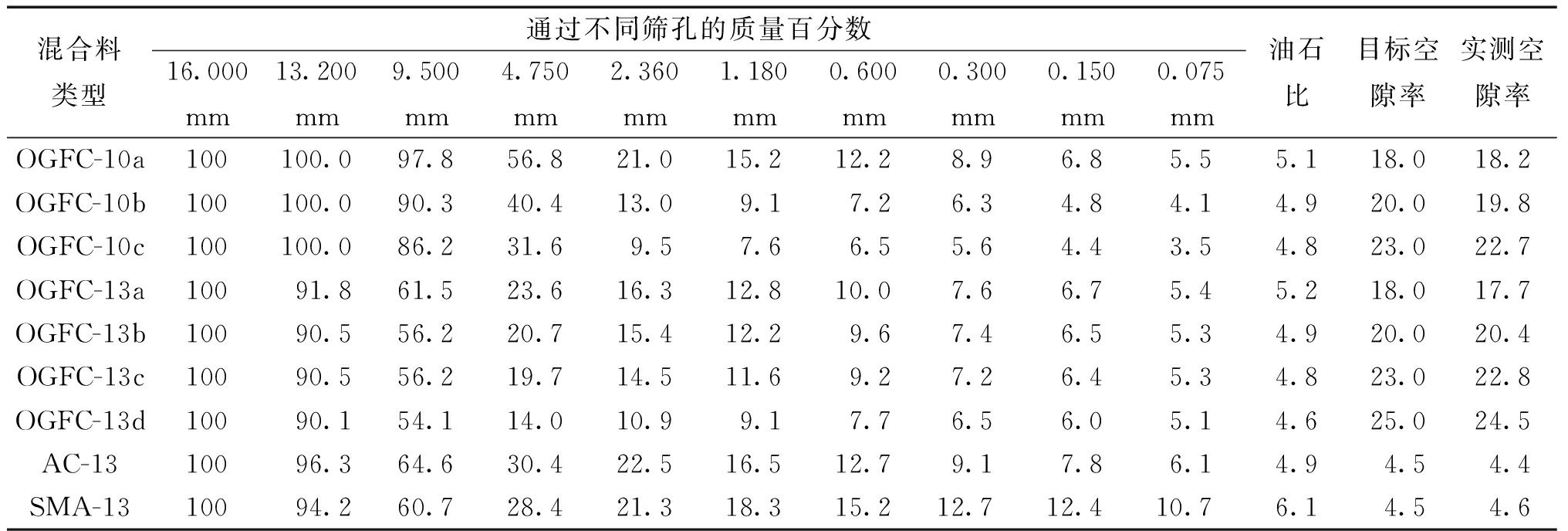
混合料类型通过不同筛孔的质量百分数16.000 mm13.200 mm9.500 mm4.750 mm2.360 mm1.180 mm0.600 mm0.300 mm0.150 mm0.075 mm油石比目标空隙率实测空隙率OGFC-10a100100.097.856.821.015.212.28.96.85.55.118.018.2OGFC-10b100100.090.340.413.09.17.26.34.84.14.920.019.8OGFC-10c100100.086.231.69.57.66.55.64.43.54.823.022.7OGFC-13a10091.861.523.616.312.810.07.66.75.45.218.017.7OGFC-13b10090.556.220.715.412.29.67.46.55.34.920.020.4OGFC-13c10090.556.219.714.511.69.27.26.45.34.823.022.8OGFC-13d10090.154.114.010.99.17.76.56.05.14.625.024.5AC-1310096.364.630.422.516.512.79.17.86.14.94.54.4SMA-1310094.260.728.421.318.315.212.712.410.76.14.54.6
吸声系数的测试使用AWA6128A型驻波管,如图1所示,该驻波管管径为96 mm,同时OGFC的铺筑厚度普遍为4 cm,为了获得尺寸准确的试件,使用旋转压实法成型直径150 mm高4 cm的试件并钻芯取样。

图1 AWA6128A型驻波管
Figure 1 AWA6128A standing wave tube
吸声系数测试时,试件背衬刚性壁置于试件筒内,用硅油密封,测试频率为100~2 000 Hz的1/3倍频程中心频率,推动探测小车分别寻找声压级极大值和极小值的位置,计算该频率的吸声系数,结果如图2所示。
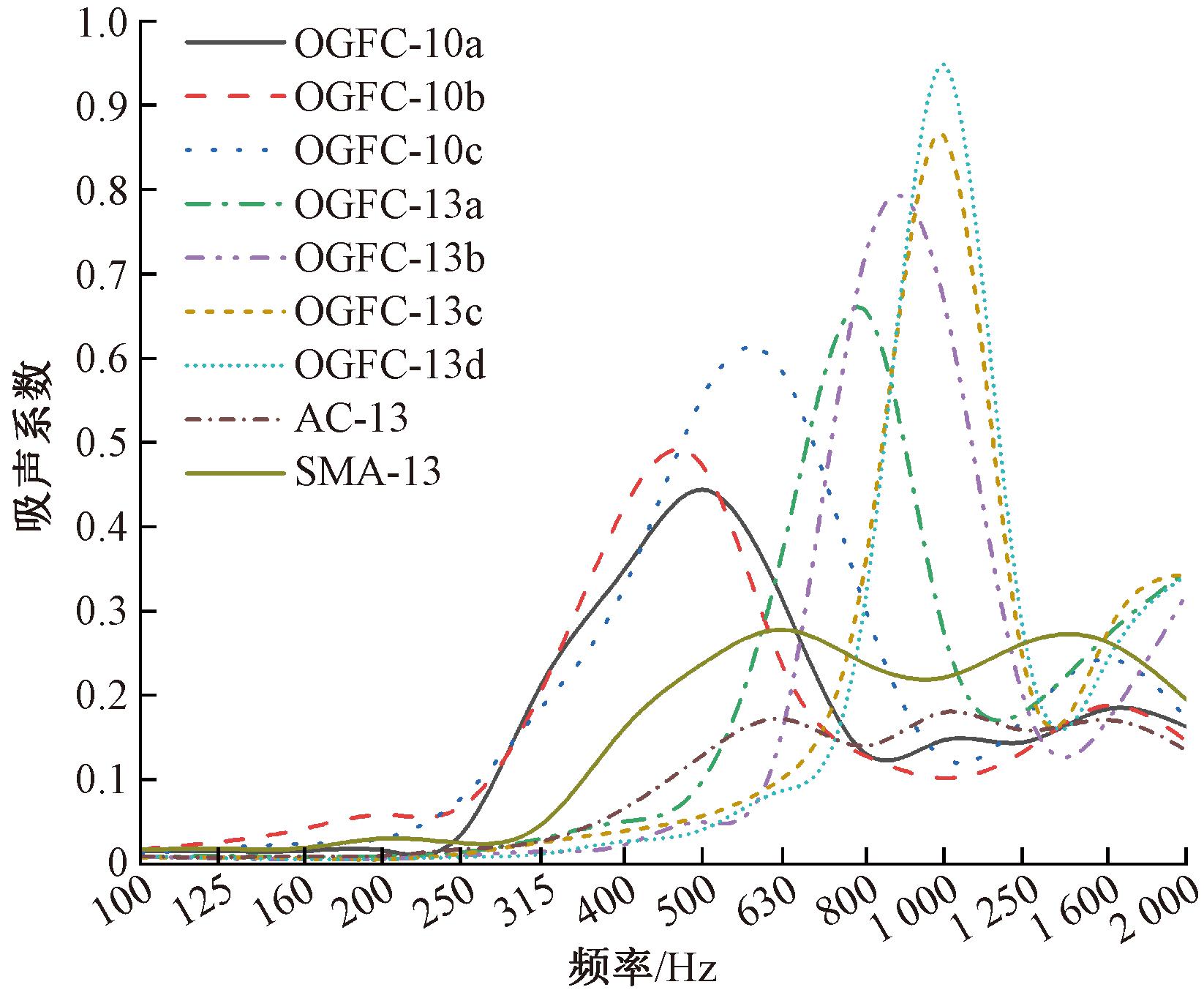
图2 吸声系数测试结果
Figure 2 Test results of sound absorption coefficient
由图2可知,SMA和AC吸声性能都明显弱于OGFC,表明OGFC较普通沥青路面具有显著的降噪效果。9种混合料的均值吸声系数分别为0.194,0.196,0.251,0.209,0.211,0.212,0.214,0.088,0.143,相同空隙率下OGFC-13的平均吸声性能较OGFC-10增加不明显,这是由于主要吸声频段存在差异。
OGFC-13主要吸声频段为750~1 000 Hz,对中高频噪声吸收能力较强,OGFC-10主要吸声频段为400~600 Hz,对低频噪声吸收能力较强,峰值吸声系数分别为0.454,0.479,0.613,0.656,0.803,0.864,0.949,0.172,0.278,OGFC-13的峰值吸声性能较OGFC-10有明显提高。相同最大公称粒径下,随空隙率的增加,峰值吸声系数增大且吸收峰向右移动。
2.2 流阻率测试
材料的流阻Rf指通过材料的稳定流体受到的流动阻力,Rf越小流体越容易通过,表示为
(10)
式中:Rf为流阻,Pa·s/m3;Δp为材料两侧的静压差,Pa;vq为气流体积速度,m3/s。
流阻率σf表示为
(11)
式中:σ为流阻率,Pa·s/m2;d为材料厚度,m;u为气流线速度,m/s,表示气流体积速度与气流方向上试件的横截面积A之比,即u=vq/A。
流阻率是材料的固有属性,测试方法通常有直流法、交流法和声学阻抗管法[16],测试方法不影响结果。直流法的测量原理是使低速、稳定的气流通过材料,测量材料两侧的静压差和气流体积速度。
基于直流法组建流阻率测量设备,如图3所示。使用LY-M3930A型空气压缩机作为气流源,使用长300 mm、内径96 mm的亚克力管作为放置芯样的容器,使用LZB-10WB型空气流量计读取气流体积速度vq,使用U型压力计读取水柱高差h,装置各部分使用橡胶塞和橡胶软管连接,并确保密封性。则材料两侧的静压差Δp可表示为
Δp=ρgh。
(12)

图3 流阻率测量装置
Figure 3 Flow resistance measuring device
式中:ρ为注入U型管中水的密度,kg/m3;g为重力加速度,m/s2。
流阻率结果如表2所示。OGFC的流阻率均为3 500~5 000 Pa·s/m2,空隙率越大流阻率越小,空隙率相近时,流阻率差值小于100 Pa·s/m2,说明公称最大粒径不影响流阻率的大小。而AC-13和SMA-13的空隙率小、流阻率大,说明空隙率是流阻率的主要影响因素。
表2 多孔沥青混合料声学参数
Table 2 Acoustic parameters of porous asphalt mixture
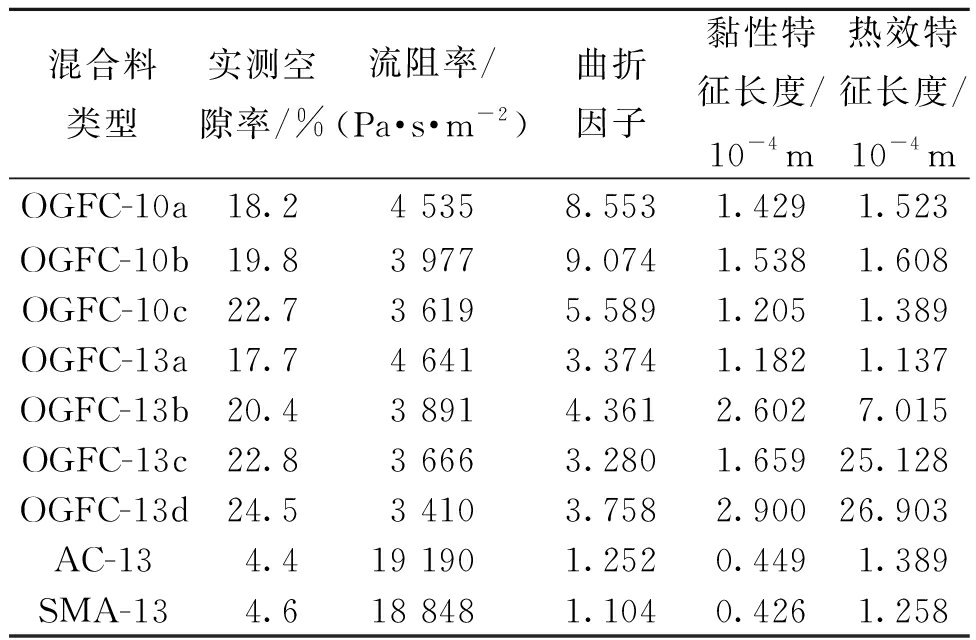
混合料类型实测空隙率/%流阻率/(Pa·s·m-2)曲折因子黏性特征长度/10-4m热效特征长度/10-4mOGFC-10a18.24 5358.5531.4291.523OGFC-10b19.83 9779.0741.5381.608OGFC-10c22.73 6195.5891.2051.389OGFC-13a17.74 6413.3741.1821.137OGFC-13b20.43 8914.3612.6027.015OGFC-13c22.83 6663.2801.65925.128OGFC-13d24.53 4103.7582.90026.903AC-134.419 1901.2520.4491.389SMA-134.618 8481.1040.4261.258
2.3 声学参数的反演
实测曲折因子α∞、黏性特征长度Λ和热效特征长度Λ′需使用超声波法,设备昂贵、测试过程困难。由于曲折因子α∞为1~10,黏性特征长度Λ与热效特征长度Λ′满足Λ′≥Λ,且形状因子c和曲折因子c′均为0.3~3.3 mm。因此,代入已实测的吸声系数、空隙率和流阻率,根据声波频率的不同,建立的方程组仅包含3个未知参数,求解方程即可获得声学参数的值。
遗传算法是一种基于生物遗传学说和进化论的优化算法[17],其借鉴了生物种群在环境影响下发生自然选择、遗传、基因交叉和变异的作用,通过多代遗传得到更适应环境的种群,即最优解。
基于遗传算法,使用Python语言编写反演程序,解的搜索范围为α∞∈[1,10],c,c′∈[0.3,3.3]且c≥c′。以各频率下吸声系数的实测值来定义适应度函数:
(13)
式中:αi为各频率下吸声系数的实测值;![]() 为各频率下代入可行解计算的吸声系数值。利用该程序反演获得了9种级配沥青混合料的声学参数,如表2所示。
为各频率下代入可行解计算的吸声系数值。利用该程序反演获得了9种级配沥青混合料的声学参数,如表2所示。
由表2可知,相近空隙率下,OGFC-10的曲折因子较OGFC-13更大,这是因为公称粒径小,集料嵌挤形成的空隙曲折程度更大。OGFC的曲折因子明显大于AC和SMA,是因为密级配混合料多为闭口空隙,流体路径仅由连通空隙提供。OGFC的黏性特征长度为1×10-4 ~3×10-4 m,热效特征长度为1×10-4~27×10-4 m。
2.4 声学参数正确性验证
使用声学有限元方法验证声学参数的正确性,建立的驻波管模型如图4所示,其与吸声系数测试时使用的驻波管具有相同的尺寸,长1 m,内径96 mm,网格最大尺寸5 mm,试件厚度与混合料一致,驻波管的材料属性为空气,试件的材料属性采用JCA模型,以表2中的5个声学参数表示,边界条件设置为全反射,即声波在管壁会发生完全反射,模拟驻波管的刚性内壁,声源定义为平面波并从一端入射,在管内形成驻波,通过定义的监测点获取声压值,用于计算相应频率下的吸声系数。实测与仿真的吸声系数频谱曲线如图5所示。
图4 驻波管有限元模型
Figure 4 Finite element model of standing wave tube
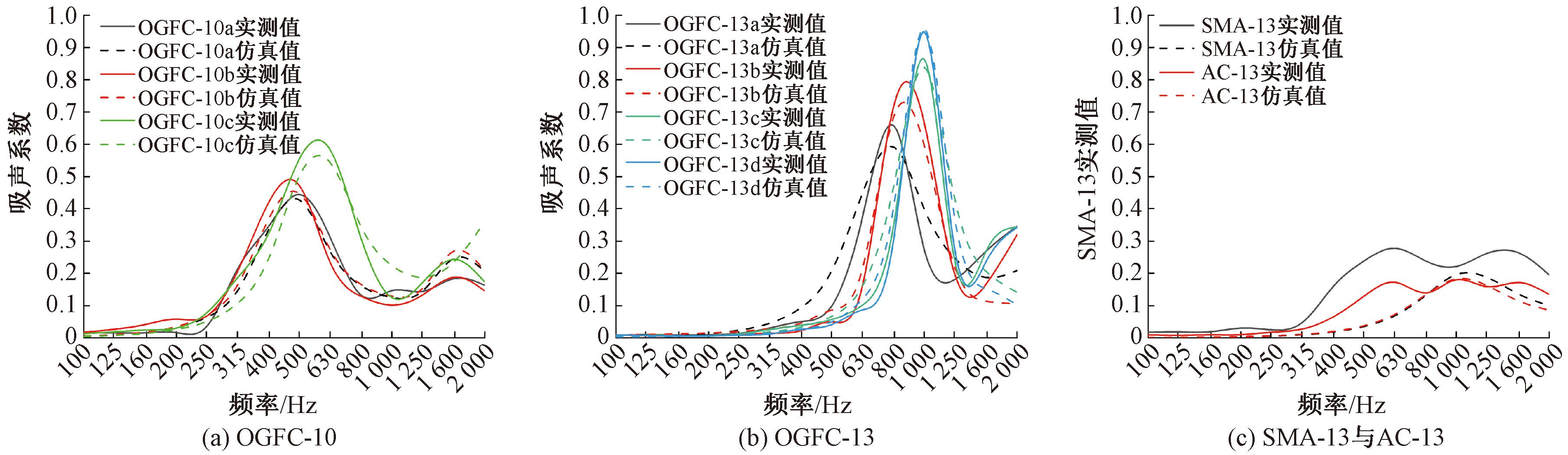
图5 实测与仿真的吸声频谱曲线对比
Figure 5 Comparison of measured and simulated sound absorption spectrum curves
由图5可知,有限元仿真获得的吸声频谱曲线能够较好地体现吸声系数随频率的变化趋势,峰值吸声系数的大小及出现的频率基本一致,可见对OGFC混合料拟合效果较好,反演获得的声学参数较为可信,能够表征OGFC混合料的吸声特性。
3 基于声学参数的吸声性能优化
3.1 声学参数单因素影响分析
为了探究声学参数作为单因素自变量时对OGFC吸声性能的影响,基于声学参数的取值范围,基础参数设置如下:空隙率为20%;流阻率为4 000 Pa·s/m2;曲折因子为5;黏性特征长度为2×10-4 m;热效特征长度为7×10-4 m。考虑单因素变化时,空隙率分别设置为16%,18%,20%,22%,24%;流阻率分别设置为3 000,3 500,4 000,4 500,5 000 Pa·s/m2;曲折因子分别设置为1,3,5,7,9;黏性特征长度分别设置为1×10-4,1.5×10-4,2×10-4,2.5×10-4,3×10-4 m;热效特征长度分别设置为2×10-4,7×10-4,13×10-4,19×10-4,25×10-4 m。各组参数计算的吸声频谱曲线如图6所示。
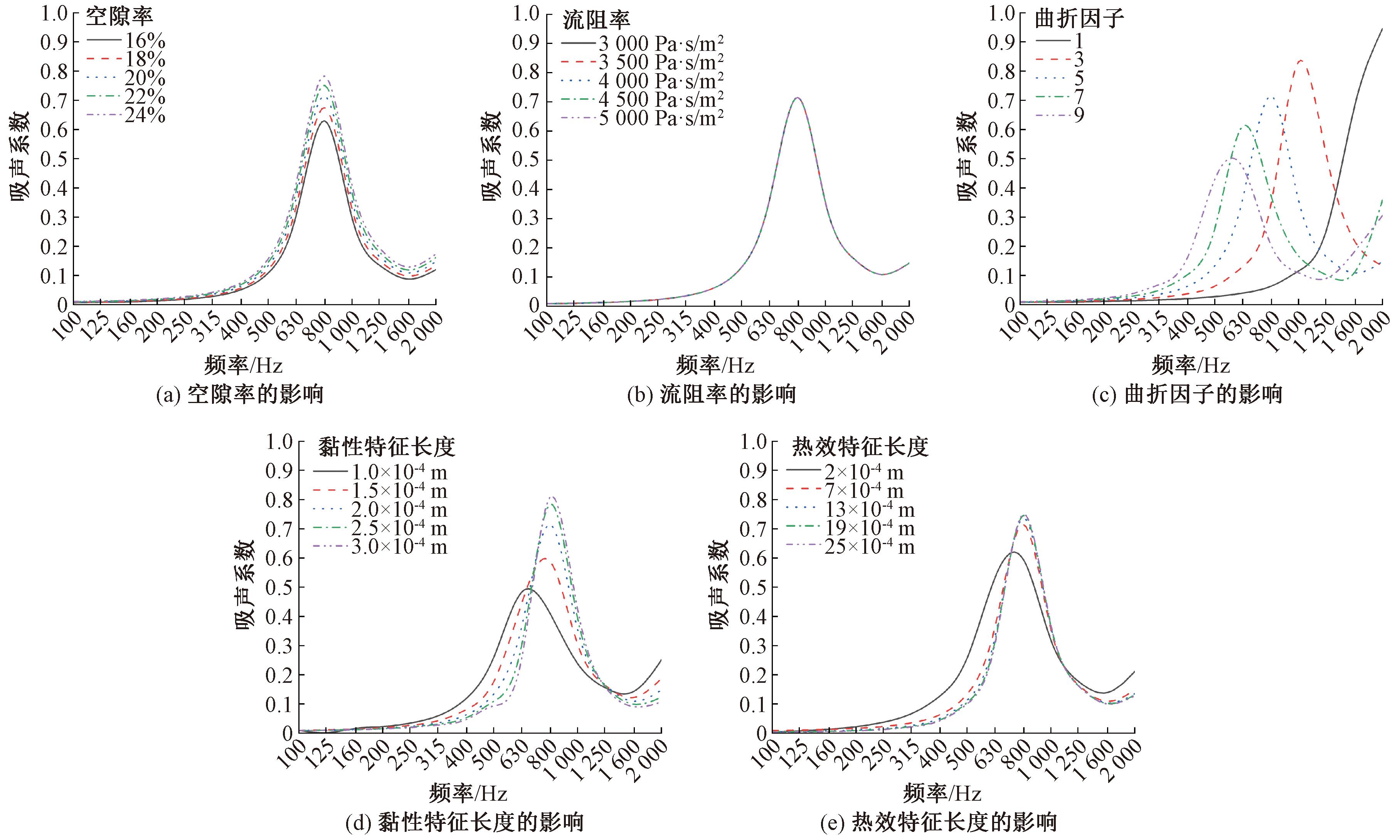
图6 单因素对吸声性能的影响
Figure 6 Influence of single factors on sound absorption performance
由图6(a)可知,随空隙率增大,峰值吸声系数分别为0.628,0.674,0.714,0.750,0.782,越大的空隙率声波进入空隙内部碰撞的概率和次数越大,吸声性能越好。空隙率主要影响峰值吸声系数的大小,不改变峰值吸声系数出现的频率。由图6(b)可知,流阻率变化时,吸声频谱曲线重合,流阻率对吸声性能没有影响,可能是因为OGFC的强度限制了空隙率大小,空隙率的大小将流阻率的大小限制在较小范围内,此范围内的流阻率对吸声性能的影响很微小。由图6(c)可知,曲折因子增大,平均吸声系数分别为 0.199,0.213,0.198,0.193,0.189,曲折因子为3,5,7,9时的峰值吸声系数分别为0.831,0.714,0.611,0.509,峰值吸声系数变小,出现的频率向低频移动,材料会由适合吸收中高频噪声转变为更适合吸收低频噪声。由图6(d)可知,黏性特征长度增大,平均吸声系数分别为0.197,0.196,0.193,0.190,0.186,逐渐减小,峰值吸声系数分别为0.482,0.587,0.714,0.784,0.809,增幅减小,出现的频率向高频移动,稳定在800 Hz附近。由图6(e)可知,热效特征长度增大,峰值吸声系数分别为0.615,0.714,0.736,0.745,0.749,增幅减小。空隙壁越粗糙,热效特征长度和黏性特征长度越大,将分别增大黏滞作用和热交换作用对声能的耗散,但空隙壁的粗糙达到一定程度,声能耗散不再增加,因此表现为频谱曲线趋于重合。
3.2 混合料吸声性能优化
从单因素对混合料吸声性能的影响结果可知,除流阻率外,其余4个参数都会产生一定程度的影响,其中,空隙率、黏性特征长度和热效特征长度宜选择较大值,曲折因子宜低于5,然而在混合料的制备过程中,难以通过调整级配等使混合料的单一声学参数改变,且单一因素最优时其余目标的变化可能会使吸声性能下降,为此需要对声学参数进行多目标的优化,达到通过控制空隙率实现多孔沥青混合料具有更好吸声性能的目的。
空隙率越大,路面的力学性能和耐久性越差,考虑各参数的取值范围,约束条件定义如下:空隙率设置为20%~23%、流阻率固定为3 800 Pa·s/m2、曲折因子为3~4.5、黏性特征长度为1.5×10-4~3×10-4 m、热效特征长度为7×10-4~25×10-4 m。通过仿真,发现此范围内的声学参数具有相似的吸声特性,吸收峰出现的位置接近,可将均值吸声系数的大小作为优化目标进行寻优。结果表明,均值吸声系数的最大值为0.224,此时空隙率为21.97%,曲折因子为3.15,黏性特征长度为1.67×10-4 m,热效特征长度为8.56×10-4 m,即空隙率应控制在22%左右。
制备目标空隙率为22%的OGFC-13试件进行验证,声学参数的测试结果为空隙率21.8%、流阻率3 763 Pa·s/m2、曲折因子3.327、黏性特征长度1.57×10-4 m、热效特征长度13.76×10-4 m。各参数大小与优化结果较为接近,实际制备的混合料曲折因子和热效特征长度偏大,黏性特征长度偏小。
优化及验证的吸声频谱曲线如图7所示,以目标空隙率为23%、均值吸声系数为0.212的OGFC-13c混合料作为对比。相较OGFC-13c,优化后峰值吸声系数从0.864降为0.776,平均吸声系数从0.212提升到0.224,提升的吸声性能主要体现在对500~800 Hz和1 100~1 550 Hz 2个频率段噪声的吸收。可见从声学参数的角度对OGFC的吸声性能进行优化,能够使吸声性能提升。
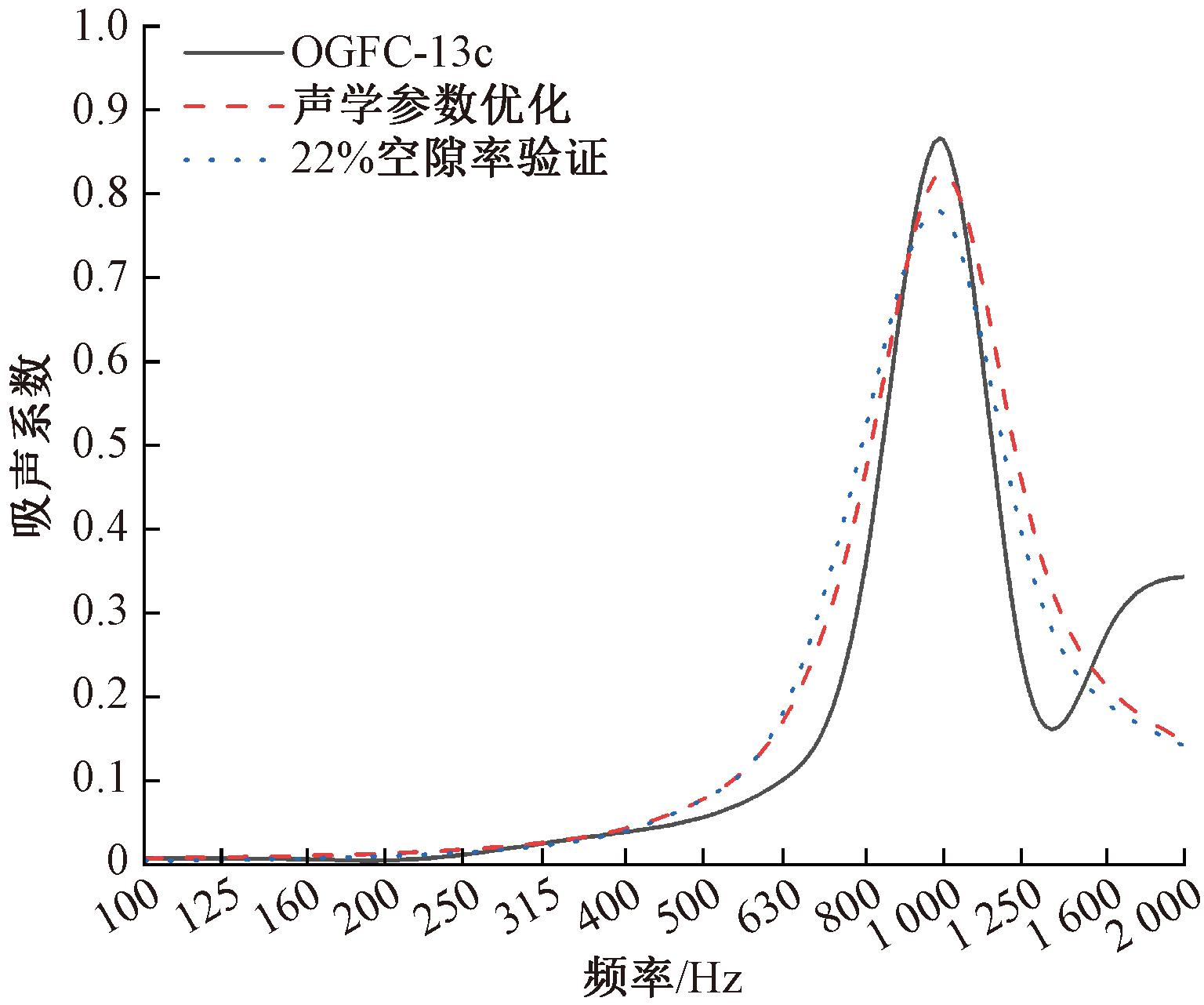
图7 声学参数的优化与验证结果
Figure 7 Optimization of acoustic parameters and validation results
4 结论
(1)OGFC的吸声性能随着空隙率的增大而增强,公称最大粒径会影响混合料的主要吸声频段,OGFC-10对低频噪声的吸声能力较好,OGFC-13对中高频噪声的吸收能力较好,且OGFC-13更适宜路面降噪。
(2)基于JCA模型,实测和反演获得的声学参数能够较好表征OGFC的吸声性能,吸声系数峰值的大小和出现的频率均与实测结果一致。
(3)从声学参数单因素对吸声性能的影响来看,空隙率增大时各频率下的吸声系数均增大,流阻率对吸声性能没有影响,曲折因子越大混合料对中高频噪声的吸收能力越弱,黏性特征长度和热效特征长度增大都能提升吸声性能但提升效果有限。
(4)基于声学参数的多目标优化,OGFC-13的空隙率应控制在22%左右,此时混合料具有最佳的吸声性能。
[1] VAITKUS A, ANDRIEJAUSKAS T, VOROBJOVAS V, et al. Asphalt wearing course optimization for road traffic noise reduction[J]. Construction and Building Materials, 2017, 152: 345-356.
[2] 李晨阳, 刘鹏, 陈宏, 等. 基于驾驶室舱内声学特性的动力吸振器设计研究[J]. 郑州大学学报(工学版), 2021, 42(4): 47-52.LI C Y, LIU P, CHEN H, et al. Design and research of dynamic vibration absorber based on acoustic characteristics of interior sound field in a cab[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(4): 47-52.
[3] 王涛. 低噪声沥青路面降噪原理及影响因素分析[J]. 山东交通科技, 2016(4): 113-115, 117.WANG T. Analysis of noise reduction principles and influence factors of low noise asphalt pavement[J]. Shangdong Jiaotong Keji, 2016(4): 113-115, 117.
[4] 何虹霖, 邹晓翎, 叶向前, 等. 低噪声沥青路面降噪机理及研究进展[J]. 中外公路, 2022, 42(1): 55-61.HE H L, ZOU X L, YE X Q, et al. Noise reduction mechanism and research progress of low-noise asphalt pavement[J]. Journal of China &Foreign Highway, 2022, 42(1): 55-61.
[5] LICITRA G, MORO A, TETI L C, et al. Modelling of acoustic ageing of rubberized pavements[J]. Applied Acoustics, 2019, 146: 237-245.
[6] 李金凤, 何兆益, 孔林. 多孔沥青混合料的声学性能评价[J]. 西南交通大学学报, 2022, 57(1): 207-214.LI J F, HE Z Y, KONG L. Evaluation of acoustic performance of porous asphalt concrete[J]. Journal of Southwest Jiaotong University, 2022, 57(1): 207-214.
[7] CHU L, FWA T F. Functional sustainability of single- and double-layer porous asphalt pavements[J]. Construction and Building Materials, 2019, 197: 436-443.
[8] YANG Y, CHEN Z F. A model for calculating the air flow resistivity of glass fiber felt[J]. Applied Acoustics, 2015, 91: 6-11.
[9] LE L H, ZHANG C, TA D A, et al. Measurement of tortuosity in aluminum foams using airborne ultrasound[J]. Ultrasonics, 2010, 50(1): 1-5.
[10] ROCHAT J, DONAVAN P, SEYBERT A, et al. Pavement sound absorption measurements in the US[EB/OL].(2012-08-19)[2024-01-16]. https:∥www.docin.com/p-1483899964.html.
[11] SACHAKAMOL P, DAI L M. Parametric influence on the sound absorption coefficient of porous asphalt[C]∥Proceedings of ASME 2009 International Mechanical Engineering Congress and Exposition. New York: ASME, 2010: 19-26.
[12] LUONG J, BUENO M, V ZQUEZ V F, et al. Ultrathin porous pavement made with high viscosity asphalt rubber binder: a better acoustic absorption?[J]. Applied Acoustics, 2014, 79: 117-123.
ZQUEZ V F, et al. Ultrathin porous pavement made with high viscosity asphalt rubber binder: a better acoustic absorption?[J]. Applied Acoustics, 2014, 79: 117-123.
[13] 于长帅, 罗忠, 骆海涛, 等. 多孔吸声材料声学模型及其特征参数测试方法研究进展[J]. 材料导报, 2022, 36(4): 226-236.YU C S, LUO Z, LUO H T, et al. Research progress on acoustic model of porous sound absorbing materials and measurement method of its characteristic parameters[J]. Materials Reports, 2022, 36(4): 226-236.
[14] 王营, 赵武, 黄丹. 多孔材料声学模型及其应用[J]. 材料导报, 2015, 29(5): 145-149.WANG Y, ZHAO W, HUANG D. The acoustic models of porous materials and their applications[J]. Materials Review, 2015, 29(5): 145-149.
[15] ALLARD J F, CHAMPOUX Y. New empirical equations for sound propagation in rigid frame fibrous materials[J]. The Journal of the Acoustical Society of America, 1992, 91(6): 3346-3353.
[16] 王萍. 稳态流阻率的声学测量方法研究[D]. 南京: 南京大学, 2013.WANG P. A study on the acoustic measurement methods of static flow resistivity[D].Nanjing: Nanjing University, 2013.
[17] 张茂清, 李东洋, 胡博, 等. 基于维度扰动的快速非支配排序遗传算法Ⅱ[J]. 郑州大学学报(工学版), 2020, 41(1): 38-43.ZHANG M Q, LI D Y, HU B, et al. Non-dominated sorting genetic algorithm Ⅱ based on dimensionality perturbation[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(1): 38-43.