近年来,随着中国国民经济的不断增长,能源需求也呈现指数型增长,化石能源在过去的几十年内一直占据主导地位,然而使用化石能源不可避免地会带来环境问题以及能源枯竭问题。在这样的背景下,清洁能源应运而生,而风能凭借其分布广泛、无污染等特点备受全球青睐。然而,风能的调度受风速、气压等因素的影响,导致风能呈现间歇性、不稳定性。因此,对风电输出功率进行预测,尽可能降低风电功率的不确定性是必要的。
目前,风电功率预测方法根据预测所采用的模型原理划分,可划分为物理方法、统计方法与深度学习方法。基于物理模型的预测方法是指通过数值天气预报(numerical weather prediction, NWP)所提供的数据,并结合风电场的地理环境、风机分布等情况将气象数据转换为风机对应轮毂高度的风速与风向,最后通过功率-风速曲线得到输出功率;Zhao 等[1]使用NWP数据提出了一种集成策略来预测后一天的风速。基于统计学模型的预测方法是指由历史数据驱动,建立输入特征与输出功率之间的非线性映射关系,实现对风电功率的预测。Naik等[2]采用多核极限学习机对风电功率进行预测;Sharifian 等[3]采用Ⅱ型模糊神经网络进行预测;Zhang 等[4]在自回归模型的基础上进行改进,将自回归模型的固定参数改进为动态自适应的逐步参数估计,提出了一种实时功率预测方法——自回归动态自适应模型(autoregressive dynamic adaptive model, ARDA),与长短期记忆网络(long short term memory, LSTM)模型相比,ARDA模型更准确,对数据波动的动态适应性更好。张颖超等[5]基于离散Frechet距离与核熵成分分析相结合的数据处理方法,结合支持向量机模型,实现预测精度的提升。
近年来,深度学习理论迅猛发展,深度学习模型相比浅层的机器学习模型有着更强的非线性拟合能力。深度学习中的循环神经网络(recurrent neural network, RNN)及改进模型在时间序列预测中的优异表现使其逐渐成为风电功率预测的研究热点[6]。Zhang 等[7]采用LSTM对风电功率进行预测,并用高斯混合模型(Gaussian mixture model, GMM)分析误差分布特征;Kisvari 等[8]对历史数据进行预处理、重采样、异常检测、特征工程等操作后,使用门控循环神经网络(gated recurrent unit, GRU)进行预测。不论是机器学习模型还是深度学习模型,想要达到预期效果,都需要对模型选择合适的超参数,因此一些学者引入了优化算法来对模型进行参数选择。Zhang 等[9]采用遗传算法(genetic algorithm, GA)对人工神经网络(artificial neural network, ANN)参数进行优化;Fu 等[10]采用改进的灰狼算法(improved grey wolf algorithm, IGWO)对LSTM网络结构进行优化,有效提高了预测精度。
此外,由于风电功率序列具有非平稳性,时间序列分解算法也被应用到风电功率预测中。Naik 等[11]采用变分模态分解(variational mode decomposition, VMD)将序列分解为多个本征模态函数,并通过多核岭回归(multi-kernel robust ridge regression, MKRR)算法对每个子序列进行预测;Liu 等[12]采用奇异频谱分析法(singular spectrum analysis, SSA)将时间序列分解为趋势分量与细节分量,分别进行预测。另一方面,由于RNN在处理较长时间序列时存在梯度消失及梯度爆炸问题,因此很多学者尝试采用新的模型,例如卷积神经网络(convolutional neural networks, CNN),以期达到更好的效果。李静茹等[13]在CNN-LSTM网络的基础上引入注意力机制,进一步突出关键特征,以达到更好的预测性能;Bentsen 等[14]在Transformer模型基础上改进,提出了FFT(fast Fourier transformer)模型,并将其用于风速序列预测。
目前GA被广泛用于模型参数优化,但使用GA对神经网络参数进行优化时存在寻优时间较长、GA结构参数设置较为复杂等问题。而粒子群算法具有寻优速度较快、结构参数设置简单等优势,因此,本文针对LSTM超参数选择,采用粒子群算法对LSTM每层隐含层神经元的个数进行寻优,以期达到更好的效果。使用LSTM以单步滚动的方式预测风电功率输出。将目前主要研究的单机组风电功率预测问题推广至多机组。
1 数据预处理
1.1 异常值处理
由于天气、地形等环境因素的影响,风电场数据采集系统(supervisory control and data acquisition, SCADA)时常会在较为恶劣的环境下工作,因此在采集数据时,可能发生信号中断、设备损坏等故障,导致采集到错误数据或未采集到数据。异常数据通常包含异常值、缺失值;在风电功率预测之前需要对异常数据采取合适的方式处理,本文采用邻近均值填补法进行处理。
由于风机运行过程中的惯性作用,前k个时刻的输出值与当前时刻的输出有着密切关系,因此在处理异常值时,通过前k个时刻的平均值对其进行修正,具体流程如下。
步骤1 遍历数据集,查找所有数据缺失项与异常项。
步骤2 若发现t时刻存在缺失项或异常项,则获取该项的前k个时刻的输出功率值Xt-1,Xt-2,…,Xt-k。
步骤3 k个数据的功率平均值为
(1)
式中:Xt为t时刻的异常值;![]() 为t时刻前k个时刻的输出功率平均值。k通过分析数据的自相关性确定,本文将采用斯皮尔曼相关系数法确定k的具体取值。
为t时刻前k个时刻的输出功率平均值。k通过分析数据的自相关性确定,本文将采用斯皮尔曼相关系数法确定k的具体取值。
步骤4 重复以上步骤,直至处理完所有异常值。
计算当前时刻风电功率与历史时刻风电功率之间的斯皮尔曼相关系数[15]:
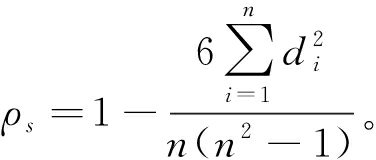
(2)
式中:n为样本数量;di为Xi与Yi两列第i个样本数列降序排列后的序号差,计算结果如表1所示。
表1 当前功率与历史功率的相关系数
Table 1 The correlation coefficient between current power and historical power
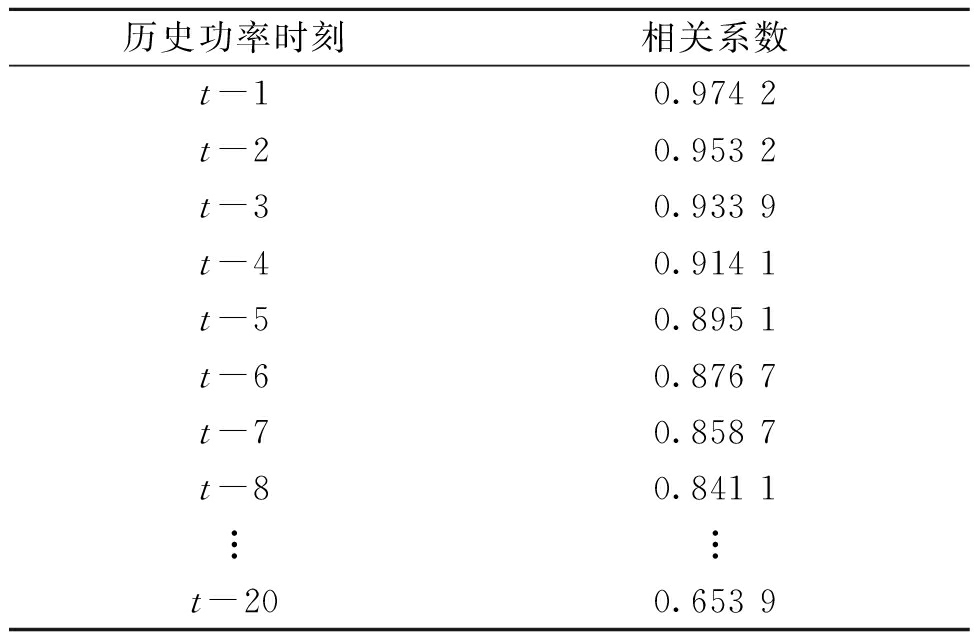
历史功率时刻相关系数t-10.974 2t-20.953 2t-30.933 9t-40.914 1t-50.895 1t-60.876 7t-70.858 7t-80.841 1︙︙t-200.653 9
当相关系数大于0.85时,可认为二者之间为强相关[16]。从表1中可知,在k>7时相关系数已经低于0.85,因此在邻近均值法处理数据时,选择参数k为7。
1.2 特征工程
特征工程是指用一系列工程化的方式从原始数据中筛选出较好的数据特征,以提升模型的训练效果。常见的特征工程有特征提取、特征选择、特征降维、归一化等。针对不同的数据集,应根据其特点选择合适的特征处理方式,才能最大程度发挥模型的能力。
主成分分析(principal component analysis, PCA)是一种常用的线性降维方法,它通过转换原始数据来创建一组新的正交特征(即主成分)。PCA的主要目的是将多维度的数据空间投影到新的低维空间中,从而实现去除冗余并保留关键信息,降维过程如下。
步骤1 设数据集中共有m条样本,每条样本有n个特征,降维的目标维数为k,m×n样本矩阵Z1;
步骤2 对样本矩阵去中心化得到m×n矩阵Z2;
步骤3 计算Z2矩阵的n维协方差矩阵B2;
步骤4 求出B2的特征值λk、特征向量φk,W=[φ1φ2…φm]n×m;
步骤5 取W矩阵的前k列组成矩阵A;
步骤6 通过线性变换Y=Z2A,得到降维后的样本矩阵Y,Y为m×k阶矩阵。
通过以上步骤,实现了将样本矩阵从n维特征空间到k维特征空间的映射。
由于输出风电功率与风速呈正相关,因此风速的变化趋势将直接影响风电输出功率的大小。若仅采用历史数据作为模型的输入,会存在以下2个缺陷:①当未来一段时间内风电场出现转折性天气[17]时,模型的预测能力将大打折扣;②当预测的时间跨度增大时,会引起误差累计,导致模型的预测精度降低。
刘洋[18]将NWP进行修正,并将修正后的数据输入LSTM、CNN-LSTM等多个模型进行预测,均取得了较好的效果;王丽婕等[19]通过考虑风电场周围多个位置的NWP数据进行建模,其准确度相比单一位置NWP数据有所提升。
另一方面,如果仅采用NWP数据,则模型预测的精度十分依赖NWP数据的准确性;而提高NWP数据的准确性需结合当地地形、气候天气等进一步建立复杂模型,但限于理论复杂、成本高,这往往是十分困难的。因此,本文将结合历史数据与NWP数据,构造多元特征输入,以期达到更高的预测精度。
2 预测模型构建
2.1 LSTM预测原理
LSTM的提出是为了解决RNN存在的梯度消失及梯度爆炸问题,LSTM通过设置门控机制,有效控制了信息的保留与遗忘。遗忘门的引入可以使得网络记忆重要信息;输入门和输出门的引入则极大增强了网络的弹性,使得LSTM有更强的建模能力。另外,门控机制的引入使得LSTM不再像RNN一样在每一时刻将记忆状态格式化,而是有选择地记忆,从而有效缓解RNN的梯度消失及梯度爆炸问题。LSTM的内部结构图如图1所示。
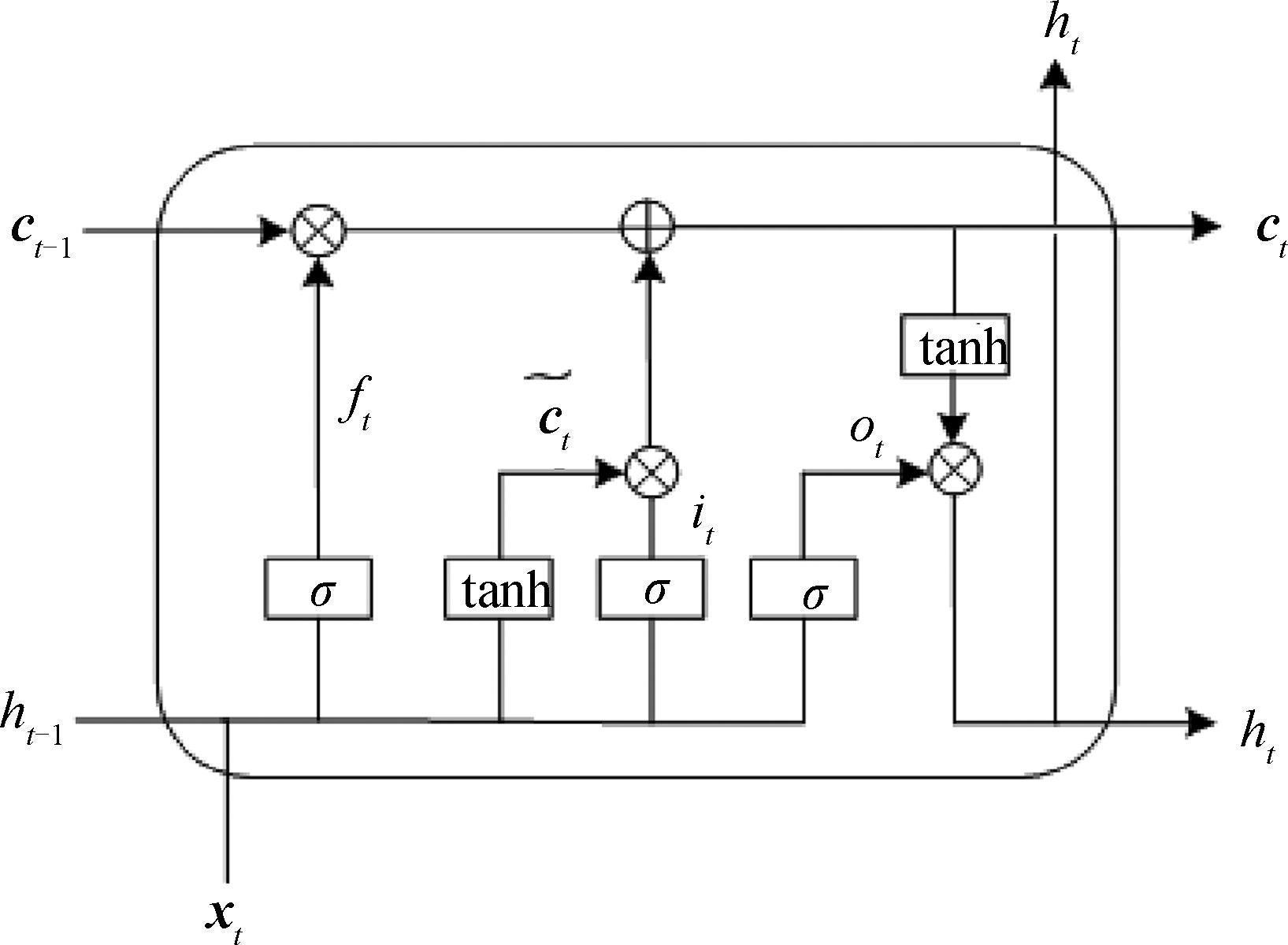
图1 LSTM内部结构图
Figure 1 LSTM internal structure diagram
图1中xt表示t时刻的输入,ht-1表示上一时刻的输出,σ表示sigmoid激活函数,ct-1为上一时刻记忆单元的值,与神经网络类似,LSTM是依靠记忆单元实现“记忆”功能。与神经网络不同的是,LSTM并没有直接将记忆单元送入下一时刻的输入,而是通过输入门、遗忘门和输出门等门控机制来控制信息的传输与更新。输入门、遗忘门和输出门的作用机制在这里不再赘述。
LSTM的预测精度与时间步长的选择息息相关,根据表1可知,输入时间步长为7时效果最好;随着输出时间步长的增大,模型预测的准确率会随之下降[20]。因此,在采用LSTM模型进行风电功率预测时,宜选用单步预测的方式。单步预测的输出为当前时刻的功率值。本文构建了一种滚动预测模型,通过滑动窗口的方式调整输入,具体过程如图2所示。当要预测t时刻的功率值时,使用t-6,t-5,…,t-1,t时刻的特征值作为输入,输出为t时刻的风电预测功率。
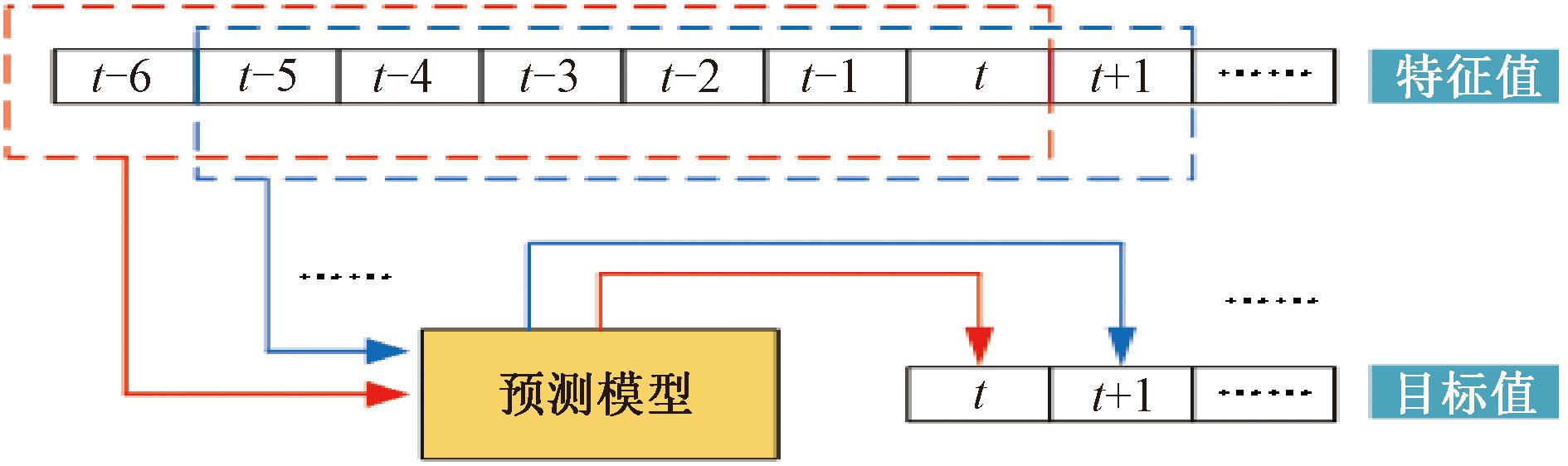
图2 单步滚动预测方式
Figure 2 Single-step rolling prediction method
2.2 粒子群优化算法
粒子群优化算法(particle swarm optimization, PSO)从鸟群觅食的行为中得到启发,基于鸟群中个体之间的协作和信息共享的思想,将鸟抽象为粒子,将食物抽象为所要搜索的最优解[21]。
设目标搜索空间维度为N,群体中共有M个粒子,则在第t次迭代时,粒子i搜索过程为
Xi(t)={xi1(t),xi2(t),…,xiN(t)};
(3)
Vi(t)={vi1(t),vi2(t),…,viN(t)};
(4)
pbest(t)={pi1(t),pi2(t),…,piN(t)};
(5)
gbest(t)={gi1(t),gi2(t),…,giN(t)};
(6)
vik(t+1)=ωvik(t)+a1r1(pik(t)-xik(t))+
a2r2(gik(t)-xik(t))。
(7)
式中:Xi(t)为粒子所处位置;Vi(t)为粒子飞行速度;pbest为粒子目前发现的最好位置;gbest为整个群体目前发现的最好位置;ω为惯性权重,ω较大时,粒子有较强的全局寻优能力,但容易忽略局部最优;a1、a2为学习因子;r1、r2为(0, 1)上的随机数;k表示N维空间中的第k个维度。
粒子群算法的流程图如图3所示,首先,设置种群数目、惯性权重等参数;除此之外,还应设置粒子的飞行速度范围,以保证粒子不会离开搜索空间。其次,计算每个粒子的适应度并比较,得到当前的个体最优值与全局最优值。在迭代过程中,每个粒子的速度和位置都会发生改变,需要更新个体粒子最佳位置。最后,更新全局粒子最优位置,不断重复直至达到限制条件后结束循环。

图3 粒子群算法流程图
Figure 3 Particle swarm algorithm flow chart
2.3 评价指标
本文选用均方根误差RMSE、平均绝对误差MAE[22]及预测准确率CR来评估模型预测效果。
(8)
(9)
(10)
式中:![]() 和yi分别表示第i个样本的预测值和实际值;m为样本数量;Ci为i时刻开机容量。
和yi分别表示第i个样本的预测值和实际值;m为样本数量;Ci为i时刻开机容量。
3 算例分析
实验所使用的数据来自于2022年KDD杯空间动态风电预测挑战赛数据集,该数据集采集于某风电场的SCADA系统,该风电场由134台风电机组组成,SCADA系统每隔10 min采集一次数据,共245 d的数据量。所采集的数据包含风速、风向、环境温度、机舱温度、机舱方向、叶片浆距角。
预测模型实际运行与代码实现基于Python中的TensorFlow框架;具体实验设备为配备RTX3090显卡、24 GB显存的计算机一台。
3.1 单机组预测
为研究单机组风电功率预测,选取机组1作为实验样本,分析机组1在不同模型下的预测效果。机组1前242 d的功率已知,最后3 d的功率作为待预测值,但提供了后3 d的NWP数据。
LSTM隐含层层数设置为3,利用PSO对3层隐含层的神经元个数进行寻优。在具体应用PSO时加入了相关先验知识,确定LSTM隐含层层数大致在何种范围内表现较为优异,然后在该范围中进行具体寻优,确定最终参数。PSO的目标函数为验证集的均方误差MSEvalid:
(11)
PSO运行结果如图4所示,随着迭代次数的增加,其目标函数值逐渐减小;通过PSO算法,得到3个隐含层最佳神经元个数分别为90,110,60,目标函数最小值为1 578.73。
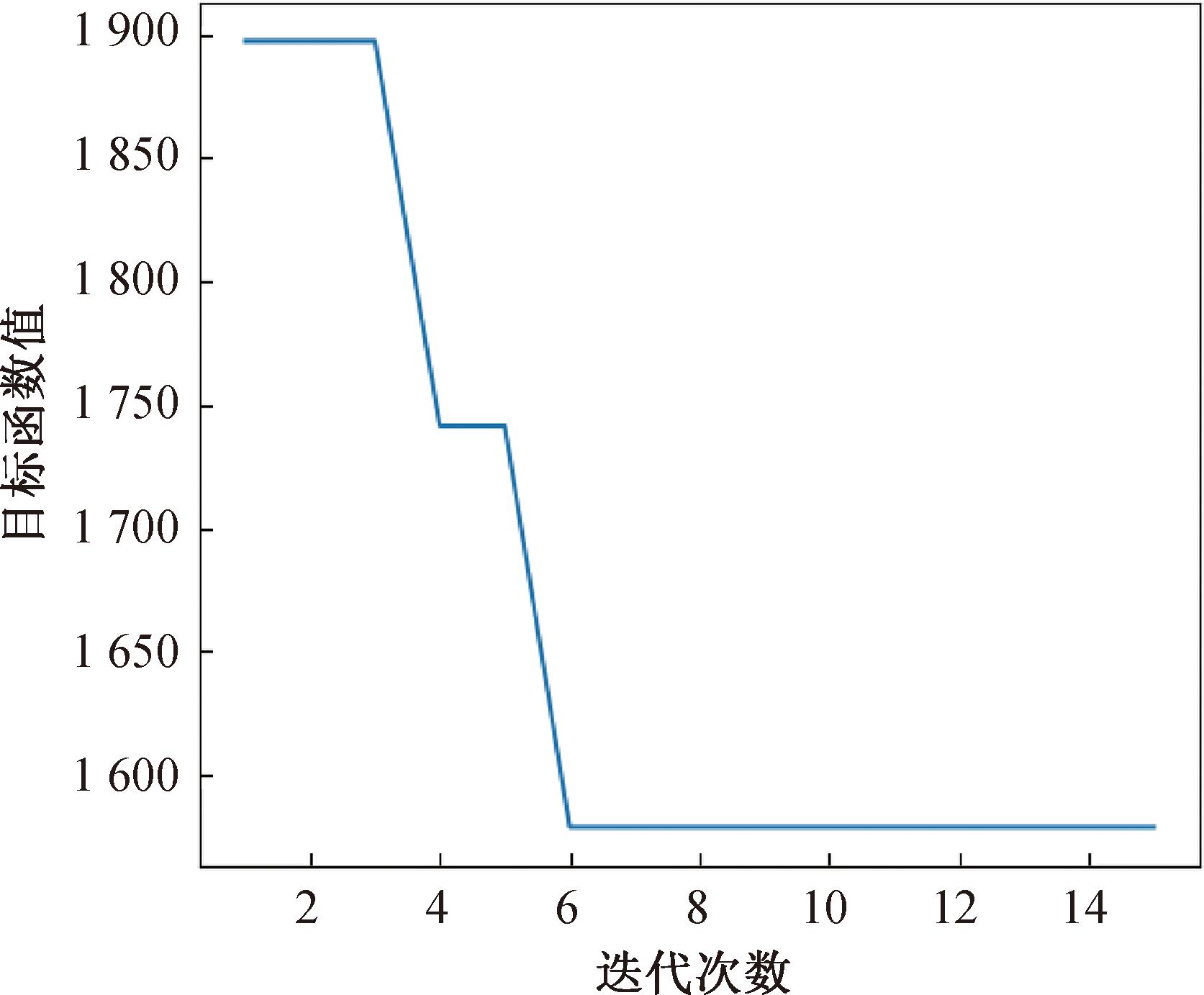
图4 PSO迭代过程
Figure 4 PSO iterative process
为验证PSO寻优的有效性,分别取PSO寻优下界、寻优上界及上下界平均值作为LSTM模型参数进行对比,具体参数如表2所示。
表2 多种LSTM具体参数
Table 2 Specific parameters of various LSTMs

模型神经元个数隐含层1隐含层2隐含层3LSTM1101010LSTM2120120120LSTM3656565PSO-LSTM9011060
采用PSO-LSTM模型,得到预测结果如图5所示。
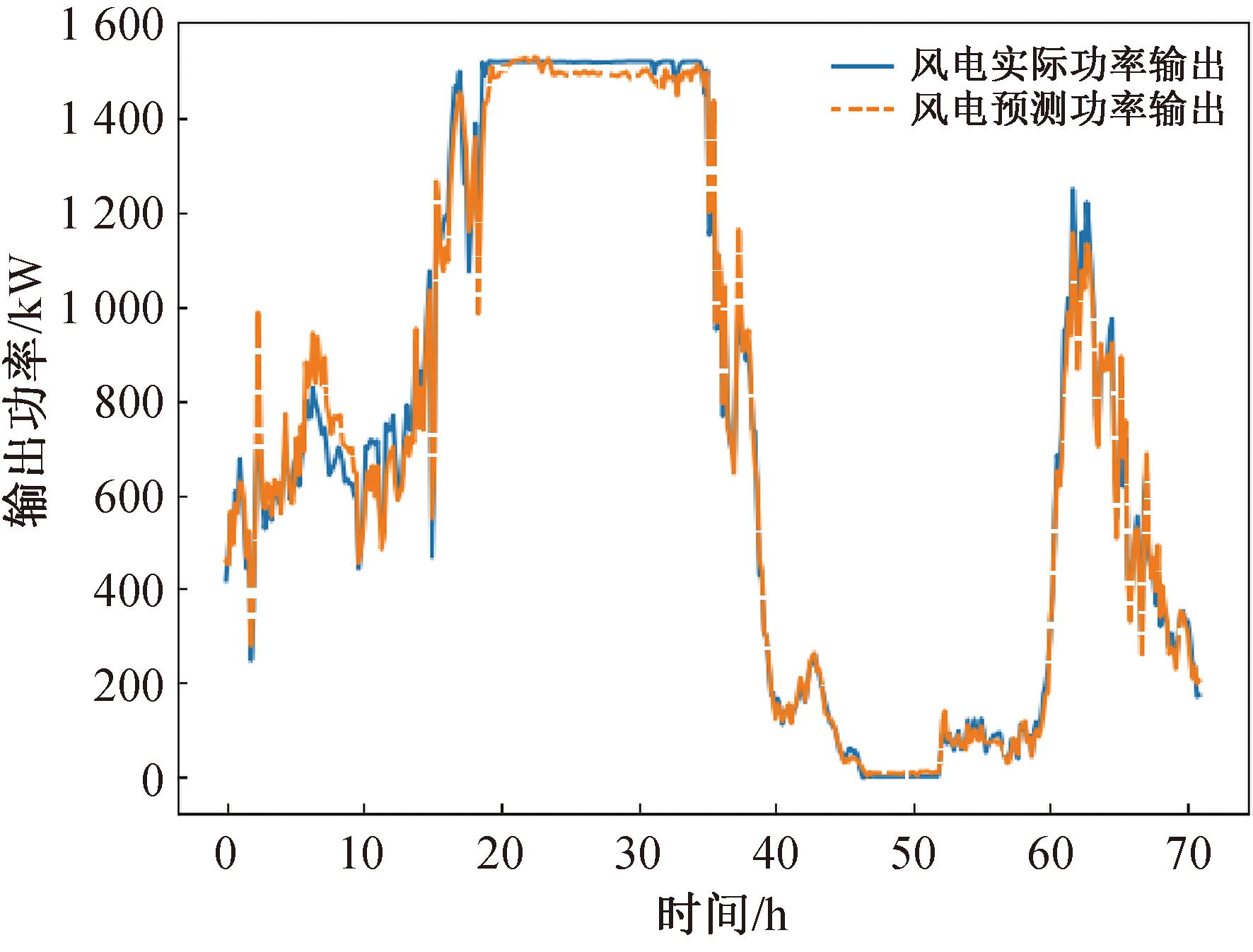
图5 机组1的PSO-LSTM预测结果
Figure 5 PSO-LSTM prediction results of unit 1
为保证模型预测性能评估的客观性,将每个模型均训练10次,并从中去除每个评估指标的最大值与最小值,取8次的平均值后得到相应的评估指标的最终值,并引入VMD-LSTM[23]进行对比实验,所得结果如表3所示。VMD-LSTM方法是通过VMD对预处理后的风电功率数据进行分解,采用LSTM对得到的多个子风电功率数据分量进行训练和预测,最后将预测的子风电功率数据分量加和,得到最终的预测结果。
表3 不同模型机组1的预测结果
Table 3 The prediction results of different model unit 1
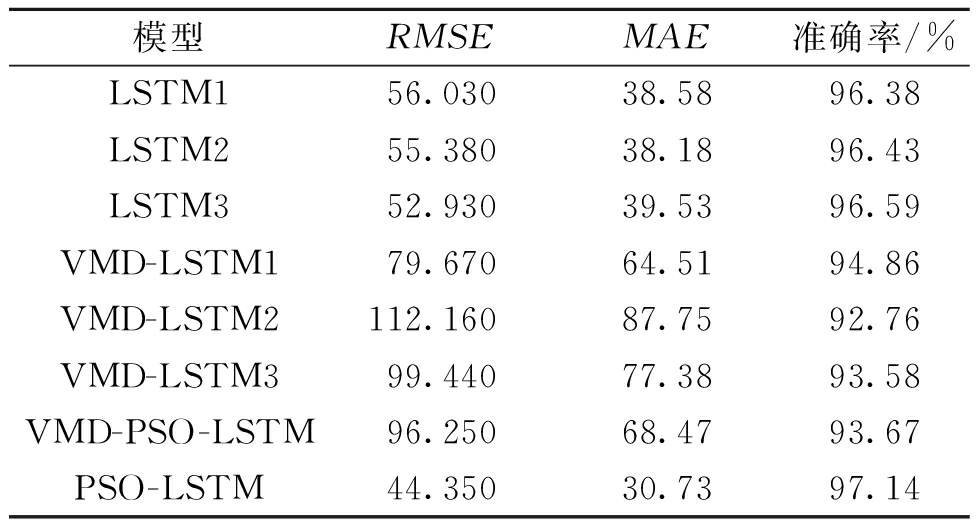
模型RMSEMAE准确率/%LSTM156.03038.5896.38LSTM255.38038.1896.43LSTM352.93039.5396.59VMD-LSTM179.67064.5194.86VMD-LSTM2112.16087.7592.76VMD-LSTM399.44077.3893.58VMD-PSO-LSTM96.25068.4793.67PSO-LSTM44.35030.7397.14
图6为PCA累计方差的贡献率。由图6可知,随着特征数量的增大,其主成分方差累计贡献率也随之增大。当主成分个数为5时,方差累计贡献率已接近100%,因此,在本文中选择的主成分个数为5,即达到了去除冗余特征的目的。为验证PCA特征工程的有效性,采取相应对比实验,并引入训练时间作为评价指标,预测结果如表4所示。
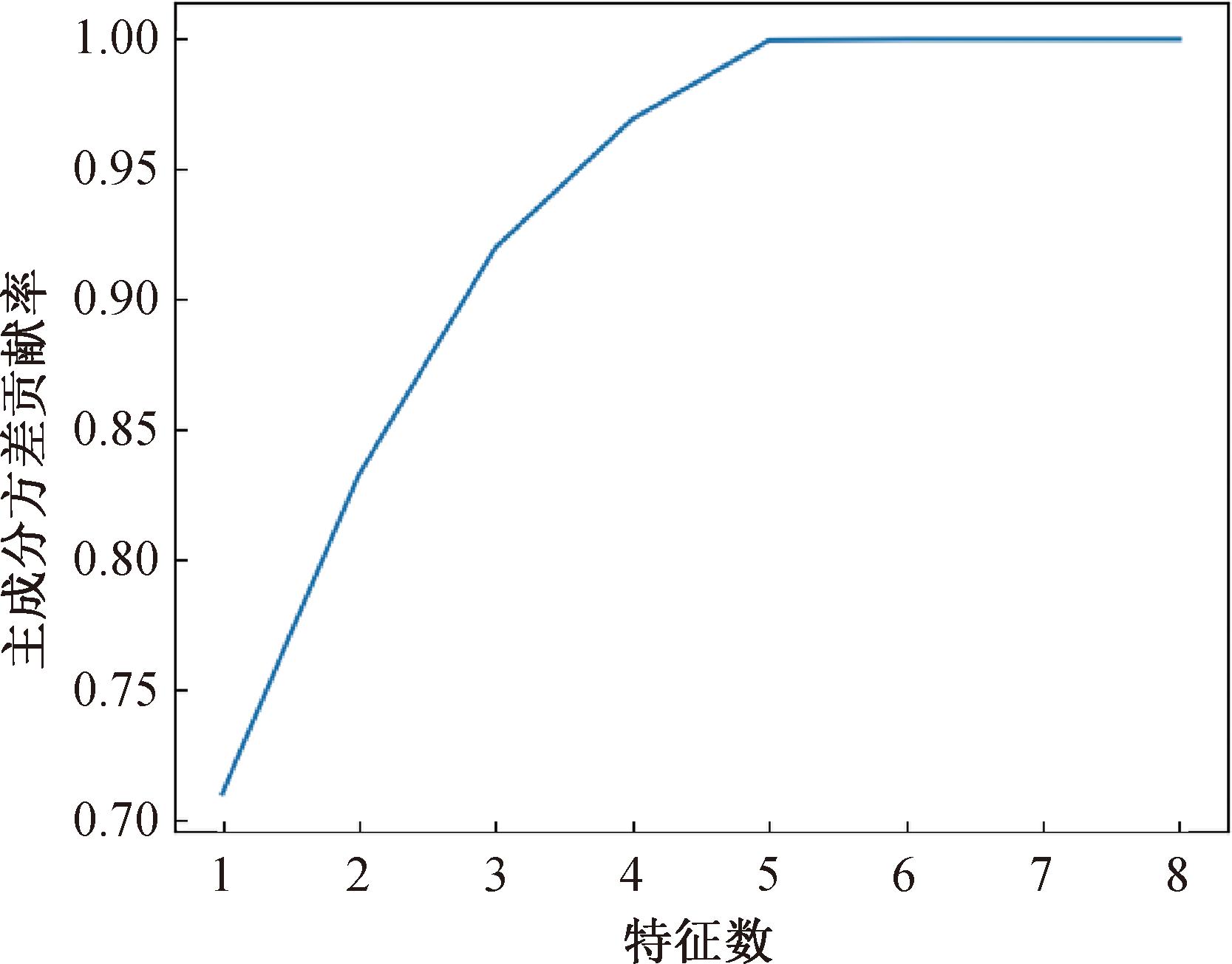
图6 主成分累计方差贡献率
Figure 6 Principal component cumulative variance contribution rate
表4 PCA使用前后预测结果
Table 4 Prediction results before and after using PCA

预测模型RMSEMAE准确率/%训练时间/s使用PCA44.3530.7397.14301.9未使用PCA50.0636.0796.71300.2
由表4可知,经过特征工程PCA后,PSO-LSTM模型的预测准确率更高,预测性能更好,RMSE与MAE相较未采用PCA的LSTM-PSO分别降低了11.4%和14.8%,二者的训练时间基本相同。造成这一现象的原因是在本次实验所使用的数据集中,PCA仅将特征空间从8维降至5维,数据量的减小并不明显;但当数据集的特征数较多时,PCA在训练时间上将取得显著效果,因而,这一方法对风电功率预测相关工作具有一定的借鉴意义。
3.2 多机组预测
通过表3可以看出在单机组功率预测中所提出的PSO-LSTM模型表现较为优异,将该模型应用于多机组风电功率预测,通过多角度对比实验测试该模型的泛化性能。
实验随机选取8台机组,首先对8台机组分别进行数据清洗,得到完备数据集,其次进行主成分分析,提取重要特征;完成上述步骤后,将数据放入模型中训练,得到最终预测结果,具体流程如图7所示。
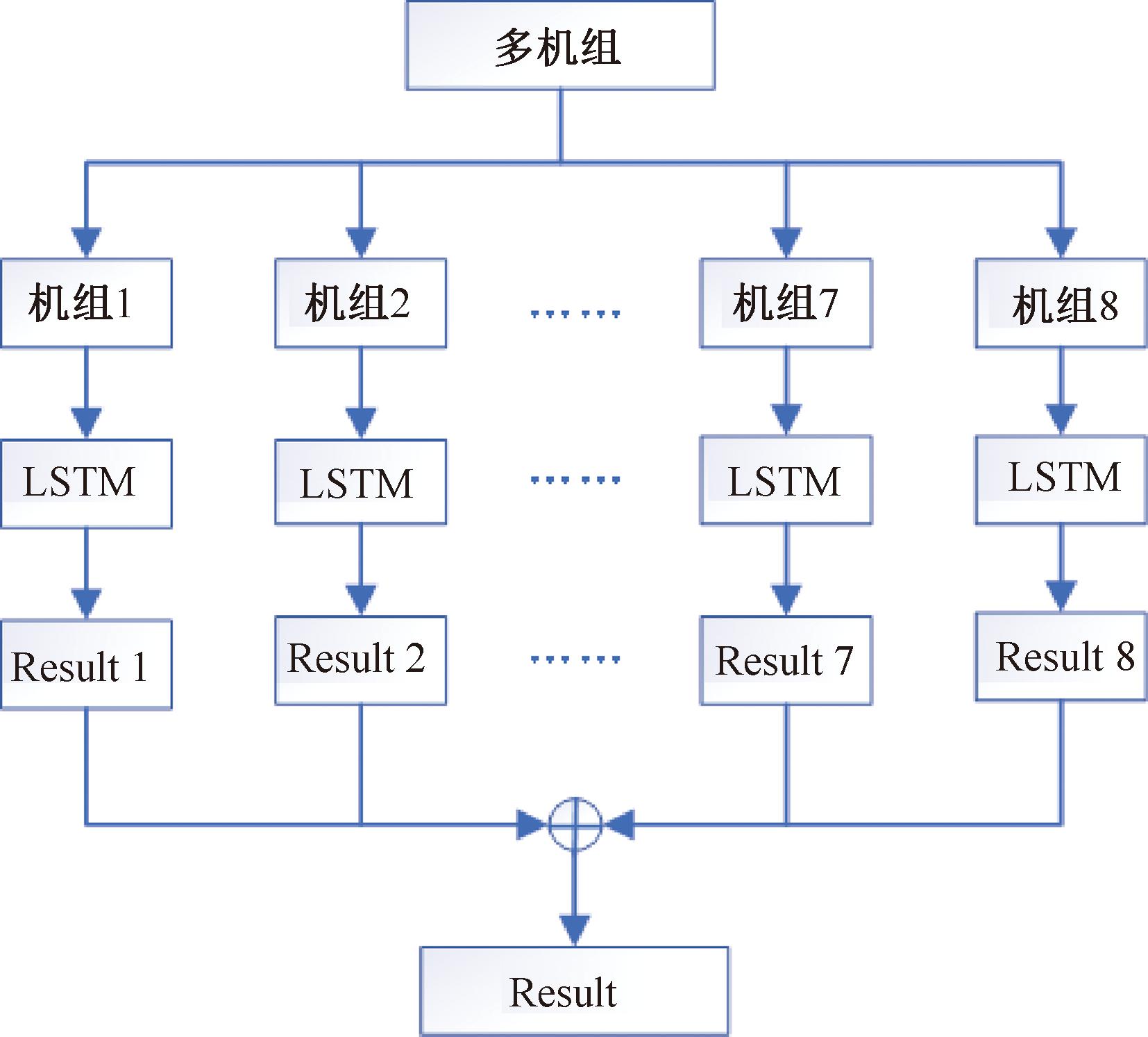
图7 多机组风电功率预测流程图
Figure 7 Multi-unit wind power prediction flow chart
VMD-LSTM在单机组风电功率预测中预测误差较大,归纳其原因[24]主要有:①VMD分解算法在超短期预测中能有较良好表现,在短期预测中预测性能会有所下降;②VMD分解后目标值与特征之间的相关性会被改变,即原先与目标值强相关的特征在时间序列下采样为几个子序列后,该特征与子序列的相关性会降低;③VMD分解结果会有一定的残差分量,即所有的本征模态函数之和并不等于原序列,二者之间相差一个残差项,因而在分解过程中会有一定的信息损失,可能会丢失一些重要信息。
因此在多机组预测中,不再引入VMD-LSTM模型进行对比实验。使用LSTM1、LSTM2、LSTM3及PSO-LSTM进行多机组风电功率预测,所有输入特征均已经PCA降维。图8为使用PSO-LSTM模型对多机组的风电功率预测效果图。分别对每个模型训练10次,去除对应指标最大最小值后取平均值,得到结果如表5所示。
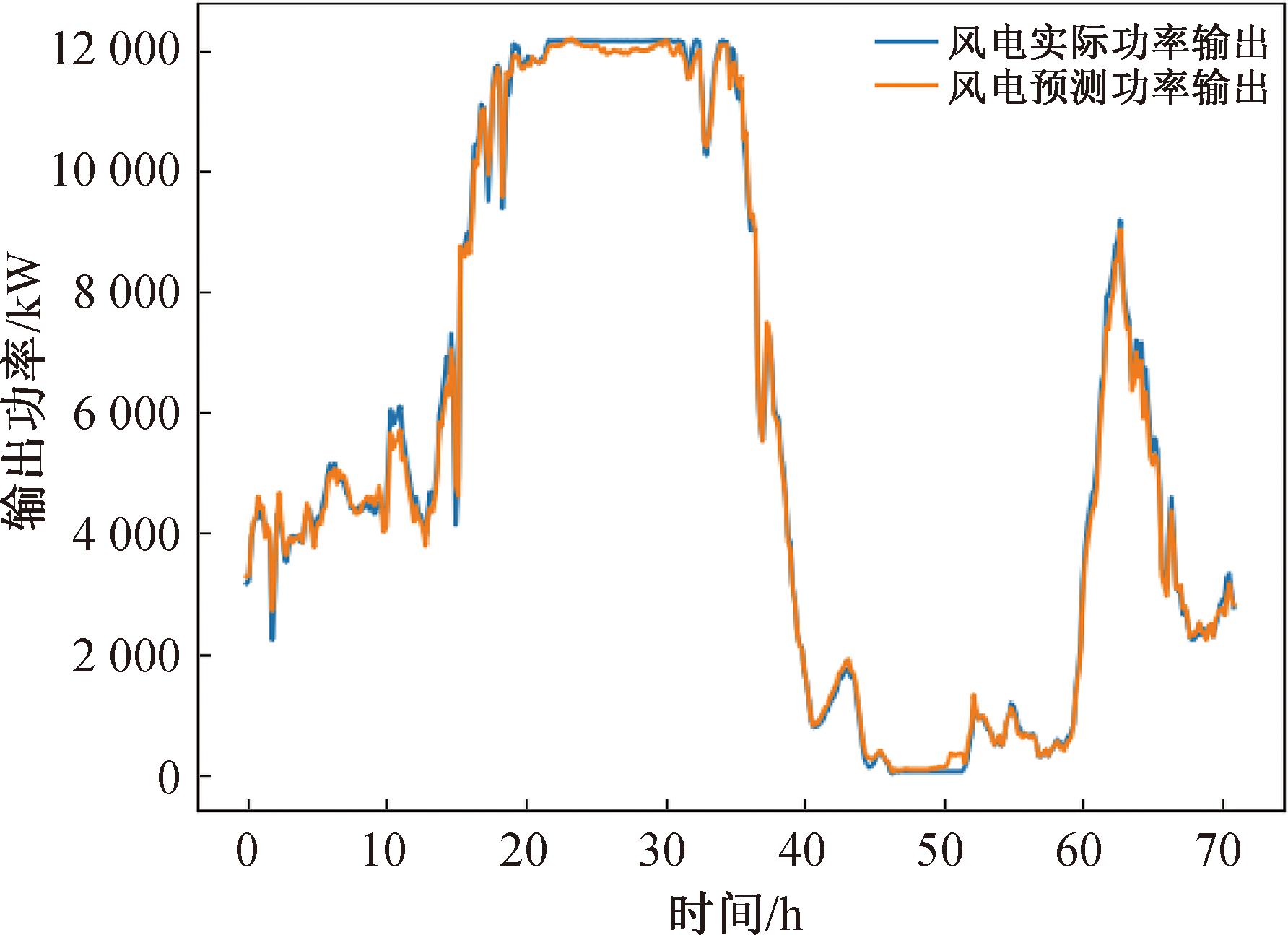
图8 多机组PSO-LSTM预测结果
Figure 8 Multi-unit PSO-LSTM prediction results
表5 不同模型多机组预测结果
Table 5 Multi-unit prediction results of different models
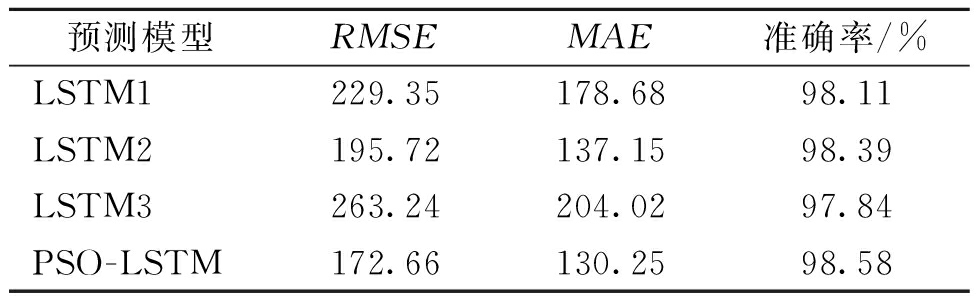
预测模型RMSEMAE准确率/%LSTM1229.35178.6898.11LSTM2195.72137.1598.39LSTM3263.24204.0297.84PSO-LSTM172.66130.2598.58
由表5可见,所提出的PSO-LSTM模型不仅在单机组预测中表现较好,并且在多机组风电功率预测中也取得了最佳的效果,具体表现为其RMSE相较表现最优的LSTM2降低了11.8%,MAE相较LSTM2降低了5.03%,其准确率也在所有模型中表现最优,达到了98.58%。这表明所提出的PSO-LSTM模型具有较好的泛化能力,它能够更准确地预测风电场未来一段时间内的输出功率,从而提高风电站运行效率,降低发电成本。通过PSO对LSTM的隐含层1~3神经元个数等参数进行优化,能够保证提高LSTM的性能,实现风电预测精度的提高。
需要说明的是,本文提出的PSO-LSTM模型训练所需的时间较常规LSTM模型训练所需的时间有较大的增加,这是由于PSO算法中种群更新和迭代进化均需要对每一个个体的LSTM进行训练。然而,由于计算机硬件的快速发展和云平台的迅速普及,上述时间的差距会逐步缩小,在工程应用中通过部署高配置的计算机硬件或者基于云平台开展算法预测,能够逐步减少训练所需的时间[25]。
4 结论
本文提出了一种基于PSO-LSTM的多机组风电功率预测方法,并取得了显著成效。
(1)针对风能随机性、无序性的特点,采用斯皮尔曼相关系数法对功率时间序列进行量化分析,其次采用PCA对输入特征进行降维,通过实验证明PCA主成分分析的有效性。
(2)构建了多元特征输入,通过结合NWP数据与历史数据,构建多元特征,来驱动LSTM实现预测。
(3)在搭建LSTM模型中,采用单步滚动预测方式以提高预测精度,并且对LSTM模型超参数的选择问题,引入了PSO算法。
(4)使用某风电场实际采集数据对所提出的模型进行验证,大量实验表明,PSO-LSTM模型相较于LSTM、VMD-LSTM等模型具有更佳的性能;同时将单机组预测推广至多机组,以考察模型泛化性能,通过大量实验发现,PSO-LSTM在多机组风电功率预测中也有着最优表现。
[1] ZHAO J, WANG J Z, GUO Z H, et al. Multi-step wind speed forecasting based on numerical simulations and an optimized stochastic ensemble method[J]. Applied Energy, 2019, 255: 113833.
[2] NAIK J, DASH S, DASH P K, et al. Short term wind power forecasting using hybrid variational mode decomposition and multi-kernel regularized pseudo inverse neural network[J]. Renewable Energy, 2018, 118: 180-212.
[3] SHARIFIAN A, GHADI M J, GHAVIDEL S, et al. A new method based on type-2 fuzzy neural network for accurate wind power forecasting under uncertain data[J]. Renewable Energy, 2018, 120: 220-230.
[4] ZHANG F, LI P C, GAO L, et al. Application of autoregressive dynamic adaptive (ARDA) model in real-time wind power forecasting[J]. Renewable Energy, 2021, 169: 129-143.
[5] 张颖超, 成金杰, 邓华, 等. 基于相似日和特征提取的短期风电功率预测[J]. 郑州大学学报(工学版), 2020, 41(5): 44-49.ZHANG Y C, CHENG J J, DENG H, et al. Short-term wind power prediction based on similar day and feature extraction[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(5): 44-49.
[6] 朱俊丞, 杨之乐, 郭媛君, 等. 深度学习在电力负荷预测中的应用综述[J]. 郑州大学学报(工学版), 2019, 40(5): 13-22.ZHU J C, YANG Z L, GUO Y J, et al. Deep learning applications in power system load forecasting: a survey[J]. Journal of Zhengzhou University (Engineering Science), 2019, 40(5): 13-22.
[7] ZHANG J H, YAN J, INFIELD D, et al. Short-term forecasting and uncertainty analysis of wind turbine power based on long short-term memory network and Gaussian mixture model[J]. Applied Energy, 2019, 241: 229-244.
[8] KISVARI A, LIN Z, LIU X L. Wind power forecasting:a data-driven method along with gated recurrent neural network[J]. Renewable Energy, 2021, 163: 1895-1909.
[9] ZHANG Y G, PAN G F, CHEN B, et al. Short-term wind speed prediction model based on GA-ANN improved by VMD[J]. Renewable Energy, 2020, 156: 1373-1388.
[10] FU W L, FANG P, WANG K, et al. Multi-step ahead short-term wind speed forecasting approach coupling variational mode decomposition, improved beetle antennae search algorithm-based synchronous optimization and Volterra series model[J]. Renewable Energy, 2021, 179: 1122-1139.
[11] NAIK J, DASH P K, DHAR S. A multi-objective wind speed and wind power prediction interval forecasting using variational modes decomposition based multi-kernel robust ridge regression[J]. Renewable Energy, 2019, 136: 701-731.
[12] LIU H, MI X W, LI Y F, et al. Smart wind speed deep learning based multi-step forecasting model using singular spectrum analysis, convolutional gated recurrent unit network and support vector regression[J]. Renewable Energy, 2019, 143: 842-854.
[13] 李静茹, 姚方. 引入注意力机制的CNN和LSTM复合风电预测模型[J]. 电气自动化, 2022, 44(6): 4-6.LI J R, YAO F. Integrated CNN and LSTM wind power prediction modelwith the introduction of attention mechanism[J]. Electrical Automation, 2022, 44(6): 4-6.
[14] BENTSEN L Ø, WARAKAGODA N D, STENBRO R, et al. Spatio-temporal wind speed forecasting using graph networks and novel transformer architectures[J]. Applied Energy, 2023, 333: 120565.
[15] 黄秋娟. 基于注意力机制的风电功率预测[D]. 重庆: 重庆大学, 2022.HUANG Q J. Wind power prediction based on attention mechanism[D].Chongqing: Chongqing University, 2022.
[16] 吴珺玥, 赵二刚, 郭增良, 等. 基于Spearman系数和TCN的光伏出力超短期多步预测[J]. 太阳能学报, 2023, 44(9): 180-186.WU J Y, ZHAO E G, GUO Z L, et al. Ultra-short-term photovoltaic power multi-step prediction based on Spearman coefficient and TCN[J]. Acta Energiae Solaris Sinica, 2023, 44(9): 180-186.
[17] 余光正, 陆柳, 汤波, 等. 考虑转折性天气的海上风电功率超短期分段预测方法研究[J]. 中国电机工程学报, 2022, 42(13): 4859-4871.YU G Z, LU L, TANG B, et al. Research on ultra-short-term subsection forecasting method of offshore wind power considering transitional weather[J]. Proceedings of the CSEE, 2022, 42(13): 4859-4871.
[18] 刘洋. 基于NWP数据优化下的风电场功率预测算法研究[D]. 太原: 太原科技大学, 2021.LIU Y. Wind farm power prediction algorithm based on NWP data optimization[D].Taiyuan: Taiyuan University of Science and Technology, 2021.
[19] 王丽婕, 冬雷, 高爽. 基于多位置NWP与主成分分析的风电功率短期预测[J]. 电工技术学报, 2015, 30(5): 79-84.WANG L J, DONG L, GAO S. Wind power short-term prediction based on principal component analysis of NWP of multiple locations[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 79-84.
[20] 赵晓阳. 基于神经网络的空气质量预测模型构建研究[D]. 包头: 内蒙古科技大学, 2020.ZHAO X Y. Research on construction of air quality forecast model based on neural network[D].Baotou: Inner Mongolia University of Science &Technology, 2020.
[21] 黄峰, 向书琛, 王睿, 等. 一种基于VMD-PSO-SVM的短期风电功率预测算法[J]. 湖南工程学院学报(自然科学版), 2022, 32(2): 7-12.HUANG F, XIANG S C, WANG R, et al. A design of PSO-SVM short-term wind power forecasting algorithm based on VMD[J]. Journal of Hunan Institute of Engineering (Natural Science Edition), 2022, 32(2): 7-12.
[22] 刘洪波, 盖雪扬, 孙黎, 等. 计及数据降维和数据清洗的超短期风电功率预测[J]. 东北电力大学学报, 2023, 43(4): 1-9.LIU H B, GAI X Y, SUN L, et al. Ultra-short-term wind power prediction considering data reduction and data cleaning[J]. Journal of Northeast Electric Power University, 2023, 43(4): 1-9.
[23] 黄志祥, 周莉. 基于VMD-LSTM的短期电力负荷预测研究[J]. 洛阳理工学院学报(自然科学版), 2022, 32(3): 76-80, 96.HUANG Z X, ZHOU L. Research on short term load forecasting based on VMD-LSTM[J]. Journal of Luoyang Institute of Science and Technology (Natural Science Edition), 2022, 32(3): 76-80, 96.
[24] QIAN Z, PEI Y, ZAREIPOUR H, et al. A review and discussion of decomposition-based hybrid models for wind energy forecasting applications[J]. Applied Energy, 2019, 235: 939-953.
[25] HOURAN M A, BUKHARI S M S, ZAFAR M H, et al. COA-CNN-LSTM: coati optimization algorithm-based hybrid deep learning model for PV/wind power forecasting in smart grid applications[J]. Applied Energy, 2023, 349: 121638.