近年来,旱涝极端水文事件给各国带来了巨大的经济损失和人员伤亡[1],其重要原因之一是缺乏准确的旱涝预警信息。另外,随着人类活动的加剧[2],流域径流受到间歇性径流、地下水过度开采和水质恶化等问题的困扰,对流域生态环境和可持续发展带来了巨大挑战[3]。因此,探究径流演变模式并进行精准预测势在必行。
由于径流序列预测周期长,影响因素多,且具有较强的非线性和非平稳性,使得传统方法或是机器学习对于原始序列的预测效果不佳。通过适当的分解技术对原始数据进行预处理,可以过滤干扰和混合噪声,提高模型预测精度[4]。雷庆文等[5]使用基于加权回归的季节趋势分解(seasonal-trend decomposition using loess,STL)和CNN(convolutional neural networks)-LSTM(long short term memory)的组合模型对月径流量进行了预测,发现经过分解预处理的数据预测效果显著提高。
一次分解技术虽然可以提高模型的预测能力,但其对数据的随机性、规则性和非平稳性不能很好地处理,特别是对数据序列中较大异常值的预测效果不够好。因此,有学者提出二次分解技术。王文川等[6]基于CEEMD(complementary ensemble empirical mode decomposition)-VMD(variational mode decomposition)的组合分解方法,结合BP神经网络(back propagation neural network)模型研究了月尺度径流量的预测,发现加入VMD方法后的二次分解模型的预测精度高于一次分解模型。除了分解方法的选择及其不同的组合,使用不同的基础预测模型也会对径流序列的预测精度产生影响。Yang等[7]采用基于二次分解的回声状态网络(echo state network,ESN)研究日径流预测,其3个水文站点径流预测的NSE均在0.99以上。
本研究基于二次分解技术的思路,针对径流序列的季节特征,采用STL-VMD的二次分解方法,与支持向量机(support vector machine,SVM)相结合组成STL-VMD-SVM模型,开展伊洛河流域黑石关站月径流预测,并在黄河干流高村站验证该模型的普适性。
1 研究区概况及数据
伊洛河流域面积约为18 800 km2,跨越陕西和河南两省21个县市[8],流域上游以土石山区为主,下游以低山丘陵、河谷平原为主,分别占流域总面积的约50%,40%和10%。伊洛河地处湿润半湿润地区,是黄河流域重要的水源涵养区之一,流域年平均气温为12~14 ℃,年平均降雨量约为680 mm,降雨主要集中在5—10月份,占全年降水量的80%以上,年平均日照时数为2 291.6 h[9]。图1为所绘制的伊洛河流域分布概况图。
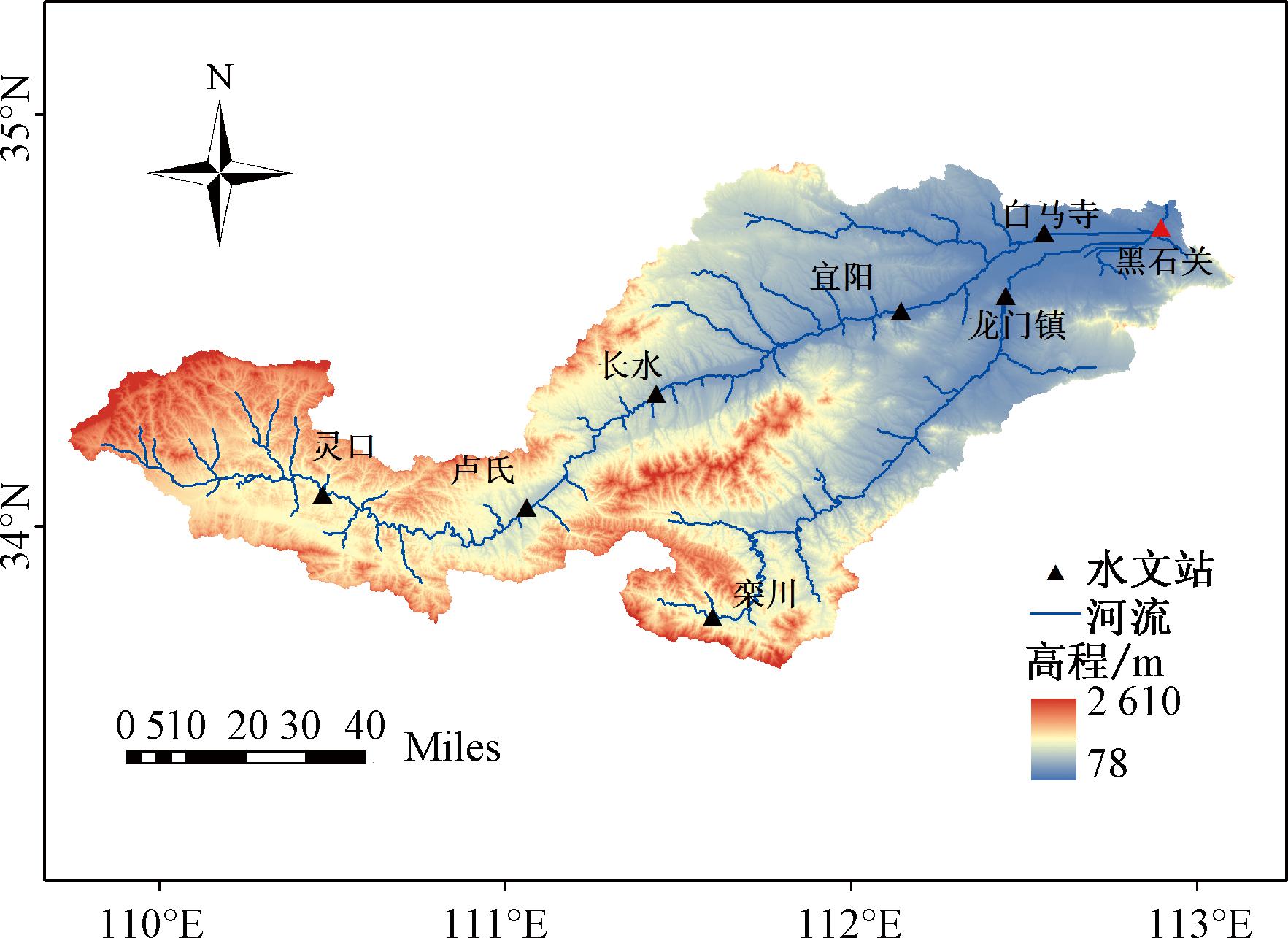
图1 伊洛河流域概况图
Figure 1 Overview of the Yiluo River Basin
本文以黑石关水文站1962年1月至2022年12月实测月径流量资料为研究对象,其中1962年1月至2012年12月为训练期,2013年1月至2022年12月为验证期。
2 研究方法
2.1 自相关分析
前期历史径流输入数的选取会直接影响模型预测结果的准确度。输入量太少,会造成模型模拟准确度不高;输入量太多,会导致模型模拟过拟合[10]。通过对径流时间序列的自相关分析可以粗略判定时间序列中与下一时刻的观测值具有较强相关关系的历史观测数据个数[11]。因此,本文运用SPSS软件,对径流序列进行自相关分析,ACF为自相关值,结果如图2所示。
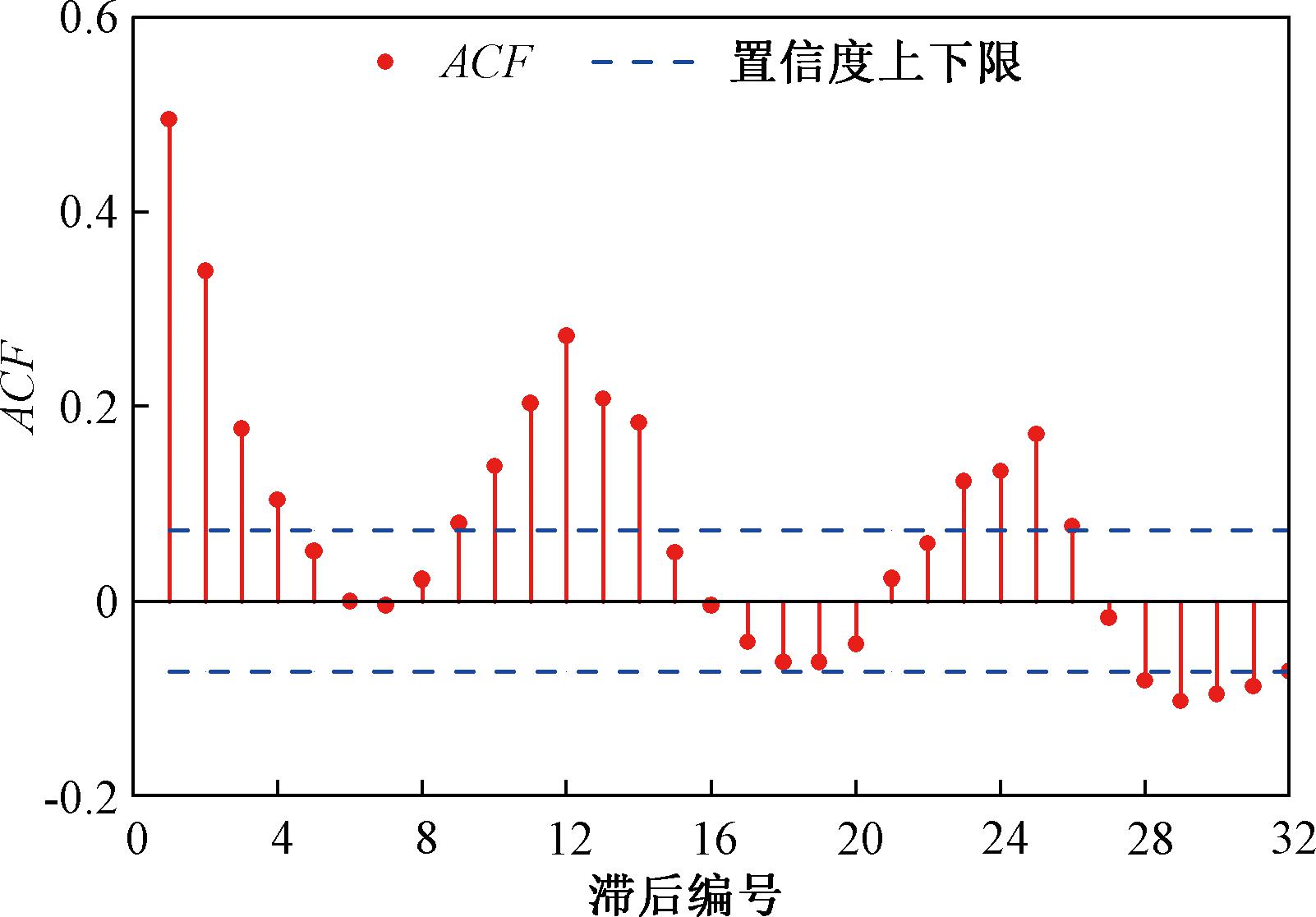
图2 黑石关站实测月径流序列自相关性分析
Figure 2 Autocorrelation analysis of monthly runoff series measured at Heishiguan station
由图2可知,某一径流量与其前推第1,2,12个相关性最大,受其影响最深。径流预测需要一定的历史资料数据,本文选择输入历史资料个数为12(即前12个数据作为输入,第13个数据作为输出)。
2.2 STL
基于局部多项式拟合回归的STL计算效率高,对趋势项和季节项的鲁棒性估计能力强[12]。其有加法和乘法2种模式[7],分解模式分别为
Yt=St+Tt+Rt;
(1)
Yt=StTtRt。
(2)
式中:Yt为原始时间序列;St为季节分量;Tt为趋势分量;Rt为残差分量。
分别使用加法和乘法建立组合模型,得到的预测精度如表1所示,虽然加法模型的RMSE比乘法模型小,但是其MAPE过大,NSE也不如乘法模型高,所以认为整体预测精度不如乘法模型。因此,使用式(2)对时间序列进行分解。
表1 STL两种分解模式预测精度对比
Table 1 Comparison of prediction accuracy between two decomposition modes of STL

STL分解模式训练期验证期RRMSEMAPE/%NSERRMSEMAPE/%NSE加法0.9830.17161.1490.9660.9740.16871.0250.949乘法0.9920.36115.8570.9830.9910.32713.7050.977
2.3 VMD
VMD由Dragomiretskiy等[13]提出,其将原始信号分解为一组离散模态分量,具有高度自适应性和较强的鲁棒性,能够有效去噪[14]。具体步骤如下。
步骤1 利用希尔伯特变换计算各子序列的关联解析信号uk(t),得到其单边频谱。
步骤2 将各子序列及其对应的中心频率ωk调整到相应的基带。
步骤3 通过解调信号的高斯平滑度估计频率带宽。带宽和中心频率有条件限制,即满足每个子序列的估计带宽之和最小化,因此,约束变分问题[15]如式(3)所示:
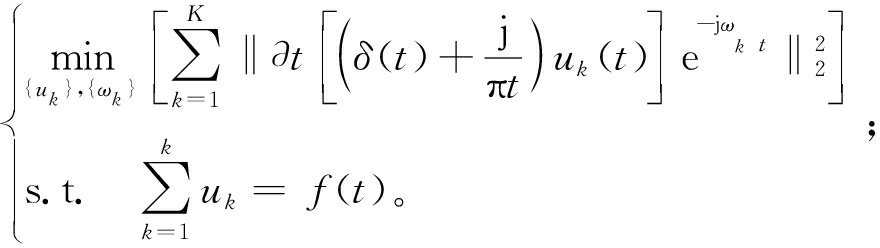
(3)
式中:f(t)为原始序列;uk为f(t)的第k个分量;ωk为uk的中心频率;δ(t)为狄拉克分布;K为模态数;t为时间;‖·‖表示向量的范数;∂t表示带宽;j为虚数单位,用于表示复数形式的函数。
通过添加二次惩罚因子α和拉格朗日乘子λ可将式(3)转化为无约束问题,然后利用交替方向乘子法对其进行求解。uk和ωk的解表示为
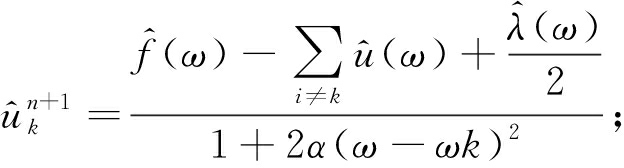
(4)
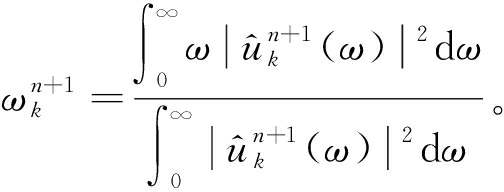
(5)
式中:n为迭代次数;![]() 和
和![]() 分别为f(t)、ui(t)、λ(t)和
分别为f(t)、ui(t)、λ(t)和![]() 的傅里叶变换。
的傅里叶变换。
2.4 SVM
SVM在解决非线性问题方面具有独特优势[16],与传统的人工神经网络等方法相比,SVM在很大程度上解决了过拟合、非线性、高维度和局部极小值问题[17],广泛应用于径流预测领域。它通过核函数实现非线性向线性问题的变换,并将支持向量机的学习过程转化为易计算的凸优化[18]问题:
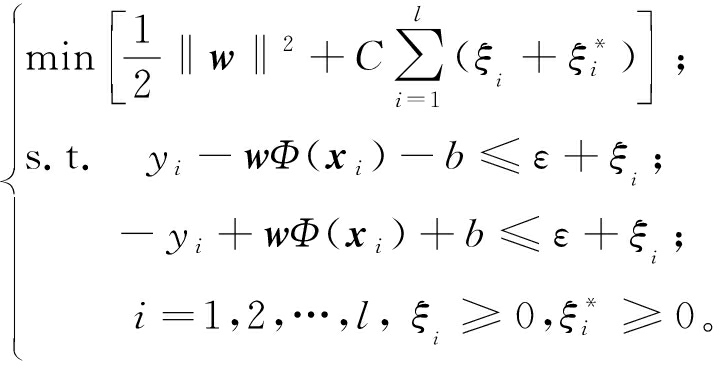
(6)
最终回归函数为
(7)
式中:Φ(x)为非线性映射函数;w为方向向量;b为回归函数截距;ε为不敏感系数;K(xi,xj)=Φ(xi)Φ(xj)为满足Mercer条件的核函数;xi与xj为样本向量;yi代表训练样本的类别。![]() 为松弛变量;
为松弛变量;![]() 和ai为二次规划中的拉格朗日乘子。
和ai为二次规划中的拉格朗日乘子。
SVM的性能受核函数、惩罚因子C和核参数g的影响。径向基核函数(radial basis function,RBF)参数相对较少又可以很好地处理高维复杂样本问题[19]。其表达形式为
K(x,xi)=e-g‖x-xi‖2。
(8)
2.5 评价指标
为了衡量模型的预测效果,本文选取均方根误差RMSE、纳什系数NSE、平均绝对百分比误差MAPE和相关系数R来评价模型的预测精度。RMSE、NSE、MAPE和R的计算公式[6]如下:
(9)
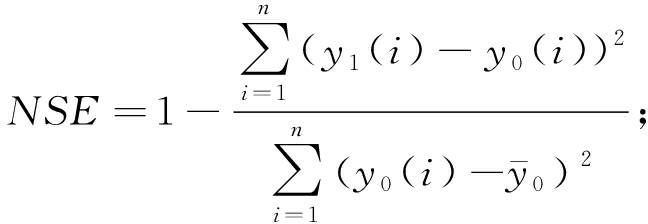
(10)
(11)
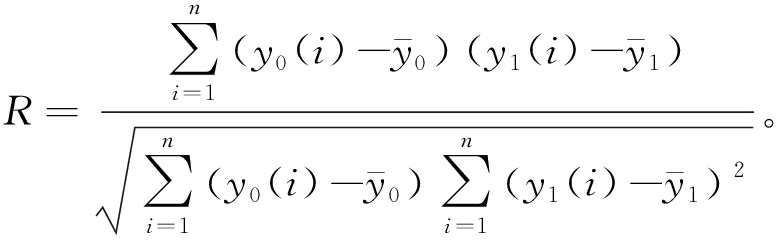
(12)
式中:y1(i)和y0(i)分别为预测值和实测值;![]() 和
和![]() 分别为两者的平均值;n为样本总数。
分别为两者的平均值;n为样本总数。
2.6 组合模型预测流程
预测模型流程如图3所示。
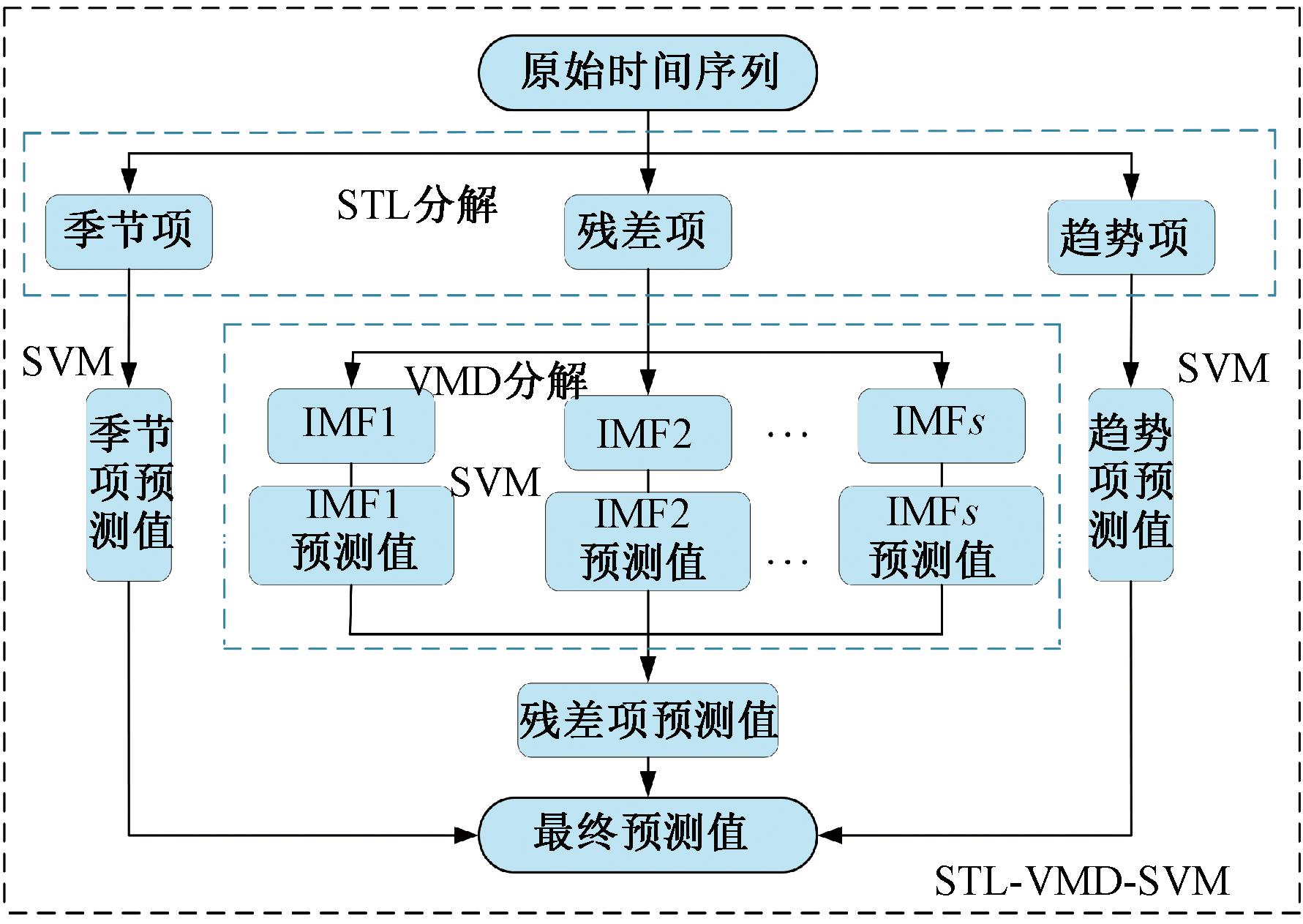
图3 组合预测模型流程
Figure 3 Combined prediction model process
首先,利用STL将原始径流序列分解为不同频率的季节项、趋势项和残差项。其次,通过VMD将STL分解出的残差项进一步分解为一系列分量IMFs。再次,建立SVM模型预测季节项、趋势项和IMFs。最后,所有IMFs的预测值之和为残差项的预测值,季节项、趋势项和残差项之积为原始径流序列的最终预测值。
3 分解及预测结果分析
3.1 STL分解结果
首先对径流时间序列进行STL分解,分解结果如图4所示。趋势项与原始径流序列的变化规律呈现出总体一致性,但趋势项的变化更加平滑,残差项波动呈现随机性,季节项呈现出明显的变化规律。
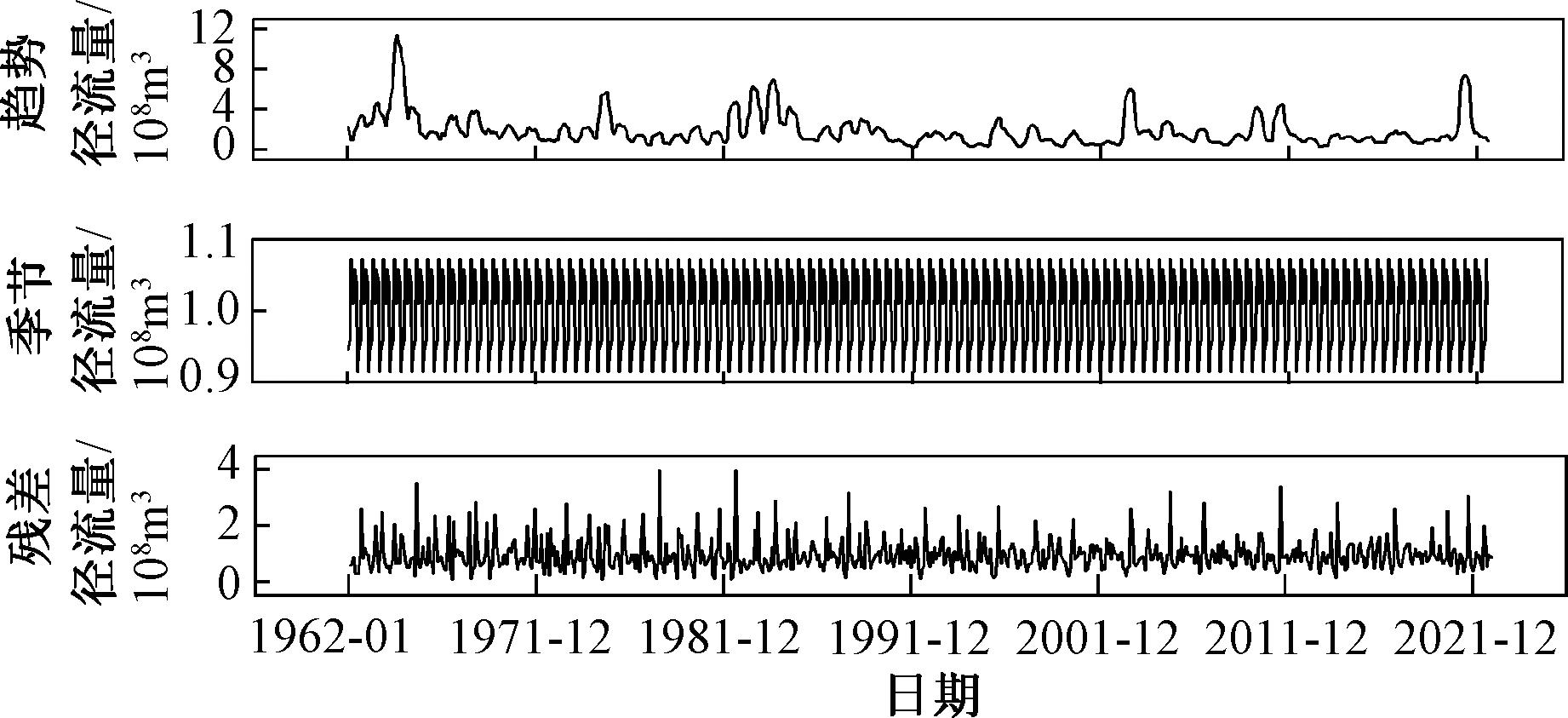
图4 径流时间序列STL分解
Figure 4 STL decomposition of runoff time series
3.2 VMD分解结果
对STL分解出的残差项进行VMD分解。分解时,模态数的选择对于预测效果有较大影响,整体的预测效果主要由分解出的残差量的预测效果决定(除残差分量外其他分量预测效果差别不大),表2是模态数K由2到10分解出的残差量预测的NSE。
表2 不同模态数残差分量预测的NSE
Table 2 NSE prediction of residual components for different modal numbers
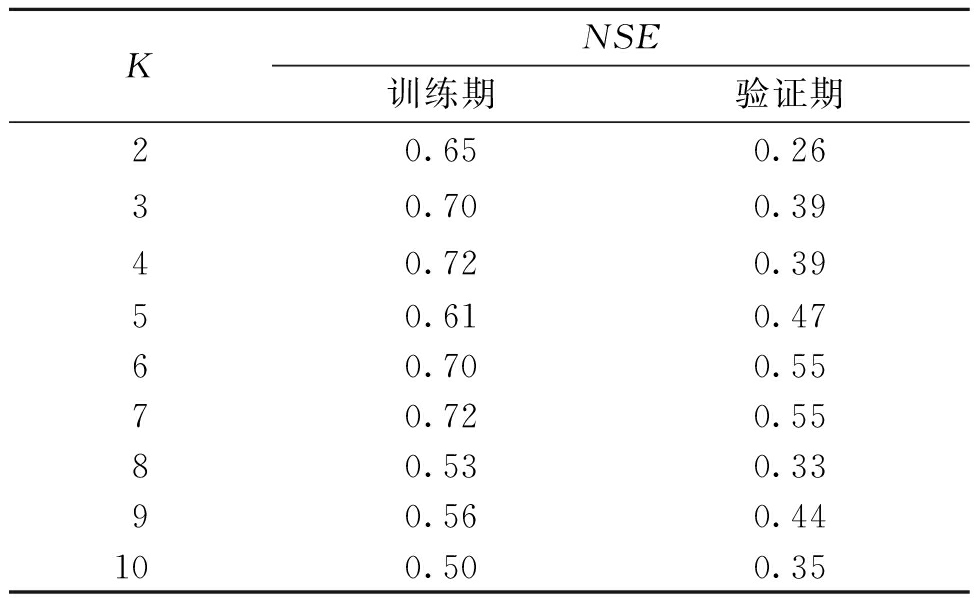
KNSE训练期 验证期20.650.2630.700.3940.720.3950.610.4760.700.5570.720.5580.530.3390.560.44100.500.35
由表2可知,当模态数K为7时训练期和验证期的预测效果最好。所以利用VMD将STL的残差项分解为7个IMFs和1个残差分量,如图5所示。
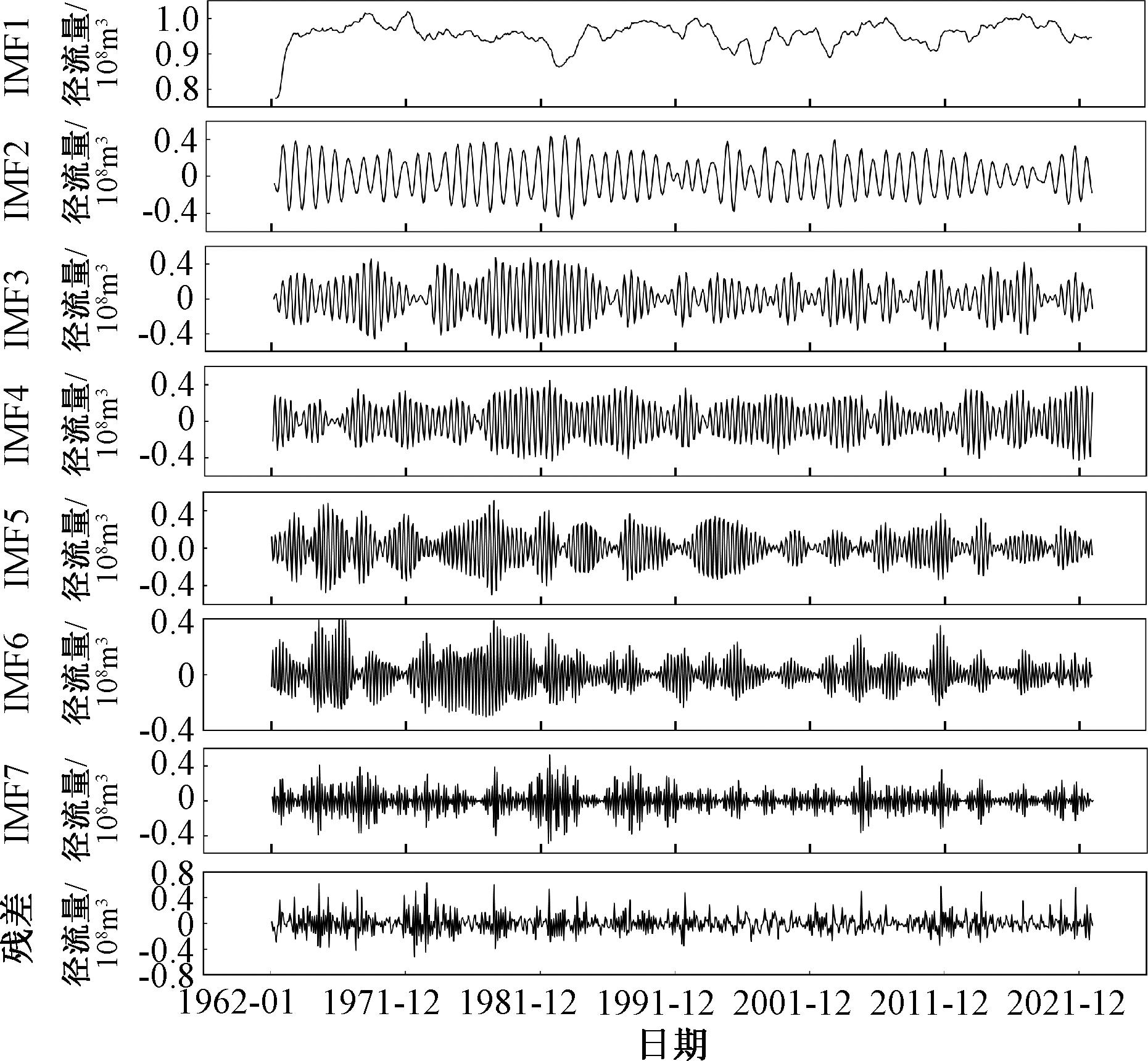
图5 VMD分解结果
Figure 5 VMD decomposition results
3.3 模型预测结果
未分解、一次分解和二次分解3种模型的性能指标值见表3。由表3可知,STL-VMD-SVM组合模型训练期的R、RMSE、MAPE和NSE分别为0.992,0.361,15.857%和0.983;验证期分别为0.991,0.327,13.705%和0.977,4项评价指标均达到预测标准且有较高的精度。与SVM和STL-SVM模型相比,STL-VMD-SVM组合模型的所有评价指标均为最优,一次分解模型的性能均优于未分解的模型。
表3 3种模型的预测评价结果
Table 3 Prediction and evaluation results of three models

预测模型训练期验证期RRMSEMAPE%NSERRMSEMAPE%NSESVM0.6092.12551.6000.3000.4652.17448.4400.168STL-SVM0.8701.25334.6530.7560.8861.14135.6210.771STL-VMD-SVM0.9920.36115.8570.9830.9910.32713.7050.977
表4为经过多次调节试验得出的SVM模型预测各个分量时的惩罚因子C和核参数g的最佳值。
表4 惩罚因子和核参数
Table 4 Penalty factors and kernel parameters
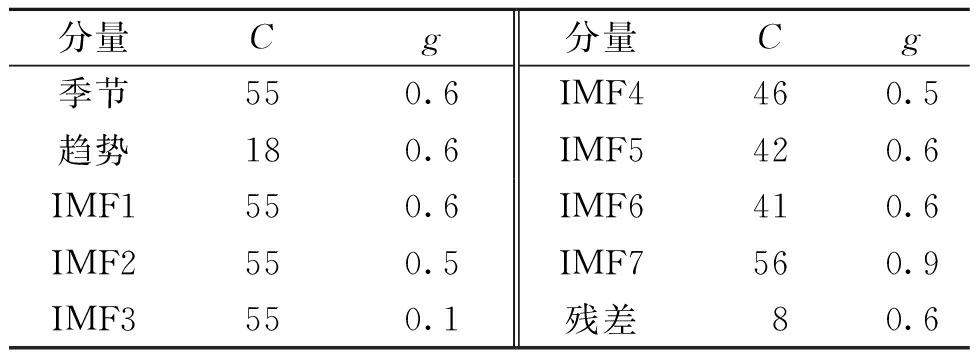
分量Cg分量Cg季节550.6IMF4460.5趋势180.6IMF5420.6IMF1550.6IMF6410.6IMF2550.5IMF7560.9IMF3550.1残差80.6
如图6所示,模型预测值与实测值对比表明,STL-VMD-SVM的组合模型能够较好地学习径流序列的波动规律和极值,对径流极值的模拟效果较好,因此,可以认为基于STL-VMD-SVM的组合模型能够较好地模拟研究区水文站点的径流过程。
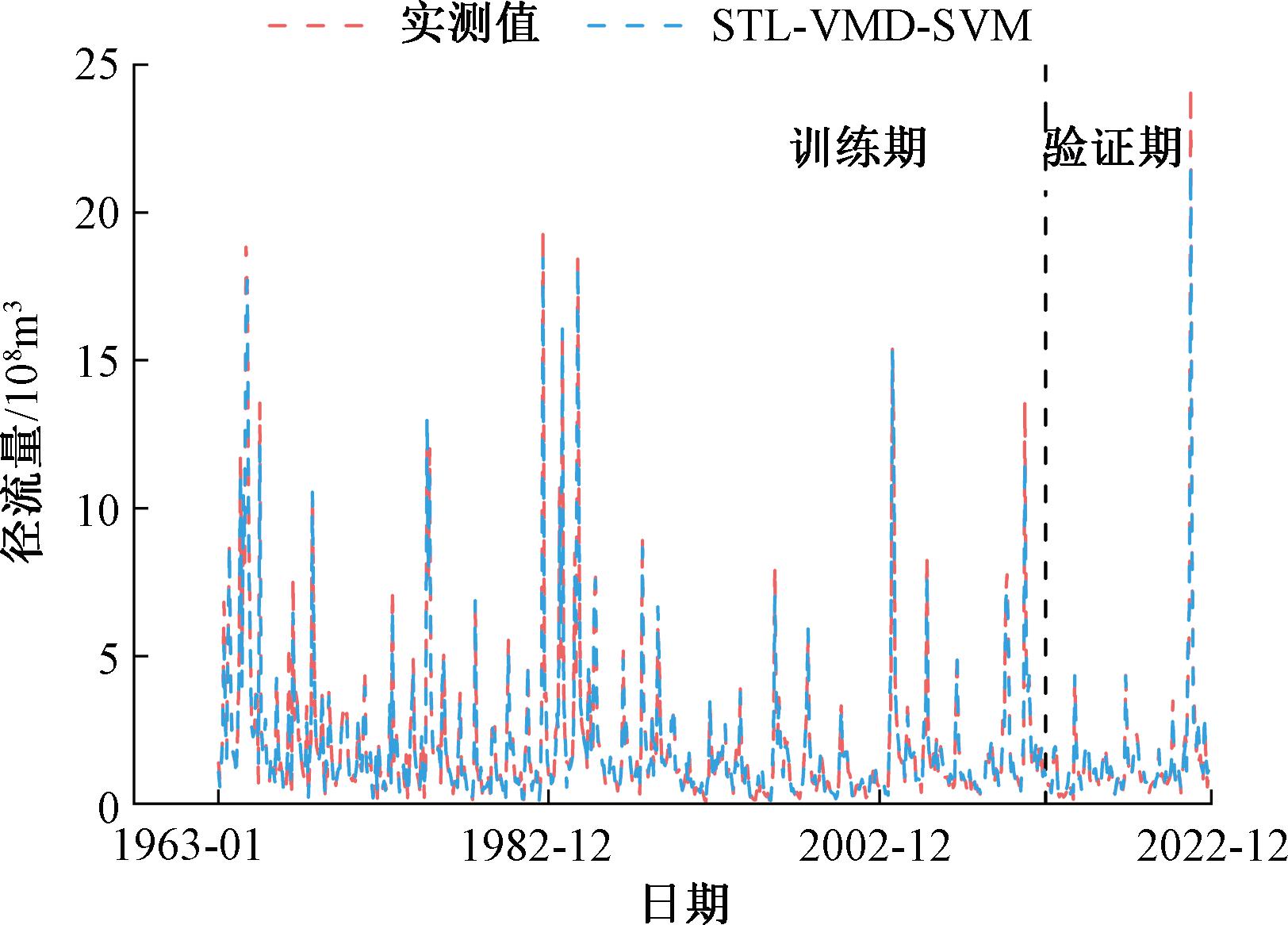
图6 实测值与预测值对比
Figure 6 Comparison between measured and predicted values
为了进一步验证组合模型的有效性,将组合模型的预测结果与SVM模型以及STL-SVM模型的预测结果进行对比。所有模型采用相同的预测输入、参数、训练期以及验证期。
图7展示了验证期3种模型的预测效果。从图7可以看出,相较于SVM模型和STL-SVM模型,STL-VMD-SVM组合模型能更精准地捕获原始径流量的变化特征,大幅度提升了模型预测能力,拟合效果最优。
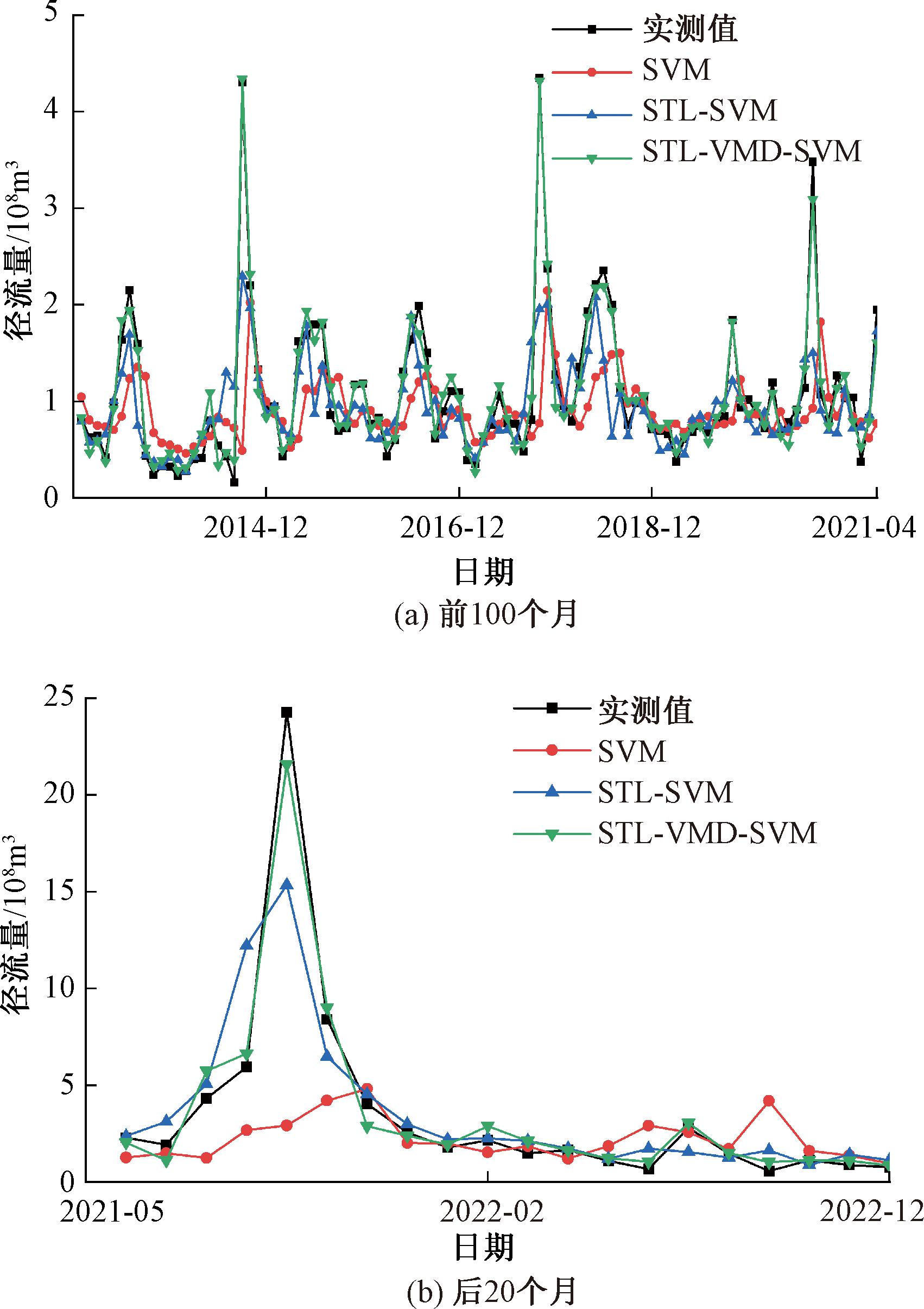
图7 3种模型验证期预测结果对比
Figure 7 Comparison of prediction results of three model validation periods
从图8可以看出,STL-VMD-SVM组合模型预测的最大值、最小值、中位数和异常值与实测值最接近。
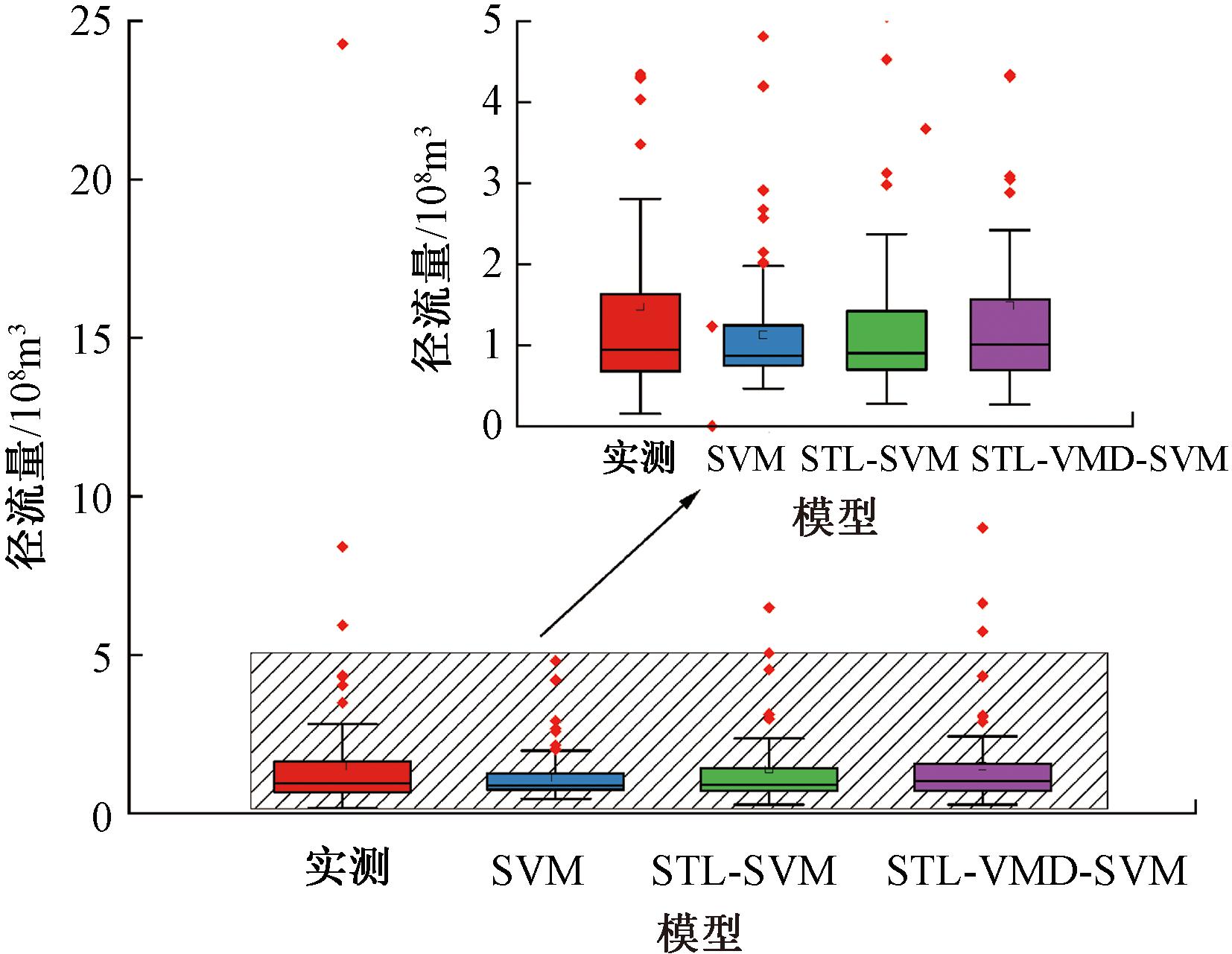
图8 验证期预测结果箱线图
Figure 8 Box plot of validation period prediction results
本文基于二次分解思路的STL-VMD 组合分解方法适用于分解月径流时间序列,采用此方法预处理后的月径流数据作为预测模型的输入,可以有效地消除数据的非平稳特征,有助于提高模型的预测性能。
3.4 与BP、LSTM模型的对比及普适性分析
为了进一步证明本文的组合模型在径流预测中的优势,选择了2个常用的径流预测模型:BP神经网络和长短期记忆神经网络(LSTM)模型,并与STL-VMD的二次分解方法组合成STL-VMD-BP和STL-VMD-LSTM模型作为对比。
表5和图9显示了这3种模型的性能,可以看出,本文的STL-VMD-SVM模型在所有评价指标上略优于其他2种模型。
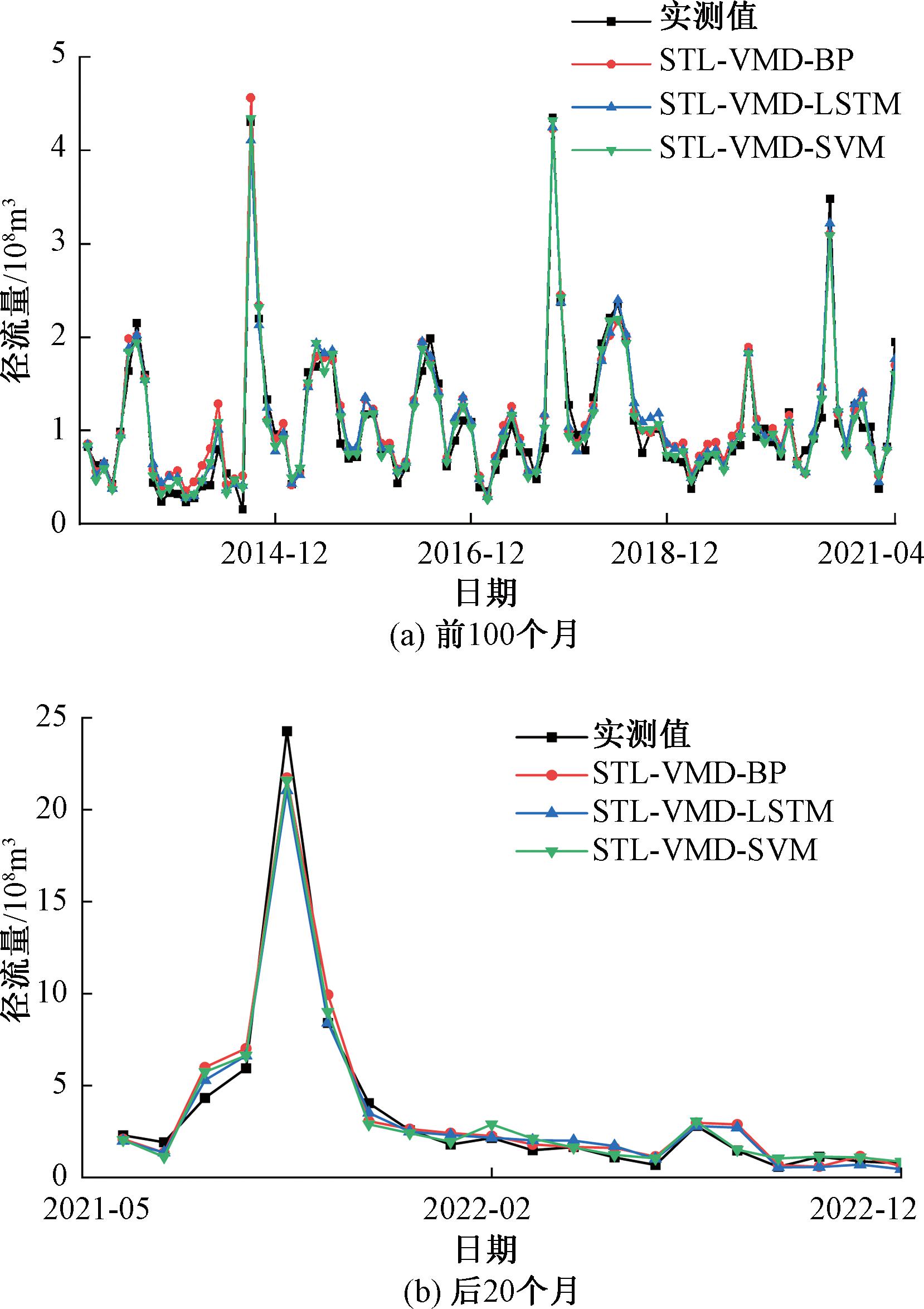
图9 常用模型验证期预测结果对比
Figure 9 Comparison of prediction results for validation period of common models
表5 3种组合模型的预测评价指标
Table 5 Prediction and evaluation indicators of three combination models

预测模型训练期验证期RRMSEMAPE%NSERRMSEMAPE%NSESTL-VMD-BP0.9850.4521.2130.9690.9860.41621.6490.970STL-VMD-LSTM0.9880.40118.3150.9740.9910.38818.1850.973STL-VMD-SVM0.9920.36115.8570.9830.9910.32713.7050.977
考虑到不同的流域及站点径流序列具有不同的波动性,为了验证模型的普适性,选取黄河干流高村站2007—2022年月径流序列,利用上文所述相同方法和步骤测试此模型,测试结果如表6和图10所示。
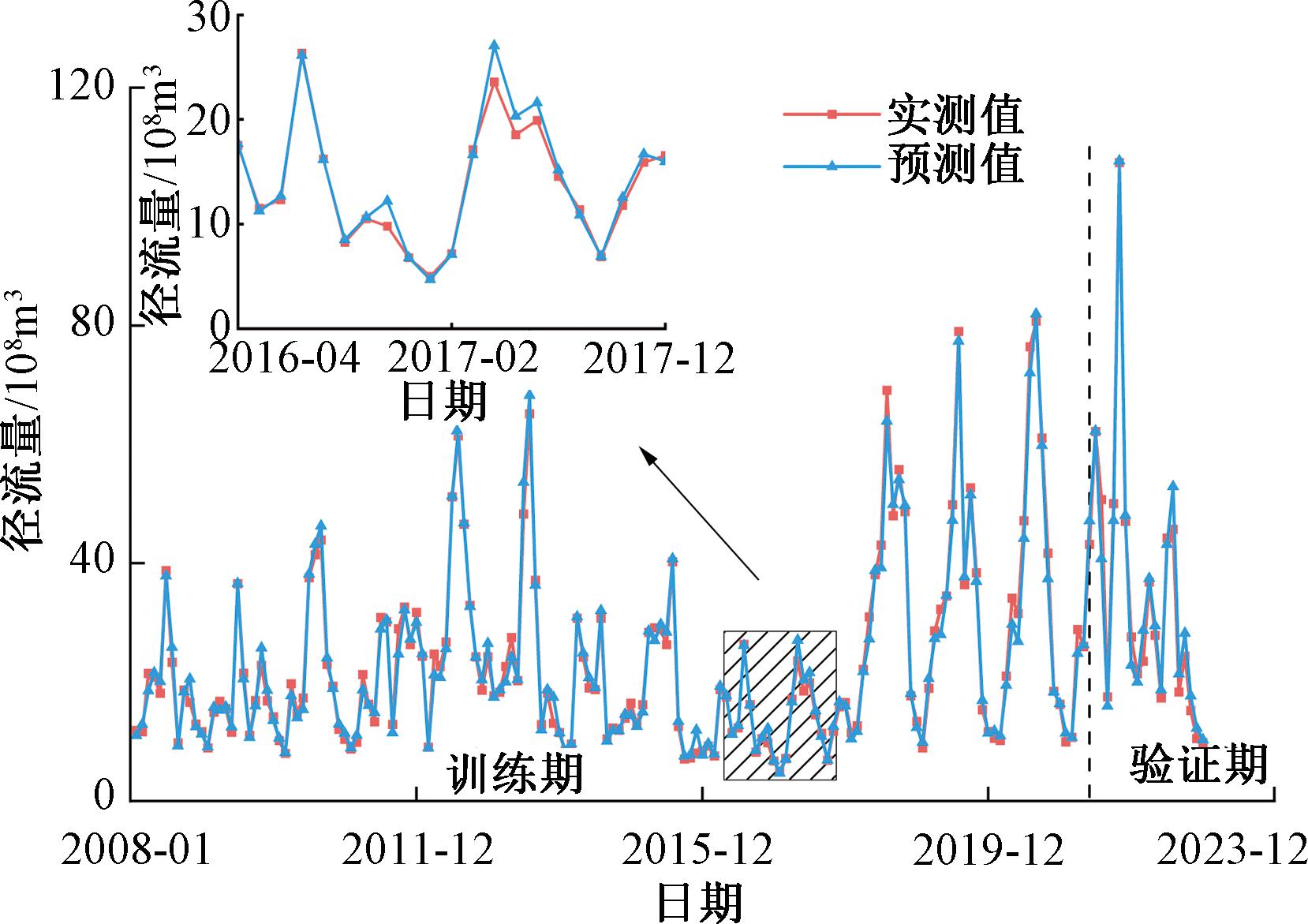
图10 高村站径流序列实测值与预测值对比
Figure 10 Comparison of measured and predicted runoff sequences at Gaocun station
表6 高村站径流序列预测评价结果
Table 6 Prediction and evaluation results of runoff sequence at Gaocun station

模拟期RRMSEMAPE%NSE训练期0.9931.6505.9270.986验证期0.9893.2638.5090.979
由表6和图10可知,该模型在高村站径流序列预测的应用性能仍比较优越,具有一定的普适性。STL-VMD-SVM组合模型使月径流时间序列预测结果达到了更高的准确度。
4 结论
径流序列具有高度的非稳态和强季节性特征,为提高其预测精度,本文基于二次分解思路,将STL-VMD组合分解技术与SVM模型相结合,并将其应用于伊洛河流域黑石关站的月径流预测。主要研究结论如下。
(1)分解增强了SVM的预测能力。STL分解法能够有效去除径流序列的季节成分,基于二次分解的模型比一次分解的模型具有更好的性能。
(2)基于二次分解后与SVM相结合的模型在R、RMSE、MAPE和NSE这4项评价指标中,略高于与常用的BP和LSTM模型相结合。STL-VMD-SVM组合模型月径流预测具有优势,对黄河干流高村站径流序列的预测也有较好的效果,证明该模型具有一定的普适性。
使用SVM模型进行预测时,是利用手动调节其惩罚因子与核参数,工作量较大。在下一步研究中,考虑采用适当的优化算法进行调参,例如粒子群优化算法或麻雀搜索算法,以减少工作量并进一步提高预测精度。
[1] HIRABAYASHI Y, MAHENDRAN R, KOIRALA S, et al. Global flood risk under climate change[J]. Nature Climate Change, 2013, 3(9): 816-821.
[2] DEY P,MISHRA A. Separating the impacts of climate change and human activities on streamflow: a review of methodologies and critical assumptions[J]. Journal of Hydrology, 2017,548:278-290.
[3] KOTTA J, HERKÜL K, JAAGUS J, et al. Linking atmospheric, terrestrial and aquatic environments: regime shifts in the Estonian climate over the past 50 years[J]. PLoS One, 2018, 13(12): e0209568.
[4] HE X X, LUO J G, LI P, et al. A hybrid model based on variational mode decomposition and gradient boosting regression tree for monthly runoff forecasting[J]. Water Resources Management, 2020, 34(2): 865-884.
[5] 雷庆文, 高培强, 李建林. 时序分解和CNN-LSTM相融合的月径流预报模型[J]. 长江科学院院报, 2023, 40(6): 49-54.LEI Q W, GAO P Q, LI J L. A monthly runoff forecast model combining time series decomposition and CNN-LSTM[J]. Journal of Changjiang River Scientific Research Institute, 2023, 40(6): 49-54.
[6] 王文川, 杜玉瑾, 和吉, 等. 基于CEEMDAN-VMD-BP模型的月径流量预测研究[J]. 华北水利水电大学学报(自然科学版), 2023, 44(1): 32-40, 48.WANG W C, DU Y J, HE J, et al. Research on monthly runoff prediction based on CEEMDAN-VMD-BP model[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2023, 44(1): 32-40, 48.
[7] YANG H, LI W D. Data decomposition, seasonal adjustment method and machine learning combined for runoff prediction: a case study[J]. Water Resources Management, 2023, 37(1): 557-581.
[8] 朱得胜, 吕锡芝, 倪用鑫, 等. 2001—2018年伊洛河流域产水系数演变分析[J]. 中国农村水利水电, 2022(9): 139-145.ZHU D S, LYU X Z, NI Y X, et al. An analysis of the changes in the water yield coefficient in the Yiluo River Basin from 2001 to 2018[J]. China Rural Water and Hydropower, 2022(9): 139-145.
[9] HOU J, QIN T L, YAN D H, et al. Evaluation of water-land resources regulation potential in the Yiluo River Basin, China[J]. Ecological Indicators, 2023, 153: 110410.
[10] 张艺馨. 基于改进BP神经网络模型的采空区特殊下垫面条件下径流预报研究[D]. 太原: 太原理工大学, 2021.ZHANG Y X. Study on runoff prediction of goaf with special underlying surface based on improved BP neural network model[D].Taiyuan: Taiyuan University of Technology, 2021.
[11] 邢珊珊. 基于时空关联的城市快速路短时交通流预测方法研究[D]. 北京: 北京交通大学, 2017.XING S S. Study on short-term traffic flow forecasting method of urban expressway based on spatial-temporal correlation[D].Beijing: Beijing Jiaotong University, 2017.
[12] 薛联青, 周天文, 刘远洪, 等. 基于两阶段分解和可解释机器学习的中长期径流预测[J]. 中国农村水利水电, 2023(7): 1-7, 18.XUE L Q, ZHOU T W, LIU Y H, et al. Medium and long-term runoff forecasting based on two-stage decomposition and interpretable machine learning[J]. China Rural Water and Hydropower, 2023(7): 1-7, 18.
[13] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[14] SHARMA V, PAREY A. Extraction of weak fault transients using variational mode decomposition for fault diagnosis of gearbox under varying speed[J]. Engineering Failure Analysis, 2020, 107: 104204.
[15] 廖晓辉, 陈川川. 改进的VMD-HT在电能质量扰动检测中的应用[J]. 郑州大学学报(工学版), 2021, 42(1): 21-27.LIAO X H, CHEN C C. Application of improved VMD-HT in power quality disturbance detection[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(1): 21-27.
[16] TOMAR D, AGARWAL S. Twin support vector machine: a review from 2007 to 2014[J]. Egyptian Informatics Journal, 2015, 16(1): 55-69.
[17] 张颖超, 成金杰, 邓华, 等. 基于相似日和特征提取的短期风电功率预测[J]. 郑州大学学报(工学版), 2020, 41(5): 44-49.ZHANG Y C, CHENG J J, DENG H, et al. Short-term wind power prediction based on similar day and feature extraction[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(5): 44-49.
[18] CHEN S, REN M M, SUN W. Combining two-stage decomposition based machine learning methods for annual runoff forecasting[J]. Journal of Hydrology, 2021, 603: 126945.
[19] 纪昌明, 周婷, 向腾飞, 等. 基于网格搜索和交叉验证的支持向量机在梯级水电系统隐随机调度中的应用[J]. 电力自动化设备, 2014, 34(3): 125-131.JI C M, ZHOU T, XIANG T F, et al. Application of support vector machine based on grid search and cross validation in implicit stochastic dispatch of cascaded hydropower stations[J]. Electric Power Automation Equipment, 2014, 34(3): 125-131.