塑性铰长度作为工程结构抗震领域的重要概念,是结构进行弹塑性地震响应分析和抗震加固的重要依据。超高性能混凝土(ultra high performance concrete,UHPC)作为一种在延性、韧性和损伤容限等方面具有显著优势的新型水泥基材料,在桥梁墩柱结构抗震设计中具有非常广阔的应用前景[1]。目前,国内外学者已对全UHPC构件、UHPC护套加固矩形桥墩、分段UHPC预制壳壁加固RC组合柱和UHPC预制管混凝土组合柱的抗震性能开展了试验研究[2-5],结果表明,UHPC材料对于提高结构或构件的塑性变形以及耗能能力都具有显著成效。基于试验研究和数值分析,Ren等[6]进一步提出了UHPC箱型桥墩等效塑性铰长度计算公式。但考虑到UHPC造价相对昂贵,而墩柱构件塑性变形主要发生在塑性铰区域[7],为此,采用UHPC替换桥墩塑性铰区域普通混凝土(normal concrete, NC),并匹配高强钢筋形成一种新型的高强钢筋增强UHPC-NC组合桥墩显然更具工程应用价值。为取得适用性和经济性的统一,合理的UHPC替换高度显得尤为重要,因此对提出的组合桥墩开展相应的塑性铰长度研究具有非常重要的现实意义。
本文应用有限元程序ABAQUS,结合材料本构关系和混凝土损伤塑性模型,建立了高强钢筋增强UHPC-NC组合桥墩抗震有限元模型。在试验验证的基础上,进一步提出了塑性铰区域长度确定方法,探讨了轴压比、纵筋直径和屈服强度以及试件高度等参数对组合桥墩塑性铰区域长度的影响规律,并在评估规范建议公式适用性的基础上,建立了组合桥墩等效塑性铰长度计算公式。
1 材料本构关系
高强钢筋增强UHPC-NC组合桥墩中包含了UHPC、NC和高强钢筋3种材料,在ABAQUS软件中对于NC和高强钢筋2种材料可以分别选用程序中Mander模型[8]和双折线模型[9]来表征其应力-应变关系。但考虑到UHPC作为一种纤维增强的新型水泥基材料,程序中并无相应材料本构模型,但可以通过输入对应的应力-应变曲线来实现,为此必须明确UHPC材料在受压和受拉状态下的本构关系。
1.1 UHPC受压本构关系
本文UHPC本构曲线采用约束UHPC本构模型[10],相应表达式为
σc=
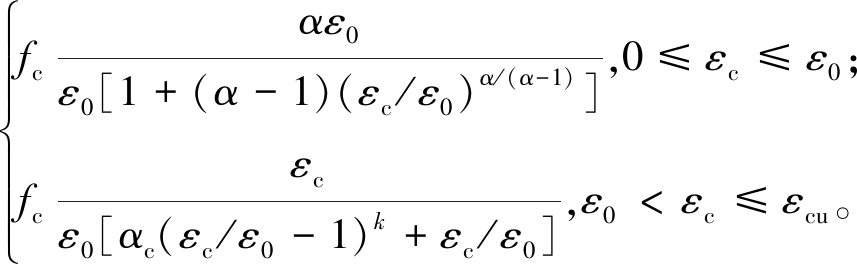
(1)
其中:
α=(1+111.17Ie2.43)A;
(2)
αc=2εc/[3ε0(εcu/ε0-1)k];
(3)
(4)
Ie=0.5keλv;
(5)
λv=ρvfyv/fc0。
(6)
式中:σc和εc分别表示约束UHPC压应力和压应变;fc为约束UHPC峰值应力;ε0为约束UHPC峰值应变;α为约束UHPC本构曲线上升段参数;A为非约束UHPC初始弹性模量和峰值割线的比值;αc为约束UHPC本构曲线下降段参数;k为箍筋对约束UHPC本构曲线下降段的影响参数;εcu为约束UHPC峰值应力下降到60%时相应应变;Ie为有效约束指标;ke为有效约束系数[8];λv为箍筋特征值;ρv为体积配箍率;fyv为高强箍筋屈服强度;fc0为未约束UHPC峰值应力。UHPC本构曲线如图1所示。
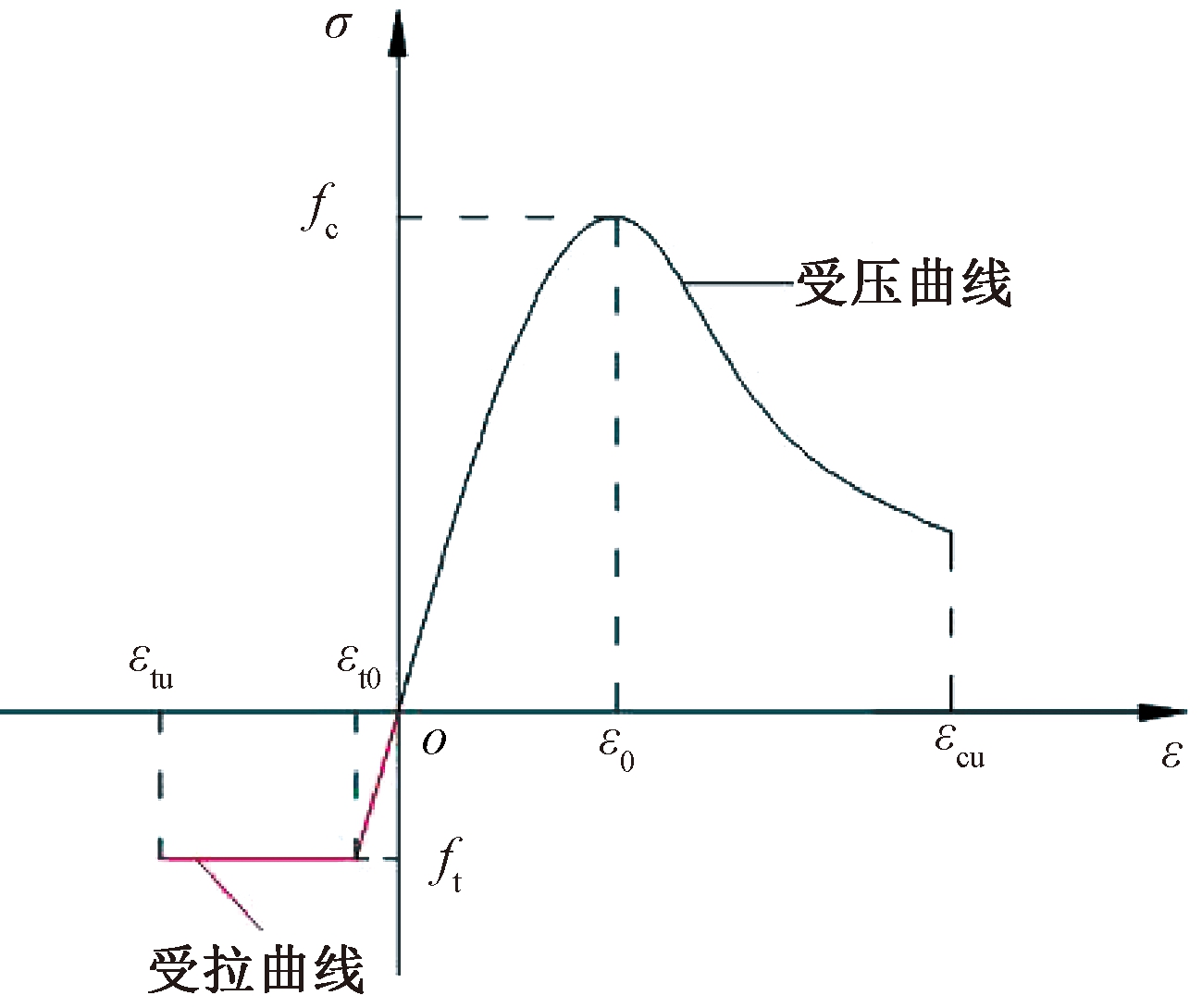
图1 UHPC应力-应变关系
Figure 1 Stress-strain relationship of UHPC
1.2 UHPC受拉本构关系
钢纤维对UHPC构件在受拉状态下会起到阻裂作用,数值模型中应考虑UHPC的抗拉性能,相应的受拉本构曲线如图1所示,其表达式[11]为
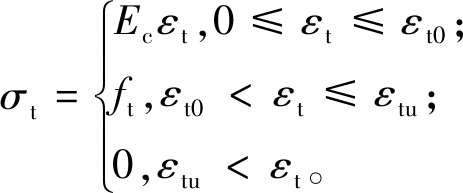
(7)
式中:Ec表示UHPC初始弹性模量;σt和εt分别表示UHPC拉应力和拉应变;ft为UHPC峰值抗拉强度,其大小可取为立方体抗压强度的1/23.6;εt0和εtu分别表示UHPC峰值和极值拉应变,其中εtu建议按2倍εt0取值。
2 延性分析模型
基于大型有限元程序ABAQUS,结合上述的UHPC、NC和高强钢筋材料本构关系,选取C3D8R单元来模拟UHPC和NC材料在反复荷载作用下的力学性能、T3D2单元模拟高强钢筋的滞回特性,建立了延性分析模型,如图2所示。
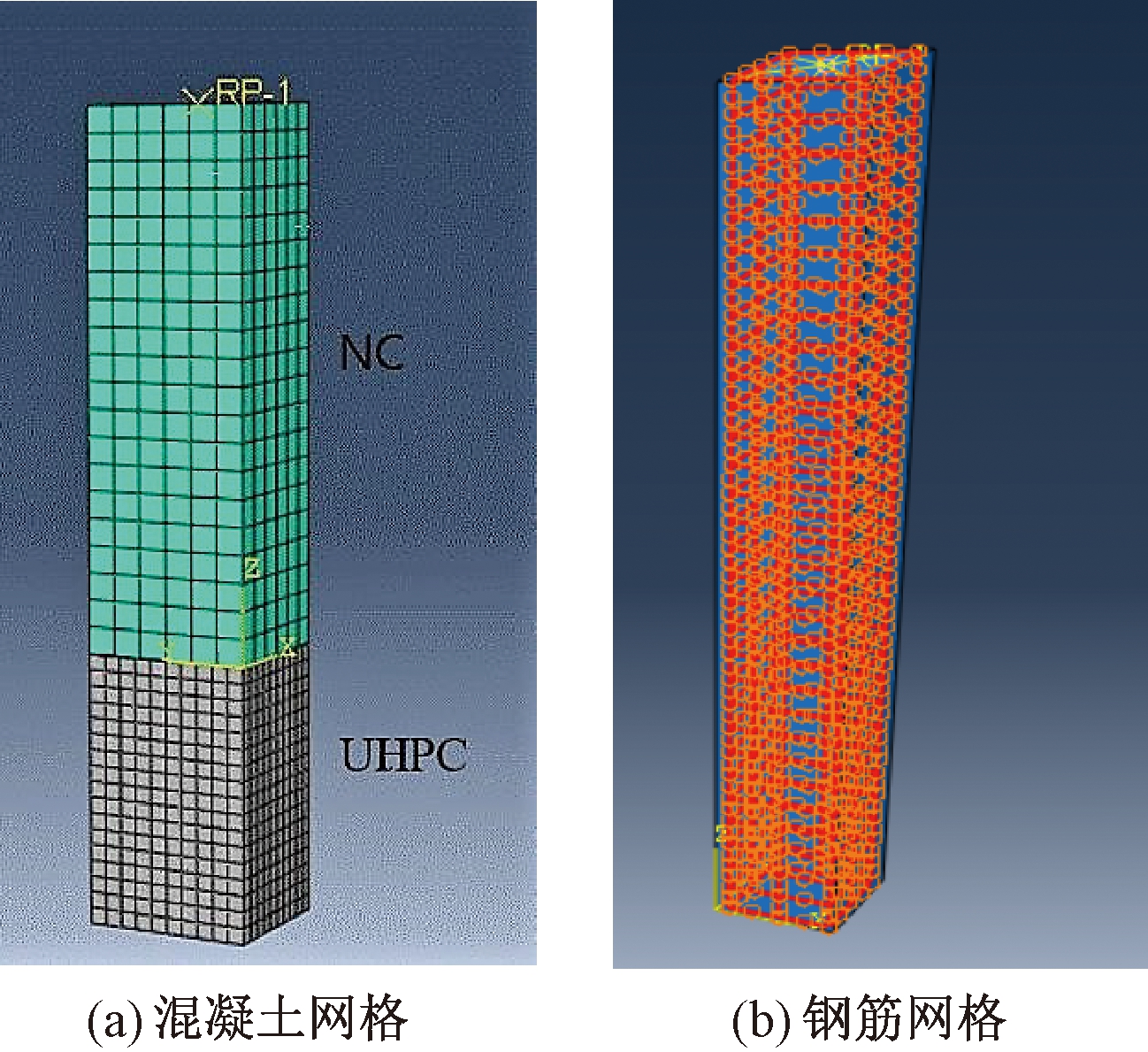
图2 延性分析模型
Figure 2 Ductility analysis model
图2中UHPC节段和NC节段截面均按相同的网格密度进行划分,高度方向在UHPC节段区域单元适当细分,试件的底端设置为完全固定,顶端通过设置参考点来施加轴向力与水平往复荷载。为准确模拟UHPC和NC材料从加载到破坏的力学行为,选用ABAQUS软件中混凝土损伤塑性模型,考虑2种材料的损伤,并采用静力隐式算法进行数值分析。综合考虑UHPC相对于NC在强度、韧性和抗裂性方面的优势,表1给出了2种材料混凝土损伤塑性模型关键控制参数的取值。
表1 混凝土损伤塑性模型控制参数取值
Table 1 Control parameters of concrete damage plastic model

注:ρ表示膨胀角;λ表示偏心率;σb0/σc0表示双轴极限抗压强度和单轴极限抗压强度之比;KC表示控制混凝土屈服面在偏平面上的投影形状的参数;μ表示黏性系数。
材料ρ/(°)λσb0/σc0KCμNC350.11.140.666 70.005UHPC400.11.160.666 70.005
钢筋与混凝土之间应用分离式模型模拟钢筋与混凝土之间接触,两者之间的黏结效应通过Embeded方式来实现,滑移效应基于应力-滑移(τ-s)关系,结合ABAQUS程序的二次开发功能来实现,相应的黏结滑移本构表达式如下[12]。
上升段:
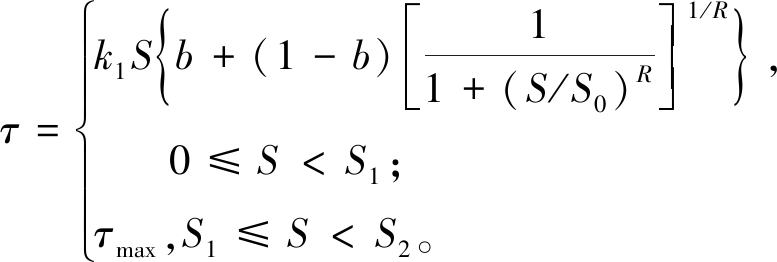
(8)
下降段:
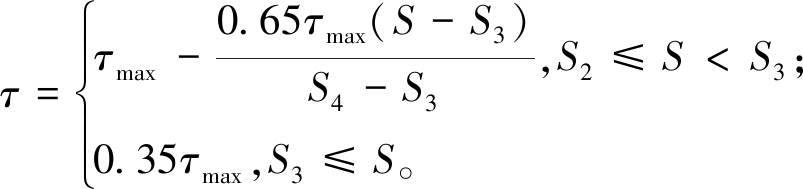
(9)
式中:τ为黏结应力;S为滑移;b为峰值切线刚度k2与初始刚度k1的比值;S0~S3为曲线各阶段滑移,其中S0=(τmax-S2k2)/(k1-k2);R为确定Menegotto-Pinto曲线的参数,按3.0取值[13]。
3 试验对比分析
由于高强钢筋增强UHPC-NC组合桥墩抗震性能试验尚未见诸文献,为探讨建立的高强钢筋增强UHPC-NC组合桥墩抗震有限元模型的可靠性,分别选取常轴力下3个不同UHPC加固高度的钢筋混凝土桥墩和3个UHPC箱型桥墩拟静力试验结果对延性分析模型进行验证。
3.1 试验概况
不同UHPC加固高度的钢筋混凝土桥墩和不同加载角度下UHPC箱型桥墩拟静力试验试件参数如表2所示,试件相应的配筋和截面尺寸如图3所示。其中UHPC加固桥墩的纵筋和箍筋的钢筋等级分别为HRB400、HPB300,相应实测屈服强度为502、528 MPa;混凝土标号为C40,UHPC实测立方体抗压强度为129.7 MPa,抗拉强度为5.52 MPa,弹性模量40.1 GPa。UHPC箱型桥墩的纵筋和箍筋的钢筋等级分别为HRB400、HRB300,相应实测屈服强度为450、458 MPa;UHPC实测立方体抗压强度为110.7 MPa,抗拉强度为5.93 MPa,弹性模量为40.9 GPa。表3给出了试验中UHPC材料的配合比设计。试验采取先力后位移的控制加载方式,详细的加载过程及试件破坏形态见文献[3]和文献[14]。
表2 试件参数
Table 2 Specimen parameters
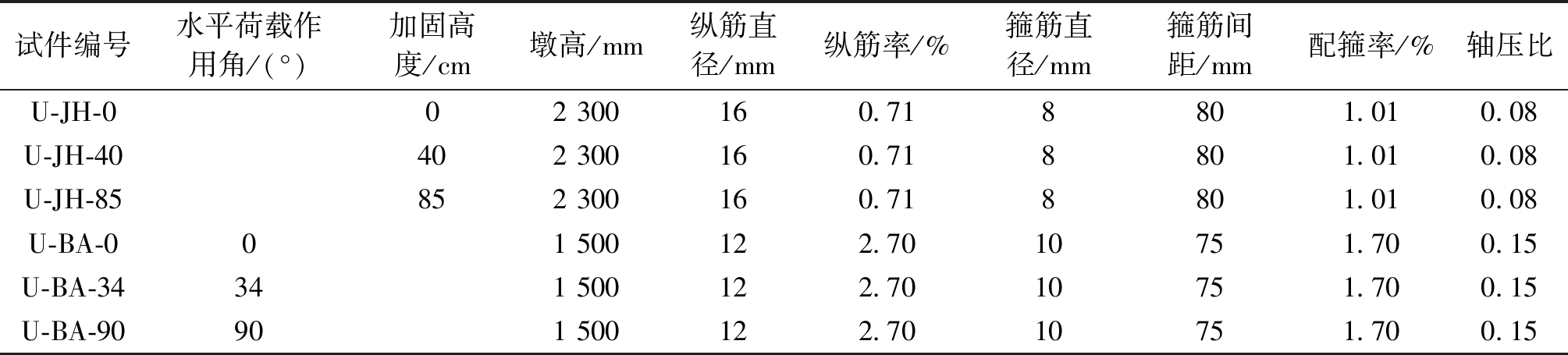
注:试件编号中U表示UHPC;JH表示加固高度;BA表示箱型桥墩水平荷载作用角度,其后数值表示水平荷载作用方向与截面长边之间的夹角。
试件编号水平荷载作用角/(°)加固高度/cm墩高/mm纵筋直径/mm纵筋率/%箍筋直径/mm箍筋间距/mm配箍率/%轴压比U-JH-002 300160.718801.010.08U-JH-40402 300160.718801.010.08U-JH-85852 300160.718801.010.08U-BA-001 500122.7010751.700.15U-BA-34341 500122.7010751.700.15U-BA-90901 500122.7010751.700.15
表3 UHPC的配合比
Table 3 UHPC mix proportions
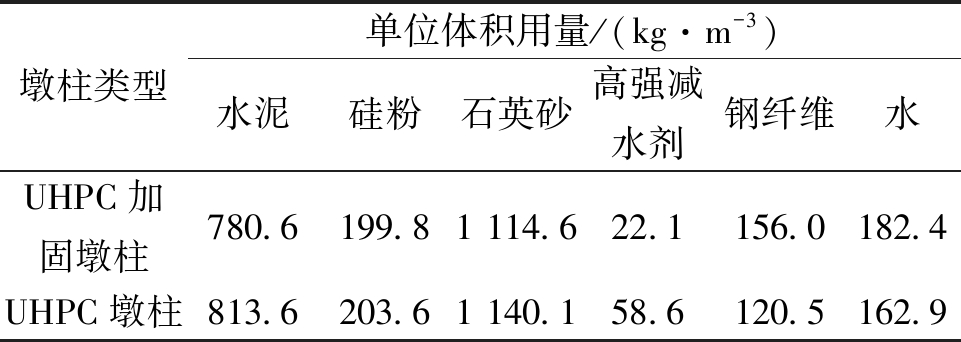
注:钢纤维均采用直径为0.16 mm、长度为12 mm、抗拉强度在2 000 MPa以上无钩端光滑的镀铜直钢纤维。
墩柱类型单位体积用量/(kg·m-3)水泥硅粉石英砂高强减水剂钢纤维水UHPC加固墩柱780.6199.81 114.622.1156.0182.4UHPC墩柱813.6203.61 140.158.6120.5162.9
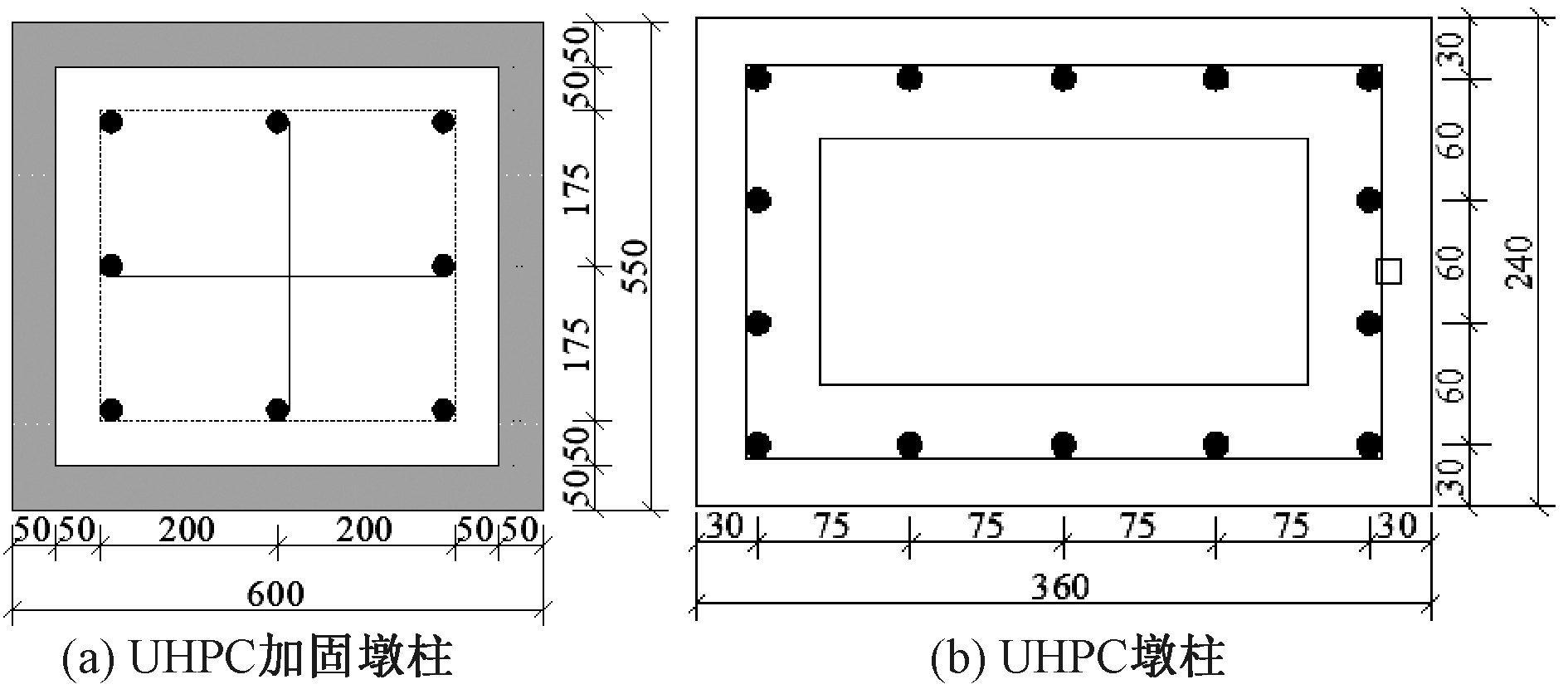
图3 试件配筋和截面尺寸(mm)
Figure 3 Reinforcement and section size of specimen(mm)
3.2 计算与试验结果对比
应用前文建立的延性分析模型,本节对上述UHPC加固钢筋混凝土桥墩和UHPC箱型桥墩拟静力试验滞回曲线开展了数值模拟,图4给出了相应的试验与计算结果对比。
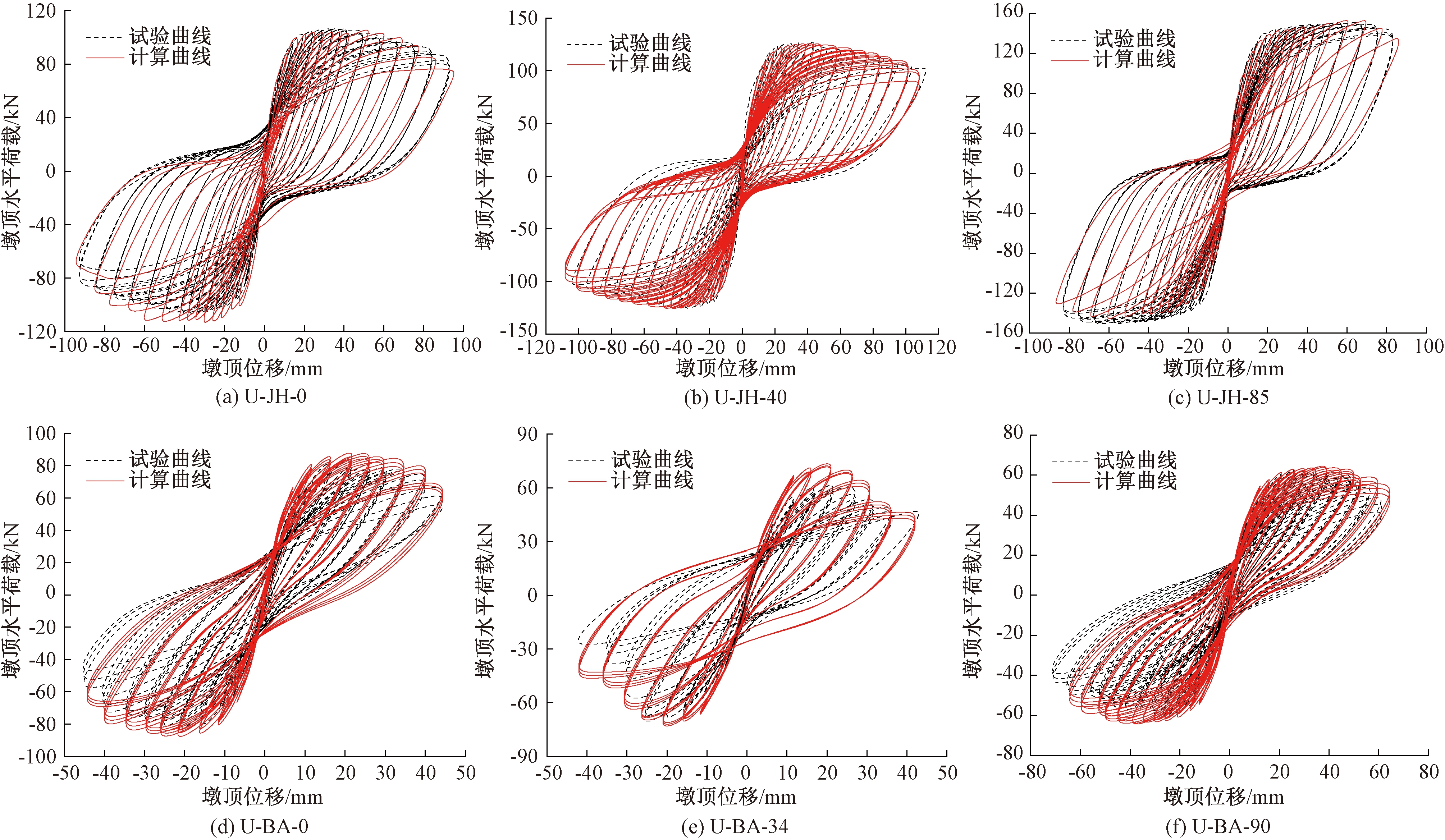
图4 滞回曲线比较
Figure 4 Comparison of hysteresis curves
从图4中可以看出,试验曲线与计算曲线的拟合程度较好,且计算曲线能较好地反映循环加载作用下试件的强度退化特征,但6个试件的试验峰值荷载均小于计算结果,这是由于数值分析时混凝土基于理想的材料本构取值,而试验中的混凝土为各向异性材料,存在受力不均匀。试件U-BA-34由于计算时未考虑扭转变形效应,导致计算结果相对于其他试件存在较明显的偏差。
为进一步验证延性分析模型的可靠性,表4列出了UHPC箱型桥墩试件等效塑性铰长度实测值和理论计算值的对比,其中等效塑性铰长度Lp由下式确定[6]:
表4 Lp实测值与理论值的比较
Table 4 Comparison of Lp test value and theoretical value

试件编号Δy/mmΔu/mmφy/(10-5rad)φu/(10-5rad)Lp/mm实测值理论值实测值理论值实测值理论值实测值理论值实测值理论值U-BA-08.99.845.642.61.31.310.610.1293274U-BA-348.19.636.432.41.11.06.35.6424376U-BA-9012.313.667.261.51.71.614.413.5322298
Δu=Δy+Δp=Δy+(φu-φy)Lp(L-0.5Lp)。
(10)
式中:Δy、Δp和Δu分别表示墩顶屈服位移、塑性位移和极限位移,其中Δy由R·Park法来确定,Δu取水平荷载下降到极值点荷载85%对应的位移;φy和φu分别表示墩底屈服曲率和极限曲率;L为墩高。
从表4中可以看出,由于数值分析时未考虑剪切变形所带来的影响,计算结果相对于试验结果偏小,表明本文计算的Lp是偏安全的。相对于试验值,3个试件计算得到的屈服位移明显偏大,这是由于数值分析时未充分考虑循环加载下试件损伤累积造成的材料性能退化。
4 塑性铰区域长度预测
塑性铰区域一般定义为类似于地震等极端荷载下,墩柱底或墩柱两端发生连续塑性变形和严重破坏的区域。塑性铰区域相应的长度则称之为塑性铰区域长度Lpz。与经典的等效塑性铰长度Lp相比,Lpz能更好地表现出墩柱真实的塑性曲率分布。目前,定义悬臂柱塑性铰区域长度有2种方法:第1种方法定义为墩柱高度方向纵筋应变已达到或超过其屈服应变的区域(塑性铰区域长度为Lpz1);第2种方法定义为墩柱高度方向曲率已达到或超过其屈服曲率的区域(塑性铰区域长度为Lpz2),其中曲率计算公式如下:
φ=(εtt-εcc)/B。
(11)
式中:εtt和εcc分别表示悬臂墩柱在受拉区和受压区上混凝土的轴向应变;B表示墩柱截面的宽度。屈服曲率一般采用Paulay等[15]提出的等效屈服曲率来确定,即
φy=2εy/B。
(12)
式中:εy表示钢筋的屈服应变。
基于前文塑性铰区域长度预测方法,确定了UHPC箱型桥墩试件的塑性铰区域长度,表5给出了2种方法所计算的塑性铰区域长度结果对比。从表5中可以看出,3个试件基于纵筋屈服的塑性铰区域长度Lpz1均大于基于曲率屈服的塑性铰区域长度Lpz2,这与文献[15-16]结果一致。为避免高估构件塑性变形能力,后续研究采用相对保守的屈服曲率来确定塑性铰区域长度。
表5 塑性铰区域长度对比
Table 5 Comparison of plastic hinge region length

试件编号εyφy/(10-5rad)Lpz1/mmLpz2/mmU-BA-00.002 51.25341310U-BA-340.002 51.04494482U-BA-900.002 51.86376358
5 参数分析
基于上述塑性铰区域长度预测方法,本文选取轴压比、纵筋直径、纵筋屈服强度和试件高度等关键影响因素,对高强钢筋增强UHPC-NC组合桥墩塑性铰区域长度进行探讨。为保证组合桥墩塑性变形发生在UHPC区域,UHPC高度为文献[6]提出的UHPC构件等效塑性铰长度的1.3倍,NC采用C40混凝土。分析时,截面尺寸、钢筋布置、UHPC材料特性和墩高与前述对比试验中UHPC箱型桥墩试件一致,加载角度为0°。
5.1 轴压比
分别选取轴压比为0、0.1、0.2、0.3、0.4及0.5对塑性铰区域长度展开分析,图5为塑性铰区域长度随轴压比变化曲线。
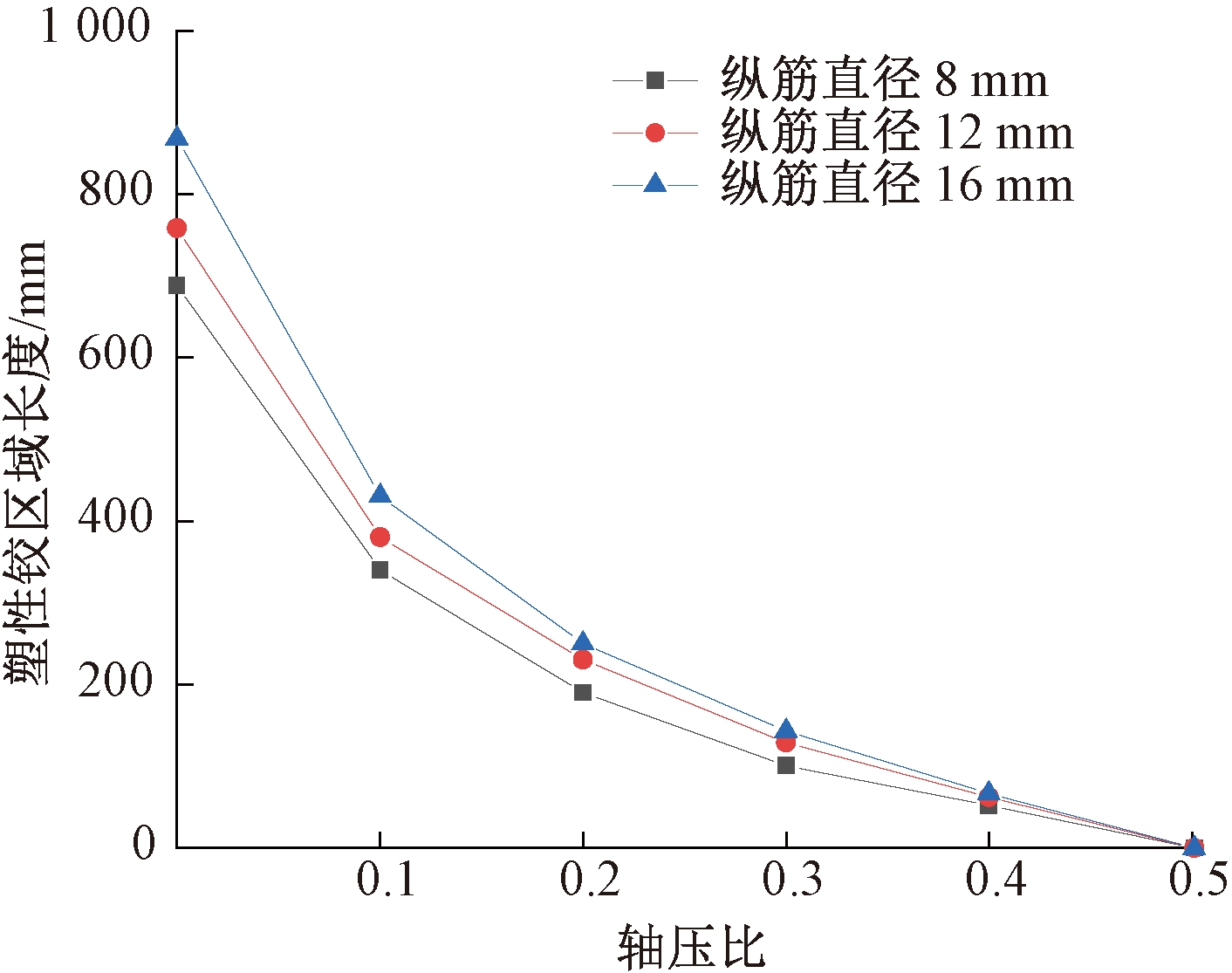
图5 塑性铰区域长度随轴压比变化曲线
Figure 5 Length of plastic hinge region versus axial pressure ratio
从图5中可以看出,塑性铰区域长度随着轴压比的增加呈现单调递减的变化趋势。这是由于轴压比增加会导致墩底截面屈服弯矩变大,截面极限弯矩相对减少,进而导致墩底塑性铰区域长度逐渐减小;当轴压比接近0.5时,由于受压区UHPC发生破坏而受拉区纵筋仍未屈服,或者受压区UHPC的破坏与受拉区纵筋的屈服同步发生,此时墩底塑性铰区域长度几乎接近于0。
5.2 纵筋直径
图6为轴压比0.10、0.15和0.20时塑性铰区域长度随纵筋直径变化曲线。
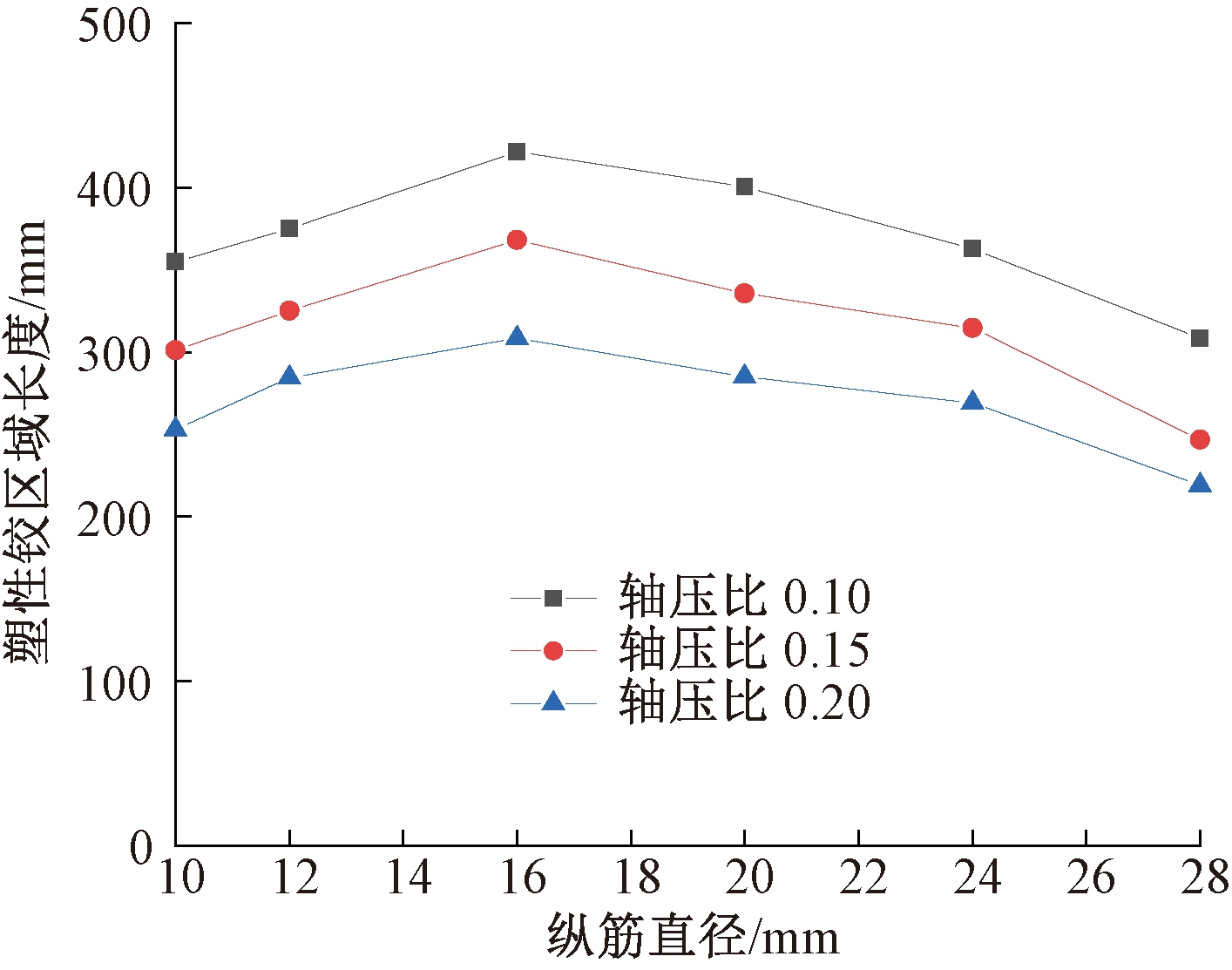
图6 塑性铰区域长度随纵筋直径变化曲线
Figure 6 Length of plastic hinge region versus longitudinal reinforcement diameter
从图6中可以看出,试件塑性铰区域长度随着纵筋直径的增大呈现出先递增后递减的变化趋势。这是由于纵筋直径较小时,截面纵筋率较低,试件表现出明显的少筋梁的破坏特征;随着纵筋直径(纵筋率)不断增大,试件破坏特征逐渐向适筋梁破坏转变,导致塑性铰区域长度随之逐渐增大;但当纵筋直径增大至一定数值(16 mm)时,截面纵筋率过大,导致试件破坏特征开始向超筋梁破坏转变,因此,塑性铰区域长度反而下降。
5.3 纵筋屈服强度
图7为轴压比0.10、0.15和0.20时塑性铰区域长度随纵筋屈服强度变化曲线。
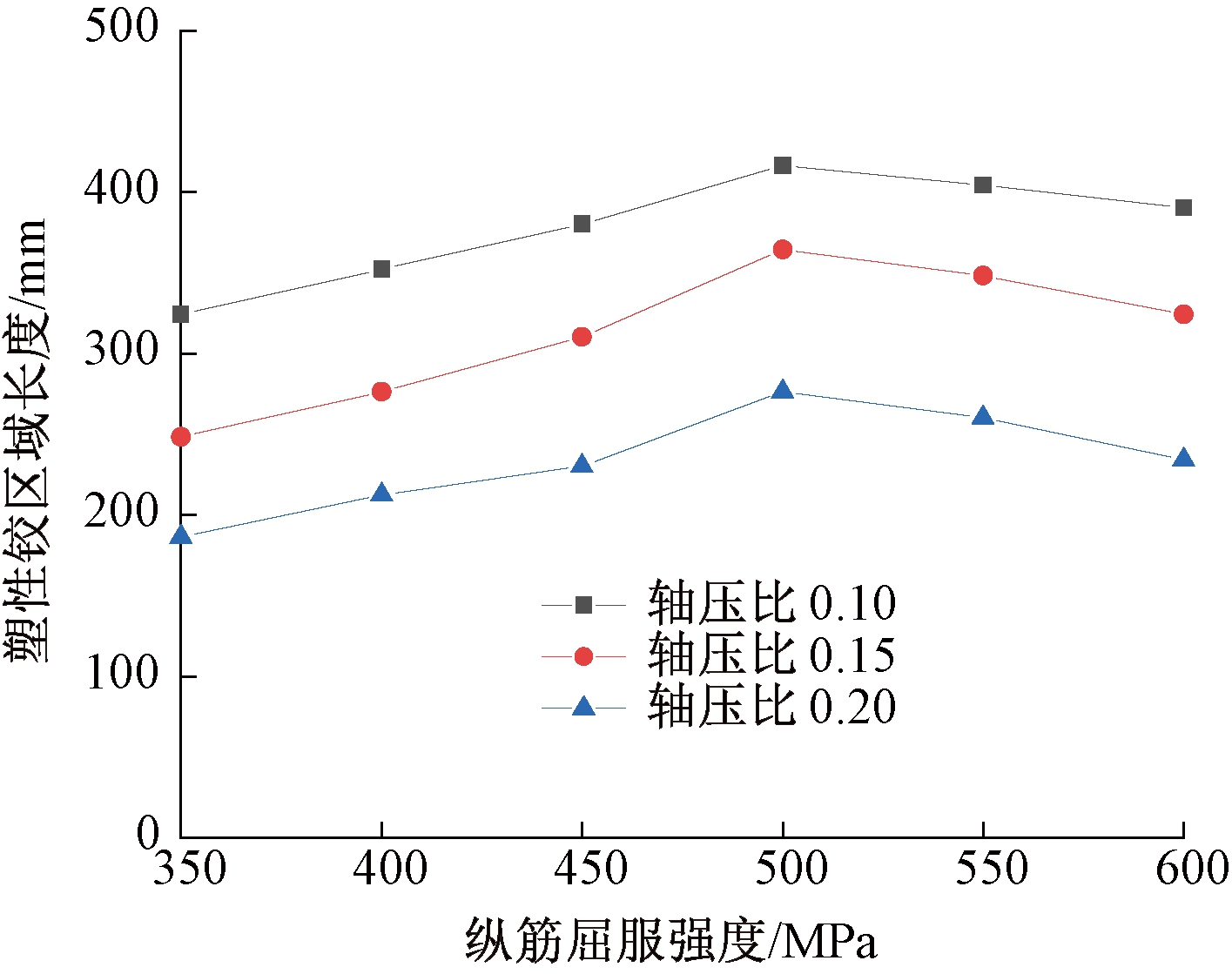
图7 塑性铰区域长度随纵筋屈服强度变化曲线
Figure 7 Length of plastic hinge region versus longitudinal reinforcement yield strength
从图7中可以看出,塑性铰区域长度随着纵筋屈服强度的增加呈现出先增后减的变化趋势,表明UHPC-NC组合桥墩采用高强钢筋在一定程度上将提升其塑性变形能力,但当纵筋屈服强度增加到临界值(500 MPa)时,随着纵筋屈服强度的增加,塑性铰区域长度减小。
5.4 试件高度
图8为轴压比0.10、0.15和0.20时塑性铰区域长度随试件高度变化曲线。
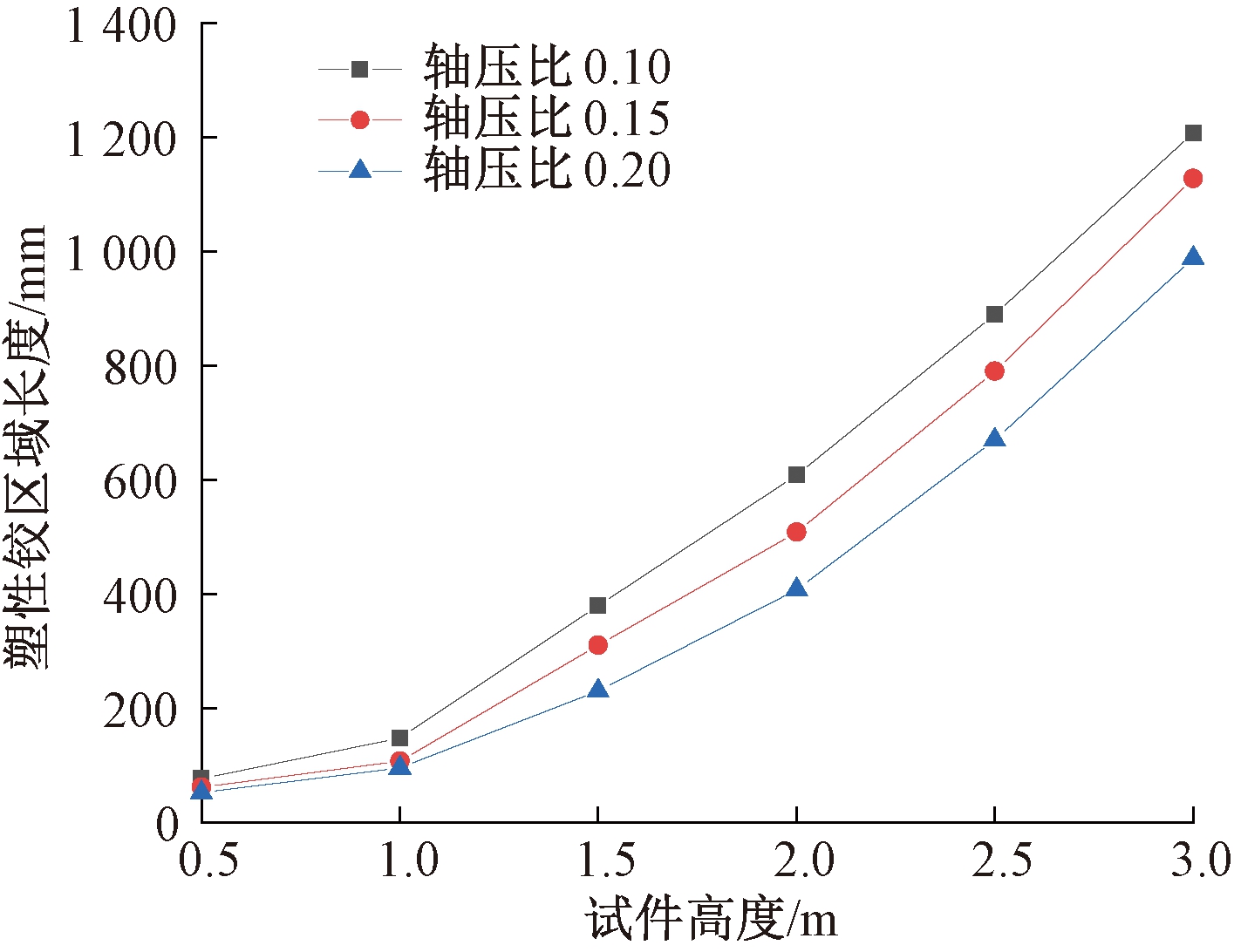
图8 塑性铰区域长度随试件高度变化曲线
Figure 8 Length of plastic hinge region versus specimen height
从图8中可以看出,试件塑性铰区域长度随着试件高度的增加表现为单调递增。这是因为在低周反复荷载作用下矮墩易发生脆性剪切破坏,塑性铰区域长度较小;但随着试件高度的增加,试件破坏特征将由脆性剪切破坏逐渐转换为延性弯曲破坏,导致试件塑性铰区域长度逐渐增大。
6 等效塑性铰长度回归公式
塑性铰区域虽然能反映墩柱塑性变形区域的实际分布,但工程实践中等效塑性铰长度显然更具实用性。通过假定真实的塑性变形区域塑性曲率从墩底到墩顶线性分布,Hines等[17]提出了塑性铰区域长度Lpz与等效塑性铰长度Lp之间的转换关系:
Lp=Lpz/2+Lsp。
(13)
式中:Lsp为纵筋应变渗透效应产生的塑性铰增量,且Lsp=0.022fyd。
为了探讨规范常用的钢筋混凝土墩柱塑性铰长度,建议公式对高强钢筋增强UHPC-NC组合桥墩适用性。图9(a)~9(c)分别给出了Paulay公式[15]、Priestley公式[16]和Panagiotakos公式[18]与数值分析结果对比。图9中经验公式结果均值与数值分析结果均值的比值以MR表示,经验公式结果与数值分析结果的相关程度以R2表示。对比分析结果排除了一些如矮墩(1.0 m)和高轴压比(n=0.4,0.5)的极端情况。
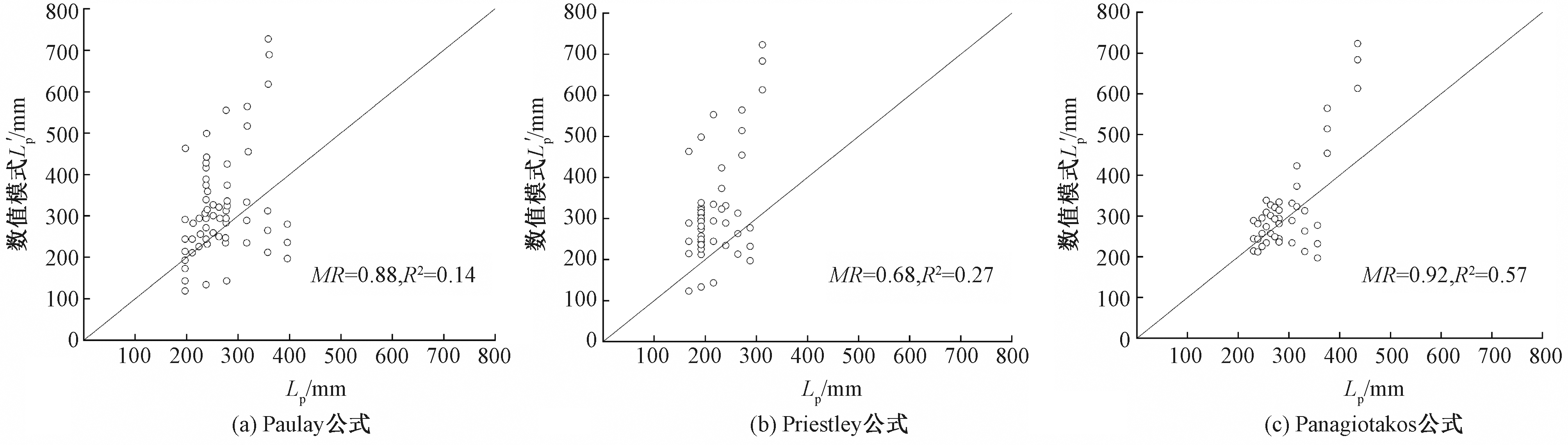
图9 塑性铰长度参数分析结果与各公式计算结果对比
Figure 9 Comparison between the analysis results of plastic hinge length parameters and the calculation results of each formula
从图9中可以看出,经验公式计算结果总体上小于数值分析结果(MR最大值为0.92),这表明采用钢筋混凝土墩柱等效塑性铰长度计算公式将一定程度上低估UHPC构件的塑性变形能力。与此同时,经验公式计算结果与数值分析结果相关程度(R2)最大值仅为0.57,表明采用钢筋混凝土墩柱等效塑性铰长度计算公式计算UHPC构件会存在较大误差。为此,本文结合数值分析结果,通过回归分析建立考虑轴压比、纵筋直径、纵筋屈服强度和试件高度的等效塑性铰长度计算公式,相应的表达式为
Lp=a1η+a2dfd+a3L+a4。
(14)
式中:η表示轴压比;d表示钢筋直径,mm;fd表示钢筋屈服强度,MPa;L表示试件高度,m;a1、a2、a3、a4均为回归系数。
基于前述数值分析结果,在剔除高轴压比(0.4和0.5)、低轴压比(0)、纵筋直径过大或过小(8 mm和28 mm)等极端状况下,经数值回归分析拟合出等效塑性铰长度计算公式为
Lp=-0.883η+0.002 3dfd+0.255L+0.009 5。
(15)
7 结论
本文基于大型有限元程序ABAQUS,建立了高强钢筋增强UHPC-NC组合桥墩抗震有限元模型,分析了轴压比、纵筋直径、纵筋屈服强度和试件高度等敏感参数对高强钢筋增强UHPC-NC组合桥墩塑性铰区域长度的影响,并拟合出等效塑性铰长度计算公式,得出以下结论。
(1) 综合考虑数值分析和试验研究的差异性,建立的延性分析模型能较好地模拟对比试验的滞回曲线、等效塑性铰长度,并能反映试件在低周反复荷载加载过程中强度和刚度的退化。
(2) UHPC-NC组合桥墩塑性铰区域长度随轴压比增大单调递减,随纵筋直径和屈服强度的增大均表现出先增大后减小的变化趋势,随试件高度的增大单调递增。当轴压比接近0.5时,UHPC的破坏与受拉区纵筋的屈服同步发生,当纵筋直径和屈服强度分别为16 mm、500 MPa时,墩底塑性铰区域耗能能力达到最优。
(3) 规范建议的计算公式在一定程度上将低估组合桥墩的塑性变形能力,基于数值分析结果建立的等效塑性铰回归公式可为高强钢筋增强UHPC-NC组合桥墩抗震研究提供参考。
[1] 赵卓, 耿佳硕, 王建强. 采用UHPC材料连接的装配式桥墩抗震性能研究[J]. 郑州大学学报(工学版), 2021, 42(2): 13-18.
ZHAO Z, GENG J S, WANG J Q. Study on seismic performance of prefabricated pier connected by UHPC[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(2): 13-18.
[2] 郑七振, 刘阳阳, 龙莉波, 等. 超高性能混凝土连接的装配式现浇混凝土框架抗震性能[J]. 工业建筑, 2019, 49(10): 85-91.
ZHENG Q Z, LIU Y Y, LONG L B, et al. Experimental research on seismic behavior of precast concrete frame connected with uhpc[J]. Industrial Construction, 2019, 49(10): 85-91.
[3] TONG T, YUAN S Q, ZHUO W D, et al. Seismic retrofitting of rectangular bridge piers using ultra-high performance fiber reinforced concrete jackets[J]. Composite Structures, 2019, 228: 111367.
[4] 孟庆利. 分段SFC预制壳壁抗震加固RC墩柱设计方法与效验[J]. 中国公路学报, 2017, 30(12): 178-186.
MENG Q L. Design method and efficacy of RC pier columns seismically strengthened with precast SFC shell segments[J]. China Journal of Highway and Transport, 2017, 30(12): 178-186.
[5] SHAN B, LIU G, LI T Y, et al. Experimental research on seismic behavior of concrete-filled reactive powder concrete tubular columns[J]. Engineering Structures, 2021, 233: 111921.
[6] REN L, FANG B W, WANG K, et al. Numerical investigation on plastic hinge length of ultra-high performance concrete column under cyclic load[J]. Journal of Earthquake Engineering, 2022, 26(3): 1281-1299.
[7] 赵毅, 段松甫, 牛中浩. 钢管混凝土异形柱-钢梁节点恢复力模型研究[J]. 郑州大学学报(工学版), 2022, 43(6): 104-110.
ZHAO Y, DUAN S F, NIU Z H. Research on restoring force modeling of concrete-filled steel tubular special-shaped column-steel beam nodes[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(6): 104-110.
[8] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826.
[9] ZHAO J, SRITHARAN S. Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures[J]. ACI Structure Journal, 2007, 104(2): 133-141.
[10] 邓宗才, 姚军锁. 高强钢筋约束超高性能混凝土柱轴心受压本构模型研究[J]. 工程力学, 2020, 37(5): 120-128.
DENG Z C, YAO J S. The axial compression stress-strain model for ultra-high performance concrete columns confined by high-strength stirrups[J]. Engineering Mechanics, 2020, 37(5): 120-128.
[11] 原海燕, 安明喆, 贾方方, 等. 活性粉末混凝土轴拉性能试验研究[J]. 工程力学, 2011, 28(增刊1): 141-144.
YUAN H Y, AN M Z, JIA F F, et al. Experimental research on uniaxial tensile performance of reactive powder concrete[J]. Engineering Mechanics, 2011, 28(S1): 141-144.
[12] 方自虎, 周海俊, 赖少颖, 等. 循环荷载下钢筋混凝土ABAQUS黏结滑移单元[J]. 武汉大学学报(工学版), 2014, 47(4): 527-531.
FANG Z H, ZHOU H J, LAI S Y, et al. ABAQUS bond-slip element of reinforced concrete under cyclic loads[J]. Engineering Journal of Wuhan University, 2014, 47(4): 527-531.
[13] ELIGEHAUSEN R, POPOV E P, BERTERO V V. Local bond stress-slip relationship of deformed bars under generalized excitations [R]. California :University of California, 1983.
[14] REN L, FANG Z, ZHONG R, et al. Experimental and numerical investigations of the seismic performance of UHPC box piers[J]. KSCE Journal of Civil Engineering, 2019, 23(2): 597-607.
[15] PAULAY T, PRIESTLY M J N. Seismic design of reinforced concrete and masonry buildings[M]. Hoboken: John Wiley &Sons, Inc., 1992.
[16] PRIESTLEY M J N, PARK R. Strength and ductility of concrete bridge columns under seismic loading[J]. ACI Structural Journal, 1987, 84(1): 61-76.
[17] HINES E M, RESTREPO J I, SEIBLE F. Force-displacement characterization of well-confined bridge piers[J]. ACI Structural Journal, 2004, 101(4): 537-548.
[18] PANAGIOTAKOS T B, FARDIS M N. Deformations of reinforced concrete members at yielding and ultimate[J]. ACI Structural Journal, 2001, 98(2): 135-148.