三维地质模型可以为地质现象、地质资源利用提供直观、虚拟的地质空间[1],在地质调查、资源勘探、城市地下空间管理、地震监测预报等行业具有重要的应用前景。三维地质建模的一般做法是利用钻探、地球物理勘探等多元原始资料构建地层界面,进而建立三维地质模型。考虑到原始数据的离散性[2],三维地质隐式建模[3]中的克里金(Kriging)插值[4]、反距离加权(IDW)插值[5]、径向基函数插值[6]和局部多项式法[7]可以获取连续的分布数据,高效精确地完成地层曲面模型的构建。在以上多种插值方法中,IDW插值以其原理简单、计算简便且符合地理学第一定律等优点在三维地质建模领域被广泛应用[8],国内外学者对其插值参数和自适应的研究也最为广泛[9-13],传统IDW插值方法以各向同性假设为基础,根据点与点之间的距离进行计算,在数据分布均匀的情况下能够快速取得高精度的插值结果,能够有效捕捉地质界面的渐进变化,但对于属性值在某一方向存在较大差异的研究区域,以上IDW插值研究结果精度明显下降,无法全面考虑地质数据的非线性特征及其固有的方向性[14-15] ,表达复杂地质结构上的能力受限。
针对地质空间各向异性特征设计了基于椭圆范围搜索与标志点位置变换的各向异性IDW插值方法,该方法在传统IDW插值的基础上模拟补齐纵向钻孔数据,利用圆形范围分配和交叉验证优化参数组合,通过标志点的膨胀与塌缩二次优化搜索范围,以郑州市城市活动断层探测项目钻孔数据为例,构建了研究范围的三维地质模型,充分考虑了地质空间的非线性属性特征,有效展现区域内的各向异性,通过实例对比分析了本文方法与常用插值算法的优劣。
1 各向异性IDW插值参数的确定
使用钻孔数据进行三维地质建模是最常见的情形[16-17],受资料限制,三维地质建模重点要解决钻孔深度和密度不足导致建模可信度低的问题[18-19]。对地层平缓、结构简单的平原区域,可利用控制性钻孔的深部信息构建虚拟钻孔[20],全面考虑区域地层层序体系、地层统一划分标准[21-22],进行浅孔纵向补齐。本文基于郑州市城市活动断层探测项目33个深度超过100 m的控制性深孔和纵向补齐深部信息的浅孔数据,交叉验证半径和旋转角度参数最优排列组合,快速获取最佳椭圆搜索参数,通过标志点的膨胀与塌缩完成搜索范围的二次优化,实现IDW插值的各向异性,技术思路如图1所示。
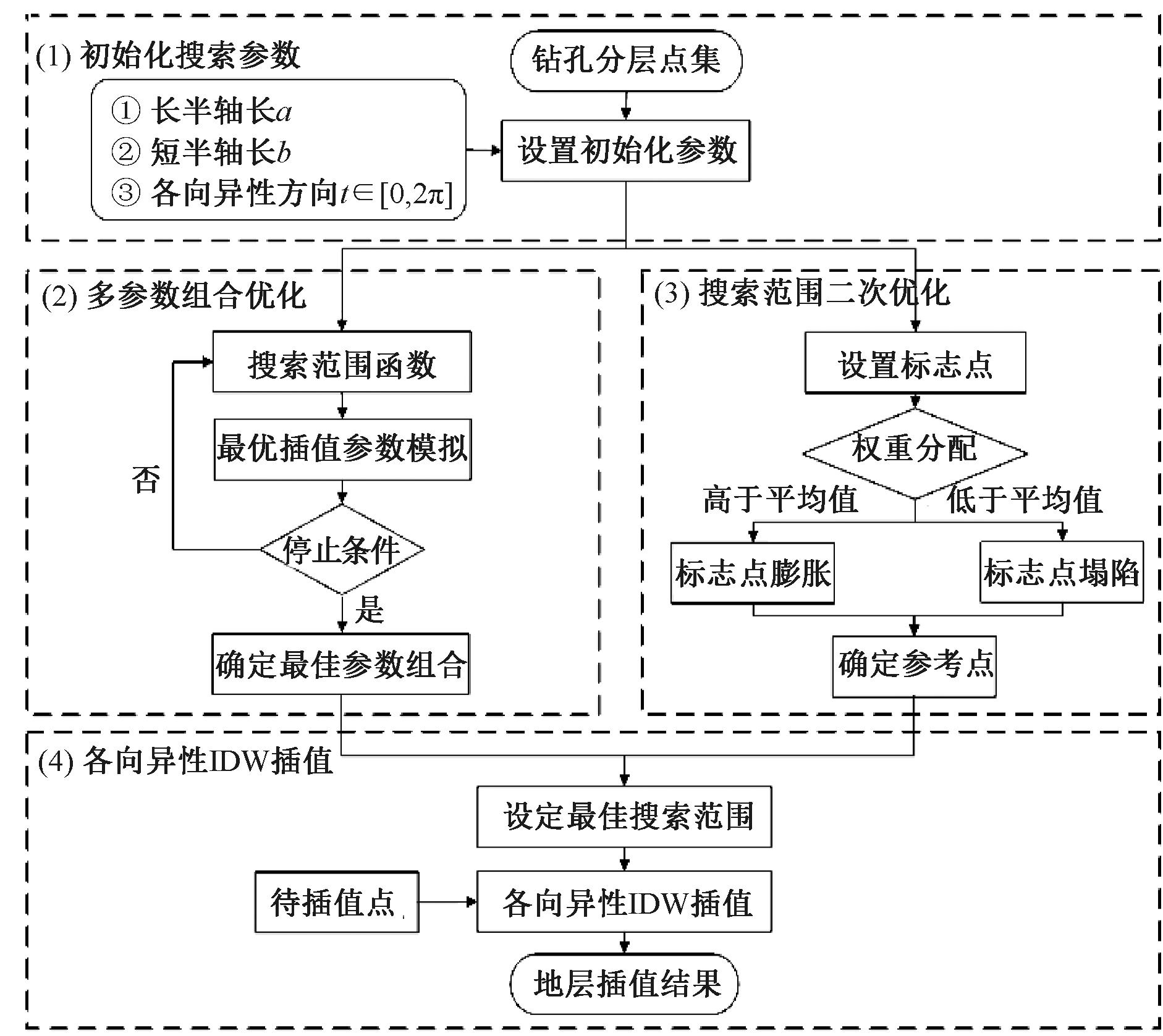
图1 各向异性IDW插值算法流程
Figure 1 Process of anisotropic IDW interpolation algorithm
1.1 各向异性IDW插值参数确定
(1)搜索范围确定。各向异性特征通常表现为数据点在不同方向上的分布密度或变化程度不同,传统的IDW插值搜索半径呈圆形,每个方向的搜索重心一致,无法体现地理空间属性值在不同方向的变化差异[23]。而采用椭圆范围搜索可综合顾及不同方向的搜索重心,实现IDW的各向异性插值。相对于圆形搜索范围,椭圆搜索能够通过调整长轴、短轴的比例,旋转角度,使得搜索范围更好地匹配数据点的实际分布,提高插值的精度和效果。孙梦楠等[24]提出了采用基于最小二乘法的椭圆拟合改进算法来确定椭圆公式,但由于其计算过程需不断随机地重复匹配参数来确定椭圆参数,存在计算量庞大、无法复现其最优解等局限性,本文提出一项新的插值参数模拟方法,通过代入不同半径和旋转角度排列组合,快速得出椭圆搜索参数最优解,搜索方式如图2所示。
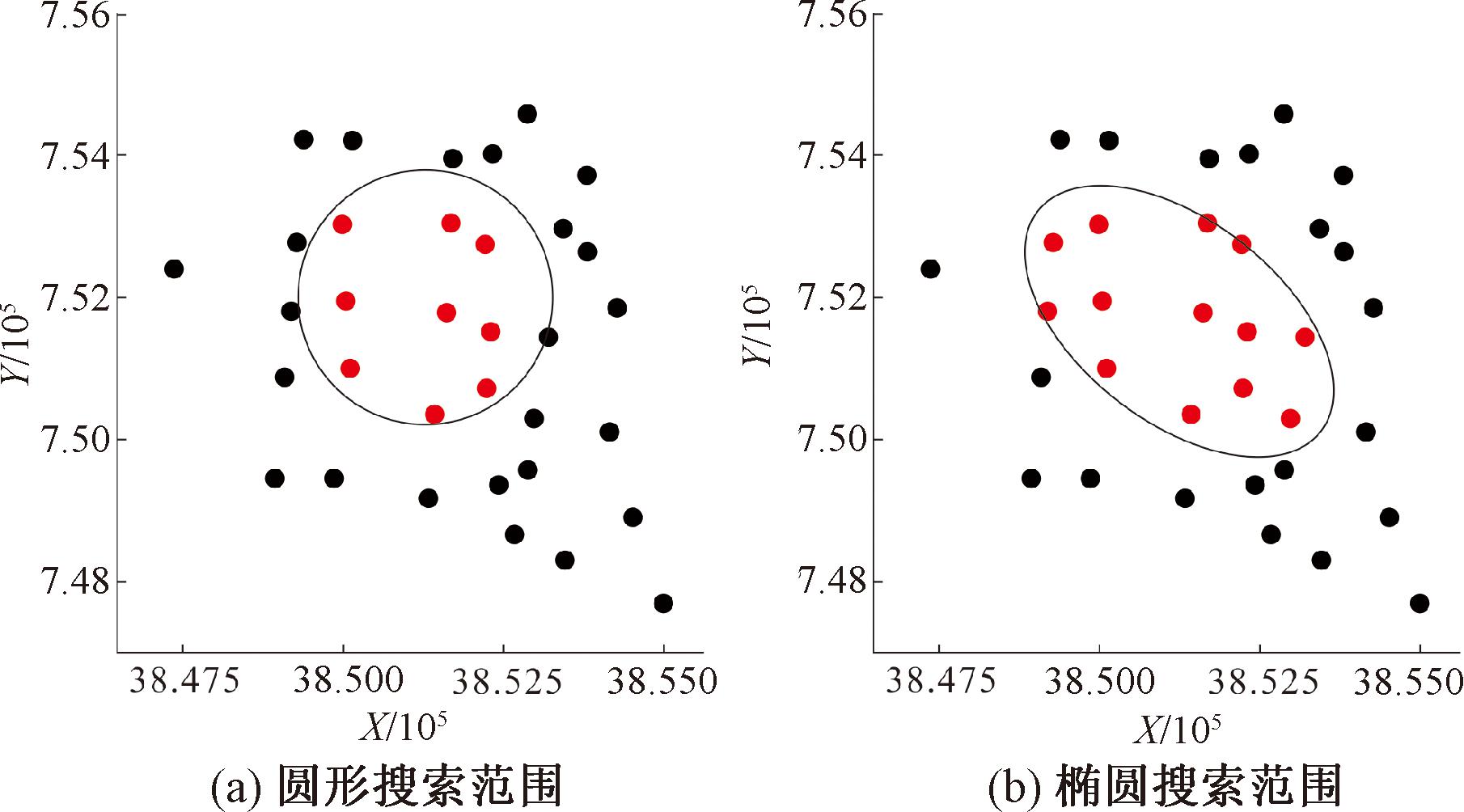
图2 IDW插值搜索范围
Figure 2 IDW interpolation search range
实现椭圆搜索范围重点在于判断参考点与预估点间的距离是否小于预估点到此方向上椭圆边的距离。假设d为参考点与预估点间的距离,参考点坐标为(xi,yi),i=1,2,…,n,预估点坐标为(x0,y0),则两者间的距离为
(1)
设预估点与参考点形成直线与椭圆的交点为(x1,y1),预估点与交点间的距离为d1,则d1可以由椭圆方程和两点间直线的方程联合求解。
(2)
以预估点作为坐标系原点,则两点间的直线公式为
(3)
设椭圆长轴与坐标系x轴间的夹角为t,长半轴长为a,短半轴长为b,则椭圆的标准方程为
(4)
当标准椭圆沿原点旋转了角度t后,建立一个新的u-v坐标系,则存在以下的等量关系:
(5)
将上式代入标准椭圆方程后,即可求得旋转角度t后的椭圆方程:
(6)
若d1≤di,则此数据点被视为参考点;若d1>di,则此数据点不参与预估点属性值的计算。
由上述推导过程可知,合理调整计算过程中椭圆旋转角度t、椭圆长半轴长a及椭圆短半轴长b的数值后,可获取最适用于研究区域地层结构的搜索重心。
(2)最优插值参数模拟。最优插值参数需合理调整椭圆旋转角度t、椭圆长半轴长a及椭圆短半轴长b的数值。
利用不同半径的圆形搜索范围确定参数a、b的取值范围,如表1所示。通过实验发现t取值间隔过大时,无法体现参考点选取的细微差异和各向异性,t取值间隔过小时,椭圆搜索范围会近似趋于圆形,无法达到预期效果,本文将t的取值划分为
和π,讨论5种椭圆旋转角度下的参考点选取方式,如表2所示。
表1 圆形搜索交叉验证结果
Table 1 Cross validation results of circular search
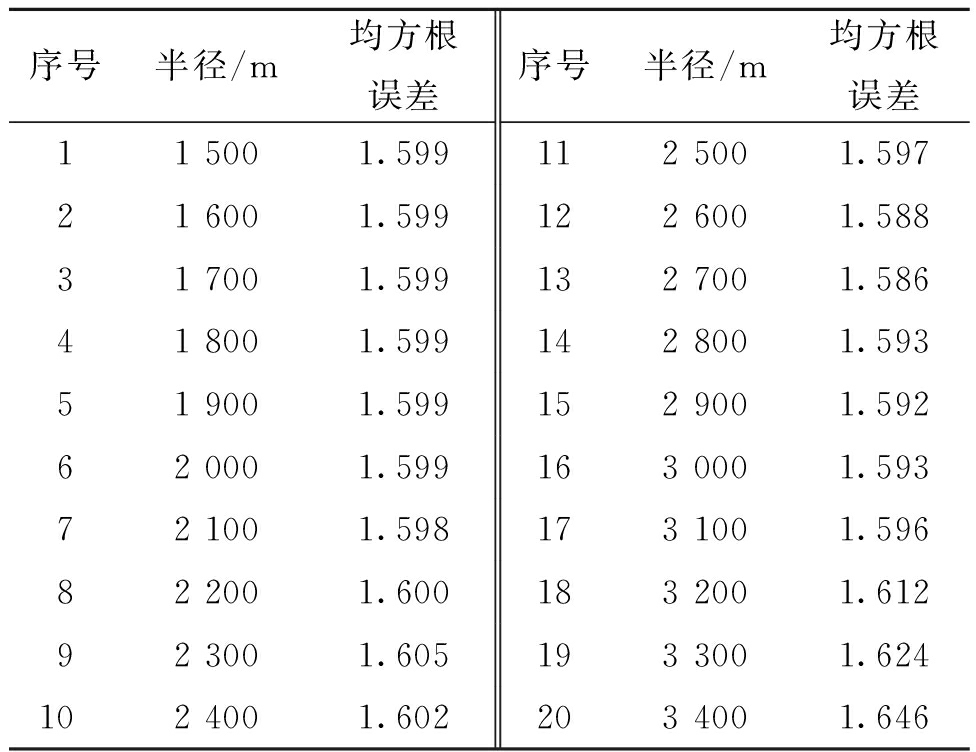
序号半径/m均方根误差序号半径/m均方根误差11 5001.599112 5001.59721 6001.599122 6001.58831 7001.599132 7001.58641 8001.599142 8001.59351 9001.599152 9001.59262 0001.599163 0001.59372 1001.598173 1001.59682 2001.600183 2001.61292 3001.605193 3001.624102 4001.602203 4001.646
表2 各向异性IDW插值最佳结果
Table 2 Best results of anisotropic IDW interpolation
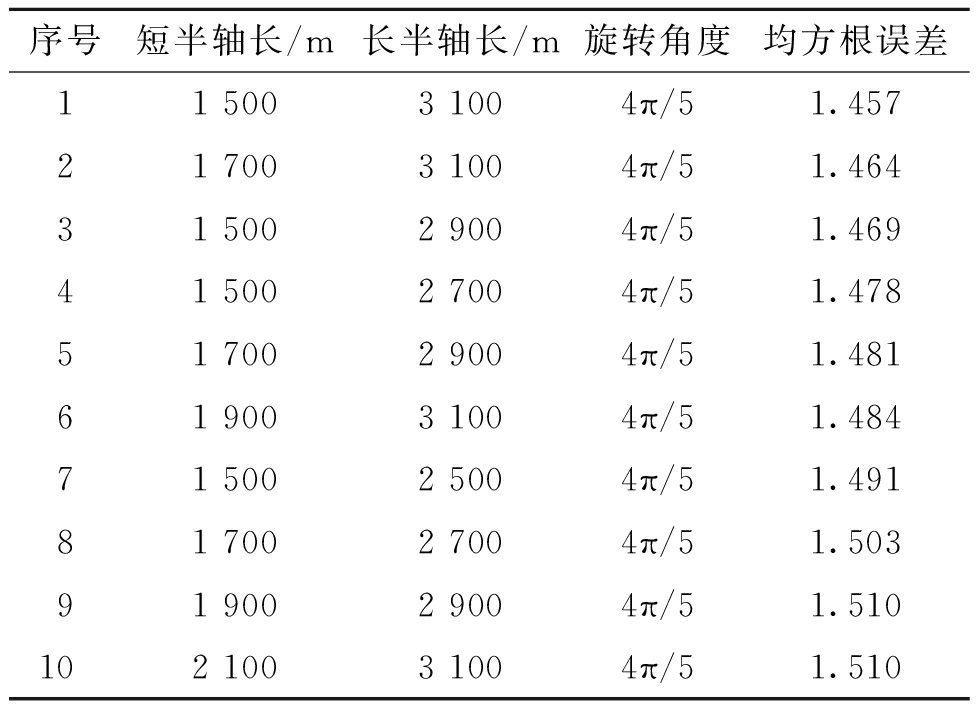
序号短半轴长/m长半轴长/m旋转角度均方根误差11 5003 1004π/51.45721 7003 1004π/51.46431 5002 9004π/51.46941 5002 7004π/51.47851 7002 9004π/51.48161 9003 1004π/51.48471 5002 5004π/51.49181 7002 7004π/51.50391 9002 9004π/51.510102 1003 1004π/51.510
表1中,2 700 m的圆形搜索半径取得了最佳的交叉验证结果,设置a的取值分别为2 300,2 500,2 700,2 900,3 100,以2 700为中心,设置b的取值为1 500,1 700,1 900,2 100,2 300,以长半轴的最小值作为短半轴的最大值,叠加5种旋转角度t构成125种三参数取值组合,表2为均方根误差最小的10种最佳参数组合。
对比发现,在椭圆旋转角度t、椭圆长半轴长a及短半轴长b叠加下,均方根误差由1.586进一步减小为1.457,插值精度提升较大。插值最佳结果的椭圆搜索范围旋转角度均为4π/5,表明本文的研究区域在4π/5方向具有强各向异性特征,进一步证实椭圆搜索范围能更好顾及地质空间的各向异性特征。
1.2 搜索范围优化
李正泉等[25]认为,在各向异性变化最为剧烈的方向投入更多权重是获得较好插值结果的有效途径;本文根据各向异性对比结果,重新制定各方向的权重分配,在这一方向上投入更多搜索重心,进一步优化IDW各向异性插值的搜索结果。针对示例数据,本文提出了一种标志点膨胀与塌缩优化确定各向异性搜索范围的方法,基于已有实验结果为不同方向分配相应的搜索权重。此方法主要包括3个步骤:确定标志点、权重分配与范围划定。
(1)确定标志点。为实现IDW的各向异性插值,基于上文划分的5种椭圆旋转角度t,在圆形最佳搜索范围上创建10个标志点,依次被记为A1～A10,每个标志点距离圆心的距离均为最佳搜索2 700 m,对应的旋转角度分别为
和
如图3(a)所示。
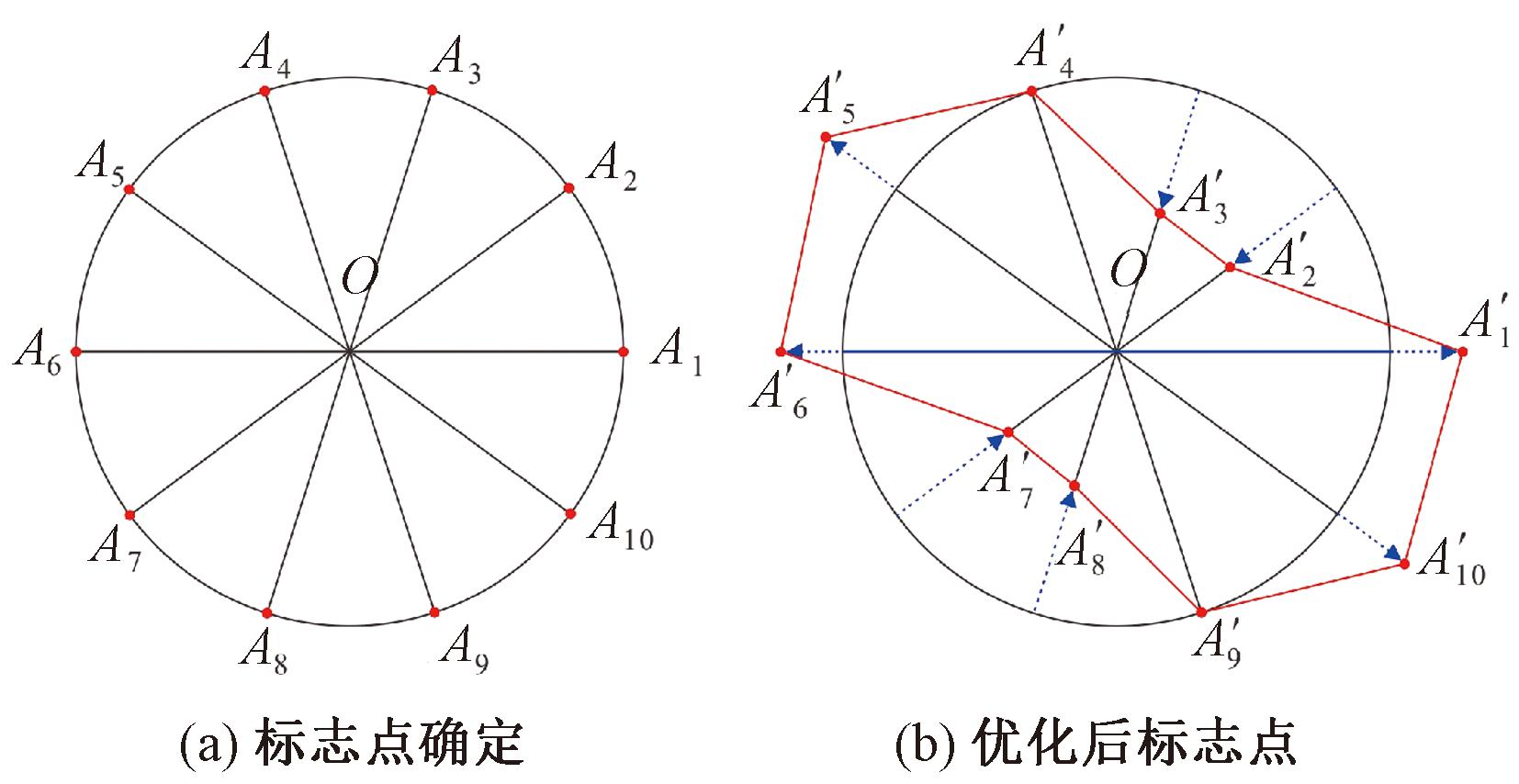
图3 搜索范围二次优化
Figure 3 Results of secondary optimization of search scope
(2)权重分配。如表3所示,在本文示例数据125组参数组合中选择误差较小的前60种组合进行权重分配,将10个旋转角度划分为5组,对异性特征较强方向的标志点膨胀处理,对异性特征较弱方向的标志点塌缩处理,膨胀或塌缩处理方式如下:基于前60组中旋转角度的占比与平均值的差异计算,实现对标志点的位置偏移,每多于平均值1组数据,则标志点沿原方向向外偏移σ,每少于平均值1组数据,则标志点沿原方向向内偏移σ,σ的值可根据研究区域实际应用状况确定。
表3 前60组旋转角度分析
Table 3 Analysis of the first 60 sets of rotation angles
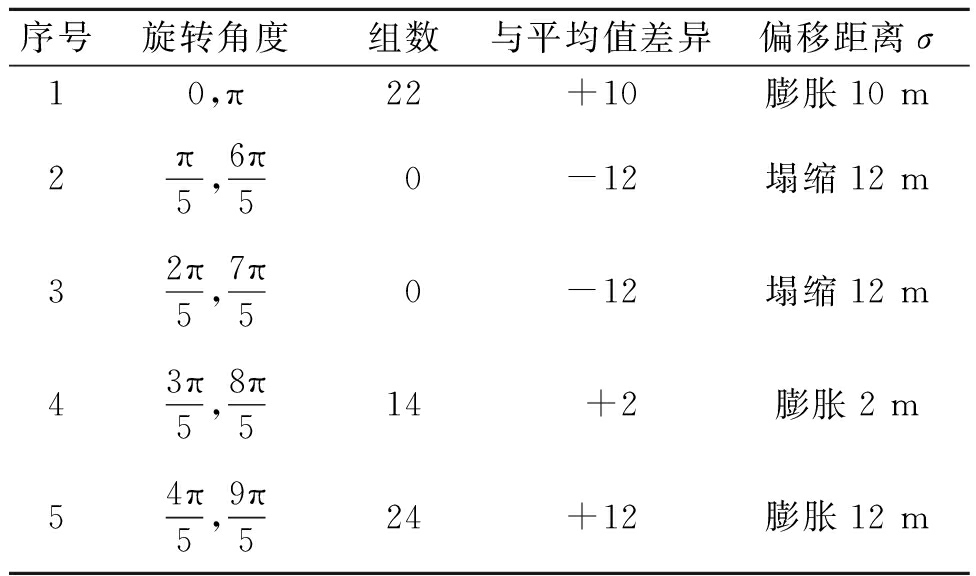
序号旋转角度组数与平均值差异偏移距离σ10,π22+10膨胀10 m2π5,6π50-12塌缩12 m32π5,7π50-12塌缩12 m43π5,8π514+2膨胀2 m54π5,9π524+12膨胀12 m
(3)搜索范围划定。按权重分配进行标志点膨胀或塌缩处理后,依次连接
到
最终形成IDW各向异性插值搜索范围二次优化后的结果(图3)。优化参考点搜索范围后,参考点的选取方式同样改变,需再次判断d1和di的大小确定搜索范围,后续处理方式如下:以区域
为例,在判断数据点M是否可以作为参考点前,首先计算
若
则比较OM与ON的长度,若OM≤ON,则M被视为参考点,如图4所示,反之则不被选用。同理,在其他9个区域也要进行角度计算和距离判断来选择参考点。
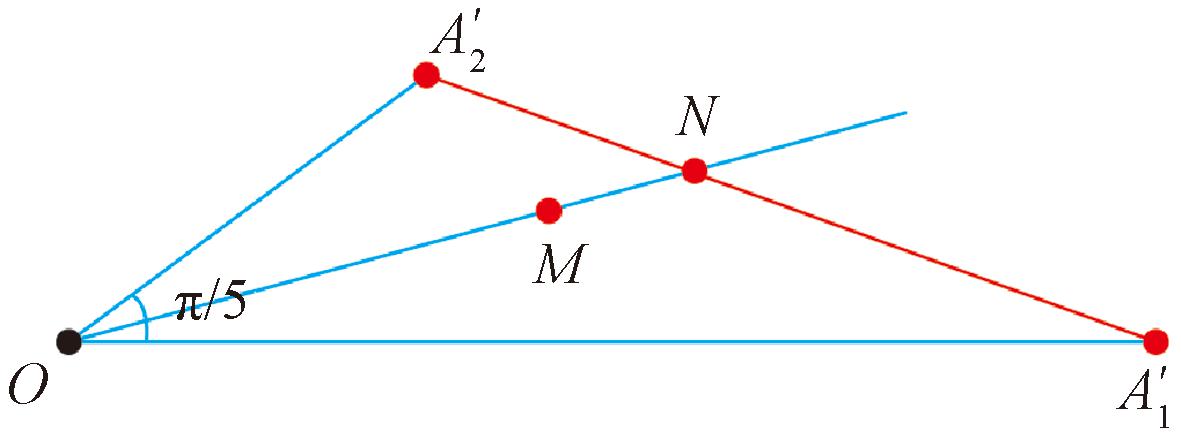
图4 参考点选取示意图
Figure 4 Schematic diagram of reference point selection
2 三维地质建模实例
三维地质建模需要利用控制性钻孔建立标准层序体系,统一时间与岩性信息,建立空间上具有等时意义的三维地质模型[19]。研究区属黄河冲积平原,地势东低西高,地表多为第四纪松散覆盖层,本文参照“河南省平原第四纪地层统一划分标准”,利用部分控制钻孔的测年结果,将所有钻孔按全新统、上更新统、中更新统和下更新统4个时序进行标定[21],提取出5个地层分界点。
以Z0～Z2地层为例,用5种传统插值方法与本文提出的插值方法进行比较,如图5和图6所示。
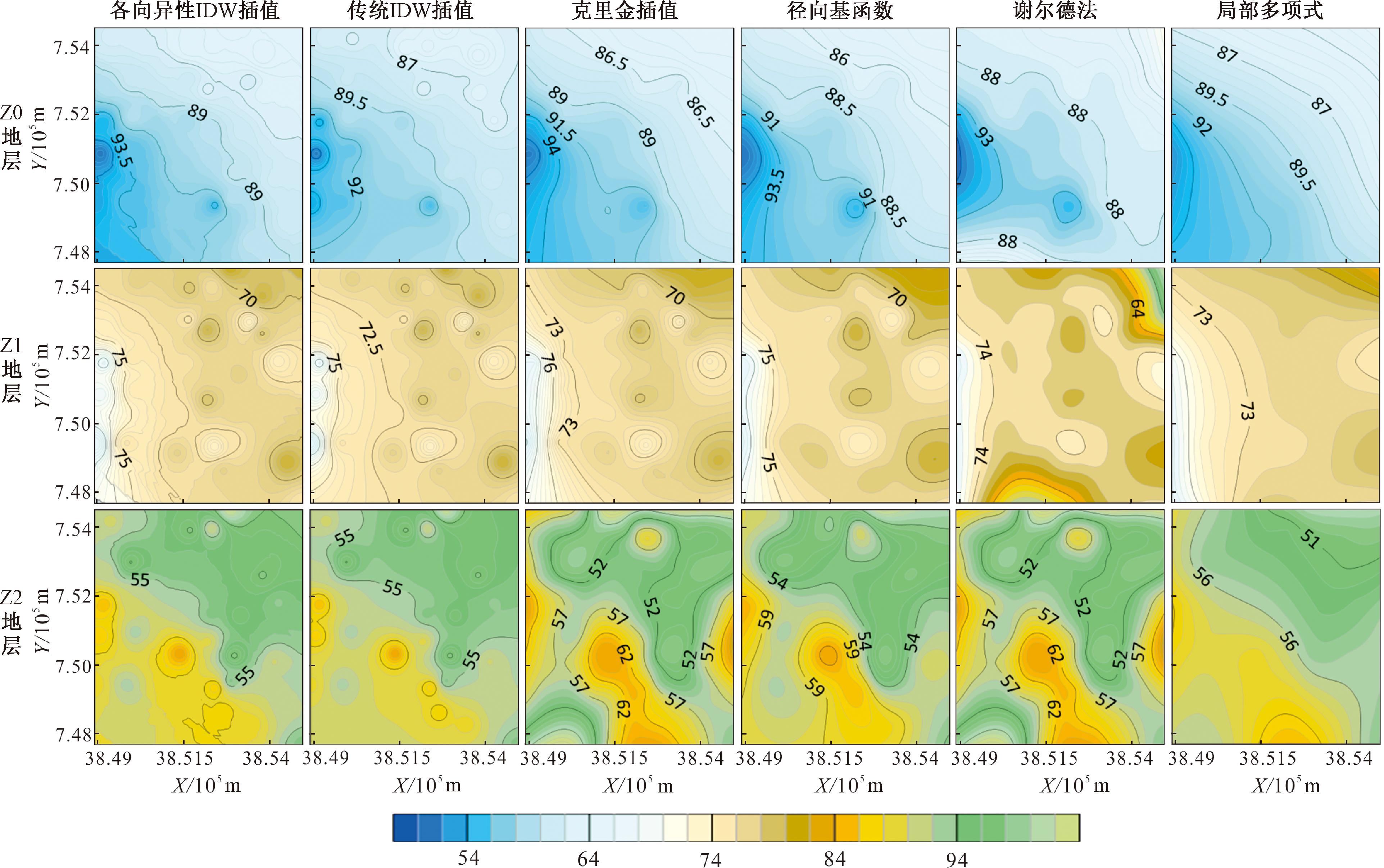
图5 Z0～Z2地层插值效果对比
Figure 5 Comparison of interpolation effects for Z0 to Z2 strata
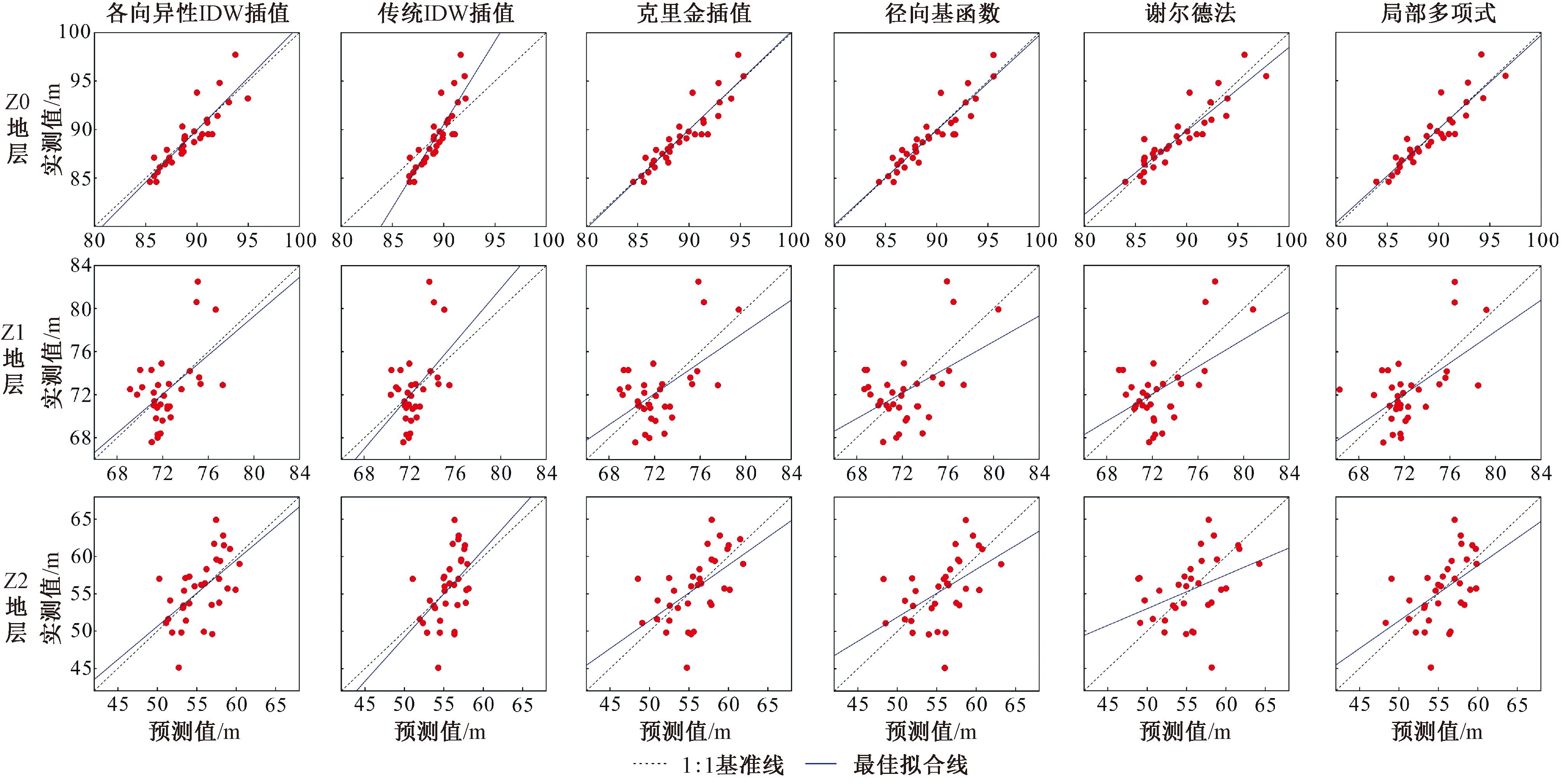
图6 Z0～Z2地层实际值与预测值对比
Figure 6 Comparison between actual and predicted values of Z0 to Z2 strata
从图5可以看出,本文提出的插值方法可最好地表征地质空间的各向异性特征,图6中的实际值和预测值插值精度近似克里金插值方法,较传统IDW插值算法精度提升明显;表4为6个地层界面建模交叉验证结果,对比5种传统插值方法,本文所示各向异性IDW插值方法在最好地表征地质空间的各向异性特征同时,还可实现均方根误差总体最小、大多数地层插值加密效果最好。经过对比分析,本文各向异性IDW插值方法总体效果最佳。
表4 交叉验证结果
Table 4 Cross validation results
地层各向异性IDW传统IDW插值克里金插值径向基函数谢尔德法局部多项式平均误差均方根误差平均误差均方根误差平均误差均方根误差平均误差均方根误差平均误差值均方根误差平均误差均方根误差Z01.077 31.369 41.177 01.600 90.845 31.218 70.935 71.256 41.127 21.421 80.913 91.269 9Z12.102 42.494 22.203 02.852 22.172 32.843 22.223 82.794 02.383 52.973 52.201 02.783 6Z22.660 83.344 83.029 03.805 02.890 63.765 12.875 93.702 73.482 64.503 72.979 13.822 2Z36.368 57.493 06.507 97.669 96.215 47.497 86.925 98.097 58.086 99.815 17.347 19.114 1Z43.105 04.616 25.714 56.783 13.628 55.003 83.152 04.701 94.245 85.627 13.409 04.697 4Z52.867 94.660 95.715 25.581 73.434 74.924 43.072 54.398 34.087 85.289 53.173 14.586 5
图7展示了利用三角网生成的各地层隐式曲面模型结果,以及通过体元填充构建的研究区域三维地质模型。
图7 三维地层曲面和地质模型
Figure 7 Three-dimensional strata surface and geological modeling
3 结论
本文针对传统地质建模插值算法区域特征表达程度不够的问题,提出了一种顾及地质空间各向异性特征的三维地质插值算法,克服了传统插值方法各向同性的局限,有效表达城市区域地下空间结构的各向异性特征。该算法的核心是确定最优的椭圆搜索区域,依据方向标志点二次优化不同方向上的搜索权重,对模型进行最优参数设置;通过与传统插值效果的大量对比实验,证实该算法在地质建模领域的有效性。
(1)在传统IDW插值的基础上,利用长半轴、短半轴、旋转角的不同组合,快速实现区域内各方向的搜索重心转移,提出了一种椭圆搜索范围参数的最优选择思路,通过交叉验证对比确定建模区域的最优搜索参数,解决了传统插值算法无法顾及地质空间各向异性特征、椭圆参数计算繁杂等问题。
(2)提出了方向标志点的概念,结合各向异性IDW插值的结果,进行膨胀和塌缩处理,二次优化搜索区域,赋予区域内各向异性特征较强、方向更大的搜索权重,体现地质空间属性在不同方向的变化差异,提升顾及地质空间各向异性插值算法的精度。
目前,本文提出的顾及地质空间各向异性特征的三维插值算法在地层起伏不剧烈的城市平原区域中得到很好的建模效果,但还缺乏在复杂地质构造或者地层起伏剧烈的研究区域的进一步分析验证。接下来将充分考虑该方法在其他复杂地质条件下的适用性,提高该方法的普适性,充分反映地质空间的真实三维构造。
[1] 李青元, 张洛宜, 曹代勇, 等. 三维地质建模的用途、现状、问题、趋势与建议[J]. 地质与勘探, 2016, 52(4): 759-767.LI Q Y, ZHANG L Y, CAO D Y, et al. Usage, status, problems, trends and suggestions of 3D geological modeling[J]. Geology and Exploration, 2016, 52(4): 759-767.
[2] 李小根, 王安明. 基于GIS的滑坡地质灾害预警预测系统研究[J]. 郑州大学学报(工学版), 2015, 36(1): 114-118.LI X G, WANG A M. The research of the early warning system about the geological disasters based on GIS[J]. Journal of Zhengzhou University (Engineering Science), 2015, 36(1): 114-118.
[3] GUO J T, WANG X L, WANG J M, et al. Three-dimensional geological modeling and spatial analysis from geotechnical borehole data using an implicit surface and marching tetrahedra algorithm[J]. Engineering Geology, 2021, 284: 106047.
[4] 王金鑫, 秦子龙, 曹泽宁, 等. 基于八叉树的修正克里金空间插值算法[J]. 郑州大学学报(工学版), 2021, 42(6): 21-27.WANG J X, QIN Z L, CAO Z N, et al. Modified Kriging spatial interpolation algorithm based on octree mechanism[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(6): 21-27.
[5] 贾立娟. 基于钻孔数据的三维地质建模插值算法研究[D]. 北京: 中国地质大学(北京), 2018.JIA L J. Research on 3D geological modeling interpolation algorithm based on drilling data[D].Beijing: China University of Geosciences, 2018.
[6] 王威, 周杰, 王水林, 等. 基于径向基函数的三维地层分块建模方法研究[J]. 岩土力学, 2012, 33(3): 939-944.WANG W, ZHOU J, WANG S L, et al. Research on three-dimensional modeling of strata block based on radial basis function[J]. Rock and Soil Mechanics, 2012, 33(3): 939-944.
[7] 程明华. 基于GIS的地层产状空间插值方法研究[D]. 北京: 中国地质大学(北京), 2010.CHENG M H. Method research of spatial interpolation for the stratum attitude based on GIS[D].Beijing: China University of Geosciences, 2010.
[8] LI Z L. An enhanced dual IDW method for high-quality geospatial interpolation[J]. Scientific Reports, 2021, 11: 9903.
[9] 冯波, 陈明涛, 岳冬冬, 等. 基于两种插值算法的三维地质建模对比[J]. 吉林大学学报(地球科学版), 2019, 49(4): 1200-1208.FENG B, CHEN M T, YUE D D, et al. Comparison of 3D geological modeling based on two different interpolation methods[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(4): 1200-1208.
[10] CHEN F W, LIU C W. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan[J]. Paddy and Water Environment, 2012, 10(3): 209-222.
[11] 张锦明, 郭丽萍, 张小丹. 反距离加权插值算法中插值参数对DEM插值误差的影响[J]. 测绘科学技术学报, 2012, 29(1): 51-56.ZHANG J M, GUO L P, ZHANG X D. Effects of interpolation parameters in inverse distance weighted method on DEM accuracy[J]. Journal of Geomatics Science and Technology, 2012, 29(1): 51-56.
[12] 段平, 盛业华, 李佳, 等. 自适应的IDW插值方法及其在气温场中的应用[J]. 地理研究, 2014, 33(8): 1417-1426.DUAN P, SHENG Y H, LI J, et al. Adaptive IDW interpolation method and its application in the temperature field[J]. Geographical Research, 2014, 33(8): 1417-1426.
[13] ROBERTS E A, SHELEY R L, LAWRENCE R L. Using sampling and inverse distance weighted modeling for mapping invasive plants[J]. Western North American Naturalist, 2004, 64(3): 312-323.
[14] LI J, DUAN P, SHENG Y H, et al. Spatial interpolation approach based on IDW with anisotropic spatial structures[C]∥SPIE Proceedings International Conference on Intelligent Earth Observing and Applications 2015. Washingtion, D. C.: SPIE, 2015: 1-6.
[15] 颜金彪, 吴波, 何清华. 顾及各向异性的多参数协同优化IDW插值方法[J]. 测绘学报, 2021, 50(5): 675-684.YAN J B, WU B, HE Q H. An anisotropic IDW interpolation method with multiple parameters cooperative optimization[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(5): 675-684.
[16] 李璐, 刘新根, 吴蔚博. 基于钻孔数据的三维地层建模关键技术[J]. 岩土力学, 2018, 39(3): 1056-1062.LI L, LIU X G, WU W B. Key technology of 3D stratum modelling based on borehole data[J]. Rock and Soil Mechanics, 2018, 39(3): 1056-1062.
[17] 徐学闯,张恒兵,符韶华等.基于钻孔伪标签半监督深度学习的沈阳市浅表地层三维建模研究[J].地理与地理信息科学,2023,39(6):9-17.XU X C, ZHANG H B, FU S H, et al. Three-dimensional modeling of shallow strata in shenyang city based on pseudo-labels and semi-supervised deep learning of boreholes[J]. Geography and Geo-information Science, 2023,39(6): 9-17.
[18] 陈应军, 严加永. 澳大利亚三维地质填图进展与实例[J]. 地质与勘探, 2014, 50(5): 884-892.CHEN Y J, YAN J Y. Progress and examples of three-dimensional geological mapping in Australia[J]. Geology and Exploration, 2014, 50(5): 884-892.
[19] 梁栋. 三维地质模型不确定性分析方法研究[D]. 武汉: 中国地质大学, 2021.LIANG D. Research on the methods of uncertainty analysis of three-dimensional geological model[D].Wuhan: China University of Geosciences, 2021.
[20] 林冰仙, 周良辰, 闾国年. 虚拟钻孔控制的三维地质体模型构建方法[J]. 地球信息科学学报, 2013, 15(5): 672-679.LIN B X, ZHOU L C, LYU G N. A 3D geological model construction approach based on virtual boreholes[J]. Journal of Geo-Information Science, 2013, 15(5): 672-679.
[21] 李亦纲, 曲国胜, 陈建强. 城市钻孔数据地下三维地质建模软件的实现[J]. 地质通报, 2005, 24(5): 470-475.LI Y G, QU G S, CHEN J Q. Realization of a 3D subsurface geological modeling software in urban areas based on borehole data[J]. Regional Geology of China, 2005, 24(5): 470-475.
[22] 李健, 刘沛溶, 梁转信, 等. 多源数据融合的规则体元分裂三维地质建模方法[J]. 岩土力学, 2021, 42(4): 1170-1177.LI J, LIU P R, LIANG Z X, et al. Three-dimensional geological modeling method of regular voxel splitting based on multi-source data fusion[J]. Rock and Soil Mechanics, 2021, 42(4): 1170-1177.
[23] LIU Z, ZHANG Z L, ZHOU C Y, et al. An adaptive inverse-distance weighting interpolation method considering spatial differentiation in 3D geological modeling[J]. Geosciences, 2021, 11(2): 51.
[24] 孙梦楠, 刘少华, 刘京城. 顾及空间各向异性的IDW插值算法[J]. 计算机工程与设计, 2020, 41(4): 983-987.SUN M N, LIU S H, LIU J C. IDW interpolation algorithm considering spatial anisotropy[J]. Computer Engineering and Design, 2020, 41(4): 983-987.
[25] 李正泉, 吴尧祥. 顾及方向遮蔽性的反距离权重插值法[J]. 测绘学报, 2015, 44(1): 91-98.LI Z Q, WU Y X. Inverse distance weighted interpolation involving position shading[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 91-98.