由于电厂复杂运行环境、燃料内杂质及自身设计特点等影响,燃气轮机在运行维护以及健康管理方面难以满足使用需求。传统的运维策略是根据设计预期的失效周期,定期进行维护。进行维护时,有的部件可能已经故障,这会造成机组整体失效或者其他重大事故。此外,在燃气轮机健康管理系统方面还存在许多问题。例如:燃气轮机各零部件特征参数的数据庞大且复杂,它们在系统中分布广泛且难以联系,难以对燃气轮机运行状态进行分析;系统内构建的模型结构简单,功能较少,数字化程度较低,难以准确反映燃气轮机的实时状态以及各项参数的实时变化[1]。
近年来,以数据为核心的数字孪生[2]技术被应用在智能制造[3]、结构设计[4]、资源优选[5]等方面。王睿瑞等[6]使用数字孪生技术构建船用燃气轮机健康管理工业互联网平台。张旭辉等[7]提出将数字孪生技术、混合现实技术与设备辅助维修方法相融合,构建基于数字孪生的复杂机电设备维修指导总体模型和技术框架。杨悦等[8]将数字孪生技术与叶片水射流表面强化工艺进行结合,为强化工艺的选择以及优化提供决策支持。Xu等[9]将数字孪生引入核电装备维修决策系统,提出数字孪生驱动的核电装备智能维修决策新模式。
压气机是燃气轮机的三大重要部件之一,与燃气轮机发电效率相关。在运行过程中,气体中的杂质会黏附在压气机叶片上,杂质不仅会堵塞气体的进气通道,还会侵蚀压气机叶片,造成燃气轮机发电效率下降。研究表明,水洗是最常见高效的恢复性能的方法[10]。为保证燃气轮机高效运行,找到合适的水洗周期对压气机进行水洗就十分必要。
韩朝兵等[11]通过多元非线性回归模型预测燃气轮机性能衰退,认为燃气轮机功率衰减约5.54%时适合进行水洗,这种方法对拟合系数要求极高,且计算量大。陈家伦等[12]利用BP神经网络对机组数据进行分析,得到性能参数随时间变化的曲线,认为性能参数偏差在3%~5%适合水洗,该方法从多角度进行预测,但未得出综合性结论。Rao等[13]提出基于压气机实时结垢情况制定水洗计划,此法部分依赖于假设,对真实运行情况的拟合不一定准确。汪祖民等[14]使用DBSCAN_GAN_XGBOOST模型对网络异常数据流中的稀有攻击类别流量进行预测,使用DBSCAN算法对数据进行聚类处理,GAN算法对数据进行扩充,XGBOOST算法对模型进行训练,预测效果良好。Choi等[15]提出基于XGBoost算法对瞬时睡意进行预测的框架,通过该框架检测睡意,预测效果良好。
因此,本文提出一种基于数字孪生的电厂燃气轮机健康管理框架,通过该框架,使用XGBoost[16]模型对燃气轮机压气机水洗周期进行预测。
1 基于数字孪生的电厂燃气轮机健康管理框架
1.1 数字孪生
数字孪生技术是利用实体装备物理模型、设备运行历史数据及设备上传感器所采集的实时数据等,在信息世界中完成映射,反映相对应实体装备全生命周期过程。通过这个多学科、多尺度、多维度的仿真过程,将信息世界与物理世界融合。
1.2 电厂燃气轮机健康管理系统框架
融合数字孪生的电厂燃气轮机健康管理系统框架如图1所示。它由物理层、数据层、模型层以及应用层组成。
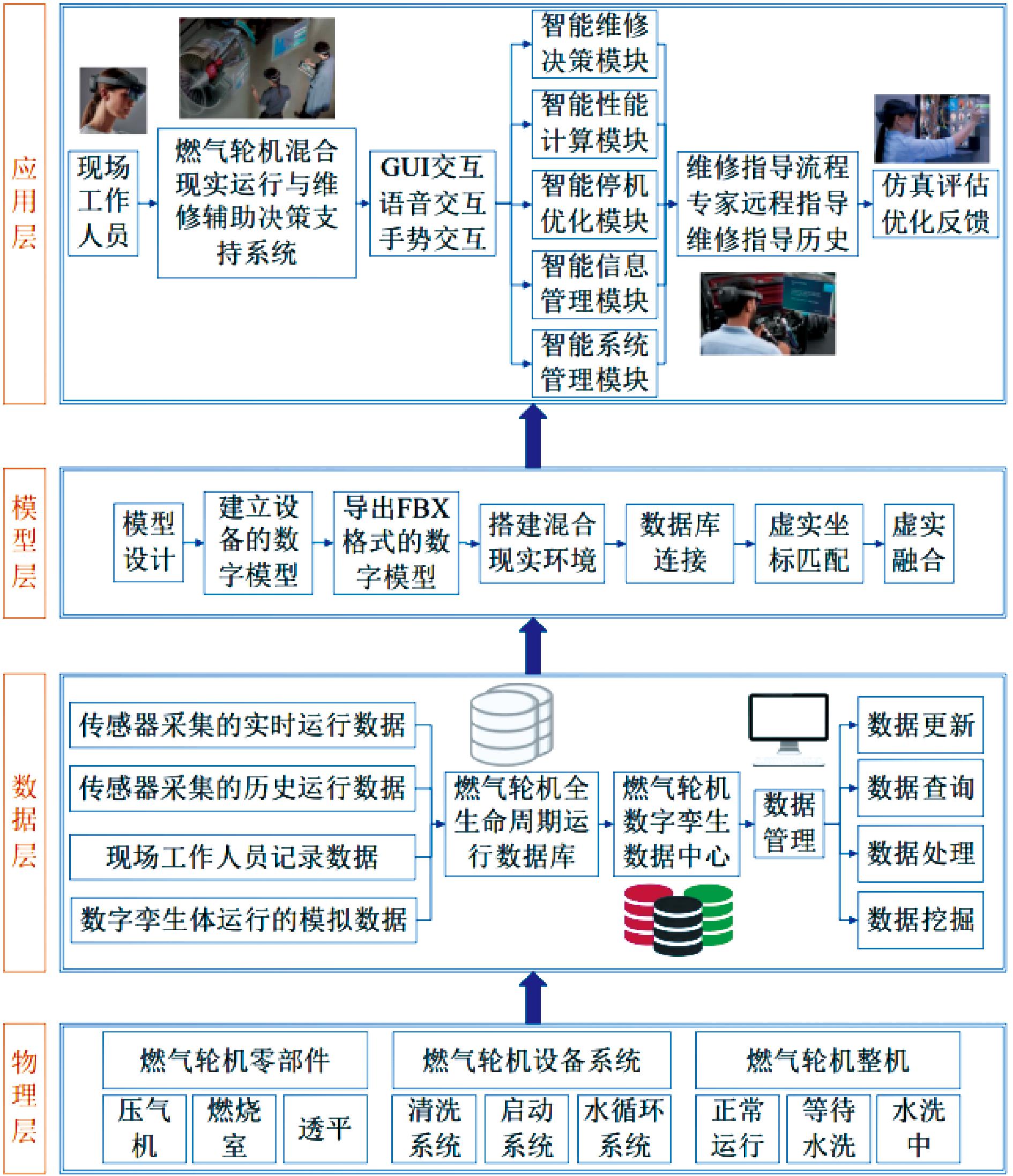
图1 融合数字孪生的电厂燃气轮机健康管理系统框架
Figure 1 Framework of power plant gas turbine health management system integrating digital twin
物理层研究的目标对象包括压气机、燃烧室、透平等燃气轮机零部件,启动系统、水循环系统、清洗系统等设备系统和各状态的燃气轮机等。
模型层通过模型设计和在unity中搭建混合现实环境,构建燃气轮机数字孪生模型,再通过数据库连接和虚实坐标匹配,将燃气轮机在物理层与模型层进行虚实结合。
数据层将各种传感器采集的燃气轮机运行数据、现场记录的数据和模型运行的模拟数据上传到燃气轮机全生命周期运行数据库中,在客户端的燃气轮机数字孪生数据中心,通过连接数据库进行数据更新、数据查询、数据处理以及数据挖掘等工作。物理层与模型层进行交互时,物理层内燃气轮机实时数据作为模型层的输入,而模型层内通过模型分析得到的决策指令则作为输出传递回物理层。
应用层通过现场工作人员佩戴HoloLens,再通过燃气轮机混合现实运行与维修辅助决策支持系统,进行语音、手势以及GUI交互,通过各种模块,帮助专家和工作人员对燃气轮机实时运行状态进行追踪,及时提供故障报警,对燃气轮机的维修决策进行高效指导,也可对燃气轮机模型进行仿真评估和优化反馈,对健康管理系统进行完善。
1.3 基于健康管理框架的水洗周期预测流程
根据上述融合数字孪生的电厂燃气轮机健康管理框架,对燃气轮机压气机水洗周期进行预测,其流程如图2所示。
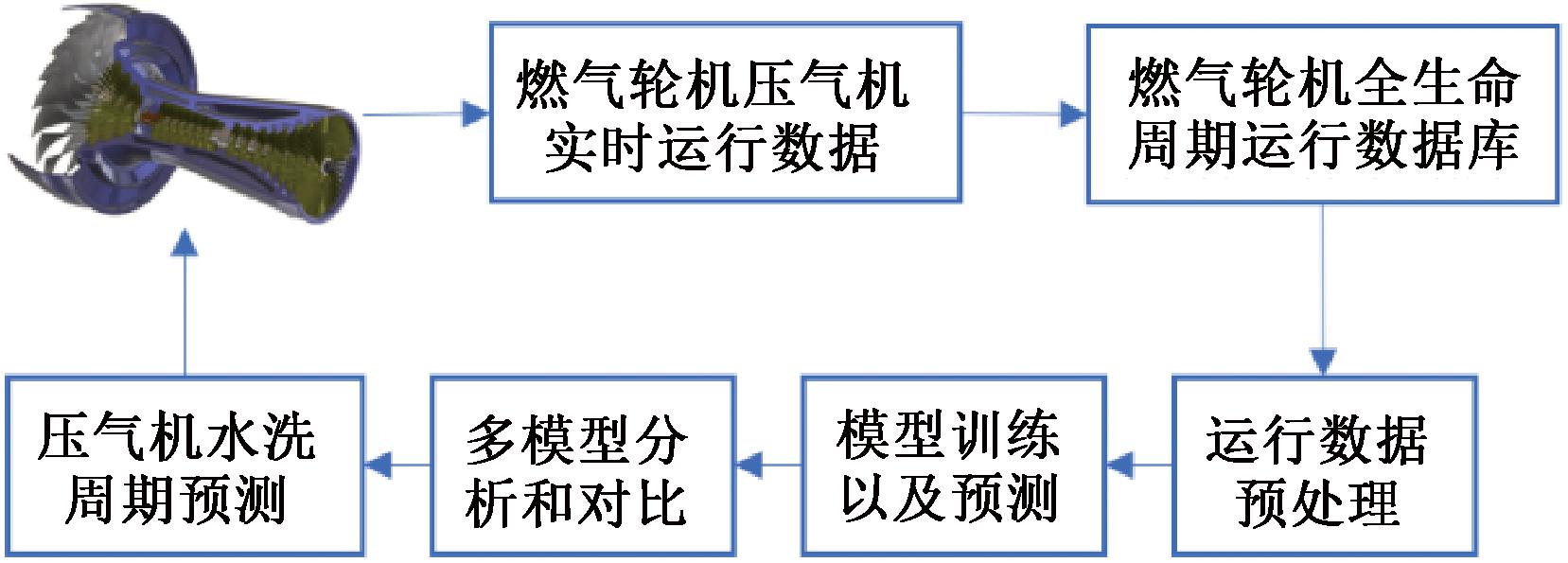
图2 水洗周期预测流程
Figure 2 Water washing cycle prediction process
2 水洗周期预测模型介绍与数据处理
2.1 XGBoost模型原理
XGBoost模型是由K个分模型累加形成的一个加法模型,通过其目标函数得出预测的结果。目标函数为
(1)
式中:Obj为目标函数;i为数据集中的第i个样本;yi为第i个样本的真实值;![]() 为第i个样本xi的预测值;
为第i个样本xi的预测值;![]() 为损失函数;Ω(fk)为正则化项。
为损失函数;Ω(fk)为正则化项。
第t次学习得到的模型函数为
(2)
式中:Obj(t)为第t次学习得到的模型目标函数;Ω(ft)为第t次学习时,模型的正则化项;yi为第i个样本的真实值;![]() 为第t次学习时,模型对于第i个样本xi的预测值;C为常量。
为第t次学习时,模型对于第i个样本xi的预测值;C为常量。
模型训练时,决策树从根部开始生长,通过节点条件将节点分成左右2个新节点,并将原节点权值按照该节点条件分给新节点,不断分裂直至停止。当损失函数没有增益、树达到预设深度或新节点样本数过少时,树停止生长,模型训练完成。
2.2 数据来源
本文选取PG9351FA型燃气轮机压气机运行数据集,从中提取包括大气压力、燃机出功和天然气量在内的10个特征值。选取时间跨度为2019年9月15日至2021年10月25日期间压气机进行水洗前后2 h的运行数据,数据样本的时间间隔为30 s,共10 812条运行数据。在此期间,压气机进行8次水洗。
2.3 数据预处理
先剔除数据集中空值、异常值以及未正常运行时的值。由于气耗量在水洗前已处于很高水平,故以水洗开始时刻为节点,将数据分为水洗前后压气机运行状况。将水洗数据中各个参数的最大值、最小值、平均数和标准差分别计算,其结果如表1所示。
表1 水洗数据统计量列表
Table 1 Statistics list of water washing data

统计量大气压力/kPa压气机进口空气温度/℃压气机排气空气压力/kPa压气机排气空气温度/℃压气机转速/(r·s-1)燃机出功/MW天然气量/kg天然气进口温度/℃烟气出口温度/℃气耗量/(kg·MW-1)最大值102.6834.871.80432.7950.150279.6254 086.3724.16603.862 541.56最小值99.542.400.89255.8549.9607.2818 050.397.98277.83192.09平均数101.1120.181.28376.6750.000157.6736 569.5016.36559.69261.54标准差0.858.860.2430.940.01462.558 883.723.8059.53120.20
2.4 特征提取
由于数据集中的数据量纲并非全部相同,且数据间数量级相差太大,会降低模型梯度下降求取最佳值的速度,因此需先将这些数据进行归一化处理。本文采用最大最小值归一化方法[17],将它们全部转化成[0,1]上的无量纲数据。最大最小值归一化方法的转换函数公式为
(3)
式中:min(x)表示某特征参数数据里面的最小值;max(x)表示其中的最大值;x则表示这些数据中的某一个值;x′则为经过归一化处理后的值。部分参数经归一化处理后的分布曲线如图3所示。
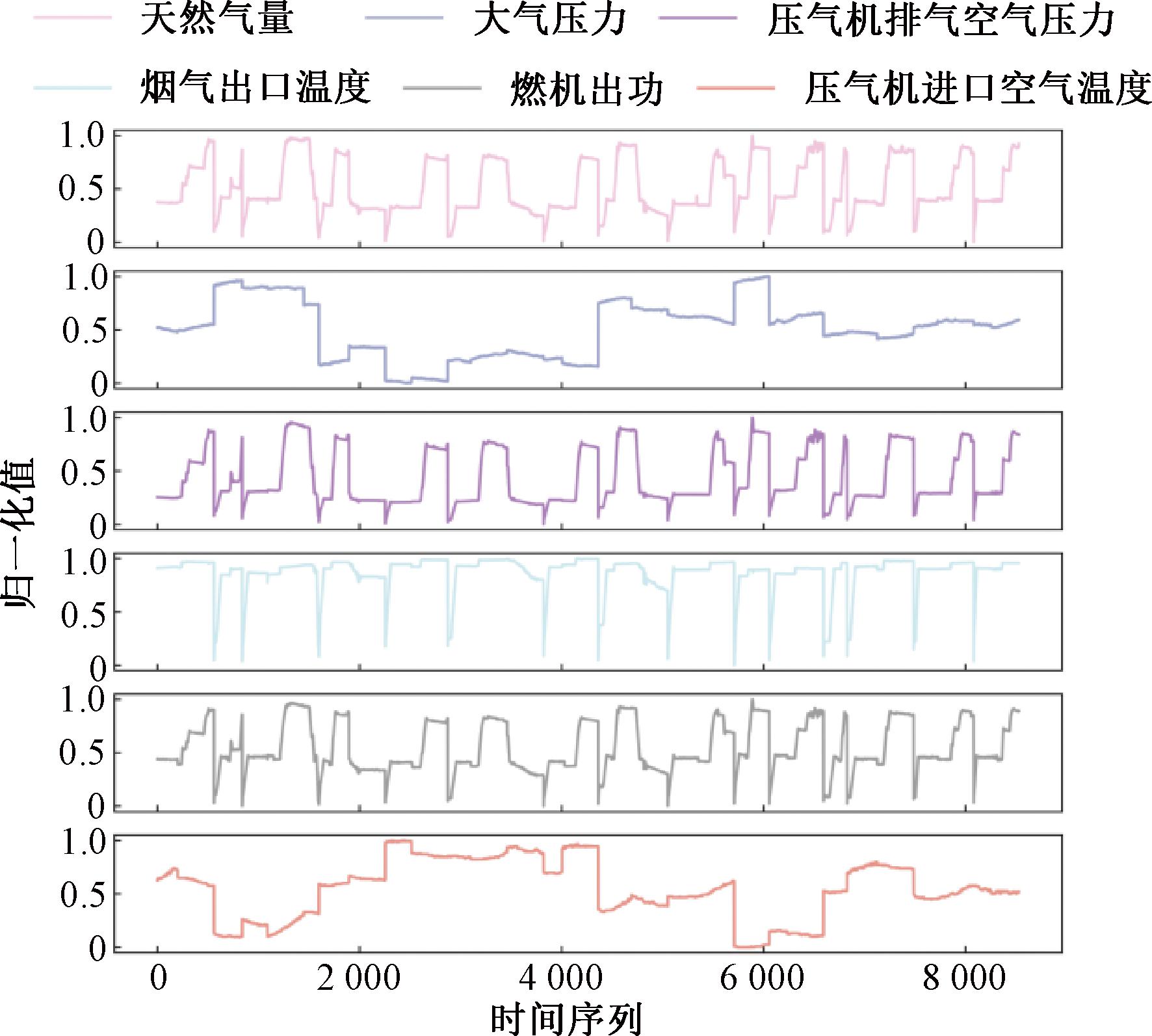
图3 部分特征归一化后的分布曲线
Figure 3 Normalized distribution curve of some features
由于这些特征参数在模型中对气耗量预测的影响程度各不相同,为优化模型训练效果,同时降低数据维度,对这些经过归一化处理之后的数据进行特征选择。本文使用模型中的“weight”权重计算方式,将重要特征筛选出来。该参数表示某个特征参数在全部树分裂节点时被使用的次数。
燃气出功在模型训练时的“weight”值最高,说明其与气耗量强相关;其次是天然气量“weight”值,再次是压气机排气空气压力“weight”值,它们与气耗量也相关;烟气出口温度和压气机排气空气温度“weight”值最低,都与气耗量弱相关。根据表1和图3可知,大气压力、压气机转速和天然气进口温度等参数在模型训练时作用小,应剔除它们。
3 压气机离线水洗周期预测方法
3.1 水洗周期预测方法
压气机正常运行时,气耗量基本不变,当其受污垢影响时,为维持燃气轮机功率,气耗量升高,对电厂经济效益产生极大影响。此外,气耗量与燃机出功、天然气量及大气压力之间具有强相关性。由表1可知,大气压力变化很小,是因为压气机海拔高度不变;压气机转速在正常运行时基本保持不变,故其变化小;受到污垢影响的天然气量变化大,预测难度大。故本文通过预测气耗量对水洗周期进行预测。
数据经过前期处理后,输入XGBoost模型中进行训练,得到气耗量预测模型并进行预测。然后对预测效果进行评价,通过对恢复率计算比较,找出最佳水洗周期,预测流程如图4所示。
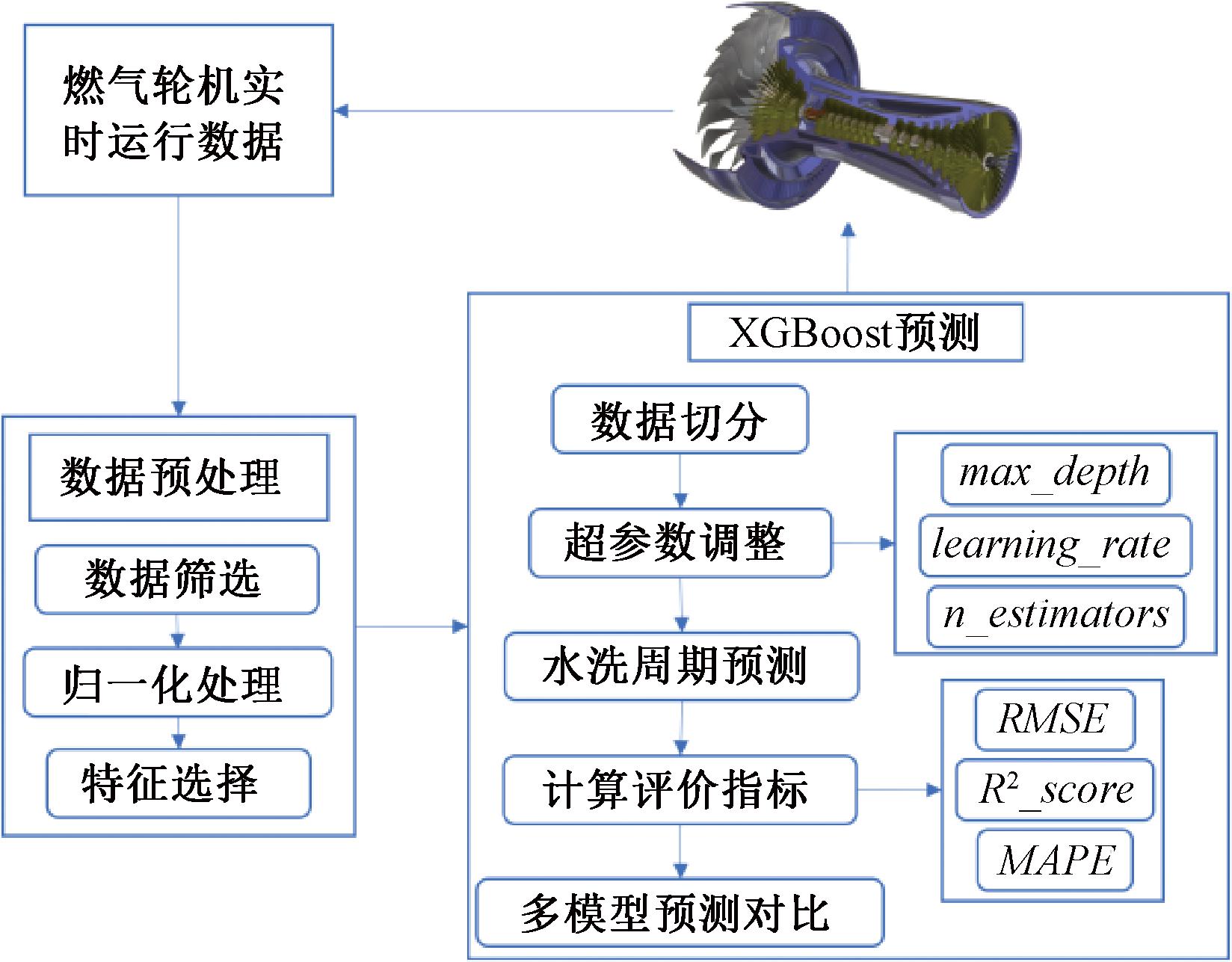
图4 XGBoost预测流程图
Figure 4 XGBoost forecast flowchart
3.2 模型训练以及调参过程
用Python将数据集里70%数据设置成训练集,30%为预测集。对模型超参数进行调整,选择最大深度(max_depth)[18]、学习率(learning_rate)[19]及弱评估器(n_estimators)[20]对模型进行调整。max_depth限制树生长的深度,learning_rate决定模型学习速度,n_estimators估计模型精确性。通过网格化搜索在不同区间内调整超参数,直至找到最优解。设置好最优参数后,读取训练集对模型进行训练。
3.3 模型训练评价指标
预测完成后,通过评价指标对模型预测效果进行判断。本文选择计算均方根误差RMSE[21]、线性回归决定系数R2_score[22]、平均绝对百分比误差MAPE[23]评估模型预测效果。计算公式分别为
(4)
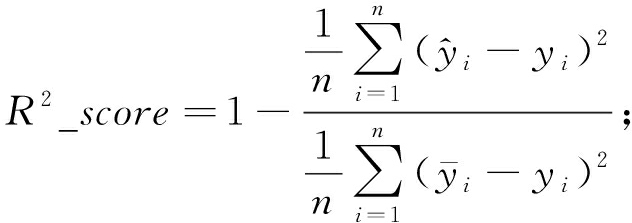
(5)
(6)
式中:n表示预测样本点数;yi表示气耗量真实值;![]() 表示气耗量预测值;
表示气耗量预测值;![]() 表示气耗量真实值的均值。RMSE越接近0、R2_score越接近1、MAPE越接近0,说明模型预测效果越好。
表示气耗量真实值的均值。RMSE越接近0、R2_score越接近1、MAPE越接近0,说明模型预测效果越好。
4 实例分析与验证
4.1 预测结果
经模型预测,水洗前后气耗量真实值与预测值对比如图5和图6所示。水洗前后预测的MAPE、RMSE和R2_score如表2所示。
表2 水洗前后各评价指标
Table 2 Evaluation indexes before and after washing
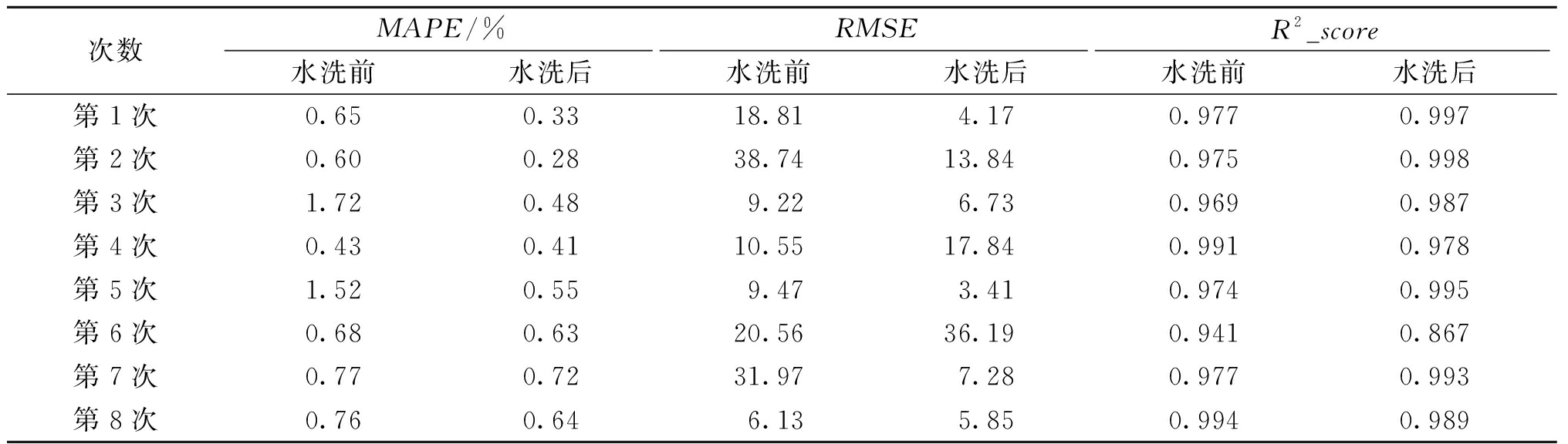
次数MAPE/%RMSER2_score水洗前水洗后水洗前水洗后水洗前水洗后第1次0.650.3318.814.170.9770.997第2次0.600.2838.7413.840.9750.998第3次1.720.489.226.730.9690.987第4次0.430.4110.5517.840.9910.978第5次1.520.559.473.410.9740.995第6次0.680.6320.5636.190.9410.867第7次0.770.7231.977.280.9770.993第8次0.760.646.135.850.9940.989
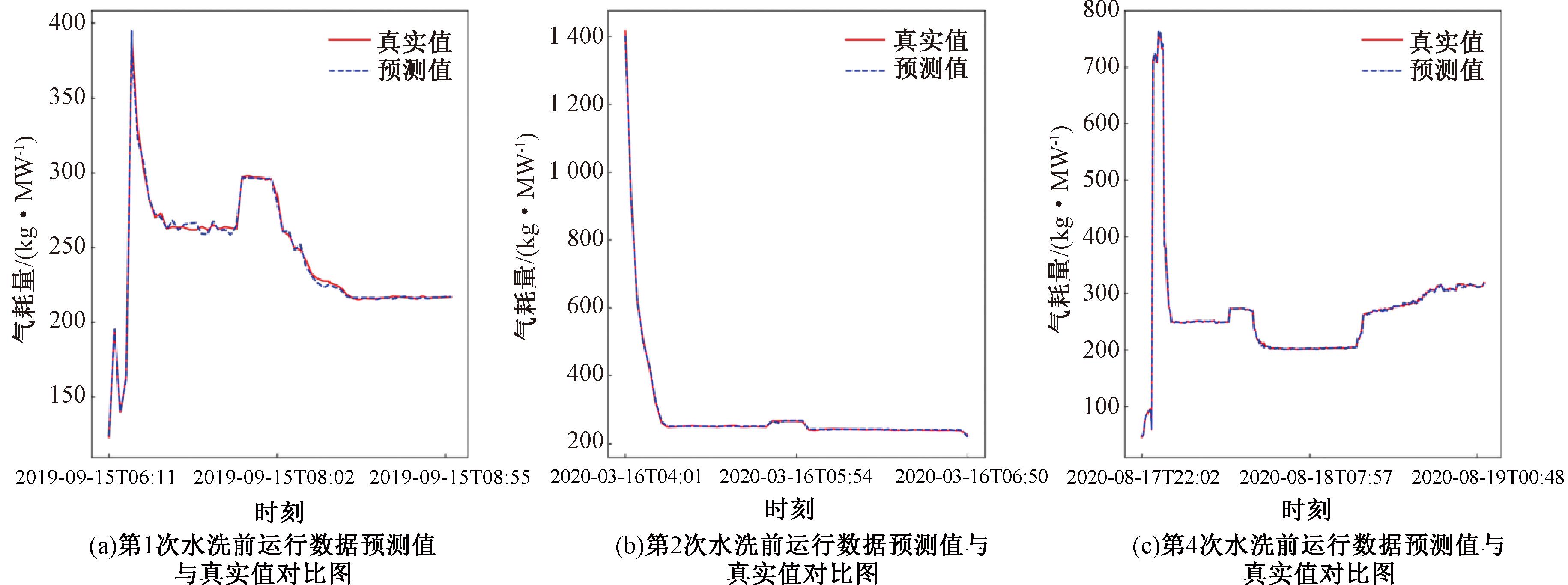
图5 水洗前运行数据真实值与预测值对比图
Figure 5 Comparison between the actual and predicted values of the operation data before washing
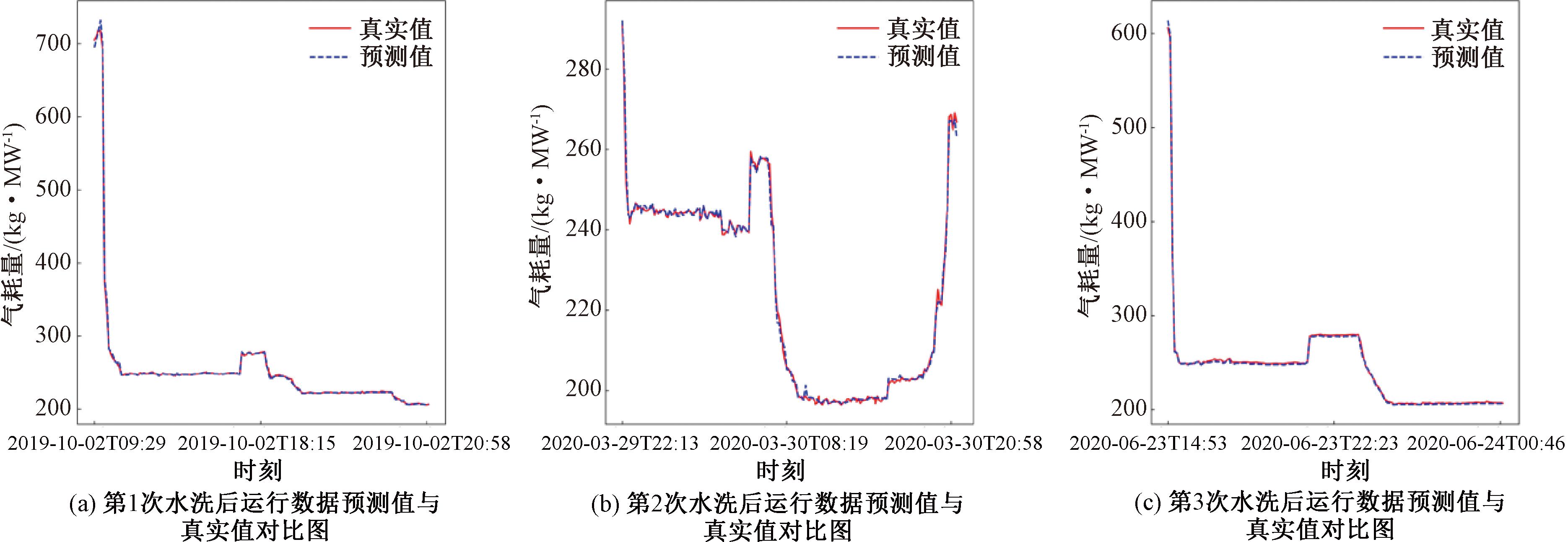
图6 水洗后运行数据真实值与预测值对比图
Figure 6 Comparison between the actual and predicted values of the operation data after washing
从图5、6可知,经过XGBoost模型的预测,气耗量预测值曲线与真实值曲线高度重合,误差很低,该模型预测效果很好。
由表2可知,MAPE在8次水洗前阶段平均值仅0.89%,8次水洗后阶段的平均值仅0.51%,8次水洗的平均MAPE为0.699 1%,都接近于0,说明模型预测效果良好。
由表2可知,8次水洗前后阶段RMSE总体来说都处在较低的范围,RMSE的平均值为15.05。
由表2可知,水洗前后运行阶段,8次水洗的平均R2_score为0.975 1,数值接近于1,说明模型预测的结果误差很低。此外,第6次水洗后预测效果差,根据数据分析,发现是作为输入变量的参数在部分时间段内数据波动很小,而气耗量在这些时间段内出现较大变化,这就使得模型预测效果一般。
综上所述,本文使用的模型对气耗量的预测效果良好,这些得益于对XGBoost模型预测超参数的选择以及调整、数据处理方法的选择等等。
4.2 离线水洗的运行数据预测结果分析及周期优化
本文使用水洗恢复率作为判定水洗效果好坏的指标。水洗恢复率为
(7)
式中:RR为水洗恢复率;GCB为水洗前气耗量;
GCA为水洗后气耗量。
由XGBoost模型预测得到的水洗前后的气耗量、水洗开始时刻、恢复率和间隔时间如表3所示。
表3 由XGBoost预测的水洗过程各项指标
Table 3 Various indicators of the washing process predicted by XGBoost
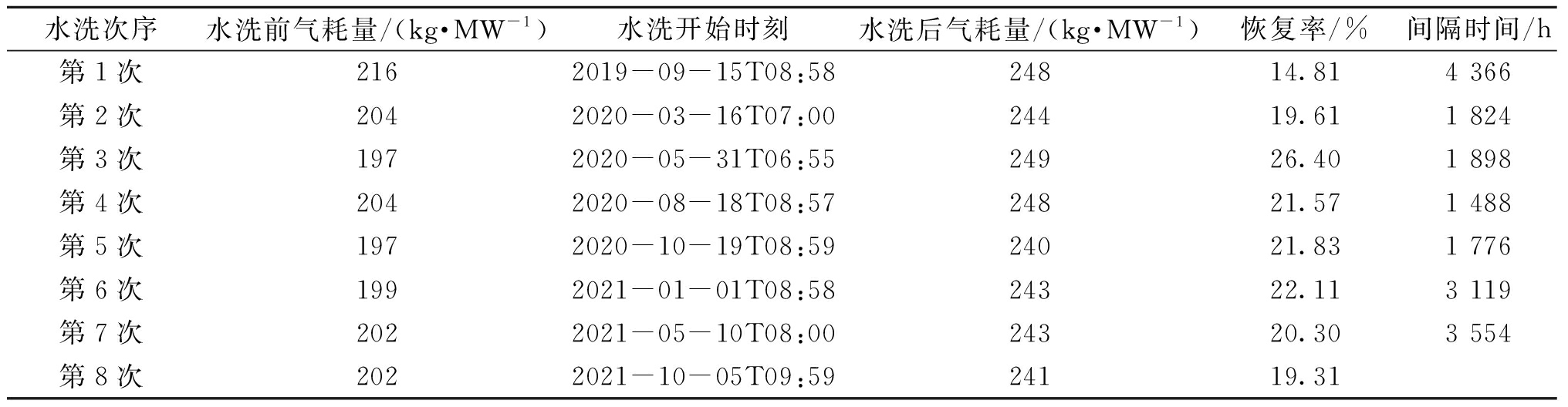
水洗次序水洗前气耗量/(kg·MW-1)水洗开始时刻水洗后气耗量/(kg·MW-1)恢复率/%间隔时间/h第1次2162019-09-15T08:5824814.814 366第2次2042020-03-16T07:0024419.611 824第3次1972020-05-31T06:5524926.401 898第4次2042020-08-18T08:5724821.571 488第5次1972020-10-19T08:5924021.831 776第6次1992021-01-01T08:5824322.113 119第7次2022021-05-10T08:0024320.303 554第8次2022021-10-05T09:5924119.31
由表3可知,第1,2次水洗,第6,7次水洗和第7,8次水洗间隔时间太长,水洗前气耗量过高,压气机已处于异常状态;第4,5次水洗间隔短,与第2,3次水洗相比,水洗前气耗量相同,但第3次水洗恢复率更高,经济效益更好;其他水洗周期接近,但恢复率都低于第3次水洗。综合得出最佳水洗周期为第2、3次,水洗间隔1 824 h。
燃气轮机在完成水洗后实际运行3 529 h[24]。
水洗成本包括洗涤剂成本、启动成本和水洗耗电量成本。每次水洗洗涤剂40 L约为1 600元;水洗需要将洗涤剂加热至80 ℃才能启动,其耗电量约为644 kW·h;水洗需要耗时8 h左右,上网电价享受补贴1.024元/(kW·h),压气机在水洗状态下,燃料消耗量为0.270 2 kg/(kW·h)。电厂水洗平均成本为1.284 5万元/h[25],该电厂水洗成本约为4 533万元。经模型预测后,选择水洗周期为1 824 h,此时水洗成本约为2 343万元。与电厂实际执行的水洗周期相比,每次水洗成本可以降低2 190万元。此外,水洗周期缩短,燃气轮机性能恢复更多,发电效率更高,更有利于电厂提高经济效益。综上所述,当前燃气轮机压气机最佳水洗周期为1 824 h。
4.3 对比实验及可行性分析
为验证本文优越性,用随机森林[26]、BP神经网络和LSTM模型进行对比验证,选择第3次水洗进行预测,预测结果对比如图7所示。
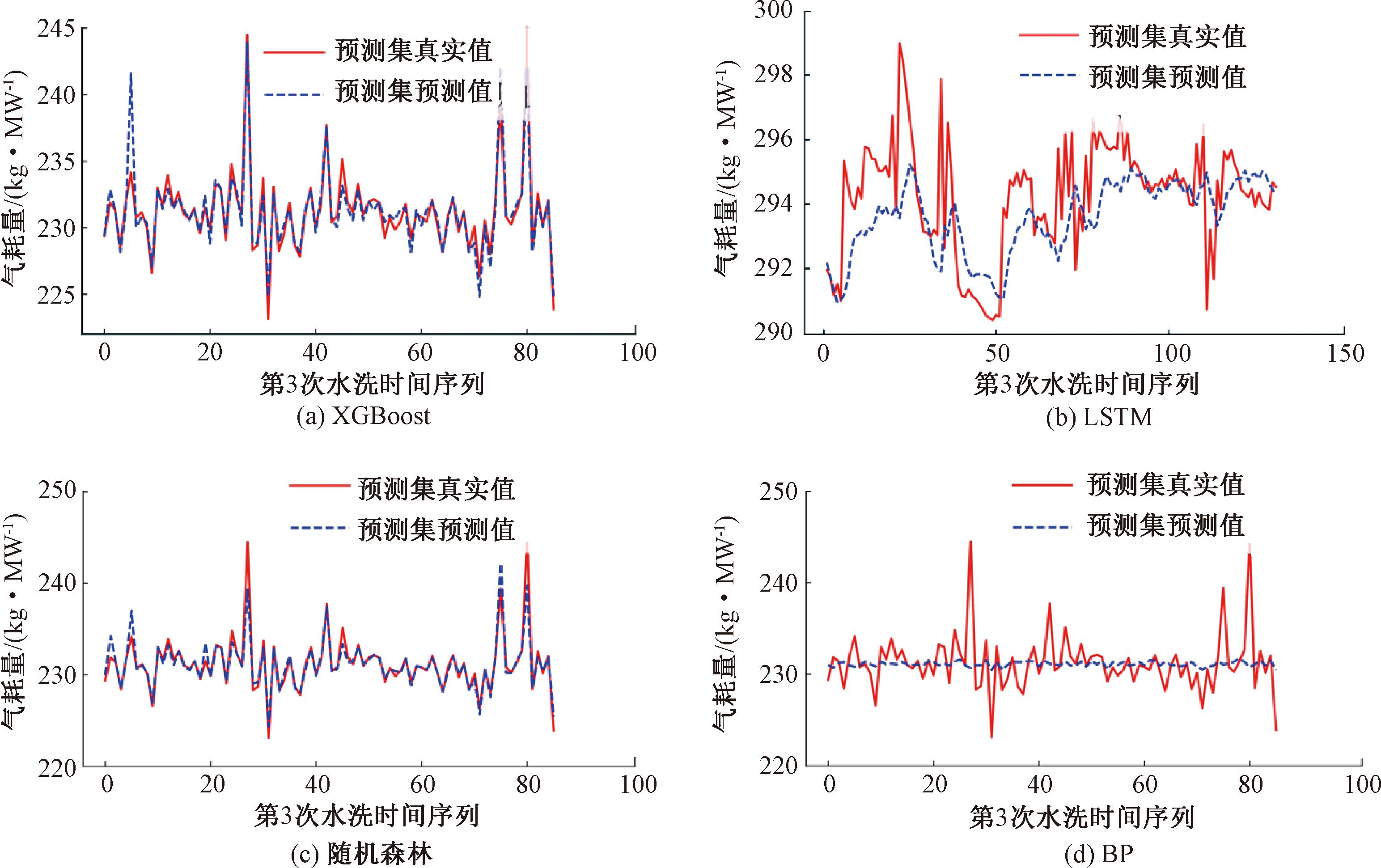
图7 多模型预测效果对比图
Figure 7 Comparison charts of prediction performance of multiple models
由图7可知,XGBoost模型预测效果优于随机森林、BP神经网络以及LSTM等模型的预测效果。说明本文选择的预测方法更适合于预测该电厂燃气轮机压气机水洗周期。
5 结论
针对压气机运维成本过高的问题,本文将数字孪生与电厂燃气轮机健康管理相结合,提出燃气轮机健康管理领域的数字孪生物理层、模型层、数据层和应用层,组合为基于数字孪生的电厂燃气轮机健康管理框架,提高健康管理系统集成度和数字化程度。
本文采用XGBoost模型对压气机气耗量进行预测,使用最大值最小值归一化、“weight”重要性排序对特征进行选择,降低模型维度,减少模型运算时间,提高模型预测效果;通过调节超参数max_depth、learning_rate以及n_estimators对模型进行优化,得到最优模型。
本文构建的XGBoost模型预测效果良好,8次水洗的平均R2_score达到0.975 1,MAPE仅仅只有0.699 1%,RMSE的平均值也只有15.05,比LSTM、BP神经网络和随机森林模型的预测效果更好,可以更好地完成对水洗周期的预测。预测得到的燃气轮机压气机离线水洗周期以及水洗成本较优化前降低48.3%,每次水洗成本可以降低2 190万元,可以有效降低压气机运维成本。
本文尚未进行实验来验证决策的性能,计划对燃气轮机进行建模,确定模型层的模型是否与物理层的燃气轮机实体相匹配;通过数据库中数据预测气耗量,计算水洗恢复率、发电效率,验证是否可以得出最佳水洗周期;对燃气轮机水洗前后各参数进行监测,对数据进行处理分析对比,验证该决策是否对燃气轮机产生效果;还可以将该系统集成在HoloLens中,验证专家与现场工作人员之间交流是否方便。
[1] 曹思佳, 胡汀, 唐瑞, 等. 基于工业互联网的船用燃气轮机健康管理平台[J]. 热能动力工程, 2022, 37(5): 180-186.CAO S J, HU T, TANG R, et al. Marine gas turbine health management based on industrial Internet platform[J]. Journal of Engineering for Thermal Energy and Power, 2022, 37(5): 180-186.
[2] SINGH M, FUENMAYOR E, HINCHY E, et al. Digital twin: origin to future[J]. Applied System Innovation, 2021, 4(2): 36.
[3] HE B, BAI K J. Digital twin-based sustainable intelligent manufacturing: a review[J]. Advances in Manufacturing, 2021, 9(1): 1-21.
[4] TAO F, CHENG J F, QI Q L, et al. Digital twin-driven product design, manufacturing and service with big data[J]. The International Journal of Advanced Manufacturing Technology, 2018, 94(9): 3563-3576.
[5] GRAESSLER I, POEHLER A. Integration of a digital twin as human representation in a scheduling procedure of a cyber-physical production system[C]∥2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM). Piscataway: IEEE, 2017: 289-293.
[6] 王睿瑞, 陈芃樾, 邱思琦, 等. 基于数字孪生的船用燃气轮机健康管理工业互联网平台[J]. 热能动力工程, 2022, 37(12): 189-196.WANG R R, CHEN P Y, QIU S Q, et al. An industrial Internet platform for PHM of marine gas turbine based on digital twins[J]. Journal of Engineering for Thermal Energy and Power, 2022, 37(12): 189-196.
[7] 张旭辉, 张雨萌, 王岩, 等. 融合数字孪生与混合现实技术的机电设备辅助维修方法[J]. 计算机集成制造系统, 2021, 27(8): 2187-2195.ZHANG X H, ZHANG Y M, WANG Y, et al. Auxiliary maintenance method for electromechanical equipment integrating digital twin and mixed reality technology[J]. Computer Integrated Manufacturing Systems, 2021, 27(8): 2187-2195.
[8] 杨悦, 姚树磊, 刘长利, 等. 叶片水射流表面强化工艺的数字孪生系统设计[J]. 华东理工大学学报(自然科学版), 2023, 49(2): 295-304.YANG Y, YAO S L, LIU C L, et al. Design of digital twin system for blade water jet surface strengthening process[J]. Journal of East China University of Science and Technology, 2023, 49(2): 295-304.
[9] XU Q F, ZHOU G H, ZHANG C, et al. Digital twin-driven intelligent maintenance decision-making system and key-enabling technologies for nuclear power equipment[J]. Digital Twin, 2022, 2: 14.
[10] 姜伟强, 孔令海, 唐武成, 等. 水洗对燃气透平效率影响浅析[J]. 中国石油石化, 2017(4): 12-14.JIANG W Q, KONG L H, TANG W C, et al. Analysis on the influence of water washing on gas turbine efficiency[J]. China Petrochem, 2017(4): 12-14.
[11] 韩朝兵, 朱泓逻, 黄伟栋, 等. 压气机离线水洗后燃气轮机性能衰退分析研究[J]. 动力工程学报, 2019, 39(8): 626-633.HAN C B, ZHU H L, HUANG W D, et al. Performance degradation analysis of a gas turbine after offline water washing of the compressor[J]. Journal of Chinese Society of Power Engineering, 2019, 39(8): 626-633.
[12] 陈家伦, 卞韶帅, 黄新. 基于BP神经网络的9F燃气轮机压气机离线水洗周期优化[J]. 燃气轮机技术, 2020, 33(1): 47-53.CHEN J L, BIAN S S, HUANG X. Optimization of offline washing cycle of 9F gas turbine compressor based on BP neural network[J]. Gas Turbine Technology, 2020, 33(1): 47-53.
[13] RAO P N S, ACHUTHA NAIKAN V N. An optimal maintenance policy for compressor of a gas turbine power plant[J]. Journal of Engineering for Gas Turbines and Power, 2008, 130(2): 1.
[14] 汪祖民, 王冬昊, 梁霞, 等. 基于DBSCAN_GAN_XGBOOST的网络入侵检测方法[J]. 郑州大学学报(工学版), 2022, 43(3): 44-51.WANG Z M, WANG D H, LIANG X, et al. Network intrusion detection method based on DBSCAN_GAN_XGBOOST[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(3): 44-51.
[15] CHOI H S, KIM S, OH J E, et al. XGBoost-based instantaneous drowsiness detection framework using multitaper spectral information of electroencephalography[C]∥Proceedings of the 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics. New York: ACM, 2018: 111-121.
[16] CHEN T Q, GUESTRIN C. Xgboost: a scalable tree boosting system[C]∥ Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2016: 785-794.
[17] HENDERI H. Comparison of min-max normalization and z-score normalization in the k-nearest neighbor (kNN) algorithm to test the accuracy of types of breast cancer[J]. IJIIS: International Journal of Informatics and Information Systems, 2021, 4(1): 13-20.
[18] ISLAM S N, SHOLAHUDDIN A, ABDULLAH A S. Extreme gradient boosting (XGBoost) method in making forecasting application and analysis of USD exchange rates against rupiah[J]. Journal of Physics: Conference Series, 2021, 1722(1): 012016.
[19] TOPIC A, RUSSO M. Emotion recognition based on EEG feature maps through deep learning network[J]. Engineering Science and Technology, an International Journal, 2021, 24(6): 1442-1454.
[20] OGUNLEYE A, WANG Q G. XGBoost model for chronic kidney disease diagnosis[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2020, 17(6): 2131-2140.
[21] CHAI T, DRAXLER R R. Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature[J]. Geoscientific Model Development, 2014, 7(3): 1247-1250.
[22] SHAHID F, ZAMEER A, MUNEEB M. Predictions for COVID-19 with deep learning models of LSTM, GRU and Bi-LSTM[J]. Chaos, Solitons &Fractals, 2020, 140: 110212.
[23] DE MYTTENAERE A, GOLDEN B, LE GRAND B, et al. Mean Absolute Percentage Error for regression models[J]. Neurocomputing, 2016, 192: 38-48.
[24] 陈创庭. 大型电站燃气轮机的水洗经济周期研究[J]. 广东电力, 2009, 22(7): 18-23.CHEN C T. Research on economic wash period of heavy-duty power gas turbine[J]. Guangdong Electric Power, 2009, 22(7): 18-23.
[25] 程元, 陈坚红, 盛德仁, 等. 联合循环发电机组燃气轮机水洗策略优化模型研究[J]. 中国电机工程学报, 2013, 33(26): 95-100.CHENG Y, CHEN J H, SHENG D R, et al. Research on washing strategy optimization model of combined cycle gas turbines[J]. Proceedings of the CSEE, 2013, 33(26): 95-100.
[26] 李爱民, 王海隆, 许有成. 优化随机森林算法的城市湖泊DOC质量浓度遥感反演[J]. 郑州大学学报(工学版), 2022, 43(6): 90-96.LI A M, WANG H L, XU Y C. Remote sensing retrieval of urban lake DOC concentration based on optimized random forest algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(6): 90-96.