石化行业中的高温运输管道,如大型锅炉系统内的管道工作温度在350~530 ℃,在进行厚度监测时,传统超声检测所用的耦合剂在高温下容易挥发,导致耦合效果变差,不利于超声波信号的传输。而且超声换能器长期工作在高温环境下,换能器会去极化而失效,因此不适用于高温环境的长期监测。导波技术将导波杆作为隔热器件,延长热源与换能器间的热传导距离,以解决换能器长期在高温下工作中出现的去极化问题。导波技术在超声测厚中的应用始于20世纪70年代。Kim等[1]使用导波杆作为辅助工具对一炼油厂的蒸汽转换炉进行了声发射检测。Cegla等[2]制造了一种高温超声测量系统,采用导波杆将传感器和压电元件隔离在高温测量区外,但由于没有对高温下的声速进行深入研究,得到的测量精度并不高。Bhadwal等[3]研究了在压电超声换能器干耦合界面填充退火处理的银箔的可行性。王刚等[4]通过对不同频率SH0波信号纯度的分析,得到信号较好的频率范围,并验证了超声导波对高温管道壁厚测量结果的可靠性。Liao等[5]在室温至350 ℃范围内研究了超声导波在干耦合下的高温检测特性,但并未对更高温度下的信号传输情况进行探究。白雪皎等[6]研究了被测管道厚度、材料、噪声水平以及温度对壁厚测量结果的影响,提出双探头测厚适用于小壁厚测量,而单探头则更适合测量厚度较大的管道。
本文在已有研究基础上对基于超声导波的高温管道壁厚监测技术进行了优化。改进高温环境的干耦合方式,提出适用于不同工作温度的超声波激励方式,并对测量数据采用乘幂算法处理以提高系统在高温下的自适应性和信号信噪比,采用分段声速修正以提高不同温度范围内的测量精度,解决了高温下监测管道厚度时传感器耦合失效以及信号信噪比较差的问题。
1 测量原理及传感器结构
1.1 测量原理
系统工作原理如图1所示。电路发出激励信号使超声换能器产生超声波,随导波杆传递到被测件,分别在被测件上、下表面发生反射,形成一次、二次回波。根据两次回波到达接收端换能器的时间差求得被测件厚度。系统所使用的压电换能器谐振频率[7]为2.5 MHz。
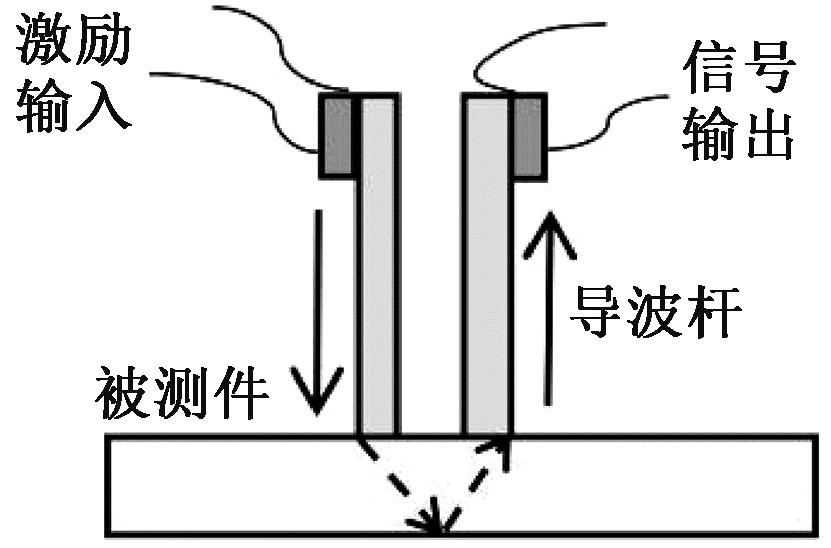
图1 基于超声导波的高温管道测厚系统原理图
Figure 1 Schematic diagram of high temperature pipe thickness measurement system based on ultrasonic guided wave
1.2 传感器结构
所设计的导波杆外形尺寸如图2所示,其厚度为1.5 mm。
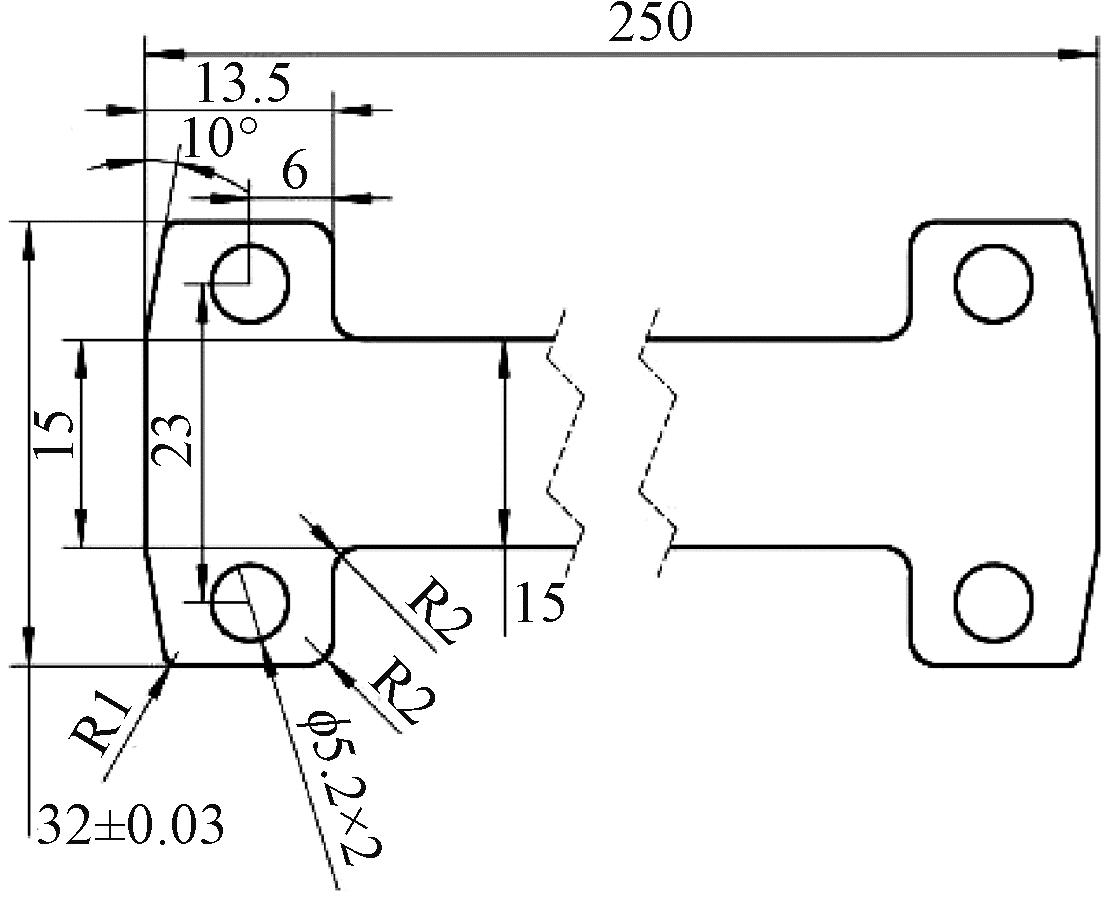
图2 导波杆外形尺寸(mm)
Figure 2 Waveguide rod external dimension (mm)
压电换能器必须稳定地固定在导波杆上端且应与导波杆接触良好,以尽可能减少在超声波传递过程中的能量损耗,使用超声耦合剂将换能器粘贴在导波杆侧面的顶部,并使其振动方向与导波杆宽度方向平行,如图3所示。
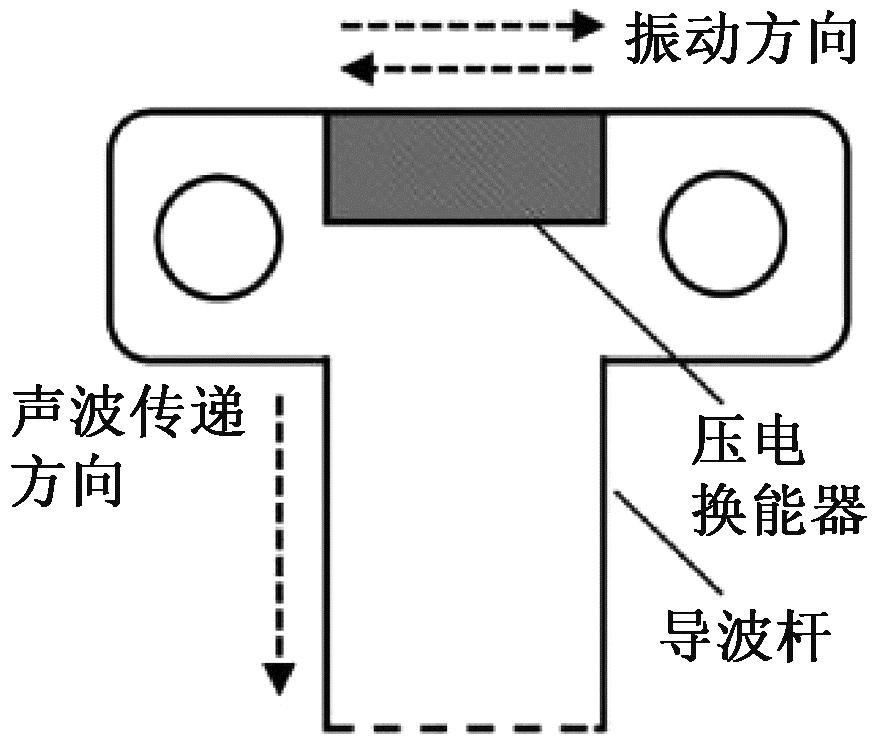
图3 导波杆粘贴方式示意图
Figure 3 Adhesion method of waveguide rod
1.3 高温干耦合方式
导波杆应与被测件紧密接触,以消除空气介质。否则形成的空气层会反射声波,造成较大能量损耗。采用适用于高温工作环境的干耦合的方式[5],通过紧固螺栓将导波杆末端紧压在被测件上,并在导波杆与被测件接触面上放置一薄铜垫片[8]。铜片较软,能更好地与被测件表面贴合,提高高温下耦合的可靠性。当铜皮厚度d与超声波波长λ满足d=nλ/2(n为整数)时,超声波会在铜皮临界面发生全透射,不会影响测量信号的强度。为保证得到清晰的回波信号,需要的夹紧力为500~2 000 N[2]。
交替拧紧两边螺母使夹具两端均匀受力,给换能器施加100 V激励信号,当可以看到两次清晰的回波且一次回波幅值在60 mV左右时,可认为耦合良好。干耦合夹持方式正视图如图4所示。
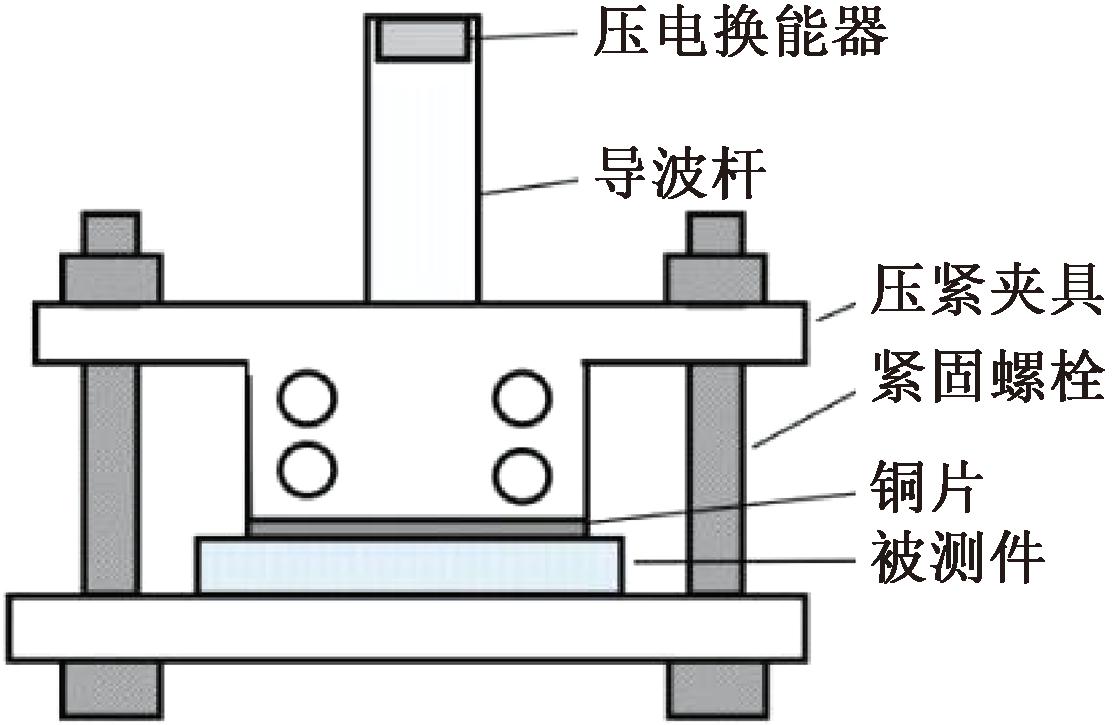
图4 干耦合夹持方式
Figure 4 Dry coupling clamping mode
2 导波杆隔热仿真模拟及实验
常规超声换能器工作温度范围一般在-20~80 ℃,所设计的导波杆应保证在500 ℃工作温度下其末端温度在80 ℃以下。选择304不锈钢为导波杆材料。使用COMSOL进行热仿真分析。在建立仿真模型时,给导波杆外部施加空气场模拟实际工作的外部环境,在导波杆一端设置500 ℃的温度载荷,对该模型进行瞬态热传导分析,可得导波杆上温度分布。对导波杆进行散热效果测试实验,加热导波杆,使用温度传感器测量实时温度。实验示意图如图5所示。将距导波杆底端分别为10、20、30、60、90、120、150、200、250 mm处的位置作为测量点;对导波杆一端加热至500 ℃,持续120 min,测量导波杆不同测量点的温度,与仿真结果对比,如图6所示。
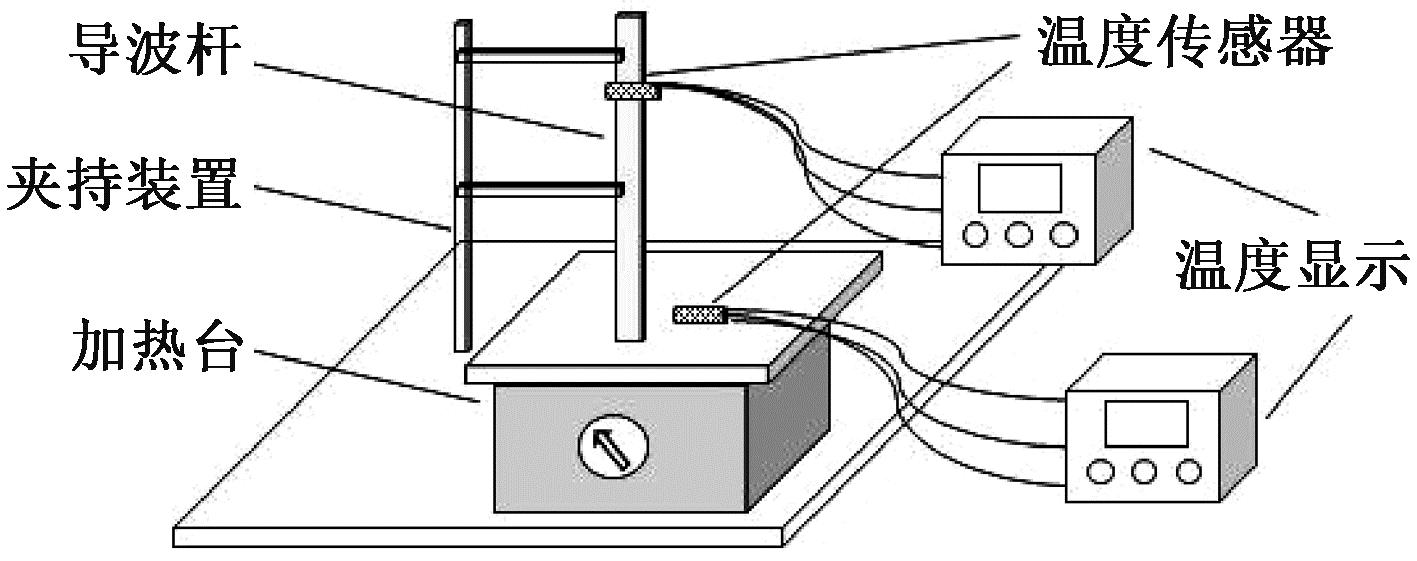
图5 导波杆隔热效果测试示意图
Figure 5 Schematic diagram of heat insulation effect test of waveguide rod
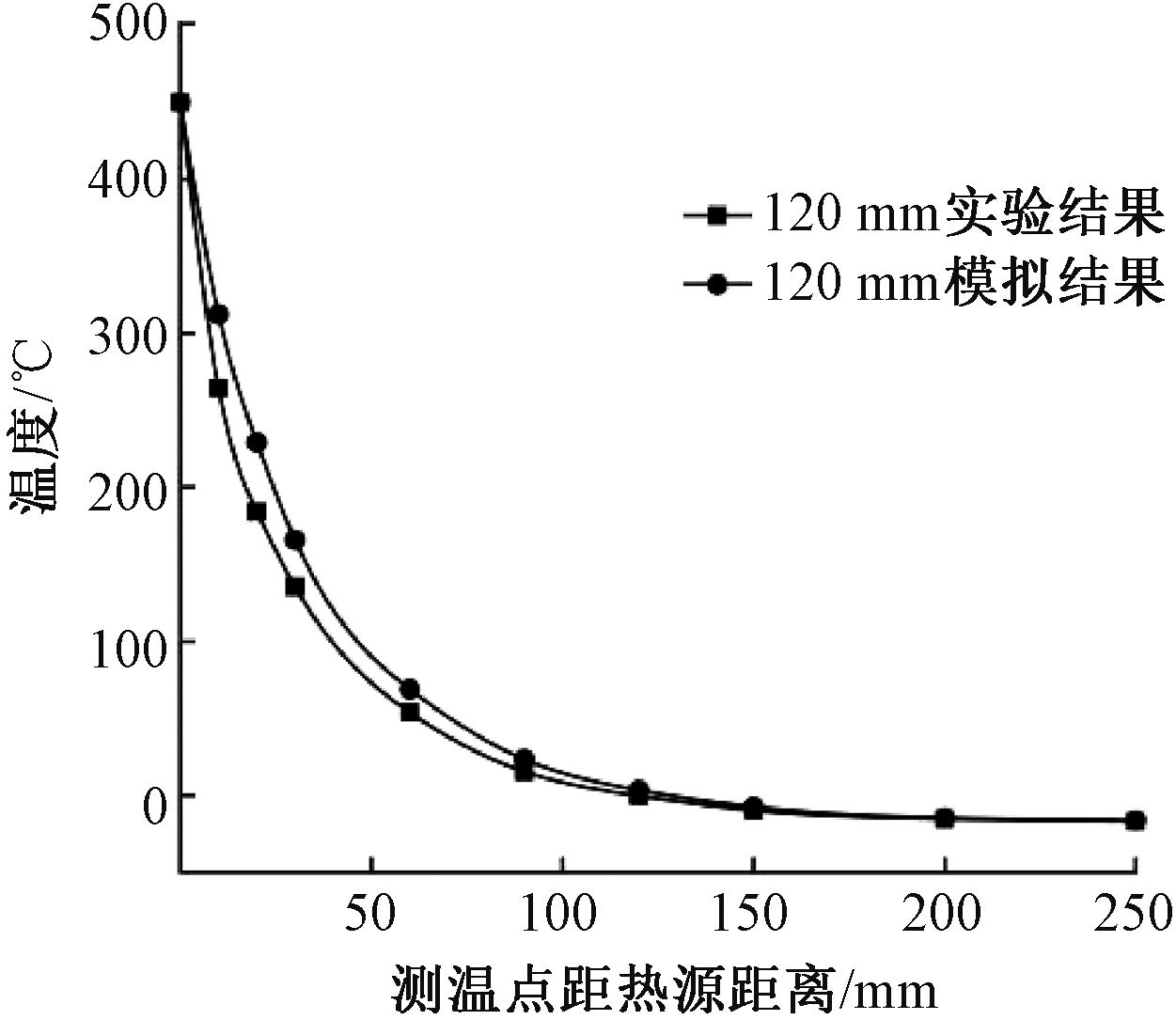
图6 500 ℃仿真与实验结果对比
Figure 6 Comparison of simulation and experimental results at 500 ℃
由图6可知,实验结果与仿真结果大致相同,温度分布规律基本一致。加热过程中靠近加热炉一端温度变化速率更快,远离加热炉一端温度变化速率较慢。导波杆末端温度在45 ℃左右,处于压电换能器工作温度范围内。实验证明,250 mm长的导波杆可以实现本文所要求的隔热效果。
3 高温壁厚测量实验
高温实验被测件是一个材料为碳钢的弧形块,其常温下厚度用千分尺测得为11.852 mm。高温测厚实验示意图如图7所示。图8为将被测件从25 ℃加热至500 ℃过程中每隔25 ℃进行一次测量得到的部分回波数据折线图。
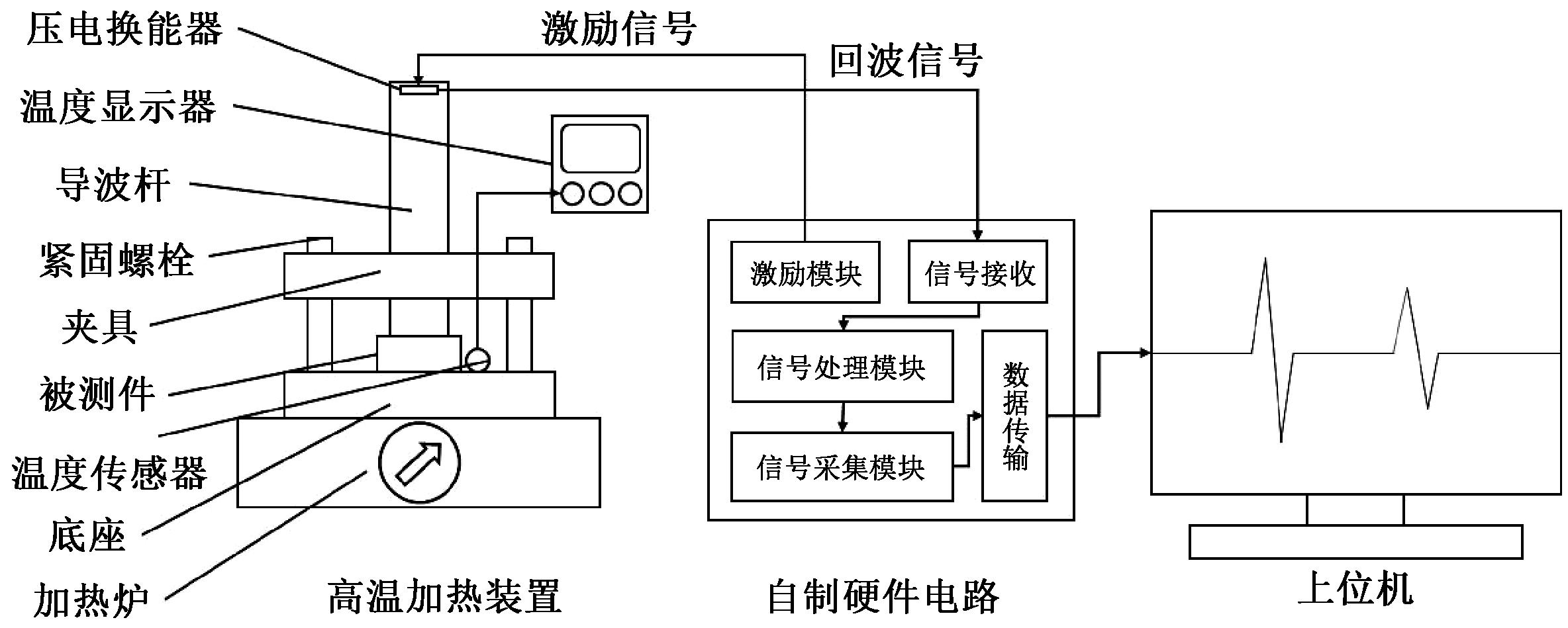
图7 高温测厚实验示意图
Figure 7 Schematic diagram of high temperature thickness measurement experiment
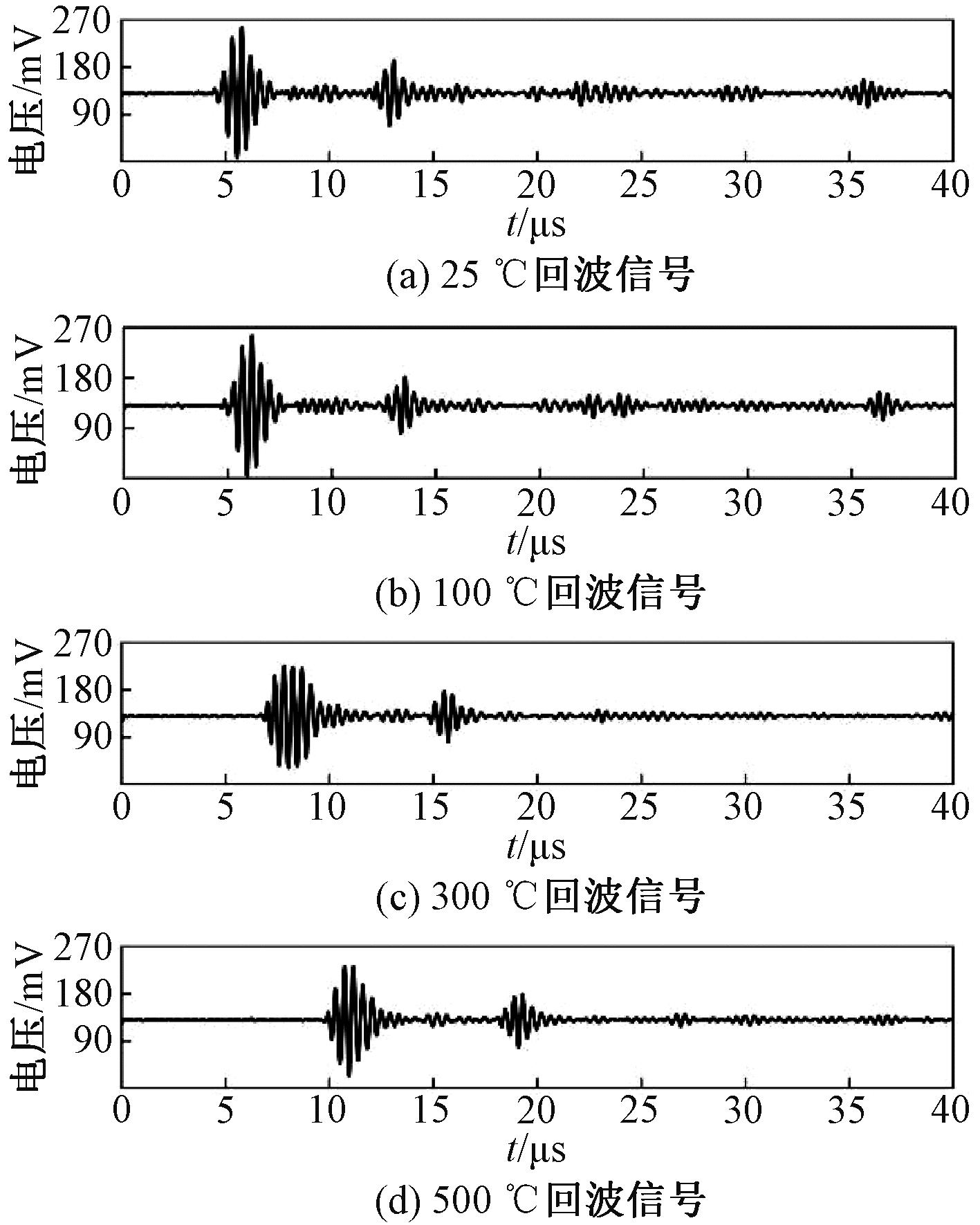
图8 不同温度下采集到的回波信号
Figure 8 Echo signals collected at different temperatures
由图8可以看出,随着温度升高,上表面回波到达时间滞后,上下表面回波到达的时间间隔变大,这表明随着温度升高,横波声速减小。
4 高温管道壁厚测量关键技术
4.1 超声波数据处理方法
为提高系统的测量精度,对测量数据采取插值算法以从软件层面提高采样频率。设计使用三倍频对数据进行处理,即在2个采样点间插入2个数据点。选择两次牛顿插值:
N2(x)=f(x0)+(x-x0)f[x0,x1]+
(x-x0)(x-x1)f[x0,x1,x2]。
(1)
对所测得的波形数据进行处理。去除信号中直流分量使信号更具有零均值特性,系统采集到的离散信号序列x[n],其长度为4 000,去直流分量公式为
xdc=x-μ(x)。
(2)
式中:xdc为去除直流分量之后的信号;μ(x)为信号平均值。
由图9(a)可以看出,原始信号波形尖峰处有较为明显的失真,对去除直流分量后的信号xdc使用牛顿插值,在每2个原始数据点之间插入2个点,插值后的波形如图9(b)所示,其中局部放大如图9(c)、9(d)所示。插值后与原始信号相比,波包A与波包B处尖峰值更明显。
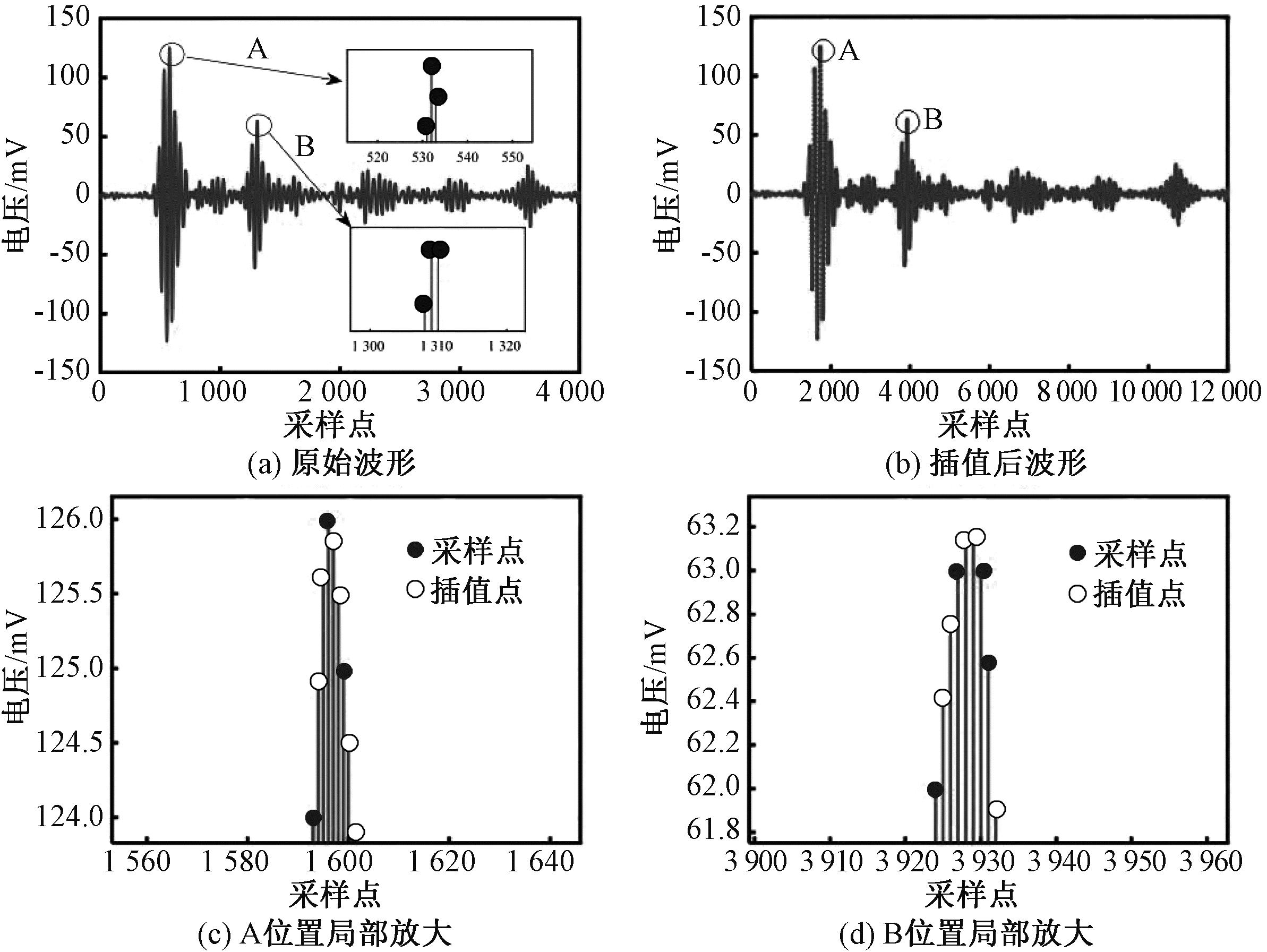
图9 插值倍频
Figure 9 Interpolation frequency doubling
由图8可知,随着温度升高,回波信号幅值逐渐降低。采用乘幂处理提高高温下测量信号的信噪比:把去除直流分量的信号负半周翻转至正半周,将各采样点数值二次幂后缩至1/10。结果如图10所示。其包络线由希尔伯特变换得到[9-10]。对比图9(a)和图10可看到信号信噪比显著提高,信噪比为
(3)
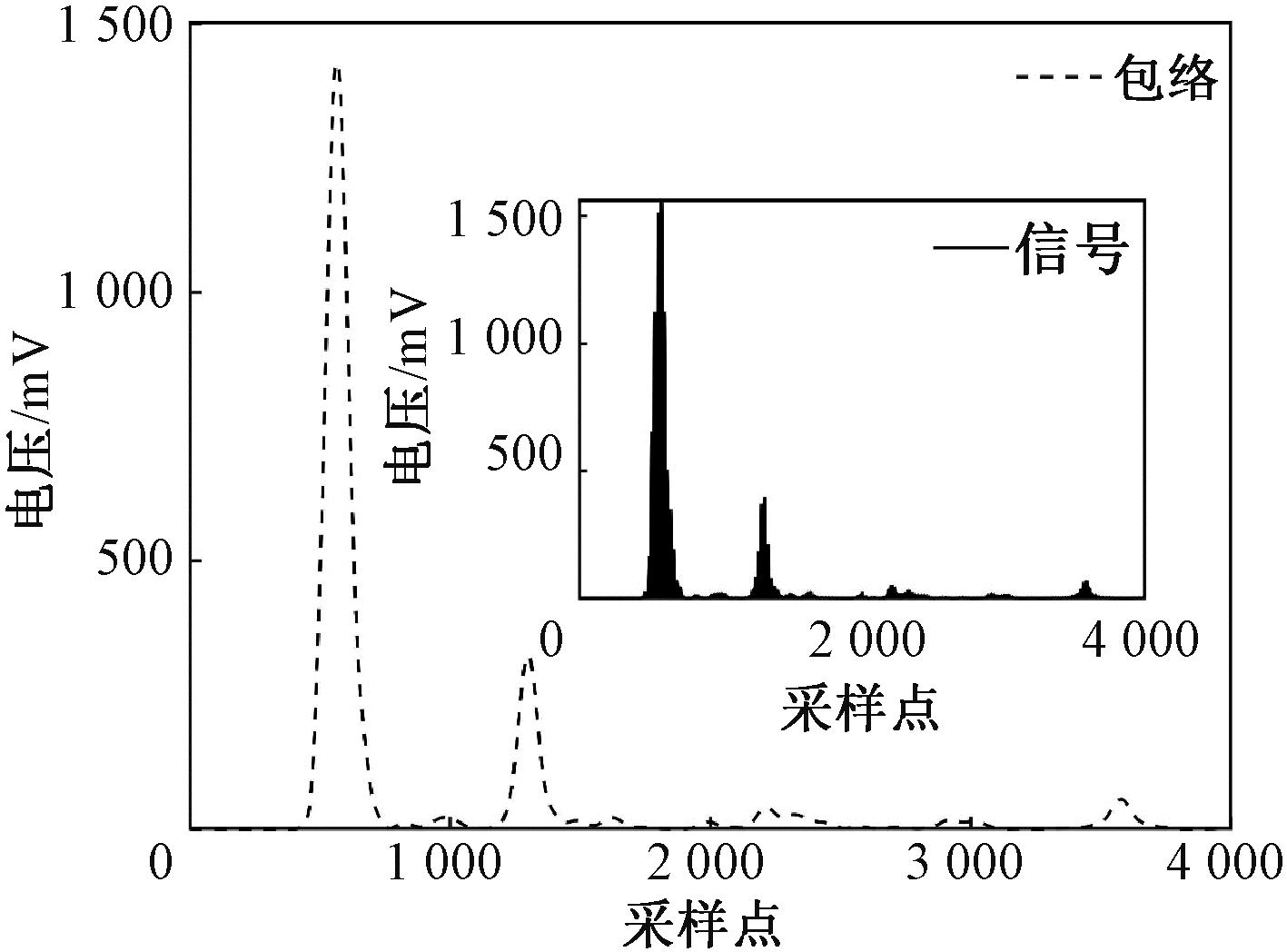
图10 乘幂处理后的信号及其包络线
Figure 10 Power processing signal and its envelope
式中:Ps为信号功率;Pn为噪声功率。
将信噪比换算成电压表示,即
(4)
式中:Vs、Vn分别为信号和噪声的有效电压值。
对Vs、Vn分别进行m次乘幂处理,此时信号的信噪比为
(5)
可知经过乘幂处理的信号信噪比为原始数据信噪比的m倍。对图9(a)信号进行二次幂处理得到图10,计算得到原始信号SNR1=7.8 dB,乘幂后信号的信噪比SNR2=15.5 dB,乘幂处理后的信号信噪比是原始信号信噪比的两倍。
4.2 声速分段补偿技术
由于固体中超声波声速受温度影响,实验中计算被测件厚度测量值时,根据实际温度对声速进行了修正。对于横波,声速为[11]
![]()
(6)
式中:E为固体材料的杨氏弹性模量;ρ为材料密度;σ为泊松比。
线膨胀系数在-100~300 ℃时与温度基本无关,固体材料杨氏弹性模量与温度近似满足[12-13]:
(7)
式中:E0为绝对零度时的弹性模量;α0为绝对零度时的线膨胀系数;m为弹性模量的温度系数与线膨胀系数之比,一般取24.66。根据国家标准,20 ℃时碳钢弹性模量E=20.000×1010 Pa,可计算得到T=0时E0=21.878×1010 Pa。
碳钢在不同温度下的线膨胀系数为
α=α0(1+bT)=α0+kT。
(8)
式中:b为相对变化比例常数;α0取值为(8.347 7~10.787 0)×10-6;k取值为3.676 3×10-9~1.450 9×10-8。取碳钢线膨胀系数为
α=10-5+7×10-9T 。
(9)
固体材料密度与温度的关系可表示为
(10)
式中:ρ0为固体材料绝对零度时的密度;常温下实验被测件材料密度ρT=7.72 kg/m3。
取泊松比σ=0.24,物体中横波声速与温度的关系可表示为
us=
(11)
通过式(11)可得25~300 ℃声速。对于超过300 ℃的声速,由于温度对线膨胀系数影响较大,进而影响材料的弹性模量,故对该温度范围内的声速采用10 mm标准量块进行修正,在300~500 ℃的等温度间距测量不同温度下对应的声速,并考虑被测件在高温下热膨胀的影响:
hT=h0(1+αΔT)。
(12)
式中:hT为考虑材料热膨胀效应后的实际厚度,mm;h0为被测件常温下厚度,mm;ΔT为温度变化量,K。
对声速测量结果进行多项式拟合,最终得到拟合曲线为
v=-3.77×10-10T5+1.236×10-6T4-1.632×
10-3T3+1.082T2-359.899T+51 223.096。
(13)
式中:T为温度,K;v为声速,m/s。
通过分段声速修正得到所有实验温度下的厚度测量结果,如表1所示。其中,P1、P2分别为2次回波波峰点所在位置;Δl为两次回波波峰间间隔点数;Δt为对应的时间间隔;v为对应温度下声速;h为厚度测量值;Δh为绝对误差。
表1 单发单收模式实验结果
Table 1 Experimental results of single issue and single receive mode
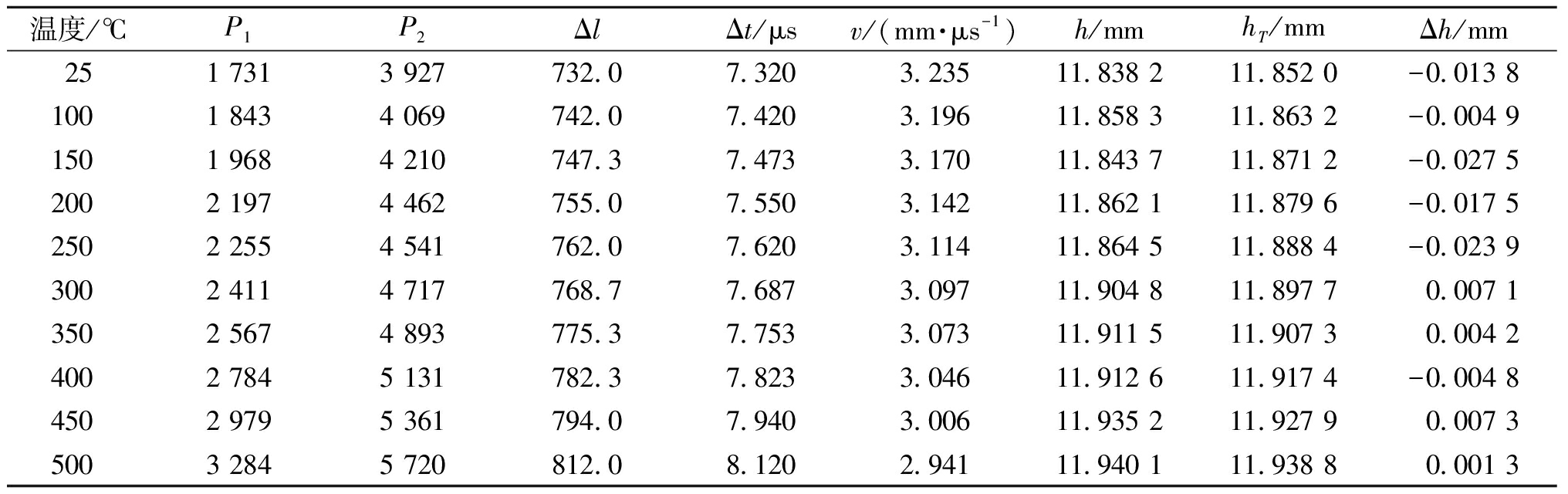
温度/℃P1P2ΔlΔt/μsv/(mm·μs-1)h/mmhT/mmΔh/mm251 7313 927732.0 7.320 3.23511.838 211.852 0-0.013 81001 8434 069742.0 7.420 3.19611.858 311.863 2-0.004 9 1501 9684 210747.3 7.473 3.17011.843 711.871 2-0.027 52002 1974 462755.0 7.550 3.14211.862 111.879 6-0.017 52502 2554 541762.0 7.620 3.11411.864 511.888 4-0.023 9 3002 4114 717768.7 7.687 3.09711.904 811.897 70.007 13502 5674 893775.3 7.753 3.073 11.911 511.907 30.004 24002 7845 131782.3 7.823 3.04611.912 6 11.917 4-0.004 84502 9795 361794.0 7.940 3.00611.935 211.927 90.007 35003 2845 720812.0 8.120 2.94111.940 111.938 80.001 3
由表1可知,单发单收的测厚方式精度较高,各温度下被测件厚度测量值的误差均在±0.03 mm。实验中被测件加热到500 ℃时,导波杆末端温度经测量仅为53 ℃,表明所设计的检测探头不仅能在500 ℃的高温下对管道壁厚进行测量,且测量结果准确。
4.3 高温环境自适应激励方法分析
高温下超声波衰减程度增大,回波信号的幅值会受到影响。为尽可能保证高温下信号信噪比接近于常温信噪比,需要根据温度对激励周期进行调整。单周期激励时温度下回波信号如图11所示。由图11可知,随着温度升高,两次回波信号幅值均有下降,不利于回波信号峰值位置的检测。通过激励周期数可调电路对激励信号周期数进行调整,以适应不同温度下的测量环境。在100、500 ℃ 的温度下分别采用1~4周期激励,得到对应的波形如图12所示。由图12可知,随着温度升高,双周期激励的二次回波信号衰减明显;三周期激励信噪比较高;在四周期激励下,虽然信噪比更高,但由于回波包络更宽而导致误判峰值信号使测量结果误差较大。因此,随着温度升高,系统分别使用不同周期数的激励模式,既保证了测量精度又提高了回波信号的信噪比,增强了系统可靠性。
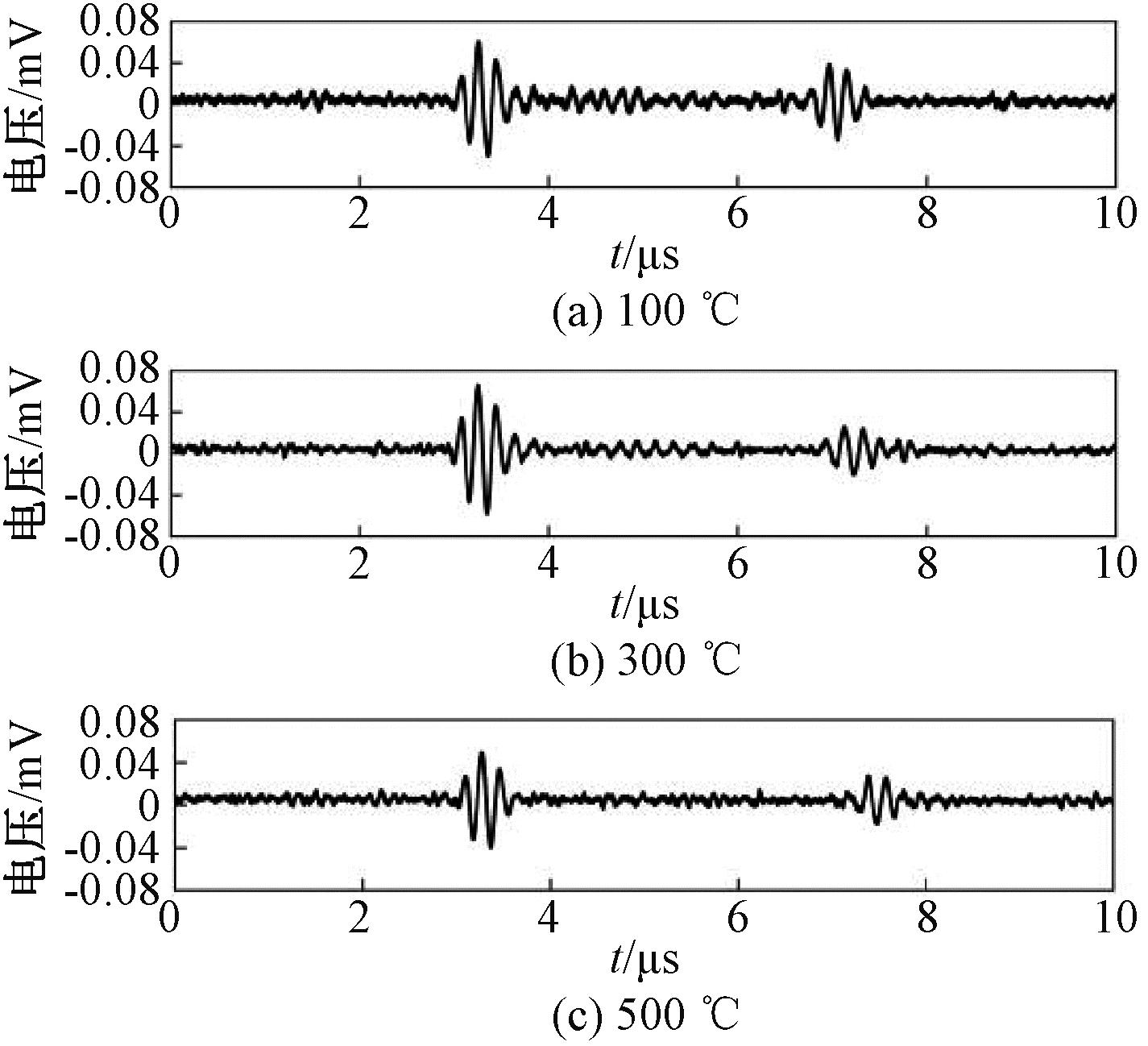
图11 单周期激励各温度回波信号
Figure 11 Single-cycle excitation of the echo signal at each temperature
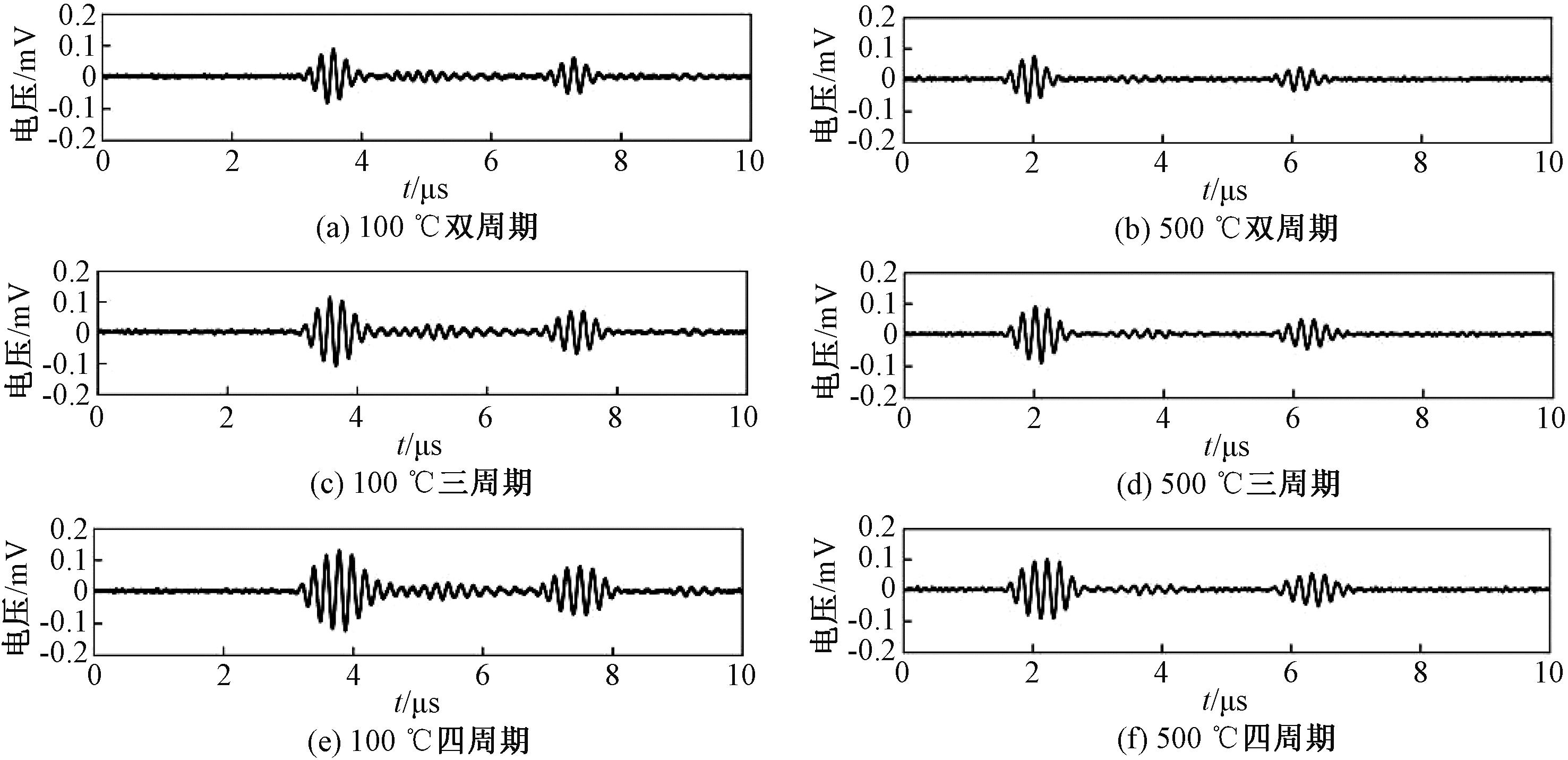
图12 不同温度下激励周期数对回波信号的影响
Figure 12 Effect of the number of excitation cycles on the echo signal at different temperatures
5 高温长期可靠性验证实验
将被测件转移至密闭高温炉持续加热72小时,保持温度在450~500 ℃,每天9时、15时、21时各测量一次当前温度下的厚度,得到表2的数据。其中温度1为被测件温度,温度2为导波杆顶端温度。
表2 高温72 h测厚数据
Table 2 Thickness measurement data at high temperature in 72 h
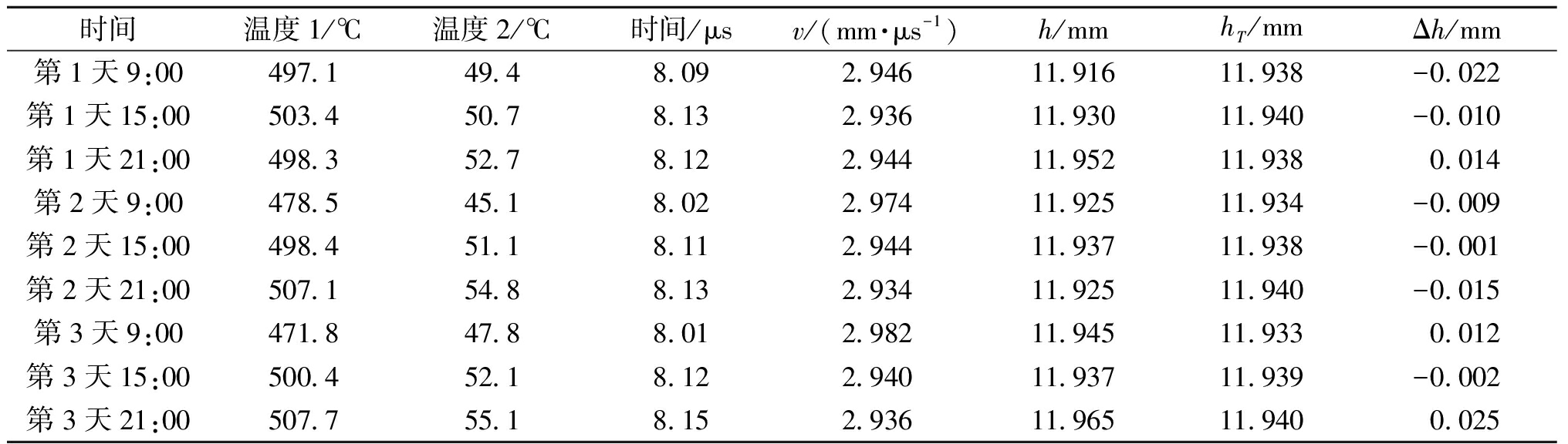
时间温度1/℃温度2/℃时间/μsv/(mm·μs-1)h/mmhT/mmΔh/mm第1天9:00497.149.48.092.94611.91611.938-0.022第1天15:00503.450.78.132.93611.93011.940-0.010第1天21:00498.352.78.122.94411.95211.9380.014第2天9:00478.545.18.022.97411.92511.934-0.009第2天15:00498.451.18.112.94411.93711.938-0.001第2天21:00507.154.88.132.93411.92511.940-0.015第3天9:00471.847.88.012.98211.94511.9330.012第3天15:00500.452.18.122.94011.93711.939-0.002第3天21:00507.755.18.152.93611.96511.9400.025
由表2可以看出,在72 h的持续监测下,测得的管道壁厚误差均在±0.03 mm,相较于文献[2,4]所设计的误差为0.08~0.10 mm的测厚系统,精度明显提高。且在72 h的加热时间内,导波杆顶端温度最高不超过56 ℃,并未超出压电换能器最高工作温度。实验证实系统具有在高温环境下对管道壁厚进行长期、准确监测的能力。
6 结论
本文针对高温超声导波技术中的干耦合方法和高温下测量信号信噪比以及测量精度进行了优化研究。利用导波杆隔离换能器与高温被测件,极大降低了换能器工作的环境温度。优化了干耦合技术,解决了高温下超声换能器与被测件耦合的可靠性问题。系统采用了激励周期数可调电路,以适应不同温度下的工作环境,实验结果显示,通过对激励方式的调节,不同温度下采集到的信号均能得到极高的信噪比。采取乘幂法处理回波信号,使高温下的信噪比可根据实际需求进行提高,避免数据采集过程中偶然出现的干扰信号对回波位置判定造成影响。通过声速分段修正法,提高了高温下的测量精度,同一被测件在不同热源温度下所测厚度误差均在±0.03 mm。系统目前已经能够在500 ℃的环境下对管道壁厚进行长期监测,且具有极高的稳定性及可靠性。
[1] KIM W S, LOTSBERG I. Fatigue test data for welded connections in ship-shaped structures[J]. Journal of Offshore Mechanics and Arctic Engineering, 2005, 127(4): 359-365.
[2] CEGLA F B, CAWLEY P, ALLIN J, et al. High-temperature (>500 ℃) wall thickness monitoring using dry-coupled ultrasonic waveguide transducers[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2011, 58(1): 156-167.
[3] BHADWAL N, TORABI MILANI M, COYLE T, et al. Dry coupling of ultrasonic transducer components for high temperature applications[J]. Sensors, 2019, 19(24): 5383.
[4] 王刚, 李法新. 基于水平剪切超声导波的高温管道壁厚在线监测[J]. 无损检测, 2019, 41(9): 1-6, 15.
WANG G, LI F X. On-line monitoring of high temperature pipeline wall thickness based on the shear horizontal ultrasonic guided wave[J]. Nondestructive Testing, 2019, 41(9): 1-6, 15.
[5] LIAO Z Y, ZHANG X, LIU T Y, et al. Characteristics of high-temperature equipment monitoring using dry-coupled ultrasonic waveguide transducers[J]. Ultrasonics, 2020, 108: 106236.
[6] 白雪皎, 祝海江. 高温管道超声波测厚方法影响因素仿真研究[J]. 计量科学与技术, 2022, 66(2): 55-60.
BAI X J, ZHU H J. Simulation-based study on factors affecting ultrasonic thickness measurements of high temperature pipelines[J]. Metrology Science and Technology, 2022, 66(2): 55-60.
[7] 王翥, 刘春龙, 罗清华. 超声波传感器特性分析与测试方法的研究[J]. 郑州大学学报(工学版), 2020, 41(2): 13-18.
WANG Z, LIU C L, LUO Q H. Research on ultrasonic sensors characteristics and testing method[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(2): 13-18.
[8] 魏建新, 王椿镛. 横波测试技术的实验室研究[J]. 石油地球物理勘探, 2003, 38(6): 630-635, 708.
WEI J X, WANG C Y. Study of S-wave test and measurement technique in laboratory[J]. Oil Geophysical Prospecting, 2003, 38(6): 630-635, 708.
[9] 郭田雨, 严荣国, 方旭晨, 等. 基于希尔伯特变换和自适应阈值的R波检测算法[J]. 计算机与现代化, 2022(2): 114-119.
GUO T Y, YAN R G, FANG X C, et al. Detection of R wave based on Hilbert transform and adaptive threshold[J]. Computer and Modernization, 2022(2): 114-119.
[10] 沙云东, 陈兴武, 栾孝驰, 等. 基于小波包分解-峭度值指标-希尔伯特包络解调融合方法处理声发射信号的滚动轴承故障诊断[J]. 科学技术与工程, 2023, 23(21): 9315-9323.
SHA Y D, CHEN X W, LUAN X C, et al. Fault diagnosis of rolling bearing based on acoustic emission signal analysis by WPD-KI-HED combination method[J]. Science Technology and Engineering, 2023, 23(21): 9315-9323.
[11] 虞雪芬, 叶凌伟, 夏立. 电磁超声检测中高温对横波声速的影响[J]. 轻工机械, 2015, 33(4): 54-56.
YU X F, YE L W, XIA L. Influence of high temperature on shear wave velocity of EMAT testing[J]. Light Industry Machinery, 2015, 33(4): 54-56.
[12] 刘彤, 刘敏珊. 金属材料弹性常数与温度关系的理论解析[J]. 机械工程材料, 2014, 38(3): 85-89, 95.
LIU T, LIU M S. Theoretical analysis of the relationship between elastic constants of metals and temperatures[J]. Materials for Mechanical Engineering, 2014, 38(3): 85-89, 95.
[13] 徐志东, 范子亮. 金属材料的弹性模量随温度变化规律的唯象解释[J]. 西南交通大学学报, 1993, 28(2): 87-92.
XU Z D, FAN Z L. A phenomenological explanation of the variation of elastic modulus with temperature for metallic materials[J]. Journal of Southwest Jiaotong University, 1993, 28(2): 87-92.