为适应不断变化的市场需求和更加多样化的客户需求,传统的大规模制造模式逐渐转变为大规模定制生产模式。在该模式下,制造车间应具备较高的生产柔性,以实现需求驱动的生产过程智能化组织。柔性作业车间调度问题(flexible job shop scheduling problem,FJSP)更符合柔性化和智能化车间生产组织的要求[1]。
求解FJSP问题的算法主要涉及精确方法和近似方法。FJSP属于NP-hard问题,是一种典型的离散型组合优化问题,由于离散变量的存在及其问题的复杂性,求解难度大,很难使用精确方法在合理的时间得到满意的结果。随着研究的不断深入,学者们趋向于采用智能优化算法以获得满足约束和目标函数的近似最优解。张朝阳等[2]应用改进的狼群算法对多目标柔性作业车间调度模型进行求解,改进后的算法具有很好的全局搜索能力;王彦杰等[3]提出一种改进的蚁狮优化算法,并将其应用在柔性作业车间调度问题中;Gayathri等[4]考虑实际生产中存在多种目标组合优化的情况,提出一种改进的混合自适应萤火虫算法求解柔性作业车间调度问题;Meng等[5]结合了人工蜂群算法和候鸟优化算法的特点,提出一种混合人工蜂群算法求解具有重复操作的柔性作业车间调度问题;杜凌浩等[6]提出了一种改进的多邻域候鸟优化算法,优化柔性作业车间调度问题的最大完工时间。然而,目前的智能优化算法求解FJSP时,初始种群的质量会影响算法的求解精度,求解过程中容易陷入局部最优,并且需要调整许多参数才能使算法获得更好的性能。为解决以上智能优化算法存在的缺陷,有必要探索新的算法以获得更优的求解结果。
天牛须搜索算法(beetle antennae search,BAS)是由Jiang等[7]在2017年提出的一种通过模拟自然界中天牛的觅食行为旨在解决复杂的优化问题的新型智能优化算法。天牛在寻找食物的过程中,通过触须不断感知外界环境中的信息,通过计算左右两侧的气味浓度差异选择移动方向。天牛不断向着气味浓度更高的方向移动,最终天牛能够准确寻找到食物的位置[8]。该算法具有搜索能力强、收敛速度快等特点,目前在很多领域的优化问题中得到应用。Fan等[9]提出了一种结合BAS算法和PID策略的复合PID控制器,并将其用于驱动电液伺服系统的位置伺服控制系统;Kim等[10]提出了一种基于混合BAS算法的Gabor滤波检测织物表面缺陷的方法,并通过实验验证该方法具有良好的稳定性和鲁棒性。
尽管天牛须搜索算法代码简单、复杂度低,但是由于寻优过程中只考虑单个天牛的搜索行为,算法的单一性使其容易陷入局部极值。Wang等[11]受群优化算法的启发,对天牛须搜索算法进行改进,将个体扩展为群体,提出天牛群算法(beetle swarm optimization,BSO),提高了优化性能,使该算法具备一定跳出局部极值的能力;Bhagavathi等[12]提出一种基于混合的BAS-PSO算法,并应用于云计算中虚拟机的整合和迁移;Mu等[13]提出了一种基于天牛群算法的三维路线规划方法。
天牛群算法目前常应用于连续函数优化问题,对求解FJSP等离散优化问题的研究较少,求解过程可能陷入局部极值,尚缺少应用验证。
本文提出一种基于莱维飞行、反向搜索和自适应参数调整混合策略的改进天牛群算法(hybrid Levy flight, reverse search, and adaptive parameter adjustment strategy improved beetle swarm optimization algorithm, LRA-BSO)来求解FJSP问题,改进思路如下:由于群智能算法对初始种群质量有要求,本文在种群初始化时采用Tent混沌序列代替随机序列,以提高初始种群质量;在迭代优化过程中,采用基于莱维飞行及反向搜索的优化策略,以改善算法的全局搜索能力,逃离局部极值;BSO算法较天牛须搜索算法有更多参数,为减少前期参数设置对算法性能的影响,采用基于适应度反馈的认知因子及步长更新策略。在此基础上,采用6种测试函数对本文提出的改进策略进行有效性验证,并应用10个标准算例和1个实际案例验证该算法在求解FJSP问题时的可行性和有效性。
1 FJSP问题建模
1.1 问题描述
FJSP问题最早由Brucker等[14]在1990年提出,该问题具有灵活性和复杂性,更符合实际的生产场景。在FJSP问题中,假设有n个工件在m台机器上加工,其中每个工件包含多道工序,每道工序可以在不同机器上加工处理,不同的机器上的加工时间可能不同。该问题主要涉及以下两个子问题:①按什么顺序加工工件;②如何合理地分配机器。因此,解决FJSP问题就是对每道工序选择合适的机器进行加工,并合理地为每一道工序安排机器进行处理,使完工时间最少。
本文以最大完工时间最小化为优化目标,在建立模型之前,做出以下假设:①机器之间是相互独立的;②在零时刻,所有机器和工件可加工;③同一工件的工序间存在优先约束,而不同工件之间是相互独立的;④同一时刻一台机器只能加工一个工件;⑤不考虑机器设置时间和工件运输时间;⑥加工具有不可中断性。
1.2 相关符号说明
本文模型中的相关参数符号和定义如表1所示。
表1 模型参数符号和定义
Table 1 Parameter symbols and definitions of model

符号定义I={i1,i2,i3,…,in}模型中所有的工件集合M={M1,M2,…,Mm}模型中所有的设备集合oi={oi1,oi2,oi3,…,oiq}工件i工序集合oij工件i的第j道工序Mij={M1,M2,…,Mk}工序oij的机器集合sijk工序oij在机器Mk上的开工时间eijk工序oij在机器Mk上的完工时间tijk工序oij在机器Mk上的处理时间ci工件i的完工时间,1≤i≤ncij工序oij的完工时间xijk决策变量,若工序oij在机器Mk上加工则为1,反之则为0
1.3 模型建立
基于问题描述,建立FJSP问题模型如下:
f=min(max ci);
(1)
(2)
(3)
si(j+1)≥eij;
(4)
sijk≥ehgk。
(5)
其中,式(1)表示优化目标;式(2)表示每道工序只能在一台机器上进行一次加工;式(3)表示加工工件i的第j道工序的完工时间应该大于等于其在机器Mk上的开始时间与加工时间之和;式(4)表示同一工件的相邻工序必须按照工序的优先约束依次加工;式(5)表示在同一台机器上加工的工序必须按照机器的工序顺序依次进行,工序ohg为工序oij在机器Mk上加工的前一道工序。
2 LRA-BSO算法求解
2.1 算法流程
本文所提出的LRA-BSO算法求解FJSP问题的流程如图1所示,具体步骤如下。
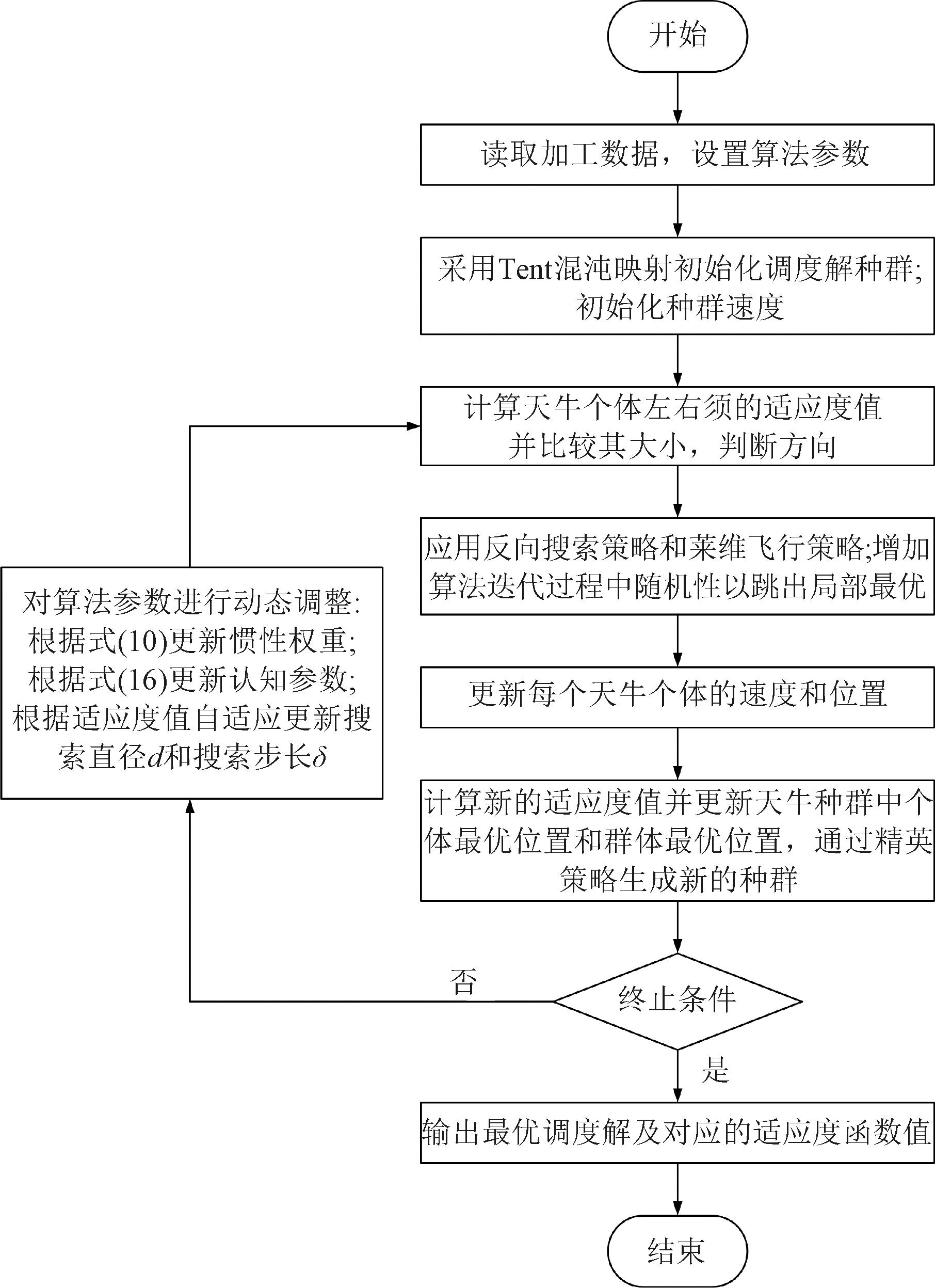
图1 LRA-BSO算法求解FJSP流程图
Figure 1 Flowchart of LRA-BSO for solving FJSP
步骤1 读取车间加工数据,设置算法参数。
步骤2 设置种群编码与解码方式,采用Tent混沌序列代替随机序列,初始化调度解种群。
步骤3 计算每个天牛个体的适应度值,并根据天牛个体左右须适应度大小判断方向。
步骤4 采用莱维飞行和反向搜索策略进行种群迭代搜索,寻找最优种群个体。
步骤5 更新天牛个体的速度和位置并计算适应度值。
步骤6 更新天牛个体最优位置,并采用精英策略合成新的种群。
步骤7 判断算法是否达到终止条件,若达到,则得到最佳调度方案,算法结束;若未达到,则对算法中的权重、搜索直径、搜索步长、认知参数等参数进行动态调整,并返回步骤3继续迭代,直至算法结束。
2.2 编码与解码
2.2.1 编码
求解FJSP问题涉及工序排序和机器选择两个子问题,因此本文采用了基于工序选择和机器选择的编码方法。编码方式如表2所示。表2中数字1-1代表工件1的第1道工序;第2列表示对应工序的机器选择编码,由于柔性作业车间中工件的每道工序都有不止一台机器可以选择,因此机器选择编码中的Mk表示对应的工序编码可选加工机器集合中的第k台机器。
表2 编码方式示例
Table 2 Coding method example
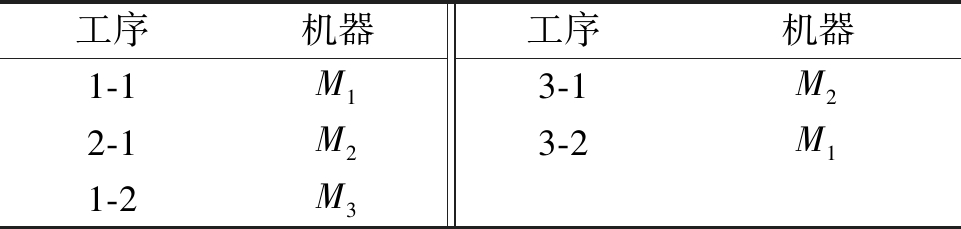
注:数字1-1表示第1个工件的第1道工序,机器M1表示此道工序选择加工机器M1。
工序机器工序机器1-1M13-1M22-1M23-2M11-2M3
2.2.2 解码
种群解码是指按照不同的调度规则解码生成可行的调度方案。在解码过程中,首先根据工序选择编码确定每道工序在调度方案中的加工顺序,然后根据机器选择编码确定每道工序的机器选择。
在解码过程中,本文采用贪婪插入的方式,按照工序序列从左到右依次进行排序,如算法1所示。
算法1 贪婪插入。
输入:一个可行解;
输出:贪婪插入后的可行解。
① For i = 1 to total_op_num do
② 获取当前工序oi所在机器M的空闲时间段B={b1,b2,…,bn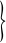 ;
;
③ For j = 1 to n do
④ if oi 的开始时间≤空闲时间bj;
oi 的开始时间=bj 的开始时间;
oi的完成时间=bj的开始时间+oi 的加工时间;
end if
⑤ end
⑥ end
2.3 基于Tent混沌映射的种群初始化
种群初始化策略影响天牛群算法的求解效率和求解质量。对于FJSP问题而言,种群初始化主要包括工序序列初始化和机器序列初始化。
(1)机器序列初始化。机器序列的初始化方案包括全局选择、局部选择和随机选择,本文初始化种群时3种生成规则所占比例分别设置为0.6、0.3、0.1。这种混合策略生成初始种群既保障了调度过程中负载的均匀性又保证了种群的多样性。
(2)工序序列初始化。在大多数研究中,工序序列初始化一般采用随机生成的方式。在生成群智能优化算法的初始种群时,使用Tent混沌映射可以提高种群的多样性,有助于提高算法的搜索能力[15]。本文在生成工序序列的过程中采用Tent混沌序列代替原本的随机序列。
Tent混沌序列的表达式如下:
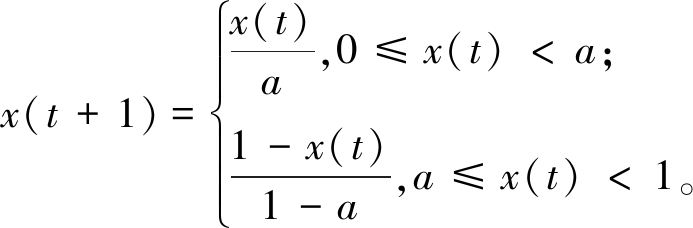
(6)
式中:a一般取值为[0,1],经过多次实验验证,本文选择a =0.499。
2.4 基于反向搜索和莱维飞行改善全局搜索能力
BSO算法在天牛须搜索算法中引入群体的概念,能够在一定程度上跳出局部最优,但是由于FJSP属于NP-hard问题,采用智能优化算法求解时,容易陷入局部极值。本文基于反向搜索和莱维飞行策略来改进BSO算法,提升全局搜索能力。
BSO算法中,天牛个体的数量即为种群的规模。每个天牛个体都有自己的位置和速度,在每次迭代中,天牛个体会朝着个体的最优解移动,所有天牛个体朝着种群最优的天牛个体的方向移动,直至达到最大迭代次数。天牛个体的速度和位置更新公式如下:
vij(t+1)=ωvij(t)+c1r1[(pij)j(t)-xij(t)]+
c2r2[(pij)j(t)-xij(t)]+c3r3ξ(t);
(7)
f(xleft(t)));
(8)
xij(t+1)=xij(t)+vij(t+1)。
(9)
式中:c1、c2两个参数同粒子群算法中的加速因子,一般取[0,2];c3为认知因子;ξ(t)为认知方向;r1、r2、r3为[0,1]上的随机数;ω为惯性权重。
ω的更新方式为
(10)
式中:T为最大迭代次数;t为当前迭代次数;ωmax、ωmin分别表示惯性权重的最大值和最小值,本文中ωmax=0.9,ωmin=0.4,这样设置参数在迭代开始时算法具有更大的搜索范围,随着迭代次数增加,ω逐渐减少,天牛速度降低,算法进行局部搜索。
2.4.1 反向搜索策略
群智能算法迭代过程中,种群多样性通常会随着迭代次数的增加而逐渐减少[16],导致算法陷入局部最优而无法找到全局最优解。为了解决这个问题,通过反向搜索策略引入随机扰动,以增加种群的多样性。其计算公式为
(11)
2.4.2 莱维飞行策略
莱维飞行是一种随机搜索路径,每次移动的步长服从莱维分布,大部分情况下生成较小的步长,但是会以较小的概率出现较大步长的跳跃[17]。利用莱维飞行策略的随机性调整天牛群个体的位置,能够有效帮助BSO算法提高寻优能力[18]。莱维飞行的步长符合莱维分布:
(12)
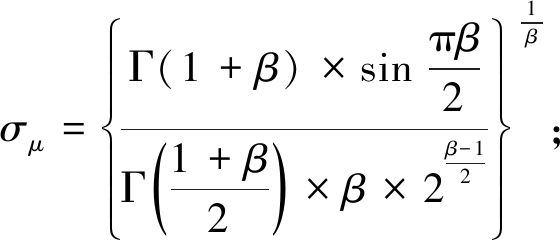
(13)
σv=1。
(14)
式中:![]() 通常取1.5。
通常取1.5。
通过莱维飞行策略和反向搜索策略改善算法的全局搜索能力,天牛个体的位置更新公式为
xij(t+1)=y×(xij(t)+xij(t)⊕Levy )+vij(t+1)。
(15)
2.5 基于适应度值反馈的算法参数调整策略
2.5.1 认知因子的调整策略
天牛个体速度更新公式(式(7))中,c3r3ξ(t)表示天牛群速度更新的个体认知,认知因子c3和认知方向ξ(t)与天牛个体左右两须所在方向的适应度大小有关[19]。认知因子c3的大小决定了个体在搜索过程中是更倾向于全局最优位置还是局部最优位置。认知因子越大,个体越容易跳出局部极值,但收敛速度可能会受到影响;反之,个体更可能陷入局部极值。本文对认知因子进行调整以兼顾算法的搜索能力,更新公式如下:
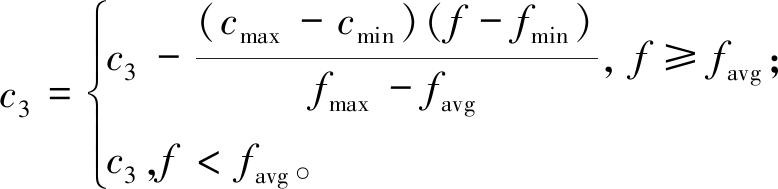
(16)
式中:cmax、cmin分别为认知因子取值的最大值和最小值;f、fmin、fmax、favg分别为当前天牛个体的适应度值、天牛群最小适应度值、天牛群最大适应度值、天牛群平均适应度值。
若此时天牛个体的适应度不如当前群体的平均适应度,则认为该天牛个体所处位置性能不佳,应该对其采用更大的认知因子来增加其全局搜索能力;反之,减小其认知因子以保证个体能够在其位置周围精细搜索,更快地收敛到全局最优解。
2.5.2 搜索步长和搜索距离的调整策略
由于LRA-BSO算法参数多,其性能和初始的搜索步长、天牛的搜索距离以及他们对应的衰减系数有关[20],合理调整搜索步长是帮助算法逃离局部最优的可行方法。
若BSO算法步长衰减过快,容易使算法提前收敛,陷入局部最优解。本文引入基于适应度值反馈的步长进行调整策略:如果适应度较好,则步长不更新;反之,若当前步长不能提高适应度值,则调整搜索步长。步长更新方法如算法2所示。
算法2 更新搜索步长和搜索距离。
输入:当前天牛个体的适应度f、当前天牛群的最佳适应度值fbest、δ(t)、d(t);
输出:更新后的搜索步长δ(t+1)、搜索距离d(t+1)。
① if f <fbest ∥ 当前δ和d不能提高适应度
δ(t+1)= ηδ × δ(t);
d(t+1)= ηd × d(t);
② else
δ(t+1)= δ(t);
d(t+1) = d(t);
③ end
3 算法测试
本文选取6种广泛应用于智能优化算法性能测试的标准测试函数。通过对这些函数进行测试并比较算法得到的最优解和理论最优解,对所提出的LRA-BSO算法本身的性能进行评估。
如表3所示,6种测试函数中,f1和f2为单峰测试函数,f3、f4和f5为多峰测试函数,f6为固定峰值测试函数。对于相同的给定条件,如果得到的解接近或达到理论解,则可以认为该算法具有更强的寻优能力和更高的求解精度。
表3 测试函数
Table 3 Test function

测试函数方程维度变量搜索范围理论最优解f1(x)=∑ni=1x2i30[-100,100]0f2(x)=∑ni=1∑ij-1xj()230[-100,100]0f3(x)=∑ni=1-xisin|xi|()30[-500,500]-1.256 9e+04f4(x)=∑ni=1[x2i-10cos(2πxi)+10]30[-5.12,5.12]0f5(x)=14 000∑ni=1x2i-∏ni=1cosxii()+130[-600,600]0f6(x)=-∑10i=1[(x-ai)(x-ai)T+ci]-130[0,10]-1.053 6e+01
算法运行环境为Win10操作系统、8 GB内存、Intel Core(TM) i7-1165G7 CPU 2.80 GHz。考虑到LRA-BSO算法是基于BSO改进的一种群智能算法,而BSO则是在BAS的基础上引入粒子群概念而提出的群智能算法,本文将LRA-BSO与BSO、粒子群优化算法(PSO)进行比较,各算法的种群规模均设置为50,最大迭代次数T=1 000。LRA-BSO算法参数设置为ωmin=0.4,ωmax=0.9,c1=c2=1.79,c3 max=2,c3 min=1。
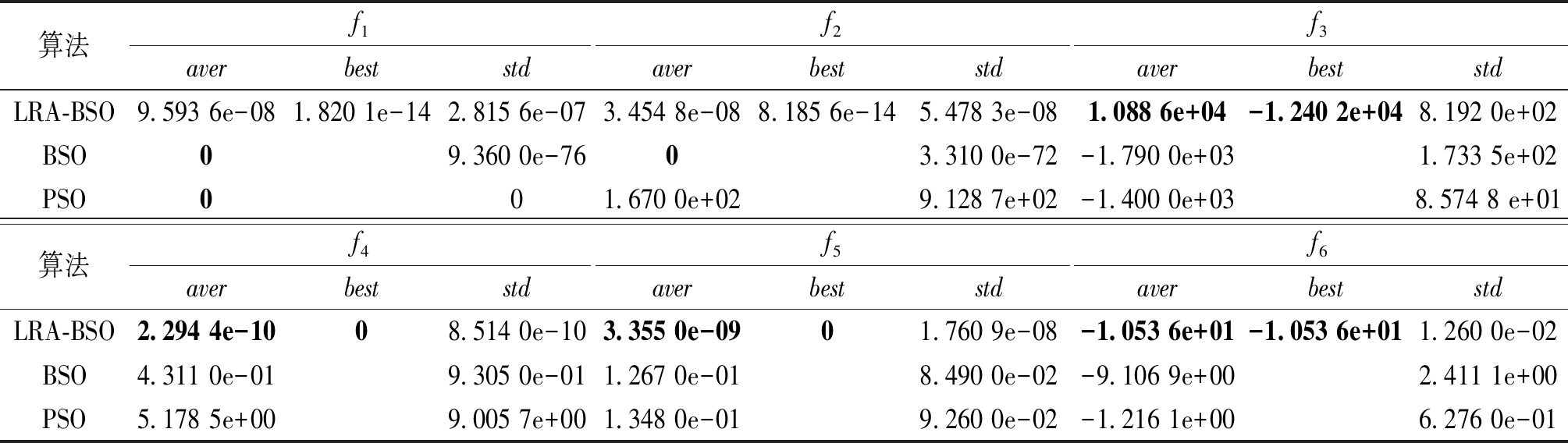
表4给出了30次独立重复实验下3种算法对给出的测试函数的求解结果对比,其中不同函数在3种算法中的最优结果已加粗,其中BSO、PSO的计算结果参见文献[11]。
表4 6种测试函数的实验结果比较
Table 4 Comparison of experimental results of 6 test functions
算法f1f2f3averbeststdaverbeststdaverbeststdLRA-BSO9.593 6e-081.820 1e-142.815 6e-073.454 8e-088.185 6e-145.478 3e-081.088 6e+04-1.240 2e+048.192 0e+02BSO09.360 0e-7603.310 0e-72-1.790 0e+031.733 5e+02PSO001.670 0e+029.128 7e+02-1.400 0e+038.574 8 e+01算法f4f5f6averbeststdaverbeststdaverbeststdLRA-BSO2.294 4e-1008.514 0e-103.355 0e-0901.760 9e-08-1.053 6e+01-1.053 6e+011.260 0e-02BSO4.311 0e-019.305 0e-011.267 0e-018.490 0e-02-9.106 9e+002.411 1e+00PSO5.178 5e+009.005 7e+001.348 0e-019.260 0e-02-1.216 1e+006.276 0e-01
由表4可以看出,在6种基准函数测试实验中,LRA-BSO算法得到了4种测试函数的最优结果,其中f4、f5、f6均达到了测试函数的理论最优值。在处理单峰测试函数f1、f2时,LRA-BSO与BSO、PSO算法相比在收敛能力上还有差距,但是LRA-BSO算法的性能更加稳定。在处理多峰值测试函数f3、f4、f5时,LRA-BSO算法的性能明显优于其他算法。实验结果表明,本文提出的改进策略使得LRA-BSO算法能够有效避免陷入局部最优解。在处理固定峰函数f6时,LRA-BSO算法不仅达到了理论最优值,而且与其他2种算法相比,LRA-BSO算法的性能也更加稳定。
综合考虑3种不同类型的测试函数,本文提出的LRA-BSO算法具有较好收敛精度和较强的稳定性,能够跳出局部最优,避免早熟。该算法具有较强的寻优能力,求解复杂FJSP问题具有优势。
4 案例验证
采用Brandimarte基准算例[21](Mk01~Mk10)及1个实际案例[2]对本文提出的LRA-BSO算法在FJSP工程问题中的应用进行有效性验证。经过多次参数实验,设置LRA-BSO算法参数如下:种群规模为50;最大迭代次数T=1 000;ωmin=0.4;ωmax=0.9;c1=c2=1.79;c3 max=2;c3 min=1。
4.1 标准算例验证
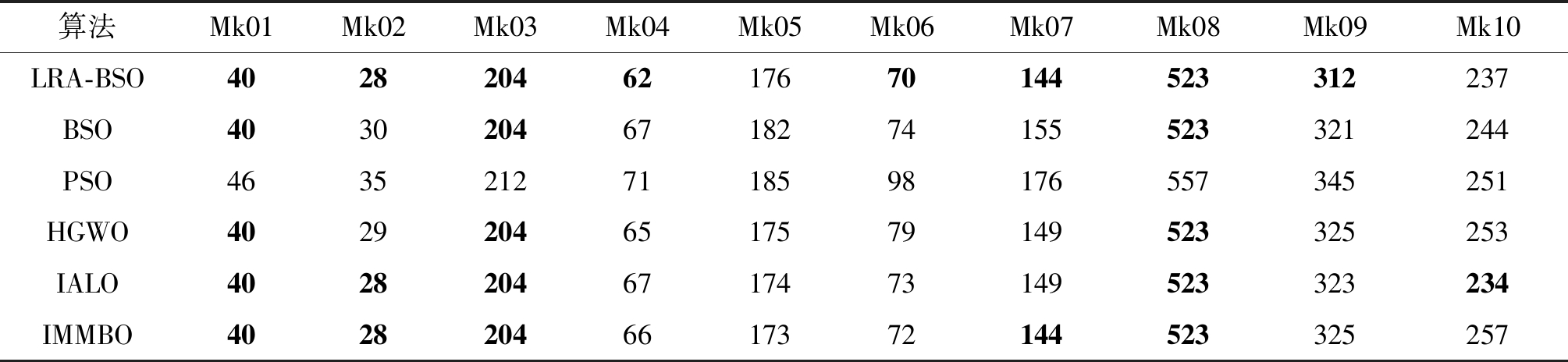
LRA-BSO、BSO、PSO、混合灰狼优化算法(HGWO)[22]、改进蚁狮优化算法(IALO)[3]、改进多邻域候鸟优化算法(IMMBO)[6]等群智能优化算法求解Mk01~Mk10的结果如表5所示。
表5 Brandimarte标准算例对比
Table 5 Comparison of Brandimarte benchmark studies
算法Mk01Mk02Mk03Mk04Mk05Mk06Mk07Mk08Mk09Mk10LRA-BSO40282046217670144523312237BSO40302046718274155523321244PSO46352127118598176557345251HGWO40292046517579149523325253IALO40282046717473149523323234IMMBO40282046617372144523325257
由表5可知,相比于其他算法,除了求解Mk05、Mk10算例的结果略差,LRA-BSO算法在求解其余8个算例时,结果均优于或持平于其他算法。因此,该算法在解决FJSP问题方面具有优势。
4.2 实例验证
采用文献[2]中的FJSP实例对本文提出的LRA-BSO算法进行有效性验证,并与其结果进行对比。在该实例中,6个工件在6台机器上加工,分别采用LRA-BSO、BSO、PSO以及改进狼群算法[2]分别对该实例进行求解,求解结果如表6所示。由表6可知,LRA-BSO算法求解该实例的最大完工时间为35,优于其他算法。
表6 实例对比结果
Table 6 Compared results of the instance

算法最大完工时间LRA-BSO算法35BSO算法37PSO算法38改进狼群算法[2]37
对比LRA-BSO、BSO和PSO算法,图2给出了LRA-BSO、BSO、PSO这3种算法在求解该实例时的迭代曲线。由图2可知,在寻优能力上,LRA-BSO算法优于BSO算法和PSO算法;在收敛速度上,LRA-BSO算法在73代收敛,优于BSO算法但次于PSO算法。虽然PSO算法在15代收敛,但该算法寻优能力不足,易陷入局部最优,表6显示其最大完工时间为38,次于LRA-BSO算法结果。
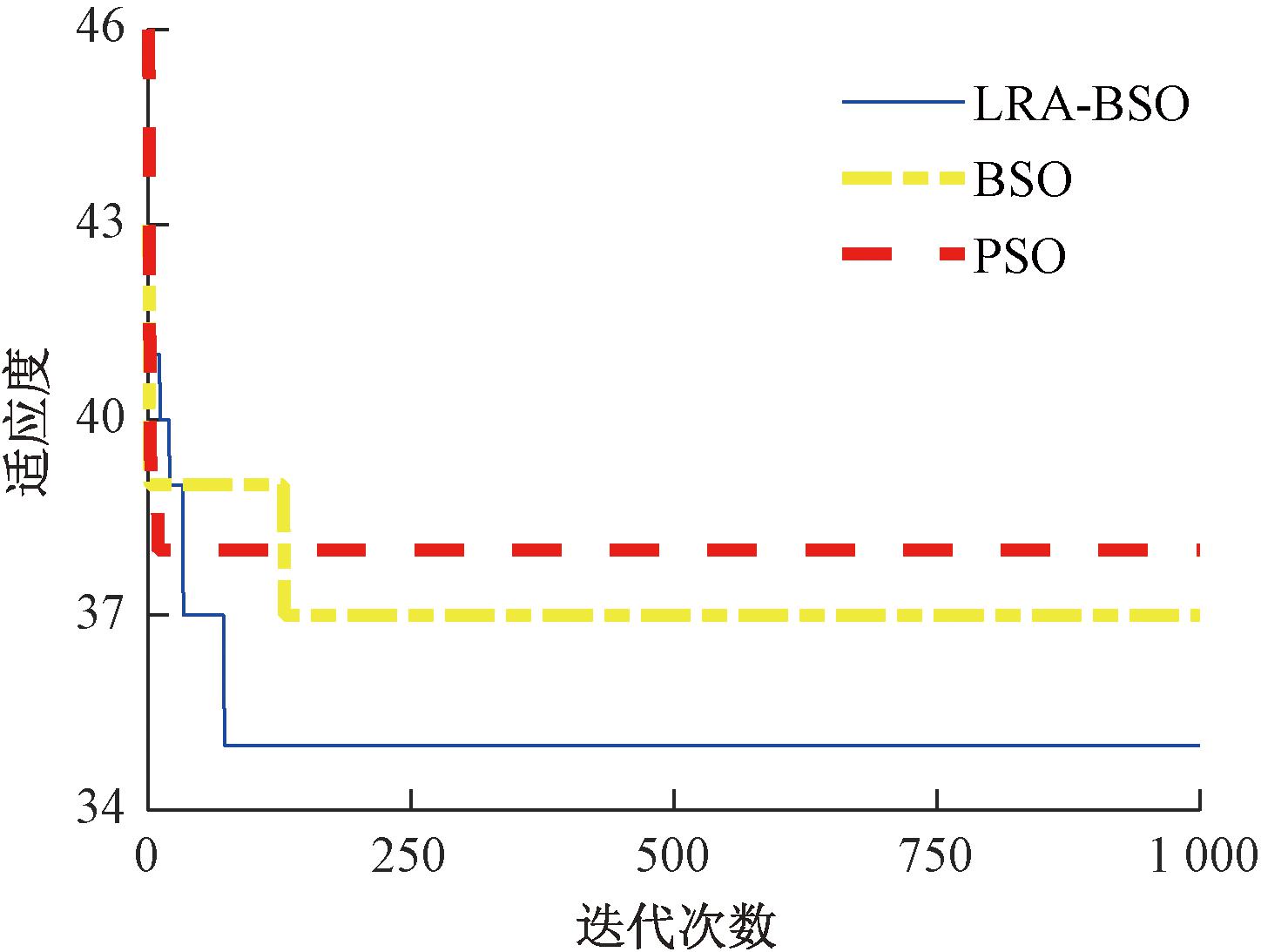
图2 不同算法迭代曲线
Figure 2 Iteration curves of different algorithms
综上所述,求解FJSP实例问题时,本文提出的LRA-BSO算法在寻优能力和收敛速度上具有一定的综合优势。对应的甘特图如图3所示。
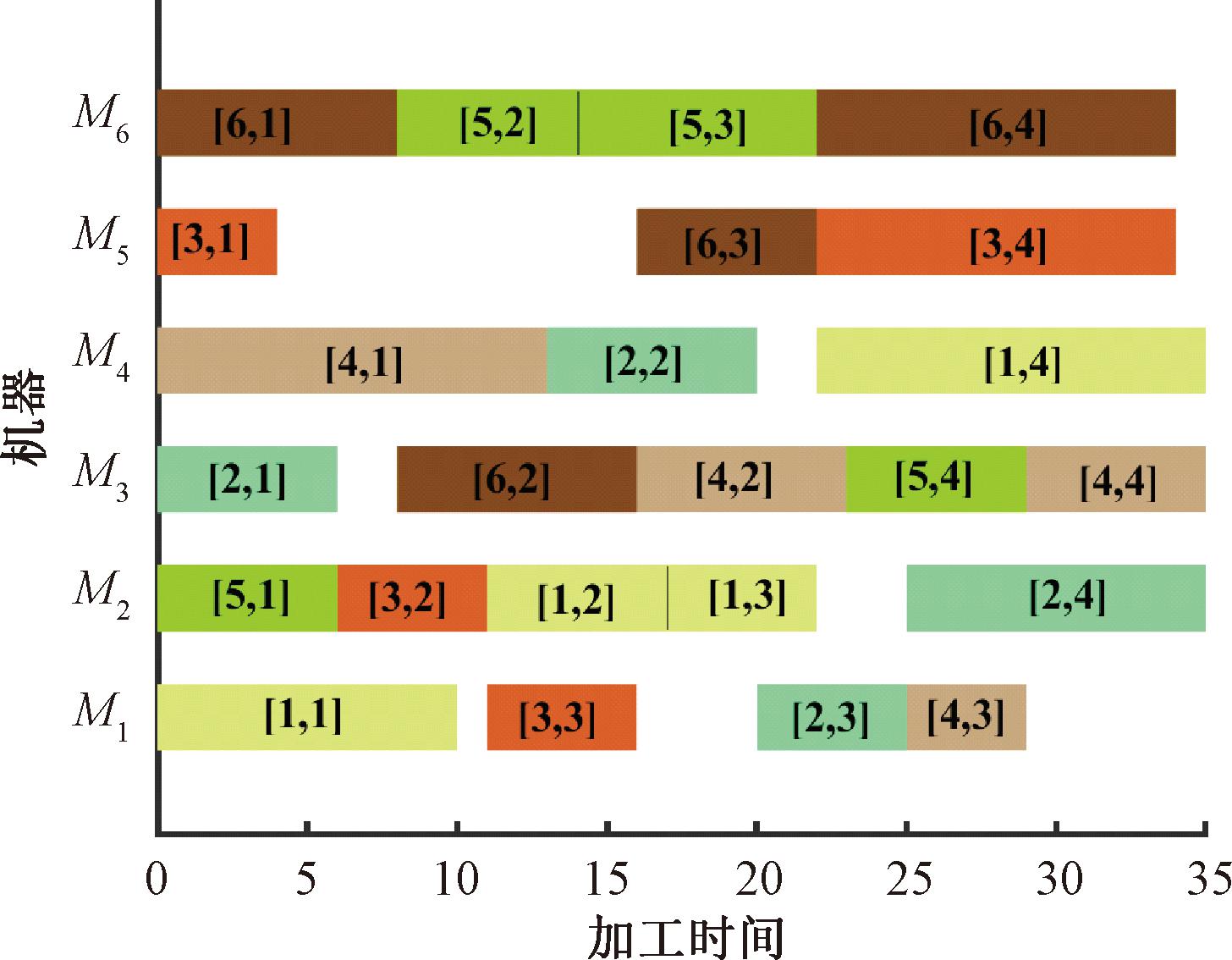
图3 基于LRA-BSO算法的FJSP甘特图
Figure 3 Gantt chart for LRA-BSO based FJSP
5 结论
针对柔性作业车间调度问题,提出了一种基于莱维飞行、反向搜索和自适应参数调整混合策略的改进天牛群算法。改进后的算法在初始种群的质量上有所提升,同时提高了算法的全局搜索能力,能够有效避免陷入局部最优解,可用于解决FJSP等复杂度比较高的离散型组合优化问题。通过6个多维度标准测试函数对改进后的算法本身的性能进行测试。结果表明,LRA-BSO算法具有较好的收敛精度和较强的稳定性。通过10个FJSP标准算例及1个实例验证了LRA-BSO算法在求解FJSP问题上的可行性和有效性。实验结果表明,在求解FJSP实例问题时,LRA-BSO算法在寻优能力和收敛速度上具有较好的综合性能。
[1] 吴秀丽, 张志强. 求解柔性作业车间调度问题的细菌算法对比及改进[J]. 郑州大学学报(工学版), 2018, 39(3): 34-39.
WU X L, ZHANG Z Q. The comparison and improvement of bacterial algorithms for flexible job scheduling problem[J]. Journal of Zhengzhou University (Engineering Science), 2018, 39(3): 34-39.
[2] 张朝阳, 徐莉萍, 李健, 等. 基于改进狼群算法的柔性作业车间调度研究[J]. 系统仿真学报, 2023, 35(3): 534-543.
ZHANG C Y, XU L P, LI J, et al. Flexible job-shop scheduling problem based on improved wolf pack algorithm[J]. Journal of System Simulation, 2023, 35(3): 534-543.
[3] 王彦杰, 向凤红. 基于改进蚁狮优化算法的柔性作业车间调度研究[J]. 机电工程, 2022, 39(9): 1325-1332.
WANG Y J, XIANG F H. Flexible job shop scheduling based on improved ant lion algorithm[J]. Journal of Mechanical &Electrical Engineering, 2022, 39(9): 1325-1332.
[4] GAYATHRI D K, MISHRA R S, MADAN A K. A dynamic adaptive firefly algorithm for flexible job shop scheduling[J]. Intelligent Automation &Soft Computing, 2022, 31(1): 429-448.
[5] MENG T, PAN Q K, SANG H Y. A hybrid artificial bee colony algorithm for a flexible job shop scheduling problem with overlapping in operations[J]. International Journal of Production Research, 2018, 56(16): 5278-5292.
[6] 杜凌浩, 向凤红. 改进多邻域候鸟优化算法的柔性作业车间调度研究[J]. 兵器装备工程学报, 2022, 43(12): 299-306.
DU L H, XIANG F H. Research on flexible job shop scheduling based on improved multi-neighborhood migratory bird optimization algorithm[J]. Journal of Ordnance Equipment Engineering, 2022, 43(12): 299-306.
[7] JIANG X Y, LI S. BAS: beetle antennae search algorithm for optimization problems[J]. International Journal of Robotics and Control, 2018, 1(1): 1.
[8] JIANG Y F, WANG S Q, LI Y C. Localizing and quantifying structural damage by means of a beetle swarm optimization algorithm[J]. Advances in Structural Engineering, 2021, 24(2): 370-384.
[9] FAN Y Q, SHAO J P, SUN G T. Optimized PID controller based on beetle antennae search algorithm for electro-hydraulic position servo control system[J]. Sensors, 2019, 19(12): 2727.
[10] KIM J, JO H, RI J, et al. Automatic fabric defect detection using optimal Gabor filter based on hybrid beetle antennae search-gravitational search algorithm[J]. Journal of Optics, 2023,52(4): 1-9.
[11] WANG T T, YANG L. Beetle swarm optimization algorithm: theory and application[EB/OL]. (2018-08-01)[2023-10-12]. https:∥arxiv.org/abs/1808.00206.
[12] BHAGAVATHI H, RATHINAVELAYATHAM S, SHANMUGAIAH K, et al. Improved beetle swarm optimization algorithm for energy efficient virtual machine consolidation on cloud environment[J]. Concurrency and Computation: Practice and Experience, 2022, 34(10): 1-15.
[13] MU Y Z, LI B K, AN D, et al. Three-dimensional route planning based on the beetle swarm optimization algorithm[J]. IEEE Access, 2019, 7: 117804-117813.
[14] BRUCKER P, SCHLIE R. Job-shop scheduling with multi-purpose machines[J]. Computing, 1990, 45(4): 369-375.
[15] 刘倩, 冯艳红, 陈嶷瑛. 基于混沌初始化和高斯变异的飞蛾火焰优化算法[J]. 郑州大学学报(工学版), 2021, 42(3): 53-58.
LIU Q, FENG Y H, CHEN Y Y. Moth-flame optimization algorithm based on chaotic initialization and Gaussian mutation[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(3): 53-58.
[16] 徐霜, 万强, 余琍. 基于学习理论的改进粒子群优化算法[J]. 郑州大学学报(工学版), 2019, 40(2): 29-34.
XU S, WAN Q, YU L. An improved particle swarm optimization algorithm based on learning theory[J]. Journal of Zhengzhou University (Engineering Science), 2019, 40(2): 29-34.
[17] ALI M Z, AWAD N H, REYNOLDS R G, et al. A balanced fuzzy cultural algorithm with a modified Levy flight search for real parameter optimization[J]. Information Sciences, 2018, 447: 12-35.
[18] XU X, DENG K L, SHEN B. A beetle antennae search algorithm based on Lévy flights and adaptive strategy[J]. Systems Science &Control Engineering, 2020, 8(1): 35-47.
[19] 赵玉强, 钱谦. 一类带学习与竞技策略的混沌天牛群搜索算法[J]. 通信技术, 2018, 51(11): 2582-2588.
ZHAO Y Q, QIAN Q. Novel chaos beetle swarm searching algorithm with learning and competitive strategies[J]. Communications Technology, 2018, 51(11): 2582-2588.
[20] WANG J Y, CHEN H X. BSAS: beetle swarm antennae search algorithm for optimization problems[EB/OL]. (2018-07-27)[2023-10-12]. https:∥arxiv.org/abs/1807.10470.
[21] BRANDIMARTE P. Routing and scheduling in a flexible job shop by tabu search[J]. Annals of Operations Research, 1993, 41(3): 157-183.
[22] 姜天华. 混合灰狼优化算法求解柔性作业车间调度问题[J]. 控制与决策, 2018, 33(3): 503-508.
JIANG T H. Flexible job shop scheduling problem with hybrid grey wolf optimization algorithm[J]. Control and Decision, 2018, 33(3): 503-508.