青少年运动损伤、人群异常检测以及老年人独居安全问题受到社会的广泛关注。传感器因其采集、存储数据量少,不涉及隐私问题以及易于集成在智能设备中的优势,被广泛应用于行为分析[1]、医疗保健[2]、智能家居[3]等人类行为感知领域。在过去的几年里,机器学习算法吸引了人类行为识别(human activity recognition, HAR)领域研究者的目光。Chen等[4]提出了一个卷积神经网络(convolutional neural networks, CNNs)模型,对卷积核进行修改以处理智能手机的三轴加速度计信号来识别人类活动。Ignatov [5]将CNNs提取的局部特征与时间序列的统计特征相结合,保留关于原始信号的全局特征信息。Wang等 [6]提出用分层深度长短时记忆神经网络提取时序信号的时域和频域特征完成分类任务。Su等[7]提出深度双向长短时记忆模型将长序列原始数据处理成双向输出向量,然后使用CNNs从输出向量中提取局部特征。基于长短时记忆神经网络的方法考虑到了时间序列的上下文的语义信息,却忽略了同种动作样本之间的相关性。此外,这些传统深度学习方法的特征提取集中在数据值上,缺乏对数据中隐藏的结构与关系信息的探索。
与视频或时间序列信号不同,非欧空间的图结构包含了丰富的拓扑信息。图卷积神经网络(graph convolutional neural networks, GCNs)因其强大的推理能力和良好的解释性成为深度学习的焦点[8]。目前,很少有研究者利用GCNs来学习和挖掘可穿戴传感器采集的人类行为信号的隐藏拓扑关系。Ahmad等[9]首次提出采用时间序列图模块将原始HAR转换为图结构,通过GCNs聚合更新样本特征实现动作识别。这种图形构造方法仅通过构建样本采样点间的时序拓扑关系来完成信息传递,没有形成样本的幅值结构信息。Donner等[10]总结了3种将时间序列转换为图形的表示方法:递归网络、转移网络和可视图。水平可视图(horizontal visibility graph, HVG)[11]作为可视图的简化,将时间序列转换为图形的同时保留了时间序列拓扑与动态特征。Li等[12]通过加权水平可视图的方式为故障信号构建时空图,并通过图同构网络对图形进行分类。这种分类方法考虑了采样点之间的结构信息,却忽视了样本之间的信息交流。
为了解决这些挑战,本文提出了一种混合结构特征和时频特征的GCNs(graph convolutional neural networks with hybrid time-frequency and construction characteristics, HTC-GCN)。其中心思想是将HVG构建的时空图转换为节点,并且在具有相似特征的节点之间构建边,实现样本自身以及样本之间的信息传递。
本文的主要工作包括以下3个方面。
(1)将HVG构建的时空图表示为拉普拉斯矩阵并通过正交分解得到动作样本的结构特征以挖掘采样点间的动态特性。
(2)在人体动作时间序列的结构特征中加入距离约束,弱化时空图中远距离邻居对中心节点的影响。进一步提高模型的拟合能力。
(3)设计了一个混合时频特征和结构特征的GCNs模型,克服结构特征受时空图拓扑关系影响较大的问题,进一步提高模型的识别能力。
1 人体行为识别方法
本文工作旨在建立一个HTC-GCN模型(如图1所示)突破传统HAR方法中时序信号结构特征提取困难的问题,探索GCNs在可穿戴式HAR领域的有效性。HTC-GCN核心思想是将非结构化时间序列转化为语义丰富的结构化图,不仅能提取动作信号中的时频特征,还能将信号中潜在的结构信息转变为结构特征。为此,本文首先通过小波包变换提取动作信号中的时频特征Fd,同时采用拉普拉斯矩阵表示HVG算法构造的时空图,并利用正交分解提取动作信号的结构特征Fc。其次,时频特征Fd与结构特征Fc结合构成图神经网络输入特征X。此外,考虑到动作样本的划分通过滑动窗口实现导致HVG构建的样本拓扑存在差异,本文利用时频特征构造GCNs的输入拓扑。最后,通过训练两层图卷积模块,使输入特征X在输入拓扑图上传播,最终得到与分类任务最相关的信息H。
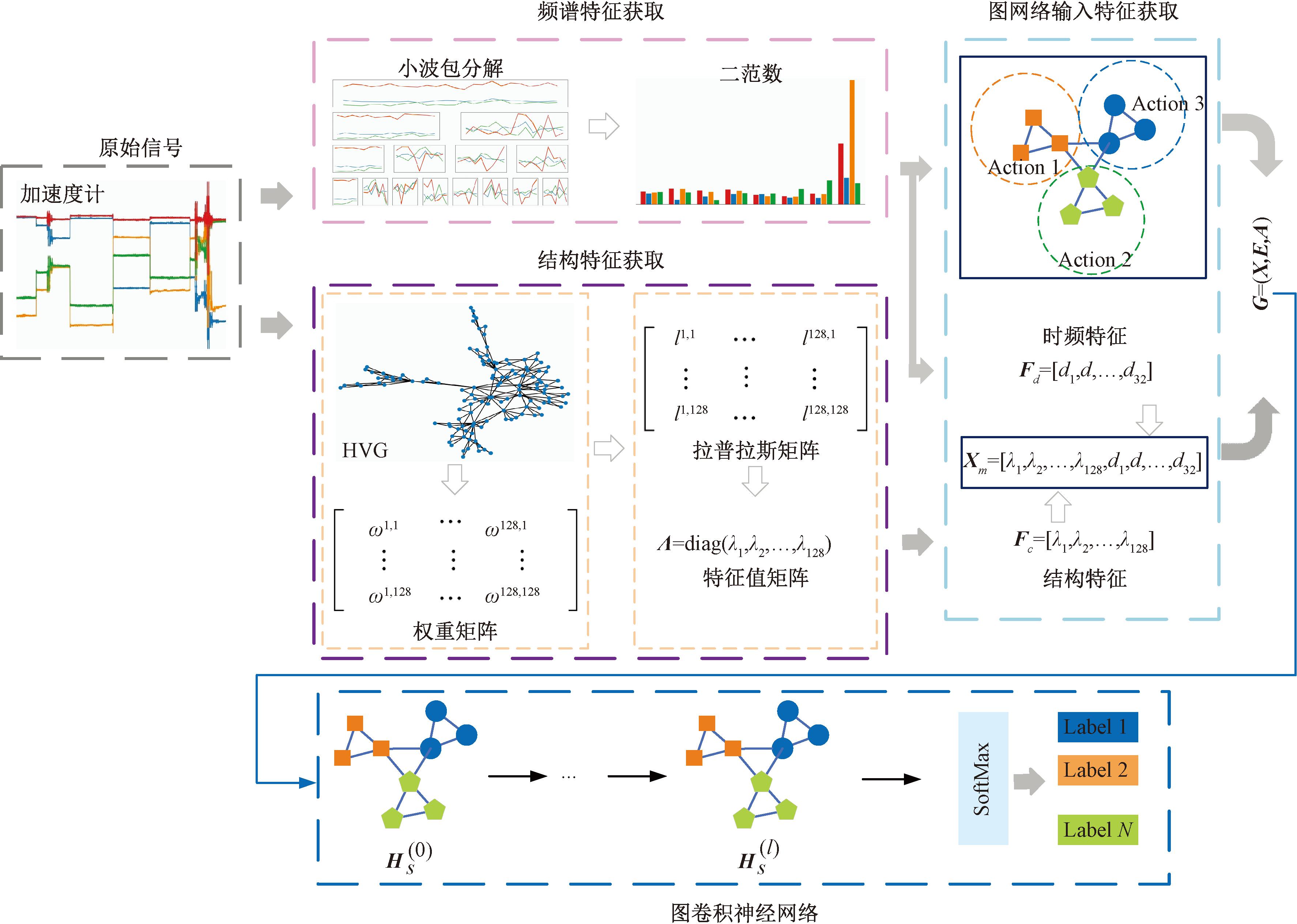
图1 所提出的人类行为识别模型
Figure 1 The proposed HAR model
1.1 提取动作的时频特征
本文采用长度为128、重叠率为50%的固定宽度滑动窗口对数据集中的加速度计信号进行处理。使用加速度计传感器的4个通道(X轴加速度、Y轴加速度、Z轴加速度和三轴合成加速度),因此将有1个4×128的输入矩阵。基于离散小波包变换(DWPT)对每个通道进行分解,小波变换公式[13-14]为
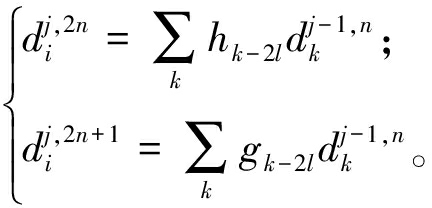
(1)
式中:d为小波包分解系数;h为高通滤波器系数;g为低通滤波器系数;j和n均为小波包节点数。通过二范数计算子带长度得到时频特征Fd。
1.2 提取动作的结构特征
1.2.1 基于水平可视图的时空图构建
人的运动信号中包含大量的动态属性,这些动态属性可以表示为时序信号的结构信息。本文通过HVG构建时空图来获取原始信号结构信息。相比于传统的特征提取方法,时空图不仅包含了时序信号的采样点信息,同时保留了动态属性,进一步提高特征的识别能力。为了减弱传感器安装所造成的方向误差,本文仅对样本的三轴合成加速度构造时空图。
(1)图形表示。时空图表示为GS=(VS,AS,WS),其中VS为节点特征矩阵;AS为节点之间的边连接矩阵;WS为图的权重矩阵。
(2)图形构造。HVG算法将时间序列转换为N个节点的图,节点特征为对应样本点的采样值即![]() 仅当没有中间数据高度与
仅当没有中间数据高度与![]() 和
和![]() 中间的水平连接相交时,2个节点之间存在无向边,边连接矩阵AS的表达如下所示:
中间的水平连接相交时,2个节点之间存在无向边,边连接矩阵AS的表达如下所示:
(2)
式中:![]() 为AS第i行j列的元素。
为AS第i行j列的元素。
图2为HVG算法图解。图2(a)描绘了时间序列(0.8,0.2,0.3,0.6,0.1,0.7)的条形图,并画出2个条形柱之间未出现相交的水平线,由此可生成如图2(b)所示的HVG,其中包含6个节点和9条无向边。由此可见,HVG中的每个节点至少与其时间相邻的节点是有边连接的。此外,HVG在仿射映射下保持不变,使得不同的采样频率和归一化不会影响图形结构[13]。
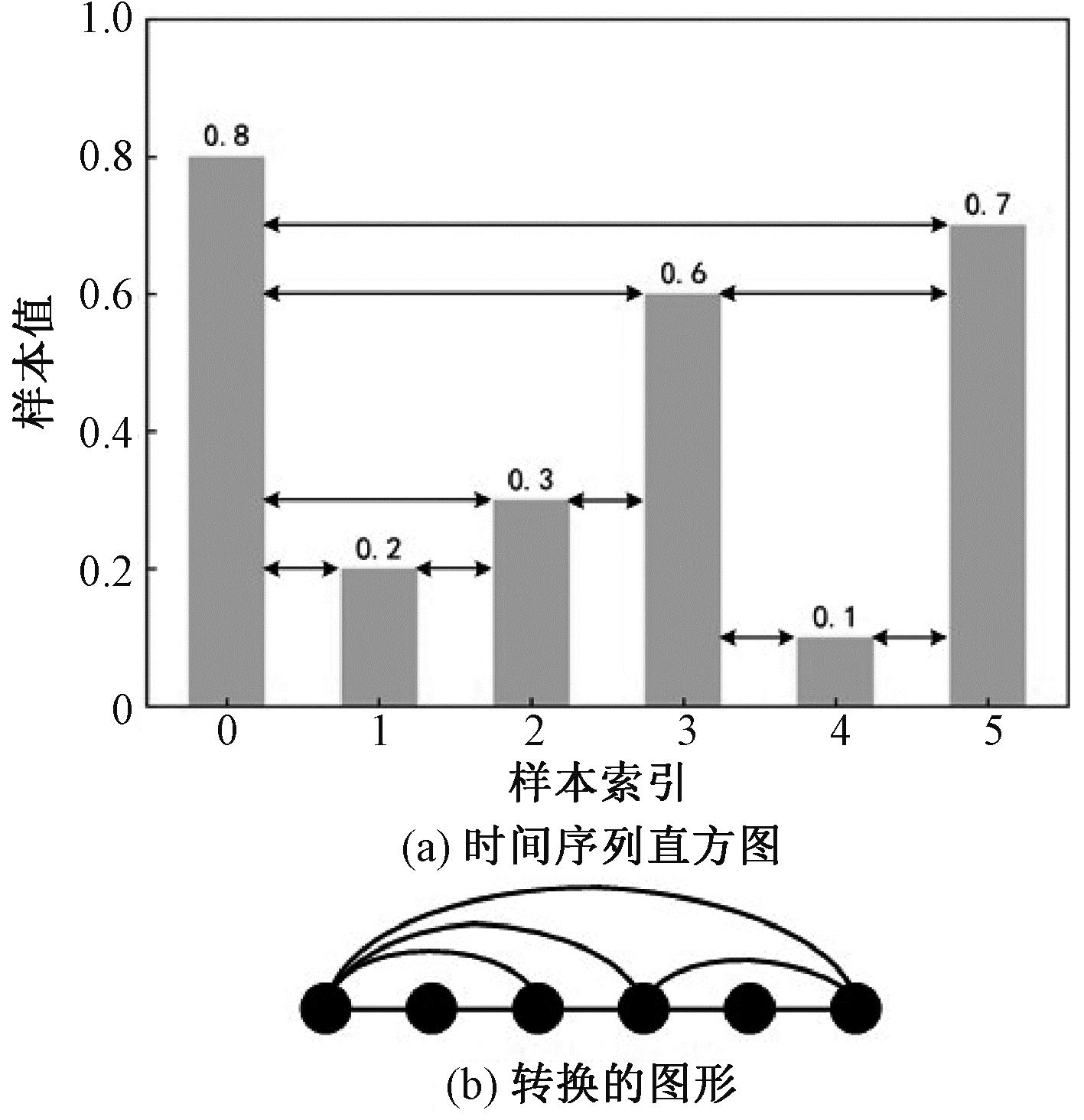
图2 HVG算法图解
Figure 2 Illustration of HVG algorithm
(3)权重矩阵构造。由于传感器采集的时间序列信号中存在噪声,导致远距离采样点之间出现干扰边缘,这将阻碍识别性能。为了抑制干扰边缘产生的影响,本文为时空图边连接添加如式(3)所示的权重约束:
(3)
式中:i为中心节点的时序序号;j为邻居节点的时序序号。权重矩阵WS元素由式(4)计算得到:
(4)
式中:Dis(·)为节点![]() 和节点
和节点![]() 间的欧氏距离。
间的欧氏距离。
1.2.2 基于时空图的结构特征提取
利用图中包含隐藏结构信息的优点,采用图论的方法进行时空图特征提取。首先依据时空图中的权重矩阵得到拉普拉斯矩阵,然后对拉普拉斯矩阵进行正交分解得到动作的结构特征。
(1)拉普拉斯矩阵构建。在谱图分析中,拉普拉斯矩阵L的定义为
L=D-WS。
(5)
式中:D为度矩阵,其对角线元素表示为
(6)
(2)正交分解。对实对称拉普拉斯矩阵通过式(7)进行正交分解:
L=UΛUT。
(7)
式中:Λ=diag(λ0,λ1,…,λN-1)为特征值矩阵;U为特征向量。最后将每个时空图转变为一维特征向量Fc=[λ0,λ1,…,λN-1]来表示样本的结构特征。
1.3 混合结构与时频特征的图卷积神经网络模型
构造GCNs有2个主要步骤:输入拓扑图构造和图卷积。将动作数据的结构特征和频谱特征作为图的节点,并通过确定节点之间的相关性构造图结构。
1.3.1 输入拓扑图构造
将原始动作信号表示为属性图G=(X,E,A)。其中,X为图的输入特征,其数目为样本总数M;E为图的边集;A为任意2个节点之间连接的相邻矩阵。
(1)输入特征X。将样本的时频特征Fd和样本的结构特征Fc进行拼接,得到GCNs最终的输入特征X:
X=hstack(Fd,Fc)。
(8)
式中:hstack(·)表示将括号中的元素按水平方向叠加。
(2)边集A。边集最重要的需求就是在相同类别节点之间创建更多的边缘连接的同时减少不同类型之间边缘连接,从而加强同类节点之间的内聚度,降低异类节点之间的耦合度。由于HVG构建的样本结构差异性较大,通过样本的结构特征Fc来构建边集难以找到合适的边连接。相同动作在同一个运动周期中的时间序列信号的时频特征具有相似性,本文根据时频特征Fd构建边集:
(9)
式中:Disi为节点i特征与其他节点特征之间的欧氏距离;sort(·)为升序算子;pi为排序后的Disi;Si为pi中前k个数的节点序号集合。最后将节点i与Si中存在的节点之间创建边连接。
(3)相邻矩阵。相邻矩阵A∈RM×M的元素为
(10)
1.3.2 图卷积神经网络
将G=(X,E,A)作为GCN的输入图形,第l层的输出为[8]
(11)
式中:ReLU(·)为激活函数;W(l)为GCNs第l层的权重矩阵;H(l-1)为第l-1层的输出特征且H(0)=X;![]() 意味着在进行图卷积时节点能从自身学习到更多特征;
意味着在进行图卷积时节点能从自身学习到更多特征;![]() 为
为![]() 的度矩阵,其对角元素
的度矩阵,其对角元素![]()
![]() 最后将输出的特征输入到SoftMax层完成动作分类。
最后将输出的特征输入到SoftMax层完成动作分类。
2 实验与结果分析
2.1 实验数据
本文提出的模型在2个真实的动作数据集上进行评估。WHARF[15]数据集在32 Hz频率下使用加速度计收集12类动作的时序信号。动作包含刷牙、梳头和吃饭等复杂活动。使用长度为256、重叠率为50%的固定宽度滑动窗口对数据进行样本划分。DataEgo[16]数据集在15 Hz频率下使用加速度计和陀螺仪收集20类动作的时序信号。动作包含刷牙、梳头和吃饭等复杂活动。使用长度为256、重叠率为50%的固定宽度滑动窗口对数据进行样本划分。
2.2 实验环境设置与评测指标
为了评估本文提出的模型,随机选取数据集中70%的样本作为训练集,30%的样本为测试集。通过准确率(Accuracy),召回率(Recall)以及F1分数与文献[4, 17-19]的方法进行比较。原始数据已经转换为输入矩阵XM×160,表示每个样本有160个特征。设置隐藏层nhid1=128、二层GCNs的输出层nhid2=64。使用学习率为0.001的Adam优化器,weight decay设置为10-4,最大迭代次数为2 000。所有方法均使用相同的参数运行10次,并报告平均结果。所有算法都是由Python 3.7用Pytorch编写的,并由具有Intel Xeon E5-2665 CPU和32 GB RAM的服务器处理。
2.3 实验结果
2.3.1 在2个数据集上的分类结果对比
表1给出了本文提出的HTC-GCN模型与其他方法的分类性能对比结果。由表1可以看出,本文方法在DataEgo数据集上的3个常用评价指标都具有优势。同时在2个数据集中所提模型在F1分数上有更好的表现。其中在WHARF数据集上,本文模型较对比模型的F1分数最大提高了19.58百分点;在DataEgo数据集上,本文模型较对比模型的F1分数最高提升了26.44百分点。这充分说明GCNs通过在拓扑结构上聚合相邻节点之间的特征,能实现节点之间信息的有效交流。
表1 不同方法在2个数据集上的分类结果
Table 1 Classification results of different methods on two datasets %
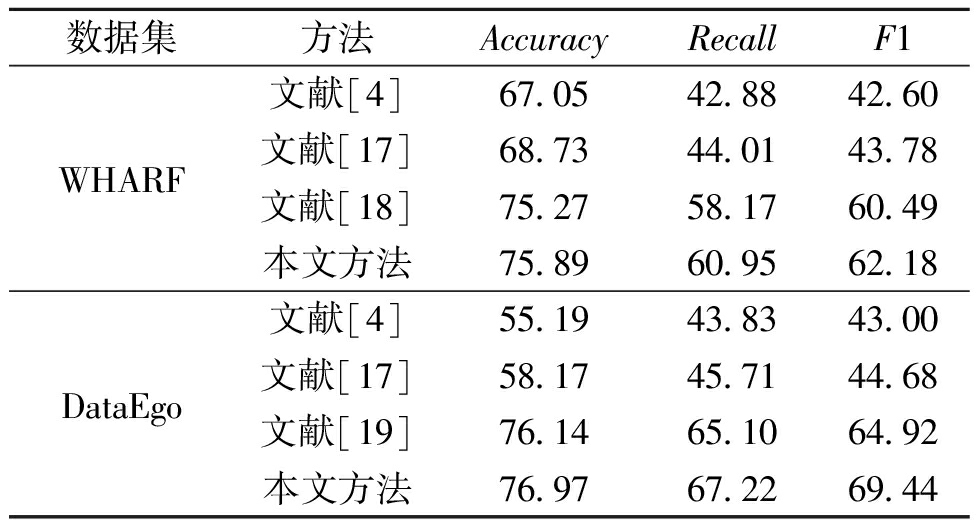
数据集方法AccuracyRecallF1文献[4]67.0542.8842.60WHARF文献[17]68.7344.0143.78文献[18]75.2758.1760.49本文方法75.8960.9562.18文献[4]55.1943.8343.00DataEgo文献[17]58.1745.7144.68文献[19]76.1465.1064.92本文方法76.9767.2269.44
为了更直观地表示HTC-GCN网络模型在WHARF数据集上的表现,图3给出了其识别结果的混淆矩阵图。可以看出,数据集中走路和上下楼、起床和躺、坐下和站起这些高度相似的行为误差率较高,但对于其他大部分行为都能够准确识别其行为类别,证明了本文方法在复杂行为识别上的有效性。

图3 HTC-GCN在WHARF数据集上准确率混淆矩阵
Figure 3 Accuracy confusion matrix of HTC-GCN on WHARF dataset
2.3.2 结构特征对所提模型的性能影响
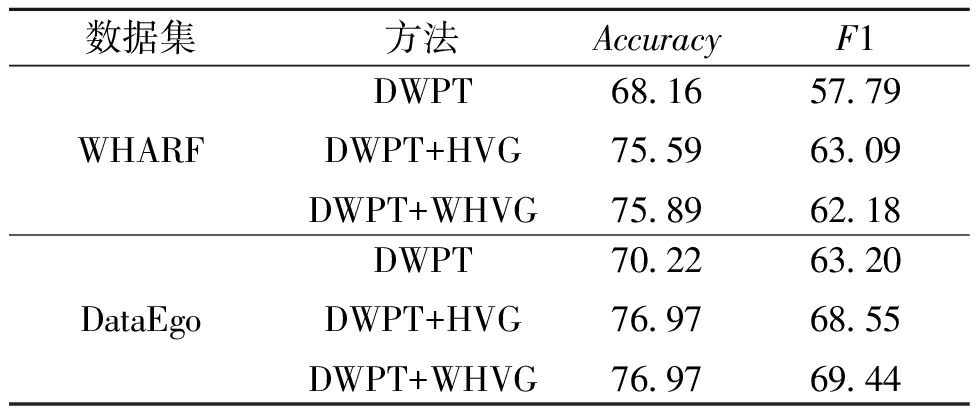
结构特征对本文方法分类结果的影响如表2所示,测试过程的损失下降曲线如图4所示。其中DWPT表示仅使用时频特征对动作进行分类;DWPT+HVG表示使用不添加约束的结构特征与时频特征融合对动作进行分类;DWPT+WHVG表示使用添加约束的结构特征与时频特征融合对动作进行分类。显然,在2个数据集中,时频特征与结构特征的融合取得了比单一使用时频特征更好的效果。添加上权重约束之后的DWPT+WHVG拥有与DWPT+HVG相近的准确率和F1分数,而损失值的下降速率却快于未加约束的DWPT+HVG。这充分说明本文通过HVG构建时空图,并利用具有额外距离约束的拉普拉斯矩阵表示时空图提取出动作信号结构特征的有效性。
表2 结构特征对所提方法分类结果的影响
Table 2 Influence of structural characteristics on classification results of the proposed method %
数据集方法AccuracyF1WHARFDWPTDWPT+HVGDWPT+WHVG68.1675.5975.8957.7963.0962.18DataEgoDWPTDWPT+HVGDWPT+WHVG70.2276.9776.9763.2068.5569.44
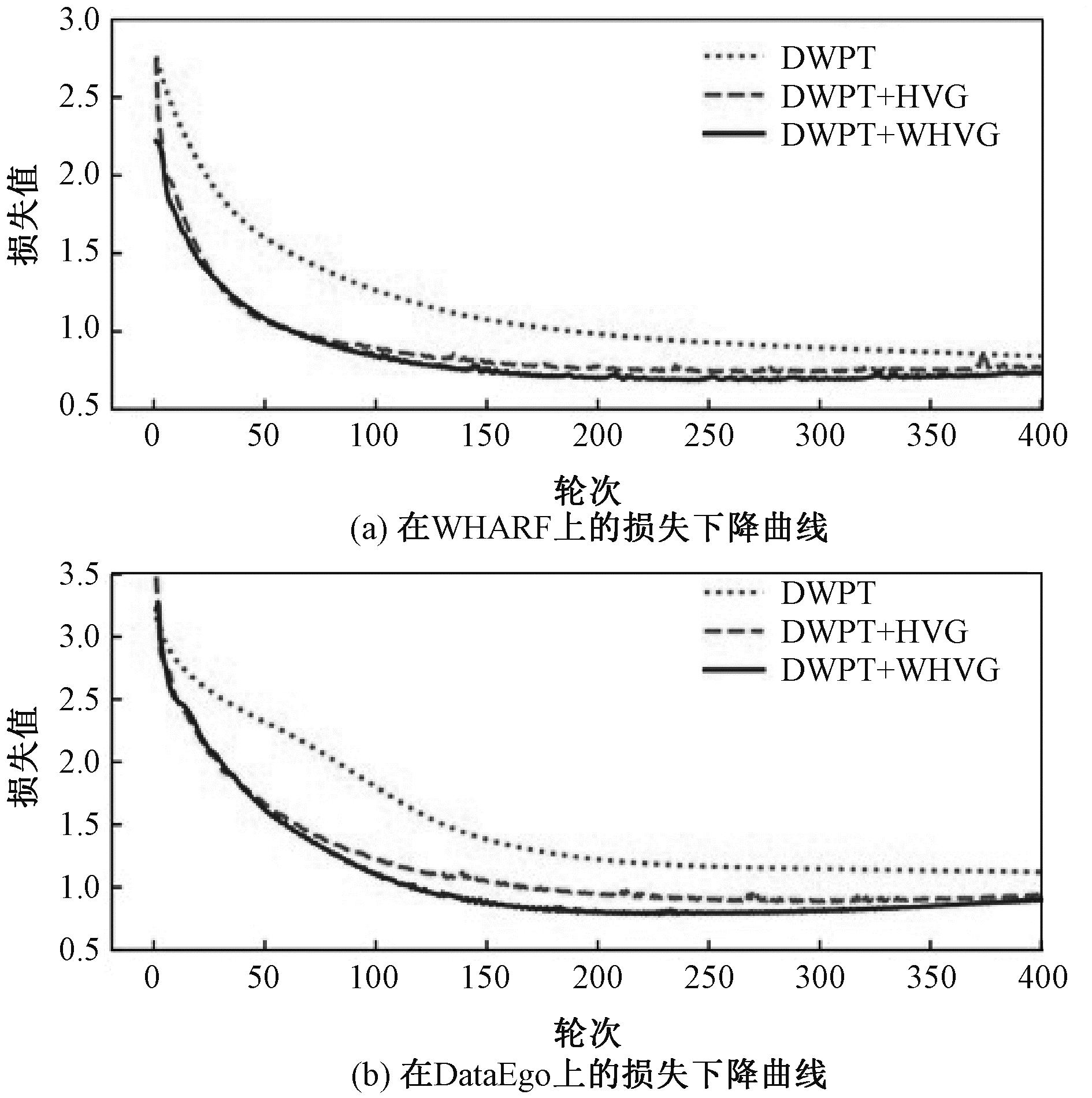
图4 HTC-GCN模型在2个数据集上的损失下降曲线
Figure 4 Loss curves of HTC-GCN model on two datasets
2.3.3 构图方式对所提模型的性能影响
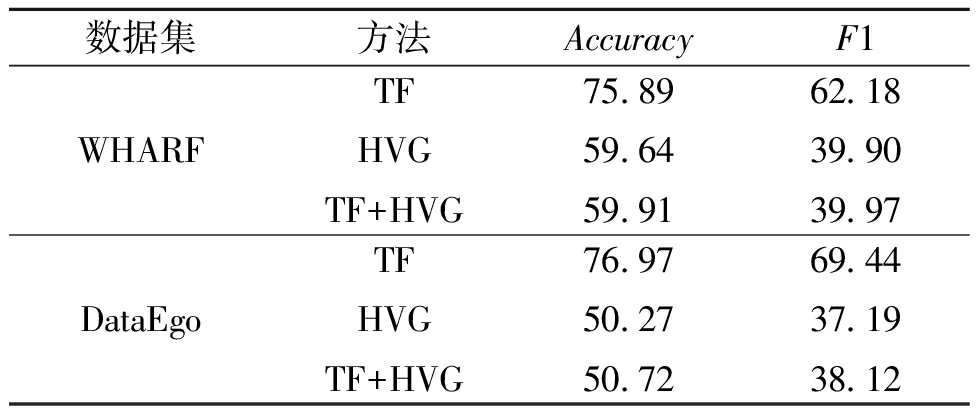
构图方式对HTC-GCN分类结果的影响如表3所示。其中TF表示按时频特征构造GCNs输入拓扑图;HVG表示按加权结构特征构造输入拓扑图;TF+HVG表示按输入特征构造输入拓扑图。实验表明,单一地通过时频特征构造输入拓扑取得了很好的效果。这不仅说明时频特征构造的输入拓扑图克服了重采样导致的样本结构差异,而且合适的拓扑构造能帮助GCNs更好地完成分类任务。
表3 构图方式对所提方法分类结果的影响
Table 3 Influence of graph construction on classification results of the proposed method %
数据集方法AccuracyF1WHARFTFHVGTF+HVG75.8959.6459.9162.1839.9039.97DataEgoTFHVGTF+HVG76.9750.2750.7269.4437.1938.12
2.3.4 滑动窗口宽度对所提模型的性能影响
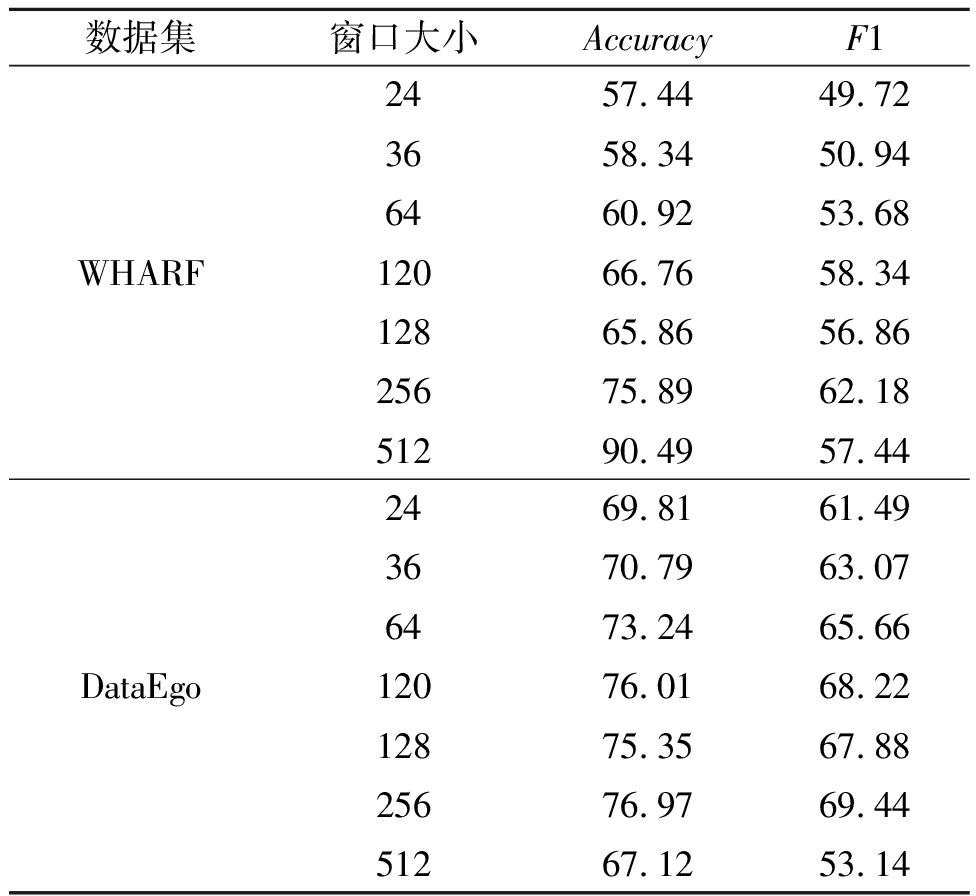
滑动窗口宽度对HTC-GCN分类结果的影响如表4所示。数据集WHARF和DataEgo在窗口宽度为256时取得最好的F1结果。实验表明,窗口宽度并非越大识别效果越好:窗口越大,样本中所含动作周期量变多的同时样本数目减少,削弱了深度模型的学习能力;窗口越小,样本数目增多,样本中所含动作周期量减少,样本特征不足,同样削弱了模型的学习能力。
表4 滑动窗口宽度对所提方法分类结果的影响
Table 4 Influence of sliding window width on classification results of the proposed method %
数据集窗口大小AccuracyF1WHARF24366412012825651257.4458.3460.9266.7665.8675.8990.4949.7250.9453.6858.3456.8662.1857.44DataEgo24366412012825651269.8170.7973.2476.0175.3576.9767.1261.4963.0765.6668.2267.8869.4453.14
3 结论
本文在关注可穿戴传感器采样点之间结构信息的同时捕获动作样本之间的潜在关系,探索GCNs在人体动作时间序列建模上的可能。在WHARF和DataEgo数据集上取得的显著改进表明,本文提出的HTC-GCN克服了传统深度学习方法的局限性,初步证明挖掘非结构化时间序列的结构信息是提升可穿戴HAR性能的有效途径。基于GCNs的HAR模型还有很多需要探索的问题,包括节点内部特征和节点关系对分类模型的贡献度等。
[1] HUAN Z, LV S Y, HOU Z J, et al. An evaluation strategy for the symmetry and consistency of lower limb segments during upper limb loading[J]. IEEE Sensors Journal, 2021, 21(5): 6440-6449.
[2] PHAM C, NGUYEN-THAI S, TRAN-QUANG H, et al. SensCapsNet: deep neural network for non-obtrusive sensing based human activity recognition[J]. IEEE Access, 2020, 8: 86934-86946.
[3] ZHU R, XIAO Z L, LI Y, et al. Efficient human activity recognition solving the confusing activities via deep ensemble learning[J]. IEEE Access, 2019, 7: 75490-75499.
[4] CHEN Y Q, XUE Y. A deep learning approach to human activity recognition based on single accelerometer[C]∥2015 IEEE International Conference on Systems, Man, and Cybernetics. Piscataway: IEEE, 2015: 1488-1492.
[5] IGNATOV A. Real-time human activity recognition from accelerometer data using convolutional neural networks[J]. Applied Soft Computing, 2018, 62: 915-922.
[6] WANG L K, LIU R Y. Human activity recognition based on wearable sensor using hierarchical deep LSTM networks[J]. Circuits, Systems, and Signal Processing, 2020, 39(2): 837-856.
[7] SU T T, SUN H Z, MA C M, et al. HDL: hierarchical deep learning model based human activity recognition using smartphone sensors[C]∥2019 International Joint Conference on Neural Networks (IJCNN). Piscataway: IEEE, 2019: 1-8.
[8] ZHOU J, CUI G Q, HU S D, et al. Graph neural networks: a review of methods and applications[J]. AI Open, 2020, 1: 57-81.
[9] AHMAD N, CHOW S H C, LEUNG H F. Beyond the gates of Euclidean space: temporal-discrimination-fusions and attention-based graph neural network for human activity recognition[EB/OL]. (2022-06-10)[2023-11-02]. https:∥arxiv.org/abs/2206.04855.
[10] DONNER R V, NORBERT M, YONG Z, et al. Nonlinear time series analysis by means of complex networks[J]. Scientia Sinica Physica, Mechanica &Astronomica, 2020, 50(1): 010509.
[11] ZHU S L, GAN L. Specific emitter identification based on horizontal visibility graph[C]∥2017 3rd IEEE International Conference on Computer and Communications (ICCC). Piscataway: IEEE, 2017: 1328-1332.
[12] LI C Y, MO L F, YAN R Q. Fault diagnosis of rolling bearing based on WHVG and GCN[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 3519811.
[13] 高金峰, 秦瑜瑞, 殷红德. 基于小波包变换和支持向量机的故障选线方法[J]. 郑州大学学报(工学版), 2020, 41(1): 63-69.
GAO J F, QIN Y R, YIN H D. Fault line selection based on wavelet packet transform and support vector machine[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(1): 63-69.
[14] LOTFOLLAHI-YAGHIN M A, KOOHDARAGH M A. Examining the function of wavelet packet transform (WPT) and continues wavelet transform (CWT) in recognizing the crack specification[J]. KSCE Journal of Civil Engineering, 2011, 15(3): 497-506.
[15] BRUNO B, MASTROGIOVANNI F, SGORBISSA A. Wearable inertial sensors: applications, challenges, and public test benches[J]. IEEE Robotics &Automation Magazine, 2015, 22(3): 116-124.
[16] POSSAS R, CACERES S P, RAMOS F. Egocentric activity recognition on a budget[C]∥2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2018: 5967-5976.
[17] 郭毅博, 孟文化, 范一鸣, 等. 基于可穿戴传感器数据的人体行为识别数据特征提取方法[J]. 计算机辅助设计与图形学学报, 2021, 33(8): 1246-1253.
GUO Y B, MENG W H, FAN Y M, et al. Wearable sensor data based human behavior recognition: a method of data feature extraction[J]. Journal of Computer-Aided Design &Computer Graphics, 2021, 33(8): 1246-1253.
[18] JORDAO A, TORRES L A B, SCHWARTZ W R. Novel approaches to human activity recognition based on accelerometer data[J]. Signal, Image and Video Processing, 2018, 12(7): 1387-1394.
[19] HUANG Y, YANG X S, GAO J Y, et al. Knowledge-driven egocentric multimodal activity recognition[J]. ACM Transactions on Multimedia Computing, Communications, and Applications, 16(4): 133.