空调压缩机曲轴是空调工作的关键零件。曲轴的圆度和平面度直接影响该零件的装配精度,如果圆度和平面度不佳,空调工作时会产生噪音,并很可能导致过早出现故障[1]。所以研究空调压缩机曲轴圆度和平面度的快速和准确测量具有重要意义。
目前,生产线上空调压缩机曲轴圆度和平面度的检测常依赖人工使用千分表的接触式测量方式。这种检测方式存在人为读数误差较大、效率低和人工成本高等问题,而且在测量时会对曲轴表面造成划痕损伤[2-4]。
随着线激光位移传感器测量精度、采样点数和采样速度的提升,线激光被广泛应用于测量领域。Qin等[5]将线激光位移传感器用于测量加工后的蜂窝表面;Gao等[6]利用线激光位移传感器测量车轮轮廓,并提出一种线点云数据处理方法;Liu等[7]将线激光位移传感器应用在大尺寸轴几何误差测量,实现在机非接触测量,测量精度<0.01 mm;董洁等[8]提出一种基于线激光位移传感器的叶片三维型面重构方法,完成了叶片型面的高精度重构;孙露萍等[9]提出一种基于2D激光位移传感器的舱段自动对接测量方法,有效提高了舱段自动对接效率;梁晓梅等[10]利用线激光位移传感器实现圆柱齿轮齿距的非接触式高精度测量;梁杰等[11]提出基于线激光位移传感器的孔毛刺检测方法,实现了孔全域毛刺3D形貌和2D波动的可视化;马金钰等[12]研究了3个线激光位移传感器角度安装误差对工件圆直径测量结果的影响,并提出了校准方法;罗哉等[13]利用线激光扫描钻孔,实现了基准孔的检测和定位;潘建州等[14]以线激光位移传感器为主体,构建了蜗杆综合偏差测量平台,实现蜗杆多项几何尺寸测量。从以上文献也可看出,线激光扫描一次就可得到一条有序的采样点,可以简化扫描路径,提高检测效率。
本文基于线激光位移传感器开发了一套空调压缩机曲轴圆度和平面度测量系统,以实现空调压缩机曲轴圆度和平面度的非接触测量,重点研究了曲轴圆度的测量方式、曲轴平面度测点的数据处理方式以及评定等关键问题。
1 测量系统搭建
1.1 测量系统原理
线激光位移传感器发射器发出的激光打到被测物上形成一条连续的轮廓线,这条轮廓线上的激光点通过漫反射被传感器接收器接收,然后接收器内部利用激光三角测量原理[15],就能获取被测物横截面的相对位移量。如图1所示,对于零件的测量传感器获取的数据为Δz,即被测物横截面各点到基准平面的距离。固定线激光位移传感器,旋转被测物,可以获得被测同一截面不同位置的表面信息;固定被测物,移动线激光位移传感器,可以获得被测物不同位置的表面信息。
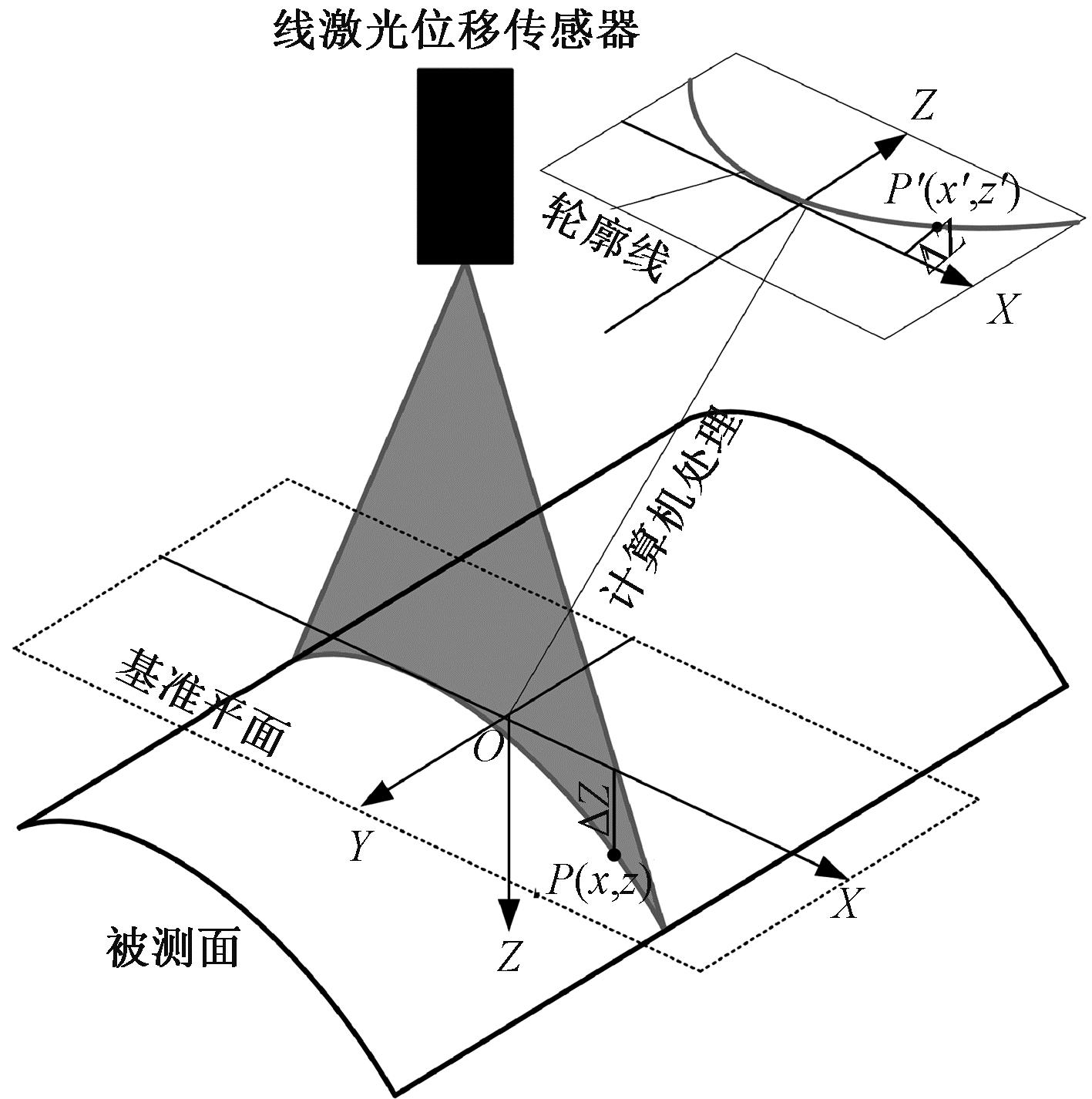
图1 零件轮廓光学测量原理图
Figure 1 Principle diagram of optical measurement of part contour
1.2 测量系统搭建
根据零件检测要求完成空调压缩机曲轴测量系统的搭建。该测量系统主要有两部分组成:机械部分和控制部分。其中机械部分如图2所示。

图2 测量装置实物图
Figure 2 Physical diagram of the measuring device
机械部分主要包括直线运动平台和旋转运动平台。直线运动平台主要包括:X向直线模组、Y向直线模组以及带动丝杠转动的步进电机。旋转运动平台主要包括:三爪卡盘、精密转台以及控制回转运动的步进电机。将2D激光位移传感器安装在Y向直线模组上,通过丝杠的上下运动以及转台的旋转实现空调压缩机曲轴不同截面的测量。
控制部分包括运动控制系统、数据采集系统和上位机。运动控制系统由PLC和步进电机驱动器组成。数据采集系统由线激光位移传感器及其控制器组成。通过上位机向PLC与传感器控制器里输入指令,进而控制整个系统的协同运转。
本文选用基恩士LJ-G030线激光位移传感器,其测量范围为30±10 mm,基准位置处线激光宽为22 mm,高度重复度测量精度为1 μm,采样周期为3.8 ms;选用GSN130-18K精密转台,其重复定位精度为5″;三爪卡盘选择三欧K11。
1.3 数据获取和处理
曲轴测量系统搭建完成后,固定曲轴、移动传感器即可获取曲轴平面上不同位置横截面数据;固定传感器,转动曲轴即可获取曲轴回转体上同一横截面上不同位置数据。通过开发相应的数据处理算法完成平面度和圆度轮廓数据的提取,再根据不同评价算法进行误差评定,最终实现曲轴平面度和圆度评定。
1.3.1 圆度轮廓数据提取
传感器采集到的数据中不仅包含工件安装时的偏心误差,同时还包含转台的旋转误差。为了使传感器在转台不同位置得到更准确的数据,就必须将这两种误差剔除。本文通过对标准量棒的测量来获取两种误差总和,即系统误差。所用标准量棒与曲轴材质、公称轴径相同。由于标准量棒圆度误差小于1 μm,可认为线激光打在量棒上的最高点和量棒轴线的距离是个定值,因此每条激光线段最高点的波动即为此截面上圆心的波动。该波动是偏心和旋转误差共同作用的结果。
设置传感器参数,使传感器连续采集量棒旋转一周的信息,取每条轮廓线最高点绘图,然后进行正弦拟合,拟合曲线为偏心误差,拟合残差为旋转误差。在相同速度、相同测量起始点条件下,对标准量棒进行5次测量,分析如图3所示,其中图3(a)~3(e)为拟合曲线图,图3(f)~3(j)为对应残差图。可以看出,拟合曲线图及其对应残差图中数据变化趋势一致。将5次测量得到的拟合曲线图和残差图对应采样点取平均值,可得旋转误差(图3(k))和系统误差(图3(l))。
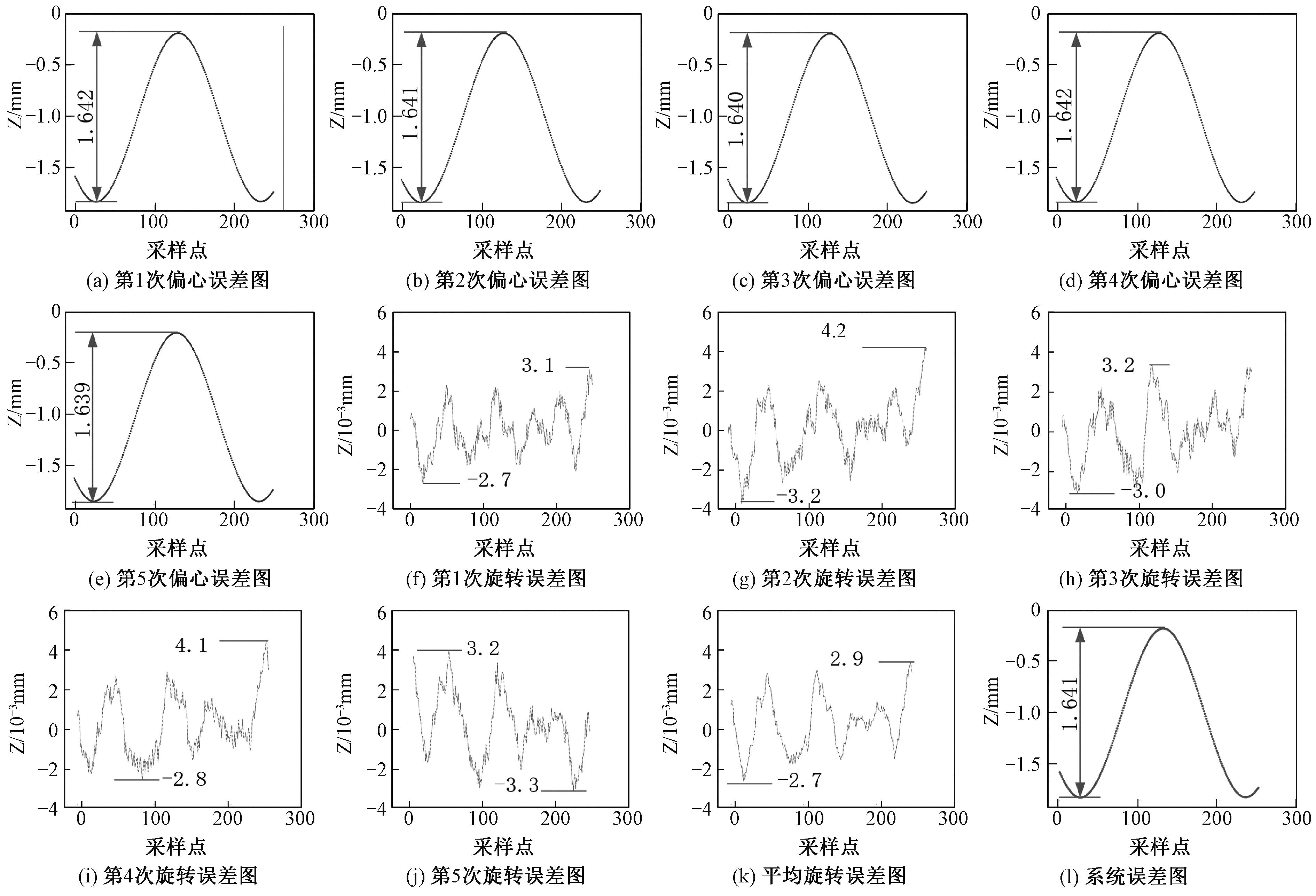
图3 系统误差分析图
Figure 3 System error analysis chart
假设系统误差在传感器基准坐标轴下为di,转台旋转中心到传感器基准面的距离为D1,由此可认为量棒截面圆心波动在传感器基准坐标轴下各位置处的坐标值pi:
pi=D1-di。
(1)
在图4中,O为转台的旋转中心,A为被测物某截面上一点,B为同一截面的轴心,Z′和B′分别为被测物旋转∠A′ OA后A和B的对应点,圆上实线为线激光测得的轮廓线。由三角形外角定理可知,∠A′B′C′=∠ABC+∠A′ OA,则C′点为被测物上C点转过∠A′ OA后的点。在转台速度恒定的情况下,每条轮廓线上的C点在被测物上是等距的。所以取每条轮廓线的C点即可获取被测物此截面1周的表面信息。可通过拟合每条轮廓线圆心寻找其垂直对应点来获取C点。
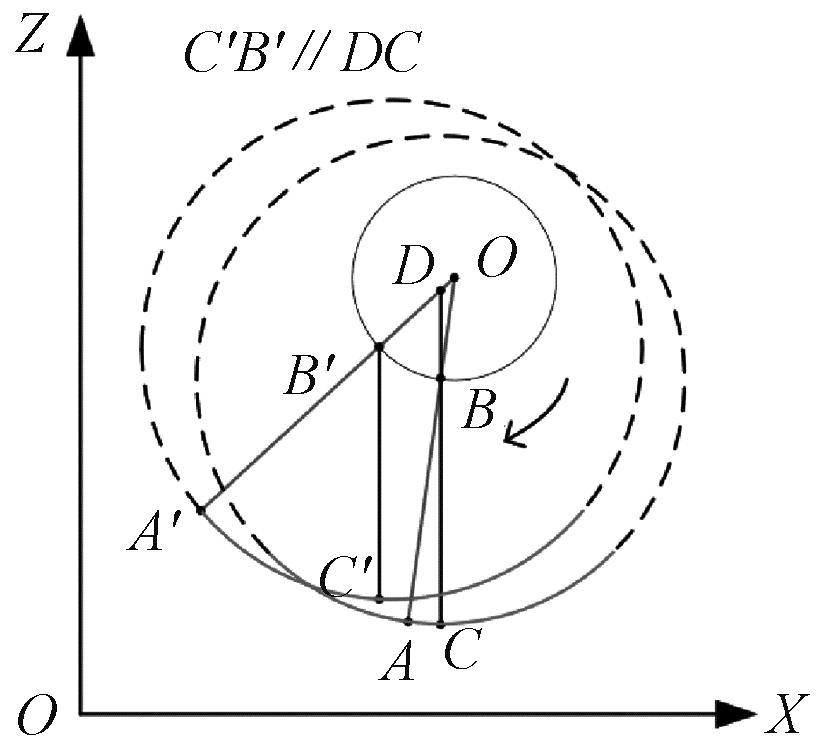
图4 测点分析图
Figure 4 Measurement point analysis diagram
假设获取的采样点数为n,图4中X轴为传感器基准轴,第i个采样点到X轴的距离为Ei,截面圆心到旋转中心O的Z向距离为ei,则被测物横截面二维坐标为
(2)
(3)
由于传感器获取的是测点在基准轴下的Z向距离值,需要将该距离值转化成基准轴下截面圆心波动的坐标值。假设第i个采样点在基准轴下坐标值为Zi,所测曲轴公称半径为R,同时结合转台各位置处的量棒截面圆心波动坐标值,求得被测物横截面的二维坐标为
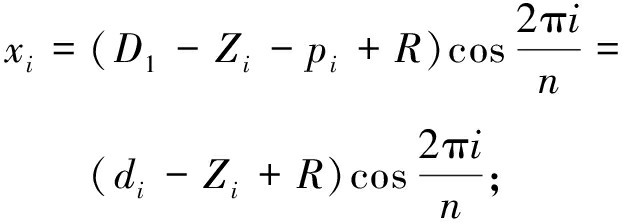
(4)
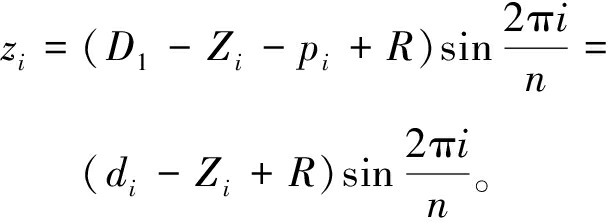
(5)
由式(4)、(5)也可以看出,转台旋转中心到传感器基准面的距离并不影响圆度的计算。
1.3.2 平面度轮廓数据提取
如图5(a)所示,所测曲轴平面并不是一个连续的平面,因此测量时线激光也会打在曲轴弧面上。为了准确测量平面度,需要将弧线轮廓线和平面轮廓线分离。本文通过相邻两点之间斜率变化区分不同轮廓线。假设第1个测点和第2个测点间斜率为k1,第2个测点和第3个测点间斜率为k2,……,以此类推得到1个斜率集合K={k1,k2,…}。取前250个将其可视化处理如图5(b)所示,可以认为斜率值位于(n,m)的测点为曲轴平面测点。图5(c)中曲轴平面轮廓线倾斜是因为曲轴平面没有正对着线激光位移传感器,而曲轴平面是否正对着线激光位移传感器,只会影响m、n的计算值,不会影响平面度的测量。
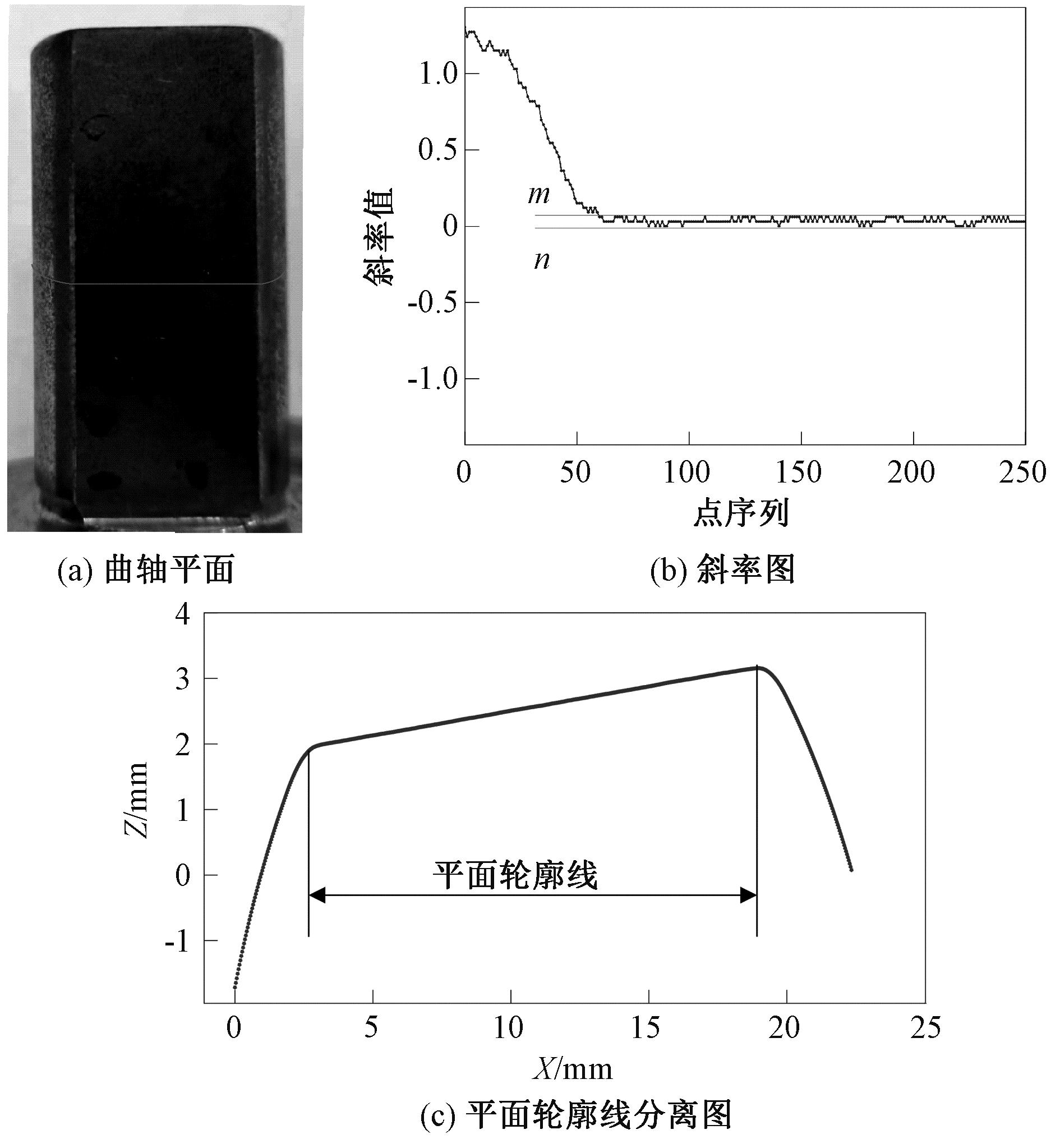
图5 曲轴平面轮廓线提取图
Figure 5 Crankshaft plane contour line extraction
分离出平面轮廓线后,要对冗余的测量数据进行下采样,以减少点云数据,提高运算效率。由于本实验采用线激光位移传感器,采集到的点云均匀有序,故使用均匀下采样处理过于冗余的原始数据。图6为曲轴平面测点数据预处理。
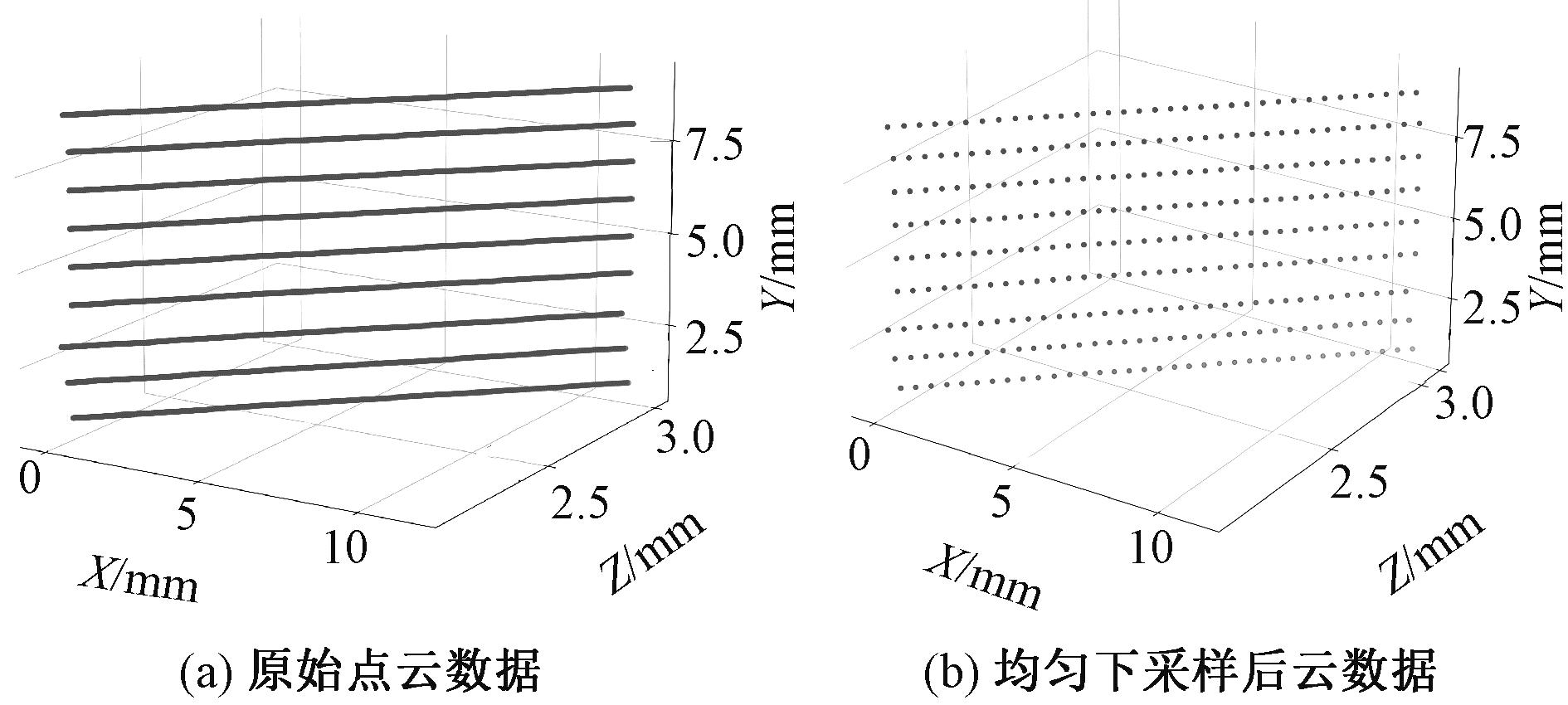
图6 曲轴平面测点数据预处理
Figure 6 Preprocessing of crankshaft planar point data
2 曲轴圆度和平面度的误差评定方法
2.1 曲轴圆度误差的评定方法
圆度是指工件圆周线上的点到轴线的距离相等的程度。国家标准规定了4种圆度误差评定方法,即最小二乘圆法、最小外接圆法、最大内接圆法和最小区域圆法[16]。其中最小区域圆法是以包容被测圆轮廓的2个同心圆的最小半径差为圆度误差,根据圆度定义进行评定,评定出的误差值最小。其他3种评定方法的区别主要在基准圆的选取上,分别选择最小二乘圆、最小外接圆以及最大内接圆作为基准圆,然后计算测量点到基准圆心最大距离和最小距离之差,所得即为圆度误差。
设置传感器采样250次,转台3.4 s旋转1周,结合传感器采样频率,可知曲轴旋转1周包含207个采样点。在测量时保证转台旋转整数圈,使得每次测量起始位置为同一点。本实验对图2中截面3进行测量。获得的曲轴采样点和系统误差如图7(a)所示,统一取采样点25~232作为曲轴旋转一周的数据。将得到的采样点数据带入式(4)、(5),其横截面二维轮廓线如图7(b)所示。将二维轮廓数据带入到4种评定方法中,分别进行圆度误差评定,得到的结果如表1所示。可以看出,最小区域圆法计算的圆度误差最小。
表1 4种评定方法对比
Table 1 Comparison of four rating methods

评定方法圆心坐标圆度误差/μm最小二乘圆法(-0.012 3,0.016 9)7.45最小外接圆法(-0.012 1,0.017 4)7.02最大内接圆法(-0.012 1,0.016 8)7.61最小区域圆法(-0.012 2,0.016 8)6.84
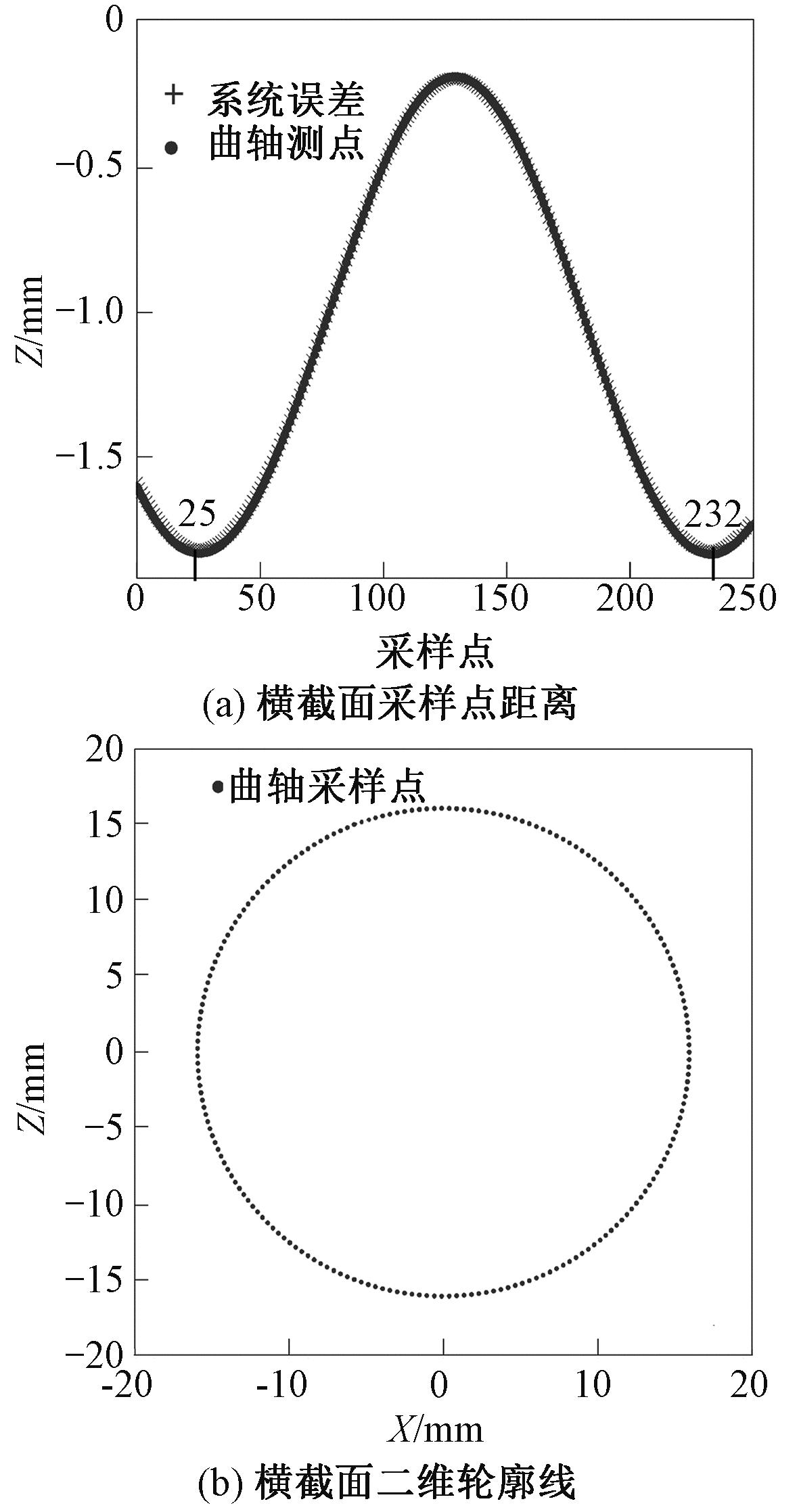
图7 圆度误差评定
Figure 7 Roundness error evaluation
2.2 曲轴平面度误差的评定方法
最小二乘法评定平面度误差,是将实际平面拟合的最小二乘平面作为基准平面。假设Pi=(xi,yi,zi)(i=1,2,…,n)为实际平面上的点在坐标系中的坐标值,z=ax+by+c为该坐标系下的某一平面。则实际平面上的点到该平面的距离为
Δdi=z-(axi+byi+c),i=1,2,…,n。
(6)
当实际平面上各点到该平面的距离平方和![]() 最小时,此时求出的a、b、c就是最小二乘平面的参数。分别对
最小时,此时求出的a、b、c就是最小二乘平面的参数。分别对![]() 中a、b、c求偏导并令其等于0,即可求出a、b、c。计算公式为
中a、b、c求偏导并令其等于0,即可求出a、b、c。计算公式为
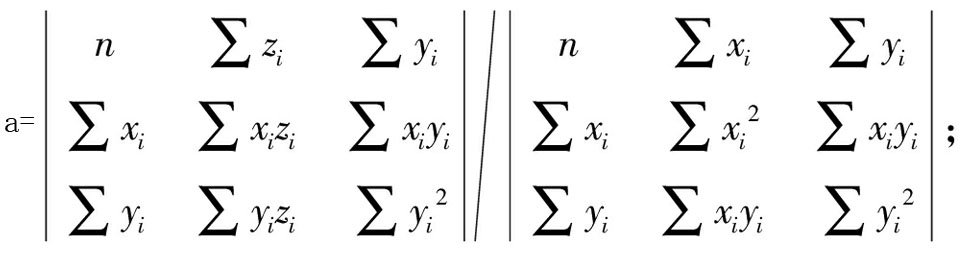
(7)
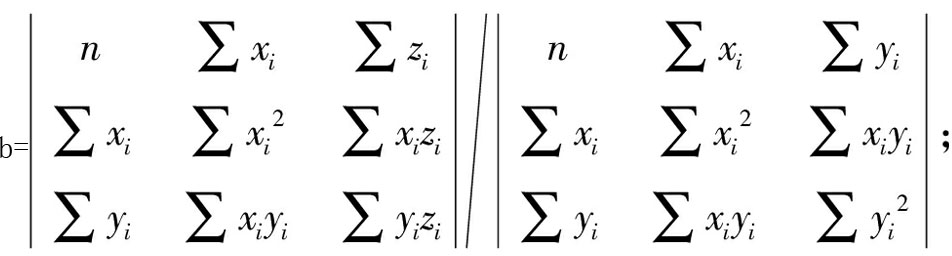
(8)
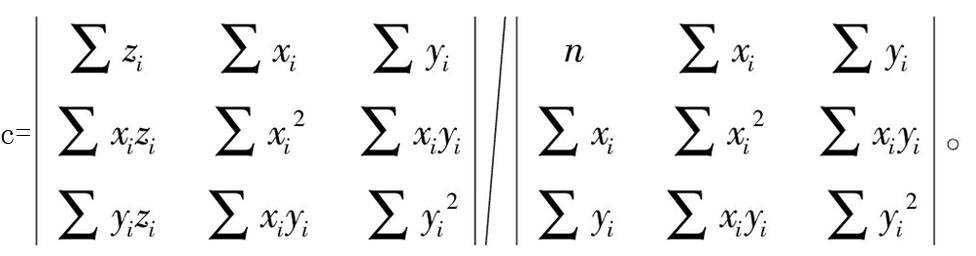
(9)
然后即可求出分布在最小二乘平面两侧的最大距离测点Pm(xm,ym,zm)、Pl(xl,yl,zl),则被测平面的平面度f为
(10)
曲轴平面整体尺寸为16 mm×40 mm,线激光沿Y轴方向每间隔4 mm采样一次,采样完毕后得到10条轮廓数据,分离出平面轮廓线,每隔60点采样一次。最后采用最小二乘法评定平面度误差,如图8所示,其结果为6.2 μm。
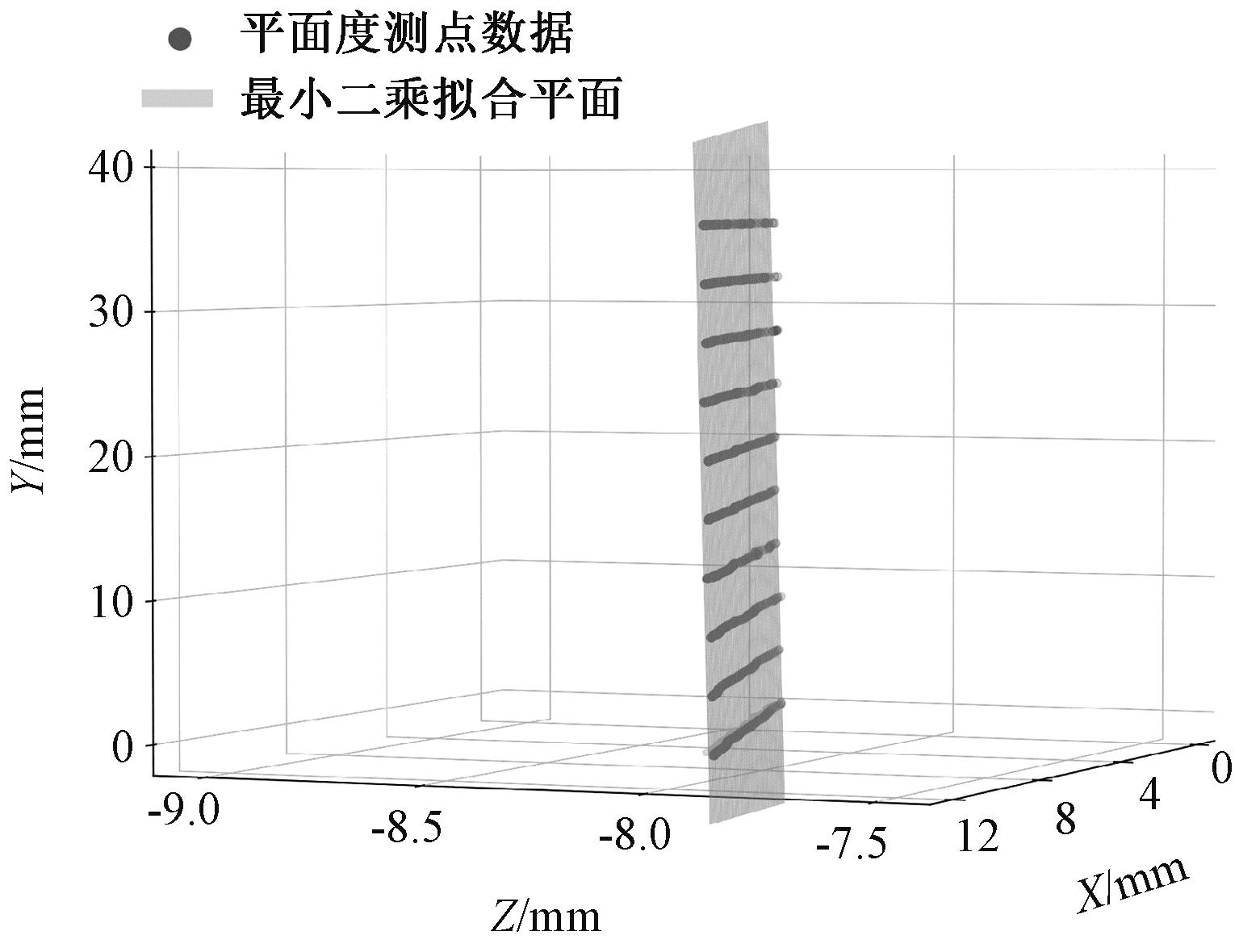
图8 最小二乘拟合平面
Figure 8 Least squares fitting plane
3 测量系统精度测试
3.1 重复度测试
在没有强光、振动干扰的实验环境下进行测量实验,对图2中的3个不同截面进行圆度误差测量。在转台转速相同的情况下,每个截面分别进行10次测量,然后进行系统误差补偿。统一采用最小区域圆法进行圆度误差评价。接着对曲轴平面进行10次平面度测量,传感器每次移动的距离保持相等,评定方法为最小二乘法。3个不同截面圆度以及曲轴平面度重复度测量结果如图9所示。
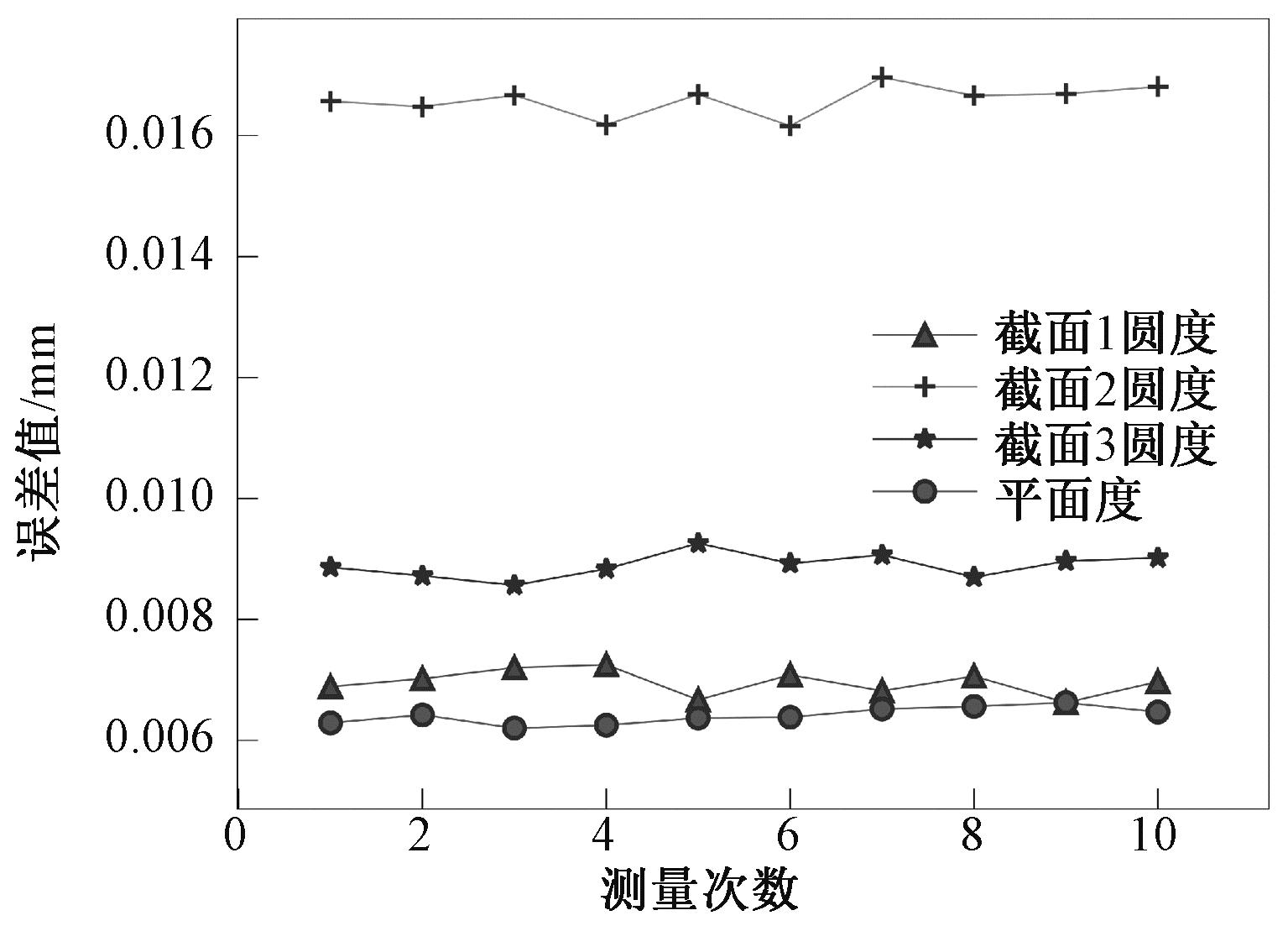
图9 曲轴圆度和平面度重复度测量结果
Figure 9 Crankshaft roundness and flatness repeatability measurement results
从实验数据可知,截面1圆度误差在6.62~7.26 μm变化,截面2圆度误差在16.12~16.91 μm变化,截面3圆度误差在8.56~9.25 μm变化,平面度误差在6.2~6.5 μm变化。
3.2 准确度测试
准确度测试使用日本东京精密的RONDCOM 43C圆度仪(图10(a))对重复度测试中3个截面进行测量,其主要参数:回转精度为(0.02+6H/10 000) μm,最小平方圆的最大偏差为(0.01+3H/10 000) μm。同时使用蔡司ZEISS MICURA三坐标测量仪(图10(b))对平面度进行测量,其测量误差为(0.7+L/400) μm。2种方法的测量值和本文测量值对比如表2所示。
表2 2种方法的测量值对比
Table 2 Comparison of measured values between two methods
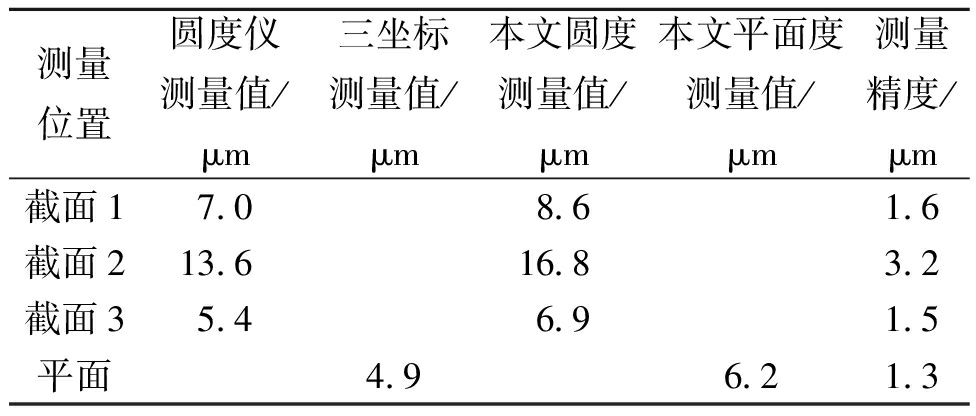
测量位置圆度仪测量值/μm三坐标测量值/μm本文圆度测量值/μm本文平面度测量值/μm测量精度/μm截面17.08.61.6截面213.616.83.2截面35.46.91.5平面4.96.21.3

图10 准确度测试
Figure 10 Accuracy testing
由图9可知,本实验台圆度重复度测量误差<0.8 μm,平面度重复度测量误差<0.3 μm;同时由表2可知,本实验台圆度测量精度<4 μm,平面度测量精度<2 μm,可认为本实验台满足该曲轴圆度和平面度测量要求。
3.3 测量不确定度
测量系统重复性误差引入的A类不确定度分量为
(11)
传感器示值误差引入的B类不确定度分量为![]() 则系统的标准不确定度为
则系统的标准不确定度为![]()
4 结论
本文基于线激光位移传感器,开发了空调压缩机曲轴圆度和平面度测量系统。通过测量标准量棒计算出系统误差,并将误差用于圆度测点补偿,实现曲轴圆度准确测量。同时针对线激光测量平面度时数据存在噪点的问题,提出利用斜率分离数据的方法,并通过均匀下采样实现平面度点云数据精简处理,为后续误差评定提供基础。最后对测量系统进行精度测试,并与圆度仪和三坐标机测量结果进行对比。结果表明,该测量系统的圆度测量精度<4 μm;平面度测量精度<2 μm;圆度重复度测量误差<0.8 μm;平面度重复度测量误差<0.3 μm,能够取代人工完成该空调压缩机曲轴圆度和平面度的一体化快速精确测量。
[1] 朱红伟, 迟莹, 李红旗, 等. 空调压缩机曲轴的可靠性设计分析[J]. 制冷与空调, 2022, 36(5): 739-745.
ZHU H W, CHI Y, LI H Q, et al. Reliability design and analysis of crankshaft of air condition compressor[J]. Refrigeration &Air Conditioning, 2022, 36(5): 739-745.
[2] 周浩淼. 孔轴类零件几何特征检测算法研究[D]. 武汉: 华中科技大学, 2020.
ZHOU H M. Research on algorithms for measuring geometrical features of hole and shaft parts[D]. Wuhan: Huazhong University of Science and Technology, 2020.
[3] 万春鹏, 周亮, 顾伟德. 圆柱体零件圆度与圆柱度非接触测量系统[J]. 机械制造, 2021, 59(12): 69-72, 98.
WAN C P, ZHOU L, GU W D. Non-contact measurement system for roundness and cylindricity of cylindrical part[J]. Machinery, 2021, 59(12): 69-72, 98.
[4] 柴众, 陆永华, 陈强, 等. 基于激光测距的管壳件圆柱度测量系统[J]. 测试技术学报, 2022, 36(1): 66-72.
CHAI Z, LU Y H, CHEN Q, et al. Research on cylindricity measurement system of cylindrical parts based on laser displacement[J]. Journal of Test and Measurement Technology, 2022, 36(1): 66-72.
[5] QIN Y, KANG R K, WANG Y D, et al. A form error evaluation method of honeycomb core surface[J]. Measurement, 2022, 201: 111667.
[6] GAO C F, BAO S Y, ZHOU C Q, et al. Research on the line point cloud processing method for railway wheel profile with a laser profile sensor[J]. Measurement, 2023, 211: 112640.
[7] LIU Y L, LI G C, ZHOU H G, et al. On-machine measurement method for the geometric error of shafts with a large ratio of length to diameter[J]. Measurement, 2021, 176: 109194.
[8] 董洁, 王宗平, 欧登荧, 等. 基于线激光扫描的叶片三维型面重构方法[J]. 四川大学学报(自然科学版), 2023, 60(3): 110-117.
DONG J, WANG Z P, OU D Y, et al. Reconstruction method of blade 3D profile based on line-laser scanning[J]. Journal of Sichuan University (Natural Science Edition), 2023, 60(3): 110-117.
[9] 孙露萍, 张文昌, 王志华, 等. 基于2D激光位移传感器的舱段自动对接测量方法[J]. 中国机械工程, 2023, 34(9): 1120-1125, 1133.
SUN L P, ZHANG W C, WANG Z H, et al. Measurement method of cabin automatic docking based on 2D laser displacement sensor[J]. China Mechanical Engineering, 2023, 34(9): 1120-1125, 1133.
[10] 梁晓梅, 孙荣. 利用激光位移传感器高精度测量圆柱齿轮齿距方法[J]. 激光杂志, 2023, 44(3): 232-236.
LIANG X M, SUN R. Method for measure tooth pitch of cylindrical gear with high precision by laser displacement sensor[J]. Laser Journal, 2023, 44(3): 232-236.
[11] 梁杰, 张康宁, 邱益. 基于线激光位移传感器的孔毛刺测量与评价[J]. 哈尔滨工业大学学报, 2022, 54(1): 156-162.
LIANG J, ZHANG K N, QIU Y. Measurement and evaluation of hole burr based on 2D laser displacement sensor[J]. Journal of Harbin Institute of Technology, 2022, 54(1): 156-162.
[12] 马金钰, 陈欣, 丁国清, 等. 基于激光位移传感器圆径测量的角度安装误差研究[J]. 红外与激光工程, 2021, 50(5): 186-192.
MA J Y, CHEN X, DING G Q, et al. Research on angle setting error of diameter measurement based on laser displacement sensors[J]. Infrared and Laser Engineering, 2021, 50(5): 186-192.
[13] 罗哉, 赵洪楠, 江文松, 等. 基于线激光扫描的基准孔检测与定位方法[J]. 仪器仪表学报, 2021, 42(12): 184-190.
LUO Z, ZHAO H N, JIANG W S, et al. A detection and positioning method for the base hole based on line laser scanning[J]. Chinese Journal of Scientific Instrument, 2021, 42(12): 184-190.
[14] 潘建州, 宋爱平, 闫创, 等. 线激光位移传感器对蜗杆型面的快捷测量方法[J]. 机械传动, 2021, 45(8): 170-176.
PAN J Z, SONG A P, YAN C, et al. Fast measurement method for worm profile by line laser displacement sensor[J]. Journal of Mechanical Transmission, 2021, 45(8): 170-176.
[15] 孙有春, 庞亚军, 白振旭, 等. 激光三角测量法应用技术[J]. 激光杂志, 2021, 42(4): 1-8.
SUN Y C, PANG Y J, BAI Z X, et al. Application technology of laser triangulation[J]. Laser Journal, 2021, 42(4): 1-8.
[16] LIU W W, ZHOU X H, LI H L, et al. An algorithm for evaluating cylindricity according to the minimum condition[J]. Measurement, 2020, 158: 107698.