深度回声状态网络(deep echo state network, DESN)作为一种深度学习背景下构建的多储备池计算框架,能够在不断增加的抽象层次上开发时间信息的高级特征表示,从而以自然的方式实现具有多时间尺度特征的时间序列建模任务。经典的DESN采用最小二乘回归训练输出权重,这种训练方式避免了传统循环神经网络在采用反向传播算法训练时出现的收敛速度慢和极易陷入局部最优值等问题。简单的训练方式和强大的非线性特征映射能力使DESN在诸多领域中发挥了重要作用,如时间序列预测、语音建模、信号处理和异常识别等。尽管有上述优势,但当前对于DESN的结构设计仍然缺乏足够的理论指导,尤其是如何为特定任务选择合适的储备池规模仍然面临着严峻的挑战[1]。在这种情况下,设计人员倾向于使用更大规模的储备池以期使网络获得令人满意的学习性能。然而,这往往会导致储备池中存在大量的冗余神经元,为储备池引入了更多的噪声,进而影响网络的泛化性能。
剪枝是一种帮助剔除神经网络冗余组件的有效策略[2]。近年来,已有学者将剪枝策略引入到DESN的建模中。例如,Shen等[3]基于储备池神经元之间的相似性提出了迭代剪枝合并算法,通过剪枝或合并一些相似的神经元,获得了具有良好适应性的网络结构。Gao等[4]通过删除相邻储备池之间的连接,阻止了输入信号的劣质特征表示由低隐层向高隐层的传递。然而,上述剪枝算法很容易改变储备池的动力学演化轨迹,进而影响网络的预测性能。因此,如何设计合理的剪枝策略以避免在优化后储备池的动力学受到影响仍有待研究。
此外,为从剪枝的角度优化DESN的结构,精准评估神经元之间的相关性尤为关键。这种相关性可为剪枝过程提供重要的先验知识,以准确地识别应该从储备池中移除的神经元。传统的皮尔逊相关系数常用于度量2个时间序列之间的相关性。然而,此类相关性分析工具在处理非平稳数据时存在一定的局限性,且仅适用于二元线性关联,难以准确地评估储备池神经元之间的相关性。去趋势多重互相关(detrended multiple cross-correlation,DMC2)[5]是一种有效的时间序列分析方法,提供了对多个时间序列之间非线性关联的鲁棒估计。此外,通过去除时间序列中的趋势成分,DMC2可以有效地处理非平稳数据。到目前为止,DMC2已被广泛应用于多个领域中。Wang等[6]利用DMC2准确地识别出了PM2.5是影响北京市空气质量的主要因素,并证明其分析结果具备统计显著性。De Almeida Brito等[7]将DMC2应用于生态环境数据的建模中,表明其能够提供比传统方法更好的统计结果。鉴于DMC2在时序数据分析方面的优势,本文采用其评估储备池神经元之间的相关性,进而为后续的剪枝操作识别冗余神经元提供准确、可靠的先验知识。
综上,本文提出了一种基于DMC2的DESN剪枝算法DMCP。一方面,利用DMC2量化储备池神经元之间的相关性,筛选出相关性较高的神经元;另一方面,仅删除所筛选神经元到网络输出层之间的连接以实现剪枝,以确保优化后的储备池动力学不受剪枝的影响,并最终通过最小二乘回归重新训练网络以完成DESN的结构优化任务。
1 深度回声状态网络
经典的DESN模型如图1所示。结构上,该模型主要由输入层,多个堆叠在一起的储备池和输出层组成。在每个时间步t,第一个储备池由外部输入u(t)驱动,而每个后续层均由其前一层的输出驱动。这些储备池的状态转移函数表示为
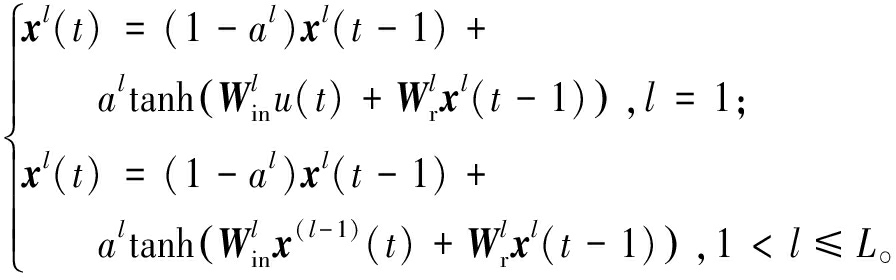
(1)
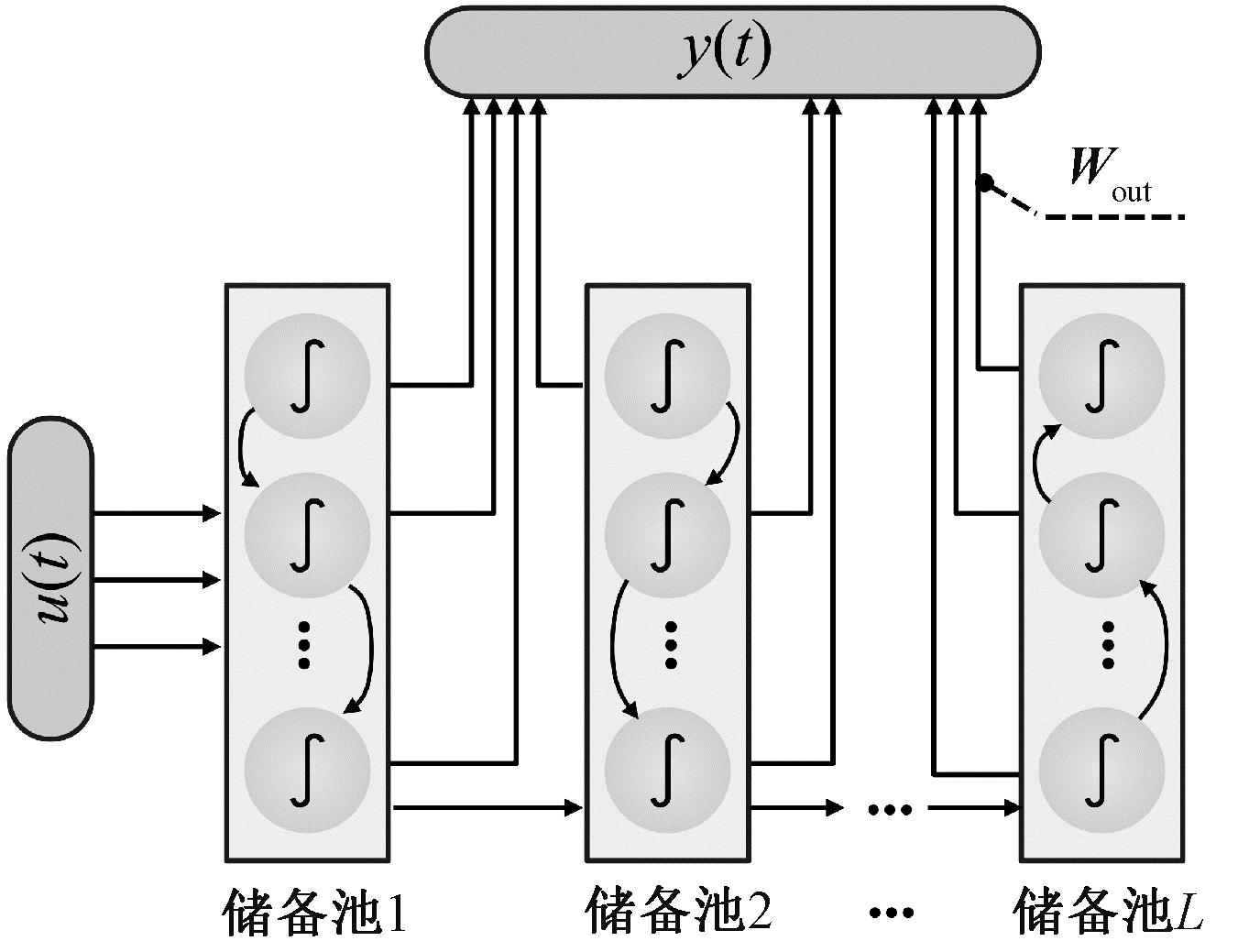
图1 深度回声状态网络的结构示意图
Figure 1 Schematic diagram of the DESN structure
式中:l∈[1,L]为储备池编号;xl(t)为第l个储备池在时刻t的激活状态;al∈[0,1]为第l个储备池的泄漏参数;![]() 为第l个储备池的输入权重矩阵;
为第l个储备池的输入权重矩阵;![]() 为第l个储备池的内部权重矩阵。
为第l个储备池的内部权重矩阵。
与标准ESN一样,DESN的储备池结构在初始化后受到稳定性约束而不需要训练。此类约束可以用满足DESN回声状态属性[8]的条件来表示,定义为
(2)
式中:rl为第l个储备池的谱半径。
DESN在t时刻的输出y(t)为所有储备池激活状态的线性组合:
y(t)=WoutX(t)。
(3)
式中:X(t)=[x1(t);x2(t);…;xL(t)]为网络在t时刻的全局状态;Wout为网络的输出权重矩阵。事实上,DESN训练的主要目的是获得最优的Wout,可通过求解以下的最小二乘问题实现:
(4)
式中:M=[X(1),X(2),…,X(H)]T为网络H个时间步长的全局状态矩阵;Yreal=[y(1),y(2),…,y(H)]T表示网络的期望输出;![]() 为欧几里得范数。通常,伪逆方法可用于对式(4)进行求解:
为欧几里得范数。通常,伪逆方法可用于对式(4)进行求解:
Wout=![]() 。
。
(5)
式中:M+为M的广义逆矩阵。一旦完成Wout的计算,则标志着DESN的训练结束。
2 DMCP算法描述
2.1 总体架构
图2显示了使用DMCP算法优化DESN结构的示意图。结构主要由储备池神经元的DMC2测度模块和储备池剪枝模块组成,前者可以根据定量的DMC2度量评估储备池神经元之间的相关性,为储备池剪枝提供先验知识;后者通过将高相关性神经元到输出层的连接权重置零,来实现DESN的剪枝优化。
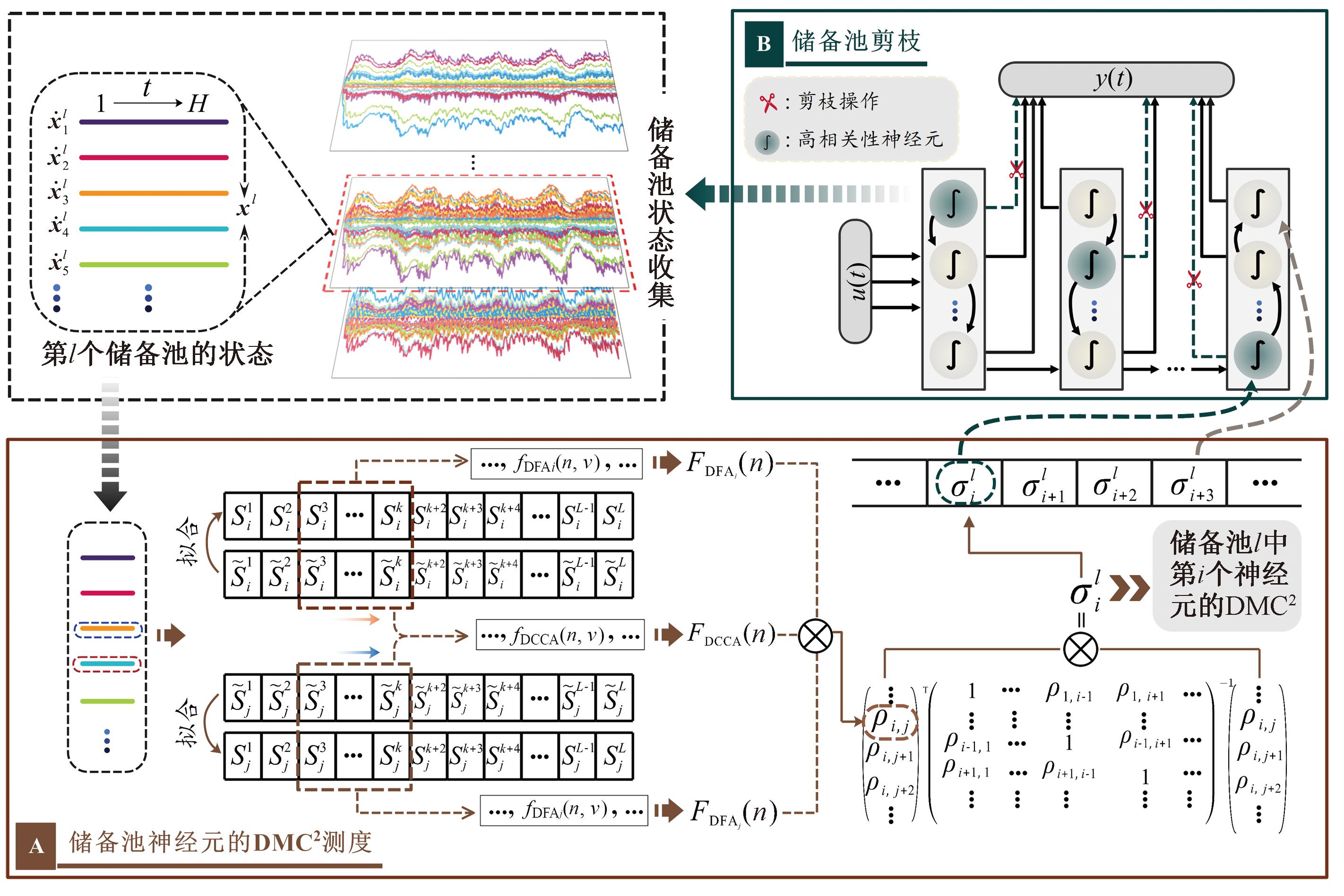
图2 基于DMCP优化DESN结构示意图
Figure 2 Schematic diagram of optimizing DESN structure based on DMCP
2.2 储备池神经元的DMC2测度
DMC2系数作为二元去趋势互相关分析(detrended cross-correlation analysis, DCCA)[9]的推广,提供了对多个(2个及2个以上)时间序列之间非线性关联的鲁棒度量。鉴于此,考虑利用DMC2评估储备池神经元之间的相关性。首先获取选定储备池中各神经元的状态序列,计算每2个神经元之间的DCCA系数(定义为去趋势协方差函数和去趋势方差函数之间的比率),最后通过获得的DCCA矩阵计算多个神经元之间的DMC2系数。储备池神经元之间DMC2系数的计算过程如下。
假设xl为DESN中具有Nl个神经元的第l个储备池共计H个时间步的状态矩阵,即
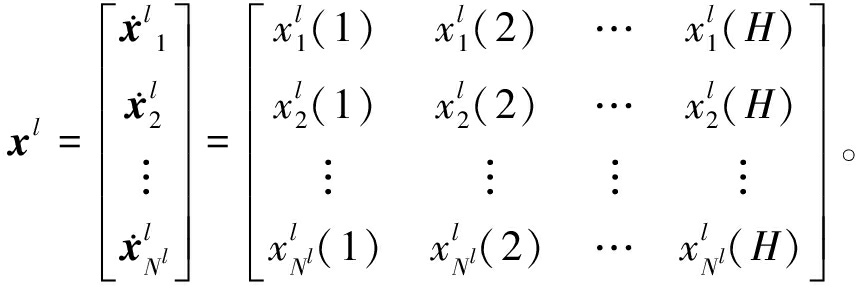
(6)
对于第i个和第j个神经元的状态序列![]() 和
和![]() 分别计算这2个序列的累计偏差以获得2个新序列,即
分别计算这2个序列的累计偏差以获得2个新序列,即
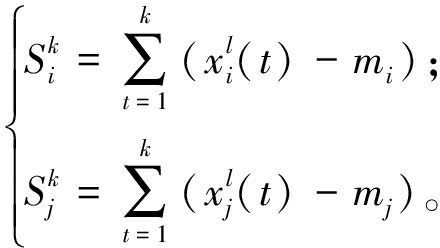
(7)
式中:mi和mj分别为![]() 和
和![]() 的平均值;k=1, 2, …,H。随后,将整合后的新序列
的平均值;k=1, 2, …,H。随后,将整合后的新序列![]() 和
和![]() 分成
分成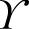 个等长为n的窗口,并通过最小二乘法计算每个窗口的局部趋势。基于获得的局部趋势,可以计算每个窗口在去趋势后残差的协方差fDCCA以及方差fDFAi和fDFAj,即
个等长为n的窗口,并通过最小二乘法计算每个窗口的局部趋势。基于获得的局部趋势,可以计算每个窗口在去趋势后残差的协方差fDCCA以及方差fDFAi和fDFAj,即
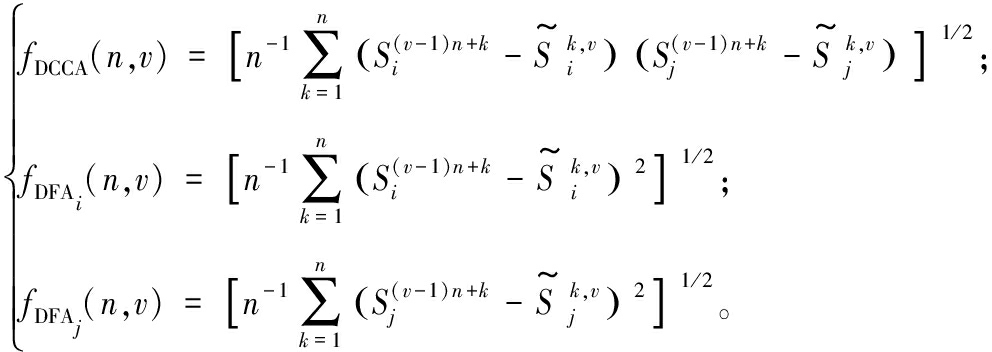
(8)
式中:![]() 和
和![]() 分别为Si和Sj在第v个窗口的局部趋势,v=1,2,…,
分别为Si和Sj在第v个窗口的局部趋势,v=1,2,…,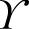 。在此基础上计算相应的去趋势协方差函数FDCCA以及去趋势方差函数FDFAi和FDFAj:
。在此基础上计算相应的去趋势协方差函数FDCCA以及去趋势方差函数FDFAi和FDFAj:
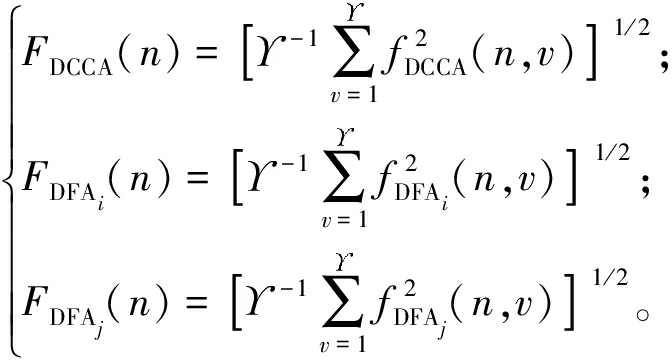
(9)
基于此,第i个和第j个神经元之间的DCCA系数可定义为
(10)
式中:-1≤ρi,j≤1。至此,此储备池中第i个神经元对剩余Nl-1个神经元的DMC2系数可表示为
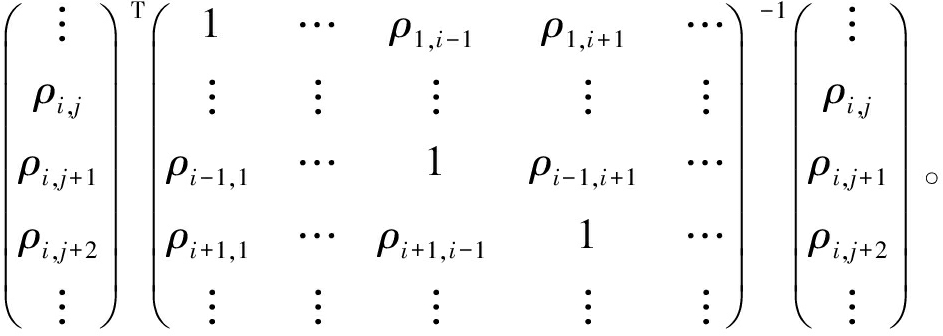
(11)
式中:i≠j;(·)-1为逆矩阵;![]() 为[0, 1]。
为[0, 1]。
2.3 储备池剪枝
本文所提剪枝算法的指导思想是逐层剪枝,依次删除各储备池中高相关性神经元到输出层之间的连接以降低网络冗余度,并最终通过最小二乘回归重训练网络以获得最优的模型结构。具体来说,构建具有L个储备池的DESN,利用样本数据驱动网络,同时收集每个储备池的状态xl(l =1,2, …,L)。从第1个储备池开始,基于x1,通过式(11)计算神经元之间的DMC2系数![]() 并将具有高
并将具有高![]() 值神经元到输出层的权重置零,实现网络剪枝。此过程需要反复运行网络,比较误差大小,以确保是否继续执行剪枝,当网络误差超过可接受范围时停止对第1个储备池的剪枝。按照上述操作对剩余L-1个储备池执行剪枝优化,当剪枝到第L个储备池且网络误差超过可接受范围时,意味着DESN的剪枝结束。算法1给出了基于DMCP算法优化DESN结构的整体流程,其时间复杂度为O(T2×(Nl)5×m×L)。
值神经元到输出层的权重置零,实现网络剪枝。此过程需要反复运行网络,比较误差大小,以确保是否继续执行剪枝,当网络误差超过可接受范围时停止对第1个储备池的剪枝。按照上述操作对剩余L-1个储备池执行剪枝优化,当剪枝到第L个储备池且网络误差超过可接受范围时,意味着DESN的剪枝结束。算法1给出了基于DMCP算法优化DESN结构的整体流程,其时间复杂度为O(T2×(Nl)5×m×L)。
算法1 DMCP算法的伪代码。
输入:样本数据u(t),储备池数量L,谱半径rl,遗忘时间T0,状态收集时间T,对每个储备池执行剪枝的次数m,每次剪枝过程中删除的神经元数量kl;
输出:DMCP-DESN。
① #初始化DESN
② 随机生成![]()
③ 设置rl∈(0,1)
④ 配置DESN
⑤ for t = T0 to T do
⑥ 通过式(1)更新储备池状态;
⑦ 收集网络状态M;
⑧ 通过式(5)计算Wout并记录误差E;
⑨ end
⑩ for l = 1 to L do
 for 1 to m do
for 1 to m do
 Nl←通过xl获得神经元数量;
Nl←通过xl获得神经元数量;
 #储备池神经元的DMC2测度
#储备池神经元的DMC2测度
 for i = 1 to Nl do
for i = 1 to Nl do
 通过式(11)计算第i个神经元的
通过式(11)计算第i个神经元的![]()
 保存
保存![]() 到Γ(i)中;
到Γ(i)中;
 end
end
 #储备池剪枝
#储备池剪枝
 for p = 1 to kl do
for p = 1 to kl do
 j←获得Γ中最大值的索引;
j←获得Γ中最大值的索引;
 置零第j个神经元到输出层的权重;
置零第j个神经元到输出层的权重;
 Γ(j)=0;
Γ(j)=0;
 end
end
 将未被剪枝的神经元的状态保存到xl中;
将未被剪枝的神经元的状态保存到xl中;
 通过式(5)更新Wout并记录误差E;
通过式(5)更新Wout并记录误差E;
 if E超过可接受范围 then
if E超过可接受范围 then
 break;
break;
 end
end
 end
end
 end
end
3 仿真结果与性能比较
3.1 数据集与度量指标
本文选取Mackey-Glass(MG)混沌时间序列和来自真实世界的蜂窝网络流量时间序列来验证DMCP算法的有效性。
MG混沌系统是测试时间序列预测模型的经典基准,可由以下形式的时滞微分方程导出:
(12)
当τ > 16.8时系统表现出混沌特性。因此,本实验通过式(12)在τ=17时生成1 000个数据点,按1∶1的比例划分为训练集和测试集。
蜂窝网络流量时间序列选择来自欧洲一家大型电信服务提供商(意大利电信)提供的开源数据集[10]。该数据集覆盖整个意大利米兰市,包括3种业务流量类型:短信息业务(SMS)、通话业务(Call)和互联网业务(Internet)。每种业务流量的收集时间为2013年11月1日至2014年1月1日,每10 min采集1次,共计3×106条记录。实验选择1 000条Call记录作为分析对象,按1∶1的比例划分为训练集和测试集。
采用归一化均方根误差NRMSE、均方根误差RMSE和决定系数R2作为模型预测性能的量化标准,对应的数学表达式为
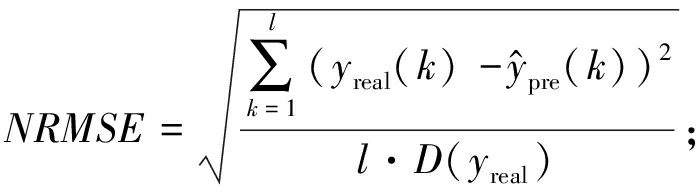
(13)
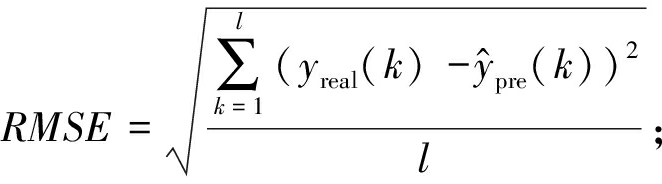
(14)
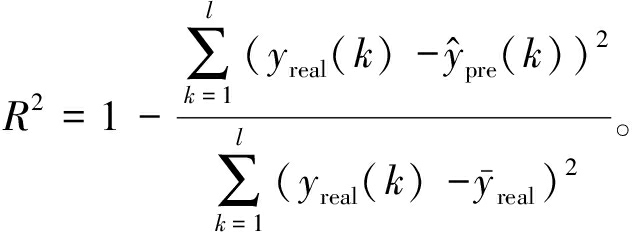
(15)
式中:l为时间序列长度;yreal(k)和![]() 分别为在时刻k的期望值和预测值;
分别为在时刻k的期望值和预测值;![]() 为真实数据的平均值;D(yreal)为yreal的方差。此外,采用记忆能力MC作为DESN重构过去时间信息能力的度量标准:
为真实数据的平均值;D(yreal)为yreal的方差。此外,采用记忆能力MC作为DESN重构过去时间信息能力的度量标准:
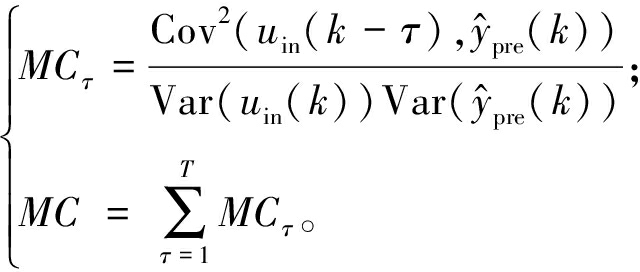
(16)
式中:τ为时间延迟;uin(k)为在k时刻的模型输入;![]() 为模型对于uin(k-τ)的预测输出;Cov(·)和Var(·)分别为协方差函数和方差函数;实验中设置T = 40。
为模型对于uin(k-τ)的预测输出;Cov(·)和Var(·)分别为协方差函数和方差函数;实验中设置T = 40。
3.2 仿真结果
3.2.1 Mackey-Glass混沌时间序列预测
图3显示了DESN和DMCP-DESN对MG时间序列的预测结果和误差分布箱型图(网络初始规模为1-50-50-50-50-1)。从图3(a)的局部放大图可知,DMCP-DESN预测曲线与期望曲线的变化趋势更相似,且图3(b)中较扁且整体上更接近0的误差箱体意味着其在预测MG数据时的偏差更小。因此,相比于原始的DESN,DMCP-DESN具有更强的非线性逼近能力。
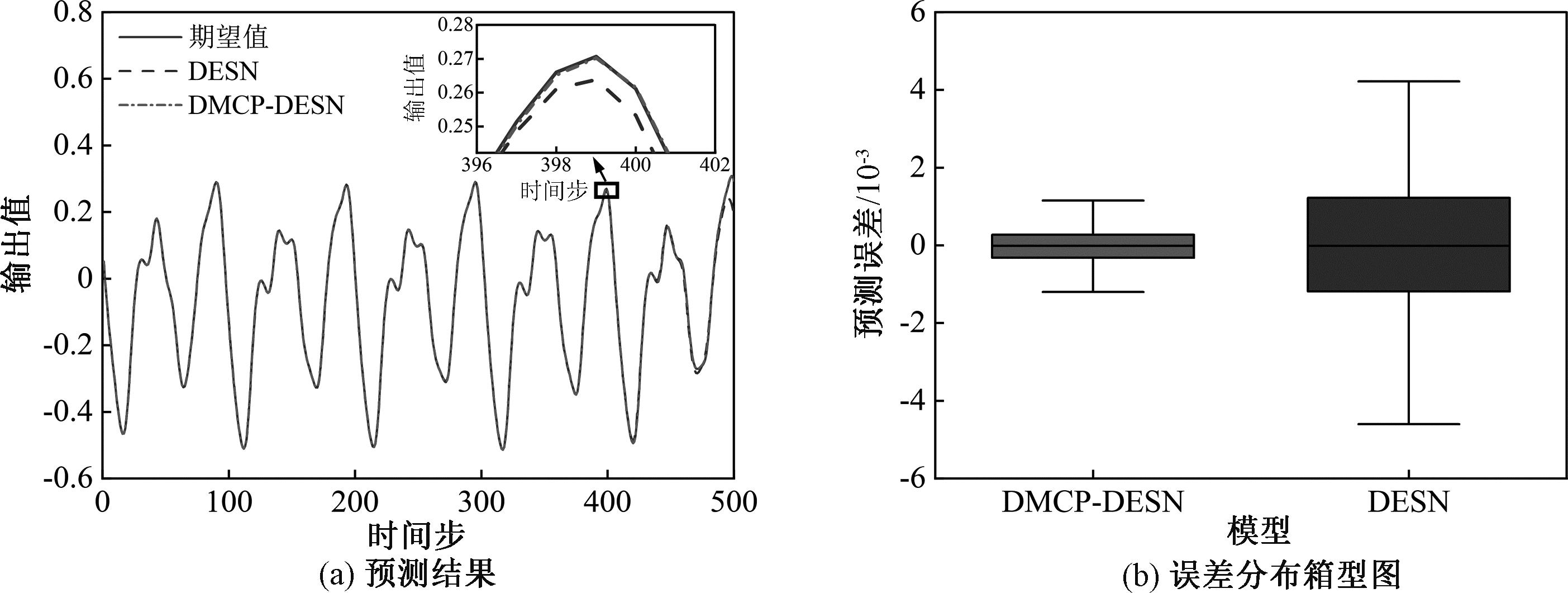
图3 DMCP-DESN和DESN在MG预测任务中的预测结果和误差分布箱型图
Figure 3 Prediction results and error distribution box plots of DMCP-DESN and DESN in the MG prediction task
图4显示了每次剪枝后DMCP-DESN在MG时间序列预测任务中的预测误差曲线(网络初始规模为1-50-50-50-50-1)。可以看出,在结构优化初期,RMSE曲线随剪枝神经元数量的增加显著下降,意味着模型预测性能的提升。当95个神经元被剪枝时,DMCP-DESN具有最佳的预测性能。然而,当更多的神经元被剪枝时,模型的预测性能下降,导致RMSE曲线急剧上升。实际上,剪枝适当数量的冗余神经元等同于模型的特征选择过程。这个过程可以有效地剔除储备池中的冗余特征和无关特征,降低数据中的噪声对网络的不利影响,进而提高DMCP-DESN的预测性能。但过多的剪枝会导致储备池中的重要神经元被剔除,网络无法检测与输入信号有关的关键特征,进而降低了DMCP-DESN的预测能力。因此,应对剪枝的神经元数量加以控制,从而保证DMCP-DESN具备良好的性能。
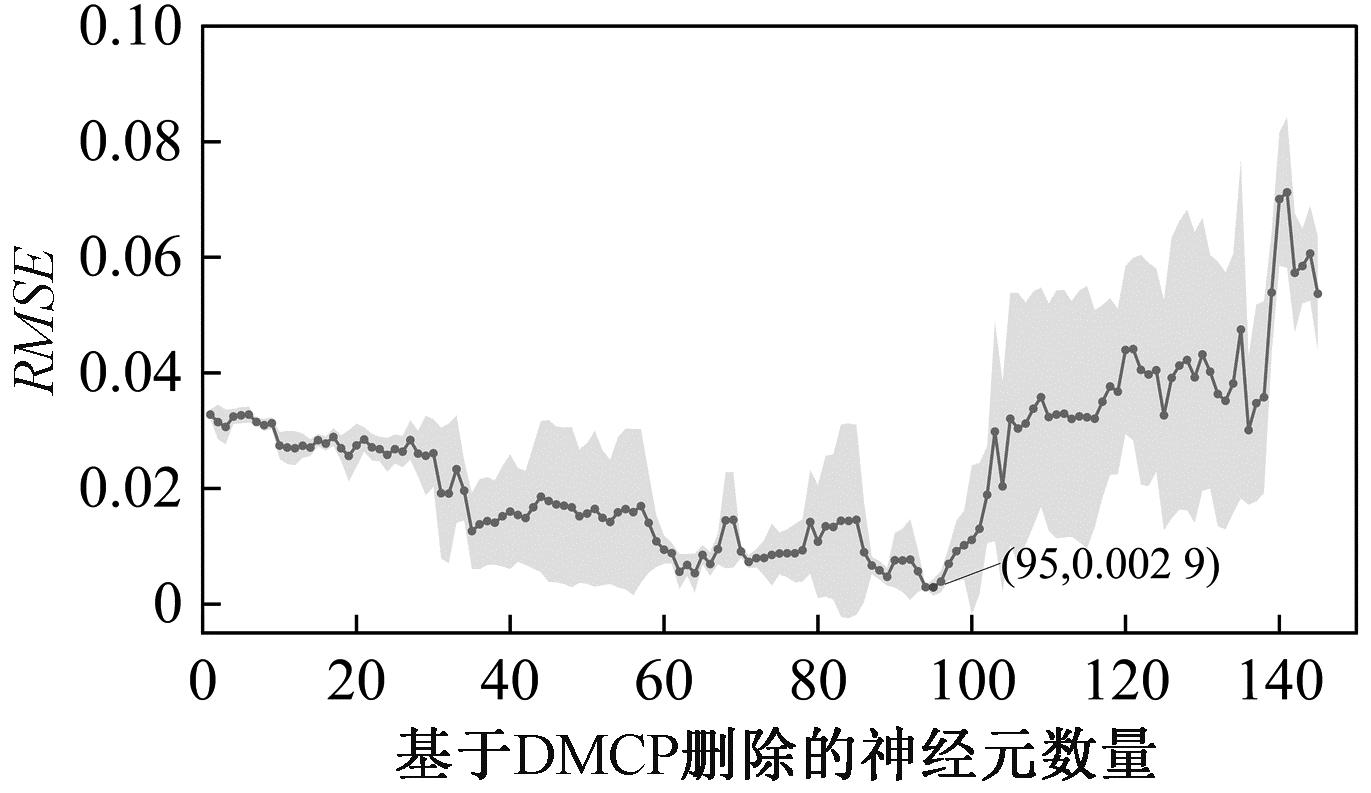
图4 每次剪枝操作后DMCP-DESN在MG预测任务中的
RMSE Figure 4 RMSE of DMCP-DESN in the MG prediction task after each pruning operation
表1给出了2种网络规模下DESN和DMCP-DESN的性能比较结果。显然,在同一网络规模下,更小的NRMSE、RMSE以及更大的R2再一次证明了DMCP-DESN在非线性逼近能力上的优势。同时,注意到DMCP-DESN具有更大的MC,表明本文所提算法能够增强网络的记忆能力,使其更善于捕捉和利用过去信息处理序列数据。
表1 DMCP-DESN在MG预测任务中的性能评价
Table 1 Performance evaluation of DMCP-DESN in the MG prediction task

模型初始网络规模NRMSERMSER2MCDESNDMCP-DESN1-50-50-50-50-10.137 3±0.021 50.029 7±0.004 70.980 7±0.005 88.053 1±2.196 60.014 0±0.006 30.003 0±0.001 40.999 8±0.000 210.544 0±2.419 8DESNDMCP-DESN1-100-100-100-100-10.104 3±0.006 40.022 6±0.001 40.989 1±0.001 39.593 3±2.274 40.004 8±0.002 50.001 0±0.000 50.999 9±011.624 3±2.040 4
实验也对比了其他现有剪枝策略优化后的DESN,包括基于贡献度剪枝的C-DESN[11]、基于皮尔逊相似性剪枝的PC-IPMA-DESN[3]和基于斯皮尔曼相似性剪枝的SC-IPMA-DESN[3]。同时,也将其与时间序列预测建模中常见的深度学习模型进行了比较,包括TCN[12]、GRU[13]、LSTM[14]、BiLSTM[15],DBN-SVM[16]和DBN-ELM[17]。
图5显示了在MG任务中各模型对选定时间步范围内数据的预测结果和误差分布箱型图。从图5可以看出,DMCP-DESN能够对目标信号进行最准确的拟合。表2给出了各模型预测性能的量化结果。从表2可以看出,DMCP-DESN与其他3种剪枝策略优化后的DESN相比,预测精度具有较大优势,这表明本文提出的剪枝算法能够更精准地识别并移除网络中的冗余成分,从而最大限度地提高网络对MG序列的预测精度。此外,与其他深度学习模型进行比较,DMCP-DESN的优势更加突出。
表2 各模型在MG预测任务中的性能评价
Table 2 Performance evaluation of each model in the MG prediction task
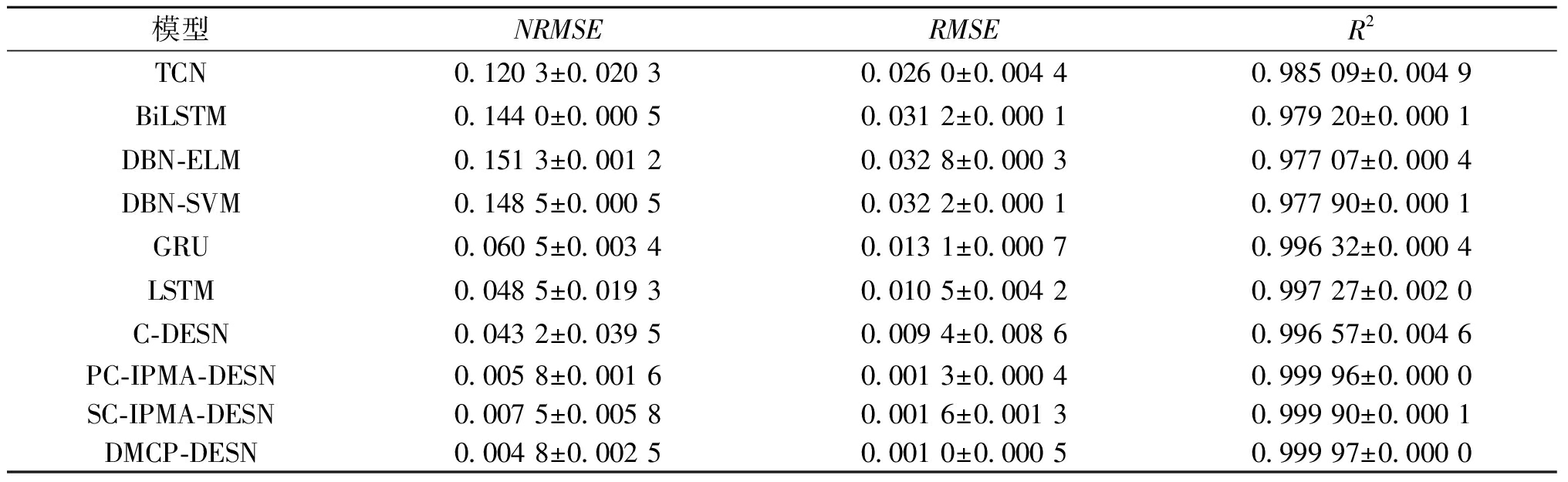
模型NRMSERMSER2TCN0.120 3±0.020 30.026 0±0.004 40.985 09±0.004 9BiLSTM0.144 0±0.000 50.031 2±0.000 10.979 20±0.000 1DBN-ELM0.151 3±0.001 20.032 8±0.000 30.977 07±0.000 4DBN-SVM0.148 5±0.000 50.032 2±0.000 10.977 90±0.000 1GRU0.060 5±0.003 40.013 1±0.000 70.996 32±0.000 4LSTM0.048 5±0.019 30.010 5±0.004 20.997 27±0.002 0C-DESN0.043 2±0.039 50.009 4±0.008 60.996 57±0.004 6PC-IPMA-DESN0.005 8±0.001 60.001 3±0.000 40.999 96±0.000 0SC-IPMA-DESN0.007 5±0.005 8 0.001 6±0.001 3 0.999 90±0.000 1 DMCP-DESN0.004 8±0.002 50.001 0±0.000 50.999 97±0.000 0

图5 各模型在MG预测任务中的预测结果和误差分布箱型图
Figure 5 Prediction results and error distribution box plots of each model in the MG prediction task
3.2.2 蜂窝网络流量时间序列预测
图6显示了对于Call流量数据,DMCP-DESN结构调整过程中RMSE的变化曲线(网络初始规模为1-50-50-50-50-1)。可以看出,当138个储备池神经元被剪枝时,网络具有最佳的非线性逼近能力。表3给出了DESN和DMCP-DESN在Call流量预测任务中的性能对比结果。可以看出,DMCP-DESN在预测精度和记忆能力方面均优于原始DESN,说明DMCP能够有效优化网络结构,提高对复杂网络流量数据的建模能力。
表3 DMCP-DESN在Call预测任务中的性能评价
Table 3 Performance evaluation of DMCP-DESN in the Call prediction task

模型初始网络规模NRMSERMSER2MCDESNDMCP-DESN1-50-50-50-50-10.184 1±0.003 30.835 2±0.015 00.966 0±0.001 212.155 7±0.014 10.157 7±0.006 60.715 4±0.030 10.975 0±0.002 112.168 0±0.000 9DESNDMCP-DESN1-100-100-100-100-10.173 0±0.001 50.785 0±0.006 80.970 0±0.000 512.103 2±0.027 70.154 9±0.001 80.702 8±0.008 10.976 0±0.000 512.158 4±0.018 8
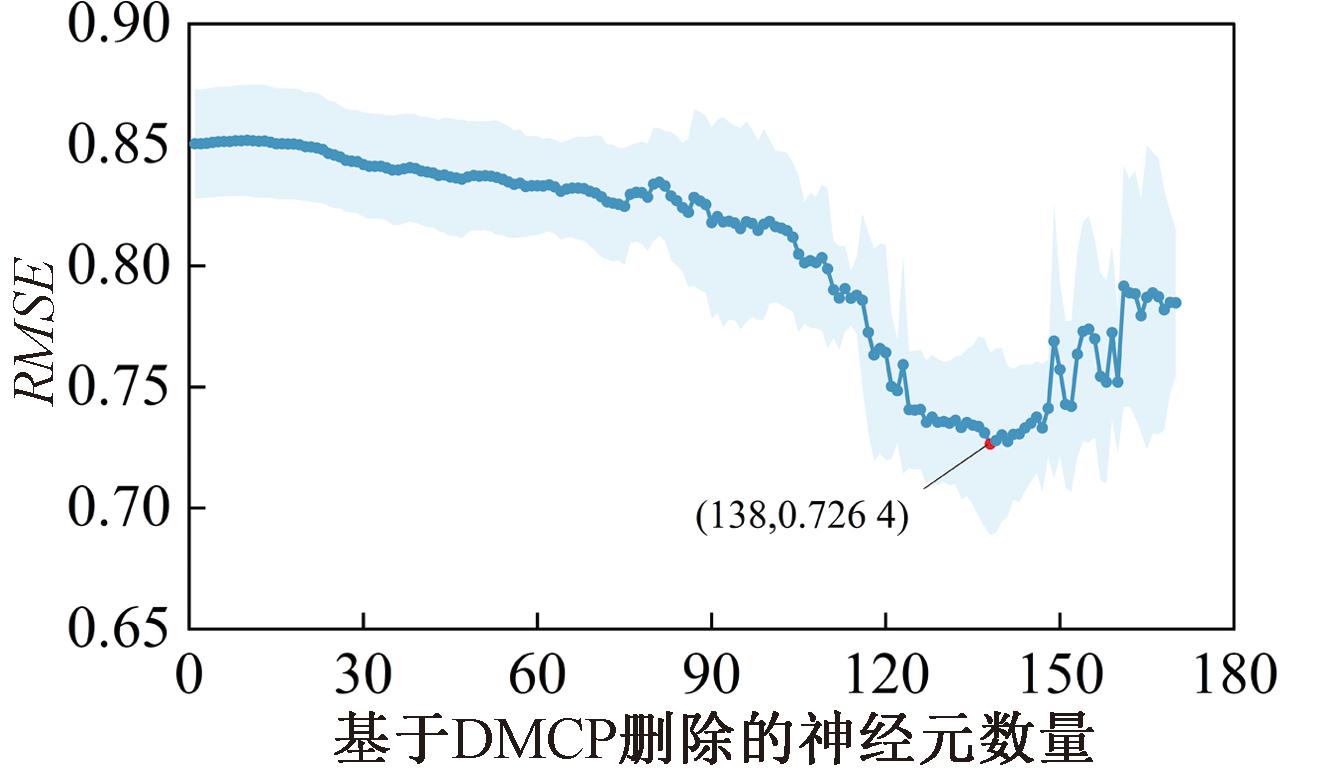
图6 每次剪枝操作后DMCP-DESN在Call预测
任务中的RMSE Figure 6 RMSE of DMCP-DESN in the Call prediction task after each pruning operation
图7显示了在Call流量预测任务中各模型对选定时间步范围内数据的预测结果分布脊线图和误差分布箱型图。从图7(a)可知,DMCP-DESN的预测输出与期望输出具有十分相似的密度分布;从图7(b)可知,DMCP-DESN的箱体最扁且整体上更接近0,表明其在预测Call数据时的偏差最小。表4给出了各模型预测性能的量化结果。可以看出,DMCP-DESN仍然以较大优势领先于对比模型,成为此类网络流量预测任务中的最佳架构。
表4 各模型在Call预测任务中的性能评价
Table 4 Performance evaluation of each model in the Call prediction task
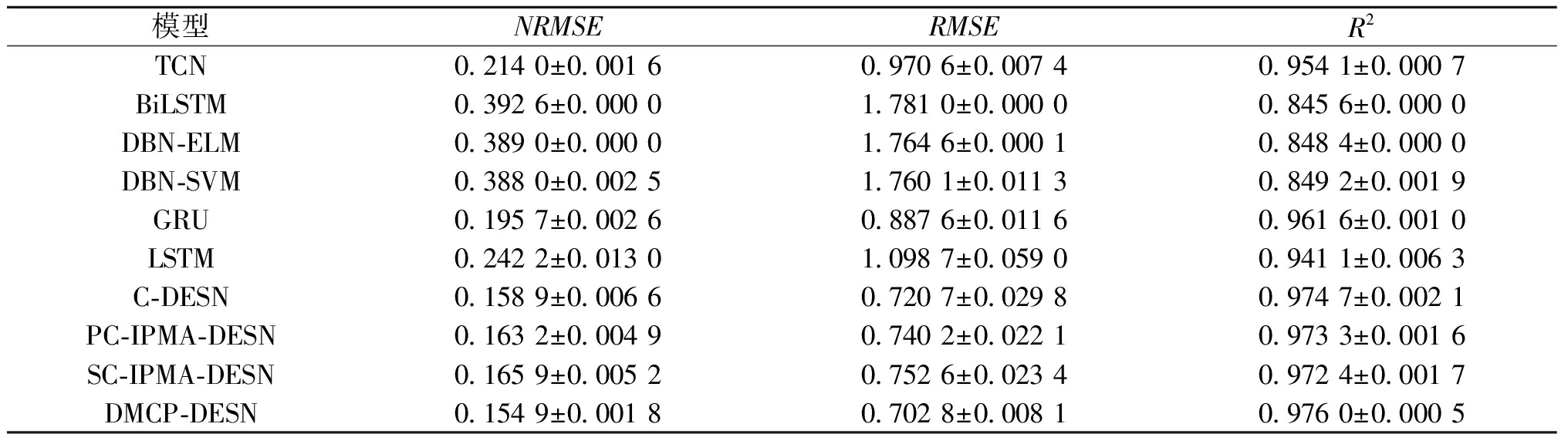
模型NRMSERMSER2TCN0.214 0±0.001 60.970 6±0.007 40.954 1±0.000 7BiLSTM0.392 6±0.000 01.781 0±0.000 00.845 6±0.000 0DBN-ELM0.389 0±0.000 01.764 6±0.000 10.848 4±0.000 0DBN-SVM0.388 0±0.002 51.760 1±0.011 30.849 2±0.001 9GRU0.195 7±0.002 60.887 6±0.011 60.961 6±0.001 0LSTM0.242 2±0.013 01.098 7±0.059 00.941 1±0.006 3C-DESN0.158 9±0.006 60.720 7±0.029 80.974 7±0.002 1PC-IPMA-DESN0.163 2±0.004 90.740 2±0.022 10.973 3±0.001 6SC-IPMA-DESN0.165 9±0.005 20.752 6±0.023 40.972 4±0.001 7DMCP-DESN0.154 9±0.001 80.702 8±0.008 10.976 0±0.000 5
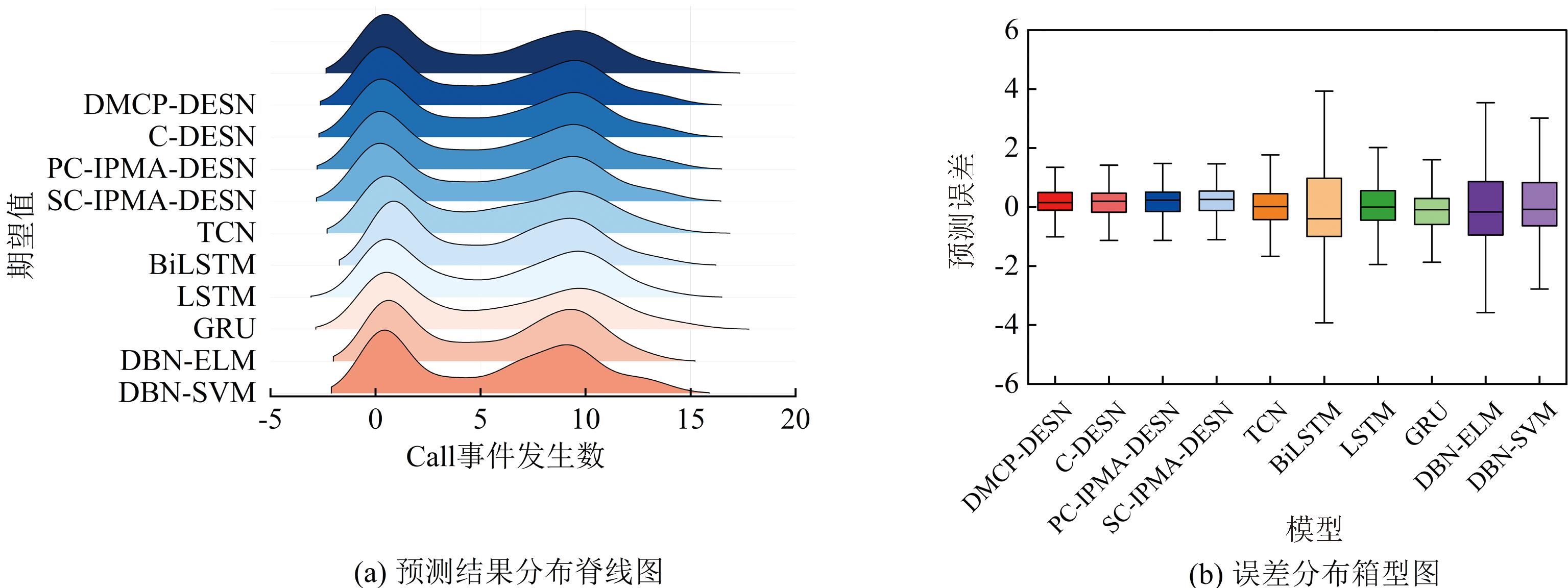
图7 各模型在Call预测任务中的预测结果分布脊线图和误差分布箱型图
Figure 7 Prediction result distribution ridge plots and error distribution box plots of each model in the Call prediction task
4 结论
本文提出了一种基于去趋势多重互相关的深度回声状态网络剪枝算法DMCP。该算法首先利用去趋势多重互相关准则评估储备池神经元之间的相关性,随后通过剪枝高相关性神经元到输出层的连接,有效地剔除了网络中的冗余成分,优化了DESN的拓扑结构。仿真结果表明:利用所提算法剔除适当数量的冗余神经元有助于提高网络的学习能力,使DMCP-DESN在预测性能和记忆能力方面的表现优于原始的DESN。此外,与其他类型的预测模型相比,DMCP-DESN预测器在预测精度方面仍具有显著优势。
[1] BARREDO ARRIETA A, GIL-LOPEZ S, LA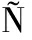 A I, et al. On the post-hoc explainability of deep echo state networks for time series forecasting, image and video classification[J]. Neural Computing and Applications, 2022, 34(13): 10257-10277.
A I, et al. On the post-hoc explainability of deep echo state networks for time series forecasting, image and video classification[J]. Neural Computing and Applications, 2022, 34(13): 10257-10277.
[2] 李北明, 金荣璐, 徐召飞, 等. 基于特征蒸馏的改进Ghost-YOLOv5红外目标检测算法[J]. 郑州大学学报(工学版), 2022, 43(1): 20-26.
LI B M, JIN R L, XU Z F, et al. An improved Ghost-YOLOv5 infrared target detection algorithm based on feature distillation[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(1): 20-26.
[3] SHEN Q Y, ZHANG H W, MAO Y. Improving deep echo state network with neuronal similarity-based iterative pruning merging algorithm[J]. Applied Sciences, 2023, 13(5): 2918.
[4] GAO R B, LI R L, HU M H, et al. Dynamic ensemble deep echo state network for significant wave height forecasting[J]. Applied Energy, 2023, 329: 120261.
[5] ZEBENDE G F, DA SILVA FILHO A M. Detrended multiple cross-correlation coefficient[J]. Physica A: Statistical Mechanics and its Applications, 2018, 510: 91-97.
[6] WANG F, XU J, FAN Q J. Statistical properties of the detrended multiple cross-correlation coefficient[J]. Communications in Nonlinear Science and Numerical Simulation, 2021, 99: 105781.
[7] DE ALMEIDA BRITO A, DE ARA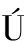 JO H A, ZEBENDE G F. Detrended multiple cross-correlation coefficient applied to solar radiation, air temperature and relative humidity[J]. Scientific Reports, 2019, 9: 19764.
JO H A, ZEBENDE G F. Detrended multiple cross-correlation coefficient applied to solar radiation, air temperature and relative humidity[J]. Scientific Reports, 2019, 9: 19764.
[8] GALLICCHIO C, MICHELI A. Echo state property of deep reservoir computing networks[J]. Cognitive Computation, 2017, 9(3): 337-350.
[9] BEN-SALHA O, MOKNI K. Detrended cross-correlation analysis in quantiles between oil price and the US stock market[J]. Energy, 2022, 242: 122918.
[10] BARLACCHI G, DE NADAI M, LARCHER R, et al. A multi-source dataset of urban life in the city of Milan and the Province of Trentino[J]. Scientific Data, 2015, 2: 150055.
[11] LI D Y, LIU F, QIAO J F, et al. Structure optimization for echo state network based on contribution[J]. Tsinghua Science and Technology, 2019, 24(1): 97-105.
[12] LI D, JIANG F X, CHEN M, et al. Multi-step-ahead wind speed forecasting based on a hybrid decomposition method and temporal convolutional networks[J]. Energy, 2022, 238: 121981.
[13] 高金峰, 庞昊, 杜耀恒. 基于GRU网络的配电网故障数量等级预测方法[J]. 郑州大学学报(工学版), 2019, 40(5): 39-44.
GAO J F, PANG H, DU Y H. A method for predicting the number of faults in distribution network based on GRU neural network[J]. Journal of Zhengzhou University (Engineering Science), 2019, 40(5): 39-44.
[14] CHEN Z L, YANG C L, QIAO J F. The optimal design and application of LSTM neural network based on the hybrid coding PSO algorithm[J]. The Journal of Supercomputing, 2022, 78(5): 7227-7259.
[15] CUI M S. District heating load prediction algorithm based on bidirectional long short-term memory network model[J]. Energy, 2022, 254: 124283.
[16] HUANG Y P, YEN M F. A new perspective of performance comparison among machine learning algorithms for financial distress prediction[J]. Applied Soft Computing, 2019, 83: 105663.
[17] LI Y M, PENG T, HUA L, et al. Research and application of an evolutionary deep learning model based on improved grey wolf optimization algorithm and DBN-ELM for AQI prediction[J]. Sustainable Cities and Society, 2022, 87: 104209.