近年来,随着科技的飞速发展,智能设备得到了广泛的普及,由此产生了海量的无标签视频数据。智能预测与决策系统在生活中具有重要的地位,视频帧预测作为智能预测的关键技术,能够为决策系统提供支持,在气象预警[1]、交通流量[2]等领域具有广泛的应用前景。
目前,视频帧预测模型的多帧预测能力不足,其复杂的时空结构导致视频帧预测仍然是一项非常具有挑战性的任务。现有的视频帧预测方法可以分为两类,主要包括单进单出预测架构和多进多出预测架构。其中,单进单出预测架构是视频帧预测的主流结构。Srivastava等[3]通过编码器将视频序列重建为固定长度的特征向量,并输入到长短期记忆网络(long short term memory,LSTM)中进行多帧预测。为提高LSTM的特征捕捉能力,Shi等[4]采用卷积结构对LSTM的状态转移函数进行了扩展。为增强不同层次循环网络间的联系,Wang等[5]通过在自底向上和自顶向下的方向上建立记忆流,使模型能够同时对短期变化和长期动态趋势进行建模。在此基础上,Wang等[6]建立了一种基于因果LSTM的循环网络,由级联的双存储器和梯度高速单元组成,能够自适应地捕获短期和长期依赖关系。上述方法能够有效增强模型的特征学习能力,但随着预测长度的增加会存在误差累积的问题,导致预测精度迅速下降。
随着神经网络结构的快速发展,多进多出预测架构能够有效避免在长期预测中受到的误差累积影响。Liu等[7]采用3D卷积自编码器学习体素流,并通过现有的流动像素值来合成未来视频帧。Aigner等[8]提出一种基于时空三维卷积的生成式对抗网络(genertive adversarial network,GAN),该架构能够一次预测多个未来帧。Ye等[9]分别对空间特征和时间特征进行建模,并采用对抗损失函数来提高预测清晰度。对抗网络和3D卷积的引入虽然能够有效提高预测性能,但也导致模型变得更加复杂。
为了平衡模型的综合性能,Gao等[10]提出了一种简单的视频预测模型(simple video prediction,SimVP),通过采用简单的组成结构和训练策略,以有效减少模型的参数量和训练时间。但SimVP仍然存在两个问题:①时空特征学习能力仍然不足;②难以平衡空间特征及时间特征的捕捉能力,导致对时间维度的信息学习不充分。受图像分割[11]领域最新进展的启发,本文提出了门控时空注意力。其中,空间注意力关注帧内空间位置下的相互关系,时间(通道)注意力[12]则关注帧间的变化趋势,并采用门控机制来融合获得的时间特征和空间信息。
1 相关工作
1.1 基于循环神经网络的单进单出预测架构
目前,基于循环神经网络的单进单出预测架构被广泛用于处理序列数据。Wang等[13]利用相邻隐藏状态之间的差异信息对时空动力学中的非平稳和近似平稳特性进行建模。从预测编码的角度,Lotter等[14]将真实信号和预测信号之间的差异信息作为网络参数的更新指标。此外,受偏微分方程(PDEs)的启发,Guen等[15]提出了物理动力学网络(physical dynamics network,PhyDNet),采用双分支架构来分离视频中的物理动力学和未知因素。然而,该模型难以平衡长期和短期的预测性能。因此,Pan等[16]提出了基于特征分离原理的泰勒网络(Taylor network,TaylorNet),该架构采用泰勒级数对视频序列进行建模,有效提高了模型的多帧预测能力。上述方法通常采用堆叠各种特征学习模块来提高预测效果,导致模型的计算量和参数量过大,这限制了模型的进一步广泛应用。
1.2 基于卷积神经网络的多进多出预测架构
近年来,基于卷积神经网络的多进多出预测架构开始被应用在视频帧预测领域中。Sun等[17]提出了一种新的U-net预测架构,能够对神经网络不同层次中的多个时间和空间尺度进行统一建模。受Transformer在计算机视觉领域成功应用的启发,Ning等[18]提出了一种基于局部时空块扩展的Transformer预测架构,通过将二维卷积融合到多头注意力中以捕捉序列中的长期依赖关系。此外,Tan等[19]提出了一种轻量型时空预测学习框架,采用膨胀卷积构建时空注意力来增强模型的特征捕捉能力。多进多出预测架构通常构建各种模块来增强空间特征的获取能力,但对时间特征的学习仍然不足。
本文受SimVP框架的启发,构建了基于门控时空注意力的视频帧预测模型。通过多尺度深度条形卷积和通道注意力来捕捉复杂的时空运动趋势,同时采用门控机制来平衡模型的时空特征学习能力,有效地增强了模型的时空动力学建模能力。
2 本文算法
2.1 问题描述
定义一个X={xt+1,xt+2, …, xt+m}表示长度为m的输入视频帧序列,Y={yt+1,yt+2,…,yt+n}表示待预测的未来n帧真实序列,Y′={y′t+1,y′t+2,…,y′t+n}表示模型预测的未来n帧视频序列,其中xt,yt和y′t分别表示第t时刻的原始帧、真实帧和预测帧。模型训练的目的就是通过输入的视频序列X来预测未来的视频序列Y′,同时对模型的可学习参数Θ进行优化,使真实序列Y和预测序列Y′之间的差异最小:
Θ*=argmin L(FΘ(X),Y)。
(1)
式中:Θ*为模型的最佳参数;FΘ为神经网络模型;L为评估差异的MSE损失函数。
2.2 网络结构
目前,在未来帧预测任务中领先的方法是SimVP架构,本文方法采用了类似的设计思想。如图1所示,模型主要由空间编码器、时空预测模块和空间解码器组成。空间编码器通过多层2D卷积来实现特征提取和下采样操作,该模块能够将输入的帧序列编码到低维潜在空间。时空预测模块主要由多个堆叠的门控时空网络(MST)构成,MST通过对输入的低维特征信息进行时空动力学建模,以学习视频序列中的时间趋势和空间相关性。此外,MST之间共享参数,这有效地减少了模型的参数量。空间解码器由2D卷积和上采样操作组成,通过将时空预测模块的输出作为解码器的输入,以实现低维信息向真实预测帧的转换,并且得到的预测序列可继续作为模型的输入进行后续的长期预测。
2.3 空间编码器
如图1所示,综合考虑模型的计算量和参数量,空间编码器采用了多层纯卷积结构,主要由Conv2d、GroupNorm、SiLU组成。由于需要充分捕捉视频帧的空间特征,并避免在下采样过程中造成过多的信息损耗,本文在编码器和解码器之间建立了残差连接,最大限度保留视频帧的背景语义Bbn。空间编码器提取视频序列高级特征信息的过程可以表示为
Zen,Bbn=σ(Norm2d(Conv2d(Xn)))。
(2)
式中:σ为激活函数SiLU;Norm2d为组归一化层;Xn为输入序列;Conv2d为2D卷积运算符;Zen为获取的低维信息。通过将2D卷积的步长(step)设置为2实现下采样,而设置为1则进行卷积操作。
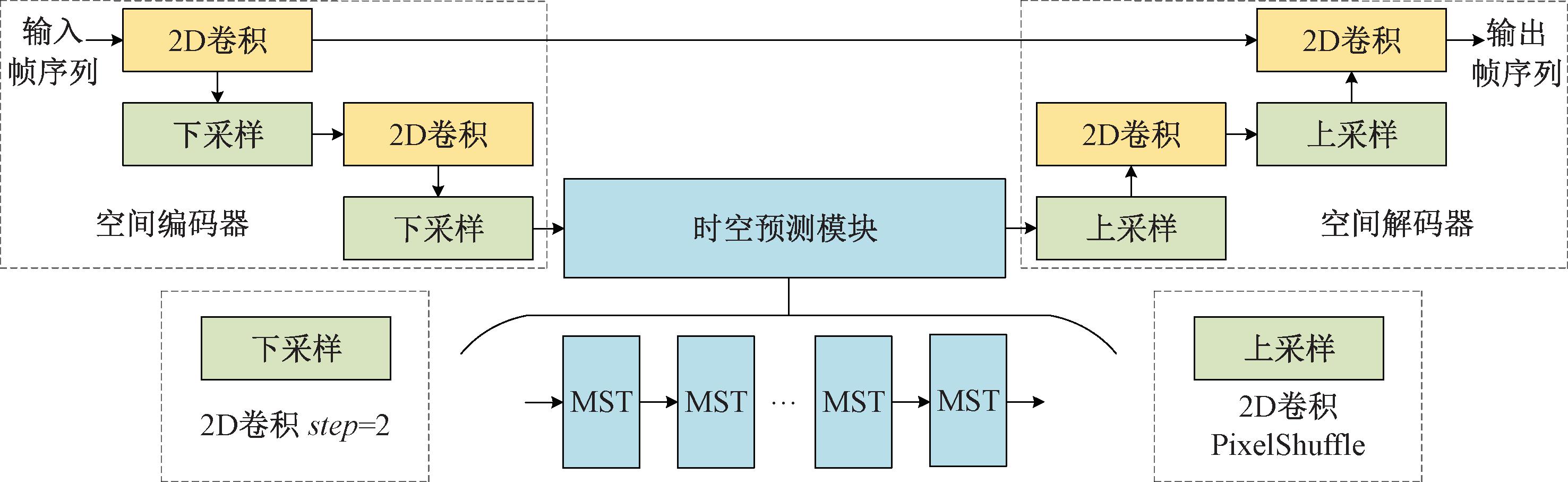
图1 网络架构图
Figure 1 Network architecture diagram
2.4 时空预测模块
时空预测模块位于整个模型的中间部分。同空间编码器和空间解码器对单帧图像进行操作不同,预测模块处理沿时间维度堆叠形成的视频帧序列。由于视频帧预测是一种像素密集型任务,预测输出和输入的视频帧分辨率相同,因此,预测模块即要高效提取时空特征,又要尽可能避免预测过程中增大感受野导致的细节缺失。因此,本文提出了一种新的门控时空网络(MST),如图2所示。MST是一种基于Transformer的变体,由归一化层(Batch Norm)、门控时空注意力层和全连接层组成。其中,门控时空注意力层主要包括空间注意力、时间注意力和门控融合机制3个部分,空间注意力能够学习帧内的多尺度特征信息,而时间注意力能够捕捉帧间的时间变化趋势。此外,门控融合机制能够有效地融合空间信息和时间特征,使模型能够采取相同的重视程度来学习序列中的空间相关性和时间趋势。门控时空注意力对视频序列中每个时空位置下的运动强度进行合理的权重分配,这有效平衡了时间特征及空间信息的捕捉能力,同时能够有效提高模型的时空预测建模能力。
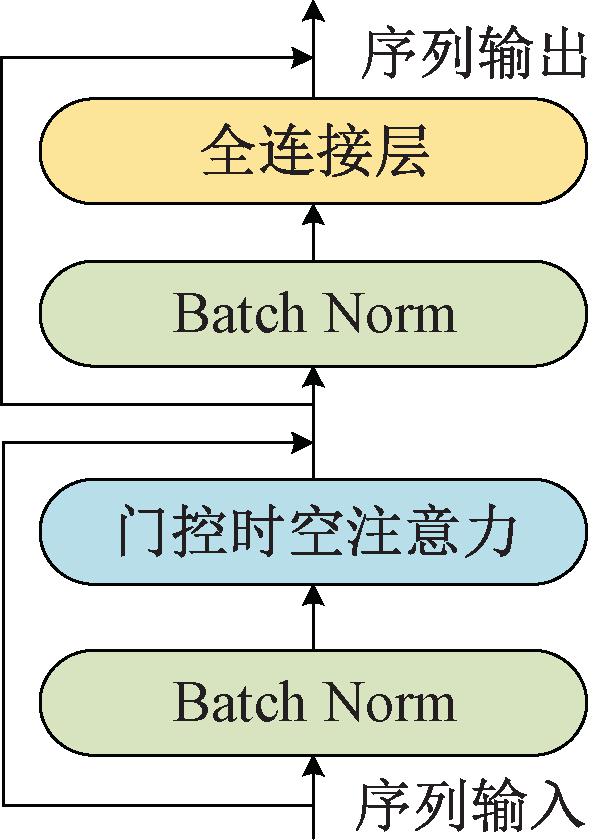
图2 MST网络结构图
Figure 2 MST network structure diagram
2.4.1 时空注意力
为了有效捕捉空间相关性和时间依赖关系,注意力机制需要分解为空间注意力和时间注意力,以充分学习帧内和帧间的相互作用。由于传统空间注意力的特征捕捉能力不足,并忽略了多尺度感受域的重要性,因此,本文采用多尺度深度条形卷积来构建空间注意力,同时使用大卷积核来增强模型的特征捕捉能力。如图3所示,空间注意力获取特征信息的过程主要包括2个阶段:首先建立基于大卷积核的多尺度深度条形卷积Cdw1×k和Cdwk×1,以提取视频序列Zi中的多尺度特征信息;然后通过大小为1×1的卷积核Conv2d1×1来聚合捕捉到的多尺度信息Zm。空间注意力捕捉多尺度特征信息的过程可以表示为
Zm=∑k∈{7,11,21}Cdwk×1(Cdw1×k(Zi));
(3)
Zh=Conv2d1×1(Zm)。
(4)
式中:k为卷积核大小,k∈{7,11,21}代表k分别取7、11和21;Zh为聚合后的多尺度信息。
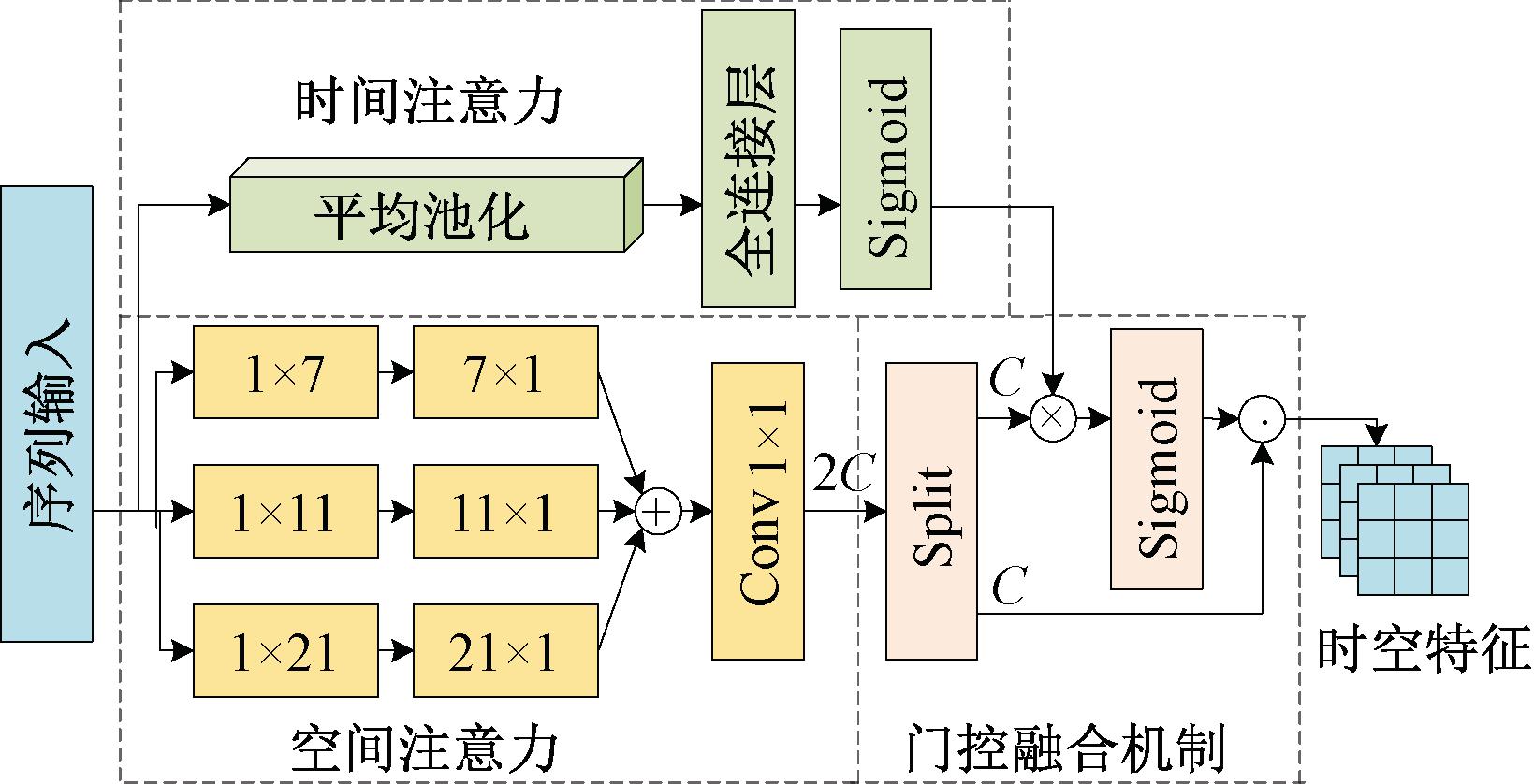
图3 门控时空注意力网路结构
Figure 3 Structure of the gated spatio-temporal attention network
空间注意力能够有效捕捉帧内的空间相关性,但难以完整学习帧间的时间变化趋势。因此,本文采用通道注意力作为时间注意力,利用通道间的相互关系获取时间权重Sa。该过程可以表示为
Sa=FC(Avgpool(Zi))。
(5)
式中:Zi为原始输入信息;Avgpool为全局平均池化;FC为全连接层。
2.4.2 门控融合机制
为了使模型对空间特征和时间特征采取相同的重视程度,本文提出了门控融合机制对空间注意力和时间注意力进行深度融合。如图3所示,门控融合过程可以分为3个阶段:首先,通过拆分操作split将通道数为2C的多尺度空间信息Zh拆分为通道数为C的空间特征Gs和Zt;其次,将空间信息Zt同时间权重Sa相乘,并通过激活函数Sigmoid将其映射至[0,1]以获得时空权重;最后,将空间特征Gs乘以时空权重以获得多尺度时空特征Z″i。整个注意力的融合过程可以表示为
Gs,Zt=split(Zh);
(6)
Z″i=σ(Sa⊗Zt)⊙(Gs)。
(7)
式中:σ为激活函数Sigmoid;⊙为哈达玛积(Had-amard product);⊗为克罗内克积(Kronecker)。
2.5 空间解码器
如图1所示,空间解码器由Conv2d、GroupNo-rm、PixelShuffle组成,通过将预测模块输出的预测信息输入到空间解码器中,能够将低维预测信息Zc解码为图像序列Y′,同时补充背景语义Bbn。空间解码器输出预测图像序列的过程可以表示为
Y′=σ(Norm2d(Conv2d(Zc,Bbn)))。
(8)
式中:σ为激活函数SiLU;Conv2d为2D卷积,通过像素重组层(PixelShuffle)实现上采样操作,否则进行步长为1的卷积操作。
3 实验结果及分析
3.1 实验环境及模型参数
本文采用的软件运行平台为Windows10专业版64位,深度学习环境软件配置为Python3.8和PyTorch1.10。硬件配置为NVIDIA TITAN V显卡,采用CUDA10.2,使用Adam优化器、OneCycle[20]及余弦退火学习率调整策略来训练模型。
该模型的超参数主要包括学习率、训练次数、drop_path、批处理大小、MST单元数等。其中,在Moving MNIST、TaxiBJ、WeatherBench和KITTI数据集上,学习率分别设置为0.001 0、0.000 5、0.005 0、0.005 0,训练次数分别为600、50、50、100,而drop_path分别设置为0、0.2、0.2、0.2,批处理大小统一设置为16,MST单元数分别设置为8、8、8、6。
本文采用MSE损失函数来对模型进行训练,并通过均方误差(MSE)、平均绝对误差(MAE)、结构相似指数(SSIM)和均方根误差(RMSE)来评估预测图像的质量。
3.2 实验评估
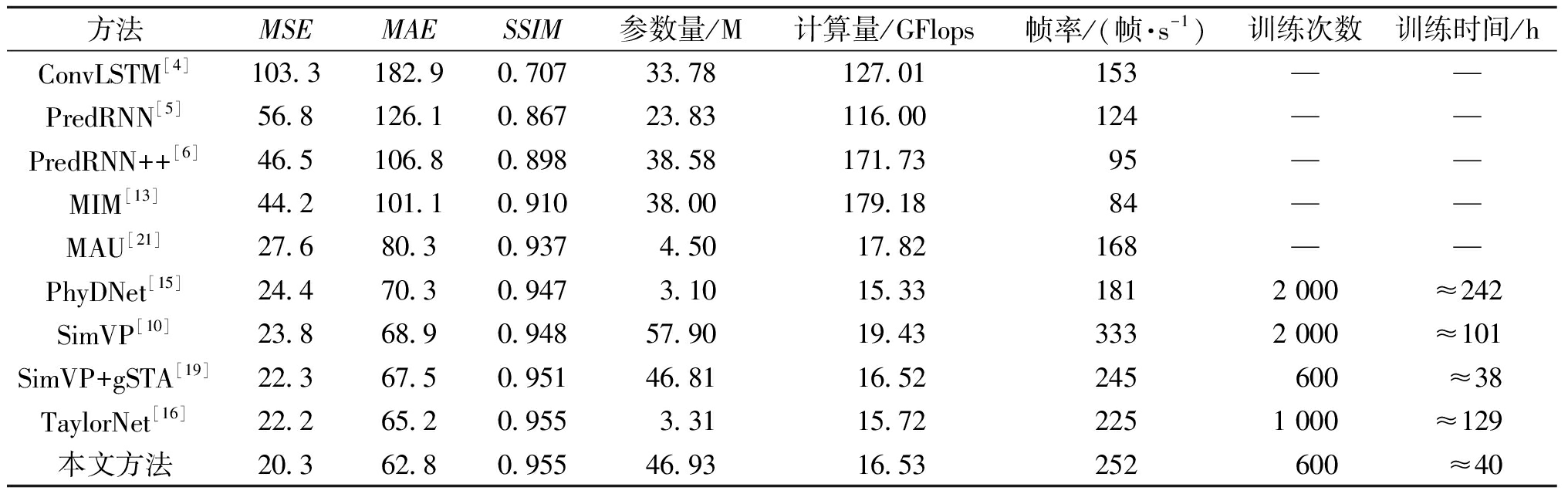
本文在Moving MNIST[3]数据集上进行根据10个条件帧来预测10个未来帧的实验,并同先进的循环式模型和多进多出预测方法对比来评估模型的时空预测学习能力。如表1所示,尽管没有采用循环式设计,本文方法在Moving MNIST数据集上依然获得了较高的预测精度,同SimVP相比,MSE和MAE分别降低了14.7%、8.9%,同时参数量和计算量也有所下降。虽然推理效率有所降低,但时空特征学习能力更强,这显著地减少了模型的训练次数,同时训练时间缩短了近61 h。同最先进的循环式模型TaylorNet相比,本文模型虽然计算量有所增加,但MSE和MAE也分别降低了8.6%、3.7%,同时推理效率提高了12%,并显著地缩短了训练时间。可以看出,本文方法有效解决了循环式架构预测精度低、推理效率低和训练时间长等问题。此外,同最先进的多进多出模型SimVP+gSTA相比,MSE和MAE也下降了9.0%、7.0%,在相同的训练次数下,本文方法获得了更高的预测精度和推理效率。
表1 在Moving MNIST数据集上的实验结果
Table 1 Experimental results on the Moving MNIST dataset
方法MSEMAESSIM参数量/M计算量/GFlops 帧率/(帧·s-1)训练次数 训练时间/hConvLSTM[4]103.3182.90.70733.78127.01153——PredRNN[5]56.8126.10.86723.83116.00124——PredRNN++[6]46.5106.80.89838.58171.7395——MIM[13] 44.2101.10.91038.00179.1884——MAU[21]27.680.30.9374.5017.82168——PhyDNet[15]24.470.30.9473.1015.331812 000≈242SimVP[10]23.868.90.94857.9019.433332 000≈101SimVP+gSTA[19]22.367.50.95146.8116.52245600≈38TaylorNet[16]22.265.20.9553.3115.722251 000≈129本文方法20.362.80.95546.9316.53252600≈40
图4所示为Moving MNIST数据集的预测结果,其中,误差特征图为真实帧和预测帧之间差值的绝对值。可以看出,随着预测长度的增加,在t=10时,TaylorNet由于受到误差累积的影响,产生了最密集的误差图。SimVP虽然解决了误差累积的问题,但特征学习能力仍然不足,其误差主要集中在图像细节。而本文方法避免了误差累积的影响,同时具有高效的特征学习能力,获得了最佳的预测图像。
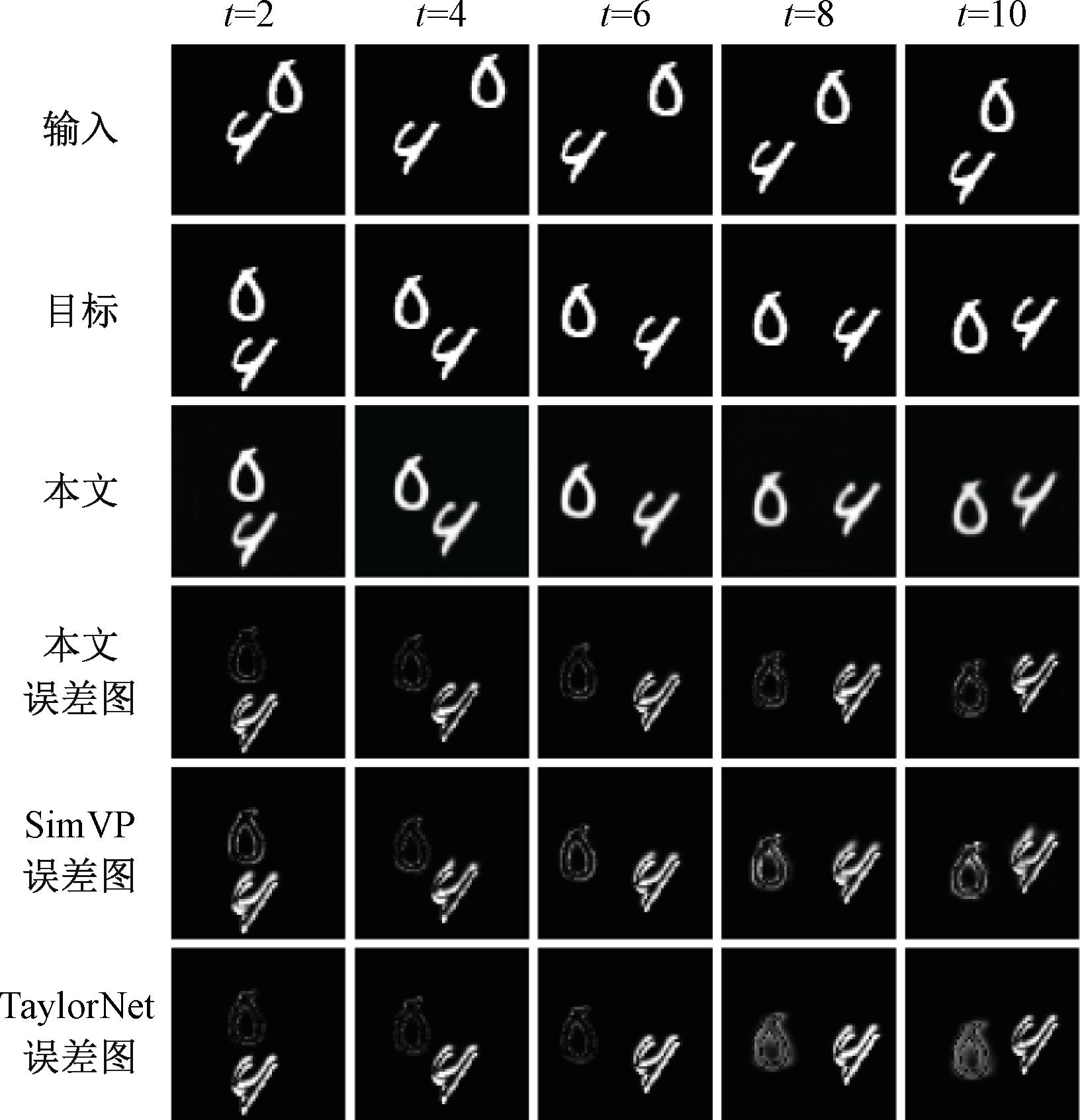
图4 Moving MNIST数据集预测结果
Figure 4 Moving MNIST dataset prediction results
本文在TaxiBJ[22]数据集上同经典的基线模型和最新的先进方法对比来评估模型的交通流预测性能,如表2所示。可以看出,本文方法获得了较高的预测精度,同最先进的循环式模型PredRNN相比,MSE和MAE分别降低了4.1%、2.6%,同时计算量减少了39.8 GFlops。因此基于端对端的多进多出预测架构显著优于循环式单进单出预测架构,能够有效增强模型的预测性能,并减少计算量。而同最先进的多进多出模型TAU相比,MSE也降低了1.3%,并且计算量仅略微增加。此外,SimVP是近期提出的一种简单的多进多出纯卷积网络,该模型构造简单,具有较高的综合性能,本文方法同SimVP相比,在MSE和MAE上也分别降低了6.7%、3.2%,同时能够显著减少计算量。
表2 在TaxiBJ数据集上的实验结果
Table 2 Experimental results on the TaxiBJ dataset
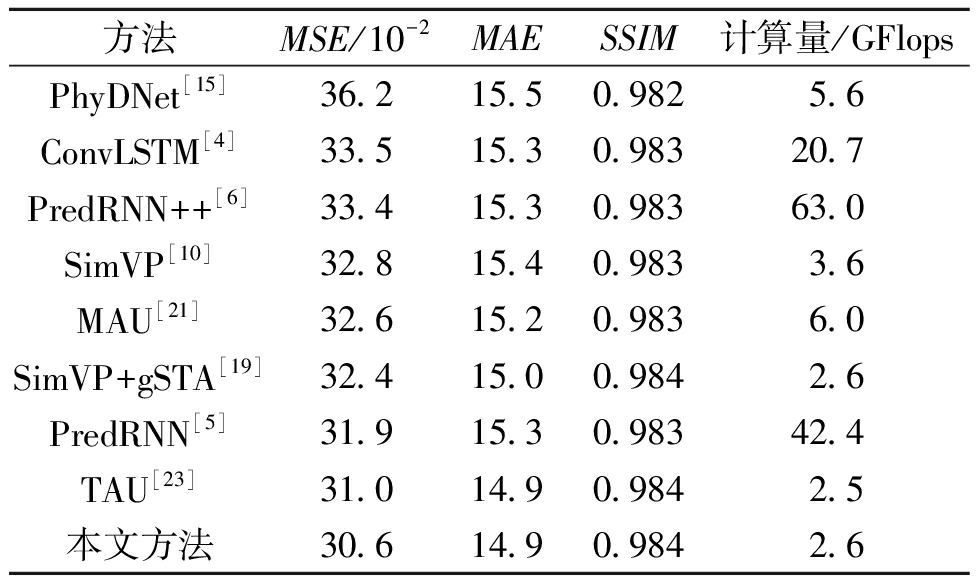
方法MSE/10-2MAESSIM计算量/GFlopsPhyDNet[15]36.215.50.9825.6ConvLSTM[4]33.515.30.98320.7PredRNN++[6]33.415.30.98363.0SimVP[10]32.815.40.9833.6MAU[21]32.615.20.9836.0SimVP+gSTA[19]32.415.00.9842.6PredRNN[5]31.915.30.98342.4TAU[23]31.014.90.9842.5本文方法30.614.90.9842.6
图5所示为TaxiBJ数据集的预测结果,可以看出,随着预测长度的增加,在t=4时,循环式模型受到误差累积的影响,导致MAU的预测效果迅速下降,SimVP虽获得了不错的预测效果,但对时间趋势的捕捉能力仍然不足。本文方法能够有效地平衡时间及空间特征的学习能力,取得了最佳的预测效果,具有很好的交通流预测性能。

图5 TaxiBJ数据集预测结果
Figure 5 TaxiBJ dataset prediction results
气候预测是时空预测学习的另一项基本任务,本文在WeatherBench[24]数据集上同时空预测学习方法进行了对比试验。如表3所示,循环式时空预测学习方法虽取得了一定效果,但复杂的结构也导致计算量过大,而本文方法采用多进多出预测架构实现了更好的综合性能。其中,同最先进的循环式模型MAU相比,MSE降低了11%,并且计算量减小了32.6 GFlops。而同最先进的多进多出模型SimVP+gSTA相比,在MAE上也降低了0.9%。此外,同SimVP模型相比,MSE和MAE分别降低了10.5%、7.5%。
表3 在WeatherBench数据集上的实验结果
Table 3 Experimental results on the WeatherBench dataset
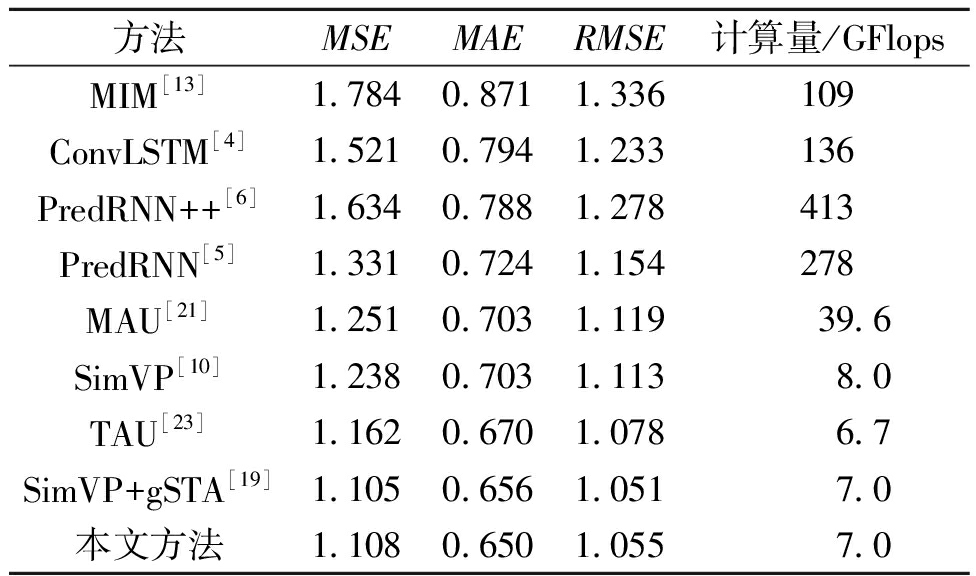
方法MSEMAERMSE计算量/GFlopsMIM[13]1.7840.8711.336109ConvLSTM[4]1.5210.7941.233136PredRNN++[6]1.6340.7881.278413PredRNN[5]1.3310.7241.154278MAU[21]1.2510.7031.11939.6SimVP[10]1.2380.7031.1138.0TAU[23]1.1620.6701.0786.7SimVP+gSTA[19]1.1050.6561.0517.0本文方法1.1080.6501.0557.0
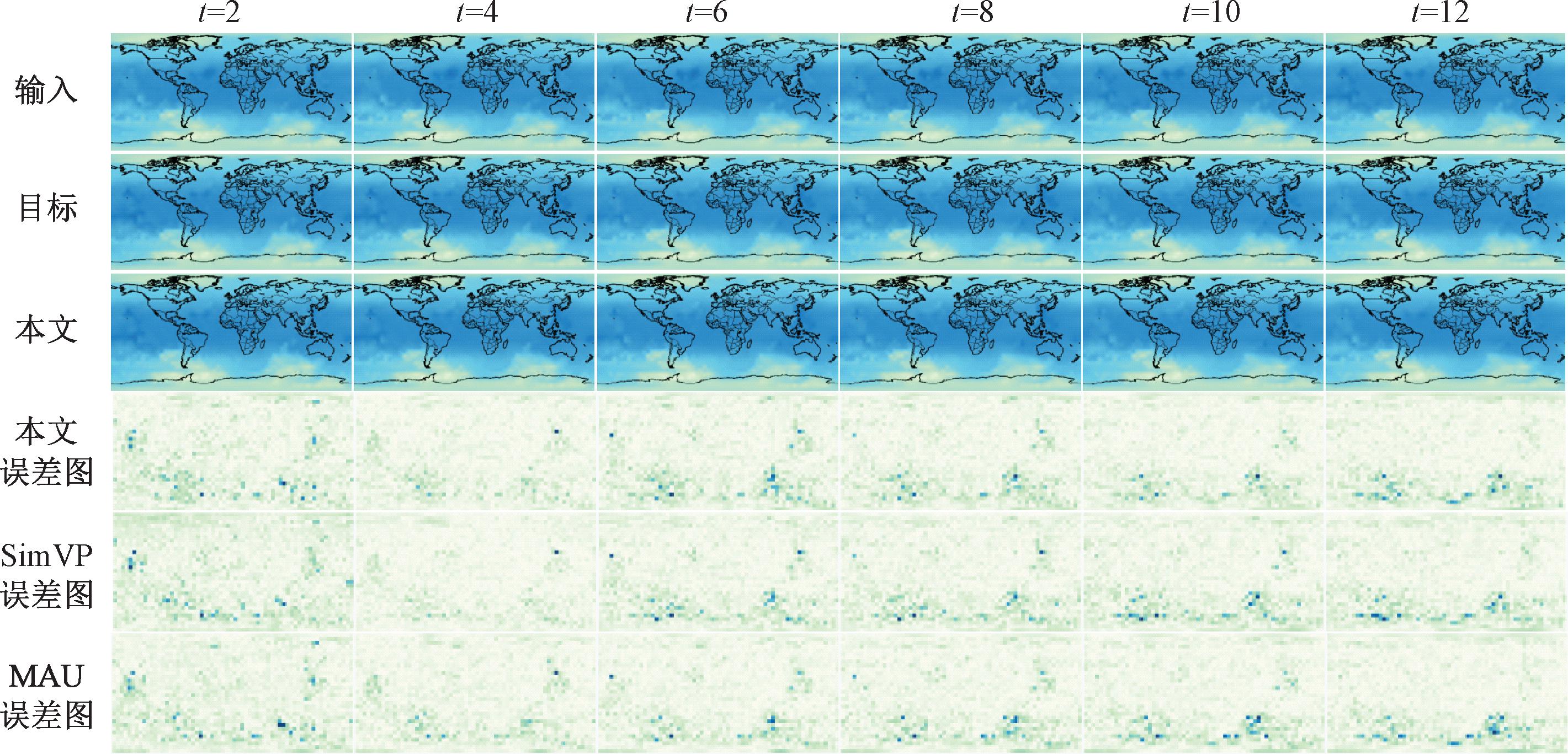
图6 WeatherBench数据集预测结果
Figure 6 WeatherBench dataset prediction results
图6所示为WeatherBench数据集预测结果。可以看出,随着预测长度的增加,在t=12时,SimVP模型难以完整地预测图像细节,MAU由于预测机制的原因,在长期预测中精度会迅速下降。而本文方法获得了最稀疏的误差图,高效的特征提取能力能够学习到更多的图像细节,并且不受误差累积的影响,在全球气候预测任务中表现出极佳的性能。
复杂的真实世界往往包含了不同运动对象的各种非线性时空运动,这导致时空预测学习更加具有挑战性。为了评估模型的泛化能力和适应性,本文在KITTI[14]数据集上进行训练,并在CalTech Pedestrian数据集[14]上进行最终测试。其中,模型在KITTI和Caltech Pedestrian上采用了相同的参数设置,统一进行通过10个条件帧来预测1个未来帧的对比实验。
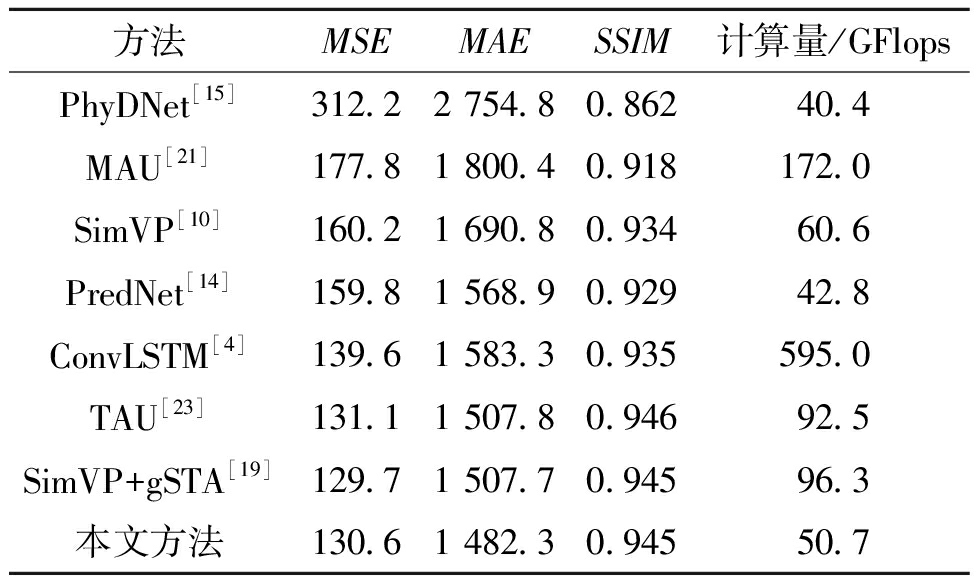
如表4所示,本文方法在真实数据集KITTI上获得了较高的预测精度,同基线模型SimVP相比,MSE和MAE分别降低了18.5%、12.3%。而同最先进的循环式模型ConvLSTM相比,本文方法在MSE和MAE上也分别降低了6.4%、6.4%,同时计算量更小。此外,同最先进的多进多出模型SimVP+gSTA相比,虽然MSE略微有所上升,但MAE降低了1.7%,并且计算量减少了45.6 GFlops。可以看出,多进多出预测架构在预测精度上显著优于循环式预测架构,而本文方法通过较少的计算量达到了和SimVP+gSTA模型同样先进的预测性能,并且显著优于其他时空预测学习方法,具有很好的自动驾驶预测能力。
表4 在KITTI数据集上的实验结果
Table 4 Experimental results on the KITTI dataset
方法MSEMAESSIM计算量/GFlopsPhyDNet[15]312.22 754.80.86240.4MAU[21]177.81 800.40.918172.0SimVP[10]160.21 690.80.93460.6PredNet[14]159.81 568.90.92942.8ConvLSTM[4]139.61 583.30.935595.0TAU[23]131.11 507.80.94692.5SimVP+gSTA[19]129.71 507.70.94596.3本文方法130.61 482.30.94550.7
3.3 消融扩展实验
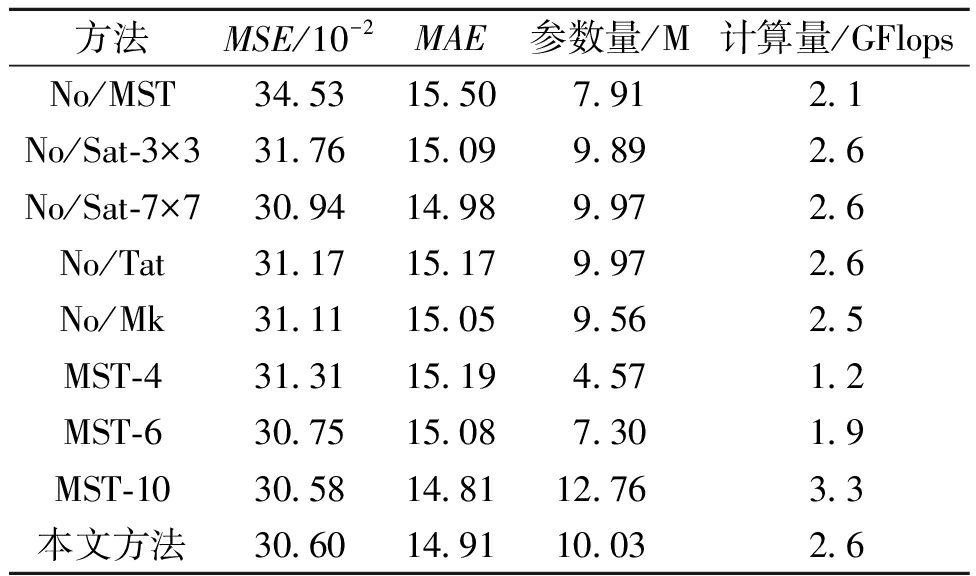
为分析门控时空注意力每个局部模块对最终预测性能的影响,本文在TaxiBJ数据集上进行了消融实验。表5所示为消融实验结果,其中“No/MST”表示用1×1卷积替换门控时空注意力层,“No/Sat-3×3”和“No/Sat-7×7”分别是将空间注意力的多尺度深度卷积替换成3×3卷积和7×7卷积,“No/Tat”表示没有设置时间注意力,“No/Mk”表示不采用门控融合机制平衡注意力。而“MST-4”、“MST-6”和“MST-10”则表示MST的数量分别设置为4、6和10。
表5 在TaxiBJ数据集上的消融实验结果
Table 5 Ablation experimental results on the TaxiBJ dataset
方法MSE/10-2MAE参数量/M计算量/GFlopsNo/MST34.5315.507.912.1No/Sat-3×331.7615.099.892.6No/Sat-7×730.9414.989.972.6No/Tat31.1715.179.972.6No/Mk31.1115.059.562.5MST-431.3115.194.571.2MST-630.7515.087.301.9MST-1030.5814.8112.763.3本文方法 30.6014.9110.032.6
如表5所示,采用门控时空注意力层使得MSE和MAE分别降低了11.4%和3.8%。同3×3卷积和7×7卷积相比,使用多尺度深度条形卷积能够增强模型的感受野和捕捉多尺度特征的能力,使得MSE分别降低了3.7%、1.1%。通过时间注意力学习帧间的相互作用,使MSE也降低了1.8%。而门控机制深度融合了两种注意力,MSE降低了1.6%。可以看出,模型中的每个模块都能够有效提高最终的预测精度。此外,设置过多的MST单元带来的效果提升并不明显,同时导致了模型的参数量和计算量增大。因此,本文将MST数量设置为8,并同上述3个模块进行集成获得了最佳的时空预测性能。
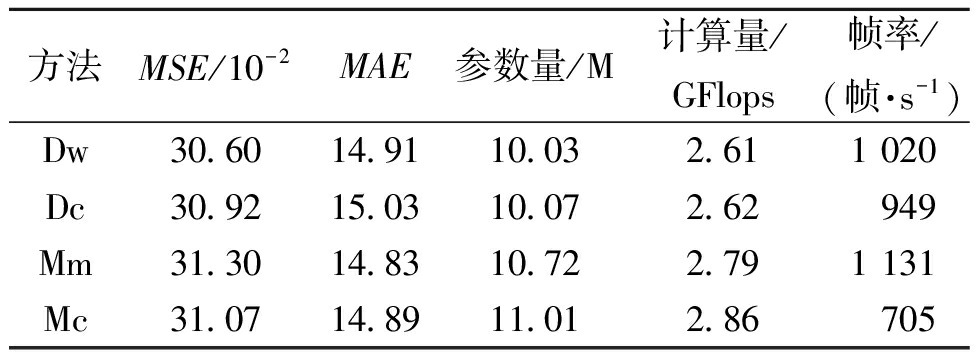
本文在TaxiBJ数据集上进行了卷积扩展实验如表6所示。其中,Dw为本文采用的多尺度深度条形卷积,Dc代表使用多尺度膨胀卷积,Mm代表采用多尺度2D卷积,并在最终测试阶段通过重参数融合法[25]压缩模型,Mc为使用多尺度2D卷积,其中7×7卷积被3个3×3卷积所代替。同Dc和Mc相比,Dw在预测性能、参数量及推理效率方面具有显著优势,而Mm由于采用了重参数融合法,获得了最佳的推理效率,但本文方法获得了更高的预测精度,同时具有很好的推理效率。
表6 卷积扩展实验对比结果
Table 6 Convolution extension experiment comparison results
方法MSE/10-2MAE参数量/M计算量/GFlops帧率/(帧·s-1)Dw30.6014.9110.03 2.611 020Dc30.9215.0310.07 2.62 949Mm31.3014.8310.72 2.791 131Mc31.0714.8911.012.86705
为了探究不同预测架构对收敛性能的影响,本文在Moving MNIST数据集上进行了扩展实验。图7所示为不同模型收敛速度的对比结果。可以看出,同单进单出预测架构PhyDNet相比,多进多出预测策略在收敛性能方面具有显著优势。其中,本文方法实现了比SimVP更快的收敛速度,获得了较好的收敛效果。这表明,在每次训练中,模型能够捕捉到更多的时空动态趋势,这将会有效缩短模型的整体训练时间。
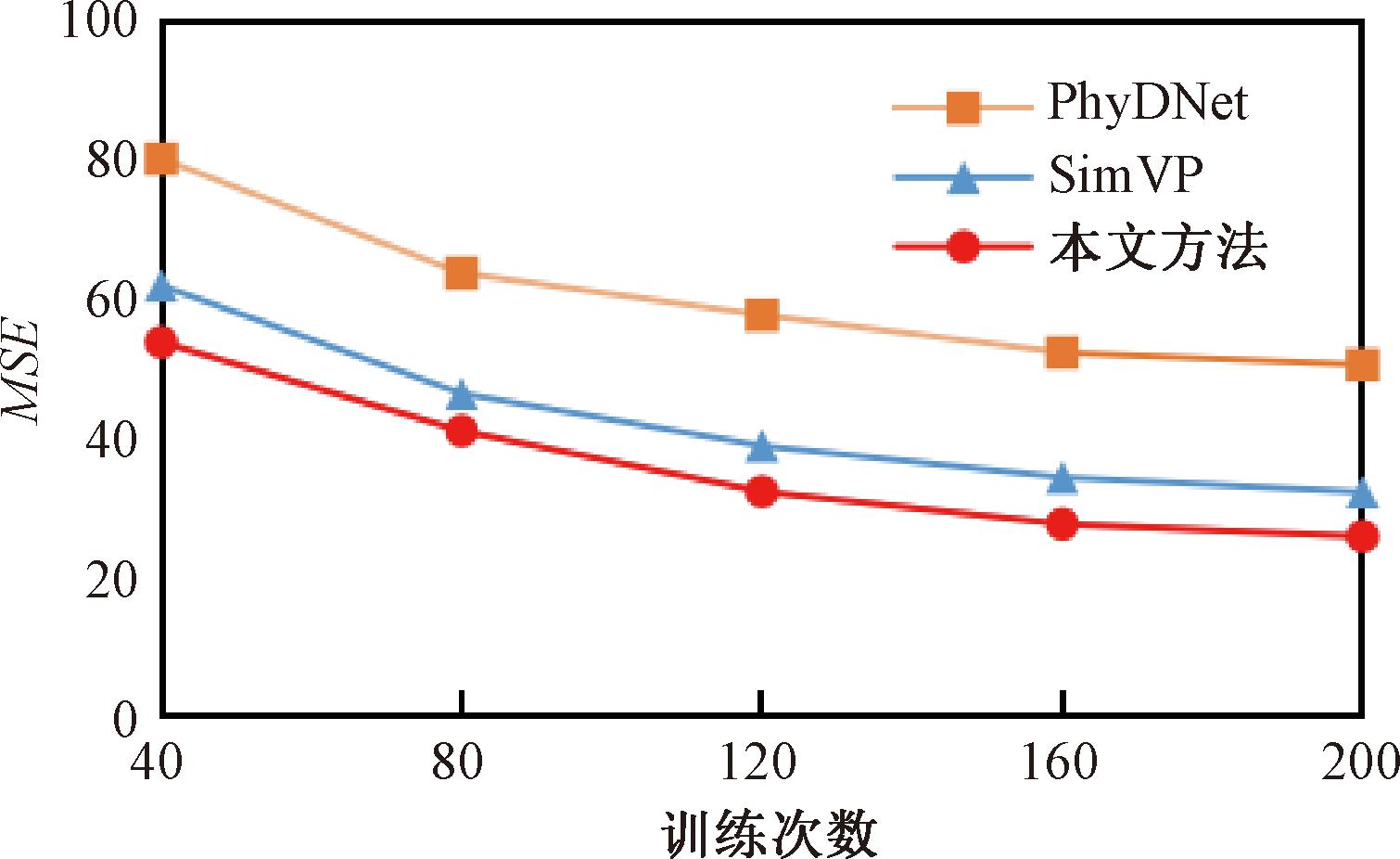
图7 收敛性能实验结果
Figure 7 Convergence performance experimental results
4 应用前景展望
随着计算机视觉和深度学习技术的不断发展,视频预测技术将会具有更加广泛的应用前景。在交通领域中,视频预测技术可用于交通流监测、交通事故预测和城市规划,通过分析实时的视频流,交通系统可以更好地调度交通信号、减少拥堵,有效提高交通系统的效率。在气象领域中,视频预测技术可用于监测自然灾害,通过分析卫星和地面摄像头的视频数据,能够提前发现灾害迹象并发出预警提示,有效减少损失。视频预测技术的发展将会产生很多新的应用领域,在医疗领域中,视频预测技术将可以用于远程患者的监测、手术中的实时病情分析,医生可以利用视频预测技术来提高手术的准确性和安全性。视频预测技术将在多个领域引领创新和变革,将会有助于提高效率和安全性,并有潜力挖掘出更多的应用场景,为未来创造更多的可能性。
5 结论
本文提出了门控时空注意力来生成帧内和帧间相互关系的时空权重,以充分学习视频序列中空间维度和时间维度下有意义的时空信息,并采用门控融合机制平衡空间及时间注意力的特征捕捉能力,在Moving MNIST、 TaxiBJ、WeatherBench、KITTI数据集上的实验结果均优于对比算法。此外,现有方法并未充分考虑帧内的多尺度信息交互作用对预测精度的影响,在今后的工作中,将研究如何更加高效地捕捉帧内及帧间的信息交互关系,同时保持模型结构简单、参数量低和推理效率高等优势。
[1] DAI K, LI X T, YE Y M, et al. MSTCGAN: multiscale time conditional generative adversarial network for long-term satellite image sequence prediction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-16.
[2] TAN C, LI S Y, GAO Z Y, et al. OpenSTL: a comprehensive benchmark of spatio-temporal predictive learning[EB/OL]. (2023-06-20)[2023-07-20]. https:∥arxiv.org/abs/2306.11249.
[3] SRIVASTAVA N, MANSIMOV E, SALAKHUTDINOV R. Unsupervised learning of video representations using LSTMs[EB/OL]. (2016-01-04)[2023-07-20]. https:∥arxiv.org/abs/1502.04681.
[4] SHI X J, CHEN Z R, WANG H, et al. Convolutional LSTM network: a machine learning approach for precipitation nowcasting[EB/OL]. (2015-09-19)[2023-07-20]. https:∥arxiv.org/abs/1506.04214.
[5] WANG Y B, LONG M S, WANG J M, et al. PredRNN: recurrent neural networks for predictive learning using spatiotemporal LSTMs[C]∥NIPS′17: Proceedings of the 31st International Conference on Neural Information Processing Systems. Cham: Springer, 2017: 879-888.
[6] WANG Y B, GAO Z F, LONG M S, et al. PredRNN++: towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning[EB/OL]. (2018-11-19)[2023-07-20]. https:∥arxiv.org/abs/1804.06300.
[7] LIU Z W, YEH R A, TANG X O, et al. Video frame synthesis using deep voxel flow[C]∥2017 IEEE International Conference on Computer Vision (ICCV).Piscataway: IEEE, 2017: 4473-4481.
[8] AIGNER S, KÖRNER M. FutureGAN: anticipating the future frames of video sequences using spatio-temporal 3d convolutions in progressively growing GANs[EB/OL]. (2018-11-26)[2023-07-20]. https:∥arxiv.org/abs/1810.01325.
[9] YE X, BILODEAU G A. VPTR: efficient transformers for video prediction[C]∥2022 26th International Confe-rence on Pattern Recognition (ICPR). Piscataway: IEEE, 2022: 3492-3499.
[10] GAO Z Y, TAN C, WU L R, et al. SimVP: simpler yet better video prediction[C]∥2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2022: 3160-3170.
[11] GUO M H, LU C Z, HOU Q B, et al. SegNeXt: rethinking convolutional attention design for semantic segmentation[EB/OL]. (2022-09-18)[2023-07-20]. https:∥arxiv.org/abs/2209.08575.
[12] HU J, SHEN L, SUN G. Squeeze-and-excitation networks[C]∥2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2018: 7132-7141.
[13] WANG Y B, ZHANG J J, ZHU H Y, et al. Memory in memory: a predictive neural network for learning higher-order non-stationarity from spatiotemporal dynamics[C]∥2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2020: 9146-9154.
[14] LOTTER W, KREIMAN G, COX D. Deep predictive coding networks for video prediction and unsupervised learning[EB/OL]. (2017-05-01)[2023-07-20]. https:∥arxiv.org/abs/1605.08104.
[15] GUEN V L, THOME N. Disentangling physical dynamics from unknown factors for unsupervised video prediction[C]∥2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2020: 11471-11481.
[16] PAN T, JIANG Z Q, HAN J N, et al. Taylor saves for later: disentanglement for video prediction using Taylor representation[J]. Neurocomputing, 2022, 472: 166-174.
[17] SUN F, BAI C, SONG Y, et al. MMINR: multi-frame-to-multi-frame inference with noise resistance for precipitation nowcasting with radar[C]∥2022 26th International Conference on Pattern Recognition (ICPR). Piscataway: IEEE, 2022: 97-103.
[18] NING S L, LAN M C, LI Y R, et al. MIMO is all you need: a strong multi-in-multi-out baseline for video prediction[EB/OL]. (2023-05-30)[2023-07-20]. https:∥arxiv.org/abs/2212.04655.
[19] TAN C, GAO Z Y, LI S Y, et al. SimVP: towards simple yet powerful spatiotemporal predictive learning[EB/OL]. (2023-04-26)[2023-07-20]. https:∥arxiv.org/abs/2211.12509.
[20] SMITH L N, TOPIN N. Super-convergence: very fast training of neural networks using large learning rates[EB/OL]. (2017-08-23)[2023-07-20]. https:∥arxiv.org/abs/1708.07120v1.
[21] CHANG Z, ZHANG X F, WANG S S, et al. MAU: a motion-aware unit for video prediction and beyond[C]∥35th Conference on Neural Information Processing Systems. Sydney: NeurIPS , 2021: 1-13.
[22] ZHANG J B, ZHENG Y, QI D K. Deep spatio-temporal residual networks for citywide crowd flows prediction[C]∥Proceedings of the 31st AAAI Conference on Artificial Intelligence. New York: ACM, 2017: 1655-1661.
[23] TAN C, GAO Z Y, WU L R, et al. Temporal attention unit: towards efficient spatiotemporal predictive learning[C]∥2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2023: 18770-18782.
[24] RASP S, DUEBEN P D, SCHER S, et al. WeatherBench: a benchmark data set for data-driven weather forecasting[J]. Journal of Advances in Modeling Earth Systems, 2020, 12(11): 1-17.
[25] DING X H, ZHANG X Y, MA N N, et al. RepVGG: making VGG-style ConvNets great again[C]∥2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2021: 13728-13737.