在轨道车辆制造、盾构掘进、风电等复杂装备制造企业,配件库存价值通常在库存成本中占比超过60%[1]。精准的需求预测是企业实现库存优化、配件灵活调度的决策依据,也是企业提高市场服务、实现智能制造的关键环节。但是在实际业务中,配件计划常与新上线项目挂钩,或与维修现场配件缺失而产生的零星需求有关,导致需求序列数据呈现出典型的间歇性特点。因此,如何从间歇性需求序列中提取演化趋势,实现需求量的精准预测是目前制造企业配件管理的迫切需求。
目前主流的时间序列预测方法大致分为以指数平滑[2]、移动平均[3]为主的统计学方法;以支持向量回归(support vector regression, SVR)[4] 、随机森林(random forests,RF)[5]、LightGBM(light gradient boosting machine)[6]为主的机器学习方法;以循环神经网络(recurrent neural network, RNN)[7]、长短期记忆神经网络(long short-term memory, LSTM)[8]为主的深度学习方法。这些方法多适用于周期性和趋势性较强的时间序列,对于随机性强、波动性大的间歇性时间序列,则无法有效提取序列中的演化规律。为实现间歇性时间序列的精准预测,Croston[9]将序列拆分为需求间隔和零间隔序列,使用指数平滑算法对两者预测然后对结果加权;Syntetos等[10]对Croston算法改进,在原来预测结果上加入了偏差值,提出了SBA方法;Gutierrez等[11]运用神经网络预测备件需求量,虽然能计算每期的备件需求,但是预测精度并不高;张瑞[12]使用SVR预测需求发生时间,但是没有考虑需求量前后之间的联系;Shi等[13]提出BHT-ARIMA(block Hanker tensor-autoregressive integrated moving average)模型,通过张量分解提取多维小样本序列间的内在相关性,进而使用张量化的ARIMA算法,实现对多条配件序列的联合预测。整体来说,上述方法已经取得一定的结果,但仍存在一定局限性:对于小样本时间序列需求演化信息挖掘不充分,未能利用相似配件序列之间的结构化信息;未能考虑配件需求序列中存在的异常需求,需要人工判别异常需求数据;未能考虑预测结果的不确定性。在实际中,预测结果可信度未知,当预测结果失真时,现有方法未能提供一种针对性的解决方案。
针对上述问题,本文首先利用间歇性分布指标聚合相似序列,增加可预测性;其次,引入张量分解,平滑配件需求序列中的异常值;最后,提出一种自适应区间预测算法,解决预测结果不确定性强、可靠性不足的问题。利用某大型轨道交通制造企业实际售后数据进行了验证。
1 相关理论
1.1 间歇性特征
间歇性序列最常用的2个特征指标为平均需求间隔ADI和平方变异系数CV2[14],计算公式如下:
(1)
(2)
式中:d为序列X非零需求的周期数;sd为非零需求序列的标准差;
为非零序列的平均值。
基于ADI和CV2,可以将需求分为4个类别:①ADI<1.32,CV2<0.49(平稳需求);②ADI≥1.32,CV2<0.49(间歇需求);③ADI≥1.32,CV2≥0.49(块状需求);④ADI<1.32,CV2≥0.49(非平稳需求)。
1.2 多路延迟嵌入变换
多路延迟嵌入变换(multi-way delay embedding transform, MDT)将多条短小的时间序列沿着时间维度转换为高阶多维数据[15]。所得的高阶多维张量称之为块汉克尔张量(block Hankel tensor, BHT)。BHT具有低秩或平滑等良好特性,这比原始数据更容易学习和训练。对于序列X={x1,x2,…,xm}, MDT转换过程如下:
={χ1,χ2,…,χm-
+1}⊆R×(m-+1);
(3)
χi=
(X)=Fold(m,)(X×S1×S2×…×Sm-+1)。
(4)
式中:和m分别为时间窗口大小和样本长度;S为映射矩阵;
为序列X经过MDT转化后的特征表示。
1.3 张量分解
张量分解是一种将高阶张量数据分解成低秩矩阵或向量的技术,经常被用于数据压缩、降维、特征提取等领域。Tucker分解[16]是张量分解中的一种,相比于其他分解方法在重构张量时的准确性和稳定性较高。Tucker分解将一个高阶张量表示为一个核心张量和沿着各个mode上的因子矩阵,每个mode上的因子矩阵称为张量在每个mode上的基矩阵或者是主成分。例如,N阶张量XT∈ki1×i2×…×iN分解为1个核心张量
∈Rj1×j2×…×jN和N个因子矩阵D(N)∈Rin×jn,定义为
XT=×D(1)×D(2)×…×D(N)。
(5)
三阶张量分解如图1所示。
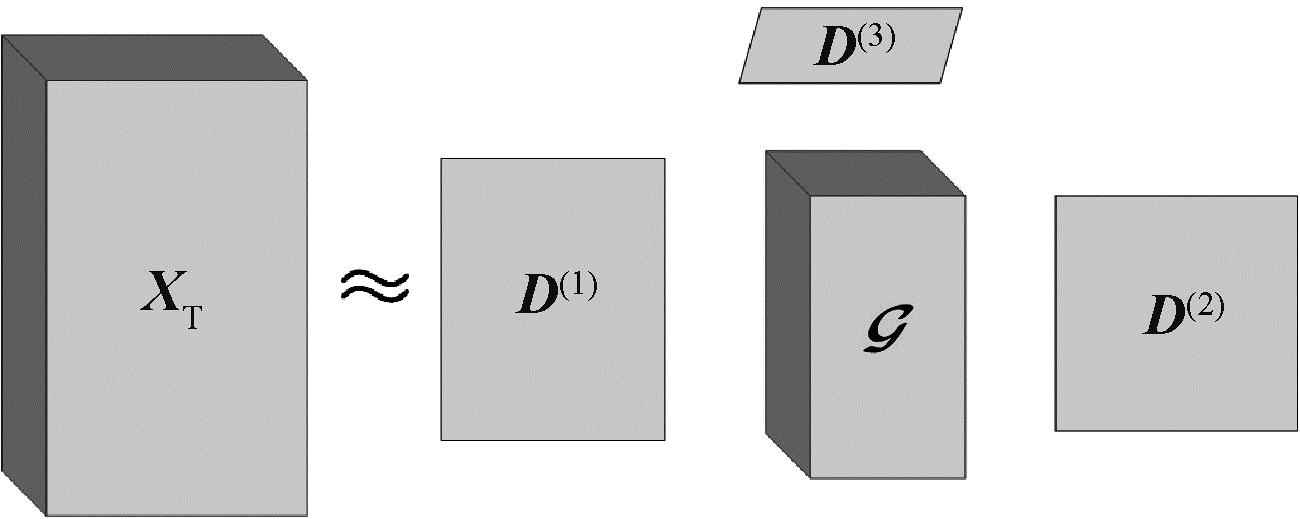
图1 三阶张量分解
Figure 1 Third-order tensor decomposition
1.4 LightGBM
LightGBM是一种基于梯度提升决策树(gradient boost decision tree,GBDT)的机器学习框架,其将多个弱回归器组合成一个强回归器,在每一轮迭代中都会根据当前模型的表现调整每个样本的权重,使得前一轮回归损失较大的样本在后一轮迭代中得到更多的关注,具有训练速度快、预测准确率高、消耗内存小等特点。
对于短小时间序列数据,特别是间歇性时间序列,使用LightGBM能够快速构建模型并进行预测。短小时间序列通常包含大量的特征,这些特征可能高度稀疏,而LightGBM使用基于直方图的算法,能够较好地处理高维稀疏特征。
2 基于张量表示的间歇性序列自适应区间预测方法
为解决配件需求发生随机、需求量波动大、预测结果不确定性高等问题,本文提出了一种基于张量表示的间歇性序列自适应区间预测方法。该方法分为3部分:①聚合相似序列,其目的是挖掘相似配件需求序列的共同演化趋势,增加可预测性;②张量分解,其目的是平滑需求序列中的异常值并提取核心演化信息;③自适应区间预测算法,其目的是构建一个可靠的预测区间,解决因预测结果不准确而造成的库存呆滞或短缺的问题。本文方法具体流程图如图2所示。
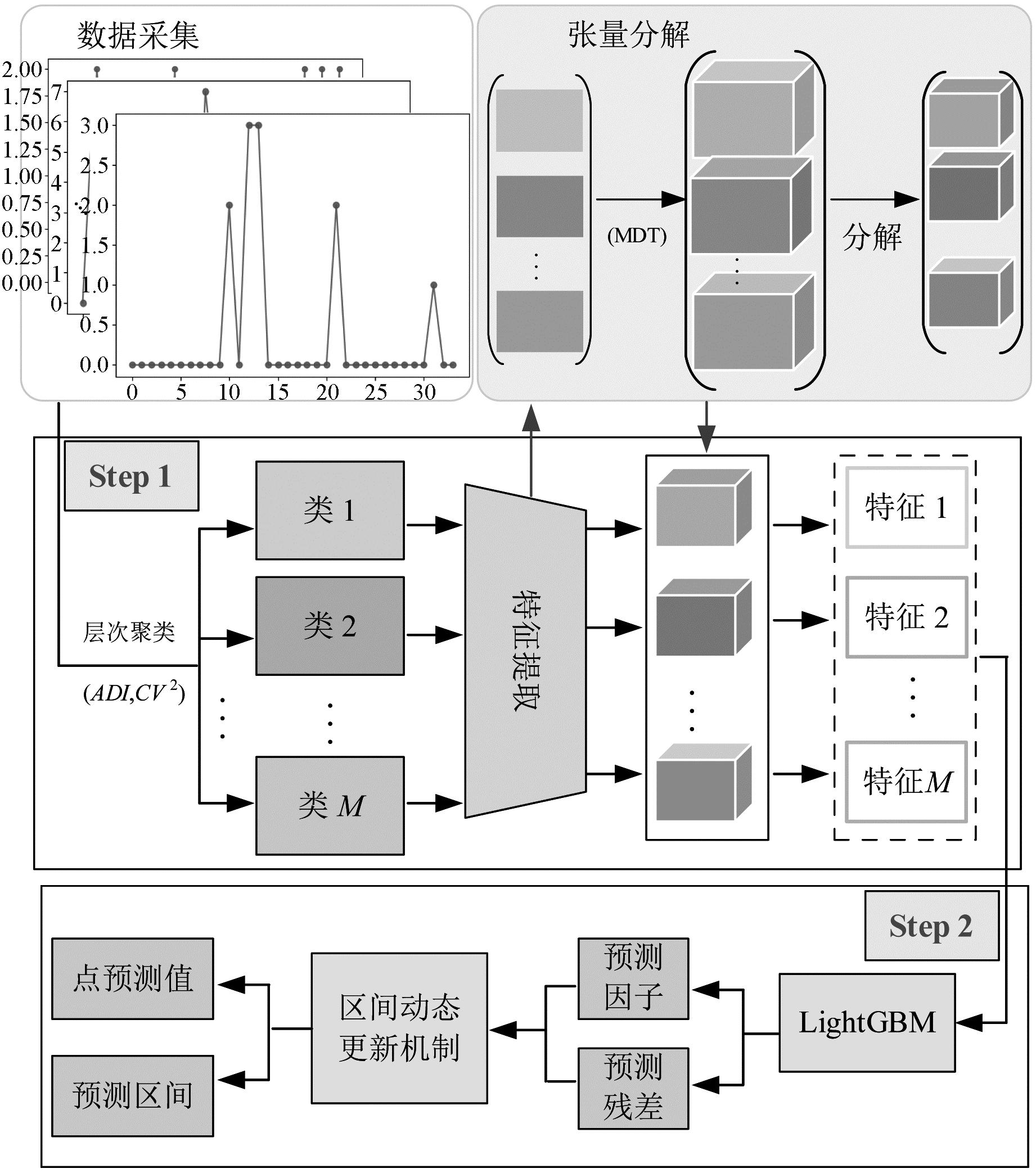
图2 基于张量表示的间歇性序列自适应区间预测方法流程图
Figure 2 Flow chart of adaptive interval prediction method for intermittent sequences based on tensor representation
2.1 序列张量分解
为表示配件序列间的结构化和时序信息,本文采用MDT将多条配件序列沿着时间维度转化为高阶张量,转化后的高阶张量更容易表征序列间的时序信息。使用Tucker分解技术获得能表示原始序列数据最本质的核心张量:
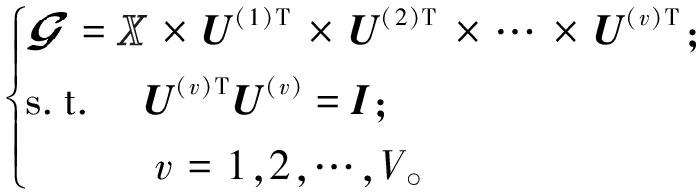
(6)
通过优化
最大限度地捕捉特征序列之间内在的相关性,同时防止需求序列中的异常值对模型的干扰,可最大限度地提取带有核心信息的张量。
2.2 自适应区间
由于配件需求序列样本量有限,从单条需求序列中提取的信息有限,本文利用间歇性序列指标CV2和ADI筛选序列形成序列簇。将筛选后的相似序列经过张量分解得到核心张量,然后使用API算法得到预测值和预测区间。API包括训练和预测2个阶段。在训练阶段,首先从训练数据的子集中拟合固定数量的LightGBM估计器,然后以留一法(leave-one-out,LOO)方式聚合所有LightGBM估计器的预测值[17],产生LOO预测因子和LOO残差。在预测阶段,API汇总了来自每个测试数据上的LOO预测值,以计算预测区间的中心,然后利用LOO残差建立预测区间,其中预测区间宽度利用区间动态更新策略进行更新。具体实现步骤如下。
首先,利用T个训练样本
训练得到一个模型f,则预测区间为
分位数,
分位数]。
(7)
式中:
为显著性为α时第t个时间步的预测区间;
为第t个LOO估计器f。LOO预测残差
和
分别定义为
(8)
分位数-
分位数)。
(9)
式中:
为区间中心;区间宽度为
和分位数在过去T个残差上的差。
为了应对不同配件序列需求波动大,设置相同区间不合理的问题,本文提出了区间动态更新机制来提高预测区间的实用性。通过这种区间动态更新机制,可以使预测结果更加符合实际需求,提高预测区间的准确性和实用性。首先需要将每条配件序列拆分为需求量序列和非零序列,然后计算它们的平方变异系数。平方变异系数越大,说明序列波动越剧烈,因此需要更大的区间宽度来进行预测。初始化区间宽度参数α,根据下列公式更新α:
α=α+cv1+cv2。
(10)
式中:cv1和cv2为需求量序列和非零序列的变异系数;α越小,区间宽度越大。
区间动态更新机制首先设置一个较大宽度的初始化区间,然后根据配件序列的需求波动性进行自适应缩减。根据式(10),α不断增加,区间宽度在不停地减小,当区间宽度降低到一定阈值后,停止更新。在本实验中,当初始化α为0.1时,区间宽度可包含配件序列中所有的需求量,满足初始化条件。区间宽度的阈值可用区间覆盖率(区间宽度覆盖的需求量个数与序列所有需求数量的比例)衡量。区间覆盖率阈值的设置与业务特点密切相关。本文参考了合作企业运维工程师的建议,将区间覆盖率阈值设置为70%。
基于张量的间歇性序列自适应区间预测算法伪代码流程如下。
输入:原始配件需求序列集合S={S1,S2,…,Sn};
输出:预测区间
①For s in S
计算间歇性度量指标ADI和CV2;
采用层次聚类对序列s进行聚类;
将序列s放入相序列簇C={c1,c2,…,cm};
②For c in C
For s in c
使用MDT将序列s沿着时间维度转化为高阶张量:s→sMDT;
采用式(5),对序列使用Tucker分解提取核心张量
:sMDT→;
③利用Tucker分解提取到的核心张量训练LightGBM;
以LOO方式聚合LightGBM预测值,产生LOO预测因子
和LOO残差
根据式(7)、式(9)计算预测区间
④利用动态更新机制,根据式(10)自适应更新预测区间。
3 实验分析
本次实验选取常见的回归评价指标:均方根误差(RMSE)、平均绝对值误差(MAE)、间歇性特有指标均方根标准误差(RMSSE)。其中,RMSSE计算公式如下:
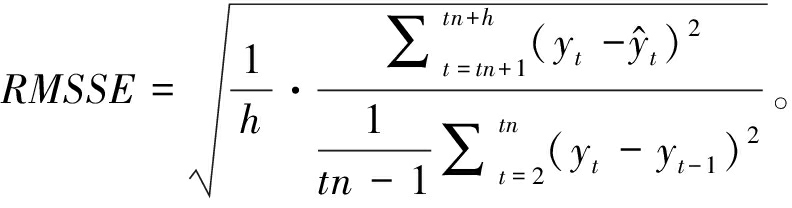
(11)
式中:yt为t时间步的实际值;
为t时间步的预测值;tn为训练样本长度;h为预测范围长度。
3.1 数据集
本次实验数据为某大型轨道交通制造企业售后配件真实需求数据。经过筛选,本文选择其中的75条配件序列数据,每条配件序列统计了2018年11月到2021年8月,共34个月数据。其中,训练数据为前33个月的需求量,预测最后1个月的需求量。
该数据配件序列需求量都是按月汇总,部分配件需求序列如图3所示。
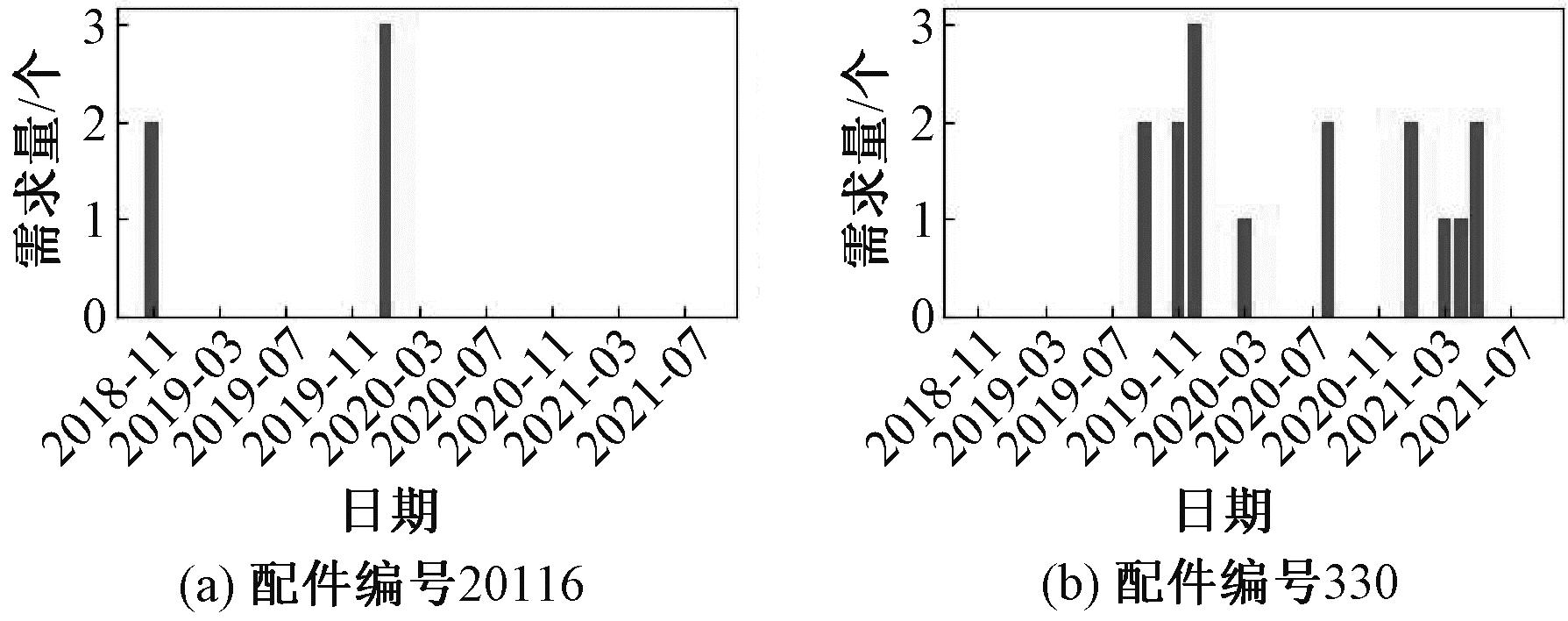
图3 某大型车辆制造企业实际售后数据
Figure 3 Actual after-sales data of large vehicle manufacturing enterprises
3.2 对比方法
本文对比方法包含经典间歇性序列预测算法Croston、BHT-ARIMA,单维时间序列方法ARIMA,多维时间序列方法SVR、LightGBM,深度学习方法长短期记忆网络LSTM,以及目前最新的时间序列预测方法Transformer和Informer。
本次实验中,Croston模型参数:平滑系数α、β分别设置为0.15、0.30。ARIMA模型参数:自回归阶数p和移动平均阶数q通过自动搜索寻优,分别设置为2、1。BHT-ARIMA模型参数:自回归阶数p=3,差分阶数d=1,移动平均阶数q=1。SVR模型通过网格搜索算法寻找最优参数:惩罚系数C=1.0,核函数kernel选择线性核函数。LightGBM模型参数:学习率learning_rate=0.05,最大深度max_depth=5,叶子节点num_leaves=20。LSTM隐藏层设置为20,结构为[6,20,1],学习率为0.001,损失函数为MSELoss,优化器选择Adam。Transformer模型的结构为[6,64,6,1],多头注意力个数num_heads=1,编码器解码器层数num_layers=1。Informer模型的结构为[6,128,1],多头注意力个数nheads=1,优化器选择Adam,学习率为0.005。本文方法初始区间宽度参数α=0.1,区间覆盖率阈值设置为70%,LightGBM估计器数量为100,参数num_leaves=31,学习率learning_rate=0.1,层次聚类算法中聚类类别参数n_clusters=3。
3.3 结果分析
3.3.1 配件序列聚类结果分析
本文基于ADI和CV2这2个指标对75条配件序列进行层次聚类。配件序列聚类类别数通过聚类指标轮廓系数确定。轮廓系数是一种用于评估聚类算法性能的指标,结合了内聚度和分离度,可以同时评估样本的簇内差异和簇间差异,其取值为[-1,1],值越接近1表示样本聚类效果越好。轮廓系数随聚类类别数变化如图4所示。
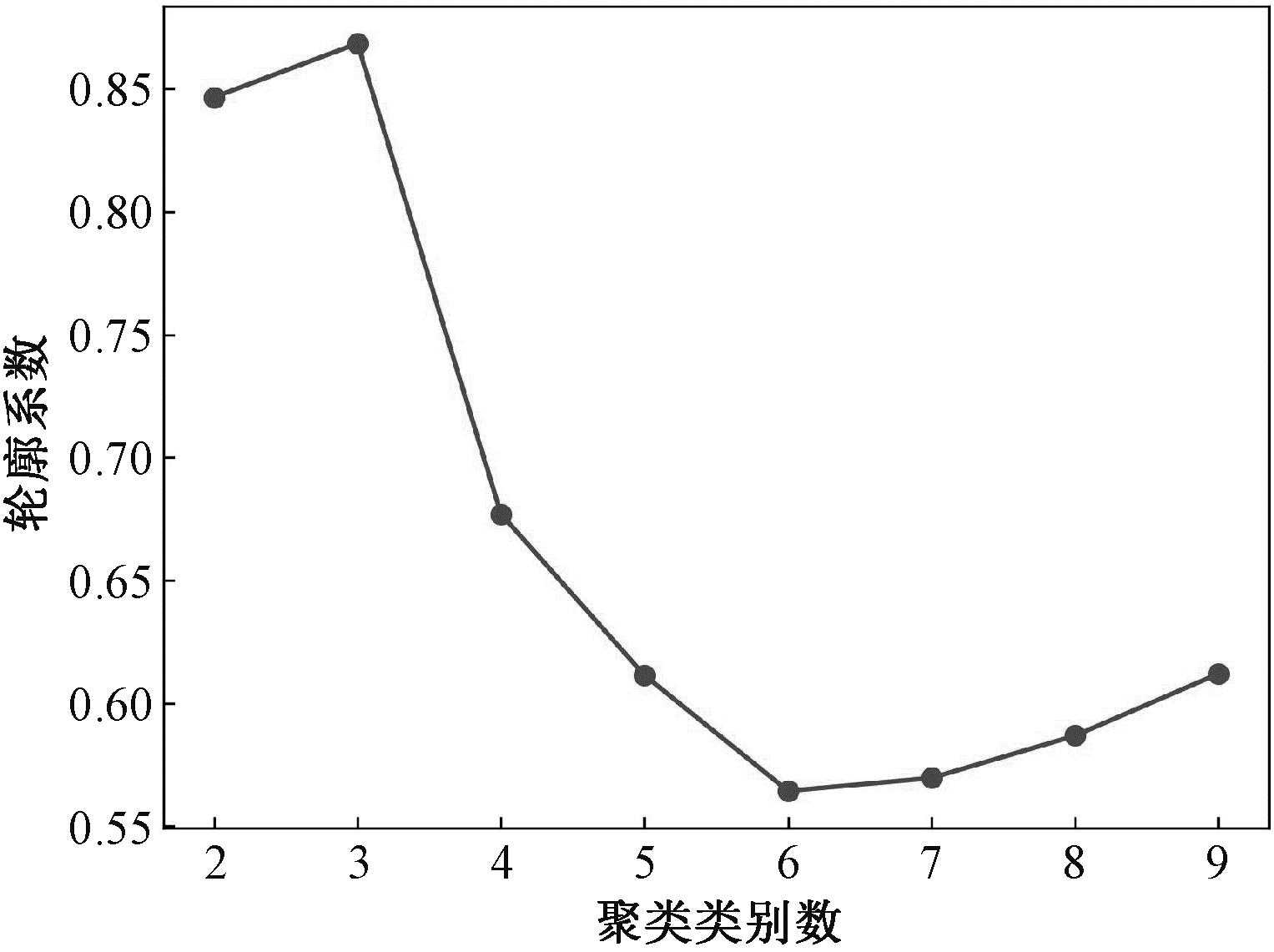
图4 轮廓系数关系曲线
Figure 4 Silhouette coefficient relationship curve
从图4可看出,当聚类类别数为3时,轮廓系数达到最大值,此时对75条配件序列聚类效果最好。此时,配件需求序列的聚类结果如图5所示。
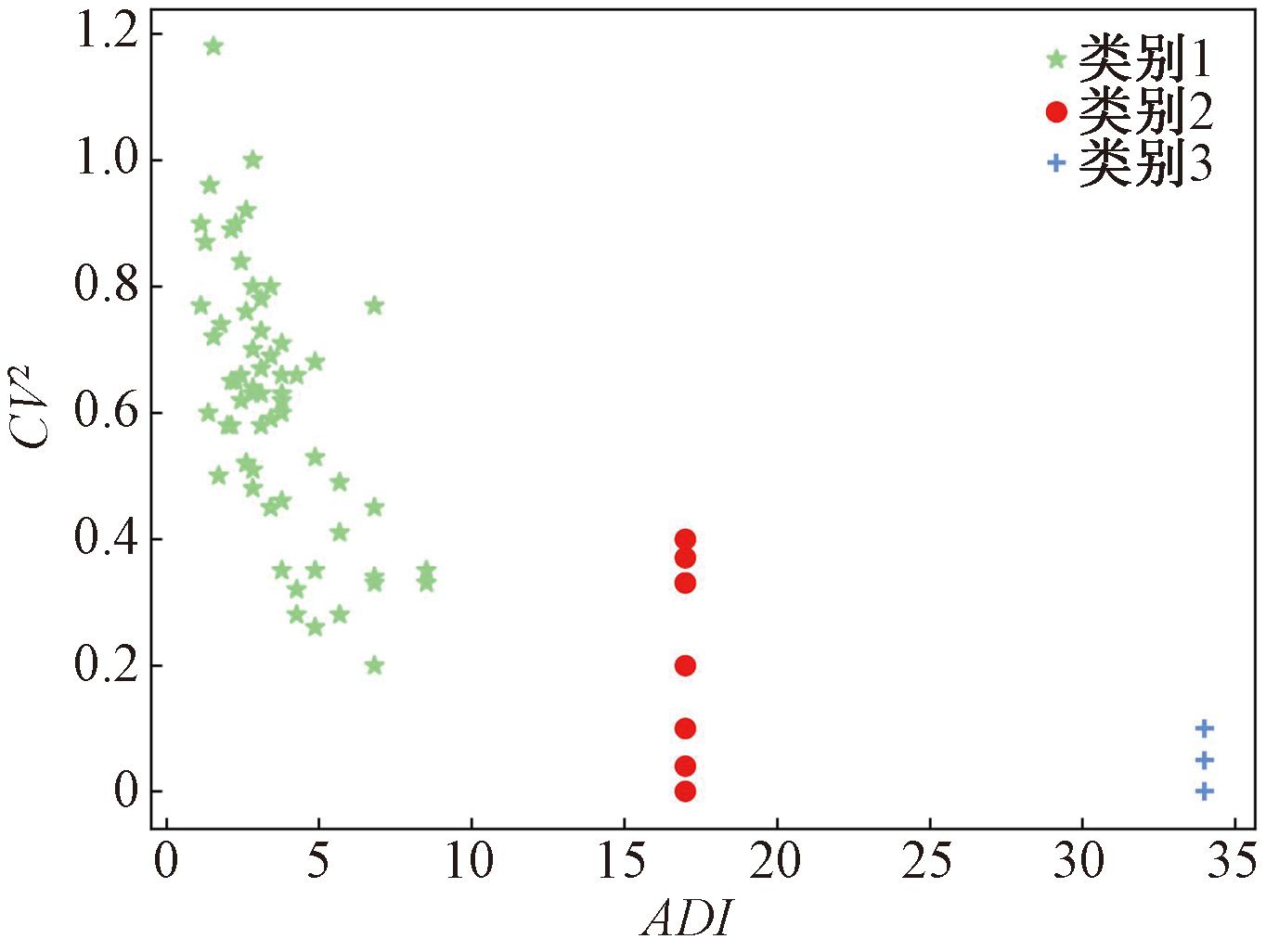
图5 配件需求序列聚类结果
Figure 5 Cluster results of accessory demand sequence
从图5中可以看出,3个类别之间的分布差异明显,同时类内具有较大的相似性。由于ADI指标可反映配件序列需求的间歇度,CV2反映需求量的波动性,可以发现:类别1中配件序列的波动性很大,间歇度变化不大,类别2、类别3中各配件序列间歇度一致,需求量波动性比较稳定。这表明通过层次聚类,可将间歇性时间序列按照数据分布特点进行有效划分,从而提高了小样本条件下配件需求序列的可预测性。
3.3.2 配件序列张量分解对比
在实际场景下获得的配件序列数据含有不规则噪声,因此,本文首先利用张量分解平滑掉配件序列中异常需求值。图6是对配件编号为400和455序列数据进行张量处理前后的对比。可以发现,经过张量分解后,可在最大限度保留原始配件序列信息的同时,平滑配件序列异常需求值,从而达到降噪的作用。
图6 配件序列张量分解前后对比
Figure 6 Before and after tensor decomposition of accessory sequences
3.3.3 模型结果分析
每条配件序列包含34个月需求量数据,以前33个月需求量数据作为训练,第34个月需求量数据作为测试,共计75条配件,由本文方法得到的预测值、预测区间如图7所示。
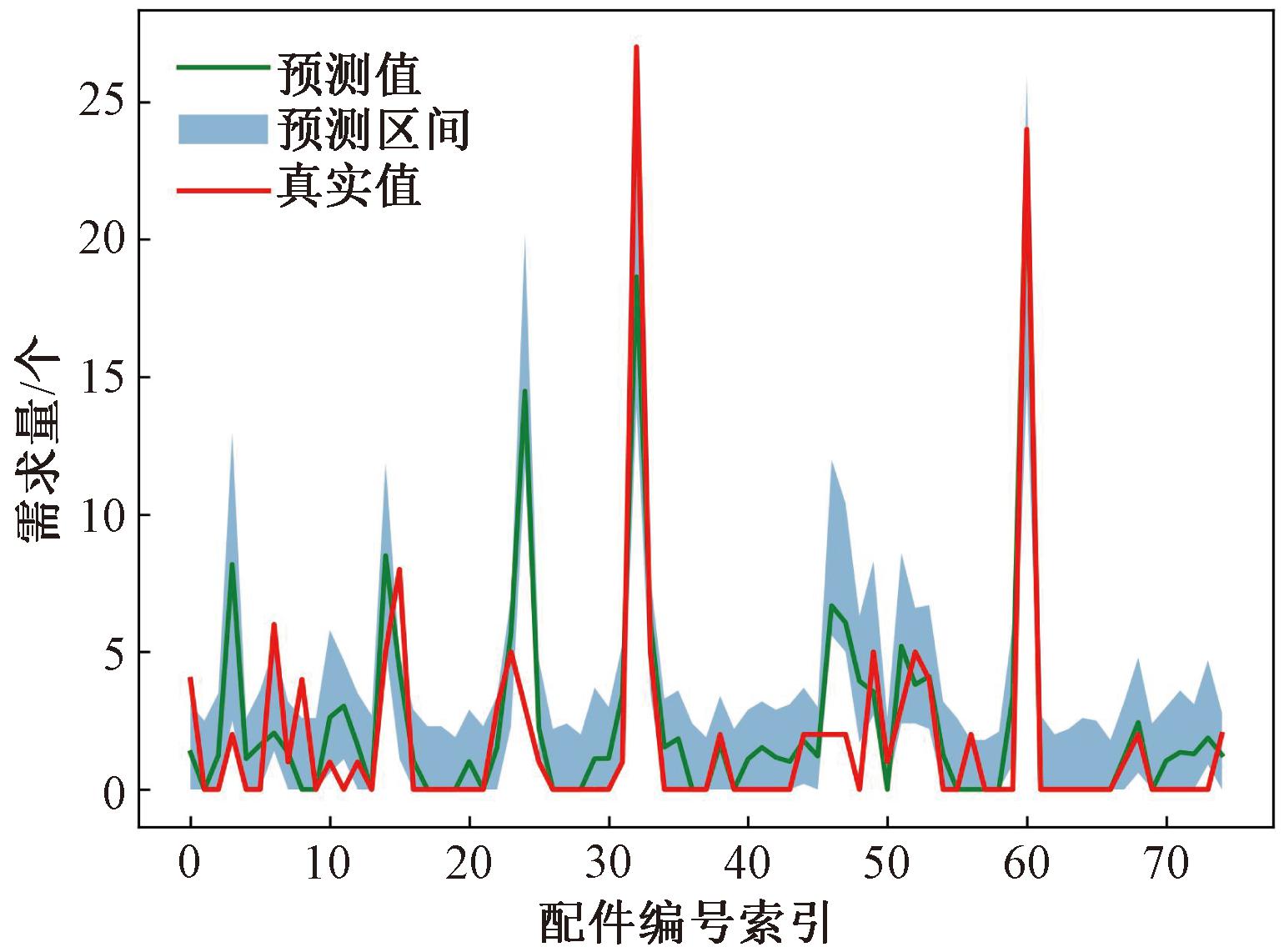
图7 总共75条配件序列的预测结果和预测区间
Figure 7 Prediction results and prediction intervals for all 75 parts
根据企业实际经验,预测配件需求量位于真实值上下浮动30%之内均可认为合理。从实验结果来看,本文预测方法在处理需求量较大的数据时表现敏感,且预测结果非常准确,原因在于张量分解提取了核心张量,对于较密集数据可更有效提取演化趋势信息。同时,当出现预测结果偏差时,本文方法的预测区间可以有效地覆盖真实值。
本文对比了SVR、BHT-ARIMA、ARIMA、Croston、LightGBM、LSTM、Transformer、Informer方法。图8为编号1259、86034、1437的配件序列使用不同方法预测结果对比。根据图8可知,由于编号为1437和86034的配件序列数据零间隔比较稳定,所以经典方法Croston具有相对较好的结果,但是Croston方法在零间隔变化较大的配件序列1259表现弱于其他方法,这是因为Croston只适用于零间隔平稳的间歇性序列。其他的常规方法也类似,多只适用于某类间歇性数据,具有较明显的局限性。BHT-ARIMA提取多条配件序列需求演化信息,在各种类型的配件需求序列上表现都不错,证明利用相似配件序列需求演化信息是一种可行的方法。本文方法引入相似配件序列提取共同需求演化趋势,并使用张量分解平滑配件序列中的异常值,最大限度保留原有特征表示信息,因此在不同分布特点的间歇性序列数据上均有较好表现。
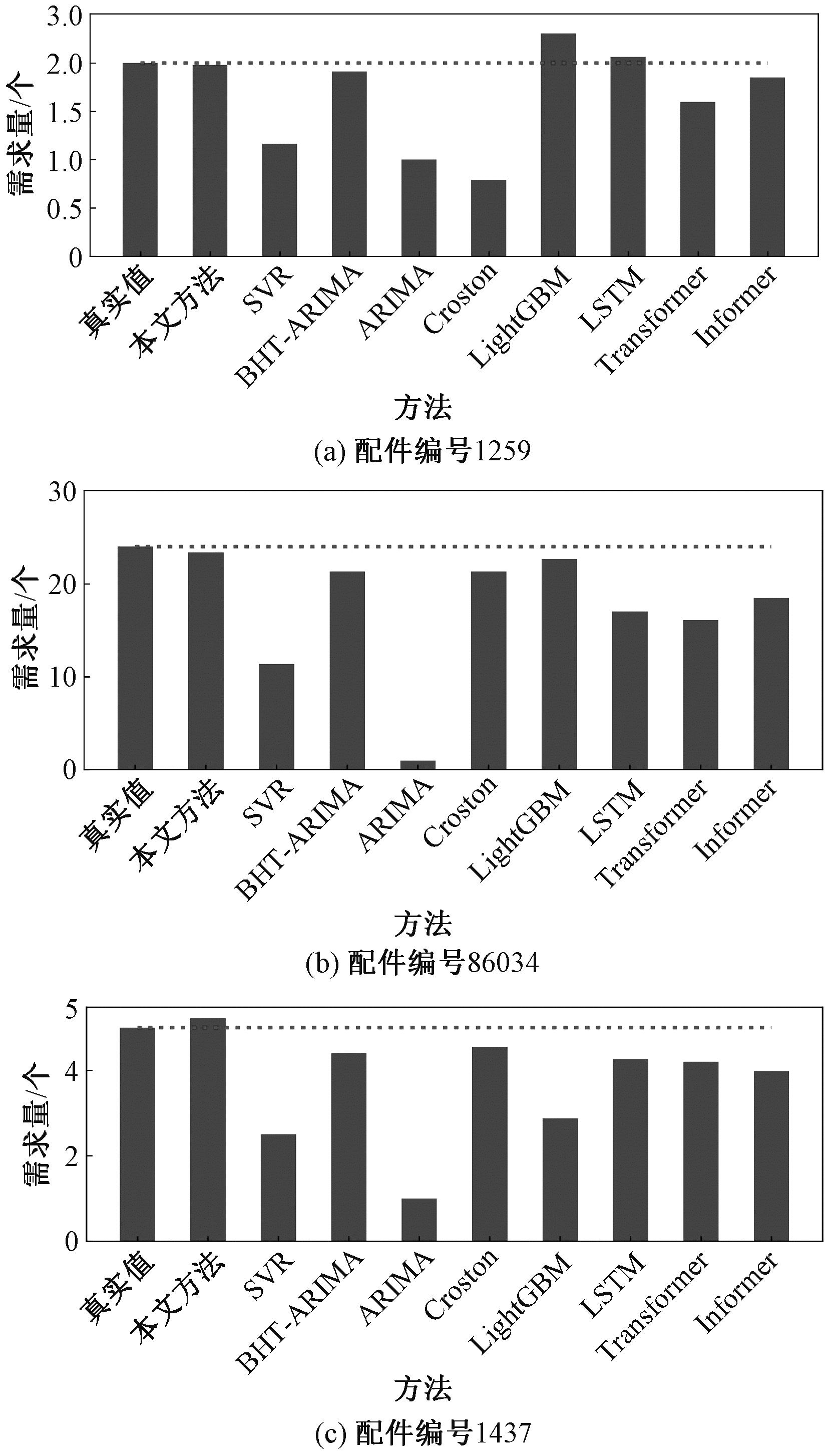
图8 不同预测方法对比图
Figure 8 Comparison of different prediction methods
本文方法增加了弹性预测区间,在点预测失真时,可提供一个较可靠的预测区间作为参考。图9为编号86034、1437、477353配件序列的预测区间图。
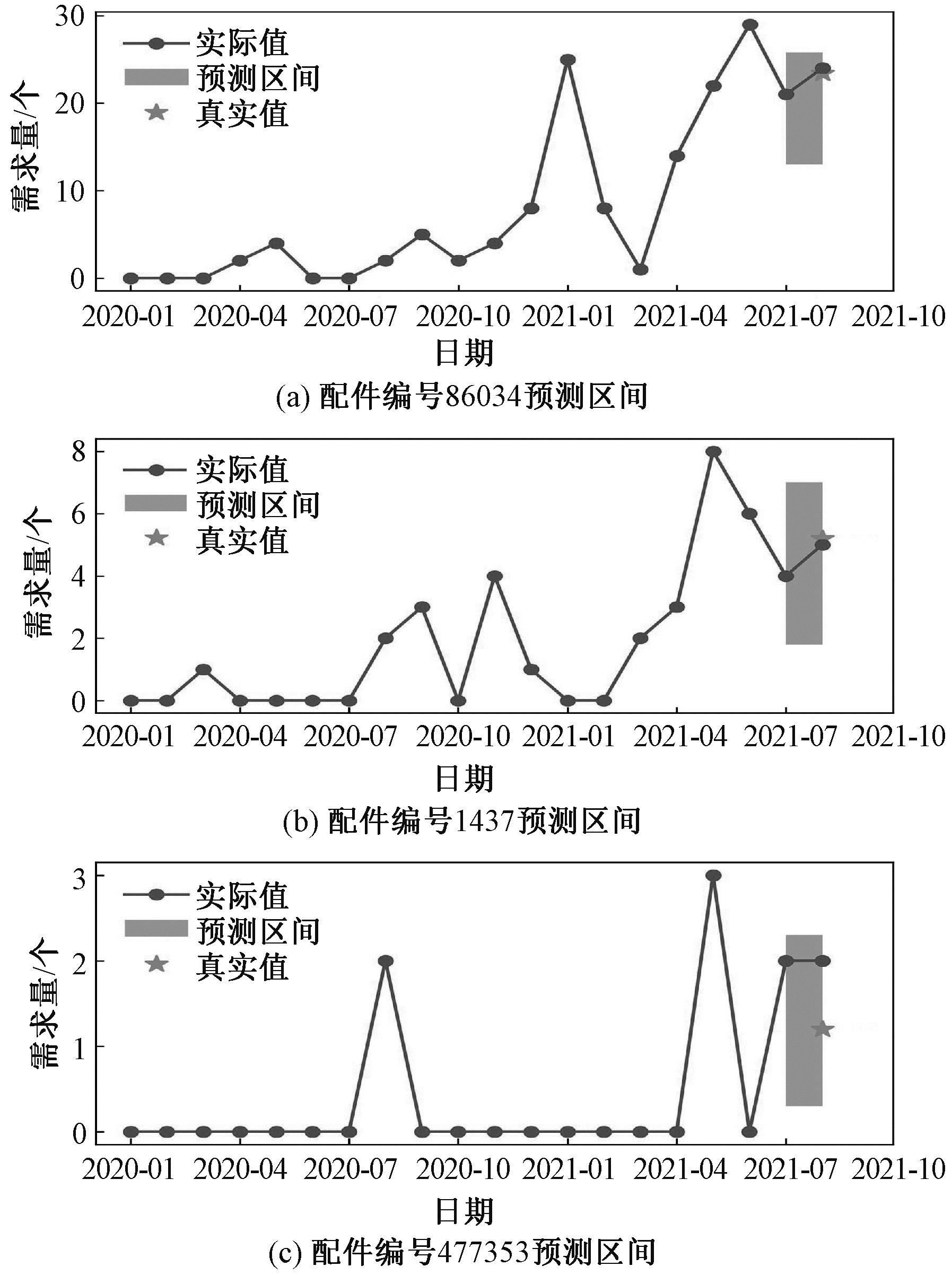
图9 不同配件序列的预测区间
Figure 9 Prediction interval of different parts sequence
根据图9区间预测结果可知,编号86034和1437配件序列的点预测值比较准,预测区间也将真实值覆盖在内;但是编号477353配件序列的需求发生次数较少,点预测模型未能挖掘其演化规律,预测结果偏差大,但同时预测区间的上下限将真实值包含在内,这样企业可以得到配件需求量的参考信息,利用该信息可方便企业进行配件调拨和管理。
表1为本文方法与其他对比方法的预测误差。由表1可知,本文方法间歇性指标RMSSE最低,而MAE略高于SVR,这是因为本文方法考虑了预测区间和点预测,只要是真实值落在预测区间内就说明本文方法预测区间有效,可以为企业决策提供协助,点预测可能与真实值有稍微偏差,导致MAE会略高于SVR。
表1 对比方法的预测误差
Table 1 Prediction error of the comparative methods
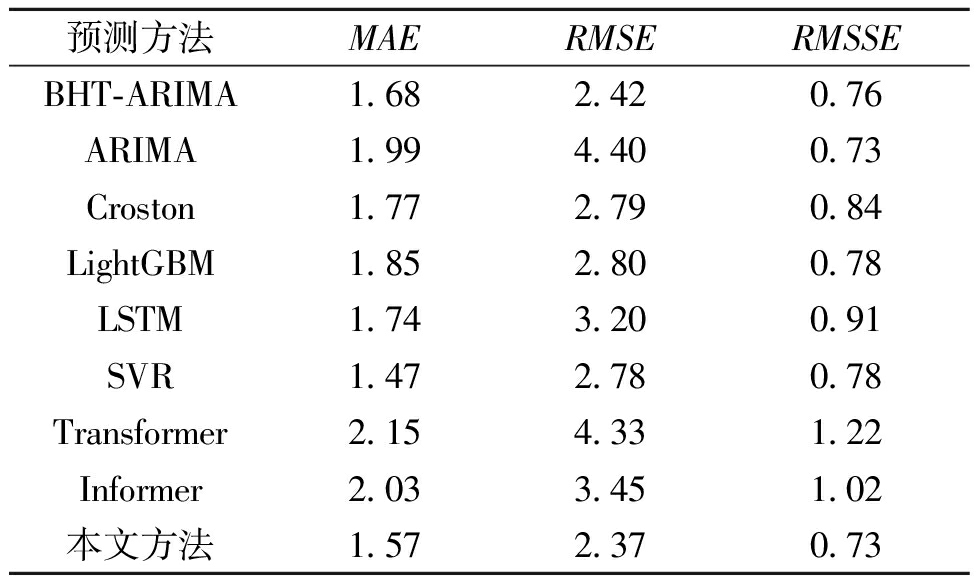
预测方法MAERMSERMSSEBHT-ARIMA1.682.420.76ARIMA1.994.400.73Croston1.772.790.84LightGBM1.852.800.78LSTM1.743.200.91SVR1.472.780.78Transformer2.154.331.22Informer2.033.451.02本文方法1.572.370.73
此外,由图6和表1可以看出,本文方法相较于目前主流深度学习模型的优势之一在于引入了张量分解。利用张量分解,可以从配件需求序列提取核心张量,进而有效平滑配件序列中的异常值,降低其对预测结果的干扰;同时利用核心张量进行LightGBM预测,能够更好地挖掘配件序列中的需求趋势信息,相比于深度模型更适合小样本的间歇性时间序列预测。但引入张量分解后,其分解过程和重构过程会带来额外的计算代价。经计算,LSTM算法平均每轮用时2.87 s,Transformer平均每轮用时7.25 s,Informer平均每轮用时4.48 s,而本文方法仅张量分解操作就用时1 s左右,整体算法用时39.39 s。同时,本文方法需要设定1个区间覆盖率,这也触发了一定的人工依赖性。
3.3.4 消融实验
本文方法包括3个关键部分:层次聚类、张量分解、构建自适应区间算法。为证明本文方法的合理性,构建如下消融实验:①冻结层次聚类;②冻结张量分解;③冻结API算法。消融实验效果如图10所示。
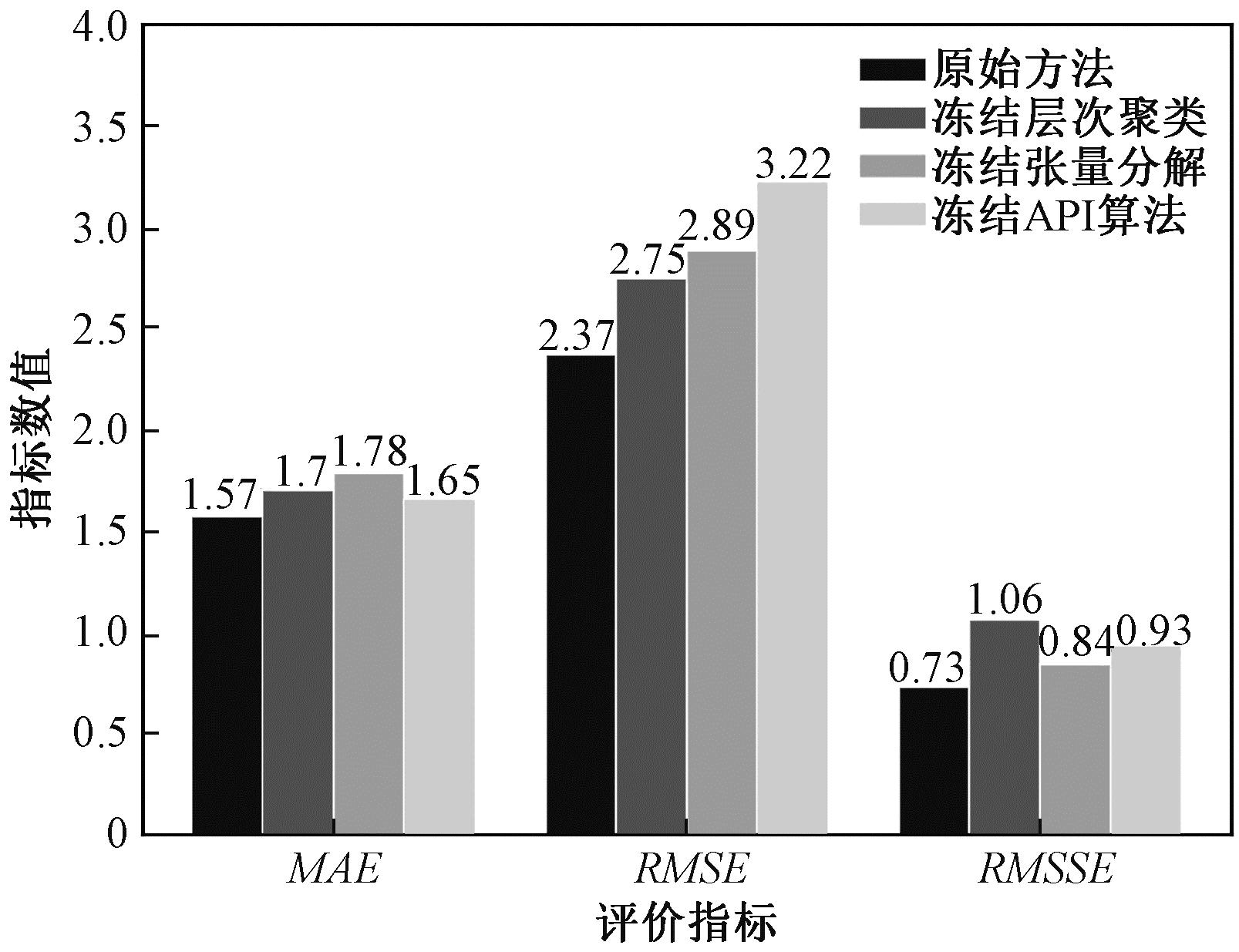
图10 不同冻结策略的预测误差结果
Figure 10 Prediction error results of different freezing strategies
从图10可以看出,冻结层次聚类之后预测误差明显提高,这表明聚合相似序列可以有效提取序列间的公共演化趋势,对预测效果形成良好支撑,这也验证了层次聚类可显著提升小样本条件下间歇性时间序列的可预测性。冻结张量分解后,预测效果变差,这表明高质量的特征表示以及对序列中异常值的处理发挥了重要作用。需要说明的是,冻结了API算法后,本文方法不再能提供区间预测结果,只能拿点预测值进行对比。可以看出,冻结API算法后的点预测效果仍然出现了下滑。上述3个算法模块旨在解决目前传统的间歇性时间序列预测方法存在的典型问题,实验结果证明了3个模块的设计思路具有合理性和有效性。
4 结论
本文针对间歇性配件序列样本少、需求波动大等问题,提出了一种基于张量表示的间歇性时间序列自适应区间预测算法。该方法可有效利用相似序列的公共演化趋势,提供具有容错性的区间预测结果。
(1)利用多条配件序列进行联合预测,有利于学习核心需求演化趋势,减少序列之间的噪声和波动性的影响,提高小样本数据下模型的预测精度。
(2)张量分解的引入可有效平滑间歇性序列中的异常值,降低了异常需求对模型的负面影响,提升了模型预测的鲁棒性和稳定性。
(3)本文所提的区间预测算法API在点预测值的基础上提供了一个可靠的预测区间,一定程度上克服了传统方法对间歇性序列预测结果的不确定性。
[1] BAO Y K, WANG W, ZOU H. SVR-based method forecasting intermittent demand for service parts inventories[C]∥ International Workshop on Rough Sets,Fuzzy Sets,Data Mining,and Granular Computing. Cham:Springer,2005:604-613.
[2] FU G Q, ZHENG Y, ZHOU L F, et al. Look-ahead prediction of spindle thermal errors with on-machine measurement and the cubic exponential smoothing-unscented Kalman filtering-based temperature prediction model of the machine tools[J]. Measurement, 2023, 210: 112536.
[3] 贾茹宾, 高金峰. 基于ARIMA模型的变压器油中溶解气体含量时间序列预测方法[J]. 郑州大学学报(工学版), 2020, 41(2): 67-72.
JIA R B, GAO J F. Time series prediction method of dissolved gas content in transformer oil based on ARIMA model[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(2): 67-72.
[4] KARMY J P, MALDONADO S. Hierarchical time series forecasting via support vector regression in the European travel retail industry[J]. Expert Systems with Applications, 2019, 137: 59-73.
[5] VAN STEENBERGEN R M, MES M R K. Forecasting demand profiles of new products[J]. Decision Support Systems, 2020, 139: 113401.
[6] SUENAGA D, TAKASE Y, ABE T, et al. Prediction accuracy of Random Forest, XGBoost, LightGBM, and artificial neural network for shear resistance of post-installed anchors[J].Structures,2023,50:1252-1263.
[7] CAO D D, CHAN M, NG S. Modeling and forecasting of nanoFeCu treated sewage quality using recurrent neural network (RNN)[J]. Computation, 2023, 11(2): 39.
[8] ABBASIMEHR H, SHABANI M, YOUSEFI M. An optimized model using LSTM network for demand forecasting[J]. Computers &Industrial Engineering, 2020, 143: 106435.
[9] CROSTON J D. Forecasting and stock control for intermittent demands[J]. Journal of the Operational Research Society, 1972, 23(3): 289-303.
[10] SYNTETOS A A, BOYLAN J E. The accuracy of intermittent demand estimates[J]. International Journal of Forecasting, 2005, 21(2): 303-314.
[11] GUTIERREZ R S, SOLIS A O, MUKHOPADHYAY S. Lumpy demand forecasting using neural networks[J]. International Journal of Production Economics, 2008, 111(2): 409-420.
[12] 张瑞. 不常用备件需求预测模型与方法研究[D]. 武汉: 华中科技大学, 2011.
ZHANG R. Research on forecasting models and methods of rarely used spare parts′ demand[D]. Wuhan: Huazhong University of Science and Technology, 2011.
[13] SHI Q Q, YIN J M, CAI J J, et al. Block Hankel tensor ARIMA for multiple short time series forecasting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 5758-5766.
[14] BOUKHTOUTA A, JENTSCH P. Support vector machine for demand forecasting of Canadian armed forces spare parts[C]∥2018 6th International Symposium on Computational and Business Intelligence (ISCBI). Piscataway: IEEE, 2018: 59-64.
[15] YOKOTA T, EREM B, GULER S, et al. Missing slice recovery for tensors using a low-rank model in embedded space[C]∥2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2018: 8251-8259.
[16] 周晓艳, 唐涛, 张思乾, 等. 多角度SAR图像非目标遮挡缺失信息重构[J]. 信号处理, 2021, 37(9): 1569-1580.
ZHOU X Y, TANG T, ZHANG S Q, et al. Missing information reconstruction for multi-aspect SAR image occlusion[J]. Journal of Signal Processing, 2021, 37(9): 1569-1580.
[17] CHENG J, DEKKERS J C M, FERNANDO R L. Cross validation of best linear unbiased predictions of breeding values using an efficient leave-one-out strategy[J]. Journal of Animal Science, 2020, 98(S4): 10-11.