现实世界中,事物之间的关系极其复杂,而复杂网络可以恰当描述此类关系。根据实体类型,复杂网络可被分为社交分析网络[1-3]、蛋白质分子网络[4]、通信网络[5]等。分析预测网络中未连边节点之间的关系可促进各个相关领域的快速发展,上述预测节点关系的过程即为链路预测[6](link prediction, LP)。
现如今,链路预测的研究方法有基于启发信息的链路预测方法[7]、基于机器学习的链路预测方法、基于网络嵌入的链路预测方法等。
基于启发信息的链路预测方法中,通常会使用CN(common neighbors)指标[8]、RA(resource allocation)指标[8]、AA(adamic-adar)指标[8]、Jaccard指标[9]、Sorenson指标[10]、Salton指标[8] 、LP(local paths)指标[11]、Katz指标[12]、LHN-Ⅱ指标[13] 、cos+指标[14]、SRW指标[11]等。基于启发信息的链路预测方法对于节点间是否有边存在着很大的假设性,倘若该假设错误,便会导致失败[15]。同时,该类方法对网络结构信息的表示较差,并且多数链接假设均只适用于社交网络,在非社交网络中预测性能不佳。
基于机器学习的链路预测方法中,通常使用的分类方法有支持向量机(support vector machine, SVM)、决策树(decision tree, DT)等。廖亮等[16]提出了一种基于SVM的机会网络链路预测,考虑了空间相似性和时间特征。杨妮亚等[17]提出了一种基于聚类和决策树的链路预测(CDTLinks),以网络中2种类型对象相互作为对象的方法去获得对象的特征表示,并且分别进行聚类,同时对双类型异质网络构建决策树,由信息增益作为选取不同分支的标准,结合上述2种方法判断不同类型节点间的连接关系,最后验证CDTLinks方法的有效性。基于机器学习的链路预测方法尽管有不错的效果,但是会占用大量的存储空间,且计算时间长。
基于网络嵌入的链路预测方法中会使用的技术有随机游走、矩阵分解、图卷积神经网络[18](graph convolutional neural network, GCN)等。Lei等[19]通过GCN、LSTM、GAN提取加权网络中的非线性特征,同时通过GCN提取各个快照的局部特征,通过LSTM提取网络的演化特征,进而使得该算法链路预测性能优异。首先,GCN将网络结构的边信息和节点信息输入到输入层中;其次,通过输出层输出的预测标签结果与网络的节点标签计算损失;最后,进行反向传播和梯度更新。在不断的迭代训练过程中得到最优模型。对于有监督任务,基于GCN的链路预测方法虽然表现出优异的性能,但是会存在耗费时间、资源等问题。而现实生活中存在大量的无标签网络,当使用基于GCN的链路预测方法进行处理时效果较差,针对上述问题,本文提出了一种近似图神经网络框架的无监督链路预测算法(an unsupervised link prediction algorithm based on an approximate graph neural network framework, ALIP)。
本文创新点有以下3点。
(1)ALIP算法模拟了GCN训练的过程,对比GCN的输入层,该算法的输入层有效保证了网络结构特征的完整性。
(2)使用矩阵分解替代GCN的隐藏层,模拟GCN中的正向传播。
(3)借鉴深度图神经网络(DeeperGCN)[20-21]中的恒等映射思想和NEU算法[22]中的高阶近邻的思想,实现算法优化问题,避免网络特征建模不充分的问题。
1 GCN算法框架
图结构不具备平移不变性,图中节点的周围结构通常不相同,对于该类数据的处理,传统神经网络框架如卷积神经网络(convolutional neural network, CNN)、循环神经网络(recurrent neural network, RNN)则会失效,无法获得较优的效果。目前常用的方法有DeepWalk、node2vec、GNN、GCN等,其中GCN与CNN均为特征提取器,只是所研究的对象不同。通过GCN对图结构数据进行特征提取所得到的特征可用于众多下游任务,如边预测、节点分类等。GCN总体框架图如图1所示。
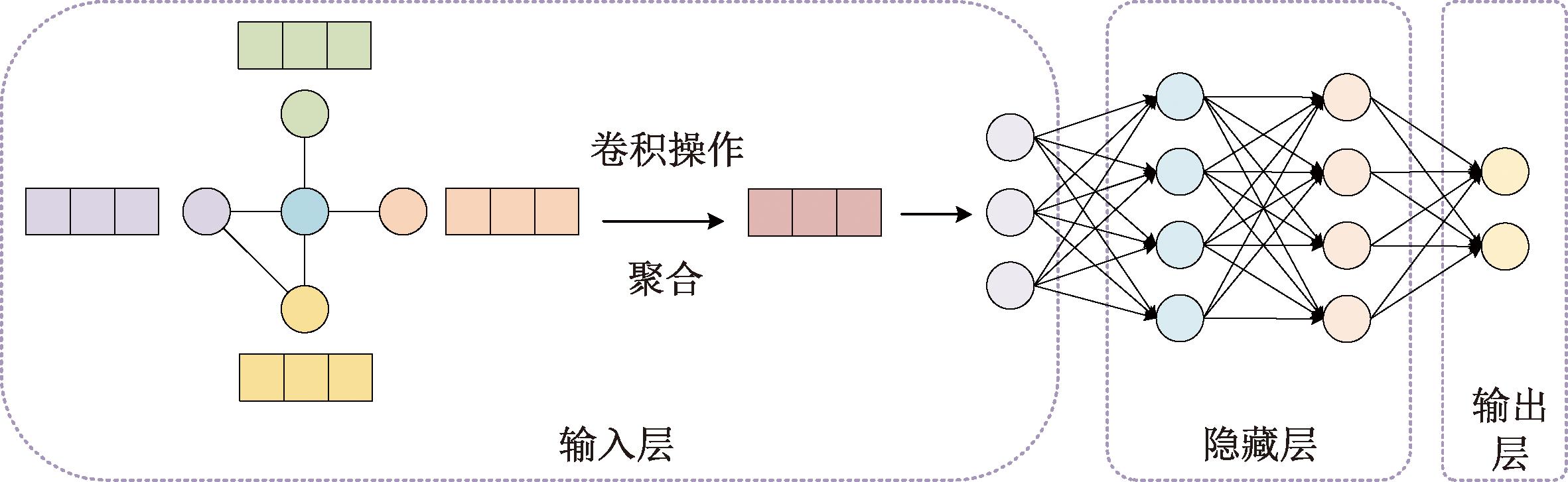
图1 GCN框架图
Figure 1 GCN framework diagram
由图1可知,GCN由三部分组成,分别为输入层、隐藏层、输出层。在输入层中,图结构数据中每个节点的节点特征均需融合自身特征信息以及其邻接节点的特征信息,其中节点自身特征为矩阵X,包含网络结构信息的邻接矩阵为A。在图1中,GCN用平均池化的方法模拟卷积操作,即将节点特征向量进行平均操作,然后将最终计算得到的平均值输入到隐藏层中进行计算。在隐藏层中,层与层之间的计算过程为
(1)
式中:σ(·)为非线性激活函数;![]() 为含有自连接的邻接矩阵,是网络节点之间的关系特征矩阵A与单位矩阵I相加的结果;
为含有自连接的邻接矩阵,是网络节点之间的关系特征矩阵A与单位矩阵I相加的结果;![]() 为
为![]() 对应的度矩阵;H为每一层的节点特征。
对应的度矩阵;H为每一层的节点特征。
2 ALIP算法框架
图结构通常是不规则的,图神经网络的处理对象为图结构数据,GCN是图神经网络的代表算法。现有的研究结果表明,图神经网络使用半监督机制,在链路预测、节点分类和推荐系统等机器学习任务中表现非常好。对于无标签网络,使用GCN的建模机制进行链路预测时效果较差,但是现实生活中,大多图结构数据无标签信息,因此,本文提出了ALIP算法。
ALIP算法模拟两层的GCN框架,使用矩阵分解替代GCN中的正向传播,使用高阶近邻和恒等映射的思想替代GCN中的反向传播,起到更新参数的作用。ALIP算法框架如图2所示。
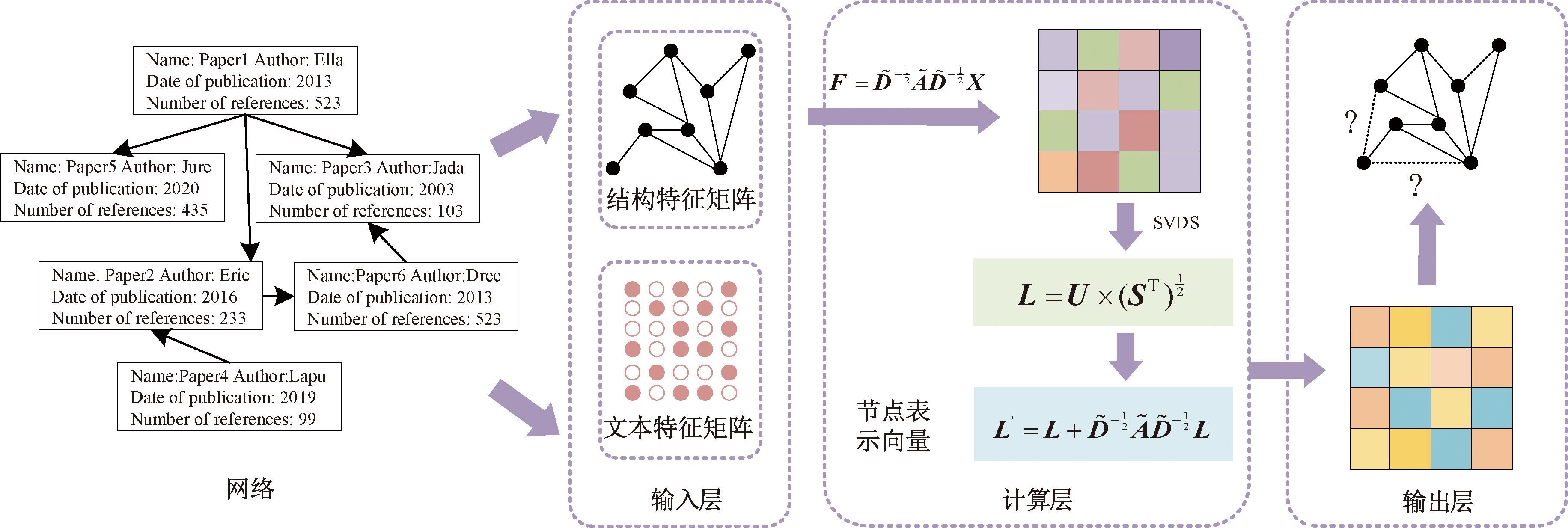
图2 ALIP算法框架
Figure 2 ALIP algorithm framework
由图2可知,ALIP算法分输入层、计算层、输出层。本文使用AUC指标评测ALIP算法性能,以此证明该算法的有效性和可行性。
(1)输入层:输入网络的结构信息和节点属性。ALIP算法输入层参照了GCN的输入层,将关系特征矩阵A和节点属性X输入到算法中,即将式(1)中的HW神经元计算过程替换为X,则提出的输入层的特征为
(2)
式中:A为网络结构的邻接矩阵;![]() 为含有自连接的邻接矩阵,保留了网络结构的自身特征;
为含有自连接的邻接矩阵,保留了网络结构的自身特征;![]() 为含有自连接的度矩阵,是
为含有自连接的度矩阵,是![]() 对应的度矩阵。由于ALIP算法不进行参数更新及多次训练拟合,故不用学习神经元之间的权重矩阵W,也不用进行激活操作。综上,可知ALIP算法的输入本质上是借鉴了GCN结合图特征及节点自身特征融合的思想,来融合结构信息和节点属性信息。上述A与
对应的度矩阵。由于ALIP算法不进行参数更新及多次训练拟合,故不用学习神经元之间的权重矩阵W,也不用进行激活操作。综上,可知ALIP算法的输入本质上是借鉴了GCN结合图特征及节点自身特征融合的思想,来融合结构信息和节点属性信息。上述A与![]() 的关系为
的关系为
(3)
式中:I为单位矩阵。
(2)计算层:对输入层所输出的向量矩阵进行矩阵分解和向量优化。浅层神经网络不断被使用,已经不能够较好地解决现有问题,深层神经网络方法使得问题能够得到较优解决,那么在实际生活中,深层神经网络的训练会遇到梯度弥散、梯度爆炸、网络退化等问题。梯度弥散和梯度爆炸的问题已经通过标准初始化和中间层正则化等优化方法得以有效控制。网络退化问题反映了深层网络不易优化的问题,因此,现有的工作主要是引入深层残差网络,融入恒等映射,从而将模型的深度加深,防止网络退化。残差单元连接方式如图3所示。

图3 跳层连接的残差单元
Figure 3 Residual units connected by jumpers
图3中跳层连接的残差单元为
F′(x)=F(x)+x。
(4)
式中:x为输入的原始特征;F(x)为残差函数,定义了原始神经结构的输入x,也是一个递归的过程;F′(x)为跳层连接的残差单元的输出。
由图3可知,残差神经网络主要是在不同层之间插入原始的特征输入,即进行了恒等映射,从而避免随着模型越来越深而出现网络退化的问题。
在网络表示学习领域,为了解决低阶网络不能建模网络节点之间的高阶关系的问题,研究人员提出了高阶近邻的方法,一类方法是在建模过程中加入节点之间的高阶关系;另外一类方式是将低阶模型学习得到的节点表示向量转化为高阶表示向量。其过程为
(5)
式中:![]() 为归一化邻接矩阵;R为低阶的网络表示向量;C为上下文节点的表示向量。通过式(5)可以将低阶向量转化为高阶向量,从而实现表示向量的优化过程。
为归一化邻接矩阵;R为低阶的网络表示向量;C为上下文节点的表示向量。通过式(5)可以将低阶向量转化为高阶向量,从而实现表示向量的优化过程。
本文将残差网络中的恒等映射思想和高阶网络表示学习中的高阶近邻思想引入ALIP算法中。
首先,将输入层输出的结构特征矩阵F使用矩阵分解方法进行分解,该方法替代GCN中隐藏层的正向传播过程,即将其分解为3个矩阵相乘的形式:
F=U×S×V。
(6)
式中:矩阵U代表结构特征矩阵F对应的奇异向量;矩阵S代表结构特征矩阵F对应的对角矩阵,矩阵S中的对角元素为结构特征矩阵F的奇异值。
其次,将矩阵U和矩阵S进行结合计算,得到网络中节点的表示向量L:
(7)
最后,为了有效防止网络原有特征丢失,将节点表示向量L和原始的网络特征矩阵进行结合,结合式(4)、(5)提出式(8)。式(8)融合了残差网络中的恒等映射和高阶网络表示学习中的高阶向量转化的思想,使得最终节点表示向量得到了优化。该步骤替代GCN中反向传播的参数更新过程,具体形式为
(8)
式中:L′代表计算层的输出。上述过程是一种无监督优化过程,其有别于GCN中的反向传播过程。本文ALIP算法向量优化计算量的增加来自于式(8),向量L 的计算复杂度为O(|v|),其中v为网络节点个数,由于![]() 的计算复杂度为O(|v|3),故
的计算复杂度为O(|v|3),故![]() 的计算复杂度为O(|v|4),综上L′的计算复杂度为O(|v|4)。
的计算复杂度为O(|v|4),综上L′的计算复杂度为O(|v|4)。
(3)输出层:根据计算层输出的矩阵,计算节点之间的相似度。根据计算层所输出的向量L′,计算节点对之间对应的相似度矩阵Wi,j,其具体过程为
Wi,j=Ei×Ej。
(9)
式中:Ei代表向量L′中的第i行向量;Ej代表向量L′中的第j行向量。
在评测链路预测ALIP算法的过程中,基于计算所得到的相似度矩阵Wi,j,使用链路预测度量指标AUC评测本文所提链路预测算法的性能。本文算法步骤如下。
算法1 ALIP算法。
输入:网络G的边集合; 训练比率T; 向量长度K;
输出:AUC值。
① 获取网络G的边集合;
② 计算出网络G节点数量|v|;
③ 将网络G分为训练集和测试集,[训练集,测试集]←网络G;
④ 初始化邻接矩阵A和文本矩阵X;
⑤ 初始化特征矩阵![]()
⑥ 分解矩阵F为[U, S, V]=SVDS(F, k);
⑦ 获取表示向量![]()
⑧ 优化矩阵![]()
⑨ 计算相似度矩阵Wi,j=Ei×Ej;
⑩ 使用测试集计算ALIP算法的AUC值,AUC←训练集。
3 实验结果与分析
3.1 实验数据
本文使用Citeseer数据集、DBLP数据集、Cora数据集对ALIP算法进行验证,具体信息如表1所示。
表1 数据集描述
Table 1 Datasets description

数据集节点数边数平均度密度平均聚类系数Citeseer3 3124 7322.8570.0010.080DBLP3 11939 51621.0700.0050.221Cora2 7085 4294.0100.0010.130
Citeseer数据集是引文网络,其中节点代表一篇论文,边代表论文相互之间的引用关系。DBLP数据集是合作网络,其中节点代表作者,边代表作者之间的合作关系。Cora数据集是引文网络,共存在5 429次引用。
由表1可知,3个数据集节点数的差异并不明显,但是边的数量却有很大的差异,其中DBLP数据集的边数最多,会导致DBLP数据集的平均度、密度以及平均聚类系数均比Citeseer数据集和Cora数据集高出很多,进一步可推断DBLP网络属于稠密网络,Citeseer网络和Cora网络属于稀疏网络。
3.2 评价指标
对于ALIP算法的实验性能的评估,选取AUC指标作为评判指标,该指标是根据链路预测算法输出的节点相似度矩阵进行计算的,是链路预测算法中的一个常用指标。整个过程是一个比较测试集中边相似值和不存在边相似值的过程,倘若边相似值大于不存在边的相似值,加1分,倘若二者相等,加0.5分。AUC的值应为0.5~1.0,其值越高,则该算法的精确度越高且性能越好。AUC指标为
(10)
式中:N为独立比较次数;n1为边相似值大于不存在边相似值的次数;n2为边相似值等于不存在边的相似值的次数。
3.3 基准算法
本文选取了现有的23种链路预测算法作为基准算法与ALIP算法进行对比。基准算法涵盖了经典和最新的链路预测算法,如表2所示。
表2 基准算法总结表
Table 2 Benchmark algorithm summary table

算法类别具体算法基于局部信息的链路预测算法CN[8]、Salton[8]、Jaccard[9]、HPI[8]、HDI[8]、LHN-Ⅰ[8]、AA[8]、RA[8]、PA[8]、LNBAA[23]、LNBCN[23]、LNBRA[23]基于路径的链路预测算法LP[11]、Katz[12]、LHN-Ⅱ[13]基于随机游走的链路预测算法ACT[24]、Cos+[14]、LRW11]、SRW[11]基于自洽相似性的链路预测算法TSCN[25]基于网络表示学习的链路预测算法LPMF[26]、TELP[27]、NRLP[28]
3.4 实验结果分析
为了确保算法对比的公平性,训练比率T设置为0.7,0.8,0.9,网络节点表示向量长度为100,并且将ALIP算法运行10次的平均值作为该算法的实验结果,如表3所示。
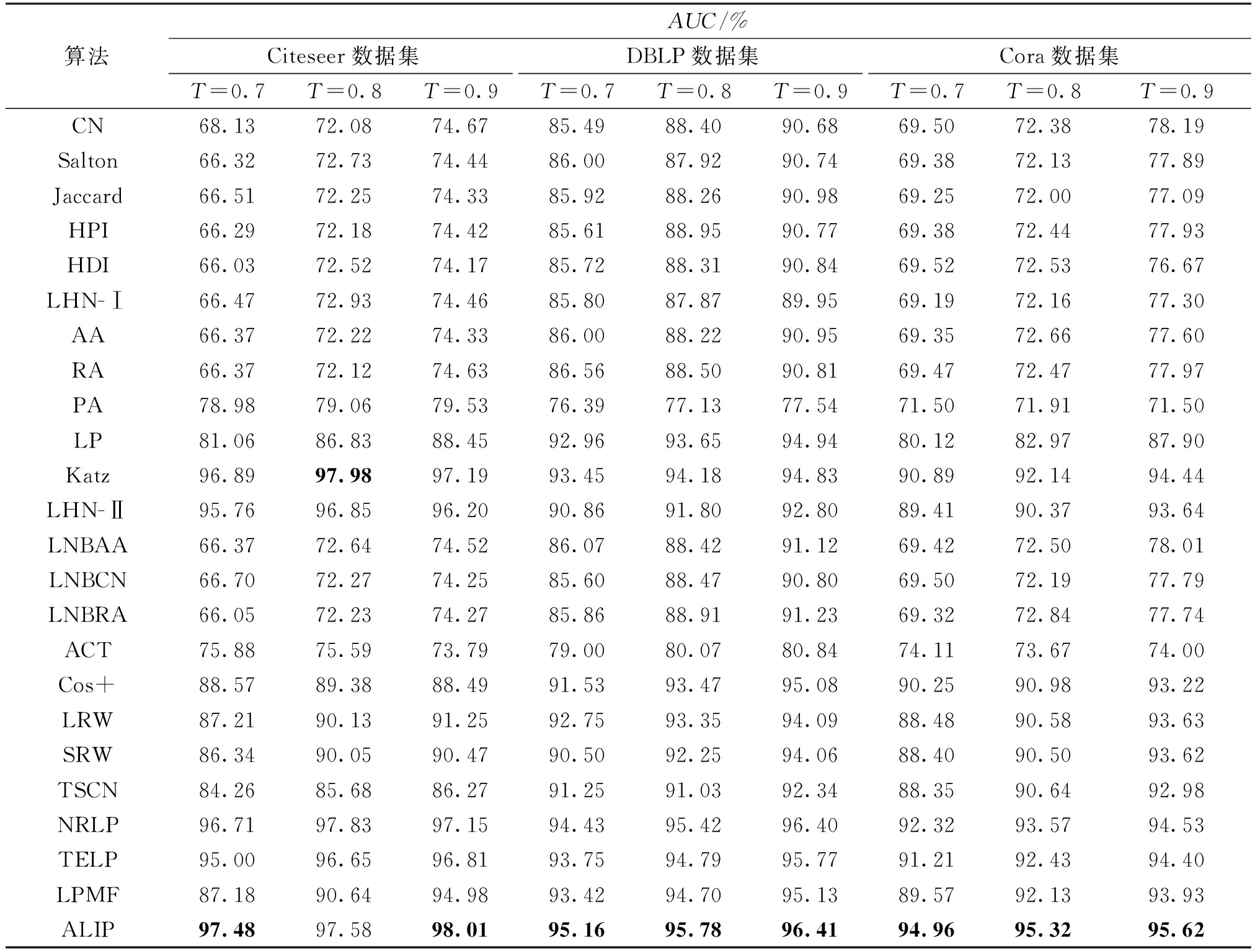
表3 Citesser、DBLP 和Cora数据集上链路预测结果
Table 3 Link prediction results on Citesser, DBLP and Cora datasets
算法AUC/%Citeseer数据集DBLP数据集Cora数据集T=0.7T=0.8T=0.9T=0.7T=0.8T=0.9T=0.7T=0.8T=0.9CN68.1372.0874.6785.4988.4090.6869.5072.3878.19Salton66.3272.7374.4486.0087.9290.7469.3872.1377.89Jaccard66.5172.2574.3385.9288.2690.9869.2572.0077.09HPI66.2972.1874.4285.6188.9590.7769.3872.4477.93HDI66.0372.5274.1785.7288.3190.8469.5272.5376.67LHN-Ⅰ66.4772.9374.4685.8087.8789.9569.1972.1677.30AA66.3772.2274.3386.0088.2290.9569.3572.6677.60RA66.3772.1274.6386.5688.5090.8169.4772.4777.97PA78.9879.0679.5376.3977.1377.5471.5071.9171.50LP81.0686.8388.4592.9693.6594.9480.1282.9787.90Katz96.8997.9897.1993.4594.1894.8390.8992.1494.44LHN-Ⅱ95.7696.8596.2090.8691.8092.8089.4190.3793.64LNBAA66.3772.6474.5286.0788.4291.1269.4272.5078.01LNBCN66.7072.2774.2585.6088.4790.8069.5072.1977.79LNBRA66.0572.2374.2785.8688.9191.2369.3272.8477.74ACT75.8875.5973.7979.0080.0780.8474.1173.6774.00Cos+88.5789.3888.4991.5393.4795.0890.2590.9893.22LRW87.2190.1391.2592.7593.3594.0988.4890.5893.63SRW86.3490.0590.4790.5092.2594.0688.4090.5093.62TSCN84.2685.6886.2791.2591.0392.3488.3590.6492.98NRLP96.7197.8397.1594.4395.4296.4092.3293.5794.53TELP95.0096.6596.8193.7594.7995.7791.2192.4394.40LPMF87.1890.6494.9893.4294.7095.1389.5792.1393.93ALIP97.4897.5898.0195.1695.7896.4194.9695.3295.62
由表3可知,在Citeseer、DBLP、Cora数据集上,仅有Katz、LHN-Ⅱ、TELP、NRLP算法的AUC均高于90%,其中Katz算法和LHN-Ⅱ算法属于基于路径的链路预测,TELP算法和NRLP算法属于基于矩阵分解的链路预测,可见这两大类的链路预测方法性能较为优异,尤其是Katz算法和NRLP算法,在Citeseer数据集上的准确率达到了97%。在Citeseer数据集上,当T=0.8时,Katz算法的AUC略高于ALIP算法,除此之外,ALIP算法的AUC取得最高值,其最高值为98.01%。而在DBLP数据集和Cora数据集上,ALIP算法效果最好。
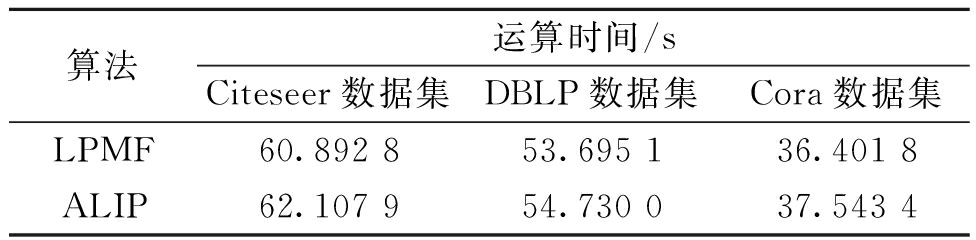
从算法复杂度的角度分析ALIP算法,只需将其与建模机制相同的LPMF进行对比,本次实验控制训练比率为0.7,节点表示向量长度为100,实验结果如表4所示。由表4可知,ALIP算法时间比LPMF算法时间多1~1.5 s,但ALIP算法相对于LPMF算法的性能有1.08百分点至10.3百分点的提升。综合考虑,在相同建模机制的算法下,ALIP算法体现出一定的优越性。
表4 ALIP与LPMF的运算时间对比
Table 4 Comparison of computation time between ALIP and LPMF
算法运算时间/sCiteseer数据集DBLP数据集Cora数据集LPMF60.892 853.695 136.401 8ALIP62.107 954.730 037.543 4
综上所述,ALIP算法可充分挖掘到网络的有效特征,同时能够保证网络特征相关信息的完整性,并且性能优异。
3.5 消融实验
为了证明输入层模块、矩阵分解模块以及高阶向量优化模块可提高节点之间链接的可能性,本文在Citeseer数据集、DBLP数据集、Cora数据集上进行消融实验,设置训练比率为0.7,0.8,0.9,表示向量长度为100,实验结果如图4所示。
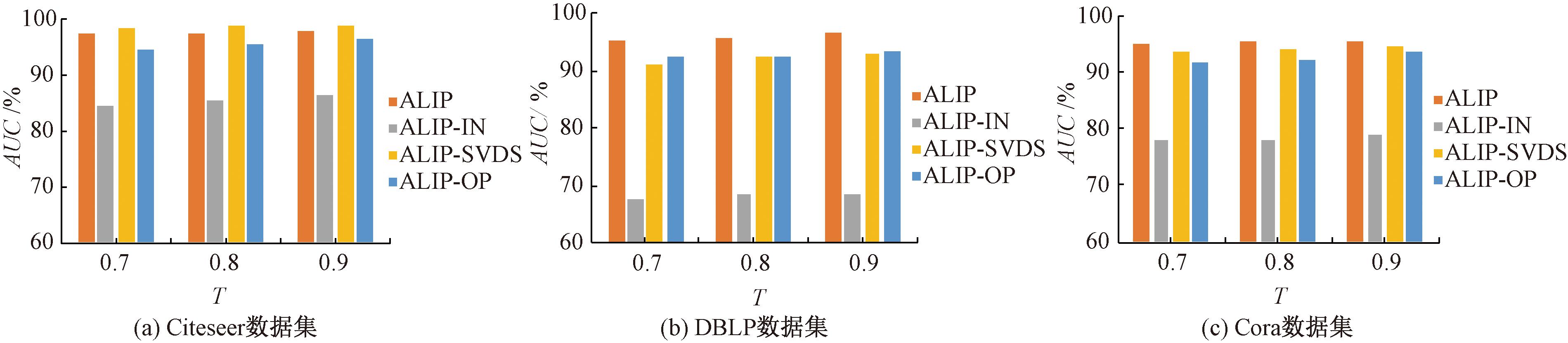
图4 消融实验结果
Figure 4 Ablation experiment results
在图4中,ALIP-IN算法为消融输入层模块的算法;ALIP-SVDS算法为消融矩阵分解的算法;ALIP-OP算法为消融向量优化的算法。
由图4可知,①在Citeseer数据集、DBLP数据集和Cora数据集上,ALIP算法AUC均高于ALIP-IN算法,并且有11.45百分点至28.18百分点的提升;②相较于ALIP-SVDS算法,ALIP算法AUC均高于ALIP-SVDS算法(Citeseer数据集除外),并且有0.9百分点至4.08百分点的提升;③在Citeseer数据集、DBLP数据集和Cora数据集上,ALIP算法AUC均高于ALIP-OP算法,并且有1.7百分点至3.42百分点的提升。综上所述,可有效证明在算法中加入输入层模块、矩阵分解模块以及向量优化模块可使得节点之间的链路预测能力增加,对ALIP算法有一定的帮助,进一步验证ALIP算法的可行性。
3.6 调参分析
在本文调参实验中,设置了训练比率T和向量长度K,T=0.70,0.75,0.80,0.85,0.90,0.95,K=25,50,100,150,200,300。调参分析结果如图5所示。
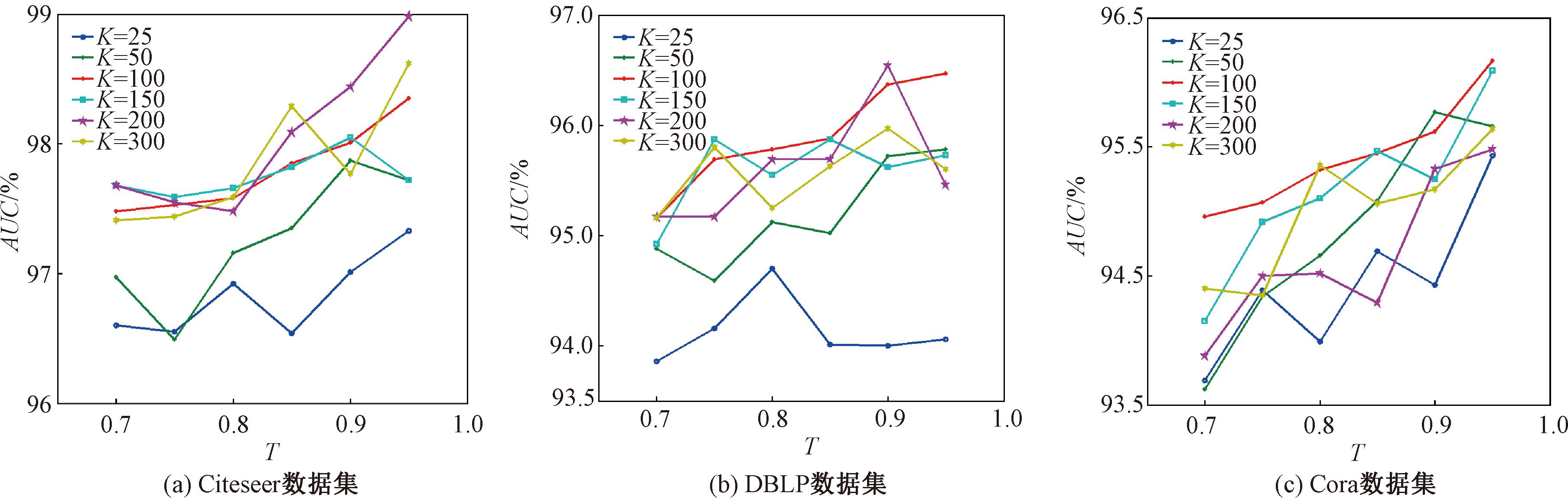
图5 调参分析结果
Figure 5 Tuning parameters analysis results
由图5可知,2个参数对链路预测算法性能均存在影响。当向量长度K=200、训练比率T=0.95时,在Citeseer数据集上,该算法的性能最好,其AUC为98.98%。在Citeseer数据集上,除了训练比率T为0.7~0.8且向量长度K为100,150,200,300以外,其余K值对应的AUC变化较大。在DBLP数据集上,不同向量长度对应的AUC的变化幅度较稳定,这是因为DBLP是稠密网络。在Cora数据集上,随着训练率的不断变化,不同向量长度对应的AUC总体趋势均呈上升状态并且波动较大,这是因为Cora数据集为稀疏网络。综上所述,训练比率T和向量长度K对稀疏网络影响较大,对稠密网络影响较小。
4 结论
针对无标签网络中基于图神经网络的链路预测方法使用其高效建模机制进行链路预测任务时性能较差的问题,提出了一种近似图神经网络框架的无监督链路预测算法。首先,输入层类比GCN的输入层,输入网络的结构信息和节点属性,确保网络特征的完整性;其次,进行矩阵分解和向量优化,得出网络节点表示向量,该步骤替代GCN的梯度更新和迭代优化过程;最后,计算相似度矩阵,使用AUC指标评测ALIP算法性能。实验结果表明,ALIP算法可以高效利用网络特征,提高节点之间关系的预测精度。
[1] XIE X Q, LI Y J, ZHANG Z Q, et al. A joint link prediction method for social network[C]∥International Conference of Young Computer Scientists, Engineers and Educators. Cham: Springer, 2015: 56-64.
[2] SCHAFER J L, GRAHAM J W. Missing data: our view of the state of the art[J]. Psychological Methods, 2002, 7(2): 147-177.
[3] KOSSINETS G. Effects of missing data in social networks[J]. Social Networks, 2006, 28(3): 247-268.
[4] LI M, MENG X M, ZHENG R Q, et al. Identification of protein complexes by using a spatial and temporal active protein interaction network[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2020, 17(3): 817-827.
[5] DZAFERAGIC M, KAMINSKI N, MCBRIDE N, et al. A functional complexity framework for the analysis of telecommunication networks[J]. Journal of Complex Networks, 2018, 6(6): 971-988.
[6] LIBEN-NOWELL D, KLEINBERG J. The link-prediction problem for social networks[J]. Journal of the American Society for Information Science and Technology, 2007, 58(7): 1019-1031.
[7] LYU L Y, ZHOU T. Link prediction in complex networks: a survey[J]. Physica A: Statistical Mechanics and Its Applications, 2011, 390(6): 1150-1170.
[8] ZHOU T, LYU L Y, ZHANG Y C. Predicting missing links via local information[J]. The European Physical Journal B, 2009, 71(4): 623-630.
[9] JACCARD P. Etude de la distribution florale dans une portion des Alpes et du Jura[J]. Bulletin De La Societe Vaudoise Des Sciences Naturelles, 1901, 37(142): 547-579.
[10] S RENSEN T, S
RENSEN T, S RENSEN T, BIERING-S
RENSEN T, BIERING-S RENSEN T, et al. A method of establishing group of equal amplitude in plant sociobiology based on similarity of species content and its application to analyses of the vegetation on Danish commons [J]. Biologiske Skrifter, 1948, 5(4): 1-34.
RENSEN T, et al. A method of establishing group of equal amplitude in plant sociobiology based on similarity of species content and its application to analyses of the vegetation on Danish commons [J]. Biologiske Skrifter, 1948, 5(4): 1-34.
[11] 王富田, 张鹏,肖井华. 链路预测算法错边识别能力的评测[EB/OL]. (2015-12-30) [2023-05-15]. http:∥www.paper.edu.cn/releasepaper/content/201512-1363.WAMG F T, ZHANG P, XIAO J H. Evaluation the ability of link prediction methods in the spurious link detection [EB/OL]. (2015-12-30) [2023-05-15]. http:∥www.paper.edu.cn/releasepaper/content/201512-1363.
[12] KATZ L. A new status index derived from sociometric analysis[J]. Psychometrika, 1953, 18(1): 39-43.
[13] LEICHT E A, HOLME P, NEWMAN M E J. Vertex similarity in networks[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2006, 73(2): 026120.
[14] FOUSS F, PIROTTE A, RENDERS J M, et al. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(3): 355-369.
[15] KOV CS I A, LUCK K, SPIROHN K, et al. Network-based prediction of protein interactions[J]. Nature Communications, 2019, 10: 1240.
CS I A, LUCK K, SPIROHN K, et al. Network-based prediction of protein interactions[J]. Nature Communications, 2019, 10: 1240.
[16] 廖亮, 张恒锋. 基于支持向量机的机会网络链路预测[J]. 信息通信, 2018, 31(9): 23-25.LIAO L, ZHANG H F. Link prediction of opportunistic network based on support vector machine[J]. Information &Communications, 2018, 31(9): 23-25.
[17] 杨妮亚, 彭涛, 刘露. 基于聚类和决策树的链路预测方法[J]. 计算机研究与发展, 2017, 54(8): 1795-1803.YANG N Y, PENG T, LIU L. Link prediction method based on clustering and decision tree[J]. Journal of Computer Research and Development, 2017, 54(8): 1795-1803.
[18] KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL].(2017-02-22)[2023-05-11]. https:∥arxiv.org/abs/1609.02907.
[19] LEI K, QIN M, BAI B, et al. GCN-GAN: a non-linear temporal link prediction model for weighted dynamic networks[C]∥IEEE INFOCOM 2019 - IEEE Conference on Computer Communications. Piscataway: IEEE, 2019: 388-396.
[20] LI G H, MÜLLER M, THABET A, et al. DeepGCNs: can GCNs go as deep as CNNs? [C]∥2019 IEEE/CVF International Conference on Computer Vision (ICCV). Piscataway: IEEE, 2019: 9266-9275.
[21] CHEN M, WEI Z W, HUANG Z F, et al. Simple and deep graph convolutional networks[EB/OL](2020-07-04)[2023-05-11]. https:∥arxiv.org/abs/2007.02133.
[22] YANG C, SUN M S, LIU Z Y, et al. Fast network embedding enhancement via high order proximity approximation[C]∥Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence. Melbourne: International Joint Conferences on Artificial Intelligence Organization, 2017: 3894-3900.
[23] LIU Z, ZHANG Q M, LYU L Y, et al. Link prediction in complex networks: a local naïve Bayes model[J]. EPL (Europhysics Letters), 2011, 96(4): 48007.
[24] KLEIN D J, RANDI? M. Resistance distance[J]. Journal of Mathematical Chemistry, 1993, 12(1): 81-95.
[25] CHEBOTAREV P, SHAMIS E. The matrix-forest theorem and measuring relations in small social groups[EB/OL]. (2006-02-04)[2023-06-01].https:∥arxiv.org/abs/math/0602070.
[26] 冶忠林, 曹蓉, 赵海兴, 等. 基于矩阵分解的DeepWalk链路预测算法[J]. 计算机应用研究, 2020, 37(2): 424-429, 442.YE Z L, CAO R, ZHAO H X, et al. Link prediction based on matrix factorization for DeepWalk[J]. Application Research of Computers, 2020, 37(2): 424-429, 442.
[27] 曹蓉, 赵海兴, 冶忠林. 基于网络节点文本增强的链路预测算法[J]. 计算机应用与软件, 2019, 36(3): 227-235, 242.CAO R, ZHAO H X, YE Z L. Link prediction algorithm based on text enhanced of network nodes[J]. Computer Applications and Software, 2019, 36(3): 227-235, 242.
[28] 王曙燕, 巩婧怡. 融合节点标签与强弱关系的链路预测算法[J]. 计算机工程与应用, 2022, 58(18): 71-77.WANG S Y, GONG J Y. Link prediction algorithm fusing node label and strength relationship[J]. Computer Engineering and Applications, 2022, 58(18): 71-77.