随着在线游戏、图像处理和增强现实等移动任务规模不断扩大,它们对移动终端的计算需求也越来越高。但是,移动终端设备计算能力和电量都是有限的,这很难满足任务长时间续航和低延迟处理要求[1]。5G和边缘计算的发展将远程云计算中心提供计算转移到了距离移动终端更近的位置提供计算,从而提供时延更低的计算服务[2]。移动边缘计算模式有效解决了移动设备计算能力有限、云计算中心提供计算服务时延较长等问题[3-4]。
与云计算相比,边缘计算提供的计算资源、网络资源及存储资源是有限的[5]。当大量用户同时向边缘服务器提交任务卸载请求时,用户之间会不可避免地竞争边缘服务器资源。若任务卸载不合理,可能导致资源出现服务繁忙或空闲不均等情况;若资源分配不合理,可能导致资源浪费,这将大大降低边缘服务器的资源利用率,边缘服务质量低下,降低用户的服务体验质量[6-7]。
近年来,国内外学者对如何在边缘计算环境下有效卸载移动任务、提高边缘设备的资源利用率、减少服务器负载方面进行了广泛研究。Gao等[8]提出负载均衡感知的任务卸载策略以最小化选择边缘服务器的时间。张展等[9]通过对任务进行划分,并将其合理分配至边缘云端及本地终端节点进行处理。邝祝芳等[10]基于贪心策略的流水车间调度算法解决任务卸载决策和卸载调度问题。Fernando等[11]基于卷积神经网络来学习时空相关性解决主动负载均衡。Lu等[12]基于深度学习减少因调度不平衡而造成的时间和负载问题。Xu等[13]基于改进粒子群优化分配边缘节点的计算资源实现负载均衡。以上工作都是考虑如何为服务器资源分配任务以实现负载均衡。在云边协同任务卸载研究中,尚缺乏基于云用户和云提供商供需相关视角的按照任务需求为任务分配合适虚拟机资源的研究。
针对以上问题,本文提出了一种云边协同卸载移动任务的模型。首先分析影响任务服务需求和虚拟机服务保障的因素,并给出任务与虚拟机的服务匹配度的度量方法。其次,基于改进匈牙利算法求一批任务的最大化服务匹配度的卸载方案,并通过有限次迭代消除资源竞争进一步优化卸载方案。最后,从资源负载、平均完成时间、平均等待时间及执行成功率等方面将本文算法与P2PITS算法、ALBOA算法和ESSDSA算法进行对比,验证本文算法的有效性。
1 云边协同卸载任务的系统架构
1.1 移动任务建模
在云边计算环境下,移动任务是终端设备上的应用提交的任务(以下称为任务),如人脸识别、目标跟踪、在线游戏等。本文假设每个终端设备产生的任务相互独立,产生的任务集T={t1,t2,…,tn}。一个任务可表示为一个八元组tj=(mk,sk,pk, wj,cj,rj,nj, dj),其中,mk表示产生任务tj的终端的编号;sk表示终端的处理速度;pk表示终端的发射功率;wj表示任务的计算量,用所需CPU周期数度量;cj表示任务需要传输的数据量;rj表示任务对资源的可用性需求;nj表示任务对资源的可靠性需求;dj表示任务的截止完成时间。
1.2 虚拟机建模
一个物理服务器通过虚拟化技术可虚拟出多个具有不同服务性能的虚拟机。一个服务器虚拟出的虚拟机集合可表示为VM={vm1,vm2,…,vmm}。一个虚拟机可表示为一个五元组vmi=(si,ai,li,ui,τi),其中,si表示虚拟机的当前处理速度,可用于CPU周期度量;ai表示虚拟机的使用时间;li表示虚拟机的当前队列长度;ui表示虚拟机当前可用度;τi表示虚拟机当前服务请求成功率。
1.3 系统架构
为使云服务器和边缘服务器虚拟出来的虚拟机能够完成有截止时间要求的任务,本文设计了一种云边协同卸载任务的系统架构,如图1所示。图1中,移动终端提交任务到调度中心,调度中心根据任务信息和虚拟机物理资源信息,按照调度策略将任务分配给合适的虚拟机,此外调度中心根据虚拟机的负载状况动态调整虚拟机的物理资源以提高服务质量。
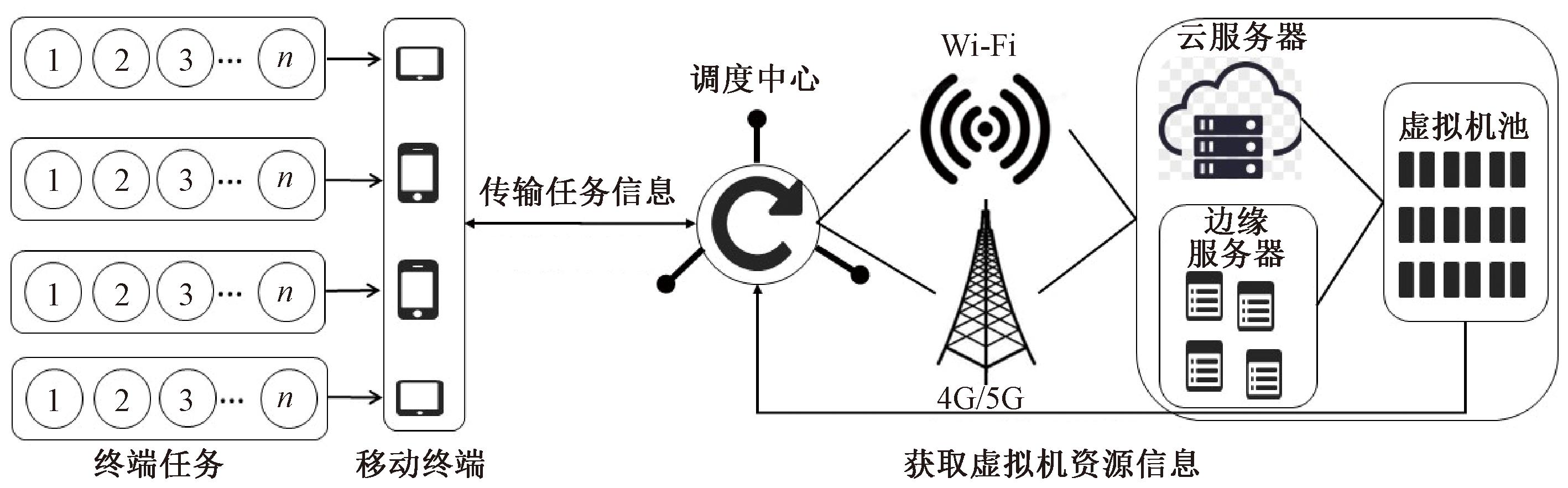
图1 云边协同卸载任务的系统架构
Figure 1 System architecture for cloud-edge collaborative offloading of multiple tasks
2 按需分配资源的任务卸载模型
2.1 任务服务需求度
任务在移动终端的卸载需求度Wor(ti)表示任务ti对虚拟机性能的需求程度,通过任务在移动终端所需处理时间和处理能耗的加权和进行评估:
(1)
任务tj在移动终端mk上的处理时间为
T(tj,mk)=wj/sk。
(2)
处理能耗为
(3)
式中:![]() 表示移动终端1个CPU周期所产生的能耗;σ1表示移动终端开关电容。
表示移动终端1个CPU周期所产生的能耗;σ1表示移动终端开关电容。
通过信息熵确定w1、w2的大小。设移动终端在本地随机处理n个任务,得到n个任务的处理时间和处理能耗2个指标的样本矩阵D={dij}n×2。由于2个指标的量纲、数量级差异较大,需要对样本矩阵进行无量纲标准化处理。本文通过式(4)最大最小化方法将数据转化成[0,1]上的正向递增数值[14]。
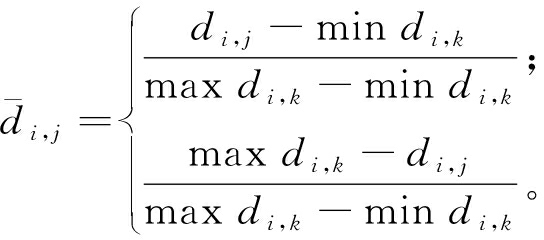
(4)
计算2个指标的信息熵:
(5)
式中:常数k与样本数n有关。完全无序的数据集的熵ρ最大,最大值为1。n个样本处于完全无序分布状态时,![]() 则
则
(6)
由于信息熵ρj可用来度量第j项指标信息的效用价值,当完全无序时ρj=1。此时第j项评价指标的数据对综合评价的效用价值为0。因此,某项指标的信息效用价值取决于该项指标的信息熵ρj与1的差值hj=1-ρj。利用熵值法,根据各项指标信息的效用价值来计算,效用价值越高,对评价的重要性越大,于是指标j的权重为
(7)
移动终端希望提交的任务能够得到虚拟机及时安全地执行,以便任务能够在截止时间内被处理完,这要求执行任务的虚拟机具有较高的安全性。任务对虚拟机的安全性需求度sf(tj)可表示为任务对虚拟机可用性和可靠性的加权和:
sf(tj)=w1×rj+w2×nj。
(8)
当任务在卸载过程中因自身服务需求过高而找不到合适的虚拟机时,用户为了保障任务成功卸载可能会对虚拟机安全性做出妥协。但若用户妥协太多,可能导致请求超时,严重影响服务质量。因此,用户需要在安全性需求和处理时间之间进行平衡,具体任务安全妥协值计算公式如下:
(9)
本文通过任务的卸载需求度和安全性需求度评估任务的服务需求度。任务tj的服务需求度Qqu(tj)可公式化表示为
Qqu(tj)=Wor(tj)×Wsf(tj)。
(10)
2.2 虚拟机服务保障度
本文设定每台服务器进行本地资源管理周期cycle=1 s,即每间隔1 s计算一次虚拟机实时算力。虚拟机在任意时刻的负载状态和物理资源配置是可实测的,虚拟机的实时算力F(vmi,ai)[15]的计算公式如下:
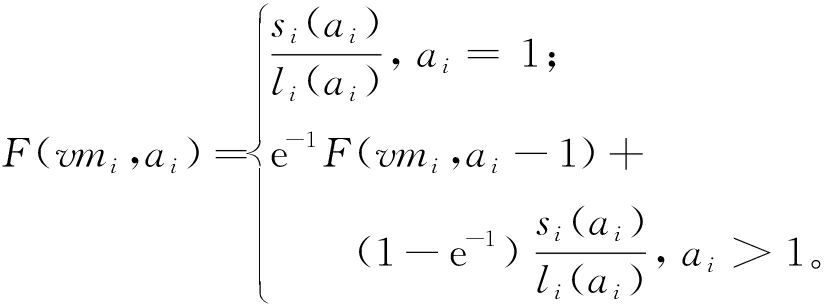
(11)
式中:si表示虚拟机的当前处理速度;ai表示虚拟机的使用时间;li表示虚拟机的当前队列长度。
移动终端通过无线信道采用正交频分多址方案将任务卸载到边缘服务器。为确保用户上行链路传输信道的正交性,假设移动设备与边缘服务器之间的每条链路只允许有1台设备占用。由香农公式可知,移动终端mk到虚拟机vmi的上行链路传输速率R(mk,vmi)为
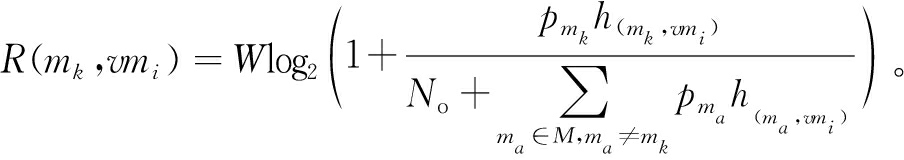
(12)
式中:W为信道之间带宽;No表示信道内部的高斯噪声功率;h(mk,vmi)表示移动终端mk和虚拟机vmi之间的信道增益。
若虚拟机vmi使用了ai时长,终端mk的任务tj上传到虚拟机vmi上处理,所需处理时间为
a(tj,vmi)=acomput(tj,vmi)+atrans(mk,vmi)=
(13)
式中:acomput(tj,vmi)、atrans(mk,vmi)分别表示计算时间和传输时间。
本文虚拟机能耗仅考虑任务上传过程中虚拟机产生的传输能耗,则传输能耗为
(14)
虚拟机处理任务花费的时间和能耗越少,虚拟机处理性能越好,通过式(4)将数据转化成[0,1]上的正向递减数值,此时每项指标值越小越好。
为保证任务在截止时间内完成,要求虚拟机对卸载的任务有较高的卸载需求保障。虚拟机的卸载需求保障度Wrp(vmi,tj),可表示为任务在虚拟机上处理花费的时间和能耗的加权和:
(15)
本文通过虚拟机的可用性和虚拟机完成服务请求的成功率2个评价指标来反馈虚拟机的安全保障度。在软件工程中,可用性依据平均故障间隔时间和平均修复时间来度量。假设每个虚拟机只有工作和故障2种状态,资源的寿命L服从参数为θ的指数分布,资源故障修复的修理时间X服从参数为μ的指数分布[16]。
(16)
假定L和X互相独立,故障资源修复后与新的资源相同,当t=0时,资源处于正常工作状态,则虚拟机vmi在t=ai/24时的可用性为
(17)
设虚拟机vmi在使用期间接收任务数为q,成功完成服务请求数为b,则虚拟机在ai时间段内完成服务请求的成功率为
τ(vmi,ai)=b/q。
(18)
虚拟机的安全保障度WS(vmi,ai)可表示为虚拟机的可用性和完成服务请求成功率的加权和:
WS(vmi,ai)=wu(vmi,ai)+wτ(vmi,ai)。
(19)
本文通过虚拟机的安全保障度和虚拟机的卸载需求保障度的乘积评估虚拟机的服务保障度Qqr(vmi,ai):
Qqr(vmi,ai)=Wrp(vmi,ai)×WS(vmi,ai)。
(20)
2.3 服务匹配度
系统按需为被卸载的任务分配资源。虚拟机提供的服务保障越接近任务的服务需求,则任务和资源的服务匹配度越大。服务匹配度qos(vmi,tj)表示虚拟机提供的服务保障度与用户提交的任务的服务需求度的匹配程度,具体计算公式如下:
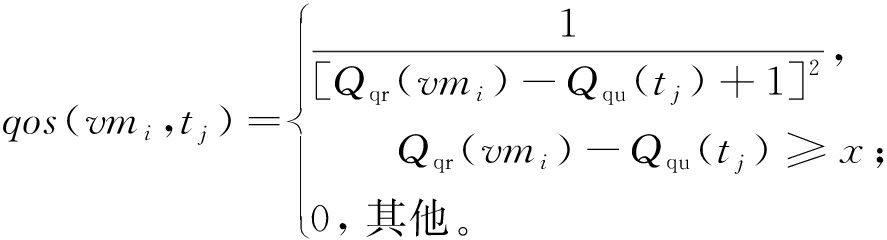
(21)
式中:x为系统服务匹配妥协下限值。
2.4 按需分配资源的任务卸载公式化描述
系统为了保障按需为被卸载任务分配资源,通过寻找最大服务匹配度来为任务匹配最佳虚拟机。最大服务匹配度满足截止时间要求的按需分配物理资源的任务卸载问题可公式化为
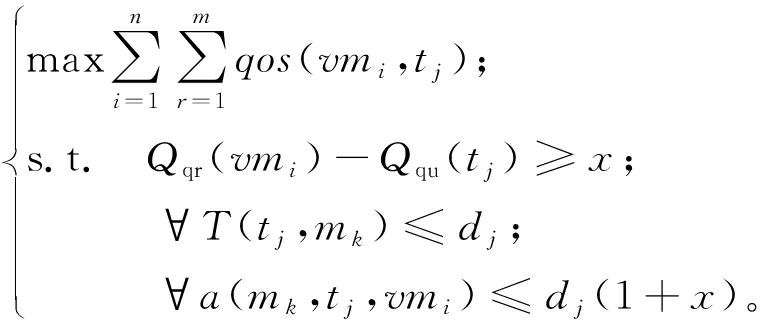
(22)
3 按需分配资源的任务卸载策略
按需为任务分配物理资源的卸载问题,可以看作是任务和虚拟机之间的匹配问题,匈牙利匹配算法可以很好地解决这类最大匹配问题。为了实现按需为被卸载任务分配物理资源,本文设计了一种最大服务匹配度满足截止时间要求的按需分配物理资源的任务卸载算法。该算法基于改进匈牙利算法求一批任务的最大化服务匹配度的卸载方案,并通过有限次迭代消除资源竞争进一步优化卸载方案。
3.1 匈牙利算法任务虚拟机匹配方式的改进
现实中,虚拟机的数量远小于用户发出的任务数量,并且一个虚拟机可同时处理多个任务。传统匈牙利算法中,每个虚拟机只能匹配一个任务。因此,本文从任务虚拟机的匹配方式改进传统的匈牙利算法,使得一个虚拟机可同时处理多个任务,据此将虚拟机虚拟化为多个虚拟节点,每个虚拟节点都执行一个任务,将这些虚拟节点与待分配的任务放在同一组中,形成二分图。这样,每个虚拟节点代表的虚拟机就可以和多个任务匹配。本文使用矩阵表示二分图,矩阵中的数值表示虚拟节点与任务之间边的匹配度。具体节点划分及资源分配规则如下。
步骤1 根据虚拟机当前服务能力决定虚拟机划分虚拟节点数。划分过程公式化表示为
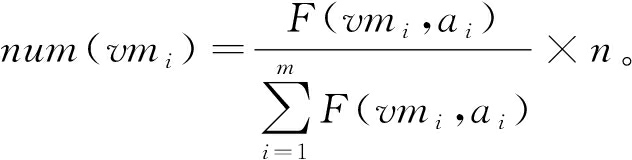
(23)
步骤2 根据任务的资源需求,将任务分为3个等级,并求解每个等级任务资源需求占比。任务等价划分规则为
(24)
每个等级任务资源需求占比为
(25)
步骤3 根据每个等级任务资源需求占比,制定每个虚拟机节点资源划分占比:
Pr=Gr/∑i∈mF(vmi,ai)。
(26)
步骤4 根据每个等级任务的占比,以及每个虚拟机划分虚拟节点个数,制定每个节点的资源量,本文设定虚拟机划分虚拟节点X~B(n,0.5),则
F(vmi,v,ai)=
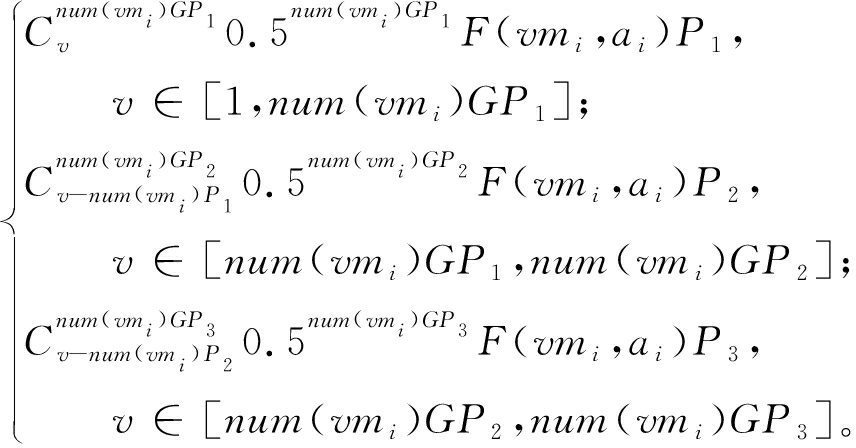
(27)
划分之后的虚拟节点集合表示为VM′=(vm1,1,vm1,2,…,vm1,num(vm1),vm2,num(vm1),…,vmm,num(vmm))。
3.2 按需分配资源的任务卸载算法设计
任务资源匹配问题可表示为一个三元组:
DT={T,VM′,qos}。
(28)
式中:T表示参与卸载的任务集合;VM′表示参与处理任务的虚拟节点集合;qos表示任务和虚拟机的服务匹配度集合。
为任务分配到一个设备资源称为任务获得匹配,令λ={λ1,λ2,…,λn}表示系统当前最优卸载方案,λi表示一个任务到具体设备资源的匹配。
寻找最大服务匹配度的最优匹配方案的过程就是不断寻找合适的资源使得任务集中的任务尽可能多地完成卸载并且保障服务质量。系统在制定卸载决策过程中,通过贪心算法寻求所有任务的最佳资源匹配并制定匹配方案。
(29)
式中:di.j表示服务质量差值矩阵DT中的值;φi.j表示决策值,φi.j∈{0,1},当φi.j取1时表示卸载到此资源上。
若当前匹配方案λ使得
(30)
此时匹配方案中存在资源竞争,通过匈牙利算法为存在资源竞争的任务集寻找最优匹配,在匹配过程不断为存在冲突的任务寻找最佳方案,使得尽可能多的任务获得匹配以达到最大匹配。将冲突设备资源存放在集合CR中,已卸载的任务存放在集合UT中,通过匈牙利算法求解冲突选出未匹配任务集合中的最小匹配代价值ΘDT的过程如下:
ΘDT=min{DT-UT,DT-CR}。
(31)
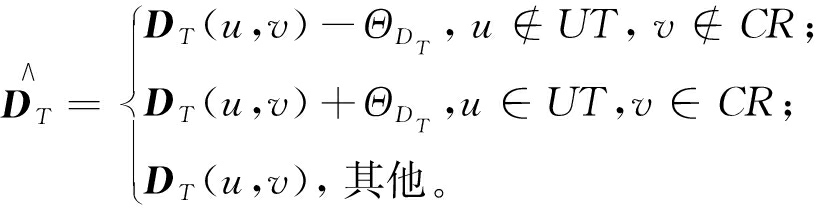
(32)
式中:![]() 表示DT变换后的矩阵。
表示DT变换后的矩阵。
解决冲突后,将找到的冲突任务的卸载方案添加到λ中,继续递归寻找其他未参与卸载的任务,直到当前匹配方案满足:
∑i∈VM′φi.j=1。
(33)
此时任务到资源集的匹配达到最大匹配。
定理1 任务到资源集的最大匹配是最优匹配。
证明:当前最大匹配结果λ一定是最优匹配,若在下次搜寻过程中出现设备资源竞争,即∑i∈VM′xi.j>1,此时,对于匹配方案DT通过式(29)变换,变换后的结果重新选择最佳卸载方案满足
(34)
将当前冲突任务的最佳卸载方案![]() 添加到λ中。在不断寻找新的任务匹配过程中实时更新S。因此最后得到的匹配一定最大匹配且是最优的。
添加到λ中。在不断寻找新的任务匹配过程中实时更新S。因此最后得到的匹配一定最大匹配且是最优的。
通过上述匹配理论,基于匈牙利算法为所有任务寻找最佳决策λ的具体步骤如下。
步骤1 初始化卸载策略,并从任务节点集合T中随机选择一个任务tj,卸载策略λ=∅,已卸载任务集合UT=∅;
步骤2 遍历当前任务可卸载虚拟节点集合VM′,并选择最大qos卸载,更新卸载策略λ。将任务从任务节点集合中删除并插入到已卸载任务集合中即
T′←T-{tj},UT←{tj}。
(35)
步骤3 若卸载到该虚拟节点上使得![]() 则存在资源竞争,使用改进匈牙利算法解决竞争,通过递归调用选择出最优卸载方案λ*并更新λ,即
则存在资源竞争,使用改进匈牙利算法解决竞争,通过递归调用选择出最优卸载方案λ*并更新λ,即
λ←λ*=min f(λ1,λ2,…,λi)。
(36)
步骤4 当T=∅时,此时已达到最大匹配数量,得出最佳卸载决策λ。
算法1 最大服务匹配度满足截止时间要求的按需分配物理资源的任务卸载算法 (mobile task unloading algorithm which allocates physical resources on demand which the maximum service match meets the deadline time requirement,ARMDR)。
输入:任务集合T,虚拟机资源集合VM,χ,θ,μ,x;
输出:最佳卸载决策方案S。
① QOSR←∅,QOSU←∅,DT←∅,S←∅,UT←∅,CR←∅,VM′←∅;
② 根据式(23)~(27)对虚拟资源进行划分,并将划分后的虚拟节点集合保存到VM′中。
③ for each vmi∈VM′,tj∈T{
QOSR[tj] = Wor(tj)×Wsf(tj);
QOSU[vmi] = Wrp(vmi,tj)×WS(vmi,ai);
计算qos(vmi, tj);
DT←1/qos(vmi,tj);}
④ while(T≠∅)∥贪心算法为tj选择最优服务匹配度值设备资源
for each tj∈T
(tj,vmi,v)←select_max_psq(tj,VM′,qos);
λ←λ+{(tj,vmi)};
T←T-{tj};∥将当前任务从集合中剔除
UT←{tj};∥将任务添加到已卸载集合
⑤ if∑i∈Nφi,j>1;∥若tj存在设备资源竞争,通过匈牙利匹配为存在设备资源竞争的任务选择最小代价设备资源
temp←select_competing _tasks (vmi, tj);∥将匹配方案中在设备资源ri上存在竞争的任务集存放在temp中
λ←λ-λ(temp);∥将匹配方案中存在竞争匹配方案S(temp)剔除
ΘDT=min{T-UT+temp,VM′-CR};∥将已卸载任务和竞争设备资源剔除,并保存剩余部分最小值
if (u∉UT,v∉CR){
f(u,v)-ΘG;}
else if (u∈UT,v∈CR){
f(u,v)+ΘG;}
temp*←max F_Munkre(temp,VM′,qos);∥
匈牙利算法寻找冲突任务集合的最优匹配
S←S+S(temp*);∥将卸载成功的任务添加到匹配方案中
if (tj∈CT Failed to match){
S←S-S(tj),T←T+tj,UT←UT-tj;
}
⑥ Get the update time difference: time;
if (time add 1 s){∥ 系统服务时间每增加1 s,更新一次服务器资源性能
update vmi∈VM′;}
定理2 ARMDR算法能够收敛。
证明:要证明算法的收敛性,首先要证明算法在有限次迭代后获得最优卸载决策。由卸载方程得
(37)
式中:Fmax=max{fi,j|for all tj∈T,vmi∈VM′}。
设![]() 当用户卸载策略从λ转换到λ′时可得
当用户卸载策略从λ转换到λ′时可得
f(λ)-f(λ′)≥Fmin。
(38)
式中:Fmin=min{fi,j|for all tj∈T,vmi∈VM′}。
根据式(37)和式(38)可得算法的最大迭代次数为
Γmax≤N2Fmax/Fmin。
(39)
要证明经过有限次迭代后得到的卸载决策为最优解,只需证明算法在更新时,目标函数值保持不减即可。
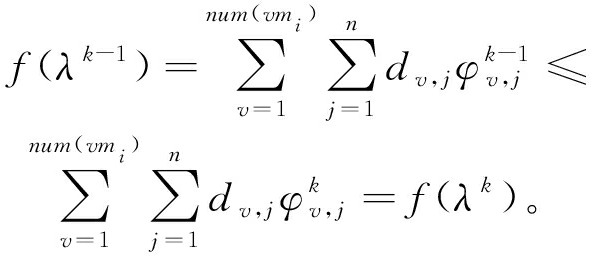
(40)
其中f(λk)为经过Γmax次迭代后获得的最优解,不等式成立的条件是f(λk)为最优解。因此,目标函数的值最多经过Γmax次迭代后始终不减少,从而在多次迭代后收敛。
4 仿真实验与结果分析
为了验证方法的可行性和有效性,本文利用Python语言实现了ARMDR算法。实验环境为Intel(R) Core(TM) i7-7700HQ CPU(双核CPU,2.80 GHz)、24 GB RAM、Windows操作系统。
4.1 实验设置
基站从终端接收服务请求,并分配给服务器处理,每个终端上传500个任务,每个任务的计算量和所需内存为[2 MB,10 MB],每2个任务间隔5 ms,任务的安全性需求值服从U(0,1)分布,任务的截止时间服从U(100 ms,3 000 ms)。
虚拟机的CPU数量服从U(0.3 GHz,1.5 GHz),内存数量服从U(1 024 MB,10 240 MB)分布,虚拟机的开始时刻负载服从U(0,0.8)分布,虚拟机的安全性服从U(0,1)分布。虚拟机的安全性低于5%代表该虚拟机为恶意虚拟机。本文假设用户提交的请求直接上传到虚拟机上处理。
4.2 实验与分析
为验证ARMDR算法的性能效用,首先,测试妥协下限值以及资源管理周期数对ARMDR算法的影响。其次,从虚拟机数量、任务数量、容忍时延以及网络带宽角度与P2PITS算法[17]、ALBOA算法[18]和ESSDSA算法[19]进行对比实验,综合评价ARMDR卸载策略的性能。实验相关参数见文献[20]。
P2PITS算法是一种数据搜索调整策略。采用多接入边缘计算的方式,在服务器之间交换数据来平衡负载,以减少本地最大负载。
ALBOA算法是一种基于软件定义网络(SDN)的任务卸载策略。该策略将任务卸载到负载较小的资源上,既能最小化所有计算任务的处理时延,又能解决负载均衡问题。
ESSDSA算法是一种基于标准差和二次分配的边缘计算任务调度策略。该策略根据服务优先级将任务集进行划分,并设计匹配函数以实现资源的良性匹配,利用空闲资源,将重载任务分配给轻负荷资源,从而提高负载均衡效果。
4.2.1 妥协下限值和资源管理周期
为验证妥协下限和资源管理周期对系统性能的影响,通过卸载成功率、执行成功率、虚拟机负载对系统性能进行评估。
卸载成功率:
(41)
式中:λj∈{0,1};N表示任务总数。
执行成功率:
(42)
式中:aj表示虚拟机处理任务花费的时间;dj表示任务的截止时间;x表示妥协下限。
虚拟机负载:
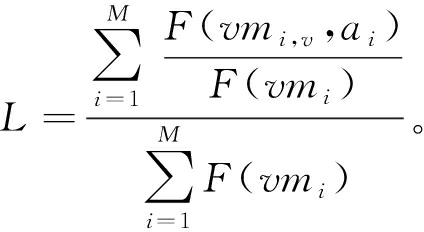
(43)
式中:F(vmi)表示虚拟机的总算力;F(vmi,ai)表示虚拟机的当前可用算力;M表示虚拟机总数。
实验设置50个虚拟机,终端数量是虚拟机数量的两倍,网络带宽为8 Mbps,实验结果如图2、3所示。
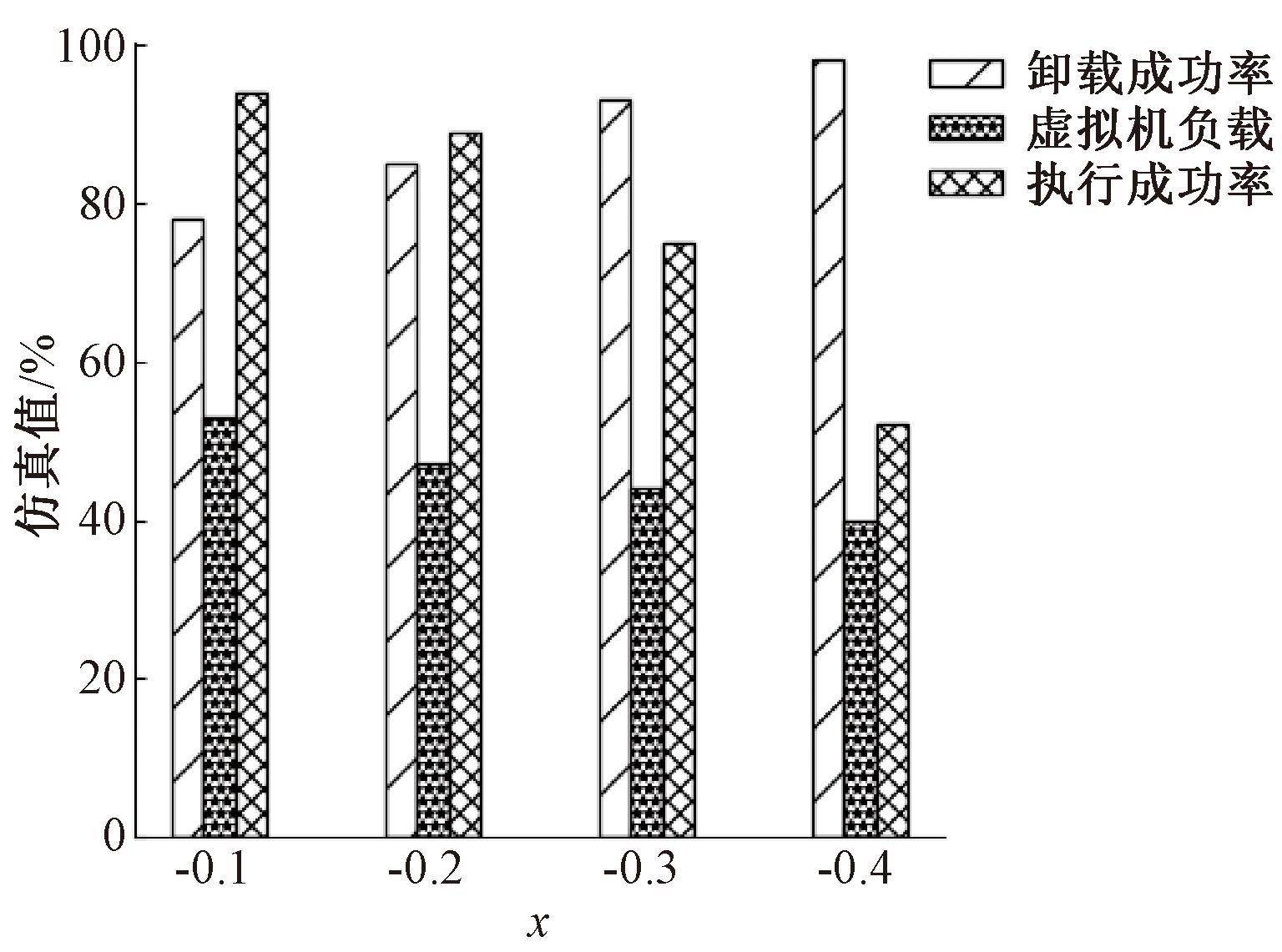
图2 妥协下限与系统性能关系
Figure 2 Relationship between the compromise lower limit and system performance
由图2可知,随着系统服务匹配度妥协下限值的增加,任务可选择虚拟机数量增加,卸载成功率从78%增加到97%,虚拟机资源负载从53%降低到40%,但随着妥协值放宽,任务执行成功率从94%降低到52%。这是因为随着妥协放宽,任务有更多资源选择,任务得到了均衡分配,但任务完成时间不能得到保证。
由图3可知,随着资源管理周期的增加,卸载成功率不断降低,执行成功率先增加到95%后减少,虚拟机负载先在50%左右波动,然后上升,这是因为cycle值过小时系统因频繁更新占据计算资源,cycle值过大时,系统无法获取虚拟机准确资源信息。综上可得,当x=-1,资源管理周期为1 s时系统性能最佳。
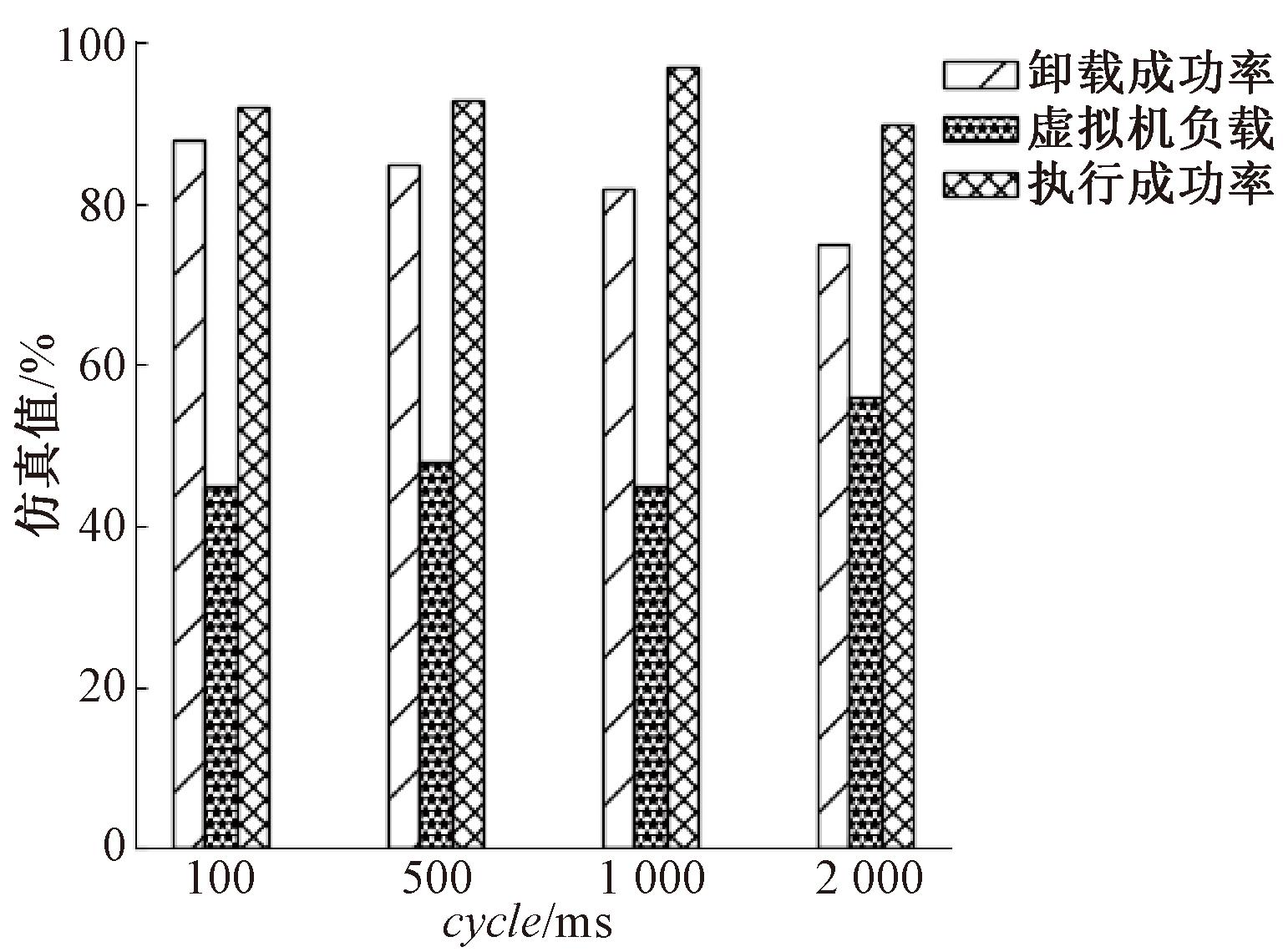
图3 资源管理周期与系统性能关系
Figure 3 Relationship between cycle values and system performance
4.2.2 虚拟机数量
为验证虚拟机数量对系统性能的影响,从平均CPU负载、平均RAM使用率和平均等待时间3个方面进行评估。其中,平均CPU使用率以及平均RAM使用率的计算方式与Linux内核对CPU使用率和RAM使用率的计算相同,等待时间是指任务到达虚拟机后等待处理的时间[15]。
实验设置移动终端数是虚拟机数的两倍,网络带宽设定为8 Mbps,系统服务匹配妥协下限值设定为x=-0.1,虚拟机本地资源管理周期为1 s,实验结果如图4所示。
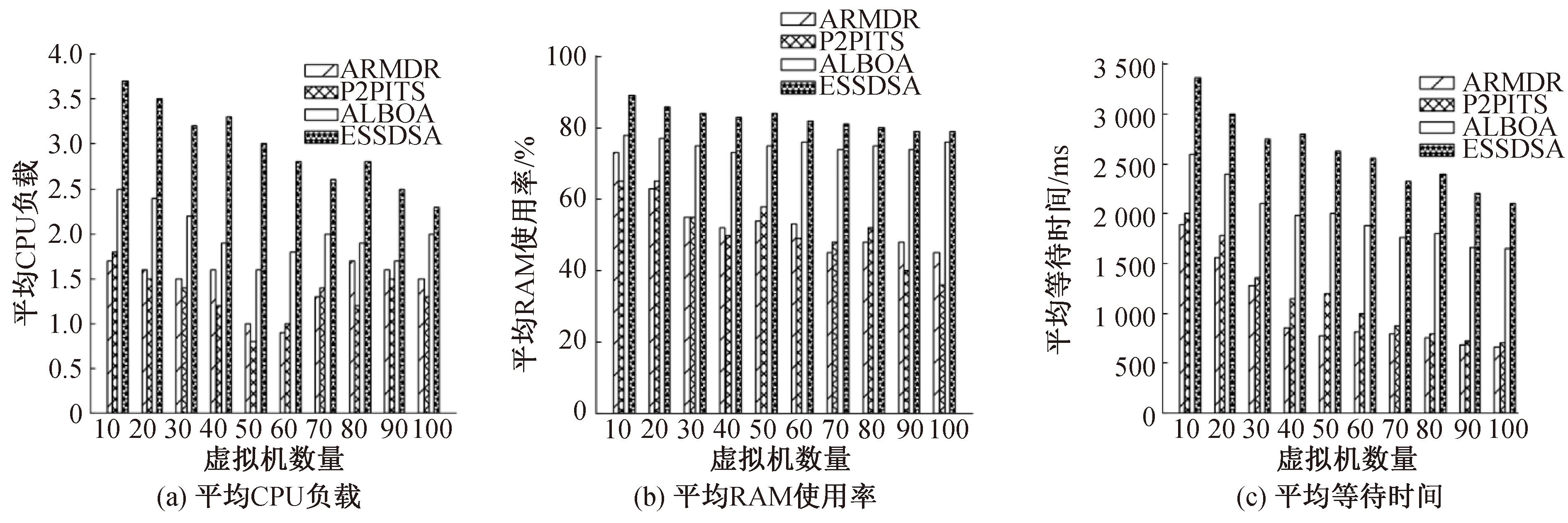
图4 不同虚拟机数量下系统性能比较
Figure 4 Comparison of system performance with different numbers of VMs
由图4可知,虚拟机规模从10扩大到100时,与ALBOA、ESSDSA算法相比,本文算法平均CPU负载分别降低了42.7%,51.5%,在平均RAM使用率方面分别降低了30.1%,36.4%。与ALBOA、ESSDSA、P2PITS算法相比,本文算法平均等待时间分别降低了13%,61.4%,49.1%。这是因为其他算法容易为负载小的资源分配过多任务,导致任务等待时间过长。虽然本文算法进行资源更新会占用资源,引起服务器内存负载上升,但根据服务匹配度进行资源分配,可减少额外的传输和等待时间并且均衡服务器之间的负载。
4.2.3 任务数量
为验证任务数量对系统性能的影响,从平均完成时间和任务执行成功率2个方面进行评估。任务执行成功率通过式(42)计算。
平均完成时间为
TF=∑j∈Naj/N,λj=1。
(44)
式中:aj表示任务的完成时间。
本实验设置虚拟机数为50,网络带宽设定为8 Mbps,妥协下限值设定为x=-0.1,虚拟机本地资源管理周期为1 s,实验结果如图5所示。
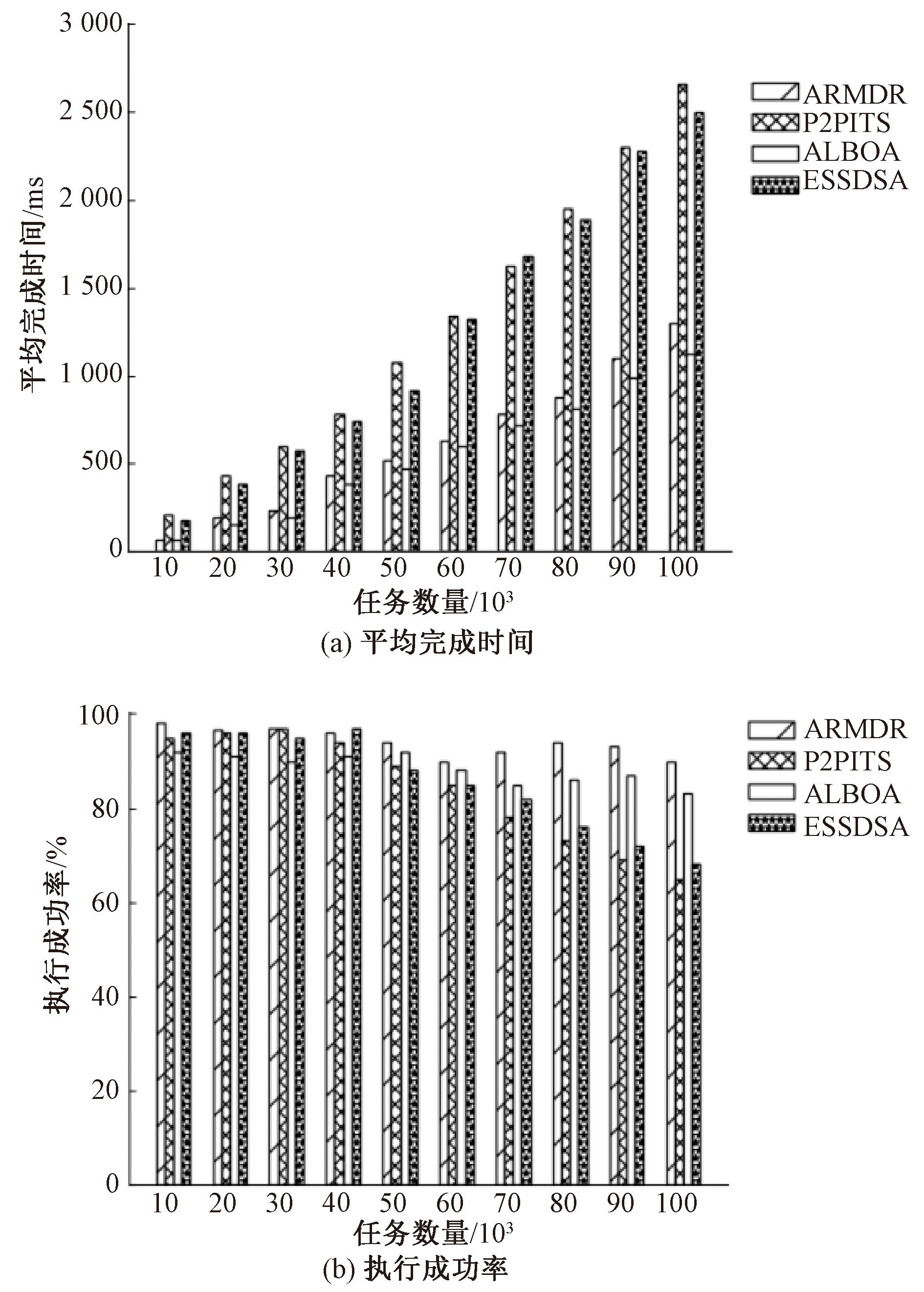
图5 不同任务数量下系统性能比较
Figure 5 Comparison of system performance with different task counts
由图5可知,与P2PITS、ESSDSA算法相比,本文算法平均完成时间分别降低了45.5%,43%,但比ALBOA算法提高了13.5%。这是因为本文算法综合考虑了虚拟机负载情况,并及时更新虚拟机资源信息,按照任务需求分配资源。相比之下,P2PITS算法因边缘计算节点之间互相传输任务而产生额外的传输时间;ESSDSA算法未考虑任务等待时间,而ALBOA算法选择了最优传输路径,在传输过程中节约时间并将任务卸载到负载较小的资源进行数据处理。
在执行成功率方面,本文相对于最优的ALBOA算法提升了6.2%,这是因为本文算法考虑虚拟机的安全性和任务的截止时间要求,避免因超时或虚拟机的安全导致任务失败,而ALBOA算法未考虑虚拟机的安全性。
4.2.4 容忍时延及网络带宽影响实验
为验证容忍时延及网络带宽对系统性能的影响,从平均完成时间和任务执行成功率2个方面进行评估。
本实验设置50个虚拟机,终端数量是虚拟机数量的两倍,妥协下限值设定为x=-0.1,虚拟机本地资源管理周期为1 s,具体的实验结果如图6所示。
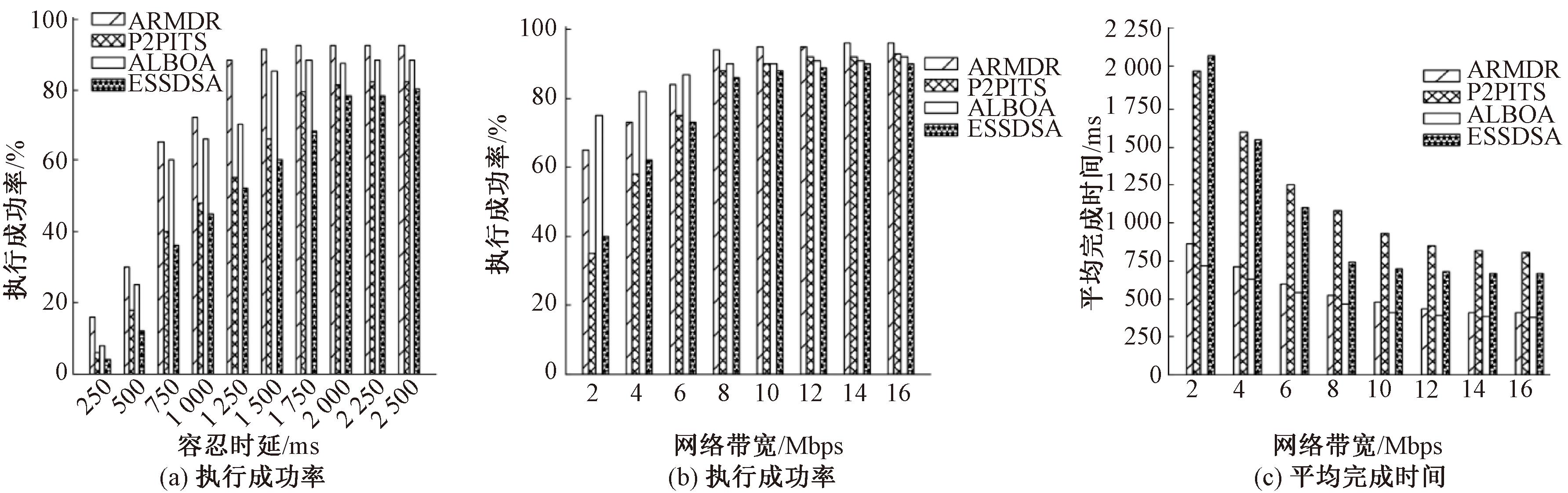
图6 不同容忍时延和网络带宽下系统性能比较
Figure 6 Comparison of system performance with different tolerances and network bandwidth
由图6可知,4种算法的执行成功率都随着容忍时延的增加而增加,相比于最优的ALBOA算法,本文算法在执行成功率方面提升了20.2%,这是因为ALBOA算法虽然考虑了任务截止时间但并未考虑虚拟机的安全性。
在平均完成时间方面,本文所提算法比P2PITS算法低49.5%,比ESSDSA算法低38.6%,比ALBOA算法高7.7%。这是因为本文算法满足截止时间前提下按照任务需求为任务分配虚拟机。P2PITS算法和ESSDSA算法由于任务在服务器间的传输产生额外的传输时间。ALBOA算法选择最优的传输链路,在传输过程中节约传输时间。
在执行成功率方面,本文算法相比最优的P2PITS算法提升了3.5%。这是因为随着网络带宽的增加,任务的传输时间降低,任务的总完成时间减小,本文所提算法中有更多的虚拟机满足任务需求,提高了匹配成功率,进而提高了执行成功率。
5 结论
本文针对有限边缘服务器资源最大限度满足众多任务有着截止时间要求的任务卸载问题,设计了一种动态云边环境下按需分配物理资源的任务卸载策略。通过仿真实验将本文算法与P2PITS算法、ALBOA算法和ESSDSA算法从多方面进行对比,结果表明,相对P2PITS算法,所提算法虚拟机负载率降低了30.1%,平均等待时间降低了13%;相对ALBOA算法,所提算法平均完成时间降低了38.6%;相对ESSDSA算法,所提算法执行成功率提高了3.5%。所提算法能够在满足用户截止时间要求下有效降低虚拟机负载和任务的平均完成时间。
[1] CHEN Z Y, HE L G. Modelling task offloading mobile edge computing[C]∥Proceedingsof the 2022 8th International Conference on Computing and Data Engineering. New York:ACM, 2022: 15-21.
[2] BASLAIM O, AWANG A. Intelligent offloading decision and resource allocation for mobile edge computing[C]∥2022 International Conference on Future Trends in Smart Communities (ICFTSC). Piscataway:IEEE, 2022: 204-209.
[3] 刘昊, 张景超, 毛万登, 等. 智慧换流站云边协同数据交互方法[J]. 郑州大学学报(工学版), 2022, 43(5): 104-110.LIU H, ZHANG J C, MAO W D,et al. Cloud edge collaboration data interaction method of intelligent converter station[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(5): 104-110.
[4] 刘振鹏, 王鑫鹏, 李明, 等. 基于时延和负载均衡的多控制器部署策略[J]. 郑州大学学报(工学版), 2021, 42(3): 19-25, 32.LIU Z P, WANG X P, LI M, et al. Multi-controller deployment strategy based on delay and load balancing[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(3): 19-25, 32.
[5] 欧阳聪, 关静, 杨鸣. 基于资源分配和动态分组的合作协同演化算法[J]. 郑州大学学报(工学版), 2023, 44(5): 10-16.OUYANG C, GUAN J, YANG M.Cooperativeco-evolution algorithm based on resource allocation and dynamic grouping[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(5): 10-16.
[6] DRBHALAJI N. Efficient and secure data utilization in mobile edge computing by data replication[J]. Journal of ISMAC, 2020, 2(1): 1-12.
[7] YU Y, LI X, QIAN C. SDLB: a scalable and dynamic software load balancer for fog and mobile edge computing[C]∥Proceedings of the Workshop on Mobile Edge Communications. New York: ACM, 2017: 55-60.
[8] GAO Y Q, LI Z M. Load balancing aware task offloading in mobile edge computing[C]∥2022 IEEE 25th International Conference on Computer Supported Cooperative Work in Design (CSCWD). Piscataway:IEEE, 2022: 1209-1214.
[9] 张展, 张宪琦, 左德承, 等. 面向边缘计算的目标追踪应用部署策略研究[J]. 软件学报, 2020, 31(9): 2691-2708.ZHANG Z, ZHANG X Q, ZUO D C, et al. Research on target tracking application deployment strategy for edge computing[J]. Journal of Software, 2020, 31(9): 2691-2708.
[10] 邝祝芳, 陈清林, 李林峰, 等. 基于深度强化学习的多用户边缘计算任务卸载调度与资源分配算法[J]. 计算机学报, 2022, 45(4): 812-824.KUANG Z F, CHEN Q L, LI L F, et al. Multi-user edge computing task offloading scheduling and resource allocation based on deep reinforcement learning[J]. Chinese Journal of Computers, 2022, 45(4): 812-824.
[11] FERNANDO N, LOKE S W, RAHAYU W. Computing with nearby mobile devices: a work sharing algorithm for mobile edge-clouds[J]. IEEE Transactions on Cloud Computing, 2019, 7(2): 329-343.
[12] LU H F, GU C H, LUO F, et al. Optimization of lightweight task offloading strategy for mobile edge computing based on deep reinforcement learning[J]. Future Generation Computer Systems, 2020, 102: 847-861.
[13] XU X L, FU S C, CAI Q, et al. Dynamic resource allocation for load balancing in fog environment[J]. Wireless Communications and Mobile Computing, 2018, 2018: 6421607.
[14] ABBAS D B, LAVIN C V, FAHY E J, et al. Standardizing dimensionless cutometer parameters to determine in vivo elasticity of human skin[J]. Advances in Wound Care, 2022, 11(6): 297-310.
[15] 卢洪利. 基于博弈论模型的分布式系统的负载均衡与性能优化[D]. 天津: 天津理工大学, 2022.LU H L. A game theoretical load balancing and optimization approach for distributed system[D]. Tianjin: Tianjin University of Technology, 2022.
[16] 曹洁, 曾国荪, 钮俊, 等. 云环境下可用性感知的并行任务调度方法[J]. 计算机研究与发展, 2013, 50(7): 1563-1572.CAO J, ZENG G S, NIU J, et al. Availability-aware scheduling method for parallel task in cloud environment[J]. Journal of Computer Research and Development, 2013, 50(7): 1563-1572.
[17] MOGI R, NAKAYAMA T, ASAKA T. Load balancing method for IoT sensor system using multi-access edge computing[C]∥2018 Sixth International Symposium on Computing and Networking Workshops (CANDARW). Piscataway:IEEE, 2018: 75-78.
[18] ZHANG J, GUO H Z, LIU J J, et al. Task offloading in vehicular edge computing networks: a load-balancing solution[J]. IEEE Transactions on Vehicular Technology, 2020, 69(2): 2092-2104.
[19] SUN L T, LI Z G, LV J X, et al. Edge computing task scheduling strategy based on load balancing[J]. MATEC Web of Conferences, 2020, 309: 03025.
[20] SAMANTA A, LI Y. Latency-oblivious incentive service offloading in mobile edge computing[C]∥2018 IEEE/ACM Symposium on Edge Computing (SEC).Piscataway:IEEE, 2018: 351-353.