基于Spark的双阶段SA及GA求解MTSP

孙 鉴1,2, 刘 品1, 李 昊1, 陈 攀1

(1.北方民族大学 计算机科学与工程学院,宁夏 银川 750021;2.北方民族大学 图像图形智能处理国家民委重点实验室,宁夏 银川 750021)

摘 要：针对总路径长度最小的单站点多旅行商问题,提出了基于Spark的模拟退火和遗传算法结合的两阶段KSAGA算法。在第一阶段,通过k-means聚类将多旅行商问题拆分为多个单旅行商问题,并使用模拟退火算法对组内城市的遍历次序进行优化。在第二阶段,通过遗传算法对城市的分组进行优化,并基于染色体分组编码方式设计了交叉、变异算子以及混合局部优化算子,以提高算法的搜索空间和收敛速度。随着城市数量的增加,计算规模变大,利用遗传算法的特性实现算法的并行,以加快算法运行效率。最后,通过选取TSPLIB的部分数据集进行仿真实验,将KSAGA与ACO、GA、SPKSA、ALNS和NSGA-Ⅱ的求解质量以及GA和NSGA-Ⅱ的收敛速度进行对比。研究结果表明:KSAGA在解决单站点多旅行商问题时能够快速收敛,并且相较于其他算法,求解质量得到了很大提升。同时,随着城市数量和旅行商数量增加,KSAGA的优势更为明显。

关键词：多旅行商问题; 并行; 遗传算法; 分组编码; 局部优化算子

旅行商问题(traveling salesman problem,TSP)是一个著名的组合优化问题:一个旅行商访问n个城市后返回起始点,每个城市只能被访问一次,目的是找到总距离最短的路线。TSP问题的现实应用有很多,例如物流调度、交通运输、生物迁徙以及电路设计等。

而实际问题中让一个旅行商访问所有城市的工作量巨大,因此当需要多个旅行商去访问城市以缩短访问时间时,经典的TSP模型不再适用。为解决上述问题,对TSP进行扩展,引入了多旅行商问题(multiple traveling salesman problem,MTSP)[1]。本文考虑了单站点的MTSP,即m个旅行商从同一城市(出发城市称作仓库)出发访问n个城市,保证每个城市只被访问一次且每个旅行商至少要访问一个除仓库以外的城市,问题的求解目标为m个旅行商访问城市路径的总距离最小。相较于TSP问题,MTSP具有更高的实际应用价值,如热门的车辆路线问题、校车路线规划问题、任务分配问题以及航班调度问题等。

求解MTSP的方法主要包括精确算法、近似算法和启发式算法。随着问题规模的扩大,问题解空间膨胀速度与问题规模呈指数关系,这成为限制精确算法求解MTSP 性能的主要瓶颈,同时由于近似算法求解精度并不理想,因此目前基于群体的启发式算法是求解MTSP最常用、最有效的方法。

求解MTSP早期通常使用一种启发式算法,如Mohammad等[2]使用了两部分染色体编码方式的遗传算法(genetic algorithm,GA),进行选择、交叉和变异操作后,在传统遗传算法的基础上使用了opt算子对结果进行优化。Yang等[3]提出了新的交叉和变异算子来增强局部和全局搜索能力,然后应用NSGA-Ⅱ框架来加快算法收敛速度,增加解的多样性。

近年来,一些研究提出用混合算法分阶段解决MTSP,这些算法结合了不同的启发式方法和技术。Harrath等[4]所提出的方法是3种算法的组合:改进的ACO、2-opt和GA,使用ACO来生成TSP初始解,在该解基础上用2-opt算子来优化所获得的解后,将TSP转化为MTSP,使用GA再次提高解的质量,最后更新信息素映射以继续进行下一次迭代。但由于在单处理器环境下只能以串行方式对解空间进行搜索,当问题规模较大时,传统算法求解效率及性能大大降低,因此通过并行方法[5]来提高算法的性能成为研究热点之一。

针对上述算法求解质量上存在的不足以及混合算法计算规模较大的问题,本文对单站点多旅行商问题进行研究,提出了一种基于Spark的两阶段启发式算法KSAGA。算法由组内优化阶段和分组优化阶段组成,首先通过k-mean聚类和贪心算法生成初始解,第一阶段应用模拟退火(simulated annealing, SA)对每个旅行商的访问顺序进行优化,第二阶段通过并行GA对城市分组进行优化。在本文中,所有实验都将数据集中的第一个城市视为仓库。

1 相关背景

1.1 MTSP数学描述

给定一个完整的无向图G(V,E),其中V表示城市的集合(V={1,2,…,n}),E为成对的边。cij表示边eij的权重(即从城市i到城市j的旅行距离),多旅行商问题实际上就是寻找加权图中的最短巡回路径问题。式(1)～(6)给出多旅行商问题的数学模型,其中m为旅行商数量;n为城市数量;xijk为一个二进制变量,表示在旅行商k的路径中城市j是否在城市i之后立即被访问,若是,则xijk=1,否则xijk= 0;ui和uj为关于城市i和j的访问顺序的变量,如果城市i在路径中排在城市j之前,则ui>uj;p表示任何销售人员可以访问的最大城市数量。

目标函数:

(1)

约束条件:

(2)

(3)

(4)

(5)

(6)

其中,式(1)为目标函数,优化目标为m个旅行商访问所有城市后的总路程之和最小;式(2)、(3)表示每个城市都要被访问一次,有且只有一个旅行商从此城市出发;式(4)、(5)表示所有旅行商都要从仓库出发最终再回到仓库位置;式(6)[6]将子路径消除约束扩展到一个三维度模型,这个约束限制了子路径的产生。

1.2 Spark框架

Apache Spark[7]是一个用于大数据处理的开源框架,是目前最流行、速度最快的分布式计算框架之一,允许集群或云架构中的应用程序并行化。Spark将计算机集群划分为一个主节点和多个工作节点:主节点负责任务调度、资源分配和错误管理;工作节点并行处理映射任务和减少任务,用户程序分发和输入数据拆分由平台自动完成。Spark附带了包括多种语言(Scala、Java、Python、 SQL和R语言)的丰富的API,用于执行复杂的分布式数据的操作。

Spark的核心数据结构是弹性分布式数据集(resillient distributed dataset,RDD),借助RDD的高效数据共享和各种操作,可以高效地设计和实现不同的工作负载。RDD是一个只读的、分区的记录集合,提供了容错的并行数据结构。RDD允许用户将数据显式存储在磁盘或内存中,控制其分区并使用操作符进行操作。操作符主要分为转换和执行两种。转换是指从现有RDD的基础上创建新的RDD,是返回一个新的RDD的操作。转换操作是惰性求值的,不会立即触发执行实际的转换,而是先记录RDD之间的转换关系,只有当触发执行操作时才会真正地进行转换操作,并返回计算结果。常用方法有map、filter等。执行操作则是对最后一个RDD数据执行计算后产生结果,并输出到外部数据源。常用到的方法有reduce、collect等。

RDD的一次执行过程如下:通过对一个集合进行并行化或者读入外部数据源进行创建,利用textFile函数加载本地数据;经过一系列的转换操作,每次操作都会产生不同的RDD;最后一个RDD经过“执行”操作进行转换,并输出到外部数据源。这一系列处理被称为一个Lineage。RDD的一次执行过程如图1所示。

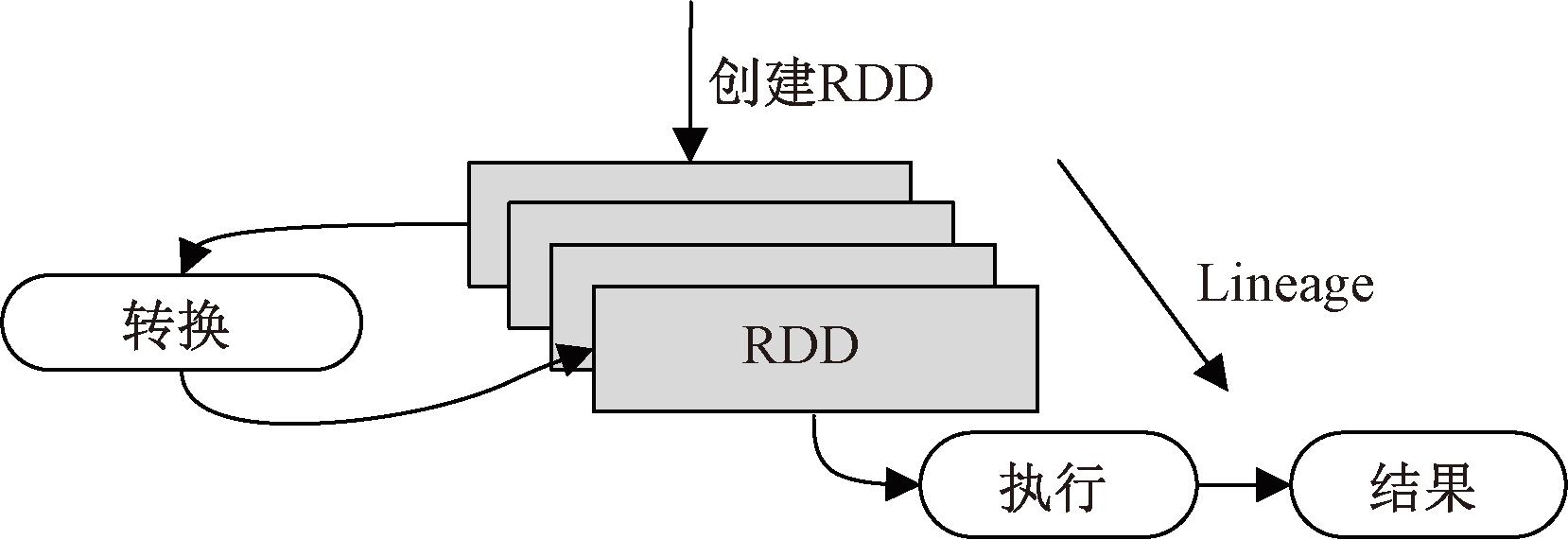
图1 RDD一次执行过程
Figure 1 An RDD′s Lineage

2 KSAGA算法

本文提出的KSAGA算法将MTSP求解过程划分成两部分:城市的分组优化和组内遍历次序优化。算法的基本思想如下。

(1)由k-means聚类和贪心算法生成问题的初始解。根据设定的m个旅行商将n个城市分成相应数量的组,若当前组内不包括仓库,则组内增加该城市,每个分组代表分配给该旅行商的城市,分组后通过贪心算法可得到每个旅行商访问的城市的顺序,生成较优的初始解。

(2)通过将城市分组把MTSP转化成多个TSP问题,通过并行SA求解TSP。

(3)优化组内城市访问顺序后,用遗传算法优化城市的分组。本文的遗传算法采用染色体分组编码方式,并设计了适用于此方式的交叉、变异算子,通过变异操作跳出局部最优,同时设计了局部优化算子加快算法收敛速度。通过将第一阶段生成的种群分成若干个域,再将数据存入RDD中来实现遗传算法的并行。

2.1 组内访问顺序优化

2.1.1 模拟退火算法

模拟退火算法是一种基于概率的搜索算法,它模拟了物理系统的热力学过程以找到最优解。算法以一定的概率接受更差的解决方案,以避免陷入局部最优解,并最终找到全局最优解。由于SA在求解TSP问题上具有较高的优势,因此在第一阶段本文采用优化的SA[8]来求解单旅行商问题,该方法的降温函数为

T0=T0α;

(7)

T=T0(1+cos πt/gapIter)。

(8)

式中:T0为初始温度;T为变化后的温度;α为降温系数;t为迭代次数;gapIter为浮动的间隔数。

2.1.2 并行模拟退火算法

在组内优化阶段,采用了基于Saprk的并行策略。通过k-means聚类将MTSP转化成多个TSP求解,每个分组的城市求最短路径即是一个TSP问题,通过并行模拟退火算法分别求出对应TSP的最优解,将结果合并即为第一阶段的最终结果。其具体步骤如下。

步骤1 将城市分为m个组,m为旅行商数量,由于每个旅行商都要求从仓库出发,所以将仓库添加至未包含仓库坐标的组中;

步骤2 分组后使用SparkContext对象的parallelize方法将以上每组城市创建为分布式RDD;

步骤3 调用RDD的map算子将m组城市分别映射到各子节点并调用贪心算法生成初始解;

步骤4 调用SA优化组内遍历顺序,最后使用RDD的collect算子将分布式的RDD本地化,合并后得到第一阶段的最优解。

2.2 城市分组优化

将k-means聚类和SA生成的结果作为GA的初始种群,通过对种群进行改进,完成对城市分组的优化。GA主要的操作算子包括以下6个部分。

(1)编码设计。常见的染色体编码方式有单染色体设计[9]、两部分染色体设计[10]、双染色体设计[11]等。以上编码方式的搜索空间相对较小,搜索效率较高,有利于加快GA的收敛速度,但是也存在明显缺陷:当把城市分配优化以及组内访问顺序优化2个环节融合在一起时会导致求解MTSP的进化算子难以设计。相较于以上几种编码方式,分组编码设计简单、易于实现,十分适用于多旅行商问题的求解,因此本文采用了染色体分组编码设计思想,将各旅行商的路径访问顺序编码成m个组,便于问题的分步优化。

(2)适应度函数。适应度函数是根据个体的适应值对其优劣判定的评价函数。本文的优化目标是最小化总路程,用访问路径总距离的倒数作为适应度函数来评价求解结果是否最优。适应度函数为

(9)

式中:li为一个旅行商访问组内所有城市的路程;m为旅行商数量。

(3)选择操作。选择策略是GA进化操作的重要步骤,会影响算法的执行效率。本文采用了轮盘赌算法作为选择策略,这是一种非随机选择策略,适应度越高的个体被选中的概率就越大。

(4)交叉操作。本文的交叉算子随机移除每个旅行商部分城市,移除比例为Pr,用贪心算法将移除的城市逐个插入到使总路程增加最少的位置,其操作如图2所示。

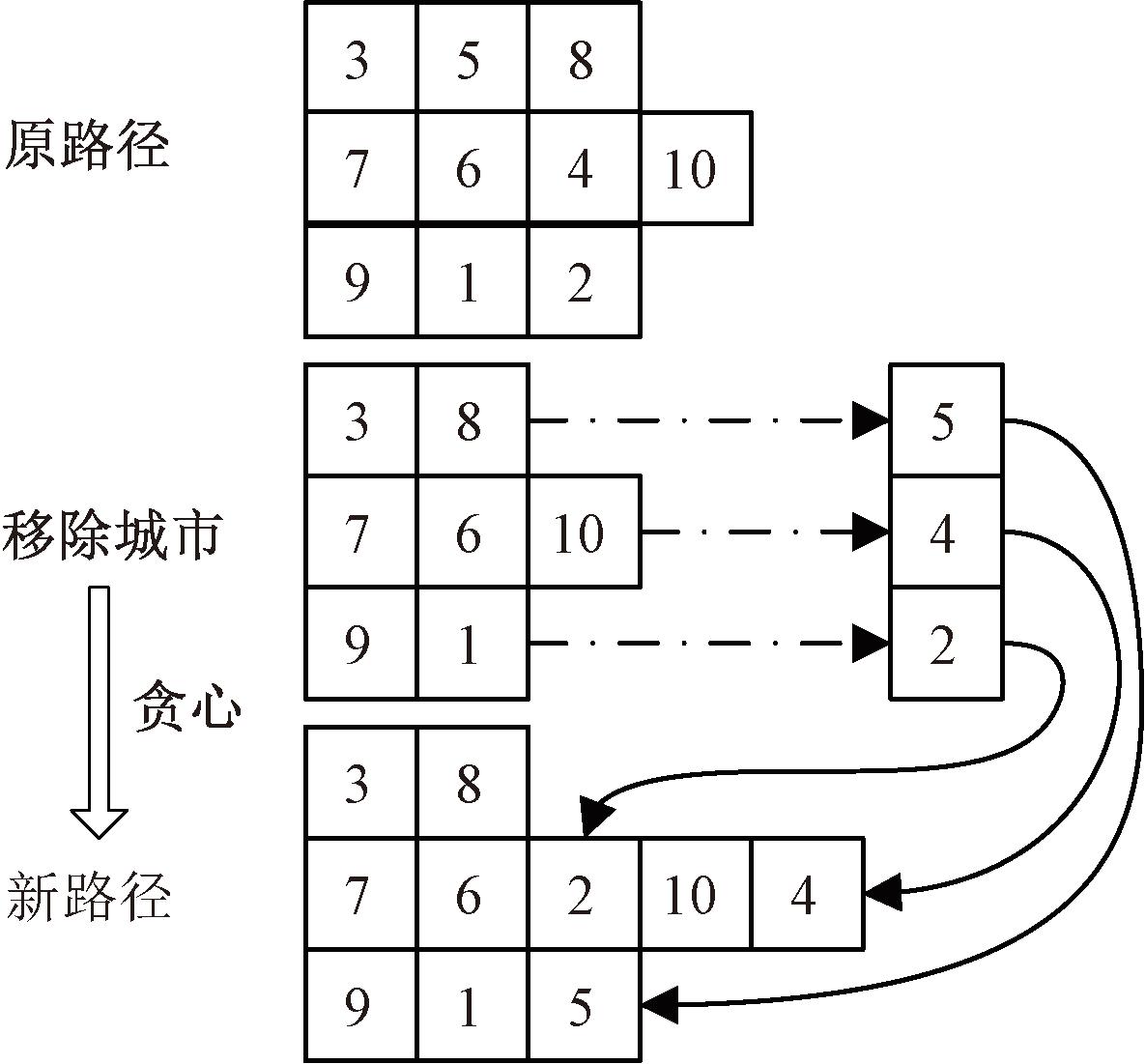
图2 交叉算子
Figure 2 Cross operate

(5)变异操作。变异算子的主要作用是防止搜索过程陷入局部最优。本文针对染色体分组编码方式,提出了适用于解决MTSP的两种变异算子:变异算子1对城市组内的访问顺序以及不同组城市之间的分组都进行了一定重组,这个过程随机移除了父代部分城市,移除比例为Pw,将移除的城市随机分配给各旅行商;变异算子2则随机选择2个旅行商,生成断点1和断点2,断点1之前的城市与断点2之后的城市组合,断点2之前的城市与断点1之后的城市组合,将这两条新生成的路径作为新的解,这样既保留了父代的部分优化解,又可以扩大搜索范围,跳出局部最优。相较于变异算子1,变异算子2对组内城市的访问顺序未进行过多破坏,其具体操作过程如图3所示。

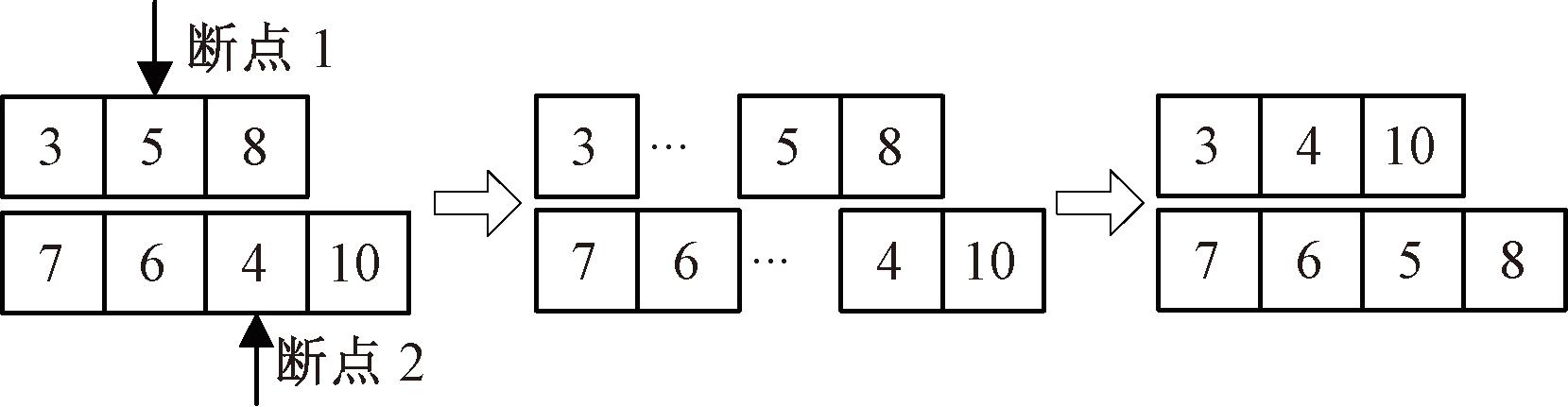
图3 变异算子2
Figure 3 The second mutation operator

(6)局部优化算子。GA用于优化不同旅行商之间的城市分组问题,因此这里的局部优化算子用于对不同旅行商之间的城市进行操作,局部搜索过程包括opt、insert、swap这3个优化算子,其具体操作过程如下。

opt:将第一组城市p0和第二组城市的p1作为断点,把各组的城市分为两部分,第一组城市p0及其之后的城市逆序后与第二组城市的第二部分合并,第一组的第一部分与第二组p1之前的城市逆序后合并,若操作后总路程减少则保留此路径。opt操作如图4(a)所示。

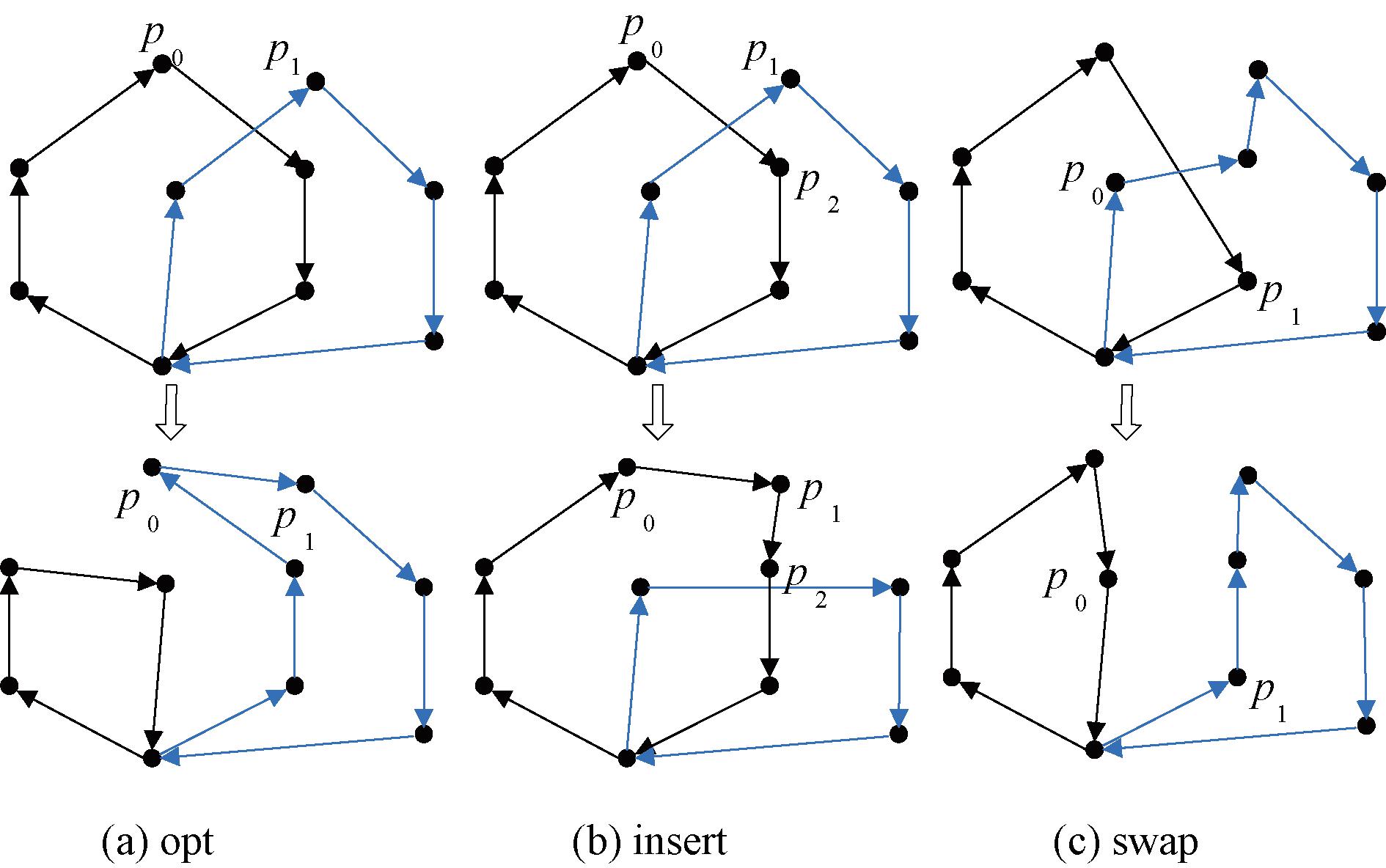
图4 局部优化算子
Figure 4 Local optimization operator

insert:插入算子操作如图4(b)所示,将第二组城市p0插入到第一组城市的p1、p2之间以改进解决方案。

swap:swap操作符如图4(c)所示。它通过交换不同组的2个城市来优化路径,图4(c)为城市p0和p1城市交换示例。

2.2.1 遗传算法流程

遗传算法具体操作流程如下。

步骤1 进行参数设置,包括迭代次数maxOutIter,种群数量Psize,执行交叉、变异算子的阈值Pm,2个变异算子的阈值Pt等;

步骤2 使用轮盘赌算法选择一个父代,适应度高的个体被选中的概率更大;

步骤3 生成0到1的随机数,若随机数小于阈值Pc,跳过步骤4执行交叉操作,否则进行变异操作;

步骤4 生成0到1的随机数,若小于阈值Pt则执行变异算子1,否则执行变异算子2;

步骤5 用局部优化算子对后代局部优化;

步骤6 若种群数量未达到规定数量,则将新的个体放入种群中,若超过规定种群数量且当前个体的解优于种群中的最差解,则用新的子代替换种群中适应度最低的个体,然后根据适应度将种群排序;

步骤7 进化结束判断(是否达到最大进化代数),若满足则循环结束,否则返回步骤2继续执行。

2.2.2 并行遗传算法

GA的种群规模通常很大,并且要经过多次进化,因此需要很大的计算量。并行可以提高计算速率,并有利于增大计算规模、扩大解的搜索空间。将数据放在RDD分区中将GA并行,在结束后对种群按个体适应度大小进行排序,从而得到更精确的解,并行GA流程图如图5所示。

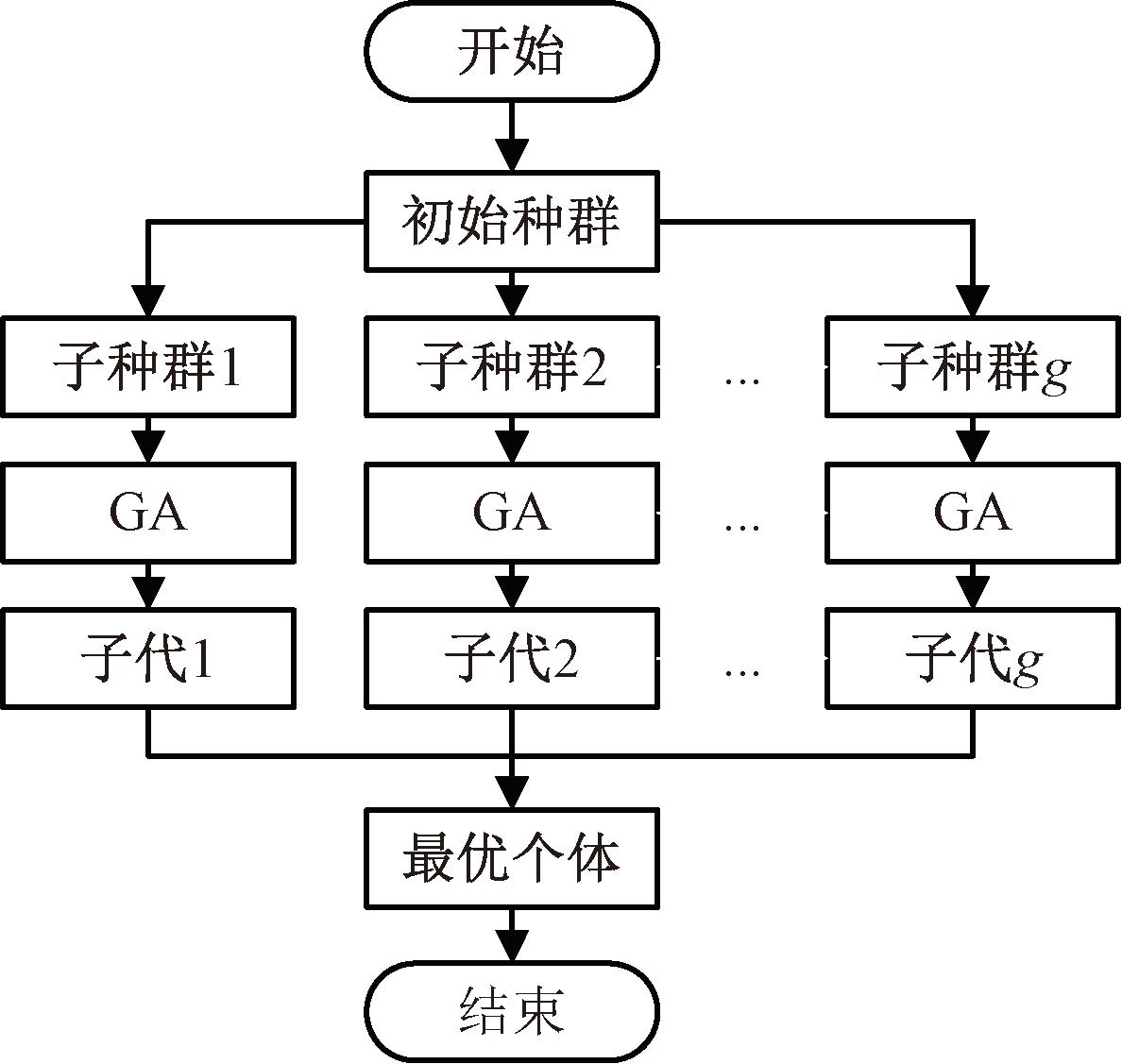
图5 并行遗传算法流程图
Figure 5 Parallel GA flowchart

并行GA流程如下。

(1)初始化种群:将k-means和SA优化后的路径作为遗传算法的初始种群。

(2)并行化处理:为了提高算法执行效率,将初始种群分为g个线程,其中g在本文中设置为15。每个线程将负责处理1个子种群,因此可以同时进行多个遗传操作。

(3)遗传操作:对每个子种群执行遗传操作,包括选择、交叉、变异和局部优化等步骤。

(4)结果本地化:一旦所有线程完成遗传操作,使用RDD的collect算子将所有线程的结果汇总并本地化,生成1个包含多个可能的解决方案的集合。然后,从中选择具有最短路径的解作为问题的最优解,这个过程确保了在并行处理中找到最优的解决方案。

3 实验与结果分析

本实验用Python语言实现KSAGA算法,在配置为Spark2.4.0、Intel(R) Xeon(R) Gold 6154 CPU@3.00 GHz的环境下进行,选取了不同规模的TSPLIB标准数据集进行仿真实验。

3.1 参数设置及其影响

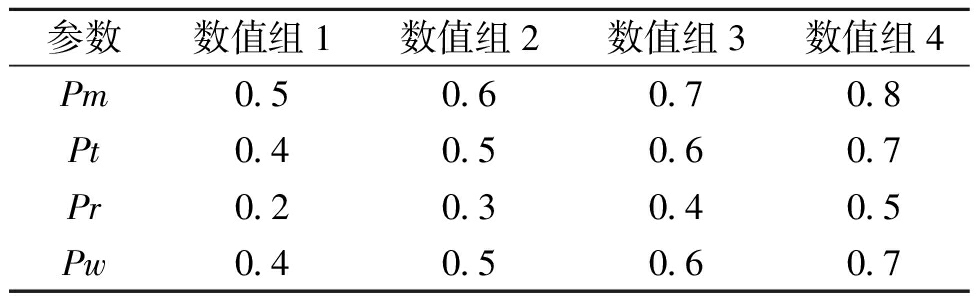
KSAGA中有4个重要的参数:交叉、变异算子阈值Pm,2个变异算子的阈值Pt,交叉算子的移除比例Pr,以及变异算子1的移除比例Pw,以上参数取值都会影响整个算法的性能。本文参考王勇臻等[12]的做法,选取eil51实例(旅行商数量为5)研究参数对KSAGA算法性能的影响。各参数取值如表1所示。

表1 参数取值
Table 1 Parameter value

参数数值组1数值组2数值组3数值组4Pm0.50.60.70.8Pt0.40.50.60.7Pr0.20.30.40.5Pw0.40.50.60.7

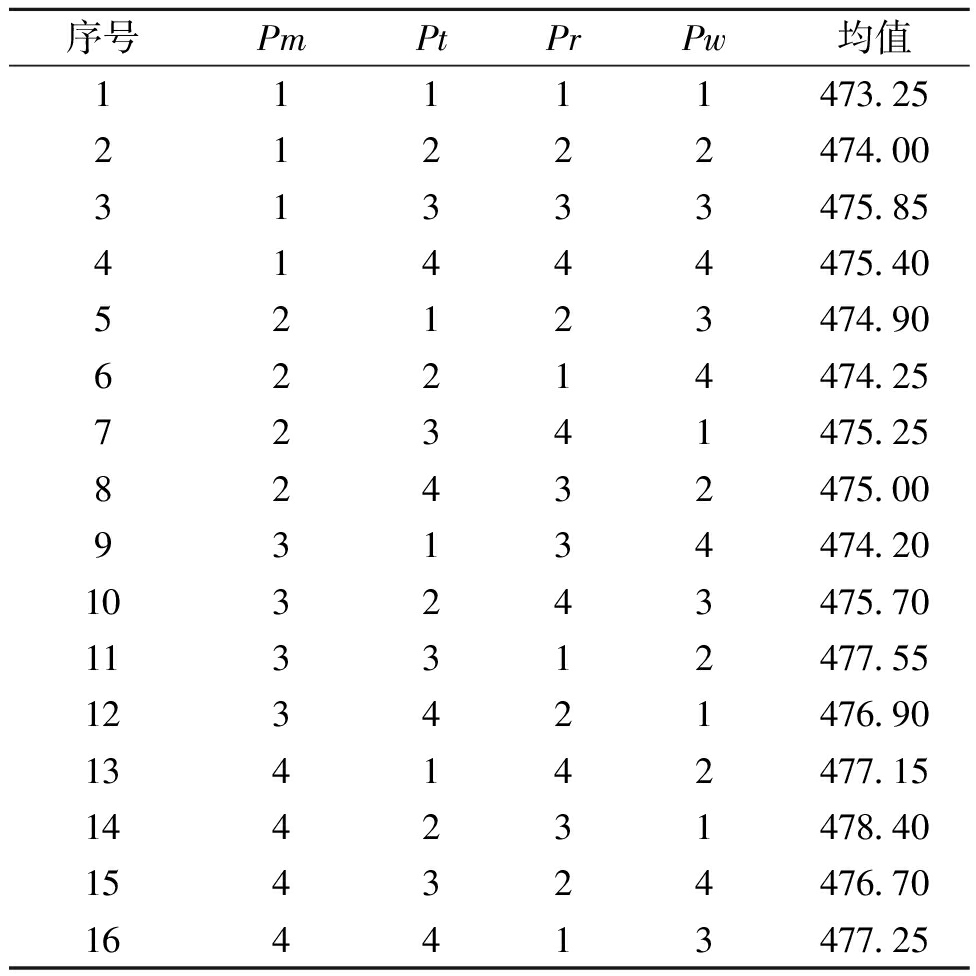
算法在每种参数组合下运行20次,本文GA的种群数量设置为20,最大迭代次数为200,将算法运行20次后得到的平均值作为评价指标,实验后得到的正交表如表2所示。

表2 正交结果及均值
Table 2 Orthogonal results and mean value

序号PmPtPrPw均值11111473.2521222474.0031333475.8541444475.4052123474.9062214474.2572341475.2582432475.0093134474.20103243475.70113312477.55123421476.90134142477.15144231478.40154324476.70164413477.25

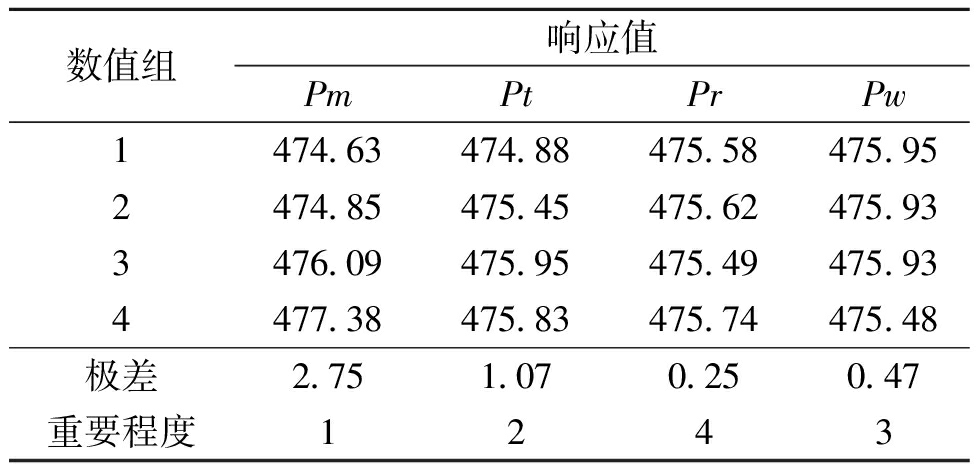
根据表1、2求得各参数在不同取值下总距离的平均值,计算这4个参数对应极差,通过极差的值可以反映本文算法中4个参数的重要程度,各参数对算法性能的影响如表3所示。

表3 各参数响应值
Table 3 Response values of each parameter

数值组响应值PmPtPrPw1474.63474.88475.58475.952474.85475.45475.62475.933476.09475.95475.49475.934477.38475.83475.74475.48极差2.751.070.250.47重要程度1243

根据表3的参数性能测试实验结果可得以下结论。

(1)参数Pm的极差在几个参数中最大,说明交叉、变异算子阈值对算法性能影响最大。在本文中,Pm取值越大执行交叉算子的概率越高,但是随着Pm增加,解的质量变差,这是由于KSAGA增加了局部优化算子,在加快收敛速度的同时,可能会使算法陷入局部最优,因此在0.5～0.8时Pm值越小越好。

(2)对算法性能影响第二大的参数是2个变异算子的阈值Pt,Pt在取0.6时效果最好,Pt越大,算法更偏向于执行变异算子1;Pt过小,变异算子2破坏程度不足以使算法跳出局部最优。

(3)Pw在算法中的影响较小,Pw会影响解空间的搜索范围,Pw取值为0.7时解的质量更好。

(4)Pr在4个参数中对算法的性能影响最小,此参数越大需要进行贪心操作的城市增多,会影响算法运行效率,但在算法中对解的质量影响不大。

综合上述分析,算法的交叉、变异算子阈值Pm、2个变异算子的阈值Pt,交叉算子的移除比例Pr,以及变异算子1的移除比例Pw设置如下:Pm =0.5,Pt=0.6,Pw=0.7,Pr=0.4。

3.2 改进的变异策略有效性验证

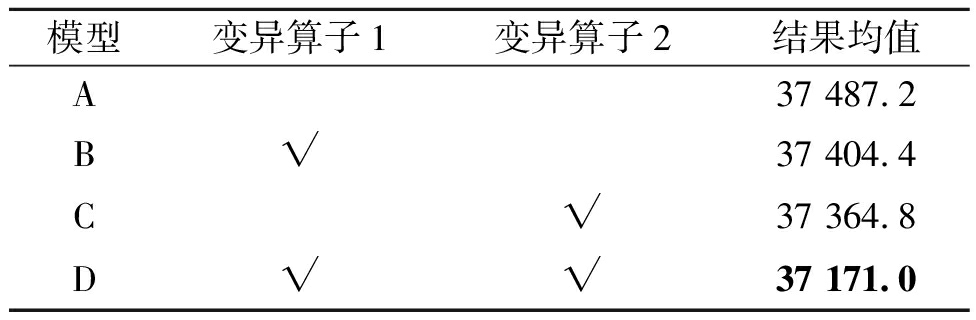
本文提出了2个变异算子,为验证策略组合的有效性设计了4个模型,在att48测试集上进行实验。表4展示了不同模型(旅行商数量为5)进行5次实验后的总路程均值结果,其中,A为基础模型,“√”表示算法中保留该算子,模型的最优结果加粗表示,下同。

表4 变异策略有效性验证表
Table 4 Validation table for the effectiveness of mutation strategy

模型变异算子1变异算子2结果均值A37 487.2B√37 404.4C√37 364.8D√√37 171.0

观察表4可以发现,未加入任何变异算子的模型A得到的均值结果为37 487.2,单独保留变异算子1的模型B或保留变异算子2的模型C相对于A模型的解更精确;进一步将2个变异操作组合后的模型D与模型B和C相比得到了更优解,与模型A相比二者相差了316.2。综上所述证明了变异策略的有效性。

3.3 算法的求解性能测试

为了验证KSAGA算法的性能,本文选取了4个不同规模的数据集eil51、eil76、kroD100、kroA150(设置不同旅行商数量)进行实验,不同数据集旅行商数量m取值参考其他文献中的常用值设置。与ACO[13]、GA[14]、NSGA-Ⅱ、SPKSA[15]以及自适应大规模邻域搜索算法[16](adaptive large-scale neighborhood search,ALNS)进行对比。为确保实验的公平性和可比性,所有算法采取统一的停止准则:最大迭代次数设置为1 000次,在算法终止时的最优解作为最终结果。各对比算法重要参数取值按照对应文献设置:GA种群规模为320,每次选择8个个体进行锦标赛选择;ACO设置信息素重要程度为1,路径可见性重要程度为3;NSGA-Ⅱ种群规模为100,变异概率为0.05;ALNS移除城市的最大比例为0.3,最小移除量为4个;SPKSA的初始温度为100,降温系数为0.99,浮动间隔为100。实验都在配置为Intel(R) Xeon(R) Gold 6154 CPU @3.00 GHz的环境下进行。其中ACO和SPKSA的重要更新公式按其对应文献设置。

由于对比算法ACO在原文献中限制了旅行商对城市的最大访问个数,为保证算法求解目标相同,在对该限制修改后进行仿真实验。其中NSGA-Ⅱ虽然为多目标优化算法,但该文献实验部分提到由于该算法交叉算子是基于最短距离的,因此在某些数据集下实验结果在最小化总距离的目标上相较于其他算法表现出明显的优势,因此本文将算法针对单目标MTSP做了优化后将其作为对比算法。各算法的实验结果如表5所示。其中,参数m为旅行商数量,同一参数设置下得到的最优解加粗表示。从表5看出,GA使用了染色体分组编码方式,便于交叉、变异操作的实现,但由于搜索空间不足导致解的质量欠佳,同时GA、ACO和NSGA-Ⅱ随机产生初始解的方式大大影响了算法的搜索效率。NSGA-Ⅱ使用了两部分染色体编码,同时设计了适用于此编码方式的交叉、变异算子,虽然加快了算法收敛速度,但是算法后期容易陷入局部最优。SPKSA算法收敛速度快,在求解每个组内城市的访问顺序有优秀的表现,但由于此算法没有对不同旅行商之间的城市分组进行优化,因此求解质量一般。而ALNS算法在小规模数据集上表现较好,但随着旅行商数量及城市数量的增加性能逐渐下降,主要原因是大规模邻域搜索算法容易陷入局部最优。在不同规模的数据集和不同旅行商数量的任务中,由于KSAGA算法结合了SA和GA的优势,同时在局部优化算子的加持下,算法收敛速度大大加快,且变异算子可以在迭代过程中使算法跳出局部最优,因此KSAGA在多次实验中相较于其他算法都可以得到更优质的解。

表5 6种算法运行结果对比
Table 5 Comparison of running results of six algorithms

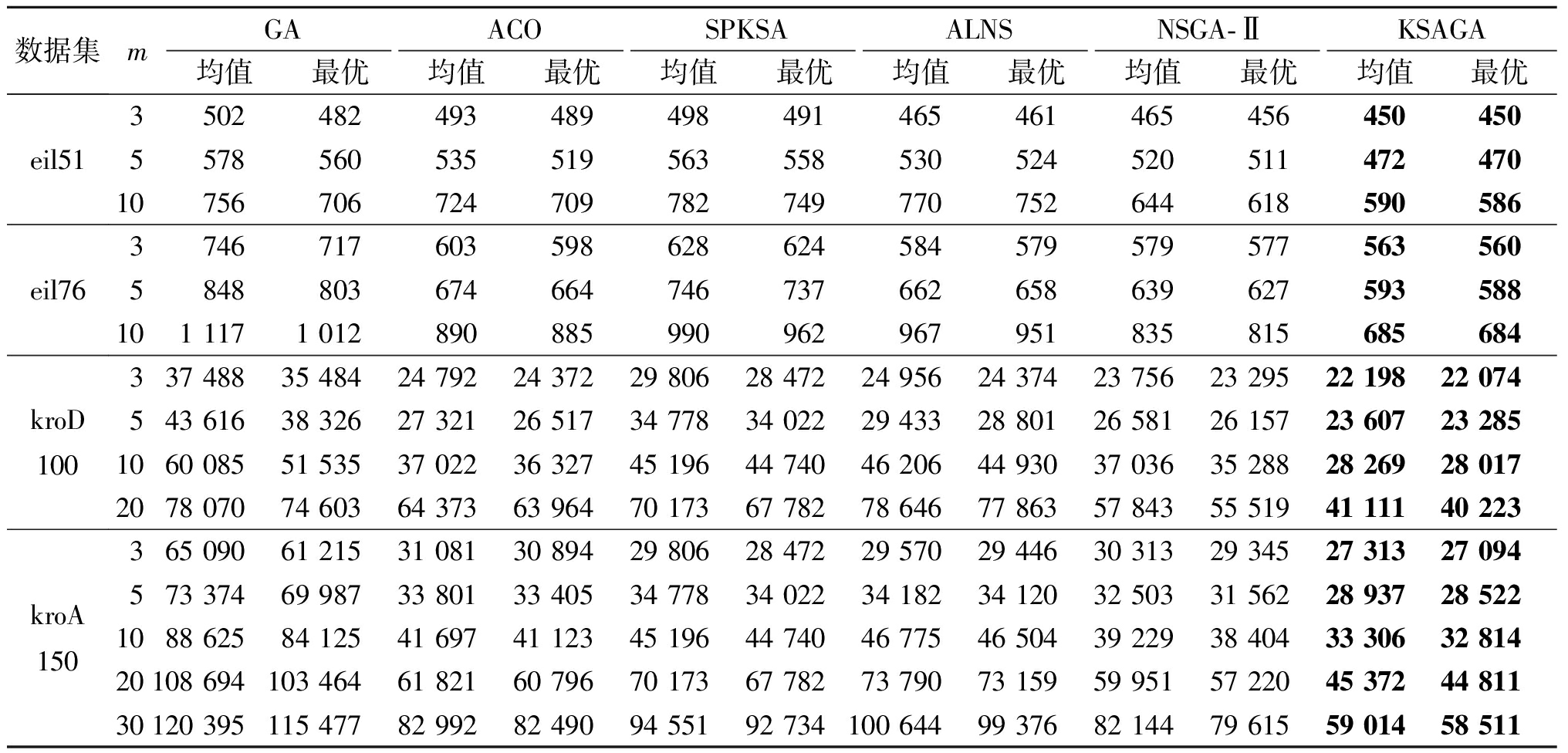
数据集mGAACOSPKSAALNSNSGA-ⅡKSAGA均值最优均值最优均值最优均值最优均值最优均值最优eil51eil76kroD100kroA150350248249348949849146546146545645045055785605355195635585305245205114724701075670672470978274977075264461859058637467176035986286245845795795775635605848803674664746737662658639627593588101 1171 012890885990962967951835815685684337 48835 48424 79224 37229 80628 47224 95624 37423 75623 29522 19822 074543 61638 32627 32126 51734 77834 02229 43328 80126 58126 15723 60723 2851060 08551 53537 02236 32745 19644 74046 20644 93037 03635 28828 26928 0172078 07074 60364 37363 96470 17367 78278 64677 86357 84355 51941 11140 223365 09061 21531 08130 89429 80628 47229 57029 44630 31329 34527 31327 094573 37469 98733 80133 40534 77834 02234 18234 12032 50331 56228 93728 5221088 62584 12541 69741 12345 19644 74046 77546 50439 22938 40433 30632 81420108 694103 46461 82160 79670 17367 78273 79073 15959 95157 22045 37244 81130120 395115 47782 99282 49094 55192 734100 64499 37682 14479 61559 01458 511

随着旅行商数量、城市规模的增加,其他算法的求解性能普遍发生下降,当数据集规模越大,或旅行商数量规模更大时,KSAGA的优势更为明显。

3.4 限制最大访问城市个数后算法性能测试

在限制销售人员可以访问的最大节点数之后,选择在测试集pr76、pr152和pr226上进行实验(独立运行10次后取最优值),与ACO、NMACO[17]算法比较来验证算法在限制访问城市数量后针对最小化总距离目标的有效性,实验结果如表6所示。

表6 限制最大访问数量后的性能测试结果
Table 6 Performance test results after limiting the maximum number of accesses

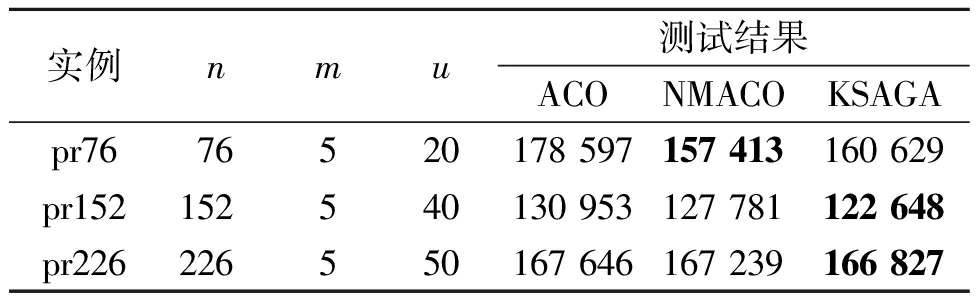
实例nmu测试结果ACONMACOKSAGApr7676520178 597157 413160 629pr152152540130 953127 781122 648pr226226550167 646167 239166 827

表6中n为城市数量;m为旅行商数量;u为每个旅行商对城市的最大访问数量。在pr76测试集中,表现最优的算法为NMACO,其次是KSAGA方法。但是随着问题规模的扩大,KSAGA算法展现出优势,逐步超越了NMACO算法,这不但证明了提出方法的有效性,还证明了所提方法对大规模问题求解的有效性。

3.5 算法收敛速度测试

由于GA、NSGA-Ⅱ以及本文所提出的方法均构建在遗传算法的基础上,因此通过对这些算法的收敛性进行比较,以评估它们在求解MTSP过程中的性能表现。测试数据集选择TSPLIB实例berlin52,旅行商数量设置为5,3种算法收敛效果如图6所示。

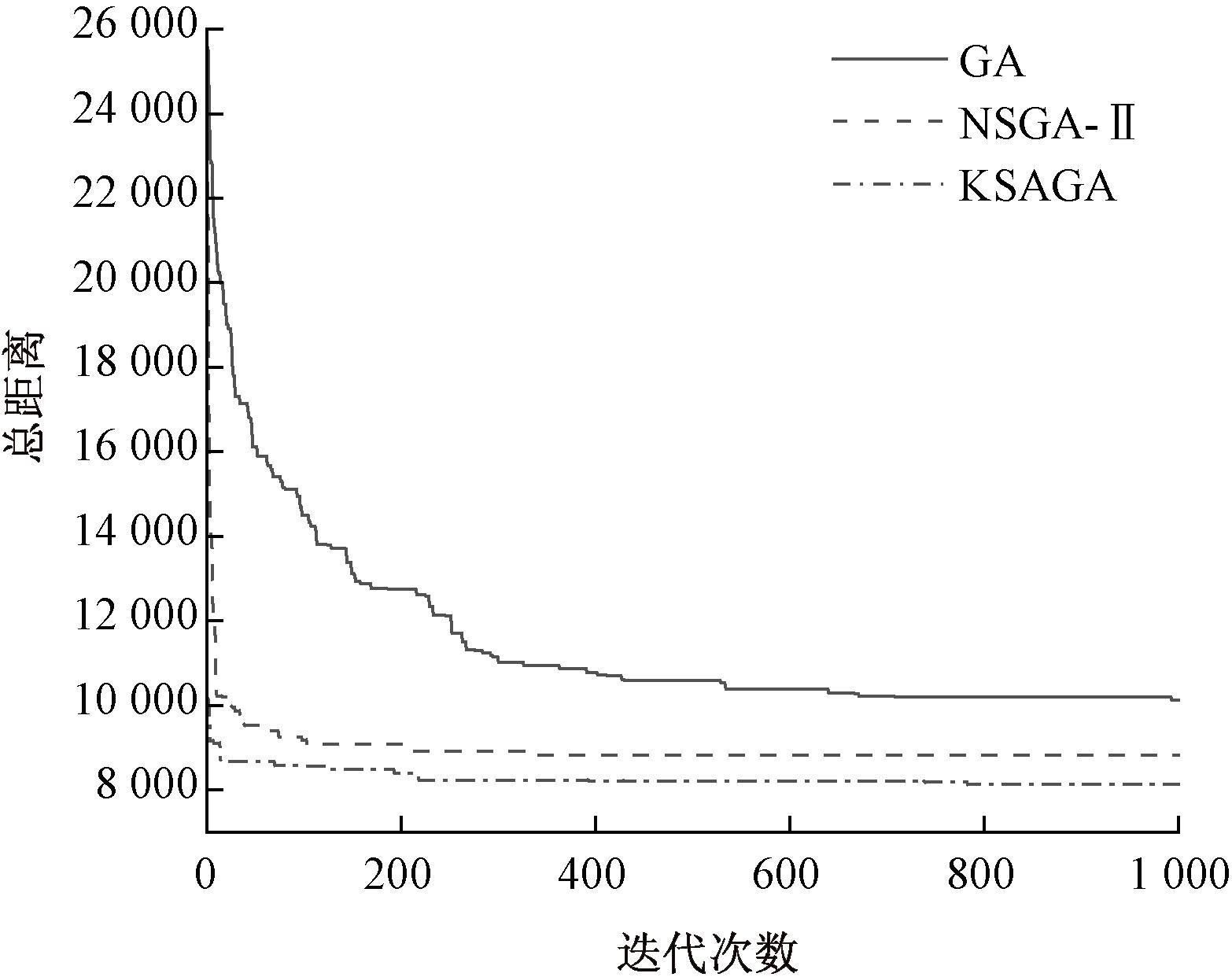
图6 相同迭代次数下算法的收敛曲线
Figure 6 Convergence curve of the algorithm with the same number of iterations

从图6可以看出,在相同的迭代次数下,KSAGA都有比GA和NSGA-Ⅱ更快的收敛速度。所提算法通过聚类和贪心操作初始化一个可行解的方式以及引入局部优化算子,都加快了算法的收敛效率。在NSGA-Ⅱ已经开始趋于平稳时,KSAGA中依然还有更好的解产生,种群的多样性得到了保证。在相同条件下,KSAGA从收敛速度及精度上都优于其他2个算法。

4 结论

针对单站点多旅行商的最小化总距离问题,本文采用了分阶段优化策略,结合SA和GA这2个算法对问题进行求解,并提出了适用于分组遗传算法的交叉、变异算子。在Spark环境下利用并行机制加快遗传算法的运行效率,同时增加解的搜索空间。通过多次实验确定了遗传算法重要参数的取值,与其他2个遗传算法在相同迭代次数下对收敛速度进行对比,实验验证了KSAGA的收敛速度更快,且求解质量相比于其他算法得到很大提升。

由于旅行商数量达到一定阈值后,继续增加不会使效率明显提高反而可能会造成资源浪费,旅行商最佳分配数量在参考其他文献得到取值范围后,分别取范围内的值进行多次仿真实验,通过分析各个取值下算法的收敛速度和结果精度确定单站点多旅行商问题中的最佳旅行商数量,但由于此方法在大规模数据集中缺乏有效性,如何在不同数据集中确定最优旅行商数量的问题仍需进一步深入研究。目前对于MTSP的研究主要集中在如何最小化所有销售商的距离之和上,但实际应用中,若优先考虑的是所有的城市访问时间而不是距离、业务员的工作量或者是推销员的成本限制,则单站点多旅行商的求解目标变换为最小化最大访问距离求解,因此后续工作可基于此对KSAGA算法做进一步的改进,使其更加贴近于实践应用。

参考文献：

[1] 苏守宝, 赵威, 李智. 求解加权MTSP问题的CUDA并行群智能方法[J]. 郑州大学学报(工学版), 2021, 42(6): 34-41.
SU S B, ZHAO W, LI Z. CUDA-based parallel swarm intelligence method for solving weighted MTSP[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(6): 34-41.

[2] MOHAMMAD S, MAJID Y, NARGES M. An effective genetic algorithm for solving the multiple traveling salesman problem[J]. Journal of Optimization in Industrial Engineering, 2011, 4: 73-79.

[3] YANG S, SHAO Y F, ZHANG K. An effective method for solving multiple travelling salesman problem based on NSGA-Ⅱ[J]. Systems Science &Control Engineering, 2019, 7(2): 108-116.

[4] HARRATH Y, SALMAN A F, ALQADDOUMI A, et al. A novel hybrid approach for solving the multiple traveling salesmen problem[J]. Arab Journal of Basic and Applied Sciences, 2019, 26(1): 103-112.

[5] 董建华, 王国胤, 雍熙, 等. 基于Spark的标准化PCA算法[J]. 郑州大学学报(工学版), 2017, 38(5): 7-12.
DONG J H, WANG G Y, YONG X, et al. Normalized PCA algorithm based on Spark[J]. Journal of Zhengzhou University (Engineering Science), 2017, 38(5): 7-12.

[6] ZHENG J Z, HONG Y W, XU W C, et al. An effective iterated two-stage heuristic algorithm for the multiple traveling salesmen problem[J]. Computers &Operations Research, 2022, 143: 105772.

[7] 冯兴杰, 王文超. Hadoop与Spark应用场景研究[J]. 计算机应用研究, 2018, 35(9): 2561-2566.
FENG X J, WANG W C. Survey on Hadoop and Spark application scenarios[J]. Application Research of Computers, 2018, 35(9): 2561-2566.

[8] 孙鉴, 刘凇佐, 武晓晓, 等. 基于Spark的并行模拟退火算法求解TSP[J]. 电子测量技术, 2022, 45(4): 53-58.
SUN J, LIU S Z, WU X X, et al. Solving TSP based on Spark-based parallel simulated annealing algorithm[J]. Electronic Measurement Technology, 2022, 45(4): 53-58.

[9] AL-FURHUD M A,AHMED H Z. Genetic algorithms for the multiple travelling salesman problem[J]. International Journal of Advanced Computer Science and Applications, 2020, 11(7): 553-560.

[10] 杨帅. 求解多旅行商问题的进化多目标优化和决策算法研究[D]. 武汉: 武汉科技大学, 2021.
YANG S. Research on evolutionary multi-objective optimization and decision making for solving multiple traveling salesman problem[D]. Wuhan: Wuhan University of Science and Technology, 2021.

[11] 孙冰, 王川, 杨强, 等. 面向多起点均衡多旅行商问题的进化算法[J]. 计算机工程与设计, 2023, 44(7): 2030-2038.
SUN B, WANG C, YANG Q, et al. Improved evolutionary algorithm for balanced multiple traveling salesmen problem with multiple starting points[J]. Computer Engineering and Design, 2023, 44(7): 2030-2038.

[12] 王勇臻, 陈燕, 于莹莹. 求解多旅行商问题的改进分组遗传算法[J]. 电子与信息学报, 2017, 39(1): 198-205.
WANG Y Z, CHEN Y, YU Y Y. Improved grouping genetic algorithm for solving multiple traveling salesman problem[J]. Journal of Electronics &Information Technology, 2017, 39(1): 198-205.

[13] PAN J J, WANG D W. An ant colony optimization algorithm for multiple travelling salesman problem[C]∥First International Conference on Innovative Computing, Information and Control. Piscataway: IEEE, 2006: 210-213.

[14] KIR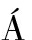LY A, ABONYI J. A novel approach to solve multiple traveling salesmen problem by genetic algorithm[J]. Computational Intelligence in Engineering, 2010, 313: 141-151.

[15] 孙鉴, 李昊, 刘凇佐, 等. 基于Spark的并行k均值聚类模拟退火算法求解MMTSP[J]. 电子测量技术, 2022, 45(20): 53-60.
SUN J, LI H, LIU S Z, et al. Spark-based parallel k-means clustering simulated annealing algorithm to solve MMTSP[J]. Electronic Measurement Technology, 2022, 45(20): 53-60.

[16] HUANG K Y, MA J B, LIU X Y. Research on vehicle route planning with capacity limitation based on adaptive large-scale neighborhood search algorithm[C]∥2021 6th International Symposium on Computer and Information Processing Technology (ISCIPT). Piscataway: IEEE, 2021: 6-10.

[17] YOUSEFIKHOSHBAKHT M, DIDEHVAR F, RAHMATI F. Modification of the ant colony optimization for solving the multiple traveling salesman problem[J]. Romanian Journal of Information Science and Technology, 2013, 16(1): 65-80.

Solving MTSP with Two-stage SA and GA Based on Spark

SUN Jian1,2, LIU Pin1, LI Hao1, CHEN Pan1

(1.School of Computer Science and Engineering,North Minzu University, Yinchuan 750021, China; 2.The Key Laboratory of Images and Graphics Intelligent Processing of State Ethnic Affairs Commission, North Minzu University, Yinchuan 750021, China)

Abstract：A two-stage KSAGA algorithm combining Spark-based simulated annealing and genetic algorithms was proposed for the single-depot multiple traveling salesman problem with minimum total path length. In the first stage, the multiple traveling salesman problem was split into multiple single traveling salesman problems by k-means clustering, and the traversal order of cities in the group was optimized using the simulated annealing algorithm. In the second stage, the classification of cities was optimized by genetic algorithm, and the cross-variance operator as well as the hybrid local optimization operator were designed based on the chromosome grouping encoding method to improve the search space and convergence speed of the algorithm. As the number of cities increased and the computational scale became larger, the characteristics of genetic algorithm were used to realize the parallelism of the algorithm in order to speed up the algorithm operation efficiency. Finally, the solution quality of KSAGA was compared with that of ACO, GA, SPKSA, ALNS and NSGA-Ⅱ and the convergence speed of GA and NSGA-Ⅱ by selecting some datasets of TSPLIB for simulation experiments. The results showed that KSAGA could converge quickly in solving the single-depot multiple traveling salesman problem, and the solution quality was greatly improved compared with other algorithms. Meanwhile, the advantage of KSAGA was more obvious as the number of cities and the number of travelers increased.

Keywords：MTSP; parallel; genetic algorithm; group encoding; local optimization operator

中图分类号： TP301.6

文献标志码：A

doi：10.13705/j.issn.1671-6833.2024.01.019

收稿日期：2023-07-26;修订日期：2023-09-15

基金项目：国家自然科学基金资助项目(62062002);宁夏自然科学基金资助项目(2022AAC03289,2022AAC03245,2022AAC03261)

作者简介：孙鉴(1982—),男,山东烟台人,北方民族大学讲师,博士,主要从事大数据存储与管理等研究,E-mail:2014132@nun.edu.cn。

引用本文：孙鉴,刘品,李昊,等. 基于Spark的双阶段SA及GA求解MTSP[J]. 郑州大学学报(工学版),2024,45(4):62-69, 94.(SUN J, LIU P, LI H,et al. Solving MTSP with two-stage SA and GA based on Spark[J].Journal of Zhengzhou University (Engineering Science),2024,45(4):62-69, 94.)

文章编号：1671-6833(2024)04-0062-08