全局中心聚类算法如k-means、谱聚类等凭借其算法的高效、易移植、易推广等特点仍流行于目前绝大多数应用领域。此类算法旨在寻找全局上的簇中心以发现真实的类簇,因此将该类算法统称为全局中心聚类算法。相较基于密度带噪声应用的空间聚类算法(density-based spatial clustering of applications with noise, DBSCAN)[1]、均值漂移算法(mean-shift, MS)[2]、密度峰值聚类算法(density peaks clustering, DPC)[3-4]等,全局中心聚类算法的一大优势在于不易引发链式效应(chain effect)而导致簇的错误合并。但此类算法对样本空间中簇的凸型与良好分离假设具有较强的依赖性,并且对所选初始簇中心的位置较为敏感,容易陷入局部最优解。特别在实际问题中,数据多数特征不具有明显的区分度,这导致簇间重叠问题难以避免,其严重影响了算法对真实簇中心的识别准确率,并加剧了算法的局部收敛问题。
近年来,许多学者对全局中心聚类算法做出了一系列的改进工作,包括引入分裂融合技术提高算法自适应性[5-6],定义新的距离度量方式以改善算法局部收敛问题[7-10]。虽然目前的各种改进算法从理论方法上对传统算法进行了优化,但其并没有放宽全局中心聚类算法对良好分离假设的依赖,当数据集内簇的分布情况欠佳时,算法的聚类效果仍然不理想。边界剥离算法(border peeling, BP)[11]通过在算法过程中排除簇边缘的样本点或离群点,使得聚类结果更加稳健。BP算法将边界点定义为局部密度较低的点,其迭代剥离低密度样本点以发现簇的核心区域,进一步利用DBSCAN算法对高密度点进行聚类,最终将边界点按剥离路径逆向合并到每个簇中。作为一种针对密度型算法的改进,BP算法能够有效改善簇间重叠问题从而克服链式效应的不良影响,但迭代剥离过程受局部密度差异性的影响,迭代终止条件较难确定且计算复杂。ROBP[12]作为BP算法的一种改进,其利用Cauchy核函数进行密度估计中的局部放缩处理,并设计了一种基于共享邻域信息的链接准则,能够从一定程度上缓解局部密度差异性带来的影响并提高算法稳健性,但仍然使用迭代方式进行边界剥离,计算效率与终止条件的设定问题难以解决。
为克服簇间重叠所导致的局部收敛问题,本文提出一种基于边界剥离思想的全局中心聚类算法(border-peeling inspired globally central clustering algorithm, BPCC)。该算法的核心过程主要为边界剥离和边界吸引两个步骤。不同于上述的BP算法,此处的边界剥离方式不再是通过逐层迭代来识别边界点,而是通过样本点间的反向k近邻关系定义样本点密度,并利用密度的经验分布函数自动确定分割阈值并一次性地剥离所有边界点。较BP算法而言,设计的一步边界剥离法对数据的局部密度差异不再敏感,且无须额外设定烦琐的终止条件,能够快速地剥除边界点以提高簇间分离度,从而显著降低被保留核心点所在区域内的簇间重叠程度,有效改善全局中心聚类算法的收敛状况。在边界吸引过程中利用已有的反向k近邻关系,从已分配标签的核心点出发,通过迭代将边界点重新划归到各个类簇,其过程中不产生额外的距离计算。
1 全局中心聚类算法
1.1 k-means聚类算法
k-means 聚类算法是最具代表性的全局中心聚类算法,其核心思想为将每个样本点分配到距离最近的中心点所在的簇中,因此类标签与簇中心实则为聚类目标的一体两面。换而言之,如何准确地找到簇中心是最为关键的问题。对于一组数据X=[x1,x2,…,xn]∈Rn×p,其中n为数据量,p为数据维数,给定一个整数K,存在一组划分为 C={C1,C2,…,CK}的集合,则k-means问题[13]一般被描述为如下的最小化目标函数问题:
(1)
式中:![]() 代表第j个簇中心。
代表第j个簇中心。
由于类标签的{0,1}属性,上述最小化目标为NP-hard问题,无法通过目标函数直接求解,因此诞生了目前被广泛使用的k-means算法(lloyd′s algorithm)[14]。该算法通过在分配样本点与更新簇中心两个步骤间的迭代得到上述问题的局部最优解, 其算法复杂度仅为O(n),但却对初始条件十分敏感,容易陷入不理想的局部最优解。
1.2 谱聚类算法
谱聚类算法(spectral clustering, SC)[15-16]依据图割(graph cut)的思想发展而来,其将原始样本空间中的点看作图的顶点,通过全连接、k近邻等方式创建图的边,并由邻接矩阵W={wij}∈Rn×n表示图中两两点间的相似关系。根据图割理论,以Ncut[15]为例,谱聚类的目标函数为
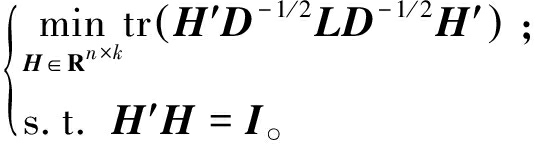
(2)
式中:H为标签矩阵;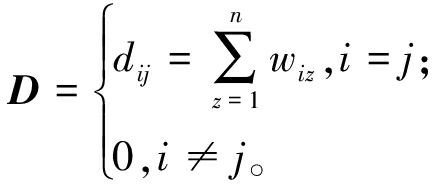 为顶点的度矩阵;L=D-W为图拉普拉斯矩阵。
为顶点的度矩阵;L=D-W为图拉普拉斯矩阵。
与k-means问题类似,由于问题(2)中的标签矩阵H是离散的,目标函数无法直接求解。而根据Ky Fan定理[17],式(2)的解存在于由拉普拉斯矩阵L最小的k个特征值所对应的特征向量所张成的空间中,因此谱聚类算法实际是对L进行特征值分解,并将前k个最小特征值所对应的特征向量作为聚类对象,最终利用k-means算法求得近似解。容易发现谱聚类算法的结果受邻接矩阵W的影响较大,因此在相同的数据集上根据不同的规则构造出的W可能带来截然不同的聚类结果。
2 BPCC算法
2.1 边界剥离
对于全局中心聚类算法,通常考虑簇的分布为正态分布或近似正态分布,即越靠近均值处(簇中心)样本点分布越集中,越远离均值处样本点分布越稀疏。为了刻画样本的聚集程度,通过样本点间的反向k近邻(reverse k-nearest neighbors, RNN)关系定义样本点的密度。对于数据集内的样本点而言,其RNN集合的大小能够从一定程度上代表该样本点局部区域内的密度,适用于发现边界点或离群点,因此借助样本点间的RNN关系,能够有效地识别数据集的边界区域。具体地,给出RNN的数学定义如下。
定义1 RNN。对于任意样本点xj,其k近邻集合为Nk(xj),则xi的反向k近邻集合为
RNk(xi)={xj|xi∈Nk(xj)}。
(3)
从定义1可以看出,RNN是一种建立在k近邻基础上的非对称关系,即xi与xj不一定互为对方的近邻点。相较于k近邻,RNN能够更加准确地反映出样本点处的密度大小,即样本点xi的RNk(xi)集合越大,其局部密度也越大。同时,RNN是一种离散关系,无法反映出RNk(xi)集合内的样本点在空间中的覆盖范围。为了更精确地定义样本点的密度,利用样本点与其Nk(xi)集合中点的平均距离作为权重,从而可以在RNN的基础上进一步定义样本点的密度。
定义2 样本点密度。对于任意样本点xi,其密度为
ρ(xi)=qi|RNk(xi)|。
(4)
式中:|·|表示集合内元素的个数;qi为xi处密度的局部距离权重,
(5)
dis(xi,xj)为样本点xi与xj的欧氏距离,
(6)
容易发现qi越小表示在xi处的k近邻范围内样本点的平均距离越大,即局部分布越稀疏,则应赋予该处较小的密度权重。
在得到每个样本点的密度后,进一步利用样本点密度的分布信息设计一种快速简洁的全局一步剥离法。
定义3 经验分布函数。设Y={Yi|i=1,2,…,n}为来自总体F的一组随机样本,则经验分布函数(empirical distribution function, EDF)可定义为
(7)
其中,I{·}为示性函数,
(8)
样本点密度的EDF能够从全局上直观地反映出密度值分布的变化情况,并且EDF为离散函数,因此一种简单有效的边界剥离方式就是取EDF数列一阶差分最大处所对应的密度值作为划分阈值。为此将样本点密度区间平均划分为S段,分段区间端点为{ρ(0),ρ(1),…,ρ(S)},则划分边界点与核心点的密度阈值为
(9)
定义4 边界点与核心点。记被剥离的样本点为bi,称为边界点,其构成的集合记为B,称为边界集;记保留的样本点为mi,称为核心点,其构成的集合记为M,称为核心集;B∩M=φ,B∪M为全数据集。
最后结合式(10)与定义4给出数据集X的全局一步剥离条件为
(10)
如图1所示,EDF为取值在[0,1]上的单调递增函数,EDF一阶差分最大处的横坐标值即为分割阈值T。
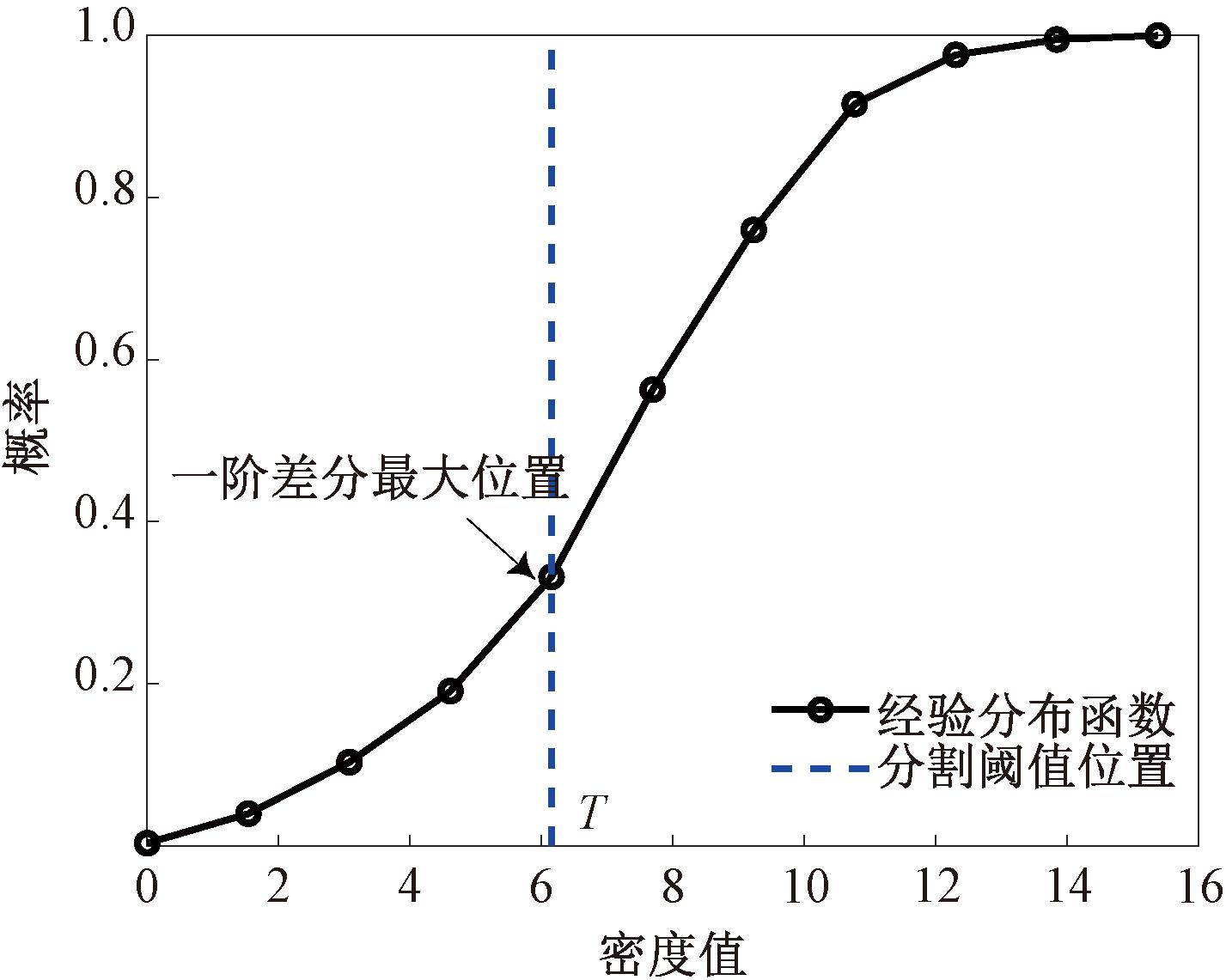
图1 由经验分布函数确定边界阈值
Figure 1 Determine the boundary threshold using empirical distribution function
2.2 聚类过程
2.2.1 嵌入全局中心聚类算法
在完成边界剥离后,嵌入k-means、谱聚类等全局中心聚类算法对核心集M进行聚类,得到所有核心点的类标签。在簇的凸型假设下,全局中心聚类算法的目标是找到真实的簇中心位置。由于M是原始数据集X的子集,并且相较于X,在M上各簇的分离结构更加清晰,能够有效避免簇间重叠问题,进而使得嵌入算法能够更容易地收敛到准确的簇中心。
2.2.2 边界吸引
在嵌入算法完成对核心集M的聚类后,各个簇中心位置已被确定且所有核心点已被归类,最后的任务则是为边界点分配类标签。从已被归类的样本点mi∈M出发,采用迭代将RNk(mi)集合内距mi最近的边界点bj划归到mi所属的类中,即I(bj)=I(mi),其中I∈Rn为类标签向量。
(11)
进一步更新核心集M和mi的RNN集合:
M=M∪{bj}。
(12)
RNk(mi)=RNk(mi)-{bj}。
(13)
如图2所示,在通过RNN关系建立的图中,核心点mi与边界点bj间存在边的连接,表示bj属于集合RNk(mi)。边界吸引过程将持续迭代至所有核心点的RNk(mi)集合均为空。在一次迭代中可能出现同一边界点被两个以上核心点吸引的情况,处理方式为将该边界点归类到最后将其吸引的核心点所在的簇中。
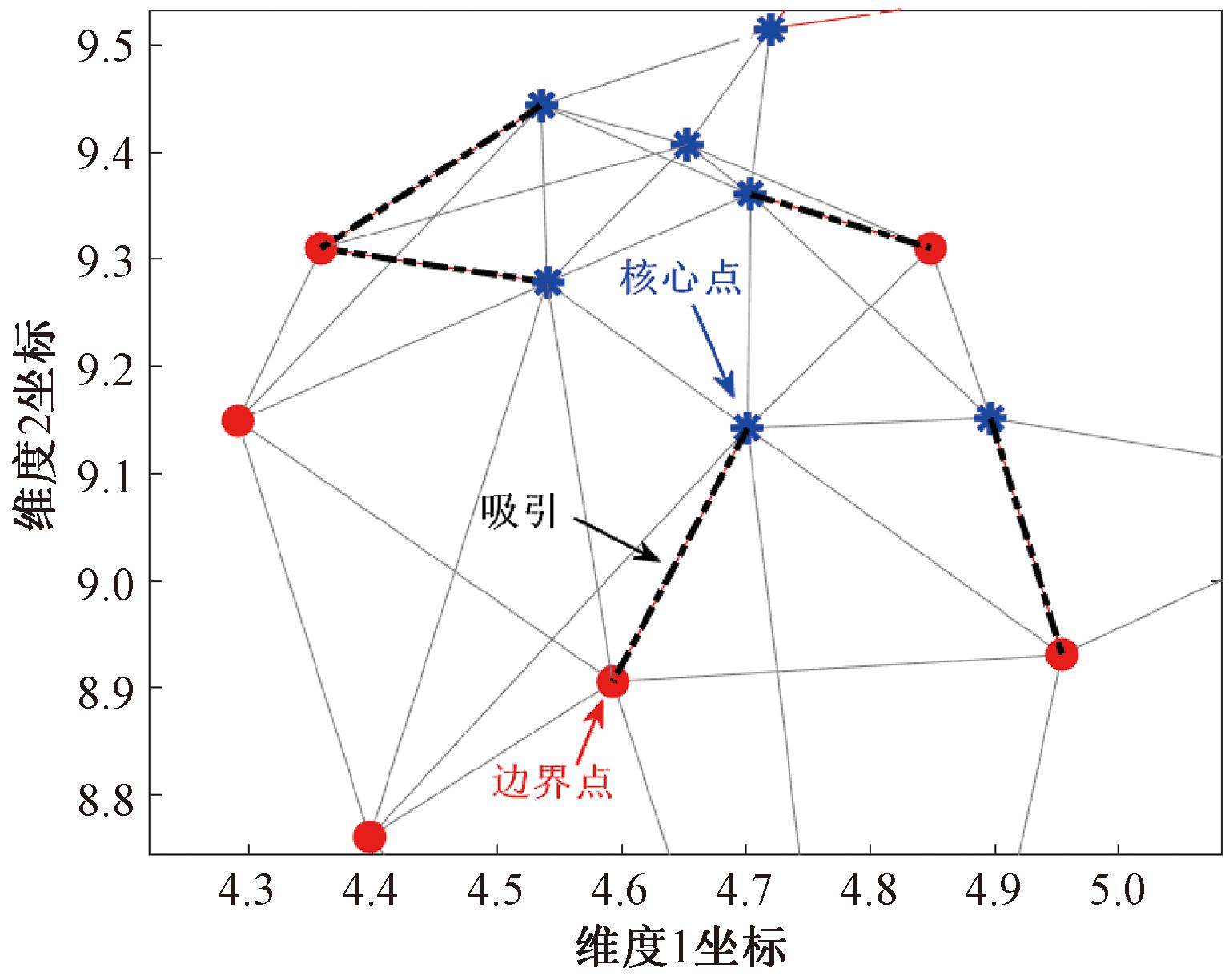
图2 D31数据集局部区域上边界吸引过程一次迭代示例
Figure 2 Example of one iteration of the boundary attraction process on local regions of D31 dataset
2.3 算法描述
综上,本文所提的BPCC算法流程如图3所示,伪代码如下。
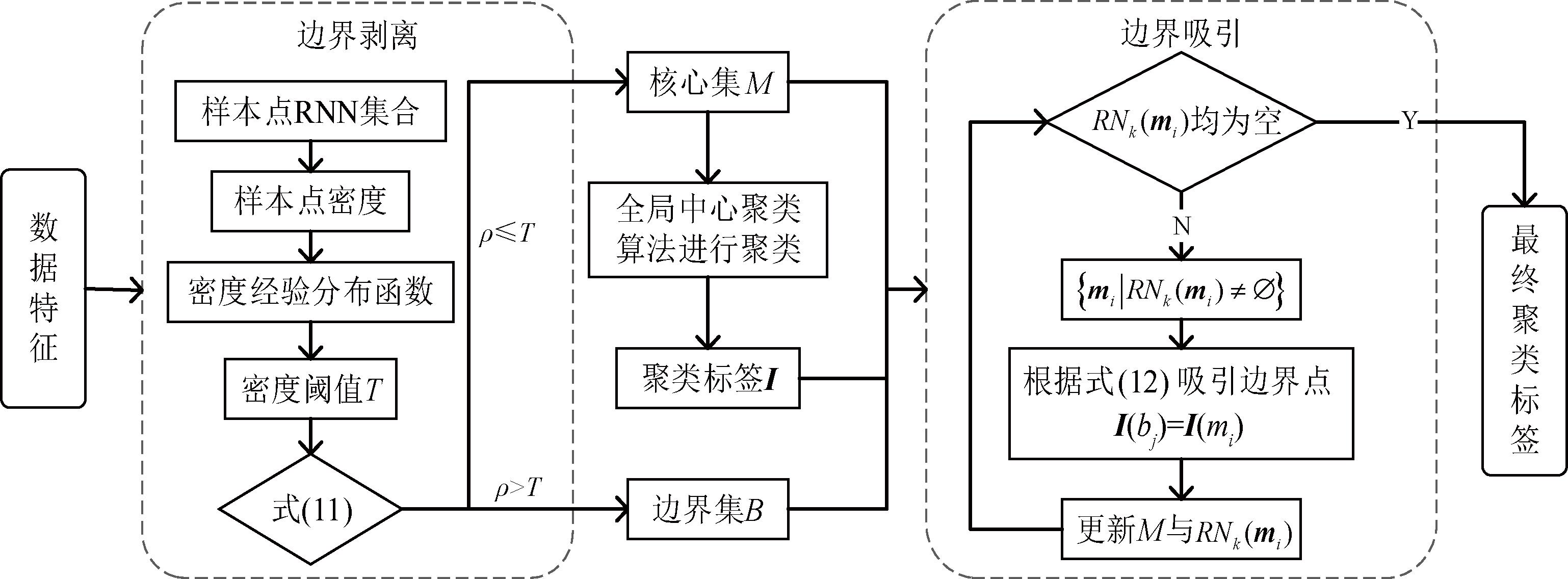
图3 BPCC算法流程
Figure 3 Flow chart of BPCC
算法1 BPCC算法。
输入:数据集X,近邻数k,簇数目K;
输出:聚类标签向量I。
#初始化
① Disn×n← 两两样本点欧式距离矩阵,其中Dis(i,j)由式(6)计算得到;
② In×1← 全0向量;
#边界剥离
③ [M, RNk] ← BP(X, k, Dis);
#嵌入算法聚类
④ I(M) ← 根据设定类簇数目K,利用全局中心聚类算法(如k-means、SC)对核心集M中的样本点进行聚类并更新标签,其余样本点标签保持为0;
#边界吸引
⑤ I ← BA(I, M, RNk);
⑥ Return I。
算法2 边界剥离(BP)算法。
输入:X,k,Dis;
输出:核心集M,样本点的RNN集合RNk。
① kNn×k← 全零矩阵,表示k近邻关系矩阵;
② For i=1:n do:
③ kN(i,:)←Dis(i,:)前k个最小距离对应的列标签,表示样本点xi的Nk(xj)集合;
④ End for
⑤ For j=1:n do:
⑥ RNk(xj) ← kN中所有包含j的行标签集合;
⑦ ρ(xj) ← 根据式(5)计算xj的密度;
⑧ End for
⑨ T ← 密度区间等分为S段(默认S=10),根据式(10)计算分割阈值;
⑩ M ← 根据式(11)找到X中的核心点集合;
 Return M,RNk。
Return M,RNk。
算法3 边界吸引(BA)算法。
输入:I,M,RNk;
输出:聚类标签向量I。
① Fn×1← 全1向量,1表示对应样本点还未被查询;
② For i=1:n do:
③ 将RNk(xi)中属于核心集M的样本点剔除;
④ IF RNk(xi)=∅do:
⑤ F(xi)← 0,表示xi已被查询并为离群点;
⑥ End if
⑦ End for
⑧ While F不为全0向量 do:
⑨ E←M∩{xi|F(xi)=1}为还未被查询的核心点;
⑩ IF E=∅ do:
 I(F==1)← 0;
I(F==1)← 0;
 Break
Break
 End if
End if
 For m in E do:
For m in E do:
 tmp←RNk(xi)中第1个样本点;
tmp←RNk(xi)中第1个样本点;
 M←M∪{tmp};
M←M∪{tmp};
 I(tmp)←I(m);
I(tmp)←I(m);
 RNk(mi)←RNk(m)-{tmp};
RNk(mi)←RNk(m)-{tmp};
 IF RNk(m)=∅ do:
IF RNk(m)=∅ do:
 F(m)← 0;
F(m)← 0;
 End if
End if
 End for
End for
 End while
End while
 Return I。
Return I。
3 算法实验
为了验证所提BPCC算法对全局中心聚类算法的实际提升效果,本文分别在9个数据集(见表1)上进行算法的对比实验,并选择k-means算法(KM),分别以全连接、k近邻方式建立相似度矩阵的谱聚类算法SC-full、SC-KNN以及Power k-means (PKM)作为对比算法。相应地,将KM、SC-full、SC-KNN算法嵌入到BPCC中,分别称为BP-KM、BP-SC-full、BP-SC-KNN。本文所有实验的运行环境为Inter i9-13900K (5.8 GHz),32 GB RAM,Windows11 64 bit,MATLAB R2022b。由于实验数据集具有真实类标签,本文利用3个外部评价指标:纯度Purity[18]、归一化互信息NMI[19]、调整的兰德指数ARI[20]评价聚类算法的效果,其中Purity和NMI取值为[0,1],ARI取值为[-1,1],各指标得分值越大,说明聚类效果越理想。
表1 实验数据集
Table 1 Experimental datasets
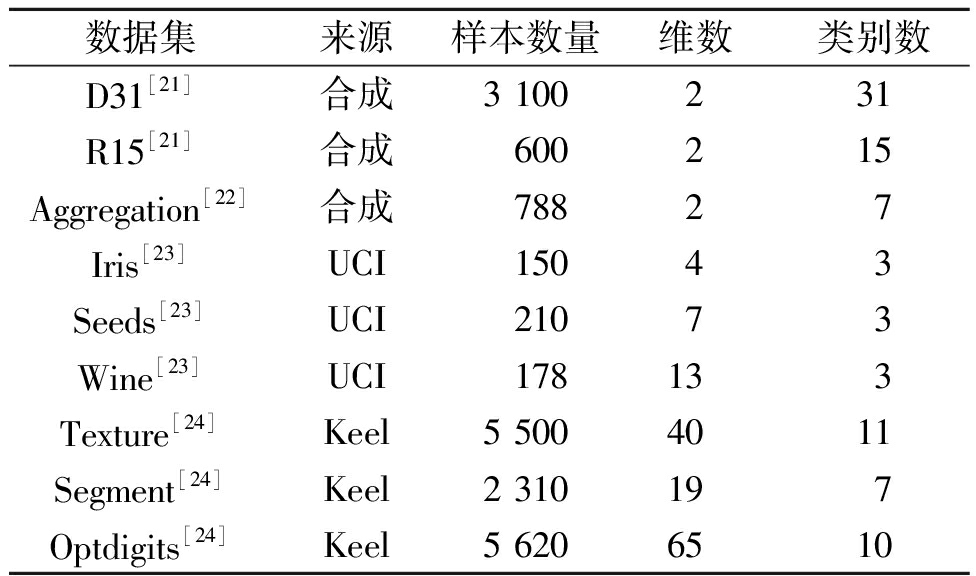
数据集来源样本数量维数类别数D31[21]合成3 100231R15[21]合成600215Aggregation[22]合成78827Iris[23]UCI15043Seeds[23]UCI21073Wine[23]UCI178133Texture[24]Keel5 5004011Segment[24]Keel2 310197Optdigits[24]Keel5 6206510
3.1 合成数据集实验分析
对比实验中,合成数据集选择了D31、R15、Aggregation,所有算法的簇数目参数均指定为各个数据集的真实簇数目,SC-KNN以及BPCC算法中需要指定的近邻参数k的取值见表2,下文中真实数据集上的参数设置相同,故后不赘述。图4展示了近邻参数k=8时所提方法的边界剥离效果,可以看到分布在各个簇边界的样本点基本被识别为边界点,保留的核心点所在区域内的簇间重叠粘连现象得到明显改善。
表2 最优聚类结果中近邻参数k的取值
Table 2 Parameter setting of k in optimal clustering results
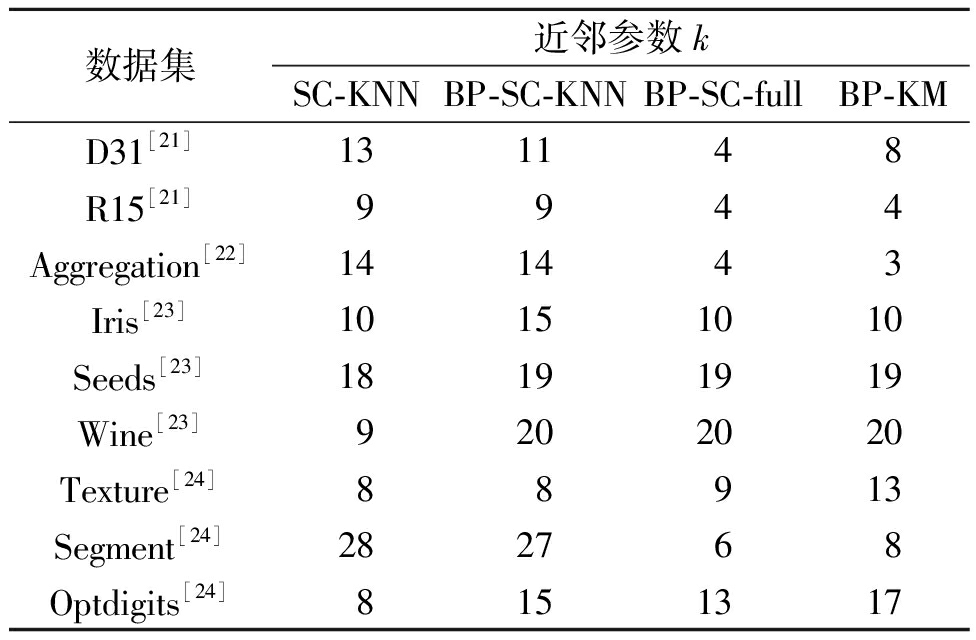
数据集近邻参数kSC-KNNBP-SC-KNNBP-SC-fullBP-KMD31[21]131148R15[21]9944Aggregation[22]141443Iris[23]10151010Seeds[23]18191919Wine[23]9202020Texture[24]88913Segment[24]282768Optdigits[24]8151317
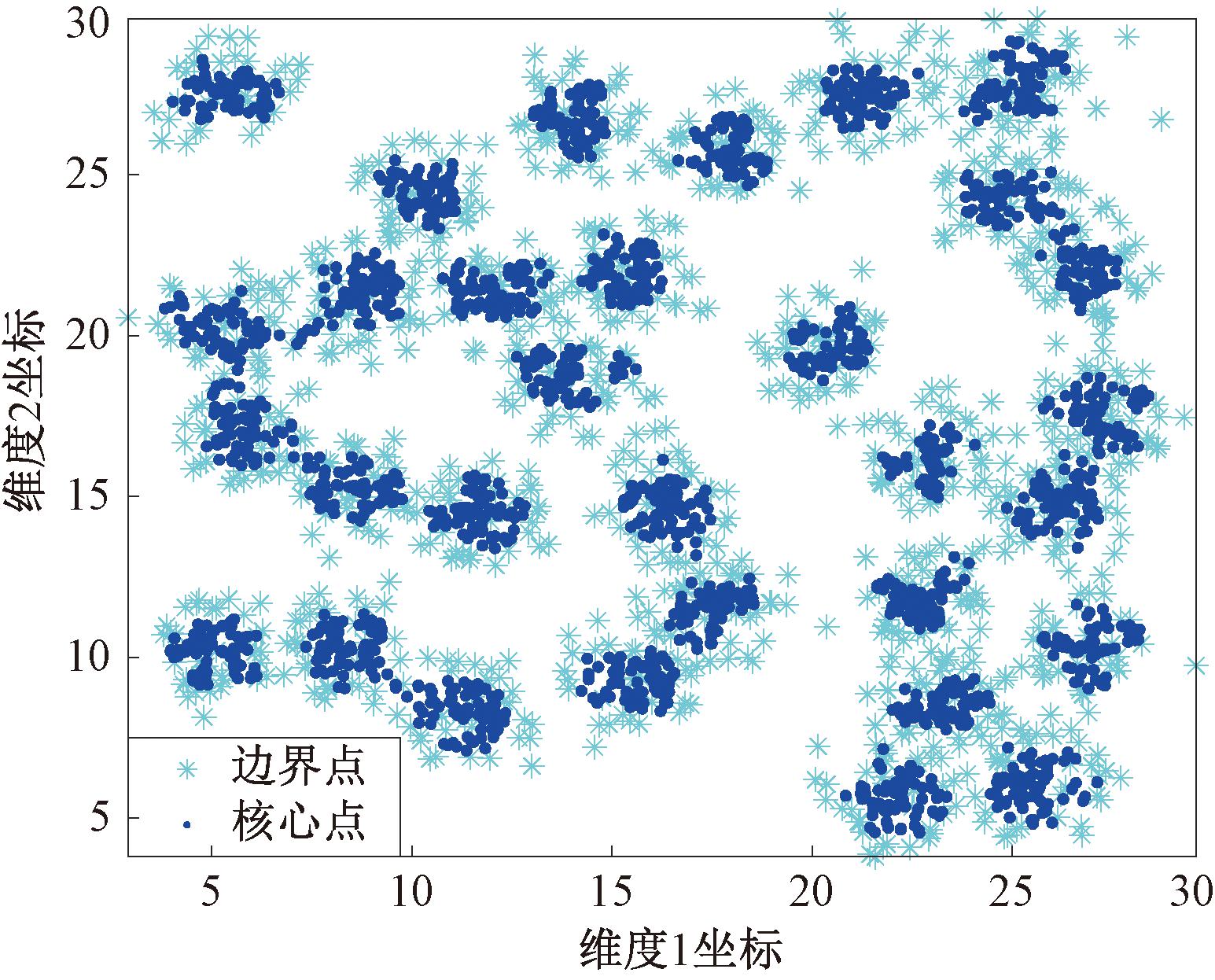
图4 D31数据集上全局一步剥离法效果
Figure 4 The performance of the global one-step peeling method on the D31 dataset
实验结果如表3所示,在合成数据集的理想环境下,BPCC的聚类结果并不一定优于传统全局中心聚类算法,但也十分接近。需要说明的是,出现此种情况是符合预期的,因为合成数据本身具有良好的簇分布,簇间重叠粘连问题本不严重,传统全局中心聚类算法也能收敛到准确的簇中心,这便导致边界剥离的作用十分有限。另一方面,由于边界吸引过程省略了样本点到中心点的距离计算,反而造成在部分数据集上BPCC的结果略逊于直接使用原始算法的结果。
表3 合成数据集聚类结果比较
Table 3 Comparison of clustering results for synthetic datasets

方法D31数据集R15数据集Aggregation数据集PurityNMIARIPurityNMIARIPurityNMIARIKM0.890 00.935 20.860 40.996 70.994 20.992 80.810 90.845 30.737 1BP-KM0.949 40.937 70.899 60.993 30.989 30.985 90.847 70.891 10.797 7SC-full0.976 50.96700.952 20.996 70.994 20.992 80.993 70.982 40.986 9BP-SC-full0.960 30.948 60.920 60.993 30.989 30.985 90.991 10.980 90.979 9SC-KNN0.695 20.828 20.605 60.985 00.977 70.967 80.748 70.791 20.653 8BP-SC-KNN0.928 70.920 20.861 80.991 70.986 40.982 10.988 60.970 30.976 9PKM0.822 30.886 90.754 90.851 70.856 20.746 20.888 30.860 10.854 0
3.2 真实数据集实验结果
真实数据集选择了Iris、Seeds、Wine、Texture、Segment、Optdigits,与合成数据集显著的差别在于更高的维数会导致簇间重叠问题加剧。考虑到其中部分数据集不同维度的量纲差异较大,因此利用Z-score标准化方法对Wine、Segment、Optdigits 3个数据集进行了标准化处理。实验结果如表4、表5所示。
表4 UCI数据集聚类结果比较
Table 4 Comparison of clustering results for UCI datasets
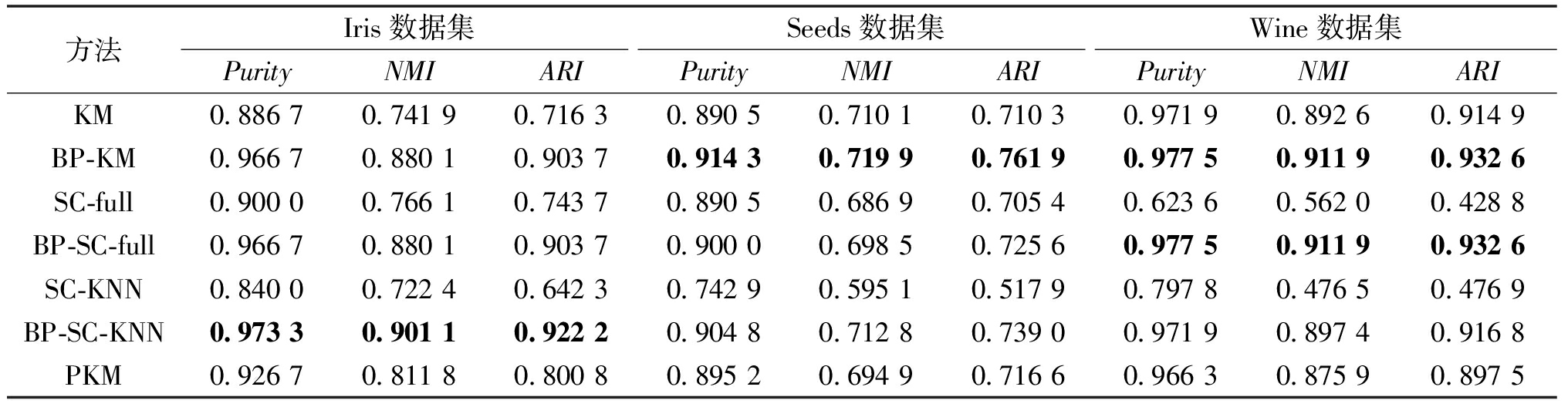
方法Iris数据集Seeds数据集Wine数据集PurityNMIARIPurityNMIARIPurityNMIARIKM0.886 70.741 90.716 30.890 50.710 10.710 30.971 90.892 60.914 9BP-KM0.966 70.880 10.903 70.914 30.719 90.761 90.977 50.911 90.932 6SC-full0.900 00.766 10.743 70.890 50.686 90.705 40.623 60.562 00.428 8BP-SC-full0.966 70.880 10.903 70.900 00.698 50.725 60.977 50.911 90.932 6SC-KNN0.840 00.722 40.642 30.742 90.595 10.517 90.797 80.476 50.476 9BP-SC-KNN0.973 30.901 10.922 20.904 80.712 80.739 00.971 90.897 40.916 8PKM0.926 70.811 80.800 80.895 20.694 90.716 60.966 30.875 90.897 5
表5 Keel数据集聚类结果比较
Table 5 Comparison of clustering results for Keel datasets
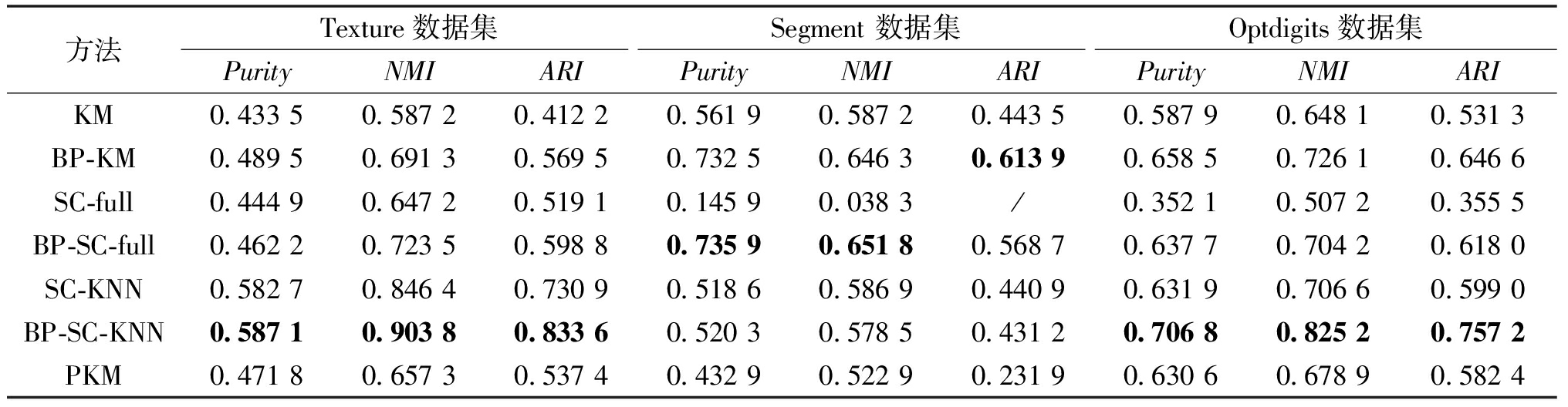
方法Texture数据集Segment 数据集Optdigits数据集 PurityNMIARIPurityNMIARIPurityNMIARIKM0.433 50.587 20.412 20.561 90.587 20.443 50.587 90.648 10.531 3BP-KM0.489 50.691 30.569 50.732 50.646 30.613 90.658 50.726 10.646 6SC-full0.444 90.647 20.519 10.145 90.038 3/0.352 10.507 20.355 5BP-SC-full0.462 20.723 50.598 80.735 90.651 80.568 70.637 70.704 20.618 0 SC-KNN0.582 70.846 40.730 90.518 60.586 90.440 90.631 90.706 60.599 0 BP-SC-KNN0.587 10.903 80.833 60.520 30.578 50.431 20.706 80.825 20.757 2PKM0.471 80.657 30.537 40.432 90.522 90.231 90.630 60.678 90.582 4
注:“/”代表数值小于5×10-4。
3.3 参数敏感性分析
此外,BPCC依赖于样本点间的RNN关系以确定样本点的密度,因此近邻参数k的选取会直接影响边界剥离的效果,并且由此参数所确定的RNN集合还将进一步决定边界吸引过程中边界点的类标签分配,因此有必要对参数k进行敏感性分析,以验证所提算法的稳健性。具体而言,本文取k在[3,30],k为整数,分别在9个数据集上以BP-KM进行实验。实验结果如图5所示,在较大的参数取值范围中,所提算法在大部分数据集上的表现并没有出现明显的波动,且呈现出样本量越大,参数表现越稳定的趋势。由此可见,BPCC对近邻参数k并不敏感,其在实际使用中的效果不易受到参数选择的制约。

图5 BP-KM分别取k 在[3,30]聚类结果的NMI值
Figure 5 NMI values of clustering results with parameter k in[3, 30] for BP-KM respectively
3.4 时间消耗分析
3.4.1 时间复杂度分析
BPCC的时间消耗主要由3部分构成:①边界剥离阶段需要借助RNN关系计算每个样本点的密度,为此需要计算样本点间的两两距离,其计算复杂度为O(n2);②需要利用全局中心聚类算法对核心集进行聚类,这部分的时间复杂度取决于嵌入算法,如利用k-means则计算复杂度为O(|R|),而谱聚类由于会进行SVD分解,计算复杂度通常达到O(![]() ),其中|R|为核心点个数;③在边界吸引过程中需要使用双层循环合并核心点的RNN集合内还未被归类的边界点,由于迭代过程中R会反复更新,导致迭代次数无法确定,但一定小于n,故该部分的计算复杂度将小于O(n2)。综上,BPCC的全局计算效率在很大程度上取决于嵌入算法的时间复杂度。
),其中|R|为核心点个数;③在边界吸引过程中需要使用双层循环合并核心点的RNN集合内还未被归类的边界点,由于迭代过程中R会反复更新,导致迭代次数无法确定,但一定小于n,故该部分的计算复杂度将小于O(n2)。综上,BPCC的全局计算效率在很大程度上取决于嵌入算法的时间复杂度。
3.4.2 模拟数据实验分析
为进一步验证算法效率,随机生成5组包含5个类簇且样本数量分别为{500, 1 000, 5 000, 10 000, 20 000}的二维模拟数据集进行时间消耗对比,实验结果如图6所示。当嵌入算法为 KM时,时间消耗由边界剥离步骤主导,会慢于直接使用KM算法;当嵌入算法为SC-full时,时间消耗则由嵌入算法主导,得益于边界点不参与嵌入算法聚类,BP-SC-full的运行时间显著短于SC-full。因此对于计算复杂度较高的全局中心聚类算法,BPCC能够从聚类效果和计算效率两方面带来提升。
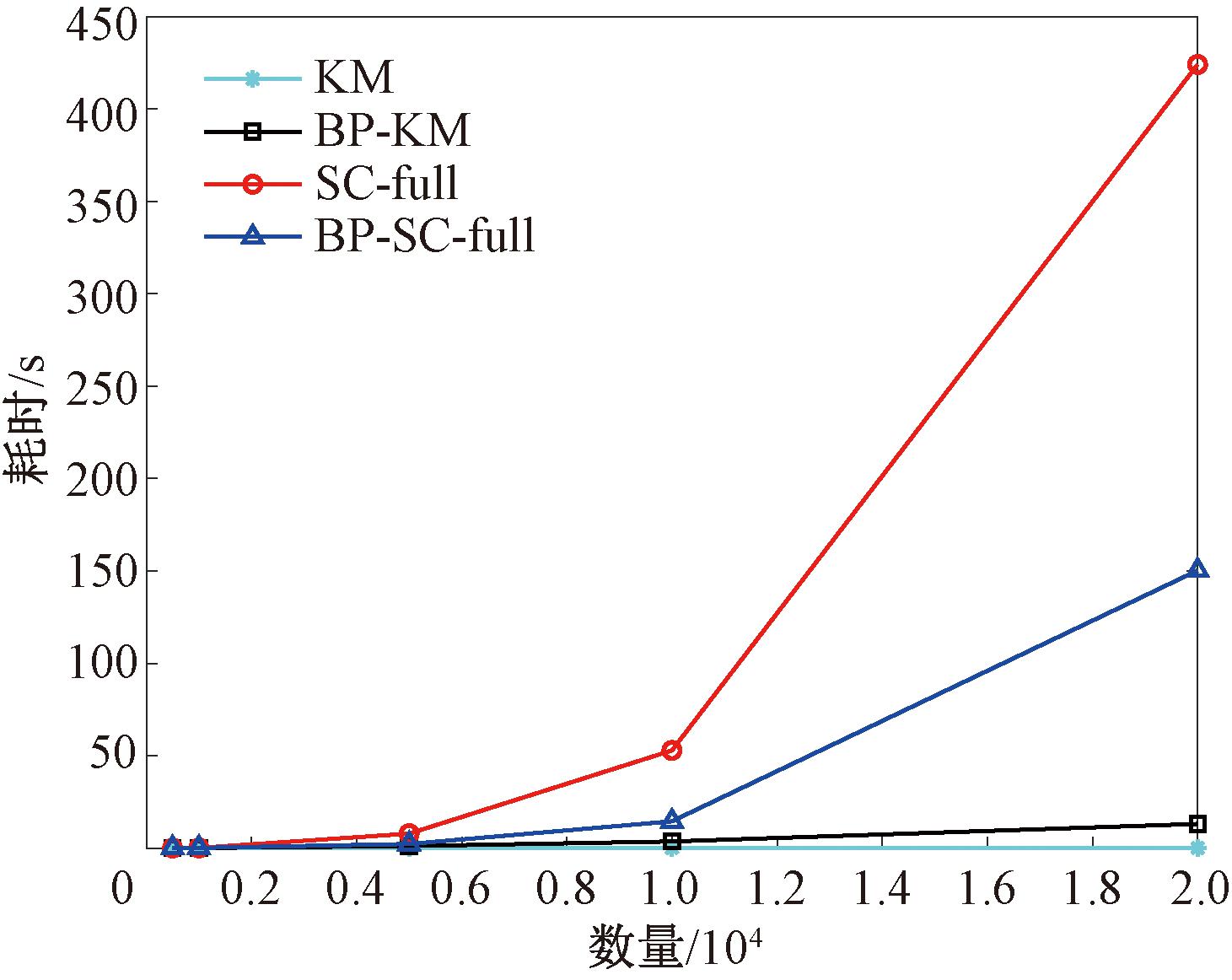
图6 不同算法时间消耗对比
Figure 6 Time consumption comparison of different algorithms
4 结论
本文提出一种基于边界剥离思想的全局中心聚类算法BPCC。所提算法根据样本点密度的经验分布将样本点快速划分为边界点与核心点。得益于核心集上簇的优良分布,利用全局中心聚类算法能够准确地对核心集进行划分,进一步利用已有的RNN关系将边界点分配至各簇,完成最终聚类。实验结果表明,BPCC能够有效解决簇边界区域重叠所造成的局部收敛问题,提升全局中心聚类算法的聚类表现,特别在实际数据集上优势明显。此外,该算法不会产生高昂的计算成本,在嵌入谱聚类等计算复杂度较高的算法时,还能额外缩减计算成本,提高算法效率。另一方面,虽然BPCC对近邻参数k不敏感,有利于实际使用,但其仍然需要人为指定簇数目K,因此该算法在参数自适应性上仍存在提升空间,在未来工作中可考虑引入基于分裂融合策略的聚类算法,以放宽需要指定簇数目作为先验条件的限制,进一步提升算法的适用性。
[1] ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]∥Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. Palo Alto: AAAI, 1996: 226-231.
[2] COMANICIU D, MEER P. Mean shift: a robust approach toward feature space analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619.
[3] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496.
[4] GUO W J, WANG W H, ZHAO S P, et al. Density peak clustering with connectivity estimation[J]. Knowledge-Based Systems, 2022, 243: 108501.
[5] CHENG M C, MA T F, LIU Y B. A projection-based split-and-merge clustering algorithm[J]. Expert Systems with Applications, 2019, 116: 121-130.
[6] SIERANOJA S, FR NTI P. Adapting k-means for graph clustering[J]. Knowledge and Information Systems, 2022, 64(1): 115-142.
NTI P. Adapting k-means for graph clustering[J]. Knowledge and Information Systems, 2022, 64(1): 115-142.
[7] HUANG J Z, NG M K, RONG H Q, et al. Automated variable weighting in k-means type clustering[J] . IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5) : 657-668.
[8] ZHANG Y Q, CHEUNG Y M. A new distance metric exploiting heterogeneous interattribute relationship for ordinal-and-nominal-attribute data clustering[J]. IEEE Transactions on Cybernetics, 2022, 52(2): 758-771.
[9] 周成龙, 陈玉明, 朱益冬. 粒K均值聚类算法[J]. 计算机工程与应用, 2023, 59(13): 317-324.ZHOU C L, CHEN Y M, ZHU Y D. Granular K-means clustering algorithm[J]. Computer Engineering and Applications, 2023, 59(13): 317-324.
[10] 邓秀勤, 郑丽苹, 张逸群, 等. 基于新的距离度量的异构属性数据子空间聚类[J]. 郑州大学学报(工学版), 2023, 44(2):53-60.DENG X Q, ZHENG L P, ZHANG Y Q, et al. Subspace clustering of heterogeneous-attribute data based on a new distance metric[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(2):53-60.
[11] AVERBUCH-ELOR H, BAR N, COHEN-OR D. Border-peeling clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(7): 1791-1797.
[12] DU M J, WANG R, JI R, et al. ROBP a robust border-peeling clustering using Cauchy kernel[J]. Information Sciences, 2021, 571: 375-400.
[13] CAP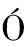 M, PÉREZ A, LOZANO J A. An efficient split-merge re-start for the K-means algorithm[J]. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(4): 1618-1627.
M, PÉREZ A, LOZANO J A. An efficient split-merge re-start for the K-means algorithm[J]. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(4): 1618-1627.
[14] LLOYD S. Least squares quantization in PCM[J]. IEEE Transactions on Information Theory, 1982, 28(2): 129-137.
[15] SHI J B, MALIK J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905.
[16] VON LUXBURG U. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4): 395-416.
[17] ZHA H Y, HE X F, DING C, et al. Spectral relaxation for K-means clustering[C]∥Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic.Cambridge: MIT, 2001: 1057-1064.
[18] ZHANG X L, WANG W, N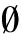 RVÅG K, et al. K-AP: generating specified K clusters by efficient affinity propagation[C]∥Proceedings of the 2010 IEEE International Conference on Data Mining. Piscataway: IEEE, 2010: 1187-1192.
RVÅG K, et al. K-AP: generating specified K clusters by efficient affinity propagation[C]∥Proceedings of the 2010 IEEE International Conference on Data Mining. Piscataway: IEEE, 2010: 1187-1192.
[19] MEIL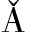 M. Comparing clusterings—an information based distance[J]. Journal of Multivariate Analysis, 2007, 98(5):873-895.
M. Comparing clusterings—an information based distance[J]. Journal of Multivariate Analysis, 2007, 98(5):873-895.
[20] HUBERT L, ARABIE P. Comparing partitions[J]. Journal of Classification, 1985, 2:193-218.
[21] VEENMAN C J, REINDERS M J T, BACKER E. A maximum variance cluster algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(9): 1273-1280.
[22] GIONIS A, MANNILA H, TSAPARAS P. Clustering aggregation[C]∥ Proceeding of the 21st International Conference on Data Engineering (ICDE′05).Piscataway:IEEE,2005:341-352.
[23] KELLY M, LONGJOHN R, NOTTINGHAM K.The UCI machine learning repository[DB/OL]. [2023-06-29]https:∥archive.ics.uci.edu/datasets.
[24] ALCALA-FDEZ J, FERNANDEZ A, LUENGO J, et al. KEEL data-mining software tool: data set repository, integration of algorithms and experimental analysis framework[J]. Journal of Multiple-Valued Logic and Soft Computing, 2011, 17(2/3): 255-287.