作为机器学习与数据挖掘的主要技术之一,聚类分析可在无监督条件下,通过学习数据内在分布结构,将具有较高相似度的样本归为相同类簇,反之将相异的样本分为不同类簇。目前,主要的聚类分析方法包括以下五类:基于划分的K-means和谱聚类算法[1-2]、密度聚类算法[3]、网格聚类算法[4]、层次聚类算法[5]以及基于模型的聚类算法[6]等。其中,K-means算法设定每个类簇由唯一的类簇中心进行标识,将聚类问题形式化为样本点与类簇中心的距离最小化问题,通过样本点分配与类簇中心更新两个阶段的交替迭代,从而实现对样本集合的划分。在样本点分配阶段,根据所有样本点到类簇中心的距离计算结果,判定样本点所属类簇;在类簇中心更新阶段,将该类中所有样本点的平均值设定为新的类簇中心。虽然K-means算法被广泛应用于多种任务场景[7-8],但其算法效果容易受到异常样本的干扰,并且计算成本与样本数量线性相关。
近年来,针对K-means算法容易受到异常样本干扰的问题,引入了多种异常检测机制对算法进行改进。例如,通过引入样本局部密度的度量机制在数据预处理时实现异常检测[9]、基于混合概率模型的异常检测方法[10]、基于采样策略的异常检测方法[11]以及通过类簇中心的迭代交换来计算类簇的紧凑程度,从而判断各样本点是否属于异常[12]。虽然引入异常检测机制提高了聚类性能,但是这些方法均采用分阶段实现的方式,没有形成融合异常检测和聚类的统一模型,无法获取良好的聚类结果。此外,异常检测机制极大地增加了算法的计算成本,降低了聚类过程的执行效率,限制了算法在大规模数据集上的应用。
针对以上问题,本文提出一种融合异常检测与区域分割的高效K-means聚类算法 (efficient K-means with region segment and outlier detection,EK-means)。与目前K-means及其各种改进型聚类算法相比,建立了融合异常检测的统一聚类模型。EK-means能够在聚类过程中捕获异常样本,同时在消除异常样本后进行聚类,通过两个阶段的交互协同提升了聚类性能。另外,为解决由于异常检测导致的计算效率下降问题,采用EK-means对类簇进行自适应的区域分割,在保持算法聚类性能不受影响的前提下,减少各区域中的冗余计算,以提升算法的效率。
1 相关工作
1.1 鲁棒K-means算法
由于传统K-means算法的类簇中心容易受到异常样本影响而无法准确获取,进而导致聚类算法性能的稳定性和准确性不足。近年来,针对此问题的研究工作主要分为两类:①利用矩阵范数建立正则化约束,削弱异常样本对聚类过程的影响;②引入异常检测机制,建立分阶段的数据聚类过程。
Huang等[13]构建了基于范数的损失函数,减少异常样本的影响。Huang等[14]提出了基于稀疏诱导范数的损失函数,增强了模型的鲁棒性。虽然以上方法能够有效提高聚类算法的性能,但无法显式获取异常样本,无法完全消除其影响。
与以上方法不同,Hautamäki等[15]提出采用分阶段异常处理机制,在聚类算法的迭代过程中逐渐删除远离类簇中心的异常样本。Im等[9]提出采用局部密度对样本进行异常检测。Li等[10]引入混合概率模型在聚类过程中检测异常样本。Zhang等[12]建立了基于局部搜索技术的K-means聚类算法,通过在目标函数中增加惩罚项以实现异常检测。上述算法分阶段执行聚类与异常检测,忽视了两者间的相关性,无法实现良好聚类,并且由于异常检测增加了大量计算,使得聚类算法的效率受到影响,限制了其在复杂大规模数据集上的应用效能。
1.2 快速K-means算法
标准K-means算法的时间复杂度为O(nkt),与样本集规模线性相关。近年来,为提高K-means算法在大规模数据集上的执行效率,主要的研究方向包括:①近似K-means算法,通过各类近似算法获取K-means的聚类结果,具有部分精度的损失;②精确K-means算法,通过减少迭代计算的次数,实现算法加速,同时保持聚类精度不变。
Peng等[16]提出一种新型近邻关系,比较样本与最近邻之间的距离,缩小样本计算范围。Giffon等[17]将稀疏因子乘积作为类簇中心矩阵的近似值,通过降低数据维度减少计算复杂度。
Hamerly[18]根据样本与类簇中心的距离设置其上下边界,并将三角不等式应用于边界,减少冗余距离计算。作为Hamerly算法的扩展,Drake[19]提出的Ann (annular K-means) 算法将三角不等式应用于以样本为圆心的环形结构。Newling等[20]提出Exp-ns(exponion K-means) 算法将三角不等式应用于以类簇中心为球心的球形结构,以定位样本标签的变动范围。由于上述限制上下界方法操作复杂且加速能力有限,Xia等[21]首次提出对类簇进行分割,减少不同区域的冗余计算。
在以上基于K-means的各类改进算法中,缺少同时考虑异常检测与计算效率的方法。因此,本文针对以上问题提出了融合异常检测与区域分割的高效K-means聚类算法。一方面,通过改进传统K-means的目标函数,将异常检测融合于聚类过程,实现统一模型的构建;另一方面,引入近邻簇搜索技术[21],实现各类簇自适应的区域分割,以减少样本聚类过程中的冗余计算。
2 EK-means
2.1 目标函数
给定数据集X={x1,x2,…,xn}∈Rn×d,其中n为样本数量,d为特征维度。不失一般性,可设定该数据集中包含z个异常样本,则该数据集的异常样本集合为Z∈Rz×d。算法将数据集划分为不同的类簇,最终聚类结果表示为{B1,B2,…,Bk,Z}。为了实现异常检测与聚类过程的交互协同,建立统一聚类模型,其目标函数为
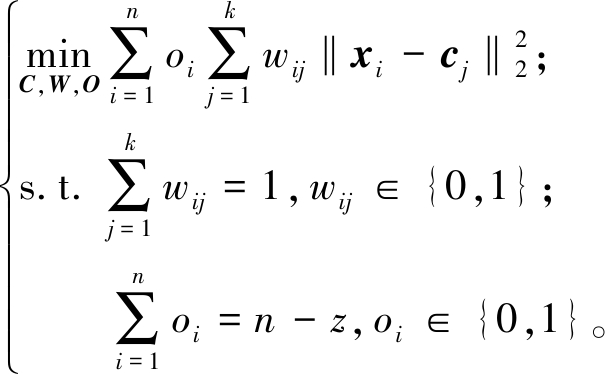
(1)
式中:xi为第i个样本;cj为第j个类簇中心;wij表示样本所在类簇;oi表示第i个样本是否属于异常样本。聚类指示矩阵W∈Rn×k由元素wij构成,当wij=1时,第i样本被分配至第j类簇;当wij=0时,第i样本不属于第j类簇。异常指示矩阵O∈Rn×1由元素oi构成,当oi=0时,第i样本为异常样本;反之为正常样本。
在标准K-means算法中,目标函数的迭代求解过程包括2个阶段,分为类簇中心更新阶段与样本分配阶段。根据本文提出的目标函数,本文算法的迭代过程包括3个阶段,分别为类簇中心更新阶段、样本分配阶段以及异常检测阶段。通过3个阶段的交替优化完成式(1)的求解,其中类簇中心矩阵C的求解与标准K-means算法一致。不同于标准K-means算法求解过程,在样本分配阶段中,引入了区域分割技术,提升聚类指示矩阵W的求解速度。在新增的异常检测阶段中,通过计算样本点的离群程度求解异常指示矩阵O。
2.2 函数求解
如式(1)所示,目标函数中包含了类簇中心矩阵C、聚类指示矩阵W以及异常指示矩阵O,采用交替优化策略进行求解,求解过程如下所示。
步骤1 固定异常指示矩阵O及聚类指示矩阵W,求解聚类中心矩阵C。当矩阵O与矩阵W固定时,式(1)转化为如下问题:
(2)
对式(2)中cj求导可得
(3)
令式(3)等于0,获取聚类中心,如式(4)所示:
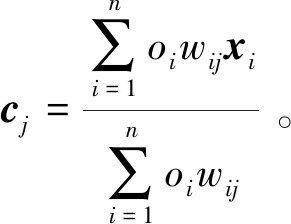
(4)
步骤2 固定异常指示矩阵O及聚类中心矩阵C,求解聚类指示矩阵W。当矩阵O及C固定时,令![]() 则目标函数可转变为
则目标函数可转变为
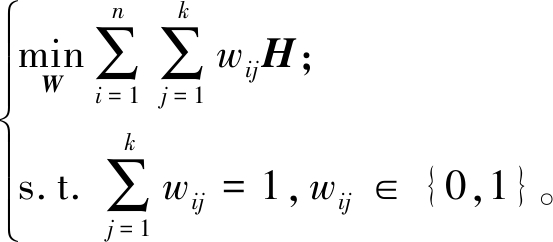
(5)
显然,通过将样本点分配到最近类簇以更新wij,所以聚类指示矩阵W的求解为
(6)
其中,由于异常指示矩阵将检测为异常样本的oi值设定为0,使得此类样本wij的取值不会对式(4)的求解产生影响。通过该方式,在此次迭代过程中被检测为异常的样本不参与分配,也不会影响正常样本点的分配。另一方面,为提高样本的分配速度,算法利用近邻簇搜索,对样本进行区域分割,以减少冗余距离计算,详细步骤见2.3节。
步骤3 固定聚类指示矩阵W及聚类中心矩阵C,求解异常指示矩阵O。当矩阵W和矩阵C固定时,令![]() 目标函数可转化为
目标函数可转化为
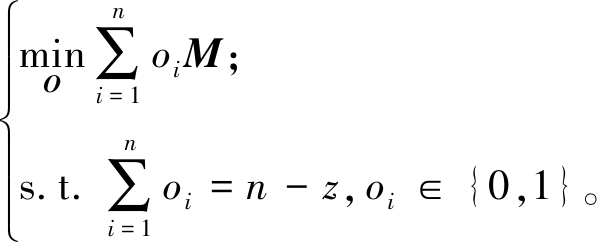
(7)
显然,通过去除最大距离值的z个异常样本,可以最小化式(7),故异常指示矩阵O为
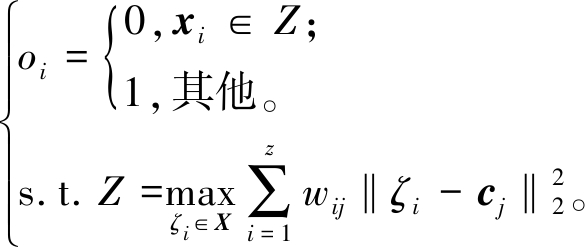
(8)
式中:Z∈Rz×d为异常集合,记录异常样本序号。在求解oi的过程中,M描述了该样本的离群程度。通过样本离群程度判断异常样本,将异常样本添加至异常集合,并将其oi设为0。为减少异常检测计算量,仅对部分异常指示矩阵O进行更新。即若正常样本到所属类簇中心的距离值超过异常样本到最近类簇中心的距离值,更新两者的异常指示。
2.3 基于近邻簇搜索的区域分割
在样本分配阶段,为提高求解聚类指示矩阵W的计算效率,本文算法引入近邻簇搜索技术[21],对类簇进行区域分割,以减少冗余计算。首先定义各类簇之间的单向近邻关系,如定义1所示。
定义1 单向近邻簇。对于任意类簇Bu和Bv,其类簇中心分别为![]() 为Bu半径长度ru,当满足以下不等式条件,Bv即为Bu的单向近邻簇:
为Bu半径长度ru,当满足以下不等式条件,Bv即为Bu的单向近邻簇:
(cu-cv)/2<ru 。
(9)
根据定义1,可获取Bu满足条件的m个单向近邻簇,同时根据类簇中心间距离,由近及远进行排序,构建Bu的单向近邻簇序列,其中令l表示该序列的序号,则Bu的区域分割方式Δ{l}为
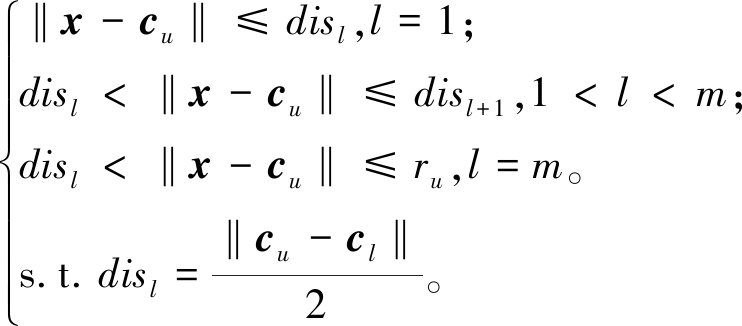
(10)
式中:当l=1时,Δ{l}为静态域;当l>1时,Δ{l}为多个动态域。如图1所示,黄色菱形表示类簇中心,红色虚线表示两类簇中心中垂线。以球簇B1为例,根据式(9),B2和B4为其单向近邻簇,而B3不为其单向近邻簇。根据式(10),球簇B1被分割为1个静态域及2个动态域。
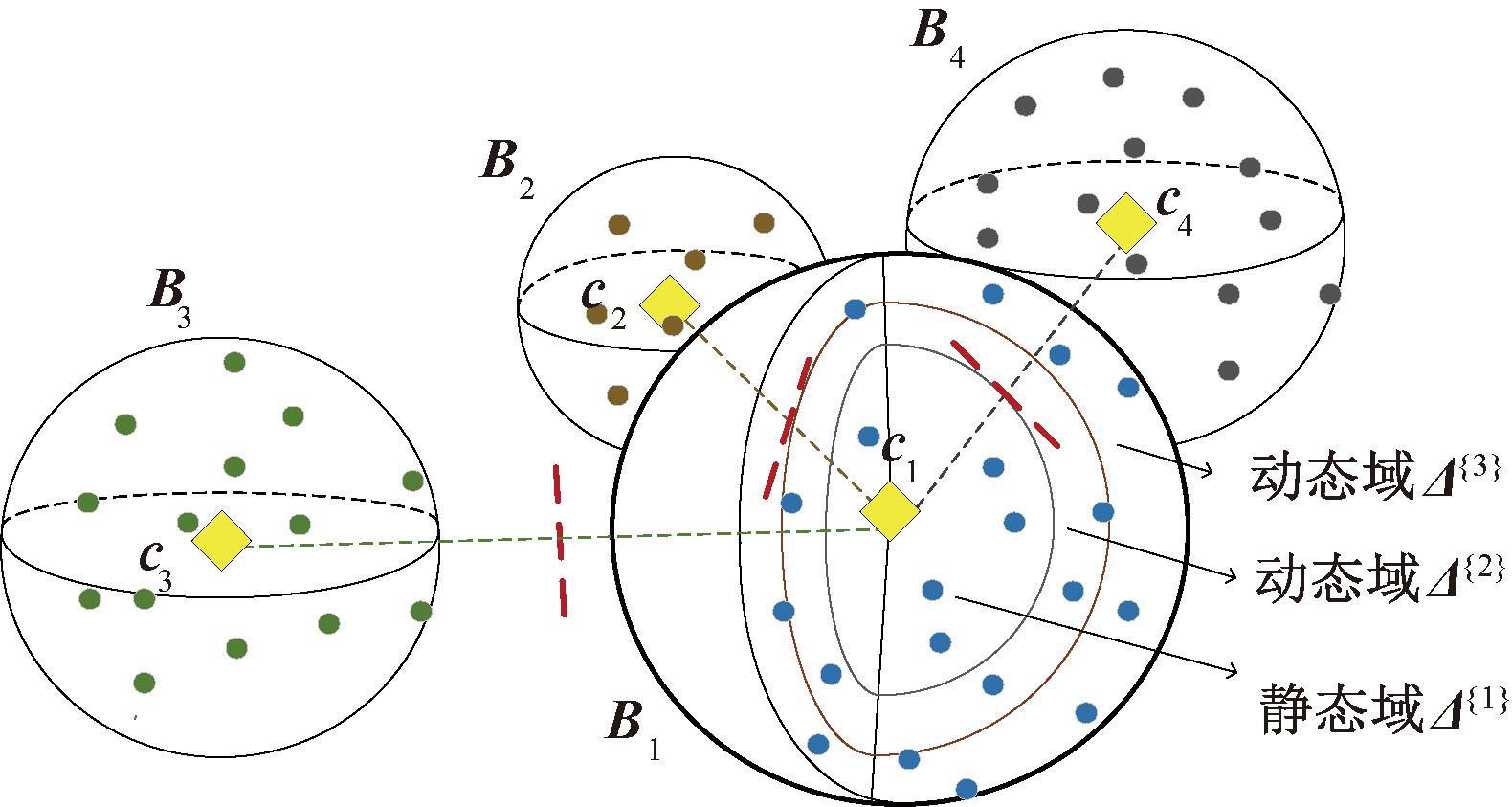
图1 基于近邻簇搜索的区域分割
Figure 1 Region segment based on neighbor clusters search
在当前迭代中,静态域中样本点的聚类指示不会改变。而动态域中样本点的聚类指示可能改变,且其变动范围如定理2所述。因此,算法在求解聚类指示矩阵时,省略了不影响聚类结果的距离计算。
定理1 对于Bu中任意样本点x,若满足x∈Δ{1},则有∀‖x-cu‖≤‖x-cv‖。
证明:![]()
且![]()
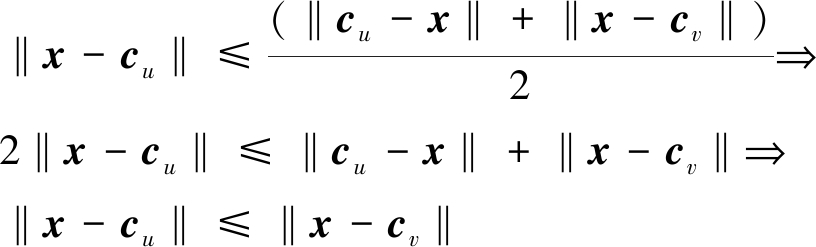
由定理1可知,若样本x∈Δ{1},在本次迭代中,其最近类簇中心将维持不变,无须更新其聚类指示。
定理2 对于Bu中任意样本点x,若满足x∈Δ{l},且l>1,则有
(1)∀x∈Δ{l},‖x-cu‖<‖x-cl+1‖;
(2)∃x∈Δ{l},‖x-cl‖<‖x-cu‖。
证:![]()
且![]()
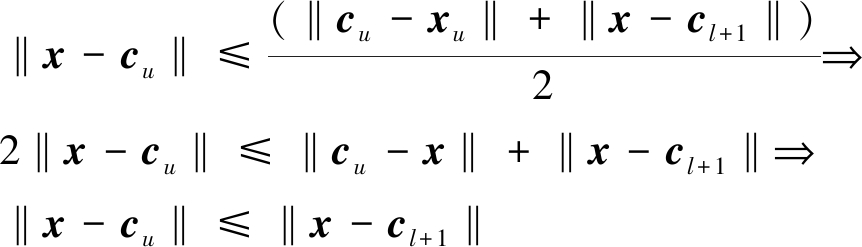
当‖cu-x‖+‖cl-x‖=‖cu-cl‖
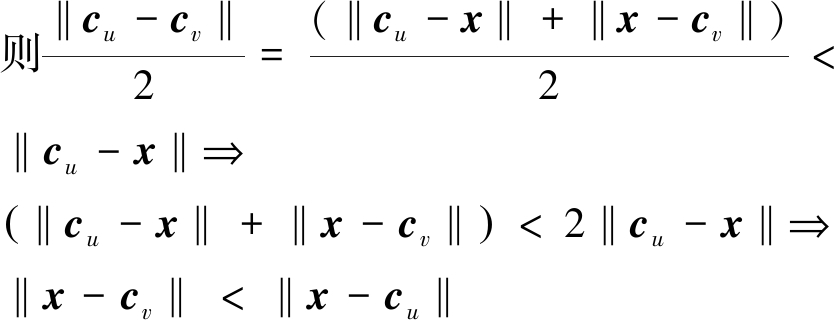 由定理2可知,若x∈Δ{l},相较于排序在l之后的单向近邻簇,其与原类簇中心距离值更小。且存在部分样本最近类簇中心由原类簇中心变动为排序在l之前某一单向近邻簇。故若x∈Δ{l},x的变动范围为原分配类簇及前i个Bu的单向近邻簇。
由定理2可知,若x∈Δ{l},相较于排序在l之后的单向近邻簇,其与原类簇中心距离值更小。且存在部分样本最近类簇中心由原类簇中心变动为排序在l之前某一单向近邻簇。故若x∈Δ{l},x的变动范围为原分配类簇及前i个Bu的单向近邻簇。
2.4 算法分析
算法分为初始化阶段与迭代阶段。首先,利用K-means++[22]初始化类簇中心,并完成初次样本分配。其次,根据目标函数迭代更新类簇中心、聚类指示矩阵及异常指示矩阵。算法将异常检测融入聚类过程中,并对样本空间进行区域分割,同时考虑算法性能及效率。EK-means算法在无异常样本时,所有的oi为1,即退化为标准K-means。算法主要步骤如下。
步骤1 输入数据集X,类簇数k,异常数z;
步骤2 执行K-means++,初始化类簇中心矩阵C和聚类指示矩阵W;
步骤3 根据式(8),初始化异常指示矩阵O;
步骤4 根据式(4),更新类簇中心矩阵C;
步骤5 根据式(10),更新各类簇区域分割Δ;
步骤6 根据式(6),更新聚类指示矩阵W;
步骤7 根据式(8),更新异常指示矩阵O;
步骤8 重复步骤4~7,直到类簇中心不发生变化,输出聚类指示矩阵W、异常指示矩阵O。
计算EK-means算法时间复杂度,步骤如下。
步骤1 更新异常指示矩阵O的时间复杂度为O(n);
步骤2 搜索单向近邻簇的时间复杂度为O(k2);
步骤3 排序单向近邻簇的时间复杂度为O(kmlog m),其中m(1≤m≤k)为单向近邻簇数;
步骤4 更新聚类指示矩阵W的时间复杂度为O(m(na-n′)+n),其中na-n′为动态域的样本数。实际上,去除异常样本点后,减少了类簇的半径,扩大了静态域的范围。相比Ball-K-means算法,动态域样本由na减少为na-n′。
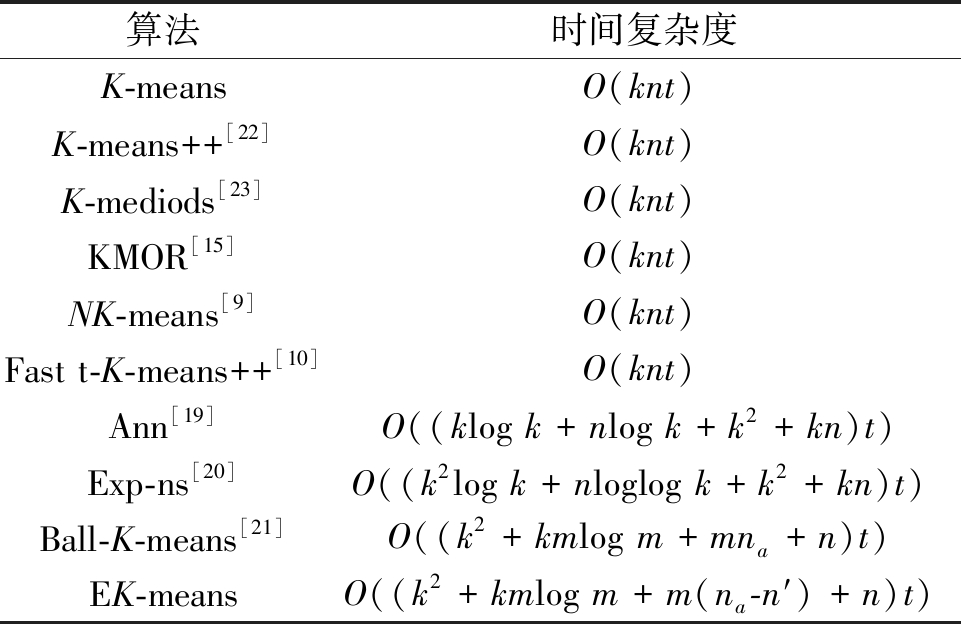
随着迭代中聚类结果变得更稳定,静态域扩大,时间消耗会越来越少。由于静态域无须距离计算,进一步提升了算法效率。EK-means在最差条件下的时间复杂度与其他算法的对比如表1所示,其中n为样本数;k为类簇数;t为迭代次数;m为邻居簇数;na为动态域样本数;n′为动态域减少样本数。Ann[19]、Exp-ns[20]、Ball-K-means[21]及EK-means优化了算法的执行效率,而其余算法并未改进执行效率。
表1 不同算法的时间复杂度
Table 1 Time complexity of different algorithms
算法时间复杂度K-meansO(knt)K-means++[22]O(knt)K-mediods[23]O(knt)KMOR[15]O(knt)NK-means[9]O(knt)Fast t-K-means++[10]O(knt)Ann[19]O((klog k+nlog k+k2+kn)t)Exp-ns[20]O((k2log k+nloglog k+k2+kn)t)Ball-K-means[21]O((k2+kmlog m+mna+n)t)EK-meansO((k2+kmlog m+m(na-n′)+n)t)
3 仿真实验
为测试算法的性能及效率,分别在4个合成数据集和6个真实数据集上进行仿真实验,采用9个聚类算法进行对比。对比算法可分为传统的聚类算法、鲁棒的聚类算法以及快速的聚类算法。其中K-means、K-means++和K-mediods是基于划分的传统聚类算法;KMOR、NK-means和Fast t-K-means++是具有异常检测的鲁棒聚类算法;Ann、Exp-ns和Ball-K-means算法是减少了距离计算次数的快速聚类算法。性能评价采用主流聚类评价指标:准确度ACC及归一化互信息NMI。以上评价指标的取值均为[0,1],当其取值越接近1时表示聚类性能越优异。
实验环境为Intel i7-10875 H,30 GHz,16.0 GB RAM,MATLAB2020,CLION2020。
3.1 合成数据集仿真实验
构建4个人工合成数据集{D1, D2, D3, D4},每个数据集中包含不同类簇分布的正常样本以及不同比例的异常样本,D1和D4为球状类簇分布,各数据集的类簇分布如表2所示。
表2 合成数据集的信息
Table 2 Information of synthetic datasets

数据集样本数特征数类簇数异常数据占比/%D1945295D21 4192410D36 0002520D44 100345
图2为各算法在合成数据集D2上的聚类效果。其中,黄色菱形表示类簇中心,黑色加号表示异常样本点。K-means算法将异常样本标记为正常样本。与KMOR算法相比,本文算法标记出了所有异常样本,证明了本文算法能够更加准确地识别异常样本。

图2 在合成数据集D2的聚类效果
Figure 2 Clustering results on D2
合成数据集D3中共包含6 000个样本,其异常样本数量占比为20%。图3为各算法在合成数据集D3上的聚类效果。如图3所示,在KMOR和K-means算法的聚类效果中,类簇中心偏移,导致大量异常样本被误标记为正常样本的情况,且后者的表现更为明显。而在EK-means算法的聚类结果中,类簇中心未发生偏移,只有极少量异常样本被误判。本文算法能有效降低异常样本对于聚类过程的影响。
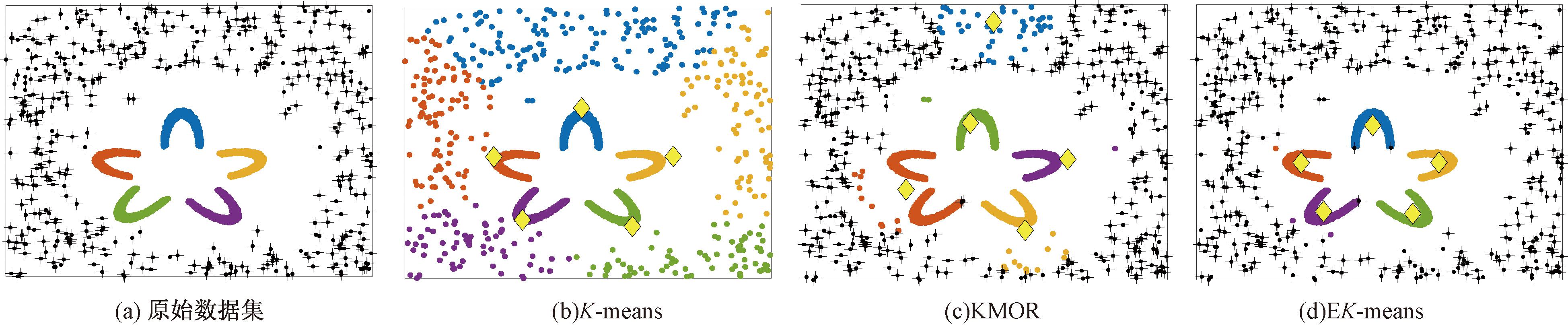
图3 在合成数据集D3的聚类效果
Figure 3 Clustering results on D3
为测试EK-means算法的执行效率,进一步记录了在人工合成数据集上完成聚类的距离计算次数与算法执行时间,如图4所示,其中,DC表示欧氏距离计算次数的倒数,T表示时间的倒数。为方便观察对比效果,将D3和D4的欧氏距离计算次数除以10后进行作图。在图4(a)中,Ann、Exp-ns、Ball-K-means及EK-means算法皆优化了K-means算法的效率,减少了距离计算次数,其中EK-means的表现较为优异。由图4(b)可以看出,EK-means算法效率更高。因此,本文通过区域分割,有效提高了聚类算法的执行效率。异常样本的去除使各类簇分布更加紧密,静态域范围被扩大,单次迭代的距离计算次数减少。
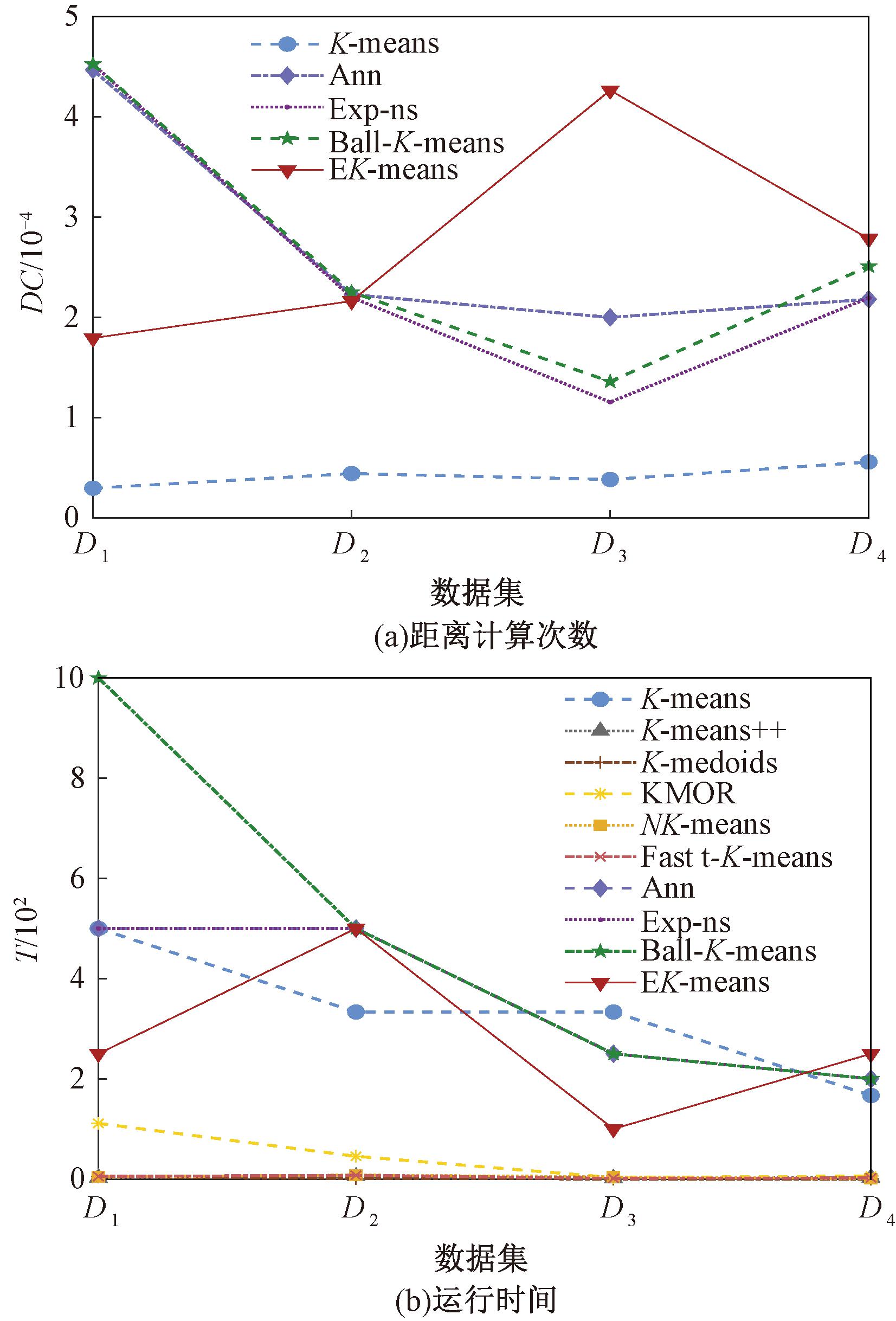
图4 各算法在合成数据集上的执行效率
Figure 4 Efficiency of algorithms on synthetic datasets
3.2 真实数据集仿真实验
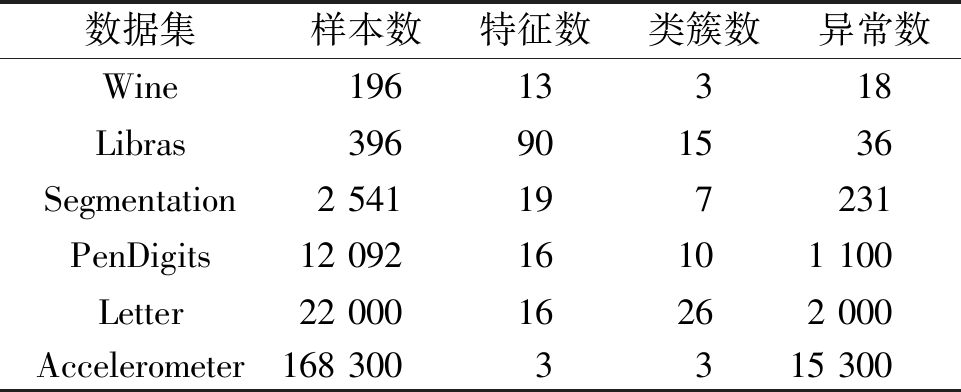
本文采用6个真实数据集验证所提方法的有效性,包括Wine、Libras、Segmentation、Accelerometer、PenDigits、Letter,如表3所示。对Wine数据集添加值在[0,1]上的随机异常点,对其余5个真实数据集添加数值在[0,2]上的随机异常点。随机异常点的占比约为10%,且其分布偏离正常样本。
表3 真实数据集的信息
Table 3 Information of real datasets
数据集样本数特征数类簇数异常数Wine19613318Libras396901536Segmentation2 541197231PenDigits12 09216101 100Letter22 00016262 000Accelerometer168 3003315 300
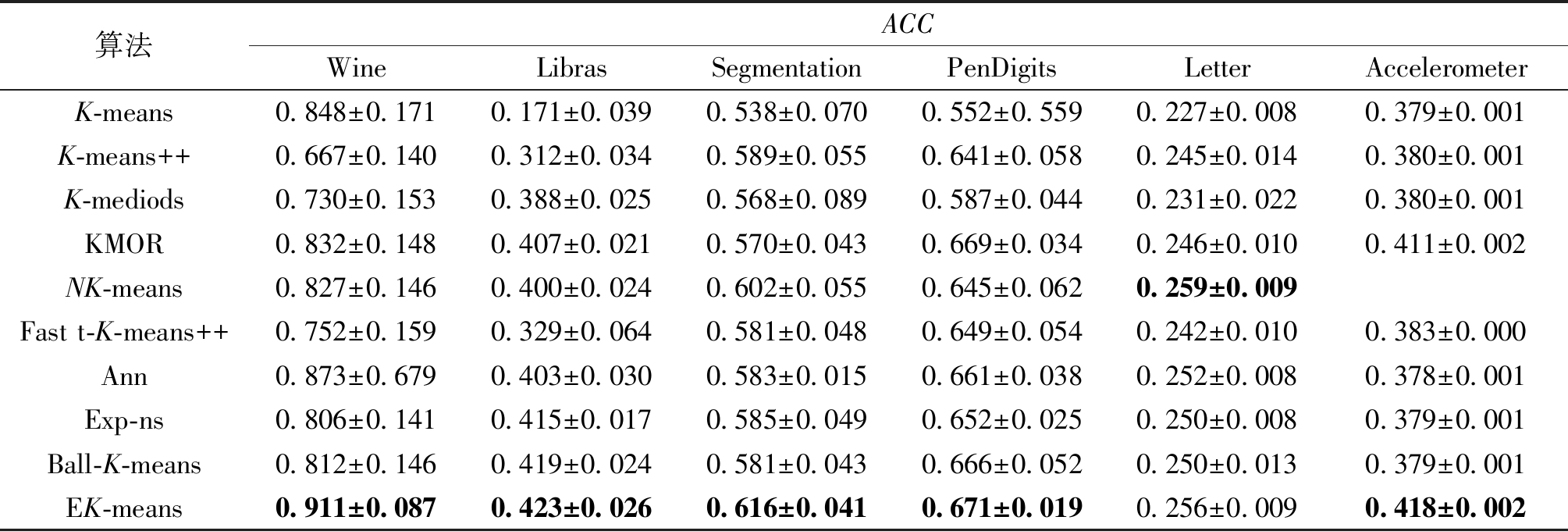
表4、5为EK-means算法及多个对比算法的聚类结果,实验选取10次结果的平均值,表4为聚类结果的ACC值,表5为聚类结果的NMI值。
表4 真实数据集聚类ACC比较
Table 4 Real datasets clustering ACC comparison
算法ACCWine LibrasSegmentationPenDigitsLetterAccelerometerK-means0.848±0.1710.171±0.0390.538±0.0700.552±0.5590.227±0.0080.379±0.001K-means++0.667±0.1400.312±0.0340.589±0.0550.641±0.0580.245±0.0140.380±0.001K-mediods0.730±0.1530.388±0.0250.568±0.0890.587±0.0440.231±0.0220.380±0.001KMOR0.832±0.1480.407±0.0210.570±0.0430.669±0.0340.246±0.0100.411±0.002NK-means0.827±0.1460.400±0.0240.602±0.0550.645±0.0620.259±0.009Fast t-K-means++0.752±0.1590.329±0.0640.581±0.0480.649±0.0540.242±0.0100.383±0.000Ann0.873±0.6790.403±0.0300.583±0.0150.661±0.0380.252±0.0080.378±0.001Exp-ns0.806±0.1410.415±0.0170.585±0.0490.652±0.0250.250±0.0080.379±0.001Ball-K-means0.812±0.1460.419±0.0240.581±0.0430.666±0.0520.250±0.0130.379±0.001EK-means0.911±0.0870.423±0.0260.616±0.0410.671±0.0190.256±0.0090.418±0.002
表5 真实数据集聚类NMI比较
Table 5 Real datasets clustering NMI comparison
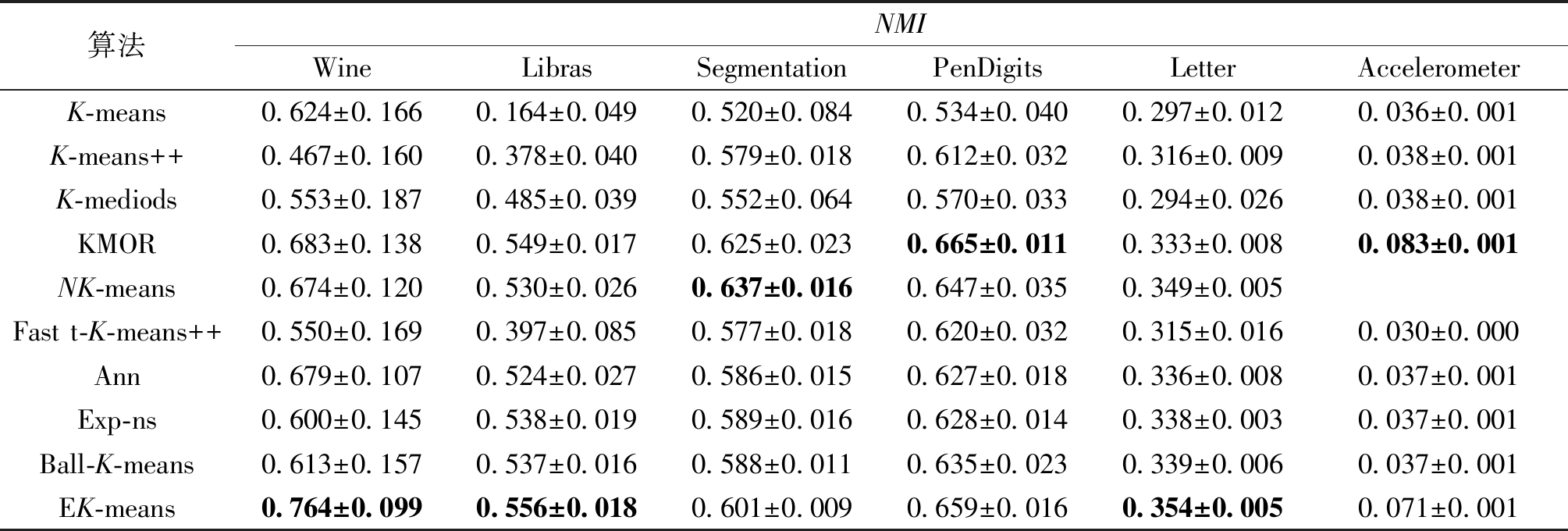
算法NMIWineLibrasSegmentationPenDigitsLetterAccelerometerK-means0.624±0.1660.164±0.0490.520±0.0840.534±0.0400.297±0.0120.036±0.001K-means++0.467±0.1600.378±0.0400.579±0.0180.612±0.0320.316±0.0090.038±0.001K-mediods0.553±0.1870.485±0.0390.552±0.0640.570±0.0330.294±0.0260.038±0.001KMOR0.683±0.1380.549±0.0170.625±0.0230.665±0.0110.333±0.0080.083±0.001NK-means0.674±0.1200.530±0.0260.637±0.0160.647±0.0350.349±0.005Fast t-K-means++0.550±0.1690.397±0.0850.577±0.0180.620±0.0320.315±0.0160.030±0.000Ann0.679±0.1070.524±0.0270.586±0.0150.627±0.0180.336±0.0080.037±0.001Exp-ns0.600±0.1450.538±0.0190.589±0.0160.628±0.0140.338±0.0030.037±0.001Ball-K-means0.613±0.1570.537±0.0160.588±0.0110.635±0.0230.339±0.0060.037±0.001EK-means0.764±0.0990.556±0.0180.601±0.0090.659±0.0160.354±0.0050.071±0.001
由表4、5可知,K-means++、Ann、Exp-ns及Ball-K-means算法优化了初始类簇中心选取,但并不具备异常点检测能力。KMOR、NK-means及Fast t-K-means++算法在性能和异常检测方面表现较好,但各有限制。KMOR算法无法检测偏离程度较小的异常样本,NK-means无法处理较密集的异常样本,而Fast t-K-means++无法处理不符合高斯分布的异常样本。本文算法在各个数据集上的聚类指标大部分优于对比算法,其余聚类指标接近于最佳聚类评分。因此,结合实验结果可以证明本文算法通过将异常检测融入聚类过程,有效提高聚类准确率。
图5为各算法在6个真实数据集上的执行效率,分别展示了算法欧氏距离计算次数及算法执行时间,其中DC为欧氏距离计算次数的倒数,T为时间的倒数。为方便观察对比效果,将Libras、Segmentation、PenDigits、Letter、Accelerometer数据集的欧氏距离计算次数分别除以10、102、103、104、104。在图5(a)中,EK-means算法在大部分数据集上达到了仅次于最少距离计算次数的Ball-K-means算法,且在PenDigits数据集上距离计算次数为最小值。在图5(b)中,EK-means算法对于效率的优化效果较好。因此,本文算法有效提高了聚类的执行效率。
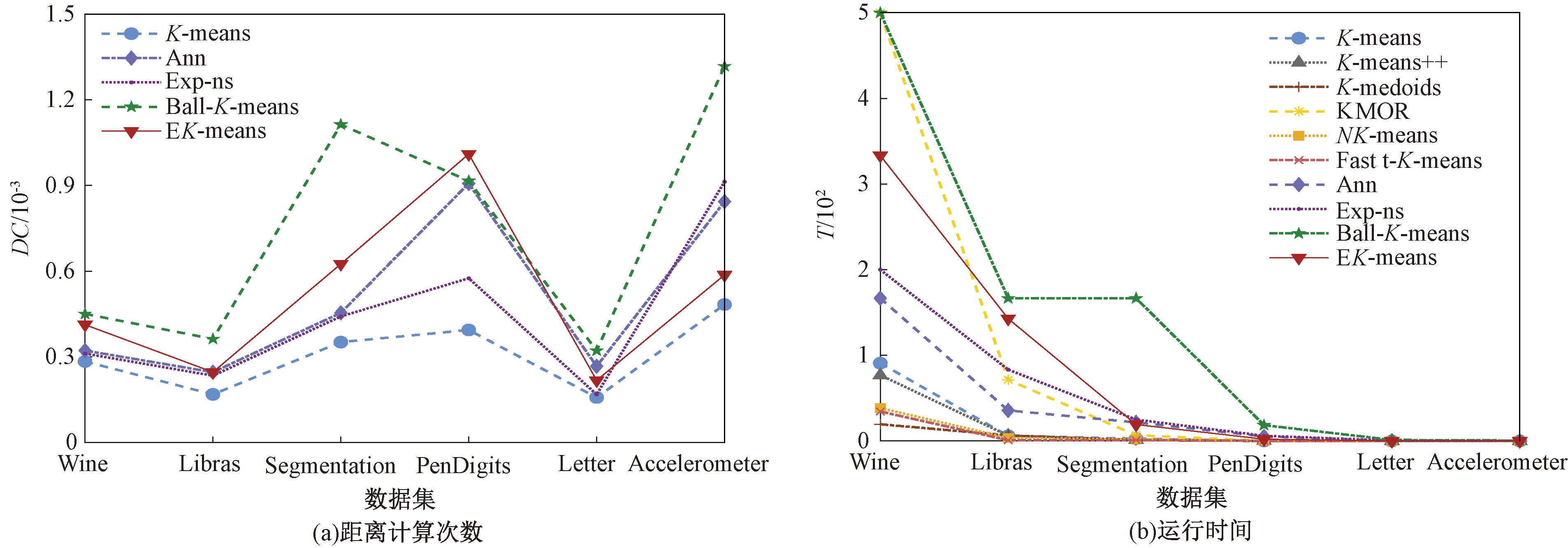
图5 EK-means算法在真实数据集上的执行效率
Figure 5 Efficiency of EK-means on real datasets
图6为本文算法在6个真实数据集上的收敛情况。可以看出,本文算法在一定迭代次数内的目标函数值不变,证明其在真实数据集上可以快速收敛。
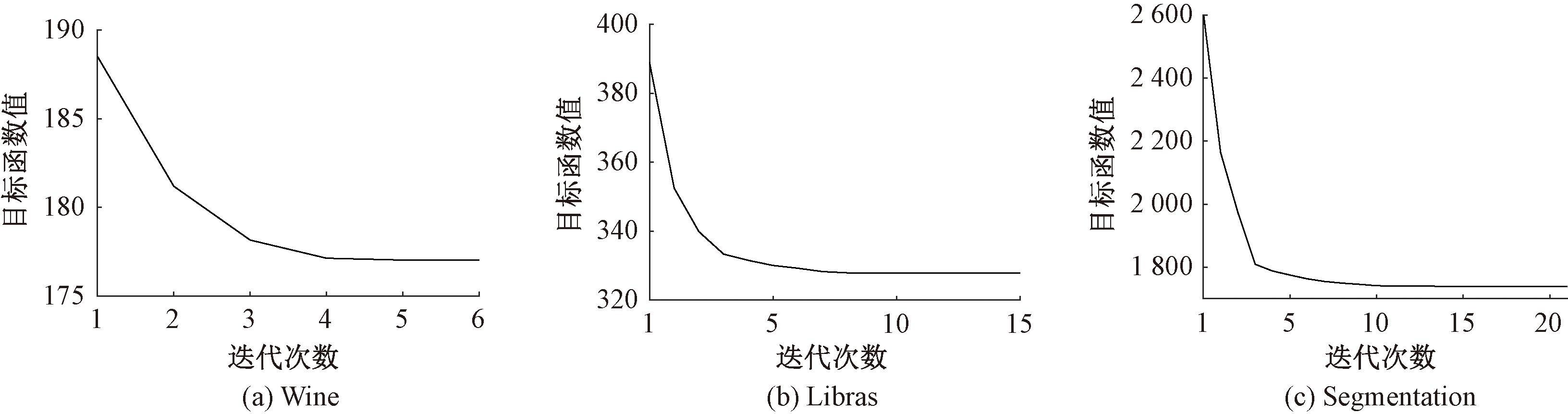
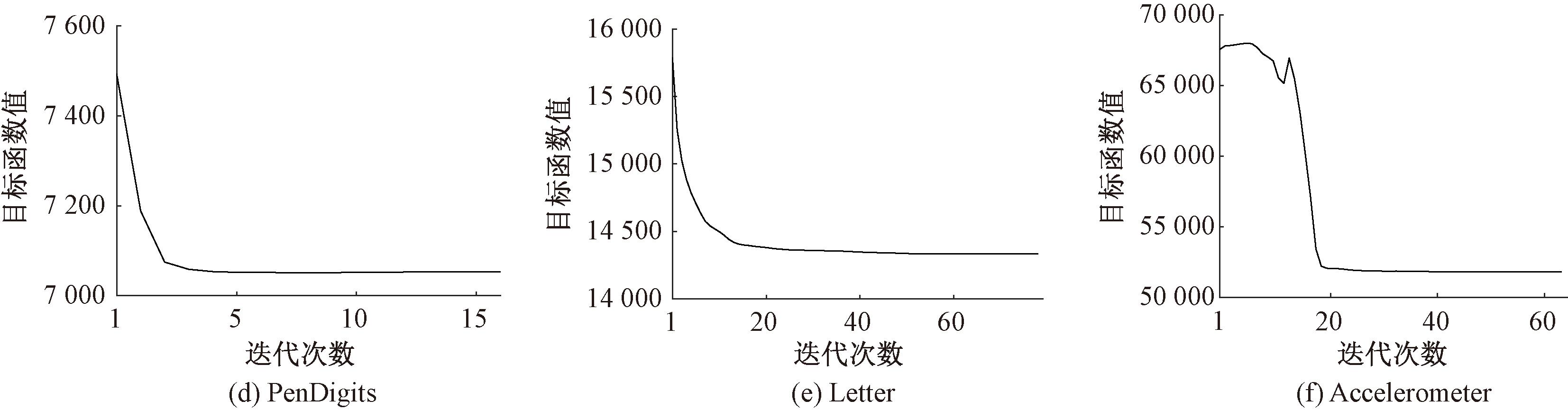
图6 EK-means算法在真实数据集上的收敛曲线
Figure 6 Convergence curves of EK-means on real datasets
表6记录了10个算法在异常数据占比分别为0、5%、10%条件下的Wine、Libras、Segmentation、PenDigits数据集的 ACC对比。随着异常数据占比的增加,K-means、K-means++、Ann、Exp-ns以及Ball-K-means算法的ACC值明显下降,K-mediods、KMOR、NK-means、Fast t-K-means++的ACC值的下降幅度较小,但K-mediods及KMOR算法的准确率较低。与以上算法相比,本文算法的ACC值下降幅度最小且聚类效果较优。本文算法通过在聚类中融入异常点检测,增强了算法的鲁棒性及准确率。
表6 不同异常数据占比条件下的真实数据集聚类结果ACC对比
Table 6 Clustering ACC comparison of datasets with different proportions of outliers
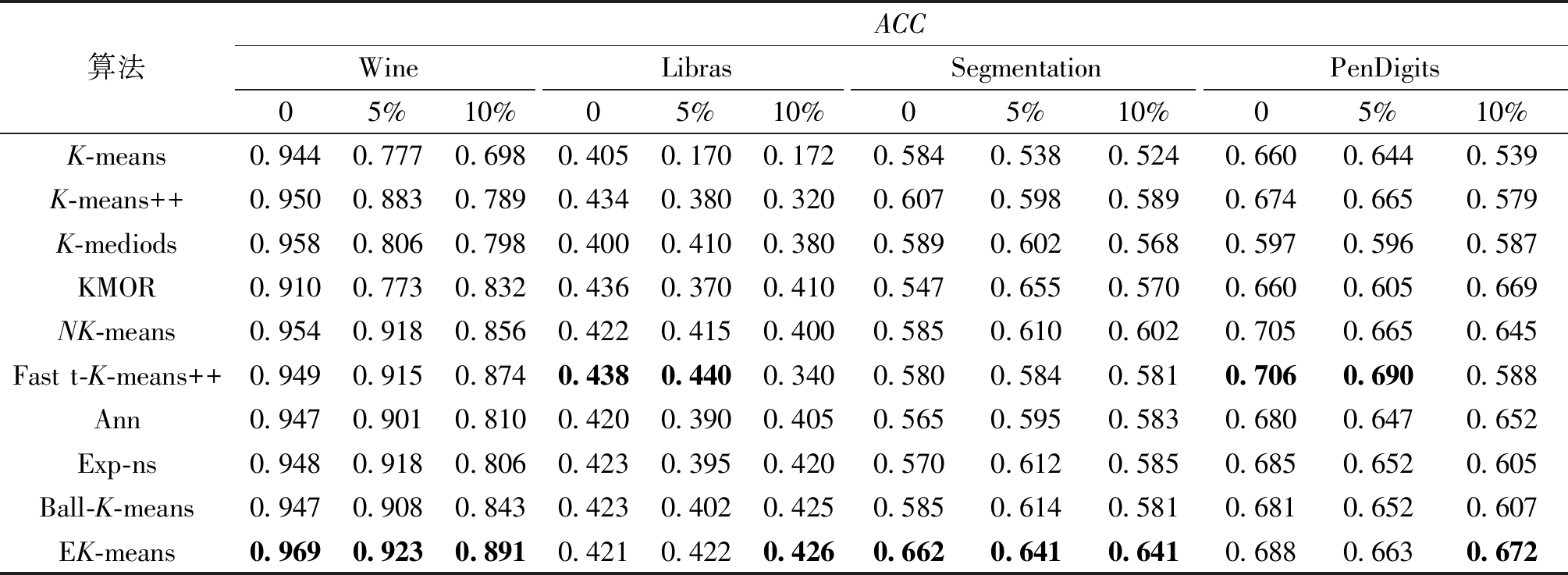
算法ACCWineLibrasSegmentationPenDigits05%10%05%10%05%10%05%10%K-means0.9440.7770.6980.4050.1700.172 0.5840.5380.5240.6600.6440.539K-means++0.950 0.8830.7890.4340.3800.3200.6070.5980.5890.6740.6650.579K-mediods0.958 0.8060.7980.4000.4100.380 0.589 0.6020.5680.5970.5960.587KMOR0.910 0.773 0.832 0.4360.3700.410 0.5470.6550.5700.6600.6050.669NK-means0.954 0.9180.856 0.4220.4150.400 0.5850.6100.602 0.7050.6650.645Fast t-K-means++0.949 0.9150.8740.438 0.4400.3400.5800.5840.5810.7060.6900.588Ann0.947 0.9010.8100.420 0.3900.4050.5650.5950.5830.6800.6470.652Exp-ns0.948 0.9180.806 0.4230.395 0.4200.5700.6120.5850.6850.652 0.605Ball-K-means0.947 0.908 0.8430.4230.402 0.4250.5850.6140.5810.6810.652 0.607EK-means0.9690.9230.8910.4210.4220.4260.6620.6410.6410.6880.6630.672
4 结论
本文提出了一种融合异常检测与区域分割的高效K-means聚类算法(EK-means)。针对传统K-means算法容易受到异常样本影响,导致其聚类准确度较低的问题,构建统一聚类模型,通过异常检测与聚类过程的交互协同,获取较优聚类效果。同时,利用近邻簇搜索技术,对各类簇进行区域分割,减少了样本分配阶段的冗余计算,提高了算法执行效率。最后,通过合成数据集和真实数据集上的仿真实验证明本文算法的有效性。
EK-means算法需要预指定异常样本的数量,但在实际应用中,异常样本的数量难以确定。此外,针对算法的不稳定性,思考是否结合多次运行的聚类结果,获得更稳定的聚类结果,因此,如何在异常样本数量未知的先验条件下,快速稳定地检测与处理异常样本将成为后续研究的目标和方向。
[1] NIE F P, LI Z H, WANG R, et al. An effective and efficient algorithm for K-means clustering with new formulation[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(4): 3433-3443.
[2] BAI L, LIANG J Y, ZHAO Y X. Self-constrained spectral clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(4): 5126-5138.
[3] ZHANG Q H, DAI Y Y, WANG G Y. Density peaks clustering based on balance density and connectivity[J]. Pattern Recognition, 2023, 134: 109052.
[4] HIRECHE C, DRIAS H, MOULAI H. Grid based clustering for satisfiability solving[J]. Applied Soft Computing, 2020, 88: 106069.
[5] MONATH N, KOBREN A, KRISHNAMURTHY A, et al. Scalable hierarchical clustering with tree grafting[C]∥Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery &Data Mining. New York:ACM, 2019: 1438-1448.
[6] WAN Y C, LIU X B, WU Y, et al. ICGT: a novel incremental clustering approach based on GMM tree[J]. Data &Knowledge Engineering, 2018, 117: 71-86.
[7] 鲁斌, 范晓明. 基于改进自适应k均值聚类的三维点云骨架提取的研究[J]. 自动化学报, 2022, 48(8): 1994-2006.
LU B, FAN X M. Research on 3D point cloud skeleton extraction based on improved adaptive k-means clustering[J]. Acta Automatica Sinica, 2022, 48(8): 1994-2006.
[8] LI Z, TANG C, ZHENG X, et al. Unified K-means coupled self-representation and neighborhood kernel learning for clustering single-cell RNA-sequencing data[J]. Neurocomputing, 2022, 501: 715-726.
[9] IM S, QAEM M M, MOSELEY B, et al. Fast noise removal for K-means clustering[C]∥ the 23rd International Conference on Artificial Intelligence and Statistics(AISTATS)2020. Palermo: AISTATS, 2020: 456-466.
[10] LI Y M, ZHANG Y, TANG Q T, et al. T-k-means: a robust and stable k-means variant[C]∥International Conference on Acoustics, Speech and Signal Processing (ICASSP). Piscataway: IEEE, 2021: 3120-3124.
[11] GRUNAU C, ROZHON V. Adapting K-means algori-thms for outliers[C] ∥the 39th International Conference on Machine Learning. Baltimore: ICML, 2022: 7845-7886.
[12] ZHANG Z, FENG Q L, HUANG J Y, et al. A local search algorithm for k-means with outliers[J]. Neurocomputing, 2021, 450: 230-241.
[13] HUANG S D, REN Y Z, XU Z L. Robust multi-view data clustering with multi-view capped-norm K-means[J]. Neurocomputing, 2018, 311: 197-208.
[14] HUANG S D, KANG Z, XU Z L, et al. Robust deep k-means: an effective and simple method for data clustering[J]. Pattern Recognition, 2021, 117: 107996.
[15] HAUTAM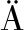 KI V, CHEREDNICHENKO S, K
KI V, CHEREDNICHENKO S, K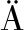 RKK
RKK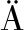 INEN I, et al. Improving k-means by outlier removal[C]∥Proceedings of the 14th Scandinavian conference on Image Analysis. New York: ACM, 2005: 978-987.
INEN I, et al. Improving k-means by outlier removal[C]∥Proceedings of the 14th Scandinavian conference on Image Analysis. New York: ACM, 2005: 978-987.
[16] PENG D W, CHEN Z Z, FU J C, et al. Fast k-means clustering based on the neighbor information[C]∥ISEEIE 2021: 2021 International Symposium on Electrical, Electronics and Information Engineering. New York: ACM, 2021: 551-555.
[17] GIFFON L, EMIYA V, KADRI H, et al. Quick-means: accelerating inference for K-means by learning fast transforms[J]. Machine Learning, 2021, 110(5): 881-905.
[18] HAMERLY G. Making k-means even faster[J]. Proceedings of the 10th SIAM International Conference on Data Mining, 2010: 130-140.
[19] DRAKE J. Faster K-means clustering[EB/OL]. (2013-09-24)[2023-06-13]. http:∥hdl.handle.net/2104/8826.
[20] NEWLING J, FLEURET F. Fast K-means with accurate bounds[C]∥Proceedings of the 33rd International Conference on International Conference on Machine Learning-Volume 48. New York:ACM, 2016: 936-944.
[21] XIA S Y, PENG D W, MENG D Y, et al. Ball $k$k-means: fast adaptive clustering with No bounds[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(1): 87-99.
[22] ARTHUR D, VASSILVITSKII S. K-means++: the advantages of careful seeding[C]∥Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. New York: ACM, 2007: 1027-1035.
[23] KAUFMAN L, ROUSSEEUW P. Clustering by means of medoids[EB/OL].(1987-01-01)[2023-06-13]. https:∥www.researchgate.net/publication/243777819_Clustering_by_Means_of_Medoids.