入侵检测系统(intrusion detection system,IDS)[1]作为计算机网络安全领域的一种主动安全防御技术,广泛部署在各种网络安全防护体系中,感知恶意入侵行为,并采取快速有效的对策,以防止系统被进一步地入侵和传播。但众多的攻击类型和网络流量特征对入侵检测构成了另一个挑战[2],冗余和不相关的特征会影响入侵检测系统对网络攻击的分类性能。因此,为了解决该问题,众多学者研究和开发了许多方法来提高IDS的检测精度和性能。
特征选择作为数据挖掘和机器学习中重要的预处理手段被广泛应用于网络入侵检测中,其通过从描述数据的完整特征集中筛选出具有最大信息量的特征子集以达到降维和提高分类性能的目的。根据算法和数据处理方式的不同,可将特征选择方法分为3类:过滤式(filter)[3]、嵌入式(embedded)[4]及包裹式(wrapper)[5]。过滤式特征选择依赖于某些统计学定义,滤除不满足标准的特征,常见的有基于相关性的特征选择(correlation-based feature selection,CFS)和最大相关最小冗余(max-relevance and min-redundancy,mRMR)等,但由于其依赖统计特性的关系,导致所得特征子集分类准确性普遍不高;嵌入式特征选择将特征挑选融入分类过程,特征选择过程无须人为参与,如基于深度学习的特征选择、树算法重要性(tree-based feature importance)等,但模型缺乏可解释性;包裹式特征选择将分类结果作为子集评价指标,能够达到较高的分类准确性,常见的如正向选择(forward selection)、群体智能优化算法等。
本文采用基于群体智能优化的包裹式特征选择算法。特征选择最优解问题作为典型的NP(non-determinisitic polynomail)问题从n维数据集中寻找最优解的复杂度高达2n。因此,常利用群体智能优化算法种群演化多样性与行为指向性的特点[6],近似求解特征选择优化问题,以应对维度灾难(curse of dimensionality)。如粒子群优化算法(particle swarm optimization,PSO)[7]、蚱蜢优化算法(grasshopper optimization algorithm,GOA)[8]、差分算法(differential evolution,DE)[9]、蝙蝠算法(bat algorithm,BA)[10]等。根据不同特征选择目标,研究者对群体智能优化算法提出了改进工作,如徐国天等[11]提出了一种利用改进哈里斯鹰算法进行特征选择的恶意软件检测方法,实验结果证明,所提出的方法取得了很好的检测结果;Li等[12]将K-means算法与蝙蝠算法相结合进行特征选择,在物联网入侵检测上取得了不错的效果;Abbasi等[13]通过设计特征分组策略改进粒子群优化算法进行特征选择,解决勒索软件检测问题。但是,这些方法仍存在易陷入局部最优、收敛速度慢等问题,导致其不能有效选择最优特征来高效检测网络中的恶意流量。
针对以上问题,本文提出了一种改进多因子优化蝙蝠算法(improved multi-factorial optimization bat algorithm,IMFBA)进行特征选择。采用基于反向学习策略的初始化和突变机制,增强算法中解的多样性和算法收敛速度。在迭代过程中应用改进的二进制差分进化算子增强算法的局部搜索能力,避免算法陷入局部最优。采用多因子优化范式[14]改进BA算法,通过设计两个相关的特征选择任务,实现任务间的知识转移,帮助算法提升全局搜索能力,从而找到更好的特征子集。
1 相关工作
1.1 蝙蝠算法
BA是一种实现全局优化的元启发式算法,灵感源于微型蝙蝠的回声定位能力,由Yang[15]于2010年提出,被研究人员广泛地使用和研究。例如,Ye等[16]通过引入曲线递减和速度加权的局部搜索算子提升了蝙蝠算法的搜索精度;Yu等[17]提出了一种混沌增强BA解决全局优化问题,以提高算法的稳定性和收敛速度;Bangyal等[18]利用Torus walk改进BA以提升算法的局部搜索能力,避免陷入局部最优。
特征选择作为离散优化问题,特征的选择与否更适合用二进制数值表示,并且二进制编码相较于实数编码更为简单和高效。因此,在本文中使用BA的改进版本二进制BA(binary bat algorithm,BBA)[19]。在BBA中描述了蝙蝠在d维二进制空间中的运动,在第t次迭代中每只蝙蝠以速度![]() 在位置
在位置![]() 随机飞行,其具有静态的频率fi、响度
随机飞行,其具有静态的频率fi、响度![]() 脉冲发射率
脉冲发射率![]() 蝙蝠的位置定义为所选特征子集,并通过适应度函数衡量其质量。
蝙蝠的位置定义为所选特征子集,并通过适应度函数衡量其质量。![]() 中某一维值为0时代表某个特征不存在于特征子集中,而为1时表示该特征存在于特征子集中。用所选特征训练分类器后,适应度函数将是分类器的评价指标。
中某一维值为0时代表某个特征不存在于特征子集中,而为1时表示该特征存在于特征子集中。用所选特征训练分类器后,适应度函数将是分类器的评价指标。
在每次迭代过程中,算法将更新每个个体的内部变量,数学公式如下:
fi=fmin+(fmax-fmin)·λ;
(1)
(2)
(3)
式中:S(·)为Sigmoid函数;g=(g1,g2,…,gd)为当前种群当中n个个体中的最优解。随着迭代的进行,响度![]() 脉冲发射率
脉冲发射率![]() 必须进行相应的更新,更新规则如下:
必须进行相应的更新,更新规则如下:
(4)
(5)
式中:α、γ为常数且0<α<1,γ>0。若![]() 小于随机数rand(0,1),则就会使用随机游走策略在局部生成每个个体的新解。
小于随机数rand(0,1),则就会使用随机游走策略在局部生成每个个体的新解。
(6)
式中:ε为均匀分布在[-1,1]的随机向量;At为第t次迭代时种群所有个体的响度平均值。
1.2 多因子优化
多任务优化是研究同时解决多个优化问题从而提高解决每个问题的能力,其假设在解决某问题时,存在一些共同的有用知识,有利于解决其他相关联的任务。2015年,Gupta等[20]提出了一种新的多任务优化范式即多因子优化(multifactorial optimization, MFO),并据此设计了多因子优化算法,该算法通过选型交配(assortative mating)和垂直文化传播(vertical cultural transmission)等算子实现不同任务间的知识共享,其流程如算法1所示。在实践中该方法已被成功用于解决各种不同的优化问题。例如,Feng等[21]提出基于多因子范式改进的PSO和DE算法,经实验证明该算法是MFO的一个有效和高效的实现方法。Osaba等[22]提出改进的多因子进化算法,有效避免了迭代过程中不同任务间负反馈的问题,并成功应用于解决离散优化问题。
算法1 选型交配和垂直文化传播。
① 从当前种群P中随机选择两个父代样本pa、pb;② 生成一个随机数rand(0,1);
③ if (![]() a==
a==![]() b) or (rand(0,1)<rmp) then
b) or (rand(0,1)<rmp) then
④ 父代pa、pb杂交得到两个子代ca、cb;
⑤ else
⑥ 父代pa发生轻微突变产生子代ca;
⑦ 父代pb发生轻微突变产生子代cb;
⑧ End if
⑨ if (‘c’有两个父代)then
⑩ 生成一个0到1的随机数rand(0,1);
 if (rand(0,1)<0.5)then
if (rand(0,1)<0.5)then
 ‘c’技能因素为
‘c’技能因素为![]() a;
a;
 else
else
 ‘c’技能因素为
‘c’技能因素为![]() b;
b;
 else
else
 ‘c’模仿其单个父代样本的技能因素;
‘c’模仿其单个父代样本的技能因素;
 End if。
End if。
MFO创造了一个多任务的环境,进化出一个单一的个体群体来同时解决多个相关的任务,其中每个任务作为一个独特因素来影响种群的进化。但不同的任务可能具有不同的属性,为解决这一问题,个体被表示在统一的搜索空间中,MFO通过计算个体的技能因素将种群划分为不同的组,每个个体被分配到与它表现最好的任务相对应的组中。
为了评估种群中的个体,MFO在解决k个任务的种群P中对个体pi定义了如下属性。
(1)因子代价。个体pi在任务Tj上的因子代价![]() 定义为其对特定任务上的适应度值。
定义为其对特定任务上的适应度值。
(2)因子等级。个体pi在任务Tj上的因子等级![]() 为因子代价按升序排列后种群列表的索引值。
为因子代价按升序排列后种群列表的索引值。
(3)技能因素。个体pi的技能因素![]() i定义为个体在所有任务中表现最优的任务的索引,即
i定义为个体在所有任务中表现最优的任务的索引,即![]()
(4)标量适应度。个体pi的标量适应度定义为![]()
2 本文方法
2.1 多因子蝙蝠算法
一般情况下,网络入侵检测数据集是极度不平衡的,在尽可能不损害多数类分类性能的情况下,保留对少数类分类有利的特征以提高少数类样本的分类能力,这是本文所设计算法的主要目的之一。在应用多因子优化范式处理该问题时,所设计任务的相关性是影响算法性能的一个重要因素之一,不同的任务在最优解方面应满足一定的共性和互补性。在本文中,基于不同类别的分类性能设计不同任务。任务1致力于选择有助于提升整个数据集分类性能的特征子集;任务2倾向于选择有利于少数类攻击流量分类的特征子集。由于任务2是任务1的一部分,因此,两个任务具有一定程度的共通性,两个任务在迭代的过程中共享信息,以寻找到更好的特征子集。
而应用多因子优化范式改进蝙蝠算法的关键问题是Gupta等[20]所提出的多因子优化算法与传统的群体智能优化算法在解的更新迭代机制方面有很大的差异,尤其是选型交配作为个体间进行多任务隐形知识转移的关键组成部分,需要新的设计方案。具体来说,定义了随机配对概率rmp来控制选型交配的过程。如果一个随机数小于rmp,式(7)将用于更新速度。否则,使用式(2)更新速度。
(7)
式中:![]() 表示第t次迭代时与个体i执行不同任务的个体中的全局最优解;fi由式(1)定义;βi=(β1,β2,…,βn)为控制g*对个体更新影响力的系数。Yang等[23]提出了基于粒子个体进化信息的自适应参数调整策略,降低了优化器对于新引入参数的敏感性,经过实验证明,通过应用自适应参数调整策略,算法在优化问题上表现更好。因此,本文设计了自适应调节参数βi,以控制式(7)中g*对每个个体更新的影响。具体而言,如果指导个体i更新的两个最优解g、g*的适应度值相差较大,则βi应该很小,以防止不同任务间出现负迁移,导致算法性能受损。若其适应度值相差较小,则βi应该较大,以增强g*对个体更新的影响,以更好实现不同任务间的知识共享,同时避免个体过快地靠近g。具体公式如下:
表示第t次迭代时与个体i执行不同任务的个体中的全局最优解;fi由式(1)定义;βi=(β1,β2,…,βn)为控制g*对个体更新影响力的系数。Yang等[23]提出了基于粒子个体进化信息的自适应参数调整策略,降低了优化器对于新引入参数的敏感性,经过实验证明,通过应用自适应参数调整策略,算法在优化问题上表现更好。因此,本文设计了自适应调节参数βi,以控制式(7)中g*对每个个体更新的影响。具体而言,如果指导个体i更新的两个最优解g、g*的适应度值相差较大,则βi应该很小,以防止不同任务间出现负迁移,导致算法性能受损。若其适应度值相差较小,则βi应该较大,以增强g*对个体更新的影响,以更好实现不同任务间的知识共享,同时避免个体过快地靠近g。具体公式如下:
A=|Fit![]() i(g)-Fit
i(g)-Fit![]() i(xi)|;
i(xi)|;
(8)
B=|Fit![]() i(g*)-Fit
i(g*)-Fit![]() i(xi)|;
i(xi)|;
(9)
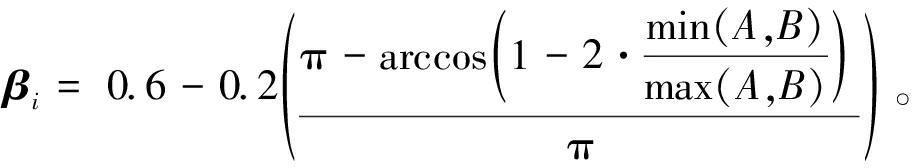
(10)
式中:Fit(·)为适应度函数,通过本文所设计的参数调整策略,可以在算法迭代过程中自适应地调整每个个体的βi。在早期阶段,个体间的差异较大,通过这种设置能帮助个体快速地寻找到有潜力的区域;而在后期阶段,当个体间差异变小时能够有效地开发有潜力的区域,避免陷入局部最优。这符合对个体更新过程的期望。
而垂直文化传播过程与算法1中保持一致,更新后的个体随机模仿指导其更新的个体的某项任务,从而实现不同任务间解决方案的交换。通过垂直文化传递,算法中的任务通过不断地从其他任务中获得有希望的解决方案,从而能够找到更好的解决方案。算法2中描述了包含选型交配和垂直文化传播算子的多因子蝙蝠算法的迭代过程。
算法2 多因子蝙蝠算法。
输入:个体数量NP、维度D、任务数量K、最大迭代次数Nt;
输出:所有任务的最优解。
① 初始化种群NP;
② 计算每个个体对所有任务的适应度值;
③ 计算每个个体的技能因素![]() ;
;
④ 更新所有任务的全局最优解;
⑤ while 1≤t≤NP do
⑥ for i=1 to NP do
⑦ 根据式(1)更新fi;
⑧ if (rand(0,1)<rmp) do
⑨ 根据式(7)和式(3)更新vi、xi;
⑩ 根据垂直文化传播选择新个体执行的任务;
 else
else
 根据式(2)和式(3)更新vi、xi;
根据式(2)和式(3)更新vi、xi;
 End if
End if
 根据式(6)更新xi;
根据式(6)更新xi;
 End if
End if
 计算更新后新解xnew的适应度函数Fit(xnew);
计算更新后新解xnew的适应度函数Fit(xnew);
 xi=xnew;
xi=xnew;
 Fit(xi)=Fit(xnew);
Fit(xi)=Fit(xnew);
 根据式(4)、式(5)更新
根据式(4)、式(5)更新![]()
 End if
End if
 if Fit(g)≤Fit(xnew) then
if Fit(g)≤Fit(xnew) then
 g=xnew;
g=xnew;
 Fit(g)=Fit(xnew);
Fit(g)=Fit(xnew);
 End if
End if
 End for
End for
 t=t+1;
t=t+1;
 End while。
End while。
2.2 突变机制
2.2.1 反向学习
反向学习(opposition-based learning,OBL)[24]是一种优化策略,其提供了一种高效的双向并发搜索方式。根据当前解x生成其反向解![]() ,并根据其适应度选择两者中的最佳解,以提高算法解的多样性和增强种群中的个体。其定义如下:
,并根据其适应度选择两者中的最佳解,以提高算法解的多样性和增强种群中的个体。其定义如下:
(11)
式中:lb和ub为x的下界和上界值,例如,在特征选择过程中lb=0,ub=1。将其推广到多维搜索空间,其表示如下:
(12)
在本文所设计的算法中,将OBL应用于算法的初始化阶段,这是因为初始化阶段的解是随机形成的,可能初始解与全局最优解相差甚远,从而导致算法的收敛速度过慢。通过在初始阶段应用OBL,帮助算法在初始阶段尽可能找到更有希望的解。与此同时,为了避免算法在迭代过程中陷入局部最优解,设计了基于OBL的解更新机制,若g在给定的Miter次迭代中没有变化,则采用OBL更新种群中的所有解,以避免算法陷入局部最优。
2.2.2 二进制差分突变
在每次迭代更新位置后,本文将差分进化算法的突变机制应用于所提出的算法中,进一步增强算法跳出局部最优解的能力。由于传统的差分进化算法只能解决连续优化问题,在本文所解决的特征选择问题中,需要设计一种适用于多任务的二进制差分进化算法。
在本文所设计的算法中,个体的位置由二进制字符串表示,因此通过逻辑操作来实现突变机制,其中“+”表示或运算,“⊕”表示异或运算,则个体突变方式如下:
(13)
对于个体i在第t次迭代中,如果rand(0,1)<P且与个体i优化相同任务的个体不少于4个,进行该突变操作。其中,r1、r2、r3为随机选择的与i具有相同技能因素的个体;F为收缩系数,且F∈(0,1),通过该系数决定个体在该突变算子中的更新方式。
2.3 本文算法整体流程
本文算法的流程如图1所示,通过两个步骤完成特征选择过程。步骤1中,根据数据集中不同类别样本所占百分比确定哪些类为少数类,并以少数类的分类准确率为评价指标构建任务2的适应度函数,同时任务1以整体准确率构建适应度函数。步骤2中,首先将初始化种群的个体随机分配给两个任务,生成两个子群,在每个子群中通过OBL对初始解进行优化以提高初始解的质量。然后通过本文所设计的多因子优化蝙蝠算法完成两个任务间的知识转移,从而通过任务2帮助任务1选择出更好的特征子集,同时在该过程中利用基于OBL的解更新机制和二进制差分进化算子来避免算法陷入局部最优,保持种群的多样性。其中,步骤2的输入为步骤1中生成的两个任务,输出为任务1所选的特征子集。
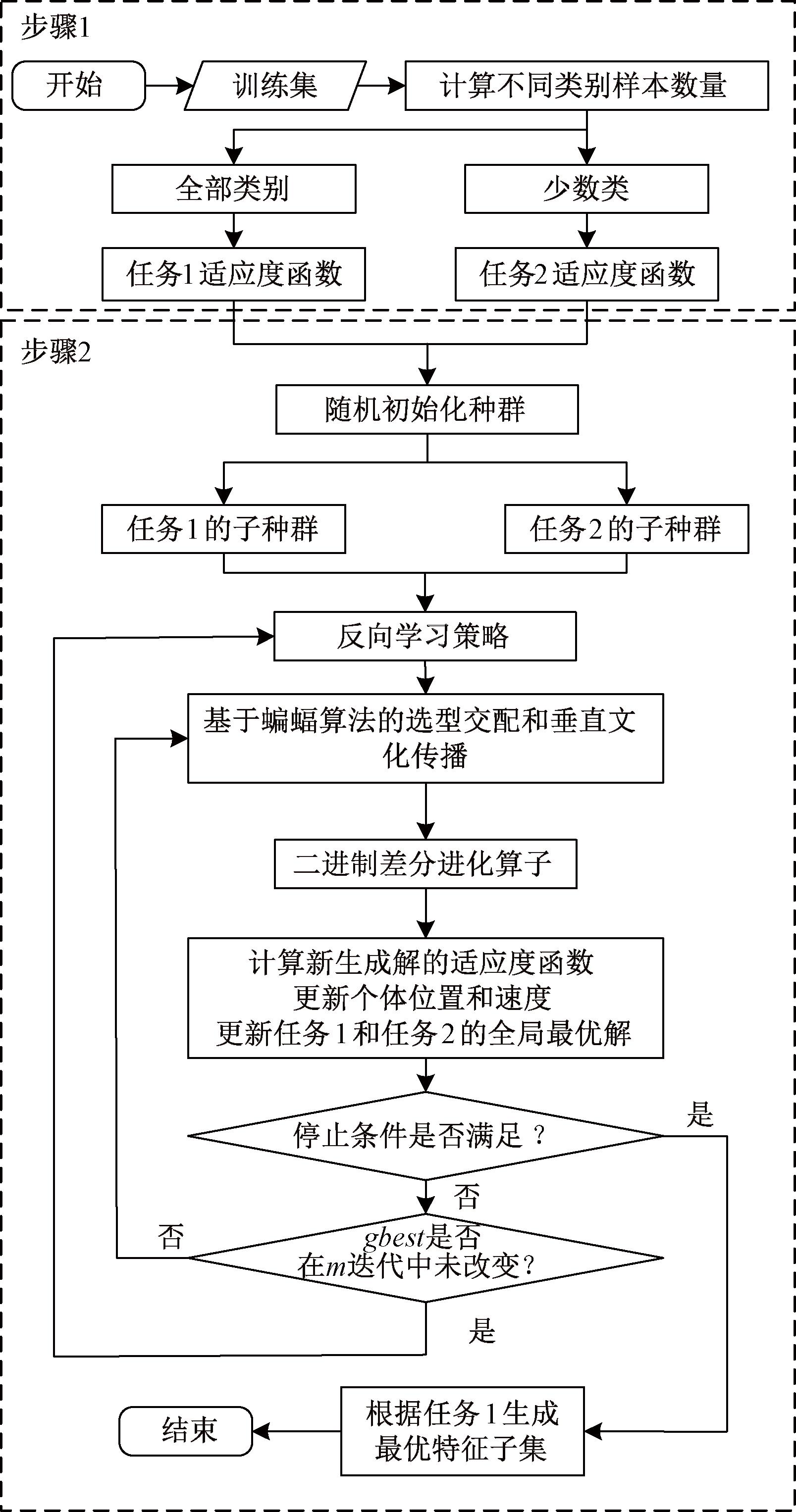
图1 IMFBA框架
Figure 1 IMFBA framework
3 实验与分析
在本节中,通过几个实验来评估所提算法在特征选择过程中的有效性。本文所有实验均在配备英特尔酷睿i7-13700KF芯片和32 GB运行内存的计算机上进行。评价指标:准确率Acc、精确率P、检出率DR、F1值、虚警率FPR等,所有评价指标的数学含义详见文献[25]。
3.1 数据集和适应度函数
本文采用被广泛应用于评估各种入侵检测方法的KDD CUP 99数据集的下采样子集和NSL-KDD数据集[26]进行实验来验证算法在网络入侵检测方面的有效性。表1、表2总结了训练数据集和测试数据集中不同种类数据的分布情况。由表1、表2可以看出,Probe、R2L、U2R这些恶意流量数据在数据集中占比极小,但这些攻击流量的正确分类却很重要。
表1 KDD CUP 99数据集分布情况
Table 1 KDD CUP 99 dataset distribution
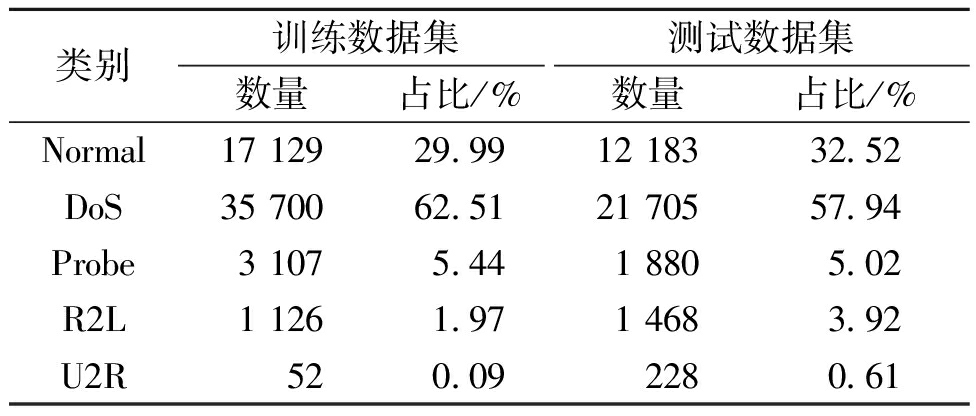
类别训练数据集测试数据集数量占比/%数量占比/%Normal17 12929.9912 18332.52DoS35 70062.5121 70557.94Probe3 1075.441 8805.02R2L1 1261.971 4683.92U2R520.092280.61
表2 NSL-KDD数据集分布情况
Table 2 NSL-KDD dataset distribution
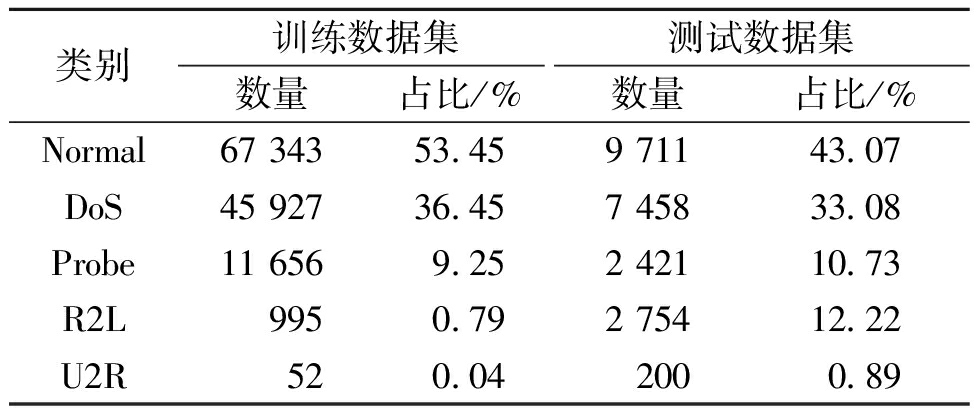
类别训练数据集测试数据集数量占比/%数量占比/%Normal67 34353.459 71143.07DoS45 92736.457 45833.08Probe11 6569.252 42110.73R2L9950.792 75412.22U2R520.042000.89
在本研究中,采用决策树算法作为分类器来评价所选的特征子集的性能。式(14)和式(15)为特征选择过程中任务1和任务2的适应度函数:
(14)
(15)
式中:ACC、ACCmin分别为整体分类准确率和少数类分类准确率;D为数据集的特征总数;S为所选特征的数量;α为反映分类正确率和所选特征数量权重的参数。
3.2 参数设定
表3所示为本文算法的实验参数设置情况,由于随机配对概率rmp和给定迭代次数Miter是本文所设计算法特征选择过程中的两个关键参数,在图2中通过对两个参数不同值的组合的实验来评估其影响。其中对rmp测试了5个值(0.4,0.5,0.6,0.7,0.8),对Miter测试了5个值(15,20,25,30,35),共25个参数组合。结果表明,在rmp为0.6、Miter为30时,实验结果最佳。此外,种群大小和最大迭代次数也是影响特征选择的重要参数,理论上两者越大越可能在迭代过程中找到最优解。在本文所设计的实验中,综合考虑算法性能和计算成本,将种群规模和最大迭代次数均设置为100。
表3 参数设置
Table 3 Parameter settings

参数数值种群规模100最大迭代次数100α0.99Miter30rmp0.6
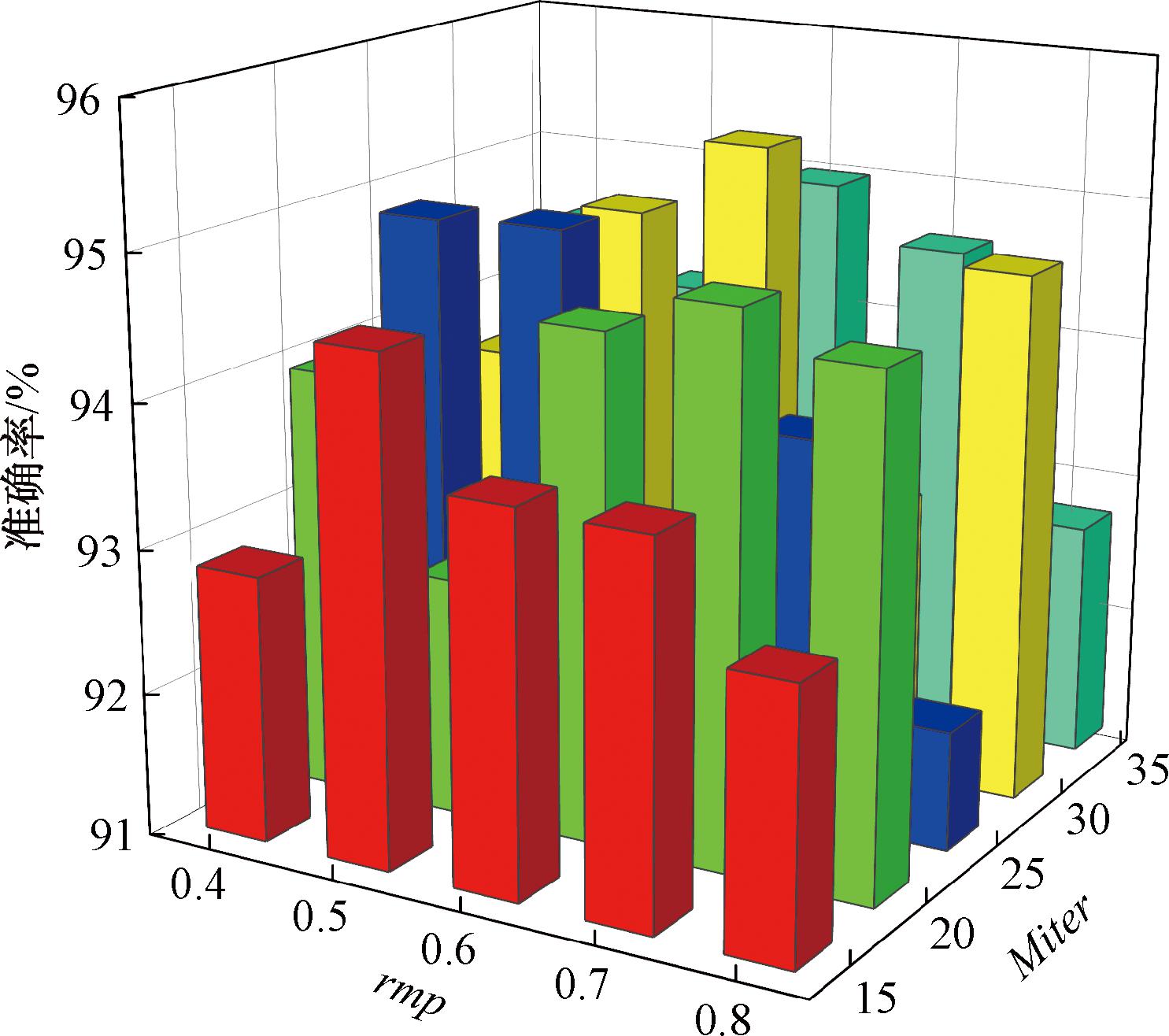
图2 两个参数25种组合的实验结果
Figure 2 Results of 25 combinations of two parameters
3.3 本文方法的有效性
本节将本文所提出的方法(IMFBA)与传统蝙蝠算法(BA)、本文设计的多因子蝙蝠算法(MFBA)、应用本文设计的突变机制改进的蝙蝠算法(IBA)及完整特征集(FULL)的分类性能相比较,以证明对BA算法所做改进的有效性。结果如表4所示。相较于完整数据集,通过选择特征子集进行分类的结果在各项指标上的均有显著提升,其中,IBA应用本文所设计的突变机制解决了BA算法易陷入局部最优解的问题,因此在分类结果上优于BA。IMFBA所选特征子集对网络入侵数据集KDD CUP 99和NSL-KDD分类结果准确率分别为95.37%和85.14%,相较于完整数据集提升了3.01百分点和9.78百分点。结合图3所示不同类别检测结果可知,通过多因子优化范式改进的MFBA虽然在绝大多数评价指标和少数类样本分类上优于IBA,尤其是对Probe类攻击的检测正确率达到了93.35%和88.22%,但在多数类上检测性能有所下降,这是由于MFBA缺乏突变机制导致其在特征选择过程中仍然会陷入局部最优。因此,本文结合上述两种改进策略提出IMFBA,实验结果表明,在整体性能和不同类别分类准确率上均优于IBA和MFBA。综上所述,本文中对于蝙蝠算法所做的所有改进是行之有效的。
表4 入侵检测性能对比
Table 4 Performance comparison of Intrusion Detection %
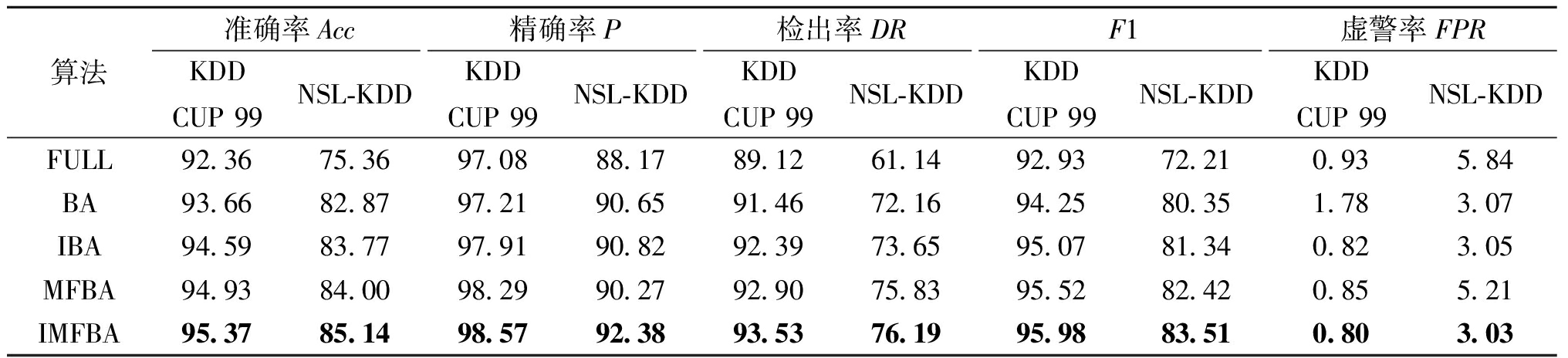
算法准确率Acc精确率P检出率DRF1虚警率FPRKDD CUP 99NSL-KDDKDD CUP 99NSL-KDDKDD CUP 99NSL-KDDKDD CUP 99NSL-KDDKDD CUP 99NSL-KDDFULL92.3675.3697.0888.1789.1261.1492.9372.210.935.84BA93.6682.8797.2190.6591.4672.1694.2580.351.783.07IBA94.5983.7797.9190.8292.3973.6595.0781.340.823.05MFBA94.9384.0098.2990.2792.9075.8395.5282.420.855.21IMFBA95.3785.1498.5792.3893.5376.1995.9883.510.803.03
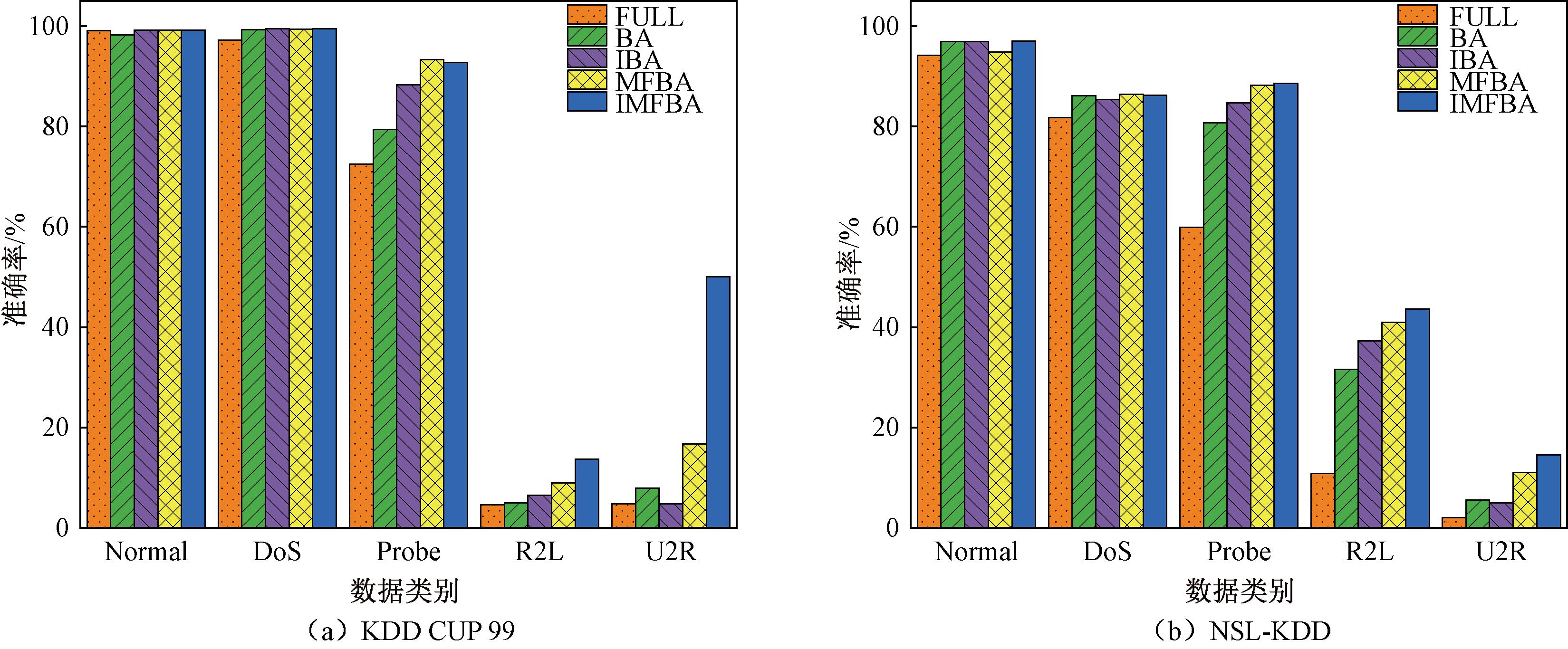
图3 不同类分类性能
Figure 3 Performance of different class
3.4 本文方法与其他特征选择算法的对比
为了进一步评价本文所提出方法,本节实验中将其与文献[8]中的LRGOA算法、文献[12]中的K-means改进BA、文献[27]中的cSG算法和一些用于特征选择的群体智能优化算法如粒子群优化算法(PSO)、人工蜂群算法(artificial bee colony,ABC)等进行了比较,实验结果如表5所示。为了更全面地评估本文方法的效果,从算法迭代过程中的收敛性和所选特征数量两个方面进行比较,结果如图4所示。
表5 不同方法的性能对比
Table 5 Performance comparison of different methods

数据集算法准确率Acc/%精确率P/%检出率DR/%F1/%虚警率FPR/%特征数KDD CUP 99NSL-KDDPSO93.2298.4690.3794.240.8820ACO93.3497.1690.6493.791.0620ABC94.0897.8691.7394.701.0321文献[8]94.9498.2193.0695.561.2318文献[12]95.0698.0593.1095.510.8419文献[27]95.1298.0593.1695.540.8519IMFBA95.3798.5793.5395.980.8021PSO82.7885.0172.1678.263.1822ACO82.5885.8371.9178.263.3218ABC83.3691.4473.4181.443.5018文献[8]84.2891.6575.0982.553.5819文献[12]84.9092.4675.9983.423.3221文献[27]84.8292.1775.8383.213.3220IMFBA85.1492.3876.1983.513.0322
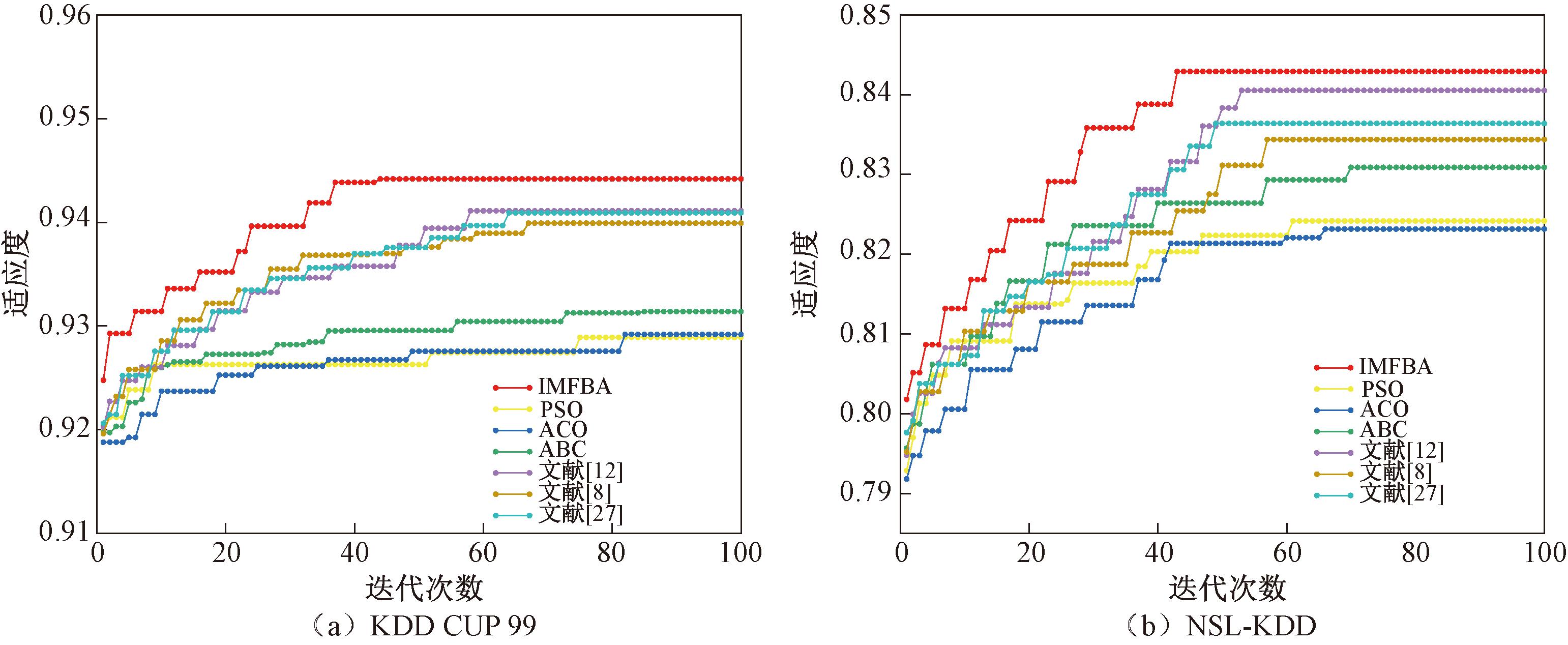
图4 不同方法的收敛性对比
Figure 4 Convergence comparison of different methods
从表5实验结果可以看出,本文所提出的特征选择方法在绝大多数评价指标方面优于现有方法,检测准确率达到了95.37%和85.14%,虽然相比于其他方法所选的特征数更多,但其通过选择贡献更大的特征来区分攻击流量,从而在保持更高的检出率的同时,保持更低的虚警率。图4验证了所提出算法的优势,在更少的迭代次数中找到具有更好适应度值的特征子集。从图4中可以看出,由于采用反向学习初始化策略,IMFBA的初始解质量更高,而且本文方法大约在45次和40次收敛,收敛速度更快且具有更高的适应度值,验证了本文所设计IMFBA增强了算法解的多样性,避免了算法陷入局部最优解,提升了算法的收敛速度。综上所述,相较于其他特征选方法,IMFBA能够更有效地选择高质量的特征子集。
同时,选择了一些从现实世界中统计出的UCI数据集,以更加全面地验证本文所提出算法的有效性,所选数据集信息如表6所示,实验结果如表7所示,在绝大多数数据集上本文所提出的算法取得更好的效果,如图5所示,本文算法在所有数据集上实现了准确率提升和数据维度缩减。
表6 UCI数据集基本信息
Table 6 Basic information of UCI datasets
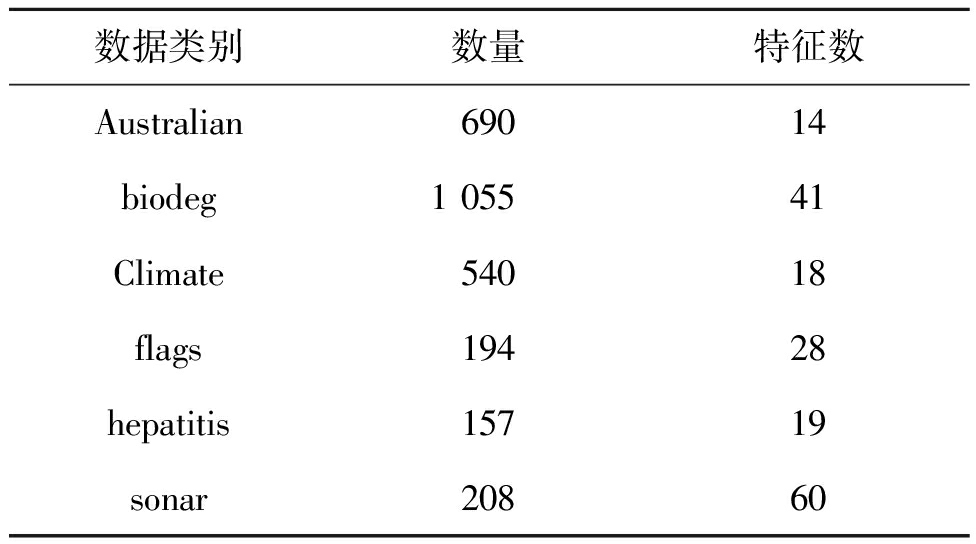
数据类别数量特征数Australian69014biodeg1 05541Climate54018flags19428hepatitis15719sonar20860
表7 UCI数据集上的准确率对比
Table 7 Accuracy comparison on UCI datasets
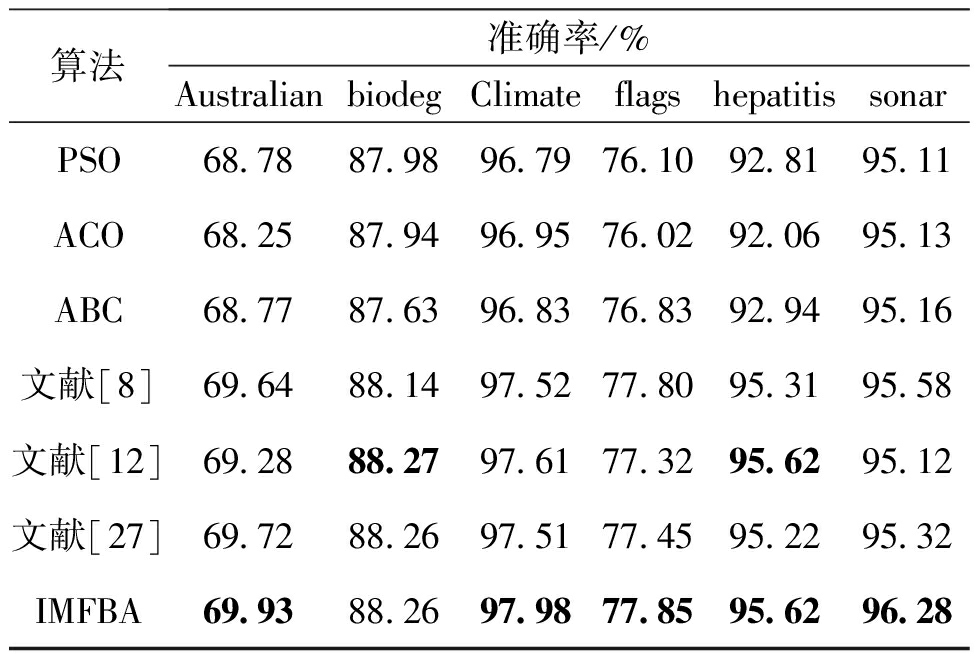
算法准确率/%AustralianbiodegClimateflagshepatitissonarPSO68.7887.9896.7976.1092.8195.11ACO68.2587.9496.9576.0292.0695.13ABC68.7787.6396.8376.8392.9495.16文献[8]69.6488.1497.5277.8095.3195.58文献[12]69.2888.2797.6177.3295.6295.12文献[27]69.7288.2697.5177.4595.2295.32IMFBA69.9388.2697.9877.8595.6296.28
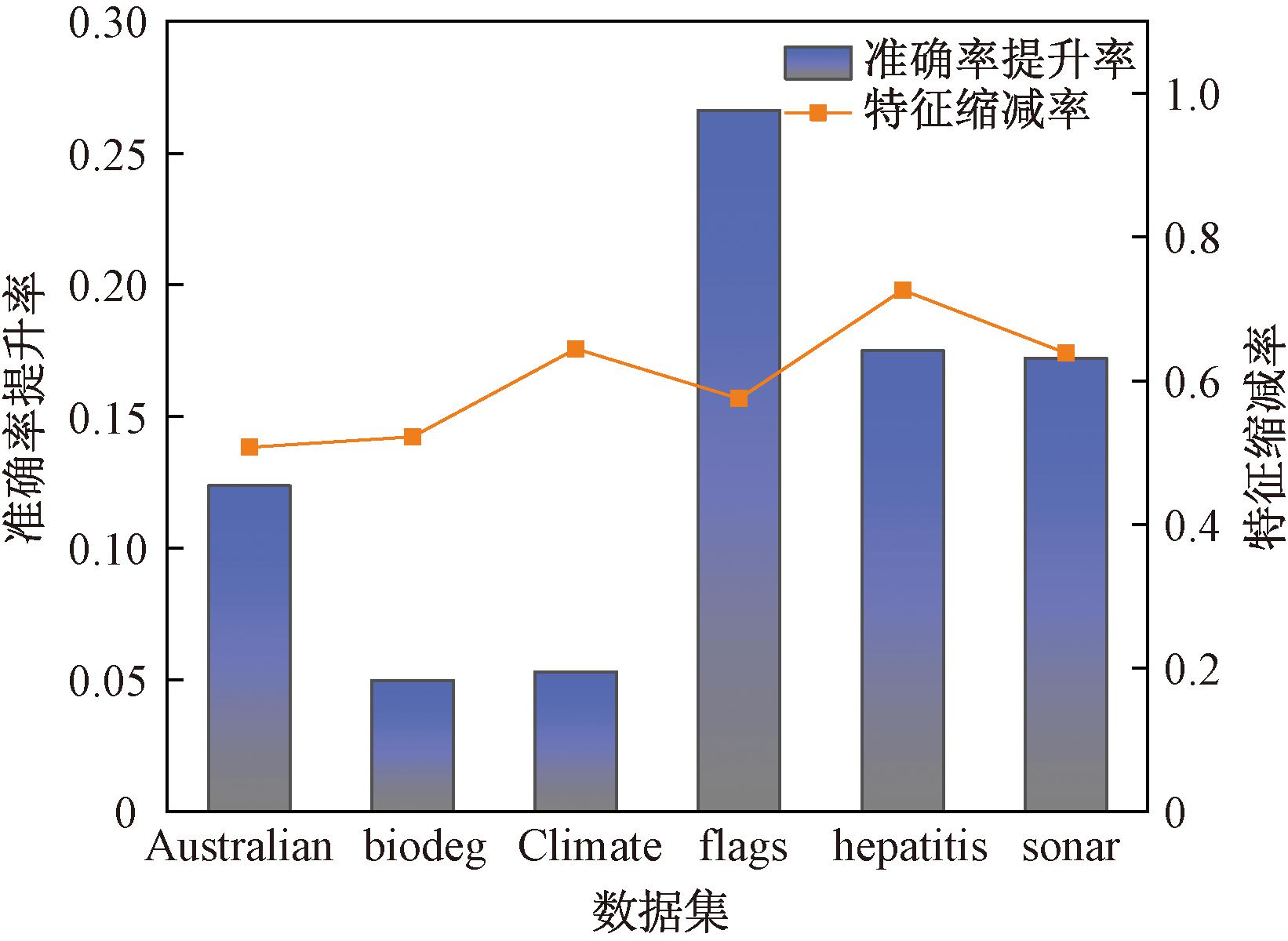
图5 IMFBA在6个数据集上的实验结果
Figure 5 Experimental results of the IMFBA on 6 datasets
4 结论
(1)本文提出一种改进蝙蝠算法进行特征选择的入侵检测方法,该方法通过对蝙蝠算法添加突变机制和应用适应性改进的多因子优化范式,来选择有利于攻击流量分类的最优特征子集。
(2)实验采用6个常用的UCI数据集以及公开的入侵检测数据集KDD CUP 99和NSL-KDD验证本文所提出方法的有效性,相较于原始数据集和其他特征选择方法,本文算法所选的特征子集都具有更好的表现。
[1] 张昊, 张小雨, 张振友, 等. 基于深度学习的入侵检测模型综述[J]. 计算机工程与应用, 2022, 58(6): 17-28.ZHANG H, ZHANG X Y, ZHANG Z Y, et al. Summary of intrusion detection models based on deep learning[J]. Computer Engineering and Applications, 2022, 58(6): 17-28.
[2] 刘翔宇, 芦天亮, 杜彦辉, 等. 基于特征选择的物联网轻量级入侵检测方法[J]. 信息网络安全, 2023, 23(1): 66-72.LIU X Y, LU T L, DU Y H, et al. Lightweight IoT intrusion detection method based on feature selection[J]. Netinfo Security, 2023, 23(1): 66-72.
[3] BOMMERT A, SUN X D, BISCHL B, et al. Benchmark for filter methods for feature selection in high-dimensional classification data[J]. Computational Statistics &Data Analysis, 2020, 143: 106839.
[4] KHAIRE U M, DHANALAKSHMI R. Stability of feature selection algorithm: a review[J]. Journal of King Saud University-Computer and Information Sciences, 2022, 34(4): 1060-1073.
[5] 王艳丽, 梁静, 薛冰, 等. 基于进化计算的特征选择方法研究概述[J]. 郑州大学学报(工学版), 2020, 41(1): 49-57.WANG Y L, LIANG J, XUE B, et al. Research on evolutionary computation for feature selection[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(1): 49-57.
[6] SHAFIQ M, TIAN Z H, BASHIR A K, et al. CorrAUC: a malicious bot-IoT traffic detection method in IoT network using machine-learning techniques[J]. IEEE Internet of Things Journal, 2021, 8(5): 3242-3254.
[7] NGUYEN B H, XUE B, ANDREAE P, et al. A new binary particle swarm optimization approach: momentum and dynamic balance between exploration and exploitation[J]. IEEE Transactions on Cybernetics, 2021, 51(2): 589-603.
[8] 李雯婷, 韩迪, 叶符明. 基于改进蚱蜢优化算法的特征选择机制[J]. 计算机工程与设计, 2022, 43(11): 3168-3176.LI W T, HAN D, YE F M. Feature selection mechanism based on improved grasshopper optimization algorithm[J]. Computer Engineering and Design, 2022, 43(11): 3168-3176.
[9] 林达坤, 黄世国, 林燕红, 等. 基于差分进化和森林优化混合的特征选择[J]. 小型微型计算机系统, 2019, 40(6): 1210-1214.LIN D K, HUANG S G, LIN Y H, et al. Feature selection based on hybrid differential evolution and forest optimization[J]. Journal of Chinese Computer Systems, 2019, 40(6): 1210-1214.
[10] 崔雪婷, 李颖, 范嘉豪. 全局混沌蝙蝠优化算法[J]. 东北大学学报(自然科学版), 2020, 41(4): 488-491, 498.CUI X T, LI Y, FAN J H. Global chaotic bat optimization algorithm[J]. Journal of Northeastern University (Natural Science), 2020, 41(4): 488-491, 498.
[11] 徐国天, 刘猛猛. 基于改进哈里斯鹰算法同步优化特征选择的恶意软件检测方法[J]. 信息网络安全, 2021, 21(12): 9-18.XU G T, LIU M M. Malware detection method based on improved Harris Hawks optimization synchronization optimization feature selection[J]. Netinfo Security, 2021, 21(12): 9-18.
[12] LI J Q, ZHAO Z F, LI R P, et al. AI-based two-stage intrusion detection for software defined IoT networks[J]. IEEE Internet of Things Journal, 2019, 6(2): 2093-2102.
[13] ABBASI M S, AL-SAHAF H, MANSOORI M, et al. Behavior-based ransomware classification: a particle swarm optimization wrapper-based approach for feature selection[J]. Applied Soft Computing, 2022, 121: 108744.
[14] YI J, ZHANG W, BAI J R, et al. Multifactorial evolutionary algorithm based on improved dynamical decomposition for many-objective optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2022, 26(2): 334-348.
[15] YANG X S. A new metaheuristic bat-inspired algorithm[M]∥GONZ LEZ J R, PELTA D A, CRUZ C, et al. Nature inspired cooperative strategies for optimization. Berlin: Springer, 2010: 65-74.
LEZ J R, PELTA D A, CRUZ C, et al. Nature inspired cooperative strategies for optimization. Berlin: Springer, 2010: 65-74.
[16] YE Y, ZHAO X J, XIONG L. An improved bat algorithm with velocity weight and curve decreasing[J]. The Journal of Supercomputing, 2022, 78(10): 12461-12475.
[17] YU H L, ZHAO N N, WANG P J, et al. Chaos-enhanced synchronized bat optimizer[J]. Applied Mathematical Modelling, 2020, 77: 1201-1215.
[18] BANGYAL W H, HAMEED A, AHMAD J, et al. New modified controlled bat algorithm for numerical optimization problem[J]. Computers, Materials &Continua, 2022, 70(2): 2241-2259.
[19] MIRJALILI S, MIRJALILI S M, YANG X S. Binary bat algorithm[J]. Neural Computing and Applications, 2014, 25(3): 663-681.
[20] GUPTA A, ONG Y S, FENG L. Multifactorial evolution: toward evolutionary multitasking[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(3): 343-357.
[21] FENG L, ZHOU W, ZHOU L, et al. An empirical study of multifactorial PSO and multifactorial DE[C]∥2017 IEEE Congress on Evolutionary Computation (CEC). Piscataway: IEEE, 2017: 921-928.
[22] OSABA E, MARTINEZ A D, GALVEZ A, et al. DMFEA-Ⅱ: an adaptive multifactorial evolutionary algorithm for permutation-based discrete optimization problems[C]∥Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion. NewYork: ACM, 2020: 1690-1696.
[23] YANG Q, CHEN W N, GU T L, et al. An adaptive stochastic dominant learning swarm optimizer for high-dimensional optimization[J]. IEEE Transactions on Cybernetics, 2022, 52(3): 1960-1976.
[24] TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence[C]∥International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC′06). Piscataway: IEEE, 2005: 695-701.
[25] DAVAHLI A, SHAMSI M, ABAEI G. Hybridizing genetic algorithm and grey wolf optimizer to advance an intelligent and lightweight intrusion detection system for IoT wireless networks[J]. Journal of Ambient Intelligence and Humanized Computing, 2020, 11(11): 5581-5609.
[26] TAVALLAEE M, BAGHERI E, LU W, et al. A detailed analysis of the KDD CUP 99 data set[C]∥2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications. Piscataway: IEEE, 2009: 1-6.
[27] EWEES A A, GAHEEN M A, YASEEN Z M, et al. Grasshopper optimization algorithm with crossover operators for feature selection and solving engineering problems[J]. IEEE Access, 2022, 10: 23304-23320.