在对机器人路径规划的过程中,首先要读取已知环境地图的数据信息,给定机器人的起始点和终点,并依据机器人的相关条件,通过相关算法规划出一条无碰撞、路程短、用时少、相对最优的完整路径。其中的关键是如何利用环境信息对路径的规划进行决策,这就需要把重点放在智能算法的选取以及改进上。目前常用的机器人路径规划算法有蚁群算法 (ant colony optimization,ACO)[1]、遗传算法 (genetic algorithm,GA)[2]、快速扩展随机树算法 (rapidly exploring random tree,RRT)[3]、人工鱼群算法 (artificial fish swarms algorithm,AFSA)[4]等,这些方法都有各自的优缺点以及使用环境,可以根据机器人的结构信息以及地图模型选取合适的路径规划算法。
人工鱼群算法是一种模拟鱼群行为的优化算法,最早是由李晓磊博士在2002年提出的一种群体智能寻优方法[5],由于其有收敛速度快和寻优效果好等优点,有学者将其应用于机器人的路径规划[6]。张文辉等[7]通过引入方向算子来提升觅食、聚群和追尾行为的准确度和成功率,由此提高了算法的求解速度和稳定性。黄宜庆等[8]引入了多策略混合机制,分别为鱼群的视野范围、步长、个体变异策略,提高人工鱼群算法的收敛速度和优化精度。针对人工鱼群算法在路径规划中表现出的收敛速度慢、运算精度低等问题,梁雪慧等[9]提出了人工鱼群与遗传策略融合的算法,在算法中加入含有保护概率和淘汰概率的精英策略遗传算法。为了避免人工鱼群算法在栅格地图中出现全局最优和局部最优之间相互干扰的情况,罗如学等[10]用视觉函数和新型的拥挤度因子函数代替了固定的视觉范围和拥挤度,由此提高了人工鱼群算法的寻优能力和搜索精度。胡致远等[11]将人工鱼群算法和蚁群算法融合,对人工鱼群算法的状态表达式和移动步长进行了改进,结果表明,算法在收敛速度和减少耗时方面均有所提高。Li等[12]提出了一种改进人工鱼群算法与连续分段贝塞尔曲线结合的算法,解决了算法收敛性差的问题,同时引入了贝塞尔曲线理论对路径进行平滑处理,克服了传统算法中拐点多、路径长等问题。Li等[13]将整个种群划分为2个亚群,分别对2个种群采取不同的自适应策略,加快了算法的收敛速度,提高了算法整体的优化性能。Wang等[14]提出了一种基于改进人工鱼群算法与路径优化器结合的路径规划方法,采用4个自定义算子和1个自适应因子来提高算法的收敛性能,具有较高的规划效率。针对移动机器人路径规划在实际环境下优化精度低、收敛性差等问题,Qi等[15]提出了一种加权改进的自适应人工鱼群算法,算法加入了自适应步长和视觉策略,并引入了权重评估因子,使算法具有良好的搜索能力和收敛性。
本文根据蠕虫机器人的结构特点以及改进的栅格地图模型,选取人工鱼群算法作为路径规划的基础算法。针对人工鱼群算法中的觅食行为进行改进,加入精英策略,通过循环,保留每次觅食行为选出的最优结果,并且在算法中引入禁忌搜索算法[16](tabu search,TS),将鱼群的位置信息作为禁忌对象,每条人工鱼的路径中相同位置点计入禁忌表,禁忌表中的位置点不可以作为鱼群的备选目标点,由此可以使人工鱼群较快地跳出局部最优,从而规划出最优路径。为消除人工鱼在陷入局部最优过程中产生的影响,在人工鱼寻找到终点后,对人工鱼的运动路径进行优化处理,删去重复点之间的路径。
1 适用于蠕虫机器人的栅格地图建模
1.1 蠕虫机器人栅格地图建模
对于机器人的路径规划问题,环境建模是最基本要素,环境建模直接关系到机器人路径规划的过程以及规划结果。常见的路径规划环境建模方法有栅格法、拓扑法、可视图法等[17-19]。栅格法是根据特定分辨率将外部环境离散为相同大小的网格,每一个网格称为一个单元,每个单元分为占用状态和空闲状态,表示为相应的栅格位置是否有障碍物[20]。不同类型的机器人所需要的路径规划地图是不同的,本文构建出一种新型的栅格地图环境,主要应用于如图1所示蠕虫类机器人[21-23]。
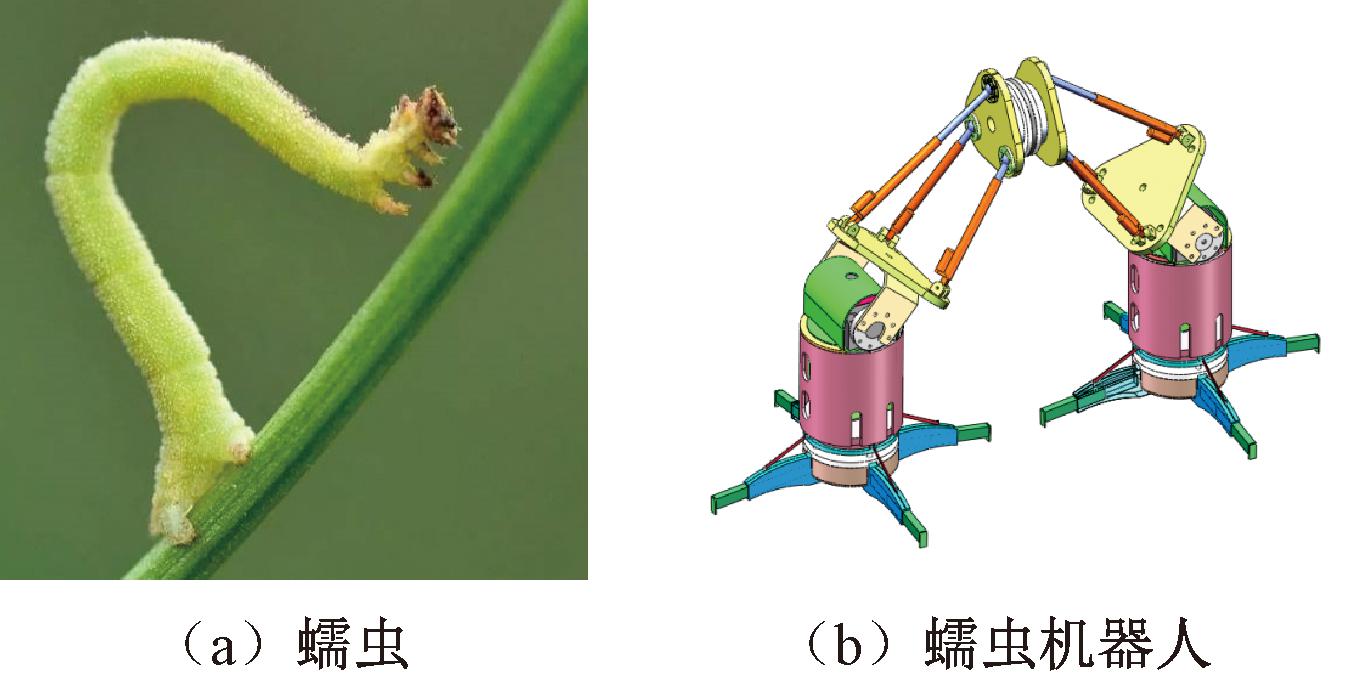
图1 蠕虫机器人
Figure 1 Worm robot
与常规的机器人相比,图1中的蠕虫机器人在运动特性上有明显的不同。首先,在面对路径中的障碍物时,常规的机器人一般都会选择绕行[24],而蠕虫机器人则可以利用自身结构特性通过各关节之间的相互配合翻越一定高度范围内的障碍物。其次,蠕虫机器人与常规机器人之间的不同在于对地面环境有一定的要求,蠕虫机器人依靠足部夹爪与地面之间的相互作用使机器人整体保持稳定,而在部分地面中会存在足部夹爪无法稳定夹持的情况[25]。因此,在对蠕虫机器人的路径规划中需要添加上述的实际约束。
在建立栅格地图过程中,一般通过数字矩阵来存储环境信息,将表示障碍物的栅格赋值为1,称为障碍物栅格;表示地面的栅格赋值为0,称为空白栅格[26]。在栅格地图中采用序号法对栅格地图中的单元格进行标识,如图2所示,将坐标系建立在10×10的栅格地图的左下角,为方便后续路径规划算法的运行,将坐标系的起始点设定为(1,1),单元格的序号p可通过坐标信息来确定,每个单元格的坐标为(xp, yp),序号p为
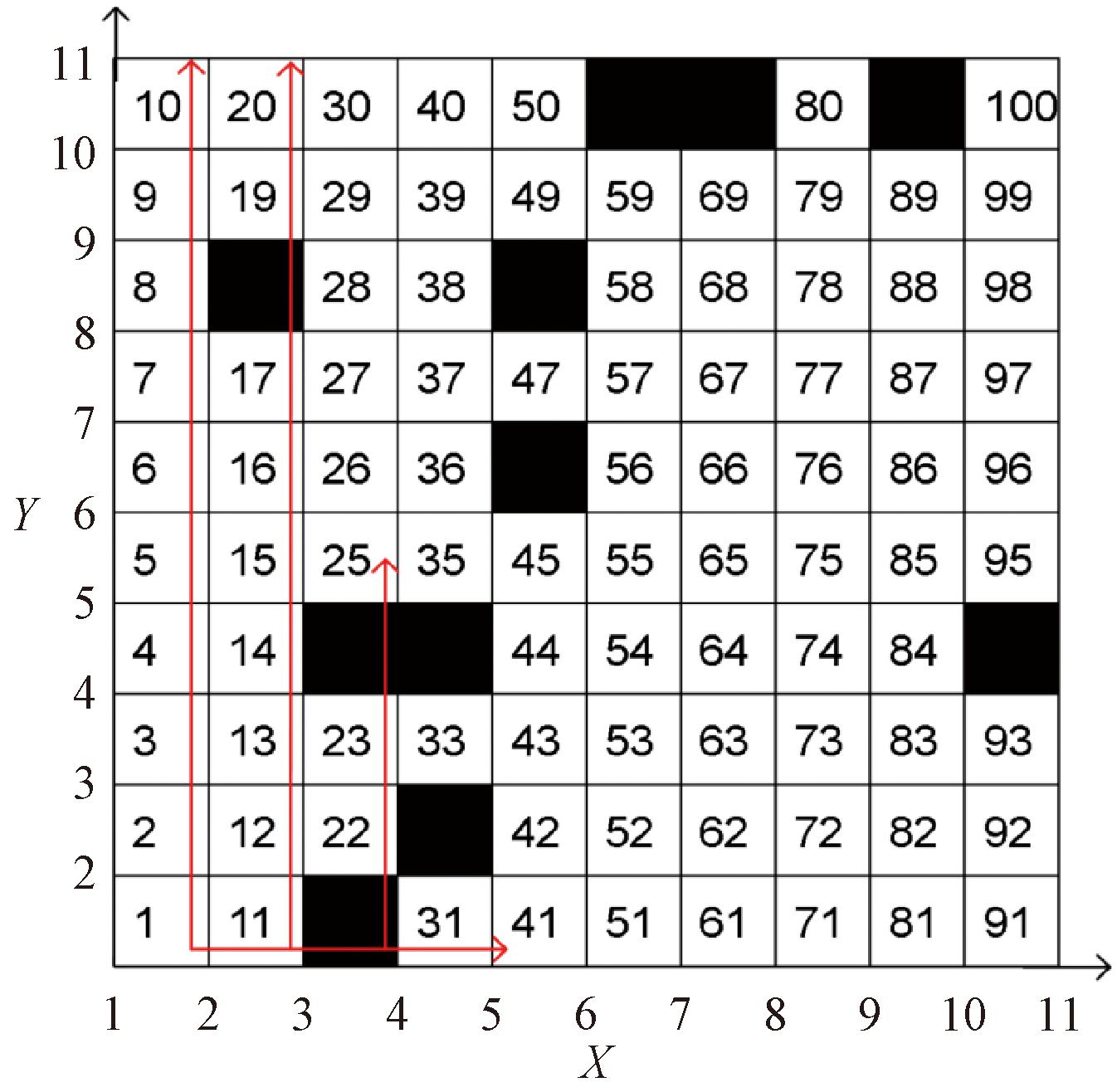
图2 序号法栅格地图模型
Figure 2 Grid map model of ordinal method
p=(xp-1)·n+yp。
(1)
式中:n为栅格地图的行数。
由于蠕虫机器人在野外环境中工作,在真实的环境中并非所有的地面都满足蠕虫机器人的运动条件,因此在栅格地图的空白栅格中选取一定比例的栅格,并将其定义为可跨越不可行走栅格,在地图信息中将此类栅格的数值改为2。在路径规划的过程中,对蠕虫机器人的约束表现为“此类栅格不可以选为落脚点”,但与障碍栅格不同的是蠕虫机器人可以通过不同的运动步态跨越此类栅格。常规的栅格地图中障碍物的表示方法虽然可以展现出环境中的障碍物分布情况,但是没有显示出障碍物的高度,不能切实反映环境的真实情况。对于部分拥有跨越障碍能力的机器人来说,此种表示方法会使机器人的运动路径与实际不符。由于蠕虫机器可以通过运动步态来跨越障碍物,因此需要根据障碍物的实际情况对栅格法地图建模进行改进。在栅格地图中给所有障碍栅格赋予高度值,假设此高度值为障碍物的实际高度并将其三维化,如图3所示。在路径规划的过程中对蠕虫机器人的约束表现为“在面对障碍物时需要根据自身的结构以及运动步态做出反应,判断跨越或者绕行障碍物”。
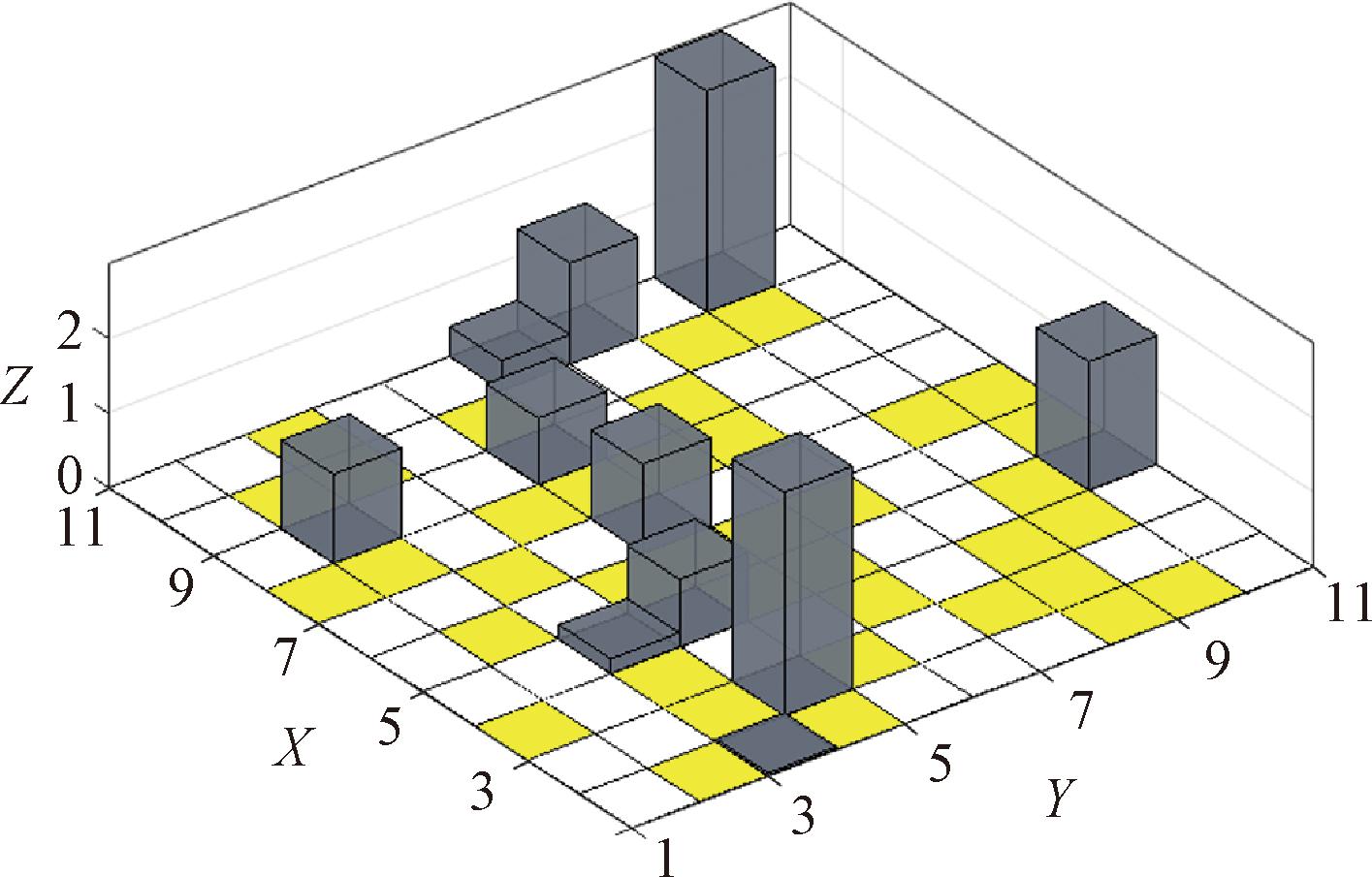
图3 改进后栅格地图模型
Figure 3 Improved grid map model
1.2 蠕虫机器人的规避原则
当蠕虫机器人面对障碍物时,可以根据机器人的结构尺寸和运动步态来设定蠕虫机器人的运动步长以及能够跨越障碍物的高度,本文设置机器人的运动步长为1.00~2.41个单位长度,能够跨越障碍物的最大高度为1.35个单位长度。在蠕虫机器人的运动步长范围内,大致可分为如图4所示的5种运动情况,图中线条表示为蠕虫机器人的运动步长,线条跨越的区域为机器人运动过程中需要跨越的栅格。为了保证机器人能够跨越运动范围内的障碍物,要求图中所有障碍栅格的高度不能超过1.35个单位长度,如果其中有一个障碍栅格的高度不符合要求,则蠕虫机器人无法跨越该障碍物,需要绕行。
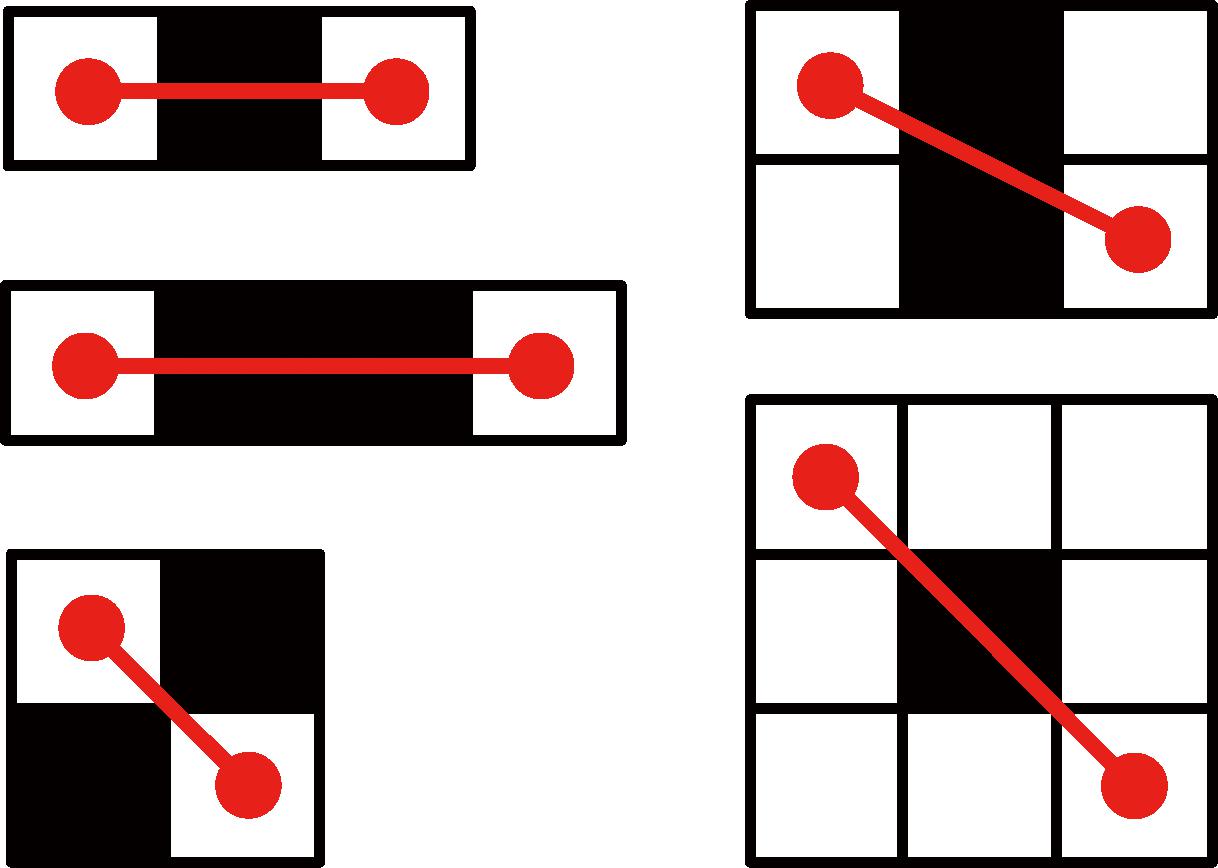
图4 蠕虫机器人跨越障碍示意图
Figure 4 Schematic diagram of worm robot crossing obstacles
2 改进人工鱼群算法
2.1 人工鱼群算法在改进栅格地图上的应用
人工鱼群算法(AFSA)是一种模拟鱼群行为的优化算法,通过模仿鱼群在活动中觅食行为、聚群行为、追尾行为、随机行为,并建立这4种行为的算法模型来实现全局寻优功能。
对于算法的模型,可以将其整体描述为一个n维的目标搜索空间,在空间内存在一个由N条人工鱼个体组成的群体,称为人工鱼群。第i条人工鱼个体的状态可以表示为向量Xi,每条人工鱼所处的位置的食物浓度表示为Y=f(Xi),其中f(x)为目标函数。每条鱼都可以通过视觉观察周围的情况,进而判断接下来向哪个方向游动,由此引入人工鱼群的两个主要参数:人工鱼个体的视野范围Visual、人工鱼个体的最大移动步长Step。
如图5所示,模拟出人工鱼的视觉和运动步长,对于第i条人工鱼来说,其在视野范围内随机选择一点Xv,如果Xv处的状态优于当前状态Xi,则该人工鱼会向前游动一步,到达位置Xinext;如果Xv处的状态不优于当前状态Xi,则人工鱼继续在视野范围内随机寻找其他位置,直至找到较优点;人工鱼寻找的次数越多,对周围的环境信息了解越透彻,越有利于人工鱼选择正确的移动方向。当然,寻找的次数也有一定限制,设置个体最大搜寻次数Max_try和整体最大迭代次数Max_gen。人工鱼视野范围内的拥挤程度用拥挤因子δ表示,每条人工鱼在执行4种行为时,可以在步长范围内向任何方向移动,同时也能感知视野范围内其他人工鱼的状态。
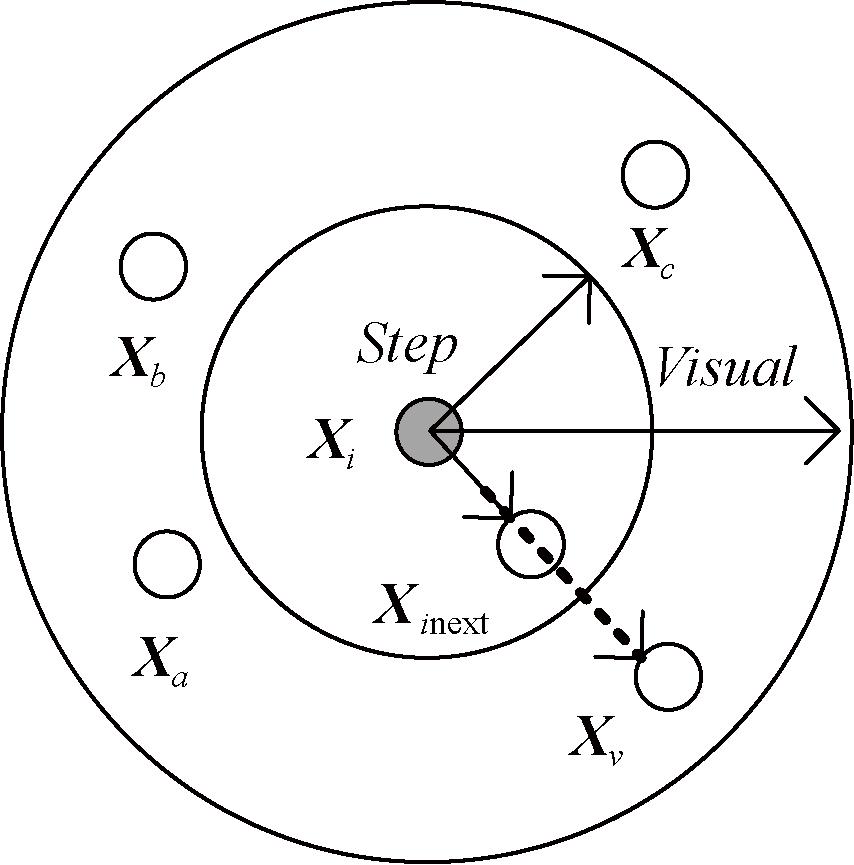
图5 人工鱼视野及运动步长模拟图
Figure 5 Artificial fish visual field and motion step simulation diagram
(1)觅食行为。觅食行为是鱼群生存的一种本能行为,鱼群会向食物浓度更高地方前行,具体表现为人工鱼i在视野范围内随机选取一点Xv,人工鱼在该点的状态可表示为
Xv=Xi+Visual·rand(0,1)。
(2)
式中:rand(0,1)表示0到1之间的一个随机数。Xv点处的食物浓度为Yv,人工鱼i原始位置的食物浓度为Yi,如果Yv大于Yi,则人工鱼i根据式(3)沿着Xv的方向前行一步到达Xinext。
(3)
式中:‖Xv-Xi‖表示两人工鱼之间的欧氏距离。如果Yv小于Yi,人工鱼将继续在视野范围内随机搜寻其他位置点Xv,直至找到较优点,若在尝试了Max_try次后还未寻找到更优点,则人工鱼执行随机行为。
(2)聚群行为。在聚群行为过程中人工鱼主要遵循:①向邻近人工鱼的中心游动;②尽量避免鱼群过度拥挤。假设人工鱼搜索得出其视野范围内的人工鱼数目nf,计算这些人工鱼中心位置的状态Xc以及食物浓度Yc。如果Yc/nf<δ·Yi,说明Xc处食物浓度更优并且不拥挤,则人工鱼会根据式(4)向状态Xc的位置前行一步,否则人工鱼将执行觅食行为。
(4)
(3)追尾行为。追尾行为是指人工鱼向其视野范围内最优的方向移动的一种行为。人工鱼当前的状态为Xi,该人工鱼搜索出其视野范围内所有人工鱼,寻找出这些人工鱼中最优的个体状态Xb以及食物浓度Yb,并探索该最优个体视野范围内的人工鱼数目nf,如果Yb/nf<δ·Yi,说明Xb处食物浓度更优并且不拥挤,则人工鱼会根据式(5)向状态Xb的位置前行一步,否则人工鱼将执行觅食行为。
(4)随机行为。对于经过上述3种行为后还没有找到较优前行目标的人工鱼,会根据式(2)在步长范围内随机前行一步。随机行为可以一定程度上抑制鱼群陷入局部最优,增加种群的多样性。
基于上述介绍,对算法步骤进行改进,使其应用到新型的栅格地图中,实现蠕虫机器人的路径规划。路径规划的流程如图6所示。
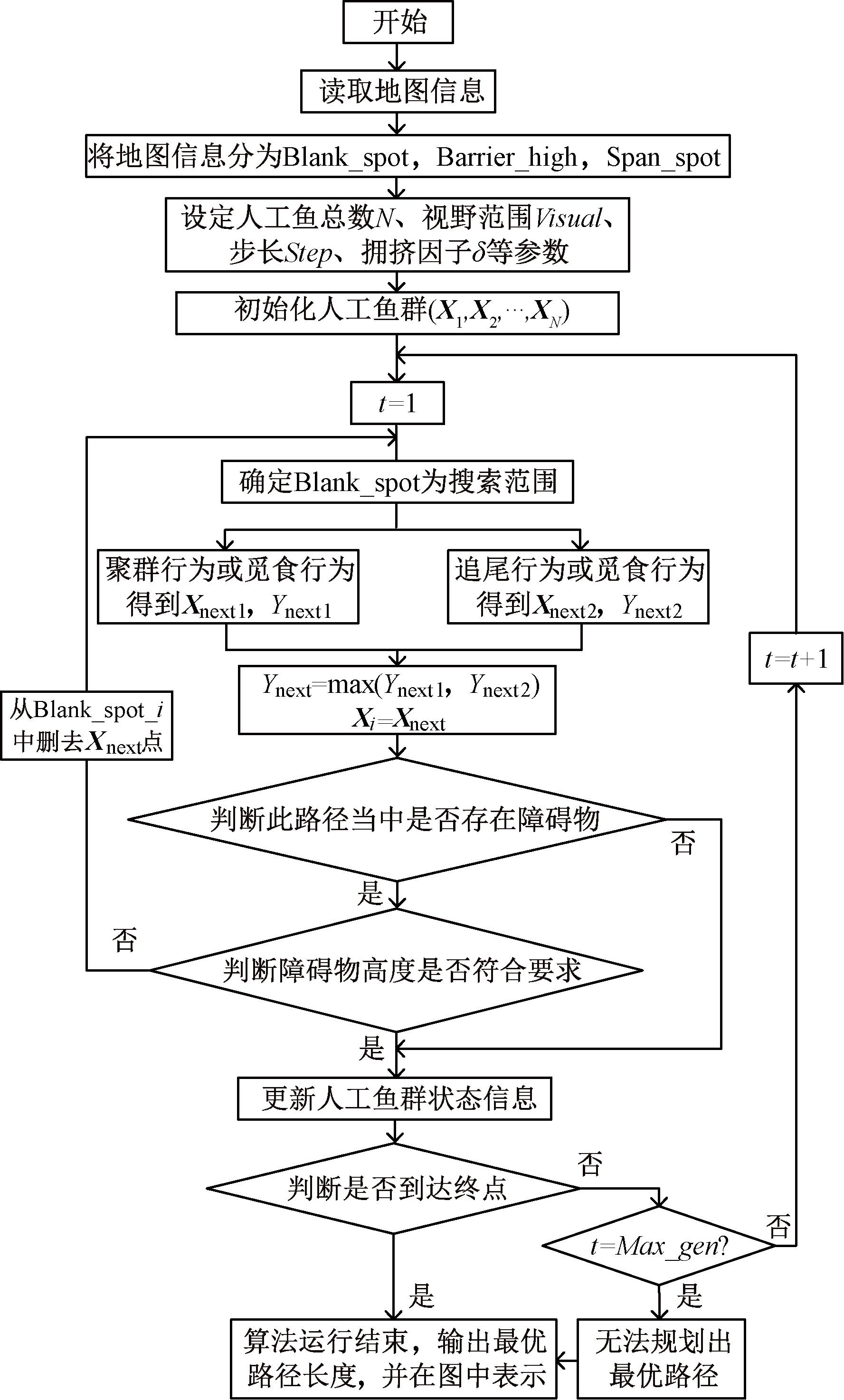
图6 路径规划流程
Figure 6 Path planning flowchart
2.2 人工鱼群算法改进点
由于常规的人工鱼群算法的行为是为了寻求相对较优点,这种方法有利于算法的快速寻优,但是很容易导致算法在面对较多地图陷阱时陷入局部最优,并且在面对空白栅格较多时,存在部分路径不合理、精度不高等情况。本文主要针对这些问题对算法进行如下改进。
(1)改进算法中的行为选择方式以及觅食行为。基础人工鱼群算法的流程中首先执行聚群和追尾行为,在此处将觅食行为加入其中,使算法在觅食、聚群、追尾3种行为中选取最优结果。常规的觅食行为是在视野范围内随机选取一点,如果被选取点的食物浓度优于当前位置则确定为下一目标点。这种选取方法有很大的偶然性,尤其在面对大面积的空白栅格时,视野范围内食物浓度优于当前位置的点有很多,极有可能导致路径规划不合理。因此对觅食行为进行改进,在其中加入寻优循环,具体表示为通过常规觅食行为选取出第1个目标点Xn1并将其保留,代表完成第1次循环,继续进行第2次常规觅食行为,选出第2个目标点Xn2时与保留的Xn1进行比较,如果Yn2大于等于Yn1则保留Yn2,如果小于则舍去,代表完成第2次寻优,直至达到最大循环次数Max_ms,选取出最终的目标点Xn。图7为改进后觅食行为的流程图。
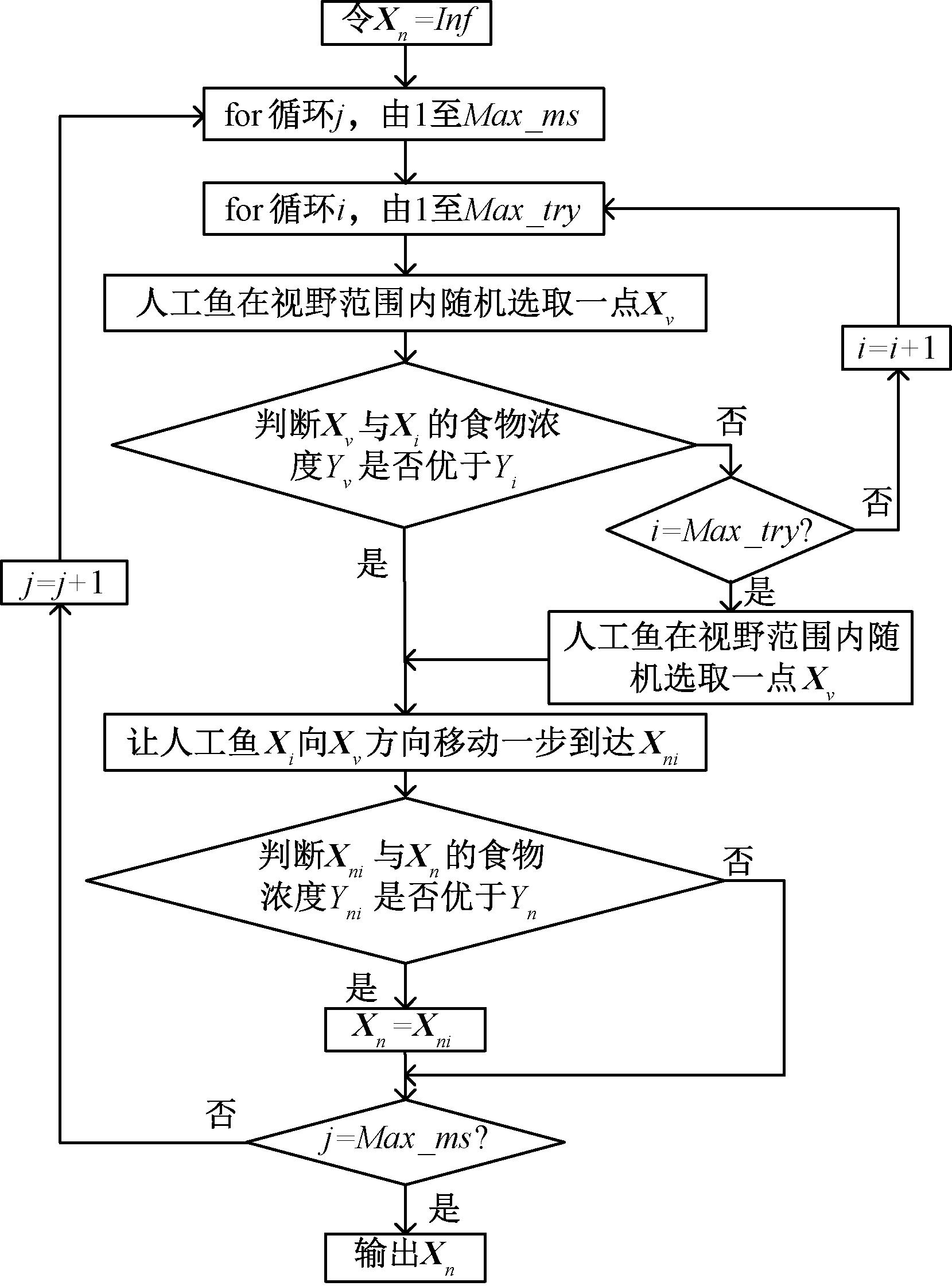
图7 改进觅食行为流程图
Figure 7 Improvement of foraging behavior flowchart
(2)融合禁忌搜索算法(tabu search algorithm,TS)。禁忌搜索算法最早由美国科罗拉多大学教授Fred Glover在1986年提出,是一种启发式算法[27],与其他算法相比,其主要优势是能够使算法跳出局部最优,算法的主要思想是对于搜索过的地方短时间内不会进行第2次搜索。为了使算法在路径规划的过程中能够跳出局部最优,在基础人工鱼群算法中融合禁忌搜索算法。首先在算法中建立禁忌表List,将栅格地图中的单元格序号作为禁忌对象,人工鱼群算法中每条人工鱼的行走路径都会被记录,当人工鱼选取出下一个前行的位置点时,对该人工鱼行走过的路径进行筛选,如果人工鱼在之前的路径中走过该位置点,表明此人工鱼在进行往返游动,为避免陷入局部循环,将此人工鱼路径中与该位置点相同的位置栅格之间的栅格序号加入禁忌表,同时为了不影响其他人工鱼的前行路径,此禁忌表只对该人工鱼有效,即每条人工鱼都有属于自己的禁忌表。
(3)对路径进行优化处理。当有人工鱼寻找到目标点时,算法跳出迭代,从人工鱼群中找出到达目标点的人工鱼路径,对这些人工鱼的运动路径进行优化处理。首先筛选出路径中重复的栅格点序号,删去重复栅格点之间的路径,保证路径中没有重复的栅格点,此做法主要是为了消除人工鱼在陷入局部最优过程中运动的路径。
2.3 改进人工鱼群算法流程
将改进后人工鱼群算法应用在新型的栅格地图中,具体步骤如下。
步骤1 读取地图信息,将地图信息划分类为Blank_spot、Barrier_high、Span_spot。
步骤2 设定人工鱼群总数N、视野范围Visual、步长Step等参数;初始化禁忌表List,人工鱼群(X1,X2,…,XN);在(1, N)的元胞数组cell的每一个元胞中存放Blank_spot作为每条人工鱼的搜索范围。
步骤3 算法进入迭代过程,通过Setdiff (Blank_spot_i, List_i)更新每条人工鱼的搜索范围,同时执行改进的觅食行为、聚群行为、追尾行为,得到3个位置点Xnext1、Xnext2、Xnext3,对比这3个位置点的食物浓度,选取最优食物浓度对应的位置点作为人工鱼前行点Xnext。
步骤4 根据蠕虫机器人的规避原则判断人工鱼Xi和前行点Xnext之间的路径是否存在障碍物,不存在则执行步骤5,若存在则判断障碍物高度是否符合要求,符合则执行步骤5,不符合则返回步骤3重新选取下一目标点。
步骤5 判断Xnext是否与该人工鱼路径上的点重合,存在则更新该人工鱼的禁忌表List_i,不存在则继续;之后更新人工鱼的状态信息,记录人工鱼群路径。
步骤6 判断人工鱼是否到达终点,到达终点则执行步骤7,若未到达终点判断是否已达到最大迭代次数,达到最大迭代次数则算法结束,说明算法无法规划最优路径,没有达到最大迭代次数则返回步骤3继续迭代。
步骤7 对完成规划的路径进行优化处理,对路径中的点进行去重处理,删去重复点之间的路径,算法运行结束,输出最优路径长度和运行时间,并在新型栅格地图中显示。
3 实验与结果分析
3.1 对比实验
为了验证改进人工鱼群算法的有效性,需要把该算法与常规人工鱼群算法、蚁群算法[28]以及文献[10]中的IAFSA算法进行对比。将这些算法在3种不同功能类型的新型栅格地图中仿真运行,在仿真模拟15次后,记录最短路径,并计算路径长度的平均值、方差和平均运行时长,分别选取最短规划结果在图中显示。算法的运行环境为Windows 10 64 bit,处理器为Intel i7-4790 CPU,运行内存为8.00 GB,软件为MATLAB2020a。
仿真前对各算法的参数进行设置,在人工鱼群算法中,将人工鱼数量N设置为50,由于蠕虫机器人的运动步长为1.00~2.41个单位长度,所能跨越的最高的障碍物高度为1.35个单位长度,因此将人工鱼群算法中的运动步长Step设置为2.41,视野范围Visual设置为2.5。最大搜寻次数Max_try设置为10,拥挤因子δ设置为0.618,对于本文提出的改进人工鱼群算法,将参数Max_ms设置为3,其余参数与人工鱼群算法的参数保持一致。参照文献[10]中的IAFSA算法,将其参数visual_min设置为6,visual_max设置为16,δmin设置为0.01,δmax设置为0.9,调整参数m设置为100,其余参数与基础人工鱼群算法的参数保持一致。对于蚁群算法,将蚂蚁数量设置为50,信息素重因子参数设置为1,启发式蒸发因子设置为7,信息蒸发系数设置为0.3,迭代次数设置为100。以上算法中的目标函数(食物浓度)均由式(6)表示,其中(xi,yi)和(xd,yd)分别代表人工鱼当前位置点坐标和路径规划终点坐标。
(6)
具体仿真结果如下,为了方便仿真结果的显示,将路径规划结果在新型栅格地图的俯视图上进行展示。
3.1.1 栅格地图1
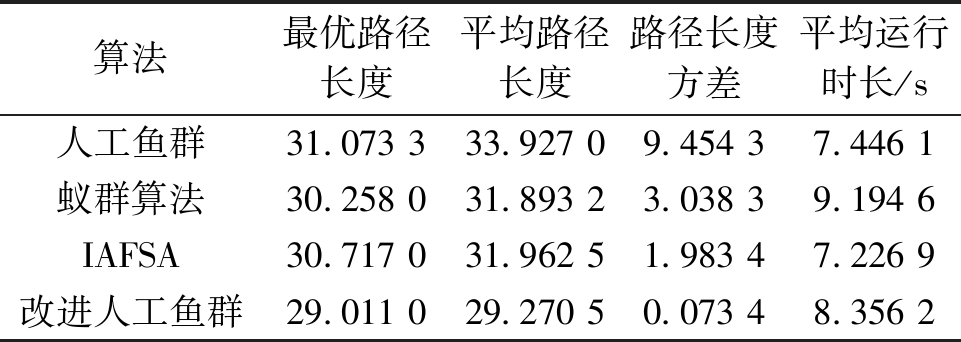
此地图为20×20的简单栅格地图,符合要求的空白栅格占比为57.4%,障碍物占比为39.75%。图8为4种算法在该地图上仿真结果的最优解。表1为仿真结果的最优路径长度、平均路径长度、路径长度方差和平均运行时长。
表1 4种算法在栅格地图1中的路径规划结果
Table 1 Path planning results of four algorithms in grid map 1
算法最优路径长度平均路径长度路径长度方差平均运行时长/s人工鱼群31.073 333.927 09.454 37.446 1蚁群算法30.258 031.893 23.038 39.194 6IAFSA30.717 031.962 51.983 47.226 9改进人工鱼群29.011 029.270 50.073 48.356 2
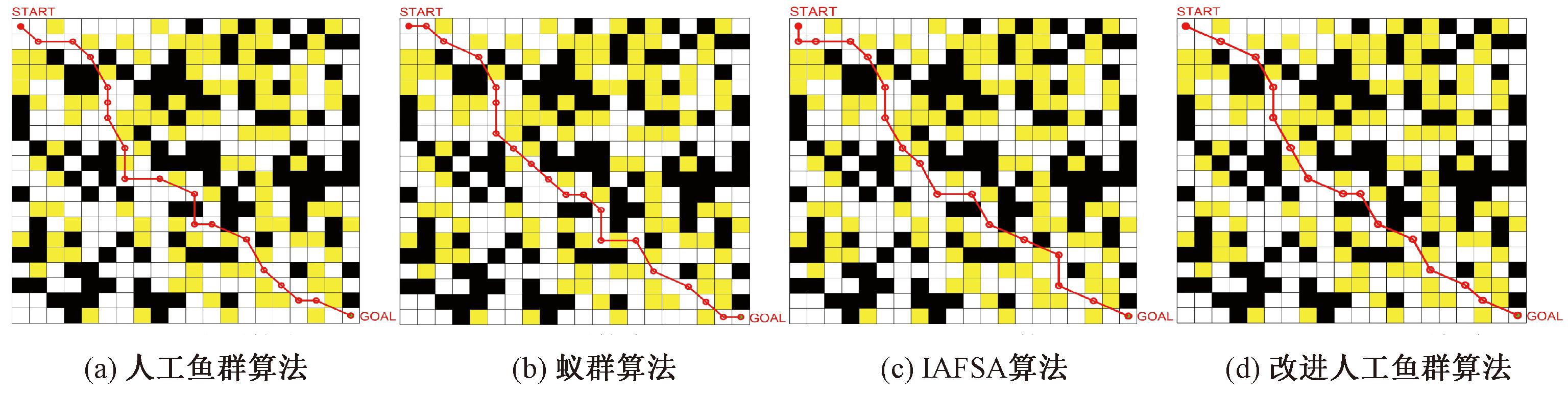
图8 4种算法在栅格地图1中最优路径结果
Figure 8 Four algorithms for optimal path results in grid map 1
在栅格地图1中,改进的人工鱼群算法在平均路径长度上比基础人工鱼群算法减少了13.73%,比蚁群算法减少了8.22%,比IAFSA算法减少了8.42%,并且在最优路径的精度上均有所提高。在路径长度的方差中可以看出改进人工鱼群算法的方差值最小。改进人工鱼群算法在平均运行时长上比蚁群算法减少了9.12%,但比基础人工鱼群算法和IAFSA算法均有增加。
3.1.2 栅格地图2
此地图为20×20的带有简单陷阱的栅格地图,符合要求的空白栅格占比为57.4%,障碍物占比为41.75%。图9为4种算法在该地图上仿真结果的最优解。表2为仿真结果的最优路径长度、平均路径长度、路径长度方差和平均运行时长。
表2 4种算法在栅格地图2中的路径规划结果
Table 2 Path planning results of four algorithms in grid map 2
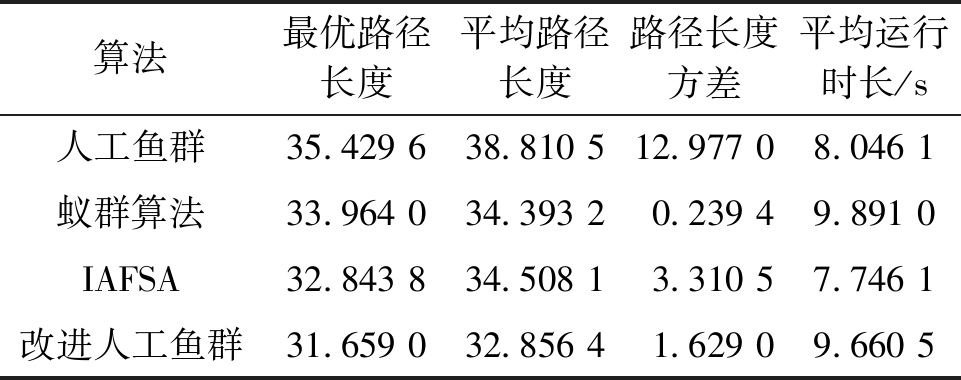
算法最优路径长度平均路径长度路径长度方差平均运行时长/s人工鱼群35.429 638.810 512.977 08.046 1蚁群算法33.964 034.393 20.239 49.891 0IAFSA32.843 834.508 13.310 57.746 1改进人工鱼群31.659 032.856 41.629 09.660 5
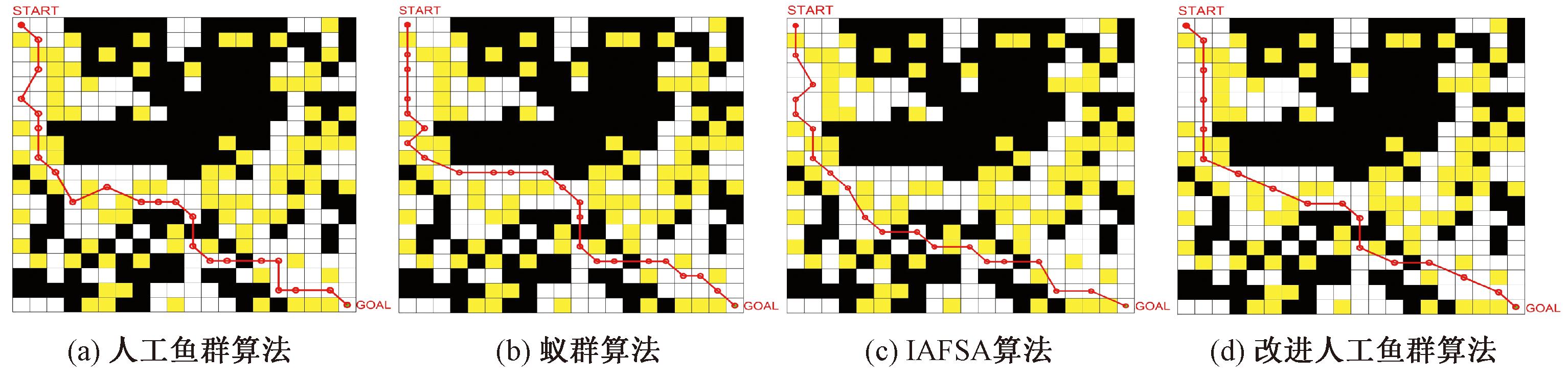
图9 4种算法在栅格地图2中最优路径结果
Figure 9 Four algorithms for optimal path results in grid map 2
3.1.3 栅格地图3
此地图为40×40的带有复杂陷阱和大面积无障碍区域的栅格地图,障碍物占比为41.75%。表3为仿真结果的最优路径长度、平均路径长度、路径长度方差和平均运行时长。图10为4种算法在该地图上仿真结果的最优解。在仿真的过程中,基础人工鱼群算法和IAFSA算法都多次存在由于陷入局部最优而规划不出最短路径的情况,其中基础人工鱼群算法共有12次无法规划出最优路径,IAFSA算法共有11次无法规划出最优路径。
表3 4种算法在栅格地图3中的路径规划结果
Table 3 Path planning results of four algorithms in grid map 3
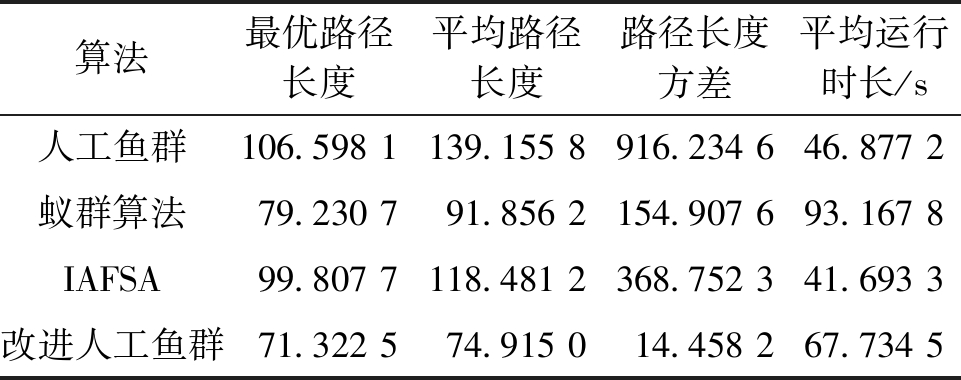
注:人工鱼群算法15次运行结果中有12次无法规划出最优路径;IAFSA算法15次运行结果中有11次无法规划出最优路径。
算法最优路径长度平均路径长度路径长度方差平均运行时长/s人工鱼群106.598 1139.155 8916.234 646.877 2蚁群算法79.230 791.856 2154.907 693.167 8IAFSA99.807 7118.481 2368.752 341.693 3改进人工鱼群71.322 574.915 014.458 267.734 5
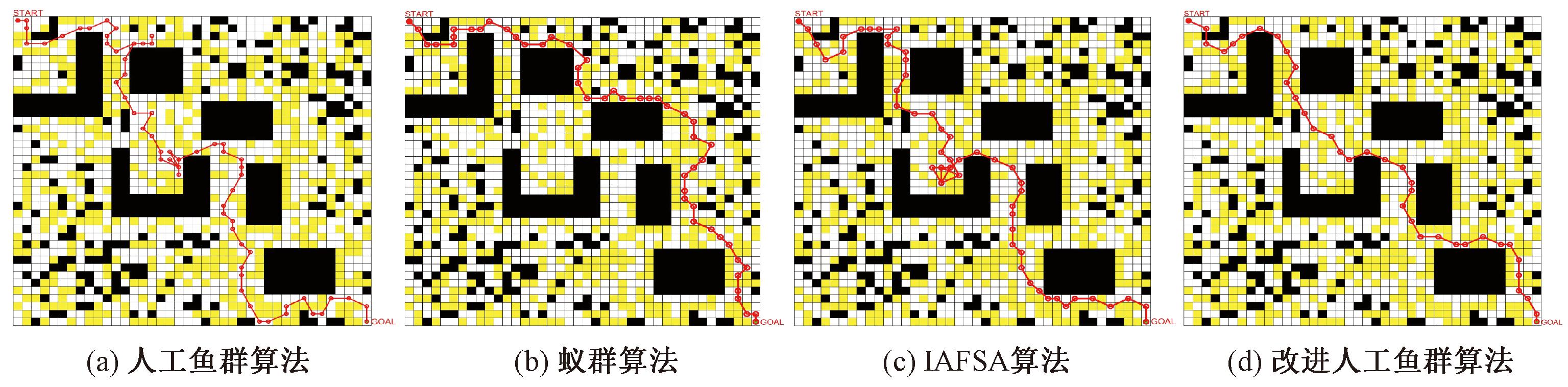
图10 4种算法在栅格地图3中最优路径结果图
Figure 10 Four algorithms for optimal path results in grid map 3
在栅格地图3中,人工鱼群算法和IAFSA算法规划成功率分别为20%、26.7%,蚁群算法和改进的人工鱼群算法均可以规划出最优路径,因此改进的人工鱼群算法能够有效地跳出局部最优,极大地提高了机器人在多陷阱的地图中路径规划的成功率。对表3进行分析可知,改进的人工鱼群算法在平均路径长度上比基础人工鱼群算法提高了46.17%,比蚁群算法提高了18.44%,比IAFSA算法提高了36.77%,并且在最优路径的精度上有大幅度提高。由路径长度方差可以看出,改进人工鱼群算法的方差值比基础人工鱼群算法、蚁群算法和IAFSA算法都有大幅度的降低。改进人工鱼群算法在平均运行时长上比蚁群算法减少了27.30%,但比基础人工鱼群算法和IAFSA算法均有增加。
3.2 结果分析
从以上分析可知,改进的人工鱼群算法在寻优能力以及路径规划稳定程度上有较好的表现,尤其在面对地图中局部陷阱较多时,改进人工鱼群算法能够及时跳出局部陷阱,保证算法能够找到最优路径。但是改进人工鱼群算法在运行时长上比人工鱼群算法和IAFSA算法有所增加,这是由于算法的改进导致算法计算量增加,从而使得算法运行用时变长。对蠕虫机器人的路径规划主要是为了保证能够成功规划出一条相对较短、较为合理的路径,相较于其他对比算法,改进的人工鱼群算法虽然耗时略有增加,但在路径长度、路径合理性、规划成功率以及规划结果的稳定性上都比其他对比算法表现更好,完全能够符合对蠕虫机器人路径规划的要求。
4 结论
本文设计了一种适用于蠕虫机器人的新型栅格地图,并选取人工鱼群算法在该地图上进行路径规划。对人工鱼群算法的不足之处进行了改进,主要对人工鱼群算法中行为的选择方式和觅食行为进行改进,加入了寻优循环,使算法在一定程度上减少所选取目标点的随机性,使规划的路径更合理。在此基础上融合了禁忌搜索算法,使算法具有较强跳出局部最优的能力。最后对路径规划的结果进行了优化处理,去除了结果中的重复路径。将改进的人工鱼群算法与人工鱼群算法、蚁群算法以及IAFSA算法在相同环境下进行路径规划的对比实验,结果表明,本文提出的算法使路径规划的结果更合理,路径规划的成功率较高,验证了算法的优越性和可行性。
本文仿真实验选取的障碍物都是静态障碍物,但是实际环境中情况可能更加复杂,存在动态障碍物。因此,在后续对路径规划算法的研究中可以考虑加入动态障碍物,在更复杂的环境下使机器人完成避障功能,这也是重要的研究方向。
[1] TIAN X, LIU L, LIU S, et al. Path planning of mobile robot based on improved ant colony algorithm for logistics[J]. Mathematical Biosciences and Engineering: MBE, 2021, 18(4): 3034-3045.
[2] 欧阳海滨, 全永彬, 高立群, 等. 基于混合遗传粒子群优化算法的层次路径规划方法[J]. 郑州大学学报(工学版), 2020, 41(4): 34-40.
OUYANG H B, QUAN Y B, GAO L Q, et al. Hierarchical path planning method for mobile robots based on hybrid genetic particle swarm optimization algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(4): 34-40.
[3] 裴以建, 杨超杰, 杨亮亮. 基于改进RRT*的移动机器人路径规划算法[J]. 计算机工程, 2019, 45(5): 285-290, 297.
PEI Y J, YANG C J, YANG L L. Path planning algorithm for mobile robot based on improved RRT*[J]. Computer Engineering, 2019, 45(5): 285-290, 297.
[4] 姚正华, 任子晖, 陈艳娜. 基于人工鱼群算法的煤矿救援机器人路径规划[J]. 煤矿机械, 2014, 35(4): 59-61.
YAO Z H, REN Z H, CHEN Y N. Path planning for mine rescue robot based on AFSA[J]. Coal Mine Machinery, 2014, 35(4): 59-61.
[5] 李晓磊. 一种新型的智能优化方法-人工鱼群算法[D]. 杭州: 浙江大学, 2003.
LI X L. A new intelligent optimization method-artificial fish school algorithm[D]. Hangzhou: Zhejiang University, 2003.
[6] 聂黎明, 周永权. 基于人工鱼群算法的机器人路径规划[J]. 计算机工程与应用, 2008, 44(32): 48-50, 63.
NIE L M, ZHOU Y Q. Path planning of robot based on artificial fish-swarm algorithm[J]. Computer Engineering and Applications, 2008, 44(32): 48-50, 63.
[7] 张文辉, 林子安, 刘彤, 等. 基于改进人工鱼群算法的机器人路径规划[J]. 计算机仿真, 2016, 33(12): 374-379, 448.
ZHANG W H, LIN Z A, LIU T, et al. Robot path planning method based on modified artificial fish swarm algorithm[J]. Computer Simulation, 2016, 33(12): 374-379, 448.
[8] 黄宜庆, 彭凯, 袁梦茹. 基于多策略混合人工鱼群算法的移动机器人路径规划[J]. 信息与控制, 2017, 46(3): 283-288.
HUANG Y Q, PENG K, YUAN M R. Path planning for mobile robots based on multi-strategy hybrid artificial fish swarm algorithm[J]. Information and Control, 2017, 46(3): 283-288.
[9] 梁雪慧, 赵嘉祺. 人工鱼群与遗传混合算法在无人艇路径规划中的应用[J]. 计算机工程与科学, 2019, 41(5): 942-947.
LIANG X H, ZHAO J Q. A hybrid algorithm of artificial fish swarm and genetic algorithm and its application in collision avoidance of unmanned surface vessels[J]. Computer Engineering &Science, 2019, 41(5): 942-947.
[10] 罗如学, 陈妙娜, 林继灿. 基于改进人工鱼群算法的机器人路径规划[J]. 科学技术与工程, 2020, 20(23): 9445-9449.
LUO R X, CHEN M N, LIN J C. Robot path planning based on improved artificial fish swarm algorithm[J]. Science Technology and Engineering, 2020, 20(23): 9445-9449.
[11] 胡致远, 王征, 杨洋, 等. 基于人工鱼群-蚁群算法的UUV三维全局路径规划[J]. 兵工学报, 2022, 43(7): 1676-1684.
HU Z Y, WANG Z, YANG Y, et al. Three-dimensional global path planning for UUV based on artificial fish swarm and ant colony algorithm[J]. Acta Armamentarii, 2022, 43(7): 1676-1684.
[12] LI F F, DU Y, JIA K J. Path planning and smoothing of mobile robot based on improved artificial fish swarm algorithm[J]. Scientific Reports, 2022, 12: 659.
[13] LI G Q, LIANG D W, ZHAO Q Y, et al. Improved artificial fish swarm algorithm approach to robot path planning problems[C]∥2020 5th International Conference on Automation, Control and Robotics Engineering (CACRE). Piscataway: IEEE, 2020: 71-75.
[14] WANG F, ZHAO L, BAI Y. Path planning for unmanned surface vehicles based on modified artificial fish swarm algorithm with local optimizer[J]. Mathematical Problems in Engineering, 2022, 2022: 1283374.
[15] QI B L, XIONG L Y, WANG L J, et al. A weights and improved adaptive artificial fish swarm algorithm for path planning[C]∥2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC).Piscataway: IEEE, 2019: 1698-1702.
[16] 玄世龙, 许志远, 孙帅, 等. 基于禁忌搜索算法的无人船路径规划[J]. 船舶工程, 2022, 44(4): 8-13, 37.
XUAN S L, XU Z Y, SUN S, et al. Path planning of unmanned ship based on the tabu search algorithm[J]. Ship Engineering, 2022, 44(4): 8-13, 37.
[17] 赵江, 王晓博, 郝崇清, 等. 栅格图特征提取下的路径规划建模与应用[J]. 计算机工程与应用, 2020, 56(10): 254-260.
ZHAO J, WANG X B, HAO C Q, et al. Path planning modeling and application based on feature extraction of grid graph[J]. Computer Engineering and Applications, 2020, 56(10): 254-260.
[18] 樊征, 曹其新, 杨扬, 等. 面向移动机器人的拓扑地图自动生成[J]. 华中科技大学学报(自然科学版), 2008, 36(增刊1): 163-166.
FAN Z, CAO Q X, YANG Y, et al. Automatically generation of topological map for mobile robot[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2008, 36(S1): 163-166.
[19] 张三川, 明珠. 基于主动安全的改进人工势场局部路径规划研究[J]. 郑州大学学报(工学版), 2021, 42(5): 32-36, 55.
ZHANG S C, MING Z. Research on improved local path planning of artificial potential field based on active safety[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(5): 32-36, 55.
[20] YOON S, YOON S E, LEE U, et al. Recursive path planning using reduced states for car-like vehicles on grid maps[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(5): 2797-2813.
[21] 朱晓东, 姜晓东, 曾庆山, 等. 一种仿生机器人的夹爪: CN113799164A[P]. 2021-12-17.
ZHU X D, JIANG X D, ZENG Q S, et al. Clamping jaw of bionic robot: CN113799164A[P]. 2021-12-17.
[22] 朱晓东, 姜晓东, 曾庆山, 等. 一种机器人伸缩摆动机构及仿生机器人: CN114851245A[P]. 2022-08-05.
ZHU X D, JIANG X D, ZENG Q S, et al. Robot telescopic swing mechanism and bionic robot: CN114851245A[P].2022-08-05.
[23] 彭金柱, 张建新, 曾庆山. 基于改进差分进化的3-RPS机器人逆运动学参数标定[J]. 郑州大学学报(工学版), 2022, 43(5): 1-7, 38.
PENG J Z, ZHANG J X, ZENG Q S. Inverse kinematic parameters calibration of 3-RPS parallel robot based on modified differential evolution[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(5): 1-7, 38.
[24] MIAO C W, CHEN G Z, YAN C L, et al. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm[J]. Computers &Industrial Engineering, 2021, 156: 107230.
[25] NAGAOKA K, MINOTE H, MARUYA K, et al. Passive spine gripper for free-climbing robot in extreme terrain[J]. IEEE Robotics and Automation Letters, 2018, 3(3): 1765-1770.
[26] 张蓝天, 王光霞, 刘旭, 等. 机器人栅格地图编码与索引方法[J]. 测绘工程, 2022, 31(3): 23-30.
ZHANG L T, WANG G X, LIU X, et al. Coding and indexing method of robot grid maps[J]. Engineering of Surveying and Mapping, 2022, 31(3): 23-30.
[27] LI X Y, GAO L. An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem[J]. International Journal of Production Economics, 2016, 174: 93-110.
[28] ZHANG D Y, FU P. Robot path planning by generalized ant colony algorithm[J]. Applied Mechanics and Materials, 2014, 494-495: 1229-1232.