随着越来越多的可再生式新能源发电机组接入电网,传统发电机组在电网中的比例下降,电网的惯量明显下降。新能源发电机组主要是通过电力电子设备将能量传送到电网,与电网系统完全解耦,无法响应电网的频率变化[1-2]。此情况以光伏发电最为明显。因为光伏发电运行过程中没有旋转运动,无法提供任何惯量[3]。对于风力发电,虽然机组通过叶片旋转获得能量,理论上有较高的惯量[4],但由于风机转速变化较大,且一般通过换流器与电网弱耦合连接,故可提供的惯量也较少[5]。
为解决该问题,国内外学者进行了大量研究[6-8]。研究的核心思路为如何能够让新能源机组模拟传统大惯量同步发电机的外部特性,使新能源电力系统获得较大的转动惯量和阻尼,达到惯性增强、频率稳定的目的。有学者提出引入下垂控制,即通过P/f下垂控制稳定电网频率运行状态[9-11]。虚拟同步发电机(virtual synchronous genetator,VSG)技术是增强系统惯性的重要手段,最早在欧洲VSYNC工程提出[12]。该技术通过模拟传统同步发电机的特性,使逆变器获得虚拟惯量和虚拟阻尼,实现了风电机组和光伏电池的惯量响应[13-15]。Alipoor等[16]提出了一种基于粒子群优化算法寻找合适参数的方式,将发电机电压角偏差抑制在可控范围内,避免系统振荡,但此方法缺乏动态调节性能。张亚楠等[17]提出一种自适应控制策略,实现了控制策略的自适应调节,但该方法仅在3种模式下进行修正,并未真正实现实时调整参数。Molina-García等[18]提出一种无须通信的分布式需求响应控制策略,通过响应系统各区域频率偏差及持续时间,利用简单控制装置调节该地区部分负载辅助系统而进行调频。李俊等[19]提出一种基于模糊控制的参数补偿策略,但该方法仅针对风力发电机运行进行分析。
在上述研究的基础上,提出了一种基于同步发电机下垂优化控制的VSG控制策略。该策略将传统同步发电机的P/f下垂控制引入VSG控制,在电网运行过程中通过人工神经网络对频率变化进行预测,从而达到自适应调整VSG的虚拟转动惯量和阻尼,有效提高了系统面对扰动时的频率和功率稳定能力。算例仿真结果验证了所提策略在电网遇到故障时降低频率扰动和加速频率恢复的有效性。
1 VSG的结构和控制算法
1.1 VSG结构
VSG通过对同步发电机的电磁特性和机械转矩特性进行分析,采用控制算法模拟发电机输出特性,实现并网逆变器模拟同步发电机的目的,其拓扑结构如图1所示。

图1 虚拟同步发电机拓扑结构
Figure 1 Topology of virtual synchronous generator
1.2 VSG基本控制算法
VSG的核心为控制算法,以此获得虚拟转动惯量和虚拟阻尼。图2为VSG基本控制算法框图,实现了对转子运动方程和无功-电压特性的模拟。
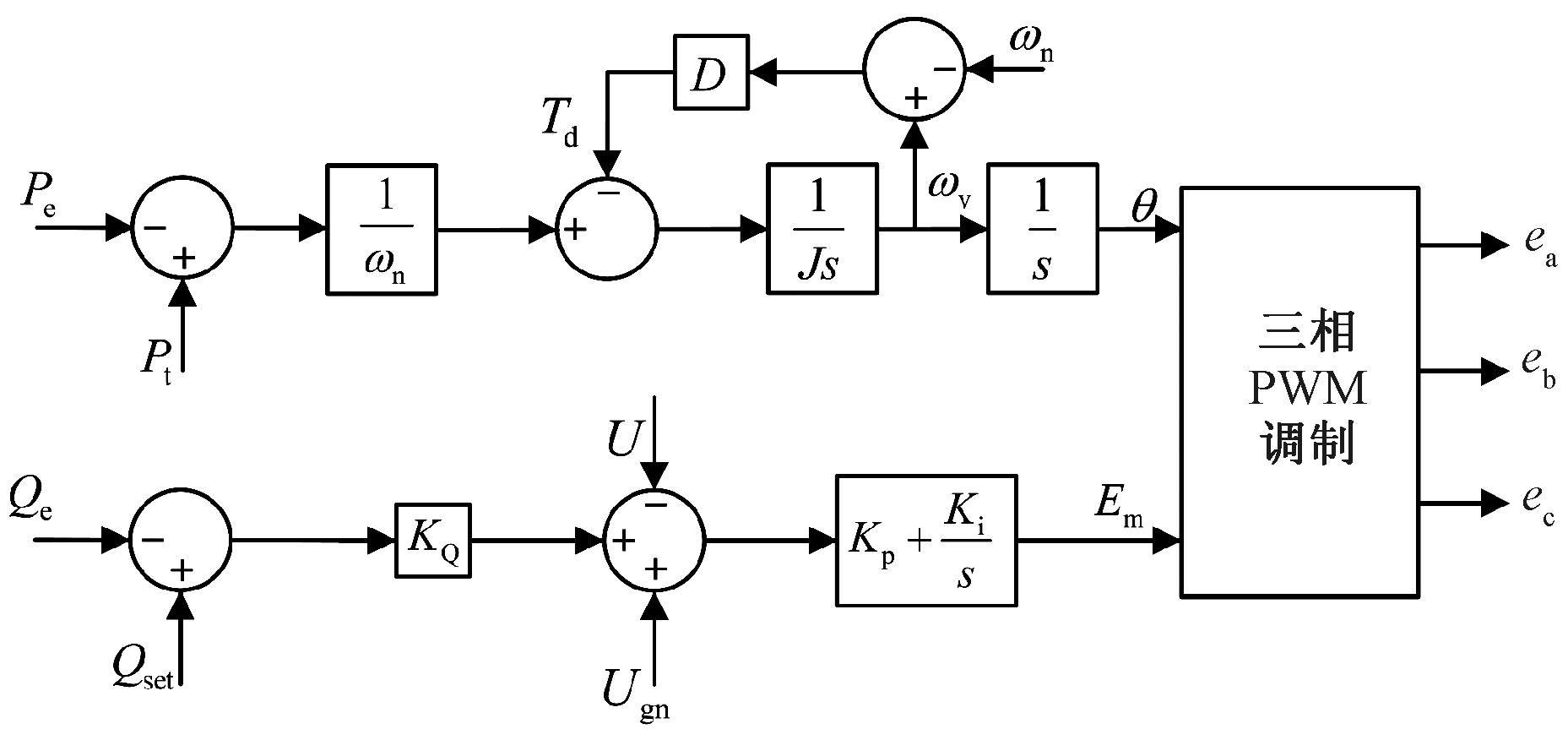
图2 VSG控制算法
Figure 2 VSG control algorithm
VSG的转子机械运动数学方程为
(1)
(2)
式中:J为虚拟转动惯量,kg·m2;ωv为虚拟角频率,rad/s;Pe为电磁功率,kW;Pt为机械功率,kW;ωn为额定角频率,rad/s;θ为虚拟相位角;D为虚拟阻尼,N·m·s/rad。
同步发电机的机端电压和输出无功功率可通过同步发电机的励磁确定。同样,可以通过控制发电机的机端电势Em来控制机端电压和输出无功。VSG的虚拟机端电势Em可由两部分组成:一部分为对应无功功率调节的部分,可表示为KQ(Qset-Qe);另一部分对应机端电压差值,表示为Ugn-U。根据以上分析可列出无功功率-电压控制回路数学方程:
(3)
式中:Em为VSG的基本电势,V;KQ为无功-电压下垂控制系数;Qset为无功功率参考值,kVar;Qe为无功功率,kVar;Ugn为电网侧额定电压,V;U为输出电压,V;Kp和Ki分别为比例系数和积分系数。
应用θ和Em可以将VSG输出三相电压表示为
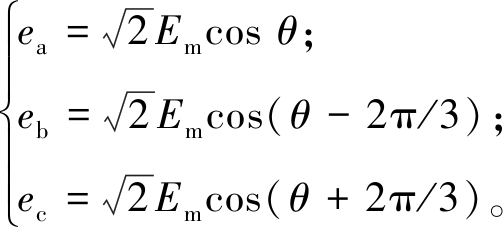
(4)
1.3 下垂控制策略
除了前述VSG的转子运动方程模拟特性,也可在VSG的有功控制回路前加上有功-频率(P/f)下垂回路。P/f下垂控制方程为
Pt-Pset=KW(fref-f)。
(5)
式中:KW为P/f下垂控制系数。
P/f下垂控制如图3所示。
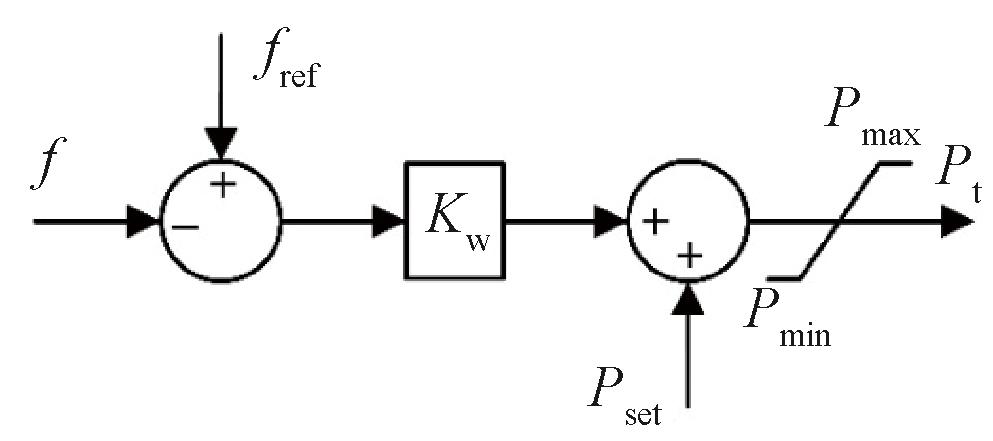
图3 P/f下垂控制
Figure 3 P/f droop control
传统下垂控制策略能够有效解决微网中因线路阻抗不同而引起的功率分配不均问题,将其应用于虚拟同步发电机控制时,虽然无法提供转动惯量和阻尼,但是可以有效控制系统的电压和频率稳定[20]。采用P/f下垂控制对电网频率稳定性进行优化,可提升VSG面对扰动的抵抗能力。
2 VSG小信号模型
VSG的等效电路[21]如图4所示。图4中,E为VSG基波电压相量,U为VSG并网处电压相量,Z为VSG输出阻抗。
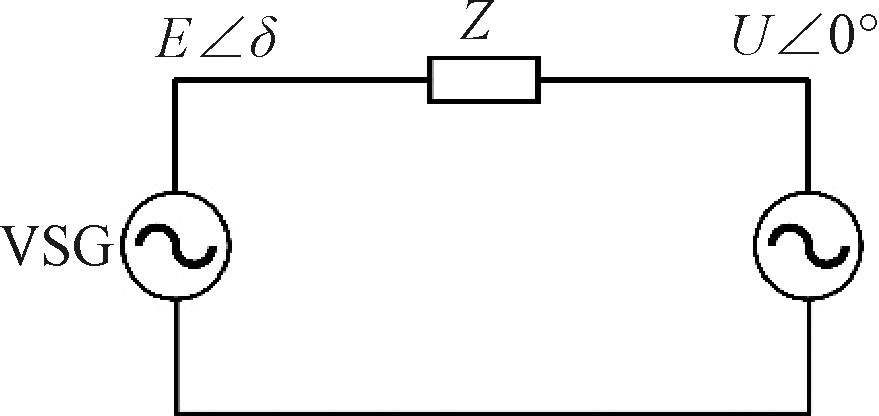
图4 VSG并网等效电路
Figure 4 VSG equivalent grid-connected circuit
Z=Ri+jωLi≈jωLi=jX。
(6)
功角δ为两个电压相量之间的相位差:
(7)
式中:ωg为电网额定角频率。
由此得到VSG的输出视在功率为
(8)
由式(8)可得
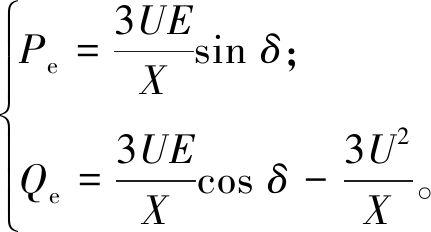
(9)
电网未发生扰动时,VSG输出电压和频率均为额定值。此时VSG功率稳定运行点为(Pe0,Qe0),结合式(9)可得VSG内电势稳定运行点:
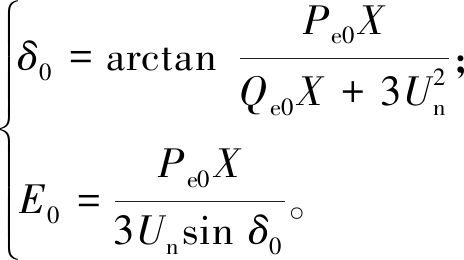
(10)
由式(1)~(3)、(5)、(9),将VSG虚拟内电势稳定运行点代入并进行拉普拉斯变换,可得VSG的小信号分析模型:
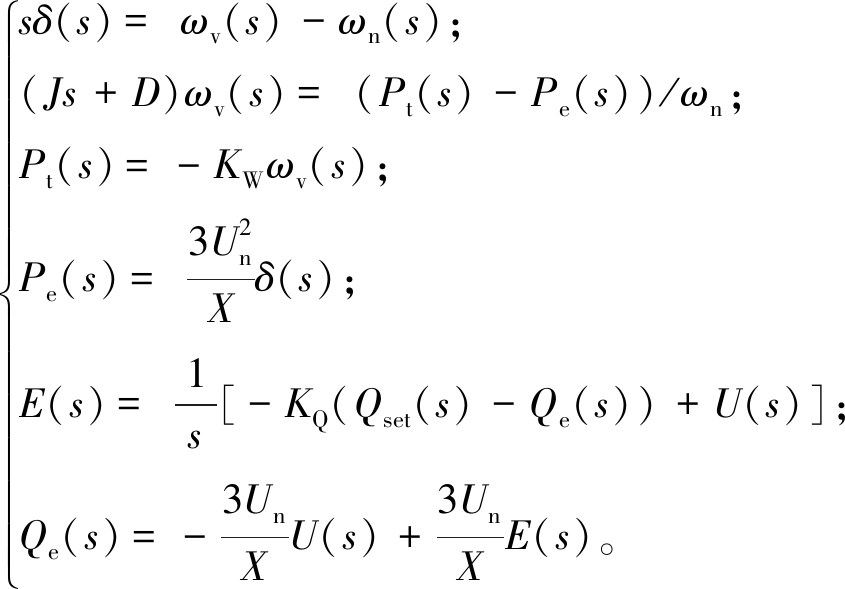
(11)
式(11)对应的模型结构图如图5所示。由图5可知,VSG动态小信号分析模型实现了频率/有功环和电压/无功环的解耦控制。
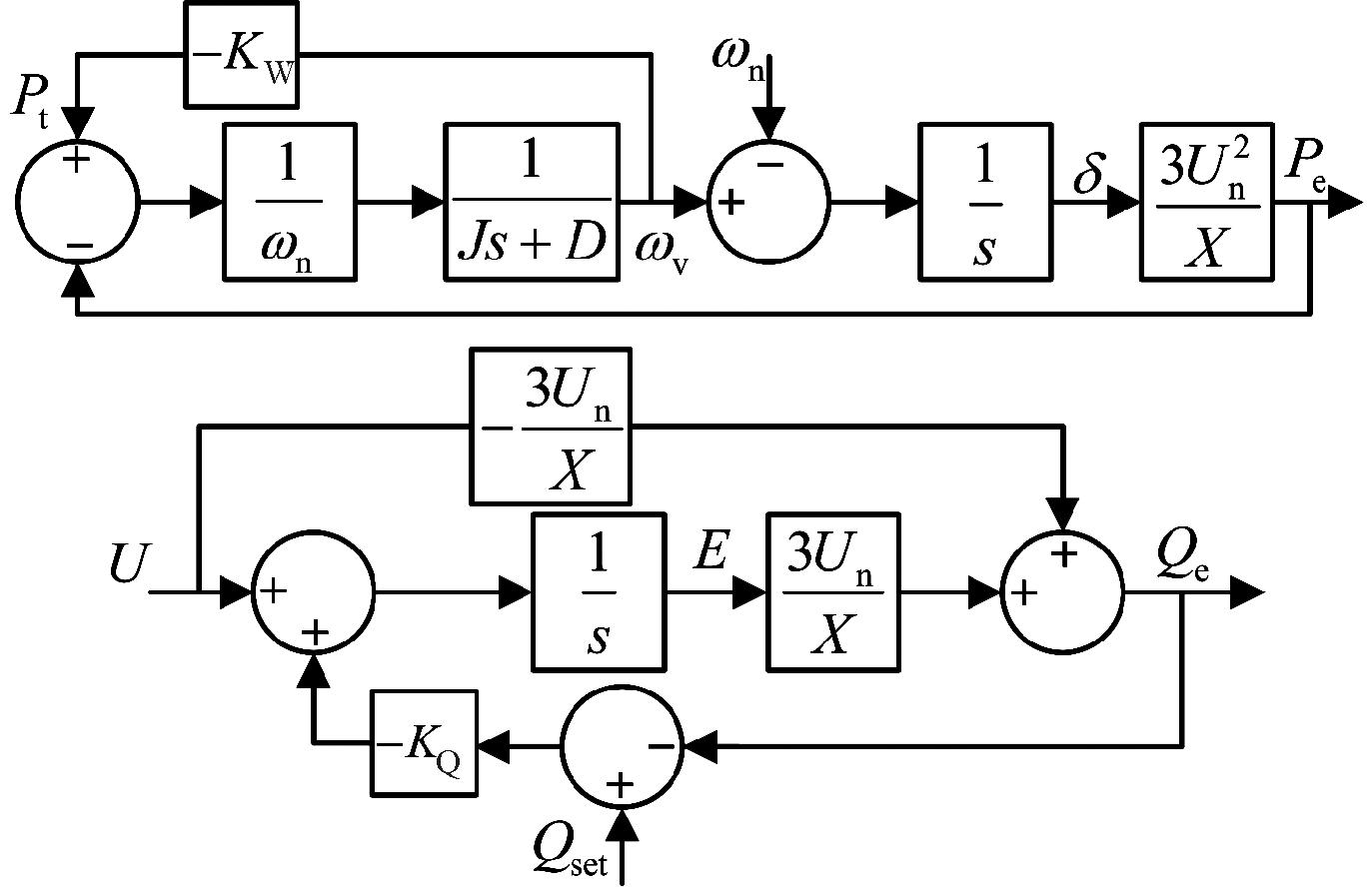
图5 VSG小信号分析模型
Figure 5 VSG small signal analysis model
3 转动惯量J和阻尼系数D的整定及优化
3.1 J和D的参数整定
根据图5,结合电力系统小信号分析方法,可得到VSG的输入输出传递函数:
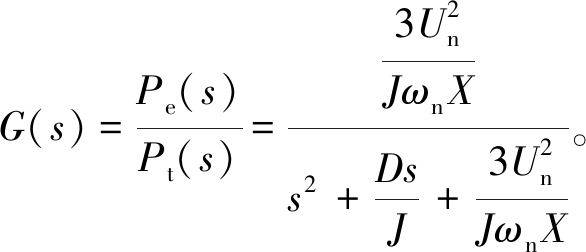
(12)
在已知阻抗X和电网电压Un的情况下,由式(12)可得到该二阶模型的自然震荡角频率和阻尼系数:
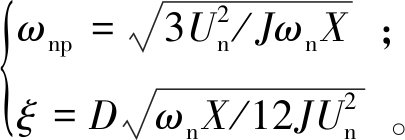
(13)
VSG的阻尼可以通过整定阻尼系数D实现,虚拟阻尼不足时,可以增大D。为了保证VSG响应电网频率变化时有较快的速度,并为了保障稳定性,取有功环为欠阻尼环节,即0.707<ζ<1,此时该二阶系统的超调量和调节时间分别为

(14)
从式(14)可以看出,该二阶系统的超调量和调节时间由虚拟转动惯量J和虚拟阻尼D决定。当J不变时,D越大,超调量越小;当D不变时,J越小,超调量越小。J越大,D越小,则调节时间越大,将延缓电力系统的稳定恢复时间。
根据式(1)可得
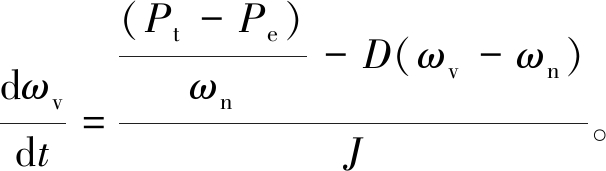
(15)
由式(15)看出,J和频率变化率成反比关系,J越大,dωv/dt越小,在电网扰动初期,J的增加可以有效抑制频率的迅速变化。
为了使VSG的频率响应与机组一次调频过程配合,调节时间应满足ts<<3 s。令ts<0.2 s,由式(14)可得ωnp>24.8 rad/s,取ωnp=24.8 rad/s。由式(13)及0.707<ζ<1可得J=0.85,D的取值为
(16)
计算得18.9< D <27.2。
3.2 J和D的神经网络优化
当电力系统处于稳定运行状态时,VSG的J和D参数可按上述方法整定为恒定值。但在实际运行中,当电网的频率和电压发生变化时,恒定的J和D并不能很好地响应电力系统的变化。针对此情况,本文根据电网频率变化率和最大偏移量,构建神经网络算法预测J和D的变化量,即对J和D进行优化。
选取一个经典的频率振荡衰减过程进行分析。如图6所示,将该振荡过程分为4个阶段。在阶段Ⅰ(t1~t2),角速度迅速增大,角速度变化率dω/dt从0迅速增加再缓慢减小。此时应增大J和D,以抑制角速度的超调量和变化率;在阶段Ⅱ(t2~t3)内,VSG角速度减小,变化率从0迅速减小再缓慢增大,此阶段应使用较小的转动惯量J,加快频率恢复速度。阶段Ⅲ(t3~t4)、阶段Ⅳ(t4~t5)类似。
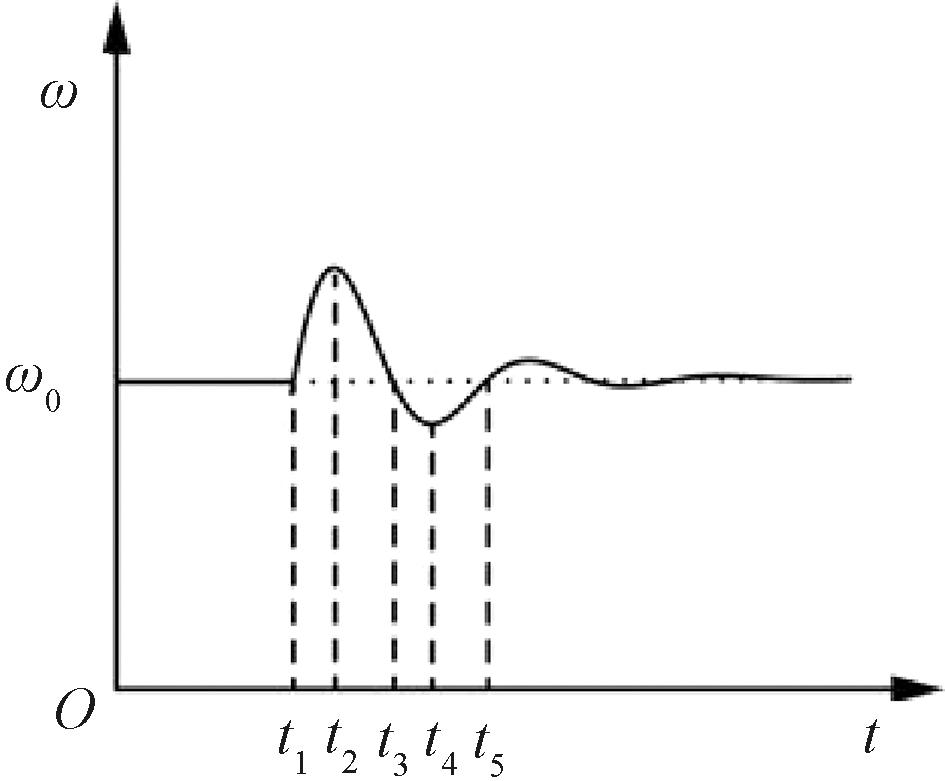
图6 电网的频率振荡
Figure 6 Frequency oscillation of the power grid
分析可知,J与频率变化率的大小和频率变化量有关,而D仅与频率变化量有关。根据上述选取原则以及J和D与频率变化率和变化量之间的关系,提出如下自适应控制策略:
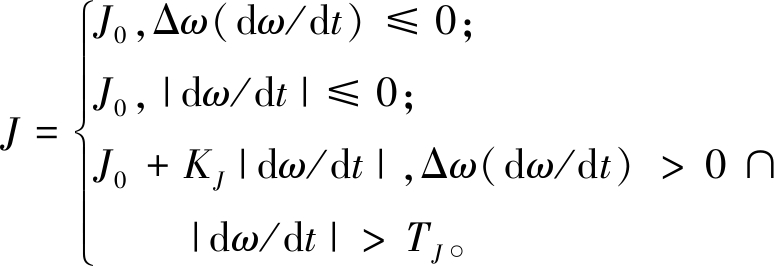
(17)
(18)
式中:J0和D0分别为VSG正常运行时的虚拟转动惯量和虚拟阻尼;KJ和KD分别为虚拟转动惯量和虚拟阻尼的调节系数;TJ和TD分别为虚拟转动惯量和虚拟阻尼的调节阈值。
本文通过建立人工神经网络实现J和D的自适应调节[22]。构造简单神经元网络模型如图7所示。图7中,x1、x2为神经元的输入信号,w1、w2表示输入信号的权重值,通过训练算法实时改变权重值,使得该神经网络的预测效果达到最佳。该神经元的输出z=g(x1,x2),其中z为一个关于x1、x2的非线性函数。定义以下神经网络参数:输入向量x=(x1,x2);输出层输出向量yo=(y1,y2);期望输出向量do=(d1,d2);误差函数![]()
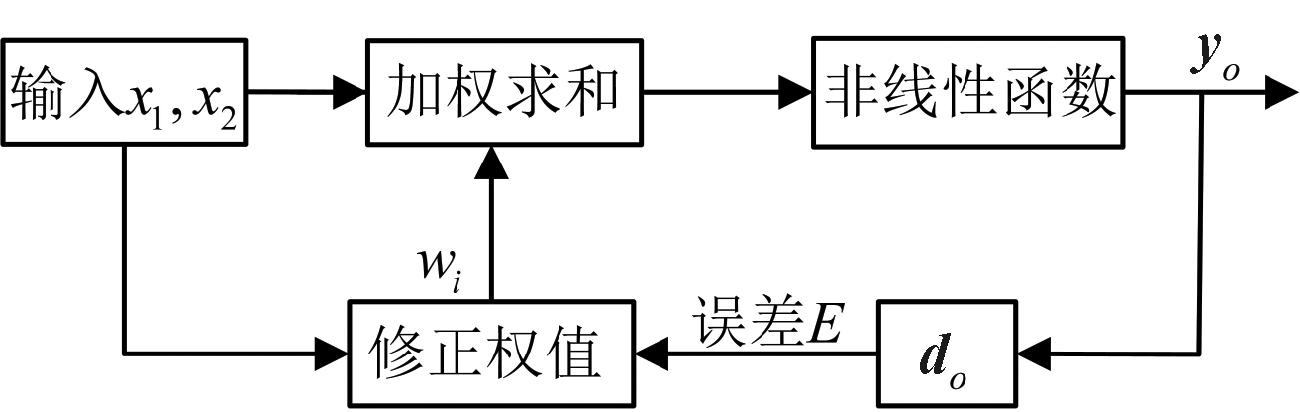
图7 单个神经元网络
Figure 7 Individual neuron network
由此可以获得权值的改变量Δwi(k):
(19)
其中μ为学习率。最后得到的权值为
wiN+1=wiN+μδo(k)·xi(k),i=1,2。
(20)
计算全局误差:
(21)
对于VSG系统,选取|Δω|和dω/dt作为神经网络的输入,KJ和KD为权重,期望输出向量的值为d1=ω=314 rad/s、d2=P=Pset。将输入x1、x2代入式(19),计算得出权值的修正量,进而得到最新的权值KJ和KD。使用该权值代入式(17)、(18)计算得出新的J和D,此时的VSG频率和电压为神经网络输出。将ω=314 rad/s、P=Pset代入期望输出向量,代入式(21)与输出进行误差计算,当误差满足可接受的条件时,结束算法,接受最新的权重w1、w2,即KJ和KD。本文选取当误差函数满足E≤0.1时,停止训练,否则选取下一组样本进行学习。神经网络优化参数流程图如图8所示。
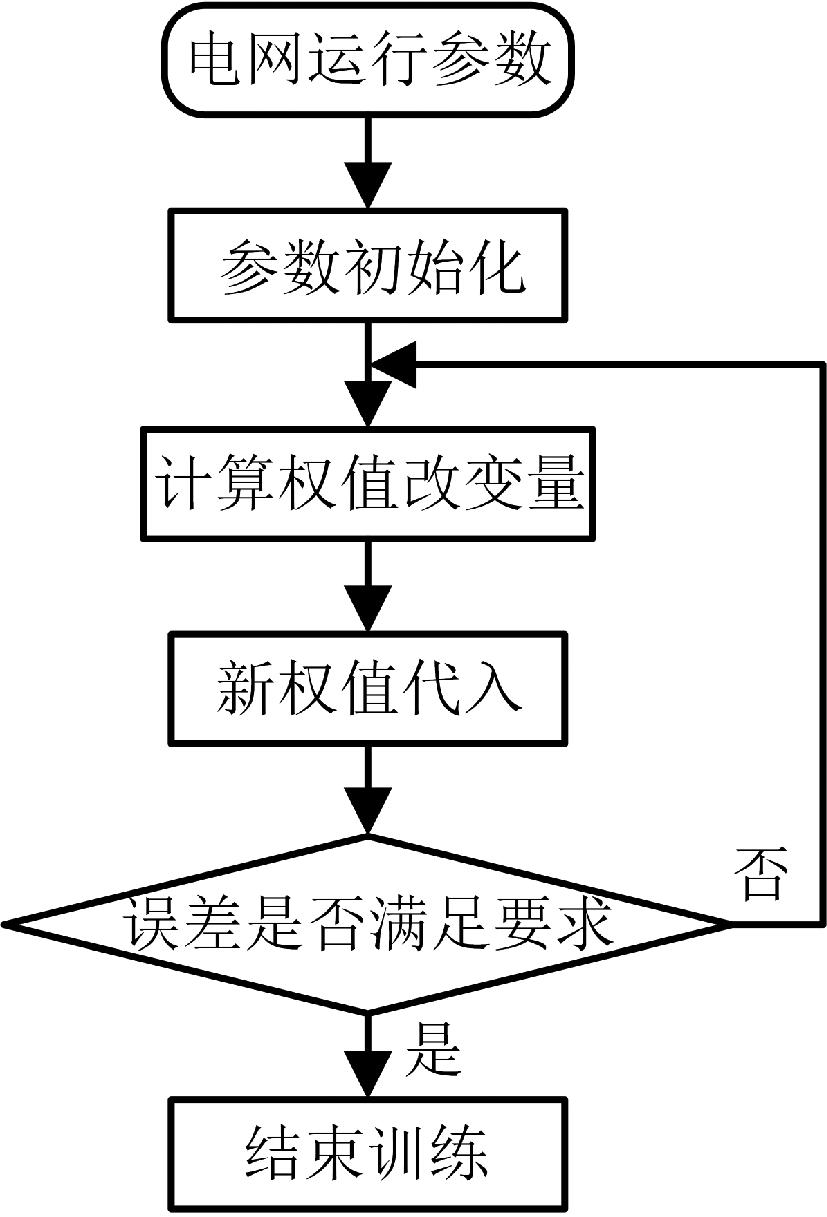
图8 神经网络控制流程图
Figure 8 Neural network control flow chart
4 算例仿真
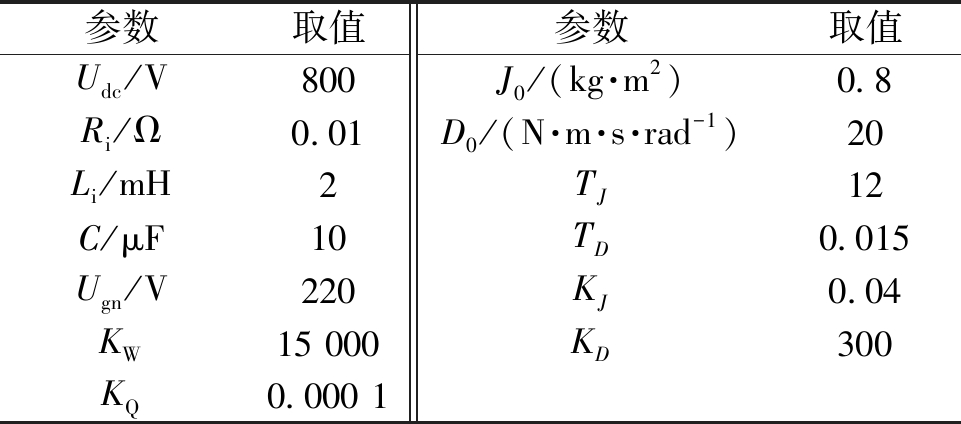
对单VSG并入无穷大电网情况进行仿真,系统参数如表1所示。
表1 仿真系统参数设置
Table 1 Simulation parameter setting
参数取值参数取值Udc/V800J0/(kg·m2)0.8Ri/Ω0.01D0/(N·m·s·rad-1)20Li/mH2TJ12C/μF10TD0.015Ugn/V220KJ0.04KW15 000KD300KQ0.000 1
仿真时长设置为2 s,无功功率参考值为2 000 Var,负荷有功功率额定值为12 kW。0 s时VSG有功功率参考值为12 kW,0.4 s突变,参考值变为15 kW,在1.1 s时有功功率第2次发生变化,降为10 kW。有功功率变化参考值如图9所示。
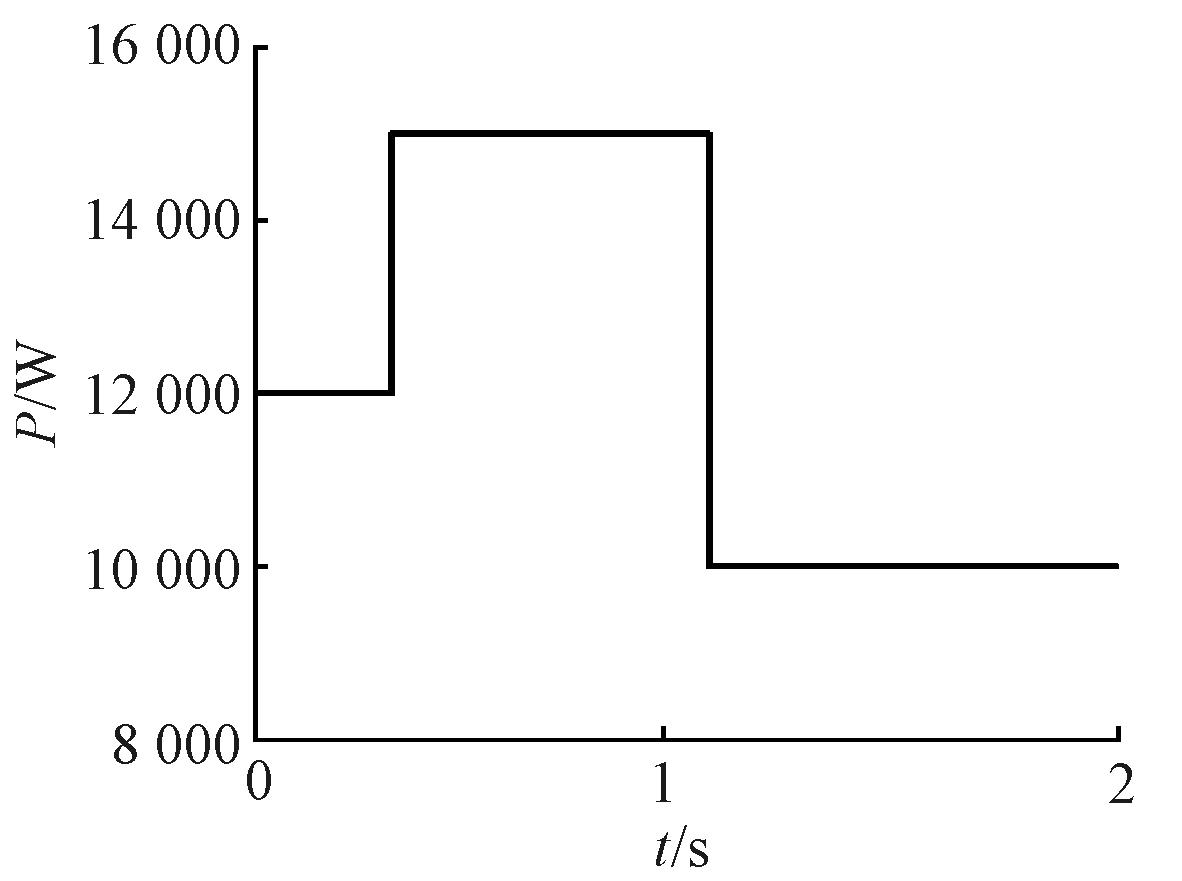
图9 有功功率参考值变化
Figure 9 Active power reference value variation
建立神经网络模型,对VSG虚拟惯量和虚拟阻尼进行预测的结果如图10所示。
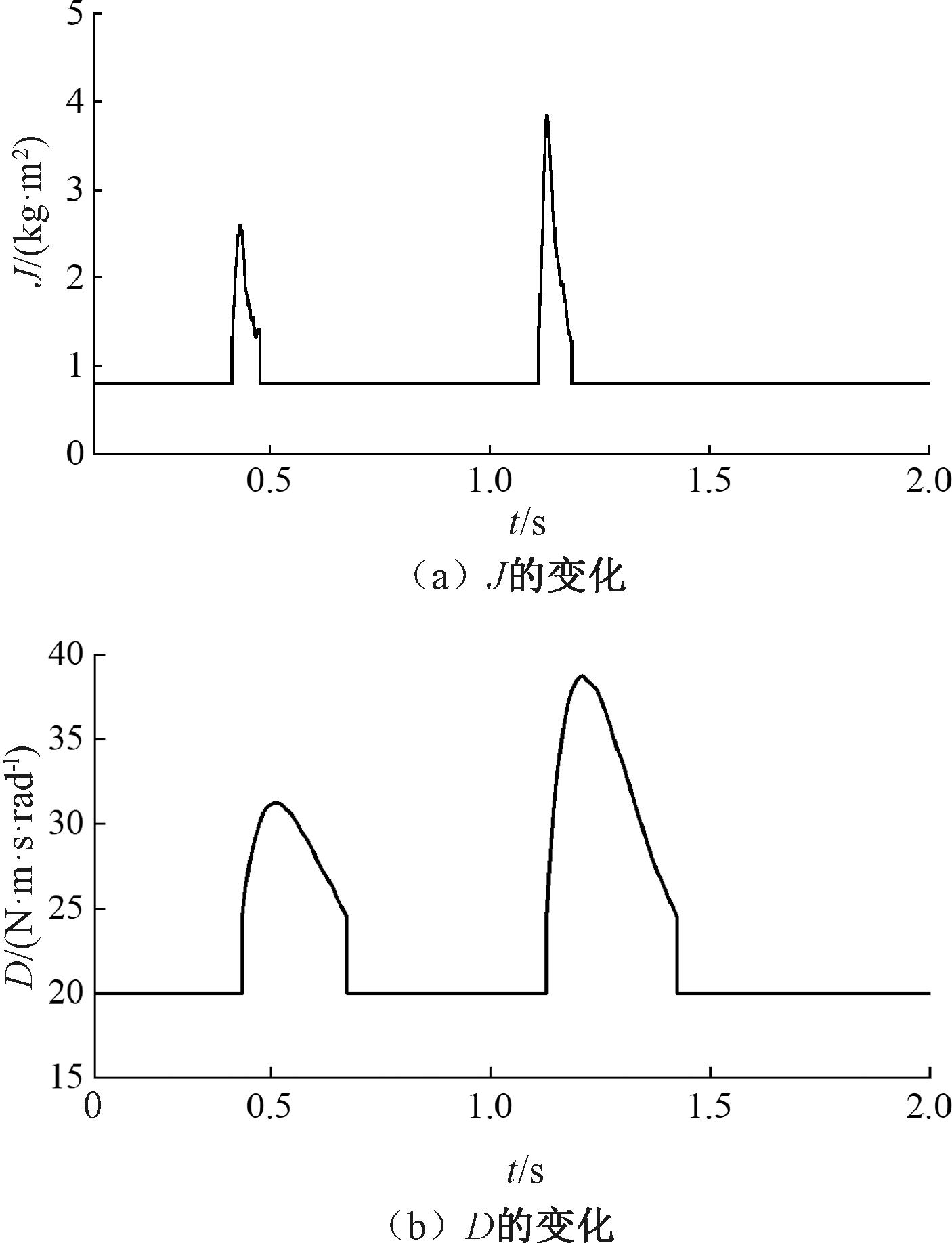
图10 VSG虚拟惯量J和虚拟阻尼D
Figure 10 VSG virtual inertia J and virtual damping D
由图10可知,基于神经网络模型预测,可以在频率发生大的扰动时对KJ和KD进行调整,通过自适应算法改变J和D的数值,以达到实时响应频率变化的目的。
图11为VSG在有功功率参考值突然变化时,分别采用传统VSG控制、恒定参数下垂控制和基于神经网络优化的自适应参数下垂控制的频率变化曲线。可以看到,传统VSG控制策略在响应系统的频率变化时较不稳定,在有功功率参考值突然增大时,系统频率增大;在3种控制方式下,频率分别在0.53、0.51、0.49 s达到最高点,频率最高点分别为50.045、50.037、50.033 Hz,并分别在1.1、1.08、0.95 s恢复到正常水平。这表明基于神经网络优化的自适应参数下垂控制策略能够很好地抑制频率的大幅度摆动,在频率超调量过大时,神经网络根据变化量对参数KJ和KD进行预测,迅速提升J和D,降低频率变化速度和频率超调量。在频率恢复过程中,为加快调节速度,根据上述分析,优化KD参数,减小虚拟惯量,以在频率偏移较大时迅速将频率稳定到正常水平。
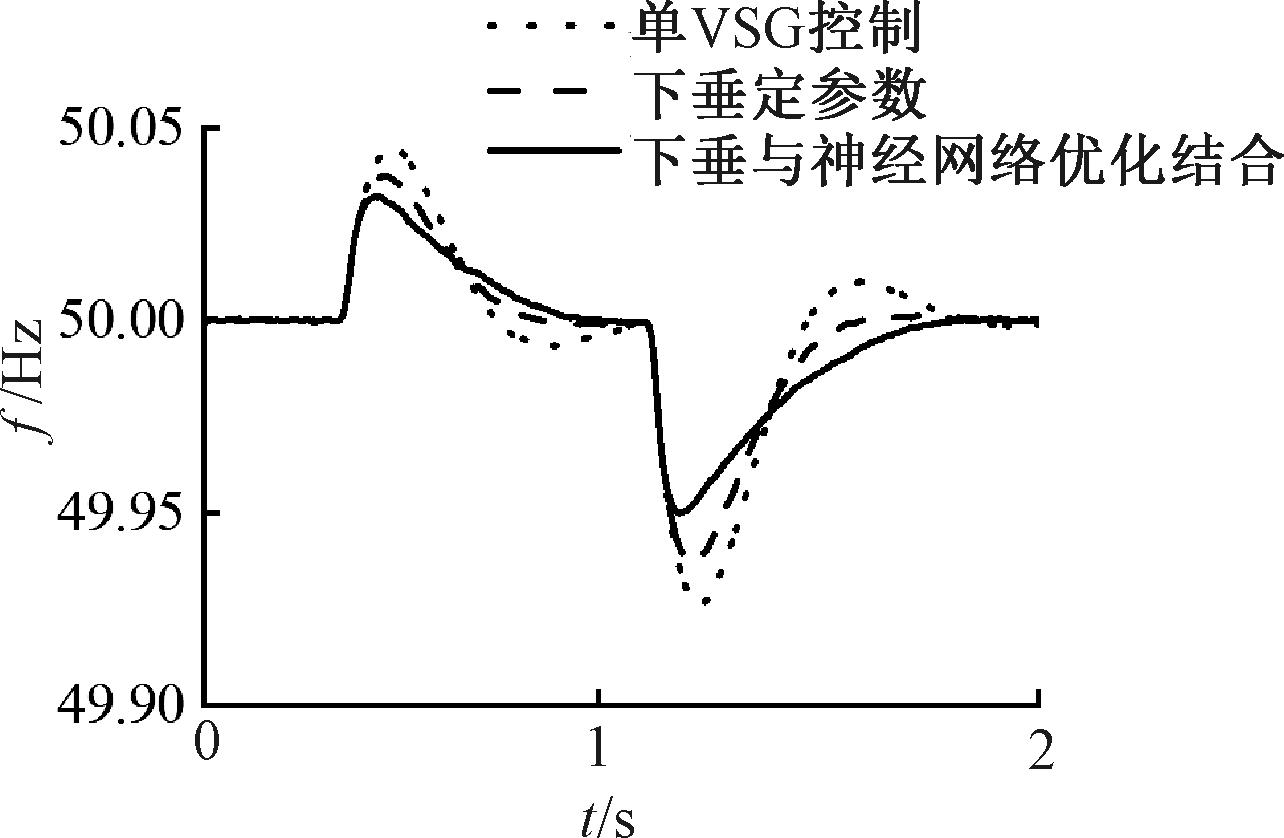
图11 VSG并网输出频率变化
Figure 11 VSG grid-connected output frequency variation
图12为不同控制策略下的系统有功功率响应曲线,3种控制方法的调节时间分别为0.7、0.7、0.45 s。可以看出,当给定参考功率增大时,传统VSG控制对于超调量的抑制不够明显;恒定参数下垂控制对于有功的超调量有所抑制,但调节时间较长;采用自适应参数下垂控制策略时,有功的超调量和调节时间都显著降低。
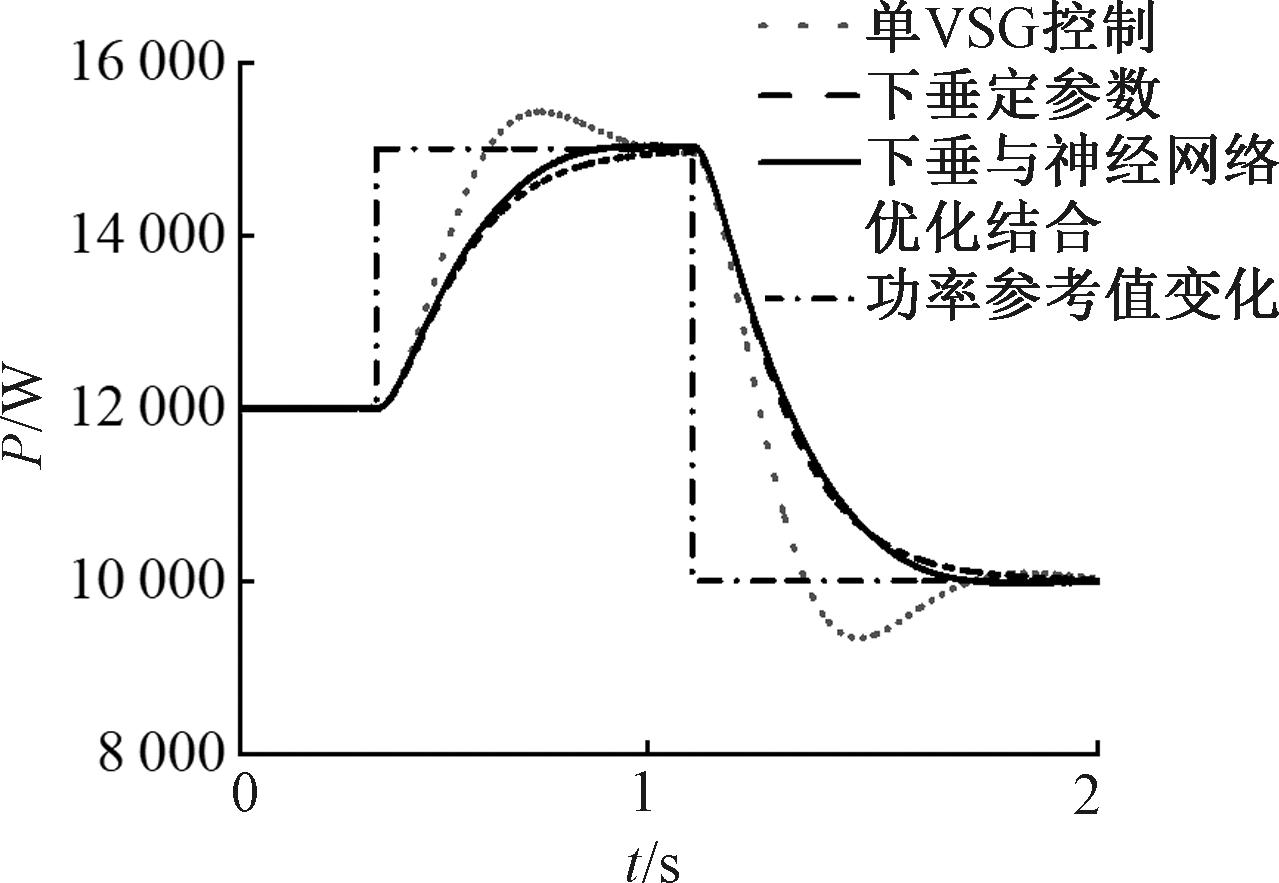
图12 VSG并网输出功率变化
Figure 12 VSG grid-connected output power variation
5 结论
本文研究VSG的下垂控制,以提升逆变器面对扰动的抵抗能力,加速频率和功率的恢复,得到以下结论。
(1)建立了VSG的控制模型。模型包括转子运动方程、P/f下垂控制模型与无功电压特性方程,可实现对电网频率的稳定控制。
(2)建立了VSG的小信号分析模型,实现了频率/有功环和电压/无功环的解耦。
(3)为适应系统的时变工况,对VSG的关键参数虚拟惯量J和虚拟阻尼D进行整定。设计了人工神经元网络,分析电网运行状态,对电网的频率、电压变化进行分析预测,对预测值进行分析以后调整权重值,得出J和D的变化量ΔJ和ΔD。
(4)将神经网络优化算法与下垂控制策略结合,对VSG控制策略进行优化。分别采用传统VSG控制、恒定参数下垂控制和基于神经网络优化的自适应参数下垂控制对算例进行仿真,结果表明,所提的优化控制策略可以达到提升新能源电力系统惯性的目的。
[1] 鲁宗相, 汤海雁, 乔颖,等. 电力电子接口对电力系统频率控制的影响综述[J]. 中国电力, 2018, 51(1): 51-58.
LU Z X, TANG H Y, QIAO Y, et al. The impact of power electronics interfaces on power system frequency control: a review[J]. Electric Power, 2018, 51(1): 51-58.
[2] 李雪, 宋彦龙. 蓄电池储能运行控制对有源配电网影响研究[J]. 郑州大学学报(工学版), 2019, 40(5): 32-38, 51.
LI X, SONG Y L. Study on the influence of battery energy storage operation control on active distribution network[J]. Journal of Zhengzhou University (Engineering Science), 2019, 40(5): 32-38, 51.
[3] SONI N, DOOLLA S, CHANDORKAR M C. Improvement of transient response in microgrids using virtual inertia[J]. IEEE Transactions on Power Delivery, 2013, 28(3): 1830-1838.
[4] ATTYAABT, HARTKOPF T. Control and quantification of kinetic energy released by wind farms during power system frequency drops[J]. IET Renewable Power Generation, 2013, 7(3): 210-224.
[5] 李少林, 秦世耀, 王瑞明,等. 大容量双馈风电机组虚拟惯量调频技术[J]. 电力自动化设备, 2018, 38(4): 145-150, 156.
LI S L, QIN S Y, WANG R M, et al. Control strategy of virtual inertia frequency regulation for large capacity DFIG-based wind turbine[J]. Electric Power Automation Equipment, 2018, 38(4): 145-150, 156.
[6] 曾正, 赵荣祥, 汤胜清,等. 可再生能源分散接入用先进并网逆变器研究综述[J]. 中国电机工程学报, 2013, 33(24): 1-12, 21.
ZENG Z, ZHAO R X, TANG S Q, et al. An overview on advanced grid-connected inverters used for decentralized renewable energy resources[J]. Proceedings of the CSEE, 2013, 33(24): 1-12, 21.
[7] KE Z P, DAI Y X, PENG Z S, et al. VSG control strategy incorporating voltage inertia and virtual impedance for microgrids[J]. Energies, 2020, 13(16): 4263.
[8] RASOOL A, YAN X W, RASOOL H, et al. VSG stability and coordination enhancement under emergency condition[J]. Electronics, 2018, 7(9): 202.
[9] HUL L, FU L. Primary frequency modulation of microgrid based on consistent droop control method[J]. Journal of Physics: Conference Series, 2022, 2387(1): 012017.
[10] 罗兰, 王渝红, 陈诗昱,等. 基于虚拟同步发电机控制策略的多端柔性直流系统自适应下垂控制[J]. 科学技术与工程, 2021, 21(17): 7116-7121.
LUO L, WANG Y H, CHEN S Y, et al. Adaptive droop control of multi-terminal direct current based on virtual synchronous generator control strategy[J]. Science Technology and Engineering, 2021, 21(17): 7116-7121.
[11] 孙孝峰, 王娟, 田艳军,等. 基于自调节下垂系数的DG逆变器控制[J]. 中国电机工程学报, 2013, 33(36): 71-78, 11.
SUN X F, WANG J, TIAN Y J, et al. Control of DG connected inverters based on self-adaptable adjustment of droop coefficient[J]. Proceedings of the CSEE, 2013, 33(36): 71-78, 11.
[12] TORRES M, LOPES L A C. Virtual synchronous generator control in autonomous wind-diesel power systems[C]∥2009 IEEE Electrical Power &Energy Conference (EPEC). Piscataway:IEEE, 2009: 1-6.
[13] KERDPHOL T, RAHMAN F S, WATANABE M, et al. Small-signal analysis of multiple virtual synchronous machines to enhance frequency stability of grid-connected high renewables[J]. IET Generation, Transmission &Distribution, 2021, 15(8): 1273-1289.
[14] CHENY, HESSE R, TURSCHNER D, et al. Improving the grid power quality using virtual synchronous machines[C]∥2011 International Conference on Power Engineering, Energy and Electrical Drives. Piscataway:IEEE, 2011: 1-6.
[15] ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[16] ALIPOOR J, MIURA Y, ISE T. Stability assessment and optimization methods for microgrid with multiple VSG units[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 1462-1471.
[17] 张亚楠, 朱淼, 张建文,等. 基于自适应调节的微源逆变器虚拟同步发电机控制策略[J]. 电源学报, 2016, 14(3): 11-19.
ZHANG Y N, ZHU M, ZHANG J W, et al. Control strategy of virtual synchronous generator based on adaptive adjusting for distributed inverters[J]. Journal of Power Supply, 2016, 14(3): 11-19.
[18] MOLINA-GARC A A, BOUFFARD F, KIRSCHEND S. Decentralized demand-side contribution to primary frequency control[J]. IEEE Transactions on Power Systems, 2011, 26(1): 411-419.
A A, BOUFFARD F, KIRSCHEND S. Decentralized demand-side contribution to primary frequency control[J]. IEEE Transactions on Power Systems, 2011, 26(1): 411-419.
[19] 李俊, 任冲, 樊国旗,等. 基于模糊控制的高占比风电系统自适应虚拟惯量及调频参数补偿策略研究[J]. 电力电容器与无功补偿, 2021, 42(4): 55-61.
LI J, REN C, FAN G Q, et al. Study on adaptive virtual inertia and frequency modulation parameter compensation strategy of high proportion wind power system based on fuzzy control[J]. Power Capacitor &Reactive Power Compensation, 2021, 42(4): 55-61.
[20] WANG W Y, JIANG L, CAO Y J, et al. A parameter alternating VSG controller of VSC-MTDC systems for low frequency oscillation damping[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4609-4621.
[21] 胡文强, 吴在军, 孙充勃, 等. 基于VSG的储能系统并网逆变器建模与参数整定方法[J]. 电力自动化设备, 2018, 38(8): 13-23.
HU W Q, WU Z J, SUN C B, et al. Modeling and parameter setting method for grid-connected inverter of energy storage system based on VSG[J]. Electric Power Automation Equipment, 2018, 38(8): 13-23.
[22] 丁小彬, 谢宇轩, 薛皓文,等. 基于神经网络算法的滚刀磨损量预测方法[J]. 郑州大学学报(工学版), 2023, 44(1): 83-88, 95.
DING X B, XIE Y X, XUE H W, et al. A method for disc cutter wear prediction based on neural network[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(1): 83-88, 95.