作为一种高效的能量传递方式,核态沸腾通过气液相变产生气泡而带走大量的潜热,因此具有传热温差小、换热系数高和热流密度大等特点,是解决电子元器件高热流密度散热[1]的有效方法。
为了进一步强化沸腾换热,一些学者采用通过改变表面润湿性来加快气泡脱离频率,或加工表面微结构以提高气泡成核位点密度的方法,来进一步提高沸腾换热的热流密度和换热系数。郑晓欢等[2]通过制备亲水性表面进行了相关实验,结果表明,此受热面产生的气泡直径较小且气泡脱离频率较快,亲水表面的最大换热系数约为光滑表面的1.7倍。曹海亮等[3]基于倒梯形微槽道结构进行可视化的池沸腾实验,结果表明,倒梯形槽道结构有助于气泡成核和液体的回流补充,使其在过热度很低的情况下也能发生沸腾,沸腾换热得到了进一步强化。Mukherjee等 [4]研究了池沸腾过程中多个气泡的聚并融合过程,给出了受热面上气泡的生长、合并和脱离的可视化结果,发现气泡合并后脱离频率加快,从而强化了沸腾换热。Huang等[5]通过格子玻尔兹曼方法(lattice Boltzmann method, LBM)详细研究了不同间距的正方形、三角形锯齿、三角形凸起结构对沸腾换热特性和气泡动力学行为的影响,结果表明,微结构对气泡形核有着不同程度的促进作用,明显提高了换热壁面的沸腾换热性能。Yuan等[6]通过LBM分析了气泡成核距离对换热壁面沸腾性能的影响,发现存在最佳成核距离,使换热性能最大化。除了上述的表面改性技术和表面微结构[7]方法之外,在固体表面加热或其附近添加低导热材料板也被证明是强化壁面换热的有效方法[8-9]。Rahman等[10]将低热导率材料嵌入传热表面进行沸腾实验,结果表明气泡成核仅发生在高热导率表面区域,添加低热导率材料使传热速率扩大至6倍,且优化了受热面的气泡动力学,换热壁面的沸腾换热性能明显增强。孟璐璐等[11]将高、低热导率材料板进行平行、交错分布,考察了沸腾过程中材料的宽度和间隙尺寸对临界热流密度(critical heat flux density,CHF)的影响。结果表明,与均匀传热板相比,交错分布结构有利于受热面再润湿液体,从而显著提升CHF。Utaka等[12]在传热板内近表面处交替放置了两种不同热性能材料,考察了间隙尺寸和宽度对CHF的影响,结果表明,不均匀传热板壁面的沸腾换热性能明显高于均匀传热板。
通过以上分析可以发现,在固体加热器内嵌入不同热性能材料可以明显提升换热壁面的沸腾换热性能。但目前学者们针对不同热性能材料的研究都是采用实验方法进行研究的,很难观察到沸腾过程中的微观流动过程和温度场分布特征,导致沸腾换热机理也无法准确解释。为了从微观角度揭示添加低导热材料板的沸腾换热过程的强化机理,本文采用介观尺度的LBM,模拟了高、低导热材料板间隔分布的沸腾换热表面上气泡的动态行为,考察了低导热材料板的数量、间隙间距对沸腾换热性能和气泡动力学的影响,从微观角度揭示添加低导热材料板强化沸腾换热的机理。
1 数值模型
1.1 多相流格子Boltzmann模型
单组分多相格子Boltzmann模型的密度演化方程[13]表示为
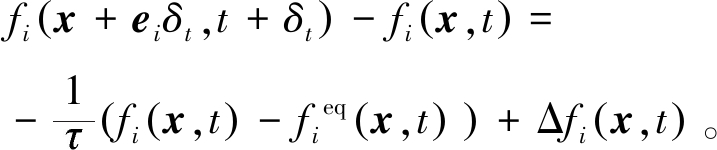
(1)
式中:fi(x,t)为密度分布函数,i和x分别表示密度分布函数中粒子的方向和位置;ei为沿着第i个方向的离散速度;Δfi(x,t)为引起分布函数变化的体积力项;
为弛豫时间;fieq(x,t)为相应的平衡态分布函数。
(2)
式中:wi为加权系数,在二维D2Q9模型中,当i=0时,wi=4/9,当i为[1,4]时,wi=1/9,当i为[5,8]时,wi =1/36;cs为晶格声速,
其中c=δx/δt为晶格速度,δx为晶格间距,δt为晶格时间步长,在本文中δx、δt取值均为1.0。本文采用Kupershtokh等[14]的作用力格式。
模型中总体积力F由式(3)表示:
F=Fint+Fg+Fw。
(3)
式中:Fint为导致相分离的粒子间相互作用力;Fg为重力;Fw为流体和固体之间的相互作用力。
(4)
Fg=(ρ(x)-ρave)g;
(5)
(6)
式中:w(|ei|2)为权系数,对于D2Q9模型可设置w(1)=1/3,w(2)=1/12;A为提高模型稳定性的加权参数;U(x+eiδt,t)为相邻粒子间的势函数;Ψ(x,t)为流体粒子的有效密度;ρave为计算域的平均密度;g为重力加速度;s(x)为壁面作用力函数,当晶格靠近固体时,s(x)=1,靠近流体时,s(x)=0。
粒子相互作用力中的势函数和有效密度[15]分别为
(7)
(8)
式中:c0取值为6.0。势函数和有效密度函数中的压力p均与非理想气体状态方程有关,本文采用的P-R状态方程,参数设置见文献[16]。
格子的密度和速度分别为
(9)
(10)
其中,u不是真实的流体速度,而真实的流体速度V为
(11)
1.2 能量方程
能量方程用温度分布函数来表示,其演化方程为
gi(x+eiδt,t+δt)-gi(x,δt)=
(12)
式中:gi(x,t)为时间t和位置x处粒子的温度分布函数;T为温度弛豫时间,以代替无量纲松弛时间来求解温度场。本文选择D2Q9方案来计算温度,gieq(x,t)为相应的平衡态分布函数。
(13)
为了更准确地进行固-液共轭传热模拟,温度弛豫时间采用修正的T[17],即
(14)
同时,液体和蒸汽界面处的流体性质[18](流体黏度或流体热扩散率)为
(15)
温度T为
(16)
此外,为了方便描述无量纲模型,引入了特征长度l0、特征速度u0和特征时间t0[19]。文中l.u.表示格子单位,若无特殊说明,本文无量纲模型中均为格子单位。
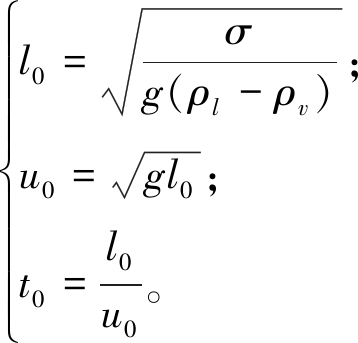
(17)
2 模型验证
在介绍本文所采用的数值模型后,对模型的稳定性和可靠性进行了Young-Laplace定律验证和气泡的生长和脱离的验证。
2.1 Young-Laplace定律验证
根据Young-Laplace定律可知,达到稳定状态后,气泡的内外压力差Δp与稳定后的气泡半径R成反比,与表面张力σ成正比[20],即
Δp=σ/R。
(18)
在不同温度下对不同半径的气泡压力场进行模拟,图1给出了在不同温度下气泡内外压力差Δp与半径倒数1/R之间的关系。
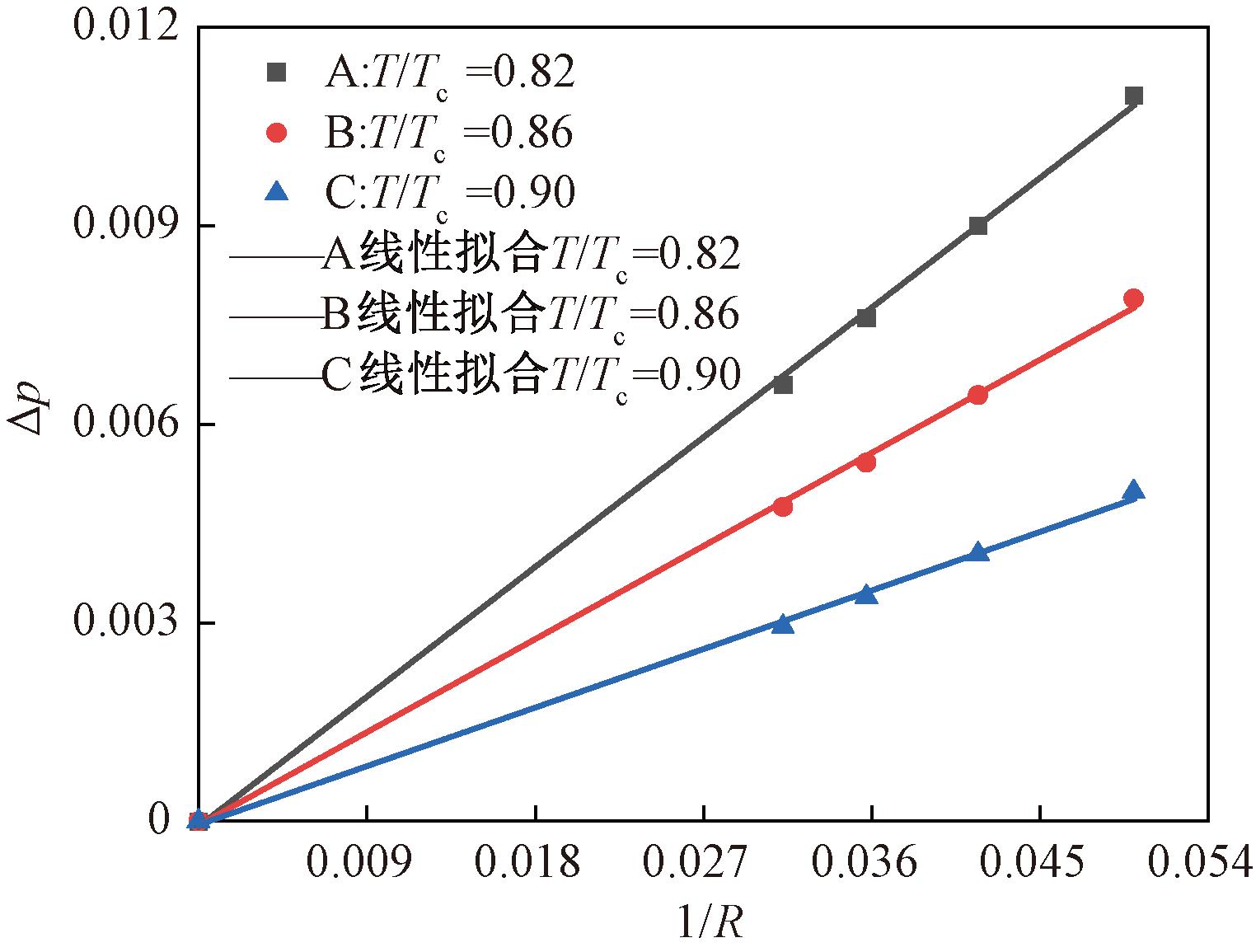
图1 气泡内外压差Δp和半径倒数1/R的拟合关系
Figure 1 Relation between pressure difference Δp inside and outside droplets and reciprocal radius 1/R
计算域采用100 l.u.×100 l.u.的网格,整个计算域初始化温度分别为0.82Tc、0.86Tc、0.90Tc,四侧边界均采用周期性边界条件。在初始时刻,半径为20、24、28、32 l.u.的气泡悬浮在计算域中心,在气泡表面张力的作用下,气泡最终会达到稳定状态。如图1所示,通过线性拟合可以看出模拟结果与Young-Laplace定律相吻合,证明本研究采用的模型具有较高的稳定性。
2.2 气泡生长和脱离的验证
为了验证气泡脱离行为的正确性和合理性,在模型验证的初始设置中,在下壁面中心区域设置4个格子的恒热流密度条件进行加热,其余区域的初始温度设置为0.90Tc,计算区域的左侧和右侧为周期性边界,上下边界为Zou-He边界。在模拟中通过改变重力加速度g的大小,获得了不同重力加速度条件下的气泡脱离直径,如图2所示。本文模拟出的气泡脱离直径D*与g-0.5成正比,与文献[21]中研究结果一致,这说明本研究模拟沸腾所采用的模型和程序可靠。
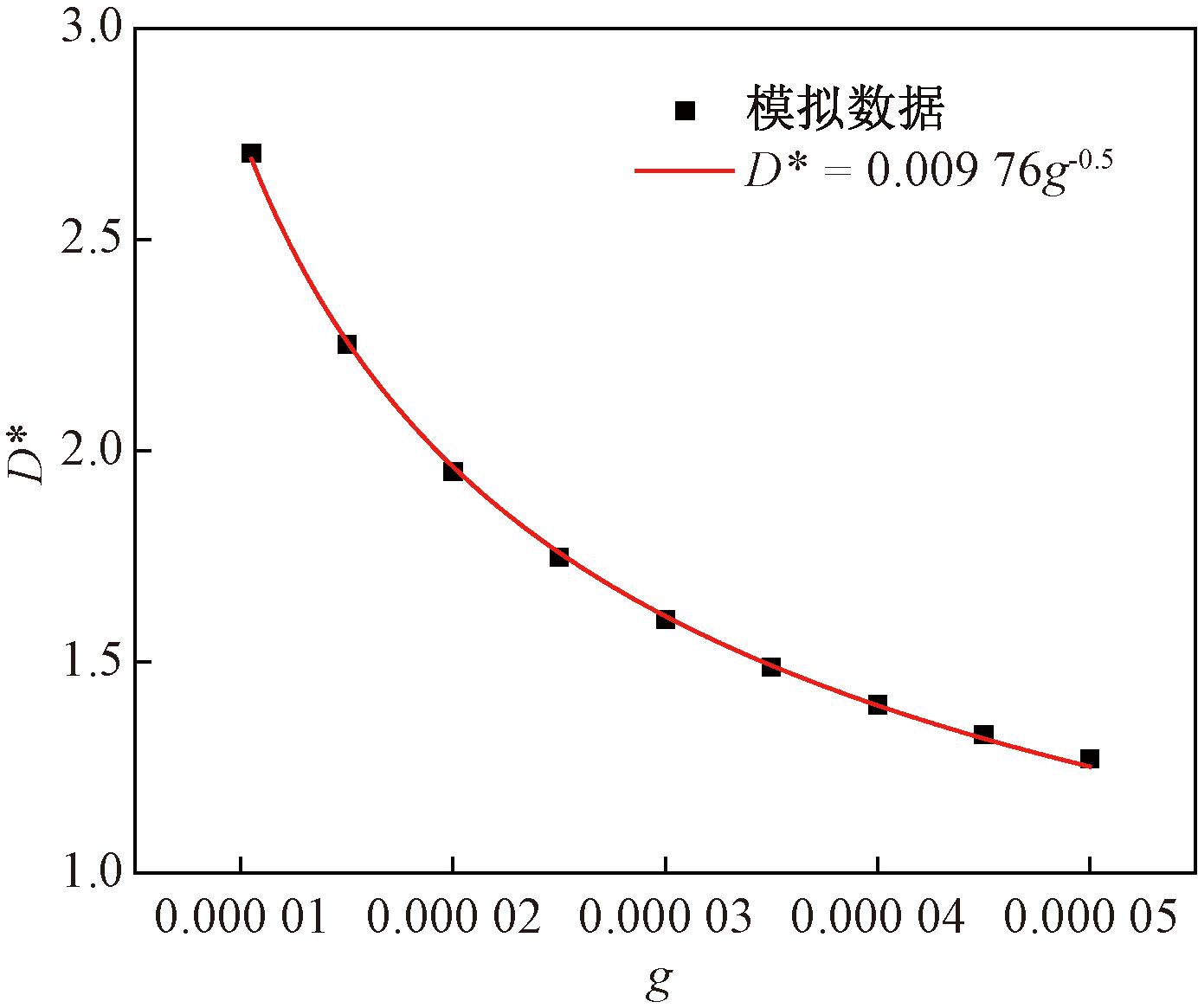
图2 重力对气泡离开直径的影响
Figure 2 The effect of gravity on bubble departure diameter
上述实验表明,本文采用的格子Boltzmann模型具有良好的稳定性和可靠性,能够很好地遵守Young-Laplace定律,能够准确描述核态沸腾过程中气泡的生长和脱离过程,因此可以采用此模型进行沸腾相关模拟。
3 计算域和参数设置
在验证了格子Boltzmann模型的稳定性和可靠性后,采用此沸腾模型对添加了多段低导热材料板的沸腾换热过程进行了数值模拟,考察了低导热材料板的数量、间隙间距的变化对沸腾过程和气泡动力学的影响,并结合气泡动态行为,通过对温度场和流场的分析从微观角度揭示了强化沸腾换热的机理。
添加多段低导热材料板的池沸腾的计算域结构如图3所示,沸腾矩形腔总体尺寸为8.06l0×10.07l0,矩形腔的底部是固体加热器,为分析低导热材料板对沸腾换热的影响,固体区域不宜设置太厚,此处厚度H=0.484l0,在靠近固体上壁面距离c=0.081l0处分别嵌入了三段、四段低导热材料板,分别形成了2个和3个间隙,间隙长度为L2,低导热材料板的厚度δ=0.162l0,低导热材料板间隙之间的间距长度为L1,两边的低导热材料板长度为L3。本文采用液态工质水,计算域顶部充满蒸汽,液相区域内充满液体,整个计算域温度设置为0.90Tc,Tc为饱和温度,可通过P-R状态方程计算得到。在模拟过程中,为了防止出现膜态沸腾,确保热量及时被气泡从受热面带走,将受热面设置成亲水性光滑表面,不考虑受热面表面特性对沸腾的影响。顶部设置为压力出口边界[22],左右两侧设置为周期性边界,底部设为恒定热流密度加热。
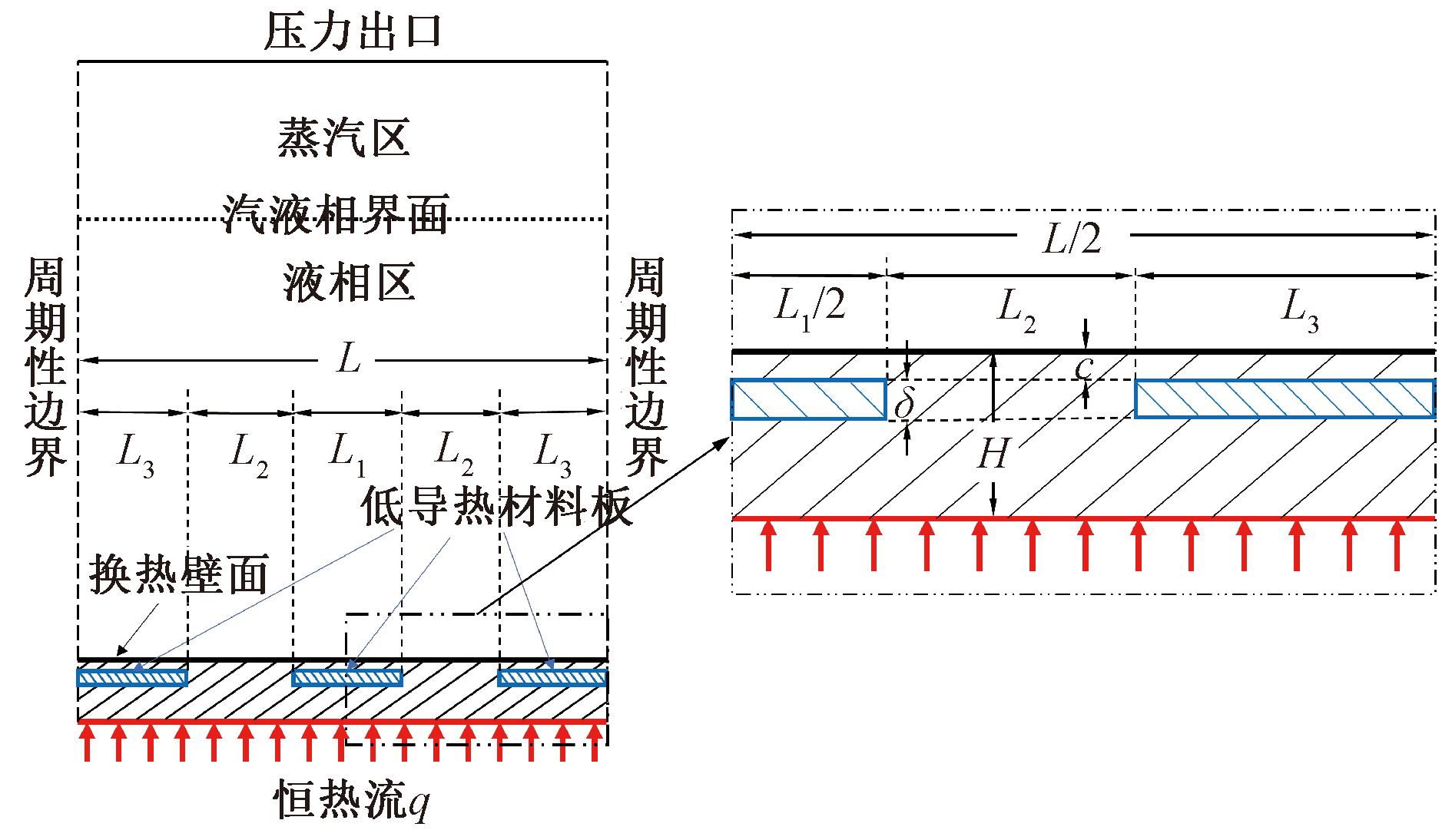
图3 计算域示意图
Figure 3 Schematic diagram of computing domain
固体加热器的结构参数H=0.484l0、c=0.081l0、δ=0.162l0、L2=0.403l0。为分析多段低导热材料板对气泡动力学的影响,本文对间隙间距L1进行了设置,L1=0.403l0、0.806l0、1.209l0、1.612l0、2.015l0、2.418l0、2.821l0、3.224l0、3.627l0。
在研究中首先保证间隙L2大小相等,对于添加三段低导热材料板的池沸腾结构,经数值模拟发现,由于两边周期性边界的存在,当间隙间距长度L1=4.030l0时,气泡的成核、生长以及脱离过程会与L1=3.224l0时的情况一样,唯一不同的是气泡的成核位置,因此不考虑间隙间距L1>4.030l0时的工况。同理,添加四段低导热材料板时,也进行相应的处理。本文中使用的数据都是在沸腾状态达到稳定后得到的。
4 结果与讨论
4.1 低导热材料板的气泡动力学行为分析
图4为不同间距的2个间隙低导热材料板的亲水表面的气泡生长和脱离过程。在较小间距L1=0.806l0时,亲水表面上生成的2个气泡核在较小状态时直接接触合并。相比L1=1.209l0、1.612l0时,气泡膨胀后,顶部(编号b4、c4)会率先融合,随后合并成一个大气泡。当间隙间距L1增大至2.015l0时,气泡脱离前不发生合并过程,气泡脱离后在上升过程中轨迹发生弯曲并出现合并(编号d2)。随着间隙间距的进一步增大,间隙处成核位点之间的距离变得更大,气泡生长变得相互独立但气泡还会受到彼此的吸引作用。
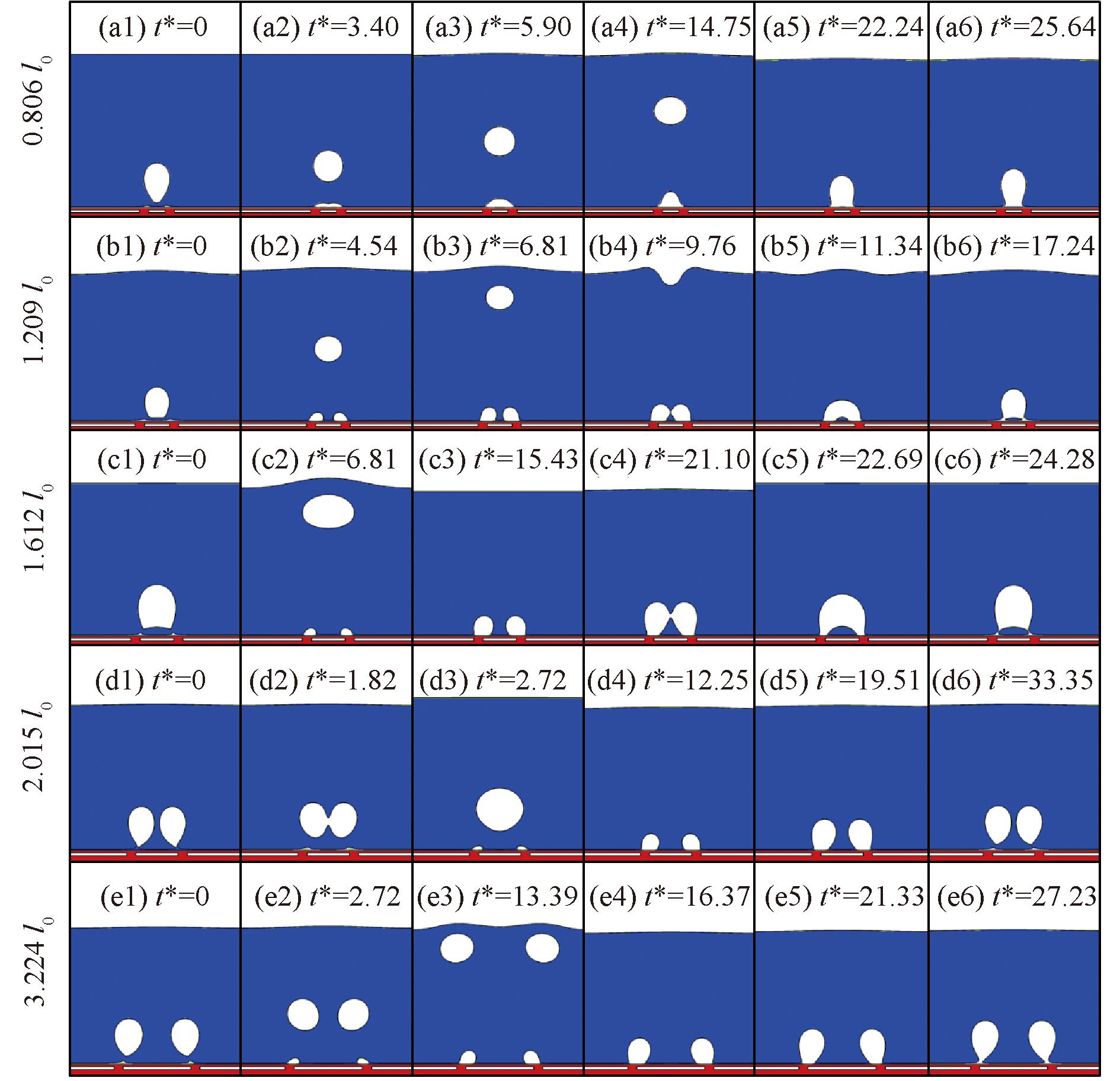
图4 不同间距的2个间隙上的气泡脱离行为
Figure 4 Bubble detachment behavior on two gaps with different spacings
图5展示了不同间距的3个间隙低导热材料板的亲水表面的气泡成核、生长和脱离过程。与2个间隙时的过程类似,气泡在生长过程中合并,在图5中,编号c4的气泡融合形成液桥,此时液桥下方存在较大的液相区域。随着间隙间距进一步增大,如编号d1～d6所示,中间间隙的气泡率先脱离,左右两侧气泡向中间倾斜迁移,在编号d2～d4的时间段内,可以明显地观察到两侧气泡不断逼近中间气泡,但不发生合并过程,在这个时间段内,两侧气泡的倾斜抑制了中间气泡的膨胀,随后两侧气泡脱离上升。
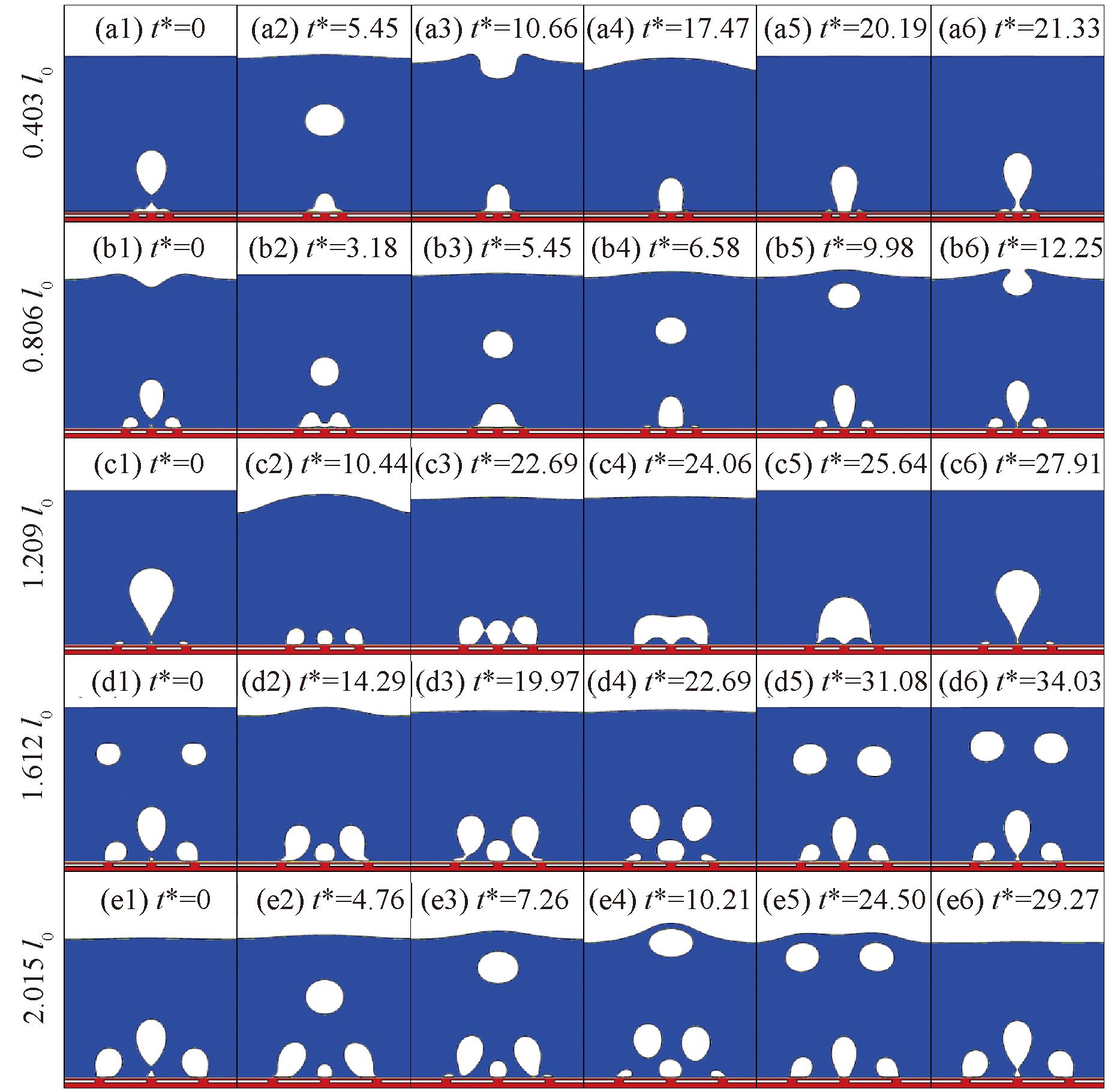
图5 不同间距的3个间隙上的气泡脱离行为
Figure 5 Bubble detachment behavior on three gaps with different spacings
从编号e1～e6中可以观察到与编号d1～d6相似的气泡脱离过程,中间气泡会率先脱离,随后带动左右两侧气泡倾斜脱离。中间气泡和左右两侧气泡在脱离后都留下气泡核,参与下一个沸腾循环。与文献[23]不相同的是,随着间隙间距的增大,3个间隙受热面上都有气泡的生长,这主要是因为设置底部加热时,间隙都处在底部加热器的中间而非边缘位置,因此温度梯度变化很快。由于低导热材料板的存在,低导热材料板上方的受热面不会生成气泡,气泡只会在间隙处生长,另外由于受热面的气泡动力学影响,导致不同间隙处生长的气泡的大小和形状不同。
对于2个间隙和3个间隙的强化沸腾换热研究,因为存在气泡合并、迁移等不规律行为,气泡脱离频率难以测量,另外计算域底部为恒热流密度加热,因此本文比较了3种工况下在单位时间内气泡带走的无量纲换热量
(本文所计算的换热量为气泡的潜热×单位时间内脱离气泡的总面积)和最初成核时间t*,如图6所示。可以看出,在本文所研究参数范围内,添加低导热材料板能使气泡更早成核(t*=8.39、8.28小于没有添加低导热材料板时的t*=10.21),另外单位时间内2个间隙时的气泡脱离频率和生成的气泡数量都要高于3个间隙,因此单位时间内2个间隙的换热量要比3个间隙时的大,且不同间隙时单位时间内的换热量都要高于没有添加低导热材料板时的换热量,这充分证明了添加适当长度和数量的低导热材料板能够强化沸腾换热。
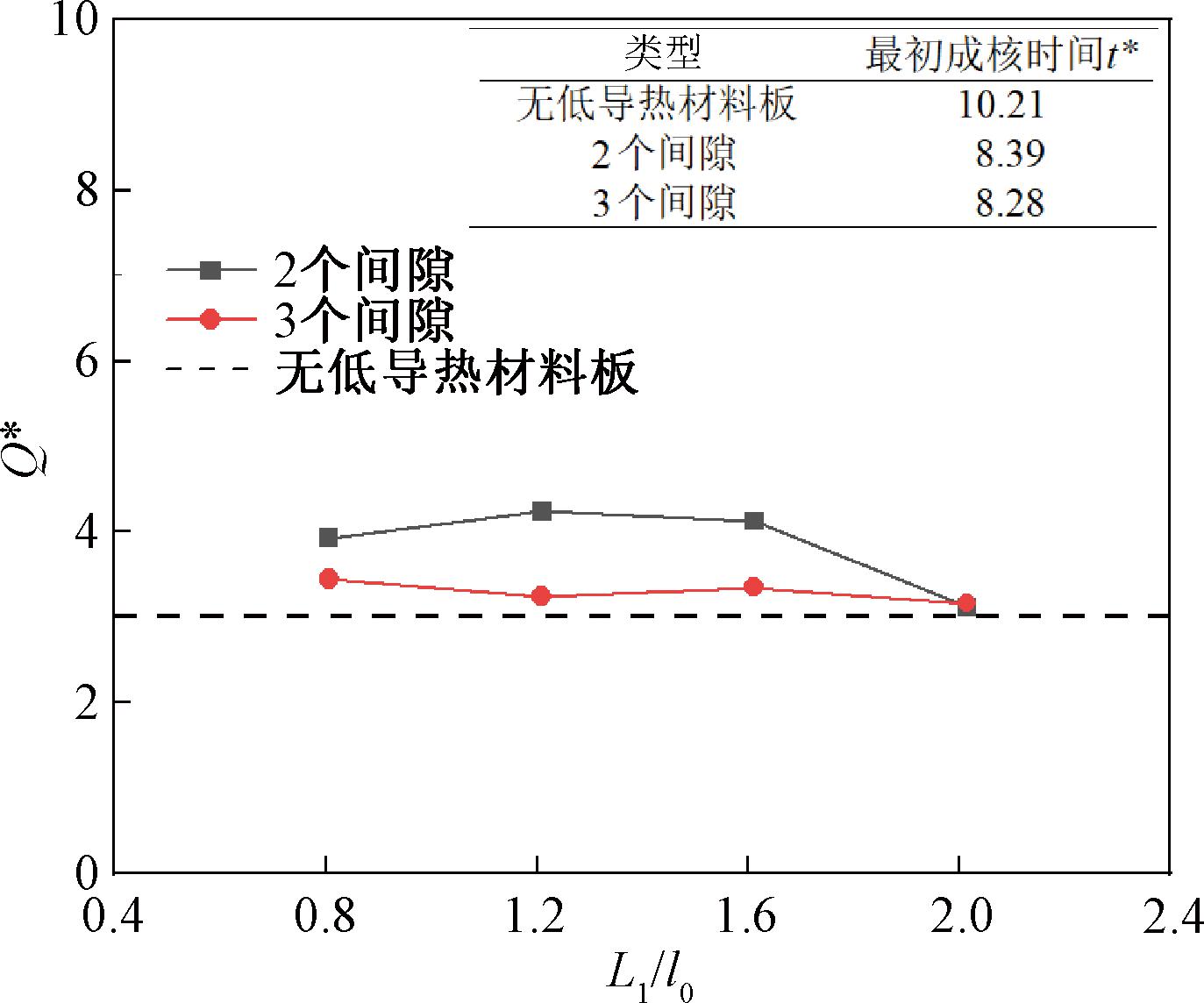
图6 添加低导热材料板强化换热分析图
Figure 6 Analysis diagram of enhancing heat transfer by adding low thermal conductivity plates
4.2 强化沸腾换热分析
图7显示了亲水表面上不同间隙间距(L1=1.209l0、2.015l0)的池沸腾温度场。图7中T为无量纲温度,黑色箭头(垂直于等温线)表示局部热流方向,红色箭头指向热流密度较集中的区域。图7(a)和7(b)分别为2个和3个间隙的温度场,从图中可以发现,两个温度场都具有对称结构的特点。由于低导热材料板的存在,间隙处的温度梯度变化大于低导热材料板处的温度梯度变化,另外间隙受热面处存在较大的局部热流密度,使得气泡首先在间隙处成核生长。
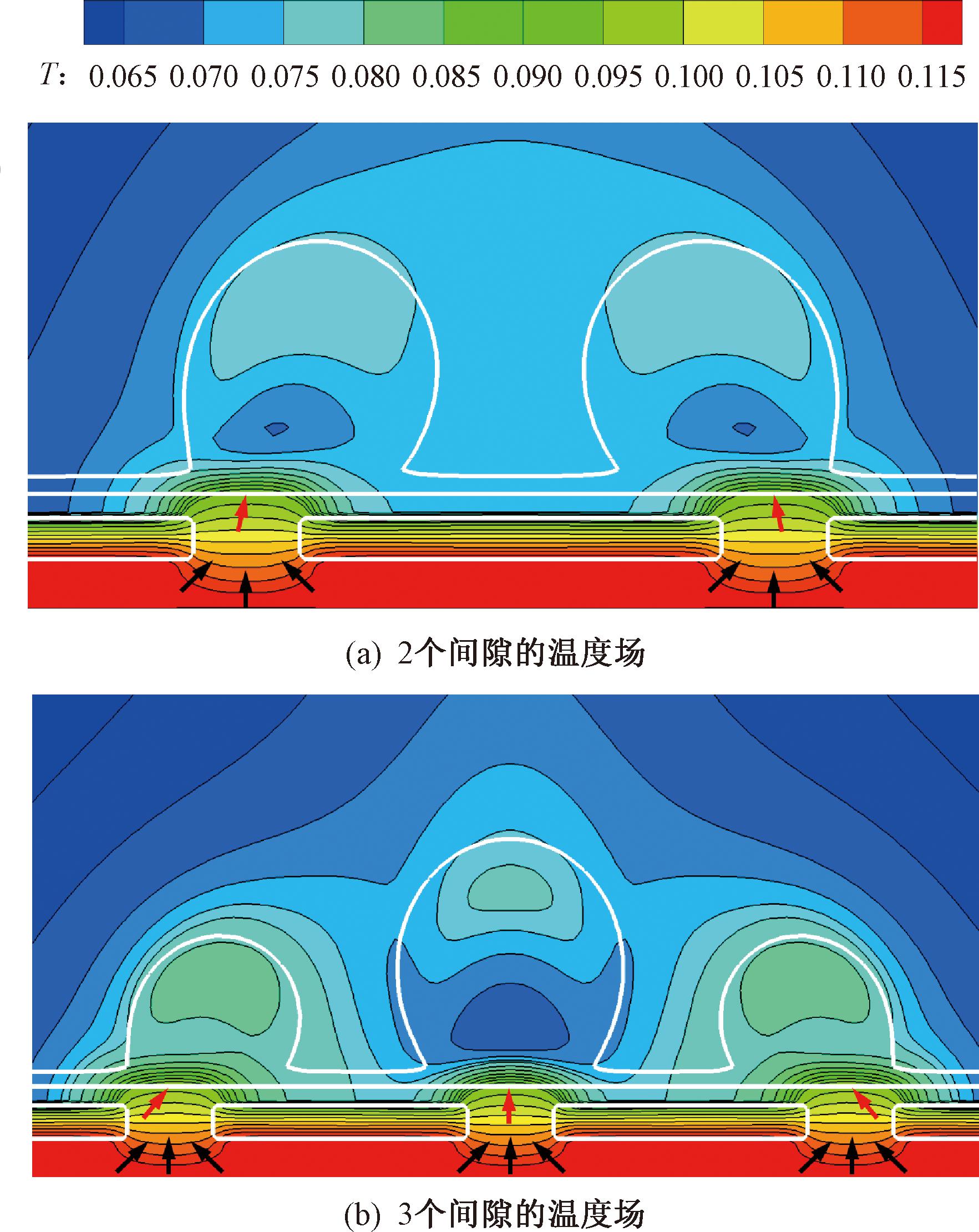
图7 池沸腾温度场
Figure 7 Pool boiling temperature field
生长气泡之间的相互作用不仅在沸腾换热过程中起着重要的作用,而且还影响着受热面附近的气泡动力学。图8为稳定状态后间隙受热面处的气泡在不同时刻下的运动轨迹和速度矢量(对应于图4和图5中的编号e1～e6)。图8(c)描述了图8(a)中过程4的气泡动态行为,由于处在上一个脱离气泡的流场中,气泡1和气泡2受到两侧速度涡流的影响,此时气泡之间的速度矢量小于两侧的速度矢量,导致气泡往中间倾斜。在2个间隙的间距较小的情况下,气泡会在生长过程中甚至在脱离上升的过程中相互交叉,从而可能会进一步导致气泡合并,这与图4中的编号a1～d6情况一致。然而,当气泡1和气泡2脱离后,受热面的成核位点又重新被激活,如图8(e)所示。由于气泡1和气泡2引起的尾流,新生长的气泡3和气泡4向彼此倾斜,与图8(c)呈现出相同的气泡倾斜趋势。图8(d)和8(f)是对图8(b)中过程气泡2和气泡5的速度矢量分析,与2个间隙的过程类似,不同的是中间间隙的气泡3沿着竖直方向生长,这主要是因为气泡3受到两侧对称且相等的速度矢量影响。稳定状态后,上升气泡脱离后的尾流导致受热面上的气泡在生长的过程中相互吸引和靠近,促进了受热面的气泡动力学循环。
图8 气泡轨迹图和速度矢量图
Figure 8 Bubble trajectory diagram and velocity vector diagram
通过对不同间隙数量时的气泡动力学行为分析,发现脱离周期较小时总伴随着气泡的合并过程(图4和图5中编号b1～b6和编号c1～c6)。由图5可知,编号b2气泡合并时形成较小的液桥,而编号c4形成较大的液桥,相较于编号b2,编号c4具有更长的气泡脱离周期,可能是因为气泡合并后需要在表面张力的作用下收缩边界,同时气泡的根部收缩过程也需要时间。但相比图5的其他工况,液桥的形成促进了气泡的脱离,为此本文针对气泡合并形成液桥的现象进行了分析。
图9给出了2个间隙和3个间隙形成液桥的微层蒸发前后的流线图,如图9(a)、9(b)所示,气泡合并形成大小不一的液桥,为了方便分析,选择了相对较大时的形成液桥过程,对应的间隙间距分别为1.612l0、1.209l0。由图9可知,液桥下方存在液相区域,由于液相区域内漩涡的存在,加速了间距上方的液体蒸发和气泡根部的微层蒸发过程,同时气泡的外侧存在反向的大涡流,能够促进计算域液相区顶部冷流体再流入间隙受热面。从图9(b)中可以发现,涡流的存在促进了液桥下方区域的液体蒸发和受热面的再润湿过程,导致左右两侧的气泡根部即将收缩。
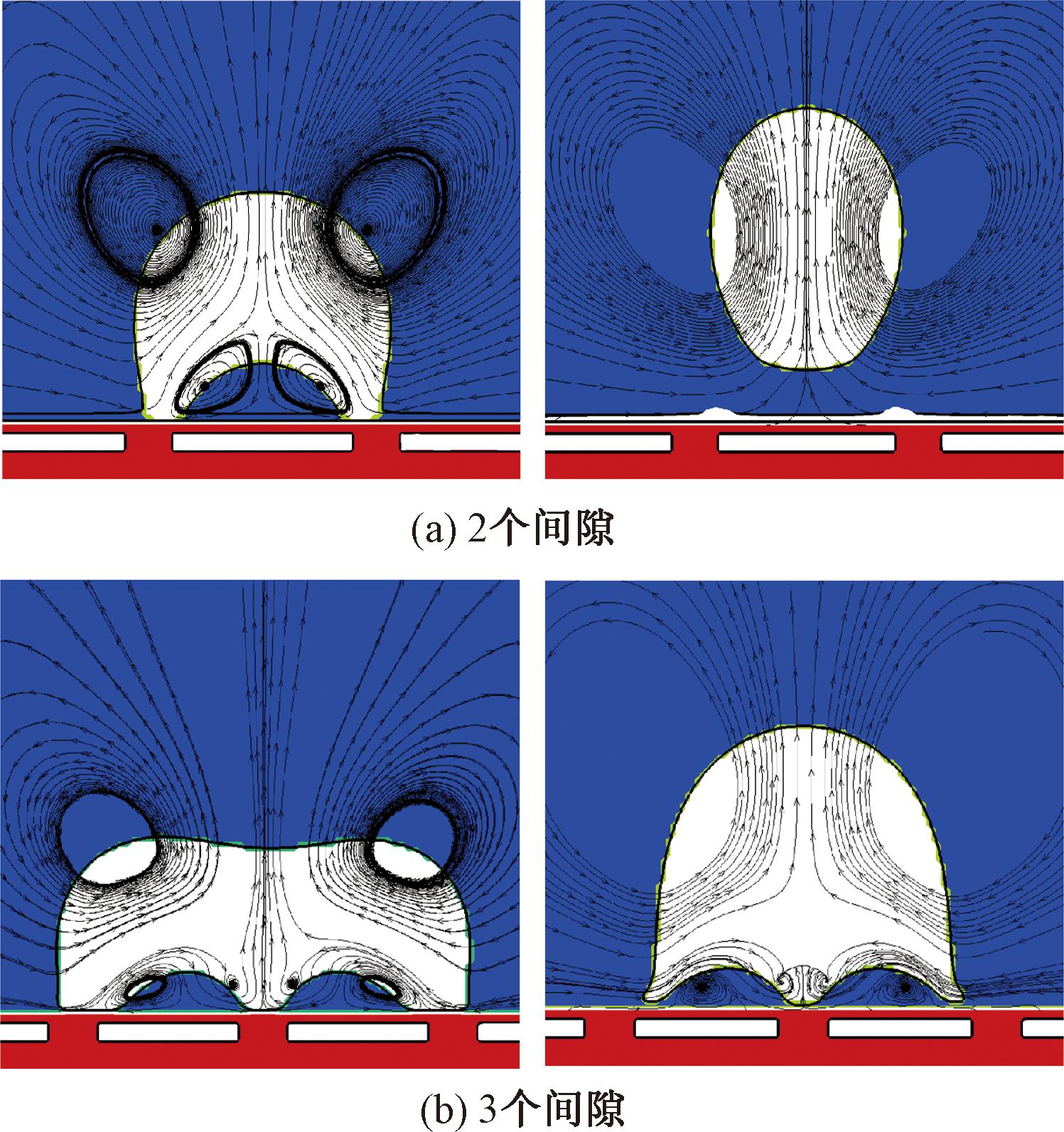
图9 微层蒸发前后流线图
Figure 9 Flow chart before and after micro layer evaporation
通过对等温线图、域内流场和气泡合并等过程的分析可知,在固体加热器中添加适当间距的低导热材料板,可以促使热量在间隙受热面处积聚,气泡更快成核。流体域内的涡流影响了受热面的气泡动力学过程,促进了间隙受热面处的气泡迁移和合并过程。气泡合并后形成的液桥促进了气泡根部的微层蒸发,且导致了液桥处冷流体对间隙受热面的再润湿。这些作用共同强化了沸腾换热性能。
5 结论
本文基于单组分多相格子Boltzmann模型,通过在固体加热器内添加多段低导热材料板,分析了沸腾换热过程中添加不同间隙间距的低导热材料板的加热表面上的气泡动态行为,并从微观角度揭示了强化沸腾换热机理,得到以下结论。
(1)亲水表面上不同低导热材料板间隙处的气泡在不同间隙间距时的气泡脱离行为不同。在沸腾过程中,气泡之间的相互作用随着间隙间距的增大而减弱。
(2)通过对温度场和流场分析,气泡首先会在间隙受热面处成核生长,脱离气泡的涡流可以促进生长气泡在受热面的横向迁移和合并过程。
(3)不同间隙处的气泡在一定间隙间距L1范围内会相互融合形成液桥,液桥的存在促进了受热面气泡根部周围微层的蒸发,推动了间隙受热面处的冷流体再润湿过程。
(4)添加多段低导热材料板时,间隙受热面处的热量积聚、气泡形成液桥促进底部微层的蒸发、间隙受热面处的再润湿过程、气泡横向迁移等动力学行为和多气泡的快速合并等这些过程的共同作用强化了沸腾换热性能。
[1] 郭茶秀, 魏金宇. 电池排布方式对21700锂电池相变热管理系统的影响[J]. 郑州大学学报(工学版), 2023, 44(2): 91-97.
GUO C X, WEI J Y. Influence of different arrangement on phase change thermal management system of 21700 lithium battery[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(2): 91-97.
[2] 郑晓欢, 纪献兵, 王野, 等. 超亲/疏水性表面池沸腾传热研究[J]. 化工进展, 2016, 35(12): 3793-3798.
ZHENG X H, JI X B, WANG Y, et al. Pool boiling heat transfer on superhydrophilic and superhydrophobic surfaces[J]. Chemical Industry and Engineering Progress, 2016, 35(12): 3793-3798.
[3] 曹海亮, 张红飞, 左潜龙, 等. 梯形微槽道表面池沸腾换热性能研究[J]. 化工学报, 2021, 72(8): 4111-4120.
CAO H L, ZHANG H F, ZUO Q L, et al. Study on pool boiling heat transfer performance of trapezoidal microchannel surface[J]. CIESC Journal, 2021, 72(8): 4111-4120.
[4] MUKHERJEE A, DHIR V K. Study of lateral merger of vapor bubbles during nucleate pool boiling[J]. Journal of Heat Transfer, 2004, 126(6): 1023-1039.
[5] HUANG Y, TIAN Y, YE W, et al. Enhancing pool boiling heat transfer by structured surfaces-a lattice Boltzmann study[J]. Journal of Applied Fluid Mechanics, 2022, 15(1): 139-151.
[6] YUAN J J, YE X, SHAN Y G. Two-dimensional lattice Boltzmann method to study the influence of nucleation distance on heat flux during bubble coalescence[J]. International Journal of Thermal Sciences, 2022, 172: 107353.
[7] 徐刚, 梁帅, 刘武发, 等. 流动聚焦型微流控芯片微通道结构优化[J]. 郑州大学学报(工学版), 2020, 41(4): 87-91.
XU G, LIANG S, LIU W F, et al. Optimization of micro-channel structure of flow focusing microfluidic chip[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(4): 87-91.
[8] ZHANG L, WANG T, KIM S, et al. The effects of wall superheat and surface wettability on nucleation site interactions during boiling[J]. International Journal of Heat and Mass Transfer, 2020, 146: 118820.
[9] MAGRINI U, NANNEI E. On the influence of the thickness and thermal properties of heating walls on the heat transfer coefficients in nucleate pool boiling[J]. Journal of Heat Transfer, 1975, 97(2): 173-178.
[10] RAHMAN M M, POLLACK J, MCCARTHY M. Increasing boiling heat transfer using low conductivity materials[J]. Scientific Reports, 2015, 5: 13145.
[11] 孟璐璐, 谢添玺, 陈志豪, 等. 材料交错分布型传热板表面异态干涉沸腾传热特性研究[J]. 化工学报, 2021, 72(9): 4564-4572.
MENG LL, XIE TX, CHEN ZH, et al. Study of different-mode-interacting boiling heat transfer characteristics on the heating plate with material cross arrangement[J]. CIESC Journal, 2021, 72(9): 4564-4572.
[12] UTAKA Y, XIE T X, CHEN Z H, et al. Critical heat flux enhancement in narrow gaps via different-mode-interacting boiling with nonuniform thermal conductance inside heat transfer plate[J]. International Journal of Heat and Mass Transfer, 2019, 133: 702-711.
[13] BHATNAGAR P L, GROSS E P, KROOK M K. A model for collision processes in gases. I. small amplitude processes in charged and neutral one-component systems[J]. Physical Review, 1954, 94(3): 511-525.
[14] KUPERSHTOKH A L, MEDVEDEV D A, KARPOV D I. On equations of state in a lattice Boltzmann method[J]. Computers &Mathematics with Applications, 2009, 58(5): 965-974.
[15] YUAN P, SCHAEFER L. Equations of state in a lattice Boltzmann model[J].Physics of fluids, 2006, 18(4): 042101.
[16] 曾建邦, 李隆键, 廖全, 等. 池沸腾中气泡生长过程的格子Boltzmann方法模拟[J]. 物理学报, 2011, 60(6): 520-529.
ZENG J B, LI L J, LIAO Q, et al. Simulation of bubble growth process in pool boiling using lattice Boltzmann method[J]. Acta PhysicaSinica, 2011, 60(6): 520-529.
[17] 曹海亮, 安琪, 左潜龙, 等. 一种新的固液共轭沸腾传热LB模型[J]. 郑州大学学报(工学版), 2023, 44(2): 75-81.
CAO H L, AN Q, ZUO Q L, et al. A new LB model for solid-liquid conjugate boiling heat transfer[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(2): 75-81.
[18] GONG S, CHENG P. A lattice Boltzmann method for simulation of liquid-vapor phase-change heat transfer[J]. International Journal of Heat and Mass Transfer, 2012, 55(17/18): 4923-4927.
[19] SON G, DHIR V K, RAMANUJAPU N. Dynamics and heat transfer associated with a single bubble during nucleate boiling on a horizontal surface[J]. Journal of Heat Transfer, 1999, 121(3): 623-631.
[20] 汪鹏军, 祁影霞, 谢荣建. 气泡生长及脱离过程的格子玻尔兹曼模拟[J]. 轻工机械, 2020, 38(5): 32-38.
WANG P J, QI Y X, XIE R J. Lattice Boltzmann simulation of bubble growth and detachment[J]. Light Industry Machinery, 2020, 38(5): 32-38.
[21] FRITZ W. Maximum volume of vapor bubbles[J]. Physic Zeitschz, 1935, 36: 379-354.
[22] ZOU Q S, HE X Y. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of Fluids, 1997, 9(6): 1591-1598.
[23] GONG S, CHENG P. Two-dimensional mesoscale simulations of saturated pool boiling from rough surfaces. Part Ⅱ: bubble interactions above multi-cavities[J]. International Journal of Heat and Mass Transfer, 2016, 100: 938-948.