脑卒中是当今中国社会中老年人多发的一种疾病[1],大脑功能受损使人体丧失肢体运动能力。末端牵引式康复机器人能够通过外部构件牵引脑卒中患者完成肢体康复运动[2],其结构简单、适用范围广、安装固定,不仅适用于大型医疗康复中心,还适用于家庭小空间环境[3]。末端牵引式康复机器人在带动患肢康复运动时,会根据交互系统的柔性产生不同的人机交互力,交互力的大小影响着患者康复的效果和安全。患者在康复初期因自身无法自如地控制肌肉收缩[4],无法自主运动,康复过程中往往会产生过大的力,此时应使康复系统尽量柔顺,保障康复安全;在康复中后期,患者具有一定的肌肉伸缩控制能力,为了帮助患者进行精细动作和肌肉的恢复,此时康复机器人应具有一定的刚性[5]。适度的柔顺性不仅能够提高患者康复训练的积极性和效率,同时能够在训练中防止产生过大的交互力从而保护患者的安全。柔顺控制一般通过构建理想的惯性-刚性-阻尼的二阶模型来调节其柔顺性：通过构建交互力与追踪误差的期望动力学方程,进而调节模型参数,调整康复机器人的柔顺性和人机交互系统刚度,已在上肢康复机器人领域广泛应用[6]。柔顺控制根据控制输入与输出关系的不同,可以分为阻抗控制和导纳控制[7]。Bai等[8]提出了一种自适应模糊阻抗控制方法,可消除康复训练过程中不确定性对系统的影响,使非线性控制系统具有较强的鲁棒性和适应性。Sado等[9]提出了一种自适应混合阻抗控制,通过在线估计受损肢体的阻抗分布,使用离散事件系统(DES)框架通过任务空间和患者阻抗曲线确定合适的阻抗参数。但阻抗控制需要基于阻抗模型和机器人系统的精准动力学建模直接计算电流/扭矩进行控制,需要伺服电机开放电流环,开发成本较高。
相对于阻抗控制,基于位置控制的导纳控制实现过程简单、成本低,且无须伺服驱动开放电流控制,应用开发较为方便。导纳控制按照控制过程中模型参数是否自动变化可分为固定参数导纳控制[10]和变参数导纳控制。吴青聪等[11]提出了一种模糊滑模导纳控制策略,对比研究了固定导纳参数模型中大中小3种导纳参数对康复训练结果的影响。但实际康复过程中,固定参数导纳控制模型需要人工调节以获得合适的柔性,较为烦琐。变导纳模型控制策略通过改变导纳参数进而调节柔顺性[12]。但如何将患者的需求感知量化,通过调节导纳模型的参数调节柔性,优化康复训练仍需要进行研究。乐宇倚等[13]提出了一种基于经验的变导纳控制的柔顺控制方法,基于人机交互力、跟踪力矩和自由力矩的基准值的差别构建数学关系调节阻尼。该方式虽然调节了系统的柔顺性,但只考虑了系统的安全性,例如在康复晚期患者具有一定肌肉伸缩控制能力时,康复机器人需要保持一定刚性,该变导纳策略无法实现。不同患者或不同康复阶段有着对机器人柔顺性的不同需求,单一的数学规则很难完善,而模糊控制常用于处理此类规则复杂的问题。梁旭等[14]设计了一种基于变参数导纳控制的外骨骼下肢康复机器人,其中模糊控制根据人机交互力和外骨骼姿态的变化调节导纳模型参数。但对于上肢康复机器人,该策略不够完备,仅仅依靠人机交互力的大小无法描述康复患者对柔顺性的准确需求。Li等[15]利用模糊控制基于追踪误差及其变化率设计了康复机器人的不同模式(负载、助力、安全模式)的虚拟力,依据虚拟力和固定导纳模型参数产生修正轨迹进行康复训练模式的切换,从而保证康复效率和安全。但该方法仅适合用于点到点的移动,在给定包含时间序列的康复轨迹时,无法从追踪误差及其变化速率判断患者的需求。
综上所述,现有上肢康复机器人柔顺控制的研究在结合实际康复需求时存在不完备的问题：固定导纳控制无法满足不同康复患者或阶段的需求;单一数学关系难以完善导纳控制参数变化;现有模糊控制规则结合实际康复需求并不完善。针对上述问题,本文基于自主研发的一种串并混联[16]上肢康复机器人[17],从实际康复需求出发,制定明确的模糊规则,并提出了基于模糊规则的导纳控制策略,用人机交互力误差及其变化速率作为模糊控制的输入,通过设计的规则来调节导纳控制模型中的自然频率达到机器人柔性的调节,以适用于各个阶段的模糊规则为康复机器人提供具有针对性的决策,并通过模拟康复训练实验分析了控制策略对训练过程中轨迹偏差的影响,从人机交互力的结果分析,验证了该上肢康复机器人控制策略在康复安全和效率上的提升。
1 上肢康复机器人系统
本文研究对象是自主研发的一种串并混联上肢康复机器人,其结构如图1所示。该机器人具有3自由度,为了使患者握持手柄时更加灵巧,在设计末端手柄时使其能够在UV平面上转动。患者在进行康复训练时,端坐于康复机器人龙门架下方,手臂上举拉住机器人末端手柄位置。U轴和V轴连杆通过并联,共同带动患者手臂在其所确定的平面中运动,再与Z轴串联,机器人的末端手臂便能够带动患者手臂在三维空间中沿预设轨迹进行运动,从而刺激患者特定肌群,较大程度地活动患者肩关节和肘关节,达到康复训练的目的。
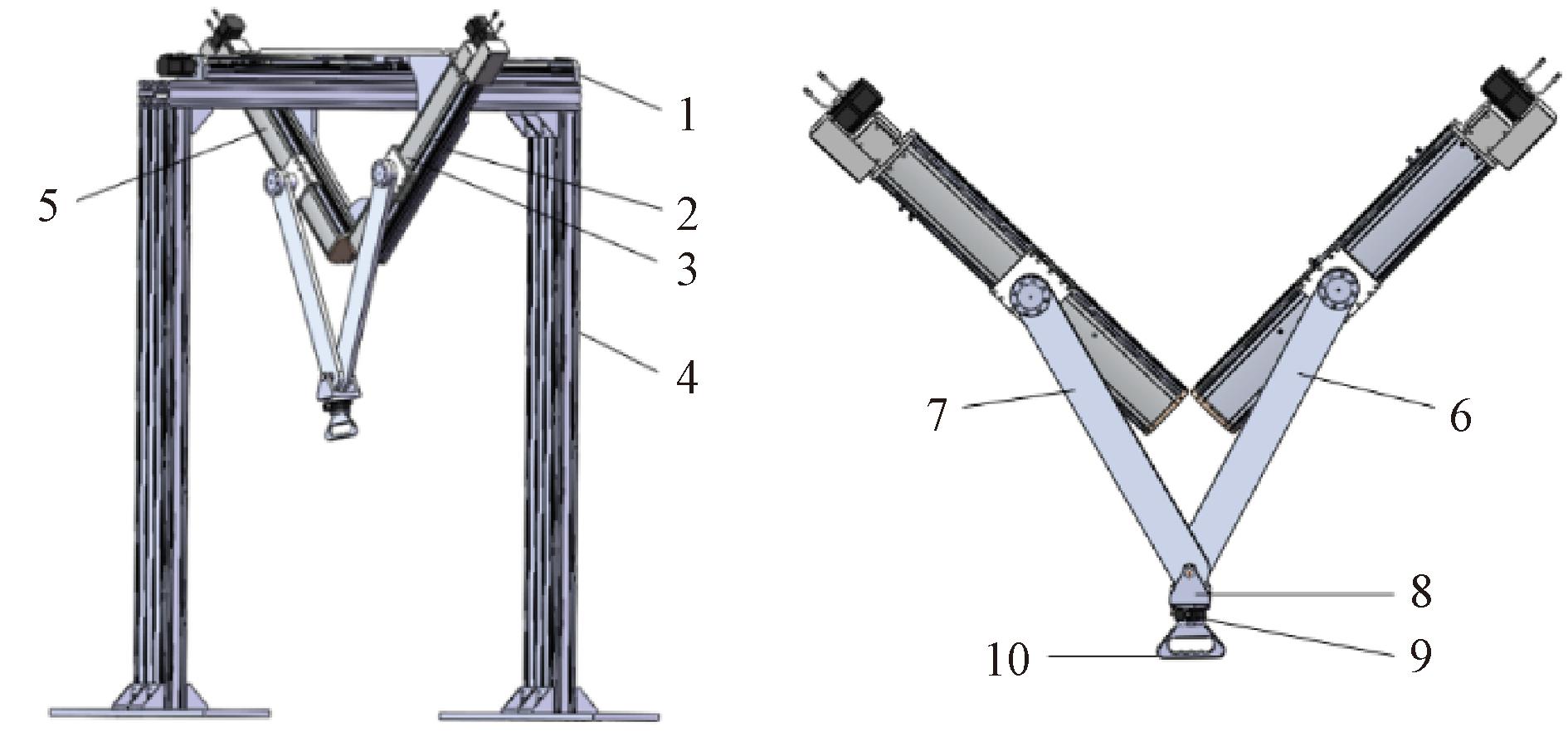
1—Z轴滑台模组;2—V型支撑架;3—U轴滑台模组;4—龙门架;5—V轴滑台模组;6—U轴连杆;7—V轴连杆;8—力传感器连接件;9—力传感器;10—末端手柄
图1 上肢康复机器人三维模型图
Figure 1 3D model of upper limb rehabilitation robot
在进行康复训练时,根据康复治疗师提供的训练路径,需要进行运动学反解。因此应首先分析机构运动学。该机构是由U、V两轴的2-PRR并联结构与Z轴耦合而成,应先将Z轴与2-PRR并联结构解耦,将上肢康复机器人末端运动分解为U、V两轴所在的平面运动和Z轴方向上的运动。先分析U、V两轴所在的平面运动,再与Z轴方向上的运动耦合。
上肢康复机器人机构简图如图2所示,以U、V两轴交点为坐标原点,水平方向为x轴,竖直方向为y轴建立坐标系。其中,OB1的长度为d1,OB1与水平面的夹角为α1;OB2的长度为d2,OB2与水平面的夹角为α2;CB1的长度为l1,CB1和水平面的夹角为β1;CB2的长度为l2,CB2和水平面的夹角为β2。
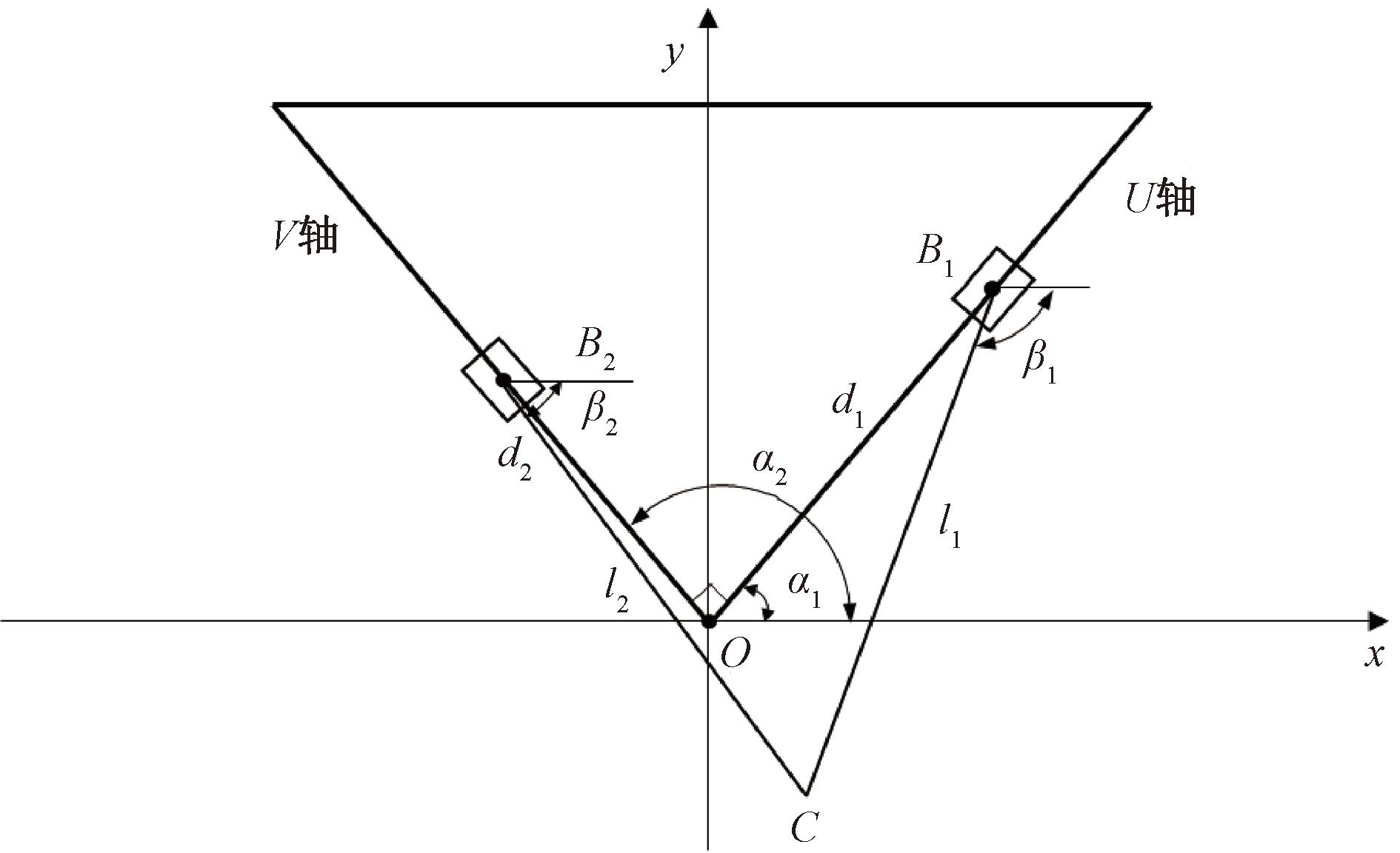
图2 上肢康复机器人机构简图
Figure 2 Schematic diagram of the upper limb rehabilitation robot
由图2中几何关系可得
(1)
式中：i=1,2(下同)。
对式(1)进行数学变换,可得两个滑块在坐标系中的运动学逆解为
(2)
式中：
(3)
因di表示滑块到原点的距离,则di≥0恒成立,故
(4)
由式(1)又可得到βi与机器人末端坐标的关系：
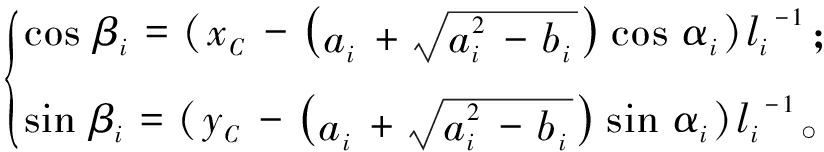
(5)
2 基于模糊控制的变参数导纳控制
2.1 固定参数导纳控制
上肢康复机器人在康复训练中通过末端手柄带动患者手臂运动时,需要采用柔顺控制策略,以防止手臂在做跟随运动或牵引运动时由于人手和末端手柄之间作用力过大而对手臂肌肉造成损伤。导纳控制框图[18]如图3所示,训练过程中,手柄和机器人末端通过力传感器连接,实时检测患肢和末端手柄之间的作用力f,并通过力反馈的方式实时更新机器人末端运动路径。其中追踪的新路径通过逆运动学来进行位置控制。这种方式可以有效锻炼患者肌肉,同时保证机器人末端执行器运动轨迹的平稳性,避免因患者肌力不足或疲劳而产生抽搐时对患者造成二次伤害。
其运行过程中Xr、Xd、Fr及Md、Bd、Kd都是包含(x,y,z)3个方向的三维向量,在实际训练中每一个自由度都是解耦状态,可根据单个自由度进行分析,因此本文基于单轴方向为例进行分析。式(6)为导纳控制方程。
(6)
式中：xe为基于笛卡尔空间末端执行器位置偏差,xe=xr-xd,xr为康复医师基于康复专业知识设定的康复轨迹,xd为期望位移;md为质量系数;bd为阻尼系数;kd为刚度系数;f为力传感测得的人机交互力;fr为导纳模型输入的力偏移量,其目的是在控制柔顺度的同时产生一个力偏移,通过调节fr来调节康复训练的负载,使患者以给定的力目标进行康复运动[13]。若fr=0,则系统可视为简单的柔顺控制;若fr过大,实际训练过程中因患者无法提供较大的力,运动路径会较多地负向偏移且柔顺性较差;若fr过小,实际训练过程中刚性较小,会使运动路径产生较大偏移,造成康复效果不理想。
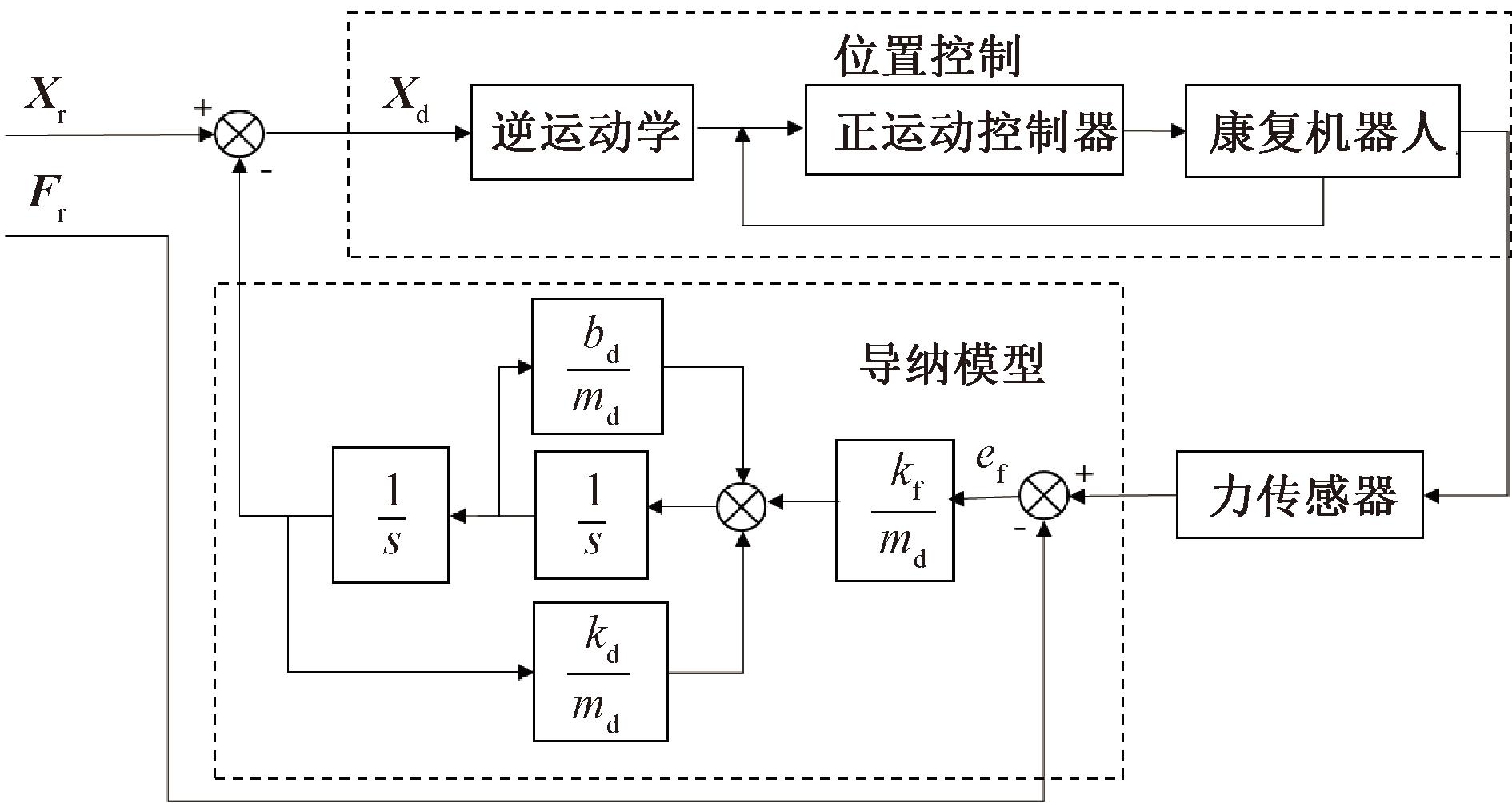
图3 导纳控制框图[18]
Figure 3 Admittance control block diagram[18]
2.2 变参数导纳控制
在康复中,人机交互需要的导纳模型是实时变化的,且人的受力动力学模型不易直接测量。因此,固定的导纳参数通常不能适应不同患者上肢患病情况,需要针对不同患者的实际情况设计针对性康复训练。现有部分研究[16-17]以人机交互力的大小变化为基准设计了基于模糊控制的变导纳控制,但实际康复训练中,人机交互力的变化率代表着患者的肌肉快速控制能力,更能反映患者肌力的强弱。
本文设计了基于模糊控制实时改变导纳系数的控制策略来实时调整在人手和末端手柄之间的作用力,如图4所示。其中人机交互力通过六维力传感器测得,其变化速率通过双向微分法计算求得,并采用二阶IIR(infinite impulse response)数字滤波器巴特沃斯滤波器(Butterworth filter)进行滤波[19],再将人机交互力误差和力误差的变化速率作为模糊控制系统的输入,采用模糊准则来实时调节导纳控制参数[20],使得在康复训练过程中能够实时输入一个理想的导纳控制参数,从而达到最佳康复效果[21]。
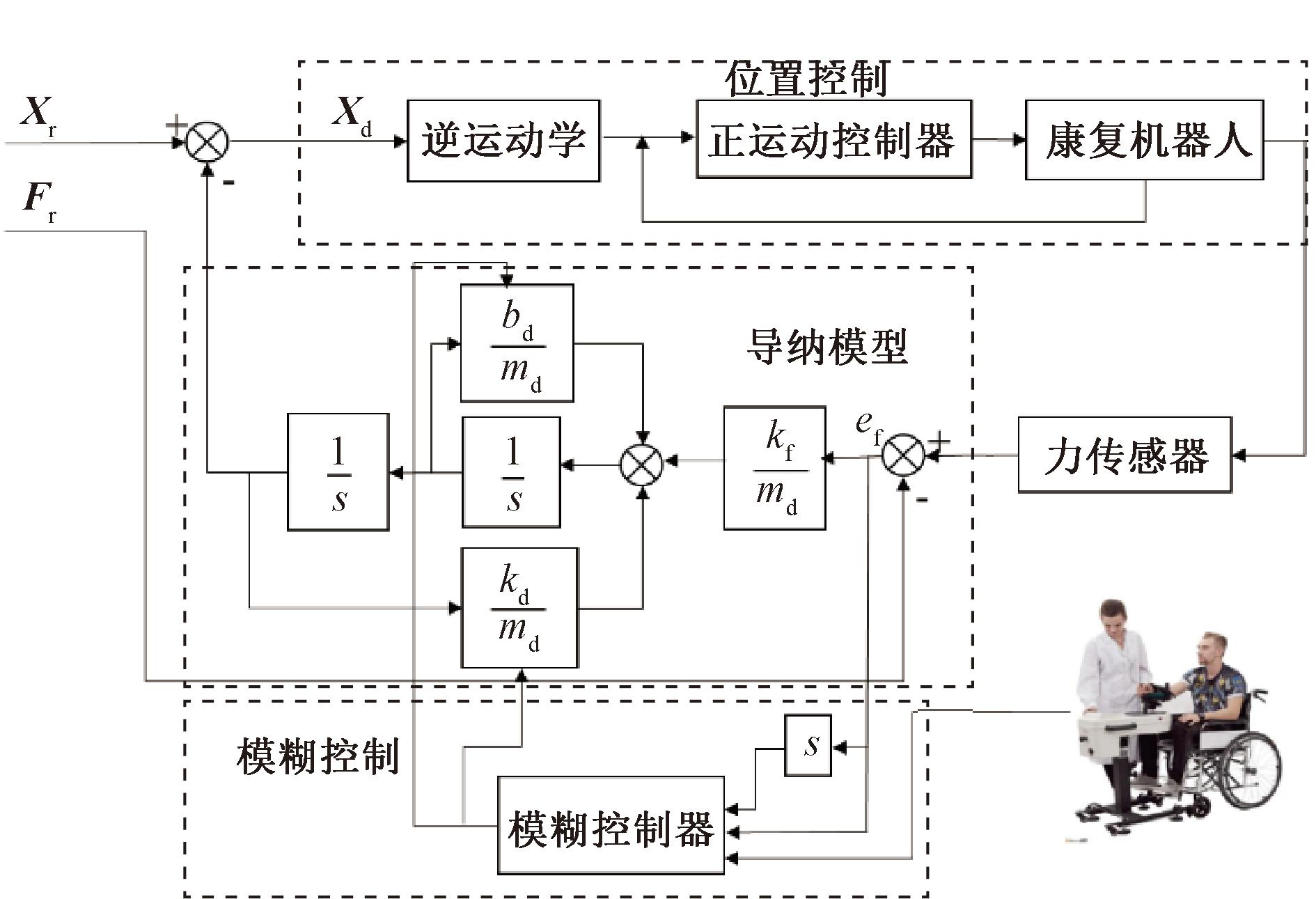
图4 基于模糊控制的变导纳控制框图
Figure 4 Fuzzy admittance control block diagram
为了使参数调节规范化,通过将导纳模型的惯性-刚性-阻尼的二阶系统转换成标准二阶系统,从其自身特性出发,对自然频率和衰减比进行分析。将二阶系统传递函数
代入式(6)得到式(7)：
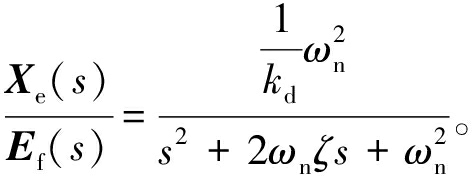
(7)
式中：
为人机交互力误差向量;ωn为自然频率;ζ为阻尼比。故可通过调节自然频率ωn从而调节导纳控制参数。自然频率ωn越大,HRI(human robot interaction)系统刚性越大,反之刚性越小。综合考虑系统反应速度和振荡,阻尼ζ为0.5～1时最佳,故ζ选择0.7(最佳0.707附近)[22]。
2.3 模糊控制
对于自然频率ωn的调节需要根据康复专业知识基于模糊控制进行调节,从康复实际出发基于以下原则：康复训练中当患者在偏离给定路径时,机器人系统刚度应增大;反之,机器人系统刚度应减小。同时在康复训练中还必须注重安全性,保护患者免受二次伤害。相较于传统导纳控制策略,基于模糊控制实时改变导纳系数的控制策略恰好适用于以上要求。
在实际的康复训练中,患者随机器人末端运动存在以下两种极限情况：一是正常人能够以给定力跟随运动,故机器人系统应提供较大的刚性,以提高训练强度;二是对于肌无力患者不能完成康复运动,机器人系统应较为缓慢地追踪给定路径。从人机交互力误差来考虑,在力误差最大时,说明患者肌力不强,自然频率ωn应取较小值,机器人系统具有更大的柔顺性;在力误差最小时,说明患者肌力能够跟随期望力,自然频率ωn应取较大值,机器人系统具有更大的刚性。对于不同患者,在康复过程中会在某一时刻产生相同的力误差但肌力不同,力误差变化率必然不同,因此,还需要通过力误差的变化率调节导纳参数。患病程度轻的患者肌力强,则力误差变化率大,能以较大的刚性进行训练,故应采用较大的导纳参数;患病程度重的患者肌力弱,力误差变化率小,应以较大的柔顺性进行训练,故应采用较小的导纳参数。本文通过力误差和力误差变化率两个参数指标来调整导纳参数,既能保护患者,又能针对不同患者的患病程度实时调整导纳参数以达到期望的康复效果[23]。
针对以上分析,模糊规则制定如下。
(1)若ef(人机交互力误差)为正,且
(人机交互力误差变化率)为正时,此时力误差有增大的趋势,说明患者此时施加力过大或出现康复运动轨迹超出患者可承受范围的情况。为保护患者,人机交互系统应具有较小的刚性,则ωn(自然频率)应取较小值。
(2)若ef为负,且为负时,此时误差有增大的趋势,且说明患者对人机交互系统施加力减小,此时人机交互系统应具有较快的响应速率,具有较大的刚性。若ef数值较大时ωn应取较大值。若ef数值较小时,此时应根据的数值大小来选取ωn,若数值较大时,说明患者施加力过大,此时可选用较大的ωn;若数值较小时,说明患者施加力并不太大,此时为保护患者,人机交互系统应具有较小的刚性,应选用较小的ωn。
(3)若ef为负,
为正时,此时误差有减小趋势,患者对人机交互系统产生的力有逐渐增大的趋势,且根据数值的大小可判断患者此时的肌力强度,从而判断患病程度,即数值大说明患者患病程度较轻,数值越小说明患者患病程度重,此时不能提供较大的力来抵消误差。据此ωn应跟随的数值进行调整,数值大时ωn选用较大的值;数值小时,ωn选用较小的值。若此时ef较小,为负时,不管数值多大,都说明患者能够达到给定康复力,此时ωn都应该选用较小值。
(4)若ef为正,为负时,此时误差有减小趋势,且说明患者最初施加力过大,正处于调整至给定康复力的时刻,为保护患者且使人机交互系统具有一定的柔顺性,应根据
的大小选取合适的ωn。ef数值大时,都应选用较大的ωn来增加人机交互系统刚性;ef数值小时,说明患者即将达到给定康复力,则应选用较小的ωn来调节。
将上述规则模糊化并制表如表1所示,ef分为负大、负小、零、正小、正大5个等级来描述,分别用NL、NS、0、PS、PL表示;分为负大、负小、零负、零正、正小、正大6个等级来描述,分别用NL、NS、N0、P0、PS、PL来描述;ωn分为很小、小、中、大、很大5个等级来描述,分别用VS、S、M、L、VL表示。图5为模糊推理输入/输出关系曲面。
表1 模糊规则表
Table 1 Fuzzy rules
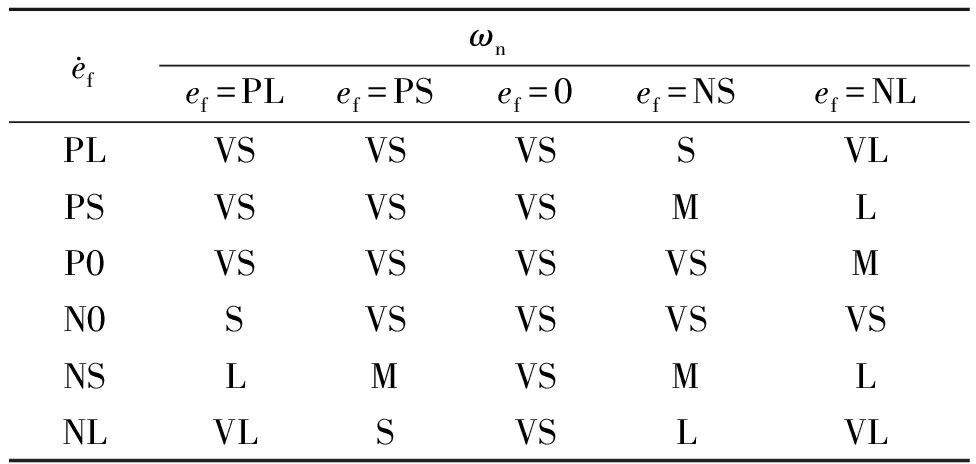
ωne·fef=PLef=PSef=0ef=NSef=NLPLVSVSVSSVLPSVSVSVSMLP0VSVSVSVSMN0SVSVSVSVSNSLMVSMLNLVLSVSLVL
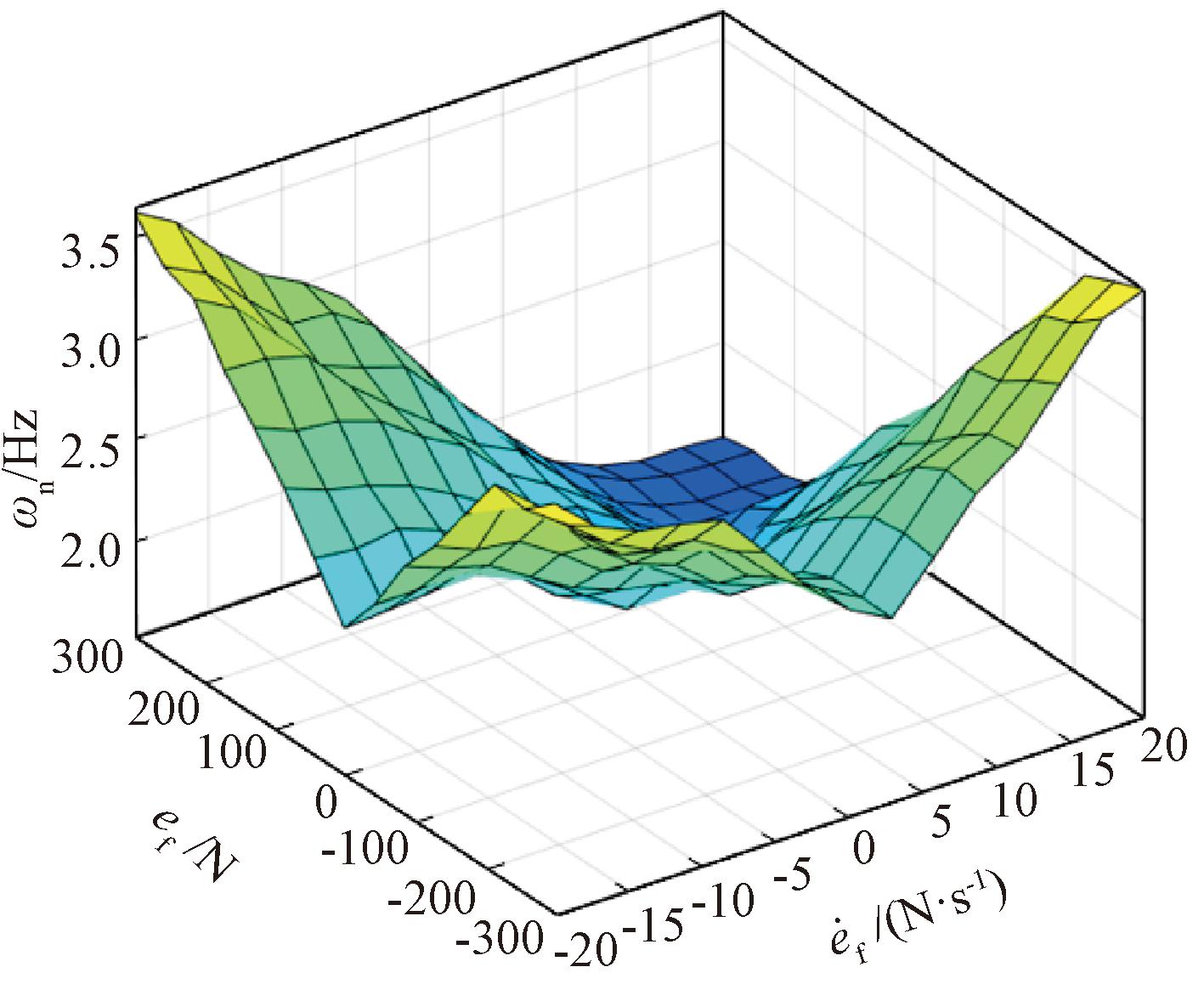
图5 模糊推理输入/输出关系曲面图
Figure 5 Input/output relation surface of fuzzy inference
3 仿真与实验验证
3.1 仿真分析
为了验证基于模糊控制的变导纳控制策略的可行性,在Simulink中进行了仿真研究(图6),仿真假设机器人为简单的一自由度质量弹簧阻尼二阶系统,康复运动轨迹为单一轴的振幅y=1 m、频率为0.01 Hz的正弦波。设期望力fr=1 N。人机交互过程中,产生的相互作用力假设为简单弹簧模型即f=kex。
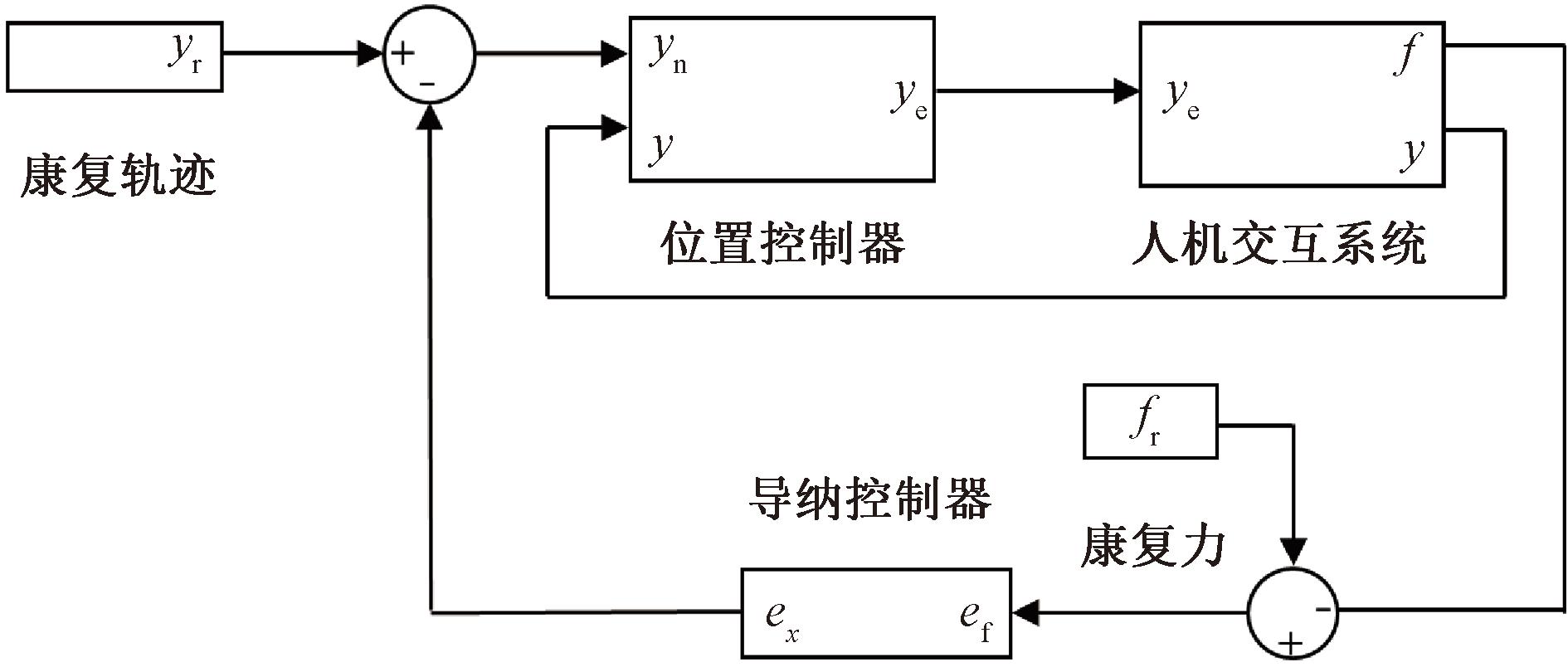
图6 基于模糊控制的变导纳控制仿真模型
Figure 6 Variable admittance control simulation model based on fuzzy control
在MATLAB的Fuzzy控制器中,输入模糊规则,输入输出语言变量隶属度函数均设定为标准正态函数,设定1 Hz≤ωn≤5 Hz,-20 N≤ef≤20 
N/s,ζ=0.7。固定导纳参数中取ωn=3 Hz,给定md=1 kg,参考式(7),可计算出kd=9,bd=4.2。
图7(a)中y、yr和y*分别为固定参数、原有和变参数的目标轨迹,在跟随原轨迹运动时,在25 s处和75 s处运动方向改变会产生突变力,对应ef如图7(b)所示,由于仿真中设定的人机交互力为简单弹簧模型,模拟健康受试者进行康复训练,从力的角度看,此时基于ef和的变化,ωn取较大值,最终仿真的结果
小于ef,说明变导纳模型中实际的力f更大,力误差能够更快收敛。在ef不论正向还是负向增大时,ωn均会增大,同时曲线y*相较于曲线y振幅更小,对应康复训练中患者肌力较强,采用较大的ωn以使人机交互系统刚性增大,符合模糊规则(2)和(3),能够满足预期提高康复效率的要求。仿真结果最终说明了基于模糊控制的变导纳模型能够有效调节系统参数,保证在产生较大力后HRI系统能够增大刚性,提高康复效率,验证了本控制方法的有效性。
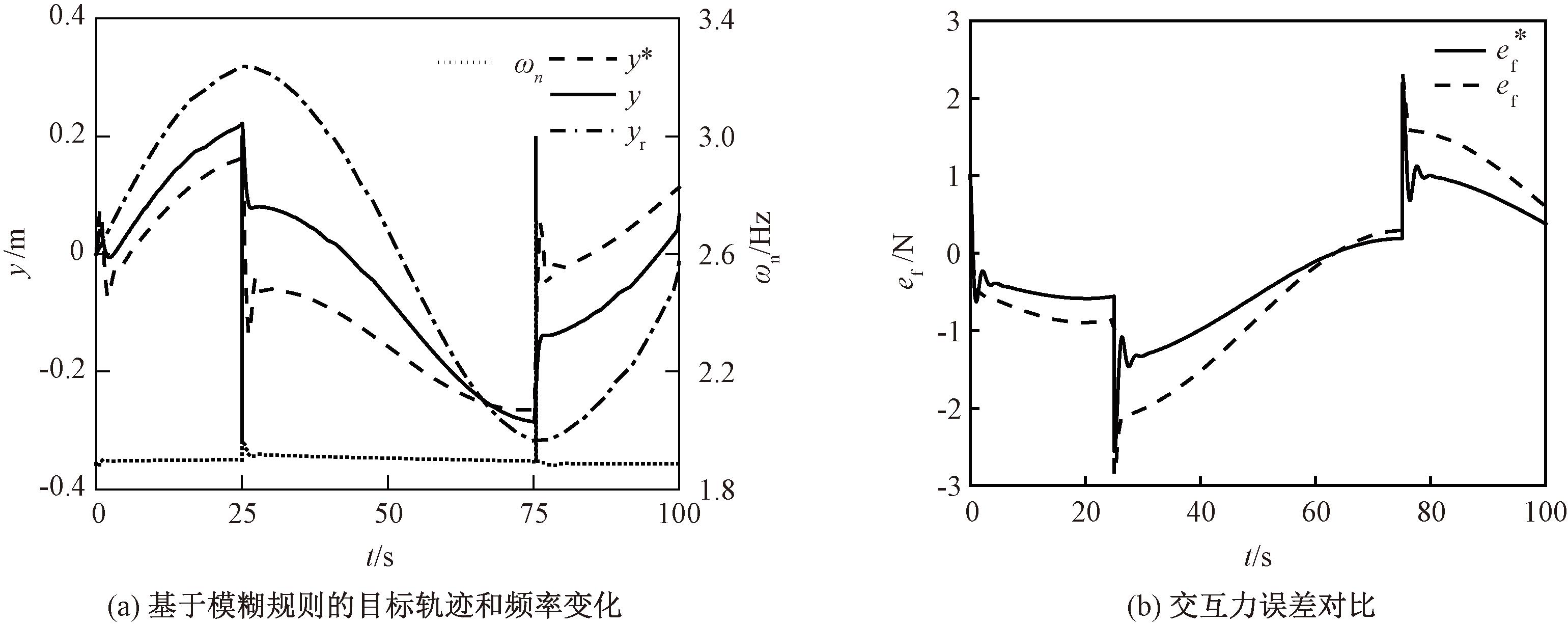
图7 MATLAB仿真结果
Figure 7 Imulation results in MATALB
3.2 实验验证
为了研究本控制策略在实际康复训练中的可行性,本文通过设计模拟实验进行验证。实验基于上肢康复机器人平台,在正运动控制器ZMC432中实现了基于模糊控制的变导纳控制算法,计算新目标追踪轨迹xd的周期为10 ms,并通过位置控制实现机器人末端轨迹的追踪。硬件连接如图8所示。
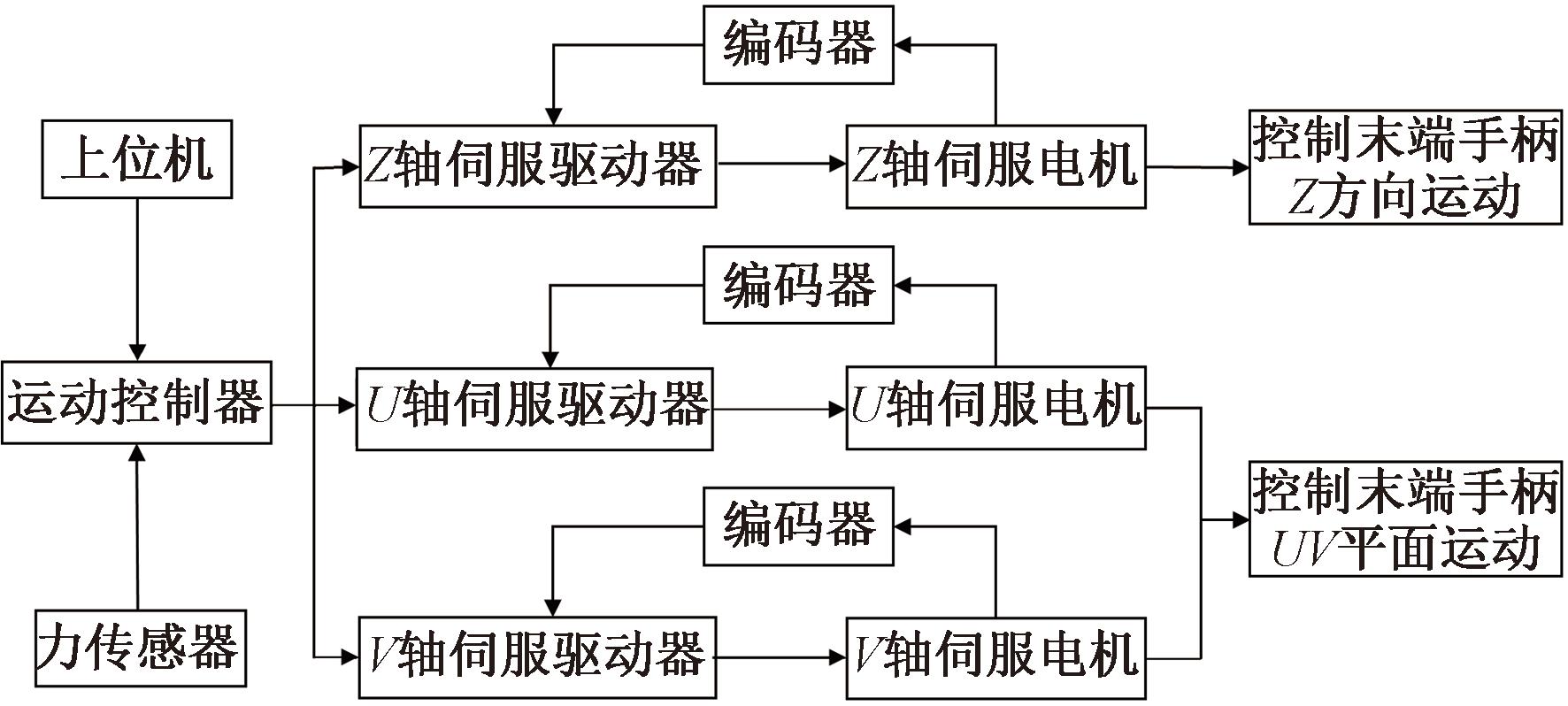
图8 硬件连接图
Figure 8 Hardware link diagram
对传统导纳模型和基于模糊控制的变导纳模型两种控制策略进行了对比实验。设计两组实验分别进行验证：实验一模拟了能够适应康复强度的患者从开始进行训练到进入稳定训练状态的肌力变化;实验二模拟了训练过程中康复运动轨迹超出患者能力承受范围而产生的力突变情况。实验现场照片如图9所示。
图9 现场实验照片
Figure 9 Experimental site photo
在仿真中发现,运动过程中可能出现基于导纳控制获得的新轨迹速度过大的现象,实验硬件条件可能无法达到,还可能会对患者造成伤害,为满足实验要求,对运动过程中的速度进行如下限制。
将xes=ve、f-fr=ef代入式(6)得追踪速度ve为
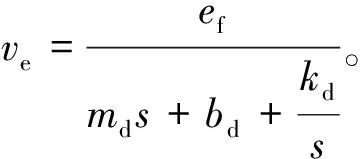
(8)
由于vd=vr-ve,限定vd在±vp之间,采用tanh(·)函数：
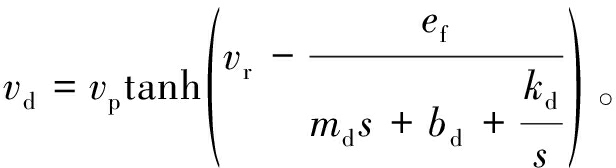
(9)
通过对vd积分求得xd
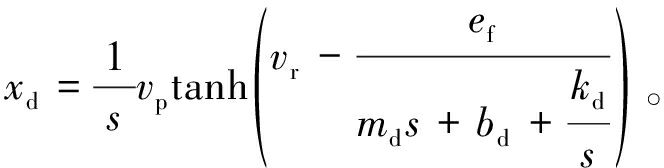
(10)
实验一中,实验对象选择一名男性健康受试者,模拟受试者在刚开始运动和运动过程中肌力变化,分析力误差变化引起的自然频率变化对康复训练的影响。
导纳模型中惯性参数md过大会使导纳控制中ef到xe的增益过小,难以运动且难以改变HRI系统柔顺性;过小的md会使整体HRI系统惯性较小,无法带动患者进行训练[24]。实验假设人机系统md=1 kg,通过调节ωn调节系统的整体柔顺性,由式(7)可知,
经实验测得,当ωn=3 Hz,md=1 kg时正常男性力误差ef的变化为[-20 N,20 N],力误差变化率的变化为[-50 N/s,50 N/s],当ef和超出给定范围时仅保留临界值。实验中由于采用二阶数字滤波器巴特沃斯滤波器进行滤波,实验结果会出现略微滞后现象。模拟实验给定x、y轴振幅为80 mm,频率为0.25 Hz的正弦和余弦路径,整体近似圆形,固定导纳模型给定自然频率ωn=3 Hz,变导纳模型中自然频率ωn给定为[1 Hz,5 Hz],ζ=0.7。实验中x,y方向上的位移和力是解耦状态,仅分析y方向上的位移和力变化即可,而位移是机器人位置控制对导纳控制输出的yd进行的位移追踪,实验假设追踪误差近似为0。
图10是模拟训练初始阶段,患者能够逐渐适应康复训练要求的实验结果。根据模糊规则(3),力误差增加速度越快,ωn应取较小值,以使y方向位移能够更快趋向于给定轨迹yr。在图10(c)中可以看出,与固定参数导纳模型相比,变参数导纳模型的追踪路径更贴近于给定路径yr,说明在患者能够负担康复训练所要求康复力的情况下,变参数导纳模型给出的新路径能够更快追踪至原给定路径,在12 s处两者与给定路径的差值最大,用差值的比作为量化结果计算为56.13%。最终可得到结论：在追踪给定路径方面的误差程度最大可降低56.13%,康复效率提高。同时,还能看出
时,ωn与正相关;反之,ωn与负相关,表明了模糊规则不仅能够提升效率、反应灵敏,同时具有舒适性。最终实验结果符合模糊规则(3)中的设定,验证了本控制方法的可行性。
患者在康复过程中如出现康复运动轨迹超出患者可承受范围时,会出现人机交互力突变的情况。实验二为模拟康复训练强度超出患者承受能力而产生力突变的对比实验。图11(a)展示了力误差ef和变化率的变化曲线;图11(b)展示了传统导纳模型和变导纳模型在力突变时y方向的位移和变导纳模型中ωn的变化曲线。
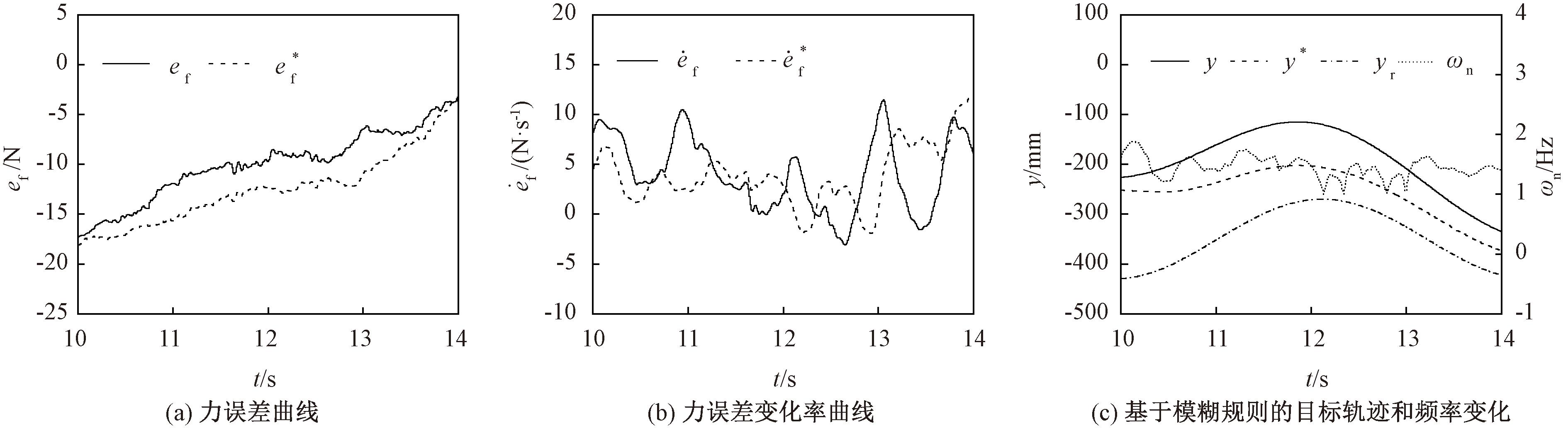
图10 能够适应康复强度的患者实验结果图
Figure 10 Experimental results of patients with rehabilitative exercise capacity
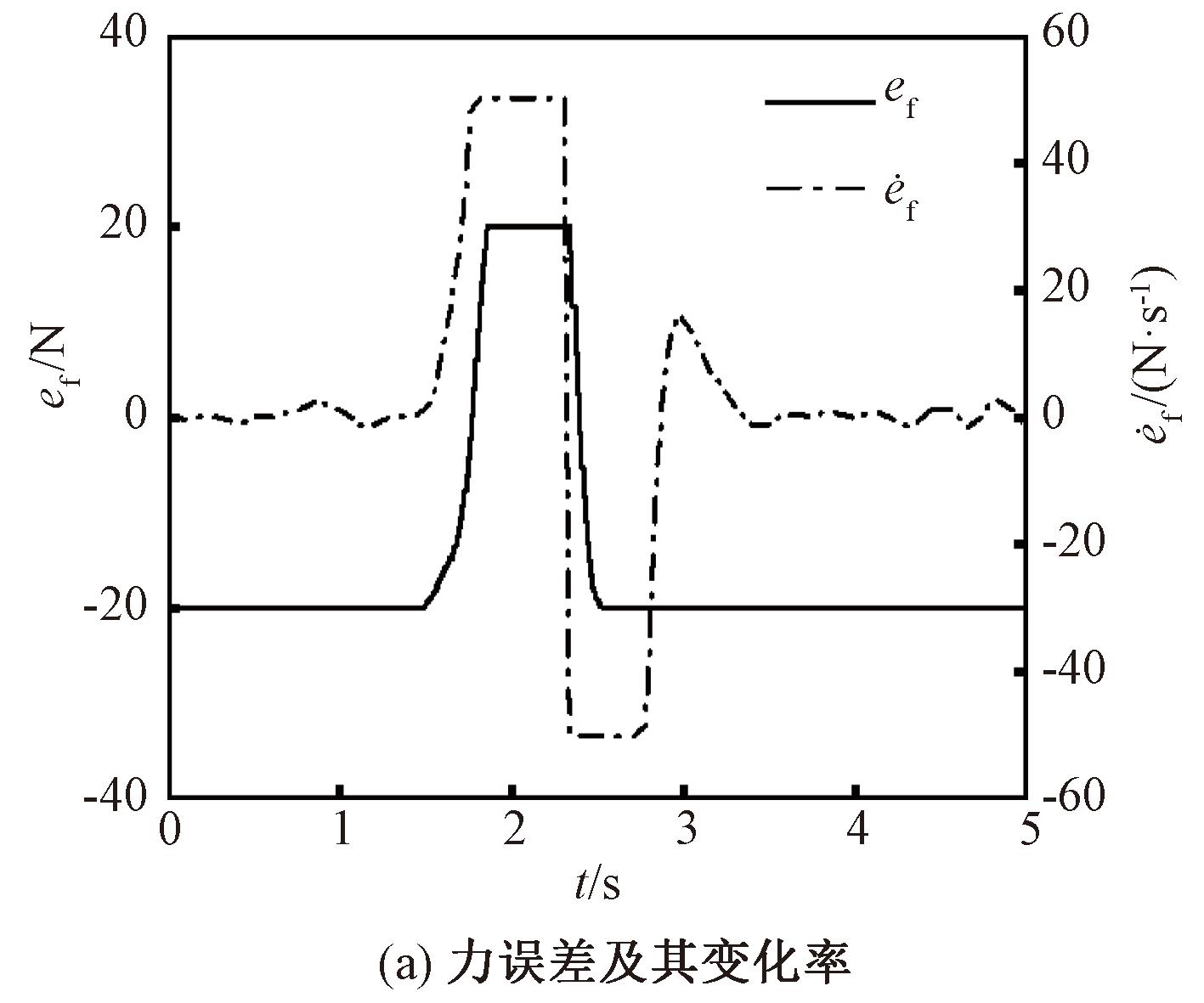
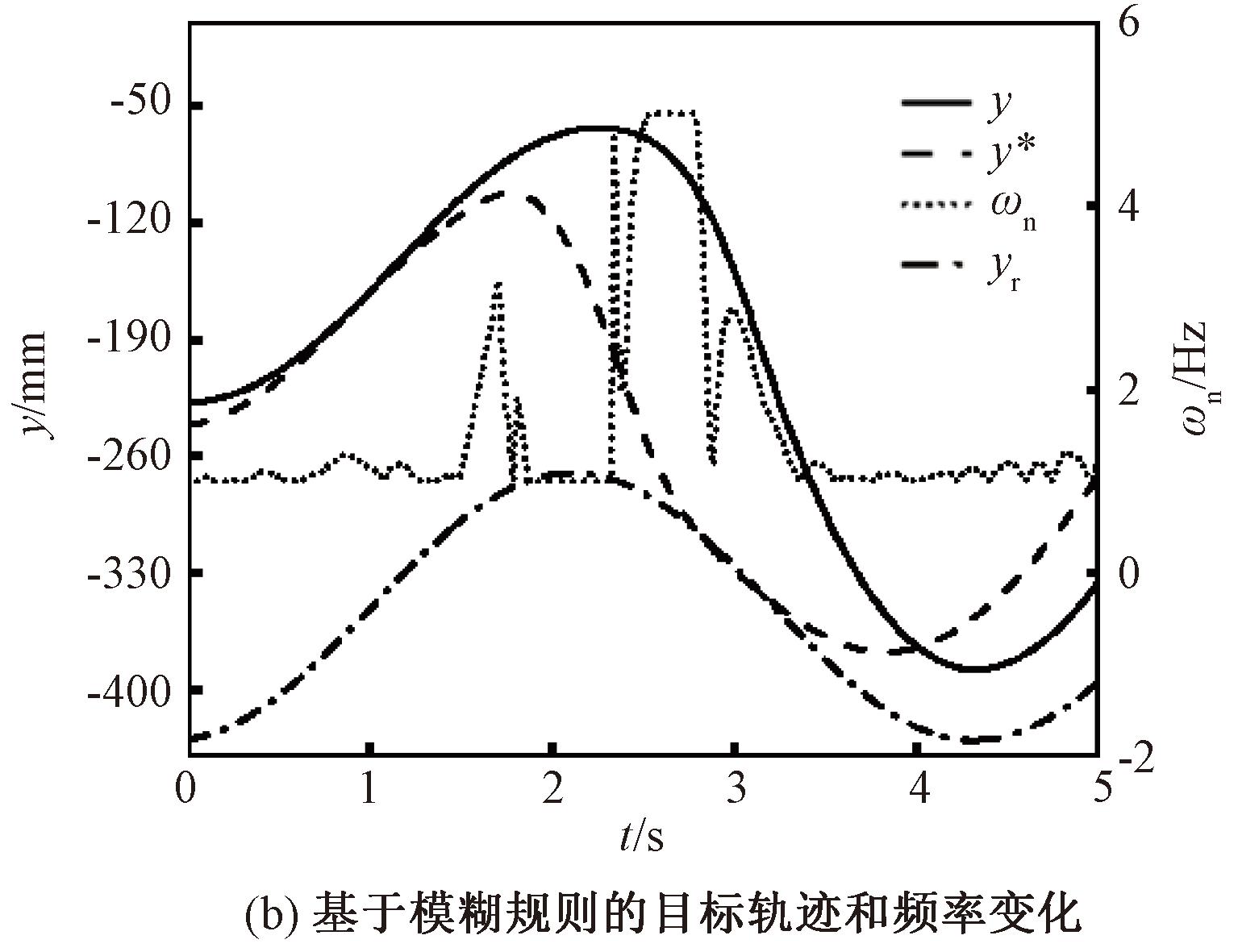
图11 力突变实验结果对比图
Figure 11 Comparison diagram of force abrupt experiment results
从图11(a)中可以看出,在1.5 s处,ef从-20 N开始增大,
突变至50 N/s,ωn也相应增大,对应模糊规则(3),实际康复中患者肌力很强,人机交互系统更新路径以更快追踪至原给定路径。当ef达到0后继续增大,此时仍为50 N/s,ωn开始减小,对应模糊规则(1),在实际康复中交互力快速增大说明此时康复运动位移超出了患者能够承受的范围,患者无法继续伸展患肢,HRI系统以最小刚度保护患者,减小位移幅度。在ef=20 N保持1 s的时间内,
N/s,此时人机交互系统以最大的柔顺性保护患者,ωn仍为最小值,y*曲线向下偏移量增大。在2.5 s处,康复轨迹回到患者能够承受的范围,ef从20 N开始减小,
N/s,ωn突变至最大值,对应模糊规则(4),康复运动位移回到患者能够承受的范围,y*曲线偏移量减小。当ef达到0后继续减小,此时仍为-50 N/s,ωn突变至0后增至较大值,对应模糊规则(2),患者对机器人系统施加力减弱,机器人系统带动患者继续运动,防止突然停止对患者造成伤害。图11(b)还展示了相较于固定参数的导纳模型,变导纳模型位移曲线从峰值下降时间提前0.5 s,说明机器人系统在检测到人机交互力突变时能够识别出患者此时无法跟随机器人系统继续运动,康复运动位移超出了患者承受能力范围,机器人系统追踪的新路径在未达到给定的路径峰值时提前沿力方向返回,防止患者患肢拉伤。从实验结果来看,变导纳模型在训练过程中遇到患者不足以跟随康复运动而产生力突变情况下能够更好地保护患者,更具安全性。
4 结论
针对上肢康复机器人面对不同患者无法调整柔顺性的问题,结合实际康复运动情况,分析了康复过程中患者对康复强度的实际需求,基于模糊控制提出了一种更完备的变导纳控制策略,主要包含以下结论。
(1)提出了一种以人机交互力误差及其变化率作为模糊控制输入量,以自然频率作为控制量,利用模糊控制实时调节导纳参数的控制策略。
(2)所提出控制策略能够通过人机交互力及其变化率改变控制的柔顺性,进而提升康复的安全性和效率,这种动态调整的过程类似于医生主导的人工康复。
(3)仿真与实验结果表明,在患者可适应训练强度的场景中,相较于固定导纳模型,变导纳模型追踪给定路径时产生的冗余路径最多可降低56.13%,提高了康复训练效率;当康复运动轨迹超出患者可承受范围时,变导纳模型可提前0.5 s改变追踪路径,增强了康复过程中的安全性。
未来工作将在本研究的基础上开展实际康复临床实验,完善机器人辅助康复效果评价体系,对临床实验结果进行分析,发现问题并进一步提升康复机器人控制性能。
[1] HARA Y. Brain plasticity and rehabilitation in stroke patients[J].Journal of Nippon Medical School, 2015, 82(1)： 4-13.
[2] ZUO S P, LI J F, DONG M J, et al. Optimum design and preliminary experiments of a novel parallel end traction apparatus for upper-limb rehabilitation[J].Frontiers of Mechanical Engineering, 2021, 16(4)： 726-746.
[3] AGGOGERI F, MIKOLAJCZYK T, O′KANE J. Robotics for rehabilitation of hand movement in stroke survivors[J].Advances in Mechanical Engineering, 2019, 11(4)： 1-14.
[4] TURNER D L, TANG X J, WINTERBOTHAM W, et al. Recovery of submaximal upper limb force production is correlated with better arm position control and motor impairment early after a stroke[J].Clinical Neurophysiology, 2012, 123(1)： 183-192.
[5] WANG S S, LIAO J, YONG Z R, et al. Inertial sensor-based upper limb rehabilitation auxiliary equipment and upper limb functional rehabilitation evaluation[C]∥CCF Conference on Computer Supported Cooperative Work and Social Computing. Cham： Springer, 2022： 518-528.
[6] CALANCA A, MURADORE R, FIORINI P. A review of algorithms for compliant control of stiff and fixed-comp-liance robots[J].IEEE/ASME Transactions on Mechatronics, 2016, 21(2)： 613-624.
[7] HOGAN N. Impedance control： an approach to manipulation[J].Journal of Dynamic Systems, Measurement, and Control,1985,107：1-7.
[8] BAI J, SONG A G, WANG T, et al. A novel backstepping adaptive impedance control for an upper limb rehabilitation robot[J].Computers &Electrical Engineering, 2019, 80： 1-13.
[9] SADO F, SIDEK S N, YUSOF H M. Adaptive hybrid impedance control for a 3DOF upper limb rehabilitation robot using hybrid automata[C]∥2014 IEEE Conference on Biomedical Engineering and Sciences (IECBES). Piscataway： IEEE, 2014： 596-601.
[10] RAGHAVAN P. Upper limb motor impairment after stroke[J].Physical Medicine and Rehabilitation Clinics of North America, 2015, 26(4)： 599-610.
[11] 吴青聪, 王兴松, 吴洪涛, 等. 上肢康复外骨骼机器人的模糊滑模导纳控制[J].机器人, 2018, 40(4)： 457-465.
WU Q C, WANG X S, WU H T, et al. Fuzzy sliding mode admittance control of the upper limb rehabilitation exoskeleton robot[J].Robot, 2018, 40(4)： 457-465.
[12] AGUIRRE-OLLINGER G, COLGATE J E, PESHKIN M A, et al. Active-impedance control of a lower-limb assistive exoskeleton[C]∥2007 IEEE 10th International Conference on Rehabilitation Robotics. Piscataway： IEEE, 2007： 188-195.
[13] 乐宇倚, 郭帅. 基于变导纳控制的上肢康复机器人柔顺控制方法研究[J].工业控制计算机, 2021, 34(10)： 9-11, 14.
LE Y Y, GUO S. Research on compliance control method of upper-limb rehabilitation robot based on variable admittance control[J].Industrial Control Computer, 2021, 34(10)： 9-11, 14.
[14] 梁旭, 王卫群, 苏婷婷, 等. 下肢康复机器人的主动柔顺自适应交互控制[J].机器人, 2021, 43(5)： 547-556.
LIANG X, WANG W Q, SU T T, et al. Active compliant and adaptive interaction control for a lower limb rehabilitation robot[J].Robot, 2021, 43(5)： 547-556.
[15] LI X M, YANG Q Q, SONG R. Performance-based hybrid control of a cable-driven upper-limb rehabilitation robot[J].IEEE Transactions on Biomedical Engineering, 2021, 68(4)： 1351-1359.
[16] 高建设, 王玉闯, 刘德平, 等. 新型四足步行机器人串并混联腿的轨迹规划与仿真研究[J].郑州大学学报(工学版), 2018, 39(2)： 23-27, 38.
GAO J S, WANG Y C, LIU D P, et al. Research on trajectory planning and simulation on the serial-parallel leg of a novel quadruped walking robot[J].Journal of Zhengzhou University (Engineering Science), 2018, 39(2)： 23-27, 38.
[17] 李朋阳, 高建设, 顾昌利. 一种串并混联的上肢康复机器人轨迹规划研究[J].机械设计与制造, 2022(6)： 265-269, 273.
LI P Y, GAO J S, GU C L. Research on the trajectory planning of a series-parallel upper limb rehabilitation robot[J].Machinery Design &Manufacture, 2022(6)： 265-269, 273.
[18] SERAJI H, COLBAUGH R. Force tracking in impedance control[J].International Journal of Robotics Research, 1997, 16(1)： 97-117.
[19] 檀盼龙, 李益敏, 赵相宾, 等. 线性扩张状态观测滤波器的分析与应用[J].郑州大学学报(工学版), 2019, 40(2)： 41-47.
TAN P L, LI Y M, ZHAO X B, et al. Analysis and application of linear extended state observer filter[J].Journal of Zhengzhou University (Engineering Science), 2019, 40(2)： 41-47.
[20] 赵相瑜, 缪志农. 模糊自适应控制中的参数调节[J].中国测试技术, 2004, 30(4)： 24-26.
ZHAO X Y, MIAO Z L. Parameters adjusting of adaptive fuzzy control[J].China Measurement Technology, 2004, 30(4)： 24-26.
[21] BOSECKER C, DIPIETRO L, VOLPE B, et al. Kinematic robot-based evaluation scales and clinical counterparts to measure upper limb motor performance in patients with chronic stroke[J].Neurorehabilitation and Neural Repair, 2010, 24(1)： 62-69.
[22] 胡寿松. 自动控制原理[M].6版. 北京： 科学出版社, 2013： 71-88.
HU S S. Principle of automatic control[M].6th ed. Beijing： Science Press, 2013： 71-88.
[23] SUZUKI K, MIZUSHIMA S. Rehabilitation technology[M].New York： Elsevier, 1987： 432-694.
[24] LIU C G, HE Y, CHEN X A, et al. Discontinuous force-based robot adaptive switching update rate impedance control[C]∥2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC). Piscataway： IEEE, 2021： 2573-2580.