近年来,随着储能技术、电转热技术的逐渐成熟,出现了能源互联网、多能源系统(multi-energy system,MES)的理念。MES建模作为MES运行的基础显得尤为重要,其中能够转换、调节和存储多个能源载体的能量枢纽(energy hub,EH)成为MES建模的关键单元[1-6]。含热电联供(combined heat and power,CHP)的EH可以将配电网(power distribution network,PDN)和区域供热网(district heating network,DHN)耦合,从而解决热能易储存、不易运输以及电能易运输、不易储存的问题[3-6]。
虽然已有学者探讨了基于EH模型的MES的优化规划[1-2]、优化运行[3-4]以及碳排放[5-6]等问题,但针对MES标准化建模的研究很少。常雨芳等[7]根据建立的含风力发电的冷热电联供系统,利用能量的耦合关系将EH设定成以矩阵建模为基础的运行方式,但这种建模方式只适用于结构简单的EH。Wang等[8]提出了一种自动计算EH标准化矩阵建模的方法,利用图论将EH设备特性转化为矩阵形式,进而建立不考虑调度因子的能量流线性方程组进行调度。Wang等[9]提出了用于制定EH中能量转换的自动线性化建模方法,并基于EH的耦合矩阵及其秩分析了EH的灵活性。以上研究将EH设备能量效率视为常数,或简化MES的输入和输出为线性关系,而实际工程中设备的运行效率会随运行条件发生变化。
有一些学者考虑了设备能量效率变化对MES的影响。陈晚晴等[10]将EH设备效率和负载率数据拟合为效率修正模型,反映设备负载率对效率的影响,基于修正模型建立以经济性为目标的MES优化调度模型。李虹等[11]基于MES中EH常用设备效率与负载率之间的函数关系构建EH矩阵模型,从而对MES优化配置进行研究。Huang等[12]提出了基于可变能量效率的EH标准化矩阵建模方法以研究MES的运行优化。Zheng等[13]建立了设备恒定能量效率和设备能量效率变化的2种EH模型,通过比较两者的运行成本及相对误差,证明了设备能量效率变化特性对EH优化运行的影响不能忽略。Chen等[14]为了研究EH设备的能效优化有效性,提出了一种由考虑设备能量效率变化特性的EH、天然气网络和PDN构成的MES调度方法。但以上研究均未考虑可变EH能效模型与电热网相耦合的网络约束。
为研究可变能量效率特性对电热网运行的影响,本文将PDN和DHN与考虑设备能量效率随输入或输出功率变化的EH相结合,建立了电热网优化运行线性模型。首先,对EH设备可变能量效率进行了分段线性化,建立了含CHP、储热设备及电热泵的EH标准化矩阵模型;其次,将所建立的矩阵模型应用到电热网中,使得EH在电热网中发挥节能消纳、提供电能和热能的作用,构建了含EH的电热网优化运行模型;最后,通过算例验证了本文模型的有效性。
1 EH结构及可变能量效率分段线性化
1.1 EH结构及描述
本文所研究的EH结构如图1所示,新能源输入为风电;能量转换设备为背压运行模式的CHP和电热泵;在CHP侧配置储热设备实现热电解耦。根据图论将能量设备定义为节点,EH的输入输出被视为特殊的节点,每个节点的输入输出定义为端口,能量流用分支v表示。定义风电输入为节点1;电能输入为节点2;天然气输入为节点3;CHP为节点4;储热设备为节点5;电热泵为节点6;电输出为节点7;热输出为节点8。
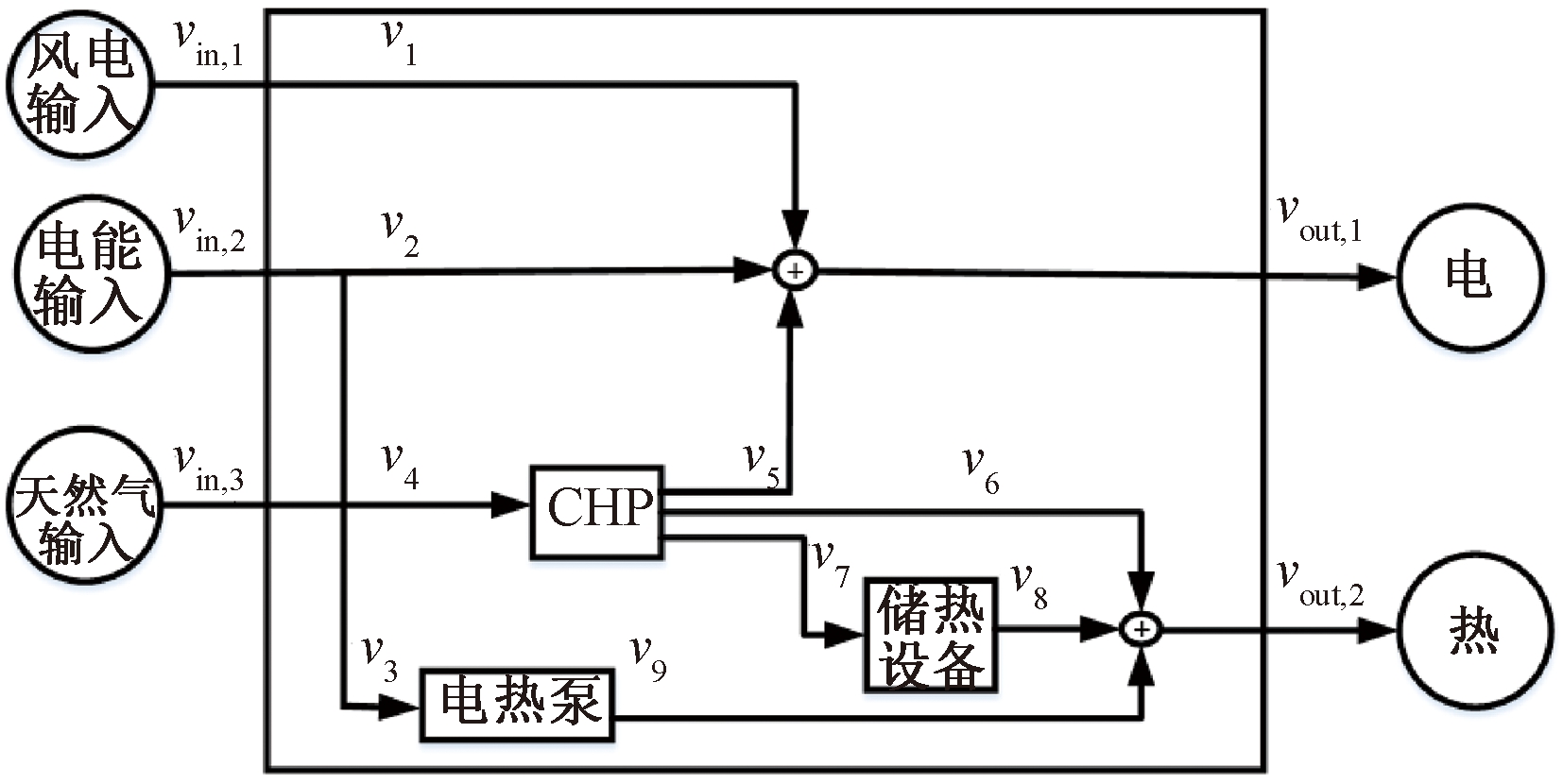
图1 EH结构示意图
Figure 1 EH structure diagram
通过图论将设备特性转换为矩阵形式,此EH的输入向量Vin和输出向量Vout[8]分别为
(1)
(2)
1.2 可变能量效率分段线性化
为了处理可变能量效率带来的非线性问题,对EH中设备的可变能量效率进行分段线性化,将一个非线性能量转换和储存过程等效为多个并行的线性转换过程[12]。以单输入单输出设备为例,假设有单个输入功率
和单个输出功率
的节点g,其能量转换效率ηg是输入功率的函数,则有
(3)
将分为s段,也可以和一样分成s段。
(4)
(5)
式中:
和
分别为每段的输入功率和输出功率;k=1,2,…,s。
用
表示
的范围,则在第k段中,能量转换效率
(变效率)可用恒定效率ηg,k代替:
(6)
式中:
和
分别表示第k段输入功率和输出功率的范围。
引入二进制数据Ug=[ug,1 ug,2 … ug,s-1]保证和的连续性。令
为所有分段的输入功率集合;
为所有分段的输入功率范围的集合,则有
(7)
(8)
(9)
将储能设备节点g看作单输入单输出设备,输入端口建模储能,输出端口建模放能,
和
分别表示储能设备的储能功率和放能功率,该设备的荷能状态变化率ΔEg[12]为
(10)
式中:
和
表示储能设备的储能和放能效率。
分段线性化后的ΔEg表示为
(11)
式中:
和
分别为第k段中储能设备的恒定储能效率和放能效率;
和
分别为每个分段中的储能功率和放能功率;k=1,2,…,s。
储能荷能状态约束[8]为
Eg(t)=Eg(t-1)+ΔEg(t);
(12)
(13)
(14)
进一步引入分线器和集线器,促进分段线性化以后能量流的分离和合并,保证线性化前后结果一致[12]。分段线性化过程相当于将非线性能量设备转换为分线器、线性能量设备、集线器3层结构。
若单输入多输出设备每个输出端口的能量输出与能量输入成比例(如本文所采用的CHP),则以类似于单输入单输出设备的方式分别分段线性化从输入端口到每个输出端口之间的能量转换过程。
2 EH标准化矩阵模型建立
与全负荷工况相比,部分负荷工况下的CHP电效率至少可降低20%,热效率升高不超过10%;储热设备的储放热效率分别随储放热功率变化[15],所以可将CHP和储热设备看作非线性设备[12],它们的能量效率是变化的。电热泵的能量效率在部分负荷工况下没有显著差异,因此可假设电热泵是线性设备,它的能量效率是恒定的。图2为对CHP和储热设备分段线性化(以两段为例)后的EH,EH中的原始分支称为一级分支,从一级分支分裂出来的分支称为二级分支,所有二级分支的能量流构成一个向量V′,基于此建立EH标准化矩阵模型。总分支向量
表示为
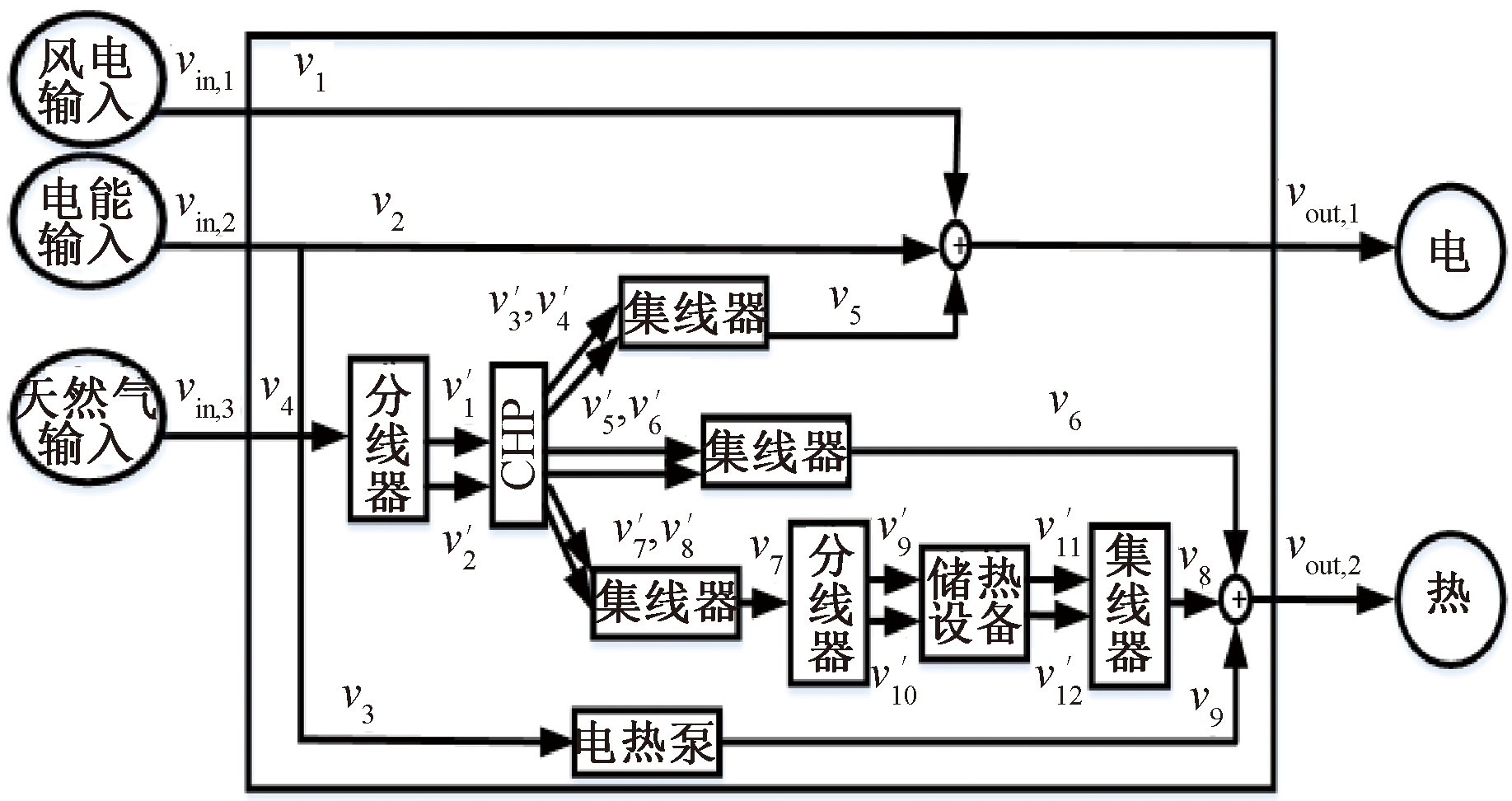
图2 分段线性化后的EH
Figure 2 EH after piecewise linearization
(15)
2.1 建立输入和输出关联矩阵
(16)
(17)
(18)
(19)
(20)
(21)
式中:Vin和Vour分别表示图2中EH的输入向量和输出向量。输入关联矩阵
的行数是EH输入端口的个数,列数是的列数;输出关联矩阵
的行数是EH输出端口的个数,列数是的列数。而矩阵X和Y中的元素值由式(17)和式(19)确定。由此可以得到图2中EH的输入关联矩阵和输出关联矩阵。
2.2 建立端口分支关联矩阵
若节点g表示非线性设备,则端口分支关联矩阵
为
(22)
节点5扩充端口分支关联矩阵为
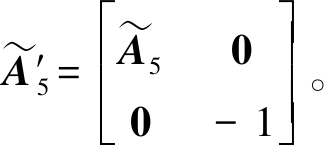
(23)
若节点g表示线性设备,则
(24)
Ag(k,b2)=
(25)
其中,行数是端口的个数,列数是分支的个数,矩阵中的元素值由式(22)或式(25)确定。由此可以得到图2 中EH各节点的端口分支关联矩阵。
2.3 建立设备特性矩阵
对于单个输入n个输出的非线性转换器,从输入端口到每个输出端口的能量转换过程分别分段线性化,将单个输入n个输出非线性转换器转换为s个输入ns个输出转换器,若每个输出端口的能量输出与能量输入成比例,则转换器特性矩阵
为
(26)
如图2中的CHP将1个输入3个输出各分成了两段,分别以η1,1、η1,2这2个恒定效率表示电效率,η2,1、η2,2、η3,1、η3,2这4个恒定效率表示热效率,η1,s×s=diag(η1,1,η1,2,…,η1,s),可建立节点4的特性矩阵。同理建立节点5特性矩阵为
(27)
线性设备的特性矩阵为
(28)
其中,Hg行数是能量转换过程的个数,列数是端口的个数,矩阵中的元素值由式(28)确定。由此可以得到图2中EH节点6的特性矩阵。
2.4 建立能量平衡矩阵
节点g的节点能量平衡矩阵
为
(29)
2.5 建立分线器或集线器特性矩阵
节点g表示的非线性设备的分线器或集线器特性矩阵
为
(30)
(31)
(32)
式中:
中的元素为Ag中元素的绝对值;
表示与节点g相关的一级分支中的能量流。可建立节点4和节点5的分线器或集线器特性矩阵。
2.6 EH的综合能量流方程
EH的综合能量流方程可作为能量流约束:
(33)
同时还应满足设备的容量约束:
(34)
式中:t为时间;
为第g个设备端口的能量流;
为第g个设备的最大容量[8]。
3 基于EH的电热网优化运行模型
电热网通常通过含CHP的EH紧密耦合,因此本文采用水力-热力模型描述DHN潮流分布,采用DistFlow描述PDN潮流模型[16]。
3.1 DHN模型
DHN一般由热源、热负荷、供回水网组成。对DHN进行水力分析,水力分析用于描述各管道水质量流量及各节点的注入水流的水质量流量[16-18]:
(35)
(36)
(37)
式中:
分别为节点i热源、热负荷的水质量流量;
分别为管道b供回水网的水质量流量;F(i)、T(i)分别表示节点i为首节点与末节点的管道集。
热力分布描述管道和节点的温度与水质量流量的关系,其热力分布可建模[17-18]为
(38)
(39)
(40)
(41)
(42)
(43)
式中:cw为载热工质(水)的比热容;
分别为供回水管网出口、入口温度;λb为管道b的温度损耗系数;Lb为管道b的长度[16]。
DHN中热负荷与热源的热功率满足:
(44)
(45)
(46)
式中:
分别为CHP和电热泵的输出功率;
分别为储热设备的储热功率和放热功率;
为热负荷的热功率需求;
分别为供回水节点i的温度最大和最小值。DHN存在2种调节方式:恒定质量流量变温度、变质量流量变温度。实际工程中通常采用恒定质量流量变温度的运行方式,使整个DHN模型变成线性化模型[17]。
3.2 PDN模型
PDN一般为辐射式结构,可采用如下线性DistFlow潮流模型对潮流分布进行描述[19]。
(47)
(48)
Uj,t=Ui,t-(rijPij,t+xijQij,t)/U0;
(49)
(50)
式中:Pij,t、Qij,t分别为线路上传输的有功和无功功率;
分别为节点j处风电机组和CHP发出的有功功率;
分别为节点j的有功和无功功率需求;π(j)为节点j的子节点集合;rij、xij分别为线路的电阻、电抗;Uj,t为节点电压幅值Vj,t的平方;Vsl为平衡节点的电压幅值;上标u和l分别代表上下界[16,20]。
3.3 优化运行目标及约束
本文以天然气价格与分时电价为基准,以全天系统购能总成本最少为目标函数,求解含EH的电热网优化运行问题。目标函数为
(51)
式中:Cgas为天然气价格;
为分时电价;FCHP,t、FHP,t、Fgrid,t分别为CHP在t时段的购气量、电热泵和PDN在t时段从上级电网购买的电量。式(7)～(9)表示分段线性化;式(12)～(14)表示储热设备荷热状态约束;式(33)～(34)表示EH能量流和设备容量约束;式(35)～(50)表示电热网运行约束。
4 算例分析
4.1 算例数据
本文将含EH的电热网优化运行问题转换为混合整数线性规划问题,使用MATLAB中YALMIP建模、CPLEX求解器求解[21]。算例测试系统如图3所示,为了维持PDN中各母线的电压质量,在PDN中配置无功补偿装置[17,22]。PDN各母线功率比由MATPOWER33节点PDN标准潮流求得。DHN各节点的热负荷比和质量流量、电负荷、热负荷、风电预测数据等参考文献[17]。本算例根据文献[8]建立节点表和分支表用于EH的标准化输入,设定天然气价格为1.54 元/m3,分时电价如表1所示,EH设备参数如表2所示,其中储热设备的最大储热功率和放热功率均为1 600 kW。
表1 分时电价
Table 1 Time of use tariff
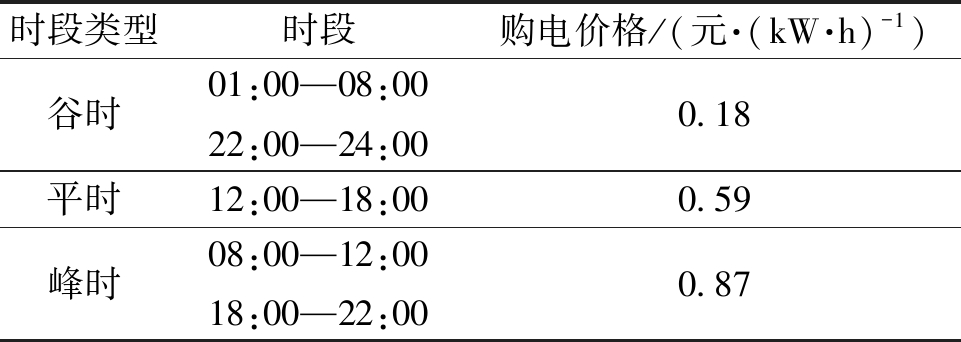
时段类型时段购电价格/(元·(kW·h)-1)谷时01:00—08:0022:00—24:000.18平时12:00—18:000.59峰时08:00—12:0018:00—22:000.87
表2 EH设备参数
Table 2 EH equipment parameters
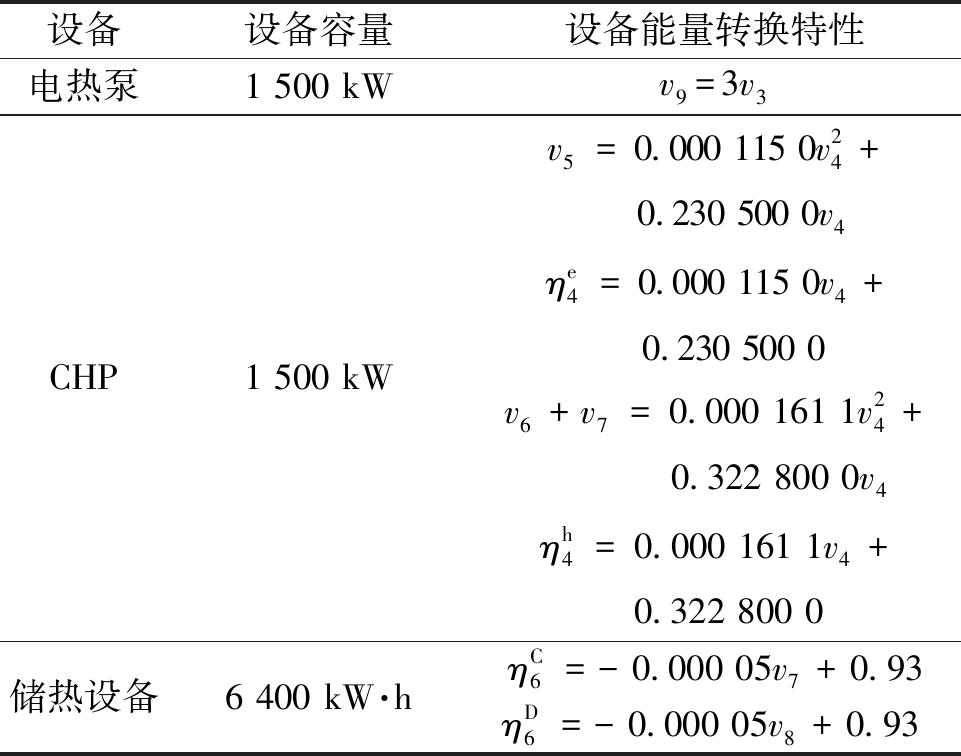
设备设备容量设备能量转换特性电热泵1 500 kWv9=3v3CHP1 500 kWv5=0.000 115 0v24+0.230 500 0v4ηe4=0.000 115 0v4+0.230 500 0v6+v7=0.000 161 1v24+0.322 800 0v4ηh4=0.000 161 1v4+0.322 800 0储热设备6 400 kW·hηC6=-0.000 05v7+0.93ηD6=-0.000 05v8+0.93
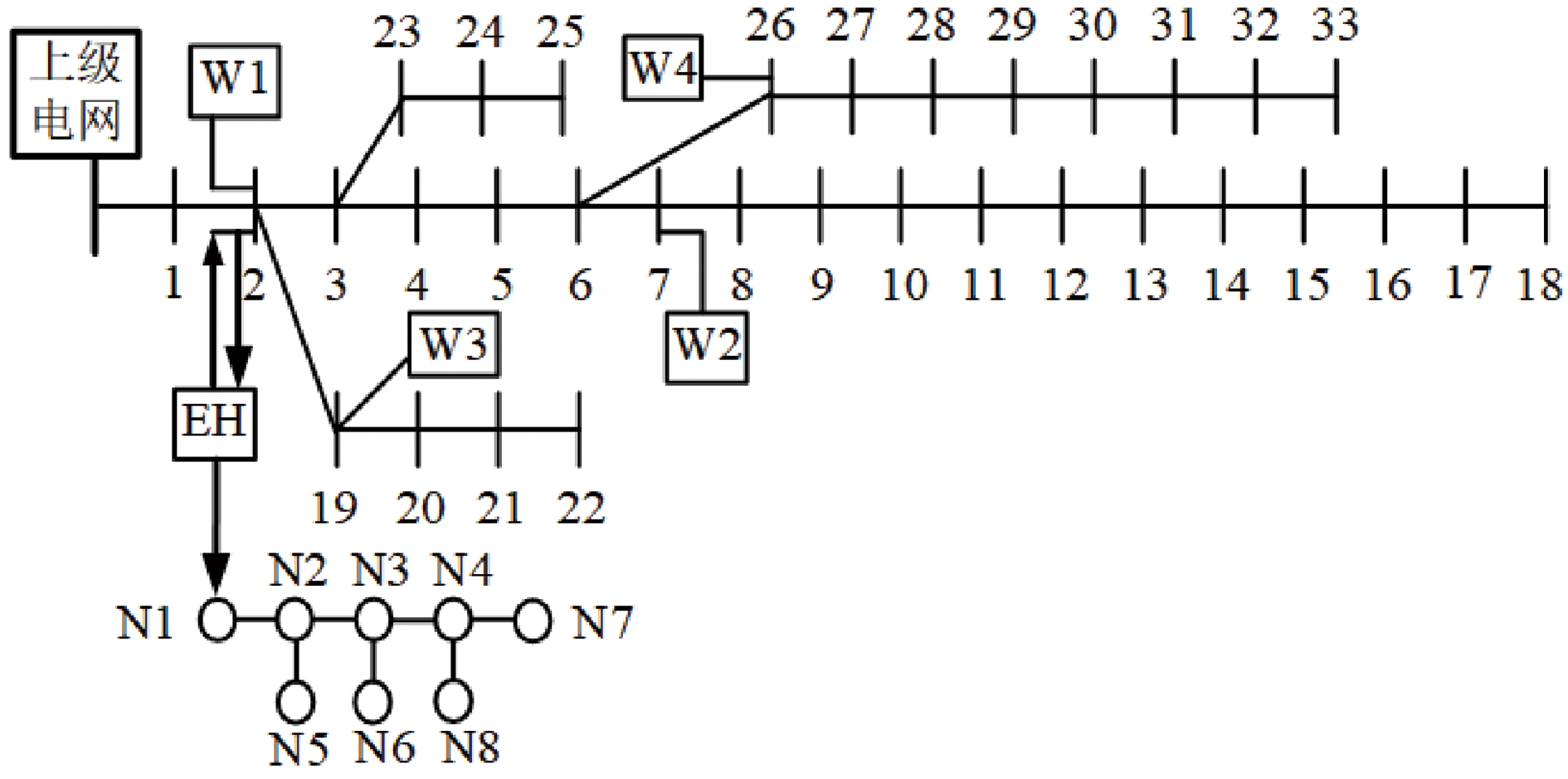
图3 测试系统图
Figure 3 Test system diagram
4.2 结果分析
如图4所示,当分段数从2增加到50时,预测的成本迅速增加,同时求解时间略微增加;当分段数从50到100时,运行成本逐渐趋于稳定,但求解时间大幅增加。由于分段数越大,优化结果就越接近实际运行成本,因此,本文以分段数为100的运行成本为参考值计算各个分段数的相对误差。考虑到预测成本的准确性与程序求解的效率,最终选取分段数为50的EH对考虑设备可变能量效率后的电热网情况进行分析,与考虑设备恒定能量效率情况(分段数为0)相比,运行成本相对误差从12.71%(分段数为0)降到了0.03%(分段数为50)。
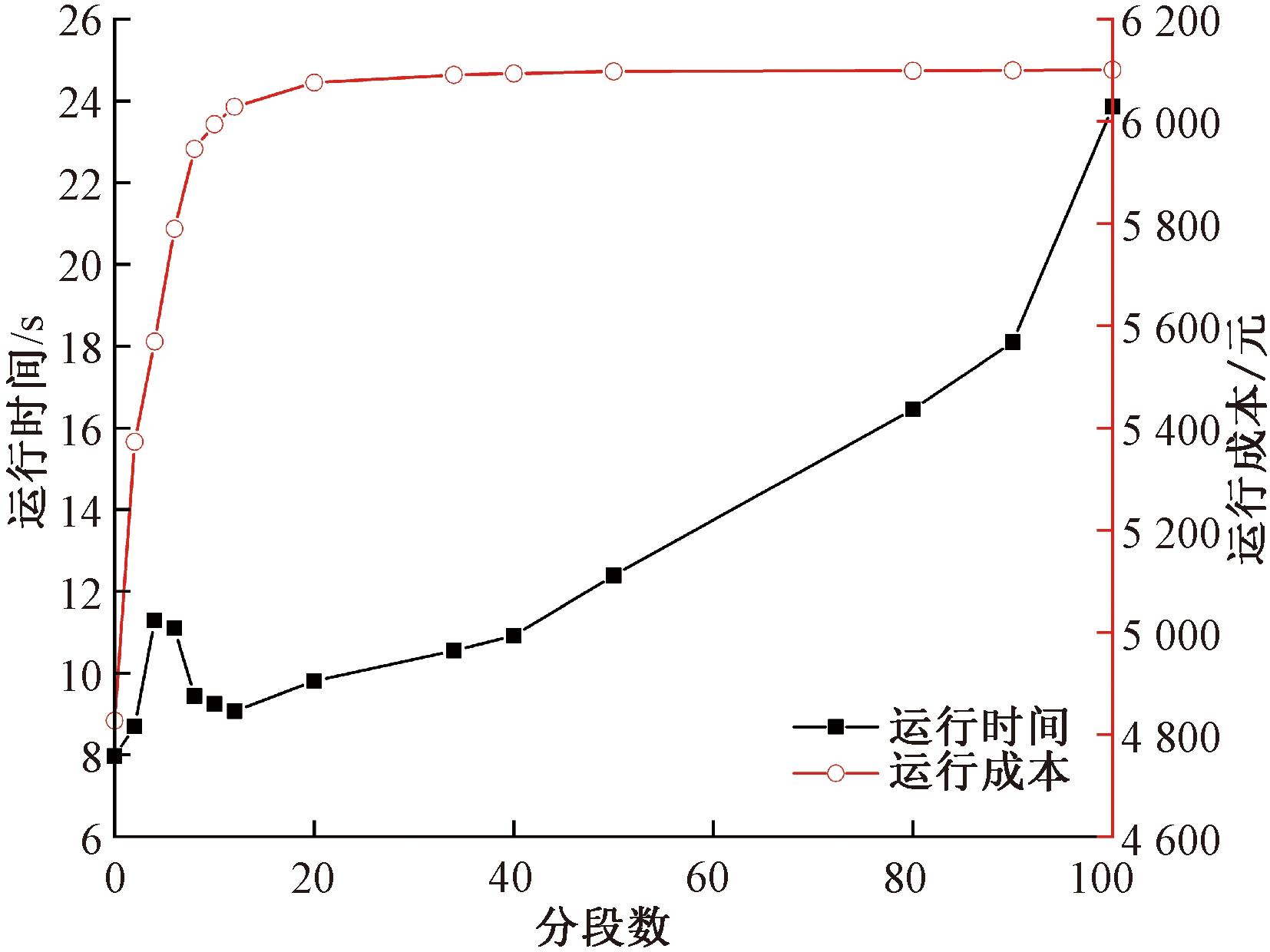
图4 不同分段数的运行成本和运行时间图
Figure 4 Operation cost and operation time chart of different segments
EH的分段数为50时PDN节点电压如图5所示,DHN管道温度如图6所示。电价峰时(11:00)和谷时(05:00)都能维持在额定电压幅值1.00的±5%以内。通过调节回水温度能满足热负荷峰值(05:00)和非峰值(15:00)的热功率需求。在供水温度相同的条件下,回水温度越小,供热量越大,表明分段数为50的EH能保证电热网的正常运行。
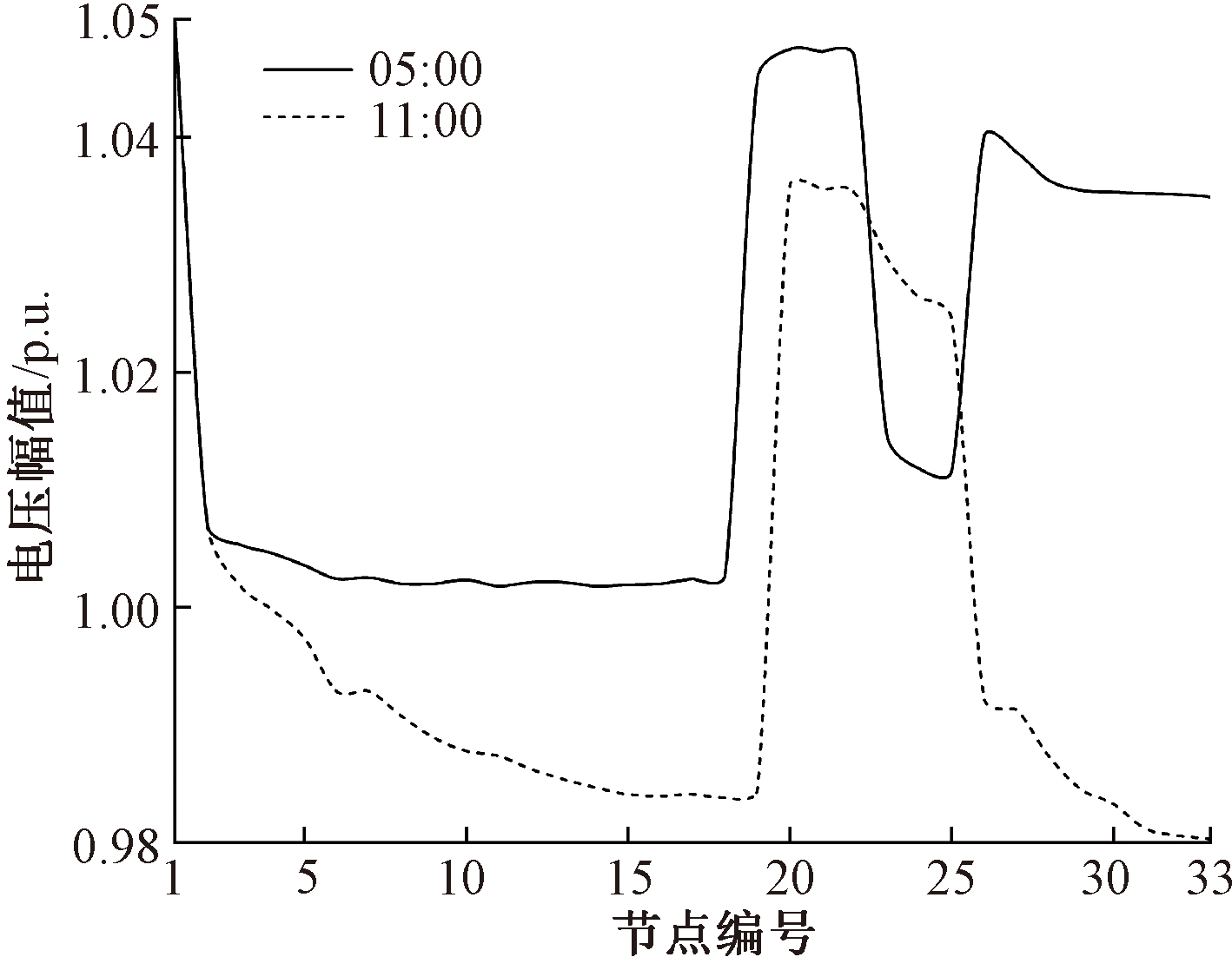
图5 PDN节点电压
Figure 5 Node voltage of PDN
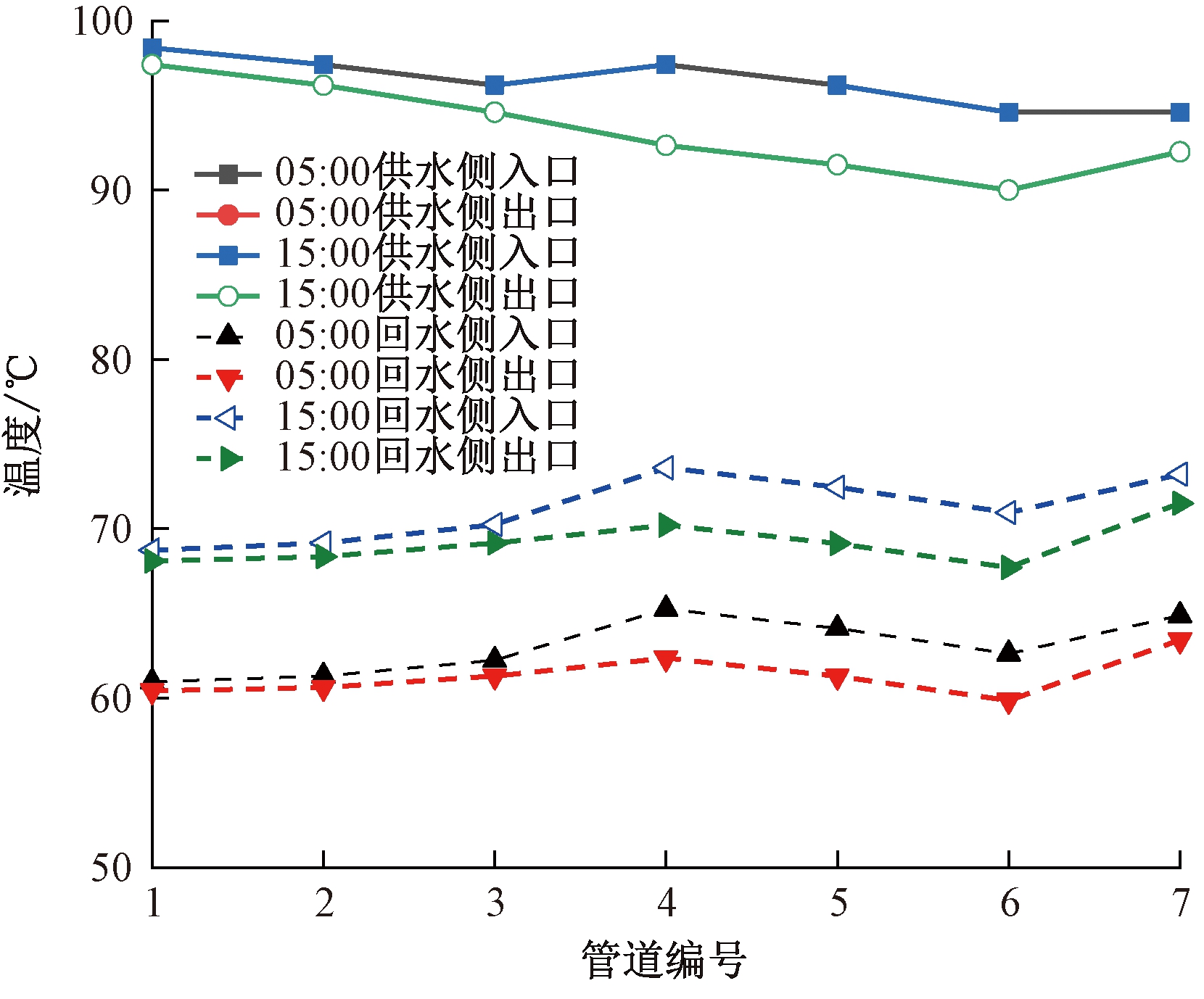
图6 DHN的管道温度
Figure 6 Pipe temperature of DHN
为了突出本文可变能量效率模型的优势,将恒定效率方案1(分段数为0)与变效率方案2(分段数为50)进行对比,恒定效率视为额定效率。两种方案下的热功率平衡如图7所示。在01:00—06:00、23:00—24:00时电价较低,方案1中CHP和电热泵一起供应热负荷,不考虑实际工程中CHP实际运行效率低于额定效率,达不到预期效果的情况;而方案2从电网购电供给电热泵产生热量作为主要供热设备,CHP不出力。在08:00—22:00时,电价较高,方案2电热泵出力减少,进而降低了购电成本;CHP以更高的热功率供给热负荷,并将一部分热储存到储热设备中。储热设备在13:00—16:00时以相较方案1更低的功率放热进行热负荷供给,减少了热功率损耗,预测情况更接近实际情况。
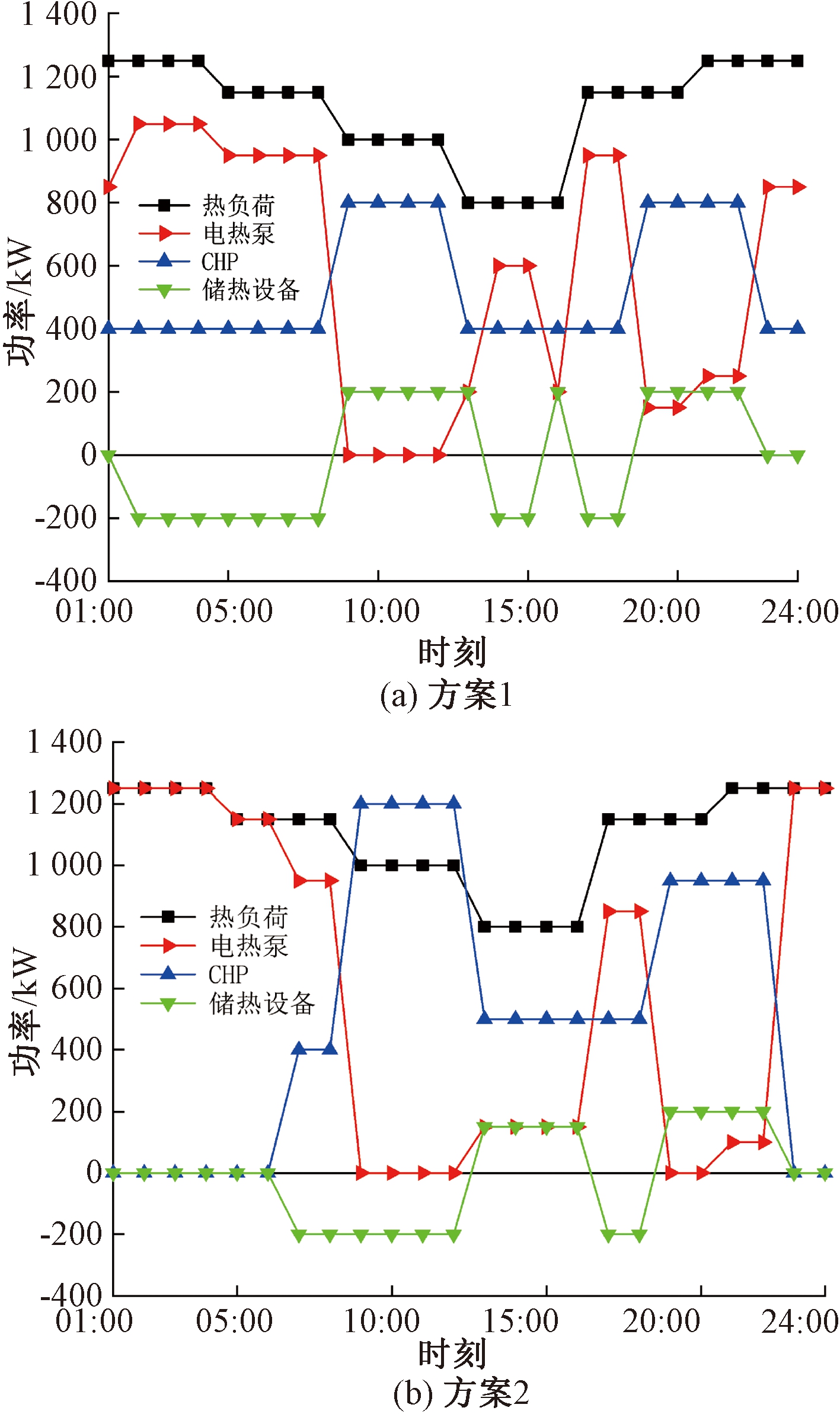
图7 热功率平衡图
Figure 7 Thermal power balance diagram
两种方案下的电功率平衡如图8所示,风电利用如图9所示。在01:00—06:00、23:00—24:00时,电价较低,风电发电功率较大,方案1中CHP设备以额定效率运行供应一部分电负荷,浪费了部分风电,并且实际工程中CHP实际运行效率会低于额定效率,不能达到预期效果;而方案2中CHP不出力,增加了风电上网空间,电负荷完全由电网和风电供应。在08:00—22:00电价较高时风电减小,CHP出力增加,和电网、风电一起供电,预测情况更接近实际情况;方案2考虑CHP和储热设备的可变能量效率相比于方案1减小了风电出力偏差,弃风功率从3 314 kW降低到1 667 kW,风电消纳率增加了4.29%。
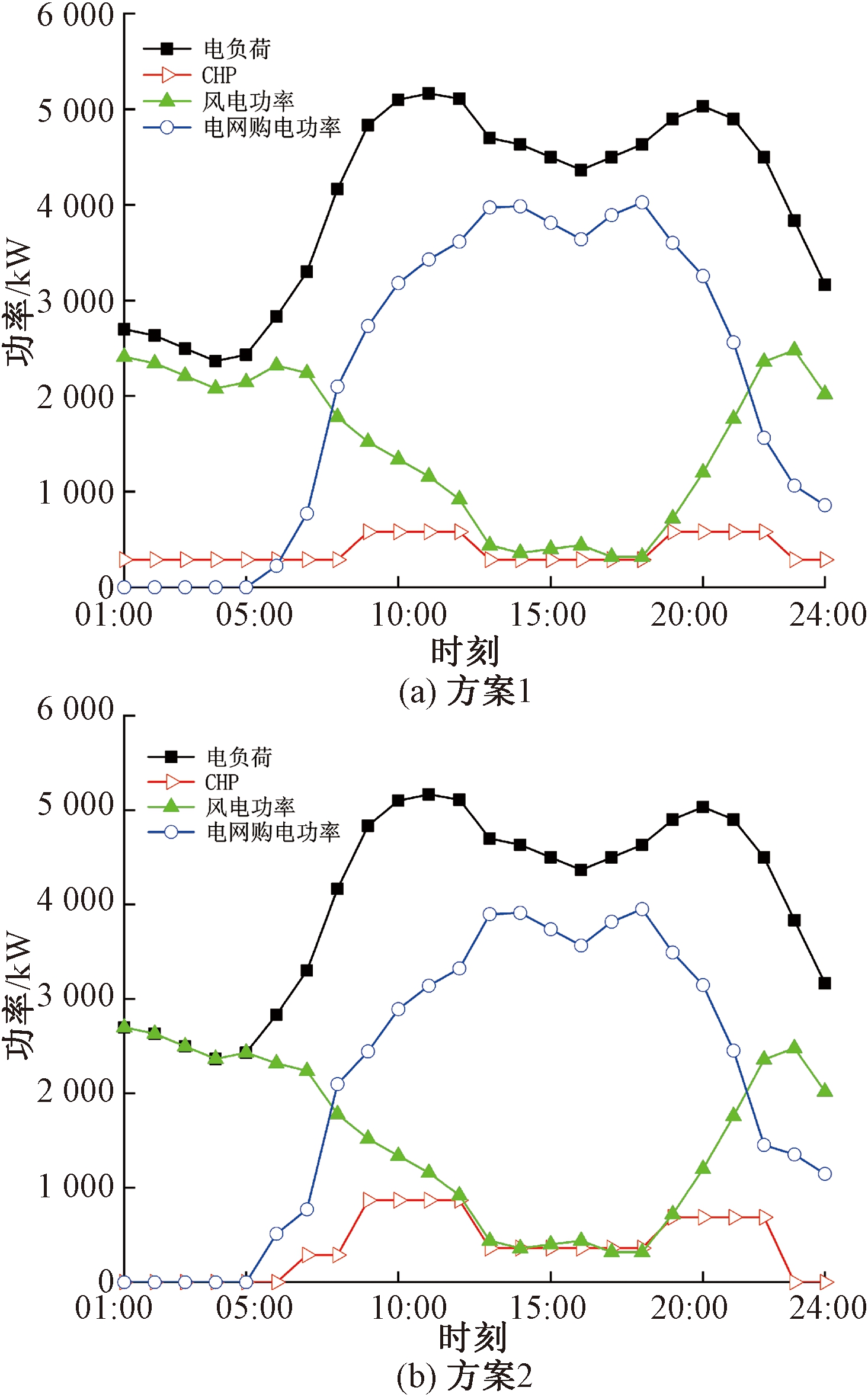
图8 电功率平衡图
Figure 8 Electric power balance diagram
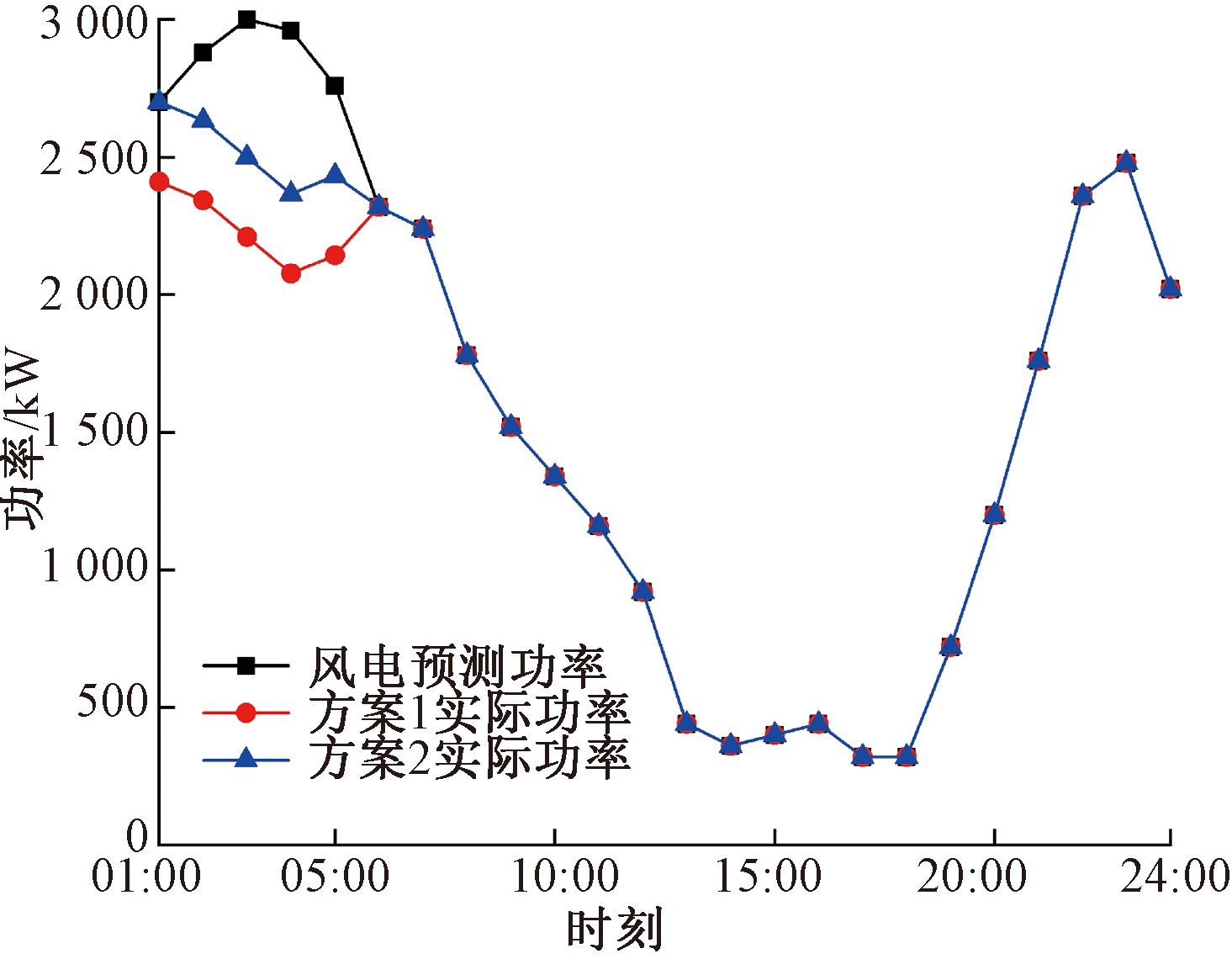
图9 两种方案风电利用图
Figure 9 Wind power utilization diagram of two schemes
5 结论
本文建立的考虑设备可变能量效率的EH能灵活地连接电热网,保证电热网的正常运行。与EH设备恒定能量效率的电热网模型相比,本文建立的考虑EH设备可变能量效率的电热网模型能更准确地描述电热网运行状态,有效提高电热网运行成本预测准确性,减小风电出力偏差。
[1] 曾博, 徐富强, 刘裕, 等. 考虑可再生能源与需求响应协同增效的能量枢纽多目标区间优化规划方法[J]. 中国电机工程学报, 2021, 41(21): 7212-7224.
ZENG B, XU F Q, LIU Y, et al. Multi-objective interval optimization approach for energy hub planning with consideration of renewable energy and demand response synergies[J]. Proceedings of the CSEE, 2021, 41(21): 7212-7224.
[2] 陆信辉, 周开乐, 杨善林. 能源互联网环境下基于分布鲁棒优化的能量枢纽负荷优化调度[J]. 系统工程理论与实践, 2021, 41(11): 2850-2864.
LU X H, ZHOU K L, YANG S L. Optimal load dispatch of energy hub based on distributionally robust optimization approach in energy internet environment[J]. Systems Engineering —Theory &Practice, 2021, 41(11): 2850-2864.
[3] THANG V V, HA T, LI Q H, et al. Stochastic optimization in multi-energy hub system operation considering solar energy resource and demand response[J]. International Journal of Electrical Power &Energy Systems, 2022, 141: 108132.
[4] DINI A, HASSANKASHI A, PIROUZI S, et al. A flexi-ble-reliable operation optimization model of the networked energy hubs with distributed generations, energy storage systems and demand response[J]. Energy, 2022, 239: 121923.
[5] 李政洁, 于强, 龚文杰, 等. 计及模糊机会约束的电-气-热能源枢纽多目标优化调度[J]. 电力系统及其自动化学报, 2021, 33(9): 49-56.
LI Z J, YU Q, GONG W J, et al. Multi-objective optimal scheduling of electricity-gas-heat energy hub consi-dering fuzzy chance constraint[J]. Proceedings of the CSU-EPSA, 2021, 33(9): 49-56.
[6] 熊宇峰, 陈来军, 郑天文, 等. 考虑电热气耦合特性的低碳园区综合能源系统氢储能优化配置[J]. 电力自动化设备, 2021, 41(9): 31-38.
XIONG Y F, CHEN L J, ZHENG T W, et al. Optimal configuration of hydrogen energy storage in low-carbon park integrated energy system considering electricity-heat-gas coupling characteristics[J]. Electric Power Automation Equipment, 2021, 41(9): 31-38.
[7] 常雨芳, 王豪, 谢昊, 等. 采用矩阵建模方式的冷热电联供系统运行优化[J]. 华侨大学学报(自然科学版), 2018, 39(2): 233-239.
CHANG Y F, WANG H, XIE H, et al. Operation optimization of combined cooling heating and power systems using matrix modeling approach[J]. Journal of Huaqiao University (Natural Science), 2018, 39(2): 233-239.
[8] WANG Y, ZHANG N, KANG C Q, et al. Standardized matrix modeling of multiple energy systems[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 257-270.
[9] WANG Y, CHENG J N, ZHANG N, et al. Automatic and linearized modeling of energy hub and its flexibility analysis[J]. Applied Energy, 2018, 211: 705-714.
[10] 陈晚晴, 穆云飞, 贾宏杰, 等. 考虑设备变工况特性的区域综合能源系统优化调度方法[J]. 电网技术, 2021, 45(3): 951-958.
CHEN W Q, MU Y F, JIA H J, et al. Optimal scheduling method of regional comprehensive energy system considering equipment off-design characteristics[J]. Power System Technology, 2021, 45(3): 951-958.
[11] 李虹, 杜世旗. 考虑能源枢纽变工况特性的综合能源系统优化配置[J]. 现代电力, 2022, 39(5): 547-553.
LI H, DU S Q. Optimal configuration of integrated energy system considering variable condition characteristics of energy hub[J]. Modern Electric Power, 2022, 39(5): 547-553.
[12] HUANG W J, ZHANG N, WANG Y, et al. Matrix mode-ling of energy hub with variable energy efficiencies[J]. International Journal of Electrical Power &Energy Systems, 2020, 119: 105876.
[13] ZHENG J H, HUANG J, DENG S, et al. Comparison and error analysis of off-design and design models of energy hubs[J]. CSEE Journal of Power and Energy Systems, 2019, 5(4): 454-465.
[14] CHEN S J, YANG Y B, XU Q S. A coordinated approach of multi-energy system considering the off-design characteristics of the devices in energy hub[J]. International Transactions on Electrical Energy Systems, 2021, 31(11): 1-24.
[15] 陈磊, 徐飞, 王晓, 等. 储热提升风电消纳能力的实施方式及效果分析[J]. 中国电机工程学报, 2015, 35(17): 4283-4290.
CHEN L, XU F, WANG X, et al. Implementation and effect of thermal storage in improving wind power accommodation[J]. Proceedings of the CSEE, 2015, 35(17): 4283-4290.
[16] 李红伟, 周海林, 韩璐, 等. 基于能量枢纽的区域电-热网优化运行研究[J]. 电力科学与工程, 2020, 36(10): 29-35.
LI H W, ZHOU H L, HAN L, et al. Study on optimal operation of regional electric and thermal power grid based on energy hub[J]. Electric Power Science and Engineering, 2020, 36(10): 29-35.
[17] LI R, CHEN L J, YUAN T J, et al. Optimal dispatch of zero-carbon-emission micro Energy Internet integrated with non-supplementary fired compressed air energy sto-rage system[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(4): 566-580.
[18] DEL HOYO A I, L
PEZ S H, LPEZ P S, et al. Models for fast modelling of district heating and cooling networks[J]. Renewable and Sustainable Energy Reviews, 2018, 82: 1863-1873.
[19] FARIVAR M, LOW S H. Branch flow model: relaxations and convexification—part I[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2554-2564.
[20] 章健, 熊壮壮, 王明东, 等. 基于二阶锥规划的主动配电网动态无功优化[J]. 郑州大学学报(工学版), 2019, 40(1): 32-37.
ZHANG J, XIONG Z Z, WANG M D, et al. Dynamic reactive power optimization in active distribution network based on second-order cone programming[J]. Journal of Zhengzhou University (Engineering Science), 2019, 40(1): 32-37.
[21] 熊文涛, 雍龙泉. 基于Yalmip工具箱的整数规划模型求解方法[J]. 湖北工程学院学报, 2014, 34(3):41-45.
XIONG W T, YONG L Q. A method for solving integer programming model using Yalmip toolbox[J]. Journal of Hubei Engineering University, 2014, 34(3):41-45.
[22] 章健, 张玉晓, 熊壮壮, 等. 计及DR的新能源配电网电压无功协调优化[J]. 郑州大学学报(工学版), 2020, 41(2): 61-66.
ZHANG J, ZHANG Y X, XIONG Z Z, et al. Voltage reactive power coordination optimization of distributed new energy network considering DR[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(2): 61-66.