随着城市电网的发展,配电网线路电缆化率提高导致对地电容电流急剧上升,单相接地后流经故障点的电流很大,电弧不易熄灭,容易产生间歇性电弧接地过电压,同时由于电磁式电压互感器铁芯饱和时容易引起谐振过电压,导致事故跳闸率明显上升[1-2]。目前谐振接地系统(resonant earthing system, NES)广泛应用于城市配电网,能够减小故障点的残余电流,抑制间歇性电弧过电压及谐振过电压。NES发生电弧接地故障时,故障线路与非故障线路的故障特征不明显,如果不能及时甄别出故障线路,可能会使事故进一步扩大。因此,研究NES电弧接地故障特征,提出高阻动态电弧下的精准接地故障选线方法是配电网有效隔离接地故障的基础工作。现有的小电流接地系统故障选线方法主要分为稳态信息选线法、信号注入选线法与暂态信息选线法。吕高[3]通过对比故障线路与非故障线路零序电流幅值的大小进行选线,但此方法易受消弧线圈补偿方式的影响,此方法在NES系统中无法可靠选线。郭威[4]提取线路零序电流谐波分量,利用零序电流中的 5 次谐波在故障线路中相位与非故障线路相反进行选线。但谐波分量易受到电网中非线性元件的影响,导致无法可靠选线。上述稳态信息选线法在NES中故障选线准确性较低。袁佳歆等[5]利用信号探测器对母线电压互感器二次侧注入特定频率的信号进行检测实现选线,但此方法选线的准确性会受到线路长度和分布电容的影响。由于暂态故障特征信息较为丰富,相关学者开始研究暂态信息选线法。方毅等[6]提出能量法,原理为通过计算各线路故障后的暂态能量,利用故障后各线路能量在极性方面的差异进行故障选线,但此方法的准确性受过渡电阻影响较大。康忠健等[7]对各馈线零序电流的综合相关度进行计算,利用最大相关度与最小相关度之间的差值与设定阈值作比较来确定故障线路,但设定阈值的选取没有相关标准。殷培峰等[8]在故障发生瞬间,利用所有线路零序电流第一个周波的半波极性差异进行选线,但该方法在故障电压过零时选线效果不佳。金涛等[9]利用希尔伯特-黄变换筛选零序电流中的非工频分量,利用故障发生后一定时间段内所有线路非工频分量极性的差异进行选线,但此方法易受到模态混叠的影响。由于故障零序暂态信号具有高频、瞬间突变等特点,而小波分析方法对非平稳暂态信号具有优异的时频分析特性,因此,于永进等[10]利用小波分析对各线路暂态零序电流进行分解,利用小波系数的幅值和极性特征选出故障线路,此文献使用固定阻值电阻模拟接地故障,但实际场景中的电弧电阻随时间而动态变化,因此上述选线方法的有效性尚待商榷。赵新红等[11]利用小波变换进行电弧故障选线,利用开关动态开合模拟间歇性电弧故障,但并未搭建考虑动态电阻的电弧模型。由于db小波函数对非平稳信号敏感性不佳,因此无法依靠模极大值极性进行故障选线,且此文献并未考虑搭建动态电阻的电弧模型。针对NES系统故障选线准确率较低的问题,本文搭建了更符合实际情况的电弧故障模型,为故障选线研究奠定基础,并使用故障线路奇异性检测效果更佳的coif小波基函数对零序电流进行分析,从而提出一种NES系统的电弧接地故障选线方法。
首先,采用NES电弧接地故障等值电路推导零序电流故障特征;其次,引入动态弧长参数改进Schwarz电弧模型的数学表达式,并采用MATLAB/Simulink搭建改进的Schwarz电弧仿真模型,在此基础上搭建某城市中压配电网电容电流超标场景下的纯电缆线路系统电弧接地故障模型;再次采用具有紧支撑性以及对非平稳信号的敏感性更佳的coif小波对电弧接地故障时各线路零序电流进行信号处理,并利用故障线路与非故障线路非工频零序电流模极大值极性之间的差异提出故障选线判据;最后设置故障电阻、故障位置、故障合闸角等典型的故障条件验证选线方法准确率为100%,证明了所提选线判据的有效性。
1 NES系统单相接地故障特征分析
设具有n条出线的NES系统第n条出线发生电弧接地故障,图1为其零序等效网络图。其中XL为消弧线圈电感,mH;C01,C02,…,C0n-1分别为配电线路1到n-1的零序电容,μF ;Rf为故障点过渡电阻, Ω。Uf为故障点等值的虚拟电源,V;I0f和I0i分别为流过故障、健全线路的零序电流,A;IL为流过消弧线圈的零序电流,A;U0为母线零序电压,V。
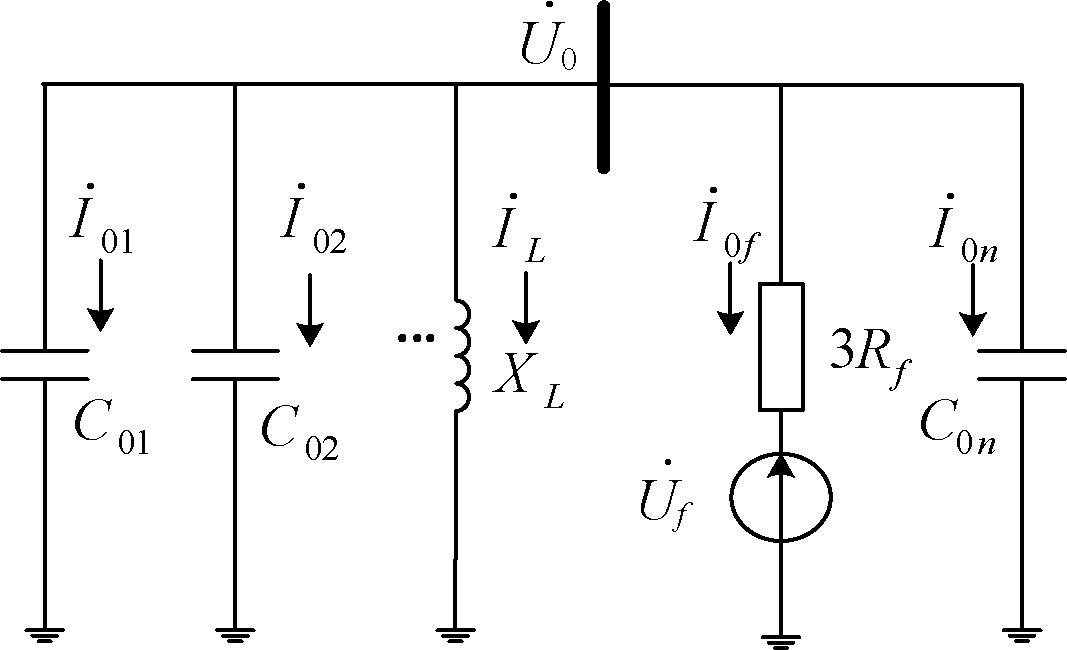
图1 零序等效网络图
Figure 1 Zero sequence equivalent network diagram
母线零序电压为
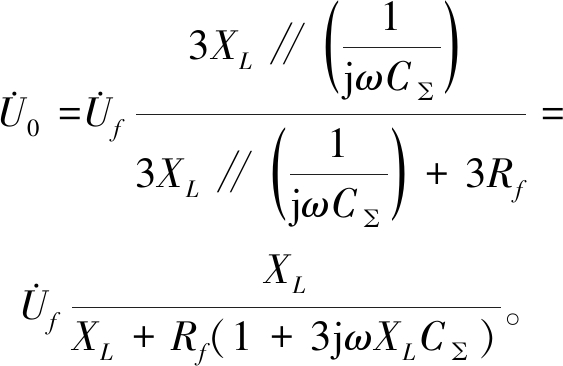
(1)
式中:C∑为各出线对地零序电容之和,μF。
根据等值电路,就健全出线来说,其数值为零序容性电流:
(2)
由KCL定理,有
(3)
式中:C∑rest为第n条出线故障时,系统所剩全线路零序电容之和。
由文献[12]可知,接地点暂态故障电流表达式如下:
ILmaxe-t/τLcos φ+(ICmax-ILmax)cos(ωt+φ)。
(4)
式中: ICmax为入地容性电流的幅值,A;τL、τC分别为电感电流分量和电容电流分量的时间常数,s;φ为故障时刻的电压相角,(°);ILmax为感性电流的幅值,A;ω为工频角频率,Hz;ωf为暂态振荡分量角频率,Hz。
由式(3)可知,电弧接地点故障电流为流经消弧线圈和对地电容的电流相量之和。由于消弧线圈感性电流对容性接地电流的补偿,可能会使故障线路零序电流与非故障线路零序电流之间相位的差异发生改变,因此无法利用稳态时各线路零序电流的极性差异进行故障选线。
由式(4)可知,电弧接地故障电流中包含按照指数级衰减的非工频电流,而消弧线圈的电感量是根据工频补偿的要求设计的,所以NES中消弧线圈只会削弱工频电流,对非工频电流的削弱作用很小,消弧线圈的补偿作用并不会影响各线路之间非工频分量的差异,因此可以利用零序电流非工频分量之间的差异进行选线研究。
2 仿真模型
2.1 NES电弧接地故障模型
Q/GDW-10-375—2008《中压系统中性点接地方式选用技术导则》规定:变电站每段母线单相接地故障电容电流大于100 A时宜采用小电阻接地方式,但经某省电网公司实地调研发现某城市配网电缆化率高、出线电容电流超标现象严重,其中对地电容电流超过150 A的线路高达数十条。为模拟电容电流严重超标场景下的NES系统电弧接地故障,利用MATLAB/Simulink建立含有l1(l1=22 km)、l2(l2=24 km)、l3(l3=26 km)、l4(l4=28 km)4条电缆线路的10 kV中性点经消弧线圈接地系统电弧接地故障模型,如图2所示。模型包括消弧线圈、外部电源、4条电缆线路、配电变压器、负荷和改进电弧模型(电弧模型与过渡电阻串联),该系统电容电流达到151.8 A。仿真模型电缆中线路及重要设备参数见表1及表2。
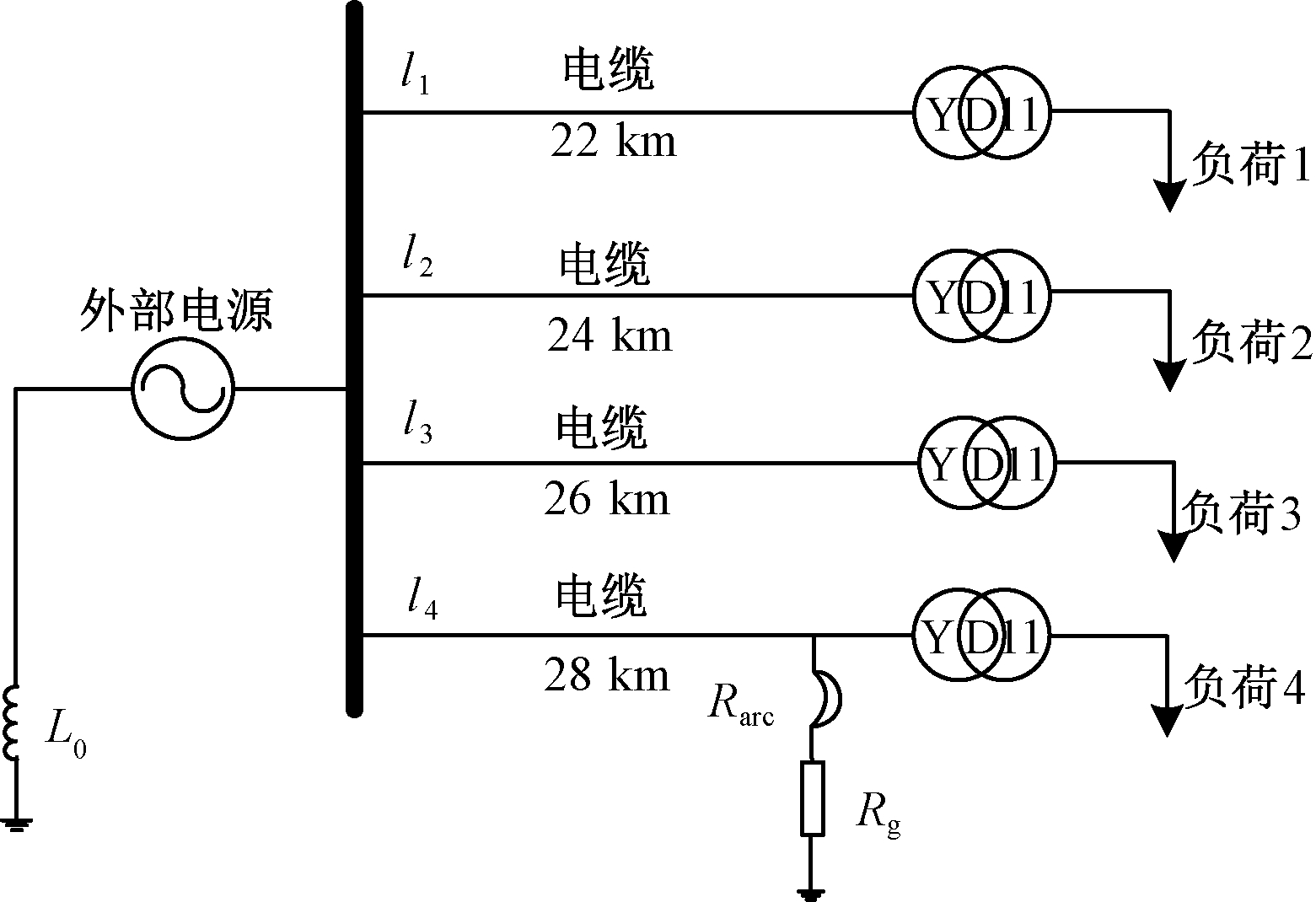
图2 NES单相电弧接地故障模型图
Figure 2 NES single-phase arc grounding fault model diagram
表1 电缆线路参数
Table 1 Parameters of cable line
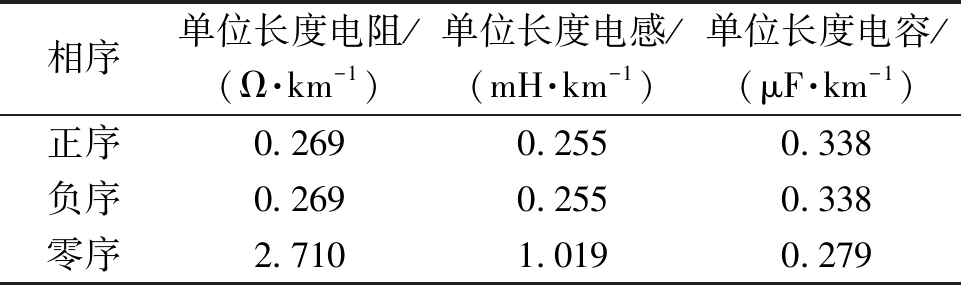
相序单位长度电阻/(Ω·km-1)单位长度电感/(mH·km-1)单位长度电容/(μF·km-1)正序0.2690.2550.338负序0.2690.2550.338零序2.7101.0190.279
表2 主要模块参数
Table 2 Main module parameters

电源模块变压器模块电压/kV电阻/Ω电感/mH接线方式一二次电阻标幺值一二次电感标幺值10.50.892 910.53Y/D110.0020.08
2.2 考虑动态电弧长度的改进Schwarz电弧模型
在小电流接地系统中,电弧接地故障是最常发生的单相接地故障[13]。但电弧接地并不等同于金属性接地,故障电弧阻值的变化过程呈非线性。对电弧进行数学建模分析,有利于准确地模拟实际电弧的发展状况。目前已有的电弧模型为Mayr模型、控制论模型、Schwarz模型。文中在Schwarz模型基础上引入动态弧长参数,使电弧仿真模型更加贴近现实。
学者们在电弧时间常数与耗散功率不变的基础上提出的Mayr电弧数学表达式[14]如下:
(5)
式中:g表示单位长度电弧电导,S;e表示单位长度电弧电压,V;i表示电弧电流,A;Ploss为耗散功率,W;τm为Mayr模型电弧时间常数,s。
后续学者们通过对大量的电弧实验数据进行分析发现,电弧时间常数和耗散功率可以表示为以电弧电导g为自变量的幂函数,即τm=τsgα,Ploss=Psgβ, 将其代入Mayr模型数学表达式中得到Schwarz模型数学表达式为
(6)
式中:Ps和τs分别为Schwarz模型的耗散功率常数以及电弧时间常数, s;α、β为常数,其取值受系统电压以及回路电流和环境等方面的影响。
上述2种电弧模型均未考虑弧长参数对电弧的影响,但现实中弧长会对电弧的物理特性以及电气特性产生影响,由文献[15]可知描述电弧时间常数与电弧长度关系的数学表达式如下:
(7)
式中:Is为Schwarz模型电流的最大幅值,A;ls为Schwarz模型电弧长度, cm;系数ζ一般取经验值2.85×10-5。
将式(6)代入式(7)对Schwarz模型加以改进,引入电弧长度这一客观实际因素表征其对电弧发展的作用。基于Schwarz模型改进的电弧模型的数学表达式如下:
(8)
式中:Ps表示改进Schwarz电弧模型的耗散功率常数,W。
改进的Schwarz电弧模型在电弧发展过程中不仅引入了以电弧电导为自变量的电弧时间常数和耗散功率,而且引入了电弧长度,使电弧数学模型更加贴近实际。在此基础上设置电弧长度ls以时间t为自变量随机变化,便可以构造出考虑动态弧长变化的改进Schwarz电弧模型,此模型可以进一步反映电弧长度随机变化引起的故障电压电流信号的随机性。
利用MATLAB/Simulink搭建文中所提出的考虑动态电弧长度的改进Schwarz电弧模型,设置仿真条件:过渡电阻为200 Ω,仿真时间0.06 s,弧长ls每0.00 2 s随机改变一次,在30~50 mm之间变化,Is=15 A,ζ=2.85×10-5,α=-0.3,Ps=3 000 W,β=0.01。改进Schwarz电弧模型仿真结果见图3。
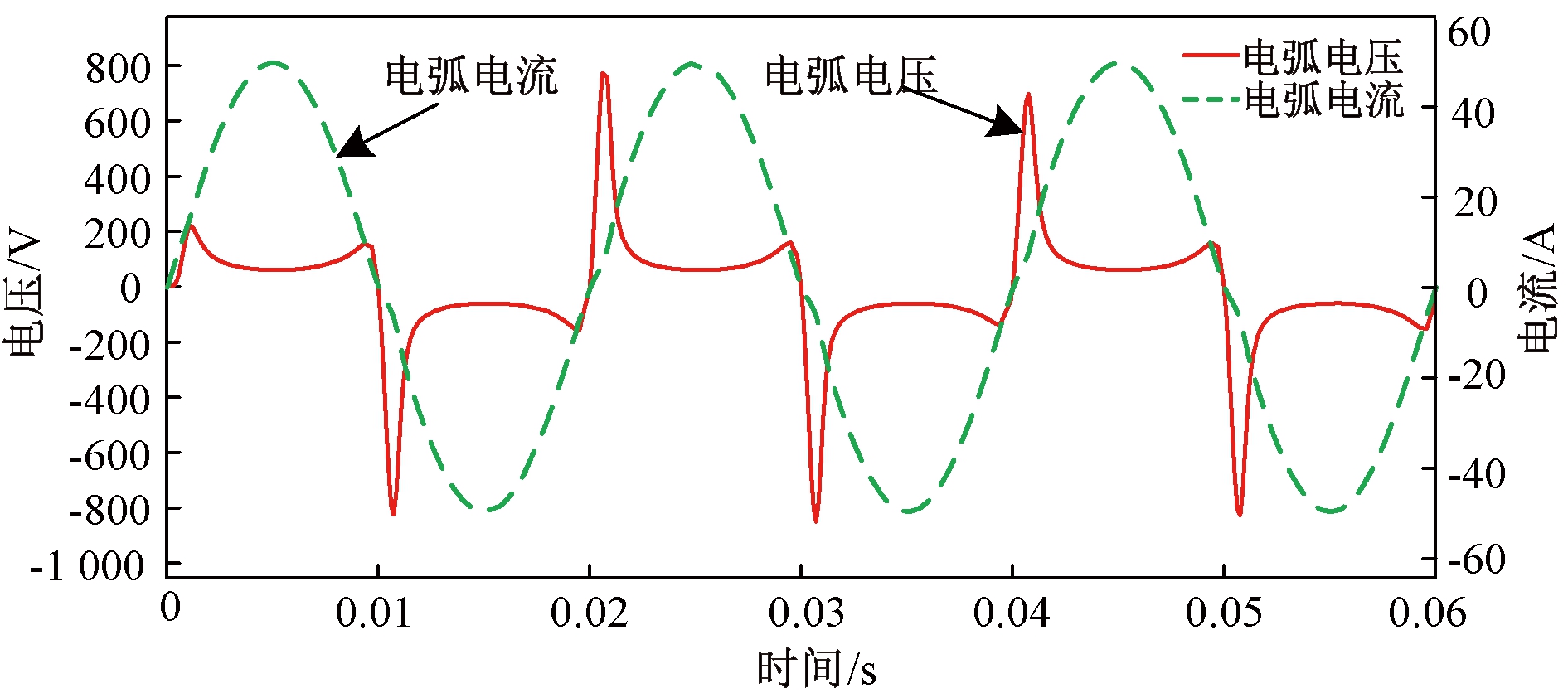
图3 改进Schwarz电弧模型的电压和电流波形
Figure 3 Voltage and current waveforms for improved Schwarz arc models
从图3可以看出,改进Schwarz电弧仿真模型的电流波形虽然变化不明显,但还是与未发生接地故障时的正弦电流波形有所不同。在过零点处电流波形斜率较小,电流值基本保持为零且变化不明显,此时间段被称为零休期。仿真模型的电压波形与未发生接地故障时的正弦电压波形相比有了明显变化,在零休期内,电弧电压先是急剧上升,然后又突然下降;当燃弧基本稳定时,电弧电压基本保持不变,在此期间其波形与马鞍相似;对比文献[16]中的实测电弧波形,文中仿真模型所得波形与实测电弧波形变化规律基本一致。
为了分析文中提出的考虑动态弧长的改进Schwarz电弧模型的仿真效果,利用MATLAB/Simulink建立了Mayr模型与Schwarz模型,将改进的Schwarz电弧模型与上述两种模型从电弧电流畸变程度和电弧电阻变化情况两个方面进行仿真对比分析。其中,与电弧模型串联的过渡电阻为200 Ω,4种模型的耗散功率常数均为3 000 W,改进电弧模型的长度在30~50 mm之间每隔0.002 s随机变化,仿真结果见图4和图5。
由图4可知,Mayr电弧模型、Schwarz电弧模型与改进的Schwarz电弧模型的电弧电流在过零点附近均发生了不同程度的畸变,其中文中提出的改进电弧模型的电弧电流畸变最明显,其零休时间最长,而Mayr模型和Schwarz模型的电弧电流波形畸变程度均劣于本文提出的改进电弧模型。
由图5可知,改进电弧模型在0.01、0.02、0.03、0.04 s时电阻值分别为193.9、163.1、211.4、191.8 Ω,而Mayr模型与Schwarz模型的电弧电阻在对应时间点分别保持为137.4、36.8 Ω,可见文中建立的改进电弧模型在电弧电阻变化情况方面随机性更高,更符合实际中电弧燃烧过程中电阻随机改变的实际情况。

图4 3种电弧模型电流波形图
Figure 4 Arc current waveform plot of three arc models
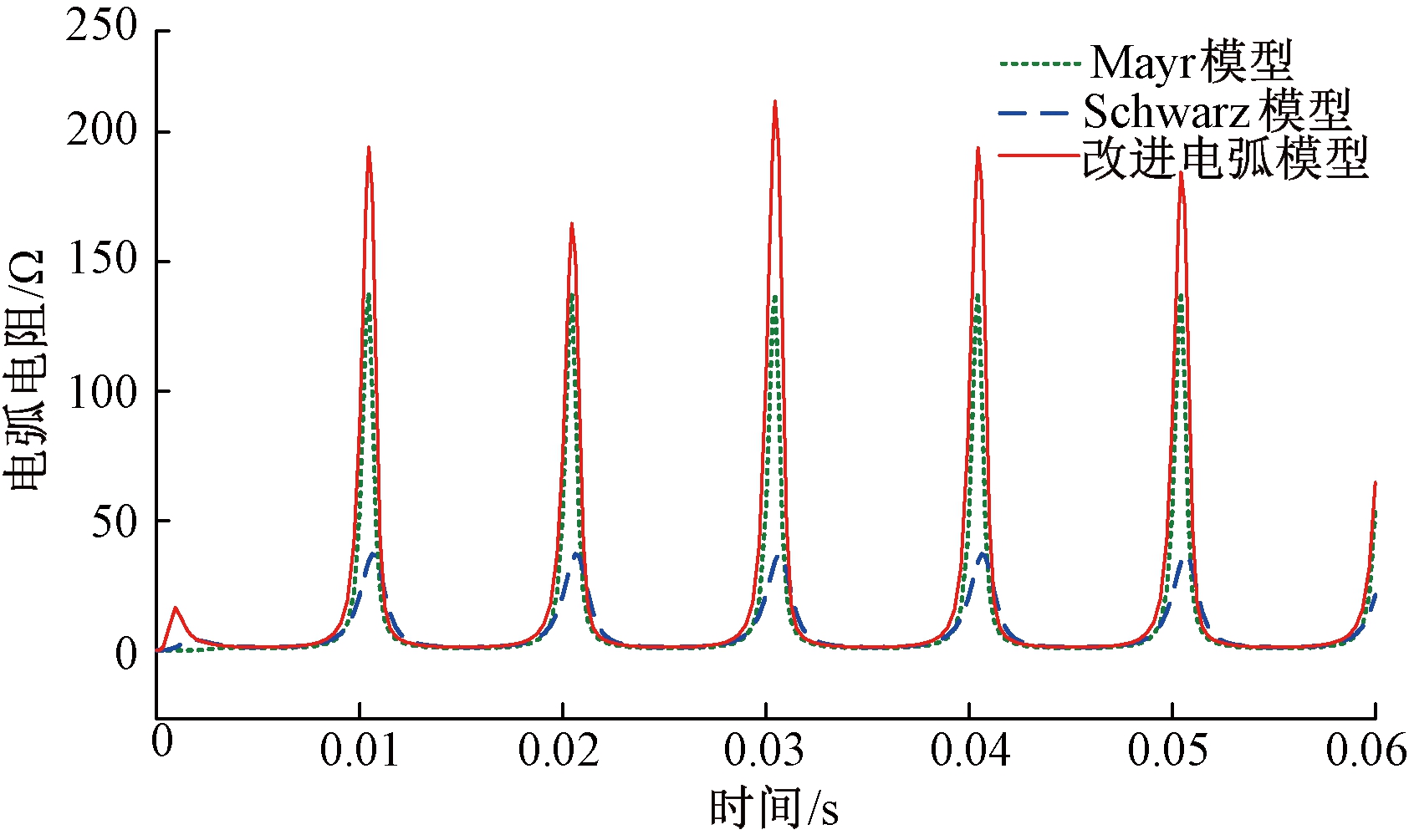
图5 3种电弧模型电阻波形图
Figure 5 Resistance waveform plot of three arc models
3 基于小波分析的接地故障选线方法
小波变换是通过小波基函数与时域信号做相关数学处理将信号投射为时频域信息。可以把小波理解为带通滤波器,它只允许频率和本身中心频率相近的信号通过。通过小波基函数的平移与伸缩调整时频窗口,进而分析非工频信号的局部时频域特性。因此可以使用小波分析对电弧接地故障时产生的非工频信号进行局部分析。
3.1 电弧接地故障信号小波分解最优参数选取
步骤1 采样频率的选取。陈奎等[17]在NES系统中利用6、9、12 kHz采样频率信息采样后进行选线,选线准确率分别为75%、77%、77%,即采样频率越高,采样后信号越不容易失真,故障选线准确率越高。为了便于后续信号处理并确保采样后的信号不失真,文中采样频率设置为10 kHz。
步骤2 小波基函数的选取。综合考虑小波的对称性、紧支撑性以及对非平稳信号的敏感性,采用db系列小波、sym系列小波、coif系列小波处理故障数据,并对比分析处理结果,本文选择故障特征提取效果最佳的coif4小波对零序电流进行小波变换。
步骤3 分解尺度的选取。陈博博等[18]指出电弧接地故障频率主要集中在1 000 Hz附近,故对信号进行4层小波分解,提取第4层的高频系数(对应频率为625~1 250 Hz)。
3.2 故障选线判据的确立
NES的电弧接地故障类型可主要分为以下2类:出线故障和母线故障。利用3.1节所述的coif小波对不同故障条件下的零序电流进行小波分解,通过对比故障线路与健全线路之间的故障特征差异从而提出选线判据。通过设置多组故障条件,经过对比分析发现同种故障类型下经过coif小波分解的零序电流时频域故障特征差异类似,从出线故障与母线故障分别列举其中一组仿真数据,并提出故障选线判据。
3.2.1 出线故障时电弧接地故障选线方法
设置NES的l4线路A相在0.005 s时刻发生电弧故障接地,故障相合闸角90°、 故障点距离10 km,过渡电阻设置为250 Ω。提取各线路零序电流进行小波分解,所得结果如图6所示。
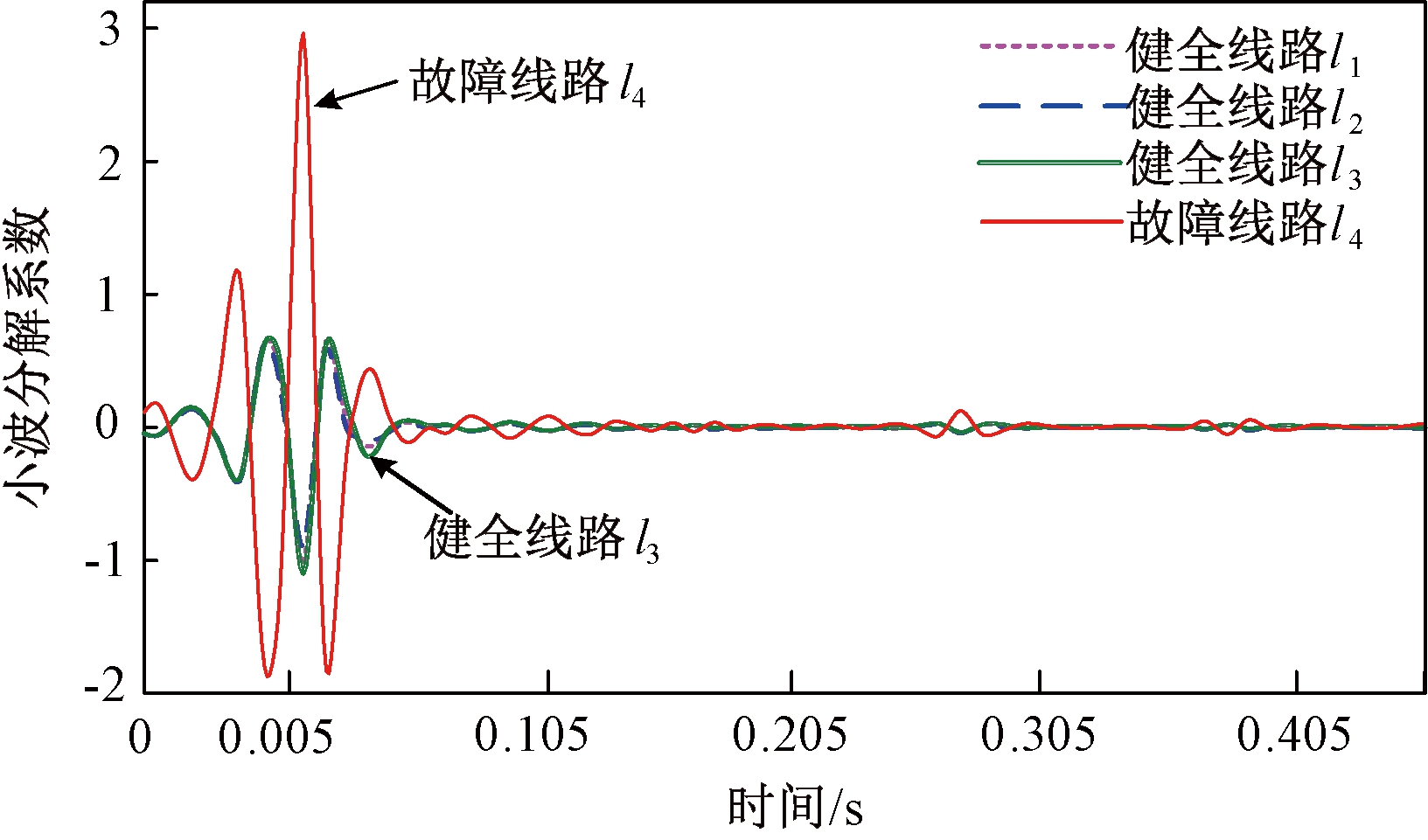
图6 各线路零序电流小波分解系数图
Figure 6 Zero sequence current wavelet decomposition coefficient of each line
由图6可知,线路l1、l2、l3、l4的小波分解系数模极大值分别为-1.102 4、-0.923 7、-1.203 5、2.875 4。通过分析发现,当发生出线故障时,故障线路l4和健全线路l1、l2、l3的模极大值的极性相反,且故障线路的模极大值较大,并且故障线路模极大值的绝对值约等于其余所有健全线路模极大值的绝对值之和。
3.2.2 母线故障时电弧接地故障选线方法
设置NES的母线在0.005 s时发生电弧故障接地,故障相合闸角90°, 过渡电阻设置为250 Ω。提取各线路零序电流进行小波分解, 所得结果如图7所示。
由图7可知,线路l1、l2、l3、l4的小波分解系数模极大值分别为0.976 1、0.997 6、1.002 5、1.013 8,通过分析可以发现,当发生母线故障时,健全线路l1、l2、l3、l4模极大值的极性相同,且大小相差不大。
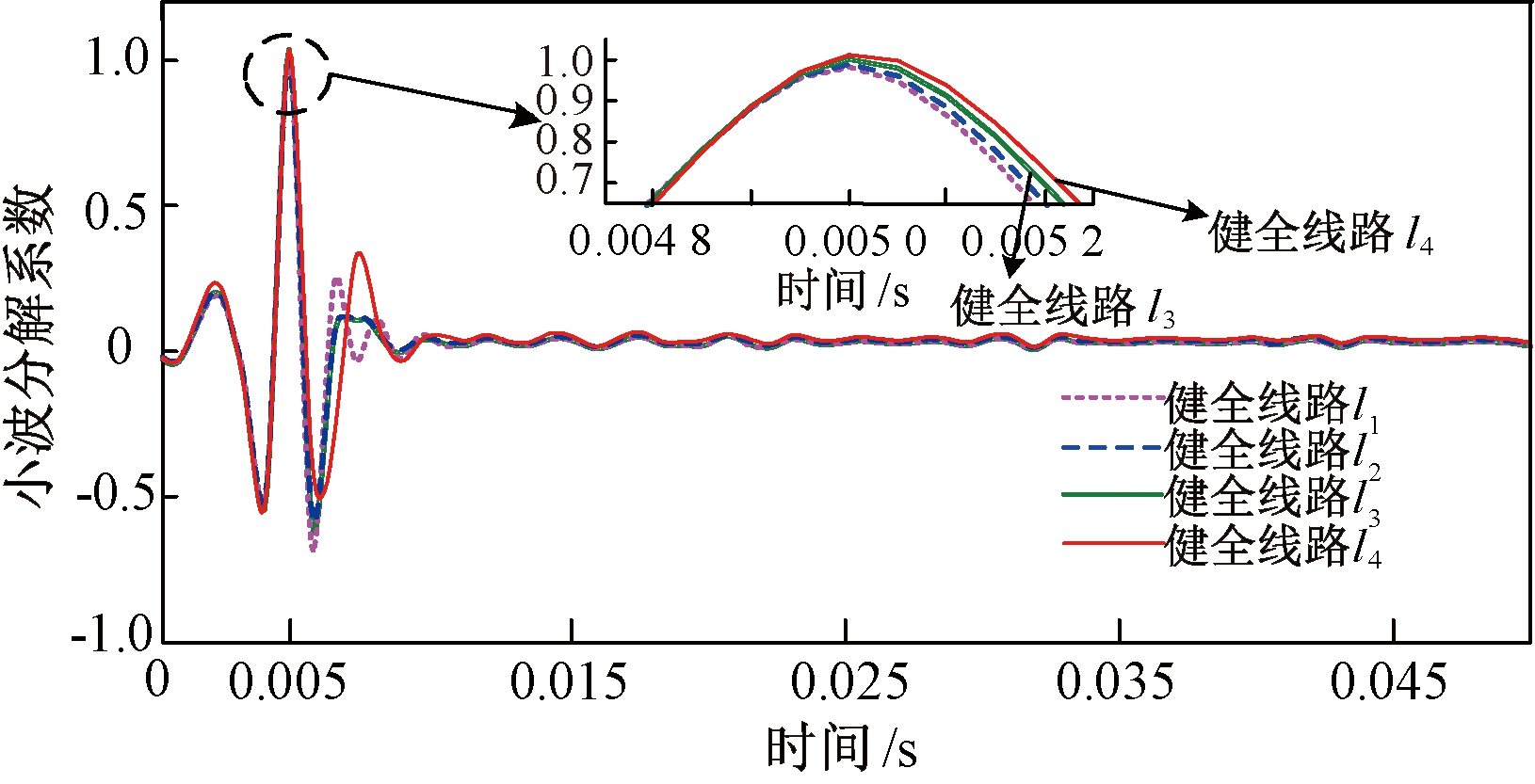
图7 各线路零序电流小波分解系数图
Figure 7 Zero sequence current wavelet decomposition coefficient of each line
通过对比多组实验数据,提出电弧接地故障选线依据如下:当出线发生电弧接地故障时,故障线路与健全线路在发生故障时非工频零序电流小波分解系数模极大值的极性相反;当母线发生电弧接地故障时,所有出线非工频零序电流在发生故障时的小波分解系数模极大值极性相同。
3.3 基于coif小波变换的电弧故障选线流程
(1)设置采样频率为10 kHz,故障发生后,对每条故障线路的零序电流进行采样,提取每条出线的零序电流。
(2)利用coif4小波对每条出线零序电流进行4层小波变换,提取第4层的高频小波分解系数。
(3)提取各出线高频小波分解系数的模极大值,利用故障时刻各线路非工频信号的小波分解系数模极大值的极性差异进行故障选线。
(4)对所有出线零序电流中的小波分解系数模极大值极性进行对比,如果所有出线模极大值的极性相同,则母线发生单相接地故障;如果出现一条出线l,其模极大值的极性与其余出线的模极大值极性不同,则出线l发生单相接地故障。
4 选线判据准确性验证
第3节提出了基于coif小波分析的电弧接地故障选线判据,为了验证该判据的有效性,在建立的NES配网模型中,通过改变过渡电阻、故障位置、故障合闸角等故障条件,验证NES在发生电弧接地故障时选线的可靠性。
4.1 出线发生电弧接地故障时选线结果
4.1.1 出线故障时不同过渡电阻下选线效果分析
设置在出线l1距离母线9 km处发生A相接地故障,故障时间设置为0.005 s,故障相角设置为90°,为验证此方法在高过渡电阻下的选线效果,令过渡电阻在500~5 000 Ω之间变化。选线结果见表3。由表3分析可知,当过渡电阻从500 Ω升高到5 000 Ω时,各线路零序电流小波分解系数的模极大值绝对值逐渐减小,但l1的模极大值始终为正值,l2、l3、l4的模极大值始终负值,并且故障线路l1模极大值的绝对值约等于其余所有健全线路模极大值的绝对值之和。通过极性的不同可以根据第3节提出的选线判据判断l1为故障线路,与实际仿真故障中设置的故障线路一致。
表3 出线故障时不同过渡电阻下的选线结果
Table 3 Line selection results under different transition resistances in case of outgoing line faults
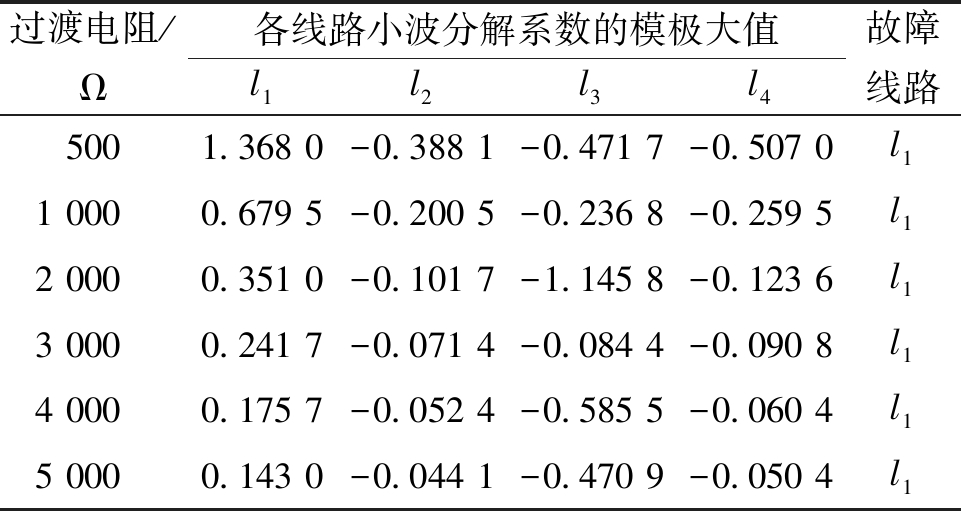
过渡电阻/Ω各线路小波分解系数的模极大值l1l2l3l4故障线路5001.368 0-0.388 1-0.471 7-0.507 0l11 0000.679 5-0.200 5-0.236 8-0.259 5l12 0000.351 0-0.101 7-1.145 8-0.123 6l13 0000.241 7-0.071 4-0.084 4-0.090 8l14 0000.175 7-0.052 4-0.585 5-0.060 4l15 0000.143 0-0.044 1-0.470 9-0.050 4l1
4.1.2 出线故障时不同故障相角下选线效果分析
设置距离母线15 km处出线l2发生A相接地故障,故障时间设置为0.005 s,过渡电阻设置为300 Ω,将故障相电压初相角在0~90°之间变化。选线结果见表4。
由表4分析可知,当故障相角从0°增加到90°时,各线路零序电流的小波分解系数模极大值的绝对值逐渐变大。健全线路l1、l3、l4在故障相角非90°时模极大值极性保持一致均为正值,在故障相角为90°时健全线路模极大值极性为负值,但健全线路l1、l3、l4始终与故障线路l2模极大值极性相反。通过模极大值极性的不同可以根据第3节提出的选线判据判断l2为故障线路,与实际仿真故障中设置的故障线路一致。
表4 出线故障时不同故障初相角下的选线结果
Table 4 Line selection results for different fault initial phase angles during outgoing line faults
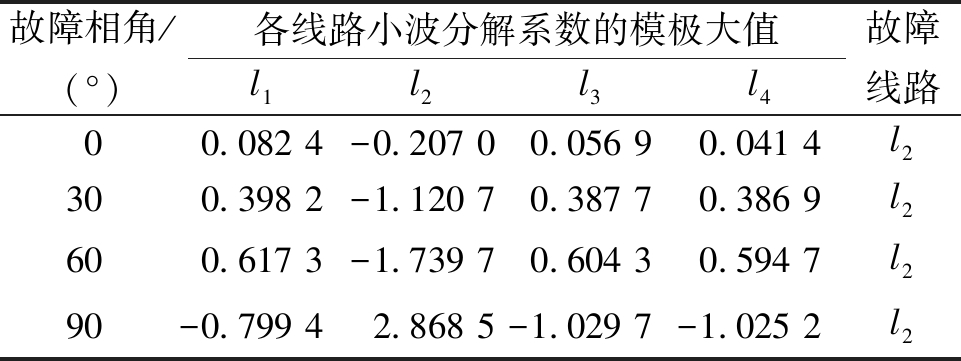
故障相角/(°)各线路小波分解系数的模极大值l1l2l3l4故障线路00.082 4-0.207 00.056 90.041 4l2300.398 2-1.120 70.387 70.386 9l2600.617 3-1.739 70.604 30.594 7l290-0.799 42.868 5-1.029 7-1.025 2l2
4.1.3 出线故障时不同故障位置下选线效果分析
设置在出线l3发生A相接地故障,故障时间设置为0.005 s,故障相角设置为90°,过渡电阻设置为300 Ω,故障位置在1~26 km之间(出线首端至出线末端)变化。选线结果见表5。由表5分析可知,当故障发生位置从出线首端1 km增加到出线末端26 km时,故障线路与健全线路模极大值的极性均相反,并且故障线路l3模极大值的绝对值约等于其余所有健全线路模极大值的绝对值之和。通过模极大值极性的不同可以根据第3节提出的选线判据判断l3为故障线路,与实际仿真故障中设置的故障线路一致。
表5 出线故障时不同故障位置下的选线结果
Table 5 Line selection results under different fault locations in case of outgoing line faults
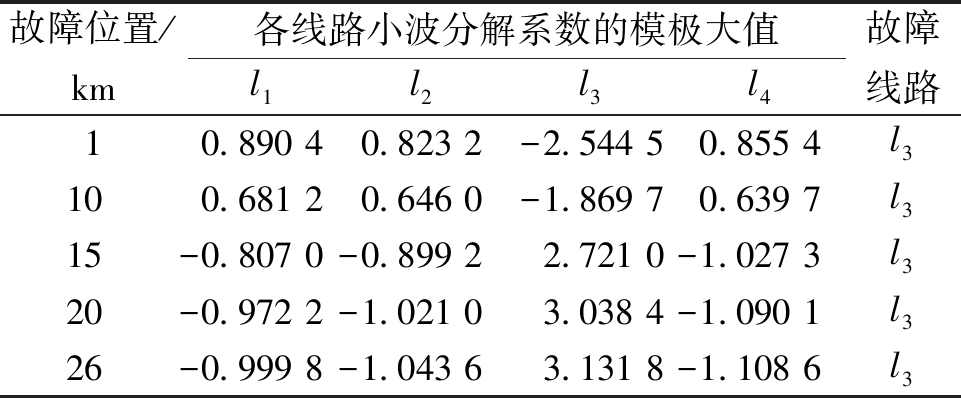
故障位置/km各线路小波分解系数的模极大值l1l2l3l4故障线路10.890 40.823 2-2.544 50.855 4l3100.681 20.646 0-1.869 70.639 7l315-0.807 0-0.899 22.721 0-1.027 3l320-0.972 2-1.021 03.038 4-1.090 1l326-0.999 8-1.043 63.131 8-1.108 6l3
4.2 母线发生电弧接地故障时选线结果
4.2.1 母线故障时不同过渡电阻下选线效果分析
设置在母线发生A相接地故障,故障时间设置为0.005 s,故障相角设置为90°,过渡电阻在500~5 000 Ω之间变化,仿真结果见表6。
表6 母线故障时不同过渡电阻下的选线结果
Table 6 Line selection results for different transition resistances in case of busbar faults
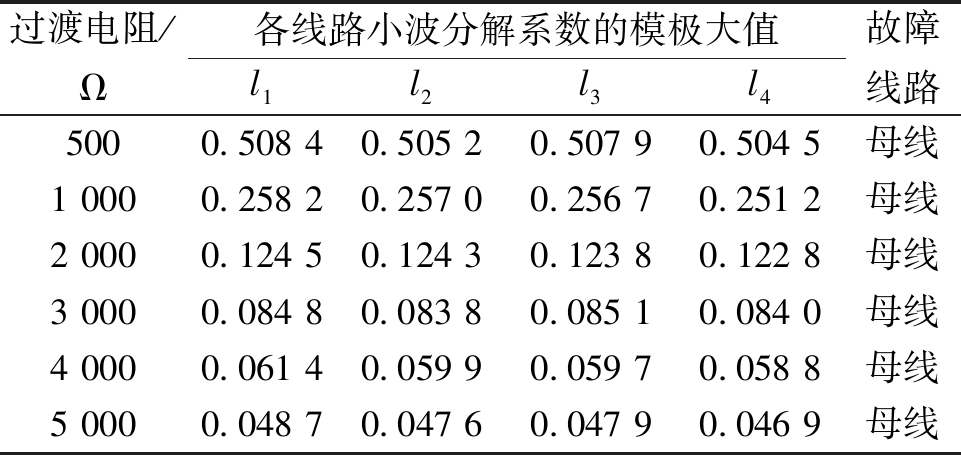
过渡电阻/Ω各线路小波分解系数的模极大值l1l2l3l4故障线路5000.508 40.505 20.507 90.504 5母线1 0000.258 20.257 00.256 70.251 2母线2 0000.124 50.124 30.123 80.122 8母线3 0000.084 80.083 80.085 10.084 0母线4 0000.061 40.059 90.059 70.058 8母线5 0000.048 70.047 60.047 90.046 9母线
由表6分析可知,当过渡电阻从500 Ω升高到5 000 Ω时,各线路零序电流小波分解系数模极大值的绝对值逐渐减小,但l1、l2、l3、l4的模极大值的极性始终相同,通过极性的相同可以根据第3节提出的选线判据判断母线为故障线路,与实际仿真故障中设置的故障线路一致。
4.2.2 母线故障时不同故障相角下选线效果分析
设置母线发生A相接地故障,过渡电阻设置为300 Ω,故障时间设置为0.005 s,故障相角在0~90°之间变化,仿真结果见表7。
由表7分析可知,当故障相角从0°增加到90°时,各线路零序电流经小波变换后的模极大值绝对值逐渐变大,但l1、l2、l3、l4的模极大值的极性始终相同,通过极性的相同可以根据第3节提出的选线判据判断母线为故障线路,与实际仿真故障中设置的故障线路一致。
表7 母线故障时不同故障初相角下的选线结果
Table 7 Line selection results for different fault initial phase angles during busbar faults
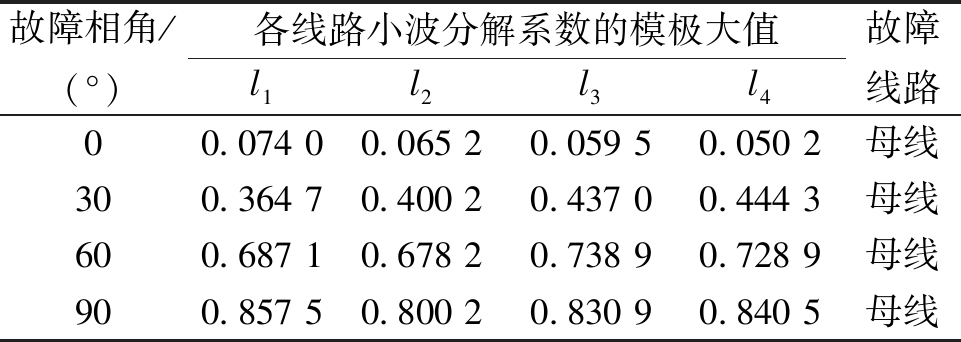
故障相角/(°)各线路小波分解系数的模极大值l1l2l3l4故障线路00.074 00.065 20.059 50.050 2母线300.364 70.400 20.437 00.444 3母线600.687 10.678 20.738 90.728 9母线900.857 50.800 20.830 90.840 5母线
5 结论
(1)本文在已有Schwarz电弧模型基础上引入动态变化的弧长参数,推导了改进Schwarz电弧模型的数学表达式,并使用MATLAB/Simulink建立了具有动态弧长的改进Schwarz电弧仿真模型,通过与Mayr电弧和Schwarz电弧对比分析,证明了文中提出的改进电弧模型在电弧电流畸变特性以及电弧电阻动态变化方面的优异性。
(2)在NES电弧接地故障电路中,消弧线圈仅仅会影响各条线路零序电流的工频分量,非工频分量的性质并不会受影响,因此可以使用对非平稳信号的敏感性更佳的coif小波将暂态故障非工频信息投射为时频域信息,利用coif小波变换后的时频域信息进行选线,准确率可达100%。
(3)本文提出了当线路发生电弧接地故障时,故障线路与健全线路在故障时刻非工频零序电流模极大值的极性相反,当母线发生电弧接地故障时,所有出线非工频零序电流在故障时刻非工频零序电流模极大值的极性相同的选线判据,并在不同过渡电阻、不同故障位置、不同故障相角等典型故障工况下验证了选线判据的准确性。
由于现实场景中配电网的线路结构为架空线路与电缆线路混合的配电网结构,后续搭建了架空线路与电缆线路混合的配电网模型,并在不同的过渡电阻、故障点距离、故障时刻相位角等典型故障工况下进行了故障选线,均可以通过本文所提方法完成正确选线,针对实际配电网中架空线路与电缆线路混合结构的故障选线问题,还需对实际数据作进一步的研究。
[1] WANG Z X, ZHANG H J, WANG H Y, et al. Analysis of modeling and fault line selection method for Single-phase Intermittent fault of distribution network[J]. Journal of Physics: Conference Series, 2022, 2355(1): 012047.
[2] DENG F, ZU Y R, MAO Y, et al. A method for distribution network line selection and fault location based on a hierarchical fault monitoring and control system[J]. International Journal of Electrical Power &Energy Systems, 2020, 123: 106061.
[3] 吕高. 基于零序电流比幅法的故障选线法[J]. 中北大学学报(自然科学版), 2014, 35(4): 473-478.
LYU G. Method of fault line selection based on zero-sequence current comparison of amplitude[J]. Journal of North University of China (Natural Science Edition), 2014, 35(4): 473-478.
[4] 郭威. 小电流接地系统五次谐波选线法研究[D]. 西安: 西安科技大学,2012.
GUO W. Study on fifth harmonic line selection method for small current grounding system[D]. Xi′an: Xi′an University of Science and Technology,2012.
[5] 袁佳歆, 李响, 张哲维. 基于注入信号的有源配电网单相接地故障选线方法[J]. 电测与仪表, 2020, 57(5):44-49.
YUAN J X, LI X, ZHANG Z W. Research on single-phase grounding fault selection technology for active distribution network based on injected signal[J]. Electrical Measurement &Instrumentation, 2020, 57(5):44-49.
[6] 方毅, 薛永端, 宋华茂, 等. 谐振接地系统高阻接地故障暂态能量分析与选线[J]. 中国电机工程学报, 2018, 38(19): 5636-5645.
FANG Y, XUE Y D, SONG H M, et al. Transient energy analysis and line selection of high resistance grounding fault in resonant grounding system[J]. Proceedings of the CSEE, 2018, 38(19): 5636-5645.
[7] 康忠健, 李丹丹, 刘晓林. 应用非工频暂态分量的配电网故障选线方法[J]. 电力自动化设备, 2011, 31(4):1-6.
KANG Z J, LI D D, LIU X L. Faulty line selection with non-power frequency transient components of distribution network[J]. Electric Power Automation Equipment, 2011, 31(4):1-6.
[8] 殷培峰, 刘石红. 基于谐波与首半波结合的单相接地选线分析与研究[J]. 自动化与仪器仪表, 2013(4): 19-21, 225.
YIN P F, LIU S H. Analysis and research on single-phase grounding line selection based on harmonic and first half wave[J]. Automation &Instrumentation, 2013(4): 19-21, 225.
[9] 金涛, 褚福亮. 基于暂态非工频零序电流的含DG新型配电网的接地选线方法[J]. 电工技术学报, 2015, 30(17):96-105.
JIN T, CHU F L. A fault line-selection method in new distribution network with DG based on transient non-power frequency zero sequence current[J]. Transactions of China Electrotechnical Society, 2015, 30(17):96-105.
[10] 于永进, 臧宝花. 基于小波变换的小电流接地系统故障选线方法[J]. 煤炭工程, 2011, 43(1): 48-50.
YU Y J, ZANG B H. Fault wire line selection method of small current grounding system base on wavelet conversion[J]. Coal Engineering, 2011, 43(1): 48-50.
[11] 赵新红, 车伟. 基于小波变换的小电流接地系统电弧故障选线[J]. 电力科学与工程, 2003, 19(4): 22-25.
ZHAO X H, CHE W. Arc-grounding fault selection for small current neutral grounding systems based on wavelet analysis[J]. Power Science and Engineering, 2003, 19(4): 22-25.
[12] 赵铁军, 孟菁, 宋岳奇, 等. 组串式光伏系统直流串联电弧故障检测与保护策略[J]. 电力系统保护与控制, 2020, 48(20): 74-82.
ZHAO T J, MENG J, SONG Y Q, et al. Series arc detection and protection on the DC side of string-type PVs[J]. Power System Protection and Control, 2020, 48(20): 74-82.
[13] 杨明波, 龙毅, 樊三军, 等. 基于组合Mayr和Cassie电弧模型的弧光接地故障仿真及分析[J]. 电测与仪表, 2019, 56(10):8-13.
YANG M B, LONG Y, FAN S J, et al. Simulation and analysis of arc grounding fault based on combined Mayr and Cassie arc models[J]. Electrical Measurement &Instrumentation, 2019, 56(10):8-13.
[14] 马祖涛, 李淑蓉. 小电流接地故障电弧建模分析[J]. 电力系统及其自动化学报, 2021, 33(9):103-108.
MA Z T, LI S R. Modeling analysis of arc grounding fault in non-solidly earthed system[J]. Proceedings of the CSU-EPSA, 2021, 33(9):103-108.
[15] 刘艳丽, 郭凤仪, 李磊, 等. 一种串联型故障电弧数学模型[J]. 电工技术学报, 2019, 34(14):2901-2912.
LIU Y L, GUO F Y, LI L, et al. A kind of series fault arc mathematical model[J]. Transactions of China Electrotechnical Society, 2019, 34(14):2901-2912.
[16] 蔺华, 王子龙, 郭振华, 等. 考虑弧长动态变化的配电网电弧接地故障建模及辨识[J]. 电力系统保护与控制, 2022, 50(7):31-39.
LIN H, WANG Z L, GUO Z H, et al. Modeling and identification of a distribution network arc grounding fault considering arc length dynamic variation[J]. Power System Protection and Control, 2022, 50(7):31-39.
[17] 陈奎, 唐轶. 小电流接地系统电弧接地选线方法的研究[J]. 继电器, 2005, 33(16):5-9.
CHEN K, TANG Y. Analysis of detecting fault line of arcing grounded fault in isolated neutral system[J]. Relay, 2005, 33(16):5-9.
[18] 陈博博, 屈卫锋, 杨宏宇, 等. 小电流接地系统单相接地综合电弧模型与选线方法的研究[J]. 电力系统保护与控制, 2016, 44(16):1-7.
CHEN B B, QU W F, YANG H Y, et al. Research on single phase grounding arc model and line selection for neutral ineffectively grounding system[J]. Power System Protection and Control, 2016, 44(16):1-7.